Ramp loss KNN-weighted multi-class twin support vector machine

Abstract

The K-nearest neighbor-weighted multi-class twin support vector machine (KWMTSVM) is an effective multi-classification algorithm which utilizes the local information of all training samples. However, it is easily affected by the noises and outliers owing to the use of the hinge loss function. That is because the outlier will obtain a huge loss and become the support vector, which will shift the separating hyperplane inappropriately. To reduce the negative influence of outliers, we use the ramp loss function to replace the hinge loss function in KWMTSVM and propose a novel sparse and robust multi-classification algorithm named ramp loss K-nearest neighbor-weighted multi-class twin support vector machine (RKWMTSVM) in this paper. Firstly, the proposed RKWMTSVM restricts the loss of outlier to a fixed value, thus the negative influence on the construction of hyperplane is suppressed and the classification performance is further improved. Secondly, since outliers will not become support vectors, the RKWMTSVM is a sparser algorithm, especially compared with KWMTSVM. Thirdly, because RKWMTSVM is a non-differentiable non-convex optimization problem, we use the concave–convex procedure (CCCP) to solve it. In each iteration of CCCP, the proposed RKWMTSVM solves a series of KWMTSVM-like problems. That also means RKWMTSVM inherits the merits of KWMTSVM, namely, it can exploit the local information of intra-class to improve the generalization ability and use inter-class information to remove the redundant constraints and accelerate the solution process. In the end, the clipping dual coordinate descent (clipDCD) algorithm is employed into our RKWMTSVM to further speed up the computational speed. We do numerical experiments on twenty-four benchmark datasets. The experimental results verify the validity and effectiveness of our algorithm.

1 Introduction

Over the past few decades, there have been plenty of machine learning methods, such as association rules, K-nearest neighbor (KNN), artificial neural network and support vector machine (SVM)(Vapnik 1995). As a binary classifier, the SVM has excellent performance in solving small sample, nonlinear and high dimensional pattern recognition and has been widely applied in many fields. Extensive variants and extensions of SVMs have been studied in recent years, such as twin support vector machines (TSVM) (Jayadeva and Chandra 2007; An and Xue 2022), rough margin-based TSVMs (Xu et al 2012; Wang and Zhou 2017), weighted SVMs (Zhu et al 2016; Mir and Nasiri 2018), pinball SVMs (Huang et al 2014b; Rastogi et al 2018; Prasad and Balasundaram 2021), TPMSVMs (Sharma et al 2021), universum SVMs (Shi 2012; Qi et al 2014; Richhariya and Tanveer 2020), projection TSVRs (Peng and Chen 2018), robust TSVMs (Borah and Gupta 2021) and so on.

The standard SVM uses the hinge loss, which makes it sensitive to the presence of outliers and noises. As we know, the support vectors (SVs) play a crucial part in determining the separating hyperplane. The solution of SVM is sparse. In recent years, some techniques are used to improve the robustness of SVMs, such as using fuzzy theory (Jha and Mehta 2020; Rezvani and Wang 2021) and different loss functions (Bamakan et al 2017; Tang et al 2021). The fuzzy SVMs (Rezvani and Wang 2021) are robustness and can do uncertainty handling, and they can be applied to address the class imbalance issue in the presence of noise and outliers and large scale datasets.

The common used loss functions are square loss, Huber loss, pinball loss, and ramp loss, etc. The square loss is often adopted in least squares SVMs (LSSVMs) (Suykens and Vandewalle 1999; Kumar and Gopal 2009; Gupta and Richhariya 2018), which solves a system of linear equations instead of quadratic programming problems (QPPs) to obtain the optimal solution. Therefore, LSSVMs have fast solving speed. However, the solutions of LSSVMs totally lose sparsity. The Huber loss function (Borah and Gupta 2020) behaves as quadratic loss for a small fraction of closer points and grows linearly after a certain point. Therefore, it is a convex robust function. Finding the solutions of Huber loss-based SVMs is computational expensive for larger datasets. The pinball SVMs (Huang et al 2014b; Tanveer et al 2019c) are proposed to handle noise insensitivity and instability to re-sampling. It deals with the quantile distance rather than the closest distance of SVM, making it less sensitive to noise, especially feature noise. Not only the incorrectly classified samples gain penalties, but also the correctly classified samples gain penalties. Its pure form loses sparsity totally. To keep the sparsity as well as the noise insensitivity, some sparse SVMs with pinball loss (Tanveer et al 2019c, 2021b; Borah and Gupta 2021; Tang et al 2021) have been studied.

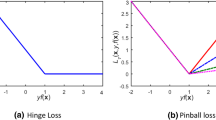
The direct reason for SVM is not robust enough is that the outliers gain the largest losses and are apt to become support vectors (SVs) (Bamakan et al 2017). The outliers will shift the hyperplane toward themselves inappropriately, thus leading to poor generalization ability. Considering the aforementioned issue, the ramp-loss-based SVM (RSVM) (Huang et al 2014a) was proposed to remedy this problem. The ramp loss function restricts the maximal loss value of the outliers, hence reduces their negative influences. What’s more, the sparsity of traditional SVM is preserved. Although it makes the problem become a non-convex optimization problem, the Concave–Convex Programming (CCCP)(Yuille and Rangarajan 2003; Lipp and Boyd 2016) procedure can be applied to solve it by means of transforming it into a sequence of convex problems. With similar idea, some binary classifiers, such as the ramp nonparallel SVM (RNPSVM) (Liu et al 2015), the ramp LSSVM (Liu et al 2016), the ramp one-class SVM (Xiao et al 2017) and ramp maximum margin of TSVM (Lu et al 2019), have been proposed and studied.

The TSVM (Jayadeva and Chandra 2007; Tanveer et al 2019b) has attracted much attention for its faster computational speed because it solves two smaller sized QPPs. To mine the structural information of samples, some fuzzy SVMs (Deepak et al 2018; Rezvani and Wang 2021) have been researched which calculates the fuzzy membership for each sample. In order to exploit the underlying correlation or similarity information between the pair of samples with the same labels, a weighted TSVM (WTSVM) was proposed (Ye et al 2012). It has obtained comparable predictive accuracy compared with the TSVM. Some density-weighted SVMs (Hazarika and Gupta 2021) are also used to deal with noisy data classification. By integrating the rough set theory and WTSVM, Xu et al (2014) proposed a KNN-based weighted rough $\nu$-TSVM in which not only different penalties are given according to the samples positions, but also different weights are given. Mir and Nasiri (2018) studied the least squares version of WTSVM which solves a pair of linear equations as opposed to solves two QPPs, thus increasing the solving speed. Gupta (2017) used the thought of WTSVM for solving regression problem.

Most of the aforementioned SVMs are binary classifiers, while the common classification scenes in the actual application are usually related to the multi-class classification problems. There are some effective decomposition strategies that can transform the multi-class problem into a series of binary problems (Hsu and Lin 2002; Balasundaram et al 2014). The common used methods include one-verse-one (OVO), one-verse-rest (OVR), all-versus-one (AVO) and direct acyclic graph (DAG) (Nasiri et al 2015; Ortigosa et al 2017; Zhou et al 2017; Kumar and Thakur 2018; Lu et al 2019). For a K-classification problem, the OVR method needs to construct K-binary classifiers. In each classifier, the j-class is regarded as positive class and the remaining is regarded as negative class, while AVO approach is just the opposite. These two approaches could easily lead to the imbalance problem and have bad performance. The OVO and DAG methods generate $K(K-1)/2$ binary classifiers, and each classifier involves only two classes of samples and ignores the remaining classes.

To mitigate the deficiencies of OVO and OVR methods, Angulo et al (2003) proposed a K-class support vector classification-regression (K-SVCR), which takes into account all the training points by adopting the “one-verse-one-verse-rest” (OVOVR) structure. It generates $K(K-1)/2$ binary classifiers in total and outputs the final predictive label by “voting” strategy. To increase its computational speed, the twin K-class support vector classification (TKSVC) (Xu et al 2013) was proposed, which has been proved to work approximately 4 times faster than the K-SVCR under the condition that the positive, the negative and rest samples are equal. The Ramp-TKSVC (Wang et al 2020) was proposed to reduce the negative influence of outliers and improve the robustness. Actually, the TKSVC and Ramp-TKSVC still work slowly, especially for large-scale multi-classification problem. A KNN-based weighted multi-class twin support vector machine (KWMTSVM) (Xu 2016) was proposed to improve the classification performance and computational efficiency by considering the local information of samples and removing the redundant constrains. Tanveer et al (2021a) proposed a least squares version of KWMTSVM (LS-KWMTSVM) which solves a pair of linear equations, thus accelerating the training process.

The KWMTSVM has gained promising results in tackling multi-classification problem. However, due to the convexity nature of the hinge loss function is used, it is susceptible to outliers in the training process. Because the outliers will gain the largest losses and easily become SVs, thus stretching the hyperplane toward themselves in an inappropriate way and leading to poor generalization ability. To circumvent this problem and develop a more precise, sparse and robust algorithm, we use the ramp loss to replace the hinge loss in the KWMTSVM and propose a ramp loss KNN-weighted multi-class twin support vector machine (RKWMTSVM) in this paper, and the contributions of this paper are listed as below:

• The proposed RKWMTSVM adopts OVOVR structure which can take a consideration of all training samples and overcome the data-imbalance problem.

• It restricts the loss of outlier to a fixed value and effectively suppresses the negative influence of constructing separating hyperplane, thus improving the robustness of the model.

• The outliers are avoided to become support vectors, then the proposed RKWMTSVM is sparser, especially compared to KWMTSVM.

• The proposed RKWMTSVM is a non-differentiable non-convex optimization problem, we adopt the popular and handy CCCP method to effectively solve it. In each iteration of CCCP, it solves a sequence of KWMTSVM-like problems. The merits of KWMTSVM are inherited. That is to say, it can exploit the local information in terms of the data affinity simultaneously. By removing the redundant constraints, the RKWMTSVM has faster solving speed.

• To further accelerate the solving process of RKWMTSVM, the clipping dual coordinate descent (clipDCD) algorithm is utilized to solve the sub-quadratic programming problems in each iteration of CCCP.

• We do numerical experiments on twenty-four datasets and compare it with six state-of-the-art algorithms, i.e., OVO PGTSVM, OVR WTSVM, OVR R$\nu$TSVM, KWMTSVM, Ramp-TKSVC and LS-KWMTSVM. Experimental results verify the effectiveness of the proposed method.

The remainder of the paper is organized as follows. In Sect. 2, we outline the KWMTSVM and RSVM. In Sect. 3, we propose and analyze the novel algorithm named RKWMTSVM. In Sect. 4, we give the theoretical analysis on the proposed RKWMTSVM and discuss the proposed RKWMTSVM with six state-of-the-art algorithms. Section 5 performs the experiments to investigate the feasibility and validity of our proposed algorithm. In sect. 6, we introduce the clipDCD algorithm in our RKWMTSVM to increase the solving speed. Finally, we make conclusions in Sect. 7.

2 Related works

The SVM was initially proposed for binary classification problem. However, most of the problems in real life are multi-classification. To deal with K-class classification problem, two conventional approaches, i.e., OVO and OVR strategies are used. As mentioned above, the two approaches suffer from some drawbacks. Therefore, OVOVR structure was proposed to avoid the shortcomings of OVO and OVR.

By considering the training datasets as $S=\{({\mathbf {x}}_1,y_1),...,\}\{({\mathbf {x}}_l,y_l)\}$, where ${\mathbf {x}}_i\in {\mathbb {R}}^n$ is the input vector, $y_i\in \{1,2,...,K\}$ is the corresponding label of ${\mathbf {x}}_i$, l and K are the number of samples and the number of classes, respectively. The KWMTSVM is an improved algorithm of TKSVC. They both need to construct $K(K-1)/2$ classifiers in total. In each classifier, it takes the OVOVR structure with ternary outputs $\{+1, -1, 0\}$, which considered all the training points. The i-class is considered as positive with label +1, the j-class is considered as negative with label −1, and the rest is considered as the zero class with label 0. Let matrix ${\mathbf {A}}\in {\mathbb {R}}^{l_1\times n}, {\mathbf {B}}\in {\mathbb {R}}^{l_2\times n}, {\mathbf {C}}\in {\mathbb {R}}^{l_3\times n}$ stand for the positive, negative and zero class, respectively, and $l_1+l_2+l_3=l$.

2.1 KNN-based weighted multi-class twin support vector machine (KWMTSVM)

The KWMTSVM constructs the following pair of nonparallel hyperplanes:

$$\begin{aligned} \left\langle {{{\mathbf {w}}}_{+}},{\mathbf {x}} \right\rangle +{{b}_{+}}=0 \quad \text {and}\quad \left\langle {{{\mathbf {w}}}_{-}},{\mathbf {x}} \right\rangle +{{b}_{-}}=0, \end{aligned}$$

(1)

where ${\mathbf {w}}_+, {\mathbf {w}}_- \in {\mathbb {R}}^n$, $b_+, b_-\in {\mathbb {R}}$, such that each hyperplane is closer to one class and is as far as possible from the other. The remaining samples (zero class) are mapped into a region and satisfy two constraints $\left\langle {{{\mathbf {w}}}_{+}},{\mathbf {x}} \right\rangle +{{b}_{+}} \le -1+ \varepsilon$ and $\left\langle {{{\mathbf {w}}}_{-}},{\mathbf {x}} \right\rangle +{{b}_{-}}\ge 1-\varepsilon$, where $\varepsilon$ is a priori smaller scaler. It can be illustrated in Fig. 1, where the blue “+”, red “−” and green “$\circ$” stands for the positive, negative and zero class, respectively.

Fig. 1

The illustration of KWMTSVM

At the same time, when constructing the positive hyperplane, the KWMTSVM considered the local information of positive samples and exploited the information of inter-class by employing K-nearest neighbor. This thought originates the weighted TSVM (Ye et al 2012), which aims to discover the underlying similarity information within samples from the same class and can be modeled by the intra-class graph $W_{s}$. Simultaneously, it constructs a inter-class $W_{d}$ to model the inter-class separability.

If the label of a sample ${\mathbf {x}}_i$ is $+1$, it needs to define two nearest sets: intra-class nearest sets $Nea_s({\mathbf {x}}_i)$ which contains its neighbors in class $+1$ and inter-class nearest sets $Nea_d({\mathbf {x}}_i)$ which contains its neighbors in the other class. Then, the two similarity matrices of graph W of class $+1$ corresponding $W_s$ and $W_d$ can be defined as follows, respectively,

$$\begin{aligned} W_{s,ij}=\left\{ \begin{aligned} 1,&\quad \text {if}\ {\mathbf {x}}_{j}\in Nea_s({\mathbf {x}}_i)\ \text {or} \ {\mathbf {x}}_{i}\in Nea_s({\mathbf {x}}_j), \\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(2)

and

$$\begin{aligned} W_{d,ij}=\left\{ \begin{aligned} 1,&\quad \text {if}\ {\mathbf {x}}_{j} \in Nea_d({\mathbf {x}}_i), \\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(3)

where $Nea_s({\mathbf {x}}_i)=\{{\mathbf {x}}_i^j| \text {if} \, {\mathbf {x}}_i^j\, \text {and}\,{\mathbf {x}}_i \, \text {belong to the same class,} 0\le j \le k_1 \},$ and $Nea_d({\mathbf {x}}_i)=\{{\mathbf {x}}_i^j| \text {if}\, {\mathbf {x}}_i^j\, \text {and}\,{\mathbf {x}}_i \, \text {belong to diff}\text {erent classes,}\ 0\le j \le k_2 \}.$

Usually, $d_j$ is used to measure the importance of sample, where

$$\begin{aligned} d_i=\sum _{j\in I_{+}}W_{s,ij}. \end{aligned}$$

(4)

The bigger the value of $d_i$, the more “important” corresponding ${\mathbf {x}}_i$ is. In order to find the training samples which possibly become SVs in class $-1$, the weight matrices $W_d$ can be redefined as follows,

$$\begin{aligned} f_{j}=\left\{ \begin{aligned} 1,&\quad \text {if}\ \exists j, W_{d,ij}\ne 0, \\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(5)

Similarly, the corresponding weight matrices of negative samples can be defined. In order to find the two hyperplanes, the KWMTSVM solves the following pair of quadratic programming problems (QPPs),

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{+}},{{b}_{+}},{\varvec{\xi }},{{\varvec{\eta }}}}{\mathop {\min }}\,\frac{1}{2}\sum _{i\in I_{1}}d_i({\mathbf {w}}_{+}^{T}{\mathbf {x}}_i+b_{+})^{2}+c_1\sum _{j\in I_2}\xi _j + c_2 \sum _{k\in I_3}\eta _k \nonumber \\&\quad s.t.\quad -f_j({\mathbf {w}}_{+}^{T}{\mathbf {x}}_j+{b}_{+})+{\xi }_{j} \ge f_j,\, {\xi }_{j}\ge 0, \, j\in I_2,\nonumber \\&\qquad -h_k({\mathbf {w}}_{+}^{T}{\mathbf {x}}_k+{b}_{+})+ {\eta }_{j} \ge (1-\varepsilon )h_k,\, {\eta }_{k} \ge 0,\, k\in I_3, \end{aligned}$$

(6)

and

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{-}},{{b}_{-}},{\varvec{\xi }^{*}},{{\varvec{\eta }}^{*}}}{\mathop {\min }}\,\frac{1}{2}\sum _{j\in I_{2}}d_j({\mathbf {w}}_{-}^{T}{\mathbf {x}}_j+b_{-})^{2}+c_3\sum _{i\in I_1}\xi _i^{*} + c_4 \sum _{k\in I_3}\eta _k^{*} \nonumber \\&\quad s.t.\quad f_i^*({\mathbf {w}}_{-}^{T}{\mathbf {x}}_i+{b}_{-})+ {\xi }_{i}^{*}\ge f_i^*,\, {\xi }_{i}^{*}\ge 0,\, i\in I_1,\nonumber \\&\qquad h_k^*({\mathbf {w}}_{-}^{T}{\mathbf {x}}_k+{b}_{-})+{\eta }_{k}^{*}\ge (1-\varepsilon )h_k^*,\, {\eta }_{k}^{*} \ge 0,\,k\in I_3, \end{aligned}$$

(7)

where $d_i$ and $d_j$ are defined as (4), $f_j$, $h_k$, $f_i^*$, $h_k^*$ are defined as (5), $\varvec{\eta }, \varvec{\eta }^* \in {\mathbb {R}}^{l_3}$, $\varvec{\xi } \in {\mathbb {R}}^{l_2}$, $\varvec{\xi }^* \in {\mathbb {R}}^{l_1}$, $I_1$, $I_2$ and $I_3$ are the indexes of samples belonging to the positive, negative and zero classes, respectively.

For a new testing sample $\mathbf{x }$, it can be predicted by the following decision function

$$\begin{aligned} f({\mathbf {x}})=\left\{ \begin{aligned} +1,&\quad \text {if}\ {\mathbf {w}}_{+}^{T}{\mathbf {x}}+b_{+}>-1+\varepsilon \\ -1,&\quad \text {if}\ {\mathbf {w}}_{-}^{T}{\mathbf {x}}+b_{-}<1-\varepsilon \\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(8)

2.2 Ramp-loss-based SVM

In the standard SVM, the hinge loss function is used by default, and it can be defined as $H_s(z)=max(0,s-z)$, where s is the position of the hinge point, is used to penalize those samples classified with an insufficient margin. The objective function of standard SVM with hinge loss function can be expressed as follows,

$$\begin{aligned} \underset{{\mathbf {w}},b}{\mathop {\min }}\,\text { }\frac{1}{2}{{\left\| {\mathbf {w}} \right\| }^{2}}+C\sum \limits _{i=1}^{l}{{H}_{1}({{y}_{i}}f({{\mathbf {x}}}_{i}))} \end{aligned}$$

(9)

where ${\mathbf {w}} \in {\mathbb {R}}^n$, $b\in {\mathbb {R}}$, and $f({\mathbf {x}})={\mathbf {w}}^{T}{\mathbf {x}}+b$ is the decision function.

The $H_s(z)$ is a convex loss function, and most SVMs with hinge loss function are sensitive to the presence of noises and outliers which will shift the decision hyperplane toward themselves inappropriately (Bamakan et al 2017). Because the outliers have the largest margin losses, the generalization ability of these algorithms decreases. Besides, these outliers will inevitably become the support vectors and make the algorithms have more computational cost. Recently, some non-convex losses are introduced the SVMs to make them more sparse and robust, and the ramp loss function attracts more attention for its better performance, where

$$\begin{aligned} {{R}_{s}}(z)=\left\{ \begin{array}{llll} 0, &{}\quad z>1 \\ 1-z, &{}\quad s\le z\le 1 \\ 1-s, &{} \quad z<s \end{array} \right. \end{aligned}$$

(10)

where $s<1$ is a prior given scalar. Fig. 2 clearly shows that the ramp loss is flat for scores z smaller than s, and the hinge loss function is a convex function. The ${{R}_{s}}(z)$ can be decomposed into the sum of a hinge loss and a concave loss, that is ${{R}_{s}}(z)=H_1(z)-H_s(z)$.

Fig. 2

The illustration of the ramp loss function, where $s=0$

In order to increase the robustness of SVM and reduce the negative influence of outliers, the RSVM (Huang et al 2014a) has been proposed where the ramp loss function is used to replace the hinge loss function in SVM. Therefore, the primal problem of the RSVM can be formulated as follows,

$$\begin{aligned}&\underset{{\mathbf {w}},b}{\mathop {\min }}\,\text { }\frac{1}{2}\left\| {\mathbf {w}} \right\| _{2}^{2}+C\sum \limits _{i=1}^{l}{{{R}_{s}}({{y}_{i}}f({{{\mathbf {x}}}_{i}}))} \nonumber \\&\quad =\frac{1}{2}\left\| {\mathbf {w}} \right\| _{2}^{2}+C\sum \limits _{i=1}^{l}{{H}_{1}({y_i}f({\mathbf {x}}_i))-C\sum \limits _{i=1}^{l}{H_s(y_if({\mathbf {x}}}_{i}))} \end{aligned}$$

(11)

This is a Concave–Convex optimization problem.

Fig. 3

The flowchart of CCCP for the problem (16)

3 Ramp loss KNN-weighted multi-class twin support vector machine

Let $f_{+}({\mathbf {x}})={{\mathbf {w}}}_{+}^T{\mathbf {x}}+{b}_{+}$, $f_{-}({\mathbf {x}})={{\mathbf {w}}}_{-}^T{\mathbf {x}}+{b}_{-}$, the objective function of primal problems (6) and (7) is equivalent to

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{+}},{{b}_{+}}}{\mathop {\min }}\,\frac{1}{2}\sum _{i \in I_1} d_i(f_{+}({\mathbf {x}}_i))^2 +c_1\sum _{j \in I_2}H_1(-f_j f_{+}({\mathbf {x}}_j))\nonumber \\&\quad +c_2\sum _{k \in I_3}H_{1-\varepsilon }(-h_k f_{+}({\mathbf {x}}_k)), \end{aligned}$$

(12)

and

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{-}},{{b}_{-}}}{\mathop {\min }}\,\frac{1}{2}\sum _{j \in I_2} d_j(f_{-}({\mathbf {x}}_j))^2 +c_3\sum _{i \in I_1}H_1(f_i f_{-}({\mathbf {x}}_i))\nonumber \\&\quad +c_4\sum _{k \in I_3}H_{1-\varepsilon }({\tilde{h}}_kf_{-}({\mathbf {x}}_k)). \end{aligned}$$

(13)

From the two equations above and Fig. 2, the KWMTSVM adopts Hinge loss function which gives more punishments on those misclassified samples far from the hyperplane, making the hyperplane shifted toward the misclassified samples in an inappropriate way. Therefore, the KWMTSVM is sensitive to the presence of noises and outliers. It can be demonstrated by a toy example and is shown in Fig. 5. In Fig. 5a, the red and black thick solid line represent the decision boundary $f_+=-1-\varepsilon$ and $f_-=1+\varepsilon$, respectively. The “$\circ$” and “$\bigtriangleup$” denote support vectors in QPP (6) and (7), respectively. The red sample located in the upper right corner is the noise of negative class. Obviously, it is circled by “$\circ$” which means it becomes the support vector and shifts the positive hyperplane inappropriately. That means KWMTSVM overemphasizes the existence of noises, making it not robust enough. In order to further improve the robustness of the KWMTSVM, a new algorithm, termed as Ramp loss KNN-weighted multi-class twin support vector machine (RKWMTSVM), is proposed in the following.

3.1 Linear case

In Eq.(12), the second term and third term are the losses of samples in the negative class and zero class, respectively. These samples adopt the hinge loss function. We use the ramp loss function to replace them, and we can derive the first optimization problem of the proposed RKWMTSVM as follows,

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{+}},{{b}_{+}}}{\mathop {\min }}\,\frac{1}{2}\sum _{i \in I_1} d_i(f_{+}({\mathbf {x}}_i))^2 +c_1\sum _{j \in I_2}R_{s_1}(-f_j f_{+}({\mathbf {x}}_j))\nonumber \\&\quad +c_2\sum _{k \in I_3}R_{s_2}(-h_k f_{+}({\mathbf {x}}_k)). \end{aligned}$$

(14)

and similarly, the second optimization problem of the proposed RKWMTSVM is

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{-}},{{b}_{-}}}{\mathop {\min }}\,\frac{1}{2}\sum _{j \in I_2} d_j(f_{-}({\mathbf {x}}_j))^2 +c_3\sum _{i \in I_1}R_{s_3}(f_if_{-}({\mathbf {x}}_i))\nonumber \\&\quad +c_4\sum _{k \in I_3}R_{s_4}({\tilde{h}}_k f_{-}({\mathbf {x}}_k)). \end{aligned}$$

(15)

The ramp loss can be decomposed into the sum of convex hinge loss and concave function. Therefore, Eq.(14) and Eq.(15) can be reformulated as follows,

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{+}},{{b}_{+}}}{\mathop {\min }}\,\underbrace{\frac{1}{2}\sum _{i \in I_1} d_i(f_{+}({\mathbf {x}}_i))^2 +c_1\sum _{j \in I_2}H_{1}(-f_jf_{+}({\mathbf {x}}_j))+c_2\sum _{k \in I_3}H_{1-\varepsilon }(-h_{k}f_{+}({\mathbf {x}}_k))}_{J_\mathrm{vex}({\mathbf {w}}_{+},b_+)} \nonumber \\&\quad \underbrace{-c_1\sum _{j \in I_2}H_{s_1}(-f_jf_{+}({\mathbf {x}}_j))-c_2\sum _{k \in I_3}H_{s_2}(-h_kf_{+}({\mathbf {x}}_k))}_{J_\mathrm{cav}({\mathbf {w}}_{+},b_+)}, \end{aligned}$$

(16)

and

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{-}},{{b}_{-}}}{\mathop {\min }}\,\underbrace{\frac{1}{2}\sum _{j \in I_2} d_j(f_{-}({\mathbf {x}}_i))^2 +c_3 \sum _{i \in I_1}H_{1}(f_if_{-}({\mathbf {x}}_i))+c_4\sum _{k \in I_3}H_{1-\varepsilon }(h_kf_{-}({\mathbf {x}}_j))}_{J_\mathrm{vex}({\mathbf {w}}_{-},b_-)} \nonumber \\&\quad \underbrace{-c_3\sum _{i \in I_1}H_{s_3}(f_i f_{-}({\mathbf {x}}_i))-c_4\sum _{k \in I_3}H_{s_4}({\tilde{h}}_kf_{-}({\mathbf {x}}_k))}_{J_\mathrm{cav}({\mathbf {w}}_{-},b_-)}. \end{aligned}$$

(17)

Obviously, the above two problems consist of two parts: the convex part $J_\mathrm{vex}$ and the concave part $J_\mathrm{cav}$, and they need to minimize a non-convex cost function. The CCCP is a powerful heuristic method which is used to find local solutions to difference of convex (DC) programming problems (Yuille and Rangarajan 2003; Lipp and Boyd 2016). Because it is simple in tuning and can iteratively solve a sequence of convex programs, it has become a successful and power algorithm for solving non-differentiable non-convex optimization problems (Bamakan et al 2017). For simplicity and convenience, we only use problem (16) of the proposed RKWMTSVM to interpret the detailed solving progress, and the problem (17) can be obtained with an exactly similar way.

The CCCP framework for problem (16) is constructed in the following flowchart, seen (Fig. 3).

From the flowchart, the CCCP procedure for problem (16) needs to solve the following problem in the t-th step,

$$\begin{aligned} \underset{{{{\mathbf {w}}}_{+}},{{b}_{+}}}{\mathop {\min }}\,J_\mathrm{vex}({\mathbf {w}}_{+},b_+)+ \left\langle J'_\mathrm{cav}({\mathbf {w}}_{+}^{t},b_+^{t}), ({{{{\mathbf {w}}}_{+}},{{b}_{+}}})) \right\rangle \end{aligned}$$

(18)

Next, we will show how to find the solution for Eq.(18). Remarkably, $J'_\mathrm{cav}({\mathbf {w}}_{+}^{t},b_+^{t})$ is non-differentiable at some points. When using any upper-derivative of a concave function, the CCCP can remain valid. For convenience, we suppose $\varvec{\delta }_+=(\delta _1,\delta _2,...,\delta _{l_2})^T$, $\varvec{\theta }_+=(\theta _1, \theta _2, ..., \theta _{l_3})^T$, where

$$\begin{aligned}&{{\delta }_{j}}=-c_1\cdot \frac{\partial H_{s_1}(-f_jf_+({\mathbf {x}}_j))}{\partial (-f_jf_+({\mathbf {x}}_j))}\nonumber \\&\quad =\left\{ \begin{aligned} c_1,&\quad \text {if} \ -f_jf_+({\mathbf {x}}_j)<s_1, f_j=1,\\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(19)

where $j\in I_2$, and

$$\begin{aligned}&{{\theta }_{k}}=-c_2\cdot \frac{\partial H_{s_2}(-h_kf_+({\mathbf {x}}_k))}{\partial (-h_kf_+({\mathbf {x}}_j))}\nonumber \\&\quad =\left\{ \begin{aligned} c_2 ,&\quad \text {if} \ -h_kf_+({\mathbf {x}}_k)<s_2,h_k=1,\\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(20)

where $k\in I_3$. Therefore, using Eq.(19) and Eq.(20), Eq. (18) can be rewritten as:

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{+}},{{b}_{+}}}{\mathop {\min }}\,\frac{1}{2}\sum _{i \in I_1} d_i({\mathbf {w}}_{+}^T\mathbf{x }_i+b_{+})^2 +c_1\sum _{j \in I_2}H_{1}(-f_jf_{+}(\mathbf{x }_j))\nonumber \\&\quad +c_2\sum _{k \in I_3}H_{1-\varepsilon }(-h_{k}f_{+}(\mathbf{x }_k)) \nonumber \\&\quad - \sum _{j \in I_2}\delta _j f_j({\mathbf {w}}_{+}^{T}\mathbf{x }_j+b_{+}) -\sum _{k \in I_3}\theta _{k}h_{k} ({\mathbf {w}}_{+}^{T}\mathbf{x }_k+b_{+}), \end{aligned}$$

(21)

where the first three items are the convex part $J_\mathrm{vex}({\mathbf {w}}_{+},b_+)$ in Eq. (18), the fourth item is the result of $-c_1$ multiplies the inner product of $\frac{\partial H_{s_1}(-f_jf_+({\mathbf {x}}_j))}{\partial (-f_jf_+({\mathbf {x}}_j))}$ and $-f_jf_+({\mathbf {x}}_j)$ ($f_+({\mathbf {x}}_j) = {\mathbf {w}}_{+}^{T}\mathbf{x }_j+b_{+}$), and the last term is the result of $-c_2$ multiplies the inner product of $\frac{\partial H_{s_2}(-h_kf_+({\mathbf {x}}_k))}{\partial (-h_kf_+({\mathbf {x}}_k))}$ and $-f_kf_+({\mathbf {x}}_k)$ ($f_+({\mathbf {x}}_k) = {\mathbf {w}}_{+}^{T}\mathbf{x }_k+b_{+}$).

By introducing slack vectors $\varvec{\xi }_+=(\xi _1,\xi _2,...,\xi _{l_2})^T$ and $\varvec{\eta }_+=(\eta _1,\eta _2,...,\eta _{l_3})^T$, the above equation is equivalent to

$$\begin{aligned}&\underset{{{{\mathbf {w}}}_{+}},{{b}_{+}}}{\mathop {\min }}\,\frac{1}{2}\sum _{i \in I_1} d_i({\mathbf {w}}_{+}^T{\mathbf {x}}_i+b_{+})^2 +c_1\sum _{j \in I_2}\xi _j +c_2\sum _{k \in I_3}\eta _k \nonumber \\&\qquad - \sum _{j \in I_2}\delta _j f_j({\mathbf {w}}_{+}^{T}{\mathbf {x}}_j+b_{+}) -\sum _{k \in I_3}\theta _{k}h_{k} ({\mathbf {w}}_{+}^{T}{\mathbf {x}}_k+b_{+}) \nonumber \\&s.t.\quad -f_j({\mathbf {w}}_{+}^{T}{\mathbf {x}}_j+b_{+}) +\xi _j \ge f_j, \xi _j \ge 0, j\in I_2, \nonumber \\&\quad \quad -h_k ({\mathbf {w}}_{+}^{T}{\mathbf {x}}_k+b_{+}) +\eta _k \ge (1-\varepsilon )h_k, \eta _k \ge 0, k \in I_3. \end{aligned}$$

(22)

We can construct the Lagrangian function of (22) as follows,

$$\begin{aligned}&L({\mathbf {w}}_{+}, b_+, \varvec{\xi }_{+},\varvec{\eta }_+, \varvec{\alpha }_+, \varvec{\beta }_+, \varvec{\lambda }_+,\varvec{\sigma }_+) \nonumber \\&\quad =\frac{1}{2}\sum _{i \in I_1} d_i({\mathbf {w}}_{+}^T{\mathbf {x}}_i+b_{+})^2 +c_1\sum _{j \in I_2}\xi _j +c_2\sum _{k \in I_3}\eta _k \nonumber \\&\qquad - \sum _{j \in I_2}\delta _j f_j({\mathbf {w}}_{+}^{T}{\mathbf {x}}_j+b_{+}) -\sum _{k \in I_3}\theta _{k}h_{k} ({\mathbf {w}}_{+}^{T}{\mathbf {x}}_k+b_{+}) \nonumber \\&\qquad -\sum _{j \in I_2} \alpha _j^{+}(-f_j({\mathbf {w}}_{+}^{T}{\mathbf {x}}_j+b_{+}) +\xi _j - f_j) \nonumber \\&\qquad -\sum _{k \in I_3}\beta _k^{+}(-h_k ({\mathbf {w}}_{+}^{T}{\mathbf {x}}_k+b_{+}) +\eta _k - (1-\varepsilon )h_k)\nonumber \\&\qquad -\sum _{j \in I_2}\lambda _j^{+} \xi _j -\sum _{k \in I_3}\sigma _k^{+}\eta _k, \end{aligned}$$

(23)

where $\varvec{\alpha }_+=(\alpha ^{+}_j)_{i\in I_2}$, $\varvec{\beta }_+=(\beta ^{+}_k)_{k\in I_3}$, $\varvec{\lambda }=(\lambda ^{+}_j)_{j\in I_2}$, and $\varvec{\sigma }_+=(\sigma ^{+}_k)_{k \in I_3}$ are Lagrange multipliers. Differentiating the Lagrangian function L with respect to variables ${\mathbf {w}}_{+}, b_+, \varvec{\xi }_{+}, \varvec{\eta }_+$ can yield the following Karush–Kuhn–Tucker (KKT) conditions:

$$\begin{aligned}&\frac{\partial L}{\partial {{{\mathbf {w}}}_{+}}}= \sum _{i \in I_1} d_i({\mathbf {x}}_i {\mathbf {x}}_i^{T}{\mathbf {w}}_{+}+{\mathbf {x}}_ib_{+}) + \sum _{j \in I_2}\alpha _j^{+}f_j{\mathbf {x}}_j \nonumber \\&\quad + \sum _{k \in I_3}\beta _{k}^{+} h_{k}{\mathbf {x}}_k - \sum _{j \in I_2}\delta _jf_j{\mathbf {x}}_j -\sum _{k \in I_3}\theta _{k} h_{k}{\mathbf {x}}_k =0, \end{aligned}$$

(24)

$$\begin{aligned}&\frac{\partial L}{\partial {{b}_{+}}}=\sum _{i \in I_1} d_i({\mathbf {x}}_i^{T}{\mathbf {w}}_{+}+b_{+}) + \sum _{j \in I_2}\alpha _j^{+}f_j +\sum _{k \in I_3}\beta _{k}^{+} h_{k} \nonumber \\&\quad - \sum _{j \in I_2}\delta _jf_j -\sum _{k \in I_3}\theta _{k} h_{k}=0, \end{aligned}$$

(25)

$$\begin{aligned}&\frac{\partial L}{\partial {{\varvec{\xi }}_{+}}}=c_1{{{\mathbf {e}}}_{2}}-\varvec{\alpha }_{+}-\varvec{\lambda }_{+}=0, \end{aligned}$$

(26)

$$\begin{aligned}&\frac{\partial L}{\partial {{\varvec{\eta }}_{+}}}=c_2{{{\mathbf {e}}}_{3}}-\varvec{\beta }_{+}-\varvec{\sigma }_{+}=0, \end{aligned}$$

(27)

$$\begin{aligned}&\sum _{j \in I_2} \alpha _j^{+}(-f_j({\mathbf {w}}_{+}^{T}{\mathbf {x}}_j+b_{+}) +\xi _j - f_j)=0, \end{aligned}$$

(28)

$$\begin{aligned}&\sum _{k \in I_3}\beta _k^{+}(-h_k ({\mathbf {w}}_{+}^{T}{\mathbf {x}}_k+b_{+}) +\eta _k - (1-\varepsilon )h_k)=0, \end{aligned}$$

(29)

$$\begin{aligned}&\sum _{j \in I_2}\lambda _j^{+} \xi _j=0, \sum _{k \in I_3}\sigma _k^{+}\eta _k=0. \end{aligned}$$

(30)

Arranging Eqs.(24) and (25) and representing them in the matrix form, we can get

$$\begin{aligned}&{\mathbf {A}}^T{\mathbf {D}}_1({\mathbf {A}}{\mathbf {w}}_{+}+{\mathbf {e}}_{1}b_{+})+{\mathbf {B}}^{T}{\mathbf {F}}_2(\varvec{\alpha }_{+} -\varvec{\delta }_{+}) \nonumber \\&\quad +{\mathbf {C}}^{T}{\mathbf {H}}(\varvec{\beta }_{+}- \varvec{\theta }_{+})=0, \end{aligned}$$

(31)

$$\begin{aligned}&{\mathbf {e}}_{1}^T{\mathbf {D}}_1({\mathbf {A}}{\mathbf {w}}_{+}+{\mathbf {e}}_{1}b_{+}) +{{\mathbf {e}}_2^{T}}{\mathbf {F}}_2(\varvec{\alpha }_{+}- \varvec{\delta }_{+}) \nonumber \\&\quad +{\mathbf {e}}_3^{T}{\mathbf {H}}(\varvec{\beta }_{+}- \varvec{\theta }_{+})=0, \end{aligned}$$

(32)

where ${\mathbf {D}}_1=diag(d_1,d_2,...,d_{l_1})$, ${\mathbf {F}}_2=diag(f_1,f_2,...,f_{l_2})$, ${\mathbf {H}}=diag(h_1,h_2,...,h_{l_3})$, ${\mathbf {e}}_{1}$, ${\mathbf {e}}_{2}$ and ${\mathbf {e}}_{3}$ are vectors of ones of appropriate dimensions.

By combining Eqs.(31) and (32) and setting ${\mathbf {u}}_+=[{\mathbf {w}}_+;\ b_+]$ , we get

$$\begin{aligned} {\mathbf {u}}_+ =-({\mathbf {X}}_1^T {\mathbf {D}}_{1}{\mathbf {X}}_1)^{-1}({\mathbf {X}}_2^T\mathbf {F_2}(\varvec{\alpha }_{+}-\varvec{\delta }_{+})+{\mathbf {X}}_3^T{\mathbf {H}}(\varvec{\beta }_{+}-\varvec{\theta }_+)), \end{aligned}$$

(33)

where ${\mathbf {X}}_1=[{\mathbf {A}}\ {\mathbf {e}}_1]$, ${\mathbf {X}}_2=[{\mathbf {B}} \ {\mathbf {e}}_2]$, and ${\mathbf {X}}_3=[{\mathbf {C}}\ {\mathbf {e}}_3]$.

From (26) and (27), we have

$$\begin{aligned}&{\mathbf {0}}\le \varvec{\alpha }_+\le c_1{{\mathbf {e}}}_{2}, \end{aligned}$$

(34)

$$\begin{aligned}&{\mathbf {0}}\le \varvec{\beta }_+ \le c_2{{\mathbf {e}}}_{3}, \end{aligned}$$

(35)

where ${\mathbf {0}}$ is vector of zeros of appropriate dimension. For simplicity, we set $\varvec{\gamma }_+= [\varvec{\alpha }_+; \ \varvec{\beta }_+]$, $\varvec{\tau }_+= [\varvec{\delta }_+; \ \varvec{\theta }_+]$, ${\mathbf {N}}_{+}= [{\mathbf {X}}_2^{T}{\mathbf {F}}_2; \ {\mathbf {X}}_3^{T}{\mathbf {H}}]$, ${\mathbf {e}}_4= [{\mathbf {F}}_2{\mathbf {e}}_2; \ {\mathbf {H}}{\mathbf {e}}_3(1-\varepsilon )]$, and ${\mathbf {S}}_{+}=[c_1{\mathbf {e}}_2;\ c_2{\mathbf {e}}_3]$.

By substituting the equations above into (23), we can derive the dual formulation as follows,

$$\begin{aligned}&\underset{\varvec{\gamma }_+}{\mathop {\max }}\,\text { }-\frac{1}{2}({\varvec{\gamma }_+}-\varvec{\tau }_+)^{T} {\mathbf {N}}_{+}({\mathbf {X}}_1^T{\mathbf {D}}_1{\mathbf {X}}_1)^{-1}{\mathbf {N}}_{+}({\varvec{\gamma }_+}-\varvec{\tau }_+) + {\mathbf {e}}_4^T\varvec{\gamma }_+\nonumber \\&s.t.\quad {\mathbf {0}}\le \varvec{\gamma }_+ \le {\mathbf {S}}_{+}. \end{aligned}$$

(36)

Similarly, the dual of the QPP (17) is derived as

$$\begin{aligned}&\underset{\varvec{\gamma }_-}{\mathop {\max }}\,\text { }-\frac{1}{2}({\varvec{\gamma }_-}-\varvec{\tau }_-)^{T} {\mathbf {N}}_{-}({\mathbf {X}}_2^T\mathbf {D_2}{\mathbf {X}}_2)^{-1}{\mathbf {N}}_{-}({\varvec{\gamma }_-}- \varvec{\tau }_-) + {\mathbf {e}}_5^T\varvec{\gamma }_-\nonumber \\&s.t.\quad {\mathbf {0}}\le \varvec{\gamma }_- \le {\mathbf {S}}_{-}, \end{aligned}$$

(37)

where ${\mathbf {D}}_2=diag(d_1,d_2,...,d_{l_2})$, ${\mathbf {F}}_1=diag(f_1,f_2,...,f_{l_1})$, ${\mathbf {H}}^{*}=diag(h_1,h_2,...,h_{l_3})$, ${\mathbf {N}}_{-}=[{\mathbf {X}}_1^{T}{\mathbf {F}}_1; \ {\mathbf {X}}_3^{T}{\mathbf {H}}^{*}]$, ${\mathbf {e}}_5= [{\mathbf {F}}_1{\mathbf {e}}_1; \ {\mathbf {H}}^{*}{\mathbf {e}}_3(1-\varepsilon )]$, and ${\mathbf {S}}_{-}=[c_3{\mathbf {e}}_1;\ c_4{\mathbf {e}}_3]$. Similarly, we set $\varvec{\gamma }_-= [\varvec{\alpha }_-; \ \varvec{\beta }_-]$, where $\varvec{\alpha }_-, \varvec{\beta }_-$ are Lagrange multipliers, and set $\varvec{\tau }_-= [\varvec{\delta }_-; \ \varvec{\theta }_-]$, where $\varvec{\delta }_-=({\bar{\delta }}_1,{\bar{\delta }}_2,...,{\bar{\delta }}_{l_1})^T$, $\varvec{\theta }_-=({\bar{\theta }}_1, {\bar{\theta }}_2, ..., {\bar{\theta }}_{l_3})^T$, and

$$\begin{aligned} {{{\bar{\delta }}}_{j}}=-c_3\cdot \frac{\partial H_{s_3}(f_-({\mathbf {x}}_i))}{\partial (f_-({\mathbf {x}}_i))}=\left\{ \begin{array}{lll} c_3, &{} \text {if} \ f_if_-({\mathbf {x}}_i)<s_3, f_i=1,\\ 0, &{} \text {otherwise} \end{array} \right. \end{aligned}$$

(38)

where $i\in I_1$, and

$$\begin{aligned} {{{\bar{\theta }}}_{k}}=-c_4\cdot \frac{\partial H_{s_4}(f_-({\tilde{h}}_k{\mathbf {x}}_k))}{\partial ({\tilde{h}}_kf_-({\mathbf {x}}_k))}=\left\{ \begin{array}{llll} c_4, &{}\ \text {if} \ {\tilde{h}}_kf_-({\mathbf {x}}_k)<s_4, {\tilde{h}}_k=1,\\ 0, &{}\ \text {otherwise} \end{array} \right. \nonumber \\ \end{aligned}$$

(39)

where $k\in I_3$.

Once the optimal solution $\varvec{\gamma }_-$ is obtained, we can derive

$$\begin{aligned} {\mathbf {u}}_- =({\mathbf {X}}_2^T{\mathbf {D}}_2 {\mathbf {X}}_2)^{-1}({\mathbf {X}}_1^T{\mathbf {F}}_1(\varvec{\alpha }_{-}-\varvec{\delta }_{-})+{\mathbf {X}}_3^T{\mathbf {H}}^*(\varvec{\beta }_{-}-\varvec{\theta }_-)), \end{aligned}$$

(40)

where ${\mathbf {u}}_-=[{\mathbf {w}}_-;\ b_-]$.

Based on the aforementioned equations, the algorithm of linear RKWTSVM based on the CCCP procedure is summarized as follows.

3.2 Nonlinear case

In an exactly similar way, we extend the linear RKWTSVM to the nonlinear case by introducing the kernel function $K({{{\mathbf {x}}}_{i}},{{{\mathbf {x}}}_{j}})=(\varphi ({{{\mathbf {x}}}_{i}})\cdot \varphi ({{{\mathbf {x}}}_{j}}))$. The nonlinear case differs from the linear case only in that

• (1) The matrices ${\mathbf {X}}_1, {\mathbf {X}}_2$ and ${\mathbf {X}}_3$ in (36) and (37) are instead of the appropriate kernel forms ${\mathbf {X}}_1=[K({\mathbf {A}}, {\mathbf {D}})\ {\mathbf {e}}_1]$, ${\mathbf {X}}_2=[K({\mathbf {B}}, {\mathbf {D}}) \ {\mathbf {e}}_2]$, and ${\mathbf {X}}_3=[K({\mathbf {C}}, {\mathbf {D}})\ {\mathbf {e}}_3]$, where ${\mathbf {D}}=[{\mathbf {A}};{\mathbf {B}};{\mathbf {C}}]$.

• (2) The decision function becomes the following equation,

  $$\begin{aligned} f({\mathbf {x}})=\left\{ \begin{aligned} +1,&\quad \text {if}\ {\mathbf {w}}_{+}^{T}K({\mathbf {x}}^T, {\mathbf {D}})+b_{+}>-1+\varepsilon \\ -1,&\quad \text {if}\ {\mathbf {w}}_{-}^{T}K({\mathbf {x}}^T, {\mathbf {D}})+b_{-}<1-\varepsilon \\ 0,&\quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

  (41)

4 Theoretical analysis and comparison

We do theoretical analysis on RKWMTSVM in terms of sparsity and algorithm analysis and compare it with state-of-the-art algorithms.

4.1 Sparsity

Compared with KWMTSVM, the proposed RKWMTSVM is sparser. Because of the introduction of ramp loss, all misclassified samples are avoided converting to SVs in the RKWMTSVM. We assume that the Ramp losses $R_{s_i}, i=1,...,4$ are made differentiable with smooth approximation on a small interval of corresponding inflection samples. Differentiating (14) and (15), we can obtain

$$\begin{aligned} \sum _{i \in I_1} d_i({\mathbf {w}}_{+}^T{\mathbf {x}}_i + b_{+}){\mathbf {x}}_i&= c_1\sum _{j \in I_2}f_jR'_{s_1}(-f_j f_{+}({\mathbf {x}}_j)){\mathbf {x}}_j \nonumber \\&\quad + c_2\sum _{k \in I_3}h_k R'_{s_2}(-h_k f_{+}({\mathbf {x}}_k)){\mathbf {x}}_k, \end{aligned}$$

(42)

$$\begin{aligned} \sum _{j \in I_2} d_j({\mathbf {w}}_{-}^{T}{\mathbf {x}}_j + b_{-}){\mathbf {x}}_j&= -c_3\sum _{i \in I_1}f_iR'_{s_3}(f_i f_{-}({\mathbf {x}}_i)){\mathbf {x}}_i \nonumber \\&\quad - c_4\sum _{k \in I_3}{\tilde{h}}_k R'_{s_4}({\tilde{h}}_k f_{-}({\mathbf {x}}_k)){\mathbf {x}}_k, \end{aligned}$$

(43)

respectively.

From Eq.(42), we can conclude that the negative samples ${\mathbf {x}}_j$ located in the flat area, i.e., $z=-f_j f_{+}({\mathbf {x}}_j) \notin [s_1,1]$, will not become SVs for the reason that $R'_{s_1}=0$; the zero samples ${\mathbf {x}}_k$ in the flat area, i.e., $z=-h_k f_{+}({\mathbf {x}}_k) \notin [s_2, 1-\varepsilon ]$, will not become SVs because $R'_{s_2}=0$. We can do similar analysis for Eq.(43). Compared with KWMTSVM, the proposed RKWMTSVM can explicitly incorporate outlier suppression better. Therefore, RKWMTSVM is more robust and sparser.

The analysis above can be proved by the following property.

Sparsity. From Eq. (33), the support vectors are the corresponding negative samples with $\alpha _j^{+}-\delta _j \ne 0$, for $j\in I_2$ and the corresponding “rest” samples with $\beta _j^{+}-\theta _j\ne 0$, for $j\in I_3$. Then, the following statements can be derived.

• (1) If $\alpha _j^+=c_1$, we get $\delta _j=c_1$ from (19), therefore, $\alpha _j^{+}-\delta _j=0$, for $j\in I_2$.

• (2) If $\alpha _j^+=0$, we get $\delta _j=0$ from (19), therefore, $\alpha _j^{+}-\delta _j=0$, for $j\in I_2$.

• (3) If $\beta _k^+=c_2$, we get $\theta _k=c_2$ from (20), therefore, $\beta _k^{+}-\theta _k=0$, for $k\in I_3$.

• (4) If $\beta _k^+=0$, we get $\theta _k=0$ from (20), therefore, $\beta _k^{+}-\theta _k=0$, for $k\in I_3$.

From the statements above, the bounded SVs (with $\alpha _j^+=c_1, j\in I_2$ or $\beta _k^+=c_2, k\in I_3$) in the KWMTSVM are not SVs any more in the proposed RKWMTSVM. Similarly, we can derive the corresponding statements from Eq. (40) and obtain the similar conclusions. Consequently, we conclude that the proposed RKWMTSVM is more sparse than KWMTSVM.

In the following, we analyze the similarities and differences of the proposed RKWMTSVM with five sparse twin SVMs. They all need to construct two non-parallel hyperplanes.

• (1) STSVM (Peng 2011a). Their similarity is that their optimal solutions are obtained by iteration. The STSVM is proposed for binary classification problem, and it is built in primal space, while RKWMTSVM is proposed for multi-class classification problem and it is solved in the dual space. Based on a simple back-fitting strategy, the STSVM iteratively builds each nonparallel hyperplanes by adding a new SV from the corresponding class at one time, and its learning style is solving linear equation computing systems. The RKWMTSVM iteratively solves a sequence of KWMTSVM-like optimization problems, and KWMTSVM is a convex optimization problem.

• (2) SNPTSVM (Tian et al 2014). The SNPTSVM is proposed for binary classification problem. Its sparsity is achieved by adopting the $\epsilon$-insensitive quadratic loss function and soft margin quadratic loss function. For the positive hyperplane, the SNPTSVM can achieve sparsity for positive samples while RKWMTSVM can not, and the sparsity of RKWMTSVM is mainly reflected in the negative and zero samples. However, the SNPTSVM sacrifices the complexity because its dual problem contains three kinds of Lagrangian multipliers.

• (3) SPinTSVM (Tanveer et al 2019a). The SPinTSVM is raised for binary classification problem. It achieves the sparsity by using the $\epsilon$-insensitive zone pinball loss function. Not only the incorrectly classified samples gain punishments, but also the correctly classified samples gain penalties. It is less sensitive to noise, especially feature noise. The proposed RKWMSTVM achieves sparsity by using the ramp loss function. It only punishes the incorrectly classified data and when the outlier is bigger than a threshold s, the corresponding penalty will be given a fixed value. Therefore, the RKWMSTVM is less sensitive to label noise.

• (4) RSLPTSVM (Tanveer 2014). The RSLPTSVM is a binary classifier while RKWMTSVM is a multi-class classification algorithm. The RSLPTSVM achieves sparsity by using exact 1-norm, and it is a strongly convex problem by incorporated regularization term while RKWMSTVM is a non-convex optimization algorithm. The optimal solution of RSLPTSVM is obtained by solved by a pair of unconstrained minimization problems using Newton–Armijo algorithm while RKWMTSVM solves a series of QPPs.

• (5) RNPSVM (Liu et al 2015). What RNPSVM and RKWMTSVM have in common is that they both use ramp loss function which can explicitly incorporate noise and outlier suppression in the training phase. They both are non-convex and non-differentiable optimization problems and have sparsity and robustness. The difference between them is that RKWMTSVM is proposed for multi-classification by adopting OVOVR structure, while RNPSVM is proposed for binary classification. Besides, RNPSVM preserves the $\epsilon$-insensitive function of NPSVM. RKWMTSVM excavates the structural information of data to improve the generalization ability and accelerate the solving speed.

• (6) R-TWSVM (Qi et al 2013). The R-TWSVM is a stronger insensitive binary classifier for dealing with missing or uncertain data with label noise. Because it uses a quadratic loss function making the proximal hyperplane close to the class itself, and a soft-margin loss function making the hyperplane as far as possible from the other class. The RKWMTSVM can effectively depress the negative influence of outliers in the negative (resp. positive) and zero classes for the positive (resp. negative) classifier by using ramp loss functions. The R-TWSVM is a second-order cone programming problem, while RKWMTSVM is a non-convex optimization problem.

4.2 Algorithm analysis

The proposed RKWMTSVM aims at constructing two nonparallel hyperplanes by solving a pair of smaller-size QPPs in each sub-classifier.

• When constructing the separating positive (negative) hyperplane, the greater weights are given to the positive (negative) samples if they have more KNNs.

• The ineffective constraints can be removed if their corresponding KNN weights $f_j=0, j \in I_2$ (resp. $f_i=0, i \in I_1$) and $h_k=0, k \in I_3$ (resp. ${\tilde{h}}_k=0, k \in I_3$), thus accelerating the computational speed of RKWMTSVM.

• The structural information is exploited by KNN, and the class imbalance problem is resolved by adopting the OVOVR structure.

• The KWMTSVM can be seen as a special case of the proposed RKWMTSVM. If $s_i\rightarrow -\infty , i=1,...,4$, then $R_s\rightarrow H_1$, i.e., s takes large negative value, the ramp loss in the RKWMTSVM will not help to remove outliers, then RKWMTSVM will degenerate to KWMTSVM.

• Computational complexity of RKWMTSVM. In a 3-class classification problem, we suppose that there are l/3 samples in each class, where l is the number of total number of training samples. As discussed in the works proposed by Xu (2016) and Tanveer et al (2021a), the computational complexity of TKSVC $O(2\times (2l/3)^3)$. Because of $f_j=1 \ \text {or} \ 0, j \in I_2$ (resp. $f_i=1 \ \text {or} \ 0, i \in I_1$) and $h_k=1 \ \text {or} \ 0, k \in I_3$ (resp. ${\tilde{h}}_k=1 \ \text {or} \ 0, k \in I_3$), the computational complexity of KWMTSVM is less than $O(16l^3/27)$. The proposed RKWMTSVM needs to solve a sequence of KWMTSVM-like problems; therefore, the computational complexity of RKWMTSVM is less than $O(16l^3/27)$ times the iteration number in CCCP.

The proposed RKWMTSVM still needs to calculate the weight matrices by KNN steps whose complexity is $O(l^2\mathrm{log}(l))$. Therefore, the total time complexity of RKWMTSVM is about $O(l^2\mathrm{log}(l))$ plus $O(16l^3/27)$ times the iteration number.

4.3 Discussion on RKWMTSVM

4.3.1 OVO PGTSVM vs. RKWMTSVM

The PGTSVM (Tanveer et al 2019c) is noise insensitive and more stable for re-sampling because it uses the pinball loss function, which not only gives punishments on correctly classified samples but also on incorrectly classified samples. Besides, the pinball loss function does not increase the computational complexity as compared with TSVM. Compared with RKWMTSVM, it totally loses sparsity.

Because PGTSVM is proposed for binary classification, we extend it to multi-classification case by adopting OVO strategy, termed as OVO PGTSVM. For a 3-class classification problem, we still set there are l/3 samples in each class (The same for the following analysis). OVO PGTSVM has to construct $K(K-1)/2$ binary PGTSVM, and each binary PGTSVM only picks two classes. Therefore, its computational complexity is about $O(2\times (l/3)^3)$.

4.3.2 OVR WTSVM vs. RKWMTSVM

The WTSVM (Ye et al 2012) is a binary classifier which can mine the underlying similarity information within samples by using inner-class nearest neighbor, which greatly improve the performance. Besides, it removes the redundant constraints by using inter-class nearest neighbor to improve the solving speed. WTSVM is the basic algorithm compared with RKWMTSVM, because RKWMTSVM also considers inner-class and inter-class nearest neighbor to excavate the structural information.

The OVR is a common used “decomposition-reconstruction” strategy. We extend WTSVM to multi-classification case by employing OVR, termed as OVR WTSVM. For a 3-class classification problem, OVR WTSVM needs to construct K binary WTSVMs, and the computational complexity of each binary WTSVM is less than $O(2\times (2l/3)^3)$. Besides, it needs to calculate k-nearest neighbor graph, whose computational complexity is about $O(l^2\mathrm{log}(l))$.

4.3.3 OVR R$\nu$TSVM vs. RKWMTSVM

Rough $\nu$-TSVM (R$\nu$-TSVM) (Xu et al 2012) is proposed as a binary classifier, which gives different penalties to different misclassified samples according to their positions by constructing rough lower margin, rough upper margin and rough boundary. It can avoid the over-fitting problem to a certain extent. Both R$\nu$-TSVM and RKWMTSVM concentrate on the study of misclassified samples. The RKWMTSVM uses ramp loss function to depress the negative influence of outliers which are also the misclassified samples.

We extend R$\nu$-TSVM to multi-classification scenes by OVR. For a 3-class classification problem, OVR R$\nu$-TSVM also has to construct K binary R$\nu$-TSVMs, and the computational complexity of each binary R$\nu$-TSVM is about $O(2\times (2l/3)^3)$.

4.3.4 KWMTSVM vs. RKWMTSVM

Both KWMTSVM (Xu 2016) and RKWMTSVM adopt OVOVR structure to handle multi-classification data and consider the local information of samples by KNN. The difference of them is the usage of loss function, where KWMTSVM uses the hinge loss function while the proposed RKWMTSVM uses the ramp loss function. The KWMTSVM solves a pair of convex optimization problems, while RKWMTSVM is a concave–convex optimization problem. The RKWMTSVM solves a sequence of KWMTSVM-like problems by CCCP. Besides, RKWMTSVM is more robust for outliers. Compared with KWMTSVM, our RKWMTSVM is sparser.

For a 3-class classification problem, KWMTSVM needs to solve two QPPs and use KNN steps to compute weight matrices. Its overall time complexity is approximately $O(l^2\mathrm{log}(l)+16l^3/27)$.

4.3.5 Ramp-TKSVC vs. RKWMTSVM

Ramp-TKSVC (Wang et al 2020) is also a multi-classification model adopting OVOVR structure. Both Ramp-TKSVC and RKWMTSVM use ramp loss function to restrict the maximal loss value of outliers to a fixed value. Therefore, they both are sparse and robust algorithms. They both are concave–convex optimization problems. In each CCCP, Ramp-TKSVC solves a sequence of TKSVC problems while RKWMTSVM solves a series of KWMTSVM problems. Compared to Ramp-TKSVC, RKWMTSVM considers the structural information by KNN which can greatly improve the generalization ability and reduce the redundant constraints.

For a 3-class classification problem, the time computational complexity of TKSVC is $O(2\times (2l/3)^3)$ and then, computational complexity of Ramp-TKSVC is about $O(l^2\mathrm{log}(l))$ times the iteration number.

4.3.6 LS-KWMTSVM vs. RKWMTSVM

Both LS-KWMTSVM (Tanveer et al 2021a) and the proposed RKWMTSVM are multi-classification algorithms. They both exploit the local information of training samples by KNN. The LS-KWMTSVM is a least squares version of KWMTSVM, because it uses 2-norm instead of 1-norm in KWMTSVM. Therefore, LS-KWMTSVM only needs to solve two systems of linear equations rather than two QPPs in KWMTSVM, making LS-KWMTSVM work faster.

For a 3-class classification problem, LS-KWMTSVM contains two systems of linear equations and KNN steps to compute weight matrices. Its total computational complexity is less than $O(l^2\mathrm{log}(l)+16l^3/27)$.

5 Numerical experiments

To evaluate the performance of our algorithm, in this section, we conduct the experiments on one artificial dataset and twenty-four benchmark datasets which are collected from UCI machine learning repository¹ and Libsvm library². The characteristics of datasets are shown in Table 1. We remove the missing values in dataset Dermatology and replace the missing values with zero in dataset Autompg before doing the partitions. Furthermore, in order to eliminate the influence of dimension and make the numerical calculation easier, we scale all the features into the range of [0, 1] in the data preprocessing.

Table 1 The characteristics of twenty-four benchmark datasets

In order to make the results more convincing, the respected dataset splits into training sets and independent test sets according to k-fold cross-validation method (Salzberg 1997). This method requires that the dataset be divided into k parts, which each of the k parts acted as an independent holdout test set. Because all k parts will be used in the testing part equally and independently, the reliability of the results could be convincing. The accuracy of the algorithm is the averaged one of k experiments. According to the work of Gutierrez et al (2016); Bamakan et al (2017); Tang et al (2021), we also use fivefold cross-validation in our experiment. All experiments are carried out in Matlab R2014a on Windows 7 running on a PC with system configuration Inter Core i3-4160 Duo CPU (3.60GHz) with 12.00 GB of RAM. We report testing accuracy to evaluate the performance of classifiers. “Accuracy” (Acc) denotes the mean value of five times testing results and plus or minus the standard deviation(std). “Time” denotes the average time of five experiments, and each experiment’s time consists of training time and testing time. For the nonlinear case, we only adopt the Gaussian kernel function $K({{{\mathbf {x}}}_{i}},{{{\mathbf {x}}}_{j}})=\mathrm{exp}(-r||{\mathbf {x}}_{i}-{\mathbf {x}}_{j}||^2)$ as it has been proved it always yields higher testing accuracy.

5.1 Experiment on one artificial dataset

In this subsection, we conduct the experiment on one artificial dataset in ${\mathbb {R}}^2$ dimensional space, which comes from the work of Bamakan et al (2017). Firstly, we generate a training set $T=\{(\mathbf{x }_1, y_1), (\mathbf{x }_2, y_2), \cdots (\mathbf{x }_l, y_l)\}$, where $\mathbf{x }_i\in {\mathbb {R}}^2$ and $l=150$. The data have three different classes, i.e., the positive, negative and zero class. Each class has 50 samples and follows a Guassian distribution, where $\mu _A=[4 \ 3]$, $\mu _B=[1 \ 1]$, $\mu _C=[3 \ -3]$, and

$$\begin{aligned} \varSigma _A=\left[ \begin{array}{ll} \text {2} &{}\quad \text {--1} \\ \text {--1} &{} \quad \text {2} \\ \end{array} \right] , \varSigma _B=\left[ \begin{array}{ll} \text {2} &{}\quad \text {1} \\ \text {1} &{} \quad \text {1} \\ \end{array} \right] , \varSigma _C=\left[ \begin{array}{ll} \text {1} &{}\quad \text {0} \\ \text {0} &{} \quad \text {4} \\ \end{array} \right] . \end{aligned}$$

Similarly, to eliminate the influence of dimension and make the numerical calculation easier, we scale all the features into the range of [0, 1]. The corresponding results are shown in Figs. 4, 5 and 6. The blue “$\star$”, red “$\blacktriangleright$” and green “$\blacklozenge$” stand for the positive, negative and zero class, respectively. The “$\circ$” and “$\bigtriangleup$” in Fig. 4 stand for the samples selected by KNN in the QPP (16) and QPP (17), respectively. Figure 4a and b shows the results of setting cluster parameter $k=3$ and $k=4$, respectively. The results show that the more samples will be removed by setting smaller k. Besides, the appropriate k will help to remove some noises, such as the green point in the lower-left corner which is a outlier of the rest class.

Fig. 4

The samples selected by KNN, where “$\circ$” stands for the samples with $f_j=1,j\in I_2$ and $h_k=1, k\in I_3$, “$\bigtriangleup$” stands for the samples with $f_i=1,i\in I_1$ and $h_k=1, k\in I_3$

Fig. 5

The plots of KWMTSVM and RKWMTSVM with different parameters with cluster parameter $k=3$, where $c_i=5$ , “$\circ$” and “$\bigtriangleup$” stand for the SVs

Fig. 6

The plots of KWMTSVM and RKWMTSVM with different parameters with cluster parameter $k=4$, where $c_i=5$

In Figs. 5 and 6, the red and black thick solid line represent the decision boundary $f_+=-1-\varepsilon$ and $f_-=1+\varepsilon$, respectively. The “$\circ$” and “$\bigtriangleup$” denote support vectors (SVs) in the first and second QPP in both KWMTSVM and RKWMTSVM, respectively. Figure. 5 and 6 show the results of KWMTSVM and RKWMTSVM with different parameter $\varepsilon$ and kernel parameter r under cluster parameter $k=3$ and $k=4$, respectively. It is obvious that the number of SVs of RKWMTSVM is less than that of KWMTSVM under the same parameter. The most obvious point is the red triangle which locates in the upper right corner which is regarded as a outlier of negative class. Obviously, it is marked by the circle which means it is a SV in the KWMTSVM while it is not a SV any more in our RKWMTSVM. The results show that our RKWMTSVM is more sparse compared with the KWMTSVM. The results also indicate that the number of SVs is different under different parameters. Besides, the positive decision boundary (the red one) obtained by the KWMTSVM is more shifted toward the outlier compared with our RKWMTSVM. The results demonstrate that the proposed RKWMTSVM is more robust compared with the KWMTSVM.

5.2 Influence of parameters

We conduct the experiments on thirteen datasets to investigate the influence of cluster parameter k in our RKWMTSVM. The results are shown in Table 2, where we record the testing accuracy of RKWMTSVM with the cluster parameter k ranges from 3 to 8. As the increase of k, the computational time of the proposed RKWMTSVM tends to rise. A smaller k will help RKWMTSVM to remove the redundant data and reduce the computational time. When $k=max\{l_1+l_3,l_2+l_3\}$, no training samples will be removed by KNN and the computational time will become longer. With the increase of k, the change of classification accuracy is not obvious.

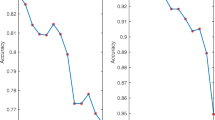
In order to analyze the influence of parameter $c_2$ and kernel parameter r on the predictive accuracy in the KWMTSVM and our RKWMTSVM, we do the experiments on four benchmark datasets, i.e., Autompg, Glass, Teaching and Wine, and the results are shown in Figs. 8, 9, 10, 11, where we search the parameter $c_2$ and r from the range $\{2^{i}|i=-4,...,6\}$ and fix $c_1=4, \varepsilon =0.2, k=3$. From Fig. 8, it is hard to judge which parameter affects more on the testing accuracy. In Figs. 8 and 9, it appears that the impact of kernel parameter r is more than penalty parameter $c_2$, and both KWMTSVM and RKWMTSVM achieve better testing accuracy for smaller value of parameter r. However, it seems that the classifiers achieve better predictive accuracy for large value of r in Fig. 10.

Because the proposed RKWMTSVM contains too many parameters, we carry out the analysis of variance (ANOVA) (Hamdia et al 2018) decomposition to do the key parameter sensitivity analysis. ANOVA is used to quantify the independent and joint effects of the parameters on 5-fold cross validation accuracy and calculate the sensitivity index of each parameter ($S_{T_i}$). The works of Hamdia et al (2018) and Long et al (2020) show the specific calculation, and they conclude that the larger $S_{T_i}$, the higher sensitivity of accuracy with respect to the i-th parameter. The results using ANOVA on our RKWMTSVM are shown in Fig. 7, where the x-axis denotes six benchmark datasets and y-axis is the indices $S_T$. The parameter r has a dramatic effect on accuracy, followed by $c_1$ and $c_2$. Relatively, the sensitivity brought by $\varepsilon$ and k is much weaker. Summarily, the parameter k can help to remove the redundant constraints and improve the classification accuracy of RKWMTSVM, but their variation cannot lead to strong accuracy fluctuation.

Based on the results discussed above, we set $k=3$ in the following experiments to reduce the long searching time.

Fig. 7

$S_T$ indices of the parameters

Table 2 Performance comparisons of RWMTSVM with different cluster parameter k on thirteen datasets

Fig. 8

The relationship of kernel parameter r, parameter $c_2$, and classification accuracy in the KWMTSVM and RKWMTSVM on Autompg dataset, respectively

Fig. 9

The relationship of kernel parameter r, parameter $c_2$, and classification accuracy in the KWMTSVM and RKWMTSVM on Glass dataset, respectively

Fig. 10

The relationship of kernel parameter r, parameter $c_2$, and classification accuracy in the KWMTSVM and RKWMTSVM on Teaching dataset, respectively

Fig. 11

The relationship of kernel parameter r, parameter $c_2$, and classification accuracy in the KWMTSVM and RKWMTSVM on Wine dataset, respectively

5.3 Parameter selection

An important preliminary issue for SVMs is the optimal parameter selection. There are three types of parameter optimization methods of SVMs. The first is the typical of grid search method (Friedrichs and Igel 2005). The second is numerical optimization method, such as gradient descent method (Schölkopf et al 2007). Many meta-heuristics methods are also introduced to obtain an acceptable optimum, including genetic algorithms, particle swarm optimization, bat algorithms, etc. (Wang et al 2013; Tharwat et al 2017; Li et al 2018). In this paper, we adopt the traditional grid search method to get the optimal parameters.

The kernel parameter r is searched from $\{2^{i}|i=-4,...,6\}$. In order to reduce the computational complexity of parameter selection, we set $c_1=c_2$ in OVO PGTSVM, OVR WTSVM and OVR R$\nu$TSVM; $\tau _1=\tau _2$ in OVO PGTSVM; ${{\nu }_{1}}={{\nu }_{2}}$ and $\sigma _1=\sigma _2$ in OVR R$\nu$-TSVM; $c_1=c_3$, $c_2=c_4$ in Ramp-TKSVC, KWMTSVM, LS-KWMTSVM and RKWMTSVM. In general, we need to choose $(c_1,\tau _1,r)$ in OVO PGTSVM; $(c_1,r)$ in OVR WTSVM; $(\nu _1,\sigma _1, r)$ in OVR R$\nu$-TSVM; $(c_1,c_2,\varepsilon ,r)$ in Ramp-TKSVC, KWMTSVM, LS-KWMTSVM and our RKWMTSVM. The parameter $c_{1}$ is selected from the set $\{2^{i}|i=-4,...,6\}$. The parameter $\nu _1$ is searched from the set $\{0.2,...,0.7\}$. The parameter $\tau _1$ is searched from the set $\{0.1,0.5,0.9\}$. The value $\sigma _1$ is searched from the set $\{1.5,2,2.5,3,5,8\}$. The parameter $\varepsilon$ ranges from set $\{0.1,0.2,0.3\}$. For large-scaled datasets, we reduce the number of parameters uniformly by enlarging the search step due to the long running time.

5.4 Result comparisons and discussions

Table 3 reports the averages and standard deviations of the testing accuracies (in %) and running times (s) for the seven compared algorithms on twenty-four datasets. The bold value indicates the best predictive accuracy.

Table 3 Performance comparisons of seven nonlinear algorithms with Gaussian kernel

Fig. 12

The accuracy variation with different training sizes

From the perspective of testing accuracy, we can learn that our proposed RKWMTSVM outperforms the other six algorithms for most datasets. The reasons are twofold. On one hand, our RKWMTSVM retains the property of the KWMTSVM which utilizes the local information of inter-class and intra-class by using KNN method. On the other hand, the introduction of ramp loss makes our RKWMTSVM insensitive to outliers. Besides, we find that OVO PGTSVM performs better than OVR WTSVM and OVR R$\nu$TSVM for most cases. A possible reason is that OVR strategy easily leads to imbalance problem which may lead to bad performance. Another possible reason is that OVO PGTSVM adopts the pinball loss function which maximize the quantile distance rather than the shortest distance between classes, making the algorithm be less sensitive to noises. OVR R$\nu$TSVM performs better than OVR WTSVM on most datasets. The reason for that is R$\nu$TSVM punishes the misclassified samples according to their positions which can improve the performance. The algorithms which take one-verse-one-verse-rest structure, i.e., KWMTSVM, Ramp-TKSVC, LS-KWMTSVM and our RKWMTSVM, perform better than binary classifiers adopted OVR strategies, i.e., OVR WTSVM and OVR R$\nu$TSVM. The reason is that KWMTSVM, Ramp-TKSVC, LS-KWMTSVM and our RKWMTSVM can not only utilize all the information of training data points in every classifier but also avoid the imbalance problem to some extent. Ramp-TKSVC performs best on six datasets, while KWMTSVM and LS-KWMTSVM perform best on four datasets, which implies that Ramp-TKSVC yields better. That is because Ramp-TKSVC also adopts ramp loss function to avoid the disturbance of outliers. The seven algorithms all yield 100% testing accuracy on Soybean dataset, which implies that seven algorithms yield the comparable performance.

From the view of running time, when the size of dataset is relatively small, it is hard to judge which algorithm has the least running time. The three strategies, i.e., OVO, OVR, and OVOVR, have their pros and cons. When the size of dataset is large scale, the advantage of KWMTSVM, LS-KWMTSVM and our RKWMTSVM is obvious. That is because they all can remove the redundant constraints by KNN, especially when they are compared with Ramp-TKSVC. It is worth to note that LS-KWMTSVM takes the least time among the seven algorithms. Because LS-KWMTSVM solves linear equations and uses KNN to remove the consonant constraint. Although both Ramp-TKSVC and RKWMTSVM adopt ramp loss function to depress the negative influence of outliers, the proposed RKWMTSVM works faster than Ramp-TKSVC.

5.5 Training efficiency

To see the performance of the proposed RKWMTSVM on different training sizes of noisy datasets, we do experiments on Cmc and Optidigits datasets which have larger sample sizes. The results are shown in Fig. 12, where x-axis denotes the training sizes and y-axis denotes the testing accuracy. The red, blue and black lines are the case with no noise, 1% and 5% label noise added, respectively. The results show that the accuracy of RKWMTSVM will increase with the increase in training sizes. Fig. 13 is the time change with different training sizes, where y-axis is the logarithmic of time. Obviously, the training time will increase with the training size increases.

In addition, we discuss the training time of RKWMTSVM, which needs to solve optimization problems (36) and (37) repeatedly by CCCP. Suppose that each outer loop requires a comparable amount of running time, leading to a sharp increase in the total training time with the number of iterations. To verify the hypothesis, we draw Fig. 14 to reveal how the training time distributes during the outer loop process on five datasets, where $t_i$ denotes the running time of ith subproblem. Figure 14 denotes the curve of $t_i/t_1$ ratio. It displays that the five datasets will be terminated less than 8 iterations. Datasets Wine and Thyroid take only 3 iterations. In addition, after the first iteration, the running time of the following iterations decreases drastically. It is obvious that Iris dataset takes 8 iterations to converge while the first iteration takes the most training time. These results prove the effectiveness of the proposed Algorithm 1.

Fig. 13

The time variation with different training sizes

Fig. 14

The variations of $t_i/t_1$ as the outer loop iterations on five datasets

5.6 Statistical tests

From Table 3, we can see that our RKWMTSVM not always performs the best among the seven algorithms on the twenty-four datasets from the perspective of testing accuracy. To further analyze the performance of seven algorithms on multiple datasets statistically, we use Friedman test (Demsar 2006) and Holm–Bonferroni test (Holm 1979) which are two commonly used statistical methods.

5.6.1 Friedman test

The Friedman test is suggested by Demsar (2006) and Salvador et al (2010), and it is proved to be simple, nonparametric and safe for comparing three or more related samples. For this, the average ranks of seven algorithms on accuracy for twenty-four datasets are listed in the last line of Table 3.

Referring to the works of Wang et al (2020); Tanveer et al (2021a), we still suppose the null-hypothesis be that all the algorithms are equivalent. We can obtain the Friedman statistic according to the following equation,

$$\begin{aligned} \chi ^2_F =\frac{12N}{k(k+1)}\left[ \sum \limits _{j}{R_{j}^{2}-\frac{k{{(k+1)}^{2}}}{4}} \right] , \end{aligned}$$

(44)

where $R_j=\frac{1}{N}\sum _{i}{r_{i}^{j}}$, and $r_{i}^{j}$ denotes the jth of k algorithms on the ith of N datasets. Friedman’s $\chi ^2_F$ is undesirably conservative and derives a better statistic

$$\begin{aligned} F_F =\frac{(N-1)\chi ^2_F}{N(k-1)-\chi ^2_F}, \end{aligned}$$

(45)

which is distributed according to the F-distribution with $k-1$ and $(k-1)(N-1)$ degrees of freedom.

On the basis of (44) and (45), we derive $\chi ^2_F=37.3551$ and $F_F=8.0563$, where $F_F$ is distributed according to F-distribution with (6, 138) degrees of freedom. The critical value of F(6, 138) is 1.817 for the level of significance $\alpha =0.1$; similarly, it is 2.165 for $\alpha =0.05$. Because the value of $F_F$ is 8.0563 which is much larger than the critical value, it indicates that there is significant difference between the seven algorithms. It is worth to mention that the average rank of the proposed RKWMTSVM is far lower than the remaining algorithms, which means that it has a better performance than the other six compared algorithms.

5.6.2 Holm–Bonferroni test

Holm–Bonferroni method (Simes 1986) is a frequently used method to compare the performance of multiple algorithms. The p value (Demsar 2006) is calculated by performing pairwise t-test, and the proposed RKWMTSVM is statistically compared with the other six algorithms. According to the statement of Demsar (2006), the null hypothesis assumes that the data of two-sample t-test come from independent random samples with equal means and equal but unknown variances. For a given significance level $\alpha =0.05$, Holm–Bonferroni test orders the p-values from minimum to maximum as $p_{(1)},p_{(2)},...,p_{(6)}$ with corresponding null hypothesis $H_{(1)},H_{(2)},...,H_{(6)}$. The results of p-values are presented in Table 4 ($\alpha =0.05$). It rejects the null hypotheses $H_{(1)},...,H_{(i-1)}$ and does not reject $H_{(i)},...,H_{(6)}$, if

$$\begin{aligned} p_{(i)}>\frac{\alpha }{6+1-i},1<i\le 6, \end{aligned}$$

(46)

where i is the minimal index.

Table 4 The p values of the seven algorithms using Gaussian kernel

For dataset Iris, $(p_{(2)}=0.7238 = p_{(3)} = p_{(5)}) < (p_{(1)} =p_{(4)} = p_{(6)}=1)$ and $p_{(2)}>{\alpha }/{5}$. Hence, we conclude that $H_{(1)},...,H_{(6)}$ are not rejected. That means the RKWMTSVM is statistically similar to OVO PGTSVM, OVR WTSVM, OVR R$\nu$TSVM, KWMTSVM, Ramp-TKSVC and LS-KWMTSVM on Iris dataset. In this way, we find 16 out of the 144 null hypotheses are judged which indicates our method has significant advantage over others. In total, the statistical results on p value suggest that the proposed algorithm is not obvious statistically difference with other six algorithms in performance.

In our experiment, the Friedman test reports a significant difference, but the Holm–Bonferroni test which is a post hoc test fails to detect it. This is due to the lower power of the latter (Demsar 2006). In this case, we can only conclude that these algorithms do differ. For example, all seven algorithms yield 100% accuracy on Soybean dataset, and the p values show that they are statistically similar which is rational. The p value of OVR WTSVM is 0.7328 on Iris dataset which indicates that our RKWMTSVM is statistically similar to OVR WTSVM. Actually, the performance of our RKWMTSVM is indeed higher than OVR WTSVM. Another possible reason is that the datasets do not have much outliers, and the advantages of RKWMTSVM are not obvious, especially compared with the robust algorithms OVO PGTSSVM and Ramp-TKSVC.

6 The clipDCD for RKWMTSVM

In this section, we employ the clipDCD algorithm (Peng et al 2014) to accelerate the solving speed of our RKWMTSVM in the training process.

6.1 The clipDCD algorithm

The clipDCD algorithm is a kind of the coordinate descent method, and it is proposed for solving the dual problem of SVM (Peng et al 2014). Till now, it has been successfully embedded into SVM, TSVM, L1-loss-based TSVM (Peng et al 2016), TPMSVM (Peng 2011b), structural TSVM(Pan et al 2015) and so on. In each iteration, the clipDCD algorithm only solves one single-variable sub-problem according to the maximal possibility-decrease strategy on objective value. The dual form of classical SVM is as follows,

$$\begin{aligned}&\underset{\varvec{\alpha }}{\mathop {\min }}\,f(\varvec{\alpha })=\frac{1}{2}{\varvec{\alpha }^{T}}\varvec{Q}\varvec{\alpha } -{{\mathbf {e}}^{T}}\varvec{\alpha } \nonumber \\&s.t. \quad \varvec{0}\le \varvec{\alpha } \le {\mathbf {C}}. \end{aligned}$$

(47)

It is assumed that only one component of $\varvec{\alpha }$ is updated at each iteration, denoted $\alpha _L=\alpha _L+\lambda , L\in \{1,..,n\}$ is the index. It has been proved that

$$\begin{aligned} f(\lambda )=f(0)+\frac{(e_L-\varvec{\alpha }^T\varvec{Q}_{.,L})^2}{2Q_{LL}}, \end{aligned}$$

(48)

where $\varvec{Q}_{.,L}$ is the Lth column of $\varvec{Q}$. The objective decrease will be approximately largest by maximizing ${(e_L-\varvec{\alpha }^T\varvec{Q}_{.,L})^2}/{Q_{LL}}$, and the L index is chosen as

$$\begin{aligned} L=\underset{i\in {\mathcal {A}}}{\mathop {\arg \max }}\left\{ \frac{(e_i-\varvec{\alpha }^T\varvec{Q}_{.,i})^2}{Q_{ii}} \right\} , \end{aligned}$$

(49)

where the index set ${\mathcal {A}}$ is

$$\begin{aligned} {\mathcal {A}}=\left\{ i: \alpha _i>0, \text {if}\, \frac{e_i-\varvec{\alpha }^T\varvec{Q}_{.,i}}{Q_{ii}}<0\, \text {or}\, \alpha _i<C, \text {if}\, \frac{e_i-\varvec{\alpha }^T\varvec{Q}_{.,i}}{Q_{ii}}>0 \right\} . \end{aligned}$$

(50)

Table 5 Performance comparison of four algorithms on seven datasets

Table 6 Performance comparison of four algorithms on seven datasets with 5% noises

6.2 The clipDCD algorithm for RKWMTSVM

We embed the clipDCD algorithm into the dual QPPs in our RKWMTSVM during each iteration of CCCP procedure. The two convex QPPs are shown in (36) and (37). For simplicity, we only explain the QPP (36), where we use matrix ${\mathbf {N}}_{+}({\mathbf {X}}_1^T{\mathbf {D}}_1{\mathbf {X}}_1)^{-1}{\mathbf {N}}_{+}$ in place of matrix $\varvec{Q}$ in (47) and use vector ${\varvec{\gamma }_+}-\varvec{\tau }_+$ in place of $\varvec{\alpha }$ in (47). Therefore, we need to solve the following optimization problem:

$$\begin{aligned}&\underset{\varvec{\alpha }}{\mathop {\min }}\,f(\varvec{\alpha })=\frac{1}{2}{\varvec{\alpha }^{T}}\varvec{Q}\varvec{\alpha } -{{\mathbf {e}}^{T}}\varvec{\alpha } \nonumber \\&s.t. \quad -\varvec{\tau }_+ \le \varvec{\alpha } \le {\mathbf {S}}_{+} -\varvec{\tau }_+ . \end{aligned}$$

(51)

It is noteworthy the matrix ${\mathbf {N}}_{+}= [{\mathbf {X}}_2^{T}{\mathbf {F}}_2; \ {\mathbf {X}}_3^{T}{\mathbf {H}}]$ is sparse, where ${\mathbf {F}}_2=diag(f_1,f_2,...,f_{l_2})$ and ${\mathbf {H}}=diag(h_1,h_2,...,h_{l_3})$, because the value of $f_j,j\in I_2$ or $h_k,k\in I_3$ is either 1 or 0. That means the component of $\varvec{\alpha }$ corresponding $f_j=0$ and $h_k=0$ will not contribute to the optimization of objective function. Therefore, they can be ignored during the progress of solving the optimal $\varvec{\alpha }$, which will further advance the computational efficiency.

Remarkably, there is the simple update $\alpha _L^{new}=\alpha _L+\lambda$ in clipDCD. Then,

$$\begin{aligned} f(\lambda )=f(0)+\frac{1}{2}\lambda ^2\varvec{Q}_{LL}-\lambda (e_L-\varvec{\alpha }^T\varvec{Q}_{.,L}) \end{aligned}$$

(52)

Setting the derivation of $\lambda$:

$$\begin{aligned} \frac{df(\lambda )}{d\lambda }=0 \quad \Rightarrow \lambda =\frac{e_L-\varvec{\alpha }^T\varvec{Q}_{.,L}}{\varvec{Q}_{LL}}. \end{aligned}$$

(53)

Similarly, the L index is chosen as Eq.(49). Moreover, the $\lambda$ value in QPP (36) must be adequately clipped so that $-\varvec{\tau }_+^{(i)} \le \alpha _L^{new} \le {\mathbf {S}}_{+}^{(i)} -\varvec{\tau }_+^{(i)}$. That means the step $\lambda$ should satisfy the inequality constraints. Accordingly, we adjust the index set ${\mathcal {A}}$ as follows.

$$\begin{aligned} {\mathcal {A}}=\{ i:&\alpha _i>-\varvec{\tau }_+^{(i)}, \text {if}\, \frac{e_i-\varvec{\alpha }^T\varvec{Q}_{.,i}}{Q_{ii}}<0 \nonumber \\&\text {or}\ \alpha _i<{\mathbf {S}}_{+}^{(i)} -\varvec{\tau }_+^{(i)}, \text {if}\, \frac{e_i-\varvec{\alpha }^T\varvec{Q}_{.,i}}{Q_{ii}}>0 \}. \end{aligned}$$

(54)

The convergence of clipDCD algorithm and corresponding theoretical proofs can be found in Peng et al (2014).

In a word, the framework of clipDCD algorithm for solving QPP(36) is summarized as follows.

In order to verify the performance of our proposed RKWMTSVM by applying the clipDCD ($\text {RKWMTSVM}^{cl}$), we conduct experiment on seven benchmark datasets. Besides, we add noises into these datasets. The corresponding results are recorded in Tables 5 and 6, respectively. The results indicate that the clipDCD algorithm can improve the solving speed of our RKWMTSVM to a certain extent, while the testing accuracy lose a little. The results also show that the proposed RKWMTSVM by quadratic programming method ($\text {RKWMTSVM}^{qp}$) obtain the best testing accuracy on most datasets. Although the $\text {RKWMTSVM}^{cl}$ performs almost the same as KWMTSVM in Table 5, it performs better than KWMTSVM after the noises are added in Table 6. In addition, we also compare our method with the native multi-class classifier K-Nearest Neighbor (KNN). The results show that our RKWMTSVM outperforms KNN from the perspective of testing accuracy, while it takes a relatively long time.

7 Conclusion and future work

In this paper, a new multi-classification algorithm termed as ramp loss K-nearest neighbor-weighted multi-class twin support vector machine (RKWMTSVM) is proposed by replacing the hinge loss with ramp loss function in KWMTSVM. This modification leads to a precise, sparse and robust algorithm with better performance. On one hand, similar to KWMTSVM, the proposed RKWMTSVM adopts the OVOVR structure to deal with multi-class classification problem, which is helpful to deal with class-imbalance problem by considering all training points. Besides, the local information of intra-class can be exploited by constructing the weight matrix in the objective function which can help to improve the generalization ability. Meanwhile, the weight matrix of inter-class can help to remove the redundant constraints which can reduce the computational speed. On the other hand, it adopts the ramp loss function which can avoid the disturbance of outliers, making it be a sparser and robust algorithm, especially compared with KWMTSVM. In addition, the proposed RKWMTSVM is a non-differentiable non-convex optimization problem, we adopt the CCCP to cope with this model and embed the clipDCD method to speed up the solution process, thus making our model more adaptable for large-scale problem. In the experiments, we compare it with six state-of-the-art algorithms to demonstrate the validity. The experimental results show that the proposed RKWMTSVM is a more sparse algorithm and is robust to outliers.

As the proposed RKWMTSVM is less sensitive to outliers and it is an efficient multi-classification algorithm, it is worthwhile to apply it on the domains such as intrusion detection problem, spam detection, stellar spectra classification, fault class detection, novelty detection, prediction of diagnostic phenotypes, customer churning analysis, anomaly detection problem and so on. Due to the proposed RKWMTSVM contains many parameters, it takes us a long searching time to find the optimal parameters combination by grid search. During our experiments, we find that the performance of RKWMTSVM is worse on some parameter intervals which is time-consuming and wasteful to search the optimal solution on these parameter intervals. Besides, the optimal solution is not always fall in the grid points of grid search. Therefore, how to design an effective algorithm for searching the optimal parameter combination for our RKWMTSVM is worthy of further research.