1 Introduction

Recently, neural networks have gotten more and more attention because of its widespread application in a variety of areas, such as optimization problems, pattern recognition and signal and image processing [1–7]. In many practical problems, the periodic solution of the model is often required to be either globally asymptotically stable or globally exponentially stable [8–13]. In fact, there are a few pure period phenomena in nature, so the research on almost periodic phenomenon or pseudo-almost periodic phenomenon is more practical. In the past few decades, many research results have been obtained for the existence, uniqueness and stability of periodic solutions, almost periodic solutions, asymptotically almost periodic solutions and pseudo-almost periodic solutions of the following cellular neural networks (CNNs) with mixed delays [14–20]:

$$\begin{aligned} x'_{i}(t)= & {} -a_{i}(t) x_{i}(t )+ \sum _{j=1}^{n}{\bar{\beta }}_{ij}(t){\bar{F}}_{j}(x_{j}(t )) + \sum _{j=1}^{n}\beta _{ij}(t)F_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&+ \sum _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(x_{j}(t-u)){\rm d}u+I_{i}(t),\quad i\in N=\{1, 2, \ldots , n\}. \end{aligned}$$
(1.1)

Here \(x_{i}(t )\) is the ith neuron state, \(a_{i}(t)\) represents the rate of decay, \({\bar{F}}_{j}\), \(F_{j}\) and \({\tilde{F}}_{j}\) are the activation of the ith neuron. The detailed biological description on the input \(I_{i}(t)\), the coefficients \(\ {\bar{\beta }}_{ij}(t)\), \(\beta _{ij}(t)\), \(d_{ij}(t)\) and delays \(\tau _{ij}(t),\) \(\sigma _{ij }(u)\) can be found in [15–17].

Most recently, as mentioned by Al-Islam et al. [21], compared with pseudo-almost periodic phenomenon, weighted pseudo-almost periodic (WPAP) phenomenon which can be accounted as an almost periodic process plus a weighted ergodic component is more frequent. As far as we know, the WPAP problem for CNNs with mixed delays has not been sufficiently studied.

Inspired by the above discussions, in this manuscript, we aim to challenge the analysis problem on the existence and exponential stability of WPAP solutions for (1.1).

2 Definitions and preliminary lemmas

Throughout this paper, \({\mathbb {U}}\) denotes the collection of functions (weights) \(\mu :{\mathbb {R}}\rightarrow (0, \ +\infty )\), which are locally integrable over \({\mathbb {R}}\) and satisfy

$$\begin{aligned} \lim \limits _{z\rightarrow +\infty }\mu ([-z, \ z])=+\infty , \ \hbox {where } \ \mu ([-z, \ z]):=\int _{-z}^{z}\mu (x){\rm d}x \ (z>0) . \end{aligned}$$

Define the following notations:

$$\begin{aligned} x= & {} \{x_{i}\}=(x_{1} , \ x_{2} , \ldots , x_{ n})^{T}, \ |x|= \{|x_{i}|\}, \ \ \Vert x \Vert =\max \limits _{ i\in N} |x_{i } |,\\ W^{+}= & {} \sup \limits _{t\in {\mathbb {R}}}|W(t)|, \ W^{-}=\inf \limits _{t\in {\mathbb {R}}}|W(t)|,\\ {\mathbb {U}}_{\infty }:= & {} \{\mu |\mu \in {\mathbb {U}},\inf \limits _{x\in {\mathbb {R}}}\mu (x)=\mu _{0}>0 \}, \end{aligned}$$

and

$$\begin{aligned}&{\mathbb {U}}^{+}_{\infty }:= \left\{ \mu |\mu \in {\mathbb {U}} _{\infty }, \limsup \limits _{|x|\rightarrow +\infty }\frac{\mu (x+\alpha )}{\mu (x)}<{+}\infty , \right. \\&\quad \left. \limsup \limits _{z\rightarrow +\infty }\frac{\mu ([-(z+\alpha ), \ z+\alpha ])}{\mu ([-z, \ z])} <{+}\infty , \ \forall ~\alpha \in {\mathbb {R}} \right\} . \end{aligned}$$

Furthermore, \({\rm BC}({\mathbb {R}},{\mathbb {R}}^{n})\), \({\rm AP}({\mathbb {R}},{\mathbb {R}}^{n})\) and \({\rm PAP}({\mathbb {R}},{\mathbb {R}}^{n})\) denote, respectively, the set of bounded and continuous functions, almost periodic functions and pseudo-almost periodic functions from \({\mathbb {R}}\) to \({\mathbb {R}}^{n}\), and

$$\begin{aligned} {\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}}^{n})=\big \{\varphi \in {\rm BC}({\mathbb {R}},{\mathbb {R}}^{n})|\lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}\mu (t)|\varphi (t)|{\rm d}t={\mathbf {0}}\big \}. \end{aligned}$$

Then, \(({\rm BC}({\mathbb {R}},{\mathbb {R}}^{n}), \Vert \cdot \Vert _{\infty })\) is a Banach space with the supremum norm \(\Vert f\Vert _{\infty } := \sup\nolimits _{ t\in {\mathbb {R}}} \Vert f (t)\Vert\). A function \(f\in {{\rm BC}({\mathbb {R}},{\mathbb {R}}^{n})}\) is called WPAP if it can be expressed as

$$\begin{aligned} f=h+\varphi , \end{aligned}$$

where \(h\in {{\rm AP}({\mathbb {R}},{\mathbb {R}}^{n})}\) and \(\varphi \in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}}^{n})}.\) The collection of such functions will be denoted by \({\rm PAP}^{\mu }({\mathbb {R}},{\mathbb {R}}^{n}).\) In particular, fixed \(\mu \in {\mathbb {U}}^{+}_{\infty }\), \(({\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n}),\Vert .\Vert _{\infty })\) is a Banach space and \({\rm PAP} ({\mathbb {R}},{\mathbb {R}}^{n})\) is a proper subspace of \({\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n})\) [22, 23].

According to the actual meaning, we consider initial condition

$$\begin{aligned} x (s)=\varphi (s), \ s\in (-\infty , \ 0], \ \varphi \in {\rm BC}({\mathbb {R}},{\mathbb {R}}^{n} ), \ i\in N. \end{aligned}$$
(2.1)

Throughout this paper, for \(i, \ j\in N,\) it will be assumed that \(\ {\bar{\beta }}_{ij }, \ \beta _{ij }, \ \ d_{ij }, I_{i}\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}} )\), \(\tau _{ij} \in C ({\mathbb {R}}, \ [0, \ +\infty ) ), \ \tau _{ij}' \in C ({\mathbb {R}}, \ {\mathbb {R}} )\), and

$$\begin{aligned} a_{i },\tau _{ij}\in {\rm AP} ({\mathbb {R}},{\mathbb {R}}) , \ \ M[a_{i }]=\lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}a_{i }(s){\rm d}s>0 , -\infty< \tau _{ij}'(s )<1,\quad \forall ~s \in {\mathbb {R}} . \end{aligned}$$
(2.2)

We suppose that the parameters of (1.1) and activation functions in this paper satisfy the following assumptions for \(i, j \in N\).

\((E_0)\) there exist \({\tilde{a}}_{i} \in {\rm BC}({\mathbb {R}},(0, +\infty ) )\) and a constant \(K_{i}>0\) such that

$$\begin{aligned} e ^{ -\int _{s}^{t}a_{i}(u){\rm d}u}\le K_{i} e ^{ -\int _{s}^{t}{\tilde{a}}_{i}(u){\rm d}u} \quad \forall \ t,\quad s\in {\mathbb {R}} ,\quad t-s\ge 0. \end{aligned}$$

\((E_1)\) \({\bar{F}} _{j}\), \(F _{j}\) and \({\tilde{F}} _{j}\) are global Lipschitz with Lipschitz constants \(L ^{{\bar{F}}}_{j}\), \(L ^{F}_{j}\) and \(L^{{\tilde{F}}}_{j}\), respectively.

\((E_{2})\) \(\sigma _{ij } :[0, +\infty )\rightarrow {\mathbb {R}}\) is bounded and continuous, and \(|\sigma _{ij }(t)|e^{\kappa t}\) is integrable on \([0, +\infty )\) for some \(\kappa >0\).

\((E_3)\) \(\mu \in {\mathbb {U}}^{+}_{\infty }\), and \({\mathbb {F}}(\alpha )=\sup \limits _{x\in \mathbb {R}}\frac{\mu (x+\alpha )}{\mu (x)}\) is bounded on arbitrary closed subinterval of \([0, \ +\infty )\).

\((E_4)\) there are constants \(\gamma _{i}>0\) and \(\xi _{i}>0\) such that

$$\begin{aligned}&\sup \limits _{t\in {\mathbb {R}}}\left\{ -{\tilde{a}}_{i} (t)+K_{i} \left[ \xi ^{-1}_{i}\sum ^n_{j=1}\left( | {\bar{\beta }}_{ij}(t)| L^{{\bar{F}}}_{j} +| \beta _{ij}(t)| L^{F}_{j} + | d_{ij}(t)|\int _{0}^{\infty }|\sigma _{ij}(u)|{\rm d}u L^{{\tilde{F}}}_{j}\right) \xi _{j} \right] \right\} \\&\quad<-\gamma _{i}<0. \end{aligned}$$

Lemma 2.1

Suppose that \(f\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}})\), \(\vartheta \in C ^{1} ({\mathbb {R}}, \ {\mathbb {R}} )\) is almost periodic, \(\vartheta (t)\ge 0\) and \(\vartheta '(t)<1\) for all \(t\in {\mathbb {R}}\). Then, \(f(t-\vartheta (t))\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}).\)

Proof

Let

$$\begin{aligned} f=h+\varphi , \end{aligned}$$

where \(h\in {{\rm AP} ({\mathbb {R}},{\mathbb {R}} )}\) and \(\varphi \in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}.\) Clearly, \(h(t-\vartheta (t))\in {\rm AP} ({\mathbb {R}},{\mathbb {R}}).\)

In view of \((E_{3})\), we have

$$\begin{aligned} \frac{\mu (t )}{\mu (t-\vartheta (t))}= \frac{\mu (t-\vartheta (t)+\vartheta (t) )}{\mu (t-\vartheta (t))}\le \sup \limits _{\alpha \in [\vartheta ^{-}, \ \vartheta ^{+}]}{\mathbb {F}}(\alpha ) , \ \hbox {for all } t\in {\mathbb {R}}. \end{aligned}$$

Letting \(z\ge 1, \ \beta =\sup \limits _{t\in {\mathbb {R}}}\frac{1}{1- \vartheta '(t)} \times \sup \limits _{\alpha \in [\vartheta ^{-}, \ \vartheta ^{+}]}{\mathbb {F}}(\alpha )\) and \(s=t-\vartheta (t)\) give us

$$\begin{aligned} 0\le & {} \frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|\varphi (t-\vartheta (t))|\mu (t ){\rm d}t\\\le & {} \frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|\varphi (t-\vartheta (t))|\mu (t-\vartheta (t)){\rm d}t \sup \limits _{t\in {\mathbb {R}}}\frac{\mu (t )}{\mu (t-\vartheta (t))}\\\le & {} \frac{1}{\mu ([-z, \ z])}\int _{- z- \vartheta (-z) }^{z- \vartheta (z)}|\varphi (s)|\mu (s)\sup \limits _{t\in {\mathbb {R}}} \frac{1}{1- \vartheta '(t)}{\rm d}s\sup \limits _{t\in {\mathbb {R}}}\frac{\mu (t )}{\mu (t-\vartheta (t))}\\\le & {} \beta \frac{1}{\mu ([-z, \ z])}\int _{- (z+ \vartheta (- z)) }^{z- \vartheta (z)}|\varphi (s)|\mu (s) {\rm d}s \\\le & {} \beta \frac{\mu ([-(z+ \vartheta ^{+}), \ z+ \vartheta ^{+}]}{\mu ([-z, \ z])}\frac{1}{\mu ([-(z+ \vartheta ^{+}), \ z+ \vartheta ^{+}]}\int _{- (z+ \vartheta ^{+}) }^{ z+ \vartheta ^{+}}|\varphi (s)|\mu (s) {\rm d}s\\\le & {} \beta \sup \limits _{z\ge 1}\frac{\mu ([-(z+ \vartheta ^{+}), \ z+ \vartheta ^{+}])}{\mu ([-z, \ z])} \frac{1}{\mu ([-(z+ \vartheta ^{+}), \ z+ \vartheta ^{+}])}\int _{- (z+ \vartheta ^{+}) }^{ z+ \vartheta ^{+}}|\varphi (s)|\mu (s) {\rm d}s, \end{aligned}$$

which, together with the fact that

$$\begin{aligned} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-(z+ \vartheta ^{+}), \ z+ \vartheta ^{+}])}\int _{- (z+\vartheta ^{+}) }^{ z+ \vartheta ^{+}}|\varphi (s)|\mu (s) {\rm d}s=0, \end{aligned}$$

implies that

$$\begin{aligned} \lim \limits _{z\rightarrow +\infty } \frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|\varphi (t-\vartheta (t))|\mu (t ){\rm d}t =0, \ \hbox {and } \varphi (t-\vartheta (t))\in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}})}. \end{aligned}$$

This finishes the proof. \(\square\)

Lemma 2.2

(see [24, Lemma 2.2]) If \(\varphi \in {\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ) ,\) then, \(\int _{0}^{+\infty }|\sigma _{ij}(s)||\varphi (t-s)| {\rm d}s\in {\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ).\)

Lemma 2.3

For \(~i,j\in N\), if \(x_{j}\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}})\), then,

$$\begin{aligned} \beta _{ij}(t )F_{j}(x_{j}(t-\tau _{ij}(t)) ), {\bar{\beta }}_{ij}(t ){\bar{F}}_{j}(x_{j}(t ) )\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}), \end{aligned}$$

and

$$\begin{aligned} d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(x_{j}(t-u)){\rm d}u \ \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}). \end{aligned}$$

Proof

By Lemma 2.1, we have

$$\begin{aligned} x_{j}(t-\tau _{ij}(t)) \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}), \ i,j\in N. \end{aligned}$$

Furthermore, let

$$\begin{aligned} x_{j}(t-\tau _{ij}(t))=x_{j}^{h}(t)+x_{j}^{\varphi }(t), \ \hbox {where} \ x_{j}^{h}\in {{\rm AP} ({\mathbb {R}},{\mathbb {R}} )},\quad x_{j}^{\varphi }\in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )},\quad i,j\in N. \end{aligned}$$

Then, for all \(t\in {\mathbb {R}}\), we get

$$\begin{aligned}&\beta _{ij}(t )F_{j}(x_{j}(t-\tau _{ij}(t)) )\\&\quad =[\beta ^{h}_{ij}(t )+\beta ^{\varphi }_{ij}(t )]F_{j}(x_{j}^{h}(t)+x_{j}^{\varphi }(t) )\\&\quad = \beta ^{h}_{ij}(t )F_{j}(x_{j}^{h}(t) )+\beta ^{\varphi }_{ij}(t )F_{j}(x_{j}^{h}(t) )+\beta _{ij}(t )[F_{j}(x_{j}^{h}(t)+x_{j}^{\varphi }(t) )-F_{j}(x_{j}^{h}(t) )], \end{aligned}$$

where \(\beta ^{h}_{ij}\in {{\rm AP} ({\mathbb {R}},{\mathbb {R}} )}, \beta ^{\varphi }_{ij}\in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}, \ i,j\in N.\) Clearly,

$$\begin{aligned} \beta ^{h}_{ij}(t )F_{j}(x_{j}^{h}(t) )\in {\rm AP} ({\mathbb {R}},{\mathbb {R}}),\quad i, j\in N. \end{aligned}$$
(2.3)

Now, we choose constants \(\alpha _{j}\) and \(\eta _{j}\) such that

$$\begin{aligned} \alpha _{j}=\sup \limits _{t\in {\mathbb {R}}}|F_{j}(x_{j}^{h}(t) )|, \ \eta _{j}=\sup \limits _{t\in {\mathbb {R}}}|L^{F}_{j}\beta _{ij}(t )|. \end{aligned}$$

Consequently,

$$\begin{aligned} 0\le & {} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|\beta ^{\varphi }_{ij}(t )F_{j}(x_{j}^{h}(t) )+\beta _{ij}(t )[F_{j}(x_{j}^{h}(t)+x_{j}^{\varphi }(t) )\\&-F_{j}(x_{j}^{h}(t) )]|\mu (t ){\rm d}t\\\le & {} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|F_{j}(x_{j}^{h}(t) )||\beta ^{\varphi }_{ij}(t ) |\mu (t ){\rm d}t\\&+\lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|L^{F}_{j} \beta _{ij}(t )|| x_{j}^{\varphi }(t) |\mu (t ){\rm d}t\\\le & {} \alpha _{j}\lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z} |\beta ^{\varphi }_{ij}(t ) |\mu (t ){\rm d}t+\eta _{j}\lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z} | x_{j}^{\varphi }(t) |\mu (t ){\rm d}t\\= &\,0. \end{aligned}$$

It follows from (2.3) that

$$\begin{aligned} \beta _{ij}(t )F_{j}(x_{j}(t-\tau _{ij}(t)) )\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}), \ i,j\in N. \end{aligned}$$

Similarly,

$$\begin{aligned} {\bar{\beta }}_{ij}(t ){\bar{F}}_{j}(x_{j}(t ) )\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}),\ i,j\in N. \end{aligned}$$

Next, let \(h_{j} \in {{\rm AP} ({\mathbb {R}},{\mathbb {R}} )}\) and \(\varphi _{j} \in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}\) such that

$$\begin{aligned} x_{j}(t )=h_{j} (t)+ \varphi _{j} (t),\quad i,j\in N . \end{aligned}$$

Therefore,

$$\begin{aligned}&d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(x_{j}(t-u)){\rm d}u\nonumber \\&\quad =d_{ij}^{h}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(h_{j}(t-u)){\rm d}u+d_{ij}^{\varphi }(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(h_{j}(t-u)){\rm d}u\nonumber \\&\qquad +d_{ij} (t) \int _{0}^{\infty }\sigma _{ij}(u) [{\tilde{F}}_{j}(\varphi _{j}(t-u)+h_{j}(t-u))-{\tilde{F}}_{j}(h_{j}(t-u))]{\rm d}u, \end{aligned}$$
(2.4)

where \(d^{h}_{ij}\in {{\rm AP} ({\mathbb {R}},{\mathbb {R}} )}, d^{\varphi }_{ij}\in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}, t\in {\mathbb {R}}, \ i,j\in N.\) In view of \((E_1)\), the definition of \({\rm AP} ({\mathbb {R}},{\mathbb {R}} )\) and Lemma 2.2, we can deduce that

$$\begin{aligned} d_{ij}^{h}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}} _{j}(h_{j}(t-u)){\rm d}u \in { {\rm AP} ({\mathbb {R}},{\mathbb {R}} )}, \end{aligned}$$
(2.5)

and

$$\begin{aligned} \int _{0}^{+\infty }|\sigma _{ij}(s)||\varphi _{j} (t-s)| {\rm d}s\in {\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ),\quad i,j \in N. \end{aligned}$$
(2.6)

Hence,

$$\begin{aligned} 0\le & {} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|d_{ij}^{\varphi }(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(h_{j}(t-u)){\rm d}u\\&+d_{ij} (t) \int _{0}^{\infty }\sigma _{ij}(u) [{\tilde{F}}_{j}(\varphi _{j}(t-u)+h_{j}(t-u))-{\tilde{F}}_{j}(h_{j}(t-u))]{\rm d}u|\mu (t ){\rm d}t\\ {}\le & {} \sup \limits _{t\in {\mathbb {R}}}|\int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(h_{j}(t-u)){\rm d}u|\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}|d_{ij}^{\varphi }(t) |\mu (t ){\rm d}t\\&+d_{ij} ^{+}L^{{\tilde{F}}}_{j} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z}\int _{0}^{\infty }|\sigma _{ij}(u)| |\varphi _{j}(t-u)|{\rm d}u \mu (t ){\rm d}t \\= &\,0, \end{aligned}$$

which, together with (2.4) and (2.5), implies that

$$\begin{aligned} d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(x_{j}(t-u)){\rm d}u \ \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}),\quad i,j\in N. \end{aligned}$$

This proves Lemma 2.3. \(\square\)

Lemma 2.4

Define a nonlinear operator G by setting

$$\begin{aligned} (G\varphi )(t)= & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{i}(u){\rm d}u}\left[ \xi ^{-1}_{i}\sum ^n_{j=1}{\bar{\beta }}_{ij}(s){\bar{F}}_{j}(\xi _{j}\varphi _{j}(s ))+ \xi ^{-1}_{i}\sum ^n_{j=1}\beta _{ij}(s)F_{j}(\xi _{j}\varphi _{j}(s-\tau _{ij}(s)))\right. \right. \\&\left. \left. + \xi ^{-1}_{i}\sum _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(v) {\tilde{F}}_{j}(\xi _{j}\varphi _{j}(s-v)){\rm d}v+\xi ^{-1}_{i}I_{i}(s)\right] {\rm d}s\right\} , \varphi \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n}). \end{aligned}$$

Then \(G\varphi \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n})\).

Proof

According to \((E_{0})\) and \((E_{4})\), it is easily to see that \(G\varphi \in {\rm BC}({\mathbb {R}}, {\mathbb {R}}^{n})\) by the argument in Lemma 2.1 of [10].

From Lemma 2.3, we obtain that there are \(H_{j} \in {{\rm AP} ({\mathbb {R}},{\mathbb {R}} )}\) and \(\Phi _{j} \in {{\rm PAP}_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}\) such that

$$\begin{aligned}&\xi ^{-1}_{i}\sum ^n_{j=1}{\bar{\beta }}_{ij}(t){\bar{F}}_{j}(\xi _{j}\varphi _{j}(t )) + \xi ^{-1}_{i}\sum ^n_{j=1}\beta _{ij}(t)F_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t))) \\&\qquad + \xi ^{-1}_{i}\sum _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(v) {\tilde{F}}_{j}(\xi _{j}\varphi _{j}(t-v)){\rm d}v+\xi ^{-1}_{i}I_{i}(t)\\&\quad = H_{j} (t)+ \Phi _{j}(t) \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}), \ i,j\in N. \end{aligned}$$

Noting that \(M[a_{i }]>0\), using the theory of exponential dichotomy in [25], we get that

$$\begin{aligned} \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{i }(u){\rm d}u}H_{ j}(s){\rm d}s \in {\rm AP (\mathbb{R},\mathbb{R})} \end{aligned}$$
(2.7)

satisfies

$$\begin{aligned} y'(t)=-a_{i }(t)y(t)+H_{ j}(t), \ i, j \in N. \end{aligned}$$

Arguing as in the verification of [24, Lemma 2.2], one can show

$$\begin{aligned} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z} \int _{0}^{+\infty }e^{- {\tilde{a}}_{i} ^{-}u }|\Phi _{j} (t-u ) |{\rm d}u\mu (t ){\rm d}t=0, \quad i,j\in N. \end{aligned}$$

Then

$$\begin{aligned} 0\le & {} \lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z} \int _{-\infty }^{t }e^{- \int _{s}^{t}a _{i} ( \theta )d\theta }|\Phi _{j} (s )| {\rm d}s\mu (t ){\rm d}t \\ {}\le & {} K_{i}\lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z} \int _{-\infty }^{t }e^{- {\tilde{a}}_{i} ^{-}( t-s ) }|\Phi _{j} (s )| {\rm d}s\mu (t ){\rm d}t \\ {}= & {} K_{i}\lim \limits _{z\rightarrow +\infty }\frac{1}{\mu ([-z, \ z])}\int _{-z}^{z} \int _{0}^{+\infty }e^{- {\tilde{a}}_{i} ^{-}u }|\Phi _{j} (t-u ) |{\rm d}u\mu (t ){\rm d}t \\ {}= &\,0, \end{aligned}$$

and

$$\begin{aligned} \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{i }(u){\rm d}u}\Phi _{ j} (s){\rm d}s\in {\rm PAP}_{0}^{ \mu }({\mathbb {R}},{\mathbb {R}}),\quad i, j\in N . \end{aligned}$$

Combining with (2.7), it leads to

$$\begin{aligned} (G\varphi )_{ j}(t)= & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{i }(u){\rm d}u}H_{ j} (s){\rm d}s\\&+\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{i }(u){\rm d}u}\Phi _{ j} (s){\rm d}s\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}),\quad i, j\in N , \end{aligned}$$

and ends the proof of lemma 2.4. \(\square\)

3 Exponential stability of WPAP

Theorem 3.1

Assume that \((E_0)\), \((E_1)\), \((E_2)\), \((E_3)\) and \((E_4)\) hold. Then, system (1.1) has a unique WPAP solution \(x^{*}(t)\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n})\), and there is a constant \(\lambda \in (0, \ \min \{\kappa , \min \limits _{i\in N}{\tilde{a}}_{i}^{-}\})\) satisfying

$$\begin{aligned} x_{ i }(t) -x^{*}_{i}(t)=O(e^{-\lambda t}) \ \hbox { as} \ t\rightarrow +\infty , \ i \in N, \end{aligned}$$

where x(t) is a solution of system (1.1) with initial condition (2.1).

Proof

After making the following transformation,

$$\begin{aligned} y_{i}(t)=\xi ^{-1}_{i}x_{i}(t), i\in N, \end{aligned}$$

one can show

$$\begin{aligned} y_{i}'(t)= & {} -a_{i}(t)y_{i}(t )+ \xi ^{-1}_{i}\sum _{j=1}^{n}{\bar{\beta }}_{ij}(t){\bar{F}}_{j}(\xi _{j}y_{j}(t ))+ \xi ^{-1}_{i}\sum _{j=1}^{n}\beta _{ij}(t)F_{j}(\xi _{j}y_{j}(t-\tau _{ij}(t)))\nonumber \\&+ \xi ^{-1}_{i}\sum _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) {\tilde{F}}_{j}(\xi _{j}y_{j}(t-u)){\rm d}u +\xi ^{-1}_{i}I_{i}(t) , \quad i\in N. \end{aligned}$$
(3.1)

For \(\varphi , \psi \in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n})\), in view of \((E_{0})\), \((E_{1})\), \((E_{2})\), \((E_{3})\) and \((E_{4})\), we have

$$\begin{aligned}&| (G \varphi )_{i}(t) -(G \psi )_{i}(t) | \\&\quad = \left| \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{i}(u){\rm d}u}\left[ \xi ^{-1}_{i}\sum ^n_{j=1}{\bar{\beta }}_{ij}(s)({\bar{F}}_{j}(\xi _{j}\varphi _{j}(s))-{\bar{F}}_{j}(\xi _{j}\psi _{j}(s)))\right. \right. \\&\qquad + \xi ^{-1}_{i}\sum ^n_{j=1}\beta _{ij}(s)(F_{j}(\xi _{j}\varphi _{j}(s-\tau _{ij}(s)))-F_{j}(\xi _{j}\psi _{j}(s-\tau _{ij}(s))))\\&\left. \left. \qquad + \xi ^{-1}_{i}\sum _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) ({\tilde{F}}_{j}(\xi _{j}\varphi _{j}(s-u))-{\tilde{F}}_{j}(\xi _{j}\psi _{j}(s-u))){\rm d}u \right] {\rm d}s\right| \\&\quad \le \int ^t_{-\infty }e^{-\int _{s}^{t}{\tilde{a}}_{i} (u){\rm d}u}K_{i} \left[ \xi ^{-1}_{i}\sum ^n_{j=1}(| {\bar{\beta }}_{ij}(s)| L^{{\bar{F}}}_{j} +| \beta _{ij}(s)| L^{F}_{j} \right. \\&\left. \qquad + | d_{ij}(s)|\int _{0}^{\infty }|\sigma _{ij}(u)|{\rm d}u L^{{\tilde{F}}}_{j} )\xi _{j} \right] {\rm d}s \Vert \varphi (t)-\psi (t)\Vert _{\infty } \\&\quad \le \int ^t_{-\infty }e^{-\int _{s}^{t}{\tilde{a}}_{i} (u){\rm d}u} [ {\tilde{a}}_{i}(s)-\gamma _{i}] {\rm d}s \Vert \varphi (t)-\psi (t)\Vert _{\infty } \\&\quad \le \left[ \int ^t_{-\infty }e^{-\int _{s}^{t}{\tilde{a}}_{i}(u){\rm d}u} d\left( -\int _{s}^{t}{\tilde{a}}_{i}(u){\rm d}u\right) -\frac{\gamma _{i}}{2}\int ^t_{-\infty }e^{-\int _{s}^{t}{\tilde{a}}_{i}(u){\rm d}u} {\rm d}s \right] \Vert \varphi (t)-\psi (t)\Vert _{\infty }\\&\quad \le \max \limits _{ i \in N}\left\{ 1-\frac{\gamma _{i}}{2 {\tilde{a}}_{i} ^{+}}\right\} \Vert \varphi (t)-\psi (t)\Vert _{\infty } , \end{aligned}$$

which, together with the fact that \(0<\max \limits _{ i \in N}\{ 1-\frac{\gamma _{i}}{2 {\tilde{a}}_{i} ^{+}}\}<1,\) entails that the mapping G is contract, and has a unique fixed point

$$\begin{aligned} y^{*}=\{y_{i}^{*}(t)\}\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{n}), \ G y^{* }=y^{* }. \end{aligned}$$

Furthermore, (1.1) and (3.1) imply that (1.1) has a unique WPAP solution \(x^{* }=\{x_{i}^{* }(t)\} =\{\xi _{i}y_{i}^{*}(t)\}\) .

Finally, by an almost identical proof to that of Theorem 3.2 in [26], one can pick constants \(\lambda \in (0, \ \min \{\kappa , \min \limits _{i\in N}{\tilde{a}}_{i}^{-}\})\) and \(M> \sum \nolimits _{j=1}^{n}K_{j}^{S}+1\) such that for \(i\in N,\)

$$\begin{aligned}&\sup \limits _{t\in {\mathbb {R}}}\left\{ \lambda -{\tilde{a}}_{i}(t)+K_{i}\left[ \xi ^{-1}_{i}\sum ^n_{j=1}\left( | {\bar{\beta }}_{ij}(t)| L^{{\bar{F}}}_{j}+| \beta _{ij}(t)| L^{F}_{j} e^{ \lambda \tau _{ij} (t) }\right. \right. \right. \\&\left. \left. \left. \quad + | d_{ij}(t)|\int _{0}^{\infty }|\sigma _{ij}(u)|e^{ \lambda u}{\rm d}u L^{{\tilde{F}}}_{j} \right) \xi _{j} \right] \right\} <0 \end{aligned}$$

and

$$\begin{aligned} \Vert x(t)-x^{*}(t)\Vert \le M\{\sup \limits _{t\le 0 }\max \limits _{i\in N }\xi _{i}^{-1}|\varphi _{i} (t) -x^{*}_{i}(t)|\}e^{-\lambda t} \hbox { for all } t > 0 , \end{aligned}$$

which ends the proof of Theorem 3.1.\(\square\)

4 An example and its numerical simulations

Set

$$\begin{aligned} \left\{ \begin{array}{ll} n=2, \ {\bar{F}}_{i}(x)=0, \ F_{i}(u)={\tilde{F}}_{i}(u)=\frac{1}{20}\arctan u , a_{1}(t)= \frac{1}{10}\left( 1+\frac{3}{2}\sin t\right) , \\ a_{2}(t)= \frac{1}{10}\left( 1+\frac{3}{2}\cos t\right) , {\bar{\beta }} _{ij}(t) =0, \beta _{ij}(t) = \frac{1}{5} \sin 2t,d _{ij}(t) = \frac{1}{6} \cos 2t , \\ I_{i}(t)= (20+i)|\cos t| +p(t), \sigma _{ij } (t) = \frac{1}{10} e^{-2t}, \tau _{ij } (t) = \frac{1}{i+j} (1+\sin 2t)\\ p(s)=e^{-s} \ \hbox {for all } s\ge 0, p(s)=1 \ \hbox {for all } s< 0. \end{array}\right. \end{aligned}$$
(4.1)

Obviously, one can select

$$\begin{aligned} {\tilde{a}}_{i} (t)= \frac{1}{10}, \quad \xi _{i}= 1, T=\pi , \quad \kappa =1, \quad L^{\bar{F}}_{i}=0, \quad L^{F}_{i}= L^{{\tilde{F}}}_{i} =\frac{1}{20}, \quad K_{i}=e^{\frac{3}{10} }, \quad i,\,j=1,2, \end{aligned}$$

and

$$\begin{aligned} \mu (t)=e^{t} \ \hbox {for all } t\ge 0, \mu (t)=1 \ \hbox {for all } t< 0\end{aligned}$$

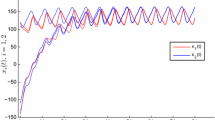
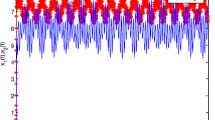
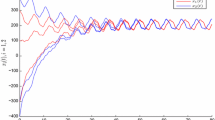
such that CNNs (1.1) with (4.1) obey all the conditions mentioned in Sect. 2. Then, system (1.1) has a unique WPAP solution \(x^{*}(t)\in {\rm PAP}^{ \mu }({\mathbb {R}},{\mathbb {R}}^{2})\), and all solutions of system (1.1) converge exponentially to \(x^{*}(t)\) as \(t\rightarrow +\infty\). Here, the exponential convergence rate \(\lambda \approx 0.01\). Figure 1 gives the state response of the neural network CNNs (1.1) with (4.1) and three groups of different initial values which are \((17,-14),(-12, 15),(11,-12)\).

Fig. 1
figure 1

Numerical solutions of CNNs (1.1) with (4.1) for three groups of different initial values

Full size image

Remark 4.1

It is well known that the exponential stability of WPAP solutions plays an important role in describing the dynamics of differential equations. In this article, by means of the fixed point theorem and some differential inequality technique, some new criteria are derived for the existence and exponential stability of WPAP solutions of the considered model. It is also worth pointing out that the sufficient condition is simple and easy to verify. As shown above, the obtained results are improvement and extension of some previously published related results in [9–18, 24–28]. In addition, the method in this paper can also be applied to the study of other CNNs models.