1 Introduction

During the 1990s, Bouzerdoum and Pinter [1–3] proposed shunting inhibitory cellular neural networks (SICNNs) to describe a new class of biologically inspired cellular neural networks (CNNs) in which shunting inhibition mediates the synaptic interactions among neurons. Therefore, SICNNs have shown great potential as information processing systems [4–11]. Recently, the exponential stability of the anti-periodic solutions can describe the global dynamics of delay systems since the convergence rate can be estimated [12–14], and a lot of research work is focused on this topic of SICNNs with mixed delays [15–20]. In particular, the following dynamical system:

$$\begin{aligned} x'_{ij}(t)&= -d_{ij}(t)x_{ij}(t )-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)F(x_{kl}(t-\tau _{kl}(t)))x_{ij}(t) \nonumber \\&\quad-\sum \limits _{B_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(t) \int _{0}^{+\infty }\sigma _{ij}(u) G(x_{kl}(t-u))\hbox {d}ux_{ij}(t)+I_{ij}(t),\ \end{aligned}$$
(1.1)

has been used to describe SICNNs with mixed delays involving time-varying delays \(\tau _{ij}(t)\) and unbounded distributed delay kernels \(\sigma _{ij }(u)\), where \(ij\in N=\{11, 12, \ldots , mn\},\) \(C_{ij}\) designates the cell at the (i, j) position of the lattice. The \( \varrho \) neighborhood \(N_\varrho (i, j)\) of \(C_{ij}\) is given as

$$N_\varrho (i, j) = \Big \{C_{kl}: \max (| k - i |, | l - j |)\le \varrho , 1 \le k \le m, 1 \le l \le n\Big \},\quad \varrho =r, q.$$

\(x(t)=\{x_{ij}(t)\}=(x_{11}(t), x_{12}(t), \ldots , x_{mn}(t))^{T}\) corresponds to the state vector, \(d_{ij}(t)\) represents the rate of decay, and F and G are the signal transmission functions. The detailed biological accounts on the coefficients \(C_{ij}^{kl} (t)\) and \(B_{ij}^{kl}(t)\) can be found in [21].

As mentioned by Al-Islam et al. [22], the research of weighted pseudo-anti-periodic differential equations has academic significance in both dynamical theory and its practical application. Moreover, weighted pseudo-periodicity and weighted pseudo-anti-periodicity were first introduced in [22] to generalized the well-known notions of periodicity and that of anti-periodicity, respectively. In addition, in view of the biological mechanism of system (1.1), it is interesting and desirable to construct neural network models which are capable of producing weighted pseudo-anti-periodic solution. Nevertheless, the weighted pseudo-anti-periodic problem for SICNNs with mixed delays has not been adequately studied. For the above reasons, in this paper, we aim to provide a criterion to guarantee that all state vectors of (1.1) converge to a weighted pseudo-anti-periodic solution with a positive exponential convergence rate.

2 Preliminary results

To further our discussion, \({\mathbb{U}}\) designates the set of locally integrable functions (weights) \(\mu :{\mathbb {R}}\rightarrow (0, \ +\infty )\) satisfying

$$\begin{aligned} \lim \limits _{\chi\rightarrow +\infty }\mu ([-\chi , \ \chi ])=+\infty , \ \text{ where } \ \mu ([-\chi , \ \chi ]):=\int _{-\chi }^{\chi }\mu (x)\hbox {d}x \ (\chi >0).\end{aligned}$$

Define the following notations:

$$\begin{aligned} |x|= & {} \{|x_{ij}|\}, \ \Vert x \Vert =\max \limits _{ ij\in N} |x_{i j} |, \ Q^{+}=\sup \limits _{t\in {\mathbb {R}}}|Q(t)|, \ Q^{-}=\inf \limits _{t\in {\mathbb {R}}}|Q(t)|, \\ {\mathbb {U}}_{\infty }:= & {} \left\{ \mu |\mu \in {\mathbb {U}},\inf \limits _{x\in {\mathbb {R}}}\mu (x)=\mu _{0}>0 \right\},\end{aligned}$$

and

$$\begin{aligned} {\mathbb {U}}^{+}_{\infty }:= & {} \left\{ \mu |\mu \in {\mathbb {U}} _{\infty }, \limsup \limits _{|x|\rightarrow +\infty }\frac{\mu (x+\alpha )}{\mu (x)}<+\infty , \right. \\&\left. \limsup \limits _{\chi \rightarrow +\infty }\frac{\mu ([-(\chi +\alpha ), \ \chi +\alpha ])}{\mu ([-\chi , \ \chi ])} <+\infty , \ \forall \alpha \in {\mathbb {R}} \right\}.\end{aligned}$$

Furthermore, let \(BC({\mathbb {R}},{\mathbb {R}}^{mn})\) denote the bounded continuous function set, which is a Banach space with the supremum norm \(\Vert f\Vert _{\infty } := \sup \nolimits _{ t\in {\mathbb {R}}} \Vert f (t)\Vert\). Also, denote

$$\begin{aligned} 0<T< +\infty , \ AP^{T}({\mathbb {R}},{\mathbb {R}}^{mn}) := \left\{ w\in BC({\mathbb {R}},{\mathbb {R}}^{mn}) | w(t+T)=-w(t) \quad \text{ for } \text{ all } t\in {\mathbb {R}} \right\},\end{aligned}$$

and

$$\begin{aligned} PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}}^{mn})=\left\{ \varphi \in BC({\mathbb {R}},{\mathbb {R}}^{mn})|\lim \limits _{\chi \rightarrow +\infty }\frac{1}{\mu ([-\chi , \ \chi ])} \int _{-\chi }^{\chi }\mu (t)|\varphi (t)|\hbox {d}t=0\right\}.\end{aligned}$$

A function \(W\in {BC({\mathbb {R}},{\mathbb {R}}^{mn})}\) is called weighted pseudo-anti-periodic if it can be expressed as

$$\begin{aligned} W=Q_{1}+Q_{2}, \end{aligned}$$

where \(Q_{1}\in {AP^{T}({\mathbb {R}},{\mathbb {R}}^{mn})}\) is the T-anti-periodic component and \(Q_{2}\in {PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}}^{mn})}\) is the ergodic perturbation. In particular, fixed \(\mu \in {\mathbb {U}}^{+}_{\infty }\), \((PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{mn}),\Vert .\Vert _{\infty })\) become a Banach space and \(AP^{T }({\mathbb {R}},{\mathbb {R}}^{mn})\) is a proper subset of \(PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{mn})\) [22].

We define the following initial condition:

$$\begin{aligned} \{x_{ij}(s)\}=\{\varphi _{ij}(s)\}, \ s\in (-\infty , \ 0], \ \{\varphi _{ij}\}\in BC({\mathbb {R}},{\mathbb {R}}^{mn}).\end{aligned}$$
(2.1)

For \(kl,ij \in N,\) it will be supposed that \(\sigma _{ij}\in BC([0, +\infty ), {\mathbb {R}})\) , \(|\sigma _{ij}(s)|e^{\kappa s}\) is integrable on \([0, +\infty )\) for \(\kappa >0\), \(d_{ij}, C_{ij}^{kl}\), \(B_{ij}^{kl}\in C({\mathbb {R}},{\mathbb {R}} ), \ I_{ij}\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}} )\), \(\tau _{kl} \in C ^{1} ({\mathbb {R}}, \ [0, \ +\infty ) )\), and

$$\begin{aligned} d_{ij}(s+T)= & {} d_{ij}(s ), \tau _{kl}(s+T) = \tau _{kl}(s ), \tau _{kl}'(s )<1, \forall s \in {\mathbb {R}}, \end{aligned}$$
(2.2)
$$\begin{aligned} C_{ij}^{kl} (s)= & {} C_{ij}^{kl, h} (s)+C_{ij}^{kl,\varphi } (s), \ B_{ij}^{kl} (s) =B_{ij}^{kl, h} (s)+B_{ij}^{kl,\varphi } (s) , \forall s \in {\mathbb {R}}, \end{aligned}$$
(2.3)

where \(C_{ij}^{kl, h} , B_{ij}^{kl, h} \in {BC({\mathbb {R}},{\mathbb {R}} )}, C_{ij}^{kl,\varphi }, B_{ij}^{kl,\varphi }\in {PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}\) satisfy

$$\begin{aligned} C_{ij}^{kl,h} (s+T)F (u)=C_{ij}^{kl,h}(s)F(-u), \ \forall s,u \in {\mathbb {R}} , \end{aligned}$$
(2.4)

and

$$\begin{aligned} \left. \begin{array}{rcl} B_{ij}^{kl,h}(s+T) = -B_{ij}^{kl,h} (s ) , G (u) = - G (-u) \\ \left( \text{ or } B_{ij}^{kl,h}(s+T) = B_{ij}^{kl,h}(s ) , G (u) = G (-u)\right) \end{array} \right\} , \quad \forall s,u \in {\mathbb {R}} \end{aligned}$$
(2.5)

For \(ij \in N\), the following assumptions will be adopted:

\((S_0)\) there exist \(\tilde{d}_{ij} \in BC({\mathbb {R}}, (0, \ +\infty ) )\) and \(K_{ij}>0\) such that

$$\begin{aligned} e ^{ -\int _{s}^{t}d_{ij}(u)\hbox {du}}\le K_{ij} e ^{ -\int _{s}^{t}\tilde{d}_{ij}(u)\hbox {d}u}, \ \forall \ t,s\in {\mathbb {R}} , \ t-s\ge 0. \end{aligned}$$

\((S_1)\) F and G are global Lipschitz with Lipschitz constants \(L ^{F}\) and \(L^{G}\), and

$$\begin{aligned} \sup \limits _{u\in {\mathbb {R}}}|F(u ) |:= M_{F}<+\infty , \ \ \sup \limits _{u\in {\mathbb {R}}}|G(u ) |:= M_{G}<+\infty . \end{aligned}$$

\((S_{2})\) \(\mu \in {\mathbb {U}}^{+}_{\infty }\), and \({\mathbb {F}}(\alpha )=\sup \nolimits _{x\in \mathbb { R}}\frac{\mu (x+\alpha )}{\mu (x)}\) is bounded on arbitrary closed subinterval of \([0, \ +\infty ).\) \((S_3)\) there exist positive constants \(\gamma _{ij}\) and \(\delta\) such that

$$\begin{aligned} -\gamma _{ij}&= \sup \limits _{t\in R} \left\{ - \tilde{d}_{ij} (t) +K_{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(t)|\left( M_{F} +L^{F} \frac{I}{1-\delta }\right) \right. \right. \\&\quad+\sum \limits _{B_{kl}\in N_{q}(i,j)}|B_{ij}^{kl}(t)| \left( \int _{0}^{+\infty }|\sigma _{ij}(u)| \hbox {d}uM_{G} \right. \\&\quad\left. \left. \left. +\int _{0}^{+\infty }|\sigma _{ij}(u)|L ^{G}\hbox {d}u\frac{I}{1-\delta }\right) \right] \right\}, \ ij\in N, \end{aligned}$$

where \(I=\max \nolimits _{ij\in N} \left\{ K_{ij}\frac{I^{+}_{ij}}{\tilde{d}_{ij} ^{-}}\right\}\), and

$$\begin{aligned} \delta =\max \limits _{ij\in N} \bigg \{K_{ij} \frac{\sum \nolimits _{C_{kl}\in N_{r}(i,j)} C_{ij}^{kl} \ ^{+} M_{F} + \sum \nolimits _{B_{kl}\in N_{q}(i,j)} B_{ij}^{kl} \ ^{+} \int _{0}^{+\infty }|\sigma _{ij}(u)| \hbox {d}uM_{G}}{\tilde{d}_{ij}^{-}}\bigg \} < 1. \end{aligned}$$

Lemma 2.1

Assume that \(f\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}})\), \(\rho \in C^{1} ({\mathbb {R}}, \ {\mathbb {R}} )\) is \(T-\) periodic, \(\rho (s)\ge 0\) and \(\rho '(s)<1\), \(\forall s\in {\mathbb {R}}\). Then, \(f(s-\rho (s))\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}).\)

Proof

Let

$$\begin{aligned} f=h+\varphi , h\in AP^{T}({\mathbb {R}},{\mathbb {R}} ), \varphi \in PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ) . \end{aligned}$$

Clearly, \(h(t-\rho (t))\in AP^{T }({\mathbb {R}},{\mathbb {R}}).\) In view of \((S_{2})\), we get

$$\begin{aligned} \frac{\mu (t )}{\mu (t-\rho (t))}= \frac{\mu (t-\rho (t)+\rho (t) )}{\mu (t-\rho (t))}\le \sup \nolimits _{\alpha \in [\rho ^{-}, \ \rho ^{+}]}{\mathbb {F}}(\alpha ) , \ \text{ for } \text{ all } t\in {\mathbb {R}}. \end{aligned}$$

Letting \(\beta =\sup \nolimits _{t\in {\mathbb {R}}}\frac{1}{1- \rho '(t)} \times \sup \nolimits _{\alpha \in [\rho ^{-}, \ \rho ^{+}]}{\mathbb {F}}(\alpha )\) and \(s=t-\rho (t)\) give us

$$\begin{aligned} 0\le & {} \frac{1}{\mu ([-\chi , \ \chi ])}\int _{-\chi }^{\chi }|\varphi (t-\rho (t))|\mu (t )\hbox {d}t\\\le & {} \frac{1}{\mu ([-\chi , \ \chi ])}\int _{-\chi }^{\chi }|\varphi (t-\rho (t))|\mu (t-\rho (t))\hbox {d}t \sup \limits _{t\in {\mathbb {R}}}\frac{\mu (t )}{\mu (t-\rho (t))}\\\le & {} \frac{1}{\mu ([-\chi , \ \chi ])}\int _{- \chi - \rho (-\chi )}^{\chi - \rho (\chi )}|\varphi (s)|\mu (s)\sup \limits _{t\in {\mathbb {R}}} \frac{1}{1- \rho '(t)}\hbox {d}s\sup \limits _{t\in {\mathbb {R}}}\frac{\mu (t)}{\mu (t-\rho (t))}\\\le & {} \beta \frac{1}{\mu ([-\chi , \ \chi ])}\int _{- (\chi + \rho (- \chi )) }^{\chi - \rho (\chi )}|\varphi (s)|\mu (s) \hbox {d}s \\\le & {} \beta \frac{\mu ([-(\chi + \rho ^{+}), \ \chi + \rho ^{+}])}{\mu ([-\chi , \ \chi ])}\frac{1}{\mu ([-(\chi + \rho ^{+}), \ \chi + \rho ^{+}])}\int _{- (\chi + \rho ^{+}) }^{ \chi + \rho ^{+}}|\varphi (s)|\mu (s) \hbox {d}s \\\le & {} \beta \sup \limits _{\chi \ge 1}\frac{\mu ([-(\chi + \rho ^{+}), \ \chi + \rho ^{+}])}{\mu ([-\chi , \ \chi ])} \frac{1}{\mu ([-(\chi + \rho ^{+}), \ \chi + \rho ^{+}])}\int _{- (\chi + \rho ^{+}) }^{ \chi + \rho ^{+}}|\varphi (s)|\mu (s) \hbox {d}s, \end{aligned}$$

which, together with the fact that

$$\begin{aligned} \lim \limits _{\chi \rightarrow +\infty }\frac{1}{\mu ([-(\chi + \rho ^{+}), \ \chi + \rho ^{+}])}\int _{- (\chi + \rho ^{+}) }^{ \chi + \rho ^{+}}|\varphi (s)|\mu (s) \hbox {d}s=0, \end{aligned}$$

implies that

$$\begin{aligned} \lim \limits _{\chi \rightarrow +\infty } \frac{1}{\mu ([-\chi , \ \chi ])}\int _{-\chi }^{\chi }|\varphi (t-\rho (t))|\mu (t )\hbox {d}t =0, \ \text{ and } \varphi (t-\rho (t))\in {PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}})}. \end{aligned}$$

This proves Lemma 2.1. \(\square\)

Lemma 2.2

If \(\varphi \in PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ) ,\) then, \(\int _{0}^{+\infty }|\sigma _{ij}(s)||\varphi (t-s)| \hbox {d}s\in PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ).\)

Proof

Obviously, one can obtain

$$\begin{aligned}&\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\bigg (\int _{0}^{+\infty }|\sigma _{ij}(s)|| \varphi (t-s)|\mu (t)\hbox {d}s\bigg )\hbox {d}t \\&\quad =\int _{0}^{+\infty }|\sigma _{ij}(s)|\bigg (\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}| \varphi (t-s)|\mu (t)\hbox {d}t\bigg )\hbox {d}s. \end{aligned}$$

Let \(M^{\varphi }=\sup \nolimits _{\theta \in {\mathbb {R}}}| \varphi (\theta )|\) and \(\sigma _{ij}^{*}=\int _{0}^{+\infty }|\sigma _{ij}(s)| \hbox {d}s\), we get

$$\begin{aligned}&\int _{0}^{+\infty }|\sigma _{ij}(s)|\bigg (\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}| \varphi (t-s)|\mu (t)\hbox {d}t\bigg )\hbox {d}s \\&\quad \le \int _{0}^{+\infty }|\sigma _{ij}(s)|\bigg (\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \mu (t)\hbox {d}t\bigg )\hbox {d}sM^{\varphi }=\sigma _{ij}^{*}M^{\varphi }. \end{aligned}$$

For any sequence \(\{r_{n}\}_{n=1}^{+\infty }\) satisfying

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty }r_{n}=+\infty , \ \ r_{n}>0, \ n=1,2,\ldots , \end{aligned}$$

we denote

$$\begin{aligned} f_{n}(s)=|\sigma _{ij}(s)|\frac{1}{\mu ([-r_{n}, \ r_{n}])}\int _{-r_{n}}^{r_{n}}| \varphi (t-s)|\mu (t)\hbox {d}t, \ n=1,2,\ldots . \end{aligned}$$

Then,

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty }f_{n}(s)=0 , \ \text{ and } \ |f_{n}(s)|\le M^{\varphi }|\sigma _{ij}(s)|, \ \text{ for } \text{ all } \ s\in [0, \ +\infty ), \ n=1,2,\ldots . \end{aligned}$$

According to the Lebesgue dominated convergence theorem, we have

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty }\int _{0}^{+\infty }|\sigma _{ij}(s)|\bigg (\frac{1}{\mu ([-r_{n}, \ r_{n}])}\int _{-r_{n}}^{r_{n}}| \varphi (t-s)|\mu (t)\hbox {d}t\bigg )\hbox {d}s=0, \end{aligned}$$

which entails that

$$\begin{aligned}&\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\bigg (\int _{0}^{+\infty }|\sigma _{ij}(s)|| \varphi (t-s)|\mu (t)\hbox {d}s\bigg )\hbox {d}t \\&\quad =\lim \limits _{r\rightarrow +\infty } \int _{0}^{+\infty }|\sigma _{ij}(s)|\bigg (\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}| \varphi (t-s)|\mu (t)\hbox {d}t\bigg )\hbox {d}s=0. \end{aligned}$$

Thus, \(\int _{0}^{+\infty }|\sigma _{ij}(s)|\varphi (t-s) \hbox {d}s\in PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ).\) This completes the proof. \(\square\)

Lemma 2.3

Let \(x_{ij}\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}})\) for all \(ij \in N\). Then,

$$\begin{aligned} x_{ij}(t)C_{ij}^{kl} (t) F (x_{kl}(t-\tau _{kl}(t)) )\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), \end{aligned}$$

and

$$\begin{aligned} x_{ij}(t)B_{ij}^{kl} (t) \int _{0}^{\infty }\sigma _{ij}(u) G(x_{kl}(t-u)){\hbox{d}}u \ \in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), \ ij,kl\in N. \end{aligned}$$

Proof

From Lemma 2.1, we get

$$\begin{aligned} x_{kl}(t-\tau _{kl}(t)) \in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), \ ij,kl\in N. \end{aligned}$$

Furthermore, let

$$\begin{aligned} x_{ij}(t )=x_{ij}^{ h}(t)+x_{ij}^{ \varphi }(t), \ \text{ where } \ x_{ij}^{ h}\in {AP^{T}({\mathbb {R}},{\mathbb {R}} )}, \quad x_{ij}^{ \varphi }\in {PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}, \;ij\in N, \end{aligned}$$

and

$$\begin{aligned} x_{kl}(t-\tau _{kl}(t))=x_{kl}^{kl,h}(t)+x_{kl}^{kl,\varphi }(t), \ \text{ where } \ x_{kl}^{kl,h}\in {AP^{T}({\mathbb {R}},{\mathbb {R}} )}, \quad x_{kl}^{kl,\varphi }\in {PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}, ij\in N. \end{aligned}$$

Then, for all \(t\in {\mathbb {R}}\), we obtain

$$\begin{aligned}&x_{ij} (t)C_{ij}^{kl} (t) F \left( x_{kl}\left( t-\tau _{kl}(t)\right) \right) \\& =\,x_{ij} (t)\left[ C_{ij}^{kl, h} (t) +C_{ij}^{kl, \varphi } (t) \right] F \left( x_{kl}^{kl,h}(t)+x_{kl}^{kl,\varphi }(t) \right) \\& =\,x_{ij}^{ h}(t)C_{ij}^{kl, h} (t)F \left( x_{kl}^{kl,h}(t) \right) +x_{ij}^{ \varphi }(t)C_{ij}^{kl, h} (t)F \left( x_{kl}^{kl,h}(t) \right) \\&\quad +\,x_{ij} (t)C_{ij}^{kl, \varphi } (t)F \left( x_{kl}^{kl,h}(t) \right) \\&\quad +\,x_{ij} (t)C_{ij}^{kl } (t)\left[ F \left( x_{kl}^{kl,h}(t)+x_{kl}^{kl,\varphi }(t) \right) -F \left( x_{kl}^{kl,h}(t) \right) \right] , ij,kl\in N. \end{aligned}$$

Clearly, (2.4) gives us

$$\begin{aligned} C_{ij}^{kl, h} (t+T )F \left( x_{kl}^{kl,h}(t+T) \right)&= C_{ij}^{kl, h} (t+T )F \left( -x_{kl}^{kl,h}(t) \right) \\&= C_{ij}^{kl, h} (t)F \left( x_{kl}^{kl,h}(t) \right) , \ \text{ for } \text{ all } t\in {\mathbb {R}}, \end{aligned}$$

and

$$\begin{aligned} x_{ij}^{ h}(t)C_{ij}^{kl, h} (t)F \left( x_{kl}^{kl,h}(t) \right) \in AP^{T }({\mathbb {R}},{\mathbb {R}}), ij, kl\in N. \end{aligned}$$
(2.6)

Now, we choose constants \(\alpha _{ij}^{kl }, \ \beta _{ij}^{kl}\) and \(\eta _{ij}^{kl}\) such that

$$\alpha _{ij}^{kl}=\sup \limits _{t\in {\mathbb {R}}}|x_{ij} (t)F \left( x_{kl}^{kl,h}(t) \right) |, \ \beta _{ij}^{kl}=\sup \limits _{t\in {\mathbb {R}}}|C_{ij}^{kl, h} (t)F \left( x_{kl}^{kl,h}(t) \right) |, \ \eta _{ij}^{kl}=\sup \limits _{t\in {\mathbb {R}}}|L^{F}x_{ij} (t)C_{ij}^{kl } (t)|.$$

Consequently,

$$\begin{aligned} 0\le & \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\left|x_{ij} (t)C_{ij}^{kl, \varphi } (t)F \left( x_{kl}^{kl, h}(t) \right) \right.\\&\left.+x_{ij} (t)C_{ij}^{kl } (t)\left[ F \left( x_{kl}^{kl,h}(t)+x_{kl}^{kl,\varphi }(t) \right) - F \left( x_{kl}^{kl,h}(t) \right) \right] \right|\mu (t )\hbox {d}t\\\le & \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\left|x_{ij} (t)F \left( x_{kl}^{kl,h}(t) \right) ||C_{ij}^{kl, \varphi } (t) \right|\mu (t)\hbox {d}t\\&+\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\left|L^{F}x_{ij} (t) C_{ij}^{kl } (t) || x_{kl}^{kl,\varphi }(t) \right|\mu (t )\hbox {d}t\\\le &\, \alpha _{ij}^{kl}\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\left |C_{ij}^{kl, \varphi } (t) \right|\mu (t )\hbox {d}t \\&+\eta _{ij}^{kl}\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \left| x_{kl}^{kl,\varphi }(t) \right|\mu (t )\hbox {d}t\\= \,&0, \end{aligned}$$

and

$$\begin{aligned} 0\le & {} \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\left|x_{ij}^{ \varphi }(t)C_{ij}^{kl, h} (t)F \left( x_{kl}^{kl,h}(t) \right) \right|\mu (t )\hbox {d}t\\\le & {} \beta _{ij}^{kl}\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \left|x_{ij}^{ \varphi }(t) \right|\mu (t )\hbox {d}t \\= & {} 0. \end{aligned}$$

This, together with (2.6), leads to

$$\begin{aligned} x_{ij} (t)C_{ij}^{kl } (t)F (x_{ij}(t-\tau _{kl}(t)) )\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), \ ij,kl\in N. \end{aligned}$$

Next, for \(ij, kl\in N\), we get

$$\begin{aligned}&x_{ij} (t)B_{ij}^{kl } (t) \int _{0}^{\infty }\sigma _{ij}(u) G\left( x_{kl}(t-u)\right) \hbox {d}u \nonumber \\&= x_{ij} ^{h}(t)B_{ij}^{kl,h } (t) \int _{0}^{\infty }\sigma _{ij}(u) G\left( x ^{h}_{kl}(t-u)\right) \hbox {d}u x_{ij}^{\varphi }(t)B_{ij}^{kl,h } (t) \int _{0}^{\infty }\sigma _{ij}(u) G\left( x ^{h}_{kl}(t-u)\right) \hbox {d}u \nonumber \\&\quad +x_{ij} (t)B_{ij}^{kl,\varphi } (t) \int _{0}^{\infty }\sigma _{ij}(u) G \left( x^{h}_{kl}(t-u)\right) \hbox {d}u\\&\quad +x_{ij} (t)B_{ij}^{kl } (t) \int _{0}^{\infty }\sigma _{ij}(u) \left[ G\left( x^{\varphi }_{kl}(t-u)+x^{h}_{kl}(t-u)\right) -G\left( x ^{h}_{kl}(t-u)\right) \right] \hbox {d}u, \forall \ t\in {\mathbb {R}}.\nonumber \end{aligned}$$
(2.7)

It follows from (2.5) and Lemma 2.2 that

$$\begin{aligned} x_{ij} ^{h}(t)B_{ij}^{kl,h } (t) \int _{0}^{\infty }\sigma _{ij}(u) G\left( x^{h}_{kl}(t-u)\right) du \in { AP^{T}({\mathbb {R}},{\mathbb {R}} )}, \end{aligned}$$
(2.8)

and

$$\begin{aligned} \int _{0}^{+\infty }|\sigma _{ij}(u)||x^{\varphi }_{kl}(t-u)| \hbox {d}u\in PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} ), ij,kl \in N. \end{aligned}$$
(2.9)

Hence,

$$\begin{aligned} 0\le & {} \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}|x_{ij} (t)B_{ij}^{kl,\varphi } (t) \int _{0}^{\infty }\sigma _{ij}(u) G \left( x ^{h}_{kl}(t-u)\right) \hbox {d}u\\&+x_{ij} (t)B_{ij}^{kl } (t) \int _{0}^{\infty }\sigma _{ij}(u) \left[ G\left( x^{\varphi }_{kl}(t-u)+x^{h}_{kl}(t-u)\right) -G\left( x^{h}_{kl}(t-u)\right) \right] \hbox {d}u|\mu (t )\hbox {d}t\\\le & {} \sup \limits _{t\in {\mathbb {R}}}|x_{ij} (t) \int _{0}^{\infty }\sigma _{ij}(u) G \left( x^{h}_{kl}(t-u)\right) \hbox {d}u|\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}|B_{ij}^{kl, \varphi }(t) |\mu (t)\hbox {d}t\\&+B_{ij}^{kl} \ ^{+} x_{ij}^{+}L^{G} \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}\int _{0}^{\infty }|\sigma _{ij}(u)| |x^{\varphi }_{kl}(t-u)|\hbox {d}u \mu (t )\hbox {d}t \\=&\, 0, \end{aligned}$$

and

$$\begin{aligned} 0\le & {} \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}|x_{ij}^{\varphi }(t)B_{ij}^{kl,h } (t) \int _{0}^{\infty }\sigma _{ij}(u) G\left( x^{h}_{kl}(t-u)\right) \hbox {d}u|\mu (t )\hbox {d}t\\\le & {} \sup \limits _{t\in {\mathbb {R}}}|B_{ij}^{kl,h } (t) \int _{0}^{\infty }\sigma _{ij}(u) G\left( x^{h}_{kl}(t-u)\right) \hbox {d}u|\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r}|x_{ij} ^{\varphi }(t) |\mu (t )\hbox {d}t \\=\,& 0, \end{aligned}$$

which, together with (2.7) and (2.8), imply that

$$\begin{aligned} x_{ij} (t)B_{ij}^{kl}(t) \int _{0}^{\infty }\sigma _{ij}(u) G(x_{kl}(t-u))\hbox {d}u \ \in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), \ ij,kl\in N. \end{aligned}$$

This proves Lemma 2.3.

Lemma 2.4

Define a nonlinear operator Q by setting

$$\begin{aligned} (Q\varphi )(t)&= \left\{ \int _{-\infty }^{t} e^{-\int _{s}^{t}d_{ij}(u){\hbox{d}}u} \left[ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)F \left( \varphi _{kl}\left( s-\tau _{kl}(s) \right) \right) \varphi _{ij}(s) \right. \right. \\&\quad-\sum \limits _{B_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s) \int _{0}^{+\infty }\sigma _{ij}(u) G\left( \varphi _{kl}(s-u)\right) \hbox {d}u\varphi _{ij}(s)\\&\quad\left. \left. +I_{ij}(s)\right] {\hbox{d}}s\right\} , \varphi \in PAP^{T,\mu }\left( {\mathbb {R}},{\mathbb {R}}^{mn}\right) . \end{aligned}$$

Then, Q maps \(PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{mn})\) into itself.

Proof

With the application of the verification in Lemma 2.1 of [21], we can easily obtain that \(Q\varphi \in BC({\mathbb {R}}, {\mathbb {R}}^{mn})\) . From Lemma 2.3, we obtain that there are \(H_{ij} \in {AP^{T}({\mathbb {R}},{\mathbb {R}} )}\) and \(\Phi _{ij} \in {PAP_{0}^{\mu }({\mathbb {R}},{\mathbb {R}} )}\) such that

$$\begin{aligned}&-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)F(\varphi _{kl}(t-\tau _{kl}(t)))\varphi _{ij}(t)\\&-\sum \limits _{B_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(t) \int _{0}^{+\infty }\sigma _{ij}(u) G(\varphi _{kl}(t-u))\hbox {d}u\varphi _{ij}(t)+I_{ij}(t)\\&\quad = H_{ij} (t)+ \Phi _{ij}(t) \in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), \ ij\in N. \end{aligned}$$

Arguing as in the verification of Lemma 2.2, one can show

$$\begin{aligned} \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \int _{0}^{+\infty }e^{- \tilde{d}_{ij} ^{-}u }|\Phi _{ij} (t-u ) |\hbox {d}u\mu (t )\hbox {d}t=0, \ ij\in N. \end{aligned}$$

Then,

$$\begin{aligned} &0\le \lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \int _{-\infty }^{t }e^{- \int _{s}^{t}d _{ij} ( \theta )d\theta }|\Phi _{ij} (s )| \hbox {d}s\mu (t )\hbox {d}t \\&\le K_{ij}\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \int _{-\infty }^{t }e^{- \tilde{d}_{ij} ^{-}( t-s ) }|\Phi _{ij} (s )| \hbox {d}s\mu (t )\hbox {d}t \\&= K_{ij}\lim \limits _{r\rightarrow +\infty }\frac{1}{\mu ([-r, \ r])}\int _{-r}^{r} \int _{0}^{+\infty }e^{- \tilde{d}_{ij} ^{-}u }|\Phi _{ij} (t-u ) |\hbox {d}u\mu (t )\hbox {d}t \\&= 0, \end{aligned}$$

and the fact that

$$\begin{aligned} \left\{ \int _{-\infty }^{t+T}e^{-\int _{s}^{t+T}d_{ij}(u)\hbox {d}u}H_{ij} (s)\hbox {d}s \right\}= & {} \left\{ \int _{-\infty }^{t } e^{-\int _{\nu +T}^{t+T} d_{ij}(u)\hbox {d}u}H_{ij} (\nu +T) \hbox {d}\nu \right\} \\= & {} \left\{ -\int _{-\infty }^{t }e^{-\int _{\nu }^{t }d_{ij}(\theta )\hbox {d}\theta }H_{ij} (\nu ) \hbox {d}\nu \right\} , \end{aligned}$$

imply that

$$\begin{aligned} (Q\varphi )_{ij}(t)= & {} \int _{-\infty }^{t }e^{-\int _{s}^{t }d_{ij}(u){\hbox {d}}u}H_{ij} (s){\hbox {d}}s\\&+\int _{-\infty }^{t }e^{-\int _{s}^{t }d_{ij}(u){\hbox {d}}u}\Phi _{ij} (s){\hbox {d}}s\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}), i j\in N , \end{aligned}$$

and Q maps \(PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{mn})\) into itself. This ends the proof.

3 Main results

Theorem 3.1

Let \((S_{0})\), \((S_{1})\), \((S_{2})\) and \((S_{3})\) hold. Then, system (1.1) has exactly one weighted pseudo-anti-periodic solution \(x^{*}(t)\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{mn})\) , and all state vectors of (1.1) and (2.1) converge to \(x^{*}(t)\) with a positive exponential convergence rate \(\lambda \in \left(0, \ \min \left\{\kappa , \min \limits _{ij\in N}\tilde{d}_{ij}^{-}\right\}\right)\).

Proof

Set

$$\begin{aligned} \varphi ^{0}= \bigg \{\int ^t_{-\infty }e^{-\int ^t_{s}d_{ij}(w)dw}I_{ij}(s)\hbox {d}s \bigg \} \end{aligned}$$

and

$$\begin{aligned} \Gamma =\bigg \{ \varphi \bigg |||\varphi -\varphi ^{0}||_{\infty } \le \frac{\delta I}{1-\delta }, \ \varphi \in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{mn}) \bigg \} . \end{aligned}$$

Then,

$$\begin{aligned} \Vert \varphi ^{0} \Vert _{\infty } \le \max _{ij\in N} \left\{ K_{ij}\frac{I^{+}_{ij}}{\tilde{d} _{ij} ^{-}}\right\} =I, \end{aligned}$$
(3.1)

and

$$\begin{aligned} \parallel \varphi \parallel _{\infty } \le \parallel \varphi -\varphi ^{0}\parallel _{\infty }+\parallel \varphi ^{0} \parallel _{\infty } \le \frac{\delta I}{1-\delta }+I=\frac{I}{1-\delta }, \ \forall \varphi \in \Gamma . \end{aligned}$$
(3.2)

Consequently, \((S_{3})\) entails

$$\begin{aligned}&|(Q \varphi )_{ij}(t) -\varphi _{ij}^{0}(t)| \\&\quad = \left| \int _{-\infty }^{t}e^{-\int _{s}^{t}d_{ij}(u)\hbox {d}u} \left[ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s) F\left( \varphi _{kl}\left( s-\tau _{kl}(s)\right) \right) \varphi _{ij}(s) \right. \right. \\&\qquad \left. \left. -\sum \limits _{B_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s) \int _{0}^{+\infty }\sigma _{ij}(u) G\left( \varphi _{kl}(s-u)\right) \hbox {d}u\varphi _{ij}(s) \right] \hbox {d}s\right| \\&\quad \le K_{ij} \int _{-\infty }^{t} e^{-\int _{s}^{t} \tilde{d}_{ij}(u)\hbox {d}u} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(s)| M_{F}\Vert \varphi \Vert _{\infty } \right. \\&\qquad \left. + \sum \limits _{B_{kl}\in N_{q}(i,j)}|B_{ij}^{kl}(s)| \int _{0}^{+\infty }|\sigma _{ij}(u)| \hbox {d}uM_{G} \right] \hbox {d}s\Vert \varphi \Vert _{\infty } \\&\quad \le K_{ij} \frac{\sum \limits _{C_{kl}\in N_{r}(i,j)} C_{ij}^{kl} \ ^{+} M_{F} + \sum \limits _{B_{kl}\in N_{q}(i,j)} B_{ij}^{kl}\ ^{+} \int _{0}^{+\infty }|\sigma _{ij}(u)| \hbox {d}uM_{G}}{\tilde{d}_{ij} \ ^{-}} \Vert \varphi \Vert _{\infty } \\&\quad \le \frac{\delta I}{1-\delta } , \ ij\in N, \end{aligned}$$

which implies that Q is a mapping from \(\Gamma\) to \(\Gamma\).

Furthermore, according to \((S_{0})\), \((S_{1})\), \((S_{2})\) and \((S_{3}),\) one can easily to see that

$$\begin{aligned}&| (Q \varphi )_{ij}(t) -(Q \psi )_{ij}(t) | \nonumber \\&\quad \le \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)\hbox {d}u} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(s)|((|F(\varphi _{kl}(s-\tau _{kl}(s)))- F(\psi _{kl}(s-\tau _{kl}(s)))||\varphi _{ij}(s)| \right. \nonumber \\&\qquad +|F(\psi _{kl}(s-\tau _{kl}(s)))||\varphi _{ij}(s)-\psi _{ij}(s)|) \nonumber \\&\qquad + \sum \limits _{B_{kl}\in N_{q}(i,j)}|B_{ij}^{kl}(s)| \left( \int _{0}^{+\infty }|\sigma _{ij}(u)| |G(\varphi _{kl}(s-u))-G(\psi _{kl}(s-u))|\hbox {d}u|\varphi _{ij}(s)| \right. \nonumber \\&\qquad \left. \left. + \int _{0}^{+\infty }|\sigma _{ij}(u)| |G(\psi _{kl}(s-u))|\hbox {d}u|\varphi _{ij}(s)-\psi _{ij}(s)|\right) \right] \hbox {d}s \nonumber \\&\quad \le K_{ij}\int ^t_{-\infty }e^{-\int _{s}^{t}\tilde{d}_{ij} (u)\hbox {d}u} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(s)|\left( L ^{F} \frac{I}{1-\delta } +M_{F} \right) \right. \nonumber \\&\qquad \left. + \sum \limits _{B_{kl}\in N_{q}(i,j)}|B_{ij}^{kl}(s)| \int _{0}^{+\infty }|\sigma _{ij}(u)| \hbox {d}u\left( L ^{G}\frac{I}{1-\delta } + M_{G} \right) \right] \hbox {d}s \Vert \varphi -\psi \Vert _{\infty } \nonumber \\&\quad \le \int ^t_{-\infty }e^{-\int _{s}^{t}\tilde{d}_{ij} (u)\hbox {d}u} \left[ \tilde{d}_{ij}(s)-\frac{\gamma _{ij}}{2}\right] \hbox {d}s \Vert \varphi -\psi \Vert _{\infty } \nonumber \\&\quad \le \left[ \int ^t_{-\infty } e^{-\int _{s}^{t} \tilde{d}_{ij}(u)\hbox {d}u} d\left( -\int _{s}^{t}\tilde{d}_{ij}(u)\hbox {d}u\right) -\frac{\gamma _{ij}}{2}\int ^t_{-\infty }e^{-\int _{s}^{t}\tilde{d}_{ij}(u)\hbox {d}u} \hbox {d}s \right] \Vert \varphi -\psi \Vert _{\infty } \nonumber \\&\quad \le \max \limits _{ ij \in N}\left\{ \left( 1-\frac{\gamma _{ij}}{2 \tilde{d}_{ij} ^{+}}\right) \right\} \Vert \varphi -\psi \Vert _{\infty } , ij\in N, \end{aligned}$$
(3.3)

which, together with the fact that \(0<\max \nolimits _{ ij \in N}\{ ( 1-\frac{\gamma _{ij}}{2 \tilde{d}_{ij} ^{+}})\}<1,\) entails that the mapping Q: \(\Gamma \rightarrow \Gamma\) is a contraction mapping, and there exists a unique fixed point

$$\begin{aligned} x^{*}=\{x_{ij}^{*}(t)\}\in \Gamma \subseteq PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{n}), \ Q x^{* }=x^{* }, \end{aligned}$$

which is a weighted pseudo-anti-periodic solution of (1.1).

Finally, with a similar proof in Theorem 3.2 of [21], one can pick constants \(\lambda \in (0, \ \min \{\kappa , \min \nolimits _{ij\in N}\tilde{d}_{ij}^{-}\})\) and \(M>\sum \nolimits _{ij=11}^{mn}K_{ij} +1\) such that

$$\begin{aligned}&\sup \limits _{t\in R}\left\{ \lambda -\tilde{d}_{ij}(t)+K_{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left|C_{ij}^{kl}(t)\right|M_{F} +L ^{F} e^{ \lambda \tau _{kl} ^{+} } \left(\frac{I}{1-\delta }\right) \right. \right. \\&\qquad +\sum \limits _{B_{kl}\in N_{q}(i,j)}|B_{ij}^{kl}(t)| \left( \int _{0}^{+\infty }|\sigma _{ij}(u)| \hbox {d}uM_{G} \right. \\&\qquad \left. \left. \left. +\int _{0}^{+\infty }|\sigma _{ij}(u)|L^{G} e^{ \lambda u }\hbox {d}u\frac{I}{1-\delta }\right) \right] \right\} <0 , \ ij\in N, \end{aligned}$$

and

$$\begin{aligned} \Vert x(t)-x^{*}(t)\Vert \le M \left\{ \sup \limits _{t\le 0 }\max \limits _{ij\in J } |\varphi _{ij} (t) -x^{*}_{ij}(t)|\right\} e^{-\lambda t} \quad \text{ for } \text{ all } t > 0 , \end{aligned}$$

which proves Theorem 3.1.

4 Numerical simulations

Consider SICNNs (1.1) with the following parameters:

$$\begin{aligned} \left\{ \begin{array}{ll} m=n=2, \ F (x)=G(x)=\frac{1}{20}|\arctan x | , d_{ij}(t)= 1+(i+j)\cos 1000t, \\ r=q=1, \ \{C_{ij}\}=\{B_{ij}\}= \left[ \begin{array}{ccc} \frac{1}{10} |\sin t|&{} \frac{1}{5} |\sin t| \\ \frac{1}{5} |\sin t|&{}\frac{1}{10} |\sin t| \end{array} \right] , \\ I_{ij}(t)=\frac{ (i+j)}{40}[\sin t+p(t)], \sigma _{ij } (t) = \frac{1}{10} e^{-2t}, \tau _{ij } (t) = \frac{1}{i+j} (1+\sin t)\\ p(t)=e^{-t} \quad \ \text{ for } \text{ all } t\ge 0, p(t)=1 \quad \ \text{ for } \text{ all } t< 0. \end{array}\right. \end{aligned}$$
(4.1)

Obviously, one can choose

$$\begin{aligned} \tilde{d}_{ij} (t)= 1, T=\pi , \kappa =1, \ L^{F} =L^{G} =\frac{1}{20}, \;M_{F}=M_{G}=\frac{\pi }{40}, \ K_{ij}=e^{\frac{3}{10} },\quad i,j=1,2, \end{aligned}$$

and

$$\begin{aligned} I\approx 0.27, \ \delta \approx 0.28, \ \mu (t)=e^{t} \quad \ \text{ for } \text{ all } t\ge 0,\\ \mu (t)=1 \quad \ \text{ for } \text{ all } t< 0 \end{aligned}$$

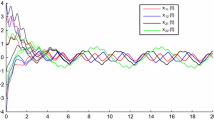
such that SICNNs (1.1) with (4.1) satisfy all the hypothesis mentioned in Section 2. Based on Theorem 3.1, we can conclude that system (1.1) has exactly one weighted pseudo-anti-periodic solution \(x^{*}(t)\in PAP^{T,\mu }({\mathbb {R}},{\mathbb {R}}^{4})\), and all state vectors of system (1.1) converge exponentially to \(x^{*}(t)\) as \(t\rightarrow +\infty\). Here, the exponential convergence rate \(\lambda \approx 0.02\). The time–response curve is given in Fig. 1, and there are three different groups initial values with \((1.1,-3.1,4.1,-3.1),(-3.2,4.1,-1.1,2.1),(3.1,-4.1,1.1,-2).\)

Fig. 1
figure 1

Numerical simulations for the state vectors of SICNNs (1.1) with (4.1)

Full size image

Remark 4.1

In the real world, there is little purely periodic phenomenon, and this motivates us to study the pseudo-almost-periodic and weighted pseudo-almost-periodic situations. In this work, we show that for the same assumptions in [21] plus other assumptions that we add to realize our demonstrations, allows us to show the dynamic characteristics of (1.1) in a weighted pseudo-anti-periodic set broader than the anti-periodic set in [21]. Since weighted pseudo-anti-periodic SICNNs with mixed delays has not been touched in [7–11, 21], our results improve and extend the corresponding ones in the above references.

5 Conclusions

In this manuscript, we have investigated shunting inhibitory cellular neural networks with mixed delays. With the aid of the contraction mapping fixed point theorem, differential inequality theory and the Lyapunov functional method, some sufficient criterion for the existence and global exponential stability of weighted pseudo-anti-periodic solutions of the system is established. In order to demonstrate the feasibility of the theoretical results, a numerical example is given. The established results were compared with those of recent methods existing in the literature. We expect to extend this work to other neural networks models with mixed delays. We will also study more types of weighted pseudo-almost-periodic solution problems on delayed neural networks models.