1 Introduction

System reliability is one of the most important issues to design various types of electrical and mechanical systems. In the reliability theory, redundancy is applied to improve system reliability. In addition, reliability redundancy allocation problem (RRAP) is an important class in modeling reliability systems so that belongs to NP-hard problems. In the RRAP literature, there are several considered RRAPs such as series, parallel, series–parallel [1–4], and k-out-of-n [5]. Hence, Fig. 1 shows a series–parallel system in which includes s subsystems and n redundant machines.

Fig. 1
figure 1

Graphical representation of series–parallel system

Full size image

There are two categories of RRAPs. The first class is a system including component mixing. The second category is a system without component mixing, which meant that the components allocated in the same subsystem in which should be the same type [6]. Furthermore, active and standby approaches are two main classifications for the redundancy strategies. The situation that all components are operated simultaneously from the time zero is called active redundancy versus standby redundancy that the redundant components are used sequentially during component failure times [7]. Moreover, standby redundancy is categorized into three different types, namely, cold [8–10], hot [11, 12], and warm [13–15] so that frees the component to fail before it operates in the cold standby redundancy versus warm standby that components are more likely to be failed before operating. Further, the failure pattern of components is freed from the idleness or the operation of the components with respect to the hot standby redundancy. In the majority of studies in the RRAP literature, it is assumed that only one type of redundancy can be used to investigate systems: active or cold standby. In the real world, both the redundancy strategies are applied simultaneously in the design of systems. Therefore, this paper studies redundancy strategy with respect to active and cold standby components.

In system-reliability optimization, Kuo and Prasad [16] provided a good overview. However, there are several studies in the scope of cold standby redundancy so that Tillman et al. [17] evidenced in their research; on the other hand, they investigate 100 papers relating to the reliability optimization researches with different types of redundancy. According to strictly cold standby redundancy, Coit [5] discussed a problem that considered imperfect switching and k-Erlang distributed time-to-failures, and then presented an integer programming solution to optimize the RRAP. To consider problems of active and cold standby redundancy is near to real-world situations in which there are few studies because of its computational complexity. Considering multiple k-out-of-n subsystems in the series, Coit and Liu [18] provided a solution methodology to optimize a RRAP for systems so that they assumed that the redundancy strategy is predetermined for each subsystem. Regarding zero–one integer programming method, Coit [19] extended another methodology to maximize system reliability with respect to either active or cold-standby redundancy can be selectively chosen for individual subsystems. Thus, he developed the previous solution methodology by adding several decision variables. Next, Tavakkoli-Moghaddam et al. [20] improved the system reliability the RRAP [19] by employing the genetic algorithm (GA). Tian, et al. [21] extended an approach to optimize systems with multi-sate components with respect to the factors that influence system reliability and system life cycle cost. Moreover, Sharma, et al. [22] proposed an efficient algorithm to find a near-optimal solution to minimize the configuration cost of heterogeneous multistate series–parallel systems while a desired reliability index should be satisfied.

With these explanations, the purpose of this article is to develop a better solution methodology to improve the RRAP optimization. In other words, this paper illustrates a continuous GA (CGA) for series–parallel RRAP used in Tavakkoli-Moghaddam et al. [20]. Since the meta-heuristics are impressed by their parameters, we utilize the response surface methodology (RSM) in the design of experiments to tune parameters of the proposed algorithm. As innovations, we can point to CGA that applies a new chromosome so that free offspring from reparation during the generation; in addition, employing RSM to calibrate parameters of CGA is another contribution. Table 1 provides several studies relevant to GA in the literature.

Table 1 Several studies relevant to genetic algorithm
Full size table

The paper is organized as follows. Section 2 defines the assumptions and the mathematical model. The proposed algorithm is presented in Section 3. Parameter tuning and the comparison of CGA are elaborated in Sections 4 and 5, respectively. Finally, Section 6 provides the conclusion and future research.

2 Mathematical model

This section presents a RRAP without component mixing for the series–parallel redundant reliability system considering S subsystem so that individual subsystems can select either active or cold standby redundancy strategy. In addition, two separable linear constraints are considered. Several typical assumptions are,

  1. a.

    The failed components, which are not repaired, do not damage to the system.

  2. b.

    Failures of individual components are statistically-independent.

  3. c.

    The states of the elements and the system are either good or have failed (and no other states are considered).

Nomenclatures used in this paper are as follows.

S :

Number of subsystems

i :

An index used for a subsystem; i = 1, 2, 3, …, S

n i :

Number of components used in subsystem; n i  ∈ {1, 2, …, n max,i }

n :

(n 1, n 2, …, n s )

m i :

Number of available component choices for a subsystem i

z i :

Index of component choice used for a subsystem i; z i  ∈ {1, 2, …, m i }

Z :

(z 1, z 2, …, z S )

A :

Set of all subsystems using active redundancy

CS :

Set of all subsystems using cold standby redundancy

n max,i :

Upper bound for n i (n i  ≤ n max,i )

\( {r}_{i{z}_i}(t) \) :

Reliability at time t for z th i available component for subsystem i

\( {\lambda}_{i{z}_i},{k}_{i{z}_i} \) :

Scale and shape parameters the Gamma distribution for z th i available component for subsystem i

\( {f}_{i{z}_i}^{(j)}(t) \) :

pdf of z th i failure arrival for subsystem i, where is the sum of jiid component failure times

W :

System-level constraint limit for weight

c ij , w ij :

Cost and weight of the j th available component for the subsystem i, respectively

ρ i (t):

Failure-detection / switching reliability at time t (scenario 1; continual sensing)

ρ i :

Failure-detection/switching reliability success probability (scenario 2; active only in response to a failure state)

R(t; z, n):

System reliability at time t for designing vectors z and n

\( \tilde{R}\left(t;z,n\right) \) :

Approximation of R(t; z, n)

t :

Mission time (fixed)

Where the decision variables are: redundancy strategies, selected components, and the number of components for each subsystem.

According to the mentioned nomenclature, the mathematical model of RRAP can be written as follows.

$$ \mathrm{Max}\;z=R\left(t;z,n\right) $$
(1)

s.t,

$$ {\displaystyle \sum_i{c}_{i{z}_i}{n}_i\le C} $$
(2)
$$ {\displaystyle \sum_i{w}_{i{z}_i}{w}_i\le W} $$
(3)
$$ {n}_i\in \left\{1,2,\dots, {n}_{\max, i}\right\} $$
(4)
$$ {z}_i\in \left\{1,2,\dots, {m}_i\right\} $$
(5)

Equation (3) presents the overall reliability system; in addition, Eqs. (4) and (5) satisfy the constraints on the available cost and weight, respectively. Then, Eqs. (7) and (8) obtain the system reliability as two scenarios [5]:

  1. Scenario 1:

    continual detector/switch operation,

  2. Scenario 2:

    switch active only in response to a failure,

$$ R\left(t;z,n\right)={\displaystyle \prod_{i\in A}\left(1-{\left(1-{r}_{i{z}_i}(t)\right)}^{n_i}\right)\times {\displaystyle \prod_{i\in CS}\left({r}_{i{z}_i}(t)+{\displaystyle \sum_{j=1}^{n_i-1}{\displaystyle {\int}_0^t{\rho}_i(u)}{f}_{i{z}_i}^{(j)}(u)}{r}_{i{z}_i}\left(t-u\right)du\right)}} $$
(6a)
$$ R\left(t;z,n\right)={\displaystyle \prod_{i\in A}\left(1-{\left(1-{r}_{i{z}_i}(t)\right)}^{n_i}\right)\times {\displaystyle \prod_{i\in CS}\left({r}_{i{z}_i}(t)+{\displaystyle \sum_{j=1}^{n_i-1}{\rho}_i^j{\displaystyle {\int}_0^t{f}_{i{z}_i}^{(j)}(u)}}{r}_{i{z}_i}\left(t-u\right)du\right)}} $$
(6b)

In the CS, the subsystem reliability is the sum of the n i mutually exclusive probabilities. Just after the product for CS, the first term in Eq. (6) is \( {r}_{i{z}_i}(t) \) that represents the probability that no cold standby redundant components are required during the mission interval. Other subsequent terms represent n i  − 1 mutually exclusion probabilities that there are between one and n i  − 1 failures. Note that the switch is available to perform its function at the time of the failure, and a redundant component is always operating at time t.

2.1 Approximation of reliability

Regarding Eqs. (7) and (9) obtains the system reliability approximation in which only one difference can be seen in the product term for CS.

$$ \tilde{R}\left(t;z,n\right)={\displaystyle \prod_{i\in A}\left(1-{\left(1-{r}_{i{z}_i}(t)\right)}^{n_i}\right)\times {\displaystyle \prod_{i\in CS}\left({r}_{i{z}_i}(t)+{\delta}_i\left(t,{n}_i\right){\displaystyle \sum_{j=1}^{n_i-1}{\displaystyle {\int}_0^t{f}_{i{z}_i}^{(j)}(u)}}{r}_{i{z}_i}\left(t-u\right)du\right)}} $$
(7)

Where \( {\delta}_i\left(t,{n}_i\right)=\left\{\begin{array}{l}{\rho}_i(t)\\ {}{\rho}_i^{n_i-1}\end{array}\right. \), as a probability function to determine the probability of the switch at hours for each subsystem, which it is considered 0.99 in this paper.

A specified form of Eq. (9) shall be determined if k-Erlang distribution is considered for component time-to-failure. The k-Erlang distribution as a special form of Gama distribution can model diverse constant and increase hazard functions. According to k-Erlang distribution, the approximation of the system reliability can be calculated as follows.

$$ \tilde{R}\left(t;z,n\right)={\displaystyle \prod_{i\in A}\left(1-{\left(1-{e}^{-{\lambda}_{i{z}_i}t}{\displaystyle \sum_{l=0}^{{k_{iz}}_i-1}\frac{{\left({\lambda}_{i{z}_i}t\right)}^l}{l!}}\right)}^{n_i}\right)\times {\displaystyle \prod_{i\in CS}\left[{e}^{-{\lambda}_{i{z}_i}t}\left({\displaystyle \sum_{l=0}^{k_{i{z}_i}-1}\frac{{\left({\lambda}_{i{z}_i}t\right)}^l}{l!}}+{\rho}_i(t){\displaystyle \sum_{l={k}_{i{z}_i}}^{k_{i{z}_i}{n}_i-1}\frac{{\left({\lambda}_{i{z}_i}t\right)}^l}{l!}}\right)\right]}} $$
(8)

3 Solution algorithm: Continuous genetic algorithm (CGA)

There are several methods to optimize NP-hard problems such as dynamic programming [26], integer programming [27], and meta-heuristics like GA [20, 28–30], particle swarm optimization [31–33], the cuckoo search (CS) algorithm [34], the bee algorithm [35]. Thus, we employ an improved meta-heuristic to optimize the model.

GA has been developed as a robust and powerful stochastic search algorithm and works based on Darwin’s theory of evolution [36]. CGA or real-coded GA, which its chromosomes are considered as a floating point number, is a special forming of GAs so that acts better than GA based on a binary method for function optimization problems [37]. There are several superior features of CGA versus the binary GA such as working quickly because of the designed chromosomes, and storing computational less space to run the algorithm. Figure 2 shows the flowchart of the proposed algorithm, which is described as follows.

Fig. 2
figure 2

The flowchart of the CGA algorithm

Full size image

3.1 Initialization

To begin the CGA, the parameters of the algorithm should be assigned an initial value. The parameters that have important roles in CGA are: (i) It: Number of iterations of CGA or the number of the generations; (ii) Npop: Number of the individual population; (iii) P c : Crossover operator ratio; (iv) P m : Mutation operator ratio. Where these parameters are tuned by RSM in Section 4.

3.2 Encoding structure

Encoding solution is the vital component to effective search in the solution area; therefore, we present a new encoding to CGA. Note that a possible solution consists of redundancy strategies, selected components, and the number of components for each subsystem. The proposed encoding presents a feasible solution that does not need to repair during the CGA process. There are three parts in the encoding of solution in which showed in Fig. 3.

Fig. 3
figure 3

The proposed chromosome

Full size image

Here, the rows, which are a random number between (0 ∼ 1), are a 1 × S vector so that S denotes number of the subsystem. Thus, these rows obtain a feasible solution after decoding process. The initial population is created randomly considering Npop.

3.3 Decoding structure

In order to evaluate the fitness function, it is necessary to decode the encoded solutions. Thus, the decoding process is elaborated considering an example with these explanations:

S Number of subsystem (S = 6)

m i Number of available component for a subsystem (m i  = 3)

n max,i Constraint on the number of components used in each subsystem (n max,i  = 6)

a i Two redundancy strategies including active and cold standby for each subsystem (a i  = 2)

The following steps describe decoding process.

  1. Step 1:

    Generate randomly a chromosome, (see Fig. 4).

    Fig. 4
    figure 4

    A graphical representation of the chromosome

    Full size image
  2. Step 2:

    Select the redundancy strategy for each subsystem between active or cold standby by rounding numbers obtained from the first row to nearest integer like this ⌊r i  × a i  + 1⌋. Such, active and cold strategies are chosen by 1 and 2, respectively, (see the first row in Fig. 5).

    Fig. 5
    figure 5

    Decoded the chromosome

    Full size image
  3. Step 3:

    Calculate ⌊m i  × c i  + 1⌋ to allocate available component for subsystem i so that 1, 2, and 3 are their number, (see the second row in Fig. 5).

  4. Step 4:

    Obtain ⌊n max,i  × n i  + 1⌋ to select the number of the components used in subsystem i, (see the third row in Fig. 5).

3.4 CGA operators

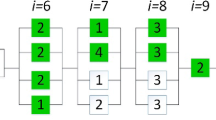
In order to satisfy the constraints described in Eqs. (4) and (5), we employ one of the penalty methods, called the death penalty [36]. Moreover, individuals with higher qualification should have a greater chance of selection than those with lower fitness. Hence, we apply the roulette wheel selection to select the chromosomes. GA generates a new population with crossover and mutation operators. This paper utilizes a specific version of the continuous uniform crossover used by Radcliffe [38] as follows. Two chromosomes, which called parents, are selected between the populations. Next, a row similar to one of the parent is generated, namely β (with values between zero and one). Afterwards, offspring are created considering Eqs. (11) and (12). Figure 6 elaborates the process of the crossover operator for the 1th row of chromosomes.

Fig. 6
figure 6

An example of crossover operator

Full size image
$$ offsprin{g}_1=\beta \times paren{t}_1+\left(1-\beta \right) paren{t}_2 $$
(9)
$$ offsprin{g}_2=\beta \times paren{t}_2+\left(1-\beta \right) paren{t}_1 $$
(10)

The second operator in GA, which called mutation, prevents the algorithm to converge on a local optimal solution. The uniform mutation operator of Radcliff [38] is used in this paper. Figure 7 explains mutation operator; such, a chromosome is selected randomly, and then exchanged one of its cells with a random number between zero and one.

Fig. 7
figure 7

An example of mutation operator

Full size image

4 Parameter tuning: Response Surface Methodology

There are two main approaches to calibrate the parameters used in meta-heuristics: a trial-and-error procedure, and the statistical methods. The parameters of meta-heuristics impress the quality of the solutions; hence, we employ one of the statistical methods in design of experiments, called the Response Surface Methodology (RSM). The RSM uses a collection of useful mathematical and statistical techniques to model and analysis of problems [39]. Considering a response that here is the system reliability, the RSM determines the best levels of variables in a problem. There are four variables in which are presented in Table 2 that shows their levels and coded factor.

Table 2 The parameters and their levels as the input variables of RSM
Full size table

In the beginning of RSM, a trial-and-error procedure is used to initialize the variables. Considering the obtained responses, a first-order model is fitted; and performed a test of lack of fit so that this test determines the sufficiency; otherwise, a second-order model is tested [40]. There are several the designs to fit a second-order model such as the central composite design (CCD) in which includes 2k factorial points, n c central points, and 2k axial points. The second-order model of CCD can be written as,

$$ \mathrm{E}\left(\mathrm{Y}\right)={\beta}_0+{\displaystyle {\sum}_{i=1}^k{\beta}_i{X}_i}+{\displaystyle {\sum}_{i=1}^k{\beta}_i{X}_i^2}+{\displaystyle {\sum}_{i<j}^k{\displaystyle {\sum}_{i<j}^k{\beta}_{ij}{X}_i}{X}_j} $$
(11)

Where E(Y) is the expected value of the response variable in which is the system reliability, and β 0, β i and β ij are fixed coefficients of the second-order model. In addition, X i and X j are the input variables in k number.

4.1 Experiments

To perform RSM, we run 33 test problems in which have 14 subsystems with varying decreasingly weights W from 191 to 159, and the available budget restricted to 130 (C = 130).

Note that the values of −1, 0, and 1 are low, middle, and high levels of parameters, respectively. To remove the influence of results obtained from the test problems with different size, the mean ratio of the CGA solution (Y as the response) is defined as the performance index of the CGA. Table 3 shows the CCD that consists of eight factorial points, eight axial points, and four central points in twenty experiments. Considering the CCD, we run CGA to obtain the responses (Y). Since the proposed model belongs to the maximization models, a response (Y) with higher values presents better performances of the CGA. Regarding the analysis of variance (ANOVA) test for the response in Table 4, there is a statistically significant curvature on the response surfaces; therefore, a second order model is employed to analysis experiments. The responses in Table 3 are used to estimate the second order models.

Table 3 The central composite design (CCD) with the responses
Full size table
Table 4 Analysis of variance for the accuracy performance index (Y)
Full size table

The best values of parameters are given by solving a single objective problem in Eq. (12), which is obtained by the estimated regression coefficients in the second-order model.

$$ \begin{array}{l}Y=0.95+0.039{X}_1-0.0015{X}_2-0.021{X}_3+0.032{X}_4-0.0149{X}_1^2+0.0027{X}_2^2+\\ {}\kern1.08em 0.0084{X}_3^2-0.0244{X}_4^2+0.007{X}_1{X}_2+0.007{X}_1{X}_3-0.0271{X}_1{X}_4\end{array} $$
(12)

Finally, the optimal values of parameters are illustrated in Table 5.

Table 5 The optimal value of input variables
Full size table

5 Numerical example

In this section, an example [5] is used to evaluate the performance of the proposed algorithm. There are 14 subsystems with three or four component selections; in addition, the maximum number of components is six (n max,i  = 6). Moreover, it is considered 0.99 as the reliability of a switch at 100 h for each subsystem.

Thus, Table 6 illustrates the component cost, the weight and k-Erlang distribution parameters of the example. The aim of solving is to maximize system reliability considering two constraints of the system cost (C = 130) and the weight (W = 170) in 100 h. There are two redundancy strategies for each subsystem: active or cold standby. The switch operates and fails similar to Scenario 1 in the cold standby redundancy strategy. Therefore, a continuous decreasing function would be suggested for switch reliability.

Table 6 Component data for example
Full size table

Table 7 makes a comparison between three solution approaches. The results explain that the proposed algorithm optimizes better the problem versus four studies. The reliability (0.9872) presented by the proposed algorithm, for example, is better than the one presented by Coit [5].

Table 7 The result of comparison the proposed algorithm
Full size table

In the second part of comparison, we resolve 33 problems used in Tavakkoli-Moghaddam et al. [20] considering varying the available weight from 191 to 159 and the constrained cost to 130. It can be understood from Table 8 that the proposed algorithm acts better than the solution algorithm of Tavakkoli-Moghaddam et al. [20] for all the problems. Figure 8 shows the domination of the proposed algorithm versus solution algorithm Tavakkoli-Moghaddam et al. [20].

Table 8 The result of comparison of the proposed algorithm with Tavakkoli-Moghaddam et al. [20]
Full size table
Fig. 8
figure 8

Performance of CGA vs. Tavakkoli-Moghaddam et al. [20]

Full size image

Figures 9 and 10 shows normal probability plots of the best results obtained (Table 8) using the proposed CGA and the GA [20], respectively, to statistically compare the results obtained. Table 9 presents the result of a t-test for the alternative “The proposed CGA < The GA [20]” as the null hypothesis. As a significant difference is not shown (p-value = 0.000 < 0.5), there is no presumption against the null hypothesis. Thus, the proposed CGA provides the better solution than the GA [20] on the average. Table 9 shows more details, in which SE Mean and StDev abbreviate the standard error of the mean and the standard deviation, respectively. Moreover, Fig. 11 presents the boxplot of comparison between the two methods, in which the reliability provided by the proposed algorithm is better than GA [20]. Note that the obtained solutions are the best among 20 runs of the algorithm. Notice also that a PC with 2.2 GHz Intel Core 2 Duo CPU, and 4 GB of RAM memory calculates all calculations in this paper; moreover, CGA is run in MATLAB 2009a.

Fig. 9
figure 9

The normal probability plot of the best costs provided by the proposed CGA

Full size image
Fig. 10
figure 10

The normal probability plot of the best costs provided by GA [20]

Full size image
Table 9 T-Test for the best costs
Full size table
Fig. 11
figure 11

The Boxplot of Proposed Algorithm and GA [18]

Full size image

6 Conclusion

This paper has considered the optimization of a series–parallel reliability redundancy allocation problem (RRAP) in which subsystems can select active or cold standby strategies. The aim of this problem was to choose the best redundancy strategies, components, and levels for each subsystem for maximizing the system reliability. Since the RRAP is an NP-hard problem, we employed a continuous genetic algorithm (CGA), which applied a new method in the production of chromosomes, to solve the model. In addition, the performance of CGA was improved by parameter tuning that one of statistical methods namely the response surface methodology (RSM) was used. According to the comparison of the proposed algorithm with the last solution algorithms, it can be concluded that the CGA has an efficient performance to optimize the RRAP problems. In other words, the presented method can probably be the best available algorithms in the literature to solve the considered problem. Finally, the future works of this study are as follows. (1) Investigate fuzzy condition in modeling. (2) Develop the objectives to consider the cost. (3) Study other redundancy strategies as decision variables.