Abstract
In this paper, the existence and the exponential stability of piecewise differentiable pseudo-almost periodic solutions for a class of impulsive neutral high-order Hopfield neural networks with mixed time-varying delays and leakage delays are established by employing the fixed point theorem, Lyapunov functional method and differential inequality. Numerical example with graphical illustration is given to illuminate our main results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider piecewise differentiable pseudo-almost periodic solutions of a class of impulsive neutral delay generalized high-order Hopfield neural networks with mixed delays. The mixed delays include leakage delay, time-varying delays and continuously distributed delays. To investigate the existence of solutions of the above-mentioned problem, we consider the following:
in which n corresponds to the number of units in a neural network, \(x_{i}(t)\) corresponds to the state vector of the ith unit at the time \(t, a_{i}(t)> 0\) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time \(t, b_{ij}(.), c_{ij}(.)\) and \(\alpha _{ijl}(.), \beta _{ijl}(.)\) are, respectively, the first-order connection weights and the second-order connection weights of the neural network, \(0 \le \rho (.) \le \rho ^{+}, 0 \le \tau _{ij}(.), \sigma _{ij}(.), \nu _{ij}(.) \le \tau ^{+}\) correspond to the transmission delays, \(J_{i}(t)\) denote the external inputs at time t, and \(f_{j}\) is the activation function of signal transmission. The sequence \(\{ t_{k}\}\) has no finite accumulation point and \(I_{k} : {\mathbb {R}}^{n} \longrightarrow {\mathbb {R}}.\)
As an important research field of dynamic systems, it is well known that high-order neural networks received much attention and have been applied in a wide range of practical fields such as signal processing, pattern recognition, associative memories, optimization problems, image processing, associative memories, speed detection of moving objects, optimization problems and many other fields [1–9, 13, 15, 37, 38]. This is due to the fact that high-order neural networks have stronger approximation property, faster convergence rate, greater storage capacity, and higher fault tolerance than lower-order neural networks.
In addition, from the real-world application angle, time delay is inevitably encountered in the implementation of networks [1, 5, 10–14, 19–25]. According to the way it occurs, time delay can be classified as two types: discrete and distributed. Time delays in the neural networks are often one of the main sources to cause poor performance, make the dynamic behaviors become more complex, may destabilize the stable equilibria and admit oscillations, bifurcation and chaos. Therefore, it is of prime importance to consider the delay effects on the stability of neural networks. In particular, the time delay in the negative feedback terms which is known as leakage has a tendency to destabilize the system [26–29] and has great impact on the dynamical behavior of neural networks. This is to say, it is necessary to consider the effect of leakage delays when studying the stability of state estimation of neural networks.
Recently, another type of time delays, namely neutral-type time delays, has drawn much research attention [18, 27, 41]. Many practical delay systems can be modeled as differential systems of neutral type, whose differential expression includes the derivative term of the past state, such as partial element equivalent circuits and transmission lines in electrical engineering, population dynamics and controlled constrained manipulators in mechanical engineering [27]. Moreover, it has been shown that the existing neural network models in many cases cannot characterize the properties of a neural reaction process precisely due to the complicated dynamic properties of the neural cells in the real world, and it is natural and necessary that systems will contain some information about the derivative of the past state to further describe and model the dynamics for such complex neural reactions [41].
However, it is well known that the dynamics of evolving processes is usually subjected to suddenly changes such as shocks, harvesting and natural disasters [16–18, 42]. Often these short-term perturbations are treated as having acted instantaneously or in the form of impulses. The theory of impulsive differential equations represents a more natural framework for mathematical modeling of many real-world phenomena, such as population dynamic system and the neural networks. High-order recurrent neural networks are often subject to impulsive perturbations that in turn affect dynamical behaviors of the systems [6].
Also, it is well known that studies on neuron dynamic systems not only involve a discussion of stability properties, but also involve many dynamic behaviors such as periodic oscillatory behavior, almost periodic oscillatory properties, pseudo-almost periodic oscillatory properties, chaos and bifurcation [30–36, 44]. In applications, the assumption of pseudo-almost periodicity, which was introduced by Zhang [30, 31], is more realistic and more important than that of periodicity and is a natural and good generalization of the classical almost periodic functions in the sense of Bohr. Liu and Zhang [35] introduced the concept of piecewise pseudo-almost periodic functions and gave some properties including the composition theorem.
To the best of our knowledge, there are no published papers considering the piecewise differentiable pseudo-almost periodic solutions for impulsive neutral high-order Hopfield neural networks with time-varying delays in the leakage terms. In other words, we have never studied the existence and the exponential stability of piecewise differentiable pseudo-almost periodic solutions for impulsive neutral high-order Hopfield neural networks with time-varying delays in the leakage terms.
The main aim of this article is to establish some sufficient conditions for the existence, the uniqueness and the exponential stability of piecewise differentiable pseudo-almost periodic solutions of Eq. (1).
Throughout this paper, for \(i,j,l = 1,2,\ldots ,n\), it will be assumed that \(\rho(.) , \tau _{ij}(.), \sigma _{ij}(.), \nu _{ij}(.)\) are almost periodic functions, such that \(1-\dot\rho(t)>0 ,\text{ } 1-\dot\tau _{ij}(t)>0 ,\text{ }1-\dot \sigma _{ij}(t)>0 ,\text{ } 1-\dot\nu _{ij}(t)>0 \text{ for all } t\in\mathbb{R}, b_{ij}, c_{ij}, \alpha _{ijl}, \beta _{ijl}, J_{i}: {\mathbb {R}} \longrightarrow {\mathbb {R}}\) are pseudo-almost periodic functions, and let the positive constant \(a_{i*}, a_i^{+}, \overline{b}_{ij}, \overline{c}_{ij}, \overline{\alpha }_{ijl}, \overline{\beta }_{ijl}\) and \(\overline{J}_{i}\) such that
We also assume that the following conditions (H1)–(H5) hold.
-
(H1)
For each \(j = \{1,2,\ldots ,n\}\), there exist nonnegative constants \(L^{f}_{j}\) and \(M^{f}_{j}\) such that
$$\begin{aligned} f_{j}(0)= 0, \, \mid f_{j}(u)- f_{j}(v)\mid \le L^{f}_{j} \mid u-v \mid , \, \, {\mathrm{{and}}} \, \mid f_{j}(u)\mid \le M^{f}_{j}, \, \, \, {\mathrm{for}} \, {\mathrm{all}} \, u,v \in {\mathbb {R}}. \end{aligned}$$ -
(H2)
For \(i,j,l \in \{1,2,\ldots ,n\}\), the delay kernels, \(d_{ij},h_{ijl},k_{ijl} : [0, \infty ) \longrightarrow {\mathbb {R}}\) are continuous, and there exist nonnegative constants \(d^{+}_{ij},h^{+}_{ijl},k^{+}_{ijl},\eta _{d}, \eta _{h}, \eta _{k}\) such that
$$\begin{aligned} \mid d_{ij}(u)\mid \le d^{+}_{ij} e^{-\eta _{d} u }, \, \mid h_{ijl}(u)\mid \le h^{+}_{ijl} e^{-\eta _{h} u }, \, \mid k_{ijl}(u)\mid \le k^{+}_{ijl} e^{-\eta _{k} u }. \end{aligned}$$ -
(H3)
For all \(1\le i \le n\) the functions \(t \mapsto a_{i}(t)\) are almost periodic with \(0 < a_{i*}= \inf\limits _{t \in {\mathbb {R}}}(a_{i}(t))\)
-
(H4)
\(I_{k} \in PAP({\mathbb {Z}},{\mathbb {R}}^{n})\) and there exists a constant \(L_{1}\) such that
$$\begin{aligned} \parallel I_{k}(u)-I_{k}(v)\parallel \le L_{1} \parallel u-v\parallel ,\, \, u,v \in {\mathbb {R}}^{n},\, k \in {\mathbb {Z}} \end{aligned}$$ -
(H5)
Assume that there exist nonnegative constants \(L, \widehat{p}\) and \(\widehat{q}\) such that
$$\begin{aligned} \max _{1 \le i \le n} \max \left\{ \frac{\overline{J}_{i}}{a_{i*}}, (1+\frac{a_{i}^{+}}{a_{i*}})\overline{J}_{i}\right\} = L \end{aligned}$$$$\begin{aligned} \widehat{p}= & {} \max _{ 1 \le i \le n} \max \left\{ \left\{ a^{-1}_{i*} \left[ a_{i}^{+} \rho ^{+} +\sum _{j=1}^{n} \overline{b}_{ij} L^{g}_{j}+ \sum _{j=1}^{n} \overline{c}_{ij} \frac{d^{+}_{ij}}{\eta _{d}} L^{f}_{j} +\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\alpha }_{ijl} L^{f}_{j} M^{f}_{l} \right. \right. \right. \\&\quad +\left. \left. \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\beta }_{ijl} \frac{h^{+}_{ijl}}{\eta _{h}} \frac{k^{+}_{ijl}}{\eta _{k}} L^{f}_{j} M^{f}_{l} \right] + \frac{L_{1}}{1-e^{-a_{i*}}}\right\} ,\left\{ (1+ \frac{a^{+}_{i}}{a_{i*}}) \left[ a_{i}^{+} \rho ^{+} +\sum _{j=1}^{n} \overline{b}_{ij} L^{f}_{j}\right. \right. \\&\quad +\sum _{j=1}^{n} \overline{c}_{ij} \frac{d^{+}_{ij}}{\eta _{d}} L^{f}_{j} +\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\alpha }_{ijl} L^{f}_{j} M^{f}_{l} \\&\left. \left. \left. \quad +\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\beta }_{ijl} \frac{h^{+}_{ijl}}{\eta _{h}} \frac{k^{+}_{ijl}}{\eta _{k}} L^{f}_{j} M^{f}_{l} \right] + \frac{a_{i}^{+}L_{1}}{1-e^{-a_{i*}}}\right\} \right\} <1, \end{aligned}$$$$\begin{aligned} \widehat{q}= & {} \max _{1 \le i \le n} max \left\{ \left\{ a^{-1}_{i*} [a_{i}^{+} \rho ^{+} +\sum _{j=1}^{n} \overline{b}_{ij} L^{f}_{j}+\sum _{j=1}^{n} \overline{c}_{ij} \frac{d^{+}_{ij}}{\eta _{d}} L^{f}_{j}+ \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\alpha }_{ijl} (L^{f}_{j} M^{f}_{l}+ M^{f}_{j} L^{f}_{l})\right. \right. \\&\quad +\left. \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\beta }_{ijl} \frac{h^{+}_{ijl}}{\eta _{h}} \frac{k^{+}_{ijl}}{\eta _{k}} (L^{f}_{j} M^{f}_{l}+ M^{f}_{j} L^{f}_{l}) ] + \frac{L_{1}}{1-e^{-a_{i*} }} \right\} , \left\{ \left( 1+\frac{a^{+}_{i}}{a_{i*} }\right) [a_{i}^{+} \rho ^{+} +\sum _{j=1}^{n} \overline{b}_{ij} L^{f}_{j}\right. \\&\quad +\sum _{j=1}^{n} \overline{c}_{ij} \frac{d^{+}_{ij}}{\eta _{d}} L^{f}_{j}+ \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\alpha }_{ijl} (L^{f}_{j} M^{f}_{l}+ M^{f}_{j} L^{f}_{l})\\&\quad +\left. \left. \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{\beta }_{ijl} \frac{h^{+}_{ijl}}{\eta _{h}} \frac{k^{+}_{ijl}}{\eta _{k}} (L^{f}_{j} M^{f}_{l}+ M^{f}_{j} L^{f}_{l}) ] + \frac{ a_{i}^{+}L_{1}}{1-e^{-a_{i*} }} \right\} \right\} < 1. \end{aligned}$$
Throughout this paper, we will first recall some basic definitions and lemmas which are used in what follows.
-
\({\mathbb {N}}, {\mathbb {Z}}\) and \({\mathbb {R}}\) stand for the set of natural numbers, integer numbers and real numbers, respectively.
-
\(C({{\mathbb {R}}},{{\mathbb {R}}}^{n})\): the set of continuous functions from \({{\mathbb {R}}}\) to \({{\mathbb {R}}}^{n}\).
-
\(BC({{\mathbb {R}}},{{\mathbb {R}}}^{n})\): the set of bounded continued functions from \({{\mathbb {R}}}\) to \({{\mathbb {R}}}^{n}\). Note that \((BC({\mathbb {R}},{\mathbb {R}}^{n}),\parallel . \parallel _{\infty })\) is a Banach space where \(\parallel . \parallel _{\infty }\) denotes the sup norm
$$\begin{aligned} \parallel f \parallel _{\infty }:= \max _{1 \le i \le n} \sup _{t \in {\mathbb {R}}} \mid f_{i}(t) \mid . \end{aligned}$$ -
Let T be the set consisting of all real sequences \(\{t_{i}\}_{i \in {\mathbb {Z}}}\) such that \(\alpha = \inf \nolimits _{i \in {\mathbb {Z}}} ( t_{i+1} - t_{i}) > 0.\) It is immediate that this condition implies that \(\lim \nolimits _{i \rightarrow +\infty } t_{i} = +\infty\) and \(\lim \nolimits _{i \rightarrow -\infty } t_{i} = -\infty\).
-
\(PC({\mathbb {R}},{\mathbb {R}}^{n})\): the space formed by all piecewise continuous functions \(f : {\mathbb {R}} \rightarrow {\mathbb {R}}^{n}\) such that f(.) is continuous at t for any \(t \not \in \{t_{i}\}_{i \in {\mathbb {Z}}}, f(t_{i}^{+}), f(t_{i}^{-})\) exists and \(f(t_{i}^{-})= f(t_{i})\) for all \(i \in {\mathbb {Z}}\).
-
\(PC([-\tau , 0],{\mathbb {R}}^{n}) = \left\{ f : [-\tau , 0] \rightarrow {\mathbb {R}}^{n} / f(t^{-})= f(t), {\text { for }} t \in [-\tau , 0], f(t^{+}) {\text { exists on }}\, {\mathbb {R}} {\text {and }} f(t^{+})= f(t) {\text { for\, all\,but\, at\, most\, a\, finite\, number\, of \,points }} {\text { on }} [-\tau , 0]. \right\} ,\)
-
\(PC^{1}([-\tau , 0],{\mathbb {R}}^{n}) = \left\{ f : [-\tau , 0] \rightarrow {\mathbb {R}}^{n} / f'(t^{+}) {\text { and }} f'(t^{-})) {\text { exist }}, f'(t) = f'(t^{-}) {\text { for }} \,t \in [-\tau , 0], f'(t^{+})=f'(t) {\text { for \,all\, but\, at\, most\, a \,finite \,number\, of\, points}} {\text {on }} [-\tau , 0]. \right\} ,\)
-
\(l^{\infty }({\mathbb {Z}},{\mathbb {R}}^{n})= \left\{ x : {\mathbb {Z}} \rightarrow {\mathbb {R}}^{n} : \parallel x \parallel = \sup \nolimits _{n \in {\mathbb {Z}}} \parallel x(n) \parallel < \infty \right\} .\)
Definition 1
[36]. A function \(f \in C({\mathbb {R}},{\mathbb {R}}^{n})\) is called (Bohr) almost periodic if for each \(\varepsilon > 0\) there exists \(L(\varepsilon )>0\) such that every interval of length \(L(\varepsilon )>0\) contains a number \(\tau\) with the property that \(\parallel f(t+\tau )-f(t) \parallel _{\infty } < \varepsilon ,\) for each \(t\in {\mathbb {R}}\).
The number \(\tau\) above is called an \(\varepsilon\)-translation number of f, and the collection of all such functions will be denoted as \(AP({\mathbb {R}},{\mathbb {R}}^{n})\).
Definition 2
[36]. A sequence \(\{x_{n}\}\) is called almost periodic if for any \(\varepsilon > 0\), there exists a relatively dense set of its \(\varepsilon\)-periods, i.e., there exists a natural number \(l = l(\varepsilon )\), such that for \(k \in {\mathbb {Z}}\), there is at least one number p in \([k,k+l]\), for which inequality \(\parallel x_{n+p} - x_{n} \parallel < \varepsilon\) holds for all \(n \in {\mathbb {N}}\). Denote by \(AP({\mathbb {Z}},{\mathbb {R}}^{n})\), the set of such sequences.
Define
Remark 1
Notice that
-
1.
A sequence vanishing at infinity is a \(PAP_{0}({\mathbb {Z}},{\mathbb {R}})\) sequence.
-
2.
The sequence \((x(n))_{n \in {\mathbb {Z}}}\) defined by
$$\begin{aligned} x(n)= \left\{ \begin{array}{ll} 1, &{} n = 2^{k}, \\ 0, &{} n \ne 2^{k}, \end{array} \right. \end{aligned}$$is an example of a \(PAP_{0}({\mathbb {Z}},{\mathbb {R}})\) sequence which not vanishing at infinity.
-
3.
For \(k \in {\mathbb {N}}\) the sequence \((x(n))_{n \in {\mathbb {Z}}}\) defined by
$$\begin{aligned} x(n)= \left\{ \begin{array}{ll} k, &{} n = 2^{k^{2}}, \\ 0, &{} n \ne 2^{k^{2}}, \end{array} \right. \end{aligned}$$is an example of an unbounded \(PAP_{0}({\mathbb {Z}},{\mathbb {R}})\) sequence.
Definition 3
[36]. A sequence \(\{x_{n}\}_{n \in {\mathbb {Z}}} \in l^{\infty }({\mathbb {Z}},{\mathbb {R}}^{n})\) is called pseudo-almost periodic if \(x_{n} = x_{n}^{1}+ x_{n}^{2}\), where \(x_{n}^{1} \in AP({\mathbb {Z}},{\mathbb {R}}^{n}), x_{n}^{2} \in PAP_{0}({\mathbb {Z}},{\mathbb {R}}^{n})\). Denote by \(PAP({\mathbb {Z}},{\mathbb {R}}^{n})\) the set of such sequences.
For \(\{t_{i}\}_{n \in {\mathbb {Z}}} \in T, \{t_{i}^{j}\}\) is defined by
It is easy to verify that the numbers \(t_{i}^{j}\) satisfy
Definition 4
[34]. A function \(f \in PC({\mathbb {R}},{\mathbb {R}}^{n})\) is said to be piecewise almost periodic if the following conditions are fulfilled:
-
1.
\(\{t_{i}^{j} = t_{i+j} - t_{i}\}, i,j \in {\mathbb {Z}}\) are equipotentially almost periodic, that is, for any \(\varepsilon > 0\), there exists a relatively dense set in \({\mathbb {R}}\) of \(\varepsilon\)-almost periods common for all of the sequences \(\{t_{i}^{j}\}\).
-
2.
For any \(\varepsilon > 0\), there exists a positive number \(\delta = \delta (\varepsilon )\) such that if the points \(t'\) and \(t''\) belong to the same interval of continuity of f and \(\mid t'-t''\mid <\delta\), then \(\parallel f(t') - f(t'')\parallel < \varepsilon\).
-
3.
For any \(\varepsilon > 0\), there exists a relatively dense set \({\varOmega }_{\varepsilon }\) in \({\mathbb {R}}\) such that if \(\tau \in {\varOmega }_{\varepsilon }\), then
$$\begin{aligned} \parallel f(t+ \tau ) - f(t)\parallel < \varepsilon \end{aligned}$$for all \(t \in {\mathbb {R}}\) which satisfy condition \(\mid t- t_{i}\mid > \varepsilon ,\, i \in {\mathbb {Z}}.\)
We denote by \(AP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) the space of all piecewise almost periodic functions. Obviously, \(AP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) endowed with the supremum norm is a Banach space. Throughout the rest of this paper, we always assume that \(\{t_{i}^{j}\}\) are equipotentially almost periodic. Let \(UPC({\mathbb {R}},{\mathbb {R}}^{n})\) be the space of all functions \(f \in PC({\mathbb {R}},{\mathbb {R}}^{n})\) such that f satisfies the condition (2) in Definition 4.
Define
Definition 5
[36]. A function \(f \in PC({\mathbb {R}},{\mathbb {R}}^{n})\) is said to be piecewise pseudo-almost periodic if it can be decomposed \(f= g+ h\), where \(g \in AP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) and \(h \in PAP_{T}^{0}({\mathbb {R}},{\mathbb {R}}^{n})\). Denote by \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) the set of all such functions. \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) is a Banach space when endowed with the supremum norm.
Remark 2
The functions g and h in Definition 5 are, respectively, called the almost periodic component and the ergodic perturbation of the pseudo-almost periodic function f. The decomposition given in Definition 5 is unique. Further, \((PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n}), \parallel .\parallel _{\infty })\) is a Banach space which contains strictly the set of almost periodic functions. For instance, the function
is a piecewise pseudo-almost periodic function, where
Hence, it is easy to see that f(t) is more general than our traditional piecewise almost periodic functions since the ergodic perturbations are introduced.
Definition 6
[40]. Suppose that both functions f and its derivative \(f'\) are in \(PAP({\mathbb {R}},{\mathbb {R}}).\) That is, \(f= g+h\) and \(f'= g'+h'\), where \(g,g' \in AP({\mathbb {R}},{\mathbb {R}})\) and \(h,h' \in PAP_{0}({\mathbb {R}},{\mathbb {R}})\). Then the functions g and h are continuous differentiable.
Remark 3
Let \(E=\{ f \mid f,f' \in PAP({\mathbb {R}},{\mathbb {R}}^{n})\}\) equipped with the induced norm defined by
Follows from [40] that \((PAP({\mathbb {R}},{\mathbb {R}}^{n}),\parallel . \parallel _{E} )\) is a Banach space.
The initial conditions associated with (1) are of the form
where \(\varphi (.)\) are real-valued piecewise continuous functions defined on \((-\infty , 0]\).
Lemma 1
[32]. Let \(c_{i}(t)\) be an almost periodic function on \({\mathbb {R}}\) and
Then the linear system
admits an exponential dichotomy on \({\mathbb {R}}\).
Lemma 2
[39]. The inhomogeneous linear system
has a unique bounded solution for a vector \(f \in C({\mathbb {R}}, {\mathbb {R}})\) if and only if the inhomogeneous linear system (2) has exponential dichotomy.
The rest of this paper is organized as follows. The existence and the uniqueness of piecewise differentiable pseudo-almost periodic solutions of Eq. (1) in the suitable convex set are discussed in Sect. 2. Some sufficient conditions on the global exponential stability of piecewise differentiable pseudo-almost periodic solutions of Eq. (1) are established in Sect. 3. A numerical example is given in Sect. 4 to illustrate the effectiveness of our results. Finally, we draw conclusion in Sect. 5.
2 Existence of piecewise differentiable pseudo-almost periodic solution
In this section, we establish some results for the existence of the piecewise differentiable pseudo-almost periodic solution of (1). To obtain the existence of piecewise differentiable pseudo-almost periodic solution of system (1), we shall introduce the following lemmas:
Lemma 3
[34]. If \(\phi (.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) and for any \(h \in {\mathbb {R}}\) , then \(\phi (.-h) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\).
Lemma 4
[34]. If \(\phi , \psi \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\) , then \(\phi \times \psi \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\).
Lemma 5
If \(f_{j}(.) \in C({\mathbb {R}},{\mathbb {R}})\) satisfies the Lipschitz condition, \(\phi (.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}), \phi '(.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\) and \(\beta (.) \in AP_{T}({\mathbb {R}},{\mathbb {R}}) \text{ such that } 1-\beta' (t)>0 \text{ for all } t\in\mathbb {R}\) then \(f_{j}(\phi (.-\beta (.))) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\)
Proof
We have \(\varphi = \varphi _{1}+ \varphi _{2},\) where \(\varphi _{1} \in AP_{T}({\mathbb {R}},{\mathbb {R}})\) and \(\varphi _{2} \in PAP_{T}^{0}({\mathbb {R}},{\mathbb {R}}).\) Let
Firstly, it follows from (Theorem 2.11, [33]) that \(M_{1}(.)\in AP_{T}({\mathbb {R}},{\mathbb {R}})\). Then, we show that \(M_{2}(.) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\) because
Thus \(M_{2}(.) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). So, \(f_{j}(\phi (.-\beta (.))) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\) and \(f_{j}(\phi '(.-\beta (.))) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\). The proof is complete. \(\square\)
Theorem 1
Under the conditions (H1)–(H2), and for all \(1\le j \le n\) , \(x_{j}(.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}) , x'_{j}(.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\), then for all \(1\le i \le n\), the function \(\phi _{i} : t \longmapsto \int _{-\infty }^{t} d_{ij}(t-s) f_{j}(x'_{j}(s)) {\mathrm{d}}s\) belongs to \(PAP_{T}({\mathbb {R}},{\mathbb {R}})\).
Proof
For \(x_{j}(.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\),it is not difficult to see that \(f_{j}(x'_{j}(.)) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\) by Lemma 5. Let \(f_{j}(x'_{j}(.))= u_{j}(.)+ v_{j}(.)\), where \(u_{j} \in AP_{T}({\mathbb {R}},{\mathbb {R}})\) and \(v_{j} \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\), then
First, it is not difficult to see that \(\phi ^{1}_{i} \in UPC({\mathbb {R}},{\mathbb {R}})\). Let \(t_{k}< t\le t_{k+1}\).
For \(\varepsilon > 0\), let \({\varOmega }_{\varepsilon }\) be a relatively dense set of \({\mathbb {R}}\) formed by \(\varepsilon\)-periods of \(u_{j}\). For \(\tau \in {\varOmega }_{\varepsilon }\) and \(0< h < \min \{\varepsilon , \frac{\alpha }{2}\},\)
Since \(u_{j} \in AP_{T}({\mathbb {R}},{\mathbb {R}})\), one has
\(\mid u_{j}(t+\tau ) - u_{j}(t) \mid \le \varepsilon\), for all \(t \in [ t_{w}+h, t_{w+1}-h]\) and \(w \in {\mathbb {Z}}, w \le k,\)
then
On the other hand,
Similarly, one has
where \(E_{1},E_{2}\) are some positive constants. Hence, \(\phi ^{1}_{i}(t) \in AP_{T}({\mathbb {R}},{\mathbb {R}})\).
In fact, for \(r > 0\), one has
Since \(v_{i}(t) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\), it follows that \(v_{i}(.-s) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\) for each \(s \in {\mathbb {R}}\) by Lemma 3. Using the Lebesgue dominated convergence theorem, we have \(\phi ^{2}_{i}(t) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). This completes the proof. \(\square\)
Similarly, we can obtain:
Corollary 1
Under the conditions (H1)–(H2), and for all \(1\le j \le n\) , \(x_{j}(.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\), then for all \(1\le i \le n\), the function \(\phi _{i} : t \longmapsto \int _{-\infty }^{t} h_{ijl}(t-s) f_{j}(x_{j}(s)) {\mathrm{d}}s\) belongs to \(PAP_{T}({\mathbb {R}},{\mathbb {R}})\).
Corollary 2
Under the conditions (H1)–(H2), and for all \(1\le l \le n\) , \(x_{j}(.) \in PAP_{T}({\mathbb {R}},{\mathbb {R}})\), then for all \(1\le i \le n\), the function \(\phi _{i} : t \longmapsto \int _{-\infty }^{t} k_{ijl}(t-s) f_{l}(x_{l}(s)) {\mathrm{d}}s\) belongs to \(PAP_{T}({\mathbb {R}},{\mathbb {R}})\).
Lemma 6
Suppose that assumptions (H1)–(H3) hold. Define the nonlinear operator \(X_{\varphi }(.)\) as follows, for each \(\varphi = (\varphi _{1},\ldots ,\varphi _{n}) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) and \(\varphi ' = (\varphi '_{1},\ldots ,\varphi '_{n}) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\):
and
then \(X_{\varphi }\) maps \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) into itself.
Proof
First, note that, for all \(1 \le i \le n\), the function
is in \(PAP_{T}({\mathbb {R}},{\mathbb {R}})\), by using Lemmas 3, 4, 5, Theorem 1, Corollaries 1, 2. Consequently, for all \(1 \le i \le n, F_{i}\) can be expressed as
where \(F_{i}^{1} \in AP_{T}({\mathbb {R}},{\mathbb {R}})\) and \(F_{i}^{2} \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). So
(i) \(H_{i}^{1}(.) \in UPC({\mathbb {R}},{\mathbb {R}})\). Let \(t^{'},t^{''} \in (t_{k},t_{k+1}), k \in {\mathbb {Z}}, t^{''} < t^{'}\), then
\(\mid H_{i}^{1}(t^{'}) - H_{i}^{1}(t^{''}) \mid\)
it is easy to see that for any \(\varepsilon > 0\), there exists
and for a suitable \(t^{'}, t^{''}\) satisfying \(0< t^{'} - t^{''} < \delta\) one has
which implies that \(H_{i}^{1}(.) \in UPC({\mathbb {R}},{\mathbb {R}})\).
(ii) \(H_{i}^{1}(.) \in AP_{T}({\mathbb {R}},{\mathbb {R}})\). Since \(F_{i}^{1} \in AP_{T}({\mathbb {R}},{\mathbb {R}})\), for \(\varepsilon > 0\), there exists a relatively dense set \({\varOmega }_{\varepsilon }\) such that for \(\tau \in {\varOmega }_{\varepsilon }, t \in {\mathbb {R}}, \mid t- t_{k} \mid > \varepsilon , k \in {\mathbb {Z}}\), then
So there exists \(\theta \in ]0, 1[\) such that
where
and
we obtain immediately that, \(H_{i}^{1}(.) \in AP_{T}({\mathbb {R}},{\mathbb {R}})\).
Now, we turn our attention to \(H_{i}^{2}(.)\), so
where
and
Pose \(m= t-s\), then by Fubini’s theorem one has
since the function \(F_{i}^{2}(.) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\), and by the Lebesgue dominated convergence theorem, we obtain
On the other hand, notice that\(\mid F_{i}^{2} \mid _{\infty }= \sup _{t \in {\mathbb {R}}} \mid F_{i}^{2}(t) \mid < \infty\) then
then
Consequently, the function \(H_{i}^{2}\) belongs to \(PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). So \(X_{\varphi }\) belongs to \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n}).\) \(\square\)
Lemma 7
Suppose that assumptions (H4) hold, Define the nonlinear operator, for each \(\varphi =(\varphi _{1},\ldots ,\varphi _{n}) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\), we have
Proof
We will show that \(\sum \nolimits _{ t_{k}<t} e^{- \int _{t_{k}}^{t} a_{i}(u) {\mathrm{d}}u} I_{k}(\varphi _{i}(t_{k})) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}).\) It is not difficult to see that\(\sum \limits _{ t_{k}<t} e^{- \int _{t_{k}}^{t} a_{i}(u) {\mathrm{d}}u} I_{k}(\varphi _{i}(t_{k})) \in UPC({\mathbb {R}},{\mathbb {R}})\). After by Corollary 2.1 (see [34]), \(I_{k}(x_{i}(t_{k})) \in PAP({\mathbb {Z}},{\mathbb {R}})\), then let \(I_{k}(x_{i}(t_{k})) = I_{k}^{1} + I_{k}^{2}\) where \(I_{k}^{1} \in AP({\mathbb {Z}},{\mathbb {R}})\) and \(I_{k}^{2} \in PAP_{0}({\mathbb {Z}},{\mathbb {R}})\), so
Since \(\{ t_{j}^{k}\} ,k,j \in {\mathbb {Z}}\) are equipotentially almost periodic, then by Lemma 3.2 (see [34]), for any \(\varepsilon > 0\), there exists relative dense sets of real numbers \({\varOmega }_{\varepsilon }\) and integers \(Q_{\varepsilon }\), such that for \(t_{k}< t\le t_{k+1}, \tau \in {\varOmega }_{\varepsilon }, q \in Q_{\varepsilon }, \mid t- t_{k}\mid> \varepsilon , \mid t- t_{k+1}\mid > \varepsilon , k \in {\mathbb {Z}}\), one has
that is \(t_{k+q}> t + \tau > t_{k+q+1};\) then
so, \({\varPhi }_{1}(t) \in AP_{T}({\mathbb {R}},{\mathbb {R}})\).
Next, we show that \({\varPhi }_{2}(t) \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). For a given \(k \in {\mathbb {Z}}\), define the function \(\chi (t)\) by
then
then \(\chi \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). Define \(\chi _{n} :{\mathbb {R}} \rightarrow {\mathbb {R}}\) by
So \(\chi _{n} \in PAP^{0}_{T}({\mathbb {R}},{\mathbb {R}})\). Moreover,
therefore, the series \(\sum \nolimits _{n=1}^{\infty } \chi _{n}\) is uniformly convergent on \({\mathbb {R}}\). By Lemma 2.2 (see [34]), one has
So, \(\sum \limits _{ t_{k}<t} e^{- \int _{t_{k}}^{t} a_{i}(u) {\mathrm{d}}u} I_{k}(x_{i}(t_{k})) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}).\) \(\square\)
Theorem 2
Suppose that assumptions (H1)–(H4) hold. Define the nonlinear operator \({\varGamma }\) as follows, for each \(\varphi =(\varphi _{1},\ldots ,\varphi _{n}) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n}),\) and \(\varphi ' =(\varphi '_{1},\ldots ,\varphi '_{n}) \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n}),\)
then \({\varGamma }\) maps \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) into itself and if
then \({\varGamma }^{'}\) maps \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\) into itself.
Theorem 3
Let conditions (H1)–(H5) hold. Then, there exists a unique piecewise differentiable pseudo-almost periodic solution of system (1) in the region
where
Proof
It is easy to see that \(B = \{\varphi / \varphi ,\varphi ' \in PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n}), \parallel \varphi - \varphi _{0} \parallel _{E} \le \frac{\widehat{p} L }{1-\widehat{p}}\}\) is a closed convex subset of \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\). According to the definition of the norm of Banach space \(PAP_{T}({\mathbb {R}},{\mathbb {R}}^{n})\), we get
Therefore, for \(\forall \varphi \in B\), we have
In view of (H1), we have
Now, we prove that the mapping \({\varGamma }\) is a self-mapping from B to B. In fact, for all \(\varphi \in B\) by using the estimate just obtained together with (4), (5), Lemma 1, Lemma 2, Lemma 6 and Lemma 7 we obtain
On the other hand
where \(i = 1, 2,\ldots ,n.\) So we can write
where \(\widehat{p} < 1\), it implies that \({\varGamma }_{\varphi }(.) \in B\). So, the mapping \({\varGamma }\) is a self-mapping from B to B. Next, we prove that the mapping \({\varGamma }\) is a contraction mapping of the B. In fact, in view of (H1), \(\forall \phi ,\psi \in B\), we have
On the other hand
where \(i = 1, 2,\ldots ,n.\) It follows that
where
It is clear that the mapping \({\varGamma }\) is a contraction. Therefore the mapping \({\varGamma }\) possesses a unique fixed point \(z^{*} \in B, {\varGamma }(z^{*}) = z^{*}\). By (7), \(z^{*}\) satisfies (1). So \(z^{*}\) is a piecewise differentiable pseudo-almost periodic solution of system (1) in the region B. The proof is now complete. \(\square\)
3 Exponential stability of piecewise differentiable pseudo-almost periodic solution
To study the exponential stability of (1), we need the following lemma and notations. So, for a continuous function g(t), we denote \(\overline{g}(t) = \sup \nolimits _{ t- \tau ^{+} \le s\le t} \mid g(s) \mid .\)
(H6) Assume that there exist positive constants \(p_{i}\) and \(q_{i}\), such that
for \(t \in [0, \infty ), i = 1,2,\ldots ,n\)
Lemma 8
Let \(\tau \ge 0\) be a given real constant. Assume that p(t) and \(q_{i}(t)(i=1,2)\) be continuous functions on \([0,+\infty ), k(s)\) be nonnegative function on \([0,+\infty )\) and satisfies that \(\int _{0}^{+\infty } k(s){\mathrm{d}}s \le k\) and \(\int _{0}^{+\infty } k(s) e^{\mu s} {\mathrm{d}}s \le +\infty\) for positive constant \(\mu\).
Moreover, assume that there exist positive constants \(\eta\) and M such that
then
Proof
Consider the following equation:
Because
and \(G(+\infty ) > 0,\) we follow that \(G(\lambda )\) is a strictly monotone increasing function.
Therefore, for any \(t\ge 0\), there is a unique positive \(\lambda (t)\) such that
Moreover, \(\lambda ^{*}\) exists and \(\lambda ^{*} \ge 0\).
Now, we will prove \(\lambda ^{*} > 0\). Suppose this is not true. Pick \(\varepsilon \in (0,\mu )\) such that \(\varepsilon < \{ \frac{\eta }{3}, \frac{1}{\tau } \ln (1+ \frac{\eta }{3M})\}\) and \(\int _{0}^{+\infty } k(s) e^{\varepsilon s} {\mathrm{d}}s \le k+ \frac{\eta }{3M}.\) Then there exist \(t^{*} > 0\) such that \(\lambda ^{*}(t^{*}) < \varepsilon\) and
Now we have
which is a contradiction. Hence, \(\lambda ^{*} > 0\). The proof of this lemma is completed. \(\square\)
Then we have
Lemma 9
Assume that (H1)–(H6) hold and there exist nonnegative vector functions \((V_{1}(t),\ldots ,V_{n}(t))^{T}\) and \((W_{1}(t),\ldots ,W_{n}(t))^{T} \in PC([-\rho ^{+},0],{\mathbb {R}}^{n})\), where \(V_{i}(t)\) is continuous at \(t \ne t_{k}\) \((k \in {\mathbb {N}}^{*})\), such that
for \(t>0, i =1,2,\ldots ,n\) and \(k \in {\mathbb {N}}^{*}\). Then for all \(t\ge 0\) and \(i =1,2,\ldots ,n\), there exists a positive constant \(\widetilde{L}\) such that
where \(\lambda ^{*}\) is defined, respectively, as
Proof
By the similar analysis in Lemma 8, we can deduce that \(\lambda _{i}^{*} > 0\) and \(\widehat{\lambda }_{i}^{*}> 0\) exist uniquely.
Choose a positive constant \(\theta\) such that
Let
Then for all \(t \in (-\infty ,0]\) and \(\gamma > 1\), we have
Then
For the sake of contradiction, assume that there exist \(i \in \{1,2,\ldots ,n\}\) and \(\overline{t} > 0\) such that
Then we have the following
(I) \((1/p_{i}) V_{i}(\overline{t}^{+}) \ge \gamma {\varPsi }(\overline{t})\) then we have the following subcases.
(i) \(\overline{t} \ne t_{k},t_{k} \in \in {\mathbb {N}}^{*}\). So \(V_{i}(t)\) is continuous at \(\overline{t}\). By 17, we have
From (H6), (17) and the definition of \(\lambda ^{*}\), we have
which is a contradiction with (18).
(ii) There exists \(k_{0} \in {\mathbb {N}}^{*}\) such that \(\overline{t} = t_{k}\). By (17), we have
Noting \(\frac{1}{p_{i}} V_{i}(\overline{t}^{-}) \ne \frac{1}{p_{i}} V_{i}(\overline{t}^{+})\), we have \(\frac{1}{p_{i}} V_{i}(\overline{t}^{-}) < \gamma {\varPsi }(\overline{t})\) or \(\gamma {\varPsi }(\overline{t}) < \frac{1}{p_{i}} V_{i}(\overline{t}^{+})\). Without loss of generality, we assume that \(\gamma {\varPsi }(\overline{t}) < \frac{1}{p_{i}} V_{i}(\overline{t}^{+})\). from (9) and (20) we get that
Simplifying (21), we obtain \(L_{1}> 1,\) which contradict that \(L_{1}<1\).
If (I) does not hold, then
(II)
Then from (8) and (H6) we have
which is a contradiction. From (I) and (II), (16) holds. Letting \(\gamma \rightarrow 1^{+}\) in (16), we have
So \(\frac{1}{p_{i}} V_{i}(t) \le {\varPsi }(t)\) for all \(t \in [0, \infty ), \, i =1,2,\ldots ,n.\) Let \(M= \max \nolimits _{1\le i\le n}\{ p_{i} \theta \}\) then for \(t \ge 0\) and \(i =1,2,\ldots ,n\), we have
The proof is complete. \(\square\)
Theorem 4
Assume that (H1)–(H6) hold, then the unique piecewise differentiable pseudo-almost periodic solution of system (1) is globally exponentially stable.
Proof
It follows from Theorem 3 that system (1) has at least one piecewise differentiable pseudo-almost periodic solution \(x^{*}(t)=(x^{*}_{1}(t),\ldots ,x^{*}_{n}(t))^{T} \in {\mathbb {B}}\) with initial value \(\phi ^{*}(t)\). Let \(x(t)=(x_{1}(t),\ldots ,x_{n}(t))^{T}\) be an arbitrary solution of system (1) with initial value \(\phi (t)\).
Let \(V_{i}(t)= \mid x_{i}(t)-z_{i}(t) \mid , W_{i}(t)= \mid x'_{i}(t)-z'_{i}(t)\mid\) for \(i=1, \ldots , n\), Then,
By (9) and (H5) we have
By (26)–(28), (H1)–(H6) and Lemma 9, there exists a positive constant M such that
where \(\lambda ^{*}\) is defined in (11). \(\square\)
Remark 4
To the best of our knowledge, there have been no results of piecewise pseudo-almost periodic solutions for impulsive neutral high-order Hopfield neural networks with time-varying coefficients, mixed delays and leakage until now. Hence, the obtained results are essentially new and the investigation methods used in this paper can also be applied to study the piecewise pseudo-almost periodic solutions for some other types of neural networks.
Remark 5
If throughout this paper, for \(i,j,l = 1,2,\ldots ,n\), it will be assumed that \(a_{i}: {\mathbb {R}} \longrightarrow {\mathbb {R}}^+\) is almost periodic functions, \(b_{ij}, c_{ij}, \alpha _{ijl}, \beta _{ijl}, J_{i}: {\mathbb {R}} \longrightarrow {\mathbb {R}}\) are almost periodic functions, then the investigation methods used here can also be applied to study the piecewise almost periodic solutions for some other types of impulsive neural networks.
4 Application
Consider the following impulsive neutral high-order Hopfield neural networks with time-varying coefficients, mixed delays and leakage:
where
for all \(t \in {\mathbb {R}}\)
Then
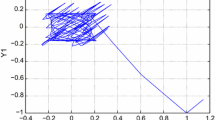
Let \(p_{1} = p_{2}= 1\) and \(q_{1}= q_{2}= 70\), and from the above assumption, the (H6) is satisfied. Therefore, all conditions from Theorems 3 and 4 are satisfied; then, the impulsive neutral high-order Hopfield neural networks with time-varying coefficients, mixed delays and leakage have a unique piecewise differentiable pseudo-almost periodic solution. Simulation results of Example 30 are depicted in Figs. 1, 2 and 3.
Figures 4 and 5 confirm that the proposed condition in Theorem 4 leads to globally exponentially stable piecewise differentiable pseudo-almost periodic solution for system 30.
5 Conclusion
In this paper we discuss the existence and the exponential stability of piecewise differentiable pseudo-almost periodic solutions for a class of impulsive neutral high-order Hopfield neural networks with mixed time-varying delays and leakage delays. We give several sufficient conditions for the existence and the exponential stability of the solution. The results of this paper are new, and they supplement previously known results. An example is given to illustrate the results.
References
Aouiti C, M’hamdi MS, Touati A (2016) Pseudo almost automorphic solutions of recurrent neural networks with time-varying coefficients and mixed delays. Neural Process Lett. doi:10.1007/s11063-016-9515-0
Li Y, Wang C, Li X (2014) Existence and global exponential stability of almost periodic solution for high-order BAM neural networks with delays on time scales. Neural Process Lett 39(3):247–268
Yu Y, Cai M (2008) Existence and exponential stability of almost-periodic solutions for high-order Hopfield neural networks. Math Comput Model 47(9–10):943–951
Xiao B, Meng H (2009) Existence and exponential stability of positive almost periodic solutions for high-order Hopfield neural. Appl Math Model 33(1):532–542
Xiang H, Yan K-M, Wang B-Y (2006) Existence and global exponential stability of periodic solution for delayed high-order Hopfield-type neural networks. Phys Lett A 352(4–5):341–349
Xu B, Liu X, Teo K L (2009) Global exponential stability of impulsive high-order Hopfield type neural networks with delays. Comput Math Appl 57(11–12):1959–1967
Cheng L, Zhang A, Qiu J, Chen X, Yang C, Chen X (2015) Existence and stability of periodic solution of high-order discrete-time Cohen–Grossberg neural networks with varying delays. Neurocomput Part C 149:1445–1450
Cao J, Liang J, Lam J (2004) Exponential stability of high-order bidirectional associative memory neural networks with time delays. Phys D 199(3–4):425–436
Ren F, Cao J (2007) Periodic oscillation of higher-order bidirectional associative memory neural networks with periodic coefficients and delays. Nonlinearity 20(3):605–629
Jinde C, Rakkiyappan R, Maheswari K, Chandrasekar A (2016) Exponential \(H_\infty\) filtering analysis for discrete-time switched neural networks with random delays using sojourn probabilities. Sci China Technol Sci March 59(3):387–402
Cao J, Ho Daniel WC, Huang X (2007) LMI-based criteria for global robust stability of bidirectional associative memory networks with time delay. Nonlinear Anal 66(7):1558–1572
Wang Y, Cao J (2013) Exponential stability of stochastic higher-order BAM neural networks with reaction diffusion terms and mixed time-varying delays. Neurocomputing 119:192–200
Ren F, Cao J (2007) Periodic solutions for a class of higher-order Cohen–Grossberg type neural networks with delays. Comput Math Appl 54(6):826–839
Xiang H, Cao J (2009) Almost periodic solution of Cohen–Grossberg neural networks with bounded and unbounded delays. Nonlinear Anal Real World Appl 10(4):2407–2419
Cao J, Song Q (2006) Stability in Cohen Grossberg-type bidirectional associative memory neural networks with time-varying delays. Nonlinearity 19(7):1601–1617
Tu Z, Cao J, Hayat T (2016) Global exponential stability in Lagrange sense for inertial neural networks with time-varying delays. Neurocomputing 171(1):524–531
Pan L, Cao J (2011) Anti-periodic solution for delayed cellular neural networks with impulsive effects. Nonlinear Anal Real World Appl 12(6):3014–3027
Rakkiyappan R, Balasubramaniam P, Cao J (2010) Global exponential stability results for neutral-type impulsive neural networks. Nonlinear Anal Real World Appl 11(1):122–130
Xiao B (2009) Existence and uniqueness of almost periodic solutions for a class of Hopfield neural networks with neutral delays. Appl Math Lett 22(4):528–533
Yang W (2012) Existence and stability of almost periodic solutions for a class of generalized Hopfield neural networks with time-varying neutral delays. J Appl Math Inf 30(5–6):1051–1065
Bai C (2008) Global stability of almost periodic solution of Hopfield neural networks with neutral time-varying delays. Appl Math Comput 203(1):72–79
Bai C (2009) Existence and stability of almost periodic solutions of hopfield neural networks with continuously distributed delays. Nonlinear Anal 71(11):5850–5859
Huang H, Cao J, Wang J (2002) Global exponential stability and periodic solutions of recurrent neural networks with delays. Phys Lett A 298(5–6):393–404
Jiang H, Cao J (2006) Global exponential stability of periodic neural networks with time-varying delays. Neurocomputing 70(1):343–350
Xiang H, Cao J (2009) Almost periodic solutions of recurrent neural networks with continuously distributed delays. Nonlinear Anal 71(12):6097–6108
Gopalsamy K (2007) Leakage delays in BAM. J Math Anal Appl 325(2):1117–1132
Li X, Cao J (2010) Delay-dependent stability of neural networks of neutral type with time delay in the leakage term. Nonlinearity 23(7):1709–1726
Li C, Huang T (2009) On the stability of nonlinear systems with leakage delay. J Frankl Inst 346(4):366–377
Gao J, Wang Q-R, Zhang L-W (2014) Existence and stability of almost periodic solutions for cellular neural networks with time-varying delays in leakage terms on time scales. Appl Math Comput 237:639–649
Chuanyi Z (1994) Pseudo almost periodic solutions of some differential equations. J Math Anal Appl 181(1):6276
Chuanyi Z (1995) Pseudo almost periodic solutions of some differential equations, II. J Math Anal Appl 192(2):543–561
Shao J, Wang L, Ou C (2009) Almost periodic solutions for shunting inhibitory cellular neural networks without global Lipschitz activaty functions. Appl Math Model 33(6):2575–2581
Li Y, Wang C (2011) Almost periodic functions on time scales and applications. Discrete Dyn Nat Soc. Article ID 727068, 20 pages
Xia Z (2015) Pseudo almost periodic mild solution of nonautonomous impulsive integro-differential equations. Mediterr J Math 12(1):1–22
Liu J, Zhang C (2013) Composition of piecewise pseudo almost periodic functions and applications to abstract impulsive differential equations. Adv Differ Equ 2013:11. doi:10.1186/1687-1847-2013-11
Chérif F (2014) Pseudo almost periodic solutions of impulsive differential equations with delay. Differ Equ Dyn Syst 22(1):73–91
Jiang H, Teng Z (2004) Global exponential stability of cellular neural networks with time-varying coefficients and delays. Neural Netw 17(10):1415–1425
Zhao W (2008) Dynamics of Cohen–Grossberg neural network with variable coefficients and time-varying delays. Nonlinear Anal Real World Appl 9(3):1024–1037
Lin Z, Lin Y-X (2000) Linear systems, exponential dichotomy, and structure of sets of hyperbolic points. World Scientific, Singapore
Zhang C (2003) Almost periodic type functions and ergodicity. Science Press, Beijing
Wang P, Li Y, Ye Y (2016) Almost periodic solutions for neutral-type neural networks with the delays in the leakage term on time scales. Math Methods Appl Sci (2 Feb 2016). doi:10.1002/mma.3857
Stamov TG, Stamova IM (2007) Almost periodic solutions for impulsive neural networks with delay. Appl Math Model 31(7):1263–1270
Stamov TG (2008) Existence of almost periodic solutions for impulsive cellular neural networks. Rocky Mt J Math 38(4):1271–1284
Ylmaz E (2014) Almost periodic solutions of impulsive neural networks at non-prescribed moments of time. Neurocomputing 141:148–152
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Aouiti, C. Oscillation of impulsive neutral delay generalized high-order Hopfield neural networks. Neural Comput & Applic 29, 477–495 (2018). https://doi.org/10.1007/s00521-016-2558-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-016-2558-3