1 Introduction

The biped robot locomotion attracts much attention from the research community [1–8]. A biped robot is not fixed to the floor, while it must be able to interact with the environment through multiple contacts to maintain dynamic balance and enhance its flexibility, dexterity, and functionality so as to follow and work with human autonomously. Therefore, the dynamic balance control for biped robots is particularly important. Ground reaction force for the biped legs must be regulated to maintain dynamic balance that is robust to unknown disturbances. In this respect, several research results have been reported. In [9], a kind of dynamically stable and collision-free trajectories are planned for full-body posture goals of biped robots. In [10], control design was constructed for stabilization of non-periodic trajectories of underactuated robots traversing rough or uneven terrain. In [11], a simple balance control algorithm compatible with a typical walking control system in the 2D plane was proposed. In [12], the authors constructed an efficient control using implicit function with support vector regression-based data-driven model for holonomic constrained under-actuated biped robots.

Different from performance indicators of manipulators and vehicles, good performance for a walking robot can be simply defined as maintaining the dynamic balance during its locomotion [13–19]. In this respect, the main control objective of a walking robot is to guarantee a suitable ground reaction force to maintain the dynamic balance, and it is also desirable to have a controller that allows the robot to adapt (compliantly) to unknown external forces. Traditionally, a general strategy is to use the dynamics based walking pattern generation which provides the desired trajectories for underlying position controllers [20–23]. In [24], a locomotion control system using nonlinear oscillators for a biped robot was proposed to achieve robust walking. In [25], an approach was proposed to find stable as well as unstable hybrid limit cycles for a planar compass-like biped on a shallow slope without integrating the full set of differential equations and approximating the dynamics. In [2], an approach for the closed-loop control of a fully actuated walking biped that leverages on its natural dynamics was presented, and the input state-dependent torques were built using a combination of low-gain spring-damper couples. Researches were also made to construct complete models to represent the whole periodic walking motion and three phases of the walking cycle (single-support, double-support, and transition phase). The performance and stability analysis of the whole closed-loop motion system are improved because that the integrated biped model is studied carefully [26, 27]. On the other hand, to maintain dynamic balance in various situations, learning algorithms for biped walking were presented in [28–32].

For biped robots, appropriate ground reaction forces are necessary to guarantee the dynamic balance especially when there are disturbances of external wrenches (forces and moments) including the gravity force and the inertia wrench exist. Since each toe and heel are independently characterized by non-penetration and no-slip constraint with the ground, and the external wrench is usually time-varying, the contact forces must satisfy certain constraints and be solved in real time to balance the change of the external wrench, typically the friction cone constraint such that it can be feasible. Therefore, how to determine the existence of feasible contact forces to resist an external wrench and maintain the system’s equilibrium need to be considered. On the other hand, for a resistable external wrench, there will be infinite solutions to counterbalance it, since there are many configurations. Then some optimization criterion should be adopted in computing the contact forces, usually to minimize their overall magnitude.

To perform dynamic balance control for the biped, the result of contact-force optimization must be used in the control law, and thus, the optimal force-distribution problem can be solved in real time. Parallel and distributed approaches to contact-force optimization for the biped are deemed necessary and desirable. In recent years, neural network-based approaches have demonstrated their great promise for optimization. Neural networks for constrained optimization problems have been widely explored for real-time applications [33]. Reported results of numerous investigations have shown many advantages over the traditional optimization algorithms, especially in real-time applications [34].

In this paper, we consider dynamical balance optimization and biped locomotion in double-support phase. The biped robot usually starts and stops motion at the double-support configuration. The analysis of biped locomotion in the double-support phase is very important for improving the smoothness of the biped locomotion system and dynamic balance [35]. This paper investigates the dynamic balance optimization and control of biped robots with the perturbing external forces in the double-support phase. First, we formulate a constrained dynamic model of the biped robot and a reduced order model for the double-support phase. Considering the dynamic external wrench on the biped, a dynamic force distribution approach based on quadratic objective function [36] is proposed for computing the optimal contact forces to equilibrate a dynamic external wrench, such that the sum of the normal force components is minimized for enhancing safety and energy saving. Then, a primary recurrent neural network (RNN) with self-stabilizing ability is adopted to deal with the complicated optimization problem subject to both equality and inequality constraints. For the obtained contact forces and desired trajectories, we propose the hybrid motion/force control based on the second RNN to approximate unknown dynamic functions with the adaptive weight parameters updating, and the adaptive learning algorithms that can learn the parameters of the RNN are derived using Lyapunov stability theorem. The proposed control can confront the uncertainties including approximation error, optimal parameter vectors, higher-order terms in Taylor series, and external disturbances. The verification of the proposed control is conducted using extensive simulations.

2 Dynamics of biped robots

The constraints for the biped robot in the double-support phase are assumed to be holonomic, arising from geometrical constraints on the joint coordinates. For a biped robot with n joint coordinates q and n input torques τ, these constraints can be represented by

$$\varPhi (q) = 0$$
(1)

where Φ ∊ R m, and m is the dimension of the constraints, for example, m = 3 for a two-dimensional (2-D) biped model and m = 6 for a three-dimensional (3-D) model. Define the augmented Lagrangian

$$L = K - P + f^{T} \varPhi$$
(2)

where K is the total kinematic energy, P is the potential energy, and f is an m-vector of constraint force. The equations of motion can be written as

$$\frac{\text{d}}{{{\text{d}}t}}\frac{\partial L}{\partial q} - \frac{\partial L}{\partial q} = \tau$$
(3)

Thus, the dynamic equations of the biped robot in the double-support phase can be represented by

$$M(q) + C(q,\dot{q})\dot{q} + G(q) = \tau + J^{T} f$$
(4)
$$M = [m_{kj} ]_{k = 1, \ldots ,n;j = 1, \ldots ,n}$$
(5)
$$C(q,\dot{q}) = \left[ {\sum\limits_{i = 1}^{n} {\frac{{\partial m_{kj} }}{{\partial q_{i} }} + \frac{{\partial m_{kj} }}{{\partial q_{j} }}} - \frac{{\partial m_{kj} }}{{\partial q_{k} }}} \right]_{k = 1, \ldots ,n;j = 1, \ldots ,n}$$
(6)
$$G(q) = \frac{\partial P}{\partial q}$$
(7)
$$J = \frac{\partial \varPhi }{\partial q}$$
(8)

where M(q) ∊ R n×n is a symmetric positive definite inertia matrix, \(C(q,\dot{q}) \in R^{n \times n}\), G(q) ∊ R n, and J ∊ R m×n.

When the biped is in the double-support phase, the number of DOF becomes (n − m) and the left m DOF contribute to the contact forces. We assume that the constraints can be written as

$$\varPhi (q) = \varPhi_{1} (q_{1} ) - \varPhi_{2} (q_{2} ) = 0$$
(9)

where q 1 are (n − m) independent coordinates and q 2 are m constraint coordinates. The physical interpretation of this assumption is that the position and orientation of the biped body can be calculated either starting from the left foot or the right foot, and each involves either of the joint coordinates q 1 or q 2. By differentiating (9), we obtain

$$J(q)\dot{q} = J_{1} (q_{1} )\dot{q}_{1} + J_{2} (q_{2} )\dot{q}_{2} = 0$$
(10)

where

$$J = \left[ {\frac{\partial \varPhi }{{\partial q_{1} }},\frac{\partial \varPhi }{{\partial q_{2} }}} \right] = [J_{1} ,J_{2} ]$$
(11)

and J 1(q 1) = ∂ Φ/ ∂ q 1, and J 2(q 2) = −∂ Φ/ ∂ q 2, with J 1 ∊ R m×(n−m) and J 2 ∊ R m×m, implying that

$$\dot{q}_{2} = \frac{{\partial q_{2} }}{{\partial q_{1} }}\dot{q}_{1} = - J_{2}^{ - 1} J_{1} \dot{q}_{1}$$
(12)

The generalized displacement and velocity can be expressed in terms of the independent coordinates q 1 and \(\dot{q}_{1}\), as

$$q = [q_{1}^{T} ,q_{2}^{T} ]^{T}$$
(13)
$$\dot{q} = \left[ {\begin{array}{*{20}c} {I_{n - m} } \\ { - J_{2}^{ - 1} J_{1} } \\ \end{array} } \right]\dot{q}_{1} = H(q)\dot{q}_{1}$$
(14)

Due to the velocity transformation (14), the generalized acceleration satisfies \(\textit{\"{q}} = H(q)\textit{\"{q}}_{1} + \dot{H}(q)\dot{q}_{1}\). The motion (4) is further represented by the independent coordinates q 1, \(\dot{q}_{1}\), and \(\textit{\"{q}}_{1}\) as

$$M(q)H(q)\textit{\"{q}}_{1} + \left( {M(q)\dot{H}(q) + C(q,\dot{q})H(q)} \right)\dot{q}_{1} + G(q) = \tau + J^{T} f$$
(15)

Remark 2.1

By (15), there is an actuator redundancy because the dimension of the control input is larger than that of the controlled output. The extra dimension of actuators should be used to produce the ground reaction force, which can balance the external dynamic wrench.

Lemma 2.1

[37] Let \({\text{e = H(s)r}}\) with \({\text{H(s)}}\) representing an (n × m)-dimensional strictly proper exponentially stable transfer function, and r and e denoting its input and output, respectively. Then r ∊ L m 2  ∩ L m ∞ implies that \(\dot{e} \in L_{2}^{m} \cap L_{\infty }^{m}\) , e is continuous, and e → 0 as t → ∞. If, in addition, r → 0 as t → ∞, then \(\dot{e} \to 0\).

Lemma 2.2

Given a differentiable function \(\phi (t):{\mathbb{R}}^{ + } \to {\mathbb{R}}\) , if ϕ(t) ∊ L 2 and \(\dot{\phi }(t) \in L_{\infty }\) , then ϕ(t) → 0 as t → ∞, where L ∞ and L 2 denote bounded and square integrable function sets, respectively.

The dynamic system (4) has the following properties [37].

Property 2.1

Matrices M(q), G(q) are uniformly bounded and uniformly continuous if q is uniformly bounded and continuous. Matrix \(C(q,\dot{q})\) is uniformly bounded and uniformly continuous if \(\dot{q}\) is uniformly bounded and continuous.

Property 2.2

Matrix \(\dot{M} - 2C\) is skew-symmetric. i.e., \(x^{T} (\dot{M} - 2C)x = 0\), ∀x ≠ 0

3 Dynamical balance optimization

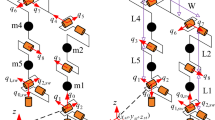
Consider double-support phase shown in Fig. 1, of the biped in a 3-D workspace with i point contacts between the ground and the feet, fixed with a right-handed coordinate frame. Assume that each foot contacts the ground with Coulomb friction. Let n i , o i , and t i be the unit inward normal and two unit tangent vectors at contact i(i = l, r), where l denotes the left leg, and r denotes the right leg, in the COM coordinate frame such that n i  = o i  × t i . The contact force f i can be expressed in the local coordinate frame {n i , o i , t i } by

$$f_{i} = [f_{in} ,f_{io} ,f_{it} ]^{\text{T}}$$
(16)

where f in , f io , and f it are the components of f i along n i , o i , and t i , respectively.

Fig. 1
figure 1

Double-support phase

Full size image

A contact force f i  ∊ R κ is applied by each foot to the ground to hold the biped without slippage and tip-over, and balance with any external forces. To ensure nonslipping at a contact point, with the contact normal along z direction and directed outward and a Coulomb friction coefficient μ i at contact i, the contact force f in must satisfy the contact constraint

$$\sqrt {f_{io}^{2} + f_{it}^{2} } \le \mu f_{in}$$
(17)

where μ is the static friction coefficient of the substrate. The friction constraint can be geometrically represented as a cone with its axis orthogonal with respect to the support surface and with an “opening angle” equal to \(\alpha = { \arctan }(\mu )\).

In order to overcome the nonlinearities induced by the friction cone equations, it is possible to substitute the friction cone with an inscribed pyramid (see Fig. 1). Hence, we have a more restrictive constraint, expressed by

$$\left\| {f_{io} } \right\| \le \mu_{p} f_{in} ,\left\| {f_{it} } \right\| \le \mu_{p} f_{in}$$
(18)

where \(\mu_{p} = \mu /\sqrt 2\).

A definite foot contacts with the ground, only if there is an f in such that

$$f_{in} \ge 0$$
(19)

Concerning the adhesion constraint, it can be satisfied if the absolute value of the sum of the distributed forces is less than the maximum allowable friction force. The friction force constraints may be rewritten as

$$\left[ {\begin{array}{*{20}c} 1 & 0 & { - \frac{\mu }{\sqrt 2 }} \\ { - 1} & 0 & { - \frac{\mu }{\sqrt 2 }} \\ 0 & 1 & { - \frac{\mu }{\sqrt 2 }} \\ 0 & { - 1} & { - \frac{\mu }{\sqrt 2 }} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {f_{io} } \\ {f_{it} } \\ {f_{in} } \\ \end{array} } \right] \le \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(20)

which gives a conservative but linear set of constraints describing a friction pyramid inscribed within the desired friction cone.

We can rewrite the above equation as

$$S_{i} f_{i} \le 0$$
(21)

where S i  ∊ R ι is the matrix coefficient of the friction constraints for the ith foot. Considering the boundedness of f i , we assume that

$$\xi_{i}^{ - } \le f_{i} \le \xi_{i}^{ + }$$
(22)

with the known boundary vectors ξ − i  ∊ R κ and ξ + i  ∊ R κ.

The wrench in the global coordinate frame produced by f i is

$$W_{i} = G_{i} f_{i}$$
(23)

where G i  ∊ R l×κ is the balance matrix for contact i

$$G_{i} = \left[ {\begin{array}{*{20}c} {n_{i} } & {o_{i} } & {t_{i} } \\ {r_{i} \times n_{i} } & {r_{i} \times o_{i} } & {r_{i} \times t_{i} } \\ \end{array} } \right]$$
(24)

Let \({\mathcal{W}}_{\text{ext}}\) denote the ‘‘dynamic” external wrench on the biped. For equilibrium, the resultant wrench \({\mathcal{W}}\) applied by the feet should always conform to

$${\mathcal{W}} = \sum\limits_{{i = \{ l,r\} }} {W_{i} } = \sum\limits_{{i = \{ l,r\} }} {G_{i} } f_{i} = - {\mathcal{W}}_{ext}$$
(25)

In real-time control of the balance of the biped, \({\mathcal{W}}_{\text{ext}}\) is sampled at a sequence of instants with sufficiently small intervals. Thus we encounter the dynamic force distribution problem.

Besides the form-closure constraints, to balance any external wrench \({\mathcal{W}}_{\text{ext}}\) to maintain a stable balance, we consider the quadratic objective function of contact forces. The optimal contact force with holding the balance can be formulated as the following optimization problem with linear and nonlinear constraints

$${\text{minimize}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J(f) = \frac{1}{2}f^{T} Qf + b^{T} f$$
(26)
$${\text{subject}}{\kern 1pt} \;{\kern 1pt} {\text{to}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} Gf = {\mathcal{W}}$$
(27)
$${\kern 1pt} Sf \le C = 0$$
(28)
$$\xi^{ - } \le f \le \xi^{ + }$$
(29)

where f = [f T l , f T r ]T ∊ R 2κ, Q is an 2κ × 2κ symmetric and positive definite matrix, G = [G l , G r ] ∊ R l×2κ, S = [S l , S r ] ∊ R ι×2κ. The above quadratic object function represents the minimum weighted norm of joint torque vectors and minimum norm force when b = 0.

From (26) to (29), a unified QP formulation for the external forces and the friction force constraints is developed. Motivated by the work in [33], the neural network was developed to solve online solution of the QP problem for foot force optimization for quadruped robots. In this paper, the primal–dual neural network is adopted to perform the optimization of the reaction forces from the environments.

For constraints (27) and (28), the corresponding dual decision vector is defined as y ∊ R l. Hence, the primal–dual decision vector u and its upper/lower bounds u ± are defined, respectively, as

$$u: = \left[ {\begin{array}{*{20}c} f \\ y \\ \beta \\ \end{array} } \right],u^{ + } : = \left[ {\begin{array}{*{20}c} {\xi^{ + } } \\ { + y^{ + } } \\ { + y^{ + } } \\ \end{array} } \right],u^{ - } : = \left[ {\begin{array}{*{20}c} {\xi^{ - } } \\ { + y^{ + } } \\ { - y^{ - } } \\ \end{array} } \right] \in R^{2\kappa + l + \iota }$$
(30)

where for the convenience of hardware implementation or simulation, for any i, the elements y + i  ≫ 0 in y + are sufficiently positive to represent + ∞. Thus, the convex set Ω made by primal–dual decision vector u is \(\varOmega = \{ u^{ - } \le u \le u^{ + } \}\). Defining the coefficient matrix M and vector p as

$$M = \left[ {\begin{array}{*{20}c} Q & { - G^{T} } & {S^{T} } \\ G & 0 & 0 \\ { - S^{T} } & 0 & 0 \\ \end{array} } \right] \in R^{(2\kappa + l + \iota ) \times (2\kappa + l + \iota )}$$
(31)
$$p = \left[ {\begin{array}{*{20}c} b \\ { - {\mathcal{W}}} \\ C \\ \end{array} } \right] \in R^{(2\kappa + l + \iota )}$$
(32)

we have the following equivalent result.

Theorem 3.1

[33] (LVI Formulation) Quadratic program (26)–(29) is equivalent to the following linear variational inequalities problem, i.e., to find a vector \(u^{*} \in \varOmega = \{ u|u^{ - } \le u \le u^{ + } \}\) such that

$$(u - u^{*} )^{T} (Mu^{*} + p){ \ge }0,\quad\forall u \in \varOmega$$
(33)

where coefficients M, p, and u ± are defined in (30) and (31), respectively.

It is known that linear variational inequality (33) is equivalent to the following system of piecewise linear equation (also called linear projection equation)

$$P_{\varOmega } \left( {u - (Mu + p)} \right) - u = 0$$
(34)

where P Ω (·) is the projection operator onto Ω and defined as P Ω (u) = [P Ω (u 1), ···, P Ω (u 2κ+l+ι )]T with

$$P_{\varOmega } (u_{i} ) = \left\{ {\begin{array}{*{20}l} {u_{i}^{ - } } \hfill & {if\quad u_{i} < u_{i}^{ - } } \hfill \\ {u_{i} } \hfill & {if\quad u_{i}^{ - } \le u_{i} \le u_{i}^{ + } } \hfill \\ {u_{i}^{ + } } \hfill & {if\quad u_{i} > u_{i}^{ + } } \hfill \\ \end{array} } \right.,\quad \forall i \quad\in \{ 1, \ldots ,2\kappa + l + \iota \} .$$

To solve linear projection Eq. (34), we may follow the dual dynamical system design approach [33, 34] to build a dynamical system. However, such a system is not stable due to M being asymmetric. The design experience motivates us to develop the following modified dynamical system to solve (34)

$$\dot{u} = \gamma (I + M^{T} )\{ P_{\varOmega } \left( {u - (Mu + p)} \right) - u\} .$$
(35)

where γ is a strictly positive design parameter used to scale the convergence rate of the system.

Theorem 3.2

[33] Starting from any initial state, the state vector u(t) of primal–dual dynamical system (35) is convergent to an equilibrium point u * , of which the first n elements constitute the optimal solution f * to the quadratic programming problem in (26)–(29). Moreover, the exponential convergence can be achieved, provided that there exists a constant ρ > 0 such that \(\left\| {u - P_{\varOmega } (u - (Mu + p))} \right\|_{2}^{2} { \ge }\rho \left\| {u - u^{*} } \right\|_{2}^{2}\).

Remark 3.1

For the double-support phase, in order to balance the biped under external wrench, and avoid the slipping or slippage and tip-over, we can obtain the ground applied constraints force to a desired value f *. Therefore, the constraint force errors and f − f * should be within a small neighborhood of zero, i.e., ‖f − f *‖ ≤ ς.

Remark 3.2

The second control objective is to design a position control such that the tracking error of q 1 and \(\dot{q}_{1}\) from their respective desired trajectories q d1 and \(\dot{q}_{1}^{d}\) are within a small neighborhood of zero, i.e., \(\left\| {q_{1} - q_{1}^{d} } \right\| \le \varepsilon_{1}\), and \(\left\| {\dot{q}_{1} - \dot{q}_{1}^{d} } \right\| \le \varepsilon_{2}\). The desired reference trajectory q d1 is assumed to be bounded and uniformly continuous, and has bounded and uniformly continuous derivatives up to the second order.

In summary, the control structure is shown in Fig. 2.

Fig. 2
figure 2

The control structure

Full size image

4 Hybrid motion/force control using RNN

4.1 Recurrent neural network

A three-layer RNN shown in [38] comprises an input layer, a hidden layer with a feedback unit, and an output layer. The Gaussian function is adopted as the activation function in the hidden layer due to its continuous and differential characteristics. The mapping of the RNN is according to the following equation

$$z(N) = \sum\limits_{i = 1}^{n} {w_{k} } \varTheta_{k} (\left\| {x_{i} (N) - v_{ik} } \right\|,\sigma_{ik} ,r_{k} ,\varTheta_{k} (N - 1)) \,$$
(36)

where x = x i , i = 1, 2, …, m are the input variables; z is the output variable; N is the number of iterations; w k represents the connective weights between the hidden layer and the output layer; Θ k represents the output of the kth neurons in the hidden layer; v ik and σ ik are the center and width of the Gaussian function; r k is the internal feedback gain; and \(\left\| \cdot \right\|\) denotes the Euclidean norm. The weight can be represented as

$${\text{net}}_{k} (N) = \sum\limits_{i = 1}^{m} {\delta_{ik}^{2} } [x_{i} (N) + \varTheta_{k} (N - 1)r_{k} - v_{ik} ]^{2} \,$$
(37)

or

$${\text{net}}_{k} (N) = \sum\limits_{i = 1}^{m} {\frac{{[x_{i} (N) + \varTheta_{k} (N - 1)r_{k} - v_{ik} ]^{2} }}{{\sigma_{ik}^{2} }}}$$
(38)

and

$$\varTheta_{k} (N) = \exp ( - {\text{net}}_{k} (N))$$
(39)

where δ ik  = 1/σ ik is the inverse radius of the Gaussian function. Define vectors δ, v and r to be the collection of all parameters in the hidden layer in RNN as

$$\delta = [\delta_{11} , \ldots ,\delta_{m1} ,\delta_{12} , \ldots ,\delta_{m2} , \ldots ,\delta_{1n} , \ldots ,\delta_{mn} ]^{T}$$
(40)
$$v = [v_{11} , \ldots ,v_{m1} ,v_{12} , \ldots ,v_{m2} , \ldots ,v_{1n} , \ldots ,v_{mn} ]^{T}$$
(41)
$$r = [r_{1} , \ldots ,r_{n} ]^{T}$$
(42)

Then the output of the RNN can be represented in a vector form as

$$y(x,\delta ,v,r,W) = W^{T} \varTheta (x,\delta ,v,r)$$
(43)

where W = [w 1, …, w n ]T and Θ = [Θ 1, …, Θ n ]T. It has been proven in [26] that there exists an RNN of (43) such that it can uniformly approximate a nonlinear, even time-varying function.

The approximation error of the RNN output is denoted as

$$\tilde{y} = y - \hat{y} = W^{*T} \varTheta (x,\delta^{*} ,v^{*} ,r^{*} ) - \hat{W}^{T} \varTheta (x,\hat{\delta },\hat{v},\hat{r}) + \varepsilon$$
(44)

where ɛ is a minimum reconstructed error due to the insufficient number of neurons at the hidden layer; δ *, v * and r * are optimal parameters of δ, v and r, and \(\hat{\delta }\), \(\hat{v}\) and \(\hat{r}\) are the estimates of the optimal parameters δ *, v * and r *.

Assumption 4.1

The ideal RNN vectors W *, δ *, v *, r * and the RNN approximation error are bounded over the compact set, i.e.,

$$\left\| {W^{*}} \right\| \le w_{m}, \left\| {\delta^{*}} \right\| \le \delta_{m},\left\| {v^{*}} \right\| \le v_{m},\left\| {r^{*}} \right\| \le r_{m},\left| {\epsilon (x)} \right| \le \epsilon^{*}$$

∀x ∊ Ω x with w m , δ m , v m , r m and \(\epsilon^{*}\) being unknown positive constants.

Remark 4.1

The optimal weight vector W *, δ *, v *, r * in (43) is an ‘‘artificial’’ quantity required only for analytical purposes. Typically, W *, δ *, v *, r * are chosen as the values that minimize \(\epsilon(x)\) for all \(x \in \varOmega_{x} \subset \, {\mathbb{R}}^{{n_{i} }}\), i.e.,

$$(W^{*} ,\delta^{*} ,v^{*} ,r^{*} ): = \arg \min_{W,\delta ,v,r} \{ \mathop {\sup }\limits_{{x \in \varOmega_{x} }} \left| {y - W^{T} \varTheta (x,\delta ,v,r)} \right|\}$$

Remark 4.2

The approximation error \(\epsilon(x)\) is a critical quantity and can be reduced by increasing the number of neurons in the hidden layer. According to the universal approximation theorem, it can be made as small as possible if the number of neurons is sufficiently large [39, 40].

From the above analysis, we see that the system uncertainties are converted to the estimation of unknown parameters W *, δ *, v *, r * and unknown bounds \(\epsilon^{*}\).

As the ideal vectors/constants W *, δ *, v *, r * and \(\epsilon^{*}\) are usually unknown, we use their estimates \(\hat{W}\), \(\hat{\delta }\), \(\hat{v}\), \(\hat{r}\) and \(\epsilon{\hat{}}\) instead. The following lemma gives the properties of the approximation errors \(\hat{W}^{T} \varTheta (x,\hat{\delta },\hat{v},\hat{r}) - W^{{*^{T} }} \varTheta (x,\delta^{*} ,v^{*} ,r^{*} )\). The definition of induced norm of matrices is given here first.

The approximation error can be expressed as

$$\tilde{y} = \hat{W}^{\text{T}} \varTheta (x,\hat{\delta },\hat{v},\hat{r}) - W^{{*^{\text{T}} }} \varTheta (x,\delta^{*} ,v^{*} ,r^{*} ) = W^{{*^{\text{T}} }} \tilde{\varTheta } + \tilde{W}^{T} \hat{\varTheta } + d_{u}$$
(45)

where \(\hat{\varTheta } = \varTheta (x,\hat{\delta },\hat{v},\hat{r})\), \(\tilde{W} = \hat{W} - W^{*}\), \(\tilde{\delta } = \hat{\delta } - \delta^{*}\), \(\tilde{v} = \hat{v} - v^{*}\) and \(\tilde{r} = \hat{r} - r^{*}\) are defined as approximation errors, and The expansion of \(\tilde{\varTheta }\) in Taylor series is obtained as follows

$$\begin{aligned} \tilde{\varTheta } & = \left[ {\begin{array}{*{20}c} {\tilde{\varTheta }_{1} } \\ {\tilde{\varTheta }_{2} } \\ \vdots \\ {\tilde{\varTheta }_{k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varTheta_{1} }}{\partial \delta }} \\ {\frac{{\partial \varTheta_{2} }}{\partial \delta }} \\ \vdots \\ {\frac{{\partial \varTheta_{k} }}{\partial \delta }} \\ \end{array} } \right]^{T} \left| {_{{\delta = \hat{\delta }}} (\delta^{*} - \delta ) + \left[ {\begin{array}{*{20}c} {\frac{{\partial \varTheta_{1} }}{\partial v}} \\ {\frac{{\partial \varTheta_{2} }}{\partial v}} \\ \vdots \\ {\frac{{\partial \varTheta_{k} }}{\partial v}} \\ \end{array} } \right]^{T} } \right.\left| {_{{v = \hat{v}}} (v^{*} - v) + \left[ {\begin{array}{*{20}c} {\frac{{\partial \varTheta_{1} }}{\partial r}} \\ {\frac{{\partial \varTheta_{2} }}{\partial r}} \\ \vdots \\ {\frac{{\partial \varTheta_{k} }}{\partial r}} \\ \end{array} } \right]^{T} } \right.\left| {_{{r = \hat{r}}} (r^{*} - r) + N} \right. \\ & = \varTheta_{\delta }^{T} \tilde{\delta } + \varTheta_{v}^{T} \tilde{v} + \varTheta_{r}^{T} \tilde{r} + N \\ \end{aligned}$$
(46)

where \(\varTheta_{\delta } = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varTheta_{1} }}{\partial \delta }} & {\frac{{\partial \varTheta_{2} }}{\partial \delta }} & \ldots & {\frac{{\partial \varTheta_{k} }}{\partial \delta }} \\ \end{array} } \right]\left| {_{{\delta = \hat{\delta }}} \in R^{j \times k} } \right.,\) \(\varTheta_{v} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varTheta_{1} }}{\partial v}} & {\frac{{\partial \varTheta_{2} }}{\partial v}} & \ldots & {\frac{{\partial \varTheta_{k} }}{\partial v}} \\ \end{array} } \right]\left| {_{{v = \hat{v}}} \in R^{j \times k} } \right.,\) \(\varTheta_{v} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varTheta_{1} }}{\partial r}} & {\frac{{\partial \varTheta_{2} }}{\partial r}} & \ldots & {\frac{{\partial \varTheta_{k} }}{\partial r}} \\ \end{array} } \right]\left| {_{{r = \hat{r}}} \in R^{j \times k} } \right.,\) and N is a vector of higher-order terms and assumed to be bounded by a positive constant. Substituting (46) into (45), one obtains [41]

$$\begin{aligned} &\hat{W}^{T} \varTheta (x,\hat{\delta },\hat{v},\hat{r}) - W^{{*^{T} }} \varTheta (x,\delta^{*} ,v^{*} ,r^{*} ) \hfill \\ &\quad= (\tilde{W} + W^{*} )^{T} \varTheta (x,\hat{\delta },\hat{v},\hat{r}) - W^{{*^{T} }} [\varTheta (x,\hat{\delta },\hat{v},\hat{r}) - \varTheta_{\delta }^{T} \tilde{\delta } - \varTheta_{v}^{T} \tilde{v} - \varTheta_{r}^{T} \tilde{r} + O(x,\tilde{\delta },\tilde{v},\tilde{r})] \hfill \\ &\quad= \tilde{W}^{T} \hat{\varTheta } + (\hat{W} - \tilde{W})^{T} \hat{\varTheta }_{\delta } \tilde{\delta } + (\hat{W} - \tilde{W})^{T} \varTheta_{v}^{T} \tilde{v} + (\hat{W} - \tilde{W})^{T} \varTheta_{r}^{T} \tilde{r} - W^{{*^{T} }} O(x,\tilde{\delta },\tilde{v},\tilde{r}) \hfill \\ &\quad= \tilde{W}^{T} \hat{\varTheta } + \hat{W}^{T} \varTheta_{\delta }^{T} \tilde{\delta } - \tilde{W}^{T} \varTheta_{\delta }^{T} (\hat{\delta } - \delta^{*} ) + \hat{W}^{T} \varTheta_{v}^{T} \tilde{v} - \tilde{W}^{T} \varTheta_{v}^{T} (\hat{v} - v^{*} ) + \hat{W}^{T} \varTheta_{r}^{T} \tilde{r} - \hfill \\ &\tilde{W}^{T} \varTheta_{r}^{T} (\hat{r} - r^{*} ) - W^{{*^{T} }} O(x,\tilde{\delta },\tilde{v},\tilde{r}) \hfill \\ &\quad= \tilde{W}^{T} (\hat{\varTheta } - \varTheta_{\delta }^{T} \hat{\delta } - \varTheta_{v}^{T} \hat{v} - \varTheta_{r}^{T} \hat{r}) + \hat{W}^{T} (\varTheta_{\delta }^{T} \tilde{\delta } + \varTheta_{v}^{T} \tilde{v} + \varTheta_{r}^{T} \tilde{r}) + \varDelta \hfill \\ \end{aligned}$$
(47)

where \(\varDelta = W^{*T} (\varTheta_{\delta }^{T} \delta^{*} + \varTheta_{v}^{T} v^{*} + \varTheta_{r}^{T} r^{*} + O) - \hat{W}^{T} (\varTheta_{\delta }^{T} \delta^{*} + \varTheta_{v}^{T} v^{*} + \varTheta_{r}^{T} r^{*} )\) is defined as the lumped uncertainty.

4.2 Hybrid motion/force control

Inspired by pure-motion tracking, some notations are defined as

$$e_{1} = q_{1} - q_{1}^{d}$$
(48)
$$r = \dot{e}_{1} + \varLambda e_{1}$$
(49)
$$\dot{q}_{1}^{r} = \dot{q}_{1}^{d} - \varLambda e_{1}$$
(50)

where Λ ∊ R (n−m)×(n−m) is a positive diagonal matrix.

If the system satisfies lim  t→∞ = 0, then position and velocity tracking errors e 1 and \(\dot{e}_{1}\) exponentially converge to zero. In other words, the error signal r is an error measurement deviating from the stable subspace \(\{ e_{1} ,\dot{e}_{1} \in R^{n - m} |r = 0\}\). The motion tracking problem is, therefore, transformed to the problem of stabilizing r. On the other hand, a force-error and its filter are accordingly defined as

$$e_{f} \, = f - f^{*}$$
(51)
$$\dot{\alpha } \, = - \rho_{1} \alpha - \rho_{2}^{ - 1} (1 + k_{f} )J^{T} e_{f}$$
(52)

where ρ 1, ρ 2 > 0, k f  > 0 are design parameters, e f  = f − f *. Then, the reduced-state-based scheme is to drive the motion trajectory into the stable subspace, while the contact force is separately controlled, maintaining a zero e f .

Combine r ∊ R n−m to form the following new hybrid variables

$$\sigma = Hr + \alpha$$
(53)
$$\nu = H\dot{q}_{1}^{r} - \alpha$$
(54)

From (50), (53), and (54), we have

$$\sigma + \nu = H\dot{q}_{1}$$
(55)

The time derivatives of ν and σ are given by

$$\dot{\nu } = \dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} - \dot{\alpha }$$
(56)
$$\dot{\sigma } = \dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} + \dot{\alpha }$$
(57)

From the dynamic Eq. (15) together with (55) and (57), we have

$$M(q)\dot{\sigma } + \mu = \tau + J^{T} f$$
(58)

where \(\mu = M(q)\dot{\nu } + C(q,\dot{q})(\nu + \sigma ) + G(q)\). We can rewrite Eq. (58) as

$$M(q)\dot{\sigma } \, = \tau - \mu + J^{T} f$$
(59)

Consider the control law

$$\tau \, = \hat{M}(q)\dot{\nu } + \hat{C}(q,\dot{q})\nu + \hat{G}(q) - K_{\sigma } \sigma - J^{T} f^{*} + k_{f} J^{T} e_{f} - K_{s} \text{sgn} (\sigma ) - \hat{\varDelta }$$
(60)

where matrix K σ  > 0, constant k f  > 0, matrix \(K_{s} = {\text{diag}}\{ k_{sii} \}\) with k sii  ≥ |E i | and E i is the element of vector E (defined later), e f  = f − f *, and \(\hat{\varDelta }\) is an on-line estimated value of the lumped uncertainty Δ, and \(\tilde{\varDelta } = \hat{\varDelta } - \varDelta\), \(\hat{M}(q)\), \(\hat{C}(q,\dot{q})\), and \(\hat{G}(q)\) are the estimates of M(q), \(C(q,\dot{q})\) and G(q), respectively, the elements of which, i.e., m ij (q), \(c_{ij} (q,\dot{q})\), and g i (q) can be expressed by RNN as

$$m_{ij} (q) = W_{{m_{ij}}}^{{*^{T}}} \varTheta (q,\delta_{{m_{ij}}}^{*},v_{{m_{ij}}}^{*},r_{{m_{ij}}}^{*}) + \epsilon_{{m_{ij}}} (q)$$
(61)
$$c_{ij} (q,\dot{q}) = W_{{c_{ij}}}^{{*^{T}}} \varTheta (q,\dot{q},\delta_{{c_{ij}}}^{*},v_{{c_{ij}}}^{*},r_{{c_{ij}}}^{*}) + \epsilon_{{c_{ij}}} (q,\dot{q})$$
(62)
$$g_{i} (q) = W_{{g_{i}}}^{{*^{T}}} \varTheta (q,\delta_{{g_{i}}}^{*},v_{{g_{i}}}^{*},r_{{g_{i}}}^{*}) + \epsilon_{{g_{i}}} (q)$$
(63)

where \(W_{{m_{ij} }}^{*}\), \(W_{{c_{ij} }}^{*}\), \(W_{{g_{i} }}^{*}\) are ideal constant weight vectors, \(\delta_{{m_{ij} }}^{*}\), \(\delta_{{c_{ij} }}^{*}\), \(\delta_{{g_{i} }}^{*}\) are the ideal vectors, \(v_{{m_{ij} }}^{*}\), \(v_{{c_{ij} }}^{*}\), \(v_{{g_{i} }}^{*}\) are the ideal vectors, \(r_{{m_{ij} }}^{*}\),\(r_{{c_{ij} }}^{*}\), \(r_{{g_{i} }}^{*}\) are the ideal vectors, and \(\epsilon_{{m_{ij}}} (q)\), \(\epsilon_{{c_{ij}}} (q,\dot{q})\), \(\epsilon_{{g_{i}}} (q)\) are the approximation errors.

Using the GL matrix (denoted by “\(\{ { \star }\}\)”) and operator (denoted by “·”) introduced in [37, 42], the function emulators (61)–(63) can be collectively expressed as

$$M(q) = [\{ W_{M}^{*} \}^{T} \cdot \{ \varTheta_{M} \} ] + E_{M}$$
(64)
$$C(q,\dot{q}) = [\{ W_{C}^{*} \}^{T} \cdot \{ \varTheta_{C} \} ] + E_{C}$$
(65)
$$G(q) = [\{ W_{G}^{*} \}^{T} \cdot \{ \varTheta_{G} \} ] + E_{G}$$
(66)

where [{W * M }, {Θ M }], \([\{ {\text{W}}_{C}^{*} \} ,\{ \varTheta_{C} \} ]\) and \([\{ {\text{W}}_{G}^{*} \} ,\{ \varTheta_{G} \} ]\) are the desired weights and basis function GL matrices pairs of the RNN emulation of M(q),\(C(q,\dot{q})\) and G(q) respectively; and E M , E C , E G are the collective RNN reconstruction errors, respectively.

The estimates \(\hat{M}(q)\), \(\hat{C}(q,\dot{q})\), \(\hat{G}(q)\), can be accordingly expressed as

$$\hat{M}(q) = [\{ \hat{W}_{M} \}^{T} \cdot \{ \hat{\varTheta }_{M} \} ]$$
(67)
$$\hat{C}(q,\dot{q}) = [\{ \{ \hat{W}_{C} \}^{T} \cdot \{ \hat{\varTheta }_{C} \} ]$$
(68)
$$\hat{G}(q) = [\{ \{ \hat{W}_{G} \}^{T} \cdot \{ \hat{\varTheta }_{G} \} ]$$
(69)

Substituting (60) and (67)–(69) into the dynamic Eq. (58) yields the closed-loop system error equation as

$$\begin{aligned} M\dot{\sigma } + C\sigma & = ([\{ \hat{W}\}^{T} \cdot \{ \varTheta \} ] - [\{ {\text{W}}^{*} \}^{\text{T}} \cdot \{ \varTheta \} ]) - K_{\sigma } \sigma \\ & \quad + J^{T} (1 + k_{f} )e_{f} - E - K_{s} \text{sgn} (\sigma ) - \hat{\varDelta } \\ \end{aligned}$$
(70)

where

$$\{ \hat{W}\}^{T} = [\{ \hat{W}_{M} \}^{T} ,\{ \hat{W}_{C} \}^{T} ,\{ \hat{W}_{G} \}^{T} ]^{T}$$
$$\{ \hat{\varTheta }\} = [\{ \hat{\varTheta }_{M} \} \dot{\nu },\{ \hat{\varTheta }_{C} \} \nu ,\{ \hat{\varTheta }_{G} \} ]^{T}$$
$$\{ {\text{W}}^{*} \}^{T} = [\{ {\text{W}}_{M}^{*} \}^{T} ,\{ {\text{W}}_{C}^{*} \}^{T} ,\{ {\text{W}}_{G}^{*} \}^{T} ]^{T}$$
$$\{ \varTheta \} = [\{ \varTheta_{M} \} \dot{\nu },\{ \varTheta_{C} \} \nu ,\{ \varTheta_{G} \} ]^{T}$$

where \(E = E_{M} \dot{\nu } + E_{C} \nu + E_{G}\).

Theorem 4.1

Consider the system described by dynamic Eq. (4) and m independent constraints (9). If the control law is chosen by (60), and the parameter adaptation laws are chosen by

$$\dot{\hat{W}} = - \varGamma_{w} \cdot \{ \hat{\varTheta } - \varTheta_{\delta }^{T} \hat{\delta } - \varTheta_{v}^{T} \hat{v} - \varTheta_{r}^{T} \hat{r}\} \sigma$$
(71)
$$\dot{\hat{\delta }} = - \varGamma_{\delta } [\hat{W} \cdot \varTheta_{\delta } ]\sigma$$
(72)
$$\dot{\hat{v}} = - \varGamma_{v} [\hat{W} \cdot \varTheta_{v} ]\sigma$$
(73)
$$\dot{\hat{r}} = - \varGamma_{r} [\hat{W} \cdot \varTheta_{r} ]\sigma$$
(74)
$$\dot{\hat{\varDelta }} = \varGamma_{h} \sigma$$
(75)

where matrices Γ w , Γ δ , Γ r , Γ v , Γ h are symmetric positive definite, then, the signals e 1 and \(\dot{e}_{1}\) asymptotically converge to zero, and all the other closed-loop signals are semi-globally uniformly ultimately bounded.

Proof

The time derivative of \(\frac{1}{2}\sigma^{T} M\sigma\) along (70) is

$$\begin{aligned} \sigma^{T} M^{T} \dot{\sigma } & = - \sigma^{T} K_{\sigma } \sigma - \sigma^{T} E - \sigma^{T} K_{s} \text{sgn} (\sigma ) - \sigma^{T} \hat{\varDelta } + \sigma^{T} J^{T} (1 + k_{f} )e_{f} - \sigma^{T} C\sigma \\ & \quad + \sigma^{T} ([\{ \hat{W}\}^{T} \cdot \{ \hat{\varTheta }\} ] - [\{ W^{*} \}^{T} \cdot \{ \varTheta \} ]) \\ \end{aligned}$$
(76)

Consider the Lyapunov function candidate

$$\begin{aligned} V =& \,\frac{1}{2}\sigma^{T} M\sigma + {\tilde{\text{W}}}^{T} \varGamma_{w}^{ - 1} {\tilde{\text{W}}} + \frac{1}{2}\tilde{\delta }^{T} \varGamma_{\delta }^{ - 1} \tilde{\delta } + \frac{1}{2}\tilde{v}^{T} \varGamma_{v}^{ - 1} \tilde{v} + \frac{1}{2}\tilde{r}^{T} \varGamma_{r}^{ - 1} \tilde{r} \hfill \\ & + \frac{1}{2}\tilde{\varDelta }^{T} \varGamma_{h}^{ - 1} \tilde{\varDelta } + \frac{1}{2}\rho_{2} \alpha^{T} \alpha \hfill \\ \end{aligned}$$
(77)

with \(\tilde{x} = \hat{x} - x^{ * }\).

The time derivative of V is given by

$$\begin{aligned} \dot{V} & = \sigma^{T} M\dot{\sigma } + \frac{1}{2}\sigma^{T} \dot{M}\sigma + \tilde{W}^{T} \varGamma_{w}^{ - 1} \hat{W} + \tilde{\delta }^{T} \varGamma_{\delta }^{ - 1} \dot{\tilde{\delta }} + \tilde{v}^{T} \varGamma_{v}^{ - 1} \dot{\tilde{v}} + \tilde{r}^{T} \varGamma_{r}^{ - 1} \dot{\tilde{r}} + \tilde{\varDelta }^{T} \varGamma_{h}^{ - 1} \dot{\tilde{\varDelta }} \\ & \quad \le \frac{1}{2}\sigma^{T} \dot{M}\sigma - \sigma^{T} C\sigma - \sigma^{T} K_{\sigma } \sigma - \sigma^{T} E - \sigma^{T} K_{s} \text{sgn} (\sigma ) - \sigma^{T} \hat{\varDelta } + \sigma^{T} J^{T} (1 + k_{f} )e_{f} \\ & \quad + \sigma^{T} ([\{ \hat{W}\}^{T} \cdot \{ \hat{\varTheta }\} ] - [\{ W^{*} \}^{T} \cdot \{ \varTheta \} ]) \\ & \quad + \tilde{W}^{T} \varGamma_{w}^{ - 1} \dot{\hat{W}} + \tilde{\delta }^{T} \varGamma_{\delta }^{ - 1} \dot{\tilde{\delta }} + \tilde{v}^{T} \varGamma_{v}^{ - 1} \dot{\tilde{v}} + \tilde{r}^{T} \varGamma_{r}^{ - 1} \dot{\tilde{r}} + \tilde{\varDelta }^{T} \varGamma_{h}^{ - 1} \dot{\tilde{\varDelta }} + \rho_{2} \alpha^{T} \dot{\alpha } \\ \end{aligned}$$
(78)

As matrix \(\dot{M} - 2C\) is skew-symmetric, \(\sigma^{T} (\dot{M} - 2C)\sigma = 0\), ∀x ≠ 0. Integrating (47) into (78), we have

$$\begin{aligned} \dot{V} \le& - \sigma^{T} K_{\sigma } \sigma - \sigma^{T} E - \sigma^{T} K_{s} \text{sgn} (\sigma ) - \sigma^{T} \hat{\varDelta } + \sigma^{T} J^{T} (1 + k_{f} )e_{f} \hfill \\ &+ \sigma^{T} \left( {[\{ \tilde{W}^{T} \} \cdot \{ \hat{\varTheta } - \varTheta_{\delta }^{T} \hat{\delta } - \varTheta_{v}^{T} \hat{v} - \varTheta_{r}^{T} \hat{r}\} ] + [\{ \hat{W}^{T} \} \cdot \{ \varTheta_{\delta }^{T} \tilde{\delta } + \varTheta_{v}^{T} \tilde{v} + \varTheta_{r}^{T} \tilde{r}\} ] + \varDelta } \right) \hfill \\ &+ \tilde{W}^{T} \varGamma_{w}^{ - 1} \hat{W} + \tilde{\delta }^{T} \varGamma_{\delta }^{ - 1} \dot{\tilde{\delta }} + \tilde{v}^{T} \varGamma_{v}^{ - 1} \dot{\tilde{v}} + \tilde{r}^{T} \varGamma_{r}^{ - 1} \dot{\tilde{r}} + \tilde{\varDelta }^{T} \varGamma_{h}^{ - 1} \dot{\tilde{\varDelta }} + \rho_{2} \alpha^{T} \dot{\alpha } \hfill \\ \end{aligned}$$
(79)

Substituting the weight vectors updating laws (71–75) into (79) yields

$$\begin{aligned} \dot{V} &\le - \sigma^{T} K_{\sigma } \sigma - \sigma^{T} E - \sigma^{T} K_{s} \text{sgn} (\sigma )\\&\quad + \sigma^{T} J^{T} (1 + k_{f} )e_{f} + \rho_{2} \alpha^{T} \dot{\alpha } \end{aligned}$$
(80)

Noting that k sii  ≥ |E i | > 0, it is obvious that \([ - \sigma^{T} E - \sigma^{T} K_{s} \text{sgn} (\sigma )] \le 0\). In addition, from (52), we know that \(\dot{\alpha } = - \rho_{1} \alpha - \rho_{2}^{ - 1} (1 + k_{f} )J^{T} e_{f}\) and from (53), σ T = r T H T + α T. Thus, we have

$$\sigma^{T} J^{T} (1 + k_{f} )e_{f} + \rho_{2} \alpha^{T} \dot{\alpha } = - \rho_{1} \rho_{2} \alpha^{T} \alpha + r^{T} H^{T} J^{T} (1 + k_{f} )e_{f}$$
(81)

Noting H T J T = 0 from (11) and (26), we then have

$$\dot{V} \le - \sigma^{T} K_{\sigma } \sigma - \rho_{1} \rho_{2} \alpha^{T} \alpha \le 0$$
(82)

As V ≥ 0 and \(\dot{V} \le 0\), V ∊ L ∞. From the definition of V, it follows that σ, ν ∊ L n∞ .

Integrating both sides of (82), we have

$$\int_{0}^{t} {\sigma^{T} } K_{\sigma } \sigma \le V(0) - V(t) \le V(0)$$
(83)

Hence σ ∊ L n2 . From (53), we have r = (H T H)−1 H T(σ − α), hence r ∊ L n−m∞ since H is bounded. From Lemma 2.1, it can be concluded that \(e_{1} ,\dot{e}_{1} \in L_{\infty }^{n - m}\). From (53–56), we have

$$\begin{aligned} \hat{M}\dot{\nu } + \hat{C}\nu + \hat{G} & = \hat{M}(\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} - \dot{\alpha }) + \hat{C}(H\dot{q}_{1}^{r} - \alpha ) + \hat{G} \\ & = \hat{M}(\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} ) + \hat{C}H\dot{q}_{1}^{r} + \hat{G}\\&\quad + (\rho_{1} \hat{M} - \hat{C})\alpha + \rho_{2}^{ - 1} (1 + k_{f} )\hat{M}J^{T} e_{f} \\ \end{aligned}$$
(84)

From (48–50), it is known that

$$\dot{q} = H\dot{q}_{1}^{r} + Hr$$
(85)
$$\textit{\"{q}} = \dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} + \dot{H}r + H\dot{r}$$
(86)

Replacing τ by (60) in dynamic Eq. (15), and Eqs. (84–86), the closed-loop system becomes

$$\begin{aligned} M\dot{H}r + MH\dot{r} + CHr - (\hat{M} - M)(\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} ) - (\hat{C} - C)H\dot{q}_{1}^{r} - (\hat{G} - G) \hfill \\ + (\hat{C} - \rho_{1} \hat{M})\alpha + K_{\sigma } \sigma + K_{s} \text{sgn} (\sigma ) = (\rho_{2}^{ - 1} (1 + k_{f} )\hat{M} + I_{n} )J^{T} e_{f} \hfill \\ \end{aligned}$$
(87)

Invoking (64–66) and (67–69), Eq. (87) then becomes

$$\begin{aligned} M\dot{H}r + MH\dot{r} + CHr - ([\{ \hat{W}_{M} \}^{T} \cdot \{ \hat{\varTheta }_{M} \} ] - [\{ W_{M}^{*} \}^{T} \cdot \{ \varTheta_{M} \} ])(\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} - ([\{ \hat{W}_{C} \}^{T} \cdot \{ \hat{\varTheta }_{C} \} ] - [\{ W_{C}^{*} \}^{T} \cdot \{ \varTheta_{C} \} ])H\dot{q}_{1}^{r} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} - ([\{ \hat{W}_{G} \}^{T} \cdot \{ \hat{\varTheta }_{G} \} ] - [\{ W_{G}^{*} \}^{T} \cdot \{ \varTheta_{G} \} ]) + (\hat{C} - \rho_{1} \hat{M})\alpha \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} + K_{\sigma } \sigma + K_{s} \text{sgn} (\sigma ) + E_{M} (\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} ) + E_{C} H\dot{q}_{1}^{r} + E_{G} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} = (\rho_{3}^{ - 1} (1 + k_{f} )\hat{M} + I_{n} )J^{T} e_{f} \hfill \\ \end{aligned}$$
(88)

Since M(q) is nonsingular, multiplying H(q)M −1(q) on both sides of (88) yields

$$\begin{aligned} H\dot{H}r + HM^{ - 1} [CHr - ([\{ \hat{W}_{M} \}^{T} \cdot \{ \hat{\varTheta }_{M} \} ] - [\{ W_{M}^{*} \}^{T} \cdot \{ \varTheta_{M} \} ])(\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} ) \hfill \\ \quad - ([\{ \hat{W}_{C} \}^{T} \cdot \{ \hat{\varTheta }_{C} \} ] - [\{ W_{C}^{*} \}^{T} \cdot \{ \varTheta_{C} \} ])H\dot{q}_{1}^{r} \hfill \\ \quad- ([\{ \hat{W}_{G} \}^{T} \cdot \{ \widehat{{\hat{\varTheta }}}_{G} \} ] - [\{ W_{G}^{*} \}^{T} \cdot \{ \varTheta_{G} \} ]) + (\hat{C} - \rho_{1} \hat{M})\alpha \hfill \\ \quad+ K_{\sigma } \sigma + K_{s} \text{sgn} (\sigma ) + E_{M} (\dot{H}\dot{q}_{1}^{r} + H\textit{\"{q}}_{1}^{r} ) + E_{C} H\dot{q}_{1}^{r} + E_{G} ] \hfill \\ = HM^{ - 1} (\rho_{3}^{ - 1} (1 + k_{f} )\hat{M} + I_{n} )J^{T} e_{f} \hfill \\ \end{aligned}$$
(89)

Since we have established that \(e_{1} ,\dot{e}_{1} \in L_{\infty }^{n - m}\), from (50), it can be concluded that \(\dot{q}_{1}^{r} ,\textit{\"{q}}_{1}^{r} \in L_{\infty }^{n - m}\). As r is shown to be bounded, so is \(\dot{q}_{1}\) from (50). Hence, \(\dot{q}(t) = H\dot{q}_{1} \in L_{\infty }^{n}\). It follows that \(M(q),\hat{M}(q),C(q,\dot{q}),\hat{C}(q,\dot{q}) \in L_{\infty }^{n \times n}\), and \(G(q),\hat{G}(q) \in L_{\infty }^{n}\). Thus, the left-hand side of (89) is bounded. In fact, ρ 3 can be properly chosen to keep \((\rho_{3}^{ - 1} (1 + k_{f} )\hat{M} + I_{n} )\) on the right-hand side of (89) from being singular. Hence, we have e f  ∊ L n−m∞ . As f * is bounded, so are e f and τ.

As λ ∊ L n−m∞ and α ∊ L m∞ , from Eq. (52), it is obvious that \(\dot{\alpha } \in L_{\infty }^{m}\). Thus, from (56), we have \(\dot{\nu } \in L_{\infty }^{n}\). Since \(\dot{q}_{1} ,\textit{\"{q}}_{1} \in L_{\infty }^{n - m}\) have been established before, we can conclude from (57) that \(\dot{\sigma } \in L_{\infty }^{n}\). Now, with σ, α ∊ L n2 , \(\dot{\sigma },\dot{\alpha } \in L_{\infty }^{n}\), according to Lemma 2.2, we can conclude that σ and μ asymptotically converge to zero. Hence, from (53), it can be concluded that r → 0 as t → ∞. According to Lemma 2.2, we can also obtain \(e_{1} ,\dot{e}_{1} \to 0\) as t → ∞.

Since \(\dot{q},\textit{\"{q}} \in L_{\infty }^{n}\), q and \(\dot{q}\) are uniformly continuous. Therefore, from Property 2.1, we can conclude that matrices M(q), \(C(q,\dot{q})\), G(q), H(q),J(q), \(\hat{M}(q)\), \(\hat{C}(q,\dot{q})\), and \(\hat{G}(q)\) are uniformly continuous.

5 Simulations and experiments

5.1 Simulations

In this section, to show the effectiveness of the proposed approach, we first present simulation results for dynamic balance optimization and control.

Consider a 12-DOF biped robot shown in Fig. 3, which is modeled using ADAMS and consists of a torso, and a pair of legs composed of six links. The left and right legs are numbered as Leg 1 and Leg 2, respectively. The height of the biped is 1.2 m, the length of the lower limbs is 460 mm, and the height of the foot is 90 mm.

Fig. 3
figure 3

Diverse external forces in three Cases are applied in the simulations

Full size image

Both the balancing optimization and the motion/force tracking under perturbing external forces are evaluated in Fig. 3. In the simulations, diverse external forces with different directions and acting points are considered. Three cases (Case 1: f ext = 50 N, α = 0o, d = 1.0 m; Case 2: f ext = 50 N, α = 30o, d = 1.0 m; Case 3: f ext = 50 N, α = 0o, d = 1.2 m) are illustrated in Fig. 3. We can obtain the corresponding matrices in (26)–(29) as

$$G = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & { - 1} & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & l & 0 & 0 & l \\ \end{array} } \right]$$
$$S = \left[ {\begin{array}{*{20}c} 1 & 0 & { - \frac{\mu }{\sqrt 2 }} \\ { - 1} & 0 & { - \frac{\mu }{\sqrt 2 }} \\ 0 & 1 & { - \frac{\mu }{\sqrt 2 }} \\ 0 & { - 1} & { - \frac{\mu }{\sqrt 2 }} \\ \end{array} } \right]$$
$$f = [f_{lx} ,f_{ly} ,f_{lz} ,f_{rx} ,f_{ry} ,f_{rz} ]^{T}$$
$$W = [0,f_{ext} cos(\alpha ),G,f_{ext} cos(\alpha )d]^{T}$$

We assume −20 N ≤ f lx  ≤ 20 N, −20 N ≤ f rx  ≤ 20 N, −20 N ≤ f ly  ≤ 20 N, −20 N ≤ f ry  ≤ 20 N, therefore, ζ + = ζ − = [20, …, 20]T. We choose \(Q = {\text{diag}}[1.0]\), b = 0. The friction coefficient of each foot is μ = 0.6.

Under the perturbing external force, both feet are on the ground and the body sways to the right, to the left and then returns to its original position. Because the motion is constrained on the lateral plane, only four joints θ l6 , θ l1 , θ r1 and θ r6 are actuated and the other eight joints are locked by axis brakes. Figure 3 shows the simplified biped model from the frontal plane. Let the state X and the control U be represented as

$$X = [x_{1} ,x_{2} ,x_{3} ,x_{4} ]^{T} = [\theta_{6}^{l} ,\theta_{1}^{l} ,\theta_{1}^{r} ,\theta_{6}^{r} ]^{T}$$
$$U = [u_{1} ,u_{2} ,u_{3} ,u_{4} ]^{T} = [\tau_{6}^{l} ,\tau_{1}^{l} ,\tau_{1}^{r} ,\tau_{6}^{r} ]^{T}$$

The constraints can be denoted by

$$\left[ {\begin{array}{*{20}c} {L\cos (x_{1} )} \\ {L\sin (x_{1} )} \\ {x_{1} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {2l + L\cos (x_{4} ) + l\sin (x_{3} + x_{4} )} \\ {L\sin (x_{4} ) - l\cos (x_{3} + x_{4} )} \\ {x_{3} + x_{4} - x_{2} } \\ \end{array} } \right] = 0$$

where L is the length of the leg and l is half the width of the body. Let x 1 and x 2 be defined by

$$X = [X_{1} ,X_{2} ]^{T} , X_{1} = [x_{1} ], X_{2} = [x_{2} ,x_{3} ,x_{4} ]^{T}$$
(90)

It is easy to have \(\dot{X}_{2} = [ - 1, - 1,1]^{T} \dot{X}_{1}\).The dynamic equation of motion involving only X 1 becomes

$$M\dot{X}_{1} + G = u_{1} - u_{2} - u_{3} + u_{4}$$
(91)

where M = 2(I 2 + I 4) + 4(m 2 + m 3)d 22  + m 4 L 2, and G = −(m 2 + m 3 + m 4)gL sin (x 1).and m 4 is the mass of the body; m 3 is the mass of the upper leg; m 2 is the length of the lower leg; I 2 is the inertial moment of the lower leg in the frontal plane; and I 3 is the inertial moment of the upper leg in the frontal plane; and g is the gravity term. For the M and G, 35 nodes are chosen for each variable, with the variances σ M  = σ G  = σ t  = 2.0; moreover, the centers are evenly distributed to span the input space [−1.0, 1.0]. The weight matrices Φ M and Φ G are all initialized to zero. The gains for the controller are chosen as \(K_{\sigma } = {\text{diag}}[50]\), \(\varLambda = {\text{diag}}[20]\), K f  = 800 and K s  = 10.0, \(\hat{\varDelta } = 0\), ρ 1 = ρ 2 = 0.5. The adaptation algorithm as given in (71)–(75) is activated with \(\varGamma_{w} = \varGamma_{\delta } = \varGamma_{v} = \varGamma_{r} = \varGamma_{h} = {\text{diag}}(0.5)\).

The simulation results for the biped can be found in Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13. The ground reaction forces of the legs are shown in Figs. 4, 5, 6, 7, 8 and 9. In Case 2, the magnitude of f z is bigger than that in Case 1 because of the change of the direction of the external force. In Case 3, the difference between ground reaction forces for the two legs is bigger than that in Case 1 because the acting point of the external force is higher. However, all the simulation results show that the force tracking errors tend to the origins in cases of diverse external forces with different directions and acting points.

Fig. 4
figure 4

Ground reaction force for the left leg in Case 1

Full size image
Fig. 5
figure 5

Ground reaction force for the right leg in Case 1

Full size image
Fig. 6
figure 6

Ground reaction force for the left leg in Case 2

Full size image
Fig. 7
figure 7

Ground reaction force for the right leg in Case 2

Full size image
Fig. 8
figure 8

Ground reaction force for the left leg in Case 3

Full size image
Fig. 9
figure 9

Ground reaction force for the right leg in Case 3

Full size image
Fig. 10
figure 10

Joint torques of the left leg in the three Cases

Full size image
Fig. 11
figure 11

Joint torques of the right leg in the three Cases

Full size image
Fig. 12
figure 12

Joint velocities of the left leg in the three Cases

Full size image
Fig. 13
figure 13

Joint velocities of the right leg in the three Cases

Full size image

The input torques for the joints in all three cases can be found in Figs. 10 and 11. The joint velocities for both legs are shown in Figs. 12 and 13. The simulation results indicate that the simulated biped robot remains dynamical balance under diverse perturbing external forces, which validate the effectiveness of the control law in Theorem 4.1. The proposed control scheme achieves good performance, which is mainly due to the “adaptive” mechanism, even if the nominal dynamics are uncertain. Although the parametric uncertainties and the external disturbances are both introduced into the simulation model, the force/motion control performance of system, under the proposed control, is not degraded. The simulation results demonstrate the effectiveness of the proposed adaptive control in the presence of unknown nonlinear dynamics and environments.

5.2 Experiments

Experiments are carried out on a physical robot “Alpha”. Alpha is a mini-type humanoid robot that is built at the Department of Electronic Engineering, Shunde Polytechnic, Guangdong of China. Alpha has 18 degree of freedom with a 0.394 m height and a 1.7 kg weight. The mechanical structure of the robot is shown in Fig. 14.

Fig. 14
figure 14

The implemented prototype robot

Full size image

The biped carries a control board for controlling and communicating, a lithium-polymer battery in the robot’s upper body for the servo motors. A RS-232 wireless transmission link connects the control software, which is running on a PC, to the robot’s control board. Degrees of freedom (DOFs) of Alpha are schematically shown in Fig. 14. The robot is driven by 18 servo motors: six per leg and three in each arm. The six leg-servos allow for flexible leg movements: Three orthogonal servos constitute the 3-DOFs hip joint. Two orthogonal servos form the 2-DOFs ankle joint. One servo drives the knee joint. The sensors such as infrared sensors, force sensors and gyro sensors are interpreted to improve the ability of autonomous walking. Closed-loop control for the humanoid robot is constructed. Daily movements of Alpha, such as going straight, walking sideways, obstacle avoidance, and turning around, have been realized. The basic parameters of Alpha are shown in Table 1.

Table 1 Basic parameters of Alpha
Full size table

Continuous-force external disturbances are applied on the right shoulder of the biped robot until the joint angles of the hips and the ankles changed obviously. The disturbances are carried out by a hand of an experimenter. The ground reaction forces are measured via the pressure sensors embedded in each of the soles of the biped robot. As we can see from Figs. 15 and 16, ground reaction forces for the both legs become steady gradually under the proposed adaptive control. Figure 17 shows the snapshots of the biped under the implemented continuous-force external disturbances in double-support phase. After swaying smoothly to the left and then to the right, the prototype humanoid robot always restores the initial balance posture. The robot is able to react appropriately to the disturbances as desired. The experimental results show that the proposed adaptive control is effective.

Fig. 15
figure 15

Ground reaction force for the left leg of Alpha

Full size image
Fig. 16
figure 16

Ground reaction force for the right leg of Alpha

Full size image
Fig. 17
figure 17

Snapshots for a biped robot in double-support phase under perturbing external forces

Full size image

6 Conclusions

In this paper, the dynamic balance optimization and control of biped robots have been investigated under the external disturbances in the double-support phase. First, a constrained dynamic model of the biped robot is formulated and a reduced order model for the double-support phase is derived. Then, a recurrent neural network has been adopted to deal with the complicated optimization problem subject to both equality and inequality constraints. For the given contact force and motion, we propose the hybrid motion/force control based on Recurrent Neural Networks to approximate unknown dynamic functions, and the adaptive learning algorithms that can learn the parameters of the Recurrent Neural Networks are derived using Lyapunov stability theorem. The verification of the proposed control is conducted by simulations and experiments. We believe that the proposed method will be promising for dynamical balance optimization and control of biped robots under perturbing external forces.