1 Introduction

With the human-like structure [1], bipedal robots are able to move in a variety of environments [2,3,4,5], and they are expected to play an important role in the areas of military use, disaster rescue, and family service, see [6, 7]. Compared with the industrial robots, bipedal robots possess floating bases and high-dimensional hybrid dynamics [8], which makes the control problem more complicated. Currently, many of the bipedal robots are controlled using the zero moment point (ZMP) method [9,10,11,12], which calls for the full-actuation at each joint. While the full-actuation approach is very effective in the physical environments, it is usually energy-costly and the walking gait looks unnatural for bipedal robots [13,14,15].

Recently, underactuated bipedal robots have attracted significant research interest [16,17,18], and many successful control strategies have been proposed. In the work [19], a transverse linearization control approach was developed for an underactuated biped with one actuator. In [20], a hybrid zero dynamics (HZD)-based controller was designed for an underactuated biped with curved feet. In the recent work [21], the HZD-based control method was further combined with the velocity decomposition metric, and the results were validated experimentally. In these investigations, the researchers mainly focus on the planar bipeds. Compared with planar bipeds, underactuated 3-D bipeds have more degrees of underactuation and higher-dimensional dynamics. In addition, the dynamic models of 3-D bipeds possess more continuous phases. These factors all complicate the controller design of underactuated 3-D bipeds.

To address the stable walking of underactuated 3-D bipeds, Chevallereau et al. [22] presented an event-based control strategy by using an extension of the method of virtual constraints and hybrid zero dynamics. In the work [23], a discrete transverse linearization method was proposed to achieve stable walking of a 3-D compass-like biped. Compared with the event-based control strategy, this method constructed a series of moving Poincaré sections along the desired periodic solution rather than simply one. In the work [24], the event-based control strategy was further developed into a time-invariant one-step hybrid control scheme on the basis of right–left symmetry, linear matrix inequalities (LMIs), and robust optimal control (ROC). From [22], for underactuated 3-D bipeds, the stability of the closed-loop system can be affected by the choice of the control output. In the work [25], parametrized output functions were first designed, and the controller parameters were then obtained by solving an optimization problem. From the results, the controller functioned well in the presence of terrain variations.

In the above investigations, the robot models are assumed to be left–right symmetric, and then the stabilization problem of 3-D bipeds can be reduced to that of hybrid systems with a single continuous phase by using the symmetry property. In practice, due to the manufacturing error or the component loss in the service process, the structural parameters of bipedal robots may exhibit asymmetry. To the best our knowledge, few researchers focus on the stable walking of underactuated 3-D bipeds with asymmetric structure.

In this work, we consider the stable walking of an underactuated 3-D biped with asymmetric structure. In Sect. 2, the asymmetric 3-D biped is described and the dynamic model is presented. In Sect. 3, a piecewise-defined feedback control strategy is proposed. The control strategy consists of a heuristic motion controller that asymptotically drive the state of the robot to the zero dynamics manifold, and an event-based feedback controller which renders the hybrid zero dynamics locally asymptotically stable. Numerical simulation results are given in Sect. 4 to show the effectiveness of the presented control strategy. In the final section, the results of this work are summarized.

2 Robot Description and Dynamic Modeling

Many previous works are focused on underactuated bipedal robots with symmetric structure. However, due to the manufacturing error or the component loss in the service process, the structural parameters of bipedal robots may exhibit asymmetry. In this section, an underactuated 3-D biped with asymmetric structure is considered and the dynamic model is presented.

2.1 Robot Description

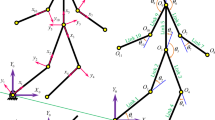
As shown in Fig. 1, the studied 3-D biped consists of five rigid links: a torso and two legs with knee joints. For simplicity, each link is modeled by a point mass at its center. The 3-D biped is asymmetric because the structural parameters of the left and right legs are different, including the masses and the lengths, see Fig. 1 for the details. In the present study, angles (q0, q1, q2) are the yaw, pitch, and roll angles of the stance leg, respectively. Angles q3 and q8 are the relative joint angles of the stance-leg knee and swing-leg knee, respectively. Angles (q4, q5) and (q6, q7) are the relative joint angles of the stance-leg hip and swing-leg hip, respectively. The angles \((q_{3} , \ldots ,q_{8} )\) are independently actuated, whereas (q0, q1, q2) are unactuated due to the point contact. \((q_{0,sw} ,q_{1,sw} ,q_{2,sw} )\) denote the angles of the swing-leg shin, and they can be calculated by the kinematic relationships.

Fig. 1
figure 1

The model of the asymmetric 3-D biped with point feet. In (a) and (b), the robot is supporting on the left and right legs, respectively. The structural parameters for the biped are as follows: L1 = 0.275 m, L2 = 0.275 m, L3 = 0.05 m, L4 = 0.274 m, L5 = 0.274 m, W = 0.15 m, m1 = 0.875 kg, m2 = 0.875 kg, m3 = 5.5 kg, m4 = 0.85 kg, m5 = 0.85 kg

Full size image

In the present study, the bipedal walking consists of single support phases, when only one leg end is in stationary contact with the ground, and double support phases, when both legs are in contact with the ground. It is assumed that the double support phases can be modeled as instantaneous and rigid impacts. Therefore, the dynamic model for the 3-D biped is hybrid. For the convenience of analysis, the following assumptions are further made in the present study:

  1. 1.

    At impact, the swing foot neither slips nor rebounds, and the configuration of the robot remain unchanged, but the velocities undergo an instantaneous change.

  2. 2.

    In the single support phase, the position and the yaw angle of the stance foot remain constant, and thus \(q = [q_{1} , \ldots ,q_{8} ]^{T}\) are defined as the generalized coordinates.

2.2 Dynamic Modeling

Due to the asymmetric structure, we have to consider the dynamics of the biped in both the left and the right support phases. In this work, the subscripts v = 1 and v = 2 stand for left and right, respectively. Considering the periodicity of bipedal walking, we use the notations v + 1=1 for v = 2 and v − 1=2 for v = 1.

In the single support phase \(v \in \{ 1,2\}\), suppose that the Lagrangian is defined as

$$L_{v} = E_{k,v} - E_{p,v}$$
(1)

where Ek,v is the total kinematic energy, Ep,v is the potential energy. Then, the dynamic model can be written as

$$\frac{d}{dt}\frac{{\partial L_{v} }}{{\partial \dot{q}}} - \frac{{\partial L_{v} }}{\partial q} = Bu$$
(2)

where B is an (8 × 6) full-rank, constant matrix indicating whether a joint is actuated or not, and u is the (6 × 1) vector of the input torques. Next, Eq. (2) can be rewritten in the following form

$$D_{v} (q)\ddot{q} + H_{v} (q,\dot{q}) = Bu$$
(3)

where \(D_{v} (q)\) is the positive-definite (8 × 8) mass-inertia matrix; \(H_{v} (q,\dot{q})\) is the (8 × 1) vector of Coriolis and gravity terms; Defining \(x_{v} = [q,\dot{q}]^{T}\), the dynamic model (3) can be written in state-space form as

$$\dot{x}_{v} = f_{v} (x_{v} ) + g_{v} (x_{v} )u$$
(4)

where

$$f_{v} (x_{v} ) = \left[ {\begin{array}{*{20}c} {\dot{q}} \\ { - D_{v}^{ - 1} H_{v} } \\ \end{array} } \right],\quad g_{v} (x_{v} ) = \left[ {\begin{array}{*{20}c} 0 \\ { - D_{v}^{ - 1} B} \\ \end{array} } \right]$$

During the double support phase, \(q_{e} = [x_{st} ,y_{st} ,z_{st} ,q_{0} , \ldots ,q_{8} ]^{T}\) are defined as the generalized coordinates, where \((x_{st} ,y_{st} ,z_{st} )\) are the Cartesian coordinates of the stance foot. Similar to the work [26], the impact model in the double support phase can be obtained as

$$\left[ {\begin{array}{*{20}c} {\dot{q}_{v,e}^{ + } } \\ {F_{v,sw} } \\ \end{array} } \right] = \mathop {\left[ {\begin{array}{*{20}c} {D_{v,e} } & { - E_{v,sw}^{T} } \\ {E_{v,sw} } & 0 \\ \end{array} } \right]}\nolimits^{ - 1} \left[ {\begin{array}{*{20}c} {D_{v,e} \dot{q}_{v,e}^{ - } } \\ 0 \\ \end{array} } \right]$$
(5)

where \(\dot{q}_{v,e}^{ - }\) and \(\dot{q}_{v,e}^{ + }\) are the extended velocities before and after the impact, respectively, Fv,sw is the impulsive reaction force on the swing leg at the contact point, Dv,e is the extended mass-inertia matrix, and \(E_{v,sw} = {{\partial [x_{sw} ,y_{sw} ,z_{sw} ,q_{0,sw} ]^{T} } \mathord{\left/ {\vphantom {{\partial [x_{sw} ,y_{sw} ,z_{sw} ,q_{0,sw} ]^{T} } \partial }} \right. \kern-0pt} \partial }q_{e}\) is the Jacobian for the position of the swing foot and its orientation in the x–y plane. After the impact, the generalized coordinates are relabeled, and the transformation is \([q_{1,sw} ,q_{2,sw} ,q_{8} , \ldots ,q_{3} ] \to [q_{1} , \ldots ,q_{8} ]\), as shown in Fig. 1. Next, combining the impact model (5) with the coordinate relabeling, the dynamical model for the double support is written as

$$x_{v + 1}^{ + } = \Delta_{v}^{v + 1} (x_{v}^{ - } )$$
(6)

where \(x_{v + 1}^{ + } = [q_{v + 1}^{ + } ,\dot{q}_{v + 1}^{ + } ]^{T}\) is the initial state of the next step, \(x_{v}^{ - } = [q_{v}^{ - } ,\dot{q}_{v}^{ - } ]^{T}\) is the final state.

From (4) and (6), the complete hybrid model can be written as

$$\sum : = \left\{\begin{array}{ll} \dot{x}_{1} = f_{1} (x_{1} ) + g_{1} (x_{1} )u, \quad x_{1} \notin S_{1}^{2} \\ {x_{2}^{ + } = \Delta_{1}^{2} (x_{1}^{ - } ) \quad x_{1} \notin S_{1}^{2} } \\ \dot{x}_{2} = f_{2} (x_{2} ) + g_{2} (x_{2} )u, \quad x_{2} \notin S_{2}^{1} \\ x_{1}^{ + } = \Delta_{2}^{1} (x_{2}^{ - } ) \quad x_{2} \notin S_{2}^{1}\\ \end{array} \right.$$
(7)

where \(S_{v}^{v + 1} = \{ x_{v} \left| {z_{sw} (x_{v} )} \right. = 0,\dot{z}_{sw} < 0\}\), v = 1, 2 are the switching surfaces. Compared with the previous work, the dynamic model (7) does not possesses the left–right symmetry property, and thus the stabilization problem of (7) can not be reduced to that of hybrid systems with a single continuous phase by using the symmetry property, which makes the controller design more complicated.

3 The Proposed Control Strategy

To address the stabilization problem of the hybrid system (7), this section presents a novel hybrid control strategy, which consists of a continous motion controller and an event-based feedback controller. The motion controller is designed to asymptotically drive the state of the robot to the zero dynamics manifold, and the event-based feedback controller is designed to render the hybrid zero dynamics locally asymptotically stable. Compared with previous work, the motion controller uses heuristic state variables as controlled variables, and the controller parameters of the event-based feedback controller are designed in an analytical method rather than relying on the left–right symmetry property.

3.1 Heuristic Motion Controller

In this subsection, a heuristic motion controller is presented using the method of virtual constraints and hybrid zero dynamics as in [20]. Compared with previous work, the controller uses heuristic state variables as controlled variables, rather than simply the actuated variables. Here, four heuristic state variables are defined, \(q_{Tor,L} = q_{1} + q_{3} + q_{4}\) defines the torso angle in the lateral plane, xcm defines the position of the center of mass (COM) along the x direction, \(q_{Tor,F} = q_{2} + q_{5}\) defines the torso angle in the frontal plane, and \(q_{Hip,F} = q_{5} - q_{6}\) is the hip angle in the frontal plane, see Fig. 2. \(q_{Tor,L}\) and xcm are used to control the motion in the lateral plane, whereas \(q_{Tor,F}\) and \(q_{Hip,F}\) are used to control the motion in the frontal plane. For simplicity, xcm is approximated by its linearization around the final configuration \(q_{v}^{ - }\). It is noted that the final configurations for the left support phase and the right support phase are different.

Fig. 2
figure 2

Heuristic state variables in the lateral and frontal planes

Full size image

(1) Virtual constraints and controller design Here, to design the virtual constraints, a controlled variable vector is firstly designed based on the heuristic state variables, and

$$C = [q_{Tor,L} ,x_{cm} ,q_{Tor,F} ,q_{Hip,F} ,q_{a} ]^{T}$$
(8)

where \(q_{a} = [q_{3} , \ldots ,q_{8} ]^{T}\) denote the actuated variables. The controlled variable vector C collects all the controlled variables, and a linear relation exists between C and q, namely

$$C = {\rm T}q$$
(9)

where T is a constant matrix.

Next, suppose that a known periodic motion \(q^{*} (t)\) can be reparametrized as a function of θ, and θ is some strictly monotonic variable in each continuous phase. Then the controlled variables in the phase \(v \in \{ 1,2\}\) can be designed as

$$C_{v} = M_{v} C(\theta )$$
(10)

where Mv is an (6 × 10) full-rank, constant selection matrix indicating whether a controlled variable is selected or not. In this work, the variable θ is defined as \(\theta = - q_{1} - 0.5q_{3}\). Let \(q_{u} = [\theta ,q_{2} ]^{T}\) denote the unactuated variables, then we have

$$q = \varPsi \left[ {\begin{array}{*{20}c} {q_{u} } \\ {q_{a} } \\ \end{array} } \right]$$
(11)

where Ψ is an (8 × 8) invertible matrix. From Eqs. (9) and (11), the controlled variables Cv in the phase \(v \in \{ 1,2\}\) can be rewritten as

$$C_{v} = M_{v} {\rm T}\varPsi \left[ {\begin{array}{*{20}c} \theta \\ {q_{2} } \\ {q_{a} } \\ \end{array} } \right] = [M_{11} \;M_{12} \;M_{13} ]\left[ {\begin{array}{*{20}c} \theta \\ {q_{2} } \\ {q_{a} } \\ \end{array} } \right]$$
(12)

where M11 and M12 are (6 × 1) submatrices of \(M_{v} {\rm T}\varPsi\), and M13 is an (6 × 6) invertible submatrix of \(M_{v} {\rm T}\varPsi\).

Based on the controlled variables (12), the virtual constraints in the phase \(v \in \{ 1,2\}\) are designed as

$$\begin{aligned} y_{v} &= C_{v} (\theta ) - C_{v}^{*} (\theta ) \hfill \\ &= M_{13} \left( {q_{a} - q_{a}^{*} (\theta )} \right) + M_{12} \left( {q_{2} - q_{2}^{*} (\theta )} \right) \hfill \\ \end{aligned}$$
(13)

To enforce the constraints, we differentiate Eq. (13) twice with respect to time as in [27], obtaining

$$\ddot{y}_{v} = \frac{{\partial y_{v} }}{\partial q}\ddot{q} + \frac{{\partial^{2} y_{v} }}{{\partial q^{2} }}\dot{q}^{2} = \frac{{\partial y_{v} }}{\partial q}\ddot{q} + \frac{{\partial^{2} V_{\theta } }}{{\partial \theta^{2} }}\dot{\theta }^{2}$$
(14)

where \(V_{\theta } = - M_{13} q_{a}^{*} (\theta ) - M_{12} q_{2}^{*} (\theta )\). Substituting (3) into (14), we have

$$\ddot{y}_{v} = \frac{{\partial y_{v} }}{\partial q}\left[ {D_{v}^{ - 1} Bu - D_{v}^{ - 1} H_{v} } \right] + \frac{{\partial^{2} V_{\theta } }}{{\partial \theta^{2} }}\dot{\theta }^{2}$$
(15)

In order to asymptotically drive the state of the robot to the constraint surface \(Z_{v} = \{ x_{v} |y_{v} = 0,\dot{y}_{v} = 0\}\), the controller in the phase \(v \in \{ 1,2\}\) can be designed as

$$\begin{aligned} u &= (\frac{{\partial y_{v} }}{\partial q}D_{v}^{ - 1} B)^{ - 1} (\frac{{\partial y_{v} }}{\partial q}D_{v}^{ - 1} H_{v} - \frac{{\partial^{2} V_{\theta } }}{{\partial \theta^{2} }}\dot{\theta }^{2} ) \hfill \\ &\quad - (\frac{{\partial y_{v} }}{\partial q}D_{v}^{ - 1} B)^{ - 1} (\frac{{K_{P} }}{{\varepsilon^{2} }}y_{v} + \frac{{K_{D} }}{\varepsilon }\dot{y}_{v} ) \hfill \\ \end{aligned}$$
(16)

which results in

$$\ddot{y}_{v} + \frac{{K_{P} }}{{\varepsilon^{2} }}y_{v} + \frac{{K_{D} }}{\varepsilon }\dot{y}_{v} = 0$$
(17)

From [26], Eq. (17) will converge sufficiently rapidly to the constraint surface Zv if \(K_{P} > 0\), KD > 0, and ε > 0 is chosen to be some sufficiently small constant. Zv is also called the zero dynamics manifold, and the dynamics of the system restricted to this set is known as the zero dynamics.

(2) HZD method and Poincaré analysis By the HZD method, the stability of the full hybrid model can be deduced on the basis of the dynamics restricted in the zero dynamics manifolds, i.e., the hybrid zero dynamics, which would significantly reduce the computational cost. To apply this method, the virtual constraints (13) are modified as

$$y_{v} = M_{13} \left( {q_{a} - q_{a}^{*} (\theta ) - h_{c} (\theta )} \right) + M_{12} \left( {q_{2} - q_{2}^{*} (\theta )} \right)$$
(18)

where \(h_{c} (\theta )\) is the correction term to achieve hybrid invariance and its coefficients are selected such that the post-impact constraints and their velocities are zero. Under the virtual constraints (18), the variable Vθ in the controller (16) is updated as

$$V_{\theta } = - M_{13} (q_{a}^{*} (\theta ) + h_{c} (\theta )) - M_{12} q_{2}^{*} (\theta )$$
(19)

Now, from [26], the stability of a given periodic orbit O of (7) can be evaluated using the restricted Poincaré map \(P^{{^{Z} }} :S_{2}^{1} \cap Z_{2} \to S_{2}^{1} \cap Z_{2}\) expressed as

$$P^{{^{Z} }} (z_{2} ): = P_{2}^{Z} \circ P_{1}^{Z} (z_{2} )$$
(20)

where the generalized Poincaré phase-v map \(P_{v}^{Z}\) follows a solution of the hybrid zero dynamics from a state in \(S_{v - 1}^{v} \cap Z_{v - 1}\) to some state in \(S_{v}^{v + 1} \cap Z_{v}\), v = 1, 2, and we have

$$P_{v}^{Z} (z_{v - 1}^{*} ) = z_{v}^{*}$$
(21)

where \(z_{v}^{*} = O \cap (S_{v}^{v + 1} \cap Z_{v} )\), v = 1, 2 are the fixed points. Let \(A = {{\partial P^{{^{Z} }} (z_{2}^{*} )} \mathord{\left/ {\vphantom {{\partial P^{{^{Z} }} (z_{2}^{*} )} {\partial z^{2} }}} \right. \kern-0pt} {\partial z^{2} }}\) be the Jacobian of Pz at the fixed point \(z_{2}^{*} = O \cap (S_{2}^{1} \cap Z_{2} )\). Then, the periodic orbit O is asymptotically stable if the magnitude of the eigenvalues or the spectral radius of A is less than 1. Let Av be the Jacobian of \(P_{v}^{Z}\) at the fixed point \(z_{v - 1}^{*}\). Then, from the chain rule, the derivative of (20) at the fixed point is

$$A = A_{2} A_{1}$$
(22)

3.2 Event-Based Feedback Controller

In this subsection, a novel event-based feedback controller is developed to render the HZD locally asymptotically stable. Firstly, a parametrized controller is designed and an explicit expression of the Jacobian of the Poincaré return map is derived. Then, an analytical method is proposed to design the controller parameters.

(1) Control objective To render the HZD locally asymptotically stable, the virtual constraints (18) are firstly parametrized as

$$\begin{aligned} y_{v,\beta } &= M_{13} \left( {q_{a} - q_{a}^{*} (\theta ) - h_{c} (\theta ) - h_{s} (\theta ,\beta_{v} )} \right) \hfill \\ &\quad\quad + M_{12} \left( {q_{2} - q_{2}^{*} (\theta )} \right) \hfill \\ \end{aligned}$$
(23)

where \(h_{s} (\theta ,\beta_{v} )\) is an additional term to shift the eigenvalues of the Poincaré map, which is designed to be a third-order polynomial of θ such that

$$\left\{ {\begin{array}{*{20}l} {h_{s} (\theta_{v,ini} ,\beta_{v} ) = 0.5\beta_{v} } \hfill \\ {h_{s} (0.5\theta_{v,ini} + 0.5\theta_{v,f} ,\beta_{v} ) = \beta_{v} } \hfill \\ {h_{s} (0.1\theta_{v,ini} + 0.9\theta_{v,f} ,\mathop \beta \nolimits_{v} ) = 0} \hfill \\ {{{\partial h_{s} (0.1\theta_{v,ini} + 0.9\theta_{v,f} ,\mathop \beta \nolimits_{v} )} \mathord{\left/ {\vphantom {{\partial h_{s} (0.1\theta_{v,ini} + 0.9\theta_{v,f} ,\mathop \beta \nolimits_{v} )} {\partial \theta }}} \right. \kern-0pt} {\partial \theta }} = 0} \hfill \\ \end{array} } \right.$$
(24)

where \(\beta_{v} \in \varXi_{v}\) and \(\varXi_{v} \in R^{6}\) represent the finite-dimensional parameter vector and the set of admissible parameters, respectively; \(\theta_{v,ini}\) and \(\theta_{v,f}\) are the initial and final values of θ, respectively. Then, similar to (16), the parametrized controller in the phase \(v \in \{ 1,2\}\) can be designed as

$$\begin{aligned} u_{\beta } &= (\frac{{\partial y_{v,\beta } }}{\partial q}D_{v}^{ - 1} B)^{ - 1} (\frac{{\partial y_{v,\beta } }}{\partial q}D_{v}^{ - 1} H_{v} - \frac{{\partial^{2} V_{\theta ,\beta } }}{{\partial \theta^{2} }}\dot{\theta }^{2} ) \hfill \\ &\quad - (\frac{{\partial y_{v,\beta } }}{\partial q}D_{v}^{ - 1} B)^{ - 1} (\frac{{K_{P} }}{{\varepsilon^{2} }}y_{v,\beta } + \frac{{K_{D} }}{\varepsilon }\dot{y}_{v,\beta } ) \hfill \\ \end{aligned}$$
(25)

with

$$V_{\theta ,\beta } = - M_{13} \left( {q_{a}^{*} (\theta ) + h_{c} (\theta ) + h_{s} (\theta ,\beta_{v} )} \right) - M_{12} q_{2}^{*} (\theta )$$
(26)

Under the controller (25), we can define the parameterized restricted Poincaré return map for the closed-loop system as \(P_{\beta }^{Z} :(S_{2}^{1} \cap Z_{2} ) \times \varXi_{1} \times \varXi_{2} \to S_{2}^{1} \cap Z_{2}\) by

$$P_{\beta }^{Z} (z_{2} ,\beta_{1} ,\beta_{2} ): = P_{2,\beta }^{Z} \left( {P_{1,\beta }^{Z} (z_{2} ,\beta_{1} ),\beta_{2} } \right)$$
(27)

where \(P_{v,\beta }^{Z} (z_{v - 1} ,\beta_{v} )\) is the parameterized version of \(P_{v}^{Z}\), and for all \(z_{v - 1} \in (S_{v - 1}^{v} \cap Z_{v - 1} )\), the following result can be immediately obtained

$$P_{v,\beta }^{Z} (z_{v - 1} ,0) = P_{v}^{Z} (z_{v - 1} )$$
(28)

Then, differentiating the above equation with respect to \(z_{v - 1}\) at the fixed point \(z_{v - 1}^{*}\), we have

$$\frac{{\partial P_{v,\beta }^{Z} }}{{\partial z_{v - 1} }}(z_{v - 1}^{*} ,0) = \frac{{\partial P_{v}^{Z} }}{{\partial z_{v - 1} }}(z_{v - 1}^{*} )$$
(29)

Next, the controller parameter βv is updated by an event-based feedback law

$$\beta_{v} = - K_{v} (z_{v - 1} - z_{v - 1}^{*} )$$
(30)

Then, the objective is to design the controller parameters K1 and K2 such that the Jacobian of the restricted Poincaré return map \(P_{\beta }^{Z}\) has its eigenvalues in the unit circle.

(2) Design of the controller parameters Here, an analytical method is proposed to design the controller parameters K1 and K2. To achieve this goal, the explicit expression of the Jacobian of the Poincaré return map is firstly derived.Since βv is a function of \(z_{v - 1}\), the parameterized Poincaré map \(P_{v,\beta }^{Z}\) can be represented by the equivalent restricted Poincaré map \(P_{v,e}^{Z} :S_{v - 1}^{v} \cap Z_{v - 1} \to S_{v}^{v + 1} \cap Z_{v}\), and we have

$$P_{v,e}^{Z} (z_{v - 1} ) = P_{v,\beta }^{Z} \left( {z_{v - 1} ,\beta_{v} (z_{v - 1} )} \right)$$
(31)

Then, the restricted Poincaré return map \(P_{\beta }^{Z}\) can be represented by the equivalent Poincaré map \(P_{e}^{Z} :(S_{2}^{1} \cap Z_{2} ) \to S_{2}^{1} \cap Z_{2}\) and

$$P_{e}^{Z} (z_{2} ): = P_{2,e}^{Z} \circ P_{1,e}^{Z} (z_{2} )$$
(32)

Next, the Jacobian of \(P_{e}^{Z}\) at the fixed point \(z_{2}^{*}\) is given by

$$A_{e} = \frac{{\partial P_{e}^{Z} }}{{\partial z_{2} }}z_{2}^{*}$$
(33)

Now, the stability of the closed-loop system can be evaluated by checking the eigenvalues of the Jacobian Ae. In the following, an explicit expression of the Jacobian Ae is derived.

Since the hybrid system (7) is C1 in each phase, the Poincaré return map \(P_{e}^{Z}\) is C1 in a neighborhood of \(z_{v}^{*}\), v = 1, 2. Then, according to the chain rule, the Jacobian Ae can be obtained as

$$A_{e} = \frac{{\partial (P_{2,e}^{Z} \circ P_{1,e}^{Z} )}}{{\partial z_{2} }}(z_{2}^{*} )\; = \;\frac{{\partial P_{2,e}^{Z} }}{{\partial z_{1} }}\left( {P_{1,e}^{Z} (z_{2}^{*} )} \right).\frac{{\partial P_{1,e}^{Z} }}{{\partial z_{2} }}(z_{2}^{*} )$$
(34)

From Eq. (31), we have

$$P_{1,e}^{Z} (z_{2}^{*} ) = P_{1,\beta }^{Z} \left( {z_{2}^{*} ,\beta_{2} (z_{2}^{*} )} \right) = P_{1,\beta }^{Z} (z_{2}^{*} ,0)$$
(35)

Next, combining Eq. (35) with Eqs. (28) and (21), we can obtain that

$$P_{1,e}^{Z} (z_{2}^{*} ) = z_{1}^{*}$$
(36)

Then, substituting Eq. (36) into Eq. (34), we have

$$A_{e} = A_{2,e} A_{1,e}$$
(37)

where \(A_{v,e} = {{\partial P_{v,e}^{Z} (z_{v - 1}^{*} )} \mathord{\left/ {\vphantom {{\partial P_{v,e}^{Z} (z_{v - 1}^{*} )} {\partial z_{v - 1} }}} \right. \kern-0pt} {\partial z_{v - 1} }}\), v = 1, 2. Next, an explicit expression of Av,e is further derived.

According to the chain rule, the Jacobian of \(P_{v,e}^{Z}\) at the fixed point \(z_{v - 1}^{*}\) can be obtained from (31), and

$$A_{v,e} = \frac{{\partial P_{v,\beta }^{Z} }}{{\partial z_{v - 1} }}(z_{v - 1}^{*} ,0) + \frac{{\partial P_{v,\beta }^{Z} }}{{\partial \beta_{v} }}(z_{v - 1}^{*} ,0).\frac{{\partial \beta_{v} }}{{\partial z_{v - 1} }}(z_{v - 1}^{*} )$$
(38)

Next, according to Eqs. (29) and (30), we have

$$A_{v,e} = A_{v} - F_{v} K_{v}$$
(39)

where \(A_{v} = {{\partial P_{v}^{Z} (z_{v - 1}^{*} )} \mathord{\left/ {\vphantom {{\partial P_{v}^{Z} (z_{v - 1}^{*} )} {\partial z_{v - 1} }}} \right. \kern-0pt} {\partial z_{v - 1} }}\), \(F_{v} = {{\partial P_{v}^{Z} (z_{v - 1}^{*} ,0)} \mathord{\left/ {\vphantom {{\partial P_{v}^{Z} (z_{v - 1}^{*} ,0)} {\partial \beta_{v} }}} \right. \kern-0pt} {\partial \beta_{v} }}\). Similar to [22], the Jacobians Av and Fv can be directly calculated using numerical differentiation approaches. Therefore, the Jacobian Av,e depends only on the constant gain matrix Kv. Based on Eqs. (37) and (39), we have

$$A_{e} = (A_{2} - F_{2} K_{2} )(A_{1} - F_{1} K_{1} )$$
(40)

Then, the asymptotical stabilization of the hybrid system (7) has been transformed into the design of the controller parameters K1 and K2 such that

$$\rho (A_{e} ) < 1$$
(41)

where \(\rho (.)\) denotes the spectral radius.Now, based on Eq. (40), we are able to design the controller parameters K1 and K2 using explicit expression, and they are designed as

$$K_{v} = (1 - {1 \mathord{\left/ {\vphantom {1 {m_{v} }}} \right. \kern-0pt} {m_{v} }})F_{v}^{ + } A_{v}$$
(42)

where \(F_{v}^{ + }\) is the pseudo inverse of Fv, and mv is the positive constant to be designed. Next, we will show that if m1 and m2 are designed such that \(m_{1} m_{2} > \lambda\), where \(\lambda\) is the spectral radius of A, then the closed-loop system is locally asymptotically stable. From (40) and (22), we have

$$A_{e} = \frac{{A_{2} A_{1} }}{{m_{1} m_{2} }} = \frac{A}{{m_{1} m_{2} }}$$
(43)

Then, from the definition of the spectral radius, we can easily prove that \(\rho (A_{e} ) = {{\rho (A)} \mathord{\left/ {\vphantom {{\rho (A)} {(m_{1} m_{2} )}}} \right. \kern-0pt} {(m_{1} m_{2} )}}\). Since \(m_{1} m_{2} > \lambda\), we have

$$\rho (A_{e} ) < \frac{1}{\lambda }\lambda = 1$$
(44)

Therefore, the closed-loop system is locally asymptotically stable. It is obvious that a pair of large constants m1 and m2 will leads to a smaller spectral radius \(\rho (A_{e} )\). However, a very large m1 and m2 may cause large torques during the feedback control. Usually, m1 and m2 are designed to be the same, and \(\rho (A_{e} )\) is designed within the interval \([0.3,0.8]\). Once \(\rho (A_{e} )\) is determined, the constants m1 and m2 can be obtained.

4 An Illustrative Example

In this section, we present a numerical example to verify the control strategy developed in Sect. 3. The asymmetric 3-D biped is shown in Fig. 1. To implement the control strategy, a periodic walking gait for the asymmetric 3-D biped is firstly designed.

For underactuated bipeds, to design a walking gait is to find a set of proper coefficients that define the evolution of the actuated variables qa. For this goal, the evolution functions of the actuated variables in the left and right single support phases are firstly designed as

$$h_{1,d} = \sum\limits_{k = 0}^{5} {\alpha_{1,k} \frac{5!}{k!(5 - k)!}s^{k} (1 - s)^{5 - k} }$$
(45)

and

$$h_{2,d} = \sum\limits_{k = 0}^{3} {\alpha_{2,k} \frac{3!}{k!(3 - k)!}s^{k} (1 - s)^{3 - k} }$$
(46)

respectively, where \(s = {{(\theta - \theta_{v,ini} )} \mathord{\left/ {\vphantom {{(\theta - \theta_{v,ini} )} {(\theta_{v,f} - \theta_{v,ini} )}}} \right. \kern-0pt} {(\theta_{v,f} - \theta_{v,ini} )}}\) is the normalized independent variable, and the coefficients \(\alpha_{v,k}\), v = 1, 2 are (6 × 1) vectors of real numbers. Next, the coefficients \(\alpha_{1,k}\) and \(\alpha_{2,k}\) are obtained through a nonlinear optimization process. To simplify the optimization process, the nominal final state \(x_{1}^{ - } = [q_{1}^{ - } ,\dot{q}_{1}^{ - } ]^{T}\) is chosen as a known condition, and

$$\begin{aligned} q_{1}^{ - } & = [ - 0.333, - 0.027,0.360, - 0.293,0.064,0.038, - 0.506,0.212]^{T} \\ \dot{q}_{1}^{ - } & = [ - 1.184, - 0.477,0.099,0.278, - 0.100,0.099,1.398,0]^{T} \\ \end{aligned}$$

During the optimization process, the final state \(x_{2}^{ - } = [q_{2}^{ - } ,\dot{q}_{2}^{ - } ]^{T}\) and the coefficients α1,2 and α1,3 are chosen to be the optimization variables, and other coefficients can be directly calculated from \(x_{1}^{ - }\) and \(x_{2}^{ - }\) by solving the boundary conditions of Eqs. (43) and (44) at \(\theta = \theta_{v,ini}\) and \(\theta = \theta_{v,f}\). The optimization process is then performed similar to [22]. In this work, the optimization results are obtained as follows:

$$\begin{aligned} q_{2}^{ - } & = [ - 0.365,0.041,0.229, - 0.391, - 0.055, - 0.009, - 0.881,0.167]^{T} , \\ \dot{q}_{2}^{ - } & = [ - 0.420,0.487, - 1.941, - 1.128,0.861,0.407, - 2.477, - 1.674]^{T} , \\ \alpha_{1,2} & = [0.997, - 1.978, - 0.220,0.455, - 0.510,0.240]^{T} , \\ \alpha_{1,3} & = [1.078, - 0.893,0.010,0.299, - 0.923,1.564]^{T} . \\ \end{aligned}$$

Now, a periodic and asymmetric walking gait has been obtained. The nominal joint profiles over two consecutive steps are shown in Fig. 3, where the unactuated variable θ is monotonic over each step. Figure 4 shows the torque required to produce the periodic motion. Figure 5 shows the profiles of the ground reaction forces on the stance foot and the profile of the swing leg tip, from which the physical constraints of bipedal walking are satisfied. In the following, the presented control strategy is applied to achieve stable walking.

Fig. 3
figure 3

The nominal joint profiles over two consecutive steps

Full size image
Fig. 4
figure 4

The torque required to produce the periodic motion over two consecutive steps

Full size image
Fig. 5
figure 5

The profiles of the ground reaction forces on the stance foot and the profile of the swing leg tip

Full size image

According to Sect. 3.1, a heuristic motion controller is first designed, and the controlled variables in the left and right single support phases are chosen as \(C_{1} = [q_{Tor,L} ,q_{4} ,x_{cm} ,q_{Hip,F} ,q_{7} ,q_{8} ]^{T}\) and \(C_{2} = [q_{Tor,L} ,q_{4} ,q_{Tor,F} ,x_{cm} ,q_{7} ,q_{8} ]^{T}\), respectively. Then, by the HZD approach, the stability property under the motion controller is evaluated by checking the spectral radius of the Jacobian of the restricted Poincaré return map PZ. By using the numerical differentiation approach [16], the Jacobian of PZ at the fixed point \(z_{2}^{*}\) is computed as

$$A = \left[ {\begin{array}{*{20}c} { 5. 0 5 8} & {{ - 0} . 0 3 7} & { 1. 0 3 0} \\ {{ - 0} . 7 0 5} & {{ 1} . 0 4 8} & { 0. 1 0 1} \\ { 0. 6 3 0} & {{ - 3} . 0 1 6} & {{ - 0} . 5 4 2} \\ \end{array} } \right]$$
(47)

with \(\rho (A) = 5.264\). As a comparison, we also consider the motion controller whose controlled variables are simply the actuated variables. In that case, the corresponding Jacobian is computed as

$$A = \left[ {\begin{array}{*{20}c} { 1 4. 0 6 1} & { 1. 7 5 5} & { 3. 1 9 7} \\ { 2. 1 3 0} & { 0. 8 2 4} & { 0. 4 3 7} \\ { 5 2. 1 8 6} & { 6. 1 7 2} & { 1 1. 9 4 5} \\ \end{array} } \right]$$
(48)

with \(\rho (A) = 2 6. 2 1 7\). It is obvious that under the presented heuristic motion controller, the spectral radius is much smaller, which indicates that the stability property is well improved.

Next, the presented event-based controller is applied by following Sect. 3.2, and we set m1 = 4, m2 = 4. Under the event-based controller, the Jacobian Ae is computed as

$$A_{e} = \left[ {\begin{array}{*{20}c} { 0. 3 1 6} & {{ - 0} . 0 0 2} & { 0. 0 6 4} \\ {{ - 0} . 0 4 4} & {\; 0. 0 6 5} & { 0. 0 0 6} \\ { 0. 0 3 9} & {{ - 0} . 1 8 8} & {{ - 0} . 0 3 3} \\ \end{array} } \right]$$
(49)

Since \(\rho (A_{e} ) = 0.329 < 1\), the closed-loop system is locally asymptotically stable. To illustrate the local stability, the hybrid zero dynamics of the 3-D biped in closed-loop is simulated with an initial state slightly deviating from the fixed point \(z_{2}^{*}\). Here, an initial error of 0.01 rad is introduced on the underactuated variable and a velocity error of 0.05 rad/s is introduced on each underactuated variable velocity. Figure 6 shows the phase plots of the underactuated variables, from which the asymmetric 3-D biped is apparently stabilized. As a comparison, we also consider the case when the controller simply uses the actuated variables as the controlled variables, and the phase plots are shown in Fig. 7. From Fig. 7, the robot falls down within 3 steps, and thus the effectiveness of the presented control strategy is demonstrated.

Fig. 6
figure 6

Phase plots for θ and q2 over 25 walking cycles, where the initial state is represented by a cycle, each variable converges to the nominal periodic orbit represented by the red curve, and the straight lines correspond to the impact phases

Full size image
Fig. 7
figure 7

Phase plots for θ and q2 when the controller simply uses the actuated variables as the controlled variables. The initial state is represented by a cycle, and the nominal periodic orbit is represented by the red curve. The robot falls down within 3 steps

Full size image

5 Conclusion

This work considered the stabilization problem of an underactuated 3-D biped with asymmetric structure, and a novel hybrid control strategy was proposed. In this strategy, a heuristic motion controller that uses heuristic state variables as controlled variables was first designed to asymptotically drive the state of the robot to the zero dynamics manifold, and then a novel event-based feedback controller, whose controller parameters were designed in an analytical method, was designed to render the hybrid zero dynamics locally asymptotically stable. Finally, a numerical asymmetric walking gait was designed and used to show the validity of this control strategy. In future research, we will consider extending this control strategy to underactuated 3-D bipedal running or bipedal walking with toe-rotation.