Fuzzy Adaptive Practical Finite-Time Control for Time Delays Nonlinear Systems

Abstract

This paper focuses on fuzzy adaptive practical finite-time output feedback control problem for a class of single-input and single-output nonlinear system with time-varying delays in nonstrict feedback form. Fuzzy logic systems are adopted to approximate the unknown nonlinear functions, and state observer is constructed to estimate the unmeasured states. By combining practical finite-time Lyapunov stability theory with the backstepping design, an observer-based fuzzy adaptive practical finite-time control strategy is proposed. Meanwhile, the stability of the closed-loop system is proved, which means that the output can follow the given reference signal in a finite time, and the closed-loop system is semi-global practical finite-time stability. Finally, two simulation examples are provided to elaborate the effectiveness of the presented control strategy.

1 Introduction

During the past several years, the neural networks (NNs) or FLSs [1,2,3] are adopted to deal with the control problem of uncertain nonlinear systems. By using adaptive backstepping design, some significant results have been received, see [4,5,6,7,8,9]. Among them, the authors in [4, 5] have studied the adaptive fuzzy or NNs control problems for SISO nonlinear pure feedback systems with time-varying delays. The authors in [6] developed the fuzzy adaptive tracking control scheme for SISO strict feedback nonlinear system with input delays, and in [7] presented the output feedback adaptive NNs control scheme for nonlinear stochastic system with time-varying delay. However, in many real-world systems, the systems states of considered plants are usually not available or measurable directly; therefore, fuzzy adaptive observer needs be designed to get the estimation of unmeasured states. Subsequently, the author in [9] investigated the output feedback adaptive fuzzy control problem for nonlinear multi-input and multi-output (MIMO) systems with time delays.

However, the aforementioned presented control design strategies are all considered in the pure/strict feedback systems. In adaptive backstepping control design process, note that FLSs or radial basis functions are adopted to approximate the systems nonlinear functions, it only contains partial state variables. However, nonlinear nonstrict feedback systems are more general nonlinear system, the nonlinear function contains the whole state vector in the i-subsystem. If the above presented control strategies for pure feedback or strict feedback systems are directly applied in nonlinear nonstrict feedback systems, thus, it will lead to much more difficulties, such as the “algebraic loop problem,” which is not be permitted. Therefore, a new adaptive backstepping design strategy needs be presented. To overcome this problem, recently, some significant fuzzy or NNs adaptive control strategies are presented for nonlinear nonstrict feedback systems, see [10,11,12,13,14,15]. Among them, the authors in works [10, 11] developed the approximation-based adaptive fuzzy or NNs control methods for nonlinear nonstrict feedback systems, and in [12] investigated the neural adaptive output feedback control issue for nonlinear stochastic system. The authors in [13,14,15] have presented the observer-based fuzzy or NNs adaptive control strategies for nonstrict feedback systems.

In the real-world systems, consider the factors of cost saving and the maximization of interest, such as the vehicle guidance system, the attitude control systems of the flight vehicle and robot control systems, which be expected to arrive the equilibrium state in a finite or fixed time. If the tracking time and the transient time of the real-world systems go to arbitrary or infinite, which will cost the high charge, apparently, we can see that the above results are all considered in the infinite time and not consider the setting time in their control process, the perform time may be very long. As the finite-time controllers contain the terms of exponential power, the finite-time control method has better robustness, fast transient performance and high precision performance. Therefore, the finite-time control methods have paid the considerable attention for many scholars.

Recently, some crucial works of finite-time control have been received, such as [16,17,18,19,20,21,22,23,24,25,26,27,28]. Bhat et al. [16, 17] first presented finite-time stability theory for nonlinear systems and addressed chattering problems of the adaptive laws caused by terminal sliding mode controller. In addition, the authors in [16, 17] also give several criterions of the finite-time stability. Later, the authors in [18,19,20,21,22] presented the semi-global practical finite-time stability (SGPFS) for uncertain nonlinear systems. Among them, the authors in [18] presented the observer-based neural adaptive finite-time control method for quantized system, and in [19] studied the fuzzy adaptive tracking control issue for nonlinear pure feedback system. In addition, the authors in [20, 21] have developed the fuzzy adaptive finite-time control strategies for SISO nonstrict feedback nonlinear systems and in work [22] are for interconnected large-scale nonlinear systems. Furthermore, the authors in [23,24,25,26,27] studied the global finite-time control problems for nonlinear strict feedback systems by combining and adding a power integrator theory with backstepping recursion design technique. The authors in [28] presented the neural adaptive control scheme for high-order nonlinear nonstrict feedback systems. Obviously, the above controlled systems do not consider the unknown time-varying delays.

In this paper, the issue of fuzzy adaptive finite-time control is studied for SISO nonlinear nonstrict feedback system with time-varying delays. FLSs are utilized to approximate nonlinear functions. Moreover, to estimate the unmeasurable states, fuzzy adaptive observer is constructed. Compared to existing works, the major contributions can be described as: (1) By combining finite-time Lyapunov–Krasovskii stability theory with backstepping design, this paper presented an observer-based fuzzy adaptive practical finite-time control scheme for SISO nonlinear system with time-varying delays. The presented control strategy can ensure that all the signals of closed-loop systems are bounded and the tracking error converges to a small neighborhood of the zero in a finite time; (2) compared with the existing finite-time control results in [18,19,20,21,22], the problems of time-varying delay are considered in this paper and the nonlinear systems are in nonstrict feedback forms. On the one hand, in [19,20,21, 23,24,25,26,27,28], the state variables are all available. In this paper, the state variables are not completely available; thus, a fuzzy state observer is constructed and does not like [18]; on the other hand, the nonlinear functions in this paper are completely unknown and do not satisfy the linear growth condition like [25,26,27].

2 Problem Formulations and Preliminaries

2.1 System Description

Consider the SISO nonlinear nonstrict feedback system as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} + f_{1} (x) + h_{1} (x_{1} (t - \tau_{1} )) + d_{1} (t)} \hfill \\ {\dot{x}_{i} = x_{i + 1} + f_{i} (x) + h_{i} (x_{1} (t - \tau_{i} )) + d_{i} (t)} \hfill \\ {\dot{x}_{n} = u + f_{n} (x) + h_{n} (x_{1} (t - \tau_{n} )) + d_{n} (t)} \hfill \\ {y = x_{1} \quad i = 2, \ldots ,n - 1} \hfill \\ \end{array} } \right. $$

(1)

where $x = [x_{1} ,x_{2} , \ldots ,x_{n} ]^{\text{T}}$ is the state vector, $y \in R$ and $u \in R$ are output and control input, respectively. $f_{i} ( \cdot )$ and $h_{i} ( \cdot )$ are the unknown smooth nonlinear functions and satisfy $f_{i} (0) = 0$. $\tau_{i}$ is unknown bounded time delay satisfying $\left| {\tau_{i} } \right| \le \tau$ and the derivative of $\tau_{i}$ satisfies $\dot{\tau }_{i} (t) \le \tau^{ *} \le 1$, where $\tau$ and $\tau^{*}$ are known constant. $d_{i} (t)$($i = 1,2, \ldots ,n$) is the dynamic disturbance and satisfies $|d_{i} (t)| \le d_{i}^{*}$ with $d_{i}^{*}$ being known constant. Moreover, the only available state is output $y$.

Assumption 1

[8, 9] The unknown nonlinear smooth function $h_{i} (x_{1} )$ satisfies

$$ \left| {h_{i} (x_{1} )} \right|^{2} \le z_{1} H_{i} (z_{1} ) + \bar{H}_{i} (y_{r} ) + \varpi_{i} $$

where $z_{1}$ is the tracking error, $\bar{H}_{i} ( \cdot )$ and $H_{i} ( \cdot )$ are bounded and known functions, which satisfy $\bar{H}_{i} (0) = 0$, $\varpi_{i}$ is a positive constant.

Lemma 1

[10, 12] (Young’s inequality) For$\forall (a,b) \in R^{2}$, the following inequality holds

$$ ab \le \frac{{\varepsilon^{p} }}{p}|a|^{p} + \frac{1}{{q\varepsilon^{q} }}|b|^{q} $$

where$\varepsilon > 0$, $p > 1$, $q > 1$and$(p - 1)(q - 1) = 1$.

Our control objective is to present a practical finite-time fuzzy adaptive control strategy for system (1), such that all the signals of the closed-loop system are bounded and output $y(t)$ can track the given reference signal $y_{r} (t)$ in a finite time.

2.2 Fuzzy Logic Systems

From [14], FLSs are consisted by the following four parts: the knowledge base, the fuzzifier, the fuzzy inference engine working on fuzzy rules and the defuzzifier. The knowledge base is consisted by the following inference rules:

$$ \begin{aligned} R^{l}:\; & {\text{If}}\;x_{1} \;{\text{is}}\;F_{1}^{l} \;{\text{and}}\;x_{2} \;{\text{is}}\;F_{2}^{l} \;{\text{and}}\; \ldots \;{\text{and}}\;x_{n} \;{\text{is}}\;F_{n}^{l} , \\ & \;{\text{then}}\;y\;{\text{is}}\;G_{{}}^{l} ,\;l = 1,2, \ldots ,N. \\ \end{aligned} $$

where $x = [x_{1} ,x_{2} , \ldots ,x_{n} ]^{\text{T}}$ and $y$ are the FLS input and output, respectively. $G_{{}}^{l}$ and $F_{i}^{l}$ are fuzzy sets, together with the fuzzy membership functions $\mu_{{G^{l} }} (y)$ and $\mu_{{F_{i}^{l} }} (x_{i} )$, respectively, and $N$ is the rules number.

According to [14], define the FLS as

$$ y(x) = \frac{{\sum\nolimits_{l = 1}^{N} {\bar{y}_{l} } \prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{l} }} (x_{i} )} }}{{\sum\nolimits_{l = 1}^{N} {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{l} }} (x_{i} )} } }} $$

(2)

where $\bar{y}_{l} = \mathop {\hbox{max} }\limits_{{y_{l} \in R}} \mu_{{G^{l} }} (y_{l} )$.

Fuzzy basis functions can be described as

$$ \varphi_{l} = \frac{{\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{l} }} (x_{i} )} }}{{\sum\nolimits_{l = 1}^{N} {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{l} }} (x_{i} )} } }} $$

Denoting $\varphi (x) = [\varphi_{1} (x), \ldots ,\varphi_{N} (x)]^{\text{T}}$ and $\xi^{T} = [\bar{y}_{1} ,\bar{y}_{2} , \ldots ,\bar{y}_{N} ] = [\xi_{1} ,\xi_{2} , \ldots ,\xi_{N} ]$, then rewritten the FLS (2) as

$$ y(x) = \xi^{T} \varphi (x) $$

(3)

Lemma 2

[8, 14] Let$f(x)$be a continuous function, which is defined on a compact set$\varOmega$. Then for any constant$\varepsilon > 0$, there exists a FLS (3) such as

$$ \mathop {\sup }\limits_{x \in \varOmega } \left| {f(x) - \xi^{T} \varphi (x)} \right| \le \varepsilon $$

(4)

where$\varepsilon$is the fuzzy minimum approximation error.

2.3 Finite Time

To deal with finite-time fuzzy adaptive control problem, consider the following valid Lemmas and Definition.

Definition 1

[18,19,20] For all initial values $\zeta (t_{0} ) = \zeta_{0}$, there exists a constant $\varsigma > 0$ and setting time $T(\varepsilon ,\zeta_{0} ) < \infty$ satisfies $\left\| {\zeta (t)} \right\| < \varsigma$, for $\forall t \ge t_{0} + T$; thus, the equilibrium point $\zeta = 0$ of nonlinear system $\dot{\zeta } = f(\zeta )$ is semi-global practical finite-time stability (SGPFS).

Lemma 3

[18,19,20] For real number$0 < p \le 1$and$\zeta_{i} \in R$, $i = 1,2, \ldots , \, k$, we have

$$ \left( {\sum\limits_{i = 1}^{k} {\left| {\zeta_{i} } \right|} } \right)^{p} \le \sum\limits_{i = 1}^{k} {\left| {\zeta_{i} } \right|^{p} } \le k^{1 - p} \left( {\sum\limits_{i = 1}^{k} {\left| {\zeta_{i} } \right|} } \right)^{p} $$

(5)

Lemma 4

[18,19,20] For$\mu$, $\sigma$and$\phi$are positive constants, and$\psi$and$\xi$are real variables, we have

$$ \left| \psi \right|^{\mu } \left| \xi \right|^{\sigma } \le \frac{\mu }{\mu + \sigma }\phi \left| \psi \right|^{\mu + \sigma } + \frac{\sigma }{\mu + \sigma }\phi^{{ - \frac{\mu }{\sigma }}} \left| \xi \right|^{\mu + \sigma } $$

(6)

Lemma 5

[18,19,20] Consider differential equation$\dot{\hat{\zeta }}(t) = - \eta \hat{\zeta }(t) + \mu w(t)$, where$\eta > 0$and$\mu > 0$are real numbers, and function$w(t)$is positive. Under the initial value$\hat{\zeta }(t_{0} ) \ge 0$, if$w(t) \ge 0$for$\forall t \ge t_{0}$, we have$\hat{\zeta }(t) \ge 0$for$\forall t \ge t_{0}$.

Lemma 6

[18,19,20] For any positive-definite function$V(\varsigma )$, with scales$\gamma > 0$, $0 < \beta < 1$and$\sigma > 0$, the nonlinear system$\dot{\varsigma } = f(\varsigma )$satisfies

$$ \dot{V}(\varsigma ) \le - \gamma V^{\beta } (\varsigma ) + \sigma ,t \ge 0 $$

(7)

thus the nonlinear system$\dot{\varsigma } = f(\varsigma )$is SGPFS.

Proof

For $\forall 0 < \delta \le 1$, according to (7), we have

$$ \dot{V}(\varsigma ) \le - \gamma (1 - \delta )V^{\beta } (\varsigma ) - \gamma \delta V^{\beta } (\varsigma ) + \sigma $$

(8)

Let $\bar{\varOmega }_{\varsigma } = \{ \varsigma |V^{\beta } (\varsigma ) > \frac{\sigma }{(1 - \delta )\gamma }\}$ and $\varOmega_{\varsigma } = \{ \varsigma |V^{\beta } (\varsigma ) \le \frac{\sigma }{(1 - \delta )\gamma }\}$. There are two cases to consider as

Case 1: If $\varsigma (t) \in \bar{\varOmega }_{\varsigma }$, we have

$$ \dot{V}(\varsigma ) \le - \delta \gamma V^{\beta } (\varsigma ) $$

(9)

Integrating it over $[0,T]$, we have

$$ \int_{0}^{T} {\frac{{\dot{V}(\varsigma )}}{{V^{\beta } (\varsigma )}}} {\text{d}}t \le - \int_{0}^{T} {\delta \gamma } {\text{d}}t $$

(10)

In addition, we have

$$ \frac{1}{1 - \beta }[V^{1 - \beta } (\varsigma (T)) - V^{1 - \beta } (\varsigma (0))] \le - \delta \gamma T $$

(11)

We can define

$$ T_{\text{reach}} = \frac{1}{(1 - \beta )\delta \gamma }\left[ {V^{1 - \beta } (\varsigma (0)) - \left( {\frac{\sigma }{(1 - \delta )\gamma }} \right)^{(1 - \beta )/\beta } } \right] $$

where $V(\varsigma (0))$ is the initial condition of $V(\varsigma )$. Therefore, according to (11), we have $\varsigma (t) \in \varOmega_{\varsigma }$ for $\forall T \ge T_{\text{reach}}$.

Case 2: If $\varsigma (t) \in \varOmega_{\varsigma }$, from the first case, the trajectory of $\varsigma (t)$ is not beyond the set $\varOmega_{\varsigma }$. The time to arrive the set $\varOmega_{\varsigma }$ is bounded as $T_{reach}$, that is, the solution of $\dot{\varsigma } = f(\varsigma )$ is bounded in a finite time.

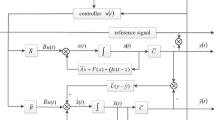
3 Fuzzy State Observer Design

In this paper, the only measurable variable is state $x_{1}$. Thus, state observer needs be constructed to get the estimation of unmeasured states $x_{i}$$(i = 2,3, \ldots ,n)$. On the basis of Lemma 2, the following FLS is adopted to approximate the unknown function $f_{i} (x)$ as

$$ \hat{f}_{i} (\hat{x}|\hat{\xi }_{i} ) = \hat{\xi }_{i}^{T} \varphi_{i} (\hat{x}) $$

(12)

Define the optimal parameter vectors $\xi_{i}^{*}$ as

$$ \xi_{i}^{*} = \arg \min_{{\xi_{i} \in \varOmega_{i} }} \left[ {\sup_{{\hat{x} \in \hat{U},{\kern 1pt} x \in U}} \left| {f_{i} (x) - \hat{f}_{i} (\hat{x}|\hat{\xi }_{i} )} \right|} \right] $$

where $U$, $\hat{U}$ and $\varOmega_{i}$ are compact regions for $x$, $\hat{x}$ and $\hat{\xi }_{i}$, respectively. Thus, define the fuzzy minimum approximation error $\varepsilon_{i}$ as

$$ \varepsilon_{i}^{{}} = f_{i} (x) - \hat{f}_{i} (\hat{x}\left| {\xi_{i}^{ * } } \right.) $$

(13)

where $\varepsilon_{i}^{{}}$ satisfies that $\left| {\varepsilon_{i} } \right| \le \varepsilon_{i}^{*}$, and $\varepsilon_{i}^{*}$ is a positive constant. Thus, rewritten system (1) as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x} = A_{0} x + \sum\limits_{i = 1}^{n} {B_{i} } f_{i} (x) + h + \varLambda + B_{n} u} \hfill \\ {y = \bar{C}x} \hfill \\ \end{array} } \right. $$

(14)

where $A_{0} = \left[ {\begin{array}{*{20}c} 0 & {} & {} & {} \\ \vdots & {} & {I_{n - 1} } & {} \\ 0 & 0 & \cdots & 0 \\ \end{array} } \right]_{n \times n}$, $\bar{C} = [1,0, \ldots ,0]_{1 \times n}$, $B_{i} = [\underbrace {0, \ldots ,0,1}_{i}, \ldots ,0]_{n \times 1}^{T}$, $h = [h_{1} ,h_{2} , \ldots ,h_{n} ]_{n \times 1}^{T}$, $\varLambda = [d_{1} ,d_{2} , \ldots ,d_{n} ]_{n \times 1}^{T}$ and $B_{n} = [0, \ldots ,0,1]_{n \times 1}^{T}$.

To estimate the immeasurable states, fuzzy state observer is designed as

$$ \left\{ {\begin{array}{*{20}l} {\dot{\hat{x}} = A\hat{x} + Ky + \sum\limits_{i = 1}^{n} {B_{i} \hat{f}_{i} (\hat{x}|\hat{\xi }_{i} ) + B_{n} u} } \hfill \\ {\hat{y} = \bar{C}\hat{x}_{1} } \hfill \\ \end{array} } \right. $$

(15)

where $A = A_{0} - K\bar{C}$ and $K = [k_{1} ,k_{2} , \ldots ,k_{n} ]_{n \times 1}^{T}$.

Define virtual observation error vector $e = x - \hat{x}$, from (14) and (15), we have

$$ \dot{e} = Ae + \sum\limits_{i = 1}^{n} {B_{i} \tilde{\xi }_{i}^{T} \varphi_{i} (\hat{x})} + h + \varLambda + \varepsilon $$

(16)

where $\tilde{\xi }_{i} = \xi_{i}^{*} - \hat{\xi }_{i}$ is the adaptive parameter vector error.

The observer gain matrix $K$ is chosen as $A$ is a strict Hurwitz matrix, for any matrix $Q = Q^{T} > 0$; thus, matrix $P = P_{i}^{T}$ satisfies

$$ A^{T} P + PA = - 2Q $$

(17)

From observer error system (16), choose the Lyapunov function as

$$ \bar{V}_{0} = \frac{1}{2}e^{T} Pe $$

Due to the existence of the term of time delay, thus, we utilize the Lyapunov–Krasovksii to deal with the problem of time delay. Choose the Lyapunov–Krasovksii function as

$$ V_{0} = \bar{V}_{0} + W_{0} = \frac{1}{2}e^{T} Pe + W_{0} $$

(18)

where $W_{0} = \frac{{e^{r(\tau - t)} }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {\int_{t - \tau (t)}^{t} {e^{rs} z_{1} (s)(H_{i} (z_{1} (s))){\text{d}}s} }$ is a positive-definition function, $r$ is a positive constant.

From (16)–(18), we have

$$ \begin{aligned} \dot{V}_{0} & = \frac{1}{2}\dot{e}^{T} Pe + \frac{1}{2}e^{T} P\dot{e} + \dot{W}_{0} \\ & \le - \lambda_{\hbox{min} } (Q)\left\| e \right\|^{2} + \dot{W}_{0} \\ & \quad + \,e^{T} P\left( {\sum\limits_{i = 1}^{n} {B_{i} \tilde{\xi }_{i}^{T} \varphi_{i} (\hat{x})} + h + \varLambda + \varepsilon } \right) \\ \end{aligned} $$

(19)

According to the fact $0 < \varphi_{i}^{T} (\hat{x})\varphi_{i} (\hat{x}) \le 1$, adopting Assumption 1 and Lemma 1, we have

$$ e^{T} P\sum\limits_{i = 1}^{n} {B_{i} \tilde{\xi }_{i}^{T} \varphi_{i} (\hat{x})} \le \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{i = 1}^{n} {\tilde{\xi }_{i}^{T} \tilde{\xi }_{i} } + \frac{n}{2}\left\| e \right\|^{2} $$

(20)

$$ e^{T} P(\varepsilon + \varLambda ) \le \left\| e \right\|^{2} + \frac{{\left\| P \right\|^{2} }}{2}\left\| {\varepsilon^{ *} } \right\|^{2} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{i = 1}^{n} {d_{i}^{*2} } $$

(21)

$$ \begin{aligned} e^{T} Ph & \le \frac{{\left\| P \right\|^{2} }}{2}\left\| e \right\|^{2} + \frac{1}{2}h^{2} \\ & \le \frac{{\left\| P \right\|^{2} }}{2}\left\| e \right\|^{2} + \sum\limits_{i = 1}^{n} {q_{i} } \\ & \quad + \,\frac{1}{2}\sum\limits_{i = 1}^{n} ( z_{1} (t - \tau_{i} )H_{i} (z_{1} (t - \tau_{i} ))) \\ \end{aligned} $$

(22)

where $q_{i} \ge \frac{1}{2}(\bar{H}_{i} (y_{r} (t - \tau_{i} )) + \varpi_{i} )$ is a constant.

$$ \begin{aligned} \dot{W}_{0} & = - rW_{0} + \frac{{e^{r(\tau - t)} }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {[e^{rt} z_{1} (t)(H_{i} (z_{1} (t)))} \\ & \quad - e^{r(t - \tau )} z_{1} (t - \tau )H_{i} (z_{1} (t - \tau_{i} ))(1 - \dot{\tau })] \\ & \le - rW_{0} + \frac{{e^{r\tau } }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {z_{1} (t)(H_{i} (z_{1} (t)))} \\ & \quad - \frac{1}{2}\sum\limits_{i = 1}^{n} ( z_{1} (t - \tau_{i} )H_{i} (z_{1} (t - \tau_{i} ))) \\ \end{aligned} $$

(23)

Substituting (20)–(23) into (19) yields

$$ \begin{aligned} \dot{V}_{0} & \le - \lambda_{0} \left\| e \right\|^{2} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } - rW_{0} + M_{0} \\ & \quad + \frac{{e^{r\tau } }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {z_{1} (t)(H_{i} (z_{1} (t)))} \\ \end{aligned} $$

(24)

where $\lambda_{0} = \lambda_{\hbox{min} } - (n + \left\| P \right\|^{2} )/2 - 1$ and $M_{0} = \left\| P \right\|^{2} (\left\| {\varepsilon^{ *} } \right\|^{2} + \sum\nolimits_{i = 1}^{n} {d_{i}^{*2} } )/2 + \sum\nolimits_{i = 1}^{n} {q_{i} }$.

4 Practical Finite-Time Fuzzy Adaptive Control and Stability Analysis

In this section, a practical finite-time fuzzy adaptive control scheme is presented by adopting backstepping design. Define the coordinates transformation as

$$ \left\{ {\begin{array}{*{20}l} {z_{1} = x_{1} - y_{r} } \hfill \\ {z_{i} = \hat{x}_{i} - \alpha_{i - 1} } \hfill \\ \end{array} } \right. $$

(25)

where $z_{1}$ is the tracking error and $\alpha_{i - 1}$, $i = 2,3, \ldots ,n$ are the intermediate control functions.

Step 1 From (1) and (15), define $z_{2} = \hat{x}_{2} - \alpha_{1}$, we have

$$ \begin{aligned} \dot{z}_{1} & = \dot{x}_{1} - \dot{y}_{r} \\ & = z_{2} + \alpha_{1} + \xi_{1}^{*T} \varphi_{1} (\hat{x}) + \hat{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} ) + e_{2} + d_{1} \\ & \quad + \,\varepsilon_{1} + h_{1} + \tilde{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} ) - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} ) - \dot{y}_{r} \\ \end{aligned} $$

(26)

Choose the Lyapunov–Krasovksii function as

$$ V_{1} = V_{0} + \frac{1}{2}z_{1}^{2} + \frac{1}{{2\eta_{1} }}\tilde{\xi }_{1}^{T} \tilde{\xi }_{1} + \frac{1}{{2\bar{\eta }_{1} }}\tilde{\vartheta }_{1}^{T} \tilde{\vartheta }_{1} + W_{1} $$

(27)

where $\eta_{1} > 0$ and $\bar{\eta }_{1} > 0$ are design parameters. $\tilde{\xi }_{i} = \xi_{i}^{*} - \hat{\xi }_{i}$ and $\hat{\xi }_{i}$ is the estimation of $\xi_{i}^{*}$. Define $\vartheta_{i}^{*} = \left\| {\xi_{i}^{*} } \right\|^{2}$, $\tilde{\vartheta }_{i} = \vartheta_{i}^{*} - \hat{\vartheta }_{i}$ and $\hat{\vartheta }_{i}$ is the estimation of $\vartheta_{i}^{*}$($i = 1, \ldots ,n$). Define $W_{1}$ is

$$ W_{1} = \frac{{e^{r(\tau - t)} }}{{2\left( {1 - \tau^{*} } \right)}}\int_{{t - \tau_{1} (t)}}^{t} {e^{rs} z_{1} (s)(H_{1} (z_{1} (s))){\text{d}}s} $$

(28)

From (26)–(28), we have

$$ \begin{aligned} \dot{V}_{1} & = \dot{V}_{0} + z_{1} \dot{z}_{1} - \frac{1}{{\eta_{1} }}\tilde{\xi }_{1}^{T} \dot{\hat{\xi }}_{1} - \frac{1}{{\bar{\eta }_{1} }}\tilde{\vartheta }_{1}^{T} \dot{\hat{\vartheta }}_{1} + \dot{W}_{1} \\ & \le - \lambda_{0} \left\| e \right\|^{2} + z_{1} z_{2} - rW_{0} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\theta }_{j}^{T} \tilde{\theta }_{j} } + M_{0} \\ & \quad + \frac{{e^{r\tau } }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {z_{1} (t)(H_{i} (z_{1} (t)))} + z_{1} (\alpha_{1} + e_{2} \\ & \quad + \xi_{1}^{*T} \varphi_{1} (\hat{x}) + \hat{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} ) + d_{1} + \varepsilon_{1} + \tilde{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} ) \\ & \quad - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} ) + h_{1} - \dot{y}_{r} ) - \frac{1}{{\eta_{1} }}\tilde{\xi }_{1}^{T} \dot{\hat{\xi }}_{1} - \frac{1}{{\bar{\eta }_{1} }}\tilde{\vartheta }_{1}^{T} \dot{\hat{\vartheta }}_{1} + \dot{W}_{1} \\ \end{aligned} $$

(29)

According to the fact of $0 < \varphi_{1}^{T} ( \cdot )\varphi_{1} ( \cdot ) \le 1$, applying Lemma 1 and Assumption 1, for any constant $\pi > 0$, we have

$$ \begin{aligned} \dot{W}_{1} & = - rW_{1} + \frac{{e^{r(\tau - t)} }}{{2\left( {1 - \tau^{*} } \right)}}[e^{rt} z_{1} (t)(H_{1} (z_{1} (t))) \\ & \quad - e^{r(t - \tau )} z_{1} (t - \tau )H_{1} (z_{1} (t - \tau ))(1 - \dot{\tau })] \\ & \le - rW_{1} + \frac{{e^{r\tau } }}{{2\left( {1 - \tau^{*} } \right)}}z_{1} (t)(H_{1} (z_{1} (t))) \\ & \quad - \frac{1}{2}z_{1} (t - \tau )H_{1} (z_{1} (t - \tau )) \\ \end{aligned} $$

(30)

$$ z_{1} (e_{2} + \varepsilon_{1} + d_{1} ) \le \frac{3}{2}z_{1}^{2} + \frac{1}{2}\left\| e \right\|^{2} + \frac{1}{2}\left\| {\varepsilon^{*} } \right\|^{2} + \frac{1}{2}d_{1}^{*2} $$

(31)

$$ z_{1} (\xi_{1}^{*T} \varphi_{1} (\hat{x}) - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} )) \le \frac{\pi }{2}z_{1}^{2} \vartheta_{1}^{*} + \frac{2}{\pi } $$

(32)

$$ \begin{aligned} z_{1} h_{1} & \le \frac{1}{2}z_{1}^{2} + \frac{1}{2}h_{1}^{2} \\ & \le \frac{1}{2}z_{1}^{2} + \frac{1}{2}z_{1} (t - \tau_{1} )H_{1} (z_{1} (t - \tau_{1} )) \\ & \quad + \frac{1}{2}\bar{H}_{1} (y_{r} (t - \tau_{1} )) + \frac{1}{2}\varpi_{1} \\ \end{aligned} $$

(33)

Substituting (30)–(33) into (29) results in

$$ \begin{aligned} \dot{V}_{1} & \le - \lambda_{1} \left\| e \right\|^{2} - rW_{0} - rW_{1} + z_{1} z_{2} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } \\ & \quad + z_{1} \left( {\alpha_{1} + \frac{{e^{r\tau } }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {H_{i} (z_{1} (t))} + \hat{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} )} \right. \\ & \quad + \frac{{e^{r\tau } }}{{2\left( {1 - \tau^{*} } \right)}}H_{1} \left( {z_{1} (t)) - \dot{y}_{r} + 2z_{1} + \frac{{\pi \hat{\vartheta }_{1} }}{2}z_{1} } \right) \\ & \quad + \frac{{\tilde{\vartheta }_{1}^{T} }}{{\bar{\eta }_{1} }}\left( {\frac{{\bar{\eta }_{1} \pi }}{2}z_{1}^{2} - \dot{\hat{\vartheta }}_{1} } \right) + \frac{{\tilde{\xi }_{1}^{T} }}{{\eta_{1} }}\left( {\eta_{1} z_{1} \varphi_{1} (\hat{x}_{1} ) - \dot{\hat{\xi }}_{1} } \right) + M_{1} \\ \end{aligned} $$

(34)

where $\lambda_{1} = \lambda_{0} - 1/2$ and $M_{1} = M_{0} + q_1 + 2/\pi + \left\| {\varepsilon^{*} } \right\|^{2} /2 + d_{1}^{*2} /2$ and $q_1 = \bar{H}_{1} (y_{r} (t - \tau_{1} ))/2 + \varpi_{1} /2$ is a constant.

Design the intermediate control function $\alpha_{1}$, parameter adaptive laws $\dot{\hat{\xi }}_{1}$ and $\dot{\hat{\vartheta }}_{1}$ as

$$ \begin{aligned} \alpha_{1} & = - c_{1} z_{1}^{2\beta - 1} - 2z_{1} - \frac{{\pi \hat{\vartheta }_{1} }}{2}z_{1} - \frac{{e^{r\tau } }}{{2(1 - \tau^{*} )}}\sum\limits_{i = 1}^{n} {H_{i} (z_{1} (t))} \\ & \quad - \hat{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} ) - \frac{{ne^{r\tau } }}{{2\left( {1 - \tau^{*} } \right)}}H_{1} (z_{1} (t)) + \dot{y}_{r} \\ \end{aligned} $$

(35)

$$ \dot{\hat{\xi }}_{1} = \eta_{1} z_{1} \varphi_{1} (\hat{x}_{1} ) - \delta_{1} \hat{\xi }_{1} $$

(36)

$$ \dot{\hat{\vartheta }}_{1} = \frac{{\bar{\eta }_{1} \pi }}{2}z_{1}^{2} - \bar{\delta }_{1} \hat{\vartheta }_{1} $$

(37)

where $\beta = (2n - 1)/(2n + 1)$, $c_{1} > 0$, $\delta_{1} > 0$ and $\bar{\delta }_{1} > 0$ are design parameters. The chosen of the adaptive laws should satisfy Lemma 5. From (35)–(37), it follows that

$$ \begin{aligned} \dot{V}_{1} & \le - \lambda_{1} \left\| e \right\|^{2} - c_{1} z_{1}^{2\beta } + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + z_{1} z_{2} \\ & \quad + \frac{{\delta_{1} }}{{\eta_{1} }}\tilde{\xi }_{1}^{T} \hat{\xi }_{1} + \frac{{\bar{\delta }_{1} }}{{\bar{\eta }_{1} }}\tilde{\vartheta }_{1}^{T} \hat{\vartheta }_{1} - rW_{0} - rW_{1} \\ & \quad - \frac{{(n - 1)e^{r\tau } }}{{2\left( {1 - \tau^{*} } \right)}}z_{1} (t)H_{1} (z_{1} (t)) + M_{1} \\ \end{aligned} $$

(38)

Step 2$i(2 \le i \le n - 1)$: According to (15) and (25), define $z_{i + 1} = \hat{x}_{i + 1} - \alpha_{i}$, we have

$$ \begin{aligned} \dot{z}_{i} & = \alpha_{i} + z_{i + 1} + \xi_{i}^{*T} \varphi_{i} (\hat{x}) - \tilde{\xi }_{i}^{T} \varphi_{i} (\hat{x}) \\ & \quad + \tilde{\xi }_{i}^{T} \varphi_{i} (\underline{{\hat{x}}}_{i} ) - \xi_{i}^{*T} \varphi_{i} (\underline{{\hat{x}}}_{i} ) + \bar{\varXi }_{i} \\ & \quad - \frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}\left( {e_{2} + \varepsilon_{1} + d_{1} + \xi_{1}^{*T} \varphi_{1} (\hat{x})} \right. \\ & \quad \left. { - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} ) + \tilde{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} ) + h_{1} } \right) \\ & \quad - \sum\limits_{j = 1}^{n} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{j} }}\left( {\xi_{j}^{*T} \varphi_{j} (\hat{x}) - \tilde{\xi }_{j}^{T} \varphi_{j} (\hat{x})} \right)} \\ \end{aligned} $$

(39)

where

$$ \begin{aligned} \varXi_{i} & = k_{i} e_{1} + \hat{\xi }_{i}^{T} \varphi_{i} (\underline{{\hat{x}}}_{i} ) - \sum\limits_{j = 1}^{n} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{j} }}(\dot{\hat{x}}_{j + 1} - k_{j} e_{1} )} - \sum\limits_{j = 1}^{i - 1} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{\xi }_{j} }}\dot{\hat{\xi }}_{j} } \\ & \quad - \sum\limits_{j = 1}^{i - 1} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{\vartheta }_{j} }}\dot{\hat{\vartheta }}_{j} } - \sum\limits_{j = 1}^{i - 1} {\frac{{\partial \alpha_{i - 1} }}{{\partial y_{r}^{(j - 1)} }}y_{r}^{(j)} } - \frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}\left( {\hat{x}_{2} + \hat{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} )} \right) \\ \end{aligned} $$

Choose the Lyapunov–Krasovksii function as

$$ V_{i} = V_{i - 1} + \frac{1}{2}z_{i}^{2} + \frac{1}{{2\eta_{i} }}\tilde{\xi }_{i}^{T} \tilde{\xi }_{i} + \frac{1}{{2\bar{\eta }_{i} }}\tilde{\vartheta }_{i}^{T} \tilde{\vartheta }_{i} + W_{1} $$

(40)

where $\bar{\eta }_{i} > 0$ and $\eta_{i} > 0$ are design parameters. According to (39)–(40), we have

$$ \begin{aligned} \dot{V}_{i} & = \dot{V}_{i - 1} + z_{i} \dot{z}_{i} - \frac{1}{{\eta_{i} }}\tilde{\xi }_{i}^{T} \dot{\hat{\xi }}_{i} - \frac{1}{{\bar{\eta }_{i} }}\tilde{\vartheta }_{i}^{T} \dot{\hat{\vartheta }}_{i} + \dot{W}_{1} \\ & \le - \,\lambda_{i - 1} \left\| e \right\|^{2} - \sum\limits_{j = 1}^{i - 1} {c_{j} z_{j}^{2\beta } } - rW_{0} - (i - 1)rW_{1} + z_{i} z_{i + 1} \\ & \quad + \,\frac{i - 2}{2}\tilde{\xi }_{1}^{T} \tilde{\xi }_{1} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \frac{1}{2}\sum\limits_{j = 2}^{i - 1} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \sum\limits_{j = 1}^{i - 1} {\frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \hat{\vartheta }_{j} } \\ & \quad - \,\frac{{(n - i + 1)e^{r\tau } }}{{2(1 - \tau^{*} )}}z_{1} (t)H_{1} (z_{1} (t)) + \sum\limits_{j = 1}^{i - 1} {\frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \hat{\xi }_{j} } + z_{i} [z_{i - 1} \\ & \quad - \,\xi_{i}^{*T} \varphi_{i} (\underline{{\hat{x}}}_{i} ) + \xi_{i}^{*T} \varphi_{i} (\hat{x}) + \tilde{\xi }_{i}^{T} \varphi_{i} (\underline{{\hat{x}}}_{i} ) + \bar{\varXi }_{i} - \tilde{\xi }_{i}^{T} \varphi_{i} (\hat{x}) \\ & \quad + \,\alpha_{i} - \frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}\left( {e_{2} + d_{1} + \varepsilon_{1} + h_{1} - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} ) + \tilde{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} )} \right. \\ & \quad \left. {\left. { + \,\xi_{1}^{*T} \varphi_{1} (\hat{x})} \right) + \sum\limits_{j = 1}^{n} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{j} }}} \left( { - \tilde{\xi }_{j}^{T} \varphi_{j} (\hat{x}) + \xi_{j}^{*T} \varphi_{j} (\hat{x})} \right)} \right) \\ & \quad - \,\frac{1}{{\eta_{i} }}\tilde{\xi }_{i}^{T} \dot{\hat{\xi }}_{i} - \frac{1}{{\bar{\eta }_{i} }}\tilde{\vartheta }_{i}^{T} \dot{\hat{\vartheta }}_{i} + \dot{W}_{1} + \frac{i - 2}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + M_{i - 1} \\ \end{aligned} $$

(41)

According to the fact $0 < \varphi_{i}^{T} (\hat{x})\varphi_{i} (\hat{x}) \le 1$, applying Lemma 1 and Assumption 1, for any constant $\pi > 0$, we have

$$ z_{i} \left( {\xi_{i}^{*T} \varphi_{i} (\hat{x}) - \xi_{i}^{*T} \varphi_{i} (\underline{{\hat{x}}}_{i} )} \right) \le \frac{2}{\pi } + \frac{\pi }{2}z_{i}^{2} \vartheta_{i}^{*} $$

(42)

$$ - z_{i} \tilde{\xi }_{i}^{T} \varphi_{i} (\hat{x}) \le \frac{1}{2}z_{i}^{2} + \frac{1}{2}\tilde{\xi }_{i}^{T} \tilde{\xi }_{i} $$

(43)

$$ - \,z_{i} \frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}\left( {e_{2} + \varepsilon_{1} + d_{1} + \tilde{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} )} \right) \le 2z_{i}^{2} \left( {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}} \right)^{2} + \frac{1}{2}\left( {\left\| e \right\|^{2} + \left\| {\varepsilon^{*} } \right\|^{2} + d_{1}^{*2} + \tilde{\xi }_{1}^{T} \tilde{\xi }_{1} } \right) $$

(44)

$$ - \,z_{i} \frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}\left( {\xi_{1}^{*T} \varphi_{1} (\hat{x}) - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} )} \right) \le \frac{\pi }{2}z_{i}^{2} \left( {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}} \right)^{2} + \frac{2}{\pi }\vartheta_{1}^{ *} $$

(45)

$$ \begin{aligned} - z_{i} \frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}h_{1} & \le \frac{1}{2}z_{i}^{2} \left( {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}} \right)^{2} + \frac{1}{2}h_{1}^{2} \\ & \le \frac{1}{2}z_{i}^{2} \left( {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}} \right)^{2} + \frac{1}{2}z_{1} (t - \tau_{1} )H_{1} (z_{1} (t - \tau_{1} )) \\ & \quad + \frac{1}{2}\bar{H}_{1} (y_{r} (t - \tau_{1} )) + \frac{1}{2}\varpi_{1} \\ \end{aligned} $$

(46)

$$ - \,z_{i} \sum\limits_{j = 1}^{n} {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{j} }}} \left( {\xi_{j}^{*T} \varphi_{j} (\hat{x}) - \tilde{\xi }_{j}^{T} \varphi_{j} (\hat{x})} \right) \le \frac{1}{2}\sum\limits_{j = 1}^{n} {\vartheta_{j}^{*} } + \frac{1}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + z_{i}^{2} \sum\limits_{j = 1}^{n} {\left( {\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{j} }}} \right)^{2} } $$

(47)

Substituting (30) and (42)–(47) into (41) results in

$$ \begin{aligned} \dot{V}_{i} & \le - \lambda_{i - 1} \left\| e \right\|^{2} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } - \sum\limits_{j = 1}^{i - 1} {c_{j} z_{j}^{2\beta } } - (i - 1)rW_{1} \\ & \quad - rW_{0} - \frac{{(n - i + 1)e^{r\tau } }}{{2(1 - \tau^{*} )}}z_{1} (t)H_{1} (z_{1} (t)) + \sum\limits_{j = 1}^{i - 1} {\frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \hat{\xi }_{j} } \\ & \quad + \frac{i - 1}{2}\tilde{\xi }_{1}^{T} \tilde{\xi }_{1} + \sum\limits_{j = 1}^{i - 1} {\frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \hat{\vartheta }_{j} } + \frac{1}{2}\sum\limits_{j = 2}^{i} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + z_{i} z_{i + 1} \\ & \quad + \frac{i - 1}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + z_{i} \left[ {\alpha_{i} + \varXi_{i} + z_{i - 1} + \frac{{z_{i} }}{2} + \frac{{\pi \hat{\vartheta }_{i} }}{2}z_{i} } \right. \\ & \quad \left. { + \frac{\pi + 5}{2}z_{i} \left( {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}} \right)^{2} } \right] + M_{i} + \frac{{\tilde{\xi }_{i}^{T} }}{{\eta_{i} }}\left( {\eta_{i} \phi_{i} (\underline{{\hat{x}}}_{i} )z_{i} - \dot{\hat{\xi }}_{i} } \right) \\ & \quad + \frac{{\tilde{\vartheta }_{i}^{T} }}{{\bar{\eta }_{i} }}\left( {\frac{{\pi \bar{\eta }_{i} }}{2}z_{i}^{2} - \dot{\hat{\vartheta }}_{i} } \right) \\ \end{aligned} $$

(48)

where $M_{i} = M_{i - 1} + q_1 + (\left\| {\varepsilon^{*} } \right\|^{2} + d_{1}^{*2} + \sum\nolimits_{j = 1}^{n} {\vartheta_{j}^{*} } )/2 + 2\vartheta_{1}^{*} /\pi + 2/\pi$,$\varXi_{i} = \bar{\varXi }_{i} + z_{i} \sum\nolimits_{j = 1}^{n} {(\frac{{\partial \alpha_{i - 1} }}{{\partial \hat{x}_{j} }})^{2} }$ and $\lambda_{i} = \lambda_{i - 1} - 1/2$.

Design the intermediate control function $\alpha_{i}$, parameter adaptive laws $\dot{\hat{\xi }}_{i}$ and $\dot{\hat{\vartheta }}_{i}$ as

$$ \alpha_{i} = - c_{i} z_{i}^{2\beta - 1} - \frac{{z_{i} }}{2} - z_{i - 1} - \varXi_{i} - \frac{{\pi \hat{\vartheta }_{i} }}{2}z_{i} - \frac{\pi + 5}{2}z_{i} \left( {\frac{{\partial \alpha_{i - 1} }}{{\partial x_{1} }}} \right)^{2} $$

(49)

$$ \dot{\hat{\xi }}_{i} = \eta_{i} z_{i} \varphi_{i} (\underline{{\hat{x}}}_{i} ) - \delta_{i} \hat{\xi }_{i} $$

(50)

$$ \dot{\hat{\vartheta }}_{i} = \frac{{\bar{\eta }_{i} \pi }}{2}z_{i}^{2} - \bar{\delta }_{i} \hat{\vartheta }_{i} $$

(51)

where $c_{i} > 0$, $\delta_{i} > 0$ and $\bar{\delta }_{i} > 0$ are design parameters.

From (49)–(51), it follows that

$$ \begin{aligned} \dot{V}_{i} & \le - \lambda_{i - 1} \left\| e \right\|^{2} - rW_{0} - (i - 1)rW_{1} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } \\ & \quad + z_{i} z_{i + 1} - \sum\limits_{j = 1}^{i - 1} {c_{j} z_{j}^{2\beta } } + \frac{i - 1}{2}\tilde{\xi }_{1}^{T} \tilde{\xi }_{1} + \frac{1}{2}\sum\limits_{j = 2}^{i} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } \\ & \quad + \frac{i - 1}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } - \frac{{(n - i + 1)e^{r\tau } }}{{2\left( {1 - \tau^{*} } \right)}}z_{1} (t)H_{1} (z_{1} (t)) \\ & \quad + \sum\limits_{j = 1}^{i} {\frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \hat{\vartheta }_{j} } + \sum\limits_{j = 1}^{i} {\frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \hat{\xi }_{j} } + M_{i} \\ \end{aligned} $$

(52)

Step 3$n$: This is the last step. Thus, from (15) and (25), we have

$$ \begin{aligned} \dot{z}_{n} & = u - \frac{{\partial \alpha_{n - 1} }}{{\partial x_{1} }}(e_{2} + \varepsilon_{1} + h_{1} + \xi_{1}^{*T} \varphi_{1} (\hat{x}) \\ & \quad + d_{1} - \xi_{1}^{*T} \varphi_{1} (\hat{x}_{1} ) + \tilde{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} )) + \bar{\varXi }_{n} \\ & \quad - \sum\limits_{j = 1}^{n} {\frac{{\partial \alpha_{n - 1} }}{{\partial \hat{x}_{j} }}\left( { - \tilde{\xi }_{j}^{T} \varphi_{j} (\hat{x}) + \xi_{j}^{*T} \varphi_{j} (\hat{x})} \right)} \\ \end{aligned} $$

(53)

where

$$ \begin{aligned} \bar{\varXi }_{n} & = k_{n} e_{1} + \hat{\xi }_{n}^{T} \varphi_{n} (\underline{{\hat{x}}}_{n} ) - \sum\limits_{j = 1}^{n} {\frac{{\partial \alpha_{n - 1} }}{{\partial \hat{x}_{j} }}(\dot{\hat{x}}_{j + 1} - k_{j} e_{1} )} - \sum\limits_{j = 1}^{n - 1} {\frac{{\partial \alpha_{n - 1} }}{{\partial \hat{\xi }_{j} }}\dot{\hat{\xi }}_{j} } \\ & \quad - \sum\limits_{j = 1}^{n - 1} {\frac{{\partial \alpha_{n - 1} }}{{\partial \hat{\vartheta }_{j} }}\dot{\hat{\vartheta }}_{j} } - \sum\limits_{j = 1}^{n - 1} {\frac{{\partial \alpha_{n - 1} }}{{\partial y_{r}^{(j - 1)} }}y_{r}^{(j)} } - \frac{{\partial \alpha_{n - 1} }}{{\partial x_{1} }}(\hat{x}_{2} + \hat{\xi }_{1}^{T} \varphi_{1} (\hat{x}_{1} )) \\ \end{aligned} $$

Choose the Lyapunov–Krasovskii function as

$$ V = V_{n - 1} + \frac{1}{2}z_{n}^{2} + \frac{1}{{2\eta_{n} }}\tilde{\xi }_{n}^{T} \tilde{\xi }_{n} + W_{1} $$

(54)

where $\eta_{n} > 0$ is a design parameter.

According to (53)–(54), we have

$$ \begin{aligned} \dot{V} & = \dot{V}_{n - 1} + z_{n} \dot{z}_{n} - \frac{1}{{\eta_{n} }}\tilde{\xi }_{n}^{T} \dot{\hat{\xi }}_{n} + \dot{W}_{1} \\ & \le - \,\lambda_{n} \left\| e \right\|^{2} - rW_{0} - nrW_{1} + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } - \sum\limits_{j = 1}^{n - 1} {c_{j} z_{j}^{2\beta } } \\ & \quad + \,\frac{n - 1}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \sum\limits_{j = 1}^{n - 1} {\frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \hat{\xi }_{j} } + \sum\limits_{j = 1}^{n - 1} {\frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \hat{\vartheta }_{j} } + M_{n} \\ & \quad + \,z_{n} \left[ {u + z_{n - 1} + \varXi_{n} + \frac{{z_{n} }}{2} + \frac{5 + \pi }{2}z_{n} \left( {\frac{{\partial \alpha_{n - 1} }}{{\partial x_{1} }}} \right)^{2} } \right] \\ & \quad + \,\frac{1}{2}\sum\limits_{j = 2}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \frac{{\tilde{\xi }_{n}^{T} }}{{\eta_{n} }}\left( {\eta_{n} \phi_{n} (\underline{{\hat{x}}}_{n} )z_{n} - \dot{\hat{\xi }}_{n} } \right) + \frac{n - 1}{2}\tilde{\xi }_{1}^{T} \tilde{\xi }_{1} \\ \end{aligned} $$

(55)

where $\lambda_{n} = \lambda_{n - 1} - 1/2$, $M_{n} = M_{n - 1} + q_1 + (\left\| {\varepsilon^{*} } \right\|^{2} + d_{1}^{*2} )/2 + 2\vartheta_{1}^{*} /2$ and $\varXi_{n} = \bar{\varXi }_{n} + z_{n} \sum\limits_{j = 1}^{n} {(\frac{{\partial \alpha_{n - 1} }}{{\partial \hat{x}_{j} }})^{2} }$.

Design the controller $u$, adaptive law $\dot{\hat{\theta }}_{n}$ as

$$ u = - c_{n} z_{n}^{2\beta - 1} - z_{n - 1} - \frac{1}{2}z_{n} - \varXi_{n} - \frac{\pi + 5}{2}z_{n} \left( {\frac{{\partial \alpha_{n - 1} }}{{\partial x_{1} }}} \right)^{2} $$

(56)

$$ \dot{\hat{\xi }}_{n} = \eta_{n} z_{n} \varphi_{n} (\underline{{\hat{x}}}_{n} ) - \delta_{n} \hat{\xi }_{n} $$

(57)

where $c_{n} > 0$ and $\delta_{n} > 0$ are design parameters. According to (57), the chosen of the adaptive laws satisfy Lemma 5. From (56)–(57), it follows that

$$ \begin{aligned} \dot{V} & \le - \lambda_{n} \left\| e \right\|^{2} - \sum\limits_{j = 1}^{n} {c_{j} z_{j}^{2\beta } } + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } - rW_{0} \\ & \quad - \,nrW_{1} + \sum\limits_{j = 1}^{n} {\frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \hat{\xi }_{j} } + \sum\limits_{j = 1}^{n - 1} {\frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \hat{\vartheta }_{j} } + M_{n} \\ & \quad + \,\frac{1}{2}\sum\limits_{j = 2}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \frac{n - 1}{2}\tilde{\xi }_{1}^{T} \tilde{\xi }_{1} + \frac{n - 1}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } \\ \end{aligned} $$

(58)

By applying Lemma 1, we have

$$ \frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \hat{\vartheta }_{j} = \frac{{\bar{\delta }_{j} }}{{\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \left( {\vartheta_{j}^{*T} - \tilde{\vartheta }_{j}^{T} } \right) \le - \frac{{\bar{\delta }_{j} }}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} + \frac{{\bar{\delta }_{j} }}{{2\bar{\eta }_{j} }}\vartheta_{j}^{*T} \vartheta_{j}^{*} $$

(59)

$$ \frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \hat{\xi }_{j} = \frac{{\delta_{j} }}{{\eta_{j} }}\tilde{\xi }_{j}^{T} \left( {\xi_{j}^{*T} - \tilde{\xi }_{j}^{T} } \right) \le - \frac{{\delta_{j} }}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} + \frac{{\delta_{j} }}{{2\eta_{j} }}\xi_{j}^{*T} \xi_{j}^{*} $$

(60)

Substituting (59)–(60) into (58) yields

$$ \begin{aligned} \dot{V} & \le - \lambda_{n} \left\| e \right\|^{2} - \sum\limits_{j = 1}^{n} {c_{j} z_{j}^{2\beta } } - rW_{0} - nrW_{1} + D \\ & \quad + \,\frac{1}{2}\sum\limits_{j = 2}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \frac{n - 1}{2}\tilde{\xi }_{1}^{T} \tilde{\xi }_{{1_{1} }} - \sum\limits_{j = 1}^{n - 1} {\frac{{\bar{\delta }_{j} }}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} } \\ & \quad - \,\sum\limits_{j = 1}^{n} {\frac{{\delta_{j} }}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \frac{n - 1}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + \frac{{\left\| P \right\|^{2} }}{2}\sum\limits_{j = 1}^{n} {\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } \\ \end{aligned} $$

(61)

where $D = M_{n} + \sum\limits_{j = 1}^{n - 1} {\frac{{\bar{\delta }_{j} }}{{2\bar{\eta }_{j} }}\vartheta_{j}^{*T} \vartheta_{j}^{*} } + \sum\limits_{j = 1}^{n} {\frac{{\delta_{j} }}{{2\eta_{j} }}\xi_{j}^{*T} \xi_{j}^{*} }$.

Choose $k = \hbox{min} \{ c_{j} ,nr,\delta_{j} - (\left\| P \right\|^{2} + 1)\eta_{j} ,\delta_{1} - (n - 1 + \left\| P \right\|^{2} )\eta_{1} \}$, rewritten (61) as

$$ \begin{aligned} \dot{V} & \le - \frac{{\lambda_{n} }}{{\lambda_{\hbox{min} } (Q)}}\left( {\lambda_{\hbox{min} } (Q)\left\| e \right\|^{2} } \right)^{\beta } + \frac{{\lambda_{n} }}{{\lambda_{\hbox{min} } (Q)}}\left( {\lambda_{\hbox{min} } (Q)\left\| e \right\|^{2} } \right)^{\beta } - \lambda_{n} \left\| e \right\|^{2} \\ & \quad - \,kW_{0}^{\beta } + kW_{0}^{\beta } - kW_{0} - 2^{\beta } k\left( {\sum\limits_{j = 1}^{n} {\frac{1}{2}z_{j}^{2} } } \right)^{\beta } - kW_{1}^{\beta } + kW_{1}^{\beta } - kW_{1} \\ & \quad + \,k\left( {\sum\limits_{j = 1}^{n} {\frac{1}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } } \right)^{\beta } - k\left( {\sum\limits_{j = 1}^{n} {\frac{1}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } } \right)^{\beta } - k\sum\limits_{j = 1}^{n} {\frac{1}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } + D \\ & \quad + \,k\left( {\sum\limits_{j = 1}^{n - 1} {\frac{1}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} } } \right)^{\beta } - k\left( {\sum\limits_{j = 1}^{n - 1} {\frac{1}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} } } \right)^{\beta } - k\sum\limits_{j = 1}^{n - 1} {\frac{1}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} } \\ \end{aligned} $$

(62)

By applying Lemma 4, we have

$$ (\lambda_{\hbox{min} } (Q)\left\| e \right\|^{2} )^{\beta } \cdot 1^{\beta } \le (1 - \beta )\beta^{\beta /1 - \beta } + \lambda_{\hbox{min} } (Q)\left\| e \right\|^{2} $$

(63)

$$ W_{0}^{\beta } \cdot 1^{\beta } \le (1 - \beta )\beta^{\beta /1 - \beta } + W_{0} $$

(64)

$$ W_{1}^{\beta } \cdot 1^{\beta } \le (1 - \beta )\beta^{\beta /1 - \beta } + W_{1} $$

(65)

$$ \left( {\sum\limits_{j = 1}^{n} {\frac{1}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } } \right)^{\beta } \cdot 1^{\beta } \le (1 - \beta )\beta^{\beta /1 - \beta } + \sum\limits_{j = 1}^{n} {\frac{1}{{2\eta_{j} }}\tilde{\xi }_{j}^{T} \tilde{\xi }_{j} } $$

(66)

$$ \left( {\sum\limits_{j = 1}^{n - 1} {\frac{1}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} } } \right)^{\beta } \cdot 1^{\beta } \le (1 - \beta )\beta^{\beta /1 - \beta } + \sum\limits_{j = 1}^{n - 1} {\frac{1}{{2\bar{\eta }_{j} }}\tilde{\vartheta }_{j}^{T} \tilde{\vartheta }_{j} } $$

(67)

Substituting (63)–(67) into (62) and adopting Lemma 3, we have

$$ \dot{V} \le - \gamma V^{\beta } + \sigma $$

(68)

where $\gamma = \hbox{min} \left\{ {\frac{{\lambda_{n} }}{{\lambda_{\hbox{min} } (Q)}},2^{\beta } k,k} \right\}$ and $\sigma = 5(1 - \beta )\beta^{\beta /1 - \beta } + D$.

From the proof of Lemma 6, let $\varsigma = [z,e,\tilde{\xi },\tilde{\vartheta }]$, we can obtain the reach time as $T_{\text{reach}} = \frac{1}{(1 - \beta )\delta \gamma }[V^{1 - \beta } (z(0),e(0),\tilde{\xi }(0),\tilde{\vartheta }(0)) - (\frac{\sigma }{(1 - \delta )\gamma })^{(1 - \beta )/\beta } ]$, with the initial values $z(0) = [z_{1} (0), \ldots ,z_{n} (0)]^{T}$, $e(0) = [e_{1} (0), \ldots ,e_{n} (0)]^{T}$, $\tilde{\vartheta }(0) = [\tilde{\vartheta }_{1} (0), \ldots ,\tilde{\vartheta }_{n - 1} (0)]^{T}$ and $\tilde{\xi }(0) = [\tilde{\xi }_{1} (0), \ldots ,\tilde{\xi }_{n} (0)]^{T}$. Thus, it should satisfy Lemma 6 such as $V^{\beta } (z,e,\tilde{\xi },\tilde{\vartheta }) \le \frac{\sigma }{(1 - \delta )\gamma }$ for $\forall t \ge T_{\text{reach}}$, which means that controlled system is SGPFS. Moreover, for $\forall t \ge T_{\text{reach}}$, we have

$$ \left| {y - y_{r} } \right| \le 2\left( {\frac{\sigma }{(1 - \delta )\gamma }} \right)^{{\frac{1}{2\beta }}} $$

(69)

That is, after finite time $T_{\text{reach}}$, the tracking error keeps in a small neighborhood of the zero.

Now, according to the above control design and stability analysis, we are ready to summarize our major results for the resulting closed-loop system as follows.

Theorem 1

Under Assumption1, Definition1 and Lemmas1–6, consider nonlinear system (1), controller$u$ (56), and state observer (15), intermediate control functions$\alpha_{1}$ (35) and$\alpha_{i}$ (49), adaptive laws$\dot{\hat{\xi }}_{1}$ (36), $\dot{\hat{\vartheta }}_{1}$ (37), $\dot{\hat{\xi }}_{i}$ (50), $\dot{\hat{\vartheta }}_{i}$ (51) and$\dot{\hat{\xi }}_{n}$ (57), can guarantee that all the signals of closed-loop system are SGPFS, tracking and observer errors converge to a small neighborhood of the origin in a finite time.

Remark 1

From Theorem 1, (69) and the proof of Lemma 6, it means that all signals of the closed-loop system are bounded. In addition, by increasing the design parameters $c_{i}$, $\eta_{i}$, $\bar{\eta }_{i}$, $k_{i}$, or decreasing the design parameters $\beta$, $\delta_{i}$, $\bar{\delta }_{i}$($i = 1,2, \ldots ,n$) and $\pi$ can make tracking error be small, and all variables of the controlled system have the fast convergence rate.

5 Simulation Example

In this section, two simulation examples are provided to elaborate the effectiveness of the presented control method.

Example 1

Consider the second-order SISO nonlinear nonstrict feedback system as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} + f_{1} (x_{1} ,x_{2} ) + h_{1} (x_{1} (t - \tau_{1} )) + d_{1} (t)} \hfill \\ {\dot{x}_{2} = u + f_{2} (x_{1} ,x_{2} ) + h_{2} (x_{1} (t - \tau_{1} )) + d_{2} (t)} \hfill \\ {y = x_{1} } \hfill \\ \end{array} } \right. $$

(70)

where $f_{1} (x_{1} ,x_{2} ) = - \,0.5x_{2} \sin (x_{1} x_{2} )/(1 + x_{1}^{4} )$, $f_{2} (x_{1} ,x_{2} ) = \sin (x_{1} x_{2} )/e^{{1 + x_{2}^{4} }}$, $d_{1} (t) = 0.5\cos (t) + \sin (t)$ and $d_{2} (t) = 0.6\sin (t)$. The reference signal is chosen as $y_{r} (t) = 2\sin (t) + \cos (4t)$. Choose nonlinear time-varying delay functions as $h_{1} = \frac{{x_{1} (t - \tau_{1} (t))}}{{1 + x_{1}^{2} (t - \tau_{1} (t))}}$, $h_{2} = x_{1} (t - \tau_{2} (t))$, $\tau_{i} = 0.5(1 + 0.4\sin t)$, $(i = 1,2)$, $\tau = 0.4$ and $\tau^{*} = 0.6$.

Choose the fuzzy membership function as $\mu_{{F_{i}^{l} }} (\hat{x}_{i} ) = \exp [ - \frac{{(\hat{x}_{i} - 6 + 2l)^{2} }}{16}]$, $+$, $l = 1, \cdots ,5$.

According to [14], FLSs $\hat{f}_{i} (\hat{x}|\hat{\xi }_{i} ) = \hat{\xi }_{i}^{T} \varphi_{i} (\hat{x})$ are adopted to approximate the unknown functions $f_{i} (x)$, $i = 1,2$.

Choose the design parameters $k_{i} = 24$$(i = 1,2)$, matrix $Q = 8I$, from (17), we can obtain the positive-definite matrix $P = \left[ {\begin{array}{*{20}c} {0.1736} & {0.1667} \\ {0.1667} & {8.1667} \\ \end{array} } \right]$. Define the state observer as

$$ \left\{ {\begin{array}{*{20}l} {\dot{\hat{x}}_{1} = \hat{x}_{2} + k_{1} (y - \hat{x}_{1} ) + \hat{f}_{1} (\hat{x} |\hat{\xi }_{1} )} \hfill \\ {\dot{\hat{x}}_{2} = u + k_{2} (y - \hat{x}_{1} ) + \hat{f}_{2} (\hat{x} |\hat{\xi }_{2} )} \hfill \\ {\hat{y} = \hat{x}_{1} } \hfill \\ \end{array} } \right. $$

(71)

In this numerical example, all the design parameters in the controller $u$, adaptive laws $\dot{\hat{\xi }}_{1}$ and $\dot{\hat{\vartheta }}_{i}$ can be set as $\beta = 0.96$, $\pi = 3$, $c_{1} = c_{2} = 8$, $\eta_{1} = 6$, $\eta_{2} = 4$, $\delta_{1} = \delta_{2} = 4$, $\bar{\eta }_{1} = 4$, $\bar{\delta }_{1} = 6$ and $r = 1$. The initial values are selected as $x_{1} (0) = x_{2} (0) = 0.5$, $\hat{x}_{1} (0) = 0.02$ and $\hat{x}_{2} (0) = 0.03$. The other initial values are selected as zero.

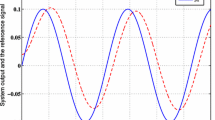
Note that we use the MATLAB environment to solve the theorem, and the simulation results can be obtained and shown in Figs. 1, 2, 3, 4 and 5, where Fig. 1 shows the trajectories of the tracking signal $y_{r}$ and output $y$; Fig. 2 displays the trajectory of the tracking error $z_{1}$; Figs. 3 and 4 exhibit the trajectories of the states $x_{i}$ and their estimation $\hat{x}_{i}$($i = 1,2$); Fig. 5 shows the trajectory of controller $u$.

Fig. 1

Trajectories of the tracking signal $y_{r}$ and output y

Fig. 2

Trajectory of $z_{1}$

Fig. 3

Trajectories of $x_{1}$ and $\hat{x}_{1}$

Fig. 4

Trajectories of $x_{2}$ and $\hat{x}_{2}$

Fig. 5

Trajectory of u

Example 2

In order to further verify the effectiveness of the presented control scheme, the following electromechanical system is considered from [18], and we are not considering the input quantized. The system is displayed in Fig. 6.

Fig. 6

Schematic of electromechanical system

The system model can be described as

$$ \left\{ {\begin{array}{*{20}l} {M\ddot{q} + B\dot{q} + N\sin (q) = I} \hfill \\ {L\dot{I} = V_{0} - RI - K_{T} \dot{q}} \hfill \\ \end{array} } \right. $$

(72)

where $M = J/K_{T} + mL_{0}^{2} /(3K_{T} ) + M_{0} L_{0}^{2} /K_{T} + 2M_{0} R_{0}^{2} /(5K_{T} )$, $B = B_{0} /K_{T}$, $N = mL_{0} G/(2K_{T} ) + M_{0} L_{0} G/K_{T}$, $m = 0.506\;{\text{kg}}$ is the link mass, $J = 1.625\;{\text{kg}}\,{\text{m}}^{2}$ is the rotor inertia, $R_{0} = 0.023\,{\text{m}}$ is the radius of the load, $M_{0} = 0.434\,{\text{kg}}$ is the load mass, $L_{0} = 0.305\,{\text{m}}$ is the link length, $B_{0} = 0.01625\,{\kern 1pt} {\text{N}}\,{\text{m}}\,{\text{s/rad}}$ is the coefficient of viscous friction at the joint, $L = 0.025\,{\text{R}}$ is the armature inductance, $K_{t} = 0.9\,{\text{N}}\,{\text{m/A}}$ is coefficient which characterizes the electromechanical conversion of armature current to torque, $R = 0.05\,\Omega$ is the armature resistance, $I(t)$ is the motor armature current and $G = 9.8$ is the gravity coefficient.

Consider the electromechanical system with time-varying delays and disturbance introduce the variable change as $x_{1} = q$, $x_{2} = \dot{q}$, $x_{3} = I$ and $u = V_{0} /M$. It is worth pointing out that there exist the time delays in the signals transmission process. In addition, in this simulation, we consider the external disturbance $\Delta = x_{1}^{2} \sin (x_{2} x_{3} )$. Thus, (72) can be rewritten as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} + x_{1}^{2} \sin (x_{2} x_{3} ) + h_{1} (x_{1} (t - \tau_{1} (t)))} \hfill \\ {\dot{x}_{2} = \frac{{x_{3} }}{M} - \frac{N}{M}\sin x_{1} - \frac{B}{M}x_{2} } \hfill \\ {\quad \quad + \frac{B}{M}\cos x_{2} \sin x_{3} + h_{2} (x_{1} (t - \tau_{2} (t)))} \hfill \\ {\dot{x}_{3} = \frac{u}{L} - \frac{K}{L}x_{2} - \frac{R}{L}x_{3} + h_{3} (x_{1} (t - \tau_{3} (t)))} \hfill \\ {y = x_{1} } \hfill \\ \end{array} } \right. $$

(73)

where $h_{1} (x_{1} (t - \tau_{1} (t))) = \frac{{x_{1} (t - \tau_{1} (t))}}{{1 + x_{1}^{2} (t - \tau_{1} (t))}}$, $h_{2} (x_{1} (t - \tau_{2} (t))) = \frac{{x_{1} (t - \tau_{2} (t))\sin (x_{2} (t))}}{{1 + x_{1}^{2} (t - \tau_{2} (t))}}$, $h_{3} (x_{1} (t - \tau_{3} (t))) = x_{1} (t - \tau_{3} (t))$,$\tau_{i} (t) = 0.4(1 + 0.5\cos (t))$,$i = 1,2,3$,$\tau = 0.2$ and $\tau^{*} = 0.6$. The reference signal is chosen as $y_{r} = \sin (0.5t)$.

Choose the fuzzy membership function as $\mu_{{F_{i}^{l} }} (\hat{x}_{i} ) = \exp [ - \frac{{(\hat{x}_{i} - 3 + l)^{2} }}{16}]$, $i = 1,2,3$; $l = 1, \ldots ,5$. According to [14], FLSs $\hat{f}_{i} (\hat{x}|\hat{\xi }_{i} ) = \hat{\xi }_{i}^{T} \varphi_{i} (\hat{x})$ are adopted to approximate the unknown functions $f_{i} (x)$, $i = 1,2,3$.

Choose the design parameters $k_{i} = 20$$(i = 1,2,3)$, matrix $Q = 8I$, from (17), we can obtain the positive-definite matrix $P = \left[ {\begin{array}{*{20}c} {0.2316} & {0.6316} & {0.2000} \\ {0.6316} & {17.0632} & {8.6316} \\ {0.2000} & {8.6316} & {16.6316} \\ \end{array} } \right]$. Define the state observer as

$$ \left\{ {\begin{array}{*{20}l} {\dot{\hat{x}}_{1} = \hat{x}_{2} + k_{1} (y - \hat{x}_{1} ) + \hat{f}_{1} (\hat{x} |\hat{\xi }_{1} )} \hfill \\ {\dot{\hat{x}}_{2} = \hat{x}_{3} + k_{2} (y - \hat{x}_{1} ) + \hat{f}_{2} (\hat{x} |\hat{\xi }_{2} )} \hfill \\ {\dot{\hat{x}}_{3} = u + k_{3} (y - \hat{x}_{1} ) + \hat{f}_{3} (\hat{x} |\hat{\xi }_{3} )} \hfill \\ {\hat{y} = \hat{x}_{1} } \hfill \\ \end{array} } \right. $$

(74)

In this numerical example, all the design parameters in the controller $u$, adaptive laws $\dot{\hat{\xi }}_{1}$ and $\dot{\hat{\vartheta }}_{i}$ can be set as $\beta = 119/121$, $\pi = 0.1$, $c_{1} = 0.5$$c_{2} = c_{3} = 20$, $\eta_{1} = 0.1$, $\eta_{2} = 0.2$, $\eta_{3} = 0.5$, $\delta_{1} = 0.2$, $\delta_{2} = 0.1$, $\delta_{3} = 0.3$, $\bar{\eta }_{1} = \bar{\eta }_{2} = 0.1$, $\bar{\delta }_{1} = \bar{\delta }_{2} = 0.5$ and $r = 0.8$. The initial values are selected as $x_{1} (0) = 0.05$, $x_{2} (0) = 0.02$, $x_{3} (0) = 0.01$, $\hat{x}_{1} (0) = 0.02$, $\hat{x}_{2} (0) = 0.03$ and $\hat{x}_{3} (0) = 0.02$. The other initial values are selected as zero.

Finally, the simulation results can be obtained and shown in Figs. 7, 8, 9, 10, 11 and 12, where Figs. 7 and 8 show the trajectories of the tracking signal $y_{r}$ and output $y$, and tracking error $z_{1}$, respectively; Figs. 9, 10 and 11 exhibit the trajectories of the states $x_{i}$ and their estimation $\hat{x}_{i}$($i = 1,2,3$); Fig. 12 shows the trajectory of controller $u$.

Fig. 7

Trajectories of $y_{r}$ and $y$

Fig. 8

Trajectory tracking error $z_{1}$

Fig. 9

Trajectories of $x_{1}$ and $\hat{x}_{1}$

Fig. 10

Trajectories of $x_{2}$ and $\hat{x}_{2}$

Fig. 11

Trajectories of $x_{3}$ and $\hat{x}_{3}$

Fig. 12

Trajectory of controller u

Remark 2

In this paper, the comparison is conducted with the method in Ref. [18] without considering the input quantized. The related parameters in both methods are the same. The tracking performance and approximation effects are presented in Figs. 13 and 14. In addition, in [18], a linear observer is designed to estimate the unmeasured states. Note that this state observer is independent of the controlled plants. The major disadvantage is that it cannot obtain the good estimations of the unmeasured states. In this paper, we design a fuzzy state observer (15), which can obtain the good estimations of the immeasurable states. Simultaneously, observer-based fuzzy adaptive practical finite-time control scheme is presented, which has the better tracking performance and approximation effects.

Fig. 13

Trajectories of tracking errors $z_{1}$

Fig. 14

Trajectories of controllers u

The above simulation results clearly shown that the presented practical finite-time fuzzy adaptive control strategy can ensure that all the signals of the closed-loop system are bounded.

6 Conclusions

In this paper, an observer-based practical finite-time fuzzy adaptive control strategy has been developed for SISO nonlinear nonstrict feedback system with time-varying delays. On the basis of finite-time Lyapunov–Krasovskii stability theory, the stability of the closed-loop systems can be proved, which demonstrated that the observer and tracking errors converge to a small neighborhood of the zero in a finite time, and all the signals of the closed-loop system are bounded.