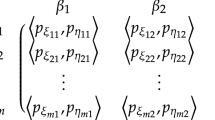Solutions of matrix games involving linguistic interval-valued intuitionistic fuzzy sets

Abstract

Game theory has found significant applications in a wide range of fields to deal with competitive environments between individuals or organizations. The researchers investigated several augmentations of ordinary game theory to deal with uncertainty and ambiguity in payoffs and goals. However, the quantifiable parts of the problems have been studied in matrix games with payoffs expressed by interval numbers, fuzzy numbers, and intuitionistic fuzzy numbers. In several situations, qualitative information is critical in describing the payoffs of a game problem. Experts frequently prefer expressing their perspective in natural linguistic terms rather than numerical values in real-life decision-making challenges. This linguistic representation has been utilized to resolve plenty of decision-making problems. This paper explores the theory of matrix games under a qualitative information environment. We use linguistic interval-valued intuitionistic fuzzy numbers (LIVIFNs) to describe the payoff values as suggested by experts. The LIVIFNs are more efficient tools that provide experts with a flexible information modeling capability to describe their ambiguous and uncertain perceptions in the form of linguistic terms. The solution of this class of matrix games is attained by resolving a duo of linear or nonlinear programming problems originating through nonlinear bi-objective programming problems. Finally, a numerical example is presented to demonstrate the applicability of the suggested approach.

1 Introduction

Zadeh (1965) defined the notion of fuzzy sets (FSs) by introducing a membership degree to each element of the set, which only expresses the degree of affinity to the FS under consideration. Atanassov (1986) gave the theory of intuitionistic fuzzy sets (IFSs) as a generalization of FSs for more effectively representing uncertain and vague concepts. A prominent characteristic of an IFS is that it assigns to each element a membership degree (MD) and a non-membership (NMD) with their summation value bounded by 1. In the past decades, FSs and IFSs have been extensively utilized to solve many real-life problems associated with different areas such as (Verma and Sharma 2014, 2015; Garg 2017; Zhang et al. 2017), to name a few.

Atanassov (1994) further generalized the theory of IFSs and proposed interval-valued intuitionistic fuzzy sets (IVIFSs) to provide more flexibility to the decision-makers (DMs) in expressing their membership degree (MD) and non-membership degree (NMD). An IVIFS specifies MD and NMD using interval numbers and offers a more logical theoretical formulation to convey unclear and vague information more efficiently. The IVIFSs have been widely studied by researchers and presented many valuable results, including aggregation operators (Garg 2018; Liu and Wang 2018) , entropy & divergence measures (Meng and Chen 2015; Wei et al. 2019; Mishra et al. 2020), distance & similarity measures (Düğenci 2016; Liu et al. 2017; Liu and Jiang 2020; Verma and Merigó 2020), possibility measures Garg and Kumar (2020b), and applications (Yx et al. 2018; Liu et al. 2020; Jeevaraj 2020; Li et al. 2021).

Real-life decision-making scenarios are more unpredictable and ambiguous. Also, due to their qualitative nature, many attributes/criteria cannot be evaluated using numerical values. It is more convenient for decision-makers to use linguistic variables (LVs) to denote their preference information. Zadeh (1975) firstly introduced the notion of LVs to express imprecise or ambiguous facts effectively. Many researchers have explored LVs to solve many complex decision-making challenges, (Herrera and Herrera-Viedma 2000; Chen et al. 2015; Meng et al. 2019; Zhang et al. 2021; Zhu and Zhao 2022), as the linguistic information process does not result in information degrading or misconception. In the literature, various extended linguistic models have been proposed to deal with qualitative information, such as uncertain linguistic variables (Xu 2006), triangular fuzzy linguistic variables (Xu 2007), trapezoidal fuzzy linguistic variables (Xu 2005), 2-dimensional linguistic variables (Zhu et al. 2009), and explored their application in a wide range of areas.

Zhang (2014) developed the idea of linguistic intuitionistic fuzzy sets (LIFSs) by integrating the advantages of IFSs and LVs into a single model, which provides an ability for the DMs to represent the MD and NMD in terms of LVs. Chen et al. (2015) developed a multiple attribute group decision-making (MAGDM) approach under a linguistic intuitionistic fuzzy environment. Liu and Qin (2017b) proposed some power average (PA) operators for dealing with multi-attribute decision making (MADM) problems with linguistic intuitionistic fuzzy numbers (LIFNs). Later, Liu and Qin (2017a) studied Maclaurin symmetric mean operators for LIFNs. Hy et al. (2017) developed an outranking approach for multi-criteria decision-making under a linguistic intuitionistic fuzzy environment. Tang and Meng (2019) formulated linguistic intuitionistic fuzzy Hamacher aggregation operators for solving decision-making problems. Garg and Kumar (2019b) utilized set pair analysis to introduce linguistic intuitionistic fuzzy PA operators. Meng et al. (2019) proposed the theory of linguistic intuitionistic fuzzy preference relations with applications. Some prioritized aggregation operators with LIFNs were studied by Arora and Garg (2019). Liu et al. (2020) developed a novel MAGDM method based on Dempster–Shafer evidence theory with LIFNs. Cheng et al. (2021) proposed a novel linguistic intuitionistic fuzzy distance measure for dealing with MADM problems. Meng and Dong (2022) extended the PROMETHEE method under a linguistic intuitionistic fuzzy environment . Verma (2020) proposed the notion of linguistic trapezoidal fuzzy intuitionistic fuzzy sets (LTFIFSs) for solving MAGDM problems. Verma and Merigó (2020) recently introduced a more flexible information representation model called 2-dimensional linguistic intuitionistic fuzzy sets for dealing with MAGDM problems with qualitative information.

A further generation of LIFS theory was proposed by Garg and Kumar (2019a), which is called linguistic interval-valued intuitionistic fuzzy sets (LIVIFSs). It provides more flexibility to the DMs in expressing the MD and NMD regarding the evaluated object/attribute. Garg and Kumar (2020a) introduced a new possibility measure for ranking linguistic interval-valued intuitionistic fuzzy numbers (LIVIFNs). Zhu et al. (2020) proposed aggregation operators for LIVIFNs based on Hamacher t-norms. Qin et al. (2022) introduced some Archimedean prioritized aggregation operators for dealing MCDM with LIVIFNs. Xu et al. (2021) discussed some copula power aggregation operators under a linguistic interval-valued intuitionistic fuzzy environment. Mohammadi et al. (2021) formulated multi-criteria decision-making models with linguistic interval-valued intuitionistic fuzzy information.

Game theory is a powerful analytical tool for dealing with day-to-day problems. In some aspects, this is the study of strategy or the optimal decision-making of independent and opposing actors/players in a strategic situation. In 1940, Neumann and Morgenstern (1944) were two of the most important architects of game theory. Many researchers have explored game theory extensively, taking into account a few (Collins and Hu 2008; Kalpiński and Tamošaitiene, 2010; Madani 2010; Sanchez-Soranio 2013). However, in real-life situations, we encounter uncertainty or ambiguity in the information about a problem, thus, motivating the study of fuzzy game theory. Butnariu (1978) and Aubin (1981) were the first to investigate the fuzzy game theory. Campos (1989) mainly explained the solution procedures for matrix games with fuzzy payoffs, whereas Sakawa and Nishizaki (1994) investigated zero-sum fuzzy matrix games with multi-objectives. Bector et al. (2004) resolved the matrix games involving fuzzy goals utilizing the fuzzy linear programming technique. Furthermore, Bector et al. (2004) established the duality results for linear programming problems with fuzzy variables and employed these to define the solution procedure of zero-sum matrix games involving payoffs expressed by fuzzy numbers. Vijay et al. (2007) used an extensive duality notion to develop the generalized representation to examine matrix games with fuzzy goals and payoffs using the fuzzy relation technique. Li (2012) investigated matrix games involving triangular fuzzy payoffs. Jana and Roy (2018) recently explained the matrix game solution approach incorporating generalized trapezoidal fuzzy payoffs.

Atanassov (1995) pioneered the comprehensive analysis of matrix games involving payoffs described by IFSs. Li and Nan (2009) suggested the nonlinear programming technique for deriving the solution of matrix games having IFSs payoffs. (Aggarwal et al. 2012a, b) extended the fuzzy duality results of (Bector et al. 2004; Vijay et al. 2005) to deal with matrix games with intuitionistic fuzzy payoffs and goals. Khan et al. (2017) introduced a technique to resolve indeterminacy from matrix games having intuitionistic fuzzy goals. Naqvi et al. (2021) outlined a novel Tanaka and Asai’s technique to explain the solution procedure for intuitionistic fuzzy matrix games. Xing and Qiu (2019) also contributed to intuitionistic fuzzy matrix games by adopting a linear accuracy function to resolve the solution of matrix games where the payoffs involved are triangular IFNs. Several initiatives to discover solutions for intuitionistic fuzzy matrix games have been conducted so far, (Khan et al. 2016; Bhaumik et al. 2017; Nan et al. 2017), to mention only some. Li (2010) developed a solution approach to matrix games with payoffs denoted by IVIFSs. Xia (2018) utilized Archimedean t-conorm and t-norm to formulate a generalized method for dealing with matrix games under an IVIF information environment.

Firstly, Arfi (2006) presented a study on matrix games based on linguistic fuzzy logic. Singh et al. (2018) studied a zero-sum matrix game with 2-tuple linguistic payoffs and formulated a solution process for it. Further, Verma and Aggarwal (2021a) developed some optimization models for solving matrix games with payoffs represented by LIFNs. Singh and Gupta (2018) discussed matrix game problems with LIVIFNs. Later, Verma and Aggarwal (2021b) generalized the work of Singh et al. (2018) and studied matrix games under a 2-tuple linguistic intuitionistic fuzzy environment.

1.1 Motivations of the present study

The following are the key motivations for the present study :

• LIVIFS theory, developed by Garg and Kumar (2019a), extends the concepts of LVs, uncertain linguistic variables (UAVs), and LIFS theory. So, it has wider applicability in different areas.

• LIVFNs provide more freedom and flexibility to the DMs in representing their MD and NMD in terms of interval linguistic numbers.

• Up to now, there has been no study on matrix games with payoffs denoted by LIVIFNs. Thus, this work will contribute to developing the basic concepts and solution procedures for such a class of matrix games.

• The existing optimization models (Li and Nan 2009; Li 2010; Xia 2018; Verma and Aggarwal 2021a) cannot be used to solve matrix games under a linguistic interval-valued intuitionistic fuzzy environment. Therefore, it is necessary to formulate new optimization models for efficiently handling matrix game problems with LIVIFN payoffs.

1.2 Contributions of this work

The main contributions of this work are summarized in the following.

• The basic concepts, definitions, and mathematical formulations are introduced for matrix games with payoffs represented by LIVIFNs.

• Linear/nonlinear programming optimization models are designed to deal with such a class of matrix games.

• The mixed strategies are also obtained corresponding to both the players with the value of the game.

• A real-life competitive decision problem is considered to show the application of the presented work.

• Finally, a comparative study with previous methods is also presented to illustrate the effectiveness of the developed optimization models.

The remaining part of the paper is structured as follows: Sect. 2 describes some basic concepts and definitions related to IFS, IVIFS, LVs, LIFSs, and LIVIFSs. Section 3 presents the mathematical formulation and solution process for matrix games with payoffs represented by LIVIFNs. In Sect. 4, a real-life numerical problem is considered to show the working process of the developed approach. In Sect. 5, a comparative study with existing methods is also carried out to validate the efficiency of the presented work. Finally, a summary of the main results from this work is given in Sect. 6 with some future directions.

2 Preliminaries

This section briefly reviews basic concepts and definitions of IFSs, IVIFSs, LVs, LIFSs, and LIVIFSs, which will be used in the further development of the work.

2.1 Intuitionistic fuzzy Set

Definition 1

(Atanassov 1986) Let X be the finite universe of discourse. An IFS $\hat{{\mathcal {M}}}$ in X is defined as

$$\begin{aligned} \hat{{\mathcal {M}}}=\left\{ \langle x,\mu _{\hat{{\mathcal {M}}}}(x),\nu _{\hat{{\mathcal {M}}}}(x) \rangle | \; x \in X\right\} , \end{aligned}$$

(2.1)

where $\mu _{\hat{{\mathcal {M}}}}, \nu _{\hat{{\mathcal {M}}}}: X\rightarrow [0,1]$, and the numbers $\mu _{\hat{{\mathcal {M}}}}$ and $\nu _{\hat{{\mathcal {M}}}}$, respectively, denote, the MD and NMD of element x to the IFS ${\hat{{\mathcal {M}}}}$, such that $\mu _{\hat{{\mathcal {M}}}}(x)+\nu _{\hat{{\mathcal {M}}}}(x) \le 1\; \forall \; x\in X$. The hesitancy degree (HD) of element x to an IFS ${\hat{{\mathcal {M}}}}$ can be calculated by using the expression $\pi _{\hat{{\mathcal {M}}}}(x)=1-\mu _{\hat{{\mathcal {M}}}}(x)-\nu _{\hat{{\mathcal {M}}}}(x)$.

2.2 Interval valued intuitonistic fuzzy set

Definition 2

(Atanassov and Gargov 1989) Let X be the finite universe of discourse and D[0, 1] be the set of all the closed subintervals of the interval [0, 1]. An IVIFS $\hat{{\mathbb {V}}}$ in X is defined as

$$\begin{aligned} \hat{{\mathbb {V}}}=\left\{ \left\langle x,\left[ \mu _{\hat{{\mathbb {V}}}}^{-}(x),\mu _{\hat{{\mathbb {V}}}}^{+}(x)\right] , \left[ \nu _{\hat{{\mathbb {V}}}}^{-}(x),\nu _{\hat{{\mathbb {V}}}}^{+}(x)\right] \right\rangle \;\; |\;x \in X\right\} \end{aligned}$$

(2.2)

where $\left[ \mu _{\hat{{\mathbb {V}}}}^{-}(x), \mu _{\hat{{\mathbb {V}}}}^{+}(x)\right] \in D[0,1]$ and $\left[ \nu _{\hat{{\mathbb {V}}}}^{-}(x), \nu _{\hat{{\mathbb {V}}}}^{+}(x)\right] \in D[0,1]$, with the condition $\mu _{\hat{{\mathbb {V}}}}^{+}(x)+\nu _{\hat{{\mathbb {V}}}}^{+}(x)\le 1$, $\forall x \in X.$ Here, the intervals $[\mu _{\hat{{\mathbb {V}}}}^{-}(x),\mu _{\hat{{\mathbb {V}}}}^{+}(x)]$ and $[\nu _{\hat{{\mathbb {V}}}}^{-}(x),\nu _{\hat{{\mathbb {V}}}}^{+}(x)]$, respectively, represent the MD and NMD of the element $x \in X$ to an IVIFS $\hat{{\mathbb {V}}}$. The interval $\left[ \pi _{\hat{{\mathbb {V}}}}^{-}(x), \pi _{\hat{{\mathbb {V}}}}^{+}(x) \right] = \left[ 1-\mu _{\hat{{\mathbb {V}}}}^{+}(x)- \nu _{\hat{{\mathbb {V}}}}^{+}(x), 1-\mu _{\hat{{\mathbb {V}}}}^{-}(x)- \nu _{\hat{{\mathbb {V}}}}^{-}(x)\right]$ is called the HD of element x to an IVIFS $\hat{{\mathbb {V}}}$.

2.3 Linguistic term set

Many decision-making challenges in real-world circumstances have qualitative characteristics that are difficult to determine using numerical figures. In such instances, LVs are a more practical and appropriate instrument for evaluating qualitative data.

Definition 3

(Herrera and Martinez 2000) Let ${\mathbb {S}} = \{ s_{f} |\;f= 0, 1, ..., t \}$ be a finite LTS with an odd cardinality, where $s_{f}$ represents a possible linguistic value for a LV and t be the positive integer. The LTS ${\mathbb {S}}$ should satisfy the following properties:

• Well ordered: $s_{p} \le s_{q} \Leftrightarrow p \le q$;

• Negation operator: $neg(s_{p})=s_{t-p}$;

• Maximum operator: $\max (s_{p},\; s_{q})=s_{p} \Leftrightarrow p \ge q$;

• Minimum operator: $\min (s_{p},\; s_{q})=s_{p} \Leftrightarrow p \le q$.

For example, a set of seven linguistic terms can be defined as:

$$\begin{aligned} \begin{array}{lll} {\mathbb {S}} = \left\{ s_{0}=\text {Extremely slow (ES)}, \; s_{1}=\text {Very slow (VS)},\;\right. \\ \left. s_{2}=\text { Moderately slow (MS)},\;\right. \\ \left. s_{3}=\text {Neither slow nor fast (NSNF)},\right. \\ \left. s_{4}=\text {Moderately fast (MF)},\; s_{5}=\text {Very fast (VF)},\;\right. \\ \left. s_{6}=\text {Extremely fast (EF)} \right\} \end{array} \end{aligned}$$

To conserve all the specified information, Xu et al. (2017) broadened the discrete term set ${\mathbb {S}}=\{s_0,s_1, \ldots ,s_t\}$ to a continuous term set ${\mathbb {S}}_{[0,t]}=\left\{ s_{f}|\;s_{0} \le s_{f} \le s_{t}, w \in [0,t] \right\}$. The components of the set ${\mathbb {S}}_{[0,t]}$ exhibits all the features of the set ${\mathbb {S}}$. If $s_{f}\in {\mathbb {S}}$, then $s_{f}$ is known as the original linguistic term, else, $s_{f}$ is known as virtual linguistic term.

2.4 Linguistic intuitionistic fuzzy set

To better deal with uncertain qualitative information, Zhang et al. (2012) introduced the notion of LIFS, characterized by a pair of LVs defining the linguistic MD and the linguistic NMD, respectively.

Definition 4

Let X be the finite universe of discourse and ${\mathbb {S}}_{[0,t]} = \{s_{f} \mid s_0 \le s_{f} \le s_{t} \}$ be a continuous LTS. A LIFS set $\hat{{\mathbb {L}}}$ in X is given by

$$\begin{aligned} \hat{{\mathbb {L}}}= \left\{ \left\langle x, s_{\alpha _{\hat{{\mathbb {L}}}}}(x), s_{\beta _{\hat{{\mathbb {L}}}}}(x)\right\rangle \mid x\in X \right\} \end{aligned}$$

(2.3)

where $s_{\alpha _{\hat{{\mathbb {L}}}}}(x), s_{\beta _{\hat{{\mathbb {L}}}}}(x) \in {\mathbb {S}}_{[0,t]}$ stand for the MD and NMD of the element x to $\hat{{\mathbb {L}}}$, respectively, and satisfying $\alpha _{\hat{{\mathbb {L}}}}\left( x \right) + \beta _{\hat{{\mathbb {L}}}} \left( x \right) \le t\; \forall \; x\in X$. For a given element $x \in X$, the pair $\left\langle s_{\alpha _{\hat{{\mathbb {L}}}}}, s_{\beta _{\hat{{\mathbb {L}}}}} \right\rangle$ is called a LIFN, which can be simply expressed by ${\hat{\Upsilon }} = \left\langle s_{\alpha _{{\hat{\Upsilon }}}}, s_{\beta _{{\hat{\Upsilon }}}} \right\rangle$.

Definition 5

Let $\displaystyle {\hat{\Upsilon }} = \left\langle s_{\alpha _{{\hat{\Upsilon }}}}, s_{\beta _{{\hat{\Upsilon }}}} \right\rangle$, ${\hat{\Upsilon }}_1 =\left\langle s_{\alpha _{{\hat{\Upsilon }}_{1}}}, s_{\beta _{{\hat{\Upsilon }}_{1}}} \right\rangle$ and ${\hat{\Upsilon }}_2 =\left\langle s_{\alpha _{{\hat{\Upsilon }}_{2}}}, s_{\beta _{{\hat{\Upsilon }}_{2}}} \right\rangle$ be the three LIFN and $\lambda >0$ be a real number. Then we have the following operational laws on LIFNs:

• (i) $\displaystyle {\hat{\Upsilon }}_1 \oplus {\hat{\Upsilon }}_2 = \left\langle s_{\alpha _{{\hat{\Upsilon }}_{1}} +\alpha _{{\hat{\Upsilon }}_{2}}- \frac{\alpha _{{\hat{\Upsilon }}_{1}} \alpha _{{\hat{\Upsilon }}_{1}}}{t}}, ~s_{\frac{\beta _{{\hat{\Upsilon }}_{1}} \beta _{{\hat{\Upsilon }}_{2}}}{t}} \right\rangle ,$

• (ii) $\displaystyle {\hat{\Upsilon }}_1 \otimes {\hat{\Upsilon }}_2 = \left\langle s_{\frac{\alpha _{{\hat{\Upsilon }}_{1}} \alpha _{{\hat{\Upsilon }}_{2}}}{t}},~ s_{\beta _{{\hat{\Upsilon }}_{1}} +\beta _{{\hat{\Upsilon }}_{2}}-\frac{\beta _{{\hat{\Upsilon }}_{1}} \beta _{{\hat{\Upsilon }}_{2}}}{t}}\right\rangle ,$

• (iii) $\displaystyle \lambda {\hat{\Upsilon }} = \left\langle s_{t-t\left( 1-\frac{\alpha _{{\hat{\Upsilon }}}}{t}\right) ^{\lambda }},~ s_{t\left( \frac{\beta _{{\hat{\Upsilon }}}}{t}\right) ^{\lambda }} \right\rangle ,$

• (iv) ${\hat{\Upsilon }} ^{\lambda } = \left\langle s_{t\left( \frac{\alpha _{{\hat{\Upsilon }}}}{t}\right) ^{\lambda }},~ s_{t-t\left( 1-\frac{\beta _{{\hat{\Upsilon }}}}{t}\right) ^{\lambda }} \right\rangle .$

2.5 Linguistic interval-valued intuitionistic fuzzy set

Definition 6

(Garg and Kumar 2019a) Let X be the finite universe of discourse and ${\mathbb {S}}_{[0,t]}$ be a continuous LTS. A LIVIFS $\tilde{{\mathcal {P}}}$ in X is defined as

$$\begin{aligned} \tilde{{\mathcal {P}}}=\left\{ \left\langle x,s_{\xi _{\tilde{{\mathcal {P}}}}}(x),\; s_{\vartheta _{\tilde{{\mathcal {P}}}}}(x)\right\rangle \;|\;x \in X \right\} , \end{aligned}$$

(2.4)

where $s_{\xi _{\tilde{{\mathcal {P}}}}}(x) =[s_{\xi _{\tilde{{\mathcal {P}}}} ^{-}}(x),\; s_{{\xi _{\tilde{{\mathcal {P}}}} ^{+}}}(x) ]$ and $s_{\vartheta _{\tilde{{\mathcal {P}}}}}(x) =[s_{{\vartheta _{\tilde{{\mathcal {P}}}}^{-}}}(x) ,\; s_{{\vartheta _{\tilde{{\mathcal {P}}}}^{+}}}(x)]$ are the subsets of $[s_{0},s_{t}]$ and represent the MD and NMD of the element $x \in X$ to the set $\tilde{{\mathcal {P}}}$, respectively, such that $s_{{\xi _{\tilde{{\mathcal {P}}}} ^{+}}}(x)+s_{{\vartheta _{\tilde{{\mathcal {P}}}} ^{+}}}(x)\le s_{t}\;\forall \;x\in X$, which implies ${\xi _{\tilde{{\mathcal {P}}}} ^{+}(x)}+{\vartheta _{\tilde{{\mathcal {P}}}}^{+}(x)} \le t\; \forall \;x\in X$ always exists. The HD of x to $\tilde{{\mathcal {P}}}$ is defined as $s_{\pi _{\tilde{{\mathcal {P}}}} }\left( x \right) =[s_{\pi _{\tilde{{\mathcal {P}}}}^{-}}\left( x \right) , s_{\pi _{\tilde{{\mathcal {P}}}}^{+}}\left( x \right) ]=[s_{t-\xi _{\tilde{{\mathcal {P}}}} ^{+}\left( x \right) -\vartheta _{\tilde{{\mathcal {P}}}}^{+}\left( x \right) }, s_{t-\xi _{\tilde{{\mathcal {P}}}}^{-}\left( x \right) -\vartheta _{\tilde{{\mathcal {P}}}}^{-}\left( x \right) }]$. Usually for a given $x \in X$, the pair $\left\langle \left[ s_{{\xi _{\tilde{{\mathcal {P}}}} ^{-}}}(x),\; s_{{\xi _{\tilde{{\mathcal {P}}}} ^{+}}}(x)\right] , \left[ s_{{\vartheta _{\tilde{{\mathcal {P}}}} ^{-}}}(x),\; s_{{\vartheta _{\tilde{{\mathcal {P}}}}^{+}}}(x)\right] \right\rangle$ is called a LIVIFN, which can be simply denoted by $\delta =\left\langle \left[ s_{{\xi _{\delta } ^{-}}},\; s_{{\xi _{\delta } ^{+}}}\right] ,\right. \left. \left[ s_{{\vartheta _{\delta } ^{-}}},\; s_{{\vartheta _{\delta }^{+}}}\right] \right\rangle$. Let ${\textbf{B}}$ be the set of all LIVIFNs defined in X.

Definition 7

(Garg and Kumar 2019a) Let $\delta _{1}=\left\langle \left[ s_{{\xi _{\delta _{1}} ^{-}}},\; s_{{\xi _{\delta _{1}} ^{+}}}\right] , \right. \left. \left[ s_{{\vartheta _{\delta _{1}} ^{-}}},\; s_{{\vartheta _{\delta _{1}}^{+}}}\right] \right\rangle$ and $\delta _{2}=\left\langle \left[ s_{{\xi _{\delta _{2}} ^{-}}},\; s_{{\xi _{\delta _{2}}^{+}}}\right] , \left[ s_{{\vartheta _{\delta _{2}} ^{-}}},\; s_{{\vartheta _{\delta _{2}}^{+}}}\right] \right\rangle$ be two LIVIFNs, then it follows that:

• (a) $\delta _{1}\le \delta _{2}$ if $\xi _{\delta _{1}}^{-}\le \xi _{\delta _{2}}^{-}$, $\xi _{\delta _{1}} ^{+}\le \xi _{\delta _{2}}^{+}$, $\vartheta _{\delta _{1}}^{-}\ge \vartheta _{\delta _{2}}^{-}$ and $\vartheta _{\delta _{1}} ^{+}\ge \vartheta _{\delta _{2}}^{+}$;

• (b) $\delta _{1}= \delta _{2}$ if and only if $\xi _{\delta _{1}}^{-}= \xi _{\delta _{2}}^{-}$, $\xi _{\delta _{1}} ^{+}= \xi _{\delta _{2}}^{+}$, $\vartheta _{\delta _{1}}^{-}= \vartheta _{\delta _{2}}^{-}$ and $\vartheta _{\delta _{1}} ^{+}= \vartheta _{\delta _{2}}^{+}$;

• (c) $\delta _{1}^{C}=\left\langle \left[ s_{{\vartheta _{\delta _{1}} ^{-}}},\; s_{\vartheta _{\delta _{1}}^{+}}\right] , \left[ s_{{\xi _{\delta _{1}} ^{-}}},\; s_{{\xi _{\delta _{1}} ^{+}}}\right] \right\rangle$;

• (d) $\delta _{1}\cup \delta _{2}=\left\langle \left[ \max \left\{ s_{\xi _{\delta _{1}} ^{-}},s_{\xi _{\delta _{2}}^{-}} \right\} , \; \max \left\{ s_{\xi _{\delta _{1}}^{+}},\; s_{\xi _{\delta _{2}} ^{+}} \right\} \right] , \;\right. \left. \left[ \min \left\{ s_{\vartheta _{\delta _{1}} ^{-}},\; s_{\vartheta _{\delta _{2}} ^{-}} \right\} , \; \min \left\{ s_{\vartheta _{\delta _{1}} ^{+}}, \; s_{\vartheta _{\delta _{2}} ^{+}} \right\} \right] \right\rangle$;

• (e) $\delta _{1}\cap \delta _{2}=\left\langle \left[ \min \left\{ s_{\xi _{\delta _{1}} ^{-}},s_{\xi _{\delta _{2}}^{-}} \right\} , \; \min \left\{ s_{\xi _{\delta _{1}}^{+}},\; s_{\xi _{\delta _{2}} ^{+}} \right\} \right] , \;\right. \left. \left[ \max \left\{ s_{\vartheta _{\delta _{1}} ^{-}},\; s_{\vartheta _{\delta _{2}} ^{-}} \right\} , \; \max \left\{ s_{\vartheta _{\delta _{1}} ^{+}}, \; s_{\vartheta _{\delta _{2}} ^{+}} \right\} \right] \right\rangle$.

Definition 8

Garg and Kumar (2019a) Let $\delta =\left\langle \left[ s_{{\xi _{\delta } ^{-}}},\; s_{{\xi _{\delta } ^{+}}}\right] ,\right. \left. \left[ s_{{\vartheta _{\delta } ^{-}}},\; s_{{\vartheta _{\delta }^{+}}}\right] \right\rangle$, $\delta _{1}=\left\langle \left[ s_{{\xi _{\delta _{1}} ^{-}}},\; s_{{\xi _{\delta _{1}} ^{+}}}\right] , \left[ s_{{\vartheta _{\delta _{1}} ^{-}}},\; s_{{\vartheta _{\delta _{1}}^{+}}}\right] \right\rangle$ and $\delta _{2}=\left\langle \left[ s_{{\xi _{\delta _{2}} ^{-}}},\; s_{{\xi _{\delta _{2}}^{+}}}\right] , \left[ s_{{\vartheta _{\delta _{2}} ^{-}}},\; s_{{\vartheta _{\delta _{2}}^{+}}}\right] \right\rangle$ be three LIVIFNs and $\lambda >0$ be a real number. Then, we have the following operational laws on LIVIFNs:

• 1. $\delta _{1}\oplus \delta _{2}=\displaystyle \left\langle \left[ s_{\left( \xi _{\delta _{1}} ^{-}+\xi _{\delta _{2}} ^{-}-\frac{\xi _{\delta _{1}} ^{-}\xi _{\delta _{2}} ^{-}}{t}\right) },s_{\left( \xi _{\delta _{1}} ^{+}+\xi _{\delta _{2}} ^{+}-\frac{\xi _{\delta _{1}} ^{+}\xi _{\delta _{2}} ^{+}}{t}\right) } \right] ,\right. \left. \;\left[ s_{\left( \frac{\vartheta _{\delta _{1}} ^{-}\vartheta _{\delta _{2}} ^{-}}{t}\right) },s_{\left( \frac{\vartheta _{\delta _{1}} ^{+}\vartheta _{\delta _{2}} ^{+}}{t}\right) } \right] \right\rangle$;

• 2. $\delta _{1}\otimes \delta _{2}=\left\langle \left[ s_{\left( \frac{\xi _{\delta _{1}} ^{-}\xi _{\delta _{2}} ^{-}}{t}\right) },s_{\left( \frac{\xi _{\delta _{1}} ^{+}\xi _{\delta _{2}} ^{+}}{t}\right) } \right] , \right. \left. \left[ s_{\left( \vartheta _{\delta _{1}} ^{-}+\vartheta _{\delta _{2}} ^{-}-\frac{\vartheta _{\delta _{1}} ^{-}\vartheta _{\delta _{2}} ^{-}}{t}\right) },s_{\left( \vartheta _{\delta _{1}} ^{+}+\vartheta _{\delta _{2}} ^{+}-\frac{\vartheta _{\delta _{1}} ^{+}\vartheta _{\delta _{2}} ^{+}}{t}\right) } \right] \right\rangle$;

• 3. $\lambda \delta =\displaystyle \left\langle \left[ s_{t\left( 1-\left( 1-\frac{\xi _{\delta } ^{-}}{t}\right) ^{\lambda }\right) } ,s_{t\left( 1-\left( 1-\frac{\xi _{\delta } ^{+}}{t}\right) ^{\lambda }\right) } \right] ,\right. \left. \; \left[ s_{t\left( \frac{\vartheta _{\delta } ^{-} }{t}\right) ^{\lambda } },s_{t\left( \frac{\vartheta _{\delta } ^{+} }{t}\right) ^{\lambda } } \right] \right\rangle$;

• 4. $\delta ^{\lambda }=\displaystyle \left\langle \left[ s_{t\left( \frac{\xi _{\delta } ^{-} }{t}\right) ^{\lambda } },s_{t\left( \frac{\xi _{\delta } ^{+} }{t}\right) ^{\lambda } } \right] , \right. \left. \left[ s_{t\left( 1-\left( 1-\frac{\vartheta _{\delta } ^{-}}{t}\right) ^{\lambda }\right) } ,s_{t\left( 1-\left( 1-\frac{\vartheta _{\delta } ^{+}}{t}\right) ^{\lambda }\right) } \right] \right\rangle$.

Definition 9

(Garg and Kumar 2019a) Let $\delta _{j}=\left\langle \left[ s_{\xi _{\delta _{j}}^{-}},s_{\xi _{\delta _{j}}^{+}} \right] ,\left[ s_{\vartheta _{\delta _{j}}^{-}},s_{\vartheta _{\delta _{j}}^{+}}\right] \right\rangle$, (where $j = 1,2, \ldots , n$) be a collection of n LIVIFNs and $\varpi =(\varpi _{1},\ldots ,\varpi _{n})^T$ be the weight vector, such that $0 \le \varpi _{j} \le 1, j=1,2, \ldots ,n, \; \displaystyle \sum ^{n}_{j=1}\varpi _{j} =1$. The LIVIFWA operator is a mapping $LIVIFWA:\; {\textbf{B}}^{n} \longrightarrow {\textbf{B}}$, and is given by

$$\begin{aligned} \begin{aligned}&LIVIFWA\left( \delta _{1}, \delta _{2},...,\delta _{n}\right) =\displaystyle \bigoplus _{j=1}^{n}\varpi _{j}\delta _{j} = \displaystyle \bigoplus _{j=1}^{n}\varpi _{j}\\&\quad \left\langle \left[ s_{\xi _{\delta _{j}}^{-}},s_{\xi _{\delta _{j}}^{+}} \right] ,\left[ s_{\vartheta _{\delta _{j}}^{-}},s_{\vartheta _{\delta _{j}}^{+}}\right] \right\rangle \\ =&\displaystyle \left\langle \left[ s_{ t\left( 1-\prod _{j=1}^{n} \left( 1-\frac{\xi _{\delta _{j}}^{-}}{t}\right) ^{\varpi _{j}} \right) },\;s_{ t\left( 1-\prod _{j=1}^{n}\left( 1-\frac{\xi _{\delta _{2}}^{+}}{t}\right) ^{\varpi _{j}} \right) } \right] \right. ,\\&\quad \;\left. \left[ s_{t\left( \prod _{j=1}^{n} \left( \frac{\vartheta _{\delta _{j}}^{-}}{t}\right) ^{\varpi _{r}} \right) },s_{t\left( \prod _{j=1}^{n}\left( \frac{\vartheta _{\delta _{j}}^{+}}{t}\right) ^{\varpi _{j}} \right) }\right] \right\rangle , \end{aligned} \end{aligned}$$

(2.5)

then, LIVIFWA is known as the linguistic interval-valued intuitionistic fuzzy weighted average (LIVIFWA) operator.

3 Matrix games with linguistic interval-valued intuitionistic fuzzy payoffs: proposed model

The matrix games with pay-off matrix involving LIVIFNs can be explained as follows:

Let $\chi =\{\chi _1,\chi _2,\ldots ,\chi _m$} and $\tau =\{\tau _1,\tau _2,\ldots ,\tau _n\}$, be two finite sets of pure strategies for player I and player II, respectively. Let ${\mathcal {I}}= \{1,2,\ldots , m \}$ and ${\mathcal {J}}= \{1,2,\ldots , n \}$. Let ${\tilde{A}}$ denotes a pay-off matrix with entries expressed by LIVIFNs. Let player I choose pure strategy $\chi _i \in \chi \; (i\in {\mathcal {I}})$ and the player II choose pure strategy $\tau _j \in \tau \; (j\in {\mathcal {J}})$. Player I gains a pay-off ${\delta }_{ij}$ represented by the LIVIFN $\delta _{ij} = \left\langle \left[ s_{\xi _{\delta _{ij}}^{-}},s_{\xi _{\delta _{ij}}^{+}}\right] , \left[ s_{\vartheta _{\delta _{ij}}^{-}},s_{\vartheta _{\delta _{ij}}^{+}}\right] \right\rangle$, where $s_{\xi _{\delta _{ij}}^{-}}, s_{\xi _{\delta _{ij}}^{+}}, s_{\vartheta _{\delta _{ij}}^{-}}, s_{\vartheta _{\delta _{ij}}^{+}} \in {\mathbb {S}}_{[0,t]}$ and the intervals $\left[ s_{\xi _{\delta _{ij}}^{-}},s_{\xi _{\delta _{ij}}^{+}}\right]$ and $\left[ s_{\vartheta _{\delta _{ij}}^{-}},s_{\vartheta _{\delta _{ij}}^{+}}\right]$ are the subset of $[ s_0, s_t]$ with the property $s_{\xi _{\delta _{ij}}^{+}} + s_{\vartheta _{\delta _{ij}}^{+}}\le s_{t}$ or specifically $\xi _{\delta _{ij}}^{+} + \vartheta _{\delta _{ij}}^{+}\le t$. Hence, the pay-off matrix ${\tilde{A}}$ of player I can be expressed as

$$\begin{aligned} {\tilde{A}} = \begin{bmatrix} \left\langle \left[ s_{\xi _{\delta _{11}}^{-}},s_{\xi _{\delta _{11}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{11}}^{-}},s_{\vartheta _{\delta _{11}}^{+}}\right] \right\rangle &{} \left\langle \left[ s_{\xi _{\delta _{12}}^{-}},s_{\xi _{\delta _{12}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{12}}^{-}},s_{\vartheta _{\delta _{12}}^{+}}\right] \right\rangle &{} \ldots \left\langle \left[ s_{\xi _{\delta _{1n}}^{-}},s_{\xi _{\delta _{1n}}^{+}}\right] ,\left[ s_{\vartheta _{a_{1n}}^{-}},s_{\vartheta _{\delta _{1n}}^{+}}\right] \right\rangle \\ \left\langle \left[ s_{\xi _{\delta _{21}}^{-}},s_{\xi _{\delta _{21}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{21}}^{-}},s_{\vartheta _{\delta _{21}}^{+}}\right] \right\rangle &{}\left\langle \left[ s_{\xi _{\delta _{22}}^{-}},s_{\xi _{\delta _{22}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{22}}^{-}},s_{\vartheta _{\delta _{22}}^{+}}\right] \right\rangle &{} \ldots \left\langle \left[ s_{\xi _{\delta _{2n}}^{-}},s_{\xi _{\delta _{2n}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{2n}}^{-}},s_{\vartheta _{\delta _{2n}}^{+}}\right] \right\rangle \\ \vdots &{} \vdots &{} \vdots &{} \\ \left\langle \left[ s_{\xi _{\delta _{m1}}^{-}},s_{\xi _{\delta _{m1}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{m1}}^{-}},s_{\vartheta _{a_{m1}}^{+}}\right] \right\rangle &{} \left\langle \left[ s_{\xi _{\delta _{m2}}^{-}},s_{\xi _{\delta _{m2}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{m2}}^{-}},s_{\vartheta _{\delta _{m2}}^{+}}\right] \right\rangle &{}\ldots \left\langle \left[ s_{\xi _{\delta _{mn}}^{-}},s_{\xi _{\delta _{mn}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{mn}}^{-}},s_{\vartheta _{\delta _{mn}}^{+}}\right] \right\rangle \end{bmatrix} \end{aligned}$$

The player II gains a payoff $\delta _{ij}^{C} = \left\langle \! \left[ \!s_{\vartheta _{\delta _{ij}}^{-}},s_{\vartheta _{\delta _{ij}}^{+}}\!\right] , \left[ \!s_{\xi _{\delta _{ij}}^{-}},s_{\xi _{\delta _{ij}}^{+}}\!\right] \!\right\rangle$. Let $\mathbf {R^n}$ denote the n-dimensional Euclidean space and $\mathbf {R^{n}_{+}}$ be its nonnegative orthant. Let $x_i\;(i \in {\mathcal {I}} )$ be the probability that the player I chooses the pure strategy $\chi _i \in \chi$ and $y_j\;(j \in {\mathcal {J}} )$ be the probability that the player II chooses the pure strategy $\tau _{j} \in \tau$, then the probability vectors $x= (x_1, x_2, \ldots , x_m)^T$ and $y= (y_1, y_2, \ldots , y_n)^T$ are called the mixed strategies for the player I and player II, respectively. Let $S^{m}= \{ x \in \mathbf {R^m_+} | \sum _{i=1}^m x_i =1 \}$ and $\displaystyle S^{n}= \{ y \in \mathbf {R^n_+} | \sum \limits {_{j=1}^n} y_j =1 \}$ be the mixed strategy spaces for the player I and player II, respectively. A linguistic interval-valued intuitionistic fuzzy matrix game can be expressed as follows

$$\begin{aligned} LIVIFMG = ( S^{m}, S^{n}, {\tilde{A}}, {\mathbb {S}}_{[0,t]}). \end{aligned}$$

If the player I and player II choose the mixed strategies $x\in S^{m}$ and $y \in S^{n}$, respectively, the expected payoff of player I can be calculated as follows:

$$\begin{aligned} \begin{array}{lll}&\,&\textrm{E}_{{\tilde{A}}}(x, y) = x^T {\tilde{A}} y,= \begin{bmatrix} x_1&{} x_2&{}\ldots x_n \end{bmatrix} \otimes \begin{bmatrix} \delta _{11}&{} \delta _{12}&{}\ldots &{}\delta _{1n}\\ \delta _{21}&{} \delta _{22}&{}\ldots &{} \delta _{2n}\\ \vdots &{} \vdots &{} &{} \vdots \\ \delta _{m1}&{} \delta _{m2}&{}\ldots &{} \delta _{mn}\\ \end{bmatrix}\; \otimes \begin{bmatrix} y_1\\ y_2\\ \vdots \\ y_n \end{bmatrix} = \begin{bmatrix} x_1&{} x_2&{}\ldots x_n \end{bmatrix}\;\\ {} &{}&{} \otimes \begin{bmatrix} \left\langle \left[ s_{\xi _{\delta _{11}}^{-}},s_{\xi _{\delta _{11}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{11}}^{-}},s_{\vartheta _{\delta _{11}}^{+}}\right] \right\rangle &{} \left\langle \left[ s_{\xi _{\delta _{12}}^{-}},s_{\xi _{\delta _{12}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{12}}^{-}},s_{\vartheta _{\delta _{12}}^{+}}\right] \right\rangle &{}\ldots &{}\left\langle \left[ s_{\xi _{\delta _{1n}}^{-}},s_{\xi _{\delta _{1n}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{1n}}^{-}},s_{\vartheta _{\delta _{1n}}^{+}}\right] \right\rangle \\ \left\langle \left[ s_{\xi _{\delta _{21}}^{-}},s_{\xi _{\delta _{21}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{21}}^{-}},s_{\vartheta _{\delta _{21}}^{+}}\right] \right\rangle &{} \left\langle \left[ (s_{\xi _{\delta _{22}}^{-}},s_{\xi _{\delta _{22}}^{+}}\right] ,\left[ (s_{\vartheta _{\delta _{22}}^{-}},s_{\vartheta _{\delta _{22}}^{+}}\right] \right\rangle &{}\ldots &{}\left\langle \left[ (s_{\xi _{\delta _{2n}}^{-}},s_{\xi _{\delta _{2n}}^{+}}\right] ,\left[ (s_{\vartheta _{\delta _{2n}}^{-}},s_{\vartheta _{\delta _{2n}}^{+}}\right] \right\rangle \\ \vdots &{} \vdots &{} &{} \vdots \\ \left\langle \left[ (s_{\xi _{\delta _{m1}}^{-}},s_{\xi _{\delta _{m1}}^{+}}\right] ,\left[ (s_{\vartheta _{\delta _{m1}}^{-}},s_{\vartheta _{\delta _{m1}}^{+}}\right] \right\rangle &{} \left\langle \left[ (s_{\xi _{\delta _{m2}}^{-}},s_{\xi _{\delta _{m2}}^{+}}\right] ,\left[ (s_{\vartheta _{\delta _{m2}}^{-}},s_{\vartheta _{\delta _{m2}}^{+}}\right] \right\rangle &{}\ldots &{}\left\langle \left[ (s_{\xi _{\delta _{mn}}^{-}},s_{\xi _{\delta _{mn}}^{+}}\right] ,\left[ (s_{\vartheta _{\delta _{mn}}^{-}},s_{\vartheta _{\delta _{mn}}^{+}}\right] \right\rangle \\ \end{bmatrix} \otimes \begin{bmatrix} y_1\\ y_2\\ \vdots \\ y_n \end{bmatrix}\\ \end{array}. \end{aligned}$$

According to the Definition 9, $\textrm{E}_{{\tilde{A}}}(x, y)$ can be expressed as follows

$$\begin{aligned}&\textrm{E}_{{\tilde{A}}}(x,y) =\displaystyle \left\langle \left[ s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{-}}}{t}\right) ^{x_{i}y_{j}}\right) },\right. \right. \\&\quad \left. \left. s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{+}}}{t}\right) ^{x_{i}y_{j}}\right) }\right] ,\right. \end{aligned}$$

$$\begin{aligned}&\quad \left. \left[ s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{{\vartheta _{\delta _{ij}}^{+}}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \right\rangle \nonumber \\ =&\displaystyle \left\langle \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \end{aligned}$$

(3.1)

where

$$\begin{aligned} s_{\xi _{\delta _{xy}}^{-}}&= s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{-}}}{t}\right) ^{x_{i}y_{j}}\right) } \in {\mathbb {S}}_{[0,t]},\;\\&\quad s_{\xi _{\delta _{xy}}^{+}} = s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{+}}}{t}\right) ^{x_{i}y_{j}}\right) } \in {\mathbb {S}}_{[0,t]},\\ s_{\vartheta _{\delta _{xy}}^{-}}&= s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) } \in {\mathbb {S}}_{[0,t]}\;\text{ and } \;\\&\quad \;\;\;\;s_{\vartheta _{\delta _{xy}}^{+}} = s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) } \in {\mathbb {S}}_{[0,t]}. \end{aligned}$$

Without loss of generality, let us assume that the player I is a maximizing player, and player II is a minimizing player. Thus, player I and player II will select the mixed strategies $x^{\star } \in X$ and $y^{\star }\in Y$ according to maximin and minimax principles, respectively, such that

$$\begin{aligned} x^{\star T}{\tilde{A}}y^{\star }=\max _{x\in S^{m}} \min _{y\in S^{n}}\left\{ x^{T}{\tilde{A}}y \right\} = \min _{y\in S^{n}}\max _{x\in S^{m}}\left\{ x^{T}{\tilde{A}}y \right\} . \end{aligned}$$

Here, $x^{\star T}{\tilde{A}}y^{\star }$ is a LIVIFN with linguistic interval-valued membership and linguistic interval-valued non-membership values, which are usually conflicting. In general, the optimal strategies $x^{\star }$ and $y^{\star }$ do not exist for player I and player II. According to the Definition 8 and Eq. (3.1), the optimization model $x^{\star T}{\tilde{A}}y^{\star }$ is a bi-objective linguistic interval valued intuitionistic fuzzy-programming problem. The first objective is the linguistic interval-valued function

$$\begin{aligned} s_{\xi } =\left[ s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{-}}}{t}\right) ^{x_{i}y_{j}}\right) },s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{+}}}{t}\right) ^{x_{i}y_{j}}\right) }\right] ;\nonumber \\ \end{aligned}$$

(3.2)

and the second is the linguistic interval-valued function

$$\begin{aligned} s_{\vartheta } = \left[ s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{{\vartheta _{\delta _{ij}}^{+}}}{t}\right) ^{x_{i}y_{j}}\right) }\right] .\nonumber \\ \end{aligned}$$

(3.3)

Consequently, the concept of solutions of the matrix game ${\tilde{A}}$ with payoffs denoted by the LIVIFNs can be defined in a manner similar to that of the Pareto optimal solutions as follows:

Definition 10

Let ${\tilde{\gamma }}_1$ and ${\tilde{\gamma }}_2$ be two LIVIFNs. If there exists $x^{*} \in S^{m}$ and $y^{*} \in S^{n}$ such that $(x^{*})^T {\tilde{A}} y \ge {\tilde{\gamma }}_{1}$ and $x^T {\tilde{A}} y^{*} \le {\tilde{\gamma }}_2$ for any $x \in S^{m}$, $y \in S^{n}$, then $x^{*}\; (y^{*})$ is called the reasonable strategies player I (player II); and ${\tilde{\gamma }}_{1}$ (${\tilde{\gamma }}_{2}$) is called the reasonable value for player I (player II). Moreover, $\left( x^{*},y^{*},{\tilde{\gamma }}_1,{\tilde{\gamma }}_2 \right)$ is known as the reasonable solution of the matrix game ${\tilde{A}}$

Definition 11

Let ${\mathbb {F}}_{1}$ and ${\mathbb {F}}_{2}$ denotes the sets of all reasonable values for player I and player II, respectively. Assume that there exists ${\tilde{\gamma }}_1^{\star } \in {\mathbb {F}}_{1}$ and ${\tilde{\gamma }}_2^{\star } \in {\mathbb {F}}_{2}$. If there do not exist any ${\tilde{\gamma }}_1 \in {\mathbb {F}}_{1}$ (${\tilde{\gamma }}_1 \ne {\tilde{\gamma }}_1^{\star }$) and ${\tilde{\gamma }}_2 \in {\mathbb {F}}_{2}$ (${\tilde{\gamma }}_2 \ne {\tilde{\gamma }}_2^{\star }$) such that ${\tilde{\gamma }}_{1} \ge {\tilde{\gamma }}_1^{\star }$ and ${\tilde{\gamma }}_2 \le {\tilde{\gamma }}_2^{\star }$. Then, $x^{\star }\;(y^{\star })$ is called the maximin (minimax) strategy for player I (player II); ${\tilde{\gamma }}_1^{\star }$ and ${\tilde{\gamma }}_2^{\star }$ are called the value of the game ${\tilde{A}}$ corresponding to the player I and player II. $(x^{\star },y^{\star }, \tilde{\gamma }^{\star }_{1}, \tilde{\gamma }^{\star }_{2})$ is called a solution of the matrix game ${\tilde{A}}$ with payoffs represented by LIVIFNs.

3.1 Model construction and solution approach for LIVIFMG

Since player I is a maximin player, let $\varTheta$ be the its minimum expected gain which can be defined as

$$\begin{aligned} \begin{aligned} \varTheta&=\displaystyle \min _{y\in S^{n} }\textrm{E}_{{\tilde{A}}}(x,y)=\min _{y \in S^{n}}\left\langle \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \\&= \left\langle \min _{y\in S^{n}}\left\{ \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \right\} ,\max _{y\in S^{n}}\left\{ \left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\} \right\rangle \\&=\left\langle \left[ s_{\xi _{\varTheta }^{-}},s_{\xi _{\varTheta }^{+}}\right] ,\left[ s_{\vartheta _{\varTheta }^{-}},s_{\vartheta _{\varTheta }^{+}}\right] \right\rangle \end{aligned} \end{aligned}$$

It may be noted that $\varTheta$ is a function of x only. Player I prefers to choose a mixed strategy $x^{\star } \in S^{m}$ in such a way that it will maximize its minimum expected gain. Therefore,

$$\begin{aligned}{} & {} \varTheta ^{\star }= \displaystyle \max _{x \in S^{m}} \varTheta = \max _{x \in S^{m}}\left\langle \left[ s_{\xi _{\varTheta }^{-}},s_{\xi _{\varTheta }^{+}}\right] ,\left[ s_{\vartheta _{\varTheta }^{-}}, s_{\vartheta _{\varTheta }^{+}}\right] \right\rangle \nonumber \\{} & {} \;= \left\langle \max _{x\in S^{m}}\min _{y\in S^{n}}\left\{ \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \right\} ,\min _{x \in S^{m}}\max _{y\in S^{n}}\left\{ \left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\} \right\rangle \nonumber \\ \end{aligned}$$

(3.4)

The mixed strategy $x^{\star } \in S^{m}$ is called the maximin strategy with the value of the game $\varTheta ^{\star }$ for player I.

Similarly, player II is a minimax player, let $\varPsi$ be the its maximum expected loss

$$\begin{aligned} \begin{aligned} \varPsi&= \displaystyle \max _{x\in S^{m} }\textrm{E}_{{\tilde{A}}}(x,y)=\max _{x\in S^{m}}\left\langle \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \\&= \displaystyle \left\langle \max _{x\in S^{m}}\left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] ,\min _{x\in S^{m}}\left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \\&=\displaystyle \left\langle \left[ s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}}\right] ,\left[ s_{\vartheta _{\varPsi }^{-}}, s_{\vartheta _{\varPsi }^{+}}\right] \right\rangle \end{aligned} \end{aligned}$$

It may be noted that $\varPsi$ is a function of y only. Player II prefers to choose a mixed strategy $y^{\star } \in S^{n}$ in such a way that it will minimize its maximum expected loss. Therefore,

$$\begin{aligned} \begin{aligned} \varPsi ^{\star }&= \min _{y \in S^{n}} \varPsi =\min _{y \in S^{n}}\left\langle \left[ s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}}\right] ,\left[ s_{\vartheta _{\varPsi }^{-}},s_{\vartheta _{\varPsi }^{+}} \right] \right\rangle \\&=\displaystyle \left\langle \min _{y \in S^{n}}\max _{x\in S^{m}}\left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] ,\;\;\max _{y \in S^{n}}\min _{x\in S^{m}}\left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \end{aligned}\nonumber \\ \end{aligned}$$

(3.5)

The mixed strategy $y^{\star } \in S^{n}$ is called the minimax strategy with the value of the game $\varPsi ^{\star }$ for player II.

3.2 Mathematical model for player I

We shall consider two cases as follows:

Case I : When $s_{0}\le s_{\xi _{\varTheta }^{-}},\; s_{\xi _{\varTheta }^{+}},\;s_{\xi _{\delta _{ij}}^{-}},\;s_{\xi _{\delta _{ij}}^{+}}< s_{t}$ and $s_{0}<s_{\vartheta _{\varTheta }^{-}},\; s_{\vartheta _{\varTheta }^{+}},\;s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}} \le s_{t}$, $i \in {\mathcal {I}}, \; j \in {\mathcal {J}}$.

The maximin strategy $x^{\star }$ and the maximum gain $\varTheta ^{\star }$ for player I are derived by resolving through nonlinear bi-objective linguistic interval-programming problem which is framed as follows:

$$\begin{aligned} {\textbf {(PI-1)}}\quad{} & {} \varTheta ^{\star }= \left\langle \displaystyle \max \left[ s_{\xi _{\varTheta }^{-}},\;s_{\xi _{\varTheta }^{+}}\right] , \displaystyle \min \left[ s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}}\right] \right\rangle \\{} & {} \text {subject to}\\ \;{} & {} \displaystyle \left[ s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \\{} & {} \quad \ge \left[ s_{\xi _{\varTheta }^{-}},\;s_{\xi _{\varTheta }^{+}}\right] \quad \text{ for } \text{ any } y \in S^{n} \\{} & {} \displaystyle \left[ s_{t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) }\;,s_{t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \\{} & {} \quad \le [s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}}] \quad \quad \quad \quad \text{ for } \text{ any } y \in S^{n} \\{} & {} s_{\xi _{\varTheta }^{-}},\;s_{\xi _{\varTheta }^{+}},\;s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]}, \\{} & {} i \in {\mathcal {I}}, \; j \in {\mathcal {J}} \\{} & {} 0 \le \xi _{\varTheta }^{+}+\vartheta _{\varTheta }^{+}\le t,\;0\le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}} \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1, \; x_{i}\ge 0,\; , \;i \in {\mathcal {I}}\\ \end{aligned}$$

where $s_{\xi _{\varTheta }^{-}}=\min \limits _{y \in S^{n}} \left\{ s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{-}}}{t}\right) ^{x_{i}y_{j}}\right) }\right\}$, $s_{\xi _{\varTheta }^{+}}=\min \limits _{y \in S^{n}} \left\{ s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{{\xi _{\delta _{ij}}^{+}}}{t}\right) ^{x_{i}y_{j}}\right) }\right\}$, $s_{\vartheta _{\varTheta }^{+}}=\max \limits _{y \in S^{n}} \left\{ s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) }\right\}$ and $s_{\vartheta _{\varTheta }^{+}}=\max \limits _{y \in S^{n}} \left\{ s_{ t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) } \right\}$.

It may be noted that the objective function is equivalent to

$$\begin{aligned}{} & {} \max \left\{ \left[ s_{\xi _{\varTheta }^{-}},s_{\xi _{\varTheta }^{+}}\right] \right\} \Leftrightarrow \min \left\{ \left[ s_{t-\xi _{\varTheta }^{+}},s_{t-\xi _{\varTheta }^{-}}\right] \right\} \\{} & {} \quad \Leftrightarrow \min \left\{ \left[ s_{\ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) },\; s_{\ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) }\right] \right\} ,\\{} & {} \min \left\{ [s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}}]\right\} \Leftrightarrow \min \left\{ \left[ s_{\ln \left( \frac{ \vartheta _{\varTheta }^{-}}{t}\right) },s_{\ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) }\right] \right\} \end{aligned}$$

and the constraints are equivalent to

$$\begin{aligned} \begin{aligned}&\displaystyle \left[ s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{ t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \\&\quad \ge \left[ s_{\xi _{\varTheta }^{-}},\;s_{\xi _{\varTheta }^{+}}\right] \\&\quad \Leftrightarrow \displaystyle \left[ s_{ \left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) },s_{ \left( \prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}} \right) }\right] \\&\quad \le \left[ s_{\left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) },\;s_{\left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) }\right] \\&\quad \Leftrightarrow \displaystyle \left[ s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\left( \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) \right) \right) },s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\left( \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) \right) \right) }\right] \\&\quad \le \left[ s_{\ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) },\;s_{\ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) }\right] , \end{aligned} \end{aligned}$$

$$\begin{aligned}&\displaystyle \left[ s_{t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{t\left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \\&\quad \le [s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}}] \\&\quad \Leftrightarrow \left[ s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}} \ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) },s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) }\right] \\&\quad \le \left[ s_{\ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) },\;s_{\ln \left( \frac{\vartheta _{\varTheta }^{+}}{t}\right) }\right] . \end{aligned}$$

Therefore, problem (PI-1) becomes equivalent to

$$\begin{aligned}{} & {} {\textbf {(PI-2)}}\\{} & {} \min \left\{ \left[ s_{\ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) }\; s_{\ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) }\right] \right\} ,\;\;\min \left\{ \left[ s_{\ln \left( \frac{ \vartheta _{\varTheta }^{-}}{t}\right) },s_{\ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) }\right] \right\} \\{} & {} \text{ subject } \text{ to } \\ \;{} & {} \displaystyle \left[ s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) \right) },\; s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m} {x_{i}y_{j}}\ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) \right) } \right] \le \left[ s_{\ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) },\; s_{\ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) } \right] , \quad \quad \text{ for } \text{ any } y\in S^{n}\\{} & {} \displaystyle \left[ s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) },\; s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) } \right] \le \; \quad \left[ s_{\ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) },\; s_{\ln \left( \frac{\vartheta _{\varTheta }^{+}}{t}\right) }\right] , \quad \quad \text{ for } \text{ any } y\in S^{n}\\{} & {} s_{\xi _{\varTheta }^{-}},\;s_{\xi _{\varTheta }^{+}},\;s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]}, \; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\varTheta }^{+}+\vartheta _{\varTheta }^{+}\le t,\;0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}} \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1, \;x_{i}\ge 0,\; i \in {\mathcal {I}}. \end{aligned}$$

Using the weighted average operator, the objective function in (PI-2) becomes

$$\begin{aligned} \begin{aligned}&\displaystyle \min \left\{ \left[ s_{\kappa \left( \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) \right) +(1-\kappa )\left( \ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) \right) },\right. \right. \\&\quad \left. \left. \quad s_{\kappa \left( \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) \right) +(1-\kappa )\left( \ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) \right) }\right] \right\} \end{aligned} \end{aligned}$$

where $\kappa \in [0,1]$ is the weight, which is suggested by the players of the game.

Similarly, the constraints in (PI-2) can also be rewritten as

$$\begin{aligned}&\displaystyle s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \right) }\\&\quad \le \;s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) \right) }\\&\displaystyle s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \right) } \\&\quad \le \;s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varTheta }^{+}}{t}\right) \right) } \end{aligned}$$

Thus, (PI-2) is transformed to

$$\begin{aligned} \begin{array} {lcl} &{}&{}{\textbf {(PI-3)}}\\ &{}&{}\displaystyle \min \left\{ \left[ s_{\kappa \left( \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) \right) +(1-\kappa )\left( \ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) \right) },\right. \right. \\ &{}&{}\quad \left. \left. s_{\kappa \left( \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) \right) +(1-\kappa )\left( \ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) \right) }\right] \right\} \\ &{}&{} \text{ subject } \text{ to } \\ &{}&{}\displaystyle s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \right) } \\ &{}&{}\quad \le \quad \;s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) \right) }\;, \quad \quad \text{ for } \text{ any } y\in S^{n}\\ &{}&{} \displaystyle s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \right) }\\ &{}&{}\quad \le \quad \;s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varTheta }^{+}}{t}\right) \right) }, \quad \quad \text{ for } \text{ any } y\in S^{n}\\ &{}&{}s_{\xi _{\varTheta }^{-}},\;s_{\xi _{\varTheta }^{+}},\;s_{\vartheta _{\varTheta }^{-}},\;s_{\vartheta _{\varTheta }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\\ &{}&{}\quad s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\;i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\ &{}&{}0 \le \xi _{\varTheta }^{+}+\vartheta _{\varTheta }^{+}\le t,\;0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\;i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\ &{}&{} \displaystyle \sum _{i=1}^{m}x_{i}=1, \;x_{i}\ge 0,\; i \in {\mathcal {I}}. \end{array} \end{aligned}$$

Now, the objective function in (PI-3) is an interval-valued function.

For simplification purpose, let $\varGamma ^{-}=\displaystyle \kappa \left( \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) \right) +(1-\kappa )\left( \ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) \right)$ and $\varGamma ^{+}=\displaystyle \kappa \left( \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) \right) +(1-\kappa )\left( \ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) \right)$.

Here, $\varGamma ^{-}\le 0$ and $\varGamma ^{+} \le 0$ because, $\kappa \in [0,1]$ and $0 \le \xi _{\varTheta }^{-}, \;\xi _{\varTheta }^{+}, \; \vartheta _{\varTheta }^{-},\; \vartheta _{\varTheta }^{+} \le t$, i.e., $\displaystyle 0 \le 1-\frac{\xi _{\varTheta }^{+}}{t}\le 1$, $0\le \displaystyle \frac{ \vartheta _{\varTheta }^{-}}{t}\le 1$, $0 \le \displaystyle 1-\frac{\xi _{\varTheta }^{-}}{t}\le 1$ and $0\le \displaystyle \frac{ \vartheta _{\varTheta }^{+}}{t}\le 1$.

Thus, the objective function in (PI-3) becomes $\min \left\{ \left[ s_{\varGamma ^{-}},\;s_{\varGamma ^{+}} \right] \right\}$ which can be further expressed as interval-objective function as $\displaystyle \min \left\{ \left[ \varGamma ^{-},\;\varGamma ^{+} \right] \right\}$, using the properties of linguistic terms. The constraints in equation (PI-3) can also be written as

$$\begin{aligned} \begin{aligned} \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \; \le \;\varGamma ^{-}\;,\\ \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \; \le \;\varGamma ^{+}, \end{aligned} \end{aligned}$$

Consequently, the (PI-3) can be modeled as follows :

$$\begin{aligned}{} & {} {\textbf {(PI-4)}}\\&&\displaystyle \min \left\{ \left[ \varGamma ^{-},\;\varGamma ^{+} \right] \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right] \\{} & {} \quad \le \quad \;\varGamma ^{-},\; \text{ for } \text{ any } y\in S^{n}\\{} & {} \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\{} & {} \quad \le \quad \;\varGamma ^{+},\; \text{ for } \text{ any } y\in S^{n}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varGamma ^{-} \le 0, \; \varGamma ^{+} \le 0,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\; x_{i}\ge 0, \;\; i \in {\mathcal {I}}. \end{aligned}$$

Since, $S^{n}$ is a finite compact convex set, it is sufficient to take into account only the extreme points of the set $S^{n}$ in the constraints (PI-4). Therefore, (PI-4) is transformed into a linear programming problem involving the interval in the objective function as follows :

$$\begin{aligned} {\textbf {(PI-5)}}\;{} & {} \displaystyle \min \left\{ \left[ \varGamma ^{-},\;\varGamma ^{+} \right] \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right] \\{} & {} \le \quad \;\varGamma ^{-}, \; j \in {\mathcal {J}}\\{} & {} \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\{} & {} \le \quad \;\varGamma ^{+}, \; j \in {\mathcal {J}}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varGamma ^{-} \le 0, \; \varGamma ^{+} \le 0,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\; x_{i}\ge 0, \;\;i \in {\mathcal {I}}. \end{aligned}$$

The center of the interval $[\varGamma ^{-},\varGamma ^{+}]$, is $\displaystyle \varGamma _{C}=\frac{\varGamma ^{-}+\varGamma ^{+}}{2}$. Thus using the existing approaches of Ishibuchi and Tanaka (1990); Sakawa and Nishizaki (1994); Sengupta and Pal (2000), (PI-5) is reduced to a bi-objective linear programming problem in the following way :

$$\begin{aligned} \begin{array}{lll} {\textbf {(PI-6)}}&{}&{}\displaystyle \min \left\{ \varGamma ^{-}\right\} , \; \min \left\{ \frac{ \varGamma ^{-}+\varGamma ^{+}}{2} \right\} \\ &{}&{} \text{ subject } \text{ to } \\ &{}&{} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right] \\ &{}&{}\le \varGamma ^{-},\;j\in {\mathcal {J}}\\ &{}&{}\displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\ &{}&{}\le \;\varGamma ^{+},\; j \in {\mathcal {J}}\\ &{}&{} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\;i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\ &{}&{} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\ &{}&{}\varGamma ^{-} \le 0, \; \varGamma ^{+} \le 0,\\ &{}&{}\displaystyle \sum _{i=1}^{m}x_{i}=1, \; x_{i}\ge 0, \; i\in {\mathcal {I}}. \end{array} \end{aligned}$$

which is equivalent to

$$\begin{aligned} {\textbf {(PI-7)}}{} & {} \displaystyle \min \left\{ \varGamma ^{-}\right\} , \; \min \left\{ \frac{\varGamma ^{-}}{2} \right\} +\min \left\{ \frac{\varGamma ^{+}}{2} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right] \\{} & {} \le \;\varGamma ^{-},\;j \in {\mathcal {J}}\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\{} & {} \le \quad \;\varGamma ^{+},\; j \in {\mathcal {J}}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varGamma ^{-} \le 0, \; \varGamma ^{+} \le 0,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\; x_{i}\ge 0,\;i \in {\mathcal {I}}. \end{aligned}$$

The problem (PI-7) is transformed into

$$\begin{aligned} {\textbf {(PI-8)}}{} & {} \displaystyle \min \left\{ \varGamma ^{-}\right\} , \; \min \left\{ \varGamma ^{+} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right] \\{} & {} \le \;\varGamma ^{-},\;j \in {\mathcal {J}}\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\{} & {} \le \;\varGamma ^{+},\; j \in {\mathcal {J}}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varGamma ^{-} \le 0, \; \varGamma ^{+} \le 0,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\; x_{i}\ge 0,\;i \in {\mathcal {I}}. \end{aligned}$$

which is further be written as :

$$\begin{aligned} {\textbf {(PI-9)}}{} & {} \displaystyle \min \left\{ \varGamma ^{-}+\varGamma ^{+} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa ) \ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right. \\{} & {} \quad \left. +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa ) \ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\{} & {} \le \;\varGamma ^{-}+\varGamma ^{+}, j \in {\mathcal {J}}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varGamma ^{-} \le 0, \; \varGamma ^{+} \le 0,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\; x_{i}\ge 0, \;\;i \in {\mathcal {I}}. \end{aligned}$$

Let ${\mathfrak {U}}=\varGamma ^{-}+\varGamma ^{+}$. Since, $\varGamma ^{-}\le 0$ and $\varGamma ^{+}\le 0$. Therefore, ${\mathfrak {U}}\le 0$.

Thus, (PI-9) is transformed into a linear programming problem

$$\begin{aligned} {\textbf {(PI-10)}}{} & {} \displaystyle \min \left\{ {\mathfrak {U}} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i} \left[ \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right. \\{} & {} \quad \left. +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right] \\{} & {} \quad \le \;{\mathfrak {U}}, j \in {\mathcal {J}}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} {\mathfrak {U}} \le 0,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\; x_{i}\ge 0, \;\;i \in {\mathcal {I}}. \end{aligned}$$

For $s_{0} \le s_{\xi _{\delta _{ij}}^{+}}<s_{t},\;s_{0} \le s_{\xi _{\delta _{ij}}^{-}}<s_{t}$ and $s_{0}<s_{\vartheta _{\delta _{ij}}^{-}}\le s_{t},\; \text{ and } s_{0}< s_{\vartheta _{\delta _{ij}}^{+}}\le s_{t}$ for all $i \in {\mathcal {I}}, \; j \in {\mathcal {J}}$, the optimal solution obtained for the linear programming problem (PI-10) is $(x^{\star },{\mathfrak {U}}^{\star })$.

Case II : When $s_{\xi _{\delta _{ij}}^{+}}=s_{t},\;s_{\xi _{\delta _{ij}}^{-}}=s_{t},$ $s_{\vartheta _{\delta _{ij}}^{-}}=s_{0},\; \text{ and } s_{\vartheta _{\delta _{ij}}^{+}}=s_{0},\; \;i \in {\mathcal {I}}, \; j \in {\mathcal {J}}$.

It is significant to take into account that whenever $\xi _{\delta _{ij}}^{+}=t, \; \vartheta _{\delta _{ij}}^{+}=0$ and $\xi _{\delta _{ij}}^{-}=t$ and $\vartheta _{\delta _{ij}}^{-}=0$, then $\displaystyle \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t} \right) \rightarrow -\infty$, $\displaystyle \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t} \right) \rightarrow -\infty$, $\displaystyle \ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t} \right) \rightarrow -\infty$ and $\displaystyle \ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t} \right) \rightarrow -\infty$. Hence, at such occurrences, problem (PI-10) becomes invalid. Thus, it is reformulated as the following nonlinear programming problem

$$\begin{aligned}{} & {} {\textbf {(PI-11)}}\\ \;{} & {} \displaystyle \min \left\{ \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varTheta }^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) ^{(1-\kappa )} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \prod _{i=1}^{m} \left[ \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{\kappa }\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{\kappa } \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{(1-\kappa )}\right] ^{x_{i}} \\{} & {} \quad \quad \le \quad \; \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varTheta }^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) ^{(1-\kappa )},\\{} & {} \quad \quad \text{ for } \text{ any } y\in S^{n}\\{} & {} {\xi _{\varTheta }^{-}},\;{\xi _{\varTheta }^{+}},\;{\vartheta _{\varTheta }^{-}},\;{\vartheta _{\varTheta }^{+}},\; {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\;i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\varTheta }^{+}+\vartheta _{\varTheta }^{+}\le t,\;0\le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}} \\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1, \; x_{i}\ge 0,\; i \in {\mathcal {I}}. \end{aligned}$$

Let ${\mathcal {V}}= \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) ^{\kappa }\left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) ^{(1-\kappa )}$.

Since $\kappa \in [0,1]$, $0 \le \displaystyle 1-\frac{\xi _{\varTheta }^{-}}{t}\le 1$, $0\le \displaystyle \frac{\xi _{\varTheta }^{+}}{t}\le 1$, $0 \le \displaystyle 1-\frac{\vartheta _{\varTheta }^{-}}{t}\le 1$ and $0\le \displaystyle 1-\frac{\vartheta _{\varTheta }^{+}}{t}\le 1$. Therefore, $0\le {\mathcal {V}}\le 1$.

Thus, (PI-11) is rewritten as :

$$\begin{aligned}{} & {} {\textbf {(PI-12)}}\\ \;{} & {} \displaystyle \min \left\{ {\mathcal {V}} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \prod _{i=1}^{m} \left( \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{\kappa } \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{(1-\kappa )}\right. \\{} & {} \left. \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{\kappa } \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{(1-\kappa )}\right) ^{x_{i}}\quad \le \quad {\mathcal {V}}, \quad \text{ for } \text{ any } y\in S^{n}\\{} & {} {\xi _{\delta _{ij}}^{-}},\; {\xi _{\delta _{ij}}^{+}},\; {\vartheta _{\delta _{ij}}^{-}},\; {\vartheta _{\delta _{ij}}^{+}}\in {[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+}\le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} 0\le {\mathcal {V}}\le 1,\\{} & {} \displaystyle \sum _{i=1}^{m}x_{i}=1,\;x_{i}\ge 0,\; i \in {\mathcal {I}}. \end{aligned}$$

The optimal solution of (PI-12) is $(x^{\star },{\mathcal {V}}^{\star })$. It is evident from (PI-10) and (PI-12), that ${\mathcal {V}}^{\star }=e^{{\mathfrak {U}}^{\star }}$, when $(x^{\star },{\mathfrak {U}}^{\star })$ exists as the optimal solutions of (PI-10).

3.3 Mathematical model for player II

Case I : If $s_{0}\le s_{\xi _{\varPsi }^{-}},\; s_{\xi _{\varPsi }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\;s_{\xi _{\delta _{ij}}^{+}}< s_{t}$ and $s_{0}<s_{\vartheta _{\varPsi }^{-}},\; s_{\vartheta _{\varPsi }^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}} ,\; s_{\vartheta _{\delta _{ij}}^{+}} \le s_{t},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}.$

For player II, the minimax strategy $y^{\star }$ and the minimum loss $\varPsi ^{\star }$ in (3.5) can be obtained by using (3.1) and Definitions 10 and 11. The nonlinear bi-objective interval-programming problem for player II is as follows :

$$\begin{aligned}{} & {} {\textbf {(PII-1)}}\\{} & {} \displaystyle \varPsi ^{\star }=\left\langle \min \left\{ \left[ s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}}\right] \right\} ,\;\max \left\{ \left[ s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}}\right] \right\} \right\rangle \\{} & {} \text{ subject } \text{ to } \\ \;{} & {} \displaystyle \left[ s_{ \left( t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) \right) },\right. \\{} & {} \; \left. s_{ \left( t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) \right) }\right] \\{} & {} \quad \le \; \left[ s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}}\right] , \; \text{ for } \text{ any } x\in S^{m}\\{} & {} \left[ s_{\left( t\prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{\left( t\prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \\{} & {} \quad \ge \quad \left[ s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}}\right] , \quad \quad \quad \quad \quad \text{ for } \text{ any } x\in S^{m}\\{} & {} s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}},\;s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\\{} & {} s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\;i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\varPsi }^{+}+\vartheta _{\varPsi }^{+}\le t,\; 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1, \;y_{j}\ge 0,\; j \in {\mathcal {J}}. \end{aligned}$$

It may be noted that

$$\begin{aligned}{} & {} \displaystyle \min \left\{ \left[ s_{\xi _{\varPsi }^{-}},s_{\xi _{\varPsi }^{+}}\right] \right\} \Leftrightarrow \max \left\{ \left[ s_{t-\xi _{\varPsi }^{+}},s_{t-\xi _{\varPsi }^{-}}\right] \right\} \\{} & {} \quad \Leftrightarrow \max \left\{ \left[ s_{\ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) },s_{\ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) }\right] \right\} ,\\&\quad&\displaystyle \max \left\{ \left[ s_{\vartheta _{\varPsi }^{-}},s_{\vartheta _{\varPsi }^{+}}\right] \right\} \\{} & {} \quad \Leftrightarrow \displaystyle \max \left\{ \left[ s_{\frac{\vartheta _{\varPsi }^{-}}{t}},s_{\frac{\vartheta _{\varPsi }^{+}}{t}}\right] \right\} \Leftrightarrow \max \left\{ \left[ s_{\ln \left( \frac{\vartheta _{\varPsi }^{-}}{t}\right) },s_{\ln \left( \frac{\vartheta _{\varPsi }^{+}}{t}\right) }\right] \right\} \end{aligned}$$

and

$$\begin{aligned}&\displaystyle \left[ s_{ \left( t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) \right) },s_{ \left( t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) \right) }\right] \\&\quad \le \quad \left[ s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}}\right] \\&\quad \Leftrightarrow \displaystyle \left[ s_{ \left( \prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) },s_{ \left( \prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) } \right] \\&\quad \ge \quad \left[ s_{\left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) },\;s_{\left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) }\right] \\&\quad \Leftrightarrow \displaystyle \left[ s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln {\left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) }\right) },s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln { \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) }\right) }\right] \\&\quad \ge \quad \left[ s_{\ln {\left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) }},\;s_{\ln {\left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) }}\right] , \\&\!\!\!\displaystyle \left[ s_{\left( t\prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{x_{i}y_{j}}\right) },s_{\left( t\prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{x_{i}y_{j}}\right) }\right] \\&\quad \ge \quad \left[ s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}}\right] \\&\quad \Leftrightarrow \displaystyle \left[ s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln {\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) }\right) },s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}{x_{i}y_{j}}\ln {\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) }\right) }\right] \\&\quad \ge \quad \left[ s_{\ln {\left( \frac{\vartheta _{\varPsi }^{-}}{t}\right) }},\;s_{\ln {\left( \frac{\vartheta _{\varPsi }^{+}}{t}\right) }}\right] \end{aligned}$$

Therefore, problem (PII-1) on operating logarithmic function gets reduced to :

$$\begin{aligned} {\textbf {(PII-2)}}{} & {} \displaystyle \max \left\{ \left[ s_{\ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) }\;, \;s_{\ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) }\right] \right\} ,\\{} & {} \quad \max \left\{ \left[ s_{\ln \left( \frac{\vartheta _ {\varPsi }^{-}}{t}\right) },\;s_{\ln \left( \frac{\vartheta _{\varPsi }^{+}}{t}\right) }\right] \right\} \\{} & {} \text{ subject } \text{ to } \\ \;{} & {} \displaystyle \left[ s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) \right) },\right. \\{} & {} \quad \left. \; s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) \right) } \right] \\{} & {} \quad \ge \quad \left[ s_{\ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) }, \; s_{\ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) }\; \right] ,\\{} & {} \quad \text{ for } \text{ any } x\in S^{m}\\{} & {} \displaystyle \left[ s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) },\;\right. \\{} & {} \quad \left. s_{\left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) } \right] \\{} & {} \quad \ge \quad \left[ s_{\ln \left( \frac{\vartheta _{\varPsi }^{-}}{t}\right) }, \; s_{\ln \left( \frac{\vartheta _{\varPsi }^{+}}{t}\right) } \right] \;,\\{} & {} \quad \text{ for } \text{ any } x\in S^{m}\\{} & {} \displaystyle s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}},\,s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}},\, s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\\{} & {} \quad \in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\varPsi }^{+}+\vartheta _{\varPsi }^{+}\le t,\; 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\\{} & {} \quad i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1, \; y_{j}\ge 0,\; j \in {\mathcal {J}}. \end{aligned}$$

Employing aggregation technique, the objective function of (PII-2) is transformed as:

$$\begin{aligned} \max \left\{ \left[ s_{\kappa \ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varPsi }^{-}}{t} \right) },\;s_{\kappa \ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varPsi }^{+}}{t} \right) }\right] \right\} \nonumber \\ \end{aligned}$$

(3.6)

where $\kappa \in [0,1]$ is the weight, which is suggested by the players of the game.

Similarly, aggregating the constraints in (PII-2) which gets reduced to:

$$\begin{aligned} \begin{aligned}{} & {} \displaystyle s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \right) }\\{} & {} \quad \ge \quad s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\varPsi }^{-}}{t}\right) \right) }\\{} & {} \displaystyle s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \right) }\\{} & {} \quad \ge \quad s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\varPsi }^{+}}{t}\right) \right) }\\ \end{aligned} \end{aligned}$$

(3.7)

Consequently, using Eqs. (3.6) and (3.7), (PII-2) is remodeled as:

$$\begin{aligned}{} & {} {\textbf {(PII-3)}}\\ {}{} & {} \max \left\{ \! \left[ \!s_{\kappa \ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\xi _{\varPsi }^{-}}{t} \right) },\;s_{\kappa \ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\xi _{\varPsi }^{+}}{t} \right) }\!\right] \!\right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \right) }\\{} & {} \quad \ge \quad s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\varPsi }^{-}}{t}\right) \right) }\;,\quad \text{ for } \text{ any } x\in S^{m}\\{} & {} \displaystyle s_{ \left( \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j}\left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \right) }\\{} & {} \quad \ge \quad s_{\left( \kappa \ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) +(1-\kappa )\ln \left( 1-\frac{\vartheta _{\varPsi }^{+}}{t}\right) \right) }\;,\quad \text{ for } \text{ any } x\in S^{m}\\{} & {} \displaystyle s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}},\;s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\\{} & {} \quad \in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\varPsi }^{+}+\vartheta _{\varPsi }^{+}\le t,\; 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1, \; y_{j}\ge 0,\; j \in {\mathcal {J}}. \end{aligned}$$

Thus, the objective function in (PII-3) is an interval-valued function.

For sake of convenience, let $\varOmega ^{-}=\displaystyle \kappa \ln \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varPsi }^{-}}{t}\right)$ and $\varOmega ^{+}=\displaystyle \kappa \ln \left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varPsi }^{+}}{t}\right)$. Then, $\varOmega ^{-} \le 0$ and $\varOmega ^{+}\le 0$. This is because, $\kappa \in [0,1]$ and $0\le \xi _{\varPsi }^{-},\;\xi _{\varPsi }^{+},\; \vartheta _{\varPsi }^{-},\; \vartheta _{\varPsi }^{+}\le t$, which imply $0 \displaystyle \le 1-\frac{\xi _{\varPsi }^{-}}{t}\le 1, \; 0\displaystyle \le 1-\frac{\xi _{\varPsi }^{+}}{t}\le 1,\; 0\le \displaystyle 1-\frac{\vartheta _{\varPsi }^{-}}{t}\le 1$ and $0\le \displaystyle 1-\frac{\vartheta _{\varPsi }^{+}}{t}\le 1$.

Therefore, the objective function in (PII-3), becomes $\max \left\{ \left[ s_{\varOmega ^{-}},\;s_{\varOmega ^{+}}\right] \right\}$, which can be equivalently expressed as $\max \left\{ \left[ \varOmega ^{-},\;\varOmega ^{+}\right] \right\}$.

Then the constraints in (PII-3) are transformed as :

$$\begin{aligned} \begin{aligned} \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \quad \ge \;\displaystyle \varOmega ^{-},\\ \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \quad \ge \;\displaystyle \varOmega ^{+}, \end{aligned} \end{aligned}$$

Consequently, (PII-3) can be re-framed as :

$$\begin{aligned} \begin{array}{lcl} {\textbf {(PII-4)}}&{}&{}\displaystyle \max \left\{ \left[ \varOmega ^{-},\;\varOmega ^{+} \right] \right\} \\ &{}&{}\text{ subject } \text{ to } \\ &{}&{}\displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \\ &{}&{}\quad \ge \;\varOmega ^{-}, \text{ for } \text{ any } x \in S^{m}\\ &{}&{}\displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}x_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\ &{}&{}\quad \ge \;\varOmega ^{+}, \text{ for } \text{ any } x\in S^{m}\\ &{}&{}\displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\ &{}&{}\displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\ &{}&{}\varOmega ^{-} \le 0, \; \varOmega ^{+} \le 0,\\ &{}&{}\displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0, \;j \in {\mathcal {J}}. \end{array} \end{aligned}$$

It is sufficient to analyze only the extreme points of the set $S^{m}$ in the constraints of (PII-4), as $S^{m}$ is a finite compact convex set.

Therefore, (PII-4) is transformed into the following linear programming problem :

$$\begin{aligned} {\textbf {(PII-5)}}{} & {} \displaystyle \max \left\{ \left[ \varOmega ^{-},\;\varOmega ^{+} \right] \right\} \\{} & {} \text{ subject } \text{ to }\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \quad \\{} & {} \ge \;\varOmega ^{-}\;,\; i \in {\mathcal {I}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\{} & {} \le \;\varOmega ^{+}\;, \; i \in {\mathcal {I}}\\{} & {} \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varOmega ^{-} \le 0, \; \varOmega ^{+} \le 0,\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0,\;j \in {\mathcal {J}}. \end{aligned}$$

The center of the interval $[\varOmega ^{-},\varOmega ^{+}]$ is $\displaystyle \varOmega _{C}=\frac{\varOmega ^{-}+\varOmega ^{+}}{2}$. Using existing approaches of Ishibuchi and Tanaka (1990); Sakawa and Nishizaki (1994); Sengupta and Pal (2000), (PII-5) is modified into a bi-objective linear programming problem as follows :

$$\begin{aligned} {\textbf {(PII-6)}}{} & {} \displaystyle \max \left\{ \varOmega ^{-}\right\} , \; \max \left\{ \frac{ \varOmega ^{-}+\varOmega ^{+}}{2} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \\{} & {} \ge \;\varOmega ^{-}\;,\; i \in {\mathcal {I}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\{} & {} \ge \varOmega ^{+}\;,\; i \in {\mathcal {I}}\\{} & {} \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varOmega ^{-} \le 0, \; \varOmega ^{+} \le 0,\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0, j \in {\mathcal {J}}. \end{aligned}$$

Further, the problem (PII-6) is analogous to the bi-objective linear programming problem:

$$\begin{aligned} {\textbf {(PII-7)}}{} & {} \displaystyle \max \left\{ \varOmega ^{-}\right\} , \; \max \left\{ \frac{\varOmega ^{-}}{2} \right\} +\max \left\{ \frac{\varOmega ^{+}}{2} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right] \\{} & {} \ge \varOmega ^{-}\;, \;i \in {\mathcal {I}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{i} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\{} & {} \ge \varOmega ^{+}\;, \; i \in {\mathcal {I}}\\{} & {} \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varOmega ^{-} \le 0, \; \varOmega ^{+} \le 0,\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0, \;j \in {\mathcal {J}}. \end{aligned}$$

The above problem is equivalent to :

$$\begin{aligned} {\textbf {(PII-8)}}{} & {} \;\displaystyle \max \left\{ \varOmega ^{-}\right\} , \; \max \left\{ \varOmega ^{+} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) \right. \\{} & {} \left. +(1-\kappa ) \ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \\{} & {} \ge \quad \;\varOmega ^{-}\;,\;i \in {\mathcal {I}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\{} & {} \ge \quad \;\varOmega ^{+}\;, \; i \in {\mathcal {I}}\\{} & {} \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \varOmega ^{-} \le 0, \; \varOmega ^{+} \le 0,\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0, \;j \in {\mathcal {J}}. \end{aligned}$$

On aggregating the constraints in (PII-8), we get the following linear programming problem :

$$\begin{aligned} {\textbf {(PII-9)}}{} & {} \quad \displaystyle \max \left\{ \varOmega ^{-}+\varOmega ^{+} \right\} \\{} & {} \quad \text{ subject } \text{ to }\\{} & {} \quad \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right. \nonumber \\{} & {} \quad +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \ge \;\varOmega ^{-}+\varOmega ^{+},\; i \in {\mathcal {I}}\\{} & {} \quad \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \quad \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \quad \varOmega ^{-} \le 0, \; \varOmega ^{+} \le 0,\\{} & {} \quad \displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0, \;j \in {\mathcal {J}}. \end{aligned}$$

Let ${\mathfrak {F}}=\varOmega ^{-}+\varOmega ^{+}$. Since, $\varOmega ^{-}\le 0$ and $\varOmega ^{+}\le 0$, therefore ${\mathfrak {F}}\le 0$.

Thus, (PII-9) is remodeled into a linear programming problem given below :

$$\begin{aligned} {\textbf {(PII-10)}}{} & {} \quad \displaystyle \max \left\{ {\mathfrak {F}} \right\} \\{} & {} \quad \text{ subject } \text{ to } \\{} & {} \quad \displaystyle \sum _{j=1}^{n}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right. \\{} & {} \quad \left. +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \ge \;{\mathfrak {F}},\; i \in {\mathcal {I}}\\{} & {} \quad \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \quad \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}\\{} & {} \quad {\mathfrak {F}} \le 0,\\{} & {} \quad \displaystyle \sum _{j=1}^{n}y_{j}=1,\; y_{j}\ge 0, \;j \in {\mathcal {J}}. \end{aligned}$$

For any specified weight $\kappa \in [0,1]$, as stated in Theorem 4 (proved later), Definitions 10 and 11, a minimax strategy $y^{\star }$ for player II, could be obtained using (PII-10). Therefore, $(y^{\star },{\mathfrak {F}}^{\star })$ is the optimal solution of the linear programming problem (PII-10).

Case II : If $s_{\xi _{\delta _{ij}}^{+}}=s_{t},\;s_{\xi _{\delta _{ij}}^{-}}=s_{t},$ $s_{\vartheta _{\delta _{ij}}^{-}}=s_{0},\; \text{ and } s_{\vartheta _{\delta _{ij}}^{+}}=s_{0},\; i \in {\mathcal {I}}, \; j \in {\mathcal {J}}$.

In this particular case, it is significant to take into account that whenever $\xi _{\delta _{ij}}^{-}=t$, $\xi _{\delta _{ij}}^{+}=t, \; \vartheta _{\delta _{ij}}^{-}=0$, and $\vartheta _{\delta _{ij}}^{+}=0$, then $\displaystyle \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t} \right) \rightarrow -\infty$, $\displaystyle \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t} \right) \rightarrow -\infty$ and $\displaystyle \ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t} \right) \rightarrow -\infty$, $\displaystyle \ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t} \right) \rightarrow -\infty$. Therefore, at such occurrences, the (PII-10) becomes invalid. Thus, it is remodeled as the following nonlinear programming problems :

$$\begin{aligned}{} & {} {\textbf {(PII-11)}}\\{} & {} \displaystyle \max \left\{ \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varPsi }^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varPsi }^{+}}{t}\right) ^{(1-\kappa )} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \prod _{j=1}^{n} \left[ \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{\kappa }\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{\kappa } \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{(1-\kappa )}\right] ^{y_{j}}\\{} & {} \ge \; \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) ^{\kappa }\left( \frac{\vartheta _{\varPsi }^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varPsi }^{+}}{t}\right) ^{(1-\kappa )},\\{} & {} \quad \quad \quad \text{ for } \text{ any } x\in S^{m}\\{} & {} s_{\xi _{\varPsi }^{-}},\;s_{\xi _{\varPsi }^{+}},\;s_{\vartheta _{\varPsi }^{-}},\;s_{\vartheta _{\varPsi }^{+}},\; s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\\{} & {} i \in {\mathcal {I}},\; j \in {\mathcal {J}} \\{} & {} 0 \le \xi _{\varPsi }^{+}+\vartheta _{\varPsi }^{+}\le t,\; 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\;\\{} & {} i \in {\mathcal {I}},\; j \in {\mathcal {J}}\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1, \; y_{j}\ge 0,\;j \in {\mathcal {J}}. \end{aligned}$$

Let $\displaystyle {\mathcal {W}}= \left( 1-\frac{\xi _{\varPsi }^{+}}{t}\right) ^{\kappa }\left( \frac{\vartheta _{\varPsi }^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\varPsi }^{-}}{t}\right) ^{\kappa }\left( \frac{ \vartheta _{\varPsi }^{+}}{t}\right) ^{(1-\kappa )}$. Since $\kappa \in [0,1]$, $0 \le \displaystyle 1-\frac{\xi _{\varPsi }^{-}}{t} \le 1$, $0\le \displaystyle \frac{ \vartheta _{\varPsi }^{+}}{t}\le 1$, $0\le \displaystyle 1-\frac{\xi _{\varPsi }^{-}}{t}\le 1$ and $0 \le \displaystyle \frac{ \vartheta _{\varPsi }^{+}}{t}\le 1$. Therefore, $0\le {\mathcal {W}}\le 1$.

Consequently, (PII-11) is transformed as :

$$\begin{aligned}{} & {} {\textbf {(PII-12)}}\\{} & {} \displaystyle \max \left\{ {\mathcal {W}} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \prod _{j=1}^{n} \left[ \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{\kappa }\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{(1-\kappa )}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{\kappa } \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{(1-\kappa )}\right] ^{y_{j}}\\{} & {} \ge \quad {\mathcal {W}}, \quad \text{ for } \text{ any } x\in S^{m}\\{} & {} \displaystyle s_{\xi _{\delta _{ij}}^{-}},\; s_{\xi _{\delta _{ij}}^{+}},\; s_{\vartheta _{\delta _{ij}}^{-}},\; s_{\vartheta _{\delta _{ij}}^{+}}\in {\mathbb {S}}_{[0,t]},\; \; i \in {\mathcal {I}},\; j \in {\mathcal {J}}\\{} & {} \displaystyle 0 \le \xi _{\delta _{ij}}^{+}+\vartheta _{\delta _{ij}}^{+} \le t,\; \; i \in {\mathcal {I}},\; j \in {\mathcal {J}}\\{} & {} 0\le {\mathcal {W}}\le 1,\\{} & {} \displaystyle \sum _{j=1}^{n}y_{j}=1,\;y_{j}\ge 0,\; \;j \in {\mathcal {J}}. \end{aligned}$$

The optimal solution for ((PII-12) is $(y^{\star },{\mathcal {W}}^{\star })$. Since, ${\mathcal {W}}^{\star }=e^{{\mathfrak {F}}^{\star }}$. Therefore, $(y^{\star },{\mathfrak {F}}^{\star })$ is the optimal solution of the linear programming problem (PII-10).

Since, (PI-10) and (PII-10) are dual of each other, therefore ${\mathfrak {U}}^{\star }={\mathfrak {F}}^{\star }$. Hence, ${\mathcal {V}}^{\star }= {\mathcal {W}}^{\star }$ because ${\mathcal {V}}^{\star }=e^{{\mathfrak {U}}^{\star }}$ and ${\mathcal {W}}^{\star }=e^{{\mathfrak {F}}^{\star }}$. Figure 1 shows the solution algorithm for matrix games involving LIVIFNs in the payoffs (considering both the cases) for two players.

Fig. 1

Algorithm for resolving LIVIFMG

Theorem 1

Let $\varTheta ^{\star }$ be the maximin for player I and $\varPsi ^{\star }$ be the minimax for player II, respectively. Then $\varTheta ^{\star }$ and $\varPsi ^{\star }$ are LIVIFNs, such that $\varTheta ^{\star } \le \varPsi ^{\star }$.

Proof

From (3.1), $\textrm{E}_{{\tilde{A}}}(x,y)= \left\langle \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] ,\left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle$ is an LIVIFN.

where, $s_{\xi _{\delta _{xy}}^{-}},\; s_{\xi _{\delta _{xy}}^{+}},\; s_{\vartheta _{\delta _{xy}}^{-}},\; s_{\vartheta _{\delta _{xy}}^{+}} \in {\mathbb {S}}_{[0,t]}$, such that $s_{\xi _{\delta _{xy}}^{+}}+s_{\vartheta _{\delta _{xy}}^{+}} \le s_{t}$.

Therefore,

$$\begin{aligned} 0\le \xi _{\delta _{xy}}^{+}+\vartheta _{\delta _{xy}}^{+}\le t. \end{aligned}$$

(3.8)

$$\begin{aligned} \text{ and }\displaystyle \max _{x \in S^{m}}\min _{y \in S^{n}}\left\{ s_{\xi _{\delta _{xy}}^{+}} \right\} ,\;\min _{x \in S^{m}}\max _{y \in S^{n}}\left\{ s_{ \vartheta _{\delta _{xy}}^{+}} \right\} \; \in {\mathbb {S}}_{[0,t]}. \end{aligned}$$

(3.9)

From (3.8), we obtain

$$\begin{aligned} 0\le&\quad \displaystyle \xi _{\delta _{xy}}^{+}+\min _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le \xi _{\delta _{xy}}^{+}+\max _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le t \end{aligned}$$

and

$$\begin{aligned} 0\le&\quad \displaystyle \min _{y \in S^{n}}\xi _{\delta _{xy}}^{+}+\min _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le \xi _{\delta _{xy}}^{+}+\max _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le t \end{aligned}$$

It gives,

$$\begin{aligned} 0\le&\quad \displaystyle \min _{y \in S^{n}}\left\{ \xi _{\delta _{xy}}^{+}\right\} +\min _{x \in S^{m}}\min _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le \min _{y \in S^{n}}\left\{ \xi _{\delta _{xy}}^{+}\right\} \\&\quad +\min _{x \in S^{m}}\max _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le \xi _{\delta _{xy}}^{+}+\min _{y \in S^{n}}\max _{y\in S^{n}}\left\{ \vartheta _{\delta _{xy}}^{+} \right\} \le t \end{aligned}$$

Therefore,

$$\begin{aligned} 0\le&\quad \displaystyle \max _{x\in S^{m}}\min _{y \in S^{n}}\left\{ \xi _{\delta _{xy}}^{+}\right\} +\min _{x \in S^{m}}\min _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le \max _{x\in S^{m}}\min _{y \in S^{n}}\left\{ \xi _{\delta _{xy}}^{+}\right\} \nonumber \\&\quad +\min _{x \in S^{m}}\max _{y \in S^{n}} \left\{ \vartheta _{\delta _{xy}}^{+}\right\} \le \max _{x\in S^{m}}\left\{ \xi _{\delta _{xy}}^{+}\right\} +\min _{y \in S^{n}}\max _{y\in S^{n}}\left\{ \vartheta _{\delta _{xy}}^{+} \right\} \le t \end{aligned}$$

(3.10)

i.e.,

$$\begin{aligned} 0\le&\quad \displaystyle \max _{x\in S^{m}} \min _{y\in S^{n}}\left\{ \xi _{\delta _{xy}}^{+} \right\} + \min _{x\in S^{m}}\max _{y\in S^{n}}\left\{ \vartheta _{\delta _{xy}}^{+} \right\} \le \;t \end{aligned}$$

(3.11)

Thus, from (3.4), (3.8) and (3.11), we get $0 \le \xi _{\varTheta ^{\star }}^{+}+\vartheta _{\varTheta ^{\star }}^{+}\le t$, where $s_{\xi _{\varTheta ^{\star }}^{+}},\; s_{\vartheta _{\varTheta ^{\star }}^{+}}\in {\mathbb {S}}_{[0,t]}$. Thus, $\varTheta ^{\star }$ is an LIVIFN.

Likewise, $\vartheta ^{\star }$ can be established as LIVIFN.

For any $x\in S^{m}$ and $y\in S^{n}$:

$$\begin{aligned} \displaystyle \min _{y\in S^{n}}\left\{ s_{\xi _{\delta _{xy}}^{-}} \right\}&\le \displaystyle \quad s_{\xi _{\delta _{xy}}^{-}} \; \le \quad \max _{x\in S^{m}}\left\{ s_{\xi _{\delta _{xy}}^{-}}\right\} \end{aligned}$$

Hence,

$$\begin{aligned} \displaystyle \min _{y\in S^{n}}\left\{ s_{\xi _{\delta _{xy}}^{-}}\right\} \quad \le \; s_{\xi _{\delta _{xy}}^{-}}&\le \quad \min _{y\in S^{n}}\max _{x\in S^{m}}\left\{ s_{\xi _{\delta _{xy}}^{-}} \right\} \end{aligned}$$

Subsequently,

$$\begin{aligned} \displaystyle \max _{x\in S^{m}} \min _{y\in S^{n}}\left\{ s_{\xi _{\delta _{xy}}^{-}}\right\}&\le \quad \min _{y\in S^{n}}\max _{x\in S^{m}}\left\{ s_{\xi _{\delta _{xy}}^{-}}\right\} \end{aligned}$$

(3.12)

Similarly, the following can also be obtained:

$$\begin{aligned} \displaystyle \max _{x\in S^{m}} \min _{y\in S^{n}}\left\{ s_{\xi _{\delta _{xy}}^{+}}\right\}&\le \quad \min _{y\in S^{n}}\max _{x\in S^{m}}\left\{ s_{\xi _{\delta _{xy}}^{+}}\right\} \end{aligned}$$

(3.13)

Combining (3.12) and (3.13), we obtain that

$$\begin{aligned} \begin{aligned} \displaystyle \max _{x\in S^{m}} \min _{y\in S^{n}}\Bigg \{\left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \Bigg \}&\le \min _{y\in S^{n}}\max _{x\in S^{m}}\Bigg \{\left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \Bigg \}. \end{aligned} \end{aligned}$$

(3.14)

Similarly, for any $x\in S^{m}$ and $y\in S^{n}$

$$\begin{aligned} \displaystyle \min _{x\in S^{m}}\left\{ s_{\vartheta _{\delta _{xy}}^{-}}\right\}&\le s_{\vartheta _{\delta _{xy}}^{-}} \le \max _{y\in S^{n}}\left\{ s_{\vartheta _{\delta _{xy}}^{-}}\right\} \end{aligned}$$

Hence,

$$\begin{aligned} \displaystyle \max _{y\in S^{n}}\min _{x\in S^{m}}\left\{ s_{\vartheta _{\delta _{xy}}^{-}}\right\}&\le \max _{y\in S^{n}}\left\{ s_{\vartheta _{\delta _{xy}}^{-}}\right\} \end{aligned}$$

and therefore,

$$\begin{aligned} \displaystyle \max _{y\in S^{n}}\min _{x\in S^{m}}\left\{ s_{\vartheta _{\delta _{xy}}^{-}}\right\}&\le \min _{x\in S^{m}} \max _{y\in S^{n}}\left\{ s_{\vartheta _{\delta _{xy}}^{-}}\right\} \end{aligned}$$

(3.15)

Also, we can establish that

$$\begin{aligned} \displaystyle \max _{y\in S^{n}}\min _{x\in S^{m}}\left\{ s_{\vartheta _{\delta _{xy}}^{+}}\right\} \le \min _{x\in S^{m}} \max _{y\in S^{n}}\left\{ s_{\vartheta _{\delta _{xy}}^{+}}\right\} \end{aligned}$$

(3.16)

Therefore, combining (3.15) and (3.16), we get

$$\begin{aligned} \displaystyle \max _{y\in S^{n}}\min _{x\in S^{m}}\Bigg \{\left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}}\right] \Bigg \}\quad \le \quad \min _{x\in S^{m}} \max _{y\in S^{n}}\Bigg \{\left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}} \right] \Bigg \} \end{aligned}$$

(3.17)

Now, using (3.14), (3.17) and Definition 7, we get

$$\begin{aligned}&\displaystyle \max _{x\in S^{m}} \min _{y\in S^{n}}\Bigg \{ \left\langle \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] , \left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \Bigg \} \\&\quad \le \min _{y\in S^{n}}\max _{x\in S^{m}}\Bigg \{\left\langle \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] , \left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\rangle \Bigg \}. \end{aligned}$$

Therefore, $\varTheta ^{\star } \le \varPsi ^{\star }$. $\square$

Theorem 2

For specific $\kappa \in [0,1]$, the matrix game LIVIFMG involving payoffs characterized by LIVIFNs always possess a solution $\left( x^{\star },y^{\star }, x^{\star T}{\tilde{A}} y^{\star }\right)$.

Proof

For any $\kappa \in [0,1]$ be a given weight. Then, it is evident that (PI-10) and (PII-10) forms a pair of primal-dual linear programming problems equivalent to the matrix game having payoffs matrix as:

$$\begin{aligned} \begin{aligned}&\displaystyle \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right. \\&\left. \quad +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa ) \ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) _{m \times n}, \end{aligned} \end{aligned}$$

Following the minimax theorem for matrix games Owen (1982), (PI-10) and (PII-10) will always have optimal solutions. Here, $(x^{\star },{\mathfrak {U}}^{\star })$ and $(y^{\star },{\mathfrak {F}}^{\star })$ are the optimal solution of (PI-10) and (PII-10), respectively, where ${\mathfrak {U}}^{\star }={\mathfrak {F}}^{\star }$. Hence, the matrix game LIVIFMG having payoff matrix ${\tilde{A}}$ characterized by LIVIFNs always possess a solution $\left( x^{\star },y^{\star }, x^{\star T}{\tilde{A}} y^{\star }\right)$, for specified weight $\kappa \in [0,1].$ $\square$

For each $\kappa \in [0,1]$, ${\mathfrak {U}}$ and ${\mathfrak {F}}$ are defined in terms of the weight $\kappa$ and retain the following property:

Theorem 3

${\mathfrak {U}}$ and ${\mathfrak {F}}$ are monotonically non-decreasing functions of $\kappa \in [0,1]$.

Proof

From problem (PI-10)

${\mathfrak {U}}=\varGamma ^{-}+\varGamma ^{+} = \displaystyle \kappa \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{ \vartheta _{\varTheta }^{-}}{t}\right) + \kappa \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right)$

where $\displaystyle 0 \le 1-\frac{\xi _{\varTheta }^{+}}{t}\le 1$, $0\le \displaystyle \frac{ \vartheta _{\varTheta }^{-}}{t}\le 1$, $0 \le \displaystyle 1-\frac{\xi _{\varTheta }^{-}}{t}\le 1$, $0\le \displaystyle \frac{ \vartheta _{\varTheta }^{+}}{t}\le 1$ and $t>0$.

Since $\displaystyle 0\le \frac{\xi _{\varTheta }^{-}}{t}\le \frac{\xi _{\varTheta }^{+}}{t}\le 1$, $\text{ therefore } \displaystyle 0 \le 1- \frac{\xi _{\varTheta }^{+}}{t}\le 1-\frac{\xi _{\varTheta }^{-}}{t}\le 1,$ which further implies that $\displaystyle \ln \left( 1- \frac{\xi _{\varTheta }^{+}}{t}\right) \le \ln \left( 1-\frac{\xi _{\varTheta }^{-}}{t}\right) \le 0$.

Also, $\displaystyle 0 \le \frac{ \vartheta _{\varTheta }^{-}}{t}\le \frac{ \vartheta _{\varTheta }^{+}}{t}\le 1$, implies $\displaystyle \ln \left( \frac{ \vartheta _{\varTheta }^{-}}{t}\right) \le \ln \left( \frac{\vartheta _{\varTheta }^{+}}{t}\right) \le 0.$

Now,

$$\begin{aligned} \frac{\partial {\mathfrak {U}}}{\partial \kappa }&=\ln \left( 1- \frac{\xi _{\varTheta }^{+}}{t}\right) - \ln \left( \frac{\vartheta _{\varTheta }^{-}}{t}\right) + \ln \left( 1- \frac{\xi _{\varTheta }^{-}}{t}\right) -\ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) \\&\ge 2\ln \left( 1- \frac{\xi _{\varTheta }^{+}}{t}\right) - 2\ln \left( \frac{ \vartheta _{\varTheta }^{+}}{t}\right) \end{aligned}$$

Here, $0 \le \xi _{\varTheta }^{+}+\vartheta _{\varTheta }^{+}\le t$, which implies that $\displaystyle 0 \le \frac{\xi _{\varTheta }^{+}}{t}+\frac{\vartheta _{\varTheta }^{+}}{t}\le 1$ and hence $\displaystyle 1-\frac{\xi _{\varTheta }^{+}}{t} \ge \frac{\vartheta _{\varTheta }^{+}}{t}$. Thus, $\displaystyle \ln \left( 1-\frac{\xi _{\varTheta }^{+}}{t} \right) \ge \ln \left( \frac{\vartheta _{\varTheta }^{+}}{t}\right)$. Thus, $\displaystyle \frac{\partial {\mathfrak {U}}}{\partial \kappa }\ge 0$, except for $\displaystyle \frac{\vartheta _{\varTheta }^{+}}{t}=0$.

Hence, ${\mathfrak {U}}$ is monotonically non-decreasing function for each $\kappa \in [0,1]$.

Analogously, ${\mathfrak {F}}$ can also be proved a monotonically non-decreasing function for $\kappa \in [0,1]$. $\square$

Finally, a well-defined relationship between optimal solutions of (PI-10) and (PII-10) and the solution of the matrix game LIVIFMG having payoffs characterized by LIVIFNs ${\tilde{A}}$, are explained as:

Theorem 4

Suppose $(x^{\star },{\mathfrak {U}}^{\star })$ and $(y^{\star },{\mathfrak {F}}^{\star })$ being optimal solutions of (PI-10) and (PII-10) with $0<\kappa <1$, respectively. Then $(x^{\star },\varTheta ^{\star })$ and $(y^{\star },\varPsi ^{\star })$ are the Pareto optimal solutions of (PI-1) and (PII-1), where

$$\begin{aligned} \varTheta ^{\star }=&\displaystyle \left\langle \max _{x\in S^{m}}\min _{y\in S^{n}}\left\{ \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \right\} ,\min _{x \in S^{m}}\max _{y\in S^{n}}\left\{ \left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\} \right\rangle \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \varPsi ^{\star }=&\displaystyle \left\langle \min _{y \in S^{n}}\max _{x\in S^{m}}\left\{ \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \right\} ,\;\;\max _{y \in S^{n}}\min _{x\in S^{m}}\left\{ \left[ s_{\vartheta _{\delta _{xy}}^{-}},\;s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\} \right\rangle \end{aligned} \end{aligned}$$

Proof

Assuming that $(x^{\star },\varTheta ^{\star })$ is not a Pareto optimal solution for (PI-1). Then there exists a feasible solution $({\hat{x}},{\hat{\varTheta }})$, for ${\hat{x}}\in S^{m}$ and ${\hat{\varTheta }}=\left\langle \left[ s_{\xi _{{\hat{\varTheta }}}^{-}},\;s_{\xi _{{\hat{\varTheta }}}^{+}} \right] ,\;\left[ s_{\vartheta _{{\hat{\varTheta }}}^{-}},\;s_{\vartheta _{{\hat{\varTheta }}}^{+}}\right] \right\rangle$ such that

$$\begin{aligned} \begin{aligned} \displaystyle s_{ \left( t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m}\left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) ^{{\hat{x}}_{i}y_{j}}\right) \right) }\quad \ge \quad s_{\xi _{{\hat{\varTheta }}}^{-}}\;,&\text{ for } \text{ any } y\in S^{n}\\ \displaystyle s_{ \left( t\left( 1-\prod _{j=1}^{n} \prod _{i=1}^{m} \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) ^{{\hat{x}}_{i}y_{j}}\right) \right) } \quad \ge \quad s_{\xi _{{\hat{\varTheta }}}^{+}}\;,&\text{ for } \text{ any } y\in S^{n}\\ \displaystyle s_{\left( t\prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) ^{{\hat{x}}_{i}y_{j}}\right) } \quad \le \quad s_{\vartheta _{{\hat{\varTheta }}}^{-}}\;,&\text{ for } \text{ any } y\in S^{n}\\ \displaystyle s_{\left( t\prod _{j=1}^{n} \prod _{i=1}^{m}\left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) ^{{\hat{x}}_{i}y_{j}}\right) } \quad \le \quad s_{\vartheta _{{\hat{\varTheta }}}^{+}}\;,&\text{ for } \text{ any } y\in S^{n}\\ s_{\xi _{{\hat{\varTheta }}}^{-}},\;s_{\xi _{{\hat{\varTheta }}}^{+}},\;s_{\vartheta _{{\hat{\varTheta }}}^{-}},\;s_{\vartheta _{{\hat{\varTheta }}}^{+}}\in {\mathbb {S}}_{[0,t]},&\\ 0 \le \xi _{{\hat{\varTheta }}}^{+}+{\vartheta }_{{\hat{\varTheta }}}^{+}\le t\\ \displaystyle \sum _{i=1}^{m}{\hat{x}}_{i}=1, \; {\hat{x}}_{i}\ge 0,\;i \in {\mathcal {I}}. \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\hat{\varTheta }}= & {} \left\langle \min _{y\in S^{n}}\left\{ \left[ s_{\xi _{\delta _{xy}}^{-}},\;s_{\xi _{\delta _{xy}}^{+}}\right] \right\} ,\max _{y\in S^{n}}\left\{ \left[ s_{\vartheta _{\delta _{xy}}^{-}},s_{\vartheta _{\delta _{xy}}^{+}}\right] \right\} \right\rangle \\= & {} \left\langle \left[ s_{\xi _{{\hat{\varTheta }}}^{-}},s_{\xi _{{\hat{\varTheta }}}^{+}}\right] ,\left[ s_{\vartheta _{{\hat{\varTheta }}}^{-}},s_{\vartheta _{{\hat{\varTheta }}}^{+}}\right] \right\rangle \end{aligned}$$

Also, $[s_{\xi _{{\hat{\varTheta }}}^{-}},\;s_{\xi _{{\hat{\varTheta }}}^{+}}]\ge [s_{\xi _{\varTheta ^{\star }}^{-}},\;s_{\xi _{\varTheta ^{\star }}^{+}}]$ and $[s_{\vartheta _{{\hat{\varTheta }}}^{-}},\;s_{\vartheta _{{\hat{\varTheta }}}^{+}}] \le [s_{\vartheta _{\varTheta ^{\star }}^{-}}, \; s_{\vartheta _{\varTheta ^{\star }}^{+}}]$, where either of the two relations can be a strict inequality.

Using ordering property of LTS and further aggregation of the above set of inequalities for $0<\kappa <1$ yields :

$$\begin{aligned}{} & {} \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}{\hat{x}}_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \nonumber \\{} & {} \le \;\kappa \ln \left( 1-\frac{\xi _{{\hat{\varTheta }}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{{\hat{\varTheta }}}^{-}}{t}\right) , \nonumber \\{} & {} \quad \text{ for } \text{ any } y\in S^{n} \nonumber \\{} & {} \displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m}{\hat{x}}_{i}y_{j} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \nonumber \\{} & {} \quad \le \;\kappa \ln \left( 1-\frac{\xi _{{\hat{\varTheta }}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{{\hat{\varTheta }}}^{+}}{t}\right) , \nonumber \\{} & {} \quad \text{ for } \text{ any } y\in S^{n} \nonumber \\{} & {} s_{\xi _{{\hat{\varTheta }}}^{-}},\;s_{\xi _{{\hat{\varTheta }}}^{+}},\;s_{\vartheta _{{\hat{\varTheta }}}^{-}},\;s_{\vartheta _{{\hat{\varTheta }}}^{+}} \in {\mathbb {S}}_{[0,t]},\; \nonumber \\{} & {} 0 \le {\xi _{{\hat{\varTheta }}}^{+}}+{\vartheta _{{\hat{\varTheta }}}^{+}}\le t \nonumber \\{} & {} \displaystyle \sum _{i=1}^{m}{\hat{x}}_{i}=1, \;{\hat{x}}_{i}\ge 0,\; \quad \in {\mathcal {I}}. \end{aligned}$$

(3.18)

Furthermore, R.H.S. of (3.18) implies the following relations

$$\begin{aligned} \left. \begin{aligned}&\kappa \ln \left( 1-\frac{\xi _{{\hat{\varTheta }}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{{\hat{\varTheta }}}^{-}}{t}\right) \quad \le \quad \kappa \ln \left( 1-\frac{\xi _{\varTheta ^{\star }}^{+}}{t}\right) \\&\quad +(1-\kappa )\ln \left( \frac{\vartheta _{\varTheta ^{\star }}^{-}}{t}\right) \\&\kappa \ln \left( 1-\frac{\xi _{{\hat{\varTheta }}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{{\hat{\varTheta }}}^{+}}{t}\right) \\&\quad \quad \le \quad \kappa \ln \left( 1-\frac{\xi _{\varTheta ^{\star }}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\varTheta ^{\star }}^{+}}{t}\right) \end{aligned} \right\} \nonumber \\ \end{aligned}$$

(3.19)

Let ${\hat{\varGamma }}^{-}=\displaystyle \kappa \ln \left( 1-\frac{\xi _{{\hat{\varTheta }}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{ \vartheta _{{\hat{\varTheta }}}^{-}}{t}\right)$ and ${\hat{\varGamma }}^{+}= \displaystyle \kappa \ln \left( 1-\frac{\xi _{{\hat{\varTheta }}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{ \vartheta ^{+}_{{\hat{\varTheta }}}}{t}\right)$.

From (3.19), we get

$$\begin{aligned} {\hat{\varGamma }}^{-} \le {\varGamma ^{-}}^{\star } \text{ and } {\hat{\varGamma }}^{+} \le {\varGamma ^{+}}^{\star }. \end{aligned}$$

(3.20)

where one of these relations can be a strict inequality.

Therefore,

$$\begin{aligned} {\hat{\varGamma }}^{-} + {\hat{\varGamma }}^{+}\le \varGamma ^{-\star } + \varGamma ^{+\star } \text{ or } \hat{{\mathfrak {U}}} \le {\mathfrak {U}}^{\star }. \end{aligned}$$

(3.21)

Also, $S^{n}$ being a finite compact convex set, it is sufficient to take into account only the extreme points of the set $S^{n}$. Thus, the constraints (3.18) can be remodeled as:

$$\begin{aligned} \begin{aligned}&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right) \\&\quad \quad \le \quad \;{\hat{\varGamma }}^{-}\;, \text{ for } \text{ any } j \in {\mathcal {J}}\\&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\&\quad \quad \le \quad \;{\hat{\varGamma }}^{+}, \text{ for } \text{ any } j \in {\mathcal {J}}\\&{\hat{\varGamma }}^{-}\le 0, \; {\hat{\varGamma }}^{+} \le 0, \\&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i}=1,\; {\hat{x}}_{i}\ge 0,\; , \;i \in {\mathcal {I}}. \end{aligned} \end{aligned}$$

Further the above constraints are reformulated as :

$$\begin{aligned} \left. \begin{aligned}&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) \right. \\&\quad \left. +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \le \;{\hat{\varGamma }}^{-}+{\hat{\varGamma }}^{+}, \text{ for } \text{ any } j \in {\mathcal {J}}\\&{\hat{\varGamma }}^{-}\le 0, \; {\hat{\varGamma }}^{+} \le 0, \\&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i}=1,\; {\hat{x}}_{i}\ge 0,\; , \;i \in {\mathcal {I}}. \end{aligned} \right\} \nonumber \\ \end{aligned}$$

(3.22)

Defining $\hat{{\mathfrak {U}}}={\hat{\varGamma }}^{-}+{\hat{\varGamma }}^{+}$. Then, (3.22) is transformedas follows:

$$\begin{aligned} \left. \begin{aligned}&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i} \left( \kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{+}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{-}}{t}\right) \right. \\&\quad \left. +\kappa \ln \left( 1-\frac{\xi _{\delta _{ij}}^{-}}{t}\right) +(1-\kappa )\ln \left( \frac{\vartheta _{\delta _{ij}}^{+}}{t}\right) \right) \\&\quad \le \;\hat{{\mathfrak {U}}}, \text{ for } \text{ any } j \in {\mathcal {J}} \\&\hat{{\mathfrak {U}}} \le 0,\\&\displaystyle \sum _{i=1}^{m}{\hat{x}}_{i}=1,\; {\hat{x}}_{i}\ge 0,\; , \;i \in {\mathcal {I}}. \end{aligned} \right\} \end{aligned}$$

Therefore, $({\hat{x}},\hat{{\mathfrak {U}}})$ is a feasible solution of (PI-10).

Also, $\hat{{\mathfrak {U}}} \le {\mathfrak {U}}^{\star }$ from (3.21), which is contrary to the statement $(x^{\star },{\mathfrak {U}}^{\star })$ exists as the optimal solution for (PI-10). Thus, $(x^{\star },\varTheta ^{\star })$ is the Pareto optimal solution of (PI-1).

On the similar lines, it can be proved that $(y^{\star },\; \varPsi ^{\star })$ is the Pareto optimal solution of (PII-1). $\square$

4 Numerical illustration

Example 1

Assume that two different companies, ${\mathcal {K}}_1$ and ${\mathcal {K}}_2$, both manufacture air conditioners (ACs) and are engaged in an intense competition to sell window ACs to a newly established educational institution. It is believed that the demand for air conditioners remains relatively stable throughout time. When one company’s profits go up, it usually means that another company’s profits are going down simultaneously. In order to gain a competitive advantage, the two companies need to consider their marketing strategies carefully. Despite the fact that there are many limitations, the company ${\mathcal {K}}_{1}$ has decided to prioritize the following three alternatives:

(i) giving special discount offer ($\sigma _{1}$),

(ii) giving additional warranty ($\sigma _{2}$),

(iii) producing energy-efficient ACs ($\sigma _{3}$).

On the other hand, company ${\mathcal {K}}_{2}$ too have three alternatives on priority basis:

(i) to provide special price offer ($\zeta _{1}$),

(ii) generating energy-efficient air conditioners ($\zeta _{2}$),

(iii) to provide one time free servicing to users ($\zeta _{3}$).

The two companies have limited funds, thus leaving them with only one possibility to select. Hence, the aforementioned challenging choice issue is referred to as a matrix game. The companies ${\mathcal {K}}_{1}$ and ${\mathcal {K}}_{2}$ are believed to be two players, player I and player II, respectively. The payoffs of game are the market gains that a company expects to receive based on the strategy that the individual company chooses. Moreover, the market facts are scarcely known/unknown and are frequently uncertain. Thus, a unique numeric value for the payoff cannot model it realistically. A committee of experts assesses the state of the financial markets and expresses their conclusions in linguistic terms, i.e., LIVIFNs. The evaluation of the above-mentioned alternatives for each player (companies) according to LTSs is defined as follows:

$S=\{s_{0}=\text {no gain} ,\; s_{1}=\text {very low gain},\; s_{2}= \text {low gain},\;s_{3}= \text {slightly low gain},\; s_{4}=\text {moderate gain},\;s_{5}=\text {slightly good gain} ,\;s_{6}=\text {good gain},\; s_{7}=\text {very good gain}, s_{8}=\text {excellent gain} \}.$

Under this paradigm, based on expert’s evaluation, the payoff matrix ${\tilde{A}}$ for player I (i.e., company ${\mathcal {K}}_1$), with payoffs as LIVIFNs is as follows :

$$\begin{aligned} {\tilde{A}}= \begin{bmatrix} \left\langle \left[ s_{5},s_{6}\right] ;[s_{1},s_{2}]\right\rangle \;&{} \; \langle [s_{4},s_ {5}];[s_{1},s_{2}]\rangle \;&{} \; \langle [s_{1},s_{3}];[s_{4},s_{5}]\rangle \\ \langle [s_{0},s_{2}];[s_{3},s_{6}] \rangle \; &{}\; \langle [s_{7},s_{7}];[s_{1},s_{1}] \rangle \;&{} \; \langle [s_{3},s_{6}];[s_{1},s_{2}]\rangle \\ \langle [s_{0},s_{1}];[s_{2},s_{2}] \rangle \; &{}\; \langle [s_{1},s_{2}];[s_{4},s_{6}]\rangle \;&{} \; \langle [s_{2},s_{7}];[s_{1},s_{1}]\rangle \end{bmatrix} \end{aligned}$$

Corresponding to the optimization Models (PI-10) and (PII-10), we get the problem for player I and player II as follows:

$$\begin{aligned}{} & {} {\textbf {(PI-1.1)}}\\&&\displaystyle \min \left\{ {\mathfrak {U}} \right\} \\{} & {} \text{ subject } \text{ to }\\{} & {} \displaystyle x_{1}\left[ \kappa \ln \left( 1-\frac{6}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{5}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] +\\{} & {} \displaystyle x_{2}\left[ \kappa \ln \left( 1-\frac{2}{8}\right) +(1-\kappa )\ln \left( \frac{3}{8}\right) +\kappa \ln \left( 1-\frac{0}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{6}{8}\right) \right] +\\{} & {} \displaystyle x_{3}\left[ \kappa \ln \left( 1-\frac{1}{8}\right) +(1-\kappa )\ln \left( \frac{2}{8}\right) +\kappa \ln \left( 1-\frac{0}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] \quad \le \quad \;{\mathfrak {U}},\\{} & {} \displaystyle x_{1} \left[ \kappa \ln \left( 1-\frac{5}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{4}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] +\\{} & {} \displaystyle x_{2}\left[ \kappa \ln \left( 1-\frac{7}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{7}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{1}{8}\right) \right] +\\{} & {} \displaystyle x_{3}\left[ \kappa \ln \left( 1-\frac{2}{8}\right) +(1-\kappa )\ln \left( \frac{4}{8}\right) +\kappa \ln \left( 1-\frac{1}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{6}{8}\right) \right] \quad \le \quad \;{\mathfrak {U}}, \\{} & {} \displaystyle x_{1}\left[ \kappa \ln \left( 1-\frac{3}{8}\right) +(1-\kappa )\ln \left( \frac{4}{8}\right) +\kappa \ln \left( 1-\frac{1}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{5}{8}\right) \right] +\\{} & {} \displaystyle x_{2} \left[ \kappa \ln \left( 1-\frac{6}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{3}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] +\\{} & {} \displaystyle x_{3} \left[ \kappa \ln \left( 1-\frac{7}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{2}{8}\right) \right. \\{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{1}{8}\right) \right] \quad \le \quad \;{\mathfrak {U}}, \\{} & {} \displaystyle x_{1}+x_{2}+x_{3}=1,\\{} & {} {\mathfrak {U}} \le 0, \; x_{1},\;x_{2},\; x_{3}\ge 0, \end{aligned}$$

$$\begin{aligned}{} & {} {\textbf {(PII-1.2)}}\\{} & {} \displaystyle \max \left\{ {\mathfrak {F}} \right\} \\{} & {} \text{ such } \text{ that } \\{} & {} \displaystyle y_{1}\left[ \kappa \ln \left( 1-\frac{6}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{5}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] +\\{} & {} \displaystyle y_{2}\left[ \kappa \ln \left( 1-\frac{5}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{4}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] +\\{} & {} \displaystyle y_{3}\left[ \kappa \ln \left( 1-\frac{3}{8}\right) +(1-\kappa )\ln \left( \frac{4}{8}\right) +\kappa \ln \left( 1-\frac{1}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{5}{8}\right) \right] \ge \;{\mathfrak {F}},\\{} & {} \displaystyle y_{1}\left[ \kappa \ln \left( 1-\frac{2}{8}\right) +(1-\kappa )\ln \left( \frac{3}{8}\right) +\kappa \ln \left( 1-\frac{0}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{6}{8}\right) \right] +\\{} & {} \displaystyle y_{2}\left[ \kappa \ln \left( 1-\frac{7}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{7}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{1}{8}\right) \right] +\\{} & {} \displaystyle y_{3}\left[ \kappa \ln \left( 1-\frac{6}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{3}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] \ge \;{\mathfrak {F}},\\{} & {} \displaystyle y_{1} \left[ \kappa \ln \left( 1-\frac{1}{8}\right) +(1-\kappa )\ln \left( \frac{2}{8}\right) +\kappa \ln \left( 1-\frac{0}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{2}{8}\right) \right] +\\{} & {} \displaystyle y_{2} \left[ \kappa \ln \left( 1-\frac{2}{8}\right) +(1-\kappa )\ln \left( \frac{4}{8}\right) +\kappa \ln \left( 1-\frac{1}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{6}{8}\right) \right] +\\{} & {} \displaystyle y_{3} \left[ \kappa \ln \left( 1-\frac{7}{8}\right) +(1-\kappa )\ln \left( \frac{1}{8}\right) +\kappa \ln \left( 1-\frac{2}{8}\right) \right. \\ {}{} & {} \quad \left. +(1-\kappa )\ln \left( \frac{1}{8}\right) \right] \ge \;{\mathfrak {F}},\\{} & {} \displaystyle y_{1}+y_{2}+y_{3}=1,\\{} & {} {\mathfrak {F}} \le 0, \; y_{1}, \; y_{2},\;y_{3}\ge 0. \end{aligned}$$

The optimization problems (PI-1.1) and (PII-1.2) can be solved for distinct values of $\kappa \in [0,1]$, with the help of mathematical software easily. Here, we use MATLAB R2018b software to compute the solutions of linear programming problems given in (PI-1.1) and (PII-1.2). The obtained optimal solutions and the corresponding expected values are illustrated in Table 1.

Analogous to the optimization Model (PI-12) and Model (PII-12), we construct the problems (PI-1.3) and (PII-1.4) for player I and player II , respectively, which are described as follows:

$$\begin{aligned}{} & {} {\textbf {(PI-1.3)}}\\{} & {} \displaystyle \min \left\{ {\mathcal {V}} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \left[ \left( 1-\frac{6}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{5}{8}\right) ^{\kappa } \left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{x_{1}}*\\{} & {} \quad \left[ \left( 1-\frac{2}{8}\right) ^{\kappa }\left( \frac{3}{8}\right) ^{(1-\kappa )}\left( 1-\frac{0}{8}\right) ^{\kappa } \left( \frac{6}{8}\right) ^{(1-\kappa )}\right] ^{x_{2}}*\\{} & {} \quad \displaystyle \left[ \left( 1-\frac{1}{8}\right) ^{\kappa }\left( \frac{2}{8}\right) ^{(1-\kappa )}\left( 1-\frac{0}{8}\right) ^{\kappa }\left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{x_{3}}\le \;{\mathcal {V}}, \\{} & {} \displaystyle \left[ \left( 1-\frac{5}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{4}{8}\right) ^{\kappa }\left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{x_{1}}*\\{} & {} \quad \left[ \left( 1-\frac{7}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{7}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\right] ^{x_{2}}*\\{} & {} \quad \displaystyle \left[ \left( 1-\frac{2}{8}\right) ^{\kappa }\left( \frac{4}{8}\right) ^{(1-\kappa )}\left( 1-\frac{1}{8}\right) ^{\kappa }\left( \frac{6}{8}\right) ^{(1-\kappa )}\right] ^{x_{3}}\le \;{\mathcal {V}}, \\{} & {} \displaystyle \left[ \left( 1-\frac{3}{8}\right) ^{\kappa }\left( \frac{4}{8}\right) ^{(1-\kappa )}\left( 1-\frac{1}{8}\right) ^{\kappa } \left( \frac{5}{8}\right) ^{(1-\kappa )}\right] ^{x_{1}}*\\{} & {} \quad \left[ \left( 1-\frac{6}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{3}{8}\right) ^{\kappa }\left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{x_{2}}*\\{} & {} \quad \displaystyle \left[ \left( 1-\frac{7}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{2}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\right] ^{x_{3}} \le \;{\mathcal {V}}, \\{} & {} \displaystyle x_{1}+x_{2}+x_{3}=1,\\{} & {} 0\le {\mathcal {V}}\le 1,\; x_{1},\;x_{2},x_{3}\ge 0. \end{aligned}$$

Table 1 Optimal solutions for (PI-1.1) and (PII-1.2)

Table 2 Optimal solutions of the nonlinear programming problems (PII-1.3) and (PII-1.4)

and

$$\begin{aligned}{} & {} {\textbf {(PII-1.4)}}\\{} & {} \displaystyle \max \left\{ {\mathcal {W}} \right\} \\{} & {} \text{ subject } \text{ to } \\{} & {} \displaystyle \left[ \left( 1-\frac{6}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{5}{8}\right) ^{\kappa } \left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{y_{1}}*\\{} & {} \quad \left[ \left( 1-\frac{5}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{4}{8}\right) ^{\kappa } \left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{y_{2}}*\\{} & {} \displaystyle \quad \left[ \left( 1-\frac{3}{8}\right) ^{\kappa }\left( \frac{4}{8}\right) ^{(1-\kappa )}\left( 1-\frac{1}{8}\right) ^{\kappa }\left( \frac{5}{8}\right) ^{(1-\kappa )}\right] ^{y_{3}}\ge \;{\mathcal {W}}, \\{} & {} \displaystyle \left[ \left( 1-\frac{2}{8}\right) ^{\kappa }\left( \frac{3}{8}\right) ^{(1-\kappa )}\left( 1-\frac{0}{8}\right) ^{\kappa } \left( \frac{6}{8}\right) ^{(1-\kappa )}\right] ^{y_{1}}*\\{} & {} \quad \left[ \left( 1-\frac{7}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{7}{8}\right) ^{\kappa } \left( \frac{1}{8}\right) ^{(1-\kappa )}\right] ^{y_{2}}*\\{} & {} \displaystyle \quad \left[ \left( 1-\frac{6}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{3}{8}\right) ^{\kappa }\left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{y_{3}}\ge \;{\mathcal {W}}, \\{} & {} \displaystyle \left[ \left( 1-\frac{1}{8}\right) ^{\kappa }\left( \frac{2}{8}\right) ^{(1-\kappa )}\left( 1-\frac{0}{8}\right) ^{\kappa } \left( \frac{2}{8}\right) ^{(1-\kappa )}\right] ^{y_{1}}*\\{} & {} \quad \left[ \left( 1-\frac{2}{8}\right) ^{\kappa }\left( \frac{4}{8}\right) ^{(1-\kappa )}\left( 1-\frac{1}{8}\right) ^{\kappa } \left( \frac{6}{8}\right) ^{(1-\kappa )}\right] ^{y_{2}}*\\{} & {} \displaystyle \quad \left[ \left( 1-\frac{7}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\left( 1-\frac{2}{8}\right) ^{\kappa }\left( \frac{1}{8}\right) ^{(1-\kappa )}\right] ^{y_{3}}\ge \;{\mathcal {W}}, \\{} & {} \displaystyle y_{1}+y_{2}+ y_{3}=1,\\{} & {} 0\le {\mathcal {W}}\le 1,\; y_{1},\;y_{2},\; y_{3}\ge 0. \end{aligned}$$

Problems (PII-1.3) and (PII-1.4) are solved by using MATLAB R2018b software, and their results have been tabulated for the optimal values and their respective expected values in Table 2.

The results summarized in Tables 1 and 2 clearly indicate that as the value of $\kappa$ changes, different mixed strategies are obtained corresponding to the Players I and II, respectively. It is worth mentioning that the values ${\mathfrak {U}}^{\star },\;{\mathfrak {F}}^{\star },\;{\mathcal {V}}^{\star }\;\text{ and } {\mathcal {W}}^{\star }$ are monotonically non-decreasing with respect to $\kappa$. Also, maximin strategies $x^{\star }$ and minimax strategies $y^{\star }$ obtained by the problems (PI-1.1) and (PII-1.2), are respectively, similar to those obtained by the problems given in (PI-1.3) and (PII-1.4). Furthermore, ${\mathcal {V}}^{\star }= e^{{\mathfrak {U}}^{\star }}$ and ${\mathcal {W}}^{\star }= e^{{\mathfrak {F}}^{\star }}$, with $s_{\xi _{\delta _{ij}}^{+}}\ne s_{t},\;s_{\xi _{\delta _{ij}}^{-}} \ne s_{t}, s_{\vartheta _{\delta _{ij}}^{+}}\ne s_{0}$ and $s_{\vartheta \delta _{\delta _{ij}}^{-}} \ne s_{0}\; (i,j =1,2,3 ).$

Table 3 Optimal solutions of linear programming problems based on Li’s approach for payoff matrix ${\tilde{B}}$

Table 4 Optimal solutions of nonlinear programming problems based on Li’s approach for payoff matrix ${\tilde{B}}$

Table 5 The characteristic comparisons of different methods for solving matrix game problems

5 Comparative study

It is important to highlight that the LIVIFN provides an adequate description of subjective information. According to the research that has been reviewed, matrix games have not been looked in the context of the linguistic interval-valued intuitionistic fuzzy environment, which describes quantitative information more flexibly. As a result, it is difficult for us to make a direct comparison between our methodology and any other methods currently available for solving matrix games.

Wang et al. (2014) developed the idea of linguistic scale function (LSF) for transforming the linguistic terms into numerical values. It can be defined as follows :

Let ${\mathbb {S}} = \left\{ s_{f} |\;f= 0, 1,\ldots , t \right\}$ be a LTS and $\varPsi _{f}\in \left[ 0 ,1\right]$ be a real number, then LSF can be expressed by the mathematical expression given by

$$\begin{aligned} {\mathcal {G}}: s_{f} \rightarrow \varPsi _{f}=\left( \frac{f}{t}\right) \left( f= 0, 1,\ldots , t \right) . \end{aligned}$$

(5.1)

Now utilizing Eq. (5.1), we get the following payoff matrix corresponding to the LIVIFNs payoff matrix ${\tilde{A}}$:

$$\begin{aligned} {\tilde{B}}= \begin{bmatrix} \left\langle \left[ {0.6250},{0.7500}\right] ;[{0.1250},{0.2500}]\right\rangle \;&{} \; \langle [{0.5000},{0.6250}];[{0.1250},{0.2500}]\rangle \;&{} \; \langle [{0.1250},{0.3750}];[{0.5000},{0.6250}]\rangle \\ \langle [{0.0000},{0.2500}];[{0.3750},{0.7500}] \rangle \; &{}\; \langle [{0.8750},{0.8750}];[{0.1250},{0.1250}]\rangle \;&{} \; \langle [{0.3750},{0.7500}];[{0.1250},{0.2500}]\rangle \\ \langle [{0.0000},{0.1250}];[{0.2500},{0.2500}] \rangle \; &{}\; \langle [{0.1250},{0.2500}];[{0.5000},{0.7500}]\rangle \;&{} \; \langle [{0.2500},{0.8750}];[{0.1250},{0.1250}]\rangle \end{bmatrix}. \end{aligned}$$

It is worth noting that all the entries in the payoff matrix ${\tilde{B}}$ are IVIFNs. After applying solution approach developed by Li (2010), we obtain the optimal solutions as listed in Tables 3 and 4, respectively.

From Table 3, we see that the optimal strategies $x^{\star }$ and $y^{\star }$ corresponding to players I and II are quite close to the optimal strategies achieved by our suggested technique, which are tabulated in Table 2. It demonstrates that the optimization models presented in this work are valid and logical when applied to solving matrix game problems whose payoffs are indicated by LIVIFNs.

In addition, we undertake a detailed analysis for comparing many aspects that are taken into consideration by researchers during the process of attempting to solve matrix game problems. Table 5 shows the important observations.

The results summarized in Table 5 depict that the presented matrix game models are more general and flexible in dealing with real-world complex decision-making problems.

6 Conclusion

In this study, we have examined the matrix games under a qualitative information environment. First, the paper has discussed some basic notions to accomplish the objectives of this work. The matrix games involving payoffs described by LIVIFNs have been formulated. The benefit of adopting LIVIFN payoff values is that it allows decision-makers to describe ambiguous and imprecise facts in a more detailed manner. As a result, the decision-maker is not compelled to express his imprecise information in single numeral terms of membership and non-membership functions. We have used the LIVIFWA operator to calculate the expected value of the game. Next, based on the order relation of LIVIFNs, the nonlinear bi-objective programming problems for each player are reduced to a corresponding pair of linear/nonlinear programming problems to determine the maximin and minimax strategies corresponding to the players. Finally, the solution technique has been validated by illustrating a real-life decision-making problem. A comparative study with some existing methods has also been carried out to demonstrate the advantages of the suggested method.

In the future, the proposed approach can even be employed to investigate multi-objective matrix games involving LIVIFSs. The described methodology can also be extended to more generalized information representation models, including linguistic interval-valued Pythagorean fuzzy sets, linguistic interval-valued q-rung orthopair fuzzy sets, and cubic linguistic intuitionistic fuzzy sets. We shall also explore the applications of the developed optimization models in different areas, such as water resources management, waste management, and irrigation systems.