Intuitionistic interval-valued hesitant fuzzy matrix games with a new aggregation operator for solving management problem

Abstract

In our daily life, we encounter many problems with uncertainty and vagueness in nature. Mathematical formulations and solutions of these problems are not easy and appear to be a challenging task to the researchers. Crisp sets and fuzzy sets suffer to deal with these. Hesitant fuzzy set—a protracted version of fuzzy set—comes into the fore to bridge over the gap. The set of all possible values of membership of hesitant fuzzy set might be considered as a set of possible intervals. Non-membership functions are also added therein to get intuitionistic interval-valued hesitant fuzzy numbered sets. In the literature, several aggregation operators exist, and here we consider a new one which is easy to apply in our formulated problems. Here, a matrix game whose payoffs are intuitionistic interval-valued hesitant fuzzy numbers is solved using our proposed aggregation operator. A tangible management problem with numerical values is demonstrated here to verify the applicability of the new aggregation operator over the matrix game.

1 Introduction

Decision-making problems associated with game theories have wide applications in sciences, engineering, management science and social sciences. Fuzzy set (FS) (Zadeh 1965) serves an excellent and marvelous role to explore the inner phenomena of problems related to everyday’s life. But it has some limitations to deal with imprecise data and hazy information when different types of vagueness and uncertainty crop up simultaneously. Researchers have nurtured fuzzy sets and extended fuzzy sets to intuitionistic fuzzy set (IFS) (Atanassov 1986), hesitant fuzzy set (HFS) (Torra 2010), interval-valued fuzzy set (IVFS) (Turksen 1986) and their inter-collaborations have been established. Hesitant fuzzy set is more applicable to the discussion over vagueness and fuzziness of the characters of the variables connected to the problems on real-life situations.

In the fuzzy set, members are characterized by membership degrees and in intuitionistic fuzzy set, members have membership degrees as well as non-membership degrees and the hesitancy degrees. Several articles (cf. Chen 2016; Chen et al. 2012a, b; Gabroveanu et al. 2016) are devoted in the intuitionistic fuzzy set, interval-valued intuitionistic fuzzy set theories since their appearances into different fields. But, all are limited in case of flexibility of choices of membership and non-membership degrees of the elements to the considered set. HFS has been successfully implemented into the cases of decision-making where FS or IFS fails to describe the problems about the vagueness and the uncertainty. HFS depicts a set of membership values in [0, 1] rather than a single one against each member of the set. In many decision-making problems of various fields with a variety of vagueness, HFS is used when decision-makers feel a hesitant environment like disaccord, discrepancy situations (cf. Farhadinia 2013; Yu et al. 2013). Basic set theoretic operations and the extension principle on HFS were proposed by Torra (2010). Xia and Xu (2011) defined some new operations on HFS. Xu and Xia (2011) proposed some distance measures on HFS. Chen et al. (2013) proposed the concept of interval-valued hesitant fuzzy set (IVHFS) which represents the membership values of an element to a set with several possible interval values and then presented some interval-valued hesitant fuzzy aggregation operators. Several articles have been published in different hesitant fuzzy environments (cf. Rodriguez et al. 2012; Zhu 2012) in different distance measures (Peng et al. 2013) and aggregation operators (Peng and Wang 2014). In decision-making, the aggregation operators are frequently used and successfully applied to get performances among all alternatives to aggregate information. Xia and Xu (2011) developed a series of aggregation operators for hesitant fuzzy information and applied to multi-criteria decision-making. Zhou (2014) introduced and developed several types of hesitant fuzzy aggregation operators which are the extended version of weighted geometric (WG) and ordered weighted geometric (OWG) operators having hesitancy environments. Yager (1988) and Xu and Yager (2006) presented some intuitionistic fuzzy aggregation operators. Wei et al. (2014) introduced hesitant triangular fuzzy aggregation operators such as hesitant triangular fuzzy weighted averaging (HTFWA) operator, hesitant triangular fuzzy weighted geometric (HTFWG) operator, hesitant triangular fuzzy ordered weighted averaging (HTFOWA) operator, hesitant triangular fuzzy ordered weighted geometric (HTFOWG) operator, hesitant triangular fuzzy hybrid geometric operator (HTFHG) and averaging operator (HTFHA). Wei (2013) presented interval-valued hesitant fuzzy Choquet ordered averaging (IVHFCOA) operator, interval-valued hesitant fuzzy prioritized aggregation (IVHFPrA) operator, and interval-valued hesitant fuzzy power aggregation (IVHFPoA) operator. In this work, we introduce a new aggregation operator simply to apply in intuitionistic interval-valued hesitant fuzzy environment.

Neumann and Morgenstern (1944) invented Game Theory as a mathematical way to discover the situation related to the turns done by decision-makers. A game involves a variety of players, a set of strategies plus a payoff that shows quantitatively the outcome of each play of the game in terms of the amounts that each player gains or loses. A player who chooses a pure strategy randomly selects a row or a column according to the probability process that specifies the chance with each pure strategy. These probability orient strategies are known as mixed strategies for players. In probability expected sense, the calculated payoffs suggest each player’s expectation to receive and the player will actually receive on average provided that the game is played a number of times. Matrix game and duality theory in linear programming problem (LPP) possess a bondage in crisp nature of complexities of problems but reality prefers to different uncertain natures. Due to the uncertainty and imprecision characteristics involved and occurred in the system and the anomaly of the judgment of players or decision-makers, the reflection of hesitance characters are marked in our problem. Campos (1989) first used fuzzy linear programming models to solve fuzzy matrix games. Jana and Roy (2018) formulated and solved dual hesitant fuzzy matrix games based on new similarity measure. Li (2014), in his classic, solved matrix games with different uncertainties using Atanassov’s IF environments. Bhaumik et al. (2017), Roy and Bhaumik (2018), Roy and Mula (2014), Roy and Mula (2016) and Roy and Mondal (2016) solved matrix games, bi-matrix games and successfully applied them in real-life situations. Several articles have been published in game theory (cf. Ammar 2019; Cheng et al. 2016; Das and Roy 2010; Jana and Roy 2018; Khan 2019; Roy and Mula 2013; Roy and Das 2009; Xia 2018).

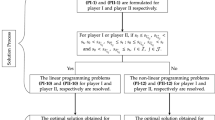
Here, we develop a matrix game model with uncertain payoff elements. Sometimes Atanassov’s IFS fails under limitations with respect to the hesitancy involved in the problem. Generally, we use IVHFS whose members are usually hesitant interval elements. Hesitant numbers emphasize liberty on the hesitancy of the choice of elements. Intuitionistic interval-valued hesitant fuzzy number facilitates more close choice of membership values and non-membership values based upon decision-makers’ intuition, assumption, judgement, behavior, evaluation, decision, etc. In this paper, matrix game with payoffs represented by intuitionistic interval-valued hesitant fuzzy numbers (IIVHFNs) is formulated. A methodology is developed mathematically to solve matrix game with payoffs IIVHFNs by considering a pair of LPPs.

Main contributions of this paper are:

• Intuitionistic interval-valued hesitant fuzzy matrix game model is designed.

• A fast-objective game model is achieved using a new aggregation operator.

• Our proposed game is solved considering a pair of linear programming problems.

• Management problem is exercised involving the matrix game in proposed environment.

In Sect. 2, the basic preliminaries related to fuzzy set, intuitionistic fuzzy set, intuitionistic fuzzy number, interval number and interval-valued intuitionistic fuzzy set are briefly discussed. Section 3 describes hesitant fuzzy set, interval-valued hesitant fuzzy set and their properties. In Sect. 4, we discuss on intuitionistic interval-valued hesitant fuzzy set. In Sect. 5, we define a new aggregating operator, say, generalized intuitionistic enveloped interval-valued hesitant fuzzy weighted aggregation operator. Matrix games with intuitionistic interval-valued hesitant fuzzy environment are described in Sect. 6. A management problem, having roots in society and economy, is discussed in Sect. 7. Section 8 considers the results of the corresponding problem and Sect. 9 concludes this paper with future research works.

2 Preliminaries

We first look back on the definitions of fuzzy set, intuitionistic fuzzy set, intuitionistic fuzzy number, interval number and interval-valued intuitionistic fuzzy set with the corresponding examples and their respective properties in this part.

Definition 2.1

(Zadeh 1965) Let X be a universe of discourse. A fuzzy set $\breve{A}$ in X is characterized by a membership function $\mu _{\breve{A}}:X\rightarrow$ [0, 1]. A fuzzy set $\breve{A}$ in X can be expressed as follows: $\breve{A}= \{ (x, \mu _{\breve{A}}(x)):~\mu _{\breve{A}}(x)\in [0,1],~x \in X \}$. And the membership degrees $\mu _{\breve{A}}(x)$ of $\breve{A}$ are crisp numbers.

Definition 2.2

(Atanassov 1986) Let X denote a universe of discourse, then an intuitionistic fuzzy set (IFS), $\hat{A}$ in X is given by a set of ordered triplet described as: $\hat{A}= \{\langle x,\mu _{\hat{A}}(x), \gamma _{\hat{A}}(x) \rangle :x \in X\},$ where both $\mu _{\hat{A}}$ and  $\gamma _{\hat{A}}$, mapping of the elements of X to [0, 1],  are functions such that  $0 \le \mu _{\hat{A}}(x)+\gamma _{\hat{A}}(x)\le 1,~\forall ~x \in X$. For each x, $\mu _{\hat{A}}(x)$ and $\gamma _{\hat{A}}(x)$ represent the degree of membership and degree of non-membership respectively. Again, the value $\pi _{\hat{A}}(x) = 1 - \mu _{\hat{A}}(x) - \gamma _{\hat{A}}(x)$ is called “degree of hesitation” of the element x in the set $\hat{A}$. If $\pi _{\hat{A}}(x) = 0, ~ \forall ~x ~\in ~X,$ then the IFS becomes a fuzzy set.

Definition 2.3

(Atanassov 1986) An IFN, $\hat{A}$ is an intuitionistic fuzzy subset of real numbers $\mathbb {R}$ if:

• (i) $\hat{A}$ is normal, i.e., $\exists ~\bar{ x} \in X$ such that

  $\mu _{\hat{A}}(\bar{x})=1$,

• (ii) $\hat{A}$ is convex for the membership function $\mu _{\hat{A}}(x)$, i.e., $\mu _{\hat{A}}(\lambda x_1+(1-\lambda )x_2) \ge \min \{\mu _{\hat{A}}(x_1), \mu _{\hat{A}}(x_2)\}$ for $x_1, x_2 \in \mathbb {R}$,  $\lambda \in [0,1]$,

• (iii) $\hat{A}$ is concave for the non-membership function $\gamma _{\hat{A}}(x)$, i.e., $\gamma _{\hat{A}}(\lambda x_1+(1-\lambda )x_2) \le \max \{\gamma _{\hat{A}}(x_1), \gamma _{\hat{A}}(x_2)\}$ for $x_1, x_2 \in \mathbb {R}$,  $\lambda \in [0,1]$,

• (iv) $\hat{A}$ is piecewise continuous.

Definition 2.4

(Moore 1979) Let $a=[a^{l},a^{u}]=\{x:a^{l}\le x\le a^{u}\}$, then a is called an interval number. If $a^{l}\ge 0$, then a is called positive interval number.

For any two positive interval numbers $a=[a^{l},a^{u}]$ and $b=[b^{l},b^{u}]$ and $\lambda \in [0,1]$, the following operations are defined.

• (i) $a+b=[a^{l}+b^{l},a^{u}+b^{u}];$

• (ii) $a^{\lambda }=([a^{l},a^{u}])^{\lambda }=[(a^{l})^{\lambda },(a^{u})^{\lambda }];$

• (iii) $\lambda a=\lambda [a^{l},a^{u}]=[\lambda a^{l},\lambda a^{u}];$

• (iv) $a\cdot b=[a^{l},a^{u}]\cdot [b^{l},b^{u}]=[a^{l}\cdot b^{l},a^{u}.b^{u}];$

• (v) $a\cup b=[\max \{a^{l},b^{l}\}, \max \{a^{u},b^{u}\}];$

• (vi) $a\cap b=[\min \{a^{l},b^{l}\}, \min \{a^{u},b^{u}\}].$

Definition 2.5

(Atanassov and Gargov 1989) Let $X=\{x_{1},x_{2},\ldots ,x_{n}\}$ be a finite universal set. An IVIFS A in X may be expressed mathematically as: $A=\{\langle x_{k},[\mu _{A}^{l}(x_{k}),\mu _{A}^{u}(x_{k})],[\nu _{A}^{l}(x_{k}),\nu _{A}^{u}(x_{k})]\rangle : x_{k}\in X,~k=1,2,\ldots ,n\}$, where, $[\mu _{A}^{l}(x_{k}),\mu _{A}^{u}(x_{k})]\subseteq [0,1]$ and $[\nu _{A}^{l}(x_{k}),\nu _{A}^{u}(x_{k})]\subseteq [0,1],~(k=1,2,\ldots ,n)$ are membership and non-membership degrees of $x_{k}$, expressed in interval form to A. If $\mu _{A}^{l}(x_{k})=\mu _{A}^{u}(x_{k})$ and $\nu _{A}^{l}(x_{k})=\nu _{A}^{u}(x_{k})$ for every $x_{k}\in X~(k=1,2,\ldots ,n)$, then the IVIFS set A is converted into Atanassov’s intuitionistic fuzzy set.

Property 2.1

We consider two IVIFSs A and B and also choose $\lambda >0$, and we get the following relational properties.

• (i) $A^{c}=\{\langle [\nu _{A}^{l},\nu _{A}^{u}],[\mu _{A}^{l},\mu _{A}^{u}]\rangle \};$

• (ii) $A \cup B =\{\langle [\mu _{A}^{l},\mu _{A}^{u}],[\nu _{A}^{l},\nu _{A}^{u}]\rangle \cup \langle [\mu _{B}^{l},\mu _{B}^{u}],[\nu _{B}^{l},\nu _{B}^{u}]\rangle \} =\{\langle [\mu _{A}^{l}\vee \mu _{B}^{l},\mu _{A}^{u}\vee \mu _{B}^{u}], [\nu _{A}^{l}\wedge \nu _{B}^{l}, \nu _{A}^{u}\wedge \nu _{B}^{u}]\rangle \};$

• (iii) $A \cap B =\{\langle [\mu _{A}^{l},\mu _{A}^{u}],[\nu _{A}^{l},\nu _{A}^{u}]\rangle \cap \langle [\mu _{B}^{l},\mu _{B}^{u}],[\nu _{B}^{l},\nu _{B}^{u}]\rangle \} =\{\langle [\mu _{A}^{l}\wedge \mu _{B}^{l},\mu _{A}^{u}\wedge \mu _{B}^{u}], [\nu _{A}^{l}\vee \nu _{B}^{l}, \nu _{A}^{u}\vee \nu _{B}^{u}]\rangle \};$

• (iv) $A \otimes B =\{\langle [\mu _{A}^{l}\mu _{B}^{l},\mu _{A}^{u}\mu _{B}^{u}], [\nu _{A}^{l}+\nu _{B}^{l}-\nu _{A}^{l}\nu _{B}^{l},\nu _{A}^{u}+\nu _{B}^{u}-\nu _{A}^{u}\nu _{B}^{u}]\rangle \};$

• (v) $A \oplus B =\{\langle [\mu _{A}^{l}+\mu _{B}^{l}-\mu _{A}^{l}\mu _{B}^{l},\mu _{A}^{u}+\mu _{B}^{u}-\mu _{A}^{u}\mu _{B}^{u}], [\nu _{A}^{l}\nu _{B}^{l}, ~~~~~\nu _{A}^{u}\nu _{B}^{u}]\rangle \};$

• (vi) $\lambda A = \{\langle [1-(1-\mu _{A}^{l})^{\lambda },1-(1-\mu _{A}^{u})^{\lambda }], [(\nu _{A}^{l})^{\lambda },~~~~~(\nu _{A}^{u})^{\lambda }] \rangle \};$

• (vii) $A^{\lambda } = \{\langle [(\mu _{A}^{l})^{\lambda },(\mu _{A}^{u})^{\lambda }], [1-(1-\nu _{A}^{l})^{\lambda },1-(1~~~~~-\nu _{A}^{u})^{\lambda }]\rangle \},$

  where the symbols “$\wedge$” and “$\vee$” are min and max operators, respectively; “$\oplus$”, “$\otimes$” are meant for direct sum and tensor product operators, respectively.

Definition 2.6

Assume $a=[a^{l},a^{u}]=\{x:0\le a^{l}\le x\le a^{u}\}$ is defined as an interval number, then the expected value of a is defined as $E(a)=(1/2)(a^{l}+a^{u})$.

Definition 2.7

Assume $\tilde{a}=[\tilde{a}^{l},\tilde{a}^{u}]=\{x: \tilde{a}^{l}\le x\le \tilde{a}^{u}, ~\tilde{a}^{l}=\inf \tilde{a}, ~\tilde{a}^{u}=\sup \tilde{a}\}$ is defined as an interval fuzzy number, then the expected value of $\tilde{a}$ is defined as $E(\tilde{a})=(1/2)(\tilde{a}^{l}+\tilde{a}^{u})$.

Definition 2.8

(Chen et al. 2013) Let $\tilde{a}_{1}=[{\tilde{a}_{1}}^{l}, \tilde{a}_{1}^{u}]$ and $\tilde{a}_{2}=[\tilde{a}_{2}^{l}, \tilde{a}_{2}^{u}]$ be two interval fuzzy numbers and let $l(\tilde{a}_{1})= \tilde{a}_{1}^{u}-\tilde{a}_{1}^{l}$ and $l(\tilde{a}_{2})= \tilde{a}_{2}^{u}-\tilde{a}_{2}^{l}$, then the degree of possibility of $\tilde{a}_{1}\ge \tilde{a}_{2}$ is defined as follows:

$$\begin{aligned} {\text {Pos}}(\tilde{a}_{1}\ge \tilde{a}_{2})=\max \Big \{ 1-\max \Big \{ \frac{\tilde{a}_{2}^{u}-\tilde{a}_{1}^{l}}{l(\tilde{a}_{1})+l(\tilde{a}_{2})}, 0\Big \}, 0\Big \}. \end{aligned}$$

Similarly, the degree of possibility of $\tilde{a}_{2}\ge \tilde{a}_{1}$ is defined as:

$$\begin{aligned} {\text {Pos}}(\tilde{a}_{2}\ge \tilde{a}_{1})=\max \Big \{1-\max \Big \{\frac{\tilde{a}_{1}^{u}-\tilde{a}_{2}^{l}}{l(\tilde{a}_{1})+l(\tilde{a}_{2})}, 0 \Big \}, 0\Big \}. \end{aligned}$$

From Definition 2.8, we easily obtain the following results:

• (i) $0\le {\text {Pos}}(\tilde{a}_{1}\ge \tilde{a}_{2})\le 1;$

• (ii) $0\le {\text {Pos}}(\tilde{a}_{2}\ge \tilde{a}_{1})\le 1;$

• (iii) ${\text {Pos}}(\tilde{a}_{1}\ge \tilde{a}_{2})+ {\text {Pos}}(\tilde{a}_{2}\ge \tilde{a}_{1})=1$; and specially,

• (iv) ${\text {Pos}}(\tilde{a}_{1}\ge \tilde{a}_{1})= {\text {Pos}}(\tilde{a}_{2}\ge \tilde{a}_{2})=0.5.$

Definition 2.9

(Ishibuchi and Tanaka 1990) Let $a=[a^{l},a^{u}]=\{x:a^{l}\le a^{u}\}$ be an interval. The maximization problem with the interval objective function is described as follows:

$$\begin{aligned} & \text {maximize} \quad a\\ & \text {subject to } \quad a \in \varOmega _{1}, \end{aligned}$$

which is equivalent to the following bi-objective mathematical programming problem:

$$\begin{aligned} &\text {maximize}~\quad a^{l}, E(a)\\ & \text {subject to } \quad a \in \varOmega _{1}, \end{aligned}$$

where $\varOmega _{1}$ is a set of constraints in which the variable “a” should satisfy according to the requirements in real situation.

Similarly, the minimization problem with the interval objective function is treated as follows:

$$\begin{aligned}& \text {minimize}\quad a\\ & \text {subject to } \quad a \in \varOmega _{2}, \end{aligned}$$

which is also converted into the following bi-objective programming problem as:

$$\begin{aligned}& \text {minimize}~\quad a^{u}, E(a)\\ & \text {subject to } \quad a \in \varOmega _{2}. \end{aligned}$$

Here, $\varOmega _{2}$ is a set of constraints in which the variable “a” should satisfy according to the requirements of reality.

Now, we consider a new interval which can be defined as an envelope of given set of intervals. In the following definition, we define such interval as enveloped interval (EI).

Definition 2.10

Let $S=\{[a_{1},b_{1}], [a_{2},b_{2}], \ldots$, $[a_{n},b_{n}]\}$ be a set of intervals. Then $E_{S}$, defined as $E_{S}=[\min _{i=1}^{n}(a_{i}),\max _{i=1}^{n}(b_{i})]$, such that $a_{k}\le \min _{i=1}^{n}(a_{i}) \le \max _{i=1}^{n}(b_{i})\le b_{l}$ (for particular k and l), is called the enveloped interval (EI) of S.

3 HFS, IVHFS and their properties

In this section, we define elaborately the HFS, IVHFS and their related properties with supporting examples.

Definition 3.1

(Torra 2010) A hesitant fuzzy set $A_{HF}$ on a reference set X is characterized in terms of a function $h_{A}(x)$ when is applied to X, give a subset of [0, 1], i.e., $A_{HF}=\{\langle x,h_{A}(x)\rangle : x\in X\}$, where $h_{A}(x)$ is termed as hesitant fuzzy element (HFE), a basic unit of HFS, is a set of some different values in [0,1] represents the membership degrees of the element $x\in X$.

Example 3.1

Suppose $A_{HF}= \{\langle x_{1},{0.1,0.4,0.3}\rangle$, $\langle x_{2},{0.3,0.35}\rangle ,\langle x_{3},{0.2,0.4,0.6,0.69,0.8}\rangle \}$ is a HFS, where $\{x_{1},x_{2},x_{3}\}\in X$, a reference set and $h_{A}(x_{1})=\{0.1,0.4,0.3\}, ~h_{A}(x_{2})=\{0.3$, $0.35\}, h_{A}(x_{3})=\{0.2,0.4,0.6,0.69,0.8\}$ are hesitant fuzzy elements.

Property 3.1

Given three HFEs represented by $h, h_{1}$ and $h_{2}$ on which some operations are defined by Torra (2010) as follows:

• (i) $h^{c}=\{1-\gamma :\gamma \in h\}$, complement of h;

• (ii) $h_{1}\cup h_{2}=\{\gamma _{1}\vee \gamma _{2}:\gamma _{1}\in h_{1}, \gamma _{2}\in h_{2}\};$

• (iii) $h_{1}\cap h_{2}=\{\gamma _{1}\wedge \gamma _{2}:\gamma _{1}\in h_{1}, \gamma _{2}\in h_{2}\};$

  Furthermore, to aggregate hesitant fuzzy information, Xia and Xu (2011) defined some new operations on $h, h_{1}$ and $h_{2}$ with $\lambda > 0$ as below:

• (iv) $h_{1}\oplus h_{2}=\{\gamma _{1}+\gamma _{2}-\gamma _{1}\gamma _{2}:\gamma _{1}\in h_{1}, \gamma _{2}\in h_{2}\};$

• (v) $h_{1}\otimes h_{2}=\{\gamma _{1}\gamma _{2}:\gamma _{1}\in h_{1}, \gamma _{2}\in h_{2}\};$

• (vi) $h^{\lambda }=\{\gamma ^{\lambda }:\gamma \in h\};$

• (vii) $\lambda h=\{1-(1-\gamma )^{\lambda }:\gamma \in h\}.$

To compare the magnitudes of HFEs, Xia and Xu (2011) defined the following comparison laws:

For any HFE h, $S(h)=\sum _{\gamma \in h}^{e_{h}} \frac{\gamma }{|e_{h}|}$, called the score function of h, where $e_{h}$ is the set of all elements in h and $|e_{h}|$ denotes the cardinality of $e_{h}$.

For any two HFEs, $h_{1}$ and $h_{2}$, $S(h_{1})>S(h_{2})$ implies that $h_{1}>h_{2}$; $S(h_{1})<S(h_{2})$ implies that $h_{2}>h_{1}$; otherwise, $S(h_{1})=S(h_{2})$ implies that $h_{1}=h_{2}.$

Definition 3.2

(Chen and Xu 2014) Specific membership degrees against an element of the reference set are not appropriate to describe the acceptance of the element. To overcome this complexity, Chen et al. (2013) defined IVHFS as: $B_{\text {IVHFS}}=\{\langle x_{i}, \tilde{h}_{B}(x_{i}): x_{i}\in X \rangle \}$ and $\tilde{h}_{B}(x_{i})$ denotes fuzzy interval in [0,1], i.e., $B_{\text {IVHFS}}=\{\langle x_{i}, \tilde{\gamma _i}\rangle :x_{i}\in X, \tilde{\gamma }_{i}=[\tilde{\gamma }^{l}, \tilde{\gamma }^{u}]\in \tilde{h}_{B}(x_{i})\}$ and $\tilde{h}_{B}(x_{i})$ is called interval-valued hesitant fuzzy element (IVHFE), where $\tilde{\gamma }^{l}= \inf \tilde{\gamma },\tilde{\gamma }^{u}=\sup \tilde{\gamma }$ represent the lower and upper limits of $\tilde{\gamma }$, respectively. As HFE is connected to HFS, IVHFE is connected to IVHFS.

Example 3.2

We consider an IVHFS as:

$$\begin{aligned}&A=\{\langle x_{1};[0.1, 0.3]\rangle ,\langle x_{2};[0.1,0.4],[0.3,0.8]\rangle ,\\&\langle x_{3};[0.4,0.6]\rangle , \langle x_{4};[0.1,0.4],[0.5,0.7],[0.75,0.9]\rangle \}. \end{aligned}$$

Property 3.2

(Chen et al. 2013) defined the operations and illustrated the comparison results among any interval-valued hesitant fuzzy elements (IVHFEs), say, $\tilde{h}=\{\cup _{\tilde{\gamma }\in \tilde{h}}[\tilde{\gamma }^{l},\tilde{\gamma }^{u}]\}$, $\tilde{h}_{1}=\{\cup _{\tilde{\gamma }_{1}\in \tilde{h}_{1}}[\tilde{\gamma }_{1}^{l},\tilde{\gamma }_{1}^{u}]\}$ and $\tilde{h}_{2}=\{\cup _{\tilde{\gamma }_{2}\in \tilde{h}_{2}}[\tilde{\gamma }_{2}^{l},\tilde{\gamma }_{2}^{u}]\}$ as described below:

• (i) $\tilde{h}^{c}=\{[1-\tilde{\gamma }^{u}, 1-\tilde{\gamma }^{l}]:\tilde{\gamma }\in \tilde{h}\}$, complement of $\tilde{h};$

• (ii) $\tilde{h}_{1}\cup \tilde{h}_{2}=\{[\max (\tilde{\gamma }_{1}^{l},\tilde{\gamma }_{2}^{l}), \max (\tilde{\gamma }_{1}^{u},\tilde{\gamma }_{2}^{u})]:\tilde{\gamma }_{1}\in \tilde{h}_{1}, \tilde{\gamma }_{2}\in \tilde{h}_{2}\};$

• (iii) $\tilde{h}_{1}\cap \tilde{h}_{2}=\{[\min (\tilde{\gamma }_{1}^{l},\tilde{\gamma }_{2}^{l}), \min (\tilde{\gamma }_{1}^{u},\tilde{\gamma }_{2}^{u})]:\tilde{\gamma }_{1}\in \tilde{h}_{1}, \tilde{\gamma }_{2}\in \tilde{h}_{2}\};$

• (iv) $\tilde{h}_{1}\oplus \tilde{h}_{2}=\{\cup _{\tilde{\gamma }_{1}\in \tilde{h}_{1}, \tilde{\gamma }_{2}\in \tilde{h}_{2}}[\tilde{\gamma }_{1}^{l}+\tilde{\gamma }_{2}^{l}-\tilde{\gamma }_{1}^{l}\tilde{\gamma }_{2}^{l}, \tilde{\gamma }_{1}^{u}+\tilde{\gamma }_{2}^{u}-\tilde{\gamma }_{1}^{u}\tilde{\gamma }_{2}^{u}]\};$

• (v) $\tilde{h}_{1}\otimes \tilde{h}_{2}=\{\cup _{\tilde{\gamma }_{1}\in \tilde{h}_{1}, \tilde{\gamma }_{2}\in \tilde{h}_{2}}[\tilde{\gamma }_{1}^{l}\tilde{\gamma }_{2}^{l}, \tilde{\gamma }_{1}^{u}\tilde{\gamma }_{2}^{u}]\};$

• (vi) $\tilde{h}^{k}=\{\cup _{\tilde{\gamma }\in \tilde{h}}[(\tilde{\gamma }^{l})^{k}, (\tilde{\gamma }^{u})^{k}]\}$, where $k\in [0,1];$

• (vii) $k\tilde{h}=\{\cup _{\tilde{\gamma }\in \tilde{h}}[1-(1-\tilde{\gamma }^{l})^{k}, 1-(1-\tilde{\gamma }^{u})^{k}]\}$, where $k\in [0,1]$.

Property 3.3

(Chen and Xu 2014) Let $\tilde{h}_{1}, \tilde{h}_{2},$ and $\tilde{h}_{3}$ are IVHFEs and let $\lambda \in [0,1]$. Then, some properties of IVHFEs can be depicted as below:

• (i) $\tilde{h}_{1}\cup \tilde{h}_{2}=\tilde{h}_{2}\cup \tilde{h}_{1};$

• (ii) $\tilde{h}_{1}\cap \tilde{h}_{2}=\tilde{h}_{2}\cap \tilde{h}_{1};$

• (iii) $\tilde{h}_{1}\cup (\tilde{h}_{2}\cup \tilde{h}_{3})=(\tilde{h}_{1}\cup \tilde{h}_{2})\cup \tilde{h}_{3};$

• (iv) $\tilde{h}_{1}\cap (\tilde{h}_{2}\cap \tilde{h}_{3})=(\tilde{h}_{1}\cap \tilde{h}_{2})\cap \tilde{h}_{3};$

• (v) $\tilde{h}_{1}\oplus (\tilde{h}_{2}\oplus \tilde{h}_{3})=(\tilde{h}_{1}\oplus \tilde{h}_{2})\oplus \tilde{h}_{3};$

• (vi) $\tilde{h}_{1}\otimes (\tilde{h}_{2}\otimes \tilde{h}_{3})=(\tilde{h}_{1}\otimes \tilde{h}_{2})\otimes \tilde{h}_{3};$

• (vii) $\lambda (\tilde{h}_{1}\cup \tilde{h}_{2})=\lambda \tilde{h}_{1}\cup \lambda \tilde{h}_{2};$

• (viii) $\lambda (\tilde{h}_{1}\cap \tilde{h}_{2})=\lambda \tilde{h}_{1}\cap \lambda \tilde{h}_{2};$

• (ix) $(\tilde{h}_{1}\cup \tilde{h}_{2})^{\lambda }=\tilde{h}_{1}^{\lambda }\cup \tilde{h}_{2}^{\lambda };$

• (x) $(\tilde{h}_{1}\cap \tilde{h}_{2})^{\lambda }=\tilde{h}_{1}^{\lambda }\cap \tilde{h}_{2}^{\lambda }.$

Definition 3.3

For any $\tilde{h}=\{\cup _{\tilde{\gamma }\in \tilde{h}}[\tilde{\gamma }^{l},\tilde{\gamma }^{u}]\}$ and if $e_{\tilde{h}}$ is the set of all elements in $\tilde{h}$, and $|e_{\tilde{h}}|$ denotes the cardinality of $e_{\tilde{h}}$ then $S(\tilde{h})=\frac{1}{|e_{\tilde{h}}|}\sum _{\tilde{\gamma } \in \tilde{h}}^{e_{\tilde{h}}} {\tilde{\gamma }}=\frac{1}{|e_{\tilde{h}}|}\sum _{\tilde{\gamma } \in \tilde{h}}^{e_{\tilde{h}}} (\frac{\tilde{\gamma }^{l}+\tilde{\gamma }^{u}}{2})$, is defined as the score function of $\tilde{h}$.

For any two IVHFEs $\tilde{h}_{1}$ and $\tilde{h}_{2}$, $S(\tilde{h}_{1})>S(\tilde{h}_{2})$ implies that $\tilde{h}_{1}>\tilde{h}_{2}$; $S(\tilde{h}_{2})>S(\tilde{h}_{1})$ implies that $\tilde{h}_{2}>\tilde{h}_{1}$; otherwise, $S(\tilde{h}_{1})=S(\tilde{h}_{2})$ implies that $\tilde{h}_{1}=\tilde{h}_{2}.$

4 Intuitionistic interval-valued hesitant fuzzy set

When IVFS or IVIFS is considered, both the membership and non-membership functions are bound by the characters of intervals. But if these intervals are not taken fixed and the decision-makers use flexible intervals for the expression of reality, IVHFS with intuitionistic character, i.e., our consideration of intuitionistic interval-valued hesitant fuzzy set (IIVHFS) is generated.

Definition 4.1

Let $\tilde{A}$ be an intuitionistic interval-valued hesitant fuzzy set with intuitionistic interval-valued hesitant fuzzy element as $\tilde{h}_{a}$. Then,

$$\begin{aligned}&\tilde{h}_{a}=\{\langle [\tilde{h}_{a\text {M}}(x_{i}), \tilde{h}_{a\text {NM}}(x_{i})]\rangle \}=\{\langle \cup _{s}[\tilde{h}_{a\text {M}}^{l}(x_{i}),\\&\tilde{h}_{a\text {M}}^{u}(x_{i})],\cup _{s}[\tilde{h}_{a\text {NM}}^{l}(x_{i}), \tilde{h}_{a\text {NM}}^{u}(x_{i})]\rangle \}, \end{aligned}$$

where $x_{i}$ belongs to reference set X and $\tilde{h}_{a\text {M}}|_{x(i)}:X \rightarrow D[0,1]$ and $\tilde{h}_{a\text {NM}}|_{x(i)}:X \rightarrow D[0,1]$. Where, ‘M’ denotes membership and ‘NM’ denotes non-membership; $\cup _{s}$ denotes the set-union of all interval-valued hesitant fuzzy elements.

For each i, we, respectively, get the membership and the non-membership functions of the related intuitionistic interval-hesitant fuzzy set and D[0, 1] denotes the domain of the closed interval [0, 1].

Example 4.1

Let $\tilde{C}=\{\langle x_{1}; [0.10,0.50]; [0.25,0.40]\rangle , \langle x_{2}; [0.30,$ 0.50], [0.50, 0.65], [0.60, 0.80]; [0.35, 0.50], [0.15, 0.25],  $[0.10,0.20]\rangle , \langle x_{3}; [0.40,0.50], [0.10,0.60]; [0.30,0.50],$ $[0.20,0.30]\rangle \}$ be an intuitionistic interval-valued hesitant fuzzy set.

Definition 4.2

(Extension principle of IIVHFS) Let $H=\{h_{1}, h_{2},\ldots , h_{n}\}$ be a set of $n\in \mathbb {N}$, IIVHFEs and let $\varTheta$ be a function on H such that $\varTheta : [0,1]^{n} \rightarrow [0,1]$ satisfies the following: $\varTheta _{H}=\bigcup _{h_{i}\in \langle \cup _{s}[\tilde{h}_{i\text {M}}^{l}, \tilde{h}_{i\text {M}}^{u}],\cup _{s}[\tilde{h}_{i\text {NM}}^{l}, \tilde{h}_{i\text {NM}}^{u}]\rangle }\{\varTheta (h_{i})\}$.

Property 4.1

(Mathematical operations on IIVHFEs) Given three IIVHFEs represented by $\tilde{h}_{a_{1}}, \tilde{h}_{a_{2}}, \tilde{h}_{a_{3}}$; and $\cup _{s}$ denotes the set of all interval-valued hesitant fuzzy elements and consider $\lambda >0$, then the following mathematical operations can be performed as:

• (i) $\tilde{h}_{a_{1}}^{c} =\{\langle [\tilde{h}_{a_{1}\text {M}}, \tilde{h}_{a_{1}\text {NM}}]\rangle \}^{c} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u}],\cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}, \tilde{h}_{a_{1}\text {NM}}^{u}]\rangle \}^{c} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}, \tilde{h}_{a_{1}\text {NM}}^{u}],\cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u}]\rangle \};$

• (ii) $\tilde{h}_{a_{1}}\cup \tilde{h}_{a_{2}} =\{\langle \tilde{h}_{a_{1}\text {M}}, \tilde{h}_{a_{1}\text {NM}}\rangle \cup \langle \tilde{h}_{a_{2}\text {M}}, \tilde{h}_{a_{2}\text {NM}}\rangle \} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u}],\cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}, \tilde{h}_{a_{1}\text {NM}}^{u}]\rangle ~~~~\cup \langle \cup _{s}[\tilde{h}_{a_{2}\text {M}}^{l}, \tilde{h}_{a_{2}\text {M}}^{u}],\cup _{s}[\tilde{h}_{a_{2}\text {NM}}^{l}, \tilde{h}_{a_{2}\text {NM}}^{u}]\rangle \} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l} \vee \tilde{h}_{a_{2}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u} \vee \tilde{h}_{a_{2}\text {M}}^{u}], \cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}$

• (iii) $\tilde{h}_{a_{1}}\cap \tilde{h}_{a_{2}} =\{\langle \tilde{h}_{a_{1}\text {M}}, \tilde{h}_{a_{1}\text {NM}}\rangle \cap \langle \tilde{h}_{a_{2}\text {M}}, \tilde{h}_{a_{2}\text {NM}}\rangle \} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u}],\cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}, \tilde{h}_{a_{1}\text {NM}}^{u}]\rangle ~~~~\cap \langle \cup _{s}[\tilde{h}_{a_{2}\text {M}}^{l}, \tilde{h}_{a_{2}\text {M}}^{u}],\cup _{s}[\tilde{h}_{a_{2}\text {NM}}^{l}, \tilde{h}_{a_{2}\text {NM}}^{u}]\rangle \} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}\wedge \tilde{h}_{a_{2}\text {M}}^{l},\tilde{h}_{a_{1}\text {M}}^{u}\wedge \tilde{h}_{a_{2}\text {M}}^{u}],\cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}$

• (iv) $\tilde{h}_{a_{1}}\otimes \tilde{h}_{a_{2}} =\{\langle \tilde{h}_{a_{1}\text {M}}, \tilde{h}_{a_{1}\text {NM}}\rangle \otimes \langle \tilde{h}_{a_{2}\text {M}}, \tilde{h}_{a_{2}\text {NM}}\rangle \} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}\tilde{h}_{a_{2}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u}\tilde{h}_{a_{2}\text {M}}^{u}], \cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l} ~~~~+\tilde{h}_{a_{2}\text {NM}}^{l}- \tilde{h}_{a_{1}\text {NM}}^{l}\tilde{h}_{a_{2}\text {NM}}^{l}, \tilde{h}_{a_{1}\text {NM}}^{u}+\tilde{h}_{a_{2}\text {NM}}^{u} ~~~~-\tilde{h}_{a_{1}\text {NM}}^{u}\tilde{h}_{a_{2}\text {NM}}^{u}]\rangle \};$

• (v) $\tilde{h}_{a_{1}}\oplus \tilde{h}_{a_{2}} =\{\langle \tilde{h}_{a_{1}\text {M}}, \tilde{h}_{a_{1}\text {NM}}\rangle \oplus \langle \tilde{h}_{a_{2}\text {M}}, \tilde{h}_{a_{2}\text {NM}}\rangle \} =\{\langle \cup _{s}[\tilde{h}_{a_{1}\text {M}}^{l}+\tilde{h}_{a_{2}\text {M}}^{l}-\tilde{h}_{a_{1}\text {M}}^{l}\tilde{h}_{a_{2}\text {M}}^{l}, \tilde{h}_{a_{1}\text {M}}^{u}+\tilde{h}_{a_{2}\text {M}}^{u} ~~~~-\tilde{h}_{a_{1}\text {M}}^{u}\tilde{h}_{a_{2}\text {M}}^{u}], \cup _{s}[\tilde{h}_{a_{1}\text {NM}}^{l}\tilde{h}_{a_{2}\text {NM}}^{l}, \tilde{h}_{a_{1}\text {NM}}^{u}\tilde{h}_{a_{2}\text {NM}}^{u}]\rangle \};$

• (vi) $\lambda \tilde{h}_{a_{1}} =\lambda \{\langle [\tilde{h}_{a_{1}\text {M}}, \tilde{h}_{a_{1}\text {NM}}]\rangle \} =\{\langle \cup _{s}[1-(1-\tilde{h}_{a_{1}\text {M}}^{l})^{\lambda }, 1-(1-\tilde{h}_{a_{1}\text {M}}^{u})^{\lambda }], ~~~~\cup _{s}[(\tilde{h}_{a_{1}\text {NM}}^{l})^{\lambda },(\tilde{h}_{a_{1}\text {NM}}^{u})^{\lambda }]\rangle \};$

• (vii) $\tilde{h}_{a_{1}}^{\lambda }=\{\langle \cup _{s}[(\tilde{h}_{a_{1}\text {M}}^{l})^{\lambda }, (\tilde{h}_{a_{1}\text {M}}^{u})^{\lambda }],\cup _{s}[1-(1-\tilde{h}_{a_{1}\text {NM}}^{l})^{\lambda }, ~~~~~~~1-(1-\tilde{h}_{a_{1}\text {NM}}^{u})^{\lambda }]\rangle \}$

5 A new aggregation operator

Based on Definitions 2.10, 4.1, 4.2 and Property 4.1, we create here a new operator on intuitionistic interval-valued hesitant fuzzy sets for aggregating the corresponding hesitant fuzzy elements and this is termed here as Generalized Intuitionistic Enveloped Interval-Valued Hesitant Fuzzy Weighted Aggregation Operator, abbreviated as GIEIVHFWAO.

Definition 5.1

(GIEIVHFWAO) Let $\tilde{h}_{i}~(i=1,2,\ldots ,n)$ be a collection of IIVHFEs and $w=(w_{1},w_{2},\ldots ,w_{n})$ be the weight vector of $\tilde{h}_{i}~(i=1,2,\ldots ,n)$ with $w_{i}\in [0,1]$ and $\sum _{i=1}^{n} w_{i}=1$. An GIEIVHFWAO is a mapping $\tilde{H}^{n}\rightarrow \tilde{H}$, (H denotes the set of all hesitant fuzzy elements) such that GIEIVHFWAO$(\tilde{h}_{1},\tilde{h}_{2},\ldots ,\tilde{h}_{n})=\bigodot _{i=1}^{n}(\tilde{h}_{i}^{w_{i}}).$

If the weights $w_{i}~(i=1,2,\ldots ,n)$ are equally distributed to each $h_{i}~(i=1,2,\ldots ,n)$ then GIEIVHFWAO reduces to intuitionistic enveloped interval-valued hesitant fuzzy aggregation operator (IEIVHFAO) as: IEIVHFAO$(\tilde{h}_{1},\tilde{h}_{2},\ldots ,\tilde{h}_{n})=\bigodot _{i=1}^{n}(\tilde{h}_{i}^{\frac{1}{n}}).$

Here, ‘$\bigodot$’ is used for the proposed aggregation operator.

Theorem 5.1

Let $\tilde{h}_{i}~(i=1,2,\ldots ,n)$ be a collection of IIVHFEs and $w=(w_{1},w_{2},\ldots ,w_{n})$ be the weight vector of $\tilde{h_{i}}~(i=1,2,\ldots ,n)$ with $w_{i}\in [0,1]$ and $\sum _{i=1}^{n} w_{i}=1$, then, the aggregated values of $\tilde{h}_{i}~(i=1,2,\ldots ,n)$, calculated using generalized intuitionistic enveloped interval-valued hesitant fuzzy weighted aggregation operator (GIEIVHFWAO) is an IIVHFE as (where $\lambda >0$):

$$\begin{aligned}&\text {GIEIVHFWAO}(\tilde{h}_{1},\tilde{h}_{2},\ldots ,\tilde{h}_{n})\\&\quad =\left\{ \left\langle \left[ \left( 1-\prod \limits _{i=1}^{n} (1-\min (\tilde{h}_{iM}^{l}))^{w_{i}}\right) ^{\frac{1}{\lambda }},\right. \right. \right. \\&\qquad \left. \left( 1-\prod \limits _{i=1}^{n}(1-\max (\tilde{h}_{iM}^{u}))^{w_{i}}\right) ^{\frac{1}{\lambda }}\right] ,\\&\qquad \left[ 1-\left( 1-\prod \limits _{i=1}^{n} (\min (\tilde{h}_{i\text {NM}}^{l}))^{w_{i}}\right) ^{\frac{1}{\lambda }},\right. \\&\qquad \left. \left. \left. 1-\left( 1-\prod \limits _{i=1}^{n} (\max (\tilde{h}_{i\text {NM}}^{u}))^{w_{i}}\right) ^{\frac{1}{\lambda }}\right] \right\rangle :\tilde{h}_{iM},\tilde{h}_{i\text {NM}}\in \tilde{h}_{i}\right\} . \end{aligned}$$

If $\lambda =1$, we get $g_{IEIVHFWAO}$ which is defined as below:

$$\begin{aligned}&g_{\text {IEIVHFWAO}}\\&\quad =\left\{ \left\langle \left[ 1-\prod \limits _{i=1}^{n}(1-\min (\tilde{h}_{iM}^{l}))^{w_{i}},\right. \right. \right. \\&\qquad \left. 1-\prod \limits _{i=1}^{n}(1-\max (\tilde{h}_{iM}^{u}))^{w_{i}}\right] ,\\&\qquad \left[ 1-\left( 1-\prod \limits _{i=1}^{n}(\min (\tilde{h}_{i\text {NM}}^{l}))^{w_{i}}\right) ,\right. \\&\qquad \left. \left. \left. 1-\left( 1-\prod \limits _{i=1}^{n}(\max (\tilde{h}_{i\text {NM}}^{u}))^{w_{i}}\right) \right] \right\rangle :\tilde{h}_{iM},\tilde{h}_{i\text {NM}}\in \tilde{h}_{i}\right\} \\&\quad =\langle [h_{kM}^{l}, h_{kM}^{u}],[h_{k\text {NM}}^{l}, h_{k\text {NM}}^{u}]\rangle . \end{aligned}$$

where k is the optimized i among n values.

Proof

Since,

$$\begin{aligned}&(1-\min (\tilde{h}_{1M}^{l}))^{w_{1}}(1-\min (\tilde{h}_{2M}^{l}))^{w_{2}}\\&\quad =\prod \limits _{i=1}^{2}(1-\min (\tilde{h}_{iM}^{l}))^{w_{i}} \end{aligned}$$

and

$$\begin{aligned}&(1-\max (\tilde{h}_{1M}^{u}))^{w_{1}}(1-\max (\tilde{h}_{2M}^{u}))^{w_{2}}\\&\quad =\prod \limits _{i=1}^{2}(1-\max (\tilde{h}_{iM}^{u}))^{w_{i}} \end{aligned}$$

then using the laws of mathematical induction, the proof is simple and obvious.

Now, we define, respectively, the score and accuracy functions approach on $g_{\text {IEIVHFWAO}}$ as:

$$\begin{aligned}&g_{\text {IEIVHFWAO}}^{s}\\&\quad =(\tilde{h}_{kM}^{l}+\tilde{h}_{kM}^{u}-(\tilde{h}_{k\text {NM}}^{l}+\tilde{h}_{k\text {NM}}^{u}))/2, \end{aligned}$$

and

$$\begin{aligned} g_{\text {IEIVHFWAO}}^{a}=(\tilde{h}_{kM}^{l}+\tilde{h}_{kM}^{u}+\tilde{h}_{k\text {NM}}^{l}+\tilde{h}_{k\text {NM}}^{u})/2, \end{aligned}$$

for particular $i=k$.

Here, we get the following relations, where we consider two IIVHFSs as, $\hat{Q_{1}}$ and $\hat{Q_{2}}$ (where ‘s’ indicates ‘score’ and ‘a’ indicates ‘accuracy’)

(i):

when $g_{\text {IEIVHFWAO}}^{s}(\hat{Q_{1}})>g_{\text {IEIVHFWAO}}^{s}(\hat{Q_{2}}),$ then $\hat{Q_{1}}>\hat{Q_{2}}$;

(ii):

when $g_{\text {IEIVHFWAO}}^{s}(\hat{Q_{1}})<g_{\text {IEIVHFWAO}}^{s}(\hat{Q_{2}}),$ then $\hat{Q_{1}}<\hat{Q_{2}}$;

(iii):

when $g_{\text {IEIVHFWAO}}^{s}(\hat{Q_{1}})=g_{\text {IEIVHFWAO}}^{s}(\hat{Q_{2}}),$

then

• 1. $g_{\text {IEIVHFWAO}}^{a}(\hat{Q_{1}})>g_{\text {IEIVHFWAO}}^{a}(\hat{Q_{2}})$ implies $\hat{Q_{1}}>\hat{Q_{2}}$;

• 2. $g_{\text {IEIVHFWAO}}^{a}(\hat{Q_{1}})<g_{\text {IEIVHFWAO}}^{a}(\hat{Q_{2}})$ implies $\hat{Q_{1}}<\hat{Q_{2}}$;

• 3. $g_{\text {IEIVHFWAO}}^{a}(\hat{Q_{1}})=g_{\text {IEIVHFWAO}}^{a}(\hat{Q_{2}})$ implies $\hat{Q_{1}}=\hat{Q_{2}}$.

Removing the weight variables, we consider the generalized intuitionistic enveloped interval-valued hesitant fuzzy aggregation (GIEIVHFA) operator, defined as below. $\square$

Definition 5.2

Let $\tilde{h}_{i}~(i=1,2,\ldots ,n)$ be a collection of IIVHFEs. Then, the aggregated values of $\tilde{h}_{i}~(i=1,2,\ldots ,n)$, calculated using generalized intuitionistic enveloped interval-valued hesitant fuzzy aggregation operator (GIEIVHFAO) is an IIVHFE as (where $\lambda >0$):

$$\begin{aligned}&\text {GIEIVHFAO}(\tilde{h}_{1},\tilde{h}_{2},\ldots ,\tilde{h}_{n})\\&\quad =\left\{ \left\langle \left[ \left( 1-\prod \limits _{i=1}^{n}(1-\min (\tilde{h}_{iM}^{l}))\right) ^{\frac{1}{\lambda }},\right. \right. \right. \\&\qquad \left. \left( 1-\prod \limits _{i=1}^{n}(1-\max (\tilde{h}_{iM}^{u}))\right) ^{\frac{1}{\lambda }}\right] ,\\&\qquad \left[ 1-(1-\prod \limits _{i=1}^{n}(\min (\tilde{h}_{i\text {NM}}^{l})))^{\frac{1}{\lambda }},\right. \\&\qquad \left. \left. \left. 1-\left( 1-\prod \limits _{i=1}^{n}(\max (\tilde{h}_{i\text {NM}}^{u}))\right) ^{\frac{1}{\lambda }}\right] \right\rangle :\tilde{h}_{iM},\tilde{h}_{i\text {NM}}\in \tilde{h}_{i}\right\} . \end{aligned}$$

If $\lambda =1$, we get $g_{\text {IEIVHFAO}}$ which is described as,

$$\begin{aligned}&g_{\text {IEIVHFAO}}\\&\quad =\left\{ \left\langle \left[ 1-\prod \limits _{i=1}^{n}(1-\min (\tilde{h}_{i\text {M}}^{l})), 1-\prod \limits _{i=1}^{n}(1-\max (\tilde{h}_{i\text {M}}^{u}))\right] ,\right. \right. \\&\qquad \left[ 1-\left( 1-\prod \limits _{i=1}^{n}(\min (\tilde{h}_{i\text {NM}}^{l}))\right) ,\right. \\&\qquad \left. \left. \left. 1-\left( 1-\prod \limits _{i=1}^{n}(\max (\tilde{h}_{i\text {NM}}^{u}))\right) \right] \right\rangle :\tilde{h}_{i\text {M}},\tilde{h}_{i\text {NM}}\in \tilde{h}_{i}\right\} \\&\quad =\langle [h_{k\text {M}}^{l}, h_{k\text {M}}^{u}],[h_{k\text {NM}}^{l}, h_{k\text {NM}}^{u}]\rangle . \end{aligned}$$

Property 5.1

GIEIVHFWAO, when applied on IIVHFEs $\tilde{h}_{i}~(i=1,2,\ldots ,n)$, follows idempotent, bounded and monotonic properties.

Proof

Proofs are easy to achieve. $\square$

6 Intuitionistic interval-valued hesitant fuzzy matrix game

In this section, two subsections are allowed. First one describes the matrix games in crisp environment, whereas the second depicts the situation in IIVHF environment.

6.1 Matrix game in crisp environment

A finite two-person zero-sum game in matrix form, (Y, Z, A), sometimes called a matrix game, means that there is a matrix $A=({a}_{ij})~(i=1,2,\ldots , p,~j=1,2,\ldots , q)$ of real numbers, called payoff matrix as

$$\begin{aligned} A=\begin{bmatrix} a_{21}&a_{22}&a_{23}&\dots&a_{2q} \\ \vdots&\vdots&\vdots&\ddots&\vdots \\ a_{p1}&a_{p2}&a_{p3}&\dots&a_{pq} \end{bmatrix}. \end{aligned}$$

When the player I, the row player, choose to play row i and player II, the column player, choose to play column j, then the payoff to player I is ${a}_{ij}$. The payoff to player I is ${a}_{ij}$ and that of player II is $-{a}_{ij}$ due to the zero-sum condition, imposed upon the two-person game. Both players want to choose strategies that will benefit their individual payoffs.

Consider the matrix game with the set of pure strategies $\alpha$ and $\beta$ and that of mixed strategies Y and Z for two players I and II, respectively, are defined as:

$$\begin{aligned}\alpha & =\{\alpha _1,\alpha _2,\ldots ,\alpha _p\} \;\text{and} \;\beta =\{\beta _1,\beta _2,\ldots ,\beta _q\}, \\Y& =\left\{y=(y_1,y_2,\ldots ,y_p)^{\text {T}}: \sum _{i=1}^{p}y_{i}=1, ~y_i \ge 0, ~i=1,2,\ldots ,p\right\}, \\Z & =\left\{z=(z_1,z_2,\ldots ,z_q)^{\text {T}}: \sum _{j=1}^{q}z_{j}=1,\; z_j \ge 0, ~j=1,2,\ldots ,q \right\},\end{aligned}$$

where $y_i~(i=1,2,\ldots , p)$ and $z_j~(j=1,2,\ldots ,q)$ are probabilities in which the players I and II choose their pure strategies $\alpha _{i}\in \alpha ~(i=1,2,\ldots , p)$ and $\beta _{j}\in \beta ~(j=1,2,\ldots , q)$, respectively. Basically, we find the value of the game and the optimal strategy(ies) for each player. The value of the game is defined to be the maximum guaranteed gain to the maximizing player I or the minimum possible loss to the minimizing player II when the best strategies are used by both the players. If a player lists the worst possible outcomes of all his or her potential strategies, he or she will choose that strategy, the most suitable for him or her. This concept is treated as maximin or minimax principle. If in a game, maximin for player I and minimax for player II be equal, then the game is said to have a saddle point [Neumann and Morgenstern (1944) used the term ‘saddle point’]. Assume that player I uses any mixed strategy $y\in Y$. Obviously, player I’s expected gain-floor is $\min (y^{t}Az: z\in Z)$ and if shortly be denoted by v, we have to maximize v, say $v^{*}$ for certain $y^{*}\in Y$, as $v(y^{*})=\max (vy: y\in Y)=\max (\min \{\sum _{i=1}^{p}a_{ij}y_{i}: j=1,2,\ldots ,q\})$.

Such $y^{*}$ and $v^{*}$, respectively, called player I’s maximin strategy and game value, are obtained from the following linear programming problem in Model 1.

Model 1

$$\begin{aligned} &\text {maximize}~\quad v\end{aligned}$$

(1)

$$\begin{aligned} \text {subject to }&\sum _{i=1}^{p}a_{ij}y_{i}\ge v~~(j=1(1)q),\end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i=1}^{p}y_{i}=1,\end{aligned}$$

(3)

$$\begin{aligned}&y_{i}\ge 0 ~~(i=1(1)p). \end{aligned}$$

(4)

And with same argument, player II’s optimal or minimax strategy, say $z^{*}\in Z$, and the game value, say $w^{*}$ are derived from Model 2 as:

Model 2

$$\begin{aligned} \text {minimize}~\quad & w\end{aligned}$$

(5)

$$\begin{aligned} \text {subject to }&\sum _{j=1}^{q}a_{ij}z_{i}\le w~~(i=1(1)p),\end{aligned}$$

(6)

$$\begin{aligned}&\sum _{j=1}^{q}z_{j}=1,\end{aligned}$$

(7)

$$\begin{aligned}&z_{j}\ge 0 ~~(j=1(1)q). \end{aligned}$$

(8)

6.2 Matrix game in IIVHF environment

Due to the imprecision of the available information, fuzzy sets, interval numbers, rough sets, etc. are used as tools to construct the model of the problem. As a special case of fuzzy sets, Atanassov’s IFS considers the non-membership characters of the elements of corresponding set. Interval number-based set also elaborately describes elements’ flexibility over a range of numbers. But in the above-mentioned situations, decision-makers use boundaries of fixed choices. So, hesitancy character can be concluded with the above characters to freely choose the elements within several boundaries incorporated with membership and non-membership degrees. Firstly, we generate matrix game models when elements are interval in nature, as Model 3 and Model 4.

Model 3

$$\begin{aligned} & \text {maximize} \quad [v^{l},v^{r}]\\ & \text {subject to } \sum _{i=1}^{p}[a_{ij}^{l},a_{ij}^{r}]y_{i}\ge _{II} [v^{l},v^{r}]~(j=1(1)q),\\&\qquad\qquad\; \text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 4

$$\begin{aligned} & \text {maximize}\quad [w^{l},w^{r}]\\ & \text {subject to } \sum _{j=1}^{q}[a_{ij}^{l},a_{ij}^{r}]z_{j}\le _{II} [w^{l},w^{r}]~(i=1(1)p),\\&\qquad \qquad \; \text {the constraints (7) and (8)}. \end{aligned}$$

where both “$\ge _{\text {II}}$” and “$\le _{\text {II}}$” denote the interval inequalities.

Value of the game is defined to be the maximum guaranteed gain to the maximizing player I or the minimum possible loss to the minimizing player II when the best strategies are used by both the players. If a player lists the worst possible outcomes of all his or her potential strategies, he or she will choose that strategy, the most suitable for him or her.

Secondly, from Model 1 and Model 2, we degenerate hesitant fuzzy matrix game $(Y, Z, h_{a_{ij}})$ as depicted in Model 5 and Model 6.

Model 5

$$\begin{aligned} & \text {maximize} \quad h_{v}\\ & \text {subject to }\sum _{i=1}^{p}h_{a_{ij}}y_{i}\ge _{HFI} h_{v}~(j=1(1)q),\\& \qquad\qquad\; \text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 6

$$\begin{aligned} & \text {minimize}~\quad h_{w}\\ & \text {subject to } \sum _{j=1}^{q}h_{a_{ij}}z_{i}\le _{HFI} h_{w}~~(i=1(1)p),\\&\qquad \qquad \; \text {the constraints (7) and (8)}. \end{aligned}$$

where both “$\ge _{\text {HFI}}$” and “$\le _{\text {HFI}}$” denote the hesitant fuzzy inequalities; $h_{a_{ij}}$ represents hesitant fuzzy payoffs of the game; $h_{v}$ and $h_{w}$ represent the game values of two players to be optimized. Now, maximin value of player I is obtained after solving Model 5 and minimax value of player II is reached on solving Model 6.

Let $\tilde{H}=(\tilde{h}_{a_{ij}})_{p\times q}$ be the intuitionistic interval-valued hesitant fuzzy decision matrix to the matrix game by the players or decision-makers, then according to Definition 4.1 and using interval constraints relations, the expected payoff of player I can be written as $E(\tilde{h}_{a_{ij}})$, given by

$$\begin{aligned}&E(\tilde{h}_{a_{ij}})\\&\quad = y^{t}\tilde{h}_{a_{ij}} z \\&\quad = \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q} \tilde{h}_{a_{ij}}y_{i}z_{j}\\&\quad =\sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}\langle \cup _{s}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}],\cup _{s}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\rangle \ y_{i}z_{j}\\&\quad =\left\langle \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}\cup _{s}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}],\right. \\&\qquad \left. \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}\cup _{s}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\right\rangle y_{i}z_{j}. \end{aligned}$$

And using our proposed aggregating operator, i.e., GIEIVHFWAO, defined in Sect. 5, we convert the intuitionistic interval-valued hesitant fuzzy elements into intuitionistic interval-valued fuzzy elements and then the expected payoff of player I is defined and written as,

$$\begin{aligned}&\mathbb {E}(\tilde{h}_{a_{ij}})\\&\quad =\left\langle \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}]\right. ,\\&\qquad \left. \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\right\rangle y_{i}z_{j}. \end{aligned}$$

Since intuitionistic interval-valued hesitant fuzzy matrix game (IIVHFMG) is zero-sum, therefore using Definition 4.1 and interval constraint relations, we get for player II,

$$\begin{aligned}&E(-\tilde{h}_{a_{ij}})\\&\quad = y^{t}(-\tilde{h}_{a_{ij}})z\\&\quad = \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q} (-\tilde{h}_{a_{ij}})y_{i}z_{j})\\&\quad =\sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}-\langle \cup _{s}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}],\\&\cup _{s}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\rangle \ y_{i}z_{j}\\&\quad =\left\langle -\sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}\cup _{s}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}],\right. \\&\qquad \left. -\sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}\cup _{s}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\right\rangle y_{i}z_{j}. \end{aligned}$$

Again applying our proposed aggregation operator (GIEIVHFWAO) of Sect. 5, we reduce the intuitionistic interval-valued hesitant fuzzy elements into intuitionistic interval-valued fuzzy elements and the corresponding expected payoff of player II is written as,

$$\begin{aligned}&\mathbb {E}(-\tilde{h}_{a_{ij}})\\&\quad =\left\langle \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}[-h_{a_{ij}\text {M}}^{u}, -h_{a_{ij}\text {M}}^{l}],\right. \\&\left. \qquad \sum \limits _{i=1}^{p}\sum \limits _{j=1}^{q}[-h_{a_{ij}\text {NM}}^{u}, -h_{a_{ij}\text {NM}}^{l}]\right\rangle y_{i}z_{j}. \end{aligned}$$

Both $\mathbb {E}(\tilde{h}_{a_{ij}})$ and $\mathbb {E}(-\tilde{h}_{a_{ij}})$ are IIVFNs.

Player II is eager to find a mixed strategy $z\in Z$ which minimizes E(y, z). This can be denoted as $\min _{z\in Z}(E(y,z))$. But as player I should choose a mixed strategy $y\in Y$ maximizing $\min _{z\in Z}(E(y,z))$ of player II, i.e., $v^{*}=\max _{y\in Y}\min _{z\in Z}(E(y,z))$ and this $v^{*}$ is called sometimes as the player I’s gain-floor. Similarly, player I wishes to get a mixed strategy $y\in Y$ which maximize E(y, z), denoted as $\max _{y\in Y}(E(y,z))$.

Thus, player II should choose a mixed strategy $z\in Z$ which minimizes $\max _{y\in Y}(E(y,z))$ of player I, i.e., $w^{*}=\min _{z\in Z}(\max _{y\in Y}(E(y,z)))$ and this $w^{*}$ is called player II’s loss-ceiling. Obviously, player I’s gain-floor and player II’s loss-ceiling should be intuitionistic interval-valued hesitant fuzzy numbers. So, the solution of the game may be defined in a similar way to that of the Pareto-optimal solution as follows.

Definition 6.1

(Solution of IIVHFMG) Let $v^{*}=\langle [\underline{v}_{\text {M}},\overline{v}_{\text {M}}],[\underline{v}_{\text {NM}},\overline{v}_{\text {NM}})]\rangle$ and $w^{*}=\langle [\underline{w}_{\text {M}},\overline{w}_{\text {M}}],[\underline{w}_{\text {NM}},\overline{w}_{\text {NM}})]\rangle$ be two IIVHFEs. Assume that there exist $y^{*}\in Y$ and $z^{*}\in Z$. Then $(y^{*},z^{*},v^{*},w^{*})$ is called a pragmatic solution of the intuitionistic interval-valued hesitant fuzzy matrix game (IIVHFMG) $\tilde{H}$ if for any $y \in Y$ and $z \in Z$, $(y^{*},z^{*},v^{*},w^{*})$ satisfies the conditions $y^{*^t}\tilde{H}z\ge _{\text {IIVHFI}} v^{*},$ and  $y^{t}\tilde{H}z^{*}\le _{\text {IIVHFI}} w^{*}.$

Definition 6.2

(Game value of IIVHFMG) Assume that there exist $v_{1}^{*}\in V$ and $w_{1}^{*}\in W$. If there exist no other $v_{2}^{*}\in V (v_{1}^{*}\ne v_{2}^{*})$ and $w_{2}^{*}\in W (w_{1}^{*}\ne w_{2}^{*})$ such that $v_{1}^{*}\le _{\text {IIVHFI}} v_{2}^{*}$ and $w_{1}^{*}\ge _{\text {IIVHFI}} w_{2}^{*},$ then, $(y^*,z^*,v_1^*,w_1^*)$ is called a solution of the intuitionistic interval-valued hesitant fuzzy matrix game $\tilde{H}$; $y^{*}$ is called a maximin strategy for player I and $z^{*}$ is called a minimax strategy for player II. $v_{1}^{*}$ and $w_{1}^{*}$ are called player I’s gain-floor and player II’s loss-ceiling and $y^{*^t}\tilde{H} z^{*^t}$ as a game value.

According to Theorem 5.1, we derive Model 7 and Model 8 for players I and II, respectively, from Models 5 and 6 using Models 3 and 4, respectively, as,

Model 7

$$\begin{aligned} \text {maximize} \quad & \langle \cup _{s}[\tilde{h}_{v\text {M}}^{l}(x_{i}),\tilde{h}_{v\text {M}}^{u}(x_{i})],\\&\cup _{s}[\tilde{h}_{v\text {NM}}^{l}(x_{i}),\tilde{h}_{v\text {NM}}^{u}(x_{i})]\rangle \\ \text {subject to }&\sum _{i=1}^{p}\langle \cup _{s}[\tilde{h}_{{a_{ij}\text {M}}}^{l}(x_{i}),\tilde{h}_{{a_{ij}\text {M}}}^{u}(x_{i})],\\&\cup _{s}[\tilde{h}_{{a_{ij}\text {NM}}}^{l}(x_{i}), \tilde{h}_{{a_{ij}\text {NM}}}^{u}(x_{i})]\rangle y_{i}\\&\ge _{\text {IIVHFI}} \langle \cup _{s}[\tilde{h}_{v\text {M}}^{l}(x_{i}), \tilde{h}_{vM}^{u}(x_{i})],\\&\cup _{s}[\tilde{h}_{v\text {NM}}^{l}(x_{i}), \tilde{h}_{v\text {NM}}^{u}(x_{i})]\rangle ~(j=1(1)q),\\&\text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 8

$$\begin{aligned} \text {minimize}~\quad & \langle \cup _{s}[\tilde{h}_{wM}^{l}(x_{i}),\tilde{h}_{wM}^{u}(x_{i})],\\&\cup _{s}[\tilde{h}_{w\text {NM}}^{l}(x_{i}),\tilde{h}_{w\text {NM}}^{u}(x_{i})]\rangle \\ \text {subject to }&\sum _{j=1}^{q} \langle \cup _{s}[\tilde{h}_{{a_{ij}\text {M}}}^{l}(x_{i}),\tilde{h}_{{a_{ij}\text {M}}}^{u}(x_{i})],\\&\cup _{s}[\tilde{h}_{{a_{ij}\text {NM}}}^{l}(x_{i}), \tilde{h}_{{a_{ij}\text {NM}}}^{u}(x_{i})]\rangle z_{j}\\&\le _{IIVHFI} \langle \cup _{s}[\tilde{h}_{wM}^{l}(x_{i}), \tilde{h}_{wM}^{u}(x_{i})],\\&\cup _{s}[\tilde{h}_{w\text {NM}}^{l}(x_{i}), \tilde{h}_{w\text {NM}}^{u}(x_{i})]\rangle ~(i=1(1)p),\\&\text {the constraints (7) and (8)}. \end{aligned}$$

where both “$\ge _{\text {IIVHFI}}$” and “$\le _{\text {IIVHFI}}$” denote the intuitionistic interval-valued hesitant fuzzy inequalities. Now maximin value of player I is obtained after solving Model 7 and minimax value of player II is reached on solving Model 8. Based on the introduced ranking approach of IIVHFE and established models of the game problems for the players, the next upcoming para establishes an approach to solve the intuitionistic interval-valued hesitant fuzzy matrix game which addresses the situation where elements are IIVHFEs. Now applying $g_{\text {IEIVHFWAO}}$ from Theorem 5.1, we obtain the models as Model 9 and Model 10 respectively from Model 7 and Model 8 as below:

Model 9

$$\begin{aligned} \text {maximize}\quad & \langle [h_{k_{v}\text {M}}^{l}, h_{k_{v}\text {M}}^{u}],[h_{k_{v}\text {NM}}^{l}, h_{k_{v}\text {NM}}^{u}]\rangle \\ \text {subject to }&\sum _{i=1}^{p} \langle [h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}],\\&[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\rangle y_{i}\\&\ge _{IIVFI} \langle [h_{k_{v}\text {M}}^{l}, h_{k_{v}\text {M}}^{u}],\\&[h_{k_{v}\text {NM}}^{l}, h_{k_{v}\text {NM}}^{u}]\rangle ~(j=1(1)q),\\&\text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 10

$$\begin{aligned} \text {minimize}~\quad & \langle [h_{k_{w}\text {M}}^{l}, h_{k_{w}\text {M}}^{u}],[h_{k_{w}\text {NM}}^{l}, h_{k_{w}\text {NM}}^{u}]\rangle \\ \text {subject to }&\sum _{j=1}^{q} \langle [h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}],[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]\rangle z_{j}\\&\le _{IIVFI} \langle [h_{k_{w}\text {M}}^{l}, h_{k_{w}\text {M}}^{u}],[h_{k_{w}\text {NM}}^{l}, h_{k_{w}\text {NM}}^{u}]\rangle \\&\qquad (i=1(1)p),\\&\text {the constraints (7) and (8)}. \end{aligned}$$

Here, $\ge _{\text {IIVFI}}$ and $\le _{\text {IIVFI}}$ indicate the abbreviated form of intuitionistic interval-valued fuzzy inequalities and the index $\textit{k}$ is used to signify the particular positional value, introducing after the aggregation operator.

Model 9 and Model 10 are reduced into bi-objective linear programming problems as Model 11 and Model 12, given below.

Model 11

$$\begin{aligned} \text {maximize}\quad & [h_{k_{v}\text {M}}^{l}, h_{k_{v}\text {M}}^{u}]\\ \text {minimize}\quad ~&[h_{k_{v}\text {NM}}^{l}, h_{k_{v}\text {NM}}^{u}]\\ \text {subject to }&\sum _{i=1}^{p}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}] y_{i}\ge [h_{k_{v}\text {M}}^{l}, h_{k_{v}\text {M}}^{u}]\\&\qquad (j=1(1)q),\\&\sum _{i=1}^{p}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]y_{i}\le [h_{k_{v}\text {NM}}^{l}, h_{k_{v}\text {NM}}^{u}]\\&\qquad (j=1(1)q),\\&\text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 12

$$\begin{aligned} \text {minimize}~\quad & [h_{k_{w}\text {M}}^{l}, h_{k_{w}\text {M}}^{u}]\\ \text {maximize}\quad &[h_{k_{w}\text {NM}}^{l}, h_{k_{w}\text {NM}}^{u}]\\ \text {subject to }&\sum _{j=1}^{q}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}] z_{j}\\&\le [h_{k_{w}\text {M}}^{l}, h_{k_{w}\text {M}}^{u}] ~(i=1(1)p),\\&\sum _{j=1}^{q}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]z_{j}\\&\le [h_{k_{w}\text {NM}}^{l}, h_{k_{w}\text {NM}}^{u}] ~(i=1(1)p),\\&\text {the constraints (7) and (8)}. \end{aligned}$$

Now we simplify the equations of Model 11 and Model 12 in the following format as:

Model 13

$$\begin{aligned} \text {maximize}\quad &[\underline{v}_{\text {M}}, \overline{v}_{\text {M}}]\\ \text {minimize}\quad ~&[\underline{v}_{NM}, \overline{v}_{NM}]\\ \text {subject to }&\sum _{i=1}^{p}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}] y_{i}\ge [\underline{v}_{\text {M}}, \overline{v}_{\text {M}}]\\&\qquad (j=1(1)q),\\&\sum _{i=1}^{p}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]y_{i}\le [\underline{v}_{\text {NM}}, \overline{v}_{\text {NM}}]\\&\qquad (j=1(1)q),\\&\underline{v}_{\text {M}}\le \overline{v}_{\text {M}},~\underline{v}_{\text {NM}}\le \overline{v}_{\text {NM}},\\&\overline{v}_{\text {M}}+\overline{v}_{\text {NM}}\ge 0,~\overline{v}_{\text {M}}+\overline{v}_{\text {NM}}\le 1,\\&\text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 14

$$\begin{aligned} \text {minimize}\quad ~&[\underline{w}_{\text {M}}, \overline{w}_{\text {M}}]\\ \text {maximize}\quad &[\underline{w}_{\text {NM}}, \overline{w}_{\text {NM}}]\\ \text {subject to }&\sum _{j=1}^{q}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}] z_{j}\\&\le [\underline{w}_{\text {M}}, \overline{w}_{\text {M}}] ~(i=1(1)p),\\&\sum _{j=1}^{q}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]z_{j}\\&\ge [\underline{w}_{\text {NM}}, \overline{w}_{\text {NM}}] ~(i=1(1)p),\\&\underline{w}_{\text {M}}\le \overline{w}_{\text {M}},~\underline{w}_{\text {NM}}\le \overline{w}_{\text {NM}},\\&\overline{w}_{\text {M}}+\overline{w}_{\text {NM}}\ge 0,~\overline{w}_{\text {M}}+\overline{w}_{\text {NM}}\le 1,\\&\text {the constraints (7) and (8)}. \end{aligned}$$

Now using Definitions 2.4, 2.5, 2.8 and 2.9, the equations of Model 13 and Model 14 are changed and we get Model 15 and Model 16 respectively as:

Model 15

$$\begin{aligned} \text {maximize}\quad &((\underline{v}_{\text {M}}+\overline{v}_{\text {M}})/2-(\underline{v}_{\text {NM}}+\overline{v}_{\text {NM}})/2)\\ \text {subject to }&\sum _{i=1}^{p}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}] y_{i}\\&\ge [\underline{v}_{\text {M}}, \overline{v}_{\text {M}}]~(j=1(1)q),\\&\sum _{i=1}^{p}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]y_{i}\\&\le [\underline{v}_{\text {NM}}, \overline{v}_{\text {NM}}]~(j=1(1)q),\\&\underline{v}_{\text {M}}\le \overline{v}_{\text {M}},~\underline{v}_{\text {NM}}\le \overline{v}_{\text {NM}},\\&\overline{v}_{\text {M}}+\overline{v}_{\text {NM}}\ge 0,~\overline{v}_{\text {M}}+\overline{v}_{\text {NM}}\le 1,\\&\text {the constraints (3) and (4)}. \end{aligned}$$

and

Model 16

$$\begin{aligned} \text {minimize}\quad ~&((\underline{w}_{\text {M}}+\overline{w}_{\text {M}})/2-(\underline{w}_{\text {NM}}+\overline{w}_{\text {NM}})/2)\\ \text {subject to }&\sum _{j=1}^{q}[h_{a_{ij}\text {M}}^{l}, h_{a_{ij}\text {M}}^{u}] z_{j}\\&\le [\underline{w}_{\text {M}}, \overline{w}_{\text {M}}]~(i=1(1)p),\\&\sum _{j=1}^{q}[h_{a_{ij}\text {NM}}^{l}, h_{a_{ij}\text {NM}}^{u}]z_{j}\\&\ge [\underline{w}_{\text {NM}}, \overline{w}_{\text {NM}}]~(i=1(1)p),\\&\underline{w}_{\text {M}}\le \overline{w}_{\text {M}},~\underline{w}_{\text {NM}}\le \overline{w}_{\text {NM}},\\&\overline{w}_{\text {M}}+\overline{w}_{\text {NM}}\ge 0,~\overline{w}_{\text {M}}+\overline{w}_{\text {NM}}\le 1,\\&\text {the constraints (7) and (8)}. \end{aligned}$$

Now solving Model 15 and Model 16, we calculate the required results of our formulated problem.

7 A real-life management problem

Not only the developed or developing countries, but also the whole world are facing the problems of strikes, lockouts, work stoppages everyday in both the hemispheres. From the very beginning of industrial revolution, the relations among workers, employers and wages, draw the attention of all concerned. When the workers are denied with some beneficial treatments, an unusual situation arises between the employees and the employers. Sometimes, we call it as a strike or lockout or work stoppage. A strike is the most popular, established, allowed and sometimes criticized component of a workplace dispute. A strike can be defined as concerted suspension of work by a group of employees or a group of laborers for the purpose of obtaining or resisting or improving in the conditions of employment or the existing disputes over the terms of the labor contract.

Here, we consider strike as a matrix game problem. Consider, there are a company or an employer A and a set of workers or employees B. Workers contribute their labors to the company for producing the production materials, say, Xs. Generally the production of Xs engages both employers and employees and naturally some management criteria arise. Company A wishes to earn more profit using B, whereas, B wishes to earn for better livelihood by producing Xs in the company and vice versa. Therefore, a management problem arises. When company earns more without paying the wages properly to laborers and workers, or company loses its profit but laborers are given their wages periodically, then disputes arise. Then company expresses its unwillingness to pay wages. So, a clash begins between employers and employees. Strike sometimes appears as an arm of workers to express their demand. To earn the labor right, workers do strikes, lockouts, work stoppage, etc. Workers want to maximize their wages, whereas company wishes minimum loss for itself. So, we can describe it as a game phenomena considering its two players as workers (player I) and company (player II). Player I is a maximizing player and player II is a minimizing player.

We consider player I’s strategies as: do strike for wage increase ($\zeta _{1}$), do strike for wage cut ($\zeta _{2}$) and do strike for changes of daily-hours ($\zeta _{3}$). Similarly, player II’s strategies are: cutting off wages of workers who sought for wage increase ($\eta _{1}$), stopping off wages of workers crying for wage cut ($\eta _{2}$) and employing new workers against those shouting for changing in daily-hours labor ($\eta _{3}$).

Under the circumstances, workers call out a work stoppage through 3-days-12-h strike. The strike persists from 6 am to 6 pm in three sections, say, from 6 to 10 am, from 10 am to 2 pm and thereafter till 6 pm. We concentrate the data in Tables 1, 2 and 3. Here,

Table 1 Demand for wage increasing in 3 days

$$\begin{aligned}&c_{11}^{\text {wi}}=\langle [0.50,0.60],[0.20,0.30] \rangle \langle [0.40,0.50],[0.20,0.30] \rangle \\&\quad \langle [0.50,0.65],[0.10,0.20] \rangle ,\\&c_{12}^{\text {wi}}=\langle [0.50,0.60],[0.04,0.10] \rangle \langle [0.40,0.60],[0.03,0.10] \rangle \\&\quad \langle [0.40,0.50],[0.04,0.10] \rangle ,\\&c_{13}^{\text {wi}}=\langle [0.30,0.40],[0.50,0.60] \rangle \langle [0.20,0.30],[0.60,0.70] \rangle \\&\quad \langle [0.10,0.20],[0.60,0.70] \rangle ,\\&c_{21}^{\text {wi}}=\langle [0.70,0.80],[0.10,0.20] \rangle \langle [0.30,0.50],[0.10,0.20] \rangle \\&\quad \langle [0.40,0.50],[0.10,0.20] \rangle ,\\&c_{22}^{\text {wi}}=\langle [0.60,0.80],[0.10,0.20] \rangle \langle [0.50,0.80],[0.05,0.20] \rangle \\&\quad \langle [0.10,0.20],[0.10,0.20] \rangle ,\\&c_{23}^{\text {wi}}=\langle [0.05,0.10],[0.40,0.50] \rangle \langle [0.30,0.40],[0.40,0.50] \rangle \\&\quad \langle [0.20,0.40],[0.40,0.50] \rangle ,\\&c_{31}^{\text {wi}}=\langle [0.20,0.40],[0.40,0.50] \rangle \langle [0.35,0.40],[0.40,0.50] \rangle \\&\quad \langle [0.20,0.60],[0.10,0.30] \rangle ,\\&c_{32}^{\text {wi}}=\langle [0.40,0.60],[0.00,0.01] \rangle \langle [0.30,0.60],[0.03,0.04] \rangle \\&\quad \langle [0.00,0.02],[0.01,0.02] \rangle ,\\&c_{33}^{\text {wi}}=\langle [0.60,0.70],[0.10,0.20] \rangle \langle [0.20,0.50],[0.20,0.30] \rangle \\&\quad \langle [0.30,0.40],[0.10,0.30] \rangle ;\\ \end{aligned}$$

Table 2 Demand for strike in 3 days against wage cut

$$\begin{aligned}&c_{11}^{\text {wc}}=\langle [0.30,0.40],[0.50,0.60] \rangle \langle [0.20,0.30],[0.60,0.70] \rangle \\&\quad \langle [0.10,0.20],[0.60,0.70] \rangle ,\\&c_{12}^{\text {wc}}=\langle [0.60,0.70],[0.20,0.30] \rangle \langle [0.40,0.70],[0.20,0.30] \rangle \\&\quad \langle [0.40,0.50],[0.20,0.30] \rangle ,\\&c_{13}^{\text {wc}}=\langle [0.50,0.60],[0.04,0.10] \rangle \langle [0.40,0.60],[0.03,0.10] \rangle \\&\quad \langle [0.40,0.50],[0.04,0.10] \rangle ,\\&c_{21}^{\text {wc}}=\langle [0.05,0.10],[0.40,0.50] \rangle \langle [0.30,0.40],[0.40,0.50] \rangle \\&\quad \langle [0.20,0.40],[0.40,0.50] \rangle ,\\&c_{22}^{\text {wc}}=\langle [0.40,0.50],[0.20,0.30] \rangle \langle [0.30,0.60],[0.30,0.40] \rangle \\&\quad \langle [0.20,0.50],[0.30,0.40] \rangle ,\\&c_{23}^{\text {wc}}=\langle [0.60,0.80],[0.10,0.20] \rangle \langle [0.50,0.80],[0.05,0.20] \rangle \\&\quad \langle [0.10,0.20],[0.10,0.20] \rangle ,\\&c_{31}^{\text {wc}}=\langle [0.40,0.50],[0.10,0.20] \rangle \langle [0.20,0.50],[0.20,0.30] \rangle \\&\quad \langle [0.10,0.30],[0.30,0.40] \rangle ,\\&c_{32}^{\text {wc}}=\langle [0.40,0.50],[0.30,0.40] \rangle \langle [0.30,0.50],[0.30,0.50] \rangle \\&\quad \langle [0.20,0.40],[0.50,0.50] \rangle ,\\&c_{33}^{\text {wc}}=\langle [0.40,0.60],[0.00,0.01] \rangle \langle [0.30,0.60],[0.03,0.04] \rangle \\&\quad \langle [0.00,0.02],[0.01,0.02] \rangle \\ &c_{11}^{\text {ch}}=\langle [0.30,0.40],[0.50,0.60] \rangle \langle [0.20,0.30],[0.60,0.70] \rangle \\&\quad \langle [0.10,0.20],[0.60,0.70] \rangle ,\\&c_{12}^{\text {ch}}=\langle [0.30,0.60],[0.00,0.10] \rangle \langle [0.10,0.50],[0.30,0.30] \rangle \\&\quad \langle [0.10,0.20],[0.40,0.40] \rangle ,\\&c_{13}^{\text {ch}}=\langle [0.60,0.70],[0.20,0.30] \rangle \langle [0.40,0.70],[0.20,0.30] \rangle \\&\quad \langle [0.40,0.50],[0.20,0.30] \rangle ,\\&c_{21}^{\text {ch}}=\langle [0.05,0.10],[0.40,0.50] \rangle \langle [0.30,0.40],[0.40,0.50] \rangle \\&\quad \langle [0.20,0.40],[0.40,0.50] \rangle ,\\&c_{22}^{\text {ch}}=\langle [0.30,0.40],[0.40,0.50] \rangle \langle [0.20,0.40],[0.30,0.50] \rangle \\&\quad \langle [0.40,0.50],[0.10,0.30] \rangle ,\\&c_{23}^{\text {ch}}=\langle [0.40,0.50],[0.20,0.30] \rangle \langle [0.30,0.60],[0.30,0.40] \rangle \\&\quad \langle [0.20,0.50],[0.30,0.40] \rangle ,\\&c_{31}^{\text {ch}}=\langle [0.60,0.70],[0.10,0.20] \rangle \langle [0.20,0.50],[0.20,0.30] \rangle \\&\quad \langle [0.30,0.40],[0.10,0.30] \rangle ,\\&c_{32}^{\text {ch}}=\langle [0.20,0.40],[0.20,0.30] \rangle \langle [0.10,0.40],[0.50,0.60] \rangle \\&\quad \langle [0.30,0.40],[0.40,0.50] \rangle ,\\&c_{33}^{\text {ch}}=\langle [0.40,0.50],[0.30,0.40] \rangle \langle [0.30,0.50],[0.30,0.50] \rangle \\&\quad \langle [0.20,0.40],[0.50,0.50] \rangle . \end{aligned}$$

From Table 1, we describe that when player II uses strategy $\eta _{1}$ (i.e., cutting off the wages of workers demanding the increase of the wages), and player I uses strategy $\zeta _{1}$, then at 2nd day of 12-h strike, from 6 to 10 am, willingness to do strike lies between 70 and 80%, whereas 10–20% are not ready for that; from 10 am to 2 pm, eagerness to do strike lies between 30 and 50%, whereas workers have 10–20% reluctancy for that; and from 2 to 6 pm, workers are prone to do strike with willingness between 40 and 50%, whereas 10–20% hesitancy arise among them for the particular movement. Similarly, other cells of three tables, i.e., Tables 1, 2 and 3 can be illustrated.

Table 3 Demand for strike in 3 days for changing working hours

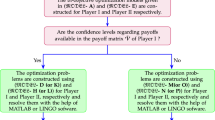
Now, we apply the proposed aggregation operator $g_{\text {IEIVHFWAO}}$ from Theorem 5.1 as a ranking technique to Tables 1, 2 and 3 to make a compact form which is represented in Table 4. Again, we consider that all strategies from both sides are not equally weighted. Here, we choose the weights 0.4, 0.3, and 0.3 in three consecutive days to the demand strategies. Now, utilizing data from Table 4 in Model 15, we have Model 17 as follows:

Table 4 Aggregated payoff matrix for IIVHFMG

Model 17

$$\begin{aligned} \text {maximize}\quad &0.5\underline{v}_{\text {M}}+0.5\overline{v}_{\text {M}}-0.5\underline{v}_{\text {NM}}-0.5\overline{v}_{\text {NM}}\\ \text {subject to }&0.31y_{1}+0.08y_{2}+0.11y_{3} \ge \underline{v}_{\text {M}},\\&0.21y_{1}+0.28y_{2}+0.13y_{3} \ge \underline{v}_{\text {M}},\\&0.11y_{1}+0.21y_{2}+0.28y_{3} \ge \underline{v}_{\text {M}},\\&0.69y_{1}+0.43y_{2}+0.51y_{3} \ge \overline{v}_{\text {M}},\\&0.67y_{1}+0.61y_{2}+0.51y_{3} \ge \overline{v}_{\text {M}},\\&0.51y_{1}+0.67y_{2}+0.61y_{3} \ge \overline{v}_{\text {M}},\\&0.10y_{2}+0.28y_{2}+0.28y_{3} \le \underline{v}_{\text {NM}},\\&0.22y_{2} \le \underline{v}_{\text {NM}},\\&0.28y_{1}+0.22y_{3} \le \underline{v}_{\text {NM}},\\&0.30y_{1}+0.53y_{2}+0.49y_{3} \le \overline{v}_{\text {NM}},\\&0.09y_{1}+0.38y_{2}+0.08y_{3} \le \overline{v}_{\text {NM}},\\&0.49y_{1}+0.09y_{2}+0.38y_{3} \le \overline{v}_{\text {NM}},\\&1 \ge \overline{v}_{\text {M}}+\overline{v}_{\text {NM}} \ge 0,\\&\overline{v}_{\text {M}} \ge \underline{v}_{\text {M}},\\&\overline{v}_{\text {NM}} \ge \underline{v}_{\text {NM}},\\&y_{1}+y_{2}+y_{3}=1,\\&y_{1} \ge 0, y_{2} \ge 0, y_{3} \ge 0. \end{aligned}$$

Solving Model 17 using LINGO 14.0 iterative scheme with 32-bit machine, we obtain the solutions as:

$$(\underline{v}_{\text {M}},\overline{v}_{\text {M}},\underline{v}_{\text {NM}},\overline{v}_{\text {NM}}) = (0.1491304, 0.5726087, 0.1704348, 0.3900000)$$

and

$$(y_{1}, y_{2}, y_{3})=(0.6086957, 0.3913043, 0.0000000).$$

Thus, we get,

$v^{*}=\langle [\underline{v}_{\text {M}},\overline{v}_{\text {M}}],[\underline{v}_{\text {NM}},\overline{v}_{\text {NM}}]\rangle = \langle [0.1491304, 0.5726087],[0.1704348, 0.3900000]\rangle$, i.e., throughout all 3 days with 12-h each day in strike period, eagerness for strike lies almost in between 14 and 57%, whereas, apathetic situation arises in 17–39%, nearly. Again using Table 4 in Model 16, we get Model 18 as:

Model 18

$$\begin{aligned} \text {minimize} \quad ~&0.5\underline{w}_{\text {M}}+0.5\overline{w}_{\text {M}}-0.5\underline{w}_{\text {NM}}-0.5\overline{w}_{\text {NM}}\\ \text {subject to }&0.31z_{1}+0.21z_{2}+0.11z_{3} \le \underline{w}_{\text {M}},\\&0.08z_{1}+0.28z_{2}+0.21z_{3} \le \underline{w}_{\text {M}},\\&0.11z_{1}+0.13z_{2}+0.28z_{3} \le \underline{w}_{\text {M}},\\&0.69z_{1}+0.67z_{2}+0.51z_{3} \le \overline{w}_{\text {M}},\\&0.43z_{1}+0.61z_{2}+0.67z_{3} \le \overline{w}_{\text {M}},\\&0.51z_{1}+0.51z_{2}+0.61z_{3} \le \overline{w}_{\text {M}},\\&0.10z_{1}+0.28z_{3} \ge \underline{w}_{\text {NM}},\\&0.28z_{1}+0.22z_{2} \ge \underline{w}_{\text {NM}},\\&0.28z_{1}+0.22z_{3} \ge \underline{w}_{\text {NM}},\\&0.30z_{1}+0.09z_{2}+0.49z_{3} \ge \overline{w}_{\text {NM}},\\&0.53z_{1}+0.38z_{2}+0.09z_{3} \ge \overline{w}_{\text {NM}},\\&0.49z_{1}+0.08z_{2}+0.38z_{3} \ge \overline{w}_{\text {NM}},\\&1 \ge \overline{w}_{\text {M}}+ \overline{w}_{\text {NM}} \ge 0,\\&\overline{w}_{\text {M}} \ge \underline{w}_{\text {M}},\\&\overline{w}_{\text {NM}} \ge \underline{w}_{\text {NM}},\\&z_{1}+z_{2}+z_{3}=1,\\&z_{1} \ge 0, z_{2} \ge 0, z_{3} \ge 0. \end{aligned}$$

Using LINGO 14.0 iterative scheme, we calculate the solutions from Model 18 as:

$$(\underline{w}_{\text {M}},\overline{w}_{\text {M}},\underline{w}_{\text {NM}},\overline{w}_{\text {NM}}) = (0.2317391, 0.6195652, 0.1704348, 0.3578261),$$

and

$$(z_{1}, z_{2}, z_{3})=(0.6086957, 0.0000000, 0.3913043).$$

Here we get, $w^{*}=\langle [\underline{w}_{\text {M}},\overline{w}_{\text {M}}],[\underline{w}_{\text {NM}},\overline{w}_{\text {NM}}]\rangle = \langle [0.2317391, 0.6195652], [0.1704348, 0.3578261]\rangle$, i.e., in strike period, eagerness for non-membership of strike almost lies in between 23 and 61%, whereas, apathetic situation arises from, nearabout, 17–35%.

8 Results and discussion

In this part of the paper, we infer that when we consider the demands of the strike supporters have weights in percentages 40%, 30% and 30% corresponding to the strategies for wage increase, for wage cut and for the changes of daily-hours, respectively, throughout all 3 days with 12-h each day in strike period, eagerness for strike lies almost in between 14 and 57%, whereas, apathetic situation arises in 17–39%, nearly; although, for the whole of 3 days with 12-h each day in strike period, eagerness for non-membership of strike almost lies in between 23 and 61%, and apathetic situation arises from, nearabout, 17–35%. In Table 5, we choose different weights imposed on different demands of the strike supporters. From Table 5, we say that when we consider the demands of the strike supporters with weights in percentages 30%, 40% and 30% corresponding to the strategies for wage increase, for wage cut and for the changes of daily-hours, respectively, throughout all 3 days with 12-h each day in strike period, eagerness for strike lies almost in between 13 and 58%, when, apathetic situation arises in 17–37%, nearly; while, for whole of 3 days with 12-h each day in strike period, eagerness for non-membership of strike almost lies in between 22 and 62%, given that, apathetic situation arises from, nearabout, 17–35%. From third line of Table 5, we say that when demands of strike supporters have weights in percentages 50%, 30% and 20% corresponding to the strategies for wage increase, for wage cut and for daily-hours-change, respectively, in strike period, eagerness for strike lies almost in between 15 and 55%, while, apathetic situation arises in 19–40%, nearly; whereas, for whole of 3 days with 12-h each day in strike period, eagerness for non-membership of strike almost lies in between 24 and 60%, whilst, apathetic situation arises from, nearabout, 20–38%. Even, when we consider no weights assigned to three consecutive days, we notice that, in 3 days 12-h strike, eagerness for strike lies almost in between 47 and 91%, despite the fact that apathetic situation arises in 1–7%.

Table 5 Different weights on 3 days to different demand-strategies

From Table 5, we observe that different weights when assigned to different days, give different results. Strike supporters and strategy makers may draw their attention into the fact that same demands when issued in different days have different impacts in socio-economic situations. From above analysis, we see that hesitant fuzzy set is a very useful tool to deal with uncertainty. Further, hesitant fuzzy set with intuitionistic interval-valued nature has a great impact when these are used to describe reality. The intuitionistic interval-valued hesitant fuzzy set, a substantial and important consequences of hesitant fuzzy set, intuitionistic hesitant fuzzy set and interval-valued hesitant fuzzy set, with the proposed aggregation operator have a great significance to tackle the managenent situation, here.

9 Conclusion

Many decision-making problems under hesitant fuzzy environment have been developed. The proposed methods are under the assumption that hesitant fuzzy set permits the membership having a set of possible exact and crisp values. However, under several conditions, for the group decision-making problems, the informations are usually uncertain or fuzzy due to the increasing complexity of the realistic environment and the vagueness of inherent subjective nature of human perception. Thus, exact as well as crisp values are inadequate or insufficient to model real-life decision-making problems. Indeed, human judgments including preference information may be stated which allow the membership having a set of possible hesitant fuzzy linguistic values. Several articles have been written on strikes, stoppages, labor organization, wages, etc. A comparative study with some existing literature is given in Table 6.

Table 6 Comparative study with other literature

We summarize our achieved results in the following points:

• (i) This paper has been presented with a detailed analysis of real-life management problem applied with a new aggregation operator on intuitionistic interval-valued hesitant fuzzy set.

• (ii) Our analysis began with a simple observation that in disputes arising over demands for a wage increase, successful strikes resulted in a tendency of significant wage gain, while failed strikes had tendency with no change in wages.

• (iii) Our proposed operator and methods can be applied to decision-making problems, mainly in game problems, in which the problem-data are in the form of intuitionistic interval-valued hesitant fuzzy numbers. Whereas, the existing methods of aggregation have a little bit difficulty to execute but our proposed aggregation method has much wider applications for its simple execution-process.

Analysis of strike problems using game theory is a new approach when hesitancy characters are included in nature. Applications of IIVHF matrix game situation with proposed aggregation operator are possible in various fields of decent work, decent industrial relations and decent social relations. Not only that, the proposed management problem can be applied to urban labor market, toy and car industries, educational hub management, global production networks, strategies and human resource management, quality management of employees, migrant workers’ situations, management of collective bargaining, legal policy support systems of workers, etc. Researchers may explain such management problems using our proposed game problem as future studies.