1 Introduction

Optimization problems are ubiquitous in nature (Kochenderfer and Wheeler 2019; Mohamed et al. 2022; Garg 2019; Kundu and Garg 2022a, b). A high number of real-world optimization problems are multi-objective, where the objectives being optimized are usually in conflict with each other. In this kind of optimization problems, rather than getting a unique optimal solution, there are usually several of them, maybe infinite, known as the Pareto set. Between other meta-heuristic approaches, Multi-Objective Evolutionary Algorithms (MOEAs) have the ability to effectively approximate this set as it has been reported in the scientific literature for more than three decades.

The Non-Dominated Sorting Genetic Algorithm II (NSGA-II) was proposed by Deb et al. (2000) as an exploration tool that employs a genetic algorithm to solve multi-objective optimization problems (MOPs). NSGA-II is still nowadays one of the most used and cited MOEAs and it has been applied to a broad variety of optimization problems since its inception in fields like economics, engineering or logistics. The NSGA-II algorithm creates a random population, selects individuals, and applies genetic operations on them, ranking and sorting individuals based on their non-domination level, and making use of a crowding distance operation to keep the evolving population diverse while aiming to generate a set of optimal solutions.

The fine-tuning of the parameters of an evolutionary algorithm is a key aspect that directly impacts on both its efficacy and its efficiency and it is usually a hard and time-consuming manual task done specifically for the particular problem being solved. Therefore, parameter tuning and control in evolutionary algorithms has been a relevant research topic since their inception.

In the literature, when NSGA-II is used as a baseline algorithm in benchmarks or even when it is applied to solve some specific engineering problem, its parameters are usually configured with static values. Normally, simulated binary crossover (SBX) and polynomial mutation (PLM) are carried out with fixed probabilities and distribution indices (Sharma et al. 2023; Liu et al. 2023; Wang et al. 2023; Ozcelikkan et al. 2022). However, Deb et al. (2007) a method for self-adapting the SBX crossover operator in order to improve the algorithm performance. Furthermore, Hamdan demonstrated in (Hamdan 2012) that the fixed distribution index broadly utilized in PLM does not always provide the best performance results. Consequently, these two relevant works show that it is not always fair to use NSGA-II for comparative evaluation purposes when its parameters are kept static.

This work proposes a novel and computationally lightweight mechanism that self-adapts one of the parameters of the PLM operator, its distribution index \(\eta _m\), used in the regular NSGA-II producing an increased efficacy over the results observed in its traditional counterpart. We compare the performance of this new algorithm variant to that of plain NSGA-II utilizing the static configuration widely found in the literature over a set of twenty-five benchmark problems from different test suites (DTLZ, WFG, ZDT, and other key problems), which experimentally confirm that this novel technique provides better results in almost every presented problem for several quality indicators such as hypervolume, generalized spread, and modified inverse generational distance.

The main motivation and contributions made by this paper could be summarized as follows:

  • Verify that the static parameterization of the regular PLM used in NSGA-II not always present the best performance results.

  • Introduce a new NSGA-II variant including a self-adaptive polynomial mutation operator which improves the observed efficacy over the regular NSGA-II with static PLM implementations. The results are measured with different metrics (hypervolume, generalized spread, and modified inverse generational distance) trying to cover different aspects of the solutions provided by the algorithms.

  • Use a quite large of known benchmark problems coming from families like DTLZ, WFG and ZDT to evaluate the performance of the proposed algorithm.

  • Propose a strict statistical test methodology to validate the new algorithm optimizing the selected problems.

The rest of this paper is structured as follows. Section 2 introduces several concepts on evolutionary multi-objective optimization and reviews related work. Section 3 describes the novel NSGA-II variant. Experimental results and analysis are presented in Sect. 4. Finally, Sect. 5 concludes the paper and suggests some future research directions.

2 Background and related work

In the present section, we initially cover some important concepts used in multi-objective optimization. Then, we review the latest work on: (i) parameter control techniques in evolutionary algorithms and (ii) quality metrics for measuring and comparing the performance of MOEAs.

2.1 Multi-objective optimization concepts

An MOP is defined as the simultaneous optimization of several objective functions over a tuple of decision variables. Without loss of generality, if minimization is considered for all the objectives, this can be formally expressed as follows:

$$\begin{aligned} \begin{aligned} \text {minimize} ~{\bar{y}}&= f({\bar{x}}) = (f_{1}({\bar{x}}),f_{2}({\bar{x}}),...,f_{m}({\bar{x}})) \end{aligned} \end{aligned}$$
(1)

where \({\bar{x}} = \langle x_1,x_2,...,x_n \rangle \in X \subseteq {\mathbb {R}}^n\) is called a decision vector, X is an n-dimensional decision space, \({\bar{y}} = \langle y_1,y_2,...,y_m \rangle \in Y \subseteq {\mathbb {R}}^m\) with \(m \ge 2\) is an objective vector, Y represents an m-dimensional objective space, n is the number of decision variables, m is the number of objective functions, and \(f_{i}\) corresponds to the ith objective function.

The set of decision vectors whose objectives cannot be improved in any direction without the degradation of another direction is called the Pareto optimal set. The concept of Pareto optimality can be defined as follows. Given a multi-objective minimization problem and two decision vectors \({\bar{a}}, {\bar{b}} \in X\), then \({\bar{a}}\) is said to dominate \({\bar{b}}\) (written as \(\varvec{{\bar{a}} \prec {\bar{b}}}\)) if and only if \({\bar{a}}\) is no worse than \({\bar{b}}\) in every objective and \({\bar{a}}\) is strictly better than \({\bar{b}}\) in at least one objective:

$$\begin{aligned} \begin{aligned} \forall i \in \{1, 2,..., m\}&~:~ f_{i}({\bar{a}}) \le f_{i}({\bar{b}}) \\ \text {and} ~\exists j \in \{1, 2,..., m\}&~:~ f_{j}({\bar{a}}) < f_{j}({\bar{b}}) \end{aligned} \end{aligned}$$
(2)

If neither \({\bar{a}}\) dominates \({\bar{b}}\) nor \({\bar{b}}\) dominates \({\bar{a}}\), \({\bar{a}}\) and \({\bar{b}}\) are said to be non-comparable, also stated as \({\bar{a}} \sim {\bar{b}}\). All the decision vectors which are not dominated by any other in a given set are called non-dominated regarding the set. The non-dominated vectors in the entire search space are called Pareto optimal solutions and form the Pareto optimal solution set or just the Pareto set:

$$\begin{aligned} PS:= \{{\bar{x}} \in X: \not \exists ~{\bar{x}}' \in X,~ {\bar{x}}' \prec {\bar{x}}\} \end{aligned}$$
(3)

and the projection of the Pareto set in the objective space is known as the Pareto front:

$$\begin{aligned} PF:= \{(f_1({\bar{x}}),f_{2}({\bar{x}}),...,f_{m}({\bar{x}})): {\bar{x}} \in PS\} \end{aligned}$$
(4)

If we relax the domination condition, we can say that \({\bar{a}}\) weakly dominates \({\bar{b}}\), or \({\bar{a}} \preceq {\bar{b}}\), if \({\bar{a}}\) is no worse than \({\bar{b}}\) in every objective:

$$\begin{aligned} \begin{aligned} \forall i \in \{1,2,...,m\}&~:~ f_{i}({\bar{a}}) \le f_{i}({\bar{b}}) \end{aligned} \end{aligned}$$
(5)

We can also consider the concept of strict domination, saying that \({\bar{a}}\) strictly dominates \({\bar{b}}\), or \({\bar{a}} \prec \prec {\bar{b}}\), if \({\bar{a}}\) is better than \({\bar{b}}\) in every objective:

$$\begin{aligned} \begin{aligned} \forall i \in \{1, 2,..., m\}&~:~ f_{i}({\bar{a}}) < f_{i}({\bar{b}}) \end{aligned} \end{aligned}$$
(6)

The set of objective vectors \(A \subset {\mathbb {R}}^m\) is called an approximation set if any of the elements in A does not dominate any other vector in the set (Hansen and Jaszkiewicz 1998). Usually, the ultimate objective when solving MOPs is not to find the real PF but a good approximation to it (Riquelme et al. 2015). Several tools to evaluate the quality of these non-dominated sets are explained in Sect. 2.3.

Even though the terms “solution” and “objective vector” have been used interchangeably (Nebro et al. 2008; Lopez et al. 2016; Ishibuchi et al. 2018), we prefer to keep the term solution for a vector in the decision space and the term objective vector for a solution projected into the objective space in order to avoid misunderstandings (Tanabe and Ishibuchi 2020).

2.2 Parameter tuning and control

Once the general scheme of an evolutionary algorithm is established, the researcher has to set the population size, choose the genetic operators for parent selection, crossover, mutation and survivor selection, and fix their probabilities. These specific parameters, or configuration, determine the behavior of the algorithm, guide its search and impact directly on the efficacy and efficiency achieved by the algorithm (Huang et al. 2022). It has been experimentally demonstrated that the use of different selection and variation operators as well as the setting of their parameters have an influence on the performance of evolutionary algorithms (Storn and Price 1997; Hamdan 2012; Deb et al. 2007). It is also true that the parameters might need distinct values at different stages of the execution process in order to adapt the exploration and exploitation intensities to the landscape it is dealing with (Back 1992).

In the course of evolutionary algorithms history, different approaches to addressing the necessity of parameter dynamism have been suggested. The first one, and probably the most extended in the literature, is the utilization of a static and promising configuration (known as parameter tuning). Researchers use a well-known set of operators and parameter values that provide good results for the problem at hand or get them adjusted after some trial-and-error search. But as the number of combinations of tested parameters can be really huge for manual adjustment, several automated tools have been developed. One of the most important tools used nowadays is irace, where an iterated execution of the F-race algorithm (Birattari et al. 2010; López-Ibánez et al. 2016) is implemented relieving the researcher of the tedious and time consuming task of repetitive manual parameter adjustment. Another interesting alternative is employing meta-heuristic techniques, like the Meta-GA used by Grefenstette (Grefenstette 1986), in which an external evolutionary algorithm adjusts the algorithm parameters.

Starting just when evolutionary algorithms were created (Jong 1975; Grefenstette 1986), but specially in the last thirty years, a lot of effort has been invested in methods for dynamically controlling the parameters during execution (parameter control). In 1995, Angeline (Angeline 1995) presented a taxonomy of these techniques differentiating the type of control based on its level of application (over the full population, the individuals, or their genes). Smith and Fogarty (Smith and Fogarty 1997) proposed a new classification scheme trying to differentiate what is being adapted (parameters or operators), the scope of the adaptation (if it is applied to the full population, individual or gene level) and the tools being applied to make the adaptation. Hinterding, Michalewicz and Eiben (Hinterding et al. 1997; Eiben et al. 1999) introduced a new classification method based on the type of adaptation and distinguished between deterministic, adaptive and self-adaptive methods. Note that this is still the most widely used taxonomy and the basis, with few and slight variations, of recent work (Zhang et al. 2012; Parpinelli et al. 2019; Doerr and Doerr 2020):

  • Eiben et al. define deterministic control as the adjustment of a parameter using a deterministic rule that does not get any feedback from the search (Eiben et al. 1999). Usually, it utilizes a rule based on the number of evaluations of the fitness function or on the number of generations passed so far. This kind of methods are very common due to the simplicity of implementation (Mezura-Montes and Palomeque-Ortiz 2009; Hassanat et al. 2019).

  • Adaptive control uses some characteristic or feedback from the search process to adjust the value of the parameters. Among the adaptive methods, very well-known and simple strategies like the 1/5 Rechenberg’s success rule (Rechenberg 1971) can be found. Alternatively, more complex methods are based on learning principles brought from fields like reinforcement learning or deep learning (Eiben et al. 2007; Auger et al. 2019).

  • Self-adaptive control is close to the underlying idea of evolutionary optimization as the parameters are encoded into the chromosomes and evolve with the rest of variables by applying genetic operations. Thus, the best parameters generate high-quality solutions which survive in future generations (Smith and Fogarty 1996; Deb et al. 2007; Bosman et al. 2017; Rajabi and Witt 2020).

Due to the vast amount of publications on parameter control in evolutionary algorithms, several exhaustive reviews have been made available to researchers and practitioners (Eiben et al. 1999; Karafotias et al. 2015; Aleti and Moser 2016), and recent reviews can be found in (Parpinelli et al. 2019), (Huang et al. 2020), (Lacerda et al. 2021) (also covering swarm inspired algorithms), and (Huang et al. 2022) (focused on differential evolution). In addition, an interesting theoretical approach is developed in (Doerr and Doerr 2020). Finally, a complete compendium on parameter control and its application is offered in (Papa 2021) and an interesting compilation about parameter setting is included in (Lobo et al. 2007).

NSGA-II, proposed by Deb et al. (2000), is a well known, competent, and extensively used genetic algorithm for solving MOPs that attains near-optimal, diverse, and uniformly distributed solution sets (Tan et al. 2009; Rahimi et al. 2022). Even though NSGA-II is a mature algorithm, it is still being utilized as a baseline to test new algorithms performance (Ishibuchi et al. 2003; Zhao et al. 2019; Long et al. 2022; Sharma et al. 2023). Its population size, crossover and mutation operators and probabilities, selection pressure, and even the distribution indices used by the original SBX and PLM operators have to be set in advance.

Although the number of publications about self-adaptation in MOEAs is relatively low compared to single-objective algorithms (Aleti and Moser 2016), several authors have shown that self-adaptation can improve the applicability of MOEAs to online decision support in real-world problems (Zeng et al. 2010). Deb et al. (2007) proposed a self-adaptive method for adapting the distribution index under SBX crossover, SA-SBX, used typically in NSGA-II due to the fact that a fixed index does not always produce the best performance results, specially when dealing with multi-modal problems. This parameter, \(\eta _c\), defines the shape of the probability distribution function which governs the spread of offspring solutions given the parents. The method, applied both to mono and multi-objective problems, produced promising results. In 2010, Zeng et al. (2010) improved Deb’s idea of a self-adapting distribution index in the binary crossover operator by using the diversity of the offspring solutions to dynamically control the parameter.

Despite the fact that several studies have focused on the mutation operator by adapting the mutation rate (Back and Schutz 1996; Yang and Uyar 2006), by changing the mutation probability distribution function like in evolution strategies and evolutionary programming (Lee and Yao 2004; Tinós and Yang 2007), or even by changing the mutation operator itself during the evolution (Korejo et al. 2009), very few studied the idea of changing the probability distribution index in PLM, \(\eta _m\), as Deb did in SA-SBX for crossover. Furthermore, Hamdan (Hamdan 2012, 2014) demonstrated that different values for \(\eta _m\) from the ones found in the literature provided better performance results.

Following the ideas of Deb, Zeng, and Hamdan, this work investigates whether or not self-adapting the mutation distribution index of the typical PLM operator used in NSGA-II could actually outperform the classical static configuration. In this regard, Sect. 3 proposes a novel and simple self-adaptive mutation operator which, as shown in Sect. 4, outperforms a static configuration when applied to several benchmark problems.

2.3 Quality indicators

Trying to compare the outputs of two multi-objective optimizers is not trivial as we are comparing two sets of non-dominated vectors or approximation sets. Several performance metrics, or quality indicators, are defined over an approximation set (unary metrics) or between two approximation sets (binary metrics) producing a scalar value utilized to compare the quality of the output of different algorithms when solving MOPs (Zitzler et al. 2003; Riquelme et al. 2015).

Ideally, the obtained non-dominated solutions of an approximation set should be as close as possible to the Pareto front, well-distributed, and widely spread (Okabe et al. 2003). Therefore, it is common to find the metrics capturing the quality of approximation sets grouped as cardinality, accuracy, and diversity metrics:

  • Cardinality metrics utilize the number of non-dominated vectors in an approximation set, since algorithms producing larger approximation sets are usually preferred.

  • Accuracy metrics (or convergence metrics) measure the distance between the approximation set and the theoretical optimal front or a reference set if the real Pareto front is unknown (Okabe et al. 2003). Several methods for calculating this distance have been proposed, like the ones defined later in this section for the GD, IGD, and \(IGD^+\) indicators.

  • Diversity metrics try to capture how well the objective vectors in the approximation set are distributed (the relative distance between them) and spread (the range of values covered by these vectors) (Riquelme et al. 2015).

  • Convergence-diversity metrics map both the proximity of the objective vectors to the PF and the diversity of these vectors to a scalar value (Jiang et al. 2014).

Over the last few decades, a large number of papers have been published studying a vast list of available indicators. We remark some of the most cited surveys authored by Riquelme et al. (2015) studying fifty-four indicators, Li and Yao (Li and Yao 2019) covering one hundred indicators, and Audet et al. (2020) describing fifty-seven metrics. The papers published by Hansen and Jaszkiewicz (Hansen and Jaszkiewicz 1998) and Zitzler et al. (2003) are relevant for analyzing the theoretical aspects of these quality indicators in a formal way.

Choosing the right indicator, or a set of them, to assess the performance of an MOEA turns out to be as difficult as developing the MOEA itself. Several authors (Knowles 2002; Knowles and Corne 2002; Okabe et al. 2003; Jiang et al. 2014; Wang et al. 2016) have criticized the usually misleading and sometimes inconsistent results provided by these metrics, and help in the selection of the right one. Following the information provided by these authors, we have finally chosen three metrics from the myriad of them in order to evaluate our new algorithm: the hypervolume indicator, the generalized spread measure and the modified inverted generational distance.

2.3.1 Hypervolume

The hypervolume indicator (HV) was introduced by Zitzler and Thiele in 1999 (Zitzler and Thiele 1999), and it is one of the most studied and used metrics due to some of its mathematical characteristics. HV captures in one single value the convergence and diversity of an approximation set, and it is a strictly monotonic metric with regards to the Pareto dominance concept (Knowles and Corne 2002; Bader and Zitzler 2011). Larger values of HV indicate that the vectors in the approximation set are closer to the true PF and evenly distributed over it (Jiang et al. 2014).

Fig. 1
figure 1

Hypervolume covering the shaded green area in a bi-objective minimization problem

Full size image

HV calculates the hypervolume that is dominated by the objective vectors in the approximation set S bounded by a reference point \({\bar{r}}\) (see Fig. 1, where HV measures the shaded green area). Although the selection of the reference point to calculate HV is critical (Auger et al. 2009; Ishibuchi et al. 2018), it is accepted that a point slightly worse in every objective than every point in S is enough to cover all the vectors in the approximation set. HV is calculated as follows:

$$\begin{aligned} HV(S, {\bar{r}}) = \Lambda \bigg (\bigcup \limits _{i=1}^{\textsf{S}} v_{i}\bigg ) \end{aligned}$$
(7)

where \(\Lambda \) denotes the Lebesgue measure and \(v_i\) represents the box defined by vector i and reference point \({\bar{r}}\). Larger values of HV indicate better approximation sets.

2.3.2 Generalized spread

The spread metric (\(\Delta \)), introduced by Deb et al. (2000), is another commonly used indicator in bi-objective MOEAs that tries to measure how uniformly the objective vectors in an approximation set are distributed over the Pareto front. Zhou et al. (2006) extended this indicator to m-objective problems in the generalized spread metric (\(\Delta ^*\)) which is formulated as follows:

$$\begin{aligned} \Delta ^*(S, P) = \frac{\sum _{i=1}^{m} d(e_i, S) + \sum _{{\bar{x}} \in P} \Vert d({\bar{x}}, S) - {\bar{d}} \Vert }{\sum _{i=1}^{m} d(e_i, S) + {\bar{d}} (\Vert P\Vert - m)}, \end{aligned}$$
(8)

where \(e_i\) is the i-th extreme objective vector in the Pareto front P with the maximum value for the i-th objective function and

$$\begin{aligned} d({\bar{x}}, P)&= \min _{y \in P, y \ne x} \Vert {\bar{x}} - {\bar{y}}\Vert _2,\end{aligned}$$
(9)
$$\begin{aligned} {\bar{d}}&= \frac{1}{\textsf{P}}\sum _{{\bar{x}} \in P}d({\bar{x}}, S) \end{aligned}$$
(10)
Fig. 2
figure 2

Examples of spread and distribution of vectors over the Pareto front

Full size image

The \(\Delta \) and \(\Delta ^*\) metrics, unlike HV, require a known Pareto front. We can observe in Fig. 2: (i) an example of a well distributed and well spread set of vectors in the left-hand graph, (ii) an example of a well spread but not well distributed set in the second graph, (iii) a well distributed but not well spread set of vectors in the third graph, and (iv) a not well spread and not well distributed set in the right-hand graph. Lower values for spread and generalized spread metrics indicate better distributed and spread vectors.

Fig. 3
figure 3

GD, IGD and \(IGD^+\) calculation for an approximation set

Full size image

2.3.3 Modified inverted generational distance

The generational distance metric (GD), proposed by Veldhuizen in 1998 (Veldhuizen and Lamont 1998), averages the distance from each objective vector in the approximation set to the nearest vector in the known PF (see the left-hand graph in Fig. 3). Conversely, the inverted generational distance (IGD) (Bosman and Thierens 2003; Coello and Sierra 2004) calculates the average distance from each vector in the reference or known PF to its nearest point in the approximation front (see the central graph in Fig. 3). The modified inverted generational distance metric (\(IGD^+\)) was introduced by Ishibuchi et al. (2015) (see the right-hand graph in Fig. 3). These three metrics are formulated in a similar way but provide different results:

$$\begin{aligned} GD(A, Z)&= \frac{1}{|A|}\sum _{{\bar{a}} \in A}^{}\min _{{\bar{z}} \in Z} {\hat{d}}({\bar{a}}, {\bar{z}}) \end{aligned}$$
(11)
$$\begin{aligned} IGD(A, Z)&= \frac{1}{|Z|}\sum _{{\bar{z}} \in Z}^{}\min _{{\bar{a}} \in A} {\hat{d}}({\bar{a}}, {\bar{z}}) \end{aligned}$$
(12)
$$\begin{aligned} IGD^+(A, Z)&= \frac{1}{|Z|}\sum _{{\bar{z}} \in Z}^{}\min _{{\bar{a}} \in A} {\hat{d}}^+({\bar{a}}, {\bar{z}}) \end{aligned}$$
(13)

where the distance \({\hat{d}}\) in GD and IGD is calculated as the Euclidean distance in \(IGD^+\). Ishibuchi et al. (2015) found that this latter distance calculation in \(IGD^+\) assures that the indicator is always better for an approximation set that is dominating another (Pareto compatibility), thus providing more accurate results than IGD in some circumstances where this property does not hold. Lower values for this metric indicate a better set of solutions in terms of both convergence and diversity (Tanabe and Ishibuchi 2020).

3 From static to self-adaptive polynomial mutation in NSGA-II

In this section, we first review the NSGA-II algorithm, which is widely used to perform the benchmarking of MOEAs. Next, we focus on the mutation phase of NSGA-II and explain the regular and the novel self-adaptive PLM operators in turn.

3.1 NSGA-II

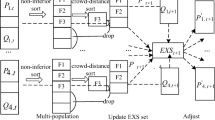
The general pseudo-code for the non-dominated sorting genetic elitist algorithm (NSGA-II) is shown in Algorithm 1, and a graphical representation of how it works is displayed in Fig. 4. The main loop works as follows:

  1. 1.

    Parents are selected, usually with binary tournament, utilizing a comparison based on non-domination ranking and crowding distance of parents. The non-domination rank segments the individuals in different fronts: F1 is the set (or front) of non-dominated individuals in the population, F2 is the set of non-dominated individuals in the population after excluding F1, and so on. The crowding distance, which is a density estimator of solutions surrounding a particular one, is used to break the ties when solutions have the same rank.

  2. 2.

    Genetic operators are applied to generate an offspring population that is joined to the original one (normally SBX is utilized for performing the recombination of selected parents and PLM for mutating their descendants).

  3. 3.

    Each individual of this new extended population, which is commonly twice the size of the original population, is evaluated to set its non-domination rank and crowding distance.

  4. 4.

    A sorting of the new extended population based on individual non-domination rank and crowding distance is performed.

  5. 5.

    A reduction to select the first half of the extended population is made.

  6. 6.

    The loop is repeated from 1 until the end condition is reached.

Fig. 4
figure 4

NSGA-II procedure, where \(\{\text {F}_1,...,\text {F}_5\}\) represent the sub-populations sorted by non-domination ranking. \(\text {F}_1\) is the set (or front) of non-dominated individuals in the population, \(\text {F}_2\) is the set of non-dominated individuals in the population after excluding \(\text {F}_1\), and so on

Full size image
Algorithm 1
figure a

NSGA-II with traditional PLM

Full size image

The use of non-domination rank and crowding distance comparisons in the selection of parents and in the ordering of the extended population assures that dominating individuals in less crowded regions are selected. Furthermore, the elitism is guaranteed by mixing the old population with the calculated offspring before performing the ordering of the extended population and selecting its best individuals. We refer the reader to the original paper (Deb et al. 2000) in order to get full details of the proposed algorithm.

3.2 Static polynomial mutation

The polynomial mutation operator over a decision vector applies a polynomial probability distribution function to generate a new decision vector starting from the current one. The pseudo-code is shown in Algorithm 2, where a perturbation following this distribution is applied with probability \(p_m\) to each variable of decision vector \({\bar{x}}\).

Algorithm 2
figure b

PLM mutation of decision vector \({\bar{x}}\)

Full size image

Note that the distribution function depends on the mutation distribution index \(\eta _m\). Figure 5 shows an example of the impact of this parameter on the shape of the probability distribution function for a point centered at \(x = 3\), where the probability of generating a closer point to the original value is larger when higher \(\eta _m\) values are used. Smaller values for that index tend to produce points located far from the original one.

Fig. 5
figure 5

PLM distribution function centered at \(x=3\) for different \(\eta _m\) values

Full size image

3.3 Novel self-adaptive polynomial mutation

Following the findings of Hamdan (Hamdan 2012) mentioned in Sect. 2.2, we have verified that using different values for \(\eta _m\) has actually a direct impact on the performance of the algorithm. For example, Fig. 6 shows the output of an experiment over an instance of a ZDT2 problem where the HV indicator captured and averaged over 30 runs is depicted for different values of \(\eta _m\). We have observed that this behavior takes place in other problems as well.

Fig. 6
figure 6

HV performance over ZDT2 problem for different \(\eta _m\) values

Full size image

The underlying idea of self-adaptive polynomial mutation follows the procedure utilized in evolutionary programming and evolution strategies, where the strategy parameters are stored in the genome of the population individuals and evolve with the rest of variables during the execution of the algorithm. Thus, we need to extend the representation of each individual from a decision vector \(\langle x_1,x_2,...,x_n \rangle \) to a new one including its specific mutation distribution index \(\langle x_1,x_2,...,x_n,\eta _m \rangle \). The initialization of individuals in the population (first generation) is performed by obtaining \(x_i\) and \(\eta _m\) values randomly chosen between their boundaries.

According to the new parameter self-adaptation strategy, we have slightly modified the original PLM algorithm by separating it in two parts: one responsible for the updating of the distribution index stored in the genome and a second one for updating the decision vector according to this mutated index. Thus, the new proposed scheme appears in Algorithm 3.

Algorithm 3
figure c

NSGA-II with self-adaptive PLM

Full size image

In Algorithm 3, it is important to note that the distribution index update of the selected parents is performed in line 7 before applying the mutation to the generated children in lines 9 and 10 that will use the specific \(\eta _m\) found in each child chromosome. The details of this updating procedure of the selected parents are included in Algorithm 4. Specifically, we average the indices of the selected parents (crossover phase) and apply a Gaussian perturbation to the averaged index (mutation phase). The resulting value is repaired before updating all the selected parents with it in order to avoid getting new \(\eta _m\) values outside of their bounds.

Algorithm 4
figure d

PLM Distribution Index update

Full size image

The main differences between the original proposal in Algorithm 1 and the novel one in Algorithm 3 are, on the one hand, the parameter updating mechanism applied in line 7 of Algorithm 3, and on the other hand, the use of the updated distribution index in lines 9 and 10. The additional computational cost incurred when performing these two operations is linear with the number of parents due to the loops in the distribution index updating function (lines 3-5 and 9-11 of Algorithm 4).

4 Experimental evaluation

This section compares how the new self-adapted mutator performs with respect to the regular PLM used in NSGA-II in terms of efficacy by using the three selected quality indicators explained in Sect. 2.3. A diverse set of problems with different features is employed to evaluate the consistency of the results obtained after several independent executions.

4.1 Test problems

In order to analyze the performance of the new PLM implementation, we execute the algorithms over well-established sets of problems found in many studies in the field. We have used a significant number of problems, twenty-five, with different features: shape and continuity of the PF, number of decision variables (n) and objectives (m), and modality. This allows us to check the validity of our proposal and to determine whether it has any deficiencies depending on one or more of these characteristics.

The diverse set of functions that we have used in the experiments consists of the following families:

  1. 1.

    The scalable family of three-objective problem collection DTLZ 1-7 from Deb et al. (2002).

  2. 2.

    Bi-objective unconstrained problems from the Walking Fish Group (WFG) test suite from Huband et al. (2005).

  3. 3.

    Bi-objective and unconstrained ZDT 1-4 and 6 problems from Zitzler et al. (1999).

  4. 4.

    Other bi-objective and unconstrained problems like Kursawe (1991), Schaffer (1985), Srinivas (1994), and Tanaka et al. (1995).

Table 1 shows the main features of the twenty-five selected problems. For each problem, we include the number of decision variables and objectives, whether the objective functions are separable or not, and its modality (uni-modal, multi-modal, or deceptiveFootnote 1). We also include the PF shape or geometry indicating the cases in which the PF is convex, non-convex or linear, whether the PF is connected or disconnected, and whether it has degenerated parts (PF with a dimension smaller than \(m - 1\)).

Table 1 Features of the tested problems: number of decision variables and objectives, separable (S) or non-separable (NS), uni-modal (U), multi-modal (M), deceptive multi-modal (D) and PF geometry
Full size table
Fig. 7
figure 7

Statistical test methodology

Full size image
Table 2 Hypervolume results obtained in experiments (significance level \(\alpha = 0.01\))
Full size table
Table 3 \(IGD^+\) results obtained in the experiments (significance level \(\alpha = 0.01\))
Full size table

4.2 Algorithm execution

We have selected jMetal,Footnote 2 a Java framework for developing multi-objective optimization algorithms created by Durillo and Nebro at the Universidad de Málaga (2011), as the environment to perform our experimentation. This framework provides a large library of tested algorithms and facilitates the development of new ones. The hardware platform used to run the experiments was an Intel Core i5 with 8GB of RAM running Windows 11 operating system.

The baseline NSGA-II was parameterized using the default values suggested by jMetal. These default values are the most commonly found in the relevant literature. Specifically, we used the following parameter values:

  • Population size was set to 300 individuals.

  • The maximum number of evaluations was set to 25000.

  • SBX was selected as the crossover operator.

  • Crossover probability \(p_c\) = 0.9.

  • Crossover distribution index, \(\eta _c\) = 20.

  • Regular PLM was used as the mutation operator.

  • Mutation probability, \(p_m\) = 1/n.

  • Static mutation distribution index, \(\eta _m\) = 20.

As far as the modified NSGA-II using the new mutation operator is concerned, it was configured exactly as the regular NSGA-II with the traditional PLM operator but, on this occasion, with a self-adaptive distribution index for the mutation process. The lower and upper boundaries for \(\eta _m\) were set to 1 and 100 respectively.

4.3 Results

Tables 2 through 4 include the experimental results for each quality indicator (HV, \(IGD+\), and \(\Delta ^*\)) when both algorithms are applied to the twenty-five problems in Table 1. A summary of these results is displayed in Table 5.

As this work deals with stochastic algorithms, we average the captured quality indicator values over 30 independent executions for each problem instance and present them with their mean and variance. Figure 7 illustrates the statistical test methodology followed in order to guarantee that the obtained results are not due to randomness. We start by applying a Shapiro normality test to the data coming from each algorithm. With a negative answer (they do not follow a Gaussian distribution) a Wilcoxon test is then applied to see their means similarity. Otherwise, having assured a normal distribution for the data, a Levene test is executed to check the homoscedasticity of the series; in the negative case where they do not have equal variances, we end by running a Welch test to check the similarity of their means. If, on the contrary, they have similar variances, we apply a paired Student t-test in order to see if they have similar means. We always consider a level of confidence of 99% in the statistical tests used in this work. Thus, with a significance level of 1% or p-value under 0.01, we are able to reject the null hypothesis of both algorithms performing similarly.

As mentioned earlier in this section, Tables 2, 3 and 4 incorporate the mean and variance calculated over 30 independent executions of both algorithms. In the “Test result” column of each table, a “+” sign indicates that the new PLM variation outperforms the regular PLM with enough statistical confidence (as specified in the statistical test methodology described earlier in this section); conversely, a “−” sign is utilized when the regular PLM gives better results than the new PLM proposal. Finally, the “=” sign indicates that no difference exists in the performance of both PLM implementations.

4.3.1 Hypervolume results

Table 2 collects the HV indicator results for the experiments. Notice that the self-adaptive PLM performs better than the regular operator in 19 problems and gives a similar performance regarding this indicator in other 4 problems. Worse results are observed only for 2 problems, WFG5 and WFG8. We also observe an important variance improvement in all the positive cases.

It is worth noticing the HV results obtained for DTLZ3 and DTLZ6 problems, where we indicate a zero HV mean and variance for the traditional PLM run. A zero HV is obtained when no solution is found inside the hypercube delimited by the reference point for any of the algorithm executions (in a minimization problem). However, the self-adaptive PLM is able to produce acceptable results in the same number of runs.

4.3.2 \(\varvec{IGD^+}\) results

The data gathered for the \(IGD^+\) indicator are presented in Table 3. We observe again that the self-adapted mutation operator performed equal to or better than the regular PLM operator in almost every problem (24 out of 25). One more time, WFG8 seems to be specially difficult to the new algorithm regarding this quality indicator. Both algorithms produce similar results for WFG4, WFG7, WFG9, and Srinivas problems.

We observe again similar variance improvements in the new algorithm, where we get a variance reduction in all the positive instances. Notice that the performance of the new algorithm for several of the positive cases is very remarkable (see DTLZ3, DTLZ6, and Schaffer problems).

4.3.3 \(\mathbf {\Delta ^*}\) results

As reported in Table 4, when dealing with the spread and diversity of the generated solutions, our new operator does not give as impressive results as those obtained for the other two metrics. It performs better than the regular operator on 13 occasions, similarly in 11 problems, and worse in 1 instance. Once again, WFG5 seems to be a hard problem for our new algorithm; however, to our surprise, it surpassed regular PLM in the WFG8 problem.

The variance analysis produces similar conclusions. For all the problems where the new algorithm outperforms the traditional one, an important reduction of the variance is again measured.

Table 4 \(\Delta ^*\) results gathered in the experiments (significance level \(\alpha = 0.01\))
Full size table

4.3.4 Tests summary

The test results for each metric are compiled in Table 5, where we additionally highlight the table cells with a “+” sign when our algorithm gives better results for a problem (and with a “=” sign when there is no difference in performance between them). A “-” sign means that our algorithm is performing worse for that quality indicator.

Table 5 Tests summary for each problem and indicator
Full size table

It is easy to see that HV and \(IGD^+\) are suggesting a similar behavior of the new algorithm. It surpasses the traditional one in 19 problems and provides similar results for other 4 or 5 problems. There is only a divergence in WFG5 problem, where HV indicates that the self-adaptive PLM is doing worse than the regular operator. Anyway, it seems to be consistent with the negative \(\Delta ^*\), as we know that HV also captures the diversity of solutions.

Additionally, \(\Delta ^*\) results are not as good as those provided by the other indicators, but they are still quite encouraging. The new algorithm provides better results on 13 occasions, and in 11 cases it shows similar performance. Only in one problem, WFG5, the new operator provides poorer results. Reviewing the characteristics of that problem, we could point to its deceptive characteristic. Probably, it is easier for the new operator to fall in the deception front and not in the real PF.

5 Conclusions and future work

NSGA-II with a fine-tuned statically parameterized polynomial mutator is typically used as a baseline when comparing the performance of MOEAs or when it is applied to solve some MOPs. In this work, a new version of NSGA-II algorithm incorporating a novel and computationally lightweight polynomial mutator that self-adapts its distribution index \(\eta _m\) has been proposed. The modified algorithm with the new dynamic operator has been experimentally compared to its static counterpart over 25 problems coming from different well established test suites (DTLZ, WFG, ZDT, and other key problems) covering diverse features of typical multi-objective problems. Furthermore, its performance has been measured over three major quality indicators: hypervolume, generalized spread, and modified inverted generational distance.

The experiments provide a clear confirmation that the proposed variation improves the observed performance of the regular NSGA-II and PLM on almost all of the tested problems and for all the three covered indicators. The main advantage of this self-adaptive mutation and the modified NSGA-II are that they are really easy to implement and introduce a very small overhead in the optimization run-time.

This work also emphasizes an algorithm comparison methodology whose main characteristics are: (i) a large number of problems with different PS and PF features, (ii) the use of several quality indicators to measure the algorithm performance, and (iii) a strict statistical test procedure to analyze the output data.

Additionally, this paper remarks the importance of parameter setting in EAs and specially in MOEAs. It has been experimentally demonstrated that dynamically adapted parameters can improve the algorithm efficacy without implying a significant increase of computational cost. Simple dynamic methods, like the proposed self-adapted operator, can improve the performance of the regular NSGA-II and, potentially, alter the benchmarking results obtained using statically configured parameters.

Currently, the main drawback of the new algorithm is the not specially good solution distribution measured through the Generalized Spread metric \(\Delta ^*\). Understanding why the algorithm makes only a moderate performance improvement regarding the spread and diversity of the obtained solutions should be a priority in future investigation. Adding other quality metrics, like Maximum Spread \(S_p\) (Schott 1995; Riquelme et al. 2015) and Spacing \(M^*_3\) (Zitzler et al. 1999), would be desirable to better understand these results.

One direction of future work is studying how the algorithm could be improved when dealing with highly deceptive problems. It would be also advisable to confront this new NSGA-II variant with some recent and state-of-art multi-objective algorithms like Multi-Objective Non-dominated Advanced Butterfly Optimization Algorithm (MONSBOA) described in (Sharma et al. 2023).

Finally, the possible application of this dynamic approach to new mutation strategies like the Lévy flight based found in the hybrid Lévy Slime Mould Algorithm Teaching-Learning Based Optimization (LSMA-TLBO) proposed in (Kundu and Garg 2022b) or the quantum inspired mutation found in the Quantum Mutation-based Backtracking Search Algorithm introduced in (Nama et al. 2022) should be studied.