Moments estimation for multi-factor uncertain differential equations based on residuals

Abstract

Parameter estimation is always the focus of constructing differential equations to simulate dynamic systems. In order to estimate unknown parameters in multi-factor uncertain differential equations, the definition of residuals is presented and important properties of residuals are demonstrated. Based on the property that the residuals obey the linear uncertainty distribution, moment estimation of the unknown parameters in the multi-factor uncertain differential equation is performed and the reasonableness of the parameter estimation results is verified. Some examples with real data are given to demonstrate the feasibility of the method.

1 Introduction

Using observational data to build dynamic models to explore patterns of development is a common research method. However, practical situations often involve a lack of data or difficulties in measurement. To solve this problem, Liu (2007) proposed to construct dynamic models based on expert belief degree and constructd a framework of uncertainty theory based on four axioms in 2007. As the research progressed, Liu (2009) discovered a class of stationary independent increment process and defined them as Liu processes. Uncertainty theory has attracted the interest of many scholars and has developed rapidly in recent years. In terms of practical applications, uncertainty theory stands out, such as modelling infectious diseases (Lio and Liu 2021), predicting stocks (Yao 2015a), optimising logistics networks (Peng et al. 2022), etc.

Uncertain differential equation (UDE) driven by the Liu process was proposed by Yao (2016) to model and analyze dynamical systems subject to uncertain factors. In order to model complex dynamic systems in different situations, more and more types of uncertain differential equations are proposed. Backward uncertain differential equations were presented by Ge and Zhu (2013), who also established the existence theorems for their solutions. Yao (2015b) proved the completely unique solution of the uncertain differential equation with jumps driven by the update process and the Liu process and its uncertainty measure in the sense of stability. Yao (2016) proposed the high-order uncertain differential equations with high-order derivatives. Li et al. (2015) proposed a multi-factor uncertain differential equation. The focus of this study is on parameter estimation for multi-factor uncertain differential equations.

Parameter estimation has long been a major research topic in the field of differential equations. Various parameter estimation methods for uncertain differential equations have been proposed in succession. Sheng et al. (2020) presented a least squares estimation method for estimating unknown parameters. Yao and Liu (2020) suggested the moment estimation technique based on the difference form. To improve the situation where the system of moment estimation equations has no solution, Liu (2021) proposed generalized moment estimation. In addition, Lio and Liu (2020) proposed the uncertain maximum likelihood method. Sheng and Zhang (2021) also introduced three methods for parameter estimation based on different types of solutions. Liu and Liu (2022) first proposed the definition of residual of uncertain differential equations and used residual to solve unknown parameters. Zhang et al. (2021a) also estimated the parameters of high-order uncertain differential equations. Zhang and Sheng (2022) rewrite the least squares estimation method for estimating the time-varying parameters in UDE. In the process of parameter estimation, the testing of the estimates is equally important. Ye and Liu (2023) proposed uncertainty hypothesis testing for verifying that the uncertain differential equations are consistent with the observed data. Zhang et al. (2022) used the uncertainty hypothesis testing to determine the reasonableness of the parameter estimates. Ye and Liu (2022) applied uncertainty hypothesis testing to uncertainty regression analysis.

In the study of unknown parameters of multi-factor uncertain differential equation, Zhang et al. (2021b) proposed a weighted method for moment estimation and least squares estimation of unknown parameters. However, that paper did not give a specific judgment on how to determine the rationality of the weighting method. In order to avoid complicated weighting and discuss the rationality of weighting, a new method based on residuals for estimating unknown parameters of multi-factor uncertain differential equations is proposed in this paper.

This paper introduces the idea of residuals into parameter estimation of multi-factor uncertain differential equation. This paper presents the definition of residuals and proves some properties of residuals. The moment estimation is performed on the unknown parameters from the residuals as samples from the linear uncertainty distribution. Section 2, some basic definitions and theorems of uncertainty theory are introduced. Section 3, the concept of residuals for multi-factor uncertain differential equations is presented, the properties of the residuals are proved and analytical expressions for the residuals are derived. Section 4, based on the fact that the residuals follow the linear uncertainty distribution ${\mathcal {L}}(0,1)$, moment estimation of the unknown parameters in the multi-factor uncertain differential equation is performed and the estimation results are tested. Section 5, two examples with real data are given to verify the reliability of the method. Section 6 is the summary of this paper.

2 Preliminary

In this section, some necessary definitions and theorems in uncertainty theory are introduced to help readers understand what follows.

Definition 1

(Liu 2007, 2009) Let $\text{ L }$ be a $\sigma$-algebra on a nonempty set $\Gamma .$ A set function $\text{ M }:$ $\text{ L }\rightarrow [0, 1]$ is called an uncertainty measure if the four following axioms are satisfied:

Axiom 1:

: (normality Axiom) $\text{ M }\{\Gamma \}=1$ for the universal set $\Gamma .$

Axiom 2:

: (duality Axiom) $\text{ M }\{\Lambda \}+\text{ M }\{\Lambda ^c\}=1$ for any event $\Lambda$.

Axiom 3:

: (subadditivity Axiom) For every countable sequence of events $\Lambda _1, \Lambda _2, \ldots ,$ we have

$$\begin{aligned} \text{ M }\left\{ \bigcup _{i=1}^{\infty }\Lambda _i\right\} \le \sum _{i=1}^{\infty }\text{ M }\left\{ \Lambda _i\right\} . \end{aligned}$$

The triplet $(\Gamma ,\text{ L },\text{ M})$ is called an uncertainty space. Besides, the product uncertain measure on the product $\sigma$-algebra $\text{ L }$ was defined by Liu as follows:

Axiom 4:

: (product Axiom) Let $(\Gamma _k,\text{ L}_k,\text{ M}_k)$ be uncertainty spaces for $k=1, 2, \ldots$, the product uncertain measure $\text{ M }$ is an uncertain measure satisfying

$$\begin{aligned} \text{ M }\left\{ \prod _{k=1}^{\infty }\Lambda _k\right\} =\bigwedge _{k=0}^{\infty }\text{ M}_k\{\Lambda _k\} \end{aligned}$$

where $\Lambda _k$ are arbitrarily chosen events from $\text{ L}_k$ for $k=1, 2, \ldots$, respectively.

Definition 2

(Liu 2009) An uncertain process $C_t$ is called a Liu process if

• (i) $C_0=0$ and almost all sample paths are Lipschitz continuous,

• (ii) $C_t$ has stationary and independent increments,

• (iii) the increment $C_{s+t}-C_s$ has a normal uncertainty distribution

$$\begin{aligned} \Phi _t(x)= \left( 1+\exp \left( -\frac{\pi x}{\sqrt{3}t}\right) \right) ^{-1},\quad x\in \Re . \end{aligned}$$

Definition 3

(Liu 2007) Let $\xi$ be an uncertain variable and its uncertainty distribution is defined by

$$\begin{aligned} \Phi (x)=\text{ M }\{\xi \le x\} \end{aligned}$$

for any real number x.

Common uncertainty distributions include linear uncertainty distributions ${\mathcal {L}}(a,b)$, zigzag uncertainty distributions ${\mathcal {Z}}(a,b,c)$ and normal uncertainty differentials ${\mathcal {N}}(e,\sigma )$. For example, suppose the uncertain variable $\xi (x)=x$, it follows ${\mathcal {L}}(0,1)$ uncertainty distribution

$$\begin{aligned} \Phi (x)= \left\{ \begin{aligned} 0,&\quad if\, x\le 0\\ x,&\quad if\, 0<x<1 \\ 1,&\quad if\, x\ge 1 \end{aligned} \right. . \end{aligned}$$

Definition 4

(Li et al. 2015) Let $C_{1t}$,$C_{2t}$,$\ldots$,$C_{nt}$ be independent Liu processes, and f and $g_{1},g_{2},\ldots ,g_{n}$ are given functions. The multi-factor uncertain differential equation with respect to $C_{jt}$ $( i=1,2,\ldots ,n)$

$$\begin{aligned} \textrm{d}X_{t}=f(t,X_{t})\textrm{d}t+\sum _{j=1}^ng_{j}(t,X_{t})\textrm{d}C_{jt} \end{aligned}$$

is said to have an $\alpha$-path $X_{t}^{\alpha }$ if it solves the corresponding ordinary differential equation

$$\begin{aligned} \textrm{d}X_t^{\alpha } = f(t,X_t^{\alpha })\textrm{d}t + \sum _{j=1}^n|g(t,X_t^{\alpha })|\Phi ^{-1}(\alpha )\textrm{d}t \end{aligned}$$

where

$$\begin{aligned} \Phi ^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha },\quad \alpha \in (0,1). \end{aligned}$$

Theorem 1

(Ye and Liu 2023) Let $\xi$ be an uncertain variable that follows a linear uncertainty distribution ${\mathcal {L}} (a,b)$ with unknown parameters a and b. The test for hypotheses

$$\begin{aligned} H_0: a=a_0 \quad and \quad b=b_0 \quad versus \quad H_1: a \ne a_0 \quad or\quad b \ne b_0 \end{aligned}$$

at significance level $\alpha$ is $W=\Bigg \{(z_1,z_2,\ldots ,z_n):$ there are at least $\alpha$ of indexes i’s with $1\le i\le n$ such as $z_i <\Phi _{\theta _0}^{-1}(\frac{\alpha }{2}) or z_i >\Phi _{\theta _0}^{-1}(1-\frac{\alpha }{2}) \Bigg \}$ where $\Phi _{\theta _0}^{-1}$ is the inverse uncertainty distribution of ${\mathcal {L}} (a,b)$, i.e.

$$\begin{aligned} \Phi _{\theta _0}^{-1}(\alpha )=(1-\alpha )a_0+\alpha b_0. \end{aligned}$$

3 Residuals of multi-factor uncertain differential equations

This section presents the definition and two important properties of residuals for multi-factor uncertain differential equations. Analytic and numerical examples of residuals are given.

Consider a multi-factor uncertain differential equation with n observations $(t_i,x_{t_i})$ $(i=1,2,\ldots ,n)$

$$\begin{aligned} \textrm{d}X_{t}=f(t,X_{t})\textrm{d}t+\sum _{j=1}^ng_{j}(t,X_{t})\textrm{d}C_{jt} \end{aligned}$$

(1)

where f and $g_{j}$ $(j=1,2,\ldots ,n)$ are given continuous functions and $C_{jt}$ $(j=1,2,\ldots ,n)$ is the Liu process. From Eq. (1) and its observations, the i-th corresponding updated uncertain differential equation can be obtained:

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=f(t,X_{t})\textrm{d}t+\sum _{j=1}^ng_{j}(t,X_{t})\textrm{d}C_{jt} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. \end{aligned}$$

(2)

where $2\le i \le n$ and $x_{t_{i-1}}$ is the new initial value at the new initial time $t_{i-1}$.

Definition 5

For any multi-factor uncertain differential equation with discrete observations $(t_i,x_{t_i})$ $(i=1,2,\ldots ,n)$, the i-th residual is defined as $\varepsilon _{i}$ and can be obtained by the uncertainty distribution $\Phi _{t_{i}}(X_{t_i})$ of the uncertain variables $X_{t_i}$ in Eq. (2),

$$\begin{aligned} \varepsilon _{i}=\Phi _{t_{i}}(x_{t_i}) \end{aligned}$$

where $2\le i\le n$ and $x_{t_i}$ is the observation at the corresponding moment of $X_{t_i}$

Example 1

Consider a multi-factor uncertain differential equation with discrete observations $(t_i,x_{t_i})$ $(i=1,2,\ldots ,n)$

$$\begin{aligned} \textrm{d}X_{t}=\mu t X_{t}\textrm{d}t+\sum _{j=1}^m\sigma _{j}t X_{t}\textrm{d}C_{jt} \end{aligned}$$

where $\mu$ and $\sigma _{j}$ are constants. By solving the i-th multi-factor updated uncertain differential equation below $(2<i<n)$

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=\mu t X_{t}\textrm{d}t+\sum _{j=1}^m\sigma _{j} t X_{t}\textrm{d}C_{jt} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. , \end{aligned}$$

we can get

$$\begin{aligned} \ln X_{t_{i}}=\ln X_{t_{i-1}}+\mu (\frac{t_{i}^2-t_{i-1}^2}{2} )+\sum _{j=1}^{m} \sigma _{j}\int _{t_{i-1}}^{t_{i}} t\textrm{d}C_{jt}. \end{aligned}$$

Since the Liu integral

$$\begin{aligned} \int _{t_{i-1}}^{t_{i}} t\textrm{d}C_{jt}\sim {\mathcal {N}} (0,\frac{t_{i}^2-t_{i-1}^2}{2} ) \end{aligned}$$

we can get the uncertainty distribution of $X_{t_{i}}$

$$\begin{aligned}{} & {} \displaystyle \Phi _{t_{i}}(X_{t_i})\\{} & {} \quad =\left( 1+\exp \bigg (\frac{\pi (\ln x_{t_{i-1}}+\mu (\frac{t_{i}^2-t_{i-1}^2}{2} )-\ln X_{t_i}) }{\sqrt{3} \sum \limits _{j=1}^{m}\sigma _{j}(\frac{t_{i}^2-t_{i-1}^2}{2} ) } \bigg )\right) ^{-1}. \end{aligned}$$

By Definition 5, we get the i-th residual corresponding to $\Phi _{t_{i}}(x_{i})$

$$\begin{aligned}{} & {} \varepsilon _{i}=\displaystyle \Phi _{t_{i}}(x_{t_i})\\{} & {} \quad =\left( 1+\exp \bigg (\frac{\pi (\ln x_{t_{i-1}}+\mu (\frac{t_{i}^2-t_{i-1}^2}{2} )-\ln x_{t_i}) }{\sqrt{3} \sum \limits _{j=1}^{m}\sigma _{j}(\frac{t_{i}^2-t_{i-1}^2}{2} ) } \bigg )\right) ^{-1}. \end{aligned}$$

Example 2

Consider a multi-factor uncertain differential equation with discrete observations $(t_i,x_{t_i})$ $(i=1,2,\ldots ,n)$

$$\begin{aligned} \textrm{d}X_{t}=\mu \textrm{d}t+\sigma _{1}t\textrm{d}C_{1t}+\sigma _{2}(2 +t)^{-\alpha }\textrm{d}C_{2t} \end{aligned}$$

where $\mu$, $\sigma _{j}$ and $\alpha$ $(0<\alpha <1)$ are constants. By solving the i-th multi-factor updated uncertain differential equation below $(2<i<n)$

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=\mu \textrm{d}t+\sigma _{1}t\textrm{d}C_{1t}+\sigma _{2}(2 +t)^{-\alpha }\textrm{d}C_{2t} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. , \end{aligned}$$

we can get

$$\begin{aligned} X_{t_{i}}=&{} X_{t_{i-1}}+\mu (t_{i}-t_{i-1})+ \sigma _{1}\displaystyle {\int _{t_{i-1}}^{t_{i}}} t \text {d}C_{1t}\\{}&{} \quad + \sigma _{2}\displaystyle {\int _{t_{i-1}}^{t_{i}}} (2+t)^{- \alpha }\text {d}C_{2t}. \end{aligned}$$

Since the Liu integrals

$$\begin{aligned}{} & {} \int _{t_{i-1}}^{t_{i}} t\textrm{d}C_{jt}\sim {\mathcal {N}} (0,\frac{t_{i}^2-t_{i-1}^2}{2} )\quad \text {and} \\{} & {} \quad \int _{t_{i{-}1}}^{t_{i}} (2{+}t)^{{-}\alpha }\textrm{d}C_{jt}\sim {\mathcal {N}} (0,\frac{(2{+}t_{i})^{1{-}\alpha }{-}(2{+}t_{i-1})^{1{-}\alpha }}{1{-}\alpha } ) \end{aligned}$$

we can get the uncertainty distribution of $X_{t_{i}}$

$$\begin{aligned}{} & {} \displaystyle \Phi _{t_{i}}(X_{t_i})\\{} & {} \quad {=}\left( 1{+}\exp \bigg (\frac{\pi ( x_{t_{i-1}}{+}\mu (t_{i}{-}t_{i-1}){-} X_{t_i}) }{\sqrt{3} (\sigma _{1}\frac{t_{i}^2{-}t_{i-1}^2}{2} {+}\sigma _{2}\frac{(2{+}t_{i})^{1{-}\alpha }{-}(2+t_{i-1})^{1{-}\alpha }}{1{-}\alpha })} \bigg )\right) ^{-1}. \end{aligned}$$

By Definition 5, we get the i-th residual corresponding to $\Phi _{t_{i}}(x_{t_i})$

$$\begin{aligned}{} & {} \displaystyle \varepsilon _{i}=\displaystyle \Phi _{t_{i}}(x_{t_i})\\{} & {} \quad {=}\left( 1{+}\exp \bigg (\frac{\pi ( x_{t_{i-1}}{+}\mu (t_{i}{-}t_{i{-}1}){-} x_{t_i}) }{\sqrt{3} (\sigma _{1}\frac{t_{i}^2{-}t_{i-1}^2}{2} {+}\sigma _{2}\frac{(2+t_{i})^{1{-}\alpha }{-}(2+t_{i-1})^{1-\alpha }}{1-\alpha }) } \bigg )\right) ^{-1}. \end{aligned}$$

3.1 Important properties of residuals

The two properties of the residuals provide an important basis for subsequent processing of the data and parameter estimation.

Property 1

The updated ordinary differential equations can be obtained by Eq. (2):

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}^{\alpha }=f(t,X_{t}^{\alpha })\textrm{d}t+|\sum _{j=1}^ng_{j}(t,X_{t}^{\alpha })|\Phi ^{-1}(\alpha )\textrm{d}t \\&X_{t_{i-1}}^{\alpha }=x_{t_{i-1}} \end{aligned} \right. , \end{aligned}$$

(3)

where

$$\begin{aligned} \Phi ^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha },\quad \alpha \in (0, 1), \end{aligned}$$

and $X_{t_{i}}^{\alpha }$ as the $\alpha$-path of $X_{t_{i}}$. The residuals $\varepsilon _{i}$ are equal to the value of $\alpha$ in $X_{t_{i}}^{\alpha }$.

Proof

Since for any $\alpha \in (0,1)$, we have

$$\begin{aligned} {\mathcal {M}}\{X_{t_{i}}\le \Phi ^{-1}_{t_i}(\alpha )\} =\Phi _{t_{i}} (\Phi _{t_{i}} ^{-1}(\alpha ))=\alpha , \end{aligned}$$

then there must be an inverse uncertainty distribution $\Phi _{t_{i}}^{-1}$ of $X_{t_{i}}$.

Writing $x=\Phi ^{-1}_{t_{i}}(\alpha )$, we can get $\alpha =\Phi _{t_{i}}$ and

$$\begin{aligned} {\mathcal {M}}\{X_{t_{i}}\le x\} =\alpha =\Phi _{t_{i}}(X_{t_i}). \end{aligned}$$

Therefore, $\varepsilon _{i}$ can be regarded as the value of $\alpha$ in $X^{\alpha }_{t_{i}}$ at time $t_{i}$. $\square$

Property 2

The residuals of a multi-factor uncertain differential equation obey the linear uncertainty distribution ${\mathcal {L}} (0,1)$.

Proof

The uncertainty distribution $\Phi _{t_{i}}(X_{t_i})$ $(2\le i\le n)$ is also an uncertain variable and $0\le \Phi _{t_{i}}(X_{t_i})\le 1$. For any $0<x<1$, we can always get

$$\begin{aligned} {\mathcal {M}}\{\Phi _{t_{i}}(X_{t_{i}}) \le x\} ={\mathcal {M}}\{X_{t_{i}}\le \Phi ^{-1}_{t_i}(x)\} \\ =\Phi _{t_{i}} (\Phi _{t_{i}} ^{-1}(x))=x. \end{aligned}$$

Obviously, the distribution of $\Phi _{t_{i}}(X_{t_i})$ is as follows

$$\begin{aligned} \Phi (x)= \left\{ \begin{aligned} 0,&\quad if\, x\le 0\\ x,&\quad if\, 0<x<1 \\ 1,&\quad if\, x\ge 1 \end{aligned} \right. . \end{aligned}$$

Therefore, the uncertain variable $\Phi _{t_{i}}(X_{t_i})$ follows a linear uncertainty distribution ${\mathcal {L}} (0,1)$, and the residuals $\varepsilon _{i}=\Phi _{t_{i}}(x_{t_i}),(i=2,\ldots ,n)$ also follow the linear uncertainty distribution ${\mathcal {L}} (0,1)$. $\square$

3.2 Approximate analytical expression of residuals

For the general multi-factor uncertain differential equation, if the uncertainty distribution cannot be obtained by solving the equation, the approximate expression of the residual can be obtained by the following method.

According to Eq. (3), $X^{\alpha }_{t_{i}}$ can be expressed as

$$\begin{aligned} X_{t_{i}}^{\alpha }= & {} X_{t_{i-1}}^{\alpha }+f(t,X_{t_{i}}^{\alpha })(t_{i}-t_{i-1})\nonumber \\{} & {} +\left| \sum _{j=1}^n g_{j}(t,X_{t_{i}}^{\alpha }) \right| \Phi ^{-1}(\alpha )(t_{i}-t_{i-1}), \end{aligned}$$

(4)

where

$$\begin{aligned} \Phi ^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }. \end{aligned}$$

Since the $\alpha$ satisfies the following minimization problem

$$\begin{aligned} \mathop {\min }\limits _{\alpha }\mid X^{\alpha }_{t_{i}}-X_{t_{i}} \mid , \end{aligned}$$

it can be obtained that $X^{\alpha }_{t_{i}} \approx X_{t_{i}}$.

According to Eq. (3) and Property 1 of the residuals, we can get

$$\begin{aligned} X_{t_{i-1}}^{\alpha }=x_{t_{i-1}},\quad \varepsilon _i=\alpha . \end{aligned}$$

Therefore the Eq. (4) can be expressed as

$$\begin{aligned} X_{t_{i}}= & {} X_{t_{i-1}}+f(t,X_{t_{i}})(t_{i}-t_{i-1})\nonumber \\{} & {} + \left| \sum _{j=1}^n g_{j}(t,X_{t_{i}}) \right| \frac{\sqrt{3}}{\pi }\ln \frac{\varepsilon _{i}}{1-\varepsilon _{i}}(t_{i}-t_{i-1}). \end{aligned}$$

After sorting, the expression for the residuals $\varepsilon _{i}$ is

$$\begin{aligned}{} & {} \displaystyle \varepsilon _{i}=1\\{} & {} \quad -\left( 1+\exp \bigg (\frac{\pi (X_{t_{i}}-X_{t_{i-1}}-f(t,X_{t})(t_{i}-t_{i-1}))}{\sqrt{3}\left| \sum \limits _{j=1}^{n} g_{j}(t,X_{t}) \right| (t_{i}-t_{i-1}) } \bigg )\right) ^{-1}. \end{aligned}$$

Example 3

Assuming a multi-factor uncertain differential equation,

$$\begin{aligned} \textrm{d}X_{t}=0.0305 t \textrm{d}t+0.7441t\textrm{d}C_{1t}+0.5000(2 +t)^{-2}\textrm{d}C_{2t}, \end{aligned}$$

the updated uncertain differential equation can be obtained

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=0.0305 t \textrm{d}t+0.7441t\textrm{d}C_{1t}+0.5000(2 +t)^{-2}\textrm{d}C_{2t} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. . \end{aligned}$$

The corresponding updated ordinary differential equation is

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}^\alpha =0.0305 t \textrm{d}t+\left| 0.7441t+0.5000(2 +t)^{-2} \right| \frac{\sqrt{3}}{\pi }\ln \nonumber \\&\quad \frac{\varepsilon _{i}}{1-\varepsilon _{i}}\textrm{d}t\\&X_{t_{i-1}}^\alpha =x_{t_{i-1}} \end{aligned} \right. . \end{aligned}$$

Using the method described above, we can get

$$\begin{aligned}{} & {} \displaystyle \varepsilon _{i}=1\\{} & {} \quad {-}\left( 1{+}\exp \bigg (\frac{\pi (x_{t_{i}}{-}x_{t_{i-1}}{-}0.0305 t_{i}(t_{i}{-}t_{i-1}))}{\sqrt{3}\left| 0.7441t_{i}{+}0.5000(2 +t_{i})^{-2} \right| (t_{i}{-}t_{i-1}) } \bigg )\right) ^{{-}1}. \end{aligned}$$

Therefore, when we have observational data, we can substitute it into the solution. The observed data of Example 3 and its residual calculation results are shown in Table 1.

Table 1 The observed datas and residual result in Example 3

4 Parameter estimation and result testing

This section presents moment estimates of the unknown parameters in multi-factor uncertain differential equations based on residuals and uses uncertainty hypothesis testing to confirm the accuracy of the estimates. Some numerical examples are provided to demonstrate the feasibility of the method.

4.1 Moment estimation based on residual

Assume a multi-factor uncertain differential equation with n observations $(t_i,x_{t_i})$ $(i=1,2,\ldots ,n)$

$$\begin{aligned} \textrm{d}X_{t}=f(t,X_{t}; \mu )\textrm{d}t+\sum _{j=1}^ng_{j}(t,X_{t}; \sigma _{j})\textrm{d}C_{jt} \end{aligned}$$

(5)

where $\mu$ and $\sigma _{j}(j=1, 2, \ldots , n)$ are the parameters to be estimated.

Based on the observed data and the definition of residuals, a series of residuals $\varepsilon _{2}, \varepsilon _{3}, \ldots ,\varepsilon _{n}$ can be obtained and used as a set of samples for the linear uncertainty distribution ${\mathcal {L}} (0,1)$.

According to the method of moments, the p-th sample moments is

$$\begin{aligned} \frac{1}{N-1}\sum _{i=1}^{N-1}\varepsilon _{i}({\mu ;\sigma _{1}, \sigma _{2},\ldots ,\sigma _{n}})^p \end{aligned}$$

and the corresponding p-th population moments

$$\begin{aligned}\frac{1}{p+1}\end{aligned}$$

where $p=1, 2, \ldots ,K$ (K is the number of unknown parameters). According to the principle of moment estimation method, we can obtain the following equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{N -1}\sum \limits _{i=2}^{N}\varepsilon _{i}\,({\mu ;\sigma _{1}, \sigma _{2},\ldots ,\sigma _{n}})=\frac{1}{1+1} \\ \frac{1}{N -1}\sum \limits _{i=2}^{N}(\varepsilon _{i}\,({\mu ;\sigma _{1}, \sigma _{2},\ldots ,\sigma _{n}}))^2=\frac{1}{2+1} \\ \ldots \\ \frac{1}{N -1}\sum \limits _{i=2}^{N}(\varepsilon _{i}\,({\mu ;\sigma _{1}, \sigma _{2},\ldots ,\sigma _{n}}))^K=\frac{1}{K+1} \end{array}\right. . \end{aligned}$$

(6)

The estimated value $({\hat{\mu }};\hat{\sigma _{1}},\hat{\sigma _{2}},\ldots ,\hat{\sigma _{n}})$ of unknown parameters can be obtained by solving the equations.

However, with some observations, the moment estimation method is no longer applicable when the Equation system (6) based on moment estimation has no solution. In this case, the unknown parameters can be obtained by solving the following minimization problem based on the generalized estimation of moments principle:

$$\begin{aligned}{} & {} \mathop {\min }\limits _{({\mu ;\sigma _{1}, \sigma _{2},\ldots ,\sigma _{n}})}\sum _{p=1}^{p}\nonumber \\{} & {} \quad \left( \frac{1}{N -1}\sum _{i=2}^{N}\varepsilon _{i}({\mu ;\sigma _{1}, \sigma _{2},\ldots ,\sigma _{n}})^p-\frac{1}{p+1} \right) ^2. \end{aligned}$$

(7)

4.2 Reasonableness test of estimated results

By means of moment estimation, we obtain estimates of the unknown parameters $({\hat{\mu }};{\hat{\sigma }}_{1}, {\hat{\sigma }}_{2},\ldots ,{\hat{\sigma }}_{n})$, and the residual values which obey a linear uncertainty distribution ${\mathcal {L}} (0,1)$. Next, we will test the estimation results using hypothesis testing methods.

For the residuals $\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _N$ that follow a linear uncertainty distribution ${\mathcal {L}} (0,1)$, the test for the hypotheses:

$$\begin{aligned}\mathrm H_0: a=0 \mathrm \quad and \quad b=1 \mathrm \quad versus\quad H_1: a \ne 0 \mathrm \quad or\quad b \ne 1 \end{aligned}$$

Table 2 The observed data and the residuals in Example 4

and at significance level $\alpha$ is

${W=\Bigg \{(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _N): \text {there are at least}\, \alpha }$${\text {of indexes i's with}1\le i\le n \text {such as}z_i <\Phi ^{-1}(\frac{\alpha }{2}) \text {or} z_i > }$${\Phi ^{-1}(1-\frac{\alpha }{2}) \Bigg \}}$ where the inverse uncertainty distribution of ${\mathcal {L}} (0,1)$ is

$$\begin{aligned}\Phi ^{-1}(\alpha )=\alpha .\end{aligned}$$

If the number of $\varepsilon _i$ satisfying

$$\begin{aligned}\varepsilon _i \notin \Big [\Phi ^{-1}(\frac{\alpha }{2}),\;\Phi ^{-1}(1-\frac{\alpha }{2})\Big ]\end{aligned}$$

is at least $(N-1)\alpha$, then $\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _N\in W$. And the original hypothesis $H_0$ is rejected, meaning that the parameter estimate result is erroneous.

Example 4

Consider a multi-factor uncertain differential equation with parameters $\mu$, $\sigma _{1}$ and $\sigma _{2}$

$$\begin{aligned} \textrm{d}X_{t}=\mu t X_{t}\textrm{d}t+\sigma _{1}t X_{t}\textrm{d}C_{1t}+\sigma _{2}t X_{t}\textrm{d}C_{2t}. \end{aligned}$$

Then we can get the related updated multi-factor uncertain differential equation

$$\begin{aligned} \left\{ \begin{aligned}&\text {d}X_{t}=\mu t \text {d}t+ \sigma _{1}t\text {d}C_{1t}+\sigma _{2}t \text {d}C_{1t} \ X_{t_{i-1}}=x_{t_{i-1}}. \end{aligned} \right. \end{aligned}$$

By solving the uncertain variable $X_{t_{i}}$ and its uncertainty distribution $\Phi (X_{t_{i}})$, the residual can be expressed as

$$\begin{aligned}{} & {} \displaystyle \varepsilon _{i}(\mu ,\sigma _{1},\sigma _{2})\\{} & {} \quad =\left( 1+\exp \bigg (\frac{\pi (\ln x_{t_{i-1}}+\mu (\frac{t_{i}^2-t_{i-1}^2}{2} )-\ln x_{i}) }{\sqrt{3}( \sigma _{1}(\frac{t_{i}^2-t_{i-1}^2}{2} ) +\sigma _{2}(\frac{t_{i}^2-t_{i-1}^2}{2} ))} \bigg )\right) ^{-1},\end{aligned}$$

and $\varepsilon _{i}\sim {\mathcal {L}}(0,1)$. The observed data are shown in Table 3.

According to the principle of the moment estimation, we obtain the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{24}\sum \limits _{i=2}^{25}\varepsilon _{i}(\mu ;\sigma _{1},\sigma _{2})=\frac{1}{2} \\ \frac{1}{24}\sum \limits _{i=2}^{25}(\varepsilon _{i}(\mu ;\sigma _{1},\sigma _{2}))^2=\frac{1}{3} \\ \frac{1}{24}\sum \limits _{i=2}^{25}(\varepsilon _{i}(\mu ;\sigma _{1},\sigma _{2}))^3=\frac{1}{4} \end{array}\right. . \end{aligned}$$

By solving the above system of equations, the unknown parameter results are obtained

$$\begin{aligned}{\hat{\mu }}=1.0400,\quad {\hat{\sigma }}_{1}=-47.1746 \quad \mathrm and \quad {\hat{\sigma }}_{2}= 50.2557.\end{aligned}$$

Therefore the residuals are determined as

$$\begin{aligned}\displaystyle{} & {} \varepsilon _{i}=\\{} & {} \quad \left( 1+\exp \bigg (\frac{\pi (\ln x_{t_{i-1}}+1.0400 (\frac{t_{i}^2-t_{i-1}^2}{2} )-\ln x_{i}) }{\sqrt{3}(-47.1746(\frac{t_{i}^2-t_{i-1}^2}{2} ) +50.2557(\frac{t_{i}^2-t_{i-1}^2}{2} ))} \bigg )\right) ^{-1},\end{aligned}$$

and the values of the residuals are shown in Table 2.

For the residuals $\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{25}$, the test for the hypotheses:

$$\begin{aligned}\mathrm H_0: a=0 \mathrm \quad and \quad b=1 \mathrm \quad versus\quad H_1: a \ne 0 \mathrm \quad or\quad b \ne 1 \end{aligned}$$

at significance level $\alpha =0.05$ is $W=\Bigg \{ (\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{25}$): there are at least 2 of indexes i’s with $1\le i\le n$ such as $z_i < \Phi ^{-1}(\frac{\alpha }{2})$ or $z_i > \Phi ^{-1}(1-\frac{\alpha }{2})\Bigg \}$

where

$$\begin{aligned} (N-1)\alpha= & {} 24*0.05=1.2,\qquad \Phi ^{-1}\left( \frac{0.05}{2}\right) =0.025,\\{} & {} \Phi ^{-1}\left( 1-\frac{0.05}{2}\right) =0.975. \end{aligned}$$

Obviously, any $\varepsilon _i\in [0.025,0.975]$ and $(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{25})\notin W$. The original hypothesis $H_0$ holds and $({\hat{\mu }},{\hat{\sigma }}_1,{\hat{\sigma }}_2)$ is reasonable for the equation.

Therefore, the multi-factor uncertain differential equation is obtained

$$\begin{aligned} \textrm{d}X_{t}=1.0400 t X_{t}\textrm{d}t-47.1746t X_{t}\textrm{d}C_{1t}+50.2557t X_{t}\textrm{d}C_{2t}. \end{aligned}$$

Example 5

Assuming a multi-factor uncertain differential equation,

$$\begin{aligned} \textrm{d}X_{t}=\frac{X_{t}}{\sigma _{1}+t}\textrm{d}t+t^2\textrm{d}C_{1t}+(\sigma _{2}+t)^{-2}\textrm{d}C_{2t}, \end{aligned}$$

where $\sigma _{1}$, $\sigma _{2}$ are unknown parameter. The observed data are shown in Table 4.

The updated uncertain differential equation can be obtained

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=\frac{X_{t}}{\sigma _{1}+t}\textrm{d}t+t^2\textrm{d}C_{1t}+(\sigma _{2}+t)^{-2}\textrm{d}C_{2t} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. . \end{aligned}$$

The corresponding updated ordinary differential equation is

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{d}X_{t}^\alpha =\frac{X_{t}^\alpha }{\sigma _{1}+t}\textrm{d}t+\left| t^2+(\sigma _{2}+t)^{-2} \right| \frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\textrm{d}t \\ X_{t_{i-1}}^\alpha =x_{t_{i-1}} \end{array}\right. } \end{aligned}$$

and the residual expression is

$$\begin{aligned}{} & {} \displaystyle \varepsilon _{i}(\sigma _{1}, \sigma _{2})\\{} & {} \quad =1-\left( 1+\exp \bigg (\frac{\pi (x_{t_{i}}-x_{t_{i-1}}-\frac{x_{t_{i}}}{\sigma _{1}+t_i})(t_{i}-t_{i-1}))}{\sqrt{3}\left| t_{i}^2+(\sigma _{2}+t_{i})^{-2} \right| (t_{i}-t_{i-1}) } \bigg )\right) ^{-1}.\end{aligned}$$

Table 3 The observed data and the residuals in Example 5

Table 4 Plasma drug concentration data at each time point in Example 6

According to the principle of the moment estimation, we obtain the following equations

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \frac{1}{19}\sum \limits _{i=2}^{20}\varepsilon _{i}(\sigma _{1},\sigma _{2})=\frac{1}{2} \\ \frac{1}{19}\sum \limits _{i=2}^{20}(\varepsilon _{i}(\sigma _{1},\sigma _{2}))^2=\frac{1}{3} \end{array}\right. . \end{aligned}$$

By solving the above system of equations, we can obtain the estimated results of the unknown parameters

$$\begin{aligned}\quad {\hat{\sigma }}_{1}=0.0013 \quad and \quad {\hat{\sigma }}_{2}=0.0012.\end{aligned}$$

Therefore the residuals are determined as

$$\begin{aligned}{} & {} \displaystyle \varepsilon _{i}\\{} & {} \quad =1-\left( 1+\exp \bigg (\frac{\pi (x_{t_{i}}-x_{t_{i-1}}-\frac{x_{t_{i}}}{0.0013+t_i})(t_{i}-t_{i-1}))}{\sqrt{3}\left| t_{i}^2+(0.0012+t_{i})^{-2} \right| (t_{i}-t_{i-1}) } \bigg )\right) ^{-1}\end{aligned}$$

and the values of the residuals are shown in Table 3.

For the residuals $\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{20}$, the test for the hypotheses:

$$\begin{aligned}\mathrm H_0: a=0 \mathrm \quad and \quad b=1 \mathrm \quad versus\quad H_1: a \ne 0 \mathrm \quad or\quad b \ne 1 \end{aligned}$$

at significance level $\alpha =0.1$ is

$W=\Bigg \{(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{20}): \text {there are at}$ $\text { least 2 of} \text {indexes i's with} 1\le i\le n \text {such as} z_i <\Phi ^{-1}(\frac{\alpha }{2}) \text {or}$ $z_i >\Phi ^{-1}(1-\frac{\alpha }{2}) \Bigg \}$ where

$$\begin{aligned}(N-1)\alpha= & {} 19*0.1=1.9,\qquad \Phi ^{-1}\left( \frac{0.1}{2}\right) =0.05,\\{} & {} \Phi ^{-1}\left( 1-\frac{0.1}{2}\right) =0.95.\end{aligned}$$

Obviously, only $\varepsilon _2 \notin [0.05,0.95]$, thus $(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{25})\notin W$. The original hypothesis $H_0$ holds and $({\hat{\sigma }}_1,{\hat{\sigma }}_2)$ is reasonable for the equation.

Therefore, the multi-factor uncertain differential equation is determined as

$$\begin{aligned} \textrm{d}X_{t}=\frac{X_{t}}{0.0013+t}\textrm{d}t+t^2\textrm{d}C_{1t}+(0.0012+t)^{-2}\textrm{d}C_{2t}. \end{aligned}$$

5 Numerical example

In this section, two examples of multi-factor uncertain differential equations with real data are shown to check the practicability of the parameter estimation method.

Example 6

Considering a multi-factor uncertain pharmacokinetic model with unknown parameters proposed by Liu and Yang (2021) is as follows:

$$\begin{aligned}\textrm{d}X_{t}=(k_{0}-k_{1}X_{t})\textrm{d}t+\sigma _{1}X_{t}\textrm{d}C_{1t}+\sigma _{2}\textrm{d}C_{2t}\end{aligned}$$

where $X_{t}$ is the drug concentration at time t and $k_{0}$, $k_{1}$, $\sigma _{1}$, $\sigma _{2}$ are the unknown constant parameters.

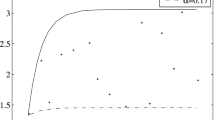
The research data of the JNJ-53718678 drug by Huntjens et al. (2017) was cited as the discrete data for the model. JNJ-53718678 is a small molecule fusion inhibitor for the treatment of respiratory diseases. A single injection of 250 mg of JNJ-53718678 was administered, and the plasma drug concentration was measured before injection and at 0.5 h, 1.0 h, 1.5 h, 2.0 h, 3.0 h, 4.0 h, 6.0 h, 8.0 h, 12.0 h, 16.0 h and 24.0 h after injection. The specific data is shown in Table 4.

The corresponding updated multi-factor uncertain differential equation is

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=(k_{0}-k_{1}X_{t})\textrm{d}t+\sigma _{1}X_{t}\textrm{d}C_{1t}+\sigma _{2}\textrm{d}C_{2t} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. \end{aligned}$$

(8)

and the corresponding updated ordinary differential equation is

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}^\alpha =(k_{0}-k_{1}X_{t}^\alpha )\textrm{d}t+|\sigma _{1}X_{t}^\alpha +\sigma _{2}|\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\textrm{d}t\\&X_{t_{i-1}}^\alpha =x_{t_{i-1}} \end{aligned} \right. .\nonumber \\ \end{aligned}$$

(9)

Therefore, the residual expression can be obtained as

$$\begin{aligned}{} & {} \varepsilon _{i}(k_{0},k_{1},\sigma _{1},\sigma _{2})\\{} & {} \quad =1-\left( 1+\exp \bigg (\frac{\pi (x_{t_{i}}-x_{t_{i-1}}-k_{0}+k_{1}x_{t_{i}})(t_{i}-t_{i-1}))}{\sqrt{3}\left| \sigma _{1}x_{t_{i}}+\sigma _{2} \right| (t_{i}-t_{i-1}) } \bigg )\right) ^{-1}.\end{aligned}$$

According to the principle of the moment estimation, we obtain the following equations

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \frac{1}{11}\sum \limits _{i=2}^{12}\varepsilon _{i}(k_{0},k_{1},\sigma _{1},\sigma _{2})=\frac{1}{2} \\ \frac{1}{11}\sum \limits _{i=2}^{12}(\varepsilon _{i}(k_{0},k_{1},\sigma _{1},\sigma _{2}))^2=\frac{1}{3} \\ \frac{1}{11}\sum \limits _{i=2}^{12}(\varepsilon _{i}(k_{0},k_{1},\sigma _{1},\sigma _{2}))^3=\frac{1}{4} \\ \frac{1}{11}\sum \limits _{i=2}^{12}(\varepsilon _{i}(k_{0},k_{1},\sigma _{1},\sigma _{2}))^4=\frac{1}{5} \end{array}\right. . \end{aligned}$$

By solving the above system of equations, the moment estimates of the unknown parameters are:

$$\begin{aligned}{} & {} {\hat{k}}_{0}=0.9780,\quad {\hat{k}}_{1}=0.3177, \quad {\hat{\sigma }}_{1}= 0.5830\quad and \quad \\{} & {} {\hat{\sigma }}_{2}=0.7134. \end{aligned}$$

The residuals can be obtained as

$$\begin{aligned}\varepsilon _{i}{=}1 {-}\left( 1{+}\exp \bigg (\frac{\pi (x_{t_{i}}{-}x_{t_{i-1}}{-}0.9780{+}0.3177x_{t_{i}})(t_{i}{-}t_{i-1}))}{\sqrt{3}\left| 0.5830x_{t_{i}}{+}0.7134 \right| (t_{i}{-}t_{i-1}) } \bigg )\right) ^{{-}1}\end{aligned}$$

and the values of the residuals are shown in Table 4.

For the residuals $\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{12}$, the test for the hypotheses:

$$\begin{aligned}\mathrm H_0: a=0 \mathrm \quad and \quad b=1 \mathrm \quad versus\quad H_1: a \ne 0 \mathrm \quad or\quad b \ne 1 \end{aligned}$$

at significance level $\alpha =0.1$ is $W=\Bigg \{ (\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{12}): \text {there are at least 2 of indexes i's with} 1\le i\le n \text {such as} z_i <\Phi ^{-1}(\frac{\alpha }{2}) \text {or} z_i >\Phi ^{-1}(1-\frac{\alpha }{2}) \Bigg \}$ where

$$\begin{aligned}(N-1)\alpha= & {} 11*0.1=1.1,\qquad \Phi ^{-1}\left( \frac{0.1}{2}\right) =0.05,\\{} & {} \quad \Phi ^{-1}\left( 1-\frac{0.1}{2}\right) =0.95.\end{aligned}$$

Obviously, only $\varepsilon _2 \notin [0.05,0.95]$, thus $(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{12})\notin W$. The original hypothesis $H_0$ holds and $({\hat{k}}_0,{\hat{k}}_1,{\hat{\sigma }}_1,{\hat{\sigma }}_2)$ is reasonable for the equation.

Eventually, the multi-factor uncertain pharmacokinetic model equation is determined as

$$\begin{aligned} \textrm{d}X_{t}{} & {} =(0.9780-0.3177X_{t})\textrm{d}t + 0.5830X_{t}\textrm{d}C_{1t}\\{} & {} \quad +0.7134 \textrm{d}C_{2t}. \end{aligned}$$

Example 7

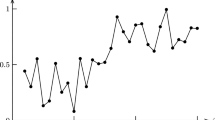
Considering a multi-factor uncertain stock model with Alibaba stock price data (Liu and Liu 2022) from January 1 to January 30, 2019 shown in Table 5:

$$\begin{aligned}\textrm{d}X_{t}=(m-a)X_t\textrm{d}t + \sigma _1 X_t\textrm{d}C_{1t}+\sigma _2 X_t\textrm{d}C_{2t}\end{aligned}$$

where $X_{t}$ is the stock price at time t and m, a, $\sigma _{1}$, $\sigma _{2}$ are the unknown constant parameters.

Table 5 The stock prices and the residuals in Example 7

The corresponding updated multi-factor uncertain differential equation is

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{d}X_{t}=(m-a)X_t\textrm{d}t + \sigma _1 X_t\textrm{d}C_{1t}+\sigma _2 X_t\textrm{d}C_{2t} \\&X_{t_{i-1}}=x_{t_{i-1}} \end{aligned} \right. \end{aligned}$$

(10)

and the residual expression can be obtained as

$$\begin{aligned}{} & {} \varepsilon _{i}(m,a,\sigma _{1},\sigma _{2})\\{} & {} \quad =(1+\exp \bigg (\frac{\pi (\ln {x_{t_i}}-(m-a)(t_{i}-t_{i-1})-\ln {x_{t_i}})}{\sqrt{3} (\sigma _{1}+\sigma _{2}) (t_{i}-t_{i-1}) } \bigg )^{-1}.\end{aligned}$$

According to the principle of the moment estimation, we obtain the following equations

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \frac{1}{29}\sum \limits _{i=2}^{30}\varepsilon _{i}(m,a,\sigma _{1},\sigma _{2})=\frac{1}{2} \\ \frac{1}{29}\sum \limits _{i=2}^{30}(\varepsilon _{i}(m,a,\sigma _{1},\sigma _{2}))^2=\frac{1}{3} \\ \frac{1}{29}\sum \limits _{i=2}^{30}(\varepsilon _{i}(m,a,\sigma _{1},\sigma _{2}))^3=\frac{1}{4} \\ \frac{1}{29}\sum \limits _{i=2}^{30}(\varepsilon _{i}(m,a,\sigma _{1},\sigma _{2}))^4=\frac{1}{5} \end{array}\right. . \end{aligned}$$

By solving the above system of equations, the moment estimates of the unknown parameters are:

$$\begin{aligned}{} & {} {\hat{m}}=0.4261,\quad {\hat{a}}=0.4371, \quad {\hat{\sigma }}_{1}= 0.4777\quad and \quad \\{} & {} {\hat{\sigma }}_{2}=-0.4432. \end{aligned}$$

The residuals can be obtained as

$$\begin{aligned}{} & {} \varepsilon _{i}(m,a,\sigma _{1},\sigma _{2})=(1+\\\exp{} & {} \quad \bigg (\frac{\pi (\ln {x_{t_{i-1}}}-(0.4261-0.4371)(t_{i}-t_{i-1})-\ln {x_{t_i}})}{\sqrt{3} (0.4777-0.4432)(t_{i}-t_{i-1}) } \bigg )^{-1}.\end{aligned}$$

and the values of the residuals are shown in Table 5.

For the residuals $\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{30}$, the test for the hypotheses:

$$\begin{aligned}\mathrm H_0: a=0 \mathrm \quad and \quad b=1 \mathrm \quad versus\quad H_1: a \ne 0 \mathrm \quad or\quad b \ne 1 \end{aligned}$$

at significance level $\alpha =0.1$ is

$W{=}\Bigg \{ (\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{30}): \text {there are at least 3 of indexes i's}$${ with} 1\le i\le n \text {such as} z_i <\Phi ^{-1}(\frac{\alpha }{2}) \text {or} z_i >\Phi ^{-1}(1-\frac{\alpha }{2}) \Bigg \}$ where

$$\begin{aligned} (N-1)\alpha= & {} 29*0.1=2.9,\qquad \Phi ^{-1}(\frac{0.1}{2})=0.05,\\{} & {} \quad \Phi ^{-1}(1-\frac{0.1}{2})=0.95. \end{aligned}$$

Obviously, $\varepsilon _2$ and $\varepsilon _{21} \notin [0.05,0.95]$, thus $(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{30})\notin W$. The original hypothesis $H_0$ holds and $({\hat{m}},{\hat{a}},{\hat{\sigma }}_1,{\hat{\sigma }}_2)$ is reasonable for the equation.

Eventually, the multi-factor uncertain stock model equation is determined as

$$\begin{aligned}\textrm{d}X_{t}= & {} (0.4261-0.4371)X_t\textrm{d}t + 0.4777 X_t\textrm{d}C_{1t}\\{} & {} -0.4432 X_t\textrm{d}C_{2t}.\end{aligned}$$

6 Conclusion

This paper presents the definition of residuals for multi-factor uncertain differential equations and proves two important properties. Examples of computing residuals demonstrate how residual expressions can be obtained in various contexts. Based on the fact that the residuals obey the linear uncertainty distribution ${\mathcal {L}}(0,1)$, moment estimates of the unknown parameters in the multi-factor uncertain differential equation are performed and the estimates are tested. Several numerical examples are shown to verify the feasibility of the method. In contrast to previously proposed estimation methods, the residual-based moment estimation method does not require weighting and normalisation of the unknown parameters in the multi-factor uncertain differential equation. The residual method can also be used for estimation when the time interval is relatively large and the difference method is not applicable. In the future the residual-based moment estimation method can be used for parameter estimation of high-order uncertain differential equations or multi-dimensional uncertain differential equations.