1 Introduction

For the sake of modeling the human’s belief degrees reasonably, uncertainty theory was established by Liu (2007) in 2007 and then perfected by Liu (2009) in 2009. Up to now, uncertainty theory has become a new branch of axiomatic mathematics and has been widely applied in many fields of science and technology.

For the purpose of handling the dynamic systems with continuous-time noises, uncertain differential equation was first proposed by Liu (2008) as a kind of differential equation driven by Liu processes. Up to now, uncertain differential equation has been extensively studied and has made significant progress. In the theoretical aspect of uncertain differential equation, Chen and Liu (2010) first proposed the existence and uniqueness theorem of the solution of uncertain differential equation under linear growth condition and Lipschitz condition. Following the existence and uniqueness theorem, Liu (2009) first defined the concept of stability of uncertain differential equation. Later, Yao et al. (2013) gave some stability theorems to develop the stability analysis of uncertain differential equation, and then other types of stability were discussed by Sheng and Wang (2014), Yao et al. (2015), Yang et al. (2017), etc. As the most significant contribution to uncertain differential equation, Yao-Chen formula was proposed by Yao and Chen (2013), which associated uncertain differential equation with ordinary differential equations, and showed that the solution of an uncertain differential equation can be represented by the solutions of a family of ordinary differential equations. Based on the Yao-Chen formula, Yao and Chen (2013) first proposed a numerical method for solving uncertain differential equation, which was then extended by Yang and Shen (2015), Yang and Ralescu (2015), Gao (2016), etc. In the practical aspect, uncertain differential equation has been widely applied in various fields and spawned many theoretical branches. For example, uncertain differential equation was widely applied in finance markets by Liu (2013) and generated uncertain finance theory. In addition, uncertain differential equation was applied in uncertain optimal control (Zhu 2010), uncertain differential game (Yang and Gao 2013), uncertain population model (Zhang and Yang 2020), uncertain heat conduction equation (Yang and Yao 2017), uncertain string vibration equation (Gao and Ralescu (2019)), uncertain spring vibration equation (Jia and Dai 2018) and uncertain epidemic model (Li et al. 2017).

However, there exist unknown parameters in the model established in the real world. Therefore, how to estimate the unknown parameters based on the observations of the solution to uncertain differential equation is a critical problem. For the purpose of solving this problem, Yao and Liu (2020) proposed a method of moment estimation based on the difference form of uncertain differential equation. Following that, Liu and Yang (2019) applied the method of moment estimation to the parameter estimation of high-order uncertain differential equation. Later, Sheng et al. (2020) presented a method of least squares estimation for estimating the unknown parameters. In addition, Lio and Liu (2020a) proposed a method of estimating the unknown initial value of uncertain differential equation based on observed data. Up to now, the parameter estimation of uncertain differential equation has received more and more attentions from scholars.

As another important method of parameter estimation, uncertain maximum likelihood estimation was proposed by Lio and Liu (2020b) under the framework of uncertainty theory, and was applied in regression analysis by estimating the unknown parameters of uncertain regression models. Since then, uncertain maximum likelihood estimation has attracted the attention of many scholars. In this paper, it is our goal to present a parameter estimation method for uncertain differential equation based on the uncertain maximum likelihood estimation. The overall structure of this paper takes the form of five sections, including this introductory section. Section 2 begins by introducing some concepts of uncertainty theory and Sect. 3 begins by proposing the parameter estimation method for uncertain differential equation, and giving some analytical formulae of the uncertain maximum likelihood estimators in special linear uncertain differential equations. In Sect. 4, we apply the proposed estimation method in some numerical examples. Finally, a concise conclusion is given in Sect. 5.

2 Preliminary

This section will introduce some concepts and theorems about uncertainty theory. The following symbols are used throughout this paper:

$$\begin{aligned}&a\wedge b:\min (a,b),\quad a\vee b:\max (a,b), \\&\bigwedge _{i=1}^{n}x_i:\min _{1\le i\le n}x_i, \quad \bigvee _{i=1}^{n}x_i:\max _{1\le i\le n}x_i. \end{aligned}$$

Definition 1

(Liu 2007) Assume that \(\varGamma \) is a universal set and \({\mathscr {L}}\) is a \(\sigma \)-algebra over \(\varGamma \), \({\mathscr {M}}\) is a measurable set function on the \(\sigma \)-algebra \({\mathscr {L}}\) by following three axioms:

Axiom 1. (Normality Axiom) \({\mathscr {M}}\{\varGamma \}=1\).

Axiom 2. (Duality Axiom) \({\mathscr {M}}\{\varLambda \}+{\mathscr {M}}\{\varLambda ^{c}\}=1\) for any event \(\varLambda \in {\mathscr {L}}\).

Axiom 3. (Subadditivity Axiom) For any countable sequence \(\{\varLambda _i\}\), we always have

$$\begin{aligned} \displaystyle {\mathscr {M}}\left\{ \bigcup _{i=1}^{\infty }\varLambda _i\right\} \le \sum _{i=1}^{\infty }{\mathscr {M}}\{\varLambda _i\}. \end{aligned}$$

Then the set function \({\mathscr {M}}\) is called an uncertain measure, and the triplet \((\varGamma ,{\mathscr {L}},{\mathscr {M}})\) is called an uncertainty space.

For the purpose of obtaining the uncertain measure of composite event, the product uncertain measure \({\mathscr {M}}\) on the product \(\sigma \)-algebra \({\mathscr {L}}\) was defined by Liu (2009) by the following product axiom.

Axiom 4. (Product Axiom) Assume \((\varGamma _i,{\mathscr {L}}_i,{\mathscr {M}}_i)\) are uncertainty spaces for \(i=1, 2, \cdots \) \({\mathscr {M}}\) is an uncertain measure on the \(\sigma \)-algebra satisfying

$$\begin{aligned} \displaystyle {\mathscr {M}}\left\{ \prod _{i=1}^\infty \varLambda _i\right\} =\bigwedge _{i=1}^\infty {\mathscr {M}}_i\{\varLambda _i\} \end{aligned}$$

where \(\varLambda _i\) are arbitrarily chosen events from \({\mathscr {L}}_i\) for \(i=1, 2, \cdots \), respectively. Then, the uncertain measure \({\mathscr {M}}\) is called a product uncertain measure.

An uncertain variable \(\xi \) is a measurable function from an uncertainty space \((\varGamma ,{\mathscr {L}},{\mathscr {M}})\) to the set of real numbers, i.e., the set

$$\begin{aligned} \{\xi \in B\}=\{\gamma \in \varGamma \mid \xi (\gamma )\in B\} \end{aligned}$$

is always an event for any Borel set B of real numbers. The uncertainty distribution of an uncertain variable \(\xi \) is defined by

$$\begin{aligned} \varPhi (x)={\mathscr {M}}\{\xi \le x\},\quad \forall x\in \Re . \end{aligned}$$

A normal uncertain variable \(\xi \sim {\mathcal {N}}(e,\sigma )\) has a normal uncertainty distribution

$$\begin{aligned} \varPhi (x)=\left( 1+\exp \left( \frac{\pi (e-x)}{\sqrt{3} \sigma }\right) \right) ^{-1},\quad x\in \Re \end{aligned}$$

and a normal uncertainty distribution is called standard if \(e = 0\) and \(\sigma = 1\).

Definition 2

(Liu 2009) An uncertain process \(C_t\) is said to be a Liu process if

  1. (i)

    \(C_0=0\) and almost all sample paths are Lipschitz continuous,

  2. (ii)

    \(C_t\) has stationary and independent increments,

  3. (iii)

    every increment \(C_{s+t}-C_s\) is a normal uncertain variable with expected value 0 and variance \(t^2\).

3 Parameter estimation

In this section, we first introduce a parameter estimation method for uncertain differential equation based on the uncertain maximum likelihood estimation.

Consider the uncertain differential equation denoted by

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t;\mu )\mathrm{d}t+g(t,X_t;\theta )\mathrm{d}C_t \end{aligned}$$
(1)

where \(C_t\) is a Liu process, \(f(t,x;\mu )\) and \(g(t,x;\theta )\) are two real-valued measurable functions on \(T\times \Re \) and satisfy that (1) has a unique solution, i.e., \(f(t,x;\mu )\) and \(g(t,x;\theta )\) satisfy the linear growth condition

$$\begin{aligned} |f(t,x;\mu )|+|g(t,x;\theta )|\le L(1+|x|), \quad \forall x\in \Re ,\quad t\ge 0 \end{aligned}$$

and Lipschitz condition

$$\begin{aligned}&|f(t,x;\mu )-f(t,y;\mu )|+|g(t,x;\theta )-g(t,y;\theta )|\\&\quad \le L|x-y| \end{aligned}$$

for any \(x,y\in \Re \) and \(t\ge 0\) with some constant L, \(\mu \) and \(\theta \) are two unknown parameters to be estimated on the basis of the observations of the solution \(X_t\). Now we write equation (1) into the difference form by using the Euler method:

$$\begin{aligned}&X_{t_{i+1}}-X_{t_{i}}\\&\quad =f(t_{i},X_{t_{i}};\mu )(t_{i+1}-t_{i}) +g(t_{i},X_{t_{i}};\theta )(C_{t_{i+1}}-C_{t_{i}}), \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{X_{t_{i+1}}-X_{t_{i}}-f(t_{i},X_{t_{i}};\mu ) (t_{i+1}-t_{i})}{g(t_{i},X_{t_{i}};\theta )(t_{i+1}-t_{i})} =\frac{C_{t_{i+1}}-C_{t_{i}}}{t_{i+1}-t_{i}}. \end{aligned}$$

According to the definition of Liu process,

$$\begin{aligned} \frac{C_{t_{i+1}}-C_{t_{i}}}{t_{i+1}-t_{i}} \end{aligned}$$

follows a standard normal uncertainty distribution. That is, we can get

$$\begin{aligned} \frac{X_{t_{i+1}}-X_{t_{i}}-f(t_{i},X_{t_{i}};\mu ) (t_{i+1}-t_{i})}{g(t_{i},X_{t_{i}};\theta )(t_{i+1}-t_{i})} \sim {\mathcal {N}}(0,1). \end{aligned}$$
(2)

Suppose that there are n observed data \(x_{t_{1}},x_{t_{2}},\cdots ,x_{t_{n}}\) of the solution \(X_t\) at time-points \(t_{1}<t_{2}<\cdots <t_{n}\). By substituting the observed data into equation (2), we write

$$\begin{aligned} h_i(\mu ,\theta )=\frac{x_{t_{i+1}}-x_{t_{i}} -f(t_{i},x_{t_{i}};\mu )(t_{i+1}-t_{i})}{g(t_{i},x_{t_{i}};\theta ) (t_{i+1}-t_{i})} \end{aligned}$$
(3)

for \(i=1,2,\cdots ,n-1\), which are \(n-1\) functions containing the unknown parameters. According to equation (2), we can regard the values of \(h_1(\mu ,\theta ),h_2(\mu ,\theta ),\cdots \), \(h_{n-1}(\mu ,\theta )\) as \(n-1\) samples of a standard normal uncertainty distribution \({\mathcal {N}}(0,1)\). Then, the following theorem gives the estimates of the parameters \(\mu \) and \(\theta \) by the uncertain maximum likelihood estimation.

Theorem 1

Assume that \(x_{t_{1}},x_{t_{2}},\cdots ,x_{t_{n}}\) are observations of the solution \(X_t\) of the uncertain differential equation (1) at the times \(t_1,t_2,\cdots ,t_n\) with \(t_{1}<t_{2}<\cdots <t_{n}\), respectively. Then, the estimates \(\mu ^{*}\) and \(\theta ^{*}\) obtained by means of the uncertain maximum likelihood estimation solve the following system of equations

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \bigwedge _{i=1}^{n-1}\frac{x_{t_{i+1}}-x_{t_{i}} -f(t_{i},x_{t_{i}};\mu )(t_{i+1}-t_{i})}{g(t_{i},x_{t_{i}};\theta ) (t_{i+1}-t_{i})}\\ \displaystyle \quad +\bigvee _{i=1}^{n-1}\frac{x_{t_{i+1}}-x_{t_{i}} -f(t_{i},x_{t_{i}};\mu )(t_{i+1}-t_{i})}{g(t_{i},x_{t_{i}};\theta ) (t_{i+1}-t_{i})}=0\\ \displaystyle \frac{\pi }{\sqrt{3}\lambda }\bigvee _{i=1}^{n-1} \left| \frac{x_{t_{i+1}}-x_{t_{i}}-f(t_{i},x_{t_{i}};\mu ) (t_{i+1}-t_{i})}{g(t_{i},x_{t_{i}};\theta )(t_{i+1}-t_{i})}\right| =1 \end{array}\right. \end{aligned}$$
(4)

where \(\lambda \) is the root of the transcendental equation \(1+x+\exp (x)-x\exp (x)=0\) and can be taken as 1.5434 approximately in numerical solution.

Proof

At first, we can regard the values of \(h_1(\mu ,\theta )\),

\(h_2(\mu ,\theta ),\cdots ,h_{n-1}(\mu ,\theta )\) as \(n-1\) samples of the population \({\mathcal {N}}(e,\sigma )\) with uncertainty distribution

$$\begin{aligned} \displaystyle \varPhi (x)=\left( 1+\exp \left( \frac{\pi (e-x)}{\sqrt{3}\sigma }\right) \right) ^{-1}. \end{aligned}$$

Notice that \(\displaystyle \varPhi (x)\) is differentiable and

$$\begin{aligned} \varPhi '(x)=\frac{\displaystyle \frac{\pi }{\sqrt{3}\sigma } \exp \left( \frac{\pi (e-x)}{\sqrt{3}\sigma }\right) }{\displaystyle \left( 1+\exp \left( \frac{\pi (e-x)}{\sqrt{3}\sigma }\right) \right) ^{2}}. \end{aligned}$$

According to the definition of uncertain likelihood function presented by Lio and Liu (2020b), the likelihood function is

$$\begin{aligned}&\mathrm{L}(e,\sigma \mid h_1(\mu ,\theta ),h_2(\mu ,\theta ), \cdots ,h_{n-1}(\mu ,\theta ))\\&\quad =\bigwedge _{i=1}^{n-1}\varPhi '(h_i(\mu ,\theta ))\\&\quad =\bigwedge _{i=1}^{n-1}\frac{\displaystyle \frac{\pi }{\sqrt{3}\sigma }\exp \left( \frac{\pi \left( e-h_i(\mu ,\theta )\right) }{\sqrt{3}\sigma }\right) }{\displaystyle \left( 1+\exp \left( \frac{\pi (e-h_i (\mu ,\theta ))}{\sqrt{3}\sigma }\right) \right) ^2}. \end{aligned}$$

Since \(\varPhi '(x)\) decreases as \(|e-x|\) increases, we can rewrite the likelihood function as

$$\begin{aligned}&\mathrm{L}(e,\sigma \mid h_1(\mu ,\theta ),h_2(\mu ,\theta ), \cdots ,h_{n-1}(\mu ,\theta ))\\&\quad =\frac{\displaystyle \frac{\pi }{\sqrt{3}\sigma } \exp \left( \frac{\pi }{\sqrt{3}\sigma }\bigvee \limits _{i=1}^{n-1} \left| e-h_i(\mu ,\theta )\right| \right) }{\displaystyle \left( 1+\exp \left( \frac{\pi }{\sqrt{3}\sigma } \bigvee \limits _{i=1}^{n-1}|e-h_i(\mu ,\theta )|\right) \right) ^2}. \end{aligned}$$

Then, we can get the maximum likelihood estimates of e and \(\sigma \) by solving the maximization problem

$$\begin{aligned} \max _{e,\sigma >0}\frac{\displaystyle \frac{\pi }{\sqrt{3}\sigma } \exp \left( \frac{\pi }{\sqrt{3}\sigma }\bigvee \limits _{i=1}^{n-1} \left| e-h_i(\mu ,\theta )\right| \right) }{\displaystyle \left( 1+\exp \left( \frac{\pi }{\sqrt{3}\sigma } \bigvee \limits _{i=1}^{n-1}|e-h_i(\mu ,\theta )|\right) \right) ^2}. \end{aligned}$$

Since the likelihood function is decreasing with respect to

$$\begin{aligned} \displaystyle \bigvee \limits _{i=1}^{n-1} \left| e-h_i(\mu ,\theta )\right| , \end{aligned}$$

the maximum likelihood estimate \(e^*\) solves the following minimization problem

$$\begin{aligned} \min _{e}\bigvee \limits _{i=1}^{n-1} \left| e-h_i(\mu ,\theta )\right| \end{aligned}$$

whose minimum solution is

$$\begin{aligned} e^{*}=\frac{1}{2}\left( \displaystyle \displaystyle \bigwedge _{i=1}^{n-1} h_{i}(\mu ,\theta )+\bigvee _{i=1}^{n-1}h_{i}(\mu ,\theta )\right) , \end{aligned}$$
(5)

and then the maximum likelihood estimate \(\sigma ^*\) solves the maximization problem

$$\begin{aligned} \max _{\sigma >0}\frac{\displaystyle \frac{\pi }{\sqrt{3}\sigma } \exp \left( \frac{\pi }{\sqrt{3}\sigma }\bigvee \limits _{i=1}^{n-1} \left| e^*-h_i(\mu ,\theta )\right| \right) }{\displaystyle \left( 1+\exp \left( \frac{\pi }{\sqrt{3}\sigma } \bigvee \limits _{i=1}^{n-1}|e^*-h_i(\mu ,\theta )|\right) \right) ^2}. \end{aligned}$$
(6)

Here we set \(\displaystyle y=\frac{\pi }{\sqrt{3}\sigma }\) and \(\displaystyle k=\bigvee \limits _{i=1}^{n-1} \left| e^*-h_i(\mu ,\theta )\right| \). Then, the maximization problem (6) is transformed into the following maximization problem

$$\begin{aligned} \max _{y>0}\frac{y\exp (ky)}{\left( 1+\exp \left( ky\right) \right) ^2}. \end{aligned}$$
(7)

Let us write

$$\begin{aligned} p(y)=\frac{y\exp (ky)}{\left( 1+\exp \left( ky\right) \right) ^2}. \end{aligned}$$

Notice that

$$\begin{aligned} p'(y)=\frac{\exp (ky)(1+ky+\exp (ky)-ky\exp (ky))}{(1+\exp (ky))^3}. \end{aligned}$$

It is easy to see that \(p'\left( \lambda /k\right) =0\), where \(\lambda \) is the root of the transcendental equation \(1+x+\exp (x)-x\exp (x)=0\) and can be taken as 1.5434 approximately in numerical solution. Then we can obtain \(p'(y)>0\) when \(0<y<\lambda /k\) and \(p'(y)<0\) when \(y>\lambda /k\). Thus, \(y^*=\lambda /k\) is the maximum point of p(y) in the feasible region, which implies that \(y^*\) is the maximum solution of the maximization problem (7). Then,

$$\begin{aligned} \sigma ^{*}=\frac{\pi }{\sqrt{3}y^*}=\frac{\pi }{\sqrt{3}\lambda } \bigvee _{i=1}^{n-1}\left| e^{*}-h_{i}(\mu ,\theta )\right| \end{aligned}$$
(8)

is the maximum solution of the maximization problem (6) immediately. Thus, \(e^*\) and \(\sigma ^{*}\) are the maximum likelihood estimates of e and \(\sigma \), respectively.

Since \(h_1(\mu ,\theta ),h_2(\mu ,\theta ),\cdots ,h_{n-1}(\mu ,\theta )\) are actually the samples of the standard normal uncertainty distribution \({\mathcal {N}}(0,1)\), we must have

$$\begin{aligned} e^{*}=0,\quad \sigma ^{*}=1. \end{aligned}$$

Therefore, it follows from (5) and (8) that

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \bigwedge _{i=1}^{n-1}h_{i}(\mu ,\theta ) +\bigvee _{i=1}^{n-1}h_{i}(\mu ,\theta )=0\\ \displaystyle \frac{\pi }{\sqrt{3}\lambda }\bigvee _{i=1}^{n-1} \left| h_{i}(\mu ,\theta ) \right| =1 \end{array} \right. \end{aligned}$$
(9)

whose solutions \(\mu ^{*}\) and \(\theta ^{*}\) are the estimates of the parameters \(\mu \) and \(\theta \), respectively. That is, we can get the estimates of the parameters \(\mu \) and \(\theta \) by solving the system of equations (4). The theorem is proved. \(\square \)

The above method of estimating the parameters of uncertain differential equations is called the method of uncertain maximum likelihood.

Remark 1

Sometimes the system of equations (4) has no solution, or we often cannot find the exact solution of the system of equations (4) when \(f(t,x;\mu )\) and \(g(t,x;\theta )\) are nonlinear functions with respect to \(\mu \) and \(\theta \), respectively. In this case, we can get the numerical solution of the system of equations (4) by solving the following minimization problem,

$$\begin{aligned} \min _{\mu ,\theta }&\left( \left( \bigwedge _{i=1}^{n-1}h_{i}(\mu ,\theta ) +\bigvee _{i=1}^{n-1}h_{i}(\mu ,\theta )\right) ^2\right. \nonumber \\&\qquad \left. +\left( \frac{\pi }{\sqrt{3}\lambda }\bigvee _{i=1}^{n-1} \left| h_{i}(\mu ,\theta ) \right| -1\right) ^2\right) \end{aligned}$$
(10)

where \(h_1(\mu ,\theta ),h_2(\mu ,\theta ),\cdots ,h_{n-1}(\mu ,\theta )\) are defined by (3), and some numerical methods such as Newton’s method, secant method and simplex method can be used.

As an important class of uncertain differential equations, linear uncertain differential equations have been widely used in financial markets. For example, Liu (2009) first proposed a stock model in which the stock price is determined by a linear uncertain differential equation. Later, Peng and Yao (2011) studied a new stock model in which the stock price follows a mean-reverting process. After that, Chen and Gao (2013) investigated an uncertain interest rate model by assuming that the interest rate follows a linear uncertain differential equation, and Liu et al. (2015) presented an uncertain currency model where the exchange rate follows a linear uncertain differential equation. Next we will give some analytical formulae of the uncertain maximum likelihood estimators in special linear uncertain differential equations.

Corollary 1

Consider the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu \mathrm{d}t+\theta \mathrm{d}C_t \end{aligned}$$

where \(\mu \) and \(\theta >0\) are two unknown parameters to be estimated. Assume that \(x_{t_{1}},x_{t_{2}},\cdots ,x_{t_{n}}\) are observations of the solution \(X_t\) of the uncertain differential equation at the times \(t_1,t_2,\cdots ,t_n\) with \(t_{1}<t_{2}<\cdots <t_{n}\), respectively. Then, the estimates of the parameters \(\mu \) and \(\theta \) are

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mu ^{*}=\frac{1}{2}\left( \displaystyle \bigwedge _{i=1}^{n-1} \frac{x_{t_{i+1}}-x_{t_{i}}}{t_{i+1}-t_{i}}+ \bigvee _{i=1}^{n-1} \frac{x_{t_{i+1}}-x_{t_{i}}}{t_{i+1}-t_{i}}\right) \\ \displaystyle \theta ^{*}=\frac{\pi }{\sqrt{3}\lambda } \bigvee _{i=1}^{n-1}\left| \frac{x_{t_{i+1}}-x_{t_{i}}}{t_{i+1} -t_{i}} -\mu ^{*} \right| . \end{array}\right. \end{aligned}$$
(11)

Proof

By substituting the observed data into equation (3), we can get

$$\begin{aligned} h_{i}(\mu ,\theta )=\frac{x_{t_{i+1}}-x_{t_{i}} -\mu (t_{i+1}-t_{i})}{\theta (t_{i+1}-t_{i})},\quad i=1,2,\cdots ,n-1. \end{aligned}$$

According to Theorem 1, the estimates of the unknown parameters solve

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \bigwedge _{i=1}^{n-1}\frac{x_{t_{i+1}} -x_{t_{i}}-\mu (t_{i+1}-t_{i})}{\theta (t_{i+1}-t_{i})}\\ \displaystyle \quad +\bigvee _{i=1}^{n-1}\frac{x_{t_{i+1}} -x_{t_{i}}-\mu (t_{i+1}-t_{i})}{\theta (t_{i+1}-t_{i})}=0\\ \displaystyle \frac{\pi }{\sqrt{3}\lambda }\bigvee _{i=1}^{n-1} \left| \frac{x_{t_{i+1}}-x_{t_{i}}-\mu (t_{i+1} -t_{i})}{\theta (t_{i+1}-t_{i})} \right| =1. \end{array}\right. \end{aligned}$$

By solving the above system of equations, we can get the estimates of \(\mu \) and \(\theta \) shown in (11). \(\square \)

Corollary 2

Consider the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu X_t\mathrm{d}t+\theta X_t\mathrm{d}C_t \end{aligned}$$

where \(\mu \) and \(\theta >0\) are two unknown parameters to be estimated. Assume that \(x_{t_{1}},x_{t_{2}},\cdots ,x_{t_{n}}\) are observations of the solution \(X_t\) of the uncertain differential equation at the times \(t_1,t_2,\cdots ,t_n\) with \(t_{1}<t_{2}<\cdots <t_{n}\), respectively. Then, the estimates of the parameters \(\mu \) and \(\theta \) are

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mu ^{*}=\frac{1}{2}\left( \displaystyle \bigwedge _{i=1}^{n-1} \frac{x_{t_{i+1}}-x_{t_{i}}}{x_{t_{i}}(t_{i+1}-t_{i})} +\bigvee _{i=1}^{n-1}\frac{x_{t_{i+1}}-x_{t_{i}}}{x_{t_{i}}(t_{i+1}-t_{i}}) \right) \\ \displaystyle \theta ^{*}=\frac{\pi }{\sqrt{3}\lambda } \bigvee _{i=1}^{n-1}\left| \frac{x_{t_{i+1}} -x_{t_{i}}}{x_{t_{i}}(t_{i+1}-t_{i})} -\mu ^{*}\right| . \end{array}\right. \end{aligned}$$
(12)

Proof

By substituting the observed data into equation (3), we can get

$$\begin{aligned} h_{i}(\mu ,\theta )=\frac{x_{t_{i+1}}-x_{t_{i}}-\mu x_{t_{i}} (t_{i+1}-t_{i})}{\theta x_{t_{i}}(t_{i+1}-t_{i})} \end{aligned}$$

for \(i=1,2,\cdots ,n-1.\) According to Theorem 1, the estimates of the unknown parameters solve

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \bigwedge _{i=1}^{n-1}\frac{x_{t_{i+1}}-x_{t_{i}} -\mu x_{t_{i}}(t_{i+1}-t_{i})}{\theta x_{t_{i}}(t_{i+1}-t_{i})}\\ \displaystyle \quad +\bigvee _{i=1}^{n-1}\frac{x_{t_{i+1}}-x_{t_{i}} -\mu x_{t_{i}}(t_{i+1}-t_{i})}{\theta x_{t_{i}}(t_{i+1}-t_{i})}=0\\ \displaystyle \frac{\pi }{\sqrt{3}\lambda }\bigvee _{i=1}^{n-1} \left| \frac{x_{t_{i+1}}-x_{t_{i}}-\mu x_{t_{i}}(t_{i+1} -t_{i})}{\theta x_{t_{i}}(t_{i+1}-t_{i})} \right| =1. \end{array} \right. \end{aligned}$$

By solving the above system of equations, we can get the estimates of \(\mu \) and \(\theta \) shown in (12). \(\square \)

Table 1 Observations of Example 1
Full size table

4 Numerical examples

Now we apply the method of uncertain maximum likelihood in three numerical examples to estimate the unknown parameters.

Example 1

For the following uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu \mathrm{d}t+\theta \mathrm{d}C_t \end{aligned}$$

with 16 observations given in Table 1, and the two parameters \(\mu \) and \(\theta >0\) are unknown which should be estimated. By substituting the observed data into (11), we have

$$\begin{aligned} \mu ^{*}=1.1178,\quad \theta ^{*}=1.1879. \end{aligned}$$

Therefore, the uncertain differential equation is

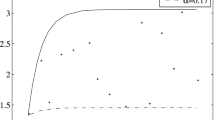
$$\begin{aligned} \mathrm{d}X_t=1.1178\mathrm{d}t+1.1879\mathrm{d}C_t \end{aligned}$$
(13)

whose 0.27-path and 0.85-path are shown in Fig. 1. As we can see, all the observations fall in these two \(\alpha \)-paths, which indicates that the estimates

$$\begin{aligned} \mu ^{*}=1.1178,\quad \theta ^{*}=1.1879 \end{aligned}$$

are acceptable.

Fig. 1
figure 1

\(\alpha \)-paths and Observations of \(X_{t}\) in Example 1

Full size image

Remark 2

In fact, the true values of parameters in Example 1 are

$$\begin{aligned} \mu =1, \theta =1, \end{aligned}$$

the moment estimation and least squares estimation of parameters are

$$\begin{aligned} \hat{\mu }_1=1.3070, \hat{\theta }_1=0.6318, \end{aligned}$$

and

$$\begin{aligned} \hat{\mu }_2=1.3350, \hat{\theta }_2=0.6543, \end{aligned}$$

respectively. Obviously, for such observations, the uncertain maximum likelihood estimation is best. The reason is that when the sample size is small, the sample moments cannot provide good estimates of the corresponding population moments, and the outliers will cause greater interference to the noise term, which will cause the least square estimation to be worse than the uncertain maximum likelihood estimation. Therefore, when the sample size is small, we should choose the method of uncertain maximum likelihood instead of other methods.

Table 2 Observations of Example 2
Full size table

Example 2

For the following uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\mu X_t\mathrm{d}t+\theta X_t\mathrm{d}C_t \end{aligned}$$

with 14 observations given in Table 2, and the two parameters \(\mu \) and \(\theta >0\) are unknown which should be estimated. By substituting the observed data into (12), we have

$$\begin{aligned} \mu ^{*}=2.5962,\quad \theta ^{*}=3.8656. \end{aligned}$$

Therefore, the uncertain differential equation is

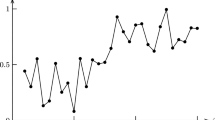
$$\begin{aligned} \mathrm{d}X_t= 2.5962X_t\mathrm{d}t+3.8656X_t\mathrm{d}C_t \end{aligned}$$
(14)

whose 0.29-path and 0.80-path are shown in Fig. 2. As we can see, all the observations fall in these two \(\alpha \)-paths, which indicates that the estimates

$$\begin{aligned} \mu ^{*}= 2.5962,\quad \theta ^{*}=3.8656 \end{aligned}$$

are acceptable.

Example 3

For the following uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=\cos (\mu t)\mathrm{d}t+\sin (\theta t)\mathrm{d}C_t \end{aligned}$$

with 16 observations given in Table 3, and the two parameters \(\mu >0\) and \(\theta >0\) are unknown which should be estimated. By substituting the observations into equation (3), we can get

Fig. 2
figure 2

\(\alpha \)-paths and Observations of \(X_{t}\) in Example 2

Full size image
Table 3 Observations of Example 3
Full size table
$$\begin{aligned} h_{i}(\mu ,\theta )=\frac{x_{t_{i+1}}-x_{t_{i}}-\cos (\mu t_i) (t_{i+1}-t_{i})}{\sin (\theta t_i)(t_{i+1}-t_{i})} \end{aligned}$$

for \(i=1,2,\cdots ,15\). Then, we can solve the minimization problem (10) by using MATLABFootnote 1, and get the estimates of \(\mu \) and \(\theta \) which are

$$\begin{aligned} \mu ^{*}= 1.6171,\quad \theta ^{*}=1.4219. \end{aligned}$$

Therefore, the uncertain differential equation is

$$\begin{aligned} \mathrm{d}X_t=\cos (1.6171 t)\mathrm{d}t+\sin (1.4219 t)\mathrm{d}C_t \end{aligned}$$
(15)

whose 0.15-path and 0.82-path are shown in Fig. 3. As we can see, all the observations fall in these two \(\alpha \)-paths, which indicates that the estimates

$$\begin{aligned} \mu ^{*}= 1.6171,\quad \theta ^{*}=1.4219 \end{aligned}$$

are acceptable.

Fig. 3
figure 3

\(\alpha \)-paths and Observations of \(X_{t}\) in Example 3

Full size image

5 Conclusion

This paper first proposed the method of uncertain maximum likelihood to estimate the unknown parameters in uncertain differential equation, and gave some analytical formulae of the uncertain maximum likelihood estimators in special linear uncertain differential equations. In addition, some numerical examples were also provided to illustrate the method of uncertain maximum likelihood in this paper.