Fixed-charge solid transportation problem with budget constraints based on carbon emission in neutrosophic environment

Abstract

This paper is to integrate among solid transportation problem, budget constraints and carbon emission with probable maximum profit. The range of air pollution and climate change are effected by ${\text {CO}_2}$ gas emission and other greenhouse gases from myriad transportation systems. Henceforth, our target is to minimize carbon emission for pollution-free environment. Transportation system with single objective is hardly applicable to the situation with more than one criterion. Therefore multi-objective decision making is incorporated for designing real-life transportation problem. Due to time pressure, data limitation, lack of information or measurement errors in practical problems, there exist some hesitations. Based on the fact, decision maker considers indeterminacy in the designed problems. To overcome such hesitancy of occurrence and non-occurrence in fuzzy and intuitionistic fuzzy, neutrosophic set is very important and suitable to accommodate such general structure of problems. Therefore neutrosophic environment with neutrosophic linear programming, fuzzy programming and global criterion method is utilized here to find the compromise solution of the multi-objective transportation problem. Thereafter, the performance of the considered model is useful by evaluating a numerical example, and then the derived results are compared. Finally sensitivity analysis and conclusions with upcoming works of this research are stated hereafter.

1 Introduction

First we display all the abbreviations which are convenient to use in this paper.

Abbreviations

MOTP:

Multi-objective transportation problem

TP:

Transportation problem

FTP:

Fixed-charge transportation problem

STP:

Solid transportation problem

FSTP:

Fixed-charge solid transportation problem

IF:

Intuitionistic fuzzy

IFS:

Intuitionistic fuzzy set

NN:

Neutrosophic number

MFSTP:

Multi-objective fixed-charge solid transportation problem

NLP:

Neutrosophic linear programming

PIS:

Positive ideal solution

NIS:

Negative ideal solution

FP:

Fuzzy programming

DM:

Decision maker

GCM:

Global criterion method

Only a single-objective function was considered in classical transportation system in the last few decades. In the present situation, more than one criterion are selected as transportation cost, average delivery time of product, deterioration rate of goods, fixed-charge for an open route, etc., at the time of passing a homogeneous product from a source to different destinations in the avenue of competitive economic condition. For this cause, the single-objective transportation problem (TP) is not enough to tractable such real-life decision making problem. To tackle such situation, the multi-objective decision making is included in the traditional TP. Hitchcock (1941) first defined TP, and then TP with linear programming is known as Hitchcock–Koopmans TP. There exist various research papers on TP with multi-objective nature in crisp or imprecise data. A few of them is presented here. Maity et al. (2019) analyzed multimodal TP and its application to artificial intelligence. Ebrahimnejad (2014) represented a new approach for solving TP with generalized trapezoidal fuzzy numbers. Multi-objective transportation problem (MOTP) with fuzzy environment was provided by Li and Lai (2000). Maity et al. (2016) proposed an MOTP in uncertain environment with cost reliability.

An extension of general TP is fixed-charge transportation problem (FTP) where the fixed-charge being independent of transported amount. A fixed cost is called setup cost added with transportation cost while the solution appears with the level of positivity and it is associated with 0–1 variable. There comes accumulation of some charges such as renting cost of vehicle, landing fees at an airport, toll charges on a high way and establishment cost for machines. All these costs are considered for the transportation of some quantity towards destinations. Adding to all the cost, the TP is called FTP and there exist two sets of cost. The names of these costs are direct cost and fixed-charge. The association of direct cost for each source to destination and fixed-charge takes place when the function of transportations is in the corresponding source–destination pair. Hirsch and Dantzig (1968) first defined FTP. Besides, there are some exact methods provided by literature review on FTP. Midya and Roy (2017) represented an application of interval programming using interval and rough interval on FTP in different environments. Midya and Roy (2014) included fixed-charge in MOTP with single-sink and multi-index stochastic environment. Roy et al. (2018) used random rough variables for solving MOTP with fixed-charge.

The TP is renamed as solid transportation problem (STP) when conveyance constraints are added with source and destination constraints. STP was first introduced by Haley (1962). Goods train, ships, trucks and cargo flights are the media for the transportation of homogeneous products from sources to destinations. The TP is restructured and renamed as fixed-charge solid transportation problem (FSTP) after the single type conveyance is used in FTP. Roy and Midya (2019) solved FSTP in intuitionistic fuzzy (IF) environment with multi-objective and product blending concept. Das et al. (2020) represented STP and facility location with carbon policies. Ghosh et al. (2021) solved a multi-objective STP in which variables and parameters are IF in nature. Roy et al. (2019) analyzed multi-objective and multi-item FSTP with twofold uncertainty.

In previous research works, STP includes sources, demands and conveyance constraints for solving decision making problem. But no research work found with STP under budget constraints including fixed-charge, purchasing cost, transportation cost and profit maximization. Budget is an important fact in TP. Whenever transporting distinct items, then transportation cost rapidly increases, which effects on the total system. Considering the budget, we optimize the several objective functions which are conflicting to each other. These objective functions minimize total transportation cost, total delivery time and deterioration charge of breakable goods. Many researchers applied budget constraints in MOTP. Majumder et al. (2019) used budget constraints in FSTP with uncertain multi-objective and multi-item environment. Das et al. (2016) analyzed Gaussian type-2 fuzzy STP with breakable multi-item and multi-stage under budget. Ghosh and Roy (2021) formulated a multi-objective product blending FTP with truck load constraints through transfer station under fuzzy-rough environment. Sifaoui and Aider (2020) considered budget constraints and safety measure in multi-objective multi-item fixed-charge STP under uncertain interval programming.

General transportation sector transports items, and passengers by bus, train, truck, car, ship, flight, etc., which emits greenhouse gasses. Thus the transportation system is mostly involved for emission of $\text {CO}_2$ gas and other greenhouse gasses. Mainly these gases emit from light-duty vehicles, passenger car, minibus, etc., and the remaining part emits from heavy-duty vehicles such as truck, ships and freight transport. The greenhouse gas emission is high risk for environmental and air pollution. The carbon emission depends on its fuel type, engine type, traffic rule, road condition, driving rules, etc. Here we include some research works on carbon emission in TP. Das and Roy (2019) analyzed the impact of $\text {CO}_2$ in an integrated transportation and facility location problem under neutrosophic environment. Ding et al. (2013) tried to reduce carbon emission and applied its potential effect in China for transportation. Song and Leng (2012) analyzed carbon emission policies for single-period problem. Tarulescu et al. (2017) introduced $\text {CO}_2$ emission reduction strategies for smart transportation. Midya et al. (2021) presented a multi-stage multi-objective FSTP in a green supply chain.

Neutrosophic set is the generalized extension of fuzzy set (Zadeh 1965) and intuitionistic fuzzy set (IFS) (Atanassov 1986). Neutrosophic set was first studied by Smarandache (1999), and this set is very important and suitable to overcome the restriction on occurrence and non-occurrence of fuzzy and intuitionistic fuzzy, respectively. The meaning of neutrosophic is neutral and it is based on the logic of universe that its elements are presented by three membership degrees. These are truth degree, indeterminacy degree and falsity degree and they lie in [0, 1]. Neutrosophic set differs from IFS which involves only the uncertainty of truth and falsity, that is belongingness and non-belongingness degrees. In neutrosophic, indeterminacy factor occurs, which is independent on truth value and falsity value. Smarandache first introduced the concept of indeterminacy. The neutrosophic number (NN) is presented by $z=p+Iq$, for $p, q \in {\mathbb {R}}$, and I is the indeterminacy, which gives indeterminate value. Here p is the determinate part and qI is the indeterminate part. Therefore neutrosophic set is a useful concept in mathematical science for describing incomplete and indeterminate information. In the case of time pressure, measurement errors, limited data or lack of information, the practical problems are solved with help of indeterminacy I. It is more important to define NN that contains indeterminacy I and handles all the programming problems with indeterminate environment. To tackle indeterminate problems, Smarandache introduced neutrosophic function, neutrosophic pre-calculus, neutrosophic calculus in 2015. Some recent studies on neutrosophic set are included here. Rizk-Allah et al. (2018) proposed an MOTP under neutrosophic environment. Time-neutrosophic soft set and its application was analyzed by Khalil et al. (2018). Ye et al. (2018) analyzed nonlinear programming problems and solution methods in neutrosophic environment.

The main contributions of this study are as follows:

• (i) In this MOTP, all the parameters are considered as NNs for controlling the indeterminacy which does not control by fuzzy or intuitionistic fuzzy.

• (ii) For neutrosophic system, there exist truth membership, indeterminacy membership and falsity membership functions which help to accommodate more imprecise information in the problem.

• (iii) Objective functions are conflicting to each other. Therefore for finding the compromise solution three advance programming methods, namely neutrosophic linear programming (NLP), fuzzy programming (FP) and global criterion method (GCM), are utilized.

• (iv) NLP always increases the degree of truth membership value, indeterminacy membership value, and at the same time, it decreases the degree of falsity membership value for determining better Pareto-optimal solution.

• (v) Carbon emission is more important factor in transportation system, as reduction of emission charge decreases the rate of air pollution indirectly. As well as minimum carbon emission charge directly helps to maximize the profit of the system as it corresponds to the total cost.

• (vi) Extra constraints for budget and carbon capacity support to maximize the profit and to minimize the deterioration.

• (vii) Sensitivity analysis is introduced for analyzing the effect of change of coefficient and finding the ranges of all parametric values.

The remaining part of the paper is structured as follows: Some basic definitions based on neutrosophic set are presented in Sect. 2. In Sect. 3, the mathematical model with notations are discussed. Section 4 introduces the solution methodology. Sections 5 and 6 describe the drawbacks of existing methods and advantages of our proposed method respectively. Numerical example with results and discussion is given in Sect. 7. Section 8 depicts the sensitivity analysis of the parameters. Conclusions and future research scopes are provided in Sect. 9.

2 Preliminaries

To formulate the proposed problem, we recall here some useful basic definitions of neutrosophic set.

The concept of neutrosophic set is a representation that consists of the indeterminate and inconsistent information, and is applied in scientific and engineering applications.

Definition 2.1

(Wang et al. 2010) Let U be the universal set. A single-valued neutrosophic set ${\tilde{A}}^n$ over U is of the form ${\tilde{A}}^n=\{\langle x,\mu _{{\tilde{A}}^n}(x),\sigma _{{\tilde{A}}^n}(x),\gamma _{{\tilde{A}}^n}(x)\rangle :x\in U\}$, where $\mu _{{\tilde{A}}^n}(x):U\rightarrow [0,1],~ \sigma _{{\tilde{A}}^n}(x):U\rightarrow [0,1],~\gamma _{{\tilde{A}}^n}(x):U\rightarrow [0,1]$ with $0\le \mu _{{\tilde{A}}^n}(x)+\sigma _{{\tilde{A}}^n}(x)+\gamma _{{\tilde{A}}^n}(x)\le 3, \forall ~ x\in U$. Here $\mu _{{\tilde{A}}^n}(x)$, $\sigma _{{\tilde{A}}^n}(x)$ and $\gamma _{{\tilde{A}}^n}(x)$ are the degrees of truth-membership, indeterminacy-membership and falsity-membership of x in ${\tilde{A}}^n$, respectively.

Fig. 1

Truth-membership, indeterminacy-membership and falsity-membership for $Z_l$

Definition 2.2

The general form of a multi-objective optimization problem with l objective functions, m constraints and n variables is given as follows:

$$\begin{aligned} \text{ minimize }&{Z(X)}=(Z_1(x),Z_2(x),\ldots ,Z_l(x))\\ \text{ subject } \text{ to }&{g}_{j}(X) \le {0}, ~~(j=1,2,\ldots ,m)\\&{x}_{i} \ge {0}, ~~(i=1,2,\ldots ,n),~x_{i} \in X \subseteq \mathbb {R}^n . \end{aligned}$$

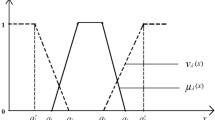
The truth-membership $\mu _{{l}}(Z_l)$, indeterminacy-membership

$\sigma _{{l}}(Z_l)$ and falsity-membership $\nu _{{l}}(Z_l)$ functions for the objective function $Z_l$ are, respectively, defined as:

$$\begin{aligned} \mu _{{l}}(Z_l)= & {} \left\{ \begin{array}{ll} 1,&{} \quad \text{ if } \, {Z_l}\le t_l,\\ 1-\frac{{Z_l}-t_l}{{a_l}},&{}\quad \text{ if }\, {t_l}\le {Z_l}\le {t_l}+{a_l},\\ 0 ,&{}\quad \text{ if } \, {Z_l}\ge {t_l}+{a_l}, \end{array} \right. \\ \sigma _{{l}}(Z_l)= & {} \left\{ \begin{array}{ll} 0,&{}\quad \text{ if } \, {Z_l}\le t_l,\\ \frac{{Z_l}-t_l}{{d_l}},&{}\quad \text{ if }\, {t_l}\le {Z_l}\le {t_l}+{d_l},\\ 1-\frac{{Z_l}-t_l}{{a_l}-{d_l}},&{}\quad \text{ if }\, {t_l}+{d_l}\le {Z_l}\le {t_l}+{a_l},\\ 0 ,&{}\quad \text{ if } \, {Z_l}\ge {t_l}+{a_l}, \end{array} \right. \\ \nu _{{l}}(Z_l)= & {} \left\{ \begin{array}{ll} 0,&{}\quad \text{ if } \, {Z_l}\le t_l,\\ \frac{{Z_l}-t_l}{{c_l}},&{}\quad \text{ if }\, {t_l}\le {Z_l}\le {t_l}+{c_l},\\ 1 ,&{}\quad \text{ if } \, {Z_l}\ge {t_l}+{c_l}. \end{array} \right. \end{aligned}$$

where $t_l$ is the target value for $Z_l$ and $a_l,d_l$ and $c_l$ are the acceptance tolerance, indeterminacy tolerance and rejection tolerance, respectively. The graphical presentation of three membership functions is shown in Fig. 1

Definition 2.3

Interval valued neutrosophic number: (Smarandache 2013) An neutrosophic number is denoted by ${\tilde{a}}^n=p+qI$, where $p,~q \in \mathbb {R}$ and $I \subseteq [0,1]$ is the indeterminacy. Now $I= [I^L,I^U],$ and therefore the interval form of ${\tilde{a}}^n=[p+qI^L, p+qI^U]=[{a}^L,{a}^U]$.

Basic properties of interval valued neutrosophic number: Let ${\tilde{a}}_1^n=p_1+q_1I_1$ and ${\tilde{a}}_2^n=p_2+q_2I_2$ with $I_1= [I_1^L,I_1^U]$, $I_2= [I_2^L,I_2^U]$ be two neutrosophic numbers. The interval forms are ${\tilde{a}}_1^n=[p_1+q_1I_1^L,p_1+q_1I_1^U]=[{a}_1^L,{a}_1^U]$ and ${\tilde{a}}_2^n=[p_2+q_2I_2^L,p_2+q_2I_2^U]=[{a}_2^L,{a}_2^U]$. Now the basic properties are defined as:

• 1. Addition: ${\tilde{a}}_1^n+{\tilde{a}}_2^n=[{a}_1^L+{a}_2^L,{a}_1^U+{a}_2^U]$.

• 2. Subtraction: ${\tilde{a}}_1^n-{\tilde{a}}_2^n=[{a}_1^L-{a}_2^U,{a}_1^U-{a}_2^L]$.

• 3. Multiplication: ${{\tilde{a}}_1^n*{\tilde{a}}_2^n=\left\{ \begin{array}{ll} [\min ({{a}_1^L}*{{a}_2^L},{{a}_1^L}*{{a}_2^U},{{a}_1^U}*{{a}_2^L},\\ {{a}_1^U}*{{a}_2^U} ),\\ \max ({{a}_1^L}*{{a}_2^L},{{a}_1^L}*{{a}_2^U},{{a}_1^U}*{{a}_2^L},\\ {{a}_1^U}*{{a}_2^U} )].\, \\ \end{array} \right. }$

• 4. Division: ${{\tilde{a}}_1^n/{\tilde{a}}_2^n=\left\{ \begin{array}{ll} [\min ({{a}_1^L}/{{a}_2^L},{{a}_1^L}/ {{a}_2^U},{{a}_1^U}/{{a}_2^L},{{a}_1^U}/{{a}_2^U} ),\\ \max ({{a}_1^L}/ {{a}_2^L},{{a}_1^L}/{{a}_2^U},{{a}_1^U}/{{a}_2^L},{{a}_1^U}/ {{a}_2^U} )], \,\\ 0\notin {\tilde{a}}_2^n.\\ \end{array} \right. }$

• 5. Scalar multiplication: $k.{\tilde{a}}^n= \left\{ \begin{array}{ll} {[}k{a}^L, k{a}^U],&{} \quad \text{ if } \, k\ge 0,\\ {[}k{a}^U, k{a}^L],&{} \quad \text{ if } \, k<0. \end{array} \right.$

• 6. Absolute value: ${|{{\tilde{a}}^n}|= \left\{ \begin{array}{ll} {[}{a}^L, {a}^U],&{} \quad \text{ if } \, {a}^L\ge 0,\\ {[}0,\max (-{a}^L,{a}^U)],&{} \quad \text{ if } \, {a}^L\le 0\le \\ {} &{}{a}^U,\\ {[}-{a}^U, -{a}^L],&{} \quad \text{ if } \, {a}^U\le 0. \end{array} \right. }$

• 7. Inequality: Ishibuchi and Tanaka (1990) ${\left\{ \begin{array}{ll} x\le [a^L, a^U] \equiv \exists ~z\in [{a}^L, {a}^U] &{} \quad \text{ and } \, x\le z,\\ x\ge [a^L, a^U] \equiv \exists ~z\in [{a}^L, {a}^U] &{}\quad \text{ and } \, x\ge z,\\ {[}{a}^L\le {b}^L, {a}^U\le {b}^U],&{}\quad \text{ iff } \, [a^L, a^U]\le [b^L, b^U],\\ {[}{a}^L\ge {b}^L, {a}^U\ge {b}^U],&{}\quad \text{ iff } \, [a^L, a^U]\ge [b^L, b^U].\\ \end{array} \right. }$

Definition 2.4

(Ye 2018) A neutrosophic linear programming is a general optimization problem if the following conditions are met:

• 1. The neutrosophic objective function is linear.

• 2. The decision variables are all nonnegative.

• 3. The structural constraints are all of the types of $``\le$” or $``\ge$.”

Definition 2.5

(Ye et al. 2018) In general, a constrained optimization problem in n decision variables with NNs is defined as follows:

$$\begin{aligned} \text{ minimize/maximize }&F(x,I)\\ \text{ subject } \text{ to }&g_i(x,I)\le 0,i=1,2,\ldots , m\\&h_j(x,I)\ge 0,j=1,2,\ldots ,l\\&p_k(x,I)=0,k=1,2,\ldots ,o\\&x\in X. \end{aligned}$$

When the indeterminacy I is considered as a possible interval range, the optimal solution of all feasible intervals forms the feasible region or feasible set for x and $I= [I^L,I^U].$ In this case, the value of the NN objective function is an optimal possible interval (NN) for F(x, I). For example, let us consider the following optimization problem with $I=[0,1]$:

Now, this problem can be transformed into two equivalent crisp subproblems to obtain worst (lower bound) and best (upper bound) solutions as follows:

Subproblem 1:

$$\begin{aligned} \text{ maximize }&2x_1+4x_2\\ \text{ subject } \text{ to }&x_1+2x_2\le 6,\\&2x_1+3x_2\le 8,\\&5x_1+4x_2\le 10,\\&x_1\ge 0,~ x_2\ge 0. \end{aligned}$$

Subproblem 2:

$$\begin{aligned} \text{ maximize }&5x_1+5x_2\\ \text{ subject } \text{ to }&x_1+2x_2\le 6,\\&2x_1+3x_2\le 8,\\&5x_1+4x_2\le 10,\\&x_1\ge 0,~ x_2\ge 0. \end{aligned}$$

By solving two subproblems we get the optimal solution (as NN) of the original problem as: $F=[10,12.5].$

Definition 2.6

(Smarandache 1999) Let two single-valued neutrosophic sets be ${\tilde{A}}^n$ and ${\tilde{B}}^n$ over the universal set U as ${\tilde{A}}^n =\{\langle x,\mu _{{\tilde{A}}^n}(x),\sigma _{{\tilde{A}}^n}(x),\gamma _{{\tilde{A}}^n}(x) \rangle :x\in U\}$, ${\tilde{B}}^n =\{\langle x,\mu _{{\tilde{B}}^n}(x)$, $\sigma _{{\tilde{B}}^n}(x), \gamma _{{\tilde{B}}^n}(x) \rangle :x\in U\}$. Then some basic properties are defined as:

• 1. ${\tilde{A}}^n\subset {\tilde{B}}^n$ if and only if $\mu _{{\tilde{A}}^n}(x)\le \mu _{{\tilde{B}}^n}(x), \sigma _{{\tilde{A}}^n}(x)\le \sigma _{{\tilde{B}}^n}(x),$ $\gamma _{{\tilde{A}}^n}(x)\ge \gamma _{{\tilde{B}}^n}(x)$.

• 2. ${\tilde{A}}^n={\tilde{B}}^n$ if and only if $\mu _{{\tilde{A}}^n}(x)=\mu _{{\tilde{B}}^n}(x),\sigma _{{\tilde{A}}^n}(x)=\sigma _{{\tilde{B}}^n}(x),$ $\gamma _{{\tilde{A}}^n}(x)=\gamma _{{\tilde{B}}^n}(x)$.

• 3. The complement of ${\tilde{A}}^n$ is denoted by $({\tilde{A}}^n)^{c}$ and defined by $({\tilde{A}}^n)^{c} =\{\langle x,\gamma _{{\tilde{A}}^n}(x),1-\sigma _{{\tilde{A}}^n}(x),\mu _{{\tilde{A}}^n}(x)\rangle :x\in U\}$.

• 4. The intersection of ${\tilde{A}}^n$ and ${\tilde{B}}^n$ is defined by ${\tilde{A}}^n \cap {\tilde{B}}^n=\{\langle x,\min \{\mu _{{\tilde{A}}^n}(x),\mu _{{\tilde{B}}^n}(x)\}, \min \{\sigma _{{\tilde{A}}^n}(x),\sigma _{{\tilde{B}}^n}(x)\},\max \{\gamma _{{\tilde{A}}^n}(x), \gamma _{{\tilde{B}}^n}(x)\}\rangle :x\in U\}$.

• 5. The union of ${\tilde{A}}^n$ and ${\tilde{B}}^n$ is defined by ${\tilde{A}}^n \cup {\tilde{B}}^n=\{\langle x$, $\max \{\mu _{{\tilde{A}}^n}(x),\mu _{{\tilde{B}}^n}(x)\}, \max \{\sigma _{{\tilde{A}}^n}(x),\sigma _{{\tilde{B}}^n}(x)\}$, $\min \{\gamma _{{\tilde{A}}^n}(x), \gamma _{{\tilde{B}}^n}(x)\}\rangle :x\in U\}$.

Definition 2.7

(Smarandache 1999) Let ${\tilde{A}}^n=\{\langle x,\mu _{{\tilde{A}}^n}(x)$, $\sigma _{{\tilde{A}}^n}(x),\gamma _{{\tilde{A}}^n}(x)\rangle :x\in U\}$ and ${\tilde{B}}^n=\{\langle x,\mu _{{\tilde{B}}^n}(x),\sigma _{{\tilde{B}}^n}(x),\gamma _{{\tilde{B}}^n}(x) \rangle :x\in U\}$ are two single-valued neutrosophic sets. Some operations of neutrosophic sets are defined as:

• 1. $\lambda {\tilde{A}}^n=\langle 1-(1-\mu _{{\tilde{A}}^n}(x))^\lambda , {\sigma _{{\tilde{A}}^n}(x)}^\lambda , {\gamma _{{\tilde{A}}^n}(x)}^\lambda \rangle$; $\lambda \ge 0, ~\lambda ~\in ~\mathbb {R}$.

• 2. $({{\tilde{A}}^n})^{\lambda }=\langle {\mu _{{\tilde{A}}^n}(x)}^\lambda , 1-(1-\sigma _{{\tilde{A}}^n}(x))^\lambda , 1-(1-\gamma _{{\tilde{A}}^n}(x))^\lambda \rangle ; \lambda \ge 0,~ \lambda ~\in ~\mathbb {R}$.

• 3. ${\tilde{A}}^n+{\tilde{B}}^n=\langle \mu _{{\tilde{A}}^n}(x)+\mu _{{\tilde{B}}^n}(x)-\mu _{{\tilde{A}}^n}(x) \mu _{{\tilde{B}}^n}(x),\sigma _{{\tilde{A}}^n}(x) \sigma _{{\tilde{B}}^n}(x),\gamma _{{\tilde{A}}^n}(x)\gamma _{{\tilde{A}}^n}(x)\rangle$.

• 4. ${\tilde{A}}^n.{\tilde{B}}^n=\langle \mu _{{\tilde{A}}^n}(x)\mu _{{\tilde{B}}^n}(x),\sigma _{{\tilde{A}}^n}(x)+ \sigma _{{\tilde{B}}^n}(x)-\sigma _{{\tilde{A}}^n}(x)\sigma _{{\tilde{B}}^n}(x),$ $\gamma _{{\tilde{A}}^n}(x)+\gamma _{{\tilde{B}}^n}(x)-\gamma _{{\tilde{A}}^n}(x)\gamma _{{\tilde{B}}^n}(x)\rangle$.

3 Problem description

To transform homogeneous products from distinct sources to different destinations with certain condition, we consider a multi-objective fixed-charge solid transportation problem (MFSTP) (here three objective functions) under budget constraints and carbon emission in neutrosophic environment. The first objective function represents the profit over carbon emission charge and fixed-charge from each source to each destination. The second objective function is chosen as the deterioration rate of goods, and third one is taken as the transporting time of goods. To overcome the complexity of incomplete and indeterminate information, here we assume that all the parameters are NNs. The main aim is to obtain compromise optimal solution for transforming homogeneous products from m sources to n destinations using the k conveyances at shipping cost ${\tilde{c}}_{ijk}^n$ per unit product in such a way that all the objective functions are optimized simultaneously. That is to shipping the product from supplier i to customer j by means of k conveyance with fixed-charge ${\tilde{f}}_{ijk}^n$. Each supplier $(i=1,2,\ldots ,m)$ has ${\tilde{a}}_{i}^n$ units of supply, each customer $(j=1,2,\ldots ,n)$ has ${\tilde{b}}_{j}^n$ units of demand and each conveyance $(k=1,2,\ldots ,l)$ has ${\tilde{e}}_{k}^n$ units of capacity.

3.1 Notations of the proposed study

The following notations are described to formulate the proposed mathematical model as:

${x}_{ijk}$::

amount of product transported from ith source to jth destination with kth conveyance,

${\tilde{c}}_{ijk}^n$::

cost for unit quantity of the product from ith source to jth destination with kth conveyance,

${\tilde{f}}_{ijk}^n$::

fixed-charge of the product from ith source to jth destination with kth conveyance,

${\tilde{d}}_{ijk}^n$::

deterioration rate for unit quantity of the product from ith source to jth destination with kth conveyance,

${\tilde{t}}_{ijk}^n$::

time of transportation for unit quantity of the product from ith source to jth destination with kth conveyance,

$\eta (x_{ijk})$::

binary variable takes the value “1” if $x_{ijk}\ne 0$ and “0” if $x_{ijk}=0$,

${\tilde{a}}_{i}^n$::

the supply at ith source,

${\tilde{b}}_{j}^n$::

the demand at jth destination,

${\tilde{e}}_{k}^n$::

the kth conveyance for TP,

${\tilde{B}}_{j}^n$::

total budget at jth destination,

${\tilde{p}}_{i}^n$::

purchasing cost per unit quantity of product at ith origin,

${\tilde{s}}_{j}^n$::

selling price per unit quantity of product at jth destination,

${\tilde{c}}_{k}^n$::

fixed carbon capacity,

${\tilde{e}}_{ijk}^n$::

charge of carbon emission per unit,

${\tilde{\alpha }}^n$::

carbon tax per unit of its carbon emission (${\tilde{\alpha }}^n>0$),

${\tilde{Z}}_{r}^n$::

the objective function with NNs $(r=1,2,3)$,

${{\overline{Z}}'}_{r}^n$::

the interval valued objective function $(r=1,2,3)$,

${Z'}_{r}^L$::

the lower-level objective function $(r=1,2,3)$ in crisp nature,

${Z'}_{r}^U$::

the upper-level objective function $(r=1,2,3)$ in crisp nature.

To obtain the maximum profit, it is obvious to minimize the purchasing cost, transportation cost, fixed-charge, carbon emission charge and to maximize the selling price. In the same time, deterioration rate of goods and total delivery time of transportation must be minimized. Since there exist three objective functions with conflicting nature, therefore the total system is controlled by MOTP. Without loss of generality, we select the first objective function as to maximize profit, second objective function as to minimize deterioration and third objective function as to minimize time. Budget constraints and fixed carbon capacity are important features in the formulated model. These two constraints help to obtain maximum profit. The mathematical model for profit maximization MFSTP with carbon emission and budget constraints under neutrosophic environment is presented as:

Model 1

$$\begin{aligned} \text{ maximize }~{{\tilde{Z}}^n}_{1}= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l \left[ ({{\tilde{s}}}_{j}^n- {{\tilde{c}}}_{ijk}^n-{{\tilde{\alpha }}^n}{{\tilde{e}}_{ijk}}^n-{{\tilde{p}}}_{i}^n){{x}_{ijk}}\right. \nonumber \\&\left. -{{\tilde{f}}}_{ijk}^n{\eta ({x}_{ijk})}\right] \end{aligned}$$

(1)

$$\begin{aligned} \text{ minimize }~{{\tilde{Z}}^n}_2= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l{{\tilde{d}}}_{ijk}^n{{x}_{ijk}} \end{aligned}$$

(2)

$$\begin{aligned} \text{ minimize }~{{\tilde{Z}}^n}_3= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l{{\tilde{t}}}_{ijk}^n{\eta ({x}_{ijk})}\end{aligned}$$

(3)

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^n\sum _{k=1}^l{{x}_{ijk}} \le {{\tilde{a}}}_i^n ~~(i=1,2,\ldots ,m),\end{aligned}$$

(4)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l{{x}_{ijk}} \ge {{\tilde{b}}}_j^n ~~(j=1,2,\ldots ,n),\end{aligned}$$

(5)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n{{x}_{ijk}} \le {{\tilde{e}}}_k^n ~~(k=1,2,\ldots ,l), \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l[{{\tilde{p}}_i}^n+{\tilde{c}}_{ijk}^n+{{\tilde{\alpha }}^n}{\tilde{e}}_{ijk}^n] {{x}_{ijk}}\le {{\tilde{B}}}_j^n \nonumber \\&(j=1,2,\ldots ,n),\end{aligned}$$

(7)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n{{\tilde{e}}_{ijk}}^n{{x}_{ijk}} \le {{\tilde{c}}}_k^n ~~(k=1,2,\ldots ,l),\end{aligned}$$

(8)

$$\begin{aligned}&{{x}_{ijk}}\ge 0, \forall ~i,~j,~k,\nonumber \\&\eta ({x}_{ijk})=\left\{ \begin{array}{ll} 1,&{} \quad \text{ if } \, x_{ijk}>0,\\ 0,&{} \quad \text{ otherwise. } \, \\ \end{array} \right. \end{aligned}$$

(9)

The feasibility condition of this TP is as follows:

$$\begin{aligned} \sum _{i=1}^m {{\tilde{a}}}_i^n\ge \sum _{j=1}^n {{\tilde{b}}}_j^n; ~\sum _{k=1}^l {{\tilde{e}}}_k^n\ge \sum _{j=1}^n {{\tilde{b}}}_j^n. \end{aligned}$$

In Model 1, the objective function (1) presents the profit that would be maximized. It consists of selling price (1st part), transportation cost (2nd part), carbon emission charge (3rd part), purchasing cost (4th part) and fixed-charge in its last part. The objective function (2) refers to minimize the total deterioration, and the objective function (3) indicates to minimize the total time of transportation. The constraints (4), (5) and (6) display as source, demand and conveyance constraints, respectively. The constraints (7) introduce as budget constraints. Carbon capacity is explained by constraints (8) and nonnegativity restriction is attended by constraints (9).

Remark 1

All the parameters in the objective functions and constraints are NNs and based on this fact, Model 1 is treated as neutrosophic MFSTP. To derive the Pareto-optimal solution (compromise solution) of this model, we consider that minimize ${\tilde{Z'}^n}_{1}$ = maximize $(-{{\tilde{Z}}^n}_{1})$, minimize ${\tilde{Z'}^n}_{2}$= minimize ${{\tilde{Z}}^n}_{2}$ and minimize ${\tilde{Z'}^n}_{3}$= minimize ${{\tilde{Z}}^n}_{3}$.

Theorem 3.1

Model 1 can be solved as multi-objective linear programming problem under NNs.

Proof

Model 1 satisfies all of the conditions stated in Definition 2.4. Therefore, Model 1 can be solved as general linear programming problem under neutrosophic environment. This evinces the proof of the theorem.

3.2 Equivalent deterministic form of Model 1

Without loss of generality, we choose NN in Model 1 of the form ${\tilde{a}}^n=p+qI$, where I is the indeterminacy, and then Model 1 transforms into Model 2 as:

Model 2

$$\begin{aligned} \text{ minimize }~{{\overline{Z}}'}_{1}^n= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l [\left( {p_i^1}+{I_p}{p_i^2}\right) +\left( {c}_{ijk}^1+{I_c}{c}_{ijk}^2\right) \\&+\bigg ({\alpha }^1+{I_\alpha }{\alpha }^2\bigg )\left( e_{ijk}^1+{I_e}e_{ijk}^2\right) -\left( {s_j^1}+{I_s}{s_j^2}\right) ]{{x}_{ijk}}\\&+\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l\left( {f}_{ijk}^1+{I_f}{f}_{ijk}^2\right) {\eta ({x}_{ijk})}\\ \text{ minimize }~{{\overline{Z}}'}_{2}^n= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l({d}_{ijk}^1+{I_d}{d}_{ijk}^2){{x}_{ijk}}\\ \text{ minimize }~{{\overline{Z}}'}_{3}^n= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l({t}_{ijk}^1+{I_t}{t}_{ijk}^2) {\eta ({x}_{ijk})} \\ \text{ subject } \text{ to }&\sum _{j=1}^n\sum _{k=1}^l{{x}_{ijk}} \le ({a}_i^1+{I_a}{a}_i^2) ~~(i=1,2,\ldots ,m),\\&\sum _{i=1}^m\sum _{k=1}^l{{x}_{ijk}} \ge ({b}_j^1+{I_b}{b}_j^2)~~(j=1,2,\ldots ,n),\\&\sum _{i=1}^m\sum _{j=1}^n{{x}_{ijk}} \le ({e}_k^1+{I_e}{e}_k^2) ~~(k=1,2,\ldots ,l),\\&\sum _{i=1}^m\sum _{k=1}^l[\left( p_{i}^1+{I_p}p_{i}^2\right) +({c}_{ijk}^1+ {I_c}{c}_{ijk}^2)+({\alpha }^1+\\&{I_\alpha }{\alpha }^2)({e}_{ijk}^1+{I_e}{e}_{ijk}^2)]{{x}_{ijk}}\le ({{B}}_j^1+{I_B}{{B}}_j^2)\\&(j=1,2,\ldots ,n),\\&\sum _{i=1}^m\sum _{j=1}^n\left( e_{ijk}^1+{I_e}e_{ijk}^2\right) {{x}_{ijk}} \le ({c}_k^1+{I_c}{c}_k^2)\\&(k=1,2,\ldots ,l),\\&{{x}_{ijk}}\ge 0, \forall ~i,~j,~k,\\&\eta ({x}_{ijk})= {\left\{ \begin{array}{ll} 1,&{} \quad \text{ if } \, x_{ijk}>0,\\ 0,&{} \quad \text{ otherwise. } \, \end{array}\right. } \end{aligned}$$

Now NN can be expressed as ${\tilde{a}}^n =[p+qI^L,p+qI^U]=[{a}^L,{a}^U]$ which becomes an interval number, and then there exist lower bound and upper bound of the interval. Therefore for existence of these bounds, Model 2 splits into two equivalent crisp problems, which are noted as Model 3A and Model 3B. Model 3A chooses as lower-level problem whereas Model 3B considers as upper-level problem. Also using inequality 7 (from Def. 2.3) the interval valued constraints transform into deterministic form. Hence the deterministic form of these models is as follows:

Model 3A

$$\begin{aligned} \text{ minimize }~{{Z'}}_{1}^L= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l [\left( {p_i^U} +{c}_{ijk}^U+{\alpha }^U e_{ijk}^U-{s_j^L}\right) {{x}_{ijk}}\nonumber \\&+{f}_{ijk}^U{\eta ({x}_{ijk})}] \end{aligned}$$

(10)

$$\begin{aligned} \text{ minimize }~{{Z'}}_{2}^L= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l{d}_{ijk}^L{{x}_{ijk}}\end{aligned}$$

(11)

$$\begin{aligned} \text{ minimize }~{{Z'}}_{3}^L= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l{t}_{ijk}^L{\eta ({x}_{ijk})}\end{aligned}$$

(12)

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^n\sum _{k=1}^l{{x}_{ijk}} \le {a}_i^U ~~(i=1,2,\ldots ,m),\end{aligned}$$

(13)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l{{x}_{ijk}} \ge {b}_j^L~~(j=1,2,\ldots ,n),\end{aligned}$$

(14)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n{{x}_{ijk}} \le {e}_k^U ~~(k=1,2,\ldots ,l), \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l[p_{i}^L+{c}_{ijk}^L+\alpha ^L{e}_{ijk}^L]{{x}_{ijk}}\le {{B}}_j^L\nonumber \\&(j=1,2,\ldots ,n),\end{aligned}$$

(16)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l[p_{i}^U+{c}_{ijk}^U+\alpha ^U{e}_{ijk}^U]{{x}_{ijk}}\le {{B}}_j^U\nonumber \\&(j=1,2,\ldots ,n),\end{aligned}$$

(17)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n{e}_{ijk}^L{{x}_{ijk}}\le {{c}}_k^L ~~(k=1,2,\ldots ,l),\end{aligned}$$

(18)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n{e}_{ijk}^U{{x}_{ijk}}\le {{c}}_k^U ~~(k=1,2,\ldots ,l),\end{aligned}$$

(19)

$$\begin{aligned}&{{x}_{ijk}}\ge 0, \forall ~i,~j,~k,\end{aligned}$$

(20)

$$\begin{aligned}&\eta ({x}_{ijk})=\left\{ \begin{array}{ll} 1,&{} \quad \text{ if } \, x_{ijk}>0,\\ 0,&{} \quad \text{ otherwise. } \,\\ \end{array} \right. \end{aligned}$$

(21)

Model 3B

$$\begin{aligned} \text{ minimize }~{{Z'}}_{1}^U= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l [({p_i^L} +{c}_{ijk}^L+{\alpha }^Le_{ijk}^L-{s_j^U}){{x}_{ijk}}\\&+{f}_{ijk}^L{\eta ({x}_{ijk})}]\\ \text{ minimize }~{{Z'}}_{2}^U= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l{d}_{ijk}^U{{x}_{ijk}}\\ \text{ minimize }~{{Z'}}_{3}^U= & {} \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l{t}_{ijk}^U{\eta ({x}_{ijk})}\\ \text{ subject } \text{ to }&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

Henceforth the definition of Pareto-optimal solution (compromise solution) is defined as follows.

Definition 3.1

Pareto-optimal solution (compromise solution) of Model 3A/Model 3B is a feasible solution $x^*=({x}^*_{ijk}:i=1,2,\ldots ,m;j=1,2,\ldots ,n;k=1,2,\ldots ,l)$ such that there exists no other feasible solution $x=({x}_{ijk}:i=1,2,\ldots ,m;$ $j=1,2,\ldots ,n;k=1,2,\ldots ,l)$ with ${Z_r'}(x)\le {Z_r'}(x^*),~r=1,2,3$ and ${Z_r'}(x)< {Z_r'}(x^*)$ for at least one r.

Theorem 3.2

The combination of the Pareto-optimal solutions of Model 3A and Model 3B represent the Pareto-optimal solution of Model 2 and consequently of Model 1 in the form of interval neutrosophic number.

Proof

Using Definition 2.5, Theorem 3.2 can be proven easily.

4 Solution methodology

In multi-objective optimization problem, there does not always exist a solution which is the best for all the objective functions. That is the solution will be the best for one objective function and that may be worst for another objective function. The objective functions are conflicting to each other and hence the solutions cannot simply compare to each other. For this cause, we discuss three methods for solving neutrosophic MFSTP as follows:

• Neutrosophic linear programming (NLP),

• Fuzzy programming (FP),

• Global criterion method (GCM).

Table 1 Pay-off matrix

4.1 Neutrosophic linear programming (NLP)

Model 3A and Model 3B provide the lower bound and upper bound of the objective functions and the solutions are not overall compromise solution of Model 2. So we utilize NLP to derive the compromise solution of multi-objective decision making problem. To solve the proposed model in NLP, we describe the following steps as:

• Step 4.1.1 Transform the neutrosophic optimization problem into crisp problem which splits into two subproblems.

• Step 4.1.2 Solve each single-objective problem for both subproblems individually such that all constraints remain same.

• Step 4.1.3 Determine the upper bound as negative ideal solution (NIS) and lower bound as positive ideal solution (PIS) for each objective function from the pay-off matrix Table 1, where PIS and NIS are defined as PIS = ${Z_r}^* = \min ~\{{Z_r}({X_1}^*),~{Z_r}({X_2}^*),~{Z_r}({X_3}^*)\} ~(r=1,2,3)$ and NIS = ${Z_r}' = \max ~\{{Z_r}({X_1}^*),~{Z_r}({X_2}^*),~{Z_r}({X_3}^*)\} ~(r=1,2,3),$ respectively.

• Step 4.1.4 Design the truth-membership function and indeterminacy-membership function with highest degree and falsity-membership function with least degree.

• Step 4.1.5 Choose the tolerance and construct the membership functions according to the bounds as:

  $$\begin{aligned} T_{{l}}(Z_l'(x))=\left\{ \begin{array}{ll} 1,&{} \quad \text{ if } \, {Z_l'(x)}\le L_{l}^T,\\ 1-\frac{{Z_l'(x)}-L_{l}^T}{U_{l}^T-{L_{l}^T}},&{} \quad \text{ if }\, L_{l}^T\le {Z_l'(x)}\le U_{l}^T,\\ 0 ,&{} \quad \text{ if } \, {Z_l'(x)}\ge U_{l}^T, \end{array} \right. \\ I_{{l}}(Z_l'(x))=\left\{ \begin{array}{ll} 0,&{} \quad \text{ if } \, {Z_l'(x)}\le L_{l}^I,\\ 1-\frac{{Z_l'(x)}-L_{l}^I}{U_{l}^I-L_{l}^I},&{} \quad \text{ if }\, L_{l}^I\le {Z_l'(x)}\le U_{l}^I,\\ 0 ,&{} \quad \text{ if } \, {Z_l'(x)}\ge U_{l}^I, \end{array} \right. \\ F_{{l}}(Z_l'(x))=\left\{ \begin{array}{ll} 0,&{} \quad \text{ if } \, {Z_l'(x)}\le L_{l}^F,\\ 1-\frac{{Z_l'(x)}-L_{l}^F}{U_{l}^F-L_{l}^F},&{} \quad \text{ if }\, L_{l}^F\le {Z_l'(x)}\le U_{l}^F,\\ 1 ,&{} \quad \text{ if } \, {Z_l'(x)}\ge U_{l}^F. \end{array} \right. \end{aligned}$$

  Here $U_{l}^T= U_l$ = NIS for $Z_l'$, and $L_{l}^T = L_l$ = PIS for $Z_l'$; $U_{l}^F = U_{l}^T$, $L_{l}^F = L_{l}^T+t_l(U_{l}^T-L_{l}^T)$; $L_{l}^I = L_{l}^T$, $U_{l}^I = L_{l}^T+s_l(U_{l}^T- L_{l}^T)$; $t_l, s_l$ are tolerances.

• Step 4.1.6 Select the values of $\theta , \xi , \zeta$ in [0, 1] for each neutrosophic number as the truth, indeterminacy and falsity degrees, respectively.

• Step 4.1.7 Constitute NLP that represents in Model 4A. Model 4A

  $$\begin{aligned} \text{ maximize }&T_{l}(Z_l'(x))~(l=1,2,3)\\ \text{ maximize }&I_{l}(Z_l'(x))~(l=1,2,3)\\ \text{ minimize }&F_{l}(Z_l'(x))~(l=1,2,3)\\ \text{ subject } \text{ to }&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

  Model 4A can be reduced to Model 4B as: Model 4B

  $$\begin{aligned} \text{ maximize }&\theta \\ \text{ maximize }&\xi \\ \text{ minimize }&\zeta \\ \text{ subject } \text{ to }&T_{{l}}(Z_l'(x))\ge \theta , ~I_{{l}}(Z_l'(x))\ge \xi , ~F_{{l}}(Z_l'(x))\le \zeta ,\\&\theta +\xi +\zeta \le 3,~\theta +\xi +\zeta \ge 0,~\theta \ge \zeta ,~\theta \ge \xi ,\\&\theta , \xi , \zeta \in [0,1]\, (l=1,2,3),\\&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

  Now the simplified model of NLP (Model 4B) that derives the compromise solution of MOTP (i.e., Model 4C) as follows: Model 4C

  $$\begin{aligned} \text{ maximize }&\theta +\xi -\zeta \\ \text{ subject } \text{ to }&{Z_l'}(x)+(U_{l}^T-L_{l}^T)\theta \le U_{l}^T,\\&{Z_l'}(x)+(U_{l}^I-L_{l}^I)\xi \le U_{l}^I,\\&{Z_l'}(x)-(U_{l}^F-L_{l}^F)\zeta \le U_{l}^F,\\&\theta +\xi +\zeta \le 3,~\theta +\xi +\zeta \ge 0,~\theta \ge \zeta ,~\theta \ge \xi ,\\&\theta , \xi , \zeta \in [0,1] \,(l=1,2,3),\\&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

• Step 4.1.8: Solve Model 4C by LINGO 13 iterative scheme.

Theorem 4.1

If $x^*=(x_{ijk}:~i=1,2,\ldots ,m; ~j=1,2,\ldots ,n; ~k$ $=1,2,\ldots ,p)$ is an optimal solution of Model 4C then it is also Pareto-optimal (non-dominated) solution of Model 2.

Proof

Let $x^*$ is not a Pareto-optimal (non-dominated) solution of Model 2. Therefore, from Def. 3.1, we consider that there exists at least one x such that $Z_l'(x)\le Z_l'(x^*)$ for $l=1,2,3$ and $Z_l'(x)< Z_l'(x^*)$ for at least one l. Therefore truth and indeterminacy membership functions $\mu _{{l}}(Z_l'(x))$ and $\sigma _{{l}}(Z_l'(x))$ are strictly decreasing with respect to the corresponding objective function $Z_l$ in [0, 1] respectively. Again the falsity membership function $\nu _{{l}}(Z_l'(x))$ strictly increases with respect to the objective function $Z_l'$ in [0, 1]. Hence $\mu _{{l}}(Z_l'(x))\ge \mu _{{l}}(Z_l'(x^*)) ~\forall ~l$ and $\mu _{{l}}(Z_l'(x))>\mu _{{l}}(Z_l'(x^*))$ for at least one l. Similarly $\sigma _{{l}}(Z_l'(x))\ge \sigma _{{l}}(Z_l'(x^*)) ~\forall ~l$ and $\sigma _{{l}}(Z_l'(x))>\sigma _{{l}}(Z_l'(x^*))$ for at least one l. Also $\nu _{{l}}(Z_l'(x))\le \nu _{{l}}(Z_l'(x^*)) ~\forall ~l$ and $\nu _{{l}}(Z_l'(x))<\nu _{{l}}(Z_l'(x^*))$ for at least one l. Now, $(\theta +\xi -\zeta )$ = $\min ~ \{\mu _{{l}}(Z_l'(x)),~\sigma _{{l}}(Z_l'(x)),~\nu _{{l}}(Z_l'(x))\}$ $\ge \min ~\{\mu _{{l}}(Z_l'(x^*)),~\sigma _{{l}}(Z_l'(x^*)),~\nu _{{l}}(Z_l'(x^*))\}$ = $(\theta ^*+\xi ^*-\zeta ^*)$ which is a contradiction that $x^*$ is an optimal solution of Model 4C. Here $\theta ^*,~\xi ^*$ and $\zeta ^*$ are the values of $\theta ,~\xi$ and $\zeta$ at $x^*$, respectively. This completes the proof of the theorem. $\square$

4.2 Fuzzy programming (FP)

Since Models 3A and 3B provide the lower bound and upper bound of the objective functions and the solutions are not overall compromise solution of Model 2, therefore to find overall compromise solution, we take the advantage of FP to solve neutrosophic MFSTP. The FP was introduced by Zimmermann (1978) for solving multi-objective linear programming problem and it is very easy for solving this type of problem. FP of Model 2 can be formulated as:

Find $x=(x_1,x_2, \ldots ,x_n)^T$ such that minimize $Z_l'~(l=1,2,3)$ and subject to ${g}_{j}(X) \le {0}, ~(j=1,2,\ldots ,m)$ and ${x}_{i} \ge {0}, ~(i=1,2,\ldots ,n),$ with tolerance $a_l~(l=1,2,3)$. The membership function $\mu _{{l}}(Z_l'(x))~(l=1,2,3)$ is defined in Def. 2.2. The goal is to maximize the degree of acceptance of objective functions. Therefore to solve the proposed Model 2 in FP, we depict the following steps as:

• Step 4.2.1 Transform the neutrosophic optimization problem into crisp problem which splits into two subproblem.

• Step 4.2.2 Solve each single-objective problem of the subproblem independently keeping all constraints as same.

• Step 4.2.3 Select the tolerance of each objective function.

• Step 4.2.4 Determine PIS and NIS defined in Step 4.1.3. and formulate the membership function corresponding to each objective function. Now maximize the degree of acceptance of objective function and then the equivalent crisp model of FP is designed as: Model 5A

  $$\begin{aligned} \text{ maximize }&\theta \\ \text{ subject } \text{ to }&T_{{l}}(Z_l'(x))\ge \theta ~(l=1,2,3),\\&\theta \in [0,1],\\&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

  Model 5A is transformed into simplified form in Model 5B as: Model 5B

  $$\begin{aligned} \text{ maximize }&\theta \\ \text{ subject } \text{ to }&{Z_l'}(x)+(U_{l}^T-L_{l}^T)\theta \le U_{l}^T (l=1,2,3),\\&\theta \in [0,1],\\&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

• Step 4.2.5: Solve Model 5B by LINGO 13 iterative scheme with respect to parameter $\theta$.

Theorem 4.2

If $x^*=(x_{ijk}:~i=1,2,\ldots ,m; ~j=1,2,\ldots ,n; ~k$ $=1,2,\ldots ,p)$ is an optimal solution of Model 5B then it is also Pareto-optimal (non-dominated) solution of Model 2.

Proof

Let $x^*$ is not a Pareto-optimal (non-dominated) solution of Model 2. Therefore, from Def. 3.1, we consider that there exists at least one x such that $Z_l'(x)\le Z_l'(x^*)$ for $l=1,2,3$ and $Z_l'(x)< Z_l'(x^*)$ for at least one l. Therefore membership function $\mu _{{l}}(Z_l'(x))$ is strictly decreasing with respect to the corresponding objective function $Z_l'$ in [0, 1]. Hence $\mu _{{l}}(Z_l'(x))\ge \mu _{{l}}(Z_l'(x^*)) ~\forall ~l$ and $\mu _{{l}}(Z_l'(x))>\mu _{{l}}(Z_l'(x^*))$ for at least one l. Now, $\theta$ = $\min ~ \{\mu _{{l}}(Z_l'(x))\}$ $\ge \min ~\{\mu _{{l}}(Z_l'(x^*))\}$ = $\theta ^*$ which is a contradiction that $x^*$ is an optimal solution of Model 5B. Here $\theta ^*$ is the value of $\theta$ at $x^*$. This completes the proof of the theorem. $\square$

4.3 Global criterion method

Here we introduce a non-fuzzy approach, namely, GCM that provides the compromise solution by minimizing distance among some reference points of the feasible objective region. Since Models 3A and 3B do not provide overall compromise solution of Model 2, therefore to find overall compromise solution, GCM of Model 2 can be depicted by the following steps:

• Step 4.3.1 Transform the neutrosophic optimization problem into crisp problem which splits into two subproblems.

• Step 4.3.2 Solve each single-objective problem for each subproblem independently with subject to all constraints.

• Step 4.3.3 Determine the max $(U_{l}^T)$ and min $(L_{l}^T)$ value of each objective function from Table 1 and formulate the crisp model is as: Model 6

  $$\begin{aligned} \text{ minimize }&F(x)=\bigg [\sum ^3_{l=1}\bigg (\frac{{Z_l'(x)}-L_{l}^T}{U_{l}^T-{L_{l}^T}}\bigg )^2\bigg ]^{\frac{1}{2}} \\ \text{ subject } \text{ to }&{\text{ constraints }}~(13){-}(21). \end{aligned}$$

• Step 4.3.4 Solve Model 6 by LINGO 13 iterative scheme.

Definition 4.1

The compromise solution of GCM is defined as the minimum distance between the ideal solution and the desired solution. If ${Z_l}^*$ is the ideal solution of the objective function $Z_l'$ then the compromise solution of Model 2 is defined as ${Z_l}^*= \min ||{Z_l'}^*-Z_l'||_\infty$ $\forall ~l.$

4.4 Differences among the solution methodologies

First of all, GCM is a non-fuzzy technique, i.e., this method does not take into account indeterminacy in the optimization problems. Therefore, we need not have to construct any membership or non-membership functions, only we have to build a single-objective optimization problem utilizing different norms such as $L_1,L_2, L_{\infty }, etc$. GCM is simple to use in comparison with respect to FP and NLP. On the other hand, FP is a fuzzy optimization technique which considers vagueness in optimization problems. Therefore, in FP we have to build membership function for the objective functions. Again, NLP is an extended version of FP, which handles the indeterminacy occupied into the optimization problem in neutrosophic manner, i.e., in NLP we have to construct three membership functions namely truth, falsity and indeterminacy. Hence, FP and NLP are interrelating, i.e., complementarily to each other.

5 Limitations of the study

From literature review, we observe that many researchers formulated STP/MFSTP in different environments such as fuzzy and IF optimization for the parameters of cost, time and deterioration. But their formulated models have some limitations which are listed here.

• Li and Lai (2000) solved MOTP using FP for controlling the uncertainty. Majumder et al. (2019) solved uncertain multi-item MFSTP with budget constraints. This problem was analyzed with the uncertainty for determining truth and falsity but the problem did not provide about indeterminacy that enrolled the system into neutrosophic.

• Rizk-Allah et al. (2018) used neutrosophic compromise programming for solving MOTP, without choosing neutrosophic number for the parameters of MOTP. In neutrosophic number, there exists indeterminacy which is an important factor for uncertainty.

• Ding et al. (2013) included carbon emission reduction in transportation system and applied its potential effect in China. But it was not connected with other factors in multi-level system such as profit, budget, carbon capacity and fixed-charge which are indirectly related to carbon emission.

• Tarulescu et al. (2017) discussed about smart transportation of $\text {CO}_2$ emission reduction strategies but did not consider carbon capacity, budget and profit which are indirectly related in transportation system with fuzzy, IF or neutrosophic environment.

• Das et al. (2016) solved breakable multi-stage multi-item STP under budget with Gaussian type-2 fuzzy parameters but did not include with neutrosophic system.

• Khalil et al. (2018) discussed time neutrosophic soft set and its applications, but we see that the paper was defined only fundamental definitions, examples and operations on time neutrosophic set without discussing the real-life application or any programming problem.

• Song and Leng (2012) analyzed about single-period problem under carbon emission policies but did not incorporate multi-level or multi-period problem and not defined for fuzzy or IF or neutrosophic environment.

6 Advances of the proposed study

• Neutrosophic sets are characterized by three independent membership degrees, namely truth-membership degree (T), indeterminacy-membership degree (I) and falsity-membership degree (F) which are more capable to handle imprecise parameters.

• IFSs can only handle the incomplete information not indeterminate. But neutrosophic set can tackle both incomplete and indeterminate information. Therefore the neutrosophic set is more applicable to tackle uncertainty than the IFS.

• Decision makers (DMs) in NLP want to increase the degree of truth-membership function and the degree of indeterminacy but to decrease the degree of falsity-membership function, which are more realistic in real-life problem.

• Relating with transportation system, carbon emission increases the rate of air pollution and thereafter increases the carbon emission charge. Hence profit of the system decreases and therefore to obtain maximum profit, carbon emission reduction is an important factor which are chosen in this study.

• To obtain maximum profit, budget constraints and carbon capacity are also included in this problem and these extra restrictions help to find minimum deterioration and minimum time of the proposed problem.

7 Real-life experiment

In this section, we include a real-life example to illustrate the applicability of the proposed study with maximum profit, minimum deterioration and minimum time in transportation. Considering two source points of West Bengal that export two types of sea fishes to other states (e.g., Bihar and Jharkhand) in transportation system. For heavy duty of vehicle in transportation, carbon emission charge includes with other costs such as selling price, purchasing cost, transportation cost and fixed-charge. Again for conservation strategy of data, deterioration cost is included. For transporting data with long distance, time factor must be added. According to various complicated factors, transportation cost per unit item from source to destination with fixed-charge, deterioration cost, time, carbon emission charge are all NNs which are supplied in Tables 2, 3, 4 and 5, respectively. Transportation cost, deterioration cost and carbon emission charge are considered in hundred dollar ($) per unit and time in hour per unit.

The selling price, purchasing cost, carbon tax, source, demand, conveyance, budget and carbon capacity are chosen here as NNs. The aim is to obtain maximum profit by minimizing purchasing cost, carbon emission charge, transportation charge and fixed-charge, and maximizing selling price. Time and deterioration are minimized such that the budget and carbon capacity must be bounded. Therefore the problem becomes MFSTP due to describe such conditions, where the objective functions are contradicted to each other. The formulation of mathematical form of this problem are Models 7A and 7B which are obtained from Models 3A and 3B, respectively. Solution of the problem is now illustrated thereafter. In addition to that we assume the following in the proposed study.

Selling price = (${\tilde{s}}_{j}^n$): {${\tilde{s}}_{1}^n= 50+5I$; ${\tilde{s}}_{2}^n=60+5I$}; Purchasing cost = (${\tilde{p}}_{i}^n$): {${\tilde{p}}_{1}^n= 5+I$; ${\tilde{p}}_{2}^n=6+2I$}; Carbon tax = (${\tilde{\alpha }}^n):~\{{\tilde{\alpha }}^n=2+I$}; Source = (${\tilde{a}}_{i}^n$): {${\tilde{a}}_{1}^n= 230+5I$; ${\tilde{a}}_{2}^n=240+10I$}; Demand = (${\tilde{b}}_{j}^n$): {${\tilde{b}}_{1}^n = 100+5I$; ${\tilde{b}}_{2}^n=120+10I$}; Conveyance = (${\tilde{e}}_{k}^n$): {${\tilde{e}}_{1}^n= 270+5I$; ${\tilde{e}}_{2}^n=290+10I$}; Budget = (${\tilde{B}}_{j}^n$): {${\tilde{B}}_{1}^n= 3900+100I$; ${\tilde{B}}_{2}^n=3500+ 100I$}; Carbon capacity=(${\tilde{c}}_{k}^n$): {${\tilde{c}}_{1}^n= 360+40I$; ${\tilde{c}}_{2}^n=420+40I$}. Here we consider $I=[0,~1]$ is the indeterminacy.

Table 2 Neutrosophic transportation cost ${{{\tilde{c}}}_{ijk}^n}$ and the fixed-charge ${{{\tilde{f}}}_{ijk}^n}$

Table 3 Neutrosophic deterioration cost ${{{\tilde{d}}}_{ijk}^n}$

Table 4 Neutrosophic time ${{{\tilde{t}}}_{ijk}^n}$

Table 5 Carbon emission charge ${\tilde{e}}_{ijk}^n$

Model 7A

$$\begin{aligned} \text{ minimize }~{Z'}_{1}^L= & {} 2{x}_{111}+{x}_{112}+5{x}_{121}-31{x}_{122}-13{x}_{211}\nonumber \\&+4{x}_{212}-27{x}_{221}-13{x}_{222}\nonumber \\ \text{ minimize }~{Z'}_{2}^L= & {} 4{x}_{111}+5{x}_{112}+5{x}_{121}+3{x}_{122}+3{x}_{211}\nonumber \\&+4{x}_{212}+2{x}_{221}+2{x}_{222}\nonumber \\ \text{ minimize }{Z'}_{3}^L= & {} 12{x}_{111}+15{x}_{112}+8{x}_{121}+11{x}_{122}+6{x}_{211}\nonumber \\&+9{x}_{212}+10{x}_{221}+14{x}_{222}\nonumber \\ \text{ subject } \text{ to }&x_{111}+x_{112}+x_{121}+x_{122}\le 235, \end{aligned}$$

(22)

$$\begin{aligned}&x_{211}+x_{212}+x_{221}+x_{222}\le 250,\end{aligned}$$

(23)

$$\begin{aligned}&x_{111}+x_{112}+x_{211}+x_{212}\ge 100,\end{aligned}$$

(24)

$$\begin{aligned}&x_{121}+x_{122}+x_{221}+x_{222}\ge 120,\end{aligned}$$

(25)

$$\begin{aligned}&x_{111}+x_{121}+x_{211}+x_{221}\le 275,\end{aligned}$$

(26)

$$\begin{aligned}&x_{112}+x_{122}+x_{212}+x_{222}\le 300,\end{aligned}$$

(27)

$$\begin{aligned}&34x_{111}+35x_{112}+29x_{211}+31x_{212}\nonumber \\&\le 4000,\end{aligned}$$

(28)

$$\begin{aligned}&13x_{111}+19x_{112}+14x_{211}+20x_{212}\nonumber \\&\le 3900,\end{aligned}$$

(29)

$$\begin{aligned}&38x_{121}+20x_{122}+24x_{221}+30x_{222}\nonumber \\&\le 3600,\end{aligned}$$

(30)

$$\begin{aligned}&26x_{121}+13x_{122}+13x_{221}+17x_{222}\nonumber \\&\le 3500,\end{aligned}$$

(31)

$$\begin{aligned}&2x_{111}+3x_{121}+2x_{211}+2x_{221}\le 360,\end{aligned}$$

(32)

$$\begin{aligned}&6x_{111}+5x_{121}+5x_{211}+4x_{221}\le 400,\end{aligned}$$

(33)

$$\begin{aligned}&3x_{112}+2x_{122}+2x_{212}+3x_{222}\le 420,\end{aligned}$$

(34)

$$\begin{aligned}&6x_{112}+3x_{122}+3x_{212}+5x_{222}\le 460,\end{aligned}$$

(35)

$$\begin{aligned}&{{x}_{ijk}}\ge {0}, \forall ~i,~j,~k. \end{aligned}$$

(36)

Model 7B

$$\begin{aligned} \text{ minimize }~{Z'}_{1}^U= & {} -30{x}_{111}-27{x}_{112}-14{x}_{121}-45{x}_{122}\\&-35{x}_{211}-22{x}_{212}-45{x}_{221}-33{x}_{222}\\ \text{ minimize }~{Z'}_{2}^U= & {} 6{x}_{111}+7{x}_{112}+6{x}_{121}+5{x}_{122}+4{x}_{211}\\&+6{x}_{212}+3{x}_{221}+3{x}_{222}\\ \text{ minimize }~{Z'}_{3}^U= & {} 15{x}_{111}+20{x}_{112}+10{x}_{121}+15{x}_{122}+10{x}_{211}\\&+14{x}_{212}+15{x}_{221}+20{x}_{222}\\ \text{ subject } \text{ to }&{\text{ constraints }}~(22){-}(36). \end{aligned}$$

Solving Model 7A and Model 7B using LINGO 13 iterative scheme, we derive the solutions and calculate the value of the objective functions that are reflected in Tables 6 and 7. Since the solutions are contradict to each other and to find the overall compromise solution we solve Model 4C with the help of proposed NLP. The PIS and NIS are obtained from Tables 6 and 7 and they are denoted by $*$ and $'$, respectively.

Table 6 Pay-off matrix for ${Z'_l}^L (l=1,2,3)$

Table 7 Pay-off matrix for ${Z'_l}^U (l=1,2,3)$

Finally we design Model 8 with help of NLP to find the compromise solution of Model 2.

Model 8

$$\begin{aligned} \text{ maximize }&\theta +\xi -\zeta \\ \text{ subject } \text{ to }&{Z'}_{l}^L(x)+(U_{l}^L-L_{l}^{L})\theta \le U_{l}^L,\\&{Z'}_{l}^L(x)+(U_{l}^L-L_{l}^{L})(\xi -1)s_{1l}\le L_{l}^{L},\\&{Z'}_{l}^L(x)-(U_{l}^L-L_{l}^{L})\zeta (1-t_{1l})\le U_{l}^L,\\&{Z'}_{l}^U(x)+(U_{l}^U-L_{l}^{U})\theta \le U_{l}^U,\\&{Z'}_{l}^U(x)+(U_{l}^U-L_{l}^{U})(\xi -1)s_{2l}\le L_{l}^{U},\\&{Z'}_{l}^U(x)-(U_{l}^U-L_{l}^{U})\zeta (1-t_{2l})\le U_{l}^U,\\&\theta +\xi +\zeta \le 3,~ \theta \ge \zeta ,~\theta \ge \xi ,\\&\theta , \xi , \zeta \in [0,1], (l=1,2,3)\\&{\text{ constraints }}~(22){-}(36). \end{aligned}$$

where $U_{l}^{\text{ L }}$=NIS of $Z_{l}^{\text{ L }}$, ${L_l}^{\text{ L }}$=PIS of ${Z_l}^{\text{ L }}$; ${U_l}^{\text{ U }}$=NIS of ${Z_l}^{\text{ U }}$, ${L_l}^{\text{ U }}$=PIS of ${Z_l}^{\text{ U }}$. The solutions for Model 8 are obtained as: $\theta =1,~\xi =1,~\zeta =0.002368;~x_{122}=59.08542,~x_{211}=54.82179,~x_{212}=45.17821,~x_{221}=31.47276,~ x_{222}=29.442,$ $x_{111}=x_{112}=x_{121}=0; Z_1^L=6323.33,Z_2^L=644.26,Z_3^L=50; Z_1^U=9294.01,Z_2^U=963.53,Z_3^U=74.$

Therefore the compromise solutions of proposed Model 1 in NLP is $Z_1=[6323.33, 9294.01]$, $Z_2=[644.26, 963.53]$, $Z_3=[50, 74].$ The solutions of FP and GCM are, respectively, given as: $Z_1=[5900.82, 9482.29],$ $Z_2=[719.97, 1048.82]$, $Z_3=[58, 84]$; and $Z_1=[5906.9,11941.13], Z_2=[720.49, 1056.57], Z_3=[52, 74]$.

7.1 Results and discussion

Solving Model 2 with help of NLP, FP and GCM, the solutions are depicted in Sect. 7. Therefore the values of three objective functions obtained by three methods are displayed in Table 8 as:

Table 8 Solution of NLP, FP and GCM

Comparing the results that calculated from the NLP, FP and GCM, we conclude that optimal values of the objective functions ($Z_1,~Z_2,~Z_3$) that received from NLP always provides better result than FP and GCM.

From the analysis, it is very much essential to include the extra restriction on carbon capacity in the formulated problem to save the environment and to obtain maximum profit in transportation system by minimizing the total transportation cost.

The main criteria for comparing the solutions are (i) to detect a better Pareto-optimal solution, (ii) to check that either fuzzy or non-fuzzy technique is appropriate to determine the final Pareto-optimal solution in uncertain environment, (iii) to find what is the appropriateness of neutrosophic environment with NLP for multi-objective decision making problem.

8 Sensitivity analysis

To explain and interpret the effect of change to the coefficients of the objective functions, sensitivity analysis is a compulsive and concerning procedure in optimization problem. Now, it is difficult to analyze the range of all parametric values and its slide change such that the optimal value remains same. There exist some research papers on sensitive analysis about transportation problem with linear programming. Whenever there exist large change of variables and constraints, then a complexity arises such that the values of basic variables are changed. To tackle these complexity, we introduce sensitivity analysis of MFSTP with NLP such that all the basic variables remain fixed. Now to find the ranges of these parameters in neutrosophic MFSTP, we define the steps as follows:

• Step 8.1: Taking all the basic variables as fixed for the optimal solution of MFSTP.

• Step 8.2: Change the values of each parameter at a time with fixing other parameters and solve the MFSTP by LINGO 13 iterative scheme.

• Step 8.3: Continue Step 8.2, until change the basic variable or no feasible solution arises in optimal solution.

• Step 8.4: Find the range of each parameter in Step 8.3. Sensitivity analysis for supply, demand and conveyance parameters changes as: Let $a_i$ change to $a_i^*$ as $a_i^*=a_i+{\gamma }_i, (i=1,2)$, $b_j$ change to $b_j^*$ as $b_j^*=b_j+{\eta }_j, (j=1,2)$ and $e_k$ change to $e_k^*$ as $e_k^*=e_k+{\tau }_k, (k=1,2)$. Using the described procedure, we derive the values of $a_i^*,b_j^*$, and $e_k^*$ which are shown in Table 9.

Table 9 Range of supply, demand and conveyance

9 Conclusion and future research scopes

Transportation system is always depended on various factors. Most of the common factors of transportation are time, profit, budget, deterioration, carbon emission, purchasing cost, selling price, fixed-charge, etc. Since all the data are collected from real-world application, therefore there exist some complexity, restriction and uncertainty. The aim of the transportation problem is to overcome such complexity under neutrosophic environment and to determine the compromise solution. Here we take all the data as NNs. Carbon emission is included here to save the environment and we see that this improves the profit, as well as reduces the air pollution. Three methods, namely FP, NLP and GCM, have been executed to obtain the compromise solutions by solving the MOTP. Out of which NLP has provided the best solution by maximizing the truth-membership value, the indeterminacy-membership value and minimizing falsity-membership value. The method is very simple, suitable and applicable for multi-objective decision making problem. Fuzzy set and IFS only find the uncertainty with membership and non-membership value, but neutrosophic system adds an extra important aspect as indeterminacy membership value which is independent on membership and non-membership values. Therefore neutrosophic system is more reliable than fuzzy system or IFS for clearly defining the incomplete and indeterminate information on real-life problems. The applicability of the proposed approach has been clarified through a real-life example. Moreover, the stable ranges of some parameters have been revealed by the sensitivity analysis. Finally, some decisions regarding the budget and carbon emission during transportation have been discussed which can be very helpful to organizations or companies for resolving the economical and environmental issues.

In future scope of research, neutrosophic system can be extended as bipolar-neutrosophic system and can be applied for linear or nonlinear problem. Also carbon emission system will be taken as cap and trade policy with neutrosophic number. Neutrosophic programming with neutrosophic number can be applied in fractional problem or multi-item transportation. Different uncertainties such as type-2 neutrosophic, type-2 uncertain variable, uncertain-random, type-2 intuitionistic fuzzy, Pythagorean fuzzy or Pythagorean hesitant fuzzy (Ghosh et al. 2022) can be developed in the proposed model. Furthermore, several heuristics, meta-heuristics and hybrid methods can be developed to solve the large instances of our proposed problem.