1 Introduction

The traditional mean variance method, which was proposed by Markowitz (1952), is the foundation of the modern portfolio theory. After that, a number of methods were proposed to find efficient portfolio such as Gao and Li (2013), Macedo et al. (2017), Al Janabi et al. (2017), Liagkouras and Metaxiotis (2017)and so on. The basic assumption for using portfolio model within a probabilistic framework is that the situation of financial markets in future can be correctly reflected by security data in the past. If there are not enough data for the practical problem, these models will be invalid. Because of lack of data in an emerging financial market, the parameters or probability distributions of random returns are difficult to be accurately estimated.

However, these quantities can be provided by the experts based on their past information and subjective belief. In other words, security returns may be considered as fuzzy variables instead of random variables when there is lack of data. The fuzzy set is a powerful tool used to describe an uncertain financial environment where not only the financial markets but also the investment decision-makers are subject to vagueness, ambiguity or fuzziness. Possibility theory has been proposed in Zadeh (1978), where fuzzy variables are associated with possibility distributions. Recently, a number of researchers have investigated fuzzy portfolio selection problem, such as Zhang et al. (2009), Qin et al. (2009), Zhang and Zhang (2014), and Kar et al. (2018). But the possibility measure is not self-dual. Credibility theory has been newly proposed in Liu (2002a). As the average of a possibility measure and a necessity measure, the credibility measure is self-dual. In this respect, the credibility measure shares some properties with the probability measure. Recently, a number of researchers have investigated credibilitic portfolio selection problem, such as Zhang et al. (2010), Mehlawat and Gupta (2014), Jalota et al. (2017), and Deng et al. (2018).

Actually, the investors may encounter uncertainty of both randomness and fuzziness simultaneously when handling the practical portfolio selection problem. Random and credibilitic optimization models provide useful methods for investors to handle uncertainty. For example, the probability distributions of security returns may be partially known. Therefore, the uncertain parameters may be estimated by experts on the basis of available data, which implies that security returns may be characterized by random credibilitic variables. Random credibilitic variable was a recently introduced variable by Liu (2002b) to describe a random fuzzy phenomenon. After that, several authors have also applied random credibilitic variable to model portfolio optimization, such as Hasuike et al. (2009), Huang (2007a, b), Liu et al. (2011), Qin (2017),Wang et al. (2017), Dutta et al. (2018).

To the best of the author’s knowledge, at present, there is little research in modeling and solving random credibilitic portfolio selection problem with different convex transaction costs. This stimulates the authors to employ the latest development of mathematics on uncertainty theory to study the portfolio selection problem in random credibilitic environment. The contribution of this work is as follows. We propose a new mean variance random credibilitic portfolio selection model with different convex transaction costs. Using the random credibilitic decision-making approach, the proposed model is transformed into a crisp convex programming problem. Three algorithms are designed to obtain the optimal portfolio strategy.

The rest of the paper is organized as follows. In Sect. 2, necessary knowledge about credibilitic variable, random credibilitic variable, and some properties will be briefly introduced. In Sect. 3, we propose a new mean variance random credibilitic portfolio selection model with three types of convex transaction costs functions, i.e., linear function, non-smooth convex function, and smooth function. Using the random credibilitic theory, the proposed model is turned into a crisp convex programming problem. A novel pivoting algorithm, a branch-and-bound algorithm, and a sequence quadratic programming are proposed to solve the proposed models with different convex transaction costs in Sect. 4. Numerical examples are presented in Sect. 5 to help understanding the modeling idea and the designed algorithm. Finally, some conclusions are given in Sect. 6.

2 Preliminaries

Some definitions, which are needed in the following section, will be introduced herein.

Definition 1

(Liu (2002a)). Let Θ be a nonempty set and P the power set of Θ. A set function Cr on P is called credibility measure if it satisfies:

  1. (1)

    (Normality) Cr{Θ} = 1;

  2. (2)

    (Monotonicity) Cr{A} ≤ Cr{B} whenever A ⊂ B;

  3. (3)

    (Self-duality) Cr{A} + Cr{Ac} = 1 for any A∈P;

  4. (4)

    (Maximality) \( Cr\{ \cup_{i} A_{i} \} = \sup_{i} Cr\{ A_{i} \} \) for any sequence {Ai} ⊂ P with \( \sup_{i} Cr\{ A_{i} \} < 0.5 \). The triplet (Θ, P, Cr) is called a credibility space.

Let ξ be a fuzzy variable with membership function μ. For any x∈ ℜ, μ (x) represents the possibility that ξ takes value x. Hence, it is also called the possibility distribution. For any set B, the possibility measure and necessity measure of ξ ∈ B were, respectively, defined by Zadeh (1978) as

$$ {\text{Pos}}\{ \xi \in B\} = \mathop {\sup }\limits_{x \in B} \mu (x) $$
(1)
$$ {\text{Nec}}\{ \xi \in B\} = 1 - \mathop {\sup }\limits_{{x \in B^{c} }} \mu (x) $$
(2)

It is proved that both possibility measure and necessity measure satisfy the properties of normality, nonnegativity, and monotonicity. However, neither of them is self-dual. Since the self-duality is intuitive and important in real problems, Liu (2002a, b) defined a credibility measure as the average of possibility measure and necessity measure

$$ Cr\{ \xi \in B\} = \frac{1}{2}\left[ {\mathop {\sup }\limits_{x \in B} \mu (x) + 1 - \mathop {\sup }\limits_{{x \in B^{c} }} \mu (x)} \right] $$
(3)

where Cr is self-dual measure and satisfies \( Cr\left\{ {\xi \le r} \right\} + Cr\left\{ {\xi \ge r} \right\} \, = \, 1 \).

Definition 2

(Liu (2002a)). Let ξ be a credibilitic variable. Then, the expected value is defined as

$$ E[\xi ] = \int_{0}^{\infty } {Cr\{ \xi \ge r\} } {\text{d}}r - \int_{ - \infty }^{0} {Cr\{ \xi \le r\} } {\text{d}}r $$
(4)

Based on Definition 2, Liu (2002a) deduced the following two theorems.

Theorem 1

(Liu (2002a)). Let ξ be a credibilitic variable with finite expected value. Then, for any real numbers λ and μ, it holds that

$$ E(\lambda \xi + \mu ) = \lambda E(\xi ) + \mu $$
(5)

Theorem 2

(Liu (2002a)) Let ξ and η be independent credibilitic variables with finite expected values. Then, for any real numbers λ and μ, it holds that

$$ E\left( {\lambda \xi + \mu \eta } \right) = \lambda E\left( \xi \right) + \mu E\left( \eta \right) $$
(6)

A popular credibilitic number is the trapezoidal credibilitic number ξ = (a, b, α, β) with membership function μξ(x) in the following form

$$ \mu_{\xi } (x) = \left\{ {\begin{array}{*{20}l} {\frac{x - (a - \alpha )}{c},} \hfill & {x \in [a - \alpha ,a]} \hfill \\ {1,} \hfill & {x \in [a,b]} \hfill \\ {\frac{b + \beta - x}{\beta },} \hfill & {x \in [b,b + \beta ]} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(7)

where α and β are positive numbers, i.e., α, β > 0.

From Eq. (3), the credibility of the event {ξ ≤ r} is as follows:

$$ Cr\{ \xi \le r\} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if }}r \ge b + \beta } \hfill \\ {\frac{r - b + \beta }{2\beta },} \hfill & {ifb \le r \le b + \beta } \hfill \\ {\frac{1}{2},} \hfill & {{\text{if }}a \le r \le b} \hfill \\ {\frac{r - a + \alpha }{2\alpha },} \hfill & {ifa - \alpha \le r \le a} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(8)

Theorem 3

Let ξ be a the trapezoidal credibilitic number ξ = (a, b, α, β) with membership function μ ξ (x). Then,

$$ E(\xi ) = \frac{a + b}{ 2} + \frac{\beta - \alpha }{4} $$
(9)

Proof

Because the credibility measure is self-dual measure, according to Eq. (8), we can obtain the following:

$$ Cr\{ \xi \ge r\} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}}\;r \ge b + \beta } \hfill \\ {\frac{b + \beta - r}{2\beta },} \hfill & {{\text{if}}\;b \le r \le b + \beta } \hfill \\ {\frac{1}{2},} \hfill & {{\text{if}}\;a \le r \le b} \hfill \\ {\frac{a + \alpha - r}{2\alpha },} \hfill & {{\text{if}}\;a - \alpha \le r \le a} \hfill \\ {1,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(10)

According to Definition 2, we can obtain as follows:

$$ \begin{aligned} E[\xi ] & = \int_{0}^{\infty } {Cr\{ \xi \ge r\} dr} - \int_{ - \infty }^{0} {Cr\{ \xi \le r\} dr} \\ & = \int_{0}^{a - \alpha } {1dr} + \int_{a - \alpha }^{a} {\frac{a + \alpha - r}{2\alpha }dr} + \int_{a}^{b} {\frac{1}{2}dr} + \int_{b}^{b + \beta } {\frac{b + \beta - r}{2\beta }dr} + \int_{b + \beta }^{ + \infty } {0dr} \\ & = r\left| {_{0}^{a - \alpha } } \right. + \frac{a + \alpha }{2\alpha }r\left| {_{a - \alpha }^{a} } \right. - \frac{1}{2\alpha }\frac{{r^{2} }}{2}\left| {_{a - \alpha }^{a} } \right. + \frac{1}{2}r\left| {_{a}^{b} } \right. + \frac{b + \beta }{2\beta }r\left| {_{b}^{b + \beta } } \right. - \frac{1}{2\beta }\frac{{r^{2} }}{2}\left| {_{b}^{b + \beta } } \right. + 0 \\ & = a - \alpha + \frac{a + \alpha }{2} - \frac{a}{2} + \frac{\alpha }{4} + \frac{b - a}{2} + \frac{b + \beta }{2} - \frac{b}{2} - \frac{\beta }{4} \\ & = \frac{a + b}{2} + \frac{\beta - \alpha }{4}. \\ \end{aligned} $$

Thus, the proof of Theorem 3 is ended.

Until now, there are many studies of portfolio selection problems whose future returns are assumed to be random variables or fuzzy numbers. However, since few studies of them are treated as random credibilitic variables, we introduce a random credibilitic variables defined by Liu (2002b) as follows.

Definition 3

(Liu (2002b)). A random credibilitic variable is a function ξ from a credibility space(Θ, Cr(Θ), Cr) to collection of random variables R. An n-dimensional random credibilitic vector ξ = (ξ1, ξ2,…, ξn) is an n-tuple of random credibilitic variables ξ1, ξ2,…, ξn.

That is, a random credibilitic variable is a fuzzy set defined on a universal set of random variables. Furthermore, the following random credibilitic definition is introduced.

Definition 4

(Liu (2002b)). Let ξ1, ξ2,…, ξn be random credibilitic variables, and f: Rn → R be a continuous function. Then, ξ = f (ξ1, ξ2,…, ξn) is a random credibilitic variable on the product credibility space(Θ, Cr(Θ), Cr), defined as

$$ x(\theta_{1} ,\theta_{2} , \, . \, . \, . \, ,\theta q_{n} ) \, = f(\xi_{1} (\theta_{1} ), \xi_{2} (\theta_{2} ), \, . \, . \, . \, ,\xi_{n} (\theta_{n} )) $$

for all(θ1, θ2,…, θn) ∈Θ.

From these definitions, the following theorem is derived.

Theorem 4

(Liu (2002b)). Let ξibe random credibilitic variables with membership functions μi, i = 1, 2,…, n, respectively, and f: Rn → R be a continuous function. Then, ξ = f (ξ1, ξ2,…, ξn) is a random credibilitic variable whose membership function is

$$ \mu (\eta ) = \mathop {\sup }\limits_{{\eta_{i} \in R_{i} ,1 \le i \le n}} \left\{ {\mathop {\hbox{min} }\limits_{1 \le i \le n} \mu_{i} (\eta_{i} )\left| {\eta = f(\eta_{1} ,\eta_{2} , \cdots ,\eta_{n} )} \right.} \right\} $$

for all η∈ R, where R = {f (η1, η2,…, ηn)| ηi∈Ri, i = 1, 2,…, n}.

Definition 5

Let ξ be a random credibilitic variable with finite mean value e. Then, the variance of ξ is defined by

$$ \sigma^{ 2} [\xi ] = E[(\xi - e)^{2} ] $$
(11)

3 The random fuzzy portfolio selection model

Assume that there are n risky assets in financial market for trading. An investor wants to allocate his/her wealth among n assets. Then, an optimal portfolio should be the one with minimized variance for the given expected return level. Suppose that the return rates of the n risky assets at each period are denoted as trapezoidal credibilitic variables. Let w be the portfolio, where w = (w1,w2,…,wn)′; \( \widetilde{{R_{i} }} \) be the random credibilitic return of risky asset i; rp be the excepted return rate of the portfolio w; σ2 be the variance of the portfolio w, where σ2 = (σij)n×n, σij = Cov(Ri,Rj); c(w) be the transaction cost of the portfolio w; rN be the net return rate of the portfolio w.

3.1 Return, risk, and transaction costs constraints

In this section, we employ the credibilitic mean value to measure the return of portfolio. The risk on the return rate of portfolio is quantified by the random variance. The return rate of security i, \( \widetilde{{R_{i} }} \) = (ai,bi,αi, βi), is trapezoidal random credibilitic variable for all i = 1,…,n.

The credibilitic value of the portfolio w = (w1, w2, …, wn)′ can be expressed as

$$ r_{p} = \sum\limits_{i = 1}^{n} {\widetilde{{R_{i} }}w_{i} } $$
(12)

Let \( \widetilde{{R_{i} }} \) be trapezoidal credibilitic variable for all i = 1,…,n, \( \widetilde{{R_{i} }} \) = (ai,bi,αi, βi). The mean value of the portfolio w = (w1, w2, …, wn)′ can be expressed as

$$ r_{p} = \sum\limits_{i = 1}^{n} {\overline{M} (\widetilde{{R_{i} }})w_{i} } = \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)} w_{i} $$
(13)

Transaction cost is one of the main concerns for portfolio managers. Arnott and Wagner (1990) and Yoshimoto (1996) found that ignoring transaction costs would result in an inefficient portfolio. Bertsimas and Pachamanova (2008), Gülpınar et al. (2003), and Zhang (2016, 2017) incorporated transaction cost into the multiperiod portfolio selection problem. In this paper, the transaction cost for asset i can be expressed as ci(wi). Hence, the total transaction costs of the portfolio w = (w1, w2,…, wn)′ can be represented as C(w)

$$ C(w) = \sum\limits_{i = 1}^{n} {c_{i} (w_{i} )} $$
(14)

The net return rate of the portfolio w can be denoted as

$$ r_{N} = \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} } - \sum\limits_{i = 1}^{n} {c_{i} (w_{i} )} $$
(15)

The variance of the portfolio w can be expressed as

$$ V(w) = w^{'} \sigma^{2} w $$
(16)

where w = (w1, w2, …, wn)′, σ2 = (σij)n×n, σij = Cov(Ri,Rj).

The capital constraint of risky assets is

$$ w_{1} + w_{2} + \cdots + w_{n} = 1 $$
(17)

3.2 The basic multiperiod portfolio optimization models

Let \( \widetilde{{R_{i} }} \) be expressed with a fuzzy set and r0 be a minimum target value of the total future profit. We formally introduce the following mean–variance model:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\widetilde{{R_{i} }}w_{i} } - \sum\limits_{i = 1}^{n} {c_{i} (w_{i} )} \ge r_{0} } \hfill & {({\text{a}})} \hfill \\ {w_{1} + w_{2} + \cdots + w_{n} { = 1}} \hfill & { ( {\text{b)}}} \hfill \\ {w_{i} \ge 0,\;\;i = 1, \ldots ,n} \hfill & { ( {\text{c)}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(18)

where constraint (a) denotes that the return of the portfolio is not less than the preset value r0; constraint (b) indicates that the proportion of risk assets sums to one; and constraint (c) states the nonnegative constraints of wi.

Model (18) is a fuzzy optimization problem. Let \( \widetilde{{R_{i} }} \) = (ai,bi,αi, βi). Using the random credibilitic theory, the proposed Model (18) can be turned into as

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - \sum\limits_{i = 1}^{n} {c_{i} (w_{i} )} \ge r_{0} } } \hfill \\ {w_{1} + w_{2} + \cdots + w_{n} = 1} \hfill \\ {w_{i} \ge 0,i = 1, \ldots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(19)

If the covariance matrix σ2 is semi-definite, and C(w1,w2,…,wn) is linear function, Model (19) is a convex quadratic programming problem, which can be solved by Algorithm 1. If the covariance matrix σ2 is semi-definite, and C(w) is non-smooth or smooth convex function, Model (19) is a convex programming problem, which can be solved by Algorithm 2 or Algorithm 3.

4 Solution algorithm

In this section, the smallest and biggest value of r0 can be obtained. Several methods will be proposed to solve the problems with the different transaction costs.

4.1 The smallest and biggest value of r 0

In Model (19), investors can choose r0 between \( r_{0}^{ \hbox{min} } \) and \( r_{0}^{\hbox{max} } \). \( r_{0}^{ \hbox{min} } \) and \( r_{0}^{\hbox{max} } \) can be, respectively, obtained as follows:

The investor considers to maximize the expected return of the portfolio

$$ \begin{aligned} & \hbox{max} \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - \sum\limits_{i = 1}^{n} {c_{i} (w_{i} )} } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {w_{1} + w_{2} + \cdots + w_{n} = 1 \, } \hfill \\ {w_{i} \ge 0,\;\;i = 1, \ldots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(20)

w* (the optimal solution w = (w1, w2,…, wn)′) can be obtained solving Model (20) by the following algorithms. The biggest of objective (\( r_{N}^{\hbox{max} } = \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)} w_{i}^{*} - \sum\limits_{i = 1}^{n} {c_{i} (w_{i}^{*} )} \)) can be obtained, i.e., \( r_{0}^{ \hbox{max} } = r_{N}^{ \hbox{max} } \).

The smallest value of the \( r_{0}^{ \hbox{min} } \) can be obtained as follows:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {w_{1} + w_{2} + \cdots + w_{n} = 1 \, } \hfill \\ {w_{i} \ge 0,\;\;i = 1, \ldots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(21)

w* (the optimal solution w = (w1, w2,…, wn)′) can be obtained solving Model (21) by Algorithm 1. Simultaneously, \( r_{N}^{ \hbox{min} } \) (the smallest of \( r_{N}^{\hbox{min} } = \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)} w_{i}^{*} - \sum\limits_{i = 1}^{n} {c_{i} (w_{i}^{*} )} \)) is obtained, i.e., \( r_{0}^{ \hbox{min} } = r_{N}^{ \hbox{min} } \).

4.2 Several methods for the problems with different transaction costs

In this section, we will present several methods for the random credibilitic mean variance portfolio selection models with different types of transaction costs, i.e., linear function, non-smooth convex functions, and smooth functions

4.2.1 The transaction cost is linear function

In Model (19), let the transaction costs be linear functions, i.e., ci(wi) = kiwi, and Model (19) can be obtained as follows:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{ 4} - k_{i} } \right)} w_{i} \ge r_{0} } \hfill \\ {w_{1} + w_{2} + \cdots + w_{n} = 1} \hfill \\ {w_{i} \ge 0,i = 1, \ldots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(22)

Let μ1 and μ2 be the Lagrange multiplier. The KKT conditions for Model (22) are as follows:

$$ \left\{ {\begin{array}{*{20}l} {\sigma_{i1} w_{1} + \cdots + \sigma_{in} w_{n} - \mu_{1} \left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4} - k_{i} } \right) + \mu_{2} \ge 0 \, i = 1, \ldots ,n} \hfill \\ {\left( {\frac{{a_{1} + b_{1} }}{2} + \frac{{\beta_{1} - \alpha_{1} }}{4} - k_{1} } \right)w_{1} + \cdots + \left( {\frac{{a_{n} + b_{n} }}{2} + \frac{{\beta_{n} - \alpha_{n} }}{4} - k_{n} } \right)w_{n} \ge r_{0} } \hfill \\ {w_{1} + w_{2} + \cdots + w_{n} = 1} \hfill \\ {w_{i} \ge 0,i = 1, \ldots ,n,\mu_{1} \ge 0} \hfill \\ {\left[ {\left( {\frac{{a_{1} + b_{1} }}{2} + \frac{{\beta_{1} - \alpha_{1} }}{4} - k_{1} } \right)w_{1} + \cdots + \left( {\frac{{a_{n} + b_{n} }}{2} + \frac{{\beta_{n} - \alpha_{n} }}{4} - k_{n} } \right)w_{n} - r_{0} } \right]\mu_{1} = 0} \hfill \\ {\left[ {\sigma_{i1} w_{1} + \cdots + \sigma_{in} w_{n} - \mu_{1} \left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4} - k_{i} } \right) + \mu_{2} } \right]w_{i} = 0} \hfill \\ \end{array} } \right. $$
(23)

where the KKT conditions of Model (22) are a system of equalities where all the expressions are linear equalities or inequalities except for complementarity conditions, and there are n + 2 variables and 2n + 4 linear equalities or inequalities in Eq. (23).

Algorithm 1. The pivoting algorithm for Eq. (23).

Step 1 Construct initial table.

Let w 3 i 0, i = 1,2,…,n, μ 31 0, μ 32 0 be the initial basic inequality. The initial basic solution is x0 = (0,…,0,0,0)′. The initial basic vector is ei, i = 1, 2,…, n + 2, which is the ith row of the identity matrix of order n + 2. Other equalities and inequalities of Eq. (23) and their coefficient vectors are non-basic gi.

Let \( d_{i} = \frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4} - k_{i} \), \( q = (0, \ldots ,0,r_{0} ,1)' \); \( g_{i} = (\sigma_{i1} ,\sigma_{i2} , \ldots ,\sigma_{in} , - d_{i} ,1) \), i = 1,2,…,n; \( g_{n + 1} = (d_{1} , \ldots ,d_{n} ,0,0) \); \( g_{n + 2} = (1, \ldots ,1,0,0) \)

The deviation with respect to x0 is Δ = gx0 − q. Thus, we have an initial table as shown in Table 1.

Table 1 Initial table
Full size table

Step 2 Preprocessing.

Let I3 be the index set of equalities, i.e., I3 = {n + 2}, I4 be the index set of inequalities, i.e., I4 = {1,2,…,n,n + 1}. Select a non-basic vector gn+2 to enter the basis, and the basic vector e1 leaves the basis. Select a non-basic vector g1 to enter the basis, and the basic vector en+2 leaves the basis. Then, carry out two pivoting on the positive elements 1. Then, delete the column of gn+2 and the row of en+2. The calculating process is as follows:

$$ g_{{\mathbf{1}}} = g_{{{\mathbf{11}}}} e_{{\mathbf{1}}} + g_{{{\mathbf{12}}}} e_{{\mathbf{2}}} + \cdots + g_{{{\mathbf{1}}n}} e_{n} + g_{{{\mathbf{1}}n + {\mathbf{1}}}} e_{{n + {\mathbf{1}}}} + g_{{{\mathbf{1}}n + {\mathbf{2}}}} e_{{n + {\mathbf{2}}}} ,i = {\mathbf{1}}, \ldots {\mathbf{3}}n + {\mathbf{2}} $$
(24)

According to Eq. (24), we can obtain Eq. (25).

$$ e_{n + 2} = \frac{1}{{a_{rn + 2} }}g_{1} + \sum\limits_{j = 1,j \ne n + 2}^{n + 2} {\left( { - \frac{{a_{1j} }}{{a_{1n + 2} }}} \right)e_{j} } $$
(25)

Substituted Eq. (25) into Eq. (24), we can get Eq. (26).

$$ g_{i} = \frac{{a_{in + 2} }}{{a_{1n + 2} }}g_{1} + \sum\limits_{j = 1,j \ne n + 2}^{n + 2} {\left( {a_{ij} - \frac{{a_{in + 2} }}{{a_{1n + 2} }}a_{1j} } \right)e_{j} } ,i = {\mathbf{1}}, \ldots ,n,n + {\mathbf{1}},n + {\mathbf{2}} $$
(26)

Using the same method, we obtain the following pivoting operation: gn+2 ↔ e1.

Step 3 Main iterations.

  1. (1)

    If all of the deviations of non-basic vectors are nonnegative, the current basic solution is a solution to Eq. (23).

  2. (2)

    Otherwise, select a non-basic vector gr with negative deviation to enter the basis. If there is no positive element in the row of entering vector that is corresponding to the basic inequality, Eq. (23) has no solution. If there is the biggest positive element grs in the row of entering vector, the basic vector of the sth column corresponding to grs leaves the basis. Then, carry out a pivoting operation: gr↔es. After that, return to Step 3. (1).

4.2.2 The transaction cost is non-smooth convex functions

Let the transaction costs be non-smooth convex functions; the random credibilitic portfolio selection model is:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} } - \sum\limits_{i = 1}^{n} {c_{i} (w_{i} )} \ge r_{0} } \hfill \\ {w_{1} + w_{2} + \cdots + w_{n} = 1} \hfill \\ {0 \le w_{i} \le u_{i} ,i = 1, \ldots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(27)

Model (27) is a non-smooth convex quadratic programming problem.

If ci(wi) is a non-smooth convex function, \( \sum\nolimits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} } - \sum\nolimits_{i = 1}^{n} {c_{i} (w_{i} )} \) is concave function. So, Model (27) is a non-smooth convex programming problem. We propose a branch-and-bound method and a pivoting algorithm to solve Model (27). Let the function of OB be ci(wi) = kiwi, where ki = ci(ui)/ui. When ci(wi) is substituted by kixi, Model (27) can be turned into as follows:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ \begin{aligned} \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - \sum\limits_{i = 1}^{n} {k_{i} w_{i} } \ge r_{0} } \hfill \\ w_{1} + w_{2} + \cdots + w_{n} = 1,0 \le w_{i} \le u_{i} ,i = 1, \ldots ,n \hfill \\ \end{aligned} \right. \\ \end{aligned} $$
(28)

Theorem 5

Let w0be the optimal solution of Model (28). Then, w0is the feasible solution of Model (27).

Proof

If x0 is the optimal solution of Model (28), we can get the following equation:

$$ \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i}^{0} } - \sum\limits_{i = 1}^{n} {k_{i} w_{i}^{0} } \ge r_{0} $$
(29)

Because ci(wi) is a non-smooth convex function, we can obtain the following equation:

$$ k_{i} w_{i}^{0} \ge c_{i} \left( {w_{i}^{0} } \right) $$
(30)

According to Eq. (29) and Eq. (30), we can get

$$ \sum\limits_{i = 1}^{n} {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i}^{0} } - \sum\limits_{i = 1}^{n} {c_{i} (w_{i}^{0} )} \ge r_{0} $$

So, w 0 i is the feasible solution of Model (27).

Thus, the proof of Theorem 5 is ended.

Theorem 6

Let w0and g(w0), respectively, be the optimal solution and the optimal objective function value of Model (28), w*and f(w*), respectively, be the optimal solution and the optimal objective function value of Model (27), f(w0) be the objective function value of the feasible solution w0of Model (27). Then,

$$ g\left( {w^{0} } \right) \le f\left( {w^{*} } \right) \le f\left( {w^{0} } \right) $$
(31)

Proof

According to Theorem 5, we can obtain that w0 is the feasible solution of Model (27). Because w* is the optimal solution of Model (27), we can get that

$$ f\left( {w^{*} } \right) \le f\left( {w^{0} } \right) $$
(32)

According to Fig. 1, we can obtain that

Fig. 1
figure 1

Non-smooth convex function

Full size image
$$ k_{i} w_{i} \ge c_{i} \left( {w_{i} } \right) $$
(33)

According to Eq. (33), we can obtain that

$$ \sum\limits_{i = 1}^{n} {[r_{i} w_{i} - c_{i} (w_{i} )]} \ge \sum\limits_{i = 1}^{n} {(r_{i} w_{i} - k_{i} w_{i} )} \ge r_{0} $$
(34)

According to Eq. (34), we can obtain that w* is the feasible solution of Model (28), i.e.,

$$ g\left( {w^{0} } \right) \le g\left( {w^{*} } \right). $$
(35)

Because the objective functions of Model (27) and Model (28) are same, we can get that

$$ g\left( {w^{*} } \right) \le f\left( {w^{*} } \right). $$
(36)

According to Eqs. (32), (35), and (36), we can obtain that

$$ g\left( {w^{0} } \right) \le f\left( {w^{*} } \right) \le f\left( {w^{0} } \right). $$

Thus, the proof of Theorem 6 is ended.

From Eq. (36), we can obtain that there are upper and lower bounds on the optimal objective function value of Model (28).

Definition 6

Let w0 be the optimal solution of Model (28), and

$$ \sum\limits_{i = 1}^{n} {(k_{i} w_{i}^{0} - c_{i} (w_{i}^{0} ))} \le \varepsilon ,e = 10^{ - 6} . $$
(37)

Then, w0 is almost the optimal solution of Model (27).

If there is an optimal solution of Model (28) w0, which cannot satisfy Eq. (37), then let

$$ k_{s} w_{s}^{0} - c_{s} \left( {w_{s}^{0} } \right) = \hbox{max} \{ k_{i} w_{i}^{0} - c_{i} \left( {w_{i}^{0} } \right)|i = 1, \ldots ,n\} $$
(38)
$$ W^{1} = \{ x|0 \le w_{s} \le u_{s} /2, \, 0 \le w_{j} \le u_{j} ,j \ne s\} $$
(39)
$$ W^{2} = \{ x|u_{s} /2 \le w_{s} \le u_{s} , \, 0 \le w_{j} \le u_{j} ,j \ne s\} . $$
(40)

Model (27) can be turned into the following two models:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - c_{i} \left( {w_{i} } \right)} \right] \ge r_{0} } } \hfill \\ {e^{T} w = 1} \hfill \\ {w \in X_{1} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(41)

and

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - c_{i} \left( {w_{i} } \right)} \right] \ge r_{0} } } \hfill \\ {e^{T} w = 1} \hfill \\ {w \in X_{2} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(42)

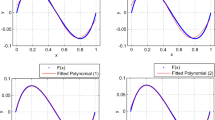
Let cs(ws) be substituted by two piecewise linear function. The function of cs(xs) can be denoted as in Fig. 2.

Fig. 2
figure 2

cs(ws) substituted by two piecewise linear functions

Full size image

In Fig. 2, the linear OA is ks1 (ws1), in which the slope of OA is cs(us/2)/(us/2), and the linear AB is ks2(ws2), in which the slope of AB is ks2 = (cs(as) − cs(as/2))/(as/2).

Model (28) can be turned into the two following models:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1,i \ne s}^{n} {(r_{i} w_{i} - k_{i} } w_{i} ) + (r_{s} w_{s} - k_{s1} (w_{s1} )) \ge r_{0} } \hfill \\ {e^{T} w = 1} \hfill \\ {w \in X_{1} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(43)
$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1,i \ne s}^{n} {(r_{i} w_{i} - k_{i} w_{i} ) + (r_{x} w_{s} - k_{s2} (w_{s2} ))} \ge r_{0} } \hfill \\ {e^{T} w = 1} \hfill \\ {w \in X_{2} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(44)

Definition 7

Let w1 and w2 be, respectively, the optimal solution of Model (43) and Model (44). If \( \sum\limits_{i = 1}^{n} {\left( {k_{i} w_{i}^{1} - c_{i} (w_{i}^{1} )} \right)} \le \varepsilon \) or \( \sum\limits_{i = 1}^{n} {\left( {k_{i} w_{i}^{2} - c_{i} (w_{i}^{2} )} \right)} \le \varepsilon \), then x1 or x2 is the optimal solution of Model (27).

Algorithm 2. The branch-and-bound algorithm for Model (27)

Step 1 Let k = 0, l 0 i  = 0, \( u_{i}^{0} = u_{i} ,w_{i}^{0} = \{ w_{i} |l_{i}^{0} \le w_{i} \le u_{i}^{0} \} . \)

Step 2 Let k j i (wi) be the approximate linear function of ci(wi). We can obtain the optimal solution of the following model by Algorithm 1.

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - k_{i}^{j} (w_{i} )} \right]} \ge r_{0} } \hfill \\ {e^{T} w = 1} \hfill \\ {w \in W^{j} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(45)

where the optimal solution of Model (45) is Wj = (w j1 ,…,w j n ).

Step 3 If \( \sum\limits_{i = 1}^{n} {(k_{i}^{j} (w_{i}^{j} ) - c_{i} (w_{i}^{j} ))} \le \varepsilon \), \( W^{j} = \left( {w_{1}^{j} , \ldots ,w_{n}^{j} } \right) \) is the optimal solution of Model (27). Otherwise, \( k_{s}^{j} \left( {w_{s}^{j} } \right) - c_{s}^{j} \left( {w_{s}^{j} } \right) = \hbox{max} \{ k_{i}^{j} \left( {w_{i}^{j} } \right) - c_{i}^{j} \left( {w_{i}^{j} } \right)|i = 1, \ldots ,n\} \), \( W^{j + 1} = \{ l_{s}^{j} \le w_{s} \le (u_{s}^{j} + l_{s}^{j)} )/2,w \in W^{j} |w_{i} \ne w_{s} \} \), \( W^{j + 2} = \{ (u_{s}^{j} + l_{s}^{j)} )/2 \le w_{s} \le u_{s}^{j} ,x \in X^{j} |w_{i} \ne w_{s} \} \), turn Step 2.

4.2.3 The transaction cost is smooth convex functions

Let the transaction costs be smooth convex functions. The function can be denoted as in Fig. 3.

Fig. 3
figure 3

Smooth convex function

Full size image

The random credibilitic portfolio selection with smooth convex transaction costs is as follows:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - c_{i} (w_{i} )} \right]} \ge r_{0} } \hfill \\ {e^{T} w = 1,w_{i} \ge 0\begin{array}{*{20}c} , & {i = 1, \ldots ,n} \\ \end{array} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(46)

If ci(xi) is a convex function, \( \sum\nolimits_{i = 1}^{n} {[r_{i} w_{i} - c_{i} (w_{i} )]} \) is a concave function. So, Model (46) is a smooth convex programming problem.

Algorithm 3. A sequence quadratic programming algorithm for Model (46)

We propose a sequence quadratic programming and a pivoting algorithm to solve Model (46).

Step 1 Let w0 = (1/n, …, 1/n)T, ci(wi) be approximated as gi(wi) = ci(w 0 i ) + ci′ (w 0 i )(wi − w 0 i ). The subproblem of Model (46) can be obtained as follows:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - \left( {c_{i} (w_{i}^{ 0} ) + c_{i}^{'} (w_{i}^{ 0} )(w_{i} - w_{i}^{ 0} } \right)} \right]} \ge r_{0} } \hfill \\ {e^{T} w = 1} \hfill \\ {w_{i} \ge 0\begin{array}{*{20}c} , & {i = 1, \cdots ,n} \\ \end{array} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(47)

The optimal solution of Model (47) w* can be obtained by Algorithm 1. Let w1 = w*.

Step 2 Let ci(wi) be approximated as gi(wi) = ci(w k i ) + ci′ (w k i )(wi − w k i ). The subproblem of Model (46) can be obtained as follows:

$$ \begin{aligned} & \hbox{min} \, \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} w_{i} w_{j} } } \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{a_{i} + b_{i} }}{2} + \frac{{\beta_{i} - \alpha_{i} }}{4}} \right)w_{i} - \left( {c_{i} (w_{i}^{k} ) + c_{i}^{'} (w_{i}^{k} )(w_{i} - w_{i}^{k} )} \right)} \right]} \ge r_{0} } \hfill \\ {e^{T} w = 1} \hfill \\ {w_{i} \ge 0,i = 1, \cdots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(48)

The optimal solution of Model (48) w*can be obtained by Algorithm 1. Let wk+1 = w*.

Step 3 If \( \left| {w^{k + 1} - w^{k} } \right| \le \varepsilon ,\;\varepsilon = 10^{ - 6} ,\;w^{k + 1} \) is the optimal solution of Model (46). Otherwise, let wk: = wk+1. Turn to Step 2.

5 Numerical examples

In this section, three numerical examples are given to express the idea of the proposed model. Assume that an investor chooses twenty stocks from Shanghai Stock Exchange for his investment. The stocks codes are, respectively, S1 (600036), S2 (600002), S3 (600060), S4 (600362), S5 (600519), S6 (601111), S7 (601318), S8 (600900), S9 (600887), S10 (600690), S11 (6000970), S12 (600000), S13 (600009), S14 (600019), S15 (600029), S16 (600104), S17 (600315), S18 (600518), S19 (600570), and S20 (600880). He/she assumes that the returns and risk of the twenty stocks at each period are represented as trapezoidal fuzzy numbers. We collect historical data of them from April 2006 to June 2018 and set every three months as a period to handle the historical data. By using the simple estimation method in Vercher et al. (2007) to handle their historical data, the trapezoidal possibility distributions of the return rates of assets can be obtained as shown in Table 2. We use the above algorithms to obtain the optimal solution of Model (19) with the three types transaction costs. (1) When the transaction cost is linear function, we assumed that ci(wi) = 0.003wi. (2) When the transaction cost is non-smooth convex function, we assumed that \( c_{i} (w_{i} ) = \left\{ {\begin{array}{*{20}l} {0.003w_{i} ,0 \le w_{i} \le 0.5} \hfill \\ {0.004w_{i} - 0.0005,0.5 \le w_{i} \le 1} \hfill \\ \end{array} } \right. \).

Table 2 Fuzzy return rates on assets
Full size table

(3) When the transaction cost is smooth convex function, we assumed that \( c_{i} (w_{i} ) = 0.003w_{i}^{2} + 0.003w_{i} \).

The trapezoidal possibility distributions \( \widetilde{{R_{i} }} \) = (ai,bi,αi, βi) can be obtained as shown in Table 2.

The covariance matrix σ2 = (σij)n×n can be obtained as follows:

$$ \sigma_{ij} = \frac{1}{m}\sum\limits_{k = 1}^{m} {\left( {R_{ik} - \overline{M} (\widetilde{{R_{i} }})} \right)\left( {R_{jk} - \overline{M} (\widetilde{{R_{j} }})} \right)} $$

As illustrations, the following numerical examples are given to show the effectiveness of the proposed model and the algorithms. The algorithm was programmed by C++ language and run on a personal computer with Pentium Dual CPU, 4 GHz, and 8 GB RAM.

(1) When the transaction cost is linear function, we assumed that the coefficients of transaction costs are generated same for all assets, i.e., ci(wi) = 0.003wi. By using the pivoting algorithm to solve Model (20) and Model (21), we can, respectively, obtain r max0  = 0.179025, r min0  = 0.0964.

By using the pivoting algorithm to solve Model (22), the computational results are summarized in Table 2.

If r0 = 0.1, 0.12, 0.13, the optimal solution will be obtained as Table 3.

Table 3 Optimal solution when r0 = 0.1, 0.12, 0.13
Full size table

When r0 = 0.1, the optimal investment strategy at period 1 is w1 = 0.1207, w3 = 0.6370, w6 = 0.1018, w9 = 0.0984, w12 = 0.0004, w19 = 0.0324, w20 = 0.0093 and being the rest of variables equal to zero, which means investor should allocate his initial wealth on asset 1, asset 3, asset 6, asset 9, asset 12, asset 19, asset 20 and otherwise asset by the proportions of 12.07%, 63.7%, 10.18%, 9.84%, 0.04%, 3.24%, 0.93% and being the rest of variables equal to zero among the twenty stocks, respectively. From Table 3, it can be seen that the investment proportion of asset 8 will increase when the minimum target value of the total future profit r0 increases.

If r0 = 0.0964, 0.1, 0.105, 0.01,…, 0.17, 0.175, 0.179025, the variance and expected return will be obtained as given in Table 4.

Table 4 Variance and expected return when r0 = 0, 0.01,…, 0.16, 0.1671
Full size table

In Table 4, it can be seen that the standard deviation will increase when the net expected return increases.

(2) When the transaction cost is non-smooth convex function, we assumed that

\( c_{i} (w_{i} ) = \left\{ {\begin{array}{*{20}l} {0.003w_{i} ,0 \le w_{i} \le 0.5} \hfill \\ {0.004w_{i} - 0.0005,0.5 \le w_{i} \le 1} \hfill \\ \end{array} } \right. \). By using Algorithm 2 to solve Model (20) and Model (21), we can, respectively, obtain r max0  = 0.178525, r min0  = 0.096203.

By using Algorithm 2 to solve Model (27), the computational results are summarized in Table 2.

If r0 = 0.1, 0.12, 0.13, the optimal solution will be obtained as given in Table 5.

Table 5 Optimal solution when r0 = 0.1, 0.12, 0.13
Full size table

From Table 5, it can be seen that the investment proportion of asset 8 will increase when the minimum target value of the total future profit r0 increases.

If r0 = 0.096203, 0.1, 0.105, 0.01,…, 0.17, 0.175, 0.178525, the variance and expected return will be obtained as given in Table 6.

Table 6 Variance and expected return when r0 = 0, 0.01, …, 0.175, 0.178525
Full size table

In Table 6, it can be seen that the standard deviation will increase when the net expected return increases.

(3) When the transaction cost is smooth convex function, we assumed that \( c_{i} (w_{i} ) = 0.003w_{i}^{2} + 0.003w_{i} \). By using Algorithm 3 to solve Model (20) and Model (21), we can, respectively, obtain

$$ r_{0}^{\hbox{max} } = 0.1760250,\;\;r_{0}^{\hbox{min} } = 0.094818. $$

By using Algorithm 3 to solve Model (16), the corresponding results can be obtained as follows.

If r0 = 0.1, 0.12, 0.13, the optimal solution will be obtained as given in Table 7.

Table 7 Optimal solution when r0 = 0.1, 0.12, 0.13
Full size table

From Table 7, it can be seen that the investment proportion of asset 8 will increase when the minimum target value of the total future profit r0 increases.

If r0 = 0.094818, 0.1, 0.105, 0.01,…, 0.175, 0.1760250, the variance and expected return will be obtained as given in Table 8.

Table 8 Variance and expected return when r0 = 0.094818, 0.1, 0.105, 0.01,…, 0.175, 0.1760250
Full size table

In Table 8, it can be seen that the standard deviation will increase when the net expected return increases.

The computational results for these three types of transaction costs are summarized in Tables 3, 5, and 7. In general, the optimal strategies under different transaction costs are different. The change of the transaction cost has great influence on the strategy making.

In the general type of convex transaction cost function ci(wi) contains three types, i.e., linear function, non-smooth convex function, and smooth convex function. The above three types of transaction costs can be used to describe the practical situation for the transaction cost precisely.

6 Conclusions

A random credibilitic portfolio optimization model with different convex transaction costs is proposed, which can be deduced into any specific form by investors’ estimation and practical situation. We present three algorithms especially for solving the different convex transaction costs function form of portfolio selection problem. Moreover, we define three general types of transaction cost and describe the practical situation for the transaction cost precisely. The computational experiments show that different types of transaction cost have great influence on strategy making.