An improved algorithm based on deviation of the error estimation for first-order integro-differential equations

Abstract

In this paper, we study efficient asymptotically correct a posteriori error estimates for the numerical approximation of first-order Fredholm–Volterra integro-differential equations. In the first step, we find the deviation of the error for Fredholm–Volterra integro-differential equations by using defect correction principle. Then we show that for m degree piecewise polynomial collocation method, our method provides order $\mathcal {O}(h^{m+1})$ for the deviation of the error. Also we improve the piecewise polynomial collocation method by using the deviation of the error estimation. Numerical results in the last section are included to confirm the theoretical results.

1 Introduction

In this work, we study the deviation of the error estimation for the linear and nonlinear Fredholm–Volterra integro-differential equations. The first-order Fredholm–Volterra integro-differential (FVID) equation is given by the following form

$$\begin{aligned}&y^{\prime }(t)=F\big (t,y(t),z_{\mathbf {f}}[y](t),z_{\mathbf {v}}[y](t)\big ),\quad t\in I:=[a,b], \end{aligned}$$

(1.1)

$$\begin{aligned}&\alpha y(a)+\beta y(b)=r, \end{aligned}$$

(1.2)

with

$$\begin{aligned} z_{\mathbf {f}}[y](t)&:=\int ^{b}_{a}K_{\mathbf {f}}\big (t,s,y(s),y^{\prime }(s)\big )\hbox {d}s, \end{aligned}$$

(1.3)

$$\begin{aligned} z_{\mathbf {v}}[y](t)&:=\int ^{t}_{a}K_{\mathbf {v}}\big (t,s,y(s),y^{\prime }(s)\big )\hbox {d}s, \end{aligned}$$

(1.4)

where $a,b,\alpha ,\beta ,r\in R=(-\,\infty ,\infty ),\,\alpha +\beta \ne 0$ and $b>a$.

Integro-differential equations can be found in many branches of science and engineering, for example, in the electrical circuit analysis (Moura and Darwazeh 2005) and mechanical engineering (Yogi Goswami 2004; Fidlin 2005). These equations appear in the computer vision and image processing. In particular, these equations are used in the image deblurring, denoising and its regularization (Chen et al. 2016; Huang et al. 2009; Athavale and Tadmor 2011). In addition, in the pattern recognition and machine intelligence, we can see the application of these equations (Doroshenko et al. 2011). Therefore, the numerical studies for the integro-differential equations have important role in sciences and computer vision. The numerical solution based on the piecewise polynomial collocation method is studied in Hangelbroek et al. (1977), Brunner (2004), Boor and Swartz (1973). Also other methods can be found in Volk (1988), Daşcioğlu and Sezer (2005), Reutskiy (2016). In this work, improved piecewise polynomial collocation method is introduced. In the previous work (Parvaz et al. 2016), the deviation of the error estimation analysis is given for the second-order Fredholm–Volterra integro-differential equations. It is shown that for m degree piecewise polynomial collocation method, the order of deviation of the error is at least $\mathcal {O}(h^{m+1})$. In this study, the first-order Fredholm–Volterra integro-differential equations are studied. We prove that for m degree piecewise polynomial, collocation method provides $\mathcal {O}(h^{m+1})$ as the order of the deviation of the error. Then according to the defect correction and the deviation of the error, piecewise polynomial collocation method can be improved. The general studies on the structure of the defect correction principle can be found in Stetter (1978), Bohmer et al. (1984). The deviation of the error estimation analysis for boundary value problems has been given in Saboor Bagherzadeh (2011). Also the error estimation based on locally weighted defect for linear and nonlinear second-order boundary value problems can be found in Saboor Bagherzadeh (2011), Auzinger et al. (2014).

This article is organized as follows: The method is presented in Sect. 2. A complete analysis of the deviation of the error for linear and nonlinear cases is given in Sect. 3. In Sect. 4, numerical results are presented. Finally, we give a summary of the main conclusions in Sect. 5.

2 Description of the method

We define W and S as follows

$$ \begin{aligned} W&:=\{(t,y,z_{\mathbf {f}},z_{\mathbf {v}})\,|\,t\in I~ \& ~y,z_{\mathbf {f}},z_{\mathbf {v}} \in R\}, \end{aligned}$$

(2.1)

$$ \begin{aligned} S&:=\{(t,s,y,y^{\prime })\,|\,t,s \in I~ \& ~y,y^{\prime }\in R\}. \end{aligned}$$

(2.2)

In this paper, we shall assume that F and $K_l,~(l=\mathbf {f},\mathbf {v})$ are uniformly continuous in W and S, respectively. We say that $z_\mathbf {f}[y](t)$ and $z_\mathbf {v}[y](t)$ are linear if we can write

$$\begin{aligned} z_{\mathbf {f}}[y](t)&=\sum ^1_{l=0}\int ^{b}_{a}\Lambda _{l,\mathbf {f}}(t,s)y^{(l)}(s)\hbox {d}s, \end{aligned}$$

(2.3)

$$\begin{aligned} z_{\mathbf {v}}[y](t)&=\sum ^1_{l=0}\int ^{t}_{a}\Lambda _{l,\mathbf {v}}(t,s)y^{(l)}(s)\hbox {d}s. \end{aligned}$$

(2.4)

In this paper, when we study linear case we assume that $\Lambda _{l,\mathbf {f}}(t,s),~\Lambda _{l,\mathbf {v}}(t,s)~(l=0,1)$ are sufficiently smooth in $J_{\mathbf {f}}:=\{(t,s)\,|t,s \in I\}$ and $J_{\mathbf {v}}:=\{(t,s)\,|a\le s \le t\le b\}$, respectively. Also we say that F is semilinear if we can write $F(t,y(t),z_\mathbf {f}[y](t),z_\mathbf {v}[y](t))$ as

$$\begin{aligned}&F(t,y(t),z_\mathbf {f}[y](t),z_\mathbf {v}[y](t))=a_1(t)y(t)+a_2(t)\nonumber \\&\quad +z_\mathbf {f}[y](t)+z_\mathbf {v}[y](t). \end{aligned}$$

(2.5)

In the nonlinear case, we assume that $F(t,y,z_\mathbf {f},z_\mathbf {v})$, $F_l(t,y,z_\mathbf {f},z_\mathbf {v})\quad (l=t,y,{z_\mathbf {f}},{z_\mathbf {v}})$ are Lipschitz-continuous. Also when $z_l[y](t)\quad (l=\mathbf {f},\mathbf {v})$ are nonlinear we assume that $K_l(t,s,y,y^{\prime })$ and $(K_{l})_j(t,s,y,y^{\prime })~(l=\mathbf {f},\mathbf {v}~ \& ~j=y,y^{\prime })$ are Lipschitz-continuous. We say FVID equation with boundary condition (1.2) is linear if we can write (1.1) as follows

$$\begin{aligned} y^{\prime }(t)=\,&a_1(t)y(t)+a_2(t)+z_\mathbf {f}[y](t)+z_\mathbf {v}[y](t),\quad t\in I, \end{aligned}$$

(2.6)

with linear $z_l[y](t) (l=\mathbf {f},\mathbf {v})$. Also in the linear case we assume that $a_1(t), a_2(t)$ are sufficiently smooth in I.

2.1 Collocation method

In this subsection, we introduce the piecewise polynomial collocation method for solution of the FVID problem (1.1), (1.2). Let

$$\begin{aligned} a&=\tau _0<\tau _1<\cdots <\tau _n=b,\,\,(n\ge 1), \end{aligned}$$

(2.7)

$$\begin{aligned} 0&=\rho _0<\rho _1<\cdots<\rho _m<\rho _{m+1}=1, \end{aligned}$$

(2.8)

and $h_i:=\tau _{i+1}-\tau _{i}$. We define $X_n,\,Z_n$ and $S^{(0)}_{m}(Z_n)$ as follows

$$\begin{aligned} X_i&:=\{t_{i,j}:=\tau _i+\rho _jh_i;\,j=1,\ldots ,m\}, \end{aligned}$$

(2.9)

$$\begin{aligned} Z_n&:=\{t_{i,0}:=\tau _i;\,i=0,\ldots ,n\}, \end{aligned}$$

(2.10)

$$\begin{aligned} S^{(0)}_{m}(Z_n)&:=\{p\in \mathcal {C}(I);\,p\upharpoonright [\tau _i,\tau _{i+1}]\nonumber \\&\qquad \in \Pi _m([\tau _i,\tau _{i+1}])\,(i=0,\ldots ,n-1)\}, \end{aligned}$$

(2.11)

where $\Pi _m([\tau _i,\tau _{i+1}])$ is space of real polynomial functions on $[\tau _i,\tau _{i+1}]$ of degree $\leqslant m$. Also we define the set of collocation points as

$$\begin{aligned} X(n):=\bigcup ^{n-1}_{i=0}X_i. \end{aligned}$$

(2.12)

We define h (the diameter of gird $Z_n$) and $h^{\prime }$ as

$$\begin{aligned} h&:=\max \{h_i;\,i=0,\ldots ,n-1\},\nonumber \\ h^{\prime }&:=\min \{h_i;\,i=0,\ldots ,n-1\}. \end{aligned}$$

(2.13)

In this paper, the set $X(n):=\bigcup ^{n-1}_{i=0}X_i$ is called the set of collocation points. According to the piecewise polynomial collocation method, we are looking to find a $p\in S^{(0)}_{m}(Z_n)$ so that (1.1), (1.2) hold for all $t\in X(n)$. In the collocation method, since we can not determine exact value for $z_\mathbf {f}[\cdot ](t)$ and $z_\mathbf {v}[\cdot ](t)$, we use the following quadrature method to determine $z_\mathbf {f}[\cdot ](t)$ and $z_\mathbf {v}[\cdot ](t)$.

$$\begin{aligned} z_\mathbf {f}[p](t_{i,j})&\approx \sum ^{n-1}_{k=0}\sum _{z=1}^{m+1}\alpha _{k,z}K_{\mathbf {f}}\big (t_{i,j},t_{k,z},p(t_{k,z}),\nonumber \\ p^{\prime }(t_{k,z})\big )&=:\widetilde{z\,}_\mathbf {f}[p](t_{i,j}), \end{aligned}$$

(2.14)

$$\begin{aligned} z_\mathbf {v}[p](t_{i,j})&\approx \sum ^{i-1}_{k=0}\sum _{z=1}^{m+1}\alpha _{k,z}K_{\mathbf {v}}\big (t_{i,j},t_{k,z},p_k(t_{k,z}),p^{\prime }_k(t_{k,z})\nonumber \\&\quad +(t_{i,j}-\tau _{i})\sum _{z=1}^{m+1}\beta _zK_{\mathbf {v}}\Big (t_{i,j},\tilde{t}^{z}_{i,j} ,p_i\big (\tilde{t}^{z}_{i,j}\big ),p^{\prime }_i\big (\tilde{t}^{z}_{i,j}\big )\Big )\nonumber \\&=:\widetilde{z\,}_\mathbf {v}[p](t_{i,j}), \end{aligned}$$

(2.15)

where $\tilde{t}^{z}_{i,j}:=\tau _i+\rho _z(t_{i,j}-\tau _i)$ and the quadrature weights are given by

$$\begin{aligned} \alpha _{k,z}:=\int ^{\tau _{k+1}}_{\tau _k}L^{[\tau _k,\tau _{k+1}]}_z(s)\hbox {d}s,\quad \beta _{z}:=\int ^{1}_{0}L_z(s)\hbox {d}s, \end{aligned}$$

(2.16)

where

$$\begin{aligned} L_j(\rho )&:=\prod _{\begin{array}{c} i=1\\ i\ne j \end{array}}^{m+1}\frac{\rho -\rho _i}{\rho _j-\rho _i},\quad L^{[a^{\prime }, b^{\prime }]}_j(\rho ):=L_j\left( \frac{\rho -a^{\prime }}{b^{\prime }-a^{\prime }}\right) ,\nonumber \\ a&\le a^{\prime } < b^{\prime } \le b. \end{aligned}$$

(2.17)

In summary, collocation method can be written as Algorithm 1.

By using the interpolation error theorem (see Stoer and Bulirsch 2002, Section 2.1), we can find the following lemma.

Lemma 2.1

For sufficiently smooth f, the following estimates hold

$$\begin{aligned} |z_{l}[f](t_{i,j})-\widetilde{z\,}_{l}[f](t_{i,j})|=\mathcal {O}(h^{m+1}),\quad l=\mathbf {f},\mathbf {v}. \end{aligned}$$

(2.18)

In a similar way to Brunner (2004), for the piecewise polynomial collocation method, we can find the following theorem.

Theorem 2.2

Assume that the FVID problem (1.1), (1.2) has a unique and sufficiently smooth solution y(t). Also assume that p(t) is a piecewise polynomial collocation solution of degree$\,\le m$. Then for sufficiently small h, the collocation solution p(t) is well-defined and the following uniform estimates at least hold:

$$\begin{aligned} \Vert y^{(j)}(t)-p^{\,(j)}(t)\Vert _{\infty }=\mathcal {O}(h^{m}),\quad j=0,1. \end{aligned}$$

(2.19)

Remark 2.3

In special case, we can see that for equidistant collocation gird points with odd m the following uniform estimates hold

$$\begin{aligned} \Vert y^{(j)}(t)-p^{(j)}(t)\Vert _{\infty }=\mathcal {O}(h^{m+1}),\quad j=0,1. \end{aligned}$$

(2.20)

By using Theorem 2.2 and Lemma 2.1, we have the following lemma.

Lemma 2.4

For linear and nonlinear $z_l[\cdot ](t)~(l=\mathbf {f},\mathbf {v})$, we have

$$\begin{aligned} |\widetilde{z\,}_{l}[p](t_{i,j})-\widetilde{z\,}_{l}[y](t_{i,j})|=\mathcal {O}(h^{m}),\quad l=\mathbf {f},\mathbf {v}. \end{aligned}$$

(2.21)

2.2 Finite difference scheme

In this section, we define $\Delta _{i,j},\mathcal {A}$ and $\mathcal {B}$ as follows

$$ \begin{aligned} \Delta _{i,j}&:=\{(l,k);\,l=0,\ldots ,i-1\, \& \,k=0,\ldots ,m\}\nonumber \\&\qquad \cup \{(i,k);\,\,k=0,\ldots ,j-1\}, \end{aligned}$$

(2.22)

$$\begin{aligned} \mathcal {A}&:=\{(i,j);\,t_{i,j}\in X(n)\cup Z_n\}, \end{aligned}$$

(2.23)

$$\begin{aligned} \mathcal {B}&:=\mathcal {A}-\{(n,0)\}. \end{aligned}$$

(2.24)

Also we define

$$\begin{aligned} \left( L^{(1)}_{\mathcal {A}}\eta \right) _{i,j}&:=\frac{\eta _{i,j+1}-\eta _{i,j}}{\delta _{i,j}}, \end{aligned}$$

(2.25)

$$\begin{aligned} \chi ^{\mathbf {f}}[\eta ]_{i,j}&:=\sum _{(l,v) \in \mathcal {B} }\delta _{l,v}K_{\mathbf {f}}\left( t_{i,j},t_{l,v},\eta _{l,v},\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}\right) , \end{aligned}$$

(2.26)

$$\begin{aligned} \chi ^{\mathbf {v}}[\eta ]_{i,j}&:=\sum _{(l,v) \in \Delta _{i,j} }\delta _{l,v}K_{\mathbf {v}}\left( t_{i,j},t_{l,v},\eta _{l,v},\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}\right) , \end{aligned}$$

(2.27)

where $\delta _{i,j}:=t_{i,j+1}-t_{i,j}$.

We write a general one-step finite difference scheme as

$$\begin{aligned}&\left( L^{(1)}_{\mathcal {A}}\eta \right) _{i,j} =F(t_{i,j},\eta _{i,j},\chi ^{\mathbf {f}}[\eta ]_{i,j},\chi ^{\mathbf {v}}[\eta ]_{i,j}),\quad (i,j) \in \mathcal {B}, \end{aligned}$$

(2.28)

$$\begin{aligned}&\alpha \,\eta _{0,0}+\beta \,\eta _{\,n,0}=r. \end{aligned}$$

(2.29)

Definition 2.5

For any function u, we define

$$\begin{aligned} \mathbf {\mathcal {R}}(u):=\{u(t_{i,j})\,;\,(i,j)\in \mathcal {A}\}, \end{aligned}$$

also we define

$$\begin{aligned} \eta :=\{\eta _{i,j}\,;\,(i,j)\in \mathcal {A}\},\quad ~L^{(1)}_{\mathcal {A}}\eta :=\left\{ \left( L^{(1)}_{\mathcal {A}}\eta \right) _{i,j}\,;(i,j)\in \mathcal {A}\right\} . \end{aligned}$$

By using Taylor expansions, the following lemma is obtained easily.

Lemma 2.6

For sufficiently smooth f, the following estimates hold

$$\begin{aligned} |\chi ^{l}[f]_{i,j}-z_{l}[f](t_{i,j})|=\mathcal {O}(h),\quad l=\mathbf {f},\mathbf {v}. \end{aligned}$$

(2.30)

By using Taylor expansion and Lemma 2.6, we can find the following estimates

$$\begin{aligned} \Vert \eta -\mathbf {\mathcal {R}}(y)\Vert _{\infty }&=\mathcal {O}(h), \end{aligned}$$

(2.31)

$$\begin{aligned} \Vert L^{(1)}_{\mathcal {A}}\eta -\mathbf {\mathcal {R}}(y^{\prime })\Vert _{\infty }&=\mathcal {O}(h), \end{aligned}$$

(2.32)

where $\eta$ and $L^{(1)}_{\mathcal {A}}\eta$ is defined in the Definition 2.5.

2.3 Deviation of the error estimation

In this subsection, we study the deviation of the error estimation for (1.1), (1.2) by using the defect correction principle. In the first step, we consider $y^{\prime }(t)=f(t),\,a\le t \le b$, where f(t) is permitted to have jump discontinuities in the points belonging to $Z_n$. Using the Taylor expansion, we can find “exact finite difference scheme” for $y^{\prime }(t)=f(t)$, which is satisfied by the exact solution.

$$\begin{aligned} \left( L^{(1)}_{\mathcal {A}}y\right) _{i,j} =\int ^{1}_{0}f(t_{i,j}+\xi \delta _{i,j})\hbox {d}\xi :=\mathcal {I}_{\mathcal {A}}(f,t_{i,j}). \end{aligned}$$

(2.33)

Therefore, we can say that a solution of problem (1.1), (1.2) satisfies in the following exact finite difference scheme

$$\begin{aligned} \left( L^{(1)}_{\mathcal {A}}y\right) _{i,j}=\mathcal {I}_{\mathcal {A}} \big (F(\cdot ,y,z_{\mathbf {f}}[y],z_{\mathbf {v}}[y]),t_{i,j}\big ). \end{aligned}$$

(2.34)

According to the collocation method, we have

$$\begin{aligned}&p^{\prime }(t_{i,j})-F\big (t_{i,j},p(t_{i,j}),\nonumber \\&\quad z_{\mathbf {f}}[p](t_{i,j}),z_{\mathbf {v}}[p](t_{i,j})\big )\equiv 0,\,(i,j)\in X(n). \end{aligned}$$

(2.35)

Now in this step we define defect at $t_{i,j}$ as

$$\begin{aligned} D_{i,j}&:=\Big (L^{(1)}_{\mathcal {A}}p\Big )_{i,j} -\mathcal {I}_{\mathcal {A}}\big (F(\cdot ,p,z_{\mathbf {f}}[p],\nonumber \\&\qquad z_{\mathbf {v}}[p]),t_{i,j}\big ),\,(i,j)\in \mathcal {B}. \end{aligned}$$

(2.36)

We use quadrature formula to compute integral in (2.36)

$$\begin{aligned}&\mathcal {I}_{\mathcal {A}}\big (F(\cdot ,p,z_{\mathbf {f}}[p],z_{\mathbf {v}}[p]),t_{i,j}\big )\nonumber \\&\quad \approx Q_{\mathcal {A}}\big (F(\cdot ,p,\widetilde{z\,}_{\mathbf {f}}[p],\widetilde{z\,}_{\mathbf {v}}[p]),t_{i,j}\big )\nonumber \\&\quad :=\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}F\big (t_{i,k},p(t_{i,k}),\widetilde{z\,}_{\mathbf {f}}[p](t_{i,k}) ,\widetilde{z\,}_{\mathbf {v}}[p](t_{i,k})\big ), \end{aligned}$$

(2.37)

where

$$\begin{aligned} \gamma ^{k}_{i,j}:=\int ^{1}_{0}L_k\left( \rho _{j}+\frac{\xi \delta _{i,j}}{h_i}\right) \hbox {d}\xi . \end{aligned}$$

(2.38)

For sufficiently smooth f, the following error holds

$$\begin{aligned} \mathcal {I}_{\mathcal {A}}\big (f,t_{i,j}\big )- Q_{\mathcal {A}}\big (f,t_{i,j}\big )=\mathcal {O}(h^{m+1}). \end{aligned}$$

(2.39)

Also when m is odd and the nodes $\rho _i$ are symmetrically, we can find the following relation.

$$\begin{aligned} \mathcal {I}_{\mathcal {A}}\big (f,t_{i,j}\big )- Q_{\mathcal {A}}\big (f,t_{i,j}\big )=\mathcal {O}(h^{m+2}). \end{aligned}$$

(2.40)

Then we consider defect at $t_{i,j}$ as follows

$$\begin{aligned} D_{i,j}&\approx \Big (L^{(1)}_{\mathcal {A}}p\Big )_{i,j} -Q_{\mathcal {A}}\big (F(\cdot ,p,z_{\mathbf {f}}[p],\nonumber \\&\qquad z_{\mathbf {v}}[p]),t_{i,j}\big ),\,(i,j)\in \mathcal {B}. \end{aligned}$$

(2.41)

In this step, we define ${{\pi }}=\{\pi _{i,j}\,;\,(i,j)\in \mathcal {A}\}$ as the solution of the following finite difference scheme

$$\begin{aligned}&\Big (L^{(1)}_{\mathcal {A}}\pi \Big )_{i,j}=F(t_{i,j},\pi _{i,j},\chi ^{\mathbf {f}}[\pi ]_{i,j},\chi ^{\mathbf {v}}[\pi ]_{i,j})\nonumber \\&\quad +D_{i,j},\,(i,j)\in \mathcal {B}, \end{aligned}$$

(2.42)

$$\begin{aligned}&\alpha \,\pi _{0,0}+\beta \,\pi _{n,0}=r. \end{aligned}$$

(2.43)

We define $\mathbf {D}:=\{D_{i,j}\,;\,(i,j)\in \mathcal {B}\}$. For small value $\mathbf {D}$, we can say that

$$\begin{aligned} {{{\pi }}}-\mathbf {\mathcal {R}}(p)\approx \mathbf {\eta }-\mathbf {\mathcal {R}}(y), \end{aligned}$$

(2.44)

where $\eta$ can be found in (2.28), (2.29). We define $\varepsilon$ and e as follows

$$\begin{aligned} \varepsilon :=\pi -\eta \approx \mathcal {R}(p)-\mathcal {R}(y):=e. \end{aligned}$$

(2.45)

An estimate for the error e can be found in Theorem 2.2. We consider the deviation of the error in the following form

$$\begin{aligned} \theta :=e-\varepsilon . \end{aligned}$$

(2.46)

By using above discussion, improved collocation method can be written as Algorithm 2.

In the next section, we will study the order of the deviation of the error estimate for FVID equation. We can easily find the following lemmas.

Lemma 2.7

The defined defect in (2.41) has order $\mathcal {O}(h^{m})$.

Lemma 2.8

The $\pi -\eta$ has order $\mathcal {O}(h^{m})$.

3 Analysis of the deviation of the error

Definition 3.1

In this section, we define $\overline{\varepsilon }$ and $\widehat{\varepsilon }$ as follows

$$\begin{aligned} \overline{\varepsilon }&:=\pi -\mathcal {R}(p), \end{aligned}$$

(3.1)

$$\begin{aligned} \widehat{\varepsilon }&:=\eta -\mathcal {R}(y). \end{aligned}$$

(3.2)

Definition 3.2

We define

$$\begin{aligned} \overline{\chi }^{\,\mathbf {f}}[\overline{\varepsilon }]_{i,j}&:=\sum _{(l,v) \in \mathcal {B}}\delta _{l,v}\Big (\overline{\Upsilon }^{\,\mathbf {f}}_0(t_{i,j},t_{l,v})\overline{\varepsilon }_{l,v}\nonumber \\&\quad +\overline{\Upsilon }^{\,\mathbf {f}}_1(t_{i,j},t_{l,v}) \Big (L^{(1)}_{\mathcal {A}}\overline{\varepsilon }\Big )_{l,v}\Big ), \end{aligned}$$

(3.3)

$$\begin{aligned} \overline{\chi }^{\,\mathbf {v}}[\overline{\varepsilon }]_{i,j}&:=\sum _{(l,v) \in \Delta _{i,j}}\delta _{l,v}\Big (\overline{\Upsilon }^{\,\mathbf {v}}_0(t_{i,j},t_{l,v})\overline{\varepsilon }_{l,v}\nonumber \\&\quad +\overline{\Upsilon }^{\,\mathbf {v}}_1(t_{i,j},t_{l,v}) \Big (L^{(1)}_{\mathcal {A}}\overline{\varepsilon }\Big )_{l,v}\Big ), \end{aligned}$$

(3.4)

where ( $l=\mathbf {f},\mathbf {v}$ )

$$\begin{aligned} \overline{\Upsilon }^{\,l}_0(t_{i,j},t_{l,v})&= \left\{ \begin{array}{l@{\qquad }l} \Lambda _{0,l}(t_{i,j},t_{l,v}),&{}when~z_l~is~linear,\\ \int ^{1}_{0}(K_l)_{y}\Big (t_{i,j},t_{l,v},p(t_{l,v}) +\nu \overline{\varepsilon }_{l,v},\Big (L^{(1)}_{\mathcal {A}}\pi \Big )_{l,v}\Big ){\hbox {d}}\nu ,&{}when~z_l~is~nonlinear,\\ \end{array}\right. \end{aligned}$$

(3.5)

$$\begin{aligned} \overline{\Upsilon }^{\,l}_1(t_{i,j},t_{l,v})&= \left\{ \begin{array}{l@{\qquad }l} \Lambda _{1,l}(t_{i,j},t_{l,v}),\quad ~&{}when~z_l~is~linear,\\ \int ^{1}_{0}(K_l)_{y^{\prime }}\Big (t_{i,j},t_{l,v},p(t_{l,v}),\Big (L^{(1)}_{\mathcal {A}}p\Big )_{l,v} +\nu \Big (L^{(1)}_{\mathcal {A}}\overline{\varepsilon }\Big )_{l,v}\Big ){\hbox {d}}\nu ,\quad &{}when~z_l~is~nonlinear.\\ \end{array}\right. \end{aligned}$$

(3.6)

Also we consider $\widehat{\chi }^{\,l}[\widehat{\varepsilon }\,]_{i,j}(l=\mathbf {f},\mathbf {v})$ as follows

$$\begin{aligned} \widehat{\chi }^{\,\mathbf {f}}[\widehat{\varepsilon }\,]_{i,j}&:=\sum _{(l,v) \in \mathcal {B}}\delta _{l,v}\Big (\widehat{\Upsilon }^{\,\mathbf {f}}_0(t_{i,j},t_{l,v})\widehat{\varepsilon }_{l,v}\nonumber \\&\quad +\widehat{\Upsilon }^{\,\mathbf {f}}_1(t_{i,j}, t_{l,v})\Big (L^{(1)}_{\mathcal {A}}\widehat{\varepsilon }\Big )_{l,v}\Big ), \end{aligned}$$

(3.7)

$$\begin{aligned} \widehat{\chi }^{\,\mathbf {v}}[\widehat{\varepsilon }\,]_{i,j}&:=\sum _{(l,v) \in \Delta _{i,j}}\delta _{l,v}\Big (\widehat{\Upsilon }^{\,\mathbf {v}}_0(t_{i,j},t_{l,v})\widehat{\varepsilon }_{l,v}\nonumber \\&\quad +\widehat{\Upsilon }^{\,\mathbf {v}}_1(t_{i,j}, t_{l,v})\Big (L^{(1)}_{\mathcal {A}}\widehat{\varepsilon }\Big )_{l,v}\Big ), \end{aligned}$$

(3.8)

where ( $l=\mathbf {f},\mathbf {v}$ )

$$\begin{aligned}&\widehat{\Upsilon }^{l}_0(t_{i,j},t_{l,v})= \left\{ \begin{array}{l@{\qquad }l} \Lambda _{0,l}(t_{i,j},t_{l,v}),&{}when~z_l~is~linear,\\ \int ^{1}_{0}(K_l)_{y}\Big (t_{i,j},t_{l,v},y(t_{l,v}) +\nu \widehat{\varepsilon }_{l,v},\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}\Big ){\hbox {d}}\nu ,&{}when~z_l~is~nonlinear,\\ \end{array} \right. \end{aligned}$$

(3.9)

$$\begin{aligned}&\widehat{\Upsilon }^{l}_1(t_{i,j},t_{l,v})= \left\{ \begin{array}{l@{\qquad }l} \Lambda _{1,l}(t_{i,j},t_{l,v}),\quad &{}when~z_l~is~linear,\\ \int ^{1}_{0}(K_l)_{y^{\prime }}\Big (t_{i,j},t_{l,v},y(t_{l,v}),\left( L^{(1)}_{\mathcal {A}}y\right) _{l,v} +\nu \Big (L^{(1)}_{\mathcal {A}}\widehat{\varepsilon }\Big )_{l,v}\Big ){\hbox {d}}\nu ,\quad &{}when~z_l~is~nonlinear.\\ \end{array}\right. \end{aligned}$$

(3.10)

By using Theorem 2.2, (2.31), (2.32) and Lemma 2.8, we can find the following lemma.

Lemma 3.3

The $\overline{\varepsilon }$ and the $\widehat{\varepsilon }$ have order $\mathcal {O}(h)$.

Lemma 3.4

We have

$$\begin{aligned} ||\overline{\varepsilon }-\widehat{\varepsilon }\,||_{\infty }=\mathcal {O}(h^{m}). \end{aligned}$$

(3.11)

Proof

By using Lemma 2.8 and Theorem 2.2, we can write

$$\begin{aligned} ||\overline{\varepsilon }-\widehat{\varepsilon }||_{\infty }\le \underbrace{||\pi -\eta ||_{\infty }}_{\mathcal {O}(h^{m})} +\underbrace{||\mathcal {R}(p)-\mathcal {R}(y)||_{\infty }}_{\mathcal {O}(h^{m})}=\mathcal {O}(h^{m}). \end{aligned}$$

(3.12)

$\square$

By using Definition 3.2, we can say that

$$\begin{aligned} \chi ^{\,l}[\pi ]-\chi ^{\,l}[p]&=\overline{\chi }^{\,l}[\overline{\varepsilon }\,],\quad (l=\mathbf {f},\mathbf {v}), \end{aligned}$$

(3.13)

$$\begin{aligned} \chi ^{\,l}[\eta ]-\chi ^{\,l}[y]&=\widehat{\chi }^{\,l}[\widehat{\varepsilon }\,],\quad (l=\mathbf {f},\mathbf {v}). \end{aligned}$$

(3.14)

Lemma 3.5

For linear and nonlinear $z_{l}[\cdot ](t)\quad (l=\mathbf {f},\mathbf {v})$, we have

$$\begin{aligned} |\chi ^{l}[y]_{i,j}-\widetilde{z\,}_{l}[y](t_{i,j})|&=\mathcal {O}(h), \end{aligned}$$

(3.15)

$$\begin{aligned} |\chi ^{l}[p]_{i,j}-\widetilde{z\,}_{l}[p](t_{i,j})|&=\mathcal {O}(h),\end{aligned}$$

(3.16)

$$\begin{aligned} |\chi ^{l}[\eta ]_{i,j}-\chi ^{l}[\pi ]_{i,j}|&=\mathcal {O}(h^{m}),\end{aligned}$$

(3.17)

$$\begin{aligned} |\chi ^{l}[y]_{i,j}-\chi ^{l}[p]_{i,j}|&=\mathcal {O}(h^{m}),\end{aligned}$$

(3.18)

$$\begin{aligned} |\chi ^{l}[\widehat{\varepsilon }\,]_{i,j}-\chi ^{l}[\overline{\varepsilon }\,]_{i,j}|&=\mathcal {O}(h^{m}),\end{aligned}$$

(3.19)

$$\begin{aligned} |\chi ^{l}[\widehat{\varepsilon }\,]_{i,j}|&=\mathcal {O}(h). \end{aligned}$$

(3.20)

Proof

For (3.15) by using Lemmas 2.1 and 2.6 we have

$$\begin{aligned}&|\chi ^{l}[y]_{i,j}-\widetilde{z\,}_{l}[y](t_{i,j})|=|\underbrace{\chi ^{l}[y]_{i,j}-z_{l}[y](t_{i,j})}_{\mathcal {O}(h)}\nonumber \\&\quad +\underbrace{z_{l}[y](t_{i,j})-\widetilde{z\,}_{l}[y](t_{i,j})}_{\mathcal {O}(h^{m+1})}|=\mathcal {O}(h). \end{aligned}$$

(3.21)

Similarly, we can prove (3.16). Now we prove (3.17) for $l=\mathbf {f}$. When $z_{l}[\cdot ](t)$ is linear, we find

$$\begin{aligned}&\chi ^{\mathbf {f}}[\eta ]_{i,j}-\chi ^{\mathbf {f}}[\pi ]_{i,j}=\chi ^{\mathbf {f}}[\eta -\pi ]_{i,j}\nonumber \\&\quad =\sum _{(l,v)\in \mathcal {B}}\delta _{l,v}\Lambda _{0,\mathbf {f}}(t_{i,j},t_{l,v})\varepsilon _{l,v}\nonumber \\&\qquad +\sum _{(l,v) \in \mathcal {B}}\delta _{l,v}\Lambda _{1,\mathbf {f}}(t_{i,j},t_{l,v})\Big (L^{(1)}_{\mathcal {A}}\varepsilon \Big )_{l,v}\nonumber \\&\quad \le (b-a)(m+1)\frac{h}{h^{\prime }}\Big (\max _{(l,v) \in \mathcal {B} }\Lambda _{0,\mathbf {f}}(t_{i,j},t_{l,v})\underbrace{\varepsilon _{l,v}}_{\mathcal {O}(h^{m})}\nonumber \\&\qquad +\max _{(l,v) \in \mathcal {B} }\Lambda _{1,\mathbf {f}}(t_{i,j},t_{l,v})\underbrace{\Big (L^{(1)}_{\mathcal {A}}\varepsilon \Big )_{l,v}}_{\mathcal {O}(h^{m})}\Big )=\mathcal {O}(h^{m}). \end{aligned}$$

(3.22)

Also for nonlinear case we can get

$$\begin{aligned}&\chi ^{\mathbf {f}}[\pi ]_{i,j}-\chi ^{\mathbf {f}}[\eta ]_{i,j}\nonumber \\&\quad =\sum _{(l,v) \in \mathcal {B}}\delta _{l,v} \Big (K_{\mathbf {f}}\Big (t_{i,j},t_{l,v},\pi _{l,v},\Big (L^{(1)}_{\mathcal {A}}\pi \Big )_{l,v}\Big )\nonumber \\&\qquad -K_{\mathbf {f}}\Big (t_{i,j},t_{l,v},\eta _{l,v},\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}\Big )\Big )\nonumber \\&\qquad \le (b-a)(m+1)\frac{h}{h^{\prime }} \max _{(l,v) \in \mathcal {B}}\Big (K_{\mathbf {f}}\Big (t_{i,j},t_{l,v},\pi _{l,v}, \Big (L^{(1)}_{\mathcal {A}}\pi \Big )_{l,v}\Big )\nonumber \\&\qquad -K_{\mathbf {f}}\Big (t_{i,j},t_{l,v},\eta _{l,v},\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}\Big )\Big ), \end{aligned}$$

(3.23)

from the Lipschitz condition for $K_{\mathbf {f}}$ and Lemma 2.8, we get

$$\begin{aligned}&|K_{\mathbf {f}}\Big (t_{i,j},t_{l,v},\pi _{l,v},\Big (L^{(1)}_{\mathcal {A}}\pi \Big )_{l,v}\Big )\nonumber \\&\qquad -K_{\mathbf {f}}\Big (t_{i,j},t_{l,v},\eta _{l,v},\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}\Big )|\nonumber \\&\quad \le C|\pi _{l,v}-\eta _{l,v}|+|\Big (L^{(1)}_{\mathcal {A}}\pi \Big )_{l,v}-\left( L^{(1)}_{\mathcal {A}}\eta \right) _{l,v}|=\mathcal {O}(h^{m}). \end{aligned}$$

(3.24)

In the same way, we can find (3.17) for $l=\mathbf {v}$. Similarly, we can prove (3.18),(3.19) and (3.20). $\square$

In this step, we study linear case.

Theorem 3.6

Assume that the FVID problem (2.6) with boundary conditions (1.2) has a unique and sufficiently smooth solution. Then the following estimate holds

$$\begin{aligned} ||\theta ||_{\infty }=||e-\varepsilon ||_{\infty }=\mathcal {O}(h^{m+1}), \end{aligned}$$

(3.25)

where e is error, $\varepsilon$ is the error estimate and $\theta$ is the deviation of the error estimate.

Proof

Since F is linear then by using (2.28) and (2.42) we get

$$\begin{aligned} \Big (L^{(1)}_{\mathcal {A}}\varepsilon \Big )_{i,j}=a_1(t_{i,j})\varepsilon _{i,j}+\chi ^{\mathbf {f}}[\varepsilon ]_{i,j}+\chi ^{\mathbf {v}}[\varepsilon ]_{i,j}+D_{i,j}. \end{aligned}$$

(3.26)

Also we can write

$$\begin{aligned} \Big (L^{(1)}_{\mathcal {A}}e\Big )_{i,j}&=(L^{(1)}_{\mathcal {A}}p)_{i,j}-\left( L^{(1)}_{\mathcal {A}}y\right) _{i,j}\nonumber \\&=D_{i,j}+Q_{\mathcal {A}}(a_1e+\widetilde{z\,}_\mathbf {f}[e]+\widetilde{z\,}_\mathbf {v}[e],t_{i,j})\nonumber \\ {}&\quad +\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.27)

From (3.26) and (3.27), we have

$$ \begin{aligned} \Big (L^{(1)}_{\mathcal {A}}\theta \Big )_{i,j}&=(L^{(1)}_{\mathcal {A}}e)_{i,j}-\Big (L^{(1)}_{\mathcal {A}}\varepsilon \Big )_{i,j}\nonumber \\&=a_1(t_{i,j})\theta _{i,j}+\sum _{l=\mathbf {f} \& \mathbf {v}}\chi ^l[\theta ]_{i,j}\nonumber \\&\quad +\underbrace{Q_{\mathcal {A}}(a_1e,t_{i,j})-a_1(t_{i,j})e(t_{i,j})}_{S_1}\nonumber \\&\quad +\underbrace{\sum _{l=\mathbf {f} \& \mathbf {v}}\Big (Q_{\mathcal {A}}(\widetilde{z\,}_l[e],t_{i,j})-\chi ^l[e]_{i,j}\Big )}_{S_2}\nonumber \\&\quad +\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.28)

Since $\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}=1$, then we rewrite $S_1$ as

$$\begin{aligned} S_1&=\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}\Big (a_1(t_{i,k})e(t_{i,k})-a_1(t_{i,j})e(t_{i,j})\Big ), \end{aligned}$$

(3.29)

and by using Taylor expansion, we have

$$\begin{aligned}&a_1(t_{i,k})e(t_{i,k})-a_1(t_{i,j})e(t_{i,j})\nonumber \\&\quad =\underbrace{(t_{i,k}-t_{i,j})}_{\mathcal {O}(h)}\Big (a_{1}^{\prime }(\xi _{i})\underbrace{e(\xi _{i})}_{\mathcal {O}(h^m)} +a_1(\xi _{i})\underbrace{e^{\prime }(\xi _{i}}_{\mathcal {O}(h^m)})\Big )\nonumber \\&\quad =\mathcal {O}(h^{m+1}), \end{aligned}$$

(3.30)

where $\xi _{i}\in [\tau _{i},\tau _{i+1}]$. By using Theorem 2.2 and (3.30), we can get $S_1=\mathcal {O}(h^{m+1})$. For $S_2$ by using the Lemma 2.1, we get

$$\begin{aligned}&\sum ^{1}_{r=0}\int ^{b}_{a}\Lambda _{r,\mathbf {f}}(t_{i,j},s)e^{(r)}(s)\hbox {d}s-\chi ^\mathbf {f}[e]_{i,j}+\mathcal {O}(h^{m+1})\nonumber \\&\quad \le \mathcal {O}(h^m)(b-a)(m+1)\frac{h}{2h^{\prime }}h\nonumber \\&\qquad \sum ^{1}_{r=0}\max _{s\in [a,b]}\left( \frac{\partial \Lambda _{r,\mathbf {f}}(t_{i,j},s)}{\partial s}\right) +\mathcal {O}(h^{m+1})\nonumber \\&\quad =\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.31)

In a similar way, we can find

$$\begin{aligned}&\sum ^{1}_{r=0}\int ^{t_{i,j}}_{a}\Lambda _{r,\mathbf {v}}(t_{i,j},s)e^{(l)}(s)\hbox {d}s-\chi ^\mathbf {v}[e]_{i,j} =\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.32)

By using (3.31), (3.32), we obtain

$$ \begin{aligned} S_2&=\sum _{w=\mathbf {f} \& \mathbf {v}}\Big (Q_{\mathcal {A}}(\widetilde{z\,}_{w}[e],t_{i,j}) -\chi ^{w}[e]_{i,j}\Big )\nonumber \\&=Q_{\mathcal {A}}(\widetilde{z\,}_{\mathbf {f}}[e],t_{i,j})-\chi ^{\mathbf {f}}[e]_{i,j} +Q_{\mathcal {A}}(\widetilde{z\,}_{\mathbf {v}}[e],t_{i,j})-\chi ^{\mathbf {v}}[e]_{i,j}\nonumber \\&=\sum ^{1}_{r=0}\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}\int ^{b}_{a}\Big (\Lambda _{r,\mathbf {f}}(t_{i,k},s) -\Lambda _{r,\mathbf {f}}(t_{i,j},s)\Big )e^{(r)}(s)\hbox {d}s \nonumber \\&\quad +\sum ^{1}_{r=0}\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}\Big (\int ^{t_{i,k}}_{a} \Lambda _{r,\mathbf {v}}(t_{i,k},s)e^{(r)}(s)\hbox {d}s\nonumber \\&\quad -\int ^{t_{i,j}}_{a}\Lambda _{r,\mathbf {v}}(t_{i,j},s)e^{(r)}(s)\hbox {d}s\Big )\nonumber \\&=(b-a)\sum ^{1}_{r=0}\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}(t_{i,k}-t_{i,j})\frac{\partial \Lambda _{r,\mathbf {f}}}{\partial t}(\zeta ^{i}_{k,r},\zeta ^{\prime }_{k,r})e^{(r)}(\zeta ^{\prime }_{k,r})\nonumber \\&\quad +\sum ^{1}_{r=0}\sum _{k=1}^{m+1}\gamma ^{k}_{i,j}\Big (\int ^{t_{i,k}}_{t_{i,j}} \Lambda _{r,\mathbf {v}}(t_{i,j},s)e^{(r)}(s)\hbox {d}s\nonumber \\&\quad +(t_{i,k}-t_{i,j})\int ^{t_{i,k}}_{a}\frac{\partial \Lambda _{r,\mathbf {v}}(\xi ^{k}_{i,j},s) }{\partial t}e^{(r)}(s) \hbox {d}s\Big )\nonumber \\&=\mathcal {O}(h^{m+1}), \end{aligned}$$

(3.33)

where $\xi ^{k}_{i,j},\, \zeta ^{i}_{k,r},\, \zeta ^{\prime }_{k,r}\in [a,b]$. Therefore, we can rewrite (3.28) as

$$ \begin{aligned} \Big (L^{(1)}_{\mathcal {A}}\theta \Big )_{i,j}=a_1(t_{i,j})\theta _{i,j}+\sum _{l=\mathbf {f} \& \mathbf {v}}\chi ^l[\theta ]_{i,j} +\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.34)

By using stability of forward Euler scheme, we find

$$\begin{aligned} ||\theta ||_{\infty }=||e-\varepsilon ||_{\infty }=\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.35)

$\square$

For nonlinear case we have the following theorem.

Theorem 3.7

Consider the FVID equation (1.1) with boundary conditions (1.2), where $F(t,y,z_\mathbf {f},z_\mathbf {v})$, $F_l(t,y,z_\mathbf {f},z_\mathbf {v}) (l=t,y,z_\mathbf {f},z_\mathbf {v})$ are Lipschitz-continuous. Also when $z_\mathbf {f}$ and $z_\mathbf {v}$ are nonlinear, we assume that $K_{l}(t,s,y,y^{\prime })$ and $(K_{l})_{j}(t,s,y,y^{\prime })$$~(l=\mathbf {f},\mathbf {v}\, \& \,j=y,y^{\prime })$ are Lipschitz-continuous. Assume that the FVID problem has a unique and sufficiently smooth solution. Then the following estimate holds

$$\begin{aligned} ||\theta ||_{\infty }=||e-\varepsilon ||_{\infty }=\mathcal {O}(h^{m+1}), \end{aligned}$$

(3.36)

where e is error, $\varepsilon$ is the error estimate and $\theta$ is the deviation of the error estimate.

Proof

For nonlinear case, we have

$$\begin{aligned}&\Big (L^{(1)}_{\mathcal {A}}\theta \Big )_{i,j}=-\Big (\underbrace{F(t_{i,j},\pi _{i,j} ,\chi ^{\mathbf {f}}[\pi ]_{i,j},\chi ^{\mathbf {v}}[\pi ]_{i,j})- F(t_{i,j},p(t_{i,j}) ,\chi ^{\mathbf {f}}[p]_{i,j},\chi ^{\mathbf {v}}[p]_{i,j})}_{I_1}\Big )\nonumber \\&\qquad -\Big (\underbrace{F(t_{i,j},p(t_{i,j}) ,\chi ^{\mathbf {f}}[p]_{i,j},\chi ^{\mathbf {v}}[p]_{i,j})-F(t_{i,j},p(t_{i,j}) ,\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j})}_{I_2})\Big )\nonumber \\ {}&\qquad -F(t_{i,j},p(t_{i,j}) ,\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j}))\nonumber \\ {}&\qquad +Q_{\mathcal {A}}\Big (F(t_{i,j},p(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}) ,\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j}))\Big ) \nonumber \\ {}&\qquad +\underbrace{F(t_{i,j},\eta _{i,j},\chi ^{\mathbf {f}}[\eta ]_{i,j},\chi ^{\mathbf {v}}[\eta ]_{i,j}) -F(t_{i,j},y(t_{i,j}),\chi ^{\mathbf {f}}[y]_{i,j},\chi ^{\mathbf {v}}[y]_{i,j})}_{I_3}\nonumber \\ {}&\qquad +\underbrace{F(t_{i,j},y(t_{i,j}),\chi ^{\mathbf {f}}[y]_{i,j},\chi ^{\mathbf {v}}[y]_{i,j}) -F(t_{i,j},y(t_{i,j}) ,\widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j}))}_{I_4}\nonumber \\ {}&\qquad +F(t_{i,j},y(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j}))\nonumber \\ {}&\qquad -Q_{\mathcal {A}}\Big (F(t_{i,j},y(t_{i,j}), \widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j}))\Big )\nonumber \\ {}&\qquad +\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.37)

We can rewrite $I_1,I_2,I_3$ and $I_4$ as

$$\begin{aligned} I_1&=\Psi ^1_{i,j}\overline{\varepsilon }_{i,j} +\Psi ^{1,\mathbf {f}}_{i,j}\overline{\chi }^{\,\mathbf {f}}[\overline{\varepsilon }\,]_{i,j} +\Psi ^{1,\mathbf {v}}_{i,j}\overline{\chi }^{\,\mathbf {v}}[\overline{\varepsilon }\,]_{i,j}, \end{aligned}$$

(3.38)

$$\begin{aligned} I_3&=\Psi ^2_{i,j}\widehat{\varepsilon }_{i,j} +\Psi ^{2,\mathbf {f}}_{i,j}\widehat{\chi }^{\,\mathbf {f}}[\widehat{\varepsilon }\,]_{i,j} +\Psi ^{2,\mathbf {v}}_{i,j}\widehat{\chi }^{\,\mathbf {v}}[\widehat{\varepsilon }\,]_{i,j}, \end{aligned}$$

(3.39)

$$\begin{aligned} I_2&=R^{1,\mathbf {f}}_{i,j}(\chi ^{\mathbf {f}}[p]_{i,j}-\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}))\nonumber \\&\quad +R^{1,\mathbf {v}}_{i,j}(\chi ^{\mathbf {v}}[p]_{i,j}-\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j})), \end{aligned}$$

(3.40)

$$\begin{aligned} I_4&=R^{2,\mathbf {f}}_{i,j}(\chi ^{\mathbf {f}}[y]_{i,j}-\widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}))\nonumber \\&\quad +R^{2,\mathbf {v}}_{i,j}(\chi ^{\mathbf {v}}[y]_{i,j}-\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j})), \end{aligned}$$

(3.41)

with

$$\begin{aligned} \Psi ^1_{i,j}&:=\int ^{1}_{0}F_{y}(t_{i,j},p(t_{i,j})+\overline{\varepsilon }\nu , \chi ^{\mathbf {f}}[\pi ]_{i,j},\chi ^{\mathbf {v}}[\pi ]_{i,j}){\hbox {d}}\nu , \end{aligned}$$

(3.42)

$$\begin{aligned} \Psi ^{1,\mathbf {f}}_{i,j}&:=\int ^{1}_{0}F_{z_{\mathbf {f}}}(t_{i,j},p(t_{i,j}), \chi ^{\mathbf {f}}[p]_{i,j}\nonumber \\&\quad +\overline{\chi }^{\,\mathbf {f}}[\overline{\varepsilon }\,]_{i,j}\nu ,\chi ^{\mathbf {v}}[\pi ]_{i,j}){\hbox {d}}\nu ,\end{aligned}$$

(3.43)

$$\begin{aligned} \Psi ^{1,\mathbf {v}}_{i,j}&:=\int ^{1}_{0}F_{z_{\mathbf {v}}}(t_{i,j},p(t_{i,j}), \chi ^{\mathbf {f}}[p]_{i,j} ,\chi ^{\mathbf {v}}[p]_{i,j}\nonumber \\&\quad +\overline{\chi }^{\,\mathbf {v}}[\overline{\varepsilon }\,]_{i,j}\nu ){\hbox {d}}\nu , \end{aligned}$$

(3.44)

$$\begin{aligned} \Psi ^2_{i,j}&:=\int ^{1}_{0}F_{y}(t_{i,j},y(t_{i,j})+\widehat{\varepsilon }\nu , \chi ^{\mathbf {f}}[\eta ]_{i,j},\chi ^{\mathbf {v}}[\eta ]_{i,j}){\hbox {d}}\nu ,\end{aligned}$$

(3.45)

$$\begin{aligned} \Psi ^{2,\mathbf {f}}_{i,j}&:=\int ^{1}_{0}F_{z_{\mathbf {f}}}(t_{i,j},y(t_{i,j}), \chi ^{\mathbf {f}}[y]_{i,j}\nonumber \\&\quad +\overline{\chi }^{\,\mathbf {f}}[\widehat{\varepsilon }\,]_{i,j}\nu ,\chi ^{\mathbf {v}}[\eta ]_{i,j}){\hbox {d}}\nu , \end{aligned}$$

(3.46)

$$\begin{aligned} \Psi ^{2,\mathbf {v}}_{i,j}&:=\int ^{1}_{0}F_{z_{\mathbf {v}}}(t_{i,j},y(t_{i,j}), \chi ^{\mathbf {f}}[y]_{i,j} ,\chi ^{\mathbf {v}}[y]_{i,j}\nonumber \\&\quad +\widehat{\chi }^{\,\mathbf {v}}[\widehat{\varepsilon }\,]_{i,j}\nu ){\hbox {d}}\nu , \end{aligned}$$

(3.47)

$$\begin{aligned} R^{1,\mathbf {f}}_{i,j}&:=\int ^{1}_{0}F_{z_{\mathbf {f}}}(t_{i,j},p(t_{i,j}) ,\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j})\nonumber \\&\quad +(\chi ^{\mathbf {f}}[p]_{i,j}-\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}))\nu ,\chi ^{\mathbf {v}}[p]_{i,j}){\hbox {d}}\nu ,\end{aligned}$$

(3.48)

$$\begin{aligned} R^{1,\mathbf {v}}_{i,j}&:=\int ^{1}_{0}F_{z_{\mathbf {v}}}(t_{i,j},p(t_{i,j}) ,\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j})\nonumber \\&\quad +(\chi ^{\mathbf {v}}[p]_{i,j}-\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j}))\nu ){\hbox {d}}\nu . \end{aligned}$$

(3.49)

By using the Lipschitz condition for $F_y,F_{z_{\mathbf {f}}},F_{z_{\mathbf {v}}}$, Lemma 3.4 and Lemma 2.8, we get

$$\begin{aligned} |\Psi ^1_{i,j}-\Psi ^2_{i,j}|&=\mathcal {O}(h^{m}), \end{aligned}$$

(3.50)

$$\begin{aligned} |\Psi ^{1,\mathbf {l}}_{i,j}-\Psi ^{2,\mathbf {l}}_{i,j}|&=\mathcal {O}(h^{m}),\quad l=\mathbf {f},\mathbf {v}, \end{aligned}$$

(3.51)

$$\begin{aligned} |R^{1,\mathbf {l}}_{i,j}-R^{2,\mathbf {l}}_{i,j}|&=\mathcal {O}(h^{m}),\quad l=\mathbf {f},\mathbf {v}. \end{aligned}$$

(3.52)

We can get

$$\begin{aligned} \Psi ^2_{i,j}\widehat{\varepsilon }_{i,j}&=\Psi ^1_{i,j}\widehat{\varepsilon }_{i,j} +(\Psi ^2_{i,j}-\Psi ^1_{i,j})\widehat{\varepsilon }_{i,j}\nonumber \\&\quad =\Psi ^1_{i,j}\widehat{\varepsilon }_{i,j}+\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.53)

Analogously we can get

$$\begin{aligned}&\Psi ^{2,l}_{i,j}\widehat{\chi }^{\,l}[\widehat{\varepsilon }\,]_{i,j}= \Psi ^{1,l}_{i,j}\widehat{\chi }^{\,l}[\widehat{\varepsilon }\,]_{i,j}+\mathcal {O}(h^{m+1}),\quad l=\mathbf {f},\mathbf {v}, \end{aligned}$$

(3.54)

$$\begin{aligned}&R^{2,l}_{i,j}(\chi ^{l}[y]_{i,j}-\widetilde{z\,}_{l}[y](t_{i,j})) =R^{1,l}_{i,j}(\chi ^{l}[p]_{i,j}\nonumber \\&\quad -\widetilde{z\,}_{l}[p](t_{i,j})) +\mathcal {O}(h^{m+1}),~l=\mathbf {f},\mathbf {v}. \end{aligned}$$

(3.55)

Then based on the above discussion, we rewrite (3.37) in the following form

$$\begin{aligned} \Big (L^{(1)}_{\mathcal {A}}\theta \Big )_{i,j}&=\Psi ^1_{i,j}\theta _{i,j} +\sum _{l=\mathbf {f},\mathbf {v}}\Psi ^{1,l}_{i,j}\chi ^{\,l}[\theta ]_{i,j}\nonumber \\&\quad +F(t_{i,j},y(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j}))\nonumber \\&\quad -F(t_{i,j},y(t_{i,j}),z_{\mathbf {f}}[y](t_{i,j}),z_{\mathbf {v}}[y](t_{i,j}))\nonumber \\&\quad +F(t_{i,j},y(t_{i,j}),z_{\mathbf {f}}[y](t_{i,j}),z_{\mathbf {v}}[y](t_{i,j}))\nonumber \\&\quad -F(t_{i,j},p(t_{i,j}) ,\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j}))\nonumber \\&\quad +F(t_{i,j},p(t_{i,j}) ,z_{\mathbf {f}}[p](t_{i,j}),z_{\mathbf {v}}[p](t_{i,j}))\nonumber \\&\quad -F(t_{i,j},p(t_{i,j}) ,z_{\mathbf {f}}[p](t_{i,j}),z_{\mathbf {v}}[p](t_{i,j}))\nonumber \\&\quad +Q_{\mathcal {A}}\Big (F(t_{i,j},p(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}) ,\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j}))\Big )\nonumber \\&\quad -Q_{\mathcal {A}}\Big (F(t_{i,j},p(t_{i,j}),z_{\mathbf {f}}[p](t_{i,j}) ,z_{\mathbf {v}}[p](t_{i,j}))\Big )\nonumber \\&\quad +Q_{\mathcal {A}}\Big (F(t_{i,j},p(t_{i,j}),z_{\mathbf {f}}[p](t_{i,j}) ,z_{\mathbf {v}}[p](t_{i,j}))\Big )\nonumber \\&\quad -Q_{\mathcal {A}}\Big (F(t_{i,j},y(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}) ,\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j}))\Big )\nonumber \\&\quad +Q_{\mathcal {A}}\Big (F(t_{i,j},y(t_{i,j}),z_{\mathbf {f}}[y](t_{i,j}) ,z_{\mathbf {v}}[y](t_{i,j}))\Big )\nonumber \\&\quad -Q_{\mathcal {A}}\Big (F(t_{i,j},y(t_{i,j}),z_{\mathbf {f}}[y](t_{i,j}) ,z_{\mathbf {v}}[y](t_{i,j}))\Big )\nonumber \\&\quad +\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.56)

By using the Lipschitz condition for F and lemma 2.1, we have

$$\begin{aligned}&|F(t_{i,j},y(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[y](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[y](t_{i,j}))\nonumber \\&\quad -F(t_{i,j},y(t_{i,j}),z_{\mathbf {f}}[y](t_{i,j}),z_{\mathbf {v}}[y](t_{i,j}))| =\mathcal {O}(h^{m+1}), \end{aligned}$$

(3.57)

$$\begin{aligned}&|F(t_{i,j},p(t_{i,j}),\widetilde{z\,}_{\mathbf {f}}[p](t_{i,j}),\widetilde{z\,}_{\mathbf {v}}[p](t_{i,j}))\nonumber \\&\quad -F(t_{i,j},p(t_{i,j}),z_{\mathbf {f}}[p](t_{i,j}),z_{\mathbf {v}}[p](t_{i,j}))| =\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.58)

Therefore, we can write (3.56) as

$$\begin{aligned} \Big (L^{(1)}_{\mathcal {A}}\theta \Big )_{i,j}&=\Psi ^1_{i,j}\theta _{i,j} +\sum _{l=\mathbf {f},\mathbf {v}}\Psi ^{1,l}_{i,j}\chi ^{\,l}[\theta ]_{i,j}\nonumber \\&\quad +\Theta (t_{i,j})-Q_{\mathcal {A}}\big (\Theta (t_{i,j})\big )+\mathcal {O}(h^{m+1}), \end{aligned}$$

(3.59)

where

$$\begin{aligned} \Theta (t_{i,j})&:=F(t_{i,j},y(t_{i,j}) ,z_{\mathbf {f}}[y](t_{i,j}),z_{\mathbf {v}}[y](t_{i,j}))\nonumber \\&\quad -F(t_{i,j},y(t_{i,j}) ,z_{\mathbf {f}}[p](t_{i,j}),z_{\mathbf {v}}[p](t_{i,j})). \end{aligned}$$

(3.60)

By using the Taylor expansion we have

$$\begin{aligned} |\Theta (t_{i,j})-Q_{\mathcal {A}}\big (\Theta (t_{i,j})\big )| \le \ C h \max |\Theta ^{\prime }(t)|. \end{aligned}$$

(3.61)

We can find

$$\begin{aligned} ||\Theta ^{\prime }(t)||_{\infty }&=||F_t\Big (t,p(t),z_{\mathbf {f}}[p](t),z_{\mathbf {v}}[p](t)\Big )\nonumber \\&\qquad -F_t\Big (t,y(t),z_{\mathbf {f}}[y](t),z_{\mathbf {v}}[y](t)\Big )\nonumber \\&\qquad +F_y\Big (t,p(t),z_{\mathbf {f}}[p](t),z_{\mathbf {v}}[p](t),\Big )p^{\prime }(t)\nonumber \\&\qquad -F_y\Big (t,y(t),z_{\mathbf {f}}[y](t),z_{\mathbf {v}}[y](t)\Big )y^{\prime }(t)\nonumber \\&\qquad +F_{z_{\mathbf {f}}}\Big (t,p(t),z_{\mathbf {f}}[p](t),z_{\mathbf {v}}[p](t)\Big )z_{\mathbf {f}}^{\prime }[p](t)\nonumber \\&\qquad -F_{z_{\mathbf {f}}}\Big (t,y(t),z_{\mathbf {f}}[y](t),z_{\mathbf {v}}[y](t)\Big )z_{\mathbf {f}}^{\prime }[y](t)\nonumber \\&\qquad +F_{z_{\mathbf {v}}}\Big (t,p(t),z_{\mathbf {f}}[p](t),z_{\mathbf {v}}[p](t)\Big )z_{\mathbf {v}}^{\prime }[p](t)\nonumber \\&\qquad -F_{z_{\mathbf {v}}}\Big (t,y(t),z_{\mathbf {f}}[y](t),z_{\mathbf {v}}[y](t)\Big )z_{\mathbf {v}}^{\prime }[y](t) ||_{\infty }\nonumber \\&\quad \le C_1||p-y||_{\infty } +C_2||p^{\prime }-y^{\prime }||_{\infty }\nonumber \\&\qquad +C_3||z^{\prime }_{\mathbf {f}}[p](t)-z^{\prime }_{\mathbf {f}}[y](t)||_{\infty }\nonumber \\&\qquad +C_4||z^{\prime }_{\mathbf {v}}[p](t)-z^{\prime }_{\mathbf {v}}[y](t)||_{\infty }\nonumber \\&\quad =\mathcal {O}(h^{m}). \end{aligned}$$

(3.62)

In this step based on the above discussion, we have

$$\begin{aligned} \Big (L^{(1)}_{\mathcal {A}}\theta \Big )_{i,j}&=\Psi ^1_{i,j}\theta _{i,j} +\sum _{l=\mathbf {f},\mathbf {v}}\Psi ^{1,l}_{i,j}\chi ^{\,l}[\theta ]_{i,j} +\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.63)

By stability of forward Euler scheme, we can find

$$\begin{aligned} ||\theta ||_{\infty }=||e-\varepsilon ||_{\infty }=\mathcal {O}(h^{m+1}). \end{aligned}$$

(3.64)

$\square$

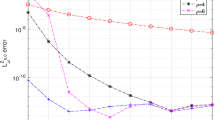
4 Numerical illustration

In this section to illustrate the theoretical results, some numerical results are presented. For all examples, we choose n collocation intervals of length 1 / n. Also we have computed the numerical results by using Mathematica-9.0 programming.

Example 4.1

To check Theorem 3.6, we consider FVID equation as follows

$$\begin{aligned} y^{\prime }(t)&=t^2y(t)+a(t)+\sum ^1_{l=0}\left( \int ^{1}_{0}s\cos (t)y^{(l)}(s)\hbox {d}s\right. \\&\left. \quad +\int ^{t}_{0}t^l\sin (s)y^{(l)}(s)\hbox {d}s\right) . \end{aligned}$$

In this example, we assume that $\alpha =1,\beta =0$ and $I:=[0,1]$. Also a(t) is chosen so that exact solution is $y(t)=\exp (2t)$. In Tables 1 and 2, we choose $m=2$ and $m=3$ and assume that $\rho _i\,(i=0,\ldots ,m+1)$ are equidistant. Also in Table 3, we choose $m=3$ and $\{\rho _0,\rho _1\,\rho _2,\rho _3\}=\{0,0.15,0.80,1\}$.

Table 1 Numerical results for Example 4.1

Table 2 Numerical results for Example 4.1

Table 3 Numerical results for Example 4.1

Example 4.2

Now we consider nonlinear case as follows

$$\begin{aligned} y^{\prime }(t)&=y^2(t)+a(t)+\int ^{1}_{0}st\Big (y(s)y^{\prime }(s)\\&\quad +1\Big )\hbox {d}s+\int ^{t}_{0}s\Big (y^2(s)+t\Big ) \hbox {d}s. \end{aligned}$$

We assume that $I=[0,1]$. Also a(t) chosen so that exact solution is $y(t)=\cos (t)$. In Table 4, we choose $\alpha =1,\beta =0$ and $m=4$. In Tables 5 and 6, we choose $m=2$ and $\alpha =\beta =1$. Also in Tables 4 and 5, we assume that $\rho _i\,(i=0,\ldots ,m+1)$ are equidistant, and in Table 6 we choose $\{\rho _0,\rho _1\,\rho _2,\rho _3\}=\{0,0.2,0.7,1\}$. By using this example, we reveal Theorem 3.7.

Table 4 Numerical results for Example 4.2

Table 5 Numerical results for Example 4.2

Table 6 Numerical results for Example 4.2

Example 4.3

We consider here the numerical results for Algorithm 2. In this example, Eq. (1.1) is considered as follows

$$\begin{aligned} y^{\prime }(t)&=y^2(t)+a(t)+\int ^{1}_{0}st^2\Big (y(s)+y^{\prime }(s) \Big )\hbox {d}s\nonumber \\&\quad +\int ^{t}_{0}s^3\big (y^2(s)+t\big ) \hbox {d}s, \end{aligned}$$

in the interval [0, 1]. a(t) chosen so that exact solution is $y(t)=\exp (-t)$. Tables 7, 8 and 9 compare our numerical results with collocation method. In the numerical results, $e^*$ denotes the error of the improved collocation method. Table 7 is obtained by using $\alpha =1,~\beta =0,~m=2,~ \{\rho _0,\rho _1\,\rho _2,\rho _3\}=\{0,0.2,0.7,1\}$. In Table 8, we consider $\alpha =1,~\beta =0,~m=3,~\rho _i=i/4~(i=0,\ldots ,4)$. Also $\alpha =\beta =1,~m=4,~ ~\rho _i=i/5~(i=0,\ldots ,5)$ are considered for Table 9.

Table 7 Numerical results for Example 4.3

Table 8 Numerical results for Example 4.3

Table 9 Numerical results for Example 4.3

Example 4.4

Consider FVID equation as

$$\begin{aligned} y^{\prime }(t)&+y(t)=a(t)+\frac{1}{4}\int ^{1}_{0}ty^3(s)\hbox {d}s \\&\quad -\frac{1}{2}\int ^{t}_{0}sy^2(s)\hbox {d}s,\quad I=[0,1], y(0)=0, \end{aligned}$$

where

$$\begin{aligned} a(t)=\frac{1}{10}t^6+t^2+2t-\frac{1}{32}. \end{aligned}$$

The exact solution of this problem is $y(t)=t^2$. We choose $m=2$ and assume that $\rho _i\,(i=0,\ldots ,m+1)$ are equidistant. In Table 10, the improved collocation method has been compared with methods in Siraj-ul-Islam et al. (2014), Babolian et al. (2009), Maleknejad et al. (2011). Note that 1 / n represents the length of the partition interval. By using the results, it can be seen that the results of the proposed method are more accurate than others.

Table 10 Comparison of point wise absolute errors for Example 4.4

5 Conclusion

In this paper, we study the deviation of the error for the linear and nonlinear first-order FVID equations. It is shown that the order of the deviation of the error estimation is at least $\mathcal {O}(h^{m+1})$, where m is the degree of piecewise polynomial. Also the piecewise polynomial collocation method is improved by using the defect correction principle and the deviation of the error estimation. In numerical section, examples confirming the theoretical results are given. Therefore, based on theoretical results and numerical examples, improved method can be applied to linear and nonlinear first-order Fredholm–Volterra integro- differential equations.