An accurate Legendre collocation method for third-kind Volterra integro-differential equations with non-smooth solutions

Abstract

This work is to analyze a Legendre collocation approximation for third-kind Volterra integro-differential equations. The rigorous error analysis in the $L^{\infty }$ and $L_{\omega ^{0,0}}^{2}$-norms is provided for the proposed method. In fact when converting the original equation to an equivalent second kind one, the integral operator of the obtained equation contains two singularities and may become non-compact under certain conditions. In addition, in order to avoid the low-order accuracy caused by the singularity of the solution at the initial point, we adopted the idea of smooth transformation at the beginning to convert the original equation into a new equation with a more regular solution. Finally, the validity and applicability of the method are verified by several numerical experiments.

1 Introduction

This work is concerned with numerical results for third-kind Volterra integro-differential equations (VIDEs) of the form

$$ t^{\beta}y^{\prime}(t) = a_{1}(t)y(t)+ g_{1}(t)+({\varOmega}_{\alpha} y)(t),~~~~~t\in I:=[0,T], $$

(1)

with the initial condition

$$y(0)=0,$$

where β > 0,

$$ ({\varOmega}_{\alpha} y)(t) = {{\int}_{0}^{t}}(t-s)^{-\alpha}K(t,s)y(s)ds, $$

α ∈ [0,1), a₁(t) = t^βa(t), g₁(t) = t^βg(t), with a(t),g(t) ∈ C(I). The kernel function K(t,s) is continuous on the domain D = {(t,s) : 0 ≤ s ≤ t ≤ T}. Moreover, as in reference [5, 6], throughout this article for α + β ≥ 1, the kernel function K has the form

$$ K(t,s) = s^{\alpha+\beta-1}H(t,s), $$

where H(t,s) ∈ C(D).

The third-kind VIDE (1) is equivalent to a linear cordial VIDE (CVIDE)

$$ y^{\prime}(t) = a(t)y(t)+g(t)+{\varOmega}_{\alpha,\beta}y(t),~~~~~t\in I:=[0,T], $$

(2)

associated with the cordial Volterra integral operator

$$ {\varOmega}_{\alpha,\beta}y(t) = {{\int}_{0}^{t}}t^{-\beta}(t-s)^{-\alpha}K(t,s)y(s)ds. $$

(3)

Remark 1

It has been pointed out in [5, 25] that the operator Ω_α,β is compact from C(I) into itself for α + β ∈ (0,1) or α + β ≥ 1 with H(0,0) = 0, and the operator Ω_α,β is non-compact for α + β ≥ 1 with H(0,0)≠ 0.

Remark 2

The following VIDE which appears in [12]

$$ y^{\prime}(t) = a(t)y(t)+g(t)+{{\int}_{0}^{t}}\frac{s^{\beta-1}}{t^{\beta}}H(t,s)y(s)ds $$

(4)

is a particular case of (1) with α = 0.

In 1910, Volterra integral equations (VIEs) of the third kind were first studied by Evans [11]. In 2015, Allaei, Yang, and Brunner [4] first discussed the existence, uniqueness, and regularity of solutions to a class of VIEs of the third kind. In 2017, Allaei, Yang, and Brunner [5] presented a spline collocation method on modified graded meshes which safeguards both the solvability and the optimal orders of convergence. In 2019, Shayanfard et al. [17] explained and analyzed a multistep collocation method. Song, Yang, and Brunner [22] studied the collocation method for a class of nonlinear Volterra integral equations of the third kind. In 2020, Cai [6] proposed a spectral Legendre-Galerkin method. By decomposing the original operator into three operators, he also proved that the proposed method guarantees the unique solvability of the approximate equation and the quasi-optimal order of global convergence of the Galerkin solution. Moreover, the collocation method for (3) has been presented by Shayanfard et al. [18], but in which the relevant integral operator is compact.

In [10], a numerical collocation method is developed for solving non-linear VIDEs of the neutral type. On account of more natural non-local approximations in addition to high accuracy in the case of smooth solutions, spectral collocation methods for VIEs and VIDEs of the second kind have been studied by Tang et al. [1,2,3, 24]. In the last few years, spectral collocation methods have been applied to fractional differential equations and weakly singular Volterra integral equation of the second kind [7,8,9, 13, 23]. However, it is known that the solutions of fractional differential equations or weakly singular Volterra integral equation of the second kind are singular even for well-behaved inputs, so they have a limited regularity in the usual Sobolev space. In order to solve this problem, the idea of smoothing the solution by introducing a suitable change of variables has been considered for different types of equations [14, 16, 20, 21].

As far as we know, up to now the numerical method for (1) with α > 0 has not been studied. In this paper, Legendre collocation method, an easy-to-use variant of the spectral methods for the numerical solution of a class of third-kind Volterra integro-differential equations (1), is proposed. A rigorous convergence analysis of the proposed method is given and rates of convergence are established in the $L^{\infty }$ and $L^{2}_{\omega ^{0,0}}$-norms. An important aspect of this method is that the convergence order of spectral approximations is only limited by the regularity of the underlying function. Finally, the numerical experiment results show that our numerical method is not only applicable to equations with non-compact integrals, but also can obtain high-order spectral accuracy for non-smooth solutions.

With these premises, the rest of this paper is organized as follows. In Section 2, the Legendre collocation method is used to approximate the solution of (1). In Section 3, we introduce some useful lemmas to establish the convergence results. In Section 4, the theoretical convergence analysis is established. In the last section, numerical examples are given to support our theoretical results and to demonstrate the significant gain in accuracy.

2 Numerical scheme

In this section, we propose a Legendre collocation method for the third-kind Volterra integro-differential equations (1). For a given positive integer N, let $\mathbb {P}_{N}$ denote the space of all polynomials of degree not exceeding N. For α > − 1 and β > − 1,

$$ L^{2}_{\omega^{\alpha,\beta}}(-1,1)=\{u~|~u~is~measurable~and~\|u\|_{\omega^{\alpha,\beta}}<\infty\} $$

is the weighted Hilbert space equipped with the following inner product and norm

$$ (u,v)_{\omega^{\alpha,\beta}}={\int}^{1}_{-1}u(x)v(x)\omega^{\alpha,\beta}(x)dx, ~~~\|u\|_{\omega^{\alpha,\beta}}=(u,u)^{\frac{1}{2}}_{\omega^{\alpha,\beta}}, $$

(5)

where ω^α,β(x) = (1 − x)^α(1 + x)^β denotes a standard Jacobi weight function on (− 1,1). For any non-negative integer m, define

$$ H^{m}_{\omega^{\alpha,\beta}}(-1,1)=\{v~|~{\partial_{x}^{k}}v~\in L^{2}_{\omega^{\alpha,\beta}}(-1,1),~0\leq k\leq m\}, $$

with the norm

$$ |v|_{H^{m;N}_{\omega^{\alpha,\beta}}}=(\sum\limits_{k=min(m,N+1)}^{m}\|{\partial_{x}^{k}}v\|^{2}_{\omega^{\alpha,\beta}})^{\frac{1}{2}}, $$

let $B^{m}_{\omega ^{\alpha ,\beta }}$ be the non-uniformly weighted Sobolev space given by

$$ B^{m}_{\omega^{\alpha,\beta}}(-1,1)=\{v~|~{\partial_{x}^{k}}v~\in L^{2}_{\omega^{\alpha+k,\beta+k}}(-1,1),~0\leq k\leq m\}. $$

We also introduce the discrete inner product as

$$ (u,v)_{N,\omega^{\alpha,\beta}}=\sum\limits_{k=0}^{N}u(x_{k})v(x_{k})\omega_{k}. $$

(6)

where $\{x_{k},\omega _{k}\}_{k=0}^{N}$ is the set of quadrature nodes and weights relative to the Jacobi weight ω^α,β(x).

In order to improve the regularity of analytic solutions of the original (2), firstly, we make the change of variables

$$ t = \frac{T}{2^{\rho}}(1+x)^{\rho},s = \frac{T}{2^{\rho}}(1+\tau)^{\rho},~~~~~1\leq\rho\in \mathbb{N}, $$

(7)

under which the problem (2) is transformed into the following integro-differential equation

$$ \begin{array}{ll} u^{\prime}(x)= b(x)u(x)+f(x)+{\int}_{-1}^{x}\lambda_{\alpha, \beta, \rho}(x,\tau)J_{\alpha,\beta,\rho}(x,\tau)u(\tau)d\tau, \end{array} $$

(8)

in which

$$ \begin{array}{ll} &u(x)=y(\frac{T}{2^{\rho}}(1+x)^{\rho}),f(x)=\frac{\rho T}{2^{\rho}}(1+x)^{\rho-1}g(\frac{T}{2^{\rho}}(1+x)^{\rho}),\\ &b(x)=\frac{\rho T}{2^{\rho}}(1+x)^{\rho-1}a(\frac{T}{2^{\rho}}(1+x)^{\rho}),\\ &\lambda_{\alpha, \beta, \rho}(x,\tau)= \begin{cases} \frac{\rho^{2} T}{2^{\rho}}\frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x)^{\beta\rho-\rho+1}}(1+\tau)^{\rho(\alpha+\beta)-1},~~~~~~~~~~~~~~&\alpha+\beta\geq1,\\ \frac{\rho^{2} T}{2^{\rho}}(\frac{T}{2^{\rho}})^{1-\alpha-\beta}\frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x)^{\beta\rho-\rho+1}}(1+\tau)^{\rho-1},~&\alpha+\beta<1,\\ \end{cases}\\ &J_{\alpha, \beta, \rho}(x,\tau)= \begin{cases} H(\frac{T}{2^{\rho}}(1+x)^{\rho},\frac{T}{2^{\rho}}(1+\tau)^{\rho}),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ &\alpha+\beta\geq1,\\ K(\frac{T}{2^{\rho}}(1+x)^{\rho},\frac{T}{2^{\rho}}(1+\tau)^{\rho}),~&\alpha+\beta<1,\\ \end{cases} \end{array} $$

(9)

and the solution of the new equation does not involve any singularities in its derivatives up to a certain order.

By integrating both sides of (8), we further obtain the equivalent integral equations

$$ \begin{array}{ll} &u(x)={\int}_{-1}^{x}f(\tau)d\tau +{\int}_{-1}^{x} b(\tau)u(\tau)d\tau+ {\int}_{-1}^{x}z(\tau)d\tau ,\\ &z(x)={\int}_{-1}^{x}\lambda_{\alpha, \beta, \rho}(x,\tau)J_{\alpha,\beta,\rho}(x,\tau)u(\tau)d\tau. \end{array} $$

(10)

To compute the integral term in (10) accurately, we make a simple linear transformation

$$ \tau=\tau(x,\vartheta)=\frac{1+x}{2}\vartheta+\frac{x-1}{2},~~~~\vartheta\in [-1,1], $$

then (10) becomes

$$ \begin{array}{ll} &u(x)=\widehat{f}(x)+\frac{1+x}{2} {\int}_{-1}^{1} [b(\tau(x,\vartheta))u(\tau(x,\vartheta))+z(\tau(x,\vartheta))]d\vartheta,\\ &z(x)={\int}_{-1}^{1}\chi_{\alpha,\beta,\rho}(\vartheta)\psi_{\alpha, \beta, \rho}(x,\vartheta)u(\tau(x,\vartheta))d\vartheta, \end{array} $$

(11)

where

$$ \begin{array}{ll} \widehat{f}(x)&={\int}_{-1}^{x}f(\tau)d\tau,\\ \chi_{\alpha,\beta,\rho}(\vartheta)&= \begin{cases} (1-\vartheta)^{-\alpha}(1+\vartheta)^{\rho(\alpha+\beta)-\lceil\rho(\alpha+\beta)\rceil},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1,\\ (1-\vartheta)^{-\alpha},~&\alpha+\beta<1,\\ \end{cases}\\ \varsigma(x,\vartheta)&= \begin{cases} H(\frac{T}{2^{\rho}}(1+x)^{\rho},\frac{T}{2^{2\rho}}(1+x)^{\rho}(1+\vartheta)^{\rho}),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1,\\ K(\frac{T}{2^{\rho}}(1+x)^{\rho},\frac{T}{2^{2\rho}}(1+x)^{\rho}(1+\vartheta)^{\rho}),~&\alpha+\beta<1,\\ \end{cases}\\ \phi_{\alpha, \beta, \rho}(\vartheta)&= \begin{cases} \frac{\rho^{2}T}{2^{(\beta+1)\rho}}({\sum}^{\rho-1}_{i=0}2^{i}(1+\vartheta)^{\rho-i-1})^{-\alpha} (1+\vartheta)^{\lceil\rho(\alpha+\beta)\rceil-1},~~~~~~~~~~~~~~~&\alpha+\beta\geq1,\\ \frac{\rho^{2}T}{2^{(\beta+1)\rho}}(\frac{T}{2^{\rho}})^{1-\alpha-\beta}({\sum}^{\rho-1}_{i=0}2^{i}(1+\vartheta)^{\rho-i-1})^{-\alpha} (1+\vartheta)^{\rho-1},~&\alpha+\beta<1,\\ \end{cases}\\ \psi_{\alpha, \beta, \rho}(x,\vartheta)&= \begin{cases} (1+x)^{\rho-1}\phi_{\alpha, \beta, \rho}(\vartheta)\varsigma(x,\vartheta), ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1,\\ (1+x)^{\rho-1}(\frac{1+x}{2})^{(1-\alpha-\beta)\rho}\phi_{\alpha, \beta,\rho}(\vartheta)\varsigma(x,\vartheta), ~&\alpha+\beta<1.\\ \end{cases} \end{array} $$

(12)

We denote by $\{\vartheta _{1,k},\omega _{1,k}\}_{k=0}^{N}, \{\vartheta _{2,k},\omega _{2,k}\}_{k=0}^{N}$ the set of quadrature nodes and weights relative to the Jacobi weights ω^0,0 and χ_α,β,ρ, respectively, thus the integral terms in above equation can be approximated by

$$ \begin{array}{@{}rcl@{}} {\int}_{-1}^{1} [b(\tau(x,\vartheta))u(\tau(x,\vartheta))+z(\tau(x,\vartheta))]d\vartheta &\approx& {\sum}_{k=0}^{N}[b(\tau(x,\vartheta_{1,k}))u(\tau(x,\vartheta_{1,k}))\\&&+z(\tau(x,\vartheta_{k}))]\omega_{1,k},\\ {\int}_{-1}^{1}\chi_{\alpha,\beta,\rho}(\vartheta)\psi_{\alpha, \beta, \rho}(x,\vartheta)u(\tau(x,\vartheta))d\vartheta &\approx& {\sum}_{k=0}^{N}\psi_{\alpha, \beta, \rho}(x,\vartheta_{2,k})u(\tau(x,\vartheta_{2,k}))\omega_{2,k}. \end{array} $$

Now, we turn to considering the Legendre collocation method for solving (11). We denote the collocation points by $\{x_{j}\}_{j=0}^{N}$ which are the set of (N + 1) Legendre-Gauss-Lobatto points corresponding to the weight function ω^0,0 in interval [− 1,1]. And consider the Lagrange interpolation operator ${I^{N}_{x}}:C[-1,1]\rightharpoonup \mathbb {P}_{N}$ defined by

$$ {I^{N}_{x}}u(x)=\sum\limits_{j=0}^{N}\mathcal{F}_{j}(x)u(x_{j}), $$

(13)

where $\{\mathcal {F}_{j}(x)\}^{N}_{j=0}$ are the Lagrange basis functions corresponding to the non-uniform mesh $\{x_{j}\}_{j=0}^{N}$.

Discretize (11) at x_i,

$$ u(x_{i})=\widehat{f}(x_{i})+\frac{1+x_{i}}{2} {\int}_{-1}^{1} [b(\tau(x_{i},\vartheta))u(\tau(x_{i},\vartheta))+z(\tau(x_{i},\vartheta))]d\vartheta,\\ $$

(14)

we use u_i to indicate the approximate values for u(x_i), 0 ≤ j ≤ N. The Legendre collocation method to (11) is to seek approximate solution in the form $u^{N}(x)={\sum }_{i=0}^{N}u_{i}\mathcal {F}_{i}(x)\in \mathbf {P}_{N}$ such that u_i, i = 0,⋯ ,N satisfy the following discrete collocation conditions:

$$ \begin{array}{ll} u_{i}= &\widehat{f}(x_{i})+\frac{1+x_{i}}{2}\sum\limits_{k=0}^{N}\omega_{1,k}[b(\tau(x_{i},\vartheta_{1,k})) \sum\limits_{l=0}^{N}u_{l}\mathcal{F}_{l}(\tau(x_{i},\vartheta_{1,k}))\\ &+\sum\limits_{p=0}^{N} \omega_{2,p}\psi_{\alpha, \beta, \rho}(\tau(x_{i},\vartheta_{1,k}),\vartheta_{2,p}) \sum\limits_{l=0}^{N}u_{l}\mathcal{F}_{l}(\tau(\tau(x_{i},\vartheta_{1,k}),\vartheta_{2,p}))]. \end{array} $$

(15)

Using notations

$$ \begin{array}{ll} U= &(u_{0},u_{1},\cdots,u_{N})^{T}, F=(\widehat{f}(x_{0}),\widehat{f}(x_{1}),\cdots,\widehat{f}(x_{N}))^{T},\\ a_{i,l}=&\frac{1+x_{i}}{2}\sum\limits_{k=0}^{N}\omega_{1,k}b(\tau(x_{i},\vartheta_{1,k}))\mathcal{F}_{l}(\tau(x_{i},\vartheta_{1,k})),\\ b_{i,l}= &\sum\limits_{k=0}^{N}\omega_{1,k}\sum\limits_{p=0}^{N} \omega_{2,p}\psi_{\alpha, \beta, \rho}(\tau(x_{i},\vartheta_{1,k}),\vartheta_{2,p}) \mathcal{F}_{l}(\tau(\tau(x_{i},\vartheta_{1,k}),\vartheta_{2,p}))],\\ A=&[a_{i,l}+b_{i,l}]_{i,l=0}^{N}, \end{array} $$

we obtain the matrix form

$$ \begin{array}{ll} U= F+AU. \end{array} $$

(16)

Having determined the approximation u^N(x) for problem (8), we can determine the approximation

$$ \begin{array}{ll} y^{N}(t)=u^{N}(2(\frac{t}{T})^{\frac{1}{\rho}}-1)=\sum\limits_{j=0}^{N}u_{j}\mathcal{F}_{j}(2(\frac{t}{T})^{\frac{1}{\rho}}-1) \end{array} $$

(17)

for the solution of the problem (1).

3 Preliminaries

In this section, we will make some necessary preparations. Throughout this paper, C denotes a positive constant that is independent of N and may have different values in different occurrences.

In order to describe the regularity of the solution u to (1), we require to introduce a few notations. For given $m\in \mathbb {N}$ and $\nu \in \mathbb {R}$, ν < 1, by C^m,ν(0,T] we denote the set of continuous functions $f:[0,T]\rightarrow \mathbb {R}$ which are m times continuously differentiable in (0,T], such that for all t ∈ (0,T] and i = 1,2,⋯ ,m the following estimates hold:

$$ \begin{array}{ll} |f^{(i)}(t)|\leq c \begin{cases} 1~~~~~~~~~~~&if~~i<1-\nu,\\ 1+|\log t| &if~~i=1-\nu,\\ t^{1-i-\nu} &if~~i>1-\nu.\\ \end{cases} \end{array} $$

By $\mathbb {C}^{r,\kappa }(-1,1)$ denote the space of functions whose rth derivatives are H$\ddot {o}$lder continuous with exponent κ, endowed with the usual norm

$$ \|v\|_{r,\kappa}= \underset{0\leq k\leq r}{\max}\underset{-1\leq x\leq 1}{\max}\mid {\partial^{k}_{x}}v(x)\mid+ \underset{x\neq y}{\sup}\frac{\mid {\partial^{r}_{x}}v(x)-{\partial^{r}_{x}}v(y)\mid}{\mid x-y\mid^{\kappa}}. $$

Lemma 1

[19] For any function $v\in B^{m}_{\omega ^{-1,-1}}(-1,1)$, we have

$$ \|{\partial_{x}^{r}}(v-{I^{N}_{x}}v)\|_{\omega^{r,r}}\leq CN^{r-m}\|{\partial_{x}^{m}}v\|_{\omega^{m,m}}, $$

(18)

and

$$ \|v-{I^{N}_{x}}v\|_{\infty}\leq C N^{\frac{1}{2}-m}\|{\partial_{x}^{m}}v\|_{\omega^{m-1,m-1}}. $$

(19)

Lemma 2

[19] Let $\{\mathcal {F}_{j}(x)\}^{N}_{j=0}$ be the Lagrange basis polynomials associated with the Jacobi-Gauss-Lobatto interpolations with the parameter pair {−μ,0}. Then for $-\frac {1}{2}\leq \mu <\frac {3}{2}$, we have

$$ \begin{array}{ll} \varLambda_{N}:=\underset{x\in[-1,1]}{\max}\sum\limits^{N}_{j=0}|\mathcal{F}_{j}(x)|\sim\ln N, \end{array} $$

and for every bounded function v(x), there exists a constant C independent of v such that

$$ \|{I^{N}_{x}}v\|_{\omega^{\alpha,\beta}}=\|\sum\limits_{j=0}^{N}v(x_{j})\mathcal{F}_{j}(x)\|_{\omega^{\alpha,\beta}}\leq C\|v\|_{\infty}. $$

Lemma 3

[19] If $v\in B^{m}_{\omega ^{-1,-1}}(-1,1)$ for some m ≥ 1, then for the Jacobi-Gauss integration, we have

$$ \begin{array}{ll} |(v,\phi)_{\omega^{\alpha,\beta}}-(v,\phi)_{N,\omega^{\alpha,\beta}}|\leq CN^{-m}\|{\partial_{x}^{m}}v\|_{\omega^{m-1,m-1}}\|\phi\|_{\omega^{\alpha,\beta}},~~~~for~~ \forall\phi\in \mathbb{P}_{N}, \end{array} $$

We now need a result on the regularity of the kernel ψ_α,β,ρ(x_i,𝜗) defined by (12).

Lemma 4

Let ψ_α,β,ρ(x,𝜗), χ^α,β,ρ be defined by (12) , If $K(\cdot ,s),H(\cdot ,s)\in C^{m,1-\frac {m+1}{\rho }}(0,T]$, and $\rho \in \mathbb {N}$, then we have that

$$ \frac{\partial^{m}}{\partial\vartheta^{m}}\psi_{\alpha, \beta, \rho}(x,\vartheta)\in L^{2}_{_{\chi^{\alpha,\beta,\rho}}}(-1,1). $$

Thus, there exists K^∗ > 0, such that

$$ K^{\ast}=\underset{-1\leq x\leq 1}{\max}\mid\psi_{\alpha, \beta, \rho}(x,\vartheta)\mid_{H^{m;N}_{_{\chi^{\alpha,\beta,\rho}}}(-1,1)}. $$

(20)

Proof

If $K(\cdot ,s),H(\cdot ,s)\in C^{m,1-\frac {m+1}{\rho }}(0,T]$, it then follows from Lemma 4.1 of [15] that ς(⋅,𝜗) ∈ C^m,−m(− 1,1]. Due to $\rho , \lceil \rho (\alpha +\beta )\rceil \in \mathbb {N}$, it is very easy to verify that ϕ_α,β,ρ(𝜗) ∈ C^m[− 1,1]. Then, it is straightforward to prove that the functions $\frac {\partial ^{m}}{\partial \vartheta ^{m}}\psi _{\alpha , \beta , \rho }(x,\vartheta )\in C[-1,1]$, so the lemma is proved. □

Lemma 5

If L > 0 and v(x) is a non-negative, locally integrable function defined on [− 1,1] satisfying

$$ u(x) \leq v(x)+ L{\int}_{-1}^{x}(1+\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1})u(\tau)d\tau, $$

then there exists a constant C such that

$$ u(x) \leq v(x)+C{\int}_{-1}^{x}(1+\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1})v(\tau)d\tau. $$

Proof

By direct calculation, we obtain

$$ \begin{array}{ll} &{\int}_{-1}^{x}(1+\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1})d\tau\\ =&{\int}_{-1}^{x}d\tau+{\int}_{-1}^{x}\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1}d\tau\\ =&(x+1)+\frac{ T}{2^{\rho}}\frac{{\varGamma}(2-\alpha){\varGamma}(\alpha)}{{\varGamma}(2)}(x+1)^{\rho}, \end{array} $$

applying the generalization of Gronwall’s lemma, we get

$$ \begin{array}{ll} u(x)\leq v(x)+C{\int}_{-1}^{x}(1+\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1})v(\tau)d\tau. \end{array} $$

□

Lemma 6

[19] Let r be a non-negative integer and κ ∈ (0,1). Then, there exists a constant C such that, for any function $v(x)\in \mathbb {C}^{r,\kappa }(-1,1)$, there exists a polynomial function $\daleth _{N}v\in \mathbb {P}_{N}$ satisfying

$$ \|v-\daleth_{N}v\|_{\infty}\leq CN^{-r-\kappa} \parallel v\parallel_{r,\kappa}. $$

Below, we prove a result for the integral operator in (8), which will play a crucial role in the convergence analysis in the next section.

Lemma 7

If α ∈ [0,1), $1\leq \rho \in \mathbb {N}$, q ≥ 0 and (1 − α)ρ + q − γ > 0, then there exists a constant C depending on ∥l(x,⋅)∥_0,κ, such that for any function v(x) ∈ C(− 1,1) and any x₁,x₂ ∈ [− 1,1] with x₁ < x₂,

$$ \frac{|Mv(x_{1})-Mv(x_{2})|}{|x_{1}-x_{2}|^{\kappa}}\leq C \parallel v\parallel_{\infty}, $$

which implies

$$ \|Mv\|_{0,\kappa}\leq C \parallel v\parallel_{\infty}, $$

where

$$ Mv(x)={\int}_{-1}^{x}\frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x)^{\gamma}}(1+\tau)^{\rho-1+q}l(x,\tau)v(\tau)d\tau, $$

and $\kappa =\min \limits \{(1-\alpha )\rho +q-\gamma , 1-\alpha , 1-\alpha +\frac {q-\gamma }{\rho }\}$.

Proof

From the triangle inequality, we obtain

$$ \begin{array}{ll} &|Mv(x_{1})-Mv(x_{2})|\\ \leq& \mid{\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}[\frac{((1+x_{1})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{1})^{\gamma}}l(x_{1},\tau) \\&-\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}l(x_{2},\tau)]v(\tau)d\tau\mid\\ &+\mid{\int}_{x_{1}}^{x_{2}}(1+\tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}l(x_{2},\tau)v(\tau)d\tau\mid\\ \leq& |{\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}[\frac{((1+x_{1})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{1})^{\gamma}} -\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}] l(x_{1},\tau)v(\tau)\ d\tau|\\ &+{\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}} | l(x_{1},\tau)-l(x_{2},\tau)| | v(\tau)| d\tau\\ &+{\int}_{x_{1}}^{x_{2}}(1+\tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}| l(x_{2},\tau)|| v(\tau)| d\tau\\ =:&D_{1}+D_{2}+D_{3}. \end{array} $$

One verifies that

$$ \begin{array}{ll} D_{1}\leq&\parallel v\parallel_{\infty}\parallel l(x_{1},\tau)\parallel_{\infty} |{\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}[\frac{((1+x_{1})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{1})^{\gamma}} \\&-\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}] d\tau|. \end{array} $$

By the triangle inequality, we further obtain

$$ \begin{array}{ll} &|{\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}[\frac{((1+x_{1})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{1})^{\gamma}} -\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}] d\tau|\\ \leq & |{\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}\frac{((1+x_{1})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{1})^{\gamma}}d\tau - {\int}_{-1}^{x_{2}}(1 + \tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}}d\tau|\\ &+|{\int}_{x_{1}}^{x_{2}}(1+\tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}} d\tau|\\ = & \frac{{\varGamma}(1-\alpha){\varGamma}(1+\frac{q}{\rho})}{{\varGamma}(2-\alpha+\frac{q}{\rho})} |((1+x_{1})^{(1-\alpha)\rho+q-\gamma}-(1+x_{2})^{(1-\alpha)\rho+q-\gamma}|\\ &+|{\int}_{x_{1}}^{x_{2}}((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}(1+x_{2})^{q-\gamma}(1+\tau)^{\rho-1} d\tau|. \end{array} $$

If 0 < (1 − α)ρ + q − γ < 1, we have

$$ \begin{array}{ll} &|(1+x_{1})^{(1-\alpha)\rho+q-\gamma}-(1+x_{2})^{(1-\alpha)\rho+q-\gamma}|\\ =&((1-\alpha)\rho+q-\gamma){\int}_{x_{1}}^{x_{2}}(\tau+1)^{(1-\alpha)\rho+q-\gamma-1}d\tau\\ \leq & ((1-\alpha)\rho+q-\gamma){\int}_{x_{1}}^{x_{2}}(\tau-x_{1})^{(1-\alpha)\rho+q-\gamma-1}d\tau\\ = &| x_{1}-x_{2}|^{(1-\alpha)\rho+q-\gamma}\leq C| x_{1}-x_{2}|^{\kappa},\\ \end{array} $$

if (1 − α)ρ + q − γ ≥ 1, it is clear that

$$ \begin{array}{ll} |(1+x_{1})^{(1-\alpha)\rho+q-\gamma}-(1+x_{2})^{(1-\alpha)\rho+q-\gamma}| \leq &C| x_{1}-x_{2}| \leq C|x_{1}-x_{2}|^{\kappa}. \end{array} $$

If q < γ, a direct calculation shows that

$$ \begin{array}{ll} &|{\int}_{x_{1}}^{x_{2}}((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}(1+x_{2})^{q-\gamma}(1+\tau)^{\rho-1} d\tau|\\ \leq &|{\int}_{x_{1}}^{x_{2}}((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{\frac{q-\gamma}{\rho}-\alpha}(1+\tau)^{\rho-1} d\tau|\\ = &\frac{((1+x_{2})^{\rho}-(1+x_{1})^{\rho})^{\frac{q-\gamma}{\rho}-\alpha+1}}{\rho(\frac{q-\gamma}{\rho}-\alpha+1)} \leq C| x_{1}-x_{2}|^{\kappa}. \end{array} $$

If q ≥ γ, similarly, we can get

$$ \begin{array}{ll} &|{\int}_{x_{1}}^{x_{2}}((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}(1+x_{2})^{q-\gamma}(1+\tau)^{\rho-1} d\tau|\\ \leq &|{\int}_{x_{1}}^{x_{2}}((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}(1+\tau)^{\rho-1} d\tau|\\ \leq &\frac{((1+x_{2})^{\rho}-(1+x_{1})^{\rho})^{1-\alpha}}{\rho(1-\alpha)} \leq C| x_{1}-x_{2}|^{\kappa}. \end{array} $$

Hence

$$ \begin{array}{ll} D_{1}\leq& C\parallel v\parallel_{\infty}| x_{1}-x_{2}|^{\kappa}. \end{array} $$

and

$$ \begin{array}{ll} D_{3}&\leq C\parallel v\parallel_{\infty}\|l(x_{2},\tau)\|_{\infty} {\int}_{x_{1}}^{x_{2}}((1+x_{2})^{\rho} - (1+\tau)^{\rho})^{-\alpha}(1 + x_{2})^{q-\gamma}(1 + \tau)^{\rho-1}d\tau\\ &\leq C\parallel v\parallel_{\infty}| x_{1}-x_{2}|^{\kappa}. \end{array} $$

Moreover

$$ \begin{array}{ll} D_{2}&\leq C\parallel v\parallel_{\infty}| x_{1}-x_{2}|^{\kappa} {\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}} \frac{| l(x_{1},\tau)-l(x_{2},\tau)|}{| x_{1}-x_{2}|^{\kappa}} d\tau\\ &\leq C\parallel v\parallel_{\infty}| x_{1}-x_{2}|^{\kappa}\|l\|_{0,\kappa} {\int}_{-1}^{x_{1}}(1+\tau)^{\rho-1+q}\frac{((1+x_{2})^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x_{2})^{\gamma}} d\tau\\ &\leq C\parallel v\parallel_{\infty}| x_{1}-x_{2}|^{\kappa}. \end{array} $$

□

The above estimates finish the proof.

4 Convergence analysis

We now turn to the convergence analysis of the proposed scheme. Compared with the common kernel (t − s)^−α of the second-kind Volterra integral equation, the analysis for the integral kernel t^−β(t − s)^−αof third-kind VIDEs is much more involved.

Let e(x) = u(x) − u^N(x), then subtracting (15) from (14) and using the definition of the continuous and discrete inner products (5) and (6) we get

$$ \begin{array}{lll} u(x_{i})-u_{i}&=& \frac{1+x_{i}}{2}[(b(\tau(x_{i},.)),u(\tau(x_{i},.))_{\omega^{0,0}}+(1,z(\tau(x_{i},.)))_{\omega^{0,0}} \\&&-(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{N,\omega^{0,0}}\\ &&-(1,(\psi_{\alpha, \beta, \rho}(\tau(x_{i},.),.),u^{N}(\tau(\tau(x_{i},.),.)))_{N,\chi_{\alpha,\beta,\rho}})_{N,\omega^{0,0}}]\\ &=&{\int}_{-1}^{x_{i}}b(\tau)e(\tau)d\tau+ {\int}_{-1}^{x_{i}}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau\\ &&+\frac{1+x_{i}}{2}[(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{\omega^{0,0}}\\&&-(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{N,\omega^{0,0}}]\\ &&+(\frac{1+x_{i}}{2},(\psi_{\alpha, \beta, \rho}(\tau(x_{i},.),.),u^{N}(\tau(\tau(x_{i},.),.)))_{\chi_{\alpha,\beta,\rho}})_{\omega^{0,0}}\\ &&-(\frac{1+x_{i}}{2},(\psi_{\alpha, \beta, \rho}(\tau(x_{i},.),.),u^{N}(\tau(\tau(x_{i},.),.)))_{N,\chi_{\alpha,\beta,\rho}})_{N,\omega^{0,0}}. \end{array} $$

(21)

For convenience, denote

$$ \begin{array}{lll} z^{N}(\tau)&=&{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)u^{N}(s)ds \\&=&(\psi_{\alpha, \beta, \rho}(\tau(x_{i},.),.),u^{N}(\tau(\tau(x_{i},.),.)))_{\chi_{\alpha,\beta,\rho}}\\ I_{i,1}&=&\frac{1+x_{i}}{2}[(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{\omega^{0,0}}-(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{N,\omega^{0,0}}],\\ I_{i,2}&=&(\frac{1+x_{i}}{2},z(\tau(x_{i},.)))_{\omega^{0,0}}-(\frac{1+x_{i}}{2},z(\tau(x_{i},.)))_{N,\omega^{0,0}},\\ I_{i,3}&=&(\frac{1+x_{i}}{2},(z^{N}-z)(\tau(x_{i},.)))_{\omega^{0,0}}-(\frac{1+x_{i}}{2},(z^{N}-z)(\tau(x_{i},.)))_{N,\omega^{0,0}},\\ I_{i,4}&=&(\frac{1+x_{i}}{2},z^{N}(\tau(x_{i},.)) - (\psi_{\alpha,\beta,\rho}(\tau(x_{i},.),.),u^{N}(\tau(\tau(x_{i},.),.)))_{N,\chi_{\alpha,\beta,\rho}})_{N,\omega^{0,0}}. \end{array} $$

Multiplying both sides of (21) by $\mathcal {F}_{i}(x)$ and then summing up from i = 0 to i = N leads to

$$ {I^{N}_{x}}u - u^{N}={I^{N}_{x}}\!{\int}_{-1}^{x}[b(\tau)e(\tau)+\! {\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)ds]d\tau + {\sum}_{k=1}^{4}{I^{N}_{x}}I_{i,k}. $$

Denote by I the identity operator; by reorganizing the terms in the above equation, we obtain

$$ \begin{array}{ll} e(x)={\int}_{-1}^{x}[b(\tau)e(\tau)+ {\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)ds]d\tau +\sum\limits_{i=1}^{4}E_{i}(x), \end{array} $$

where

$$ \begin{array}{ll} E_{1}(x)&=(I-{I^{N}_{x}})u(x),~~~~ E_{2}(x)=\sum\limits_{k=1}^{4}{I^{N}_{x}}I_{i,k}, ~~~~E_{3}(x)\\&=({I^{N}_{x}}-I){\int}_{-1}^{x}b(\tau)e(\tau)d\tau,\\ E_{4}(x)&=({I^{N}_{x}}-I){\int}_{-1}^{x}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau. \end{array} $$

(22)

By using the relation

$$ {\int}_{-1}^{x}{\int}_{-1}^{\tau}\!\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau = \!{\int}_{-1}^{x}\!e(\tau){\int}_{\tau}^{x}\!\!\lambda_{\alpha, \beta, \rho}(s,\tau)J_{\alpha,\beta,\rho}(s,\tau)ds d\tau, $$

and the estimate

$$ \begin{array}{ll} &{\int}_{\tau}^{x}\lambda_{\alpha, \beta, \rho}(s,\tau)ds\\ =& \begin{cases} {\int}_{\tau}^{x}\frac{\rho^{2} T}{2^{\rho}}\frac{((1+s)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+s)^{\beta\rho-\rho+1}}(1+\tau)^{\rho(\alpha+\beta)-1}ds, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1\\ {\int}_{\tau}^{x}\frac{\rho^{2} T}{2^{\rho}}(\frac{T}{2^{\rho}})^{1-\alpha-\beta}\frac{((1+s)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+s)^{\beta\rho-\rho+1}}(1+\tau)^{\rho-1}ds, ~&\alpha+\beta<1\\ \end{cases}\\ =& \begin{cases} (1+\tau)^{\rho\alpha-1}{\int}_{\tau}^{x}\frac{\rho^{2} T}{2^{\rho}}(\frac{1+\tau}{1+s})^{\beta\rho}((1+s)^{\rho}- (1+\tau)^{\rho})^{-\alpha}(1+s)^{\rho-1}ds,~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1\\ (1+\tau)^{\rho-1-\beta\rho}{\int}_{\tau}^{x}\frac{\rho^{2} T}{2^{\rho}}(\frac{T}{2^{\rho}})^{1-\alpha-\beta}(\frac{1+\tau}{1+s})^{\beta\rho}((1+s)^{\rho}- (1+\tau)^{\rho})^{-\alpha}(1+s)^{\rho-1}ds, ~&\alpha+\beta<1\\ \end{cases}\\ \leq& \begin{cases} \frac{\rho T}{2^{\rho}}\frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}}{1-\alpha}(1+\tau)^{\rho\alpha-1}, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1\\ \frac{\rho T}{2^{\rho}}(\frac{T}{2^{\rho}})^{1-\alpha-\beta}\frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}}{1-\alpha}(1+\tau)^{\rho-1-\beta\rho} ~~&\alpha+\beta<1\\ \end{cases}\\ \leq &C\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1}, \end{array} $$

we can conclude

$$ \begin{array}{ll} &|{\int}_{-1}^{x}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau|\\ \leq&C{\int}_{-1}^{x}|e(\tau)|{\int}_{\tau}^{x}\lambda_{\alpha, \beta, \rho}(s,\tau)dsd\tau\\ \leq&C{\int}_{-1}^{x}\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1}|e(\tau)|d\tau. \end{array} $$

Thus,

$$ |e(x)|\!\leq\! C{\int}_{-1}^{x}(1+\frac{\rho T}{2^{\rho}}((1+x)^{\rho}-(1+\tau)^{\rho})^{1-\alpha}(1+\tau)^{\rho\alpha-1}) |e(\tau)| d\tau+{\sum}_{i=1}^{4}| E_{i}(x)|. $$

(23)

Theorem 1

Suppose that the given functions $K(\cdot ,s),H(\cdot ,s), a(t) \in C^{m,1-\frac {m+1}{\rho }}(0,T]$, and H(t,s) ∈ C¹(D). If $u,z\in B^{m}_{\omega ^{-1,-1}}(-1,1)$, then there exists a positive constant C such that for sufficiently large N the following error estimate holds

$$ \|e\|_{\infty}\leq C N^{-m}(\ln N M^{\ast}+N^{\frac{1}{2}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}),\\ $$

(24)

where

$$ M^{\ast}=\|{\partial_{x}^{m}}b\|_{\omega^{m-1,m-1}}\|u\|_{\omega^{0,0}}+K^{\ast}\|u\|_{\chi_{\alpha,\beta,\rho}} +\|{\partial_{x}^{m}}z\|_{\omega^{m-1,m-1}}+\|{\partial_{x}^{m}}u\|_{\omega^{m,m}},\\ $$

(25)

and K^∗ is defined by (20).

Proof

If $a(t)\in C^{m,1-\frac {m+1}{\rho }}(0,T]$, from Lemma 4.1 of [15], we obtain $\alpha (\frac {T}{2^{\rho }}(1+x)^{\rho })\in C^{m,-m}(-1,1]$. Thus, $b(x)=\frac {\rho T}{2^{\rho }}(1+x)^{\rho -1}a(\frac {T}{2^{\rho }}(1+x)^{\rho })\in C^{m,-m}(-1,1]\subseteq H^{m}_{\omega ^{0,0}}(-1,1)\subseteq B^{m}_{\omega ^{-1,-1}}(-1,1)$.

From (23), using Gronwall inequality, we have

$$ \begin{array}{ll} \parallel e(x)\parallel_{\infty}\leq C\sum\limits_{i=1}^{4}\|E_{i}(x)\|_{\infty}. \end{array} $$

(26)

Firstly, by Lemma 1, we obtain

$$ \begin{array}{ll} \|E_{1}(x)\|_{\infty}=\|u(x)-{I^{N}_{x}}u(x)\|_{\infty} \leq C N^{\frac{1}{2}-m}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}. \end{array} $$

(27)

In order to bound $\|E_{2}(x)\|_{\infty }$, we next estimate the terms $\max \limits _{1\leq i\leq N}|I_{i,k}|,k=1,2,3,4$ one by one. Using Lemma 3 leads to

$$ \begin{array}{lll} \underset{1\leq i\leq N}{\max}|I_{i,1}|&= &\underset{1\leq i\leq N}{\max} |\frac{1+x_{i}}{2}[(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{\omega^{0,0}}\\&&-(b(\tau(x_{i},.)),u^{N}(\tau(x_{i},.)))_{N,\omega^{0,0}}]|\\ &\leq &CN^{-m}\|{\partial_{x}^{m}}b\|_{\omega^{m-1,m-1}}\|u^{N}\|_{\omega^{0,0}} \\&\leq& C N^{-m}\|{\partial_{x}^{m}}b\|_{\omega^{m-1,m-1}}(\|u\|_{\omega^{0,0}}+\|e\|_{\omega^{0,0}})\\ &\leq &C N^{-m}\|{\partial_{x}^{m}}b\|_{\omega^{m-1,m-1}}(\|u\|_{\omega^{0,0}}+\|e\|_{\infty}), \end{array} $$

(28)

and

$$ \begin{array}{lll} \underset{1\leq i\leq N}{\max}|I_{i,2}|&= &\underset{1\leq i\leq N}{\max} |(\frac{1+x_{i}}{2},z(\tau(x_{i},.)))_{\omega^{0,0}}-(\frac{1+x_{i}}{2},z(\tau(x_{i},.)))_{N,\omega^{0,0}}| \\&\leq& CN^{-m}\|{\partial_{x}^{m}}z\|_{\omega^{m-1,m-1}}. \end{array} $$

(29)

By H$\ddot {o}$lder inequality, we deduce that

$$ \begin{array}{lll} \underset{1\leq i\leq N}{\max}|I_{i,3}|&=&\underset{1\leq i\leq N}{\max} |(\frac{1+x_{i}}{2},(z^{N}-z)(\tau(x_{i},.)))_{\omega^{0,0}}\\&&-(\frac{1+x_{i}}{2},(z^{N}-z)(\tau(x_{i},.)))_{N,\omega^{0,0}}|\\ &= &\underset{1\leq i\leq N}{\max} |{\int}_{-1}^{x_{i}}|(I- I^{N}_{\tau})(z-z^{N})(\tau)|d\tau|\\ &\leq& \underset{1\leq i\leq N}{\max} ({\int}_{-1}^{x_{i}}|(I- I^{N}_{\tau})(z-z^{N})(\tau)|^{2}d\tau)^{\frac{1}{2}}\\ &\leq & \|(I- I^{N}_{\tau})(z-z^{N})\|_{\omega^{0,0}}. \end{array} $$

(30)

In order to bound $\underset {1\leq i\leq N}{\max \limits }|I_{i,3}|$, next we need the error estimates for$\parallel (I- I^{N}_{\tau })(z-z^{N})\parallel _{\omega ^{0,0}}$ in three different cases.

-Case 1: α + β ≥ 1 and ρ = 1

If ρ = 1, the assumption of H(t,s) ∈ C¹(D) results that J_α,β,1(x,τ) ∈ C¹([− 1,1] × [− 1,1]); therefore, there exist ξ ∈ (− 1,x) and ζ ∈ (− 1,τ), so that we have the first-order Taylor expansion

$$ \begin{array}{ll} J_{\alpha, \beta, 1}(x,\tau)=J_{\alpha, \beta, 1}(-1,-1)+\tilde{J}_{\alpha, \beta, 1}(x,\tau), \end{array} $$

where

$$ \begin{array}{ll} \tilde{J}_{\alpha, \beta, 1}(x,\tau)=[(x+1)\frac{\partial}{\partial x}+(\tau+1)\frac{\partial}{\partial \tau}]J_{\alpha, \beta, 1}(\xi,\zeta). \end{array} $$

Obviously,

$$ \begin{array}{lll} (I- {I^{N}_{x}})(z-z^{N})(x)&=&(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha, \beta, 1}(x,\tau)e(\tau)d\tau.\\ &=&(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha, \beta, 1}(-1,-1)u(\tau)d\tau\\ &&-(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha, \beta, 1}(-1,-1)u^{N}(\tau)d\tau\\ &&+(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)\tilde{J}_{\alpha, \beta, 1}(x,\tau)e(\tau)d\tau. \end{array} $$

Then, we can see that

$$ \begin{array}{ll} \|(I- {I^{N}_{x}})(z-z^{N})\|_{\omega^{0,0}}=\|I^{1}_{i,3}+I^{2}_{i,3}+I^{3}_{i,3}\|_{\omega^{0,0}}\leq{\sum}_{k=1}^{3}\|I^{k}_{i,3}\|_{\omega^{0,0}}, \end{array} $$

where

$$ \begin{array}{ll} &I^{1}_{i,3}=(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha, \beta, 1}(-1,-1)u(\tau)d\tau,\\ &I^{2}_{i,3}=(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha, \beta, 1}(-1,-1)u^{N}(\tau)d\tau,\\ &I^{3}_{i,3}=(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)\tilde{J}_{\alpha, \beta, 1}(x,\tau)e(\tau)d\tau. \end{array} $$

With the help of Lemmas 1 and 2, we obtain that

$$ \begin{array}{lll} \|I^{1}_{i,3}\|_{\omega^{0,0}}&=&\|(I- {I^{N}_{x}}){\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha, \beta, 1}(-1,-1)u(\tau)d\tau\|_{\omega^{0,0}}\\ &\leq&C N^{-m}\|{\partial_{x}^{m}}{\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)J_{\alpha,\beta,1}(-1,-1) u(\tau)d\tau\|_{\omega^{m,m}} \\ &\leq &C N^{-m}\|{\partial_{x}^{m}}{\int}_{-1}^{1}\chi_{\alpha, \beta, 1}(\vartheta)\phi_{\alpha, \beta, 1}(\vartheta)J_{\alpha,\beta,1}(-1,-1) u(\tau(x,\vartheta))d\vartheta\|_{\omega^{m,m}}\\ &\leq& C N^{-m}\parallel {\int}_{-1}^{1}\chi_{\alpha, \beta, 1}(\vartheta)\phi_{\alpha, \beta, 1}(\vartheta)J_{\alpha,\beta,1}(-1,-1) \frac{\partial^{m}}{\partial x^{m}}[u(\tau(x,\vartheta))]d\vartheta\parallel_{\omega^{m,m}}\\ &\leq& C N^{-m}\parallel {\int}_{-1}^{1}\chi_{\alpha, \beta, 1}(\vartheta)\phi_{\alpha, \beta, 1}(\vartheta)J_{\alpha,\beta,1}(-1,-1) \frac{\partial^{m}}{\partial\tau^{m}}[u(\tau(x,\vartheta))](\frac{\partial\tau }{\partial x})^{m}d\vartheta\parallel_{\omega^{m,m}}\\ &\leq& C N^{-m}\parallel {\int}_{-1}^{1}\chi_{\alpha, \beta, 1}(\vartheta)\phi_{\alpha, \beta, 1}(\vartheta)J_{\alpha,\beta,1}(-1,-1) \frac{\partial^{m}}{\partial\tau^{m}}[u(\tau(x,\vartheta))](\frac{1+\vartheta}{2})^{m}d\vartheta\parallel_{\omega^{m,m}}\\ &\leq& C N^{-m}\|{\partial_{x}^{m}}u\|_{\omega^{m,m}}. \end{array} $$

Furthermore, since $u^{N}(x)\in \mathbf {P}_{N}$, ${\int \limits }_{-1}^{x}\lambda _{\alpha , \beta , 1}(x,\tau )J_{\alpha , \beta , 1}(-1,-1)u^{N}(\tau )d\tau$ is still a polynomial of the Nth degree, so we have

$$ \begin{array}{ll} \|I^{2}_{i,3}\|_{\omega^{0,0}}=0. \end{array} $$

And finally, we need to estimate $\|I^{3}_{i,3}\|_{\omega ^{0,0}}$. From (9), we obtain

$$ \begin{array}{ll} &{\int}_{-1}^{x}\lambda_{\alpha, \beta, 1}(x,\tau)\tilde{J}_{\alpha,\beta,1}(x,\tau)e(\tau)d\tau\\ =&{\int}_{-1}^{x}\frac{((1+x)-(1+\tau)^{-\alpha}}{(1+x)^{\beta-1}}(1+\tau)^{\alpha+\beta-1}\frac{\partial}{\partial x}J_{\alpha, \beta, 1}(\xi,\zeta)e(\tau)d\tau\\ &+{\int}_{-1}^{x}\frac{((1+x)-(1+\tau)^{-\alpha}}{(1+x)^{\beta}}(1+\tau)^{\alpha+\beta}\frac{\partial}{\partial \tau}J_{\alpha, \beta, 1}(\xi,\zeta)e(\tau)d\tau. \end{array} $$

Let

$$ \begin{array}{ll} M_{1}e(x)=&{\int}_{-1}^{x}\frac{((1+x)-(1+\tau)^{-\alpha}}{(1+x)^{\beta-1}}(1+\tau)^{\alpha+\beta-1}\frac{\partial}{\partial x}J_{\alpha, \beta, 1}(\xi,\zeta)e(\tau)d\tau,\\ M_{2}e(x)=&{\int}_{-1}^{x}\frac{((1+x)-(1+\tau)^{-\alpha}}{(1+x)^{\beta}}(1+\tau)^{\alpha+\beta}\frac{\partial}{\partial \tau}J_{\alpha, \beta, 1}(\xi,\zeta)e(\tau)d\tau. \end{array} $$

It can be verified that the integrals M₁e(x) and M₂e(x) satisfy all conditions of Lemma 7, and κ₁ = 1 − α ∈ (0,1). By using Lemmas 6 and 7, we obtain

$$ \begin{array}{ll} \|I^{3}_{i,3}\|_{\omega^{0,0}}&=\|({I^{N}_{x}}-I)(M_{1}+M_{2})e\|_{\omega^{0,0}} =\|({I^{N}_{x}}-I)(I-\daleth_{N})(M_{1}+M_{2})e\|_{\omega^{0,0}}\\ &\leq C\|{I^{N}_{x}}\|_{\omega^{0,0}}\|(I-\daleth_{N})(M_{1}+M_{2})e\|_{\infty} \leq CN^{\alpha-1}\|(M_{1}+M_{2})e\|_{0,1-\alpha}\\ &\leq CN^{\alpha-1}\|e\|_{\infty}. \end{array} $$

Consequently,

$$ \begin{array}{ll} \|(I- {I^{N}_{x}})(z-z^{N})\|_{\omega^{0,0}}\leq CN^{-m}\|{\partial_{x}^{m}}u\|_{\omega^{m,m}}+CN^{\alpha-1}\|e(x)\|_{\infty}. \end{array} $$

-Case 2: α + β ≥ 1 and ρ ≥ 2

Let

$$ \begin{array}{lll} M_{3}e(x)&=&{\int}_{-1}^{x}\lambda_{\alpha, \beta, \rho}(x,\tau)J_{\alpha,\beta,\rho}(x,\tau)e(\tau)d\tau\\ &=&{\int}_{-1}^{x}\frac{\rho^{2} T}{2^{\rho}}\frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x)^{\beta\rho-\rho+1}}(1+\tau)^{\rho(\alpha+\beta)-1}J_{\alpha,\beta,\rho}(x,\tau)e(\tau)d\tau. \end{array} $$

It is easy to see that $\kappa _{2}=\min \limits \{1-\alpha ,1-\frac {1}{\rho }\}\in (0,1)$. By using Lemmas 6 and 7, we obtain

$$ \begin{array}{ll} \|(I- {I^{N}_{x}})(z-z^{N})\|_{\omega^{0,0}}&=\|({I^{N}_{x}}-I)M_{3}e\|_{\omega^{0,0}} =\|({I^{N}_{x}}-I)(I-\daleth_{N})(M_{3}e)\|_{\omega^{0,0}}\\ &\leq C\|{I^{N}_{x}}\|_{\omega^{0,0}}\|(I-\daleth_{N})M_{3}e\|_{\infty} \leq CN^{-\kappa_{2}}\|M_{3}e\|_{0,\kappa_{2}}\\ &\leq CN^{-\kappa_{2}}\|e\|_{\infty}. \end{array} $$

-Case 3: α + β < 1

Let

$$ \begin{array}{@{}rcl@{}} M_{4}e(x)&=&{\int}_{-1}^{x}\lambda_{\alpha, \beta, \rho}(x,\tau)J_{\alpha,\beta,\rho}(x,\tau)e(\tau)d\tau\\ &=&{\int}_{-1}^{x}\frac{\rho^{2}T}{2^{\rho}}(\frac{T}{2^{\rho}})^{1-\alpha-\beta} \frac{((1+x)^{\rho}-(1+\tau)^{\rho})^{-\alpha}}{(1+x)^{\beta\rho-\rho+1}}(1+\tau)^{\rho-1}J_{\alpha,\beta,\rho}(x,\tau)e(\tau)d\tau. \end{array} $$

For any positive integer ρ, $\kappa _{3}=\min \limits \{(2-\alpha -\beta )\rho -1,1-\alpha ,2-\alpha -\beta -\frac {1}{\rho }\}>0$, similar to the proof of Case 2, we obtain

$$ \begin{array}{ll} \|(I- {I^{N}_{x}})(z-z^{N})\|_{\omega^{0,0}} &\leq CN^{-\kappa_{3}}\|e\|_{\infty}. \end{array} $$

Therefore, combining the results of the above three cases, we can derive

$$ \begin{array}{ll} \|(I- {I^{N}_{x}})(z-z^{N})\|_{\omega^{0,0}}\leq \begin{cases} CN^{-m}\|{\partial_{x}^{m}}u\|_{\omega^{m,m}}+CN^{-\kappa_{1}}\|e\|_{\infty},~~&\alpha+\beta\geq1 ~and ~\rho=1,\\ CN^{-\kappa_{2}}\|e\|_{\infty},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1 ~and ~\rho\geq2,\\ CN^{-\kappa_{3}}\|e\|_{\infty},~~~~~~~~~~~~~~~~&\alpha+\beta<1,\\ \end{cases} \end{array} $$

which, substituted into (30), gives

$$ \begin{array}{ll} \underset{1\leq i\leq N}{\max}|I_{i,3}|\leq \begin{cases} CN^{-m}\|{\partial_{x}^{m}}u\|_{\omega^{m,m}}+CN^{-\kappa_{1}}\|e\|_{\infty},~~&\alpha+\beta\geq1 ~and ~\rho=1,\\ CN^{-\kappa_{2}}\|e\|_{\infty},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1 ~and ~\rho\geq2,\\ CN^{-\kappa_{3}}\|e\|_{\infty},~~~~~~~~~~~~~~~~&\alpha+\beta<1.\\ \end{cases} \end{array} $$

(31)

In addition, by Lemma 3, Lemma 4, and the fact $|{\sum }_{k=1}^{N}\omega _{1,k}|={\int \limits }_{-1}^{1}d\tau =2$, we get

$$ \begin{array}{lll} \underset{1\leq i\leq N}{\max}|I_{i,4}|&=& \underset{1\leq i\leq N}{\max} |(\frac{1+x_{i}}{2},z^{N}(\tau(x_{i},.))- (\psi_{\alpha,\beta,\rho}(\tau(x_{i},.),.),u^{N}(\tau(\tau(x_{i},.),.)))_{N,\chi_{\alpha,\beta,\rho}})_{N,\omega^{0,0}}\\ &=&\underset{1\leq i\leq N}{\max}|\sum\limits_{k=1}^{N}\omega_{1,k}\{z^{N}(\tau(x_{i},\theta_{k})) - (\psi_{\alpha,\beta,\rho}(\tau(x_{i},\theta_{k}),.),u^{N}(\tau(\tau(x_{i},\theta_{k}),.)))_{N,\chi_{\alpha,\beta,\rho}}\}|\\ &\leq& 2\underset{1\leq i\leq N}{\max}\underset{1\leq k\leq N}{\max} |z^{N}(\tau(x_{i},\theta_{k}))-(\psi_{\alpha,\beta,\rho}(\tau(x_{i},\theta_{k}),.),u^{N}(\tau(\tau(x_{i},\theta_{k}),.)))_{N,\chi_{\alpha,\beta,\rho}}|\\ &\leq& CN^{-m}\underset{1\leq i\leq N}{\max}\underset{1\leq k\leq N}{\max}\|{\partial_{x}^{m}}\psi_{\alpha,\beta,\rho}(\tau(x_{i},\theta_{k}),.)\|_{\chi_{\alpha,\beta,\rho}} \|u^{N}(\tau(\tau(x_{i},\theta_{k}),.))\|_{\chi_{\alpha,\beta,\rho}}\\ &\leq& CN^{-m}K^{\ast}(\|u\|_{\chi_{\alpha,\beta,\rho}}+\|e\|_{\infty}). \end{array} $$

(32)

This, along with Lemma 2 and the inequalities (28), (29), and (31), leads to

$$ \begin{array}{lll} \|E_{2}(x)\|_{\infty}&=&\|\sum\limits_{k=1}^{4}{I^{N}_{x}}I_{i,k}\|_{\infty}\leq \varLambda_{N} \sum\limits_{k=1}^{4}\underset{1\leq i\leq N}{\max}|I_{i,k}|\\ &\leq& \begin{cases} C \ln N N^{-m}M^{\ast} +C\ln NN^{-\kappa_{1}}\|e\|_{\infty}, ~~~&\alpha+\beta\geq1 ~and ~\rho=1,\\ C \ln N N^{-m}M^{\ast} +C\ln NN^{-\kappa_{2}}\|e\|_{\infty}, &\alpha+\beta\geq1 ~and ~\rho\geq2,\\ C \ln N N^{-m}M^{\ast} +C\ln N N^{-\kappa_{3}}\|e\|_{\infty},&\alpha+\beta<1.\\ \end{cases} \end{array} $$

(33)

Moreover, by using Lemma 1, the last two terms $\| E_{3}(x)\|_{\infty }$ and $\| E_{4}(x)\|_{\infty }$ are bounded by

$$ \begin{array}{lll} \| E_{3}(x)\|_{\infty}&=&\|({I^{N}_{x}}-I){\int}_{-1}^{x}b(\tau)e(\tau)d\tau\|_{\infty} \leq CN^{-\frac{1}{2}}\|\partial_{x}{\int}_{-1}^{x}b(\tau)e(\tau)d\tau\|_{\omega^{0,0}}\\ &\leq &CN^{-\frac{1}{2}}\|b(x)e(x)\|_{\omega^{0,0}} \leq CN^{-\frac{1}{2}}\|e\|_{\infty}, \end{array} $$

(34)

and

$$ \begin{array}{lll} \| E_{4}(x)\|_{\infty} &=&\|({I^{N}_{x}}-I){\int}_{-1}^{x}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau\|_{\infty}\\ &\leq& CN^{-\frac{1}{2}}\|\partial_{x} {\int}_{-1}^{x}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau\|_{\omega^{0,0}}\\ &\leq& CN^{-\frac{1}{2}}\|{\int}_{-1}^{x}\lambda_{\alpha, \beta, \rho}(x,s)J_{\alpha,\beta,\rho}(x,s)e(s)ds\|_{\omega^{0,0}}\\ &\leq& CN^{-\frac{1}{2}}\|e\|_{\infty}. \end{array} $$

(35)

Hence, a combination of the above error bounds for (26) leads to the desired result. □

Theorem 2

Suppose that the given functions $K(\cdot ,s),H(\cdot ,s), a(t) \in C^{m,1-\frac {m+1}{\rho }}(0,T]$, and H(t,s) ∈ C¹(D). If $u,z\in B^{m}_{\omega ^{-1,-1}}(-1,1)$, then there exists a positive constant C such that for sufficiently large N the following error estimate holds:

$$ \begin{array}{ll} \|e\|_{\omega^{0,0}} \!\leq\! \begin{cases} C N^{-m}(M^{\ast}+CN^{\frac{1}{2}-\kappa_{1}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}), ~~~~~~~~~~~&\alpha+\beta\!\geq\! 1 ~and ~\rho=1,\\ C N^{-m}(M^{\ast}+CN^{\frac{1}{2}-\kappa_{2}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}), ~&\alpha+\beta\!\geq 1 ~and ~\rho\geq2,\\ C N^{-m}(M^{\ast}+C N^{\frac{1}{2}-\kappa_{3}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}), ~~&\alpha+\beta\!<\!1,\\ \end{cases} \end{array} $$

(36)

where

$$ \begin{array}{lll} \kappa_{1}&=&1-\alpha;~~\kappa_{2}=\min\{1-\alpha,1-\frac{1}{\rho}\};~~ \\\kappa_{3}&=&\min\{(2-\alpha-\beta)\rho-1,1-\alpha,2-\alpha-\beta-\frac{1}{\rho}\}; \end{array} $$

and M^∗ is defined by (25).

Proof

It follows from (23) and the generalized Hardy’s inequality that

$$ \begin{array}{ll} \| e(x)\|_{\omega^{0,0}}\leq C\sum\limits_{i=1}^{4}\|E_{i}(x)\|_{\omega^{0,0}}. \end{array} $$

(37)

Firstly, by Lemma 1, we obtain

$$ \begin{array}{ll} \|E_{1}(x)\|_{\omega^{0,0}}=\|u(x)-{I^{N}_{x}}u(x)\|_{\omega^{0,0}} \leq CN^{-m}\|{\partial_{x}^{m}}u\|_{\omega^{m,m}}. \end{array} $$

(38)

Using (28), (29), (31), (32), and Lemma 2, we obtain

$$ \begin{array}{lll} \|E_{2}(x)\|_{\omega^{0,0}}&=&\|\sum\limits_{k=1}^{4}{I^{N}_{x}}I_{i,k}\|_{\omega^{0,0}} \leq C\sum\limits_{k=1}^{4} \max_{1\leq i\leq N}|I_{i,k}|\\ &\leq& \begin{cases} C N^{-m}M^{\ast}+CN^{-\kappa_{1}}\|e\|_{\infty}, ~~~~~~~~~~~~~~~~~~~~~~~~~~~&\alpha+\beta\geq1 ~and ~\rho=1\\ C N^{-m}M^{\ast}+CN^{-\kappa_{2}}\|e\|_{\infty}, &\alpha+\beta\geq1 ~and ~\rho\geq2\\ C N^{-m}M^{\ast}+C N^{-\kappa_{3}}\|e\|_{\infty}, &\alpha+\beta<1\\ \end{cases}\\ &\leq& \begin{cases} C N^{-m}(M^{\ast}+CN^{\frac{1}{2}-\kappa_{1}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}), ~~~~~~~&\alpha+\beta\geq1 ~and ~\rho=1\\ C N^{-m}(M^{\ast}+CN^{\frac{1}{2}-\kappa_{2}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}), ~&\alpha+\beta\geq1 ~and ~\rho\geq2\\ C N^{-m}(M^{\ast}+C N^{\frac{1}{2}-\kappa_{3}}\|{\partial_{x}^{m}}u\|_{\omega^{m-1,m-1}}), ~&\alpha+\beta<1.\\ \end{cases} \end{array} $$

(39)

Furthermore, using Lemma 1, it is obvious that

$$ \begin{array}{ll} \| E_{3}(x)\|_{\omega^{0,0}}=&\|({I^{N}_{x}}-I){\int}_{-1}^{x}b(\tau)e(\tau)d\tau\|_{\omega^{0,0}} \leq CN^{-1}\|\partial_{x}{\int}_{-1}^{x}b(\tau)e(\tau)d\tau\|_{\omega^{1,1}}\\ &\leq CN^{-1}\|b(x)e(x)\|_{\omega^{1,1}} \leq CN^{-1}\|e\|_{\omega^{0,0}}, \end{array} $$

and

$$ \begin{array}{lll} \| E_{4}(x)\|_{\omega^{0,0}} &=&\|({I^{N}_{x}}-I){\int}_{-1}^{x}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau\|_{\omega^{0,0}}\\ &\leq& CN^{-1}\|\partial_{x} {\int}_{-1}^{x}{\int}_{-1}^{\tau}\lambda_{\alpha, \beta, \rho}(\tau,s)J_{\alpha,\beta,\rho}(\tau,s)e(s)dsd\tau\|_{\omega^{1,1}}\\ &\leq& CN^{-1}\|{\int}_{-1}^{x}\lambda_{\alpha, \beta, \rho}(x,s)J_{\alpha,\beta,\rho}(x,s)e(s)ds\|_{\omega^{1,1}}\\ &\leq& CN^{-1}\|e\|_{\omega^{0,0}}. \end{array} $$

Thus, the desired result follows. □

5 Numerical experiments

In this section, we present the numerical results obtained by implementing the proposed Legendre collocation method on two numerical examples for demonstrating the accuracy of the method and effectiveness of applying coordinate transformation. All calculations were performed on a PC running Matlab software. To estimate the $L^{\infty }$ error, we have computed the absolute error at the points $t_{i}=\frac {T}{2N}i,i=0,\cdots ,2N$. Obtained numerical results confirm the theoretical predictions of Theorems 1 and 2.

It is worth noting that the choice of ρ is also important to the efficiency of the proposed method. Although the optimal choice of the parameter ρ for general problems remains an open problem, it can be made according to the following strategy: If the structure of the analytic solution is known, we want to choose the value of ρ such that $u(x)=y(\frac {T}{2^{\rho }}(1+x)^{\rho })$ is smooth or as regular as possible. In case the regularity of the exact solution is unavailable, the parameter ρ can be taken moderately large integer so that u(x) is smooth enough.

Example 1

We consider the third-kind VIDE with non-compact integral:

$$ t^{\frac{2}{3}}y^{\prime}(t) =g_{1}(t)+t^{\frac{5}{3}}y(t)+ {{\int}_{0}^{t}}\frac{\sqrt{3}}{3\pi}(t-s)^{-\frac{2}{3}}s^{\frac{1}{3}}y(s)ds,~~~~~t\in I:=[0,3], $$

(40)

with

$$ g_{1}(t)= \frac{5}{3} t^{\frac{4}{3}}- t^{\frac{10}{3}}-\frac{{\varGamma}(\frac{1}{3}){\varGamma}(3)}{\pi\sqrt{3} {\varGamma}(\frac{10}{3})}t^{\frac{7}{3}}. $$

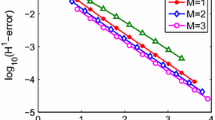
It can be verified that the exact solution of (40) is y(t) = t^5/3. We first consider performance of proposed Legendre collocation method with ρ = 1,3,4,6, respectively, and report obtained $L^{\infty }$ and $L_{\omega ^{0,0}}^{2}$ norm errors for 6 ≤ N ≤ 24 in Tables 1 and 2. The corresponding errors are also plotted in Figs. 1 and 2.

Table 1 The $L^{\infty }$ errors of Legendre collocation method for Example 5.1

Table 2 The $L_{\omega ^{0,0}}^{2}$ errors of Legendre collocation method for Example 5.1

Fig. 1

The $L^{\infty }$ errors of Legendre collocation method for Example 5.1 versus the number of collocation points

Fig. 2

The $L_{\omega ^{0,0}}^{2}$ errors of Legendre collocation method for Example 5.1 versus the number of collocation points

It can be seen that the numerical errors for ρ = 1 decay slowly than other cases, due to the limited regularity of the analytical solution. In this case, the transformed solution $u(x)=\frac {3}{2}(1+x)^{5/3}\in B^{3}_{\omega ^{-1,-1}}(I)$. In view of convergence analysis results (24) and (36), numerical errors will decay at the speed

$$ \|e\|_{\infty}\approx O(\log N N^{-3}),~~~~~\|e\|_{\omega^{0,0}}\approx O(N^{-3}). $$

In order to get higher convergence accuracy, we can choose bigger values of ρ, so, for example, here we have chosen ρ = 3,4,6 respectively; comparison of our obtained results shows that after the regularization, the rate of convergence grows powerfully. Especially when ρ = 3 or ρ = 6, we have the exponential rate of convergence, which coincides with the theoretical results. When we choose ρ = 4, the transformed solution is $u(x)=(\frac {3}{16})^{\frac {5}{3}}(1+x)^{20/3}\in B^{13}_{\omega ^{-1,-1}}(I)$; here, we expect the errors to converge with order

$$ \|e\|_{\infty}\approx O(\log N N^{-13}),~~~~~\|e\|_{\omega^{0,0}}\approx O(N^{-13}). $$

Moreover, to closely observe the error decay rates in detail, we compare the errors of ρ = 1 and ρ = 4 with the N^− 3 and N^− 13 decay rates in Fig. 3. Figure 3 shows that our numerical results verify the theoretical results again.

Fig. 3

Errors of Legendre collocation method for Example 5.1 where the parameter ρ is chosen as ρ = 1 and ρ = 4 respectively

Example 2

We consider the following Volterra integro-differential equation of the third kind [18]:

$$ t^{\frac{1}{2}}y^{\prime}(t) =\frac{1}{20}ty(t)+\frac{9}{2}t^{\frac{7}{2}}-\frac{1}{20}t^{5}-\frac{1}{30}t^{\frac{11}{2}}+\frac{1}{5} {{\int}_{0}^{t}}s^{\frac{1}{2}}y(s)ds,~~~~~t\in I:=[0,1]. $$

(41)

The exact solution of this example is $y(t)= t^{\frac {9}{2}}$. Numerical results of this example corresponding to ρ = 1,2,3,4 are given in Tables 3 and 4 and Figs. 4 and 5. As listed in Table 2 of [18], the error $\|e\|_{\infty }$ is 1.80 × 10^− 4 when N = 128 and m = 2. From Table 3, we observe that the error $\|e\|_{\infty }$ is 5.5511 × 10^− 17 when N = 10 and ρ = 2. Therefore, compared with the collocation method in [18], our proposed Legendre collocation method has the advantages of higher accuracy and lower computation. It also can be seen from Figs. 4 and 5 that when ρ ≥ 2, the rate of convergence grows powerfully and we have the exponential rate of convergence. A reasonable explanation for this excellent result is that the transformed solution u(x) becomes smooth or regular enough if a suitably small ρ is used in the approximation. Moreover, in order to investigate the convergence order in detail, we compare the errors of ρ = 1 and ρ = 3 with the N^− 8 and N^− 26 decay rates in Fig. 6. This comparison indicates that the convergence rate is in a good agreement with the theoretical prediction given in (24) and (36).

Table 3 The $L^{\infty }$ errors of Legendre collocation method for Example 5.2

Table 4 The $L_{\omega ^{0,0}}^{2}$ errors of Legendre collocation method for Example 5.2

Fig. 4

The $L^{\infty }$ errors of Legendre-collocation method for Example 5.2 versus the number of collocation points

Fig. 5

The $L_{\omega ^{0,0}}^{2}$ errors of Legendre collocation method for Example 5.2 versus the number of collocation points

Fig. 6

Errors of Legendre collocation method for Example 5.2 where the parameter ρ is chosen as ρ = 1 and ρ = 3 respectively

6 Concluding remarks

This paper proposes the Legendre collocation method for solving a class of third-kind Volterra integro-differential equations (1). When the underlying solutions of the VIDEs have a non-smooth behavior at the origin, the traditional spectral method may converge slowly. To overcome this difficulty, we apply the coordinate transformation (7) to obtain an equivalent (8) with a smoother solution. In addition, we prove that after this transformation, we will have an exponential rate of convergence for the obtained numerical solution. The numerical results also demonstrate that our method is very easy to implement and has the advantages of high precision and lower computational cost despite the solution singularity.