1 Introduction

Nowadays covering approximation spaces as generalizations of classical approximation spaces have attracted increasing attentions, and a great deal of approximation operators [4, 16–19, 25, 26, 32, 35, 43, 55, 56, 60–62, 64, 68, 70–75] have been proposed for computing the lower and upper approximations of sets in covering approximation spaces. For example, Zakowski [64] proposed the classical lower and upper approximation operators for covering approximation spaces by extending Pawlak’s model. Pomykala [32] presented two pair of dual approximation operators by modifying Zakowski’s definition. Tsang et al. [43] gave the concept of the lower and upper approximation operators using the minimal descriptions. Zhu et al. [72, 74, 75] provided three types of lower and upper approximation operators. They also systematically investigated these six types of approximation operators and presented relationships among them. Subsequently, Chen et al. [4] presented a new covering to construct the lower and upper approximations of an arbitrary set with respect to the covering application background of rough sets. Lin et al. [16, 17] investigated neighborhood-based multigranulation rough sets to deal with data sets with hybrid attributes. Liu et al. [25, 26] proposed covering fuzzy rough set based on multigranulation rough sets. Wang et al. [55] studied the second and sixth lower and upper approximation operators of covering approximation spaces using characteristic matrices. Yao [60] presented a more systematic formulation of covering based rough sets from three aspects: the element, the granule and the subsystem. So far covering-based rough set theory has been applied to many fields such as data mining and knowledge discovery, and the application fields are being increasing with the development of computer sciences and covering-based rough set theory.

Knowledge reduction of information systems as the major work of rough set theory has attracted more attentions in recent years, and researchers have presented different reducts with respect to different criterions and proposed effective algorithms for conducting knowledge reduction of information systems [3, 5, 6, 8–10, 27, 31, 33, 34, 41, 42, 44–50, 53, 54, 57, 63, 69]. For example, Chen et al. [3] presented the concept of reducts for consistent and inconsistent covering decision information systems with covering rough sets. Qian et al. [33] gave the concepts of the lower and upper approximation reducts of decision information systems. Slezak et al. [42] investigated decision reduct of decision information systems. Zhang et al. [69] proposed the concept of assignment reducts and maximum assignment reducts for decision information systems. Consequently, Kryszkiewicz et al. [6] provided the notion of discernibility matrix and discernibility function for computing decision reducts. Leung et al. [10] discussed dependence space-based attribute reduction in inconsistent decision information systems. Miao et al. [31] presented the generalized discernibility matrix and discernibility function of three types of relative reducts. Skowron et al. [41] proposed the concept of the classical discernibility matrix and discernibility function for constructing relative reducts of decision information systems. In practice, information systems vary with the time due to the dynamic characteristic of data collections, and it is time-consuming to conduct knowledge reduction of dynamic information systems with the non-incremental approaches. To solve this issue, researchers [1–3, 11–15, 20–24, 28–30, 36–40, 51, 52, 58, 59, 65–67] focus on investigating knowledge reduction of dynamic information systems using incremental approaches. For example, when coarsening and refining attribute values and varying sets of attribute, Chen et al. [1–3] constructed approximations of sets and provided an effective approach to knowledge reduction of dynamic information systems. Lang et al. [7] presented incremental approaches for computing approximations of sets in dynamic covering approximation spaces caused by variations of object sets and conducted knowledge reduction of dynamic covering decision information systems with the immigration and emigration of objects. Li et al. [14] extended rough sets for incrementally updating decision rules which handles dynamic maintenance of decision rules in data mining based on characteristic relations. Liu et al. [20, 21, 24] presented incremental approaches for knowledge reduction of dynamic information systems and dynamic incomplete information systems. Yang et al. [58] studied the neighborhood system for knowledge reduction of incomplete information systems from the perspective of knowledge engineering and neighborhood systems-based rough sets. Zhang et al. [65] presented matrix-based approaches for computing the approximations, positive, boundary and negative regions in composite information systems. In practice, covering approximation spaces vary with the time because of variations of attribute values. For example, two specialists A and B decided the quality of five cars \(U=\{A, B,C,D,E\}\) as follows: \(good=\{A,C\},middle=\{C,E\},bad=\{B,D,E\}\), and obtained the covering approximation space \((U,\mathscr {C})\), where \(\mathscr {C}=\{good,middle,bad\}\). By considering time variations, the specialists found that the quality of C was very bad, and \((U,\mathscr {C})\) should be revised into dynamic covering approximation space \((U,\mathscr {C}^{*})\), where \(\mathscr {C}^{*}=\{good^{*},middle^{*},bad^{*}\}\), \(good^{*}=\{A\},middle^{*}=\{E\},\) and \(bad^{*}=\{B,C,D,E\}\). But it is time-consuming to construct the type-1 and type-2 characteristic matrices of \(\mathscr {C}^{*}\) with the non-incremental approach. The experimental results have demonstrated the incremental approaches are effective to conduct knowledge reduction of dynamic information systems, because it reduces the computational times greatly. Such an observation motivates us to compute approximations of sets in dynamic covering approximation spaces and knowledge reduction of dynamic covering decision information systems using the incremental approaches.

The purpose of this paper is to study knowledge reduction of dynamic covering decision information systems caused by altering attribute values. First, we investigate structures of the type-1 and type-2 characteristic matrices of dynamic covering approximation spaces because of variations of attribute values and present incremental approaches to computing the type-1 and type-2 characteristic matrices of dynamic coverings. We also employ several examples to illustrate the process of calculating the type-1 and type-2 characteristic matrices can be simplified greatly by utilizing the incremental approaches. Second, we provide incremental algorithms for constructing the type-1 and type-2 characteristic matrices-based approximations of sets in dynamic covering approximation spaces caused by variations of attribute values. We also compare the time complexities of the incremental algorithms with those of non-incremental algorithms. Third, we perform experiments on ten dynamic covering approximation spaces generated randomly and employ the experimental results to illustrate the incremental approaches are effective to calculate the second and sixth lower and upper approximations of sets in dynamic covering approximation spaces with the variation of attribute values. Finally, we employ two examples to show how to conduct knowledge reduction of dynamic covering decision information systems with the incremental approaches.

The rest of this paper is organized as follows: Sect. 2 briefly reviews the basic concepts of covering-based rough set theory. Section 3 introduces incremental approaches for computing the type-1 and type-2 characteristic matrices of dynamic coverings because of varying attribute values. Section 4 presents non-incremental and incremental algorithms for calculating the second and sixth lower and upper approximations of sets using the type-1 and type-2 characteristic matrices. Section 5 performs experiments to show the incremental approaches are effective to compute the second and sixth approximations of sets in dynamic covering approximation spaces. Section 6 devotes to knowledge reduction of dynamic covering decision information systems. We give the conclusions in Sect. 7.

2 Preliminaries

A brief summary of concepts related to covering-based rough sets is given in this section.

Definition 2.1

[64] Let U be a finite universe of discourse, and \(\mathscr {C}\) a family of subsets of U. If none of elements of \(\mathscr {C}\) is empty and \(\bigcup \{C|C\in \mathscr {C}\}=U\), then \(\mathscr {C}\) is referred to as a covering of U. In addition, \((U,\mathscr {C})\) is called a covering approximation space if \(\mathscr {C}\) is a covering of U.

Definition 2.2

[55] Let \((U,\mathscr {C})\) be a covering approximation space, and \(N(x)=\bigcap \{C_{i}|x\in C_{i}\in \mathscr {C}\}\). For any \(X\subseteq U\), the second and sixth upper and lower approximations of X with respect to \(\mathscr {C}\) are defined as follows:

  1. (1)

    \(SH_{\mathscr {C}}(X)=\bigcup \{C\in \mathscr {C}\mid C\cap X\ne \emptyset \},~ SL_{\mathscr {C}}(X)=[SH_{\mathscr {C}}(X^{c})]^{c};\)

  2. (2)

    \(XH_{\mathscr {C}}(X)=\{x\in U\mid N(x)\cap X\ne \emptyset \},~ XL_{\mathscr {C}}(X)=\{x\in U\mid N(x)\subseteq X\}.\)

The second and sixth lower and upper approximation operators are typical approximation operators for covering approximation spaces, and they are also dual operators. Furthermore, researchers have established the foundation for further studying the second and sixth lower and upper approximation operators in dynamic environment.

Definition 2.3

Let \((U,\mathscr {C})\) be a covering approximation space, where \(U=\{x_1,x_2,\ldots ,x_n\}\) and \(\mathscr {C}=\{C_1,C_2,\ldots , C_m\}\). Then the representation matrix of \(\mathscr {C}\) is defined as: \(M_\mathscr {C}=(a_{ij})_{n\times m}\), where \(a_{ij}=\left\{ \begin{array}{ccc} 1, &{} x_{i}\in C_{j},\\ 0, &{} x_{i}\notin C_{j}. \end{array} \right.\)

According to Definition 2.3, a covering may induce different representation matrices due to different positions of blocks in \(\mathscr {C}\). Furthermore, the characteristic function of \(X\subseteq U\) is defined as: \(\mathcal {X}_{X} =[a_{1}~a_{2}~\cdots ~a_{n}]^{T}\), where \(a_{i}=\left\{ \begin{array}{ccc} 1,&{} x_{i}\in X,\\ 0,&{} x_{i}\notin X, \end{array}\ i=1,2,\ldots ,n. \right.\)

Definition 2.4

Let \((U,\mathscr {C})\) be a covering approximation space, and \(M_{\mathscr {C}}=(a_{ij})_{n\times m}\) a matrix representation of \(\mathscr {C}\), where \(U=\{x_1,x_2,\ldots ,x_n\}\), \(\mathscr {C}=\{C_1,C_2,\ldots ,C_m\}\), and \(a_{ij}=\left\{ \begin{array}{ccc} 1,&{} x_{i}\in C_{j},\\ 0,&{} x_{i}\notin C_{j},\end{array} \right.\). Then

  1. (1)

    \(\Gamma (\mathscr {C})=M_{\mathscr {C}}\bullet M_{\mathscr {C}}^{T}=(b_{ij})_{n\times n}\) is called the type-1 characteristic matrix of \(\mathscr {C}\), where \(b_{ij}=\bigvee ^{m}_{k=1}(a_{ik}\cdot a_{jk})\).

  2. (2)

    \(\prod (\mathscr {C})=M_{\mathscr {C}}\odot M_{\mathscr {C}}^{T}=(c_{ij})_{n\times n}\) is called the type-2 characteristic matrix of \(\mathscr {C}\), where \(c_{ij}=\bigwedge ^{m}_{k=1}(a_{jk}-a_{ik}+1).\)

By Definition 2.4, we see the type-1 and type-2 characteristic matrices are symmetric and asymmetric, respectively. Furthermore, we show the second and sixth lower and upper approximations of sets using the type-1 and type-2 characteristic matrices, respectively, as follows:

Definition 2.5

[55] Let \((U,\mathscr {C})\) be a covering approximation space, and \(\mathcal {X}_{X}\) the characteristic function of X in U. Then

  1. (1)

    \({X}_{SH(X)}=\Gamma (\mathscr {C})\bullet \mathcal {X}_{X},~ \mathcal {X}_{SL(X)}=\Gamma (\mathscr {C})\odot \mathcal {X}_{X};\)

  2. (2)

    \(\mathcal {X}_{XH(X)}=\prod (\mathscr {C})\bullet \mathcal {X}_{X},~\mathcal {X}_{XL(X)}=\prod (\mathscr {C})\odot \mathcal {X}_{X}.\)

By Definition 2.5, Lang et al. presented the concepts of type-1 and type-2 reducts of covering decision information systems as follows:

Definition 2.6

[7] Let \((U,\mathscr {D}\cup U/d)\) be a covering decision information system, where \(\mathscr {D}=\{\mathscr {C}_{i}|i\in I\}\), \(U/d=\{D_{i}|i\in J\}\), \(I=\{1,2,\ldots ,n_1\}\), \(J=\{1,2,\ldots ,n_2\}\) two integer sets, and \(\mathscr {P}\subseteq \mathscr {D}\). \(\mathscr {P}\) is called a type-1 reduct of \((U,\mathscr {D}\cup U/d)\) if it satisfies (1) and (2) simultaneously as follows:

  1. (1)

    \(\Gamma (\mathscr {D})\bullet \mathcal {X}_{D_{i}}=\Gamma (\mathscr {P})\bullet \mathcal {X}_{D_{i}}\)  and  \(\Gamma (\mathscr {D})\odot \mathcal {X}_{D_{i}}=\Gamma (\mathscr {P})\odot \mathcal {X}_{D_{i}},~\forall i\in J,\)

  2. (2)

    \(\Gamma (\mathscr {D})\bullet \mathcal {X}_{D_{i}}\ne \Gamma (\mathscr {P^{'}})\bullet \mathcal {X}_{D_{i}}\)  and  \(\Gamma (\mathscr {D})\odot \mathcal {X}_{D_{i}}\ne \Gamma (\mathscr {P^{'}})\odot \mathcal {X}_{D_{i}},~ \forall \mathscr {P^{'}}\subset \mathscr {P}.\)

Definition 2.7

[7] Let \((U,\mathscr {D}\cup U/d)\) be a covering decision information system, where \(\mathscr {D}=\{\mathscr {C}_{i}|i\in I\}\), \(U/d=\{D_{i}|i\in J\}\), \(I=\{1,2,\ldots ,n_1\}\), \(J=\{1,2,\ldots ,n_2\}\) two integer sets, and \(\mathscr {P}\subseteq \mathscr {D}\). \(\mathscr {P}\) is called a type-2 reduct of \((U,\mathscr {D}\cup U/d)\) if it satisfies (1) and (2) simultaneously as follows:

  1. (1)

    \(\prod (\mathscr {D})\bullet \mathcal {X}_{D_{i}}=\prod (\mathscr {P})\bullet \mathcal {X}_{D_{i}} ~and~ \prod (\mathscr {D})\odot \mathcal {X}_{D_{i}}=\prod (\mathscr {P})\odot \mathcal {X}_{D_{i}},~\forall i\in J,\)

  2. (2)

    \(\prod (\mathscr {D})\bullet \mathcal {X}_{D_{i}}\ne \prod (\mathscr {P^{'}}) \bullet \mathcal {X}_{D_{i}} ~and~ \prod (\mathscr {D})\odot \mathcal {X}_{D_{i}}\ne \prod (\mathscr {P^{'}})\odot \mathcal {X}_{D_{i}},~ \forall \mathscr {P^{'}}\subset \mathscr {P}.\)

For simplicity, we define the operators \(+\) and \(-\) between \(A=(a_{ij})_{n\times m}\) and \(B=(b_{ij})_{n\times m}\) as follows: \(A+B=(a_{ij}+b_{ij})_{n\times m}\) and \(A-B=(a_{ij}-b_{ij})_{n\times m}\). Furthermore, we define the operators \(\bullet\) and \(\odot\) between \(C=(c_{ij})_{n\times m}\) and \(D=(d_{jk})_{m\times p}\) as follows: \(C\bullet D=(e_{ik})_{n\times p}\) and \(C\odot D=(f_{ik})_{n\times p}\), where \(e_{ik}=\bigvee ^{m}_{j=1}(c_{ij}\cdot d_{jk})\) and \(f_{ik}=\bigwedge ^{m}_{j=1}(d_{jk}-c_{ij}+1)\).

3 Incremental approaches for computing the second and sixth approximations of sets

In this section, we present incremental approaches for computing the second and sixth lower and upper approximations of sets.

Definition 3.1

Let \((U,\mathscr {C})\) and \((U,\mathscr {C}^{*})\) be covering approximation spaces, where \(U=\{x_{1},x_{2},\ldots ,x_{n}\}\), \(\mathscr {C}\) = \(\{\mathcal {C}_{1}\), \(C_{2}\), ..., \(C_{m}\}\), \(\mathscr {C}^{*}=\{C^{*}_{1}\),\(C^{*}_{2},\ldots ,C^{*}_{m}\}\), and \(C^{*}_{i}-\{x_{k}\}=C_{i}-\{x_{k}\}(1\le i\le m),\) where \(x_{k}\in U\). Then \((U,\mathscr {C}^{*})\) is called a dynamic covering approximation space of \((U,\mathscr {C})\).

According to Definition 3.1, the dynamic covering approximation space \((U,\mathscr {C}^{*})\) is generated by revising attribute values of \(x_{k}\). In practice, variations of attribute values maybe result in \(|\mathscr {C}^{*}|<|\mathscr {C}|\), \(|\mathscr {C}^{*}|=|\mathscr {C}|\) or \(|\mathscr {C}^{*}|>|\mathscr {C}|\). For example, it will result in new blocks or combing different blocks into a block. In this work, we only discuss the situation \(|\mathscr {C}^{*}|=|\mathscr {C}|\) caused by revising attribute values of an object.

Below, we discuss the relationship between \(\Gamma (\mathscr {C})\) and \(\Gamma (\mathscr {C}^{*})\). For convenience, we denote \(M_{\mathscr {C}}=(a_{ij})_{n\times m}\), \(M_{\mathscr {C}^{*}}=(b_{ij})_{n\times m}\), \(\Gamma (\mathscr {C})=(c_{ij})_{n\times n}\), and \(\Gamma (\mathscr {C}^{*})=(d_{ij})_{n\times n}\).

Theorem 3.2

Let \((U,\mathscr {C}^{*})\) be a dynamic covering approximation space of \((U,\mathscr {C})\), \(\Gamma (\mathscr {C})\) and \(\Gamma (\mathscr {C}^{*})\) the type-1 characteristic matrices of \(\mathscr {C}\) and \(\mathscr {C}^{*}\), respectively. Then

$$\begin{aligned} \Gamma (\mathscr {C}^{*})=\Gamma (\mathscr {C})+\Delta \Gamma (\mathscr {C}), \end{aligned}$$

where

$$\begin{aligned} \Delta \Gamma (\mathscr {C})&= {} \left[ \begin{array}{cccccc} 0 &{} 0 &{} \cdots &{} d^{*}_{1k} &{} \ldots &{} 0 \\ 0 &{} 0 &{} \cdots &{} d^{*}_{2k} &{} \ldots &{} 0 \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ d^{*}_{k1} &{} d^{*}_{k2} &{} \cdots &{} d^{*}_{kk} &{} \cdots &{} d^{*}_{kn} \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ 0 &{} 0 &{} \cdots &{} d^{*}_{nk} &{} \cdots &{} 0 \\ \end{array} \right] ,\\ d^{*}_{kj}&= {} d^{*}_{jk}=\left[ \begin{array}{cccccc} b_{k1} &{} b_{k2} &{} \cdots &{} b_{km} \\ \end{array} \right] \bullet \left[ \begin{array}{cccccc} b_{1j}&{}b_{2j} &{} \cdots &{} b_{mj} \\ \end{array} \right] ^{T}-c_{kj}. \end{aligned}$$

Proof

By Definition 2.4, \(\Gamma (\mathscr {C})\) and \(\Gamma (\mathscr {C}^{*})\) are presented as follows:

$$\begin{aligned} \Gamma (\mathscr {C})&= {} M_{\mathscr {C}} \bullet M_{\mathscr {C}}^{T}\\ {}&= {} \left[ \begin{array}{cccc} a_{11} &{} a_{12} &{} \cdots &{} a_{1m} \\ a_{21} &{} a_{22} &{} \cdots &{} a_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ a_{n1} &{} a_{n2} &{} \cdots &{} a_{nm} \\ \end{array} \right] \bullet \left[ \begin{array}{cccc} a_{11} &{} a_{12} &{} \cdots &{} a_{1m} \\ a_{21} &{} a_{22} &{} \cdots &{} a_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ a_{n1} &{} a_{n2} &{} \cdots &{} a_{nm} \\ \end{array} \right] ^{T} \\&= {} \left[ \begin{array}{cccccc} c_{11} &{} c_{12} &{} \cdots &{} c_{1n} \\ c_{21} &{} c_{22} &{} \cdots &{} c_{2n} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ c_{n1} &{} c_{n2} &{} \cdots &{} c_{nn} \\ \end{array} \right] , \\ \Gamma (\mathscr {C}^{*})&= {} M_{\mathscr {C}^{*}} \bullet M_{\mathscr {C}^{*}}^{T}\\ {}&= {} \left[ \begin{array}{cccccc} b_{11} &{} b_{12} &{} \cdots &{} b_{1m} \\ b_{21} &{} b_{22} &{} \cdots &{} b_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ b_{n1} &{} b_{n2} &{} \cdots &{} b_{nm} \\ \end{array} \right] \bullet \left[ \begin{array}{cccccc} b_{11} &{} b_{12} &{} \cdots &{} b_{1m} \\ b_{21} &{} b_{22} &{} \cdots &{} b_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ b_{n1} &{} b_{n2} &{} \cdots &{} b_{nm} \\ \end{array} \right] ^{T} \\&= {} \left[ \begin{array}{ccccccc} d_{11} &{} d_{12} &{} \cdots &{} d_{1n}\\ d_{21} &{} d_{22} &{} \cdots &{} d_{2n}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ d_{n1} &{} d_{n2} &{} \cdots &{} d_{nn}\\ \end{array} \right] . \end{aligned}$$

By Definition 2.4, since \(a_{ij}=b_{ij}\) for \(i\ne k\), we have \(c_{ij}=d_{ij}\) for \(i\ne k,j\ne k\). To compute \(\Gamma (\mathscr {C}^{*})\) on the basis of \(\Gamma (\mathscr {C})\), we only need to compute \((d_{ij})_{(i=k, 1\le j\le n)}\) and \((d_{ij})_{(1\le i\le n, j=k)}\). Since \(\Gamma (\mathscr {C}^{*})\) is symmetric, we only need to compute \((d_{ij})_{(i=k, 1\le j\le n)}\). In other words, we need to compute \(\Delta \Gamma (\mathscr {C})\), where

$$\begin{aligned} \Delta \Gamma (\mathscr {C})&= {} \left[ \begin{array}{cccccc} 0 &{} 0 &{} \cdots &{} d^{*}_{1k} &{} \ldots &{} 0 \\ 0 &{} 0 &{} \cdots &{} d^{*}_{2k} &{} \ldots &{} 0 \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ d^{*}_{k1} &{} d^{*}_{k2} &{} \cdots &{} d^{*}_{kk} &{} \cdots &{} d^{*}_{kn} \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ 0 &{} 0 &{} \cdots &{} d^{*}_{nk} &{} \cdots &{} 0 \\ \end{array} \right] ,\\ d^{*}_{kj}&= {} d^{*}_{jk}=\left[ \begin{array}{cccccc} b_{k1} &{} b_{k2} &{} \cdots &{} b_{km} \\ \end{array} \right] \bullet \left[ \begin{array}{cccccc} b_{1j} &{} b_{2j} &{} \cdots &{} b_{mj} \\ \end{array} \right] ^{T}-c_{kj}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Gamma (\mathscr {C}^{*})=\Gamma (\mathscr {C})+\Delta \Gamma (\mathscr {C}). \end{aligned}$$

\(\square\)

The following example shows the process of constructing the second lower and upper approximations of sets.

Example 3.3

Let \(U=\{x_{1},x_{2},x_{3},x_{4}\}\), \(\mathscr {C}=\{C_{1},C_{2},C_{3}\}\), and \(\mathscr {C}^{*}=\{C^{*}_{1},C^{*}_{2},C^{*}_{3}\}\), where \(C_{1}=\{x_{1},x_{4}\}\), \(C_{2}=\{x_{1},x_{2},x_{4}\}\), \(C_{3}=\{x_{3},x_{4}\}\), \(C^{*}_{1}=\{x_{1},x_{3},x_{4}\}\), \(C^{*}_{2}=\{x_{1},x_{2},x_{3},x_{4}\}\), \(C^{*}_{3}=\{x_{4}\}\), and \(X=\{x_{3},x_{4}\}\). By Definition 2.4, we first obtain

$$\begin{aligned} \Gamma (\mathscr {C})= M_{\mathscr {C}} \bullet M_{\mathscr {C}}^{T}=(c_{ij})_{4\times 4} = \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \bullet \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 1 &{} 1\\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

According to Definition 2.3, we get

$$\begin{aligned} M_{\mathscr {C}^{*}}&= {} \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

Second, we obtain

$$\begin{aligned} \left[ \begin{array}{cccccc} d^{*}_{31}&{}d^{*}_{32}&{}d^{*}_{33}&{} d^{*}_{34} \\ \end{array} \right]&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 0 \\ \end{array} \right] \bullet M^{T}_{\mathscr {C}^{*}}-\left[ \begin{array}{cccccc} c_{31}&{}c_{32}&{}c_{33}&{}c_{34} \\ \end{array} \right] \\&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 0 \\ \end{array} \right] \bullet \left[ \begin{array}{cccc} 1 &{} 0 &{} 1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right] -\left[ \begin{array}{ccccc} 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \right] \\ {}&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] -\left[ \begin{array}{ccccc} 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \right] \\ {}&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 0 &{} 0 \\ \end{array} \right] ,\\ \left[ \begin{array}{cccccc} d^{*}_{13}&{}d^{*}_{23}&{}d^{*}_{33}&{} d^{*}_{43} \\ \end{array} \right]&= {} \left[ \begin{array}{cccccc} d^{*}_{31}&{}d^{*}_{32}&{}d^{*}_{33}&{} d^{*}_{34} \\ \end{array} \right] . \end{aligned}$$

By Theorem 3.2, we have

$$\begin{aligned} \Delta \Gamma (\mathscr {C})&= {} \left[ \begin{array}{cccccccccc} 0&{}0&{}d^{*}_{13}&{} 0 \\ 0&{}0&{}d^{*}_{23}&{} 0 \\ d^{*}_{31}&{}d^{*}_{32}&{}d^{*}_{33}&{} d^{*}_{34} \\ 0&{}0&{}d^{*}_{43}&{} 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] . \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \Gamma (\mathscr {C}^{*})&= {} \Gamma (\mathscr {C})+\Delta \Gamma (\mathscr {C}) =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] +\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

By Definition 2.5, we have

$$\begin{aligned} \mathcal {X}_{SH(X)}&= {} \Gamma (\mathscr {C}^{*})\bullet \mathcal {X}_{X} =\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] \bullet \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1\\ \end{array} \right] ^{T},\\ \mathcal {X}_{SL(X)}&= {} \Gamma (\mathscr {C}^{*})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, \(SH(X)=\{x_{1},x_{2},x_{3},x_{4}\}\) and \(SL(X)=\emptyset\).

In Example 3.3, we only need to compute \(\Delta \Gamma (\mathscr {C})\) by Theorem 3.2. But there is a need to compute all elements in \(\Gamma (\mathscr {C}^{*})\) by Definition 2.4. Therefore, the computational time of the incremental algorithm is less than the non-incremental algorithm. Subsequently, we discuss the construction of \(\prod (\mathscr {C}^{*})\) based on \(\prod (\mathscr {C})\). For convenience, we denote \(\prod (\mathscr {C})=(e_{ij})_{n\times n}\) and \(\prod (\mathscr {C}^{*})=(f_{ij})_{n\times n}\).

Theorem 3.4

Let \((U,\mathscr {C}^{*})\) be a dynamic covering approximation space of \((U,\mathscr {C})\), \(\prod (\mathscr {C})\) and \(\prod (\mathscr {C}^{*})\) the type-2 characteristic matrices of \(\mathscr {C}\) and \(\mathscr {C}^{*}\), respectively. Then

$$\begin{aligned} \prod (\mathscr {C}^{*})=\prod (\mathscr {C})+\Delta \prod (\mathscr {C}), \end{aligned}$$

where

$$\begin{aligned} \Delta \prod (\mathscr {C})&= {} \left[ \begin{array}{cccccc} 0&{}0&{}\cdots &{}f^{*}_{1k}&{}\cdots &{} 0 \\ 0&{}0&{}\cdots &{}f^{*}_{2k}&{}\cdots &{} 0 \\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ f^{*}_{k1}&{}f^{*}_{k2}&{}\cdots &{}f^{*}_{kk}&{}\cdots &{} f^{*}_{kn} \\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ 0&{}0&{}\cdots &{}f^{*}_{nk}&{}\cdots &{} 0 \\ \end{array} \right] , \\\left[ \begin{array}{cccccc} f^{*}_{k1}&{}f^{*}_{k2}&{}\cdots &{} f^{*}_{kn} \\ \end{array} \right]&= {} \left[ \begin{array}{cccccc} b_{k1}&{}b_{k2}&{}\cdots &{} b_{km} \\ \end{array} \right] \odot M^{T}_{\mathscr {C}^{*}}-\left[ \begin{array}{cccccc} e_{k1}&{}e_{k2}&{}\cdots &{} e_{kn} \\ \end{array} \right] ,\\\left[ \begin{array}{cccccc} f^{*}_{1k}&{}f^{*}_{2k}&{}\cdots &{} f^{*}_{nk} \\ \end{array} \right] ^{T}&= {} M_{\mathscr {C}^{*}}\odot \left[ \begin{array}{cccccc} b_{1k}&{}b_{2k}&{}\cdots &{} b_{mk} \\ \end{array} \right] ^{T}-\left[ \begin{array}{cccccc} e_{1k}&{}e_{2k}&{}\cdots &{} e_{nk} \\ \end{array} \right] ^{T}. \end{aligned}$$

Proof

According to Definition 2.4, \(\prod (\mathscr {C})\) and \(\prod (\mathscr {C}^{*})\) are presented as follows:

$$\begin{aligned} \prod (\mathscr {C})&= {} M_{\mathscr {C}}\odot M_{\mathscr {C}}^{T}\\ {}&= {} \left[ \begin{array}{cccc} a_{11} &{} a_{12} &{} \cdots &{} a_{1m} \\ a_{21} &{} a_{22} &{} \cdots &{} a_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ a_{n1} &{} a_{n2} &{} \cdots &{} a_{nm} \\ \end{array} \right] \odot \left[ \begin{array}{cccc} a_{11} &{} a_{12} &{} \cdots &{} a_{1m} \\ a_{21} &{} a_{22} &{} \cdots &{} a_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ a_{n1} &{} a_{n2} &{} \cdots &{} a_{nm} \\ \end{array} \right] ^{T} \\&= {} \left[ \begin{array}{cccc} e_{11} &{} e_{12} &{} \cdots &{} e_{1n} \\ e_{21} &{} e_{22} &{} \cdots &{} e_{2n} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ e_{n1} &{} e_{n2} &{} \cdots &{} e_{nn} \\ \end{array} \right] , \\ \prod (\mathscr {C}^{*})&= {} M_{\mathscr {C}^{*}}\odot M_{\mathscr {C}^{*}}^{T}\\ {}&= {} \left[ \begin{array}{cccc} b_{11} &{} b_{12} &{} \cdots &{} b_{1m} \\ b_{21} &{} b_{22} &{} \cdots &{} b_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ b_{n1} &{} b_{n2} &{} \cdots &{} b_{nm} \\ \end{array} \right] \odot \left[ \begin{array}{cccc} b_{11} &{} b_{12} &{} \cdots &{} b_{1m} \\ b_{21} &{} b_{22} &{} \cdots &{} b_{2m} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ b_{n1} &{} b_{n2} &{} \cdots &{} b_{nm} \\ \end{array} \right] ^{T} \\&= {} \left[ \begin{array}{cccc} f_{11} &{} f_{12} &{} \cdots &{} f_{1n}\\ f_{21} &{} f_{22} &{} \cdots &{} f_{2n}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ f_{n1} &{} f_{n2} &{} \cdots &{} f_{nn}\\ \end{array} \right] . \end{aligned}$$

By Definition 2.4, we have \(e_{ij}=f_{ij}\) for \(i\ne k,j\ne k\) since \(a_{ij}=b_{ij}\) for \(i\ne k\). To compute \(\prod (\mathscr {C}^{*})\) on the basis of \(\prod (\mathscr {C})\), we only need to compute \((f_{ij})_{(i=k, 1\le j\le n)}\) and \((f_{ij})_{(1\le i\le n, j=k)}\). In other words, we need to compute \(\Delta \prod (\mathscr {C})\), where

$$\begin{aligned} \Delta \prod (\mathscr {C})&= {} \left[ \begin{array}{cccccc} 0&{}0&{}\cdots &{}f^{*}_{1k}&{}\cdots &{} 0 \\ 0&{}0&{}\cdots &{}f^{*}_{2k}&{}\cdots &{} 0 \\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ f^{*}_{k1}&{}f_{k2}&{}\cdots &{}f^{*}_{kk}&{}\cdots &{} f^{*}_{kn} \\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ 0&{}0&{}\cdots &{}f^{*}_{nk}&{}\cdots &{} 0 \\ \end{array} \right] , \\\left[ \begin{array}{cccccc} f^{*}_{k1}&{}f^{*}_{k2}&{}\cdots &{} f^{*}_{kn} \\ \end{array} \right]&= {} \left[ \begin{array}{cccccc} b_{k1}&{}b_{k2}&{}\cdots &{} b_{km} \\ \end{array} \right] \odot M^{T}_{\mathscr {C}^{*}}-\left[ \begin{array}{cccccc} e_{k1}&{}e_{k2}&{}\cdots &{} e_{kn} \\ \end{array} \right] ,\\\left[ \begin{array}{cccccc} f^{*}_{1k}&{}f^{*}_{2k}&{}\cdots &{} f^{*}_{nk} \\ \end{array} \right] ^{T}&= {} M_{\mathscr {C}^{*}}\odot \left[ \begin{array}{cccccc} b_{1k}&{}b_{2k}&{}\cdots &{} b_{mk} \\ \end{array} \right] ^{T}-\left[ \begin{array}{cccccc} e_{1k}&{}e_{2k}&{}\cdots &{} e_{nk} \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \prod (\mathscr {C}^{*})=\prod (\mathscr {C})+\Delta \prod (\mathscr {C}). \end{aligned}$$

\(\square\)

The following example is employed to show the process of constructing the sixth lower and upper approximations of sets.

Example 3.5

Let \(U=\{x_{1},x_{2},x_{3},x_{4}\}\), \(\mathscr {C}=\{C_{1},C_{2},C_{3}\}\), and \(\mathscr {C}^{*}=\{C^{*}_{1},C^{*}_{2},C^{*}_{3}\}\), where \(C_{1}=\{x_{1},x_{4}\}\), \(C_{2}=\{x_{1},x_{2},x_{4}\}\), \(C_{3}=\{x_{3},x_{4}\}\), \(C^{*}_{1}=\{x_{1},x_{3},x_{4}\}\), \(C^{*}_{2}=\{x_{1},x_{2},x_{3},x_{4}\}\), \(C^{*}_{3}=\{x_{4}\}\), and \(X=\{x_{3},x_{4}\}\). By Definition 2.4, we first have

$$\begin{aligned} \prod (\mathscr {C})=M_{\mathscr {C}}\odot M_{\mathscr {C}}^{T}=(e_{ij})_{4\times 4}=\left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 1 &{} 1\\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

According to Definition 2.2, we have

$$\begin{aligned} M_{\mathscr {C}^{*}}&= {} \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

Second, we get

$$\begin{aligned} \left[ \begin{array}{cccccc} f^{*}_{31}&{}f^{*}_{32}&{}f^{*}_{33}&{} f^{*}_{34} \\ \end{array} \right]&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 0 \\ \end{array} \right] \odot M^{T}_{\mathscr {C}^{*}}-\left[ \begin{array}{cccccc} e_{31}&{}e_{32}&{}e_{33}&{}e_{34} \\ \end{array} \right] \\&= {} \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ \end{array} \right] \odot \left[ \begin{array}{cccc} 1 &{} 0 &{} 1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right] -\left[ \begin{array}{ccccc} 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \right] \\ {}&= {} \left[ \begin{array}{ccccc} 1 &{} 0 &{} 1 &{} 1 \\ \end{array} \right] -\left[ \begin{array}{ccccc} 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \right] \\ {}&= {} \left[ \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ,\\ \left[ \begin{array}{cccccc} f^{*}_{13}&{}f^{*}_{23}&{}f^{*}_{33}&{} f^{*}_{43} \\ \end{array} \right] ^{T}&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 1 \\ 0 \\ \end{array} \right] -\left[ \begin{array}{cccc} e_{13}&{}e_{23}&{}e_{33}&{} e_{43} \\ \end{array} \right] ^{T}\\ {}&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 1 &{} 0 \\ \end{array} \right] ^{T}-\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ \end{array} \right] ^{T}\\ {}&= {} \left[ \begin{array}{ccccc} 1 &{} 1 &{} 0 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

By Theorem 3.4, we have

$$\begin{aligned} \Delta \prod (\mathscr {C})&= {} \left[ \begin{array}{cccccccccc} 0&{}0&{}f^{*}_{13}&{} 0 \\ 0&{}0&{}f^{*}_{23}&{} 0 \\ f^{*}_{31}&{}f^{*}_{32}&{}f^{*}_{33}&{} f^{*}_{34} \\ 0&{}0&{}f^{*}_{43}&{} 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] . \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \prod (\mathscr {C}^{*})&= {} \prod (\mathscr {C})+\Delta \prod (\mathscr {C})=\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] +\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

By Definition 2.5, we have

$$\begin{aligned} \mathcal {X}_{SH(X)}&= {} \prod (\mathscr {C}^{*})\bullet \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] \bullet \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1\\ \end{array} \right] ^{T}, \\ \mathcal {X}_{SL(X)}&= {} \prod (\mathscr {C}^{*})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, we have \(SH(X)=\{x_{1},x_{2},x_{3},x_{4}\}\) and \(SL(X)=\{x_{4}\}\).

In Example 3.5, we only need to compute \(\Delta \prod (\mathscr {C})\) by Theorem 3.4. But there is a need to compute all elements in \(\prod (\mathscr {C}^{*})\) by Definition 2.4. Therefore, the computational time of the incremental algorithm is less than the non-incremental algorithm.

4 Non-incremental and incremental algorithms of computing approximations of sets

In this section, we present non-incremental and incremental algorithms of computing the second and sixth lower and upper approximations of sets.

figure a
figure b

In Algorithm 4.1, the time complexity of step 2 is \(O(mn^{2})\); the time complexity of step 3 is \(O(2n^{2})\). The total time complexity is \(O((m+2)n^{2})\). In Algorithm 4.2, the time complexity of step 3 is O(nm); the time complexity of step 5 is O(n); the time complexity of step 6 is O(n); the time complexity of step 7 is \(O(2n^{2})\). The total time complexity is \(O(2n^{2}+nm+2n)\). Furthermore, \(O((m+2)n^{2})\) is the time complexity of the non-incremental algorithm. Therefore, the incremental algorithm is more effective than the non-incremental algorithm.

figure c
figure d

In Algorithm 4.3, the time complexity of step 2 is \(O(mn^{2})\); the time complexity of step 3 is \(O(n^{2})\). The total time complexity is \(O((m+2)n^{2})\). In Algorithm 4.4, the time complexity of step 3 is O(nm); the time complexity of step 5 is O(nm); the time complexity of step 7 is O(n); the time complexity of step 8 is O(n); the time complexity of step 9 is \(O(2n^{2})\). The total time complexity is \(O(2n^{2}+2nm+2n)\). Furthermore, \(O((m+2)n^{2})\) is the time complexity of the non-incremental algorithm. Therefore, the incremental algorithm is more effective than the non-incremental algorithm.

5 Experimental analysis

In this section, we perform experiments to validate the effectiveness of Algorithms 4.2 and 4.4 for computing the second and sixth approximations of sets in dynamic covering approximation spaces caused by varying attribute values.

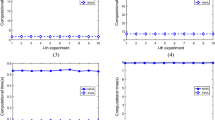
In practical situations, a large amount of computational time is used to transform incomplete information systems into covering approximation spaces, and the main objective of this study is to illustrate the efficiency of the Algorithms 4.2 and 4.4 in computing approximations of sets, ten covering approximation spaces are generated randomly with information shown in Table 1 to evaluate the performance of Algorithms 4.2 and 4.4, where \(|U_{i}|\) denotes the number of objects in \(U_{i}\) and \(|\mathscr {C}_{i}|\) means the cardinality of \(\mathscr {C}_{i}\). All experiments are run on a PC with 64-bit Windows 7, Inter(R) Core(TM) i5-4200M CPU@2.50 GHZ and 4 GB memory; the computational software is Matlab R2013b 64-bit.

Table 1 Covering approximation spaces
Full size table
Table 2 Computational times using Algorithms 4.1–4.4 in \((U_{i},\mathscr {C}_{i})\)
Full size table
Fig. 1
figure 1

Computational times using Algorithms 4.1–4.4 in \((U_{i},\mathscr {C}_{i})\)

Full size image

We apply Algorithms 4.1–4.4 to the covering approximation space \((U_{i},\mathscr {C}_{i})\), where \(i=1,2,\ldots ,10\), and compare the computational times by Algorithms 4.1 and 4.3 with those of Algorithms 4.2 and 4.4, respectively. First, we calculate \(\Gamma (\mathscr {C}_{i})\) and \(\prod (\mathscr {C}_{i})\) by Definition 2.4, where \(i=1,2,\ldots ,10\). Then we obtain the dynamic covering approximation space \((U_{i},\mathscr {C}^{*}_{i})\) because of revising attribute values of \(x_{k}\), where \(C^{*}_{j}=C_{j}\cup \{x_{k}\}\) or \(C_{j}\), \(C^{*}_{j}\in \mathscr {C}^{*}_{i}\) and \(C_{j}\in \mathscr {C}_{i}\). Subsequently, we get \(\Gamma (\mathscr {C}^{*}_{i})\) and \(\prod (\mathscr {C}^{*}_{i})\) by Algorithms 4.1 and 4.3, respectively, where \(i=1,2,\ldots ,10\). Second, we calculate SH(X), SL(X), XH(X), and XL(X) based on \(\Gamma (\mathscr {C}^{*}_{i})\) and \(\prod (\mathscr {C}^{*}_{i})\) for \(X\subseteq U_{i}\), respectively, where \(i=1,2,\ldots ,10\). Third, we obtain \(\Gamma (\mathscr {C}^{*}_{i})\) and \(\prod (\mathscr {C}^{*}_{i})\) by Algorithms 4.2 and 4.4, respectively. Fourth, we calculate SH(X), SL(X), XH(X), and XL(X) based on \(\Gamma (\mathscr {C}^{*}_{i})\) and \(\prod (\mathscr {C}^{*}_{i})\) for \(X\subseteq U_{i}\), respectively, where \(i=1,2,\ldots ,10\). We conduct all experiments ten times and show the results in Table 2 and Fig. 1. In Table 2, the measure of time is in seconds; \(\overline{t}\) indicates the average time of ten experiments; SD indicates the standard deviations of ten experimental results; in Fig. 1, i stands for the experimental number in x axis; in Fig. 1, i refers to the covering approximation space \((U_{i},\mathscr {C}_{i})\) in \(x-\)axis; while \(y-\)axes corresponds to the computational time to compute approximations of sets in dynamic covering approximation spaces; NIS, IS, NIX, and IX stand for the time of constructing the second and sixth lower and upper approximations of sets by Algorithms 4.1, 4.2, 4.3 and 4.3, respectively.

In Table 2, we see that Algorithms 4.1–4.4 are stable to compute approximations of sets in all experiments. That is, the computational times of each algorithm are almost the same. Moreover, the computational times of approximations of sets using incremental algorithms are much smaller than those of the non-incremental algorithms. In other words, the computational times of Algorithms 4.2 and 4.4 are far less than those of Algorithms 4.1 and 4.3, respectively. Therefore, the incremental algorithms are effective to construct approximations of sets in the dynamic covering approximation space \((U_{i},\mathscr {C}^{*}_{i})\), where \(i=1,2, \ldots , 10\).

In Fig. 1, we observe that the average times of the incremental and non-incremental algorithms rise monotonically with the increasing cardinalities of object sets and coverings. The incremental algorithms perform always faster than the non-incremental algorithms in all experiments, and the average times of the incremental algorithms are much smaller than those of the non-incremental algorithms. Moreover, the speed-up ratios of times using the non-incremental algorithms are higher than the incremental algorithms with the increasing cardinalities of object sets and coverings. Especially, there exists little influence of the cardinalities of object sets and coverings on computing the second and sixth lower and upper approximations of sets using Algorithm 4.2 and 4.4. In other words, the incremental algorithms are effective to construct the second and sixth lower and upper approximations of sets in dynamic covering approximation spaces when varying attribute values. All experimental results demonstrate Algorithms 4.2 and 4.4 are effective to compute the second and sixth lower and upper approximations of sets in dynamic covering approximation spaces with varying attribute values.

6 Knowledge reduction of dynamic covering decision information systems caused by variations of attribute values

In this section, we employ examples to illustrate how to compute the type-1 and type-2 reducts of dynamic covering decision information systems caused by variations of attribute values.

Example 6.1

Let \((U,\mathscr {D}\cup U/d)\) be a covering decision information system, where \(\mathscr {D}=\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\}\), \(\mathscr {C}_{1}=\{\{x_{1},x_{2},x_{3},x_{4}\},\{x_{5}\}\}\), \(\mathscr {C}_{2}=\{\{x_{1},x_{2}\},\{x_{3},x_{4},x_{5}\}\}\), \(\mathscr {C}_{3}=\{\{x_{1},x_{2},x_{5}\},\{x_{3},x_{4}\}\}\), \(\mathscr {C}_{4}=\{\{x_{1},x_{2}\},\{x_{3},x_{4}\}, \{x_{5}\}\}\), and \(U/d=\{D_1,D_2\}\), where \(D_1=\{x_{1},x_{2}\}\) and \(D_2=\{x_{3},x_{4},x_{5}\}\). According to Definition 2.3, we have

$$\begin{aligned} M_{\mathscr {D}} = \left[ \begin{array}{ccccccccc} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right] . \end{aligned}$$

By Definition 2.4, we obtain

$$\begin{aligned} \Gamma (\mathscr {D})=M_{\mathscr {D}} \bullet M_{\mathscr {D}}^T= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

According to Definition 2.5, we get

$$\begin{aligned} \mathcal {X}_{SH(D_{1})}=\Gamma (\mathscr {D})\bullet \mathcal {X}_{D_{1}}=\left[ \begin{array}{llllll} 1&1&1&1&1 \end{array} \right] ^{T},\\ \mathcal {X}_{SL(D_{1})}=\Gamma (\mathscr {D})\odot \mathcal {X}_{D_{1}}=\left[ \begin{array}{cccccc} 0&0&0&0&0 \end{array} \right] ^{T},\\ \mathcal {X}_{SH(D_{2})}=\Gamma (\mathscr {D})\bullet \mathcal {X}_{D_{2}}=\left[ \begin{array}{cccccc} 1&1&1&1&1 \end{array} \right] ^{T},\\ \mathcal {X}_{SL(D_{2})}=\Gamma (\mathscr {D})\odot \mathcal {X}_{D_{2}}=\left[ \begin{array}{cccccc} 0&0&0&0&0 \end{array} \right] ^{T}.\\ \end{aligned}$$

By Definition 2.4, we obtain

$$\begin{aligned} \Gamma (\mathscr {D}/\mathscr {C}_{4})&= {} \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ,\quad \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{4}\})= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ,\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\})&= {} \left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] ,\quad \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\})= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

According to Definition 2.5, we have

$$\begin{aligned} \Gamma (\mathscr {D}/\mathscr {C}_{4})\bullet \mathcal {X}_{D_{1}}&= {} \mathcal {X}_{SH(D_{1})}, \Gamma (\mathscr {D}/\mathscr {C}_{4})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}/\mathscr {C}_{4})\bullet \mathcal {X}_{D_{2}}&= {} \mathcal {X}_{SH(D_{2})}, \Gamma (\mathscr {D}/\mathscr {C}_{4})\odot \mathcal {X}_{D_{2}}=\mathcal {X}_{SL(D_{2})},\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{4}\})\bullet \mathcal {X}_{D_{1}}&= {} \mathcal {X}_{SH(D_{1})}, \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{4}\})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{4}\})\bullet \mathcal {X}_{D_{2}}&= {} \mathcal {X}_{SH(D_{2})}, \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{4}\})\odot \mathcal {X}_{D_{2}}=\mathcal {X}_{SL(D_{2})},\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\})\bullet \mathcal {X}_{D_{1}}&\ne {} \mathcal {X}_{SH(D_{1})}, \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\})\bullet \mathcal {X}_{D_{2}}&= {} \mathcal {X}_{SH(D_{2})}, \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\})\odot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SL(D_{2})},\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\})\bullet \mathcal {X}_{D_{1}}&\ne {} \mathcal {X}_{SH(D_{1})}, \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\})\bullet \mathcal {X}_{D_{2}}&= {} \mathcal {X}_{SH(D_{2})}, \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\})\odot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SL(D_{2})}. \end{aligned}$$

By Definition 2.6, we get \(\{\mathscr {C}_{1},\mathscr {C}_{3}\}\) is a type-1 reduct of \((U,\mathscr {D}\cup U/d)\). Similarly, we can obtain a type-2 reduct of \((U,\mathscr {D}\cup U/d)\).

We employ the following example to illustrate how to compute a type-1 reduct of dynamic covering decision information system.

Example 6.2

(Continued from Example 6.1) Let \((U,\mathscr {D}^{*}\cup U/d)\) be a dynamic covering decision information system, where \(\mathscr {D}^{*}=\{\mathscr {C}^{*}_{1},\mathscr {C}^{*}_{2},\mathscr {C}^{*}_{3},\mathscr {C}^{*}_{4}\}\), \(\mathscr {C}^{*}_{1}=\{\{x_{1},x_{2},x_{3},x_{4}\},\{x_{5}\}\}\), \(\mathscr {C}^{*}_{2}=\{\{x_{1},x_{2}\},\{x_{3},x_{4},x_{5}\}\}\), \(\mathscr {C}^{*}_{3}=\{\{x_{1},x_{2},x_{3},x_{5}\},\{x_{4}\}\}\), and \(\mathscr {C}^{*}_{4}=\{\{x_{1},x_{2}\},\{x_{3},x_{4}\},\{x_{5}\}\}\). According to Definition 2.3, we have

$$\begin{aligned} M_{\mathscr {D}^{*}} = \left[ \begin{array}{ccccccccc} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right] . \end{aligned}$$

Furthermore, we obtain

$$\begin{aligned} \Delta \Gamma (\mathscr {D})=\left[ \begin{array}{cccccc} 0 &{} 0 &{} d_{13}^{*} &{} 0 &{} 0 \\ 0 &{} 0 &{} d_{23}^{*} &{} 0 &{} 0\\ d_{31}^{*} &{} d_{32}^{*} &{} d_{33}^{*} &{} d_{34}^{*} &{} d_{35}^{*} \\ 0 &{} 0 &{} d_{43}^{*} &{} 0 &{} 0 \\ 0 &{} 0 &{} d_{53}^{*} &{} 0 &{} 0 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] . \end{aligned}$$

By Theorem 3.2, we have

$$\begin{aligned} \Gamma (\mathscr {D}^{*})=\Gamma (\mathscr {D}) + \Delta \Gamma (\mathscr {D})=\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{}1 \\ 1 &{} 1 &{} 1 &{} 1 &{}1 \\ 1 &{} 1 &{} 1 &{} 1 &{}1 \\ 1 &{} 1 &{} 1 &{} 1 &{}1 \\ 1 &{} 1 &{} 1 &{} 1 &{}1 \\ \end{array} \right] . \end{aligned}$$

By Definition 2.5, we get

$$\begin{aligned} \mathcal {X}_{SH(D_{1})}=\Gamma (\mathscr {D}^{*})\bullet \mathcal {X}_{D_{1}}=\left[ \begin{array}{cccccc} 1&1&1&1&1 \end{array} \right] ^{T}, \\ \mathcal {X}_{SL(D_{1})}=\Gamma (\mathscr {D}^{*})\odot \mathcal {X}_{D_{1}}=\left[ \begin{array}{cccccc} 0&0&0&0&0 \end{array} \right] ^{T},\\ \mathcal {X}_{SH(D_{2})}=\Gamma (\mathscr {D}^{*})\bullet \mathcal {X}_{D_{2}}=\left[ \begin{array}{cccccc} 1&1&1&1&1 \end{array} \right] ^{T},\\ \mathcal {X}_{SL(D_{2})}=\Gamma (\mathscr {D}^{*})\odot \mathcal {X}_{D_{2}}=\left[ \begin{array}{cccccc} 0&0&0&0&0 \end{array} \right] ^{T}. \end{aligned}$$

Moreover, we obtain

$$\begin{aligned} \Gamma (\mathscr {D}^{*}/\mathscr {C}_{4}^{*})&= {} \Gamma (\mathscr {D}/\mathscr {C}_{4}) + \Delta \Gamma (\mathscr {D}/\mathscr {C}_{4})= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ,\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})&= {} \Gamma (\mathscr {D}/\mathscr {C}_{4}) + \Delta \Gamma (\mathscr {D}/\mathscr {C}_{4})= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ \end{array} \right] ,\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{1}^{*},\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})&= {} \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\}) + \Delta \Gamma (\mathscr {D}/\{\mathscr {C}_{1},\mathscr {C}_{2},\mathscr {C}_{4}\})= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ \end{array} \right] ,\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{3}^{*},\mathscr {C}_{4}^{*}\})&= {} \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\}) + \Delta \Gamma (\mathscr {D}/\{\mathscr {C}_{2},\mathscr {C}_{3},\mathscr {C}_{4}\})= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

According to Definition 2.5, we have

$$\begin{aligned} \Gamma (\mathscr {D}^{*}/\mathscr {C}^{*}_{4})\bullet \mathcal {X}_{D_{1}}&=& {} \mathcal {X}_{SH(D_{1})},\quad \Gamma (\mathscr {D}^{*}/\mathscr {C}^{*}_{4})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}^{*}/\mathscr {C}^{*}_{4})\bullet \mathcal {X}_{D_{2}}&=& {} \mathcal {X}_{SH(D_{2})},\quad \Gamma (\mathscr {D}^{*}/\mathscr {C}^{*}_{4})\odot \mathcal {X}_{D_{2}}=\mathcal {X}_{SL(D_{2})},\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\bullet \mathcal {X}_{D_{1}}&=& {} \mathcal {X}_{SH(D_{1})},\quad \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\bullet \mathcal {X}_{D_{2}}&=& {} \mathcal {X}_{SH(D_{2})},\quad \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\odot \mathcal {X}_{D_{2}}=\mathcal {X}_{SL(D_{2})},\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{1}^{*},\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\bullet \mathcal {X}_{D_{1}}\ne & {} \mathcal {X}_{SH(D_{1})},\quad \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{1}^{*},\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{1}^{*},\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\bullet \mathcal {X}_{D_{2}}&=& {} \mathcal {X}_{SH(D_{2})},\quad \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{1}^{*},\mathscr {C}_{2}^{*},\mathscr {C}_{4}^{*}\})\odot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SL(D_{2})},\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{3}^{*},\mathscr {C}_{4}^{*}\})\bullet \mathcal {X}_{D_{1}}\ne & {} \mathcal {X}_{SH(D_{1})},\quad \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{3}^{*},\mathscr {C}_{4}^{*}\})\odot \mathcal {X}_{D_{1}}=\mathcal {X}_{SL(D_{1})},\\ \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{3}^{*},\mathscr {C}_{4}^{*}\})\bullet \mathcal {X}_{D_{2}}&=& {} \mathcal {X}_{SH(D_{2})},\quad \Gamma (\mathscr {D}^{*}/\{\mathscr {C}_{2}^{*},\mathscr {C}_{3}^{*},\mathscr {C}_{4}^{*}\})\odot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SL(D_{2})}. \end{aligned}$$

By Definition 2.6, we have \(\{\mathscr {C}^{*}_{1},\mathscr {C}^{*}_{3}\}\) is the type-1 reduct of \((U,\mathscr {D}^{*}\cup U/d)\).

In Example 6.2, there is no need to compute all elements in the type-1 characteristic matrices using the incremental approach, and it illustrates the incremental approach is effective to compute the type-1 reducts of dynamic covering decision information systems caused by variations of attribute values. Similarly, we can obtain a type-2 reduct of dynamic covering decision information systems caused by variations of attribute values.

7 Conclusions

In this paper, we have introduced the incremental approaches for computing the type-1 and type-2 characteristic matrices in dynamic covering approximation spaces caused by revising attribute values. We have presented the non-incremental and incremental algorithms for computing the second and sixth lower and upper approximations of sets and compared the computational complexities of the non-incremental algorithms with those of incremental algorithms. We have applied the incremental algorithms to compute the second and sixth lower and upper approximations of sets in dynamic covering approximation spaces. Experimental results have illustrated the incremental approaches are effective to compute the second and sixth lower and upper approximations of sets in dynamic covering approximation spaces. We have demonstrated how to conduct knowledge reduction of dynamic covering decision information systems with the incremental approaches.

In the future, we will improve the effectiveness of Algorithms 4.2 and 4.4 and test them in large-scale dynamic covering approximation spaces. Furthermore, we will present incremental approaches to computing the second and sixth lower and upper approximations of sets in complex dynamic covering approximation spaces and reducts of dynamic covering decision information systems caused by variation attribute values.