Fuzzy decision tree based on fuzzy-rough technique

Abstract

Using an efficient criterion in selection of fuzzy conditional attributes (i.e. expanded attributes) is important for generation of fuzzy decision trees. Given a fuzzy information system (FIS), fuzzy conditional attributes play a crucial role in fuzzy decision making. Besides, different fuzzy conditional attributes have different influences on decision making, and some of them may be more important than the others. Two well-known criteria employed to select expanded attributes are fuzzy classification entropy and classification ambiguity, both of which essentially use the ratio of uncertainty to measure the significance of fuzzy conditional attributes. Based on fuzzy-rough technique, this paper proposes a new criterion, in which expanded attributes are selected by using significance of fuzzy conditional attributes with respect to fuzzy decision attributes. An illustrative example as well as the experimental results demonstrates the effectiveness of our proposed method.

1 Introduction

As a generalization of ID3 (Quinlan 1986), Fuzzy ID3 (Umano et al. 1994) uses the fuzzy classification entropy as the criterion to measure the uncertainty of the nodes. A similar version of fuzzy ID3 was proposed by Yuan and Shaw (1995), in which the classification ambiguity is used as the criterion to measure the uncertainty of the nodes. Entropy and ambiguity are two types of uncertainties. Entropy describes the classification impurity of a partition with respect to the classes, while ambiguity describes the specificity of objects in selection of expanded attributes. One can find many types of uncertainties in the literature.

Rough sets developed by Pawlak (1982) are useful tools to deal with uncertainty (i.e. vagueness and ambiguity) of knowledge. Fuzzy rough sets (Dubois and Prade 1990; Kuncheva 1992; Nanda 1992) are generalizations of rough sets to deal with both fuzziness and vagueness in data, which integrate fuzzy sets and rough sets together. It is reasonable to believe that fuzzy rough sets are better than fuzzy sets or rough sets as tools to deal with uncertainty in complicated environments. In fuzzy rough sets, fuzzy similarity relations are employed to characterize the degree of similarity between two objects, which takes values on the unit interval. Most existing research on fuzzy rough sets focus on approximations of fuzzy sets (Chen et al. 2006; Hu et al. 2006a), fuzzy rough attribute reductions (Tsang et al. 2008; Jensen and Shen 2005, 2004; Hu et al. 2006b), and fuzzy rough attribute selections (Jensen and Shen 2007; Shen and Jensen 2004; Bhatt and Gopal 2005). Comparative studies can be found in Radzikowska and Kerre (2002), Yeung et al. (2005).

It is essential to study how to effectively make use of multiple fuzzy attribute reductions to extract fuzzy classification rules. Obviously, the quality of extracted rules heavily depends on the quality of fuzzy attribute reductions. Given a FIS, there are usually many fuzzy conditional attributes and multiple fuzzy attribute reductions [sometimes tens or hundreds of fuzzy attribute reductions can be found (Hu et al. 2007)]. Each fuzzy conditional attribute has a different significance, and therefore has different contribution to classification. More specifically, some of these attributes may have great contribution to classification, and the others may have little or even no contribution. It implies that the important fuzzy conditional attributes will play a crucial role in a FIS. In this paper, based on fuzzy-rough technique, we propose a method with new criterion which uses significance instead of fuzzy entropy to select the most important fuzzy conditional attribute recursively as expanded node in generating a fuzzy decision tree.

The paper is organized as follows. Some related notions and theoretical background are given in Sect. 2. In Sect. 3, the method based on fuzzy-rough technique for generating fuzzy decision tree is presented. An example is provided to illustrate our proposed method in Sect. 4. The experimental comparison of our proposed method, fuzzy ID3, and the method by Yuan and Shaw (1995) are presented in Sect. 5. Section 6 concludes the paper.

2 Fuzzy information system and fuzzy rough sets

2.1 Fuzzy information system

An information system (IS) refers to a 4-tuple ${\rm IS} = \left( {U,A \cup C,V,f} \right)$ where $U = \left\{ {x_{1} ,x_{2} , \ldots ,x_{N} } \right\}$ is a non-empty finite set of objects and each $x_{i}$ is usually represented as $x_{i} = \left( {a_{i1} ,a_{i2} , \ldots ,a_{in} } \right)$; $A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\}$ is a set of conditional attributes; $C = \left\{ c \right\}$ is the decision attribute (without loss of generality we suppose that $c \in \left\{ {1,2, \ldots ,p} \right\}$); $V = \bigcup\nolimits_{j = 1}^{n} {V_{{a_{j} }} }$ where $V_{{a_{j} }} \left( {1 \le j \le n} \right)$ is the domain of value of attribute $a_{j}$; $f:U \times A \to V$ is called an information function, i.e. $f\left( {x_{i} ,a_{j} } \right) = a_{ij} \left( {1 \le i \le N;1 \le j \le n} \right)$.

A fuzzy information system (FIS) (Wang et al. 2001) is a fuzzy version of an IS, which is also a 4-tuple ${\rm FIS} = \left( {U,A \cup C,V,f} \right)$ where U has the same meaning in IS and $A$ is a finite set of fuzzy conditional attributes. In the FIS, we denote by $A = \left\{ {A_{1} ,A_{2} , \ldots ,A_{n} } \right\}$ where $A_{i} \left( {1 \le i \le n} \right)$ represents a fuzzy conditional attribute which consists of a set of fuzzy linguistic terms ${\rm FLT}_{i} = \left\{ {A_{i1} ,A_{i2} , \ldots ,A_{{ik_{i} }} } \right\}\left( {1 \le i \le n} \right)$. C denotes a fuzzy decision attribute with a set of fuzzy linguistic terms ${\rm FLT}_{C} = \left\{ {C_{1} ,C_{2} , \ldots ,C_{m} } \right\}$. Each fuzzy linguistic term $A_{ij} \left( {1 \le i \le n;1 \le j \le k_{i} } \right)$ or $C_{l} \left( {1 \le l \le m} \right)$ is considered as a fuzzy set on U, represented as

$$ A_{ij} = {\frac{{a_{ij}^{\left( 1 \right)} }}{{x_{1} }}} + {\frac{{a_{ij}^{\left( 2 \right)} }}{{x_{2} }}} + \cdots+ {\frac{{a_{ij}^{\left( N \right)} }}{{x_{N} }}} $$

and

$$ C_{l} = {\frac{{c_{l}^{\left( 1 \right)} }}{{x_{1} }}} + {\frac{{c_{l}^{\left( 2 \right)} }}{{x_{2} }}} + \cdots + {\frac{{c_{l}^{\left( N \right)} }}{{x_{N} }}} $$

where $a_{ij}^{\left( p \right)} \left( {1 \le i \le n;1 \le j \le k_{i} ;1 \le p \le N} \right)$ is the conditional membership degree, while $c_{l}^{\left( p \right)} \left( {1 \le l \le m;1 \le p \le N} \right)$ is the class membership degree. $V$ and $f$ are defined same as that in the IS, respectively.

Generally a FIS can be described in Table 1. As an illustration, Table 2 gives a small FIS with four fuzzy conditional attributes and one fuzzy decision attribute. The four fuzzy conditional attributes and their linguistic terms are

Table 1 A fuzzy information system

Table 2 A small fuzzy information system with 16 instances

$$ A_{1} = {\text{Outlook}},{\rm FLT}_{1} = \left\{ {A_{11} ,A_{12} ,A_{13} } \right\} = \left\{ {Sunny,Cloudy,Rain} \right\} $$

$$ A_{2} = {\text{Temperature}},{\rm FLT}_{2} = \left\{ {A_{21} ,A_{22} ,A_{23} } \right\} = \left\{ {Hot,Mild,Cool} \right\} $$

$$ A_{3} = {\text{Humidity}},{\rm FLT}_{3} = \left\{ {A_{31} ,A_{32} } \right\} = \left\{ {Humid,Normal} \right\} $$

$$ A_{4} = {\text{Wind}},{\rm FLT}_{4} = \left\{ {A_{41} ,A_{42} } \right\} = \left\{ {Windy,Not - Windy} \right\} $$

The fuzzy decision attribute and its linguistic terms are

$$ C = \left\{{Plan} \right\}\,{\text{and}}\,{\rm FLT}_{C} = \left\{ {C_{1} ,C_{2} ,C_{3} } \right\} = \left\{ {V,S,W} \right\}. $$

Fuzzy classification rules can be extracted from a FIS by using fuzzy inductive learning methods, such as fuzzy decision trees (Yuan and Shaw 1995; Umano et al. 1994; Wang et al. 2001, 2000, 2008; Janikow 1998; Chiang and Hsu 2002; Pedrycz and Sosnowski 2005a, b, Wang et al. 2007), fuzzy rough sets (Shen and Chouchoulas 2002; Wang et al. 2007; Cao et al. 2003), fuzzy neural networks (Buckley and Hayashi 1994; Simpson 1992; Kasabov 1996), fuzzy support vector machines (Lin and Wang 2002; Chen and Wang 2003), and other techniques (Hung et al. 2008; Chen and Tsai 2008; Chen and Shie 2009; Tsai et al. 2006). This paper proposes a new methodology for rule extraction based on fuzzy-rough technique. To clearly describe our proposed methodology, we first give some definitions and notations.

Definition 2.1

Given a ${\rm FIS} = \left( {U,A \cup C,V,f} \right)$ and a fuzzy set F, $\forall x \in U$, the significant level $\alpha$ of the membership degree is defined as follows (Wang et al. 2001).

$$ \mu_{{F_{\alpha } }} = \left\{ {\begin{array}{*{20}l} {\mu_{F} \left( x \right)} & {{\text{if }}\mu_{F} \left( x \right) \ge \alpha } \\ 0 & {{\text{if }} \mu_{F} \left( x \right) < \alpha } \\ \end{array} } \right. $$

(1)

Definition 2.2

Let $A,B_{i} \left( {1 \le i \le m} \right)$ be fuzzy sets on U. A partition of A (Wang et al. 2001) is defined as $\left\{ {A \cap B_{i} |1 \le i \le m} \right\}$.

Definition 2.3

Let $F\left( U \right)$ be fuzzy power set on $U$, $F_{i} \subseteq F\left( U \right)\left( {1 \le i \le n} \right)$. $T$ is called a fuzzy decision tree, if the following conditions are satisfied (Wang et al. 2000).

• (1) Each node of the fuzzy decision tree belongs to $F\left( U \right)$;

• (2) For each non leaf node $N$, whose sub-nodes constitute a subset of $F\left( U \right)$ denoted by $\Upgamma$ (i.e. $\exists i\left( {1 \le i \le n} \right), \, \Upgamma = F_{i} \cap N$);

• (3) Each leaf node corresponds to one or several values of classification decision.

2.2 Fuzzy rough sets

Fuzzy rough sets developed originally by D. Dubois integrate together the concepts of vagueness and indiscernibility. In the framework of Dubois of fuzzy rough sets, we review some preliminaries including several basic concepts and notations related to our proposed method.

Definition 2.4

Let U be a given universe. A partition $P = \left\{ {F_{1} ,F_{2} , \ldots ,F_{n} } \right\}$ of U is a fuzzy partition if and only if the following two requirements hold,

• (1) $\forall x_{i} \in U,\quad\forall F_{j} \in P,\quad\mu_{{F_{j} }} \left( {x_{i} } \right) \le 1;$

• (2) $\forall x_{i} \in U,\quad\exists F_{j} \in P,\quad\mu_{{F_{j} }} \left( {x_{i} } \right) \ge 0.$

where $\mu_{{F_{j} }} \left( {x_{i} } \right)$ denotes the membership degree to which $x_{i}$ belongs $F_{j}$.

Definition 2.5

Let U be a given universe. R is a fuzzy equivalence relation over U if the following four requirements hold:

• (1) R is a fuzzy relation on U;

• (2) R is reflective, i.e. $R\left( {x,x} \right) = 1,\forall x \in U;$

• (3) R is symmetric, i.e. $R\left( {x,y} \right) = R\left( {y,x} \right),\forall x,y \in U;$

• (4) R is transitive, i.e. $R\left( {x,z} \right) \ge { \min }\left\{ {R\left( {x,y} \right),R\left( {y,z} \right)} \right\},\forall x,y,z \in U.$

An equivalence relation can generate a partition of universe U while a fuzzy equivalence relation can generate a fuzzy partition of universe U.

Definition 2.6

Let U be a given universe. R is a fuzzy equivalence relation over U. The fuzzy equivalence class $\left[ x \right]_{R}$ is defined by

$$ \mu_{{[x]_{R} }} \left( y \right) = \mu_{R} \left( {x,y} \right) $$

(2)

Definition 2.7

Let U be a given universe, X and P be two fuzzy sets on U. The fuzzy P-lower and P-upper approximations are defined as follows (Dubois and Prade 1990).

$$ \mu_{{\underline{P} X}} \left( {F_{i} } \right) = \mathop { \inf }\limits_{x \in U} { \max }\left\{ {1 - \mu_{{F_{i} }} \left( x \right),\mu_{X} \left( x \right)} \right\}\left( {i = 1,2, \ldots ,n} \right) $$

(3)

$$ \mu_{{\overline{P} X}} \left( {F_{i} } \right) = \mathop { \sup }\limits_{x \in U} { \min }\left\{ {\mu_{{F_{i} }} \left( x \right),\mu_{X} \left( x \right)} \right\}\left( {i = 1,2, \ldots ,n} \right) $$

(4)

where $F_{i} \in U/P\left( {1 \le i \le n} \right)$ denotes a fuzzy equivalence class, and $U/P$ denotes the fuzzy partition of U with respect to P.

Definition 2.8

Let U be a given universe, X and P be two fuzzy sets on U, $U/P$ be a fuzzy partition of U. For a given $x \in U$, the fuzzy P-lower approximation and the fuzzy P-upper approximation of X are defined as follows (Jensen and Shen 2005).

$$ \mu_{{\underline{P} X}} (x) = \mathop { \sup }\limits_{F \in U/P} { \min }\left( {\mu_{F} \left( x \right),\mathop { \inf }\limits_{y \in U} { \max }\left\{ {1 - \mu_{F} \left( y \right),\mu_{X} \left( y \right)} \right\}} \right) $$

(5)

$$ \mu_{{\overline{P} X}} (x) = \mathop { \sup }\limits_{F \in U/P} { \min }\left( {\mu_{F} \left( x \right),\mathop { \sup }\limits_{y \in U} { \min }\left\{ {\mu_{F} \left( y \right),\mu_{X} \left( y \right)} \right\}} \right) $$

(6)

The tuple $\left( {\underline{P} X,\overline{P} X} \right)$ is called a fuzzy rough set.

3 The fuzzy decision tree based on fuzzy-rough technique

3.1 New criterion for selection of expanded attribute

In this section, we will introduce a new criterion based on significance of fuzzy conditional attributes with respect to fuzzy decision attribute to select expanded attribute. Given a FIS, every fuzzy conditional attribute has different contribution to the decision attribute. In our proposed method, we will select the most important fuzzy conditional attribute as expanded attribute to generate a fuzzy decision tree. The significance of a fuzzy attribute with respect to another fuzzy attribute is introduced below.

Definition 3.1

Suppose P and Q are two fuzzy attributes in a given FIS. For a given $x \in U$, the significance of the fuzzy attribute P with respect to the fuzzy attribute Q is defined as follows,

$$ \mu_{{{\rm POS}_{P} (Q)}} (x) = \mathop { \sup }\limits_{X \in U/Q} \mu_{{\underline{P} X}} (x) $$

(7)

In literature (Jensen and Shen 2005), equality (7) represents the membership degree of an object $x$ belonging to the fuzzy positive region.

Definition 3.2

Suppose P and Q are two fuzzy attributes in a given FIS. The significance of P with respect to Q is defined by:

$$ \tau_{P} (Q) = {\frac{{\sum\nolimits_{x \in U} {\mu_{{{\rm POS}_{P} \left( Q \right)}} \left( x \right)} }}{|U|}} $$

(8)

where $|U|$ is the cardinality of the universe U.

In literature (Jensen and Shen 2005), equality (8) represents the fuzzy dependency degree of Q on P. Obviously, $0 \le \tau_{P} (Q) \le 1$.

In order to illustrate the two concepts in Definitions 3.1 and 3.2, an example is provided as follows:

Example 1

Table 2 is a small FIS. The universe is $U = \left\{ {x_{1} ,x_{2} , \ldots ,x_{16} } \right\}$. Outlook, Temperature, Humidity, and Wind are four fuzzy conditional attributes, while Plan is a fuzzy decision attribute. As an illustration, for $x_{2} \in U$, we calculate the significance of fuzzy conditional attribute P with respect to fuzzy decision attribute Q.

Let $P = \left\{ {Outlook} \right\}$ and $Q = \left\{ {Plan} \right\}$. The fuzzy partitions induced by P and Q are $U/P = \left\{ {F_{1} ,F_{2} ,F_{3} } \right\} = \left\{ {Sunny,Cloudy,Rain} \right\}$ and $U/Q = \left\{ {V,S,W} \right\}$ respectively.

Noting that $F_{1} = Sunny,\;F_{2} = Cloudy$ and $F_{3} = Rain$, we have

$$ { \min }\left( {\mu_{Sunny} \left( {x_{2} } \right),\mathop { \inf }\limits_{y \in U} { \max }\left\{ {1 - \mu_{Sunny} \left( y \right),\mu_{V} \left( y \right)} \right\}} \right) = { \min }(\mu_{Sunny} (x_{2} ),0.0) = { \min }\left( {0.6,0.0} \right) = 0.0, $$

$$ { \min }\left( {\mu_{Cloudy} \left( {x_{2} } \right),\mathop { \inf }\limits_{y \in U} { \max }\left\{ {1 - \mu_{Cloudy} \left( y \right),\mu_{V} \left( y \right)} \right\}} \right) = { \min }(\mu_{Cloudy} \left( {x_{2} } \right),0.1) = { \min }\left( {0.4,0.1} \right) = 0.1 $$

$$ { \min }\left( {\mu_{Rain} \left( {x_{2} } \right),\mathop { \inf }\limits_{y \in U} { \max }\left\{ {1 - \mu_{Rain} \left( y \right),\mu_{V} \left( y \right)} \right\}} \right) = { \min }\left( {\mu_{Rain} \left( {x_{2} } \right),0.0} \right) = { \min }\left( {0.0,0.0} \right) = 0.0 $$

which imply that the object $x_{2}$ belongs to $\underline{P} V$ with a membership degree of $\mu_{{\underline{P} V}} \left( {x_{2} } \right)$ where

$$ \mu_{{\underline{P} V}} \left( {x_{2} } \right) = { \sup }\left\{ {{ \min }\left( {\mu_{Sunny} \left( {x_{2} } \right),0.0} \right),{ \min }\left( {\mu_{Cloudy} \left( {x_{2} } \right),0.1} \right),{ \min }\left( {\mu_{Rain} \left( {x_{2} } \right),0.0} \right)} \right\} = 0.1 $$

Similarly, for S and W, we have

$$ \mu_{{\underline{P} S}} \left( {x_{2} } \right) = 0.3,\quad\mu_{{\underline{P} W}} \left( {x_{2} } \right) = 0.1, $$

Therefore, for $x_{2} \in U$, the significance of fuzzy conditional attribute P with respect to fuzzy decision attribute Q is

$$ \mu_{{{\rm POS}_{P} (Q)}} \left( {x_{2} } \right) = \mathop { \sup }\limits_{{X \in {U \mathord{\left/ {\vphantom {U Q}} \right. \kern-\nulldelimiterspace} Q}}} \mu_{{\underline{P} X}} \left( {x_{2} } \right) = 0.3. $$

Similarly, the significance of fuzzy conditional attribute P with respect to fuzzy decision attribute Q for other objects in U can be obtained. As a result, we have that the significance of fuzzy conditional attribute P with respect to fuzzy decision attribute Q is

$$ \tau_{Outlook} \left( {Plan} \right) = {\frac{{\sum\nolimits_{x \in U} {\mu_{{{\rm POS}_{Outlook} (Plan)}} \left( x \right)} }}{|U|}} = {\frac{5.2}{16}} $$

In this paper, we will use equality (8) to select the most important fuzzy conditional attribute as the expanded attribute to generate fuzzy decision tree.

3.2 The algorithm for generating fuzzy decision tree

This section introduces the algorithm for generating fuzzy decision trees based on the significance of fuzzy conditional attribute with respect to fuzzy decision attribute.

• Input: ${\rm FIS} = \left( {U,A \cup C,V,f} \right)$

• Output: A group of fuzzy classification rules extracted from the generated fuzzy decision tree $T$

  • Step 1: Pre-preparing the FIS by using formula (1).

  • Step 2: Selecting the expanded attribute.

    • Step 2.1: For each fuzzy conditional attribute $A_{i}$ and its fuzzy linguistic terms $A_{{ik_{i} }} \left( {1 \le i \le n} \right)$, the significance of $A_{i}$ with respect to the fuzzy decision attribute $C$ is calculated by using formula (8).

    • Step 2.2: Selecting $i_{0}$ according to $i_{0} = \mathop {Arg{ \max }}\nolimits_{1 \le i \le n} \left\{ {\tau_{{A_{i} }} \left( C \right)} \right\}$ ($A_{{i_{0} }}$ is the expanded attribute).

  • Step 3: If the terminal conditions can not be satisfied, then partition $U$, and recursively select the expanded attribute until a fuzzy decision tree is generated (The terminal condition will be given in the following section).

  • Step 4: Extracting fuzzy classification rules from the fuzzy decision tree T.

3.3 Terminal conditions

In this section, we first give the definition of classification truth degree, and then provide terminal conditions in Sect. 3.2.

Definition 3.3

Suppose P and Q are two fuzzy sets on U. The truth degree of the fuzzy set P with respect to the fuzzy set Q is defined by:

$$ \beta = T\left( {P,Q} \right) = {\frac{{\tau_{P} (Q)}}{{\sum\nolimits_{x \in U} {\mu_{P} \left( x \right)} }}} $$

(9)

For example, in Table 2, the truth degree of the fuzzy set Sunny with respect to fuzzy set W is 0.75.

Terminal conditions used for generating a fuzzy decision tree are given below:

• (1) If the classification truth degree of a branch with respect to one class exceeds a given threshold $\beta$, then the branch is terminated as a leaf node;

• (2) At a branch, if no attribute can be expanded, the branch is terminated as a leaf node or as null node;

• (3) If one of the conditions mentioned above is satisfied, the expanding of the branch in a fuzzy decision tree will be terminated.

During the generating of a fuzzy decision tree, if there is not a threshold to control the growth of the tree, the generated tree will be very complicated and usually the classification accuracy of the rules converted from the tree will be poor. The terminal condition (1), i.e. the threshold of classification truth degree $\beta$, plays the major role, which controls the growth of the tree. Different $\beta$ will result in different fuzzy decision trees with different classification accuracies. In general, smaller $\beta$ may lead to a smaller tree, but the classification accuracy will be lower. Larger $\beta$ may lead to a larger tree, while the classification accuracy may be higher (on training set). The selection of $\beta$ depends on the problem to be solved.

4 An illustrative example

In this section, we will demonstrate the process of generation of fuzzy decision tree by using the small FIS with 16 training instances given in Table 2. The universe is $U = \left\{ {x_{1} ,x_{2} , \ldots ,x_{16} } \right\}$. The four fuzzy conditional attributes are Outlook, Temperature, Humidity, and Wind. The fuzzy decision attribute is Plan.

Let the significant level $\alpha = 0.0$, and the threshold of classification truth degree $\beta = 0.78$. By calculating the significance of each fuzzy conditional attribute $A_{i} \left( {1 \le i \le 4} \right)$ with respect to the fuzzy decision attribute $C = \left\{ {Plan} \right\}$, we have

$$ \tau_{{A_{1} }} \left( C \right) = \tau_{Outlook} \left( {Plan} \right) = {\frac{{\sum\nolimits_{x \in U} {\mu_{{{\rm POS}_{Outlook} \left( {Plan} \right)}} \left( x \right)} }}{|U|}} = {\frac{5.2}{16}} $$

$$ \tau_{{A_{2} }} \left( C \right) = \tau_{Temperature} \left( {Plan} \right) = {\frac{{\sum\nolimits_{x \in U} {\mu_{{{\rm POS}_{Temperature} \left( {Plan} \right)}} \left( x \right)} }}{|U|}} = {\frac{4.8}{16}} $$

$$ \tau_{{A_{3} }} \left( C \right) = \tau_{Humidity} \left( {Plan} \right) = {\frac{{\sum\nolimits_{x \in U} {\mu_{{{\rm POS}_{Humidity} \left( {Plan} \right)}} \left( x \right)} }}{|U|}} = {\frac{3.2}{16}} $$

$$ \tau_{{A_{4} }} \left( C \right) = \tau_{Wind} \left( {Plan} \right) = {\frac{{\sum\nolimits_{x \in U} {\mu_{{{\rm POS}_{Wind} \left( {Plan} \right)}} \left( x \right)} }}{|U|}} = {\frac{3.2}{16}} $$

Since the fuzzy conditional attribute Outlook has the biggest significance, it is selected as the root node. There are three branches (Sunny, Cloudy and Rain) from the root node Outlook. At the branch Rain, the classification truth degree for W is 0.79$\left( {0.79 > \beta } \right)$ which meets the terminal condition (1) and becomes a leaf node with label W. At the branch Cloudy, $T\left( {Cloudy,W} \right) = 0.19 < \beta ,T\left( {Cloudy,S} \right) = 0.19 < \beta ,T\left( {Cloudy,V} \right) = 0.19 < \beta$. None of the classification truth degrees exceed the threshold $\beta = 0.78$, further partition based on additional attributes should be considered. We have three fuzzy partitions:

$$ Cloudy - Temperature = \left\{ {Cloudy \cap A_{2i} } \right\}\left( {i = 1,2,3} \right) $$

where $\left\{ {A_{21} ,A_{22} ,A_{23} } \right\} = \left\{ {Hot,Mild,Cool} \right\}$.

$$ Cloudy - Humidity = \left\{ {Cloudy \cap A_{3i} } \right\}\left( {i = 1,2} \right) $$

where $\left\{ {A_{31} ,A_{32} } \right\} = \left\{ {Humid,Normal} \right\}.$

$$ Cloudy - Wind = \left\{ {Cloudy \cap A_{4i} } \right\}\left( {i = 1,2} \right) $$

where $\left\{ {A_{41} ,A_{42} } \right\} = \left\{ {Windy,Not - Windy} \right\}.$

Similarly, we have

$$ \tau_{Cloudy - Temperature} \left( {Plan} \right) = {\frac{4.0}{16}},\tau_{Cloudy - Humidity} \left( {Plan} \right) = {\frac{5.6}{16}},\tau_{Cloudy - Wind} \left( {Plan} \right) = {\frac{4.6}{16}} $$

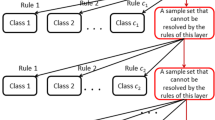
Because the value $\tau_{Cloudy - Humidity} \left( {Plan} \right)$ is the biggest one, the node Humidity is added to the branch Cloudy. From this node, the branch Humid terminates with label V (truth degree is $1 > \beta$) and branch Normal terminates with label W (truth degree is $0.89 > \beta$). At the branch Sunny, the node Temperature is selected as the expended attribute, and from this node, the branch Hot terminates with label S (truth degree is $0.83 > \beta$), the branch Mild terminates with label S (truth degree is $0.94 > \beta$) and the branch Cool terminates with label V (truth degree is $1 > \beta$). Finally we generate a fuzzy decision tree shown in Fig. 1.

Fig. 1

Fuzzy decision tree 1 generated by our proposed method

Now we convert the fuzzy decision tree to a set of fuzzy classification rules. Each path of the fuzzy decision tree from root node to leaf node can be converted into a fuzzy classification rule with the highest classification truth degree. For the fuzzy decision tree shown in Fig. 1, based on the principle of maximal membership degree, six rules are obtained.

• Rule 1: If Outlook is Sunny and Temperature is Hot, then Plan is S (0.83);

• Rule 2: If Outlook is Sunny and Temperature is Mild, then Plan is S (0.94);

• Rule 3: If Outlook is Sunny and Temperature is Cool, then Plan is V (1.00);

• Rule 4: If Outlook is Rain, then Plan is W (0.79);

• Rule 5: If Outlook is Cloudy and Humidity is Humid, then Plan is V (1.0);

• Rule 6: If Outlook is Cloudy and Humidity is Normal, then Plan is W (0.89);

Matching to these fuzzy classification rules, each object in the FIS can acquire a result of classification. Since many rules can be applied to one object at the same time, the object can usually be classified into different classes with different degrees. We use the method in literature (Wang et al. 2001) to obtain the classification result for a given object.

On the same FIS given in Table 2, another fuzzy decision tree can be generated by using fuzzy ID3 (shown in Fig. 2). In Fig. 1, at Sunny branch the sub-node is Temperature and the Cloudy is Humidity, while in Fig. 2 at the branch Sunny the sub-node is Humidity, and the Cloudy is Temperature. The expanded attribute selected at the root node for both trees shown in Figs. 1 and 2 is the same, but at the sub-nodes, the expanded attributes selected for both trees are different. Fuzzy decision tree 1 has 6 leaf nodes and 9 inner nodes while fuzzy decision tree 2 has 10 leaf nodes and 18 inner nodes.

Fig. 2

Fuzzy decision tree 2 generated by fuzzy ID3

The classification results respectively by fuzzy ID3 and by our proposed method are listed in Table 3. Among 16 training instances, 15 instances are correctly classified by our proposed method (instance 2 is not correctly classified). The classification accuracy is 94%, which is higher than the classification accuracy 75% of the fuzzy decision tree 2 (instances 2, 8, 13, and 16 are not correctly classified). Obviously with respect to this example, the classification accuracy has been much improved.

Table 3 Comparison between two methods

5 Experiments

The effectiveness of our proposed method is demonstrated through numerical experiments in the environment of Matlab 7.0 on a Pentium 4 PC. Totally our experiments select 13 datasets among them 11 datasets are from UCI (Blake and Merz 1996) and 2 from real world. The 11 UCI datasets are Iris Dataset (DB1), Pima Dataset (DB2), Wine Dataset (DB3), Ionosphere Dataset (DB4), Breast Cancer Dataset-WDBC (DB5), Breast Cancer Dataset-WPBC (DB6), Glass Dataset (DB7), Blood Transfusion Service Center Dataset (DB8), Image Segmentation Dataset (DB9), Parkinsons Dataset (DB10), and Wine (red) Quality Dataset (DB11). The two real world datasets are RenRu Dataset (DB12) and CT Dataset (DB13). The CT Dataset is obtained by collecting 212 medical CT images from Baoding local hospital. All CT images are classified into two classes (i.e., normal class and abnormal class). The CT Dataset has 170 normal instances and 42 abnormal instances. Totally 35 features are initially selected. They are 10 symmetric features, 9 texture features and 16 statistical features including mean, variance, skewness, kurtosis, energy and entropy. The RenRu Dataset is created by the key laboratory of machine learning and computational intelligence of Hebei Province, China. The RenRu Dataset is obtained by collecting 148 Chinese characters REN and RU with different typeface, font and size, in which there are 92 Chinese characters REN and 56 Chinese characters RU. For each Chinese character, it is described by 26 numerical features. The 13 datasets are summarized in Table 4.

Table 4 Summary of the 13 datasets used in our experiments

The conducted experiments consist of the following two steps.

5.1 Fuzzification

An IS with real-valued conditional attributes used in our experiments is first transformed into a FIS, which includes two steps. Firstly, we use the following algorithm to determine the fuzzy membership degree of instances.

• Input: A IS with real-valued conditional attributes

• Output: A FIS with fuzzy decision attribute (The conditional attributes remain unchanged).

  • Step 1: For each class $k \in \left\{ {1,2, \ldots ,p} \right\}$, calculating the center $c_{k}$of class k;

  • Step 2: For each instance $x_{i} \in U$, calculating the distance $d_{ik}$ between $x_{i}$ and $c_{k}$;

  • Step 3: For each instance $x_{i} \in U$, calculating the fuzzy membership degree of class as follows,

    $$ \mu_{k} \left( {x_{i} } \right) = {\frac{{\left( {d_{ik}^{2} } \right)^{ - 1} }}{{\sum\nolimits_{k = 1}^{p} {\left( {d_{ik}^{2} } \right)^{ - 1} } }}}\left( {1 \le i \le N;1 \le k \le p} \right) $$

Secondly, we use the algorithm in literature (Chen and Shie 2009) to fuzzify real-valued conditional attributes. The algorithm is listed below.

• Input: A IS with real-valued conditional attributes.

• Output: A FIS with fuzzy conditional attributes (The decision attribute remains unchanged).

  • Step 1: For $i = 1 \to n$;

  • Step 2: Let $k = 2$ and $T = T_{0}$;

  • Step 3: Constructing the membership function of real-valued conditional attributes $a_{i}$ as follows:

    • Step 3.1: Clustering the values $\left\{ {a_{1i} ,a_{2i} , \ldots ,a_{Ni} } \right\}$ of $a_{i}$ into k clusters, $m_{1} ,m_{2} , \ldots ,m_{k}$ are the centers of the k clusters respectively;

    • Step 3.2: For $t = 1 \to k$If (t = 1) then

      $$ \mu_{{V_{i1} }} \left( {a_{i} } \right) = \left\{ {\begin{array}{*{20}c} {1 - {\frac{{a_{i} - m_{1} }}{{a_{ \min } - m_{1} }}} \times 0.5} & {a_{ \min } \le a_{i} \le m_{1} } \\ {1 - {\frac{{a_{i} - m_{1} }}{{m_{2} - m_{1} }}}} & {a_{1} \le a_{i} \le m_{2} } \\ 0 & {\text{others}} \\ \end{array} } \right. $$

      Else if (t = k) then

      $$ \mu_{{V_{ik} }} \left( {a_{i} } \right) = \left\{ {\begin{array}{*{20}l} {1 - {\frac{{a_{i} - m_{k} }}{{m_{k - 1} - m_{k} }}}} & {m_{k - 1} \le a_{i} \le m_{k} } \\ {1 - {\frac{{a_{i} - m_{k} }}{{a_{ \max } - m_{k} }}} \times 0.5} & {a_{k} \le a_{i} \le a_{ \max } } \\ 0 & {\text{others}} \\ \end{array} } \right. $$

      Else

      $$ \mu_{{V_{ij} }} \left( {a_{i} } \right) = \left\{ {\begin{array}{ll} {1 - {\frac{{a_{i} - m_{j} }}{{m_{j - 1} - m_{j} }}}} & {m_{j - 1} < a_{i} < m_{j} } \\ {1 - {\frac{{a_{i} - m_{j} }}{{m_{j + 1} - m_{j} }}}} & {m_{j} < a_{i} < m_{j + 1} } \\ 0 & {\text{others}} \\ \end{array} } \right. $$

  • Step 4: Calculating the increment $\Updelta Gain\left( {a_{i} } \right)$ of information gain of attribute$a_{i}$;

  • Step 5: If (k = 2 or $\Updelta Gain\left( {a_{i} } \right) > T_{0}$) then $k \leftarrow k + 1$, and go to Step 3;

    Else exit and $k \leftarrow k - 1$;

  • Step 6: If (i < n) then $i \leftarrow i + 1$, and go to Step 2;

    Else exit.

5.2 Tree generation

We implement our algorithm on a Pentium 4 PC in the environment of Matlab 7.0. The algorithm is tested on the 13 selected datasets by tenfold cross-validation. For each dataset, we run tenfold cross-validation ten times, the experimental results are the average of the ten outputs. A comparison among our proposed method, Yuan and Shaw 1995 and fuzzy ID3 (Umano et al. 1994) is conducted. In our experiments, we select different threshold T to verify the effectiveness of our proposed approach. We find out that the threshold is sensitive to classification accuracy for a few datasets. For instance, when T = 0.1, the average accuracy of our proposed method on DB7 is 0.6028, and when T = 0.07, the average accuracy increase to 0.6918, but the latter costs much more time than the former because of much more intervals generated in the process of fuzzification. It is not really true that more intervals will lead to higher accuracy. The experimental results with T = 0.1 are listed in Table 5. Our proposed method outperforms fuzzy ID3 (Umano et al. 1994) and Yuan’s method (Yuan and Shaw 1995) on eight datasets (see the results with boldface in Table 5). Fuzzy ID3 outperforms our proposed method and Yuan’s method (Yuan and Shaw 1995) on three datasets. Yuan’s method outperforms our proposed method and the fuzzy ID3 (Yuan and Shaw 1995) on two datasets. The performances of the three methods are almost same on some datasets (e.g. DB1, DB2, DB5, and DB7). In order to further verify the effectiveness of our proposed method, we have analyzed statistically the experimental results by using paired t test (Dietterich 1998). Firstly, for each dataset and for each method, we run tenfold cross-validation ten times and then obtain three statistics denoted by $X_{1}$, $X_{2}$, and $X_{3}$ (where $X_{i}$ is a 100-dimensional vector,$1 \le i \le 3$) corresponding to Yuan’s method, fuzzy ID3, and our proposed method respectively. Next we apply paired t test to the experimental results by computing the values of MATLAB function $t\;{\text{test}}2\left( {X_{1} ,X_{3} } \right)$ and $t\;{\text{test}}2\left( {X_{2} ,X_{3} } \right)$. The p values of paired t test for the 10 × 10-fold cross-validation are listed in Table 6. Secondly, for each dataset and for each method, we average the results of 10 × 10-fold cross-validation and then obtain three statistics also denoted by $X_{1}$, $X_{2}$, and $X_{3}$ (where $X_{i}$ is a ten-dimensional vector,$1 \le i \le 3$). The p values of paired t test for the average of 10 × 10-fold cross-validation are listed in Table 7. The small p values cast doubt on the validity of the null hypothesis. Statistically the p values of paired t test (shown in Tables 6, 7) verified the effectiveness of our proposed method.

Table 5 Experimental results with T ₀ = 0.1

Table 6 P values of paired t test for 10 × 10-fold cross-validation

Table 7 P values of paired t test for the average of 10 × 10-fold cross-validation

6 Conclusions

In this paper, based on fuzzy-rough technique, a new method for generating fuzzy decision tree is presented, which uses significance of fuzzy conditional attributes with respect to fuzzy decision attribute as a criterion. Our proposed method takes both fuzziness and roughness existing in an information system into consideration. In comparison with other similar techniques, the fuzzy classification rules converted from fuzzy decision trees generated by using our proposed method demonstrate stronger generalization ability. In addition, numerically experimental results statistically verify the effectiveness of our proposed method.