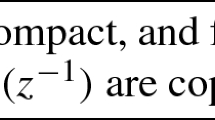Adaptive tracking with exponential stability and convolution bounds using vigilant estimation

Abstract

Classical discrete-time adaptive controllers provide asymptotic stabilization and tracking; neither exponential stabilization nor a bounded noise gain is typically proven. In our recent work, it is shown, in both the pole placement stability setting and the first-order one-step-ahead tracking setting, that if the original, ideal, projection algorithm is used (subject to the common assumption that the plant parameters lie in a convex, compact set and that the parameter estimates are restricted to that set) as part of the adaptive controller, then a linear-like convolution bound on the closed-loop behaviour can be proven; this immediately confers exponential stability and a bounded noise gain, and it can be leveraged to provide tolerance to unmodelled dynamics and plant parameter variation. In this paper, we solve the much harder problem of adaptive tracking; under classical assumptions on the set of unmodelled parameters, including the requirement that the plant be minimum phase, we are able to prove not only the linear-like properties discussed above, but also very desirable bounds on the tracking performance. We achieve this by using a modified version of the ideal projection algorithm, termed as vigilant estimator: it is equally alert when the plant state is large or small and is turned off when it is clear that the disturbance is overwhelming the estimation process.

1 Introduction

Adaptive control is an approach used to deal with systems with uncertain and/or time-varying parameters. In the classical approach to adaptive control, one combines a linear time-invariant (LTI) compensator together with a tuning mechanism to adjust the compensator parameters to match the plant. While adaptive control has been studied as far back as the 1950s, the first general proofs that parameter adaptive controllers work came around 1980, e.g. see [3, 5, 27, 32, 33]. However, the original controllers are typically not robust to unmodelled dynamics, do not tolerate time-variations well, have poor transient behaviour and do not handle noise (or disturbances) well, e.g. see [34]. During the following 2 decades, a good deal of research was carried out to alleviate these shortcomings. A number of small controller design changes were proposed, such as the use of signal normalization, deadzones and $\sigma$-modification, e.g. see [9, 11, 14, 15, 37]; arguably the simplest is that of using projection onto a convex set of admissible parameters, e.g. see [13, 31, 41,42,43,44]. However, in general these redesigned controllers provide asymptotic stability and not exponential stability, with no bounded gain on the noise; that being said, some of them, especially those which use projection, provide a bounded-noise bounded-state property, as well as tolerance of some degree of unmodelled dynamics and/or time-variations.

The goal of this paper is to design adaptive controllers for which the closed-loop system exhibits highly desirable LTI-like system properties, such as exponential stability, a bounded gain on the noise and ideally a convolution bound on the input-output behaviour;¹ in addition, we wish to obtain “good tracking” of a reference signal. As far as the authors are aware, in the classical approach to adaptive control a bounded gain on the noise is proven only in [44]; however, neither a “crisp” exponential bound on the effect of the initial condition nor a convolution bound on the closed-loop behaviour is proven. While it is possible to prove a form of exponential stability if the reference input is sufficiently persistently exciting, e.g. see [2], this places a stringent requirement on an exogenous input, which we would like to avoid.

There are several non-classical approaches to adaptive control which provide some of the LTI-like system properties. First of all, in [4, 23] a logic-based switching approach was used to sequence through a predefined list of candidate controllers; while exponential stability is proven, the transient behaviour can be quite poor and a bounded gain on the noise is not proven. In a related approach, a high-gain controller is used to provide excellent transient and steady-state tracking for minimum phase systems [22]; in this case as well, a bounded gain on the noise is not proven. A more sophisticated logic-based approach, labelled supervisory control, was proposed by Morse—see [7, 8, 28, 29, 39]; here a supervisor switches in an efficient way between candidate controllers, and in certain circumstances a bounded gain on the noise can be proven—see [30, 40], and the Concluding Remarks section of [29]. A related approach, called localization-based switching adaptive control, uses a falsification approach to prove exponential stability as well as a degree of tolerance of disturbances, e.g. see [45], though a bounded gain on the noise is not proven. In none of the above cases is a convolution bound on the closed-loop behaviour proven.

Another non-classical approach to adaptive control, proposed by the first author, is based on periodic probing, estimation and control: rather than estimate the plant or controller parameters, the goal is to estimate what the control signal would be if the plant parameters and plant state were known and the ‘ideal controller’ were applied. Under suitable assumptions on the plant uncertainty, exponential stability and a bounded gain on the noise are achieved, and a degree of unmodelled dynamics and slow time-variations are allowed; for non-minimum phase systems, near optimal transient performance is also provided—see [17, 18, 38], while for minimum-phase systems, near exact tracking is provided, even in the presence of rapid time-variations—see [16, 24]. While a convolution bound is not proven, the biggest drawback is that while a bounded gain on the noise is always achieved, it tends to increase dramatically the closer that one gets to optimality. Furthermore, because of the nature of the approach, it only works in the continuous-time domain.

This brings us to the proposed approach of the paper, wherein we show how to achieve our objectives in the discrete-time setting under some classical assumptions on the set of plant parameters. We adopt a common approach to classical adaptive control—the use of a projection algorithm-based estimator together with a tuneable compensator whose parameters are chosen via the certainty equivalence principle. However, while in the literature it is very common to use a modified version of the ideal projection algorithm in order to avoid division by zero,² here, we adopt another approach to alleviate this numerical concern. We label the resulting estimator a “vigilant estimator”: in the absence of noise it is equally alert to small signals as large signals (unlike the modified version), and in the noisy case we turn off the estimator update if it is clear that the noise is overwhelming the data. Indeed, in earlier work by the authors on the first-order setting [19] and in the pole placement setting of [20, 25], versions of this estimator are used as a building block of adaptive controllers which provide exponential stability, a bounded gain on the noise, and linear-like convolution bounds on the closed-loop behaviour; as far as the authors are aware, such LTI-like bounds have never before been proven in the adaptive setting. The objective of the present paper is to use the general approach of [19, 20, 25] to analyse the much harder adaptive tracking control problem for high-order systems.

We initially expected the analysis to follow in a straight-forward manner from either the first-order tracking approach of [19] or the pole placement approach of [20, 25]; this has not proven to be the situation. It turns out that the importance of the system delay in this setting creates significant additional complexity not found in either case, and the tracking objective is not present in the latter case. That being said, we have adopted ideas from the pole placement setting of [20, 25] as a starting point, but we have carried out several innovative modifications in order to allow us to prove not only the same highly desirable linear-like properties, but also several highly desirable tracking results:

• (i) if there is no noise, we prove an explicit 2-norm bound on the size of the tracking error in terms of the size of the initial condition and the reference signal (in the literature on classical adaptive control it is typically proven only that the tracking error is square summable);

• (ii) if there is no noise but there are slow time-variations, then we prove that we can bound the size of the average tracking error by the size of the time-variation (in the literature this situation is rarely considered);

• (iii) if there is noise, then under some technical conditions, we prove a bound on the average tracking error in terms of the average disturbance times another complicated quantity (in the literature it is usually proven only that the tracking error is bounded).

The proofs of the results contained herein are significantly more involved than the proofs of the classical results in the literature, such as the seminal work of Goodwin et al. [5]. The main reason is that here we are interested in obtaining crisp quantitative bounds on the closed-loop response, rather than the typical qualitative bounds provided in most of the literature.³ Last of all, we would like to point out that an early version of this work appears in [26].

At this point, we provide an outline of the paper. In Sect. 2, we introduce the plant, rewrite it into a form more amenable to analysis and introduce the parameter estimator as well as the adaptive control law. In Sect. 3, we introduce three high-level models for use in system analysis; we provide several technical results which will be useful in the closed-loop analysis. In Sect. 4, we use the three models of the previous section to prove that highly desirable convolution bounds on the system state hold. In Sect. 5, we show that convolution bounds still hold even in the presence of a degree of unmodelled dynamics and plant parameter variations. In Sect. 6, we derive bounds on the tracking error in a variety of situations: the noise-free case, the noise-free case with time-variation and the time-invariant noisy case. In Sect. 7, we will provide several illustrative simulation examples. Last of all, we wrap up with a Summary and Conclusions in Sect. 8.

Before proceeding, we present some mathematical preliminaries. Let $\mathbf{Z}$ denote the set of integers, $\mathbf{Z}^+$ the set of non-negative integers, $\mathbf{N}$ the set of natural numbers, $\mathbf{R}$ the set of real numbers, and $\mathbf{R}^+$ the set of non-negative real numbers. We use the Euclidean 2-norm for vectors and the corresponding induced norm for matrices and denote the norm of a vector or matrix by $\Vert \cdot \Vert$. We let $s ( \mathbf{R}^{n \times m} )$ denote the set of all $\mathbf{R}^{ n \times m}$-valued sequences, and we let ${l_{\infty }}( \mathbf{R}^{n \times m})$ denote the subset of bounded sequences; we define the norm of $u \in {l_{\infty }}( \mathbf{R}^{n \times m})$ by $\Vert u \Vert _{\infty } := \sup _{k \in \mathbf{Z}} \Vert u(k) \Vert$.

If $\mathcal{S} \subset \mathbf{R}^p$ is a convex and compact set, we define $\Vert \mathcal{S} \Vert := \max _{x \in \mathcal{S} } \Vert x \Vert$ and the function $\pi _\mathcal{S} : \mathbf{R}^p \rightarrow \mathcal{S}$ denotes the projection onto $\mathcal{S}$; it is well-known that $\pi _\mathcal{S}$ is well-defined.

2 The setup

In this paper, we start with a linear time-invariant discrete-time plant described by

$$\begin{aligned} \sum _{i=0}^{n} a_{i} y(t-i) = \sum _{i=0}^{m} b_{i} u(t-d-i) + w(t),\; t \in \mathbf{Z}, \end{aligned}$$

(1)

with

• $y(t) \in \mathbf{R}$ the measured output,

• $u(t) \in \mathbf{R}$ the control input,

• $w(t) \in \mathbf{R}$ the disturbance (or noise) input;

• the parameters regularized so that $a_0 = 1$, and

• the system delay $d \ge 1$ being known (so $b_0 \ne 0$).

Associated with this plant model are the polynomials $A(z^{-1} ) := \sum _{i=0}^n a_i z^{-i}$ and $B(z^{-1}) := \sum _{i=0}^{m} b_i z^{-i}$, the transfer function $z^{-d} \frac{B(z^{-1} )}{A(z^{-1} )}$, and the list of plant parameters:

$$\begin{aligned} \theta _{ab}^* := \left[ \begin{array}{cccccc} {a_1}&\cdots&a_n&b_0&\cdots&b_m \end{array} \right] ^T. \end{aligned}$$

Remark 1

It is straight-forward to verify that if the system has a disturbance at both the input and output, then it can be converted to a system of the above form.

The goal is closed-loop stability and asymptotic tracking of an exogenous reference input $y^*(t)$. We impose several assumptions on the set of admissible parameters. The first set is standard in the literature, e.g. [5, 6]:

Assumption 1

• (i) n is known;

• (ii) m is known;

• (iii) the system delay d is known;

• (iv) $sgn( b_0)$ is known;

• (v) the polynomial $B(z^{-1} )$ has all of its zeros in the open unit disk.

Remark 2

Since we do not require $a_n \ne 0$, Assumption 1 (i) can be interpreted as assuming that an upper bound on n is known; similarly, Assumption 1 (ii) can be interpreted as assuming that an upper bound on m is known. The constraint on the zeros of $B(z^{-1} )$ in Assumption 1 (v) is a requirement that the plant be minimum phase; this is necessary to ensure tracking of an arbitrary bounded reference signal [21].

The second assumption is less standard:

Assumption 2

The set of admissible parameters, which we label $\mathcal{S}_{ab} \subset \mathbf{R}^{n+m+1}$, is compact.

Remark 3

The boundedness requirement on $\mathcal{S}_{ab}$ is quite reasonable in practical situations; it is used here to prove uniform bounds and decay rates on the closed-loop behaviour.

There are many ways to pose and solve an adaptive tracking problem, with the d-step-ahead approach and the more general model reference control approach being the standard ones—see [5, 6]. To minimize complexity, we choose the first one, since it is the simpler of the two. To proceed we use a parameter estimator together with an adaptive d-step-ahead control law. To design the estimator, it is convenient to put the plant into the so-called predictor form. To this end, following [6], we carry out long division by dividing $A(z^{-1} )$ into one, and define $F(z^{-1}) = \sum _{i=0}^{d-1} f_i z^{-i}$ and $G( z^{-1} ) = \sum _{i=0}^{n-1} g_i z^{-i}$ satisfying

$$\begin{aligned} \frac{1}{A (z^{-1})} = F(z^{-1}) + z^{-d} \frac{ G(z^{-1})}{A (z^{-1} ) } . \end{aligned}$$

Hence, if we define

$$\begin{aligned} \beta (z^{-1}):= & {} \sum _{i=0}^{m+d-1} \beta _i z^{-i} := F(z^{-1}) B( z^{-1} ) , \\ \alpha (z^{-1} ):= & {} \sum _{i=0}^{n-1} \alpha _i z^{-i} := G(z^{-1}) , \\ \bar{w} (t):= & {} f_0 w (t+d ) + \cdots + f_{d-1} w ( t+1 ), \end{aligned}$$

then we can rewrite the plant model as

$$\begin{aligned} y(t+d)= & {} \sum _{i=0}^{n-1} \alpha _i y(t-i) + \sum _{i=0}^{m+d-1} \beta _i u(t-i) + \bar{w} (t) \nonumber \\= & {} \underbrace{ \left[ \begin{array}{c} y(t) \\ \vdots \\ y(t-n+1) \\ u(t) \\ \vdots \\ u( t - m -d +1 ) \end{array} \right] ^T}_{=: \phi (t)^T} \underbrace{ \left[ \begin{array}{c} \alpha _0 \\ \vdots \\ \alpha _{n-1} \\ \beta _0 \\ \vdots \\ \beta _{ m +d -1 } \end{array} \right] ^T}_{=: \theta ^*} + \bar{w} (t), \;\; t \in \mathbf{Z}. \end{aligned}$$

(2)

Let $\mathcal{S}_{\alpha \beta }$ denote the set of admissible $\theta ^*$ which arise from the original plant parameters which lie in $\mathcal{S}_{ab}$; since the associated mapping is analytic, it is clear that the compactness of $\mathcal{S}_{ab}$ means that $\mathcal{S}_{\alpha \beta }$ is compact as well. Furthermore, it is easy to see that $f_0 =1$, so $\beta _0 = b_0$, which means that the sign of $\beta _0$ is always the same. It is convenient that the set of admissible parameters in the new parameter space be convex and closed; so at this point let $\mathcal{S} \subset \mathbf{R}^{n+m+d}$ be any compact and convex set containing $\mathcal{S}_{\alpha \beta }$ for which the $n+1^{th}$ element (the one which corresponds to $\beta _0$) is never zero, e.g. the convex hull of $\mathcal{S}_{\alpha \beta }$ would do.

The d-step-ahead control law is the one given by

$$\begin{aligned} y^*(t+d) = \sum _{i=0}^{n-1} \alpha _i y(t-i) + \sum _{i=0}^{m+d-1} \beta _i u(t-i) , \end{aligned}$$

or equivalently

$$\begin{aligned} u(t) = \frac{1}{\beta _0} \left[ y^*(t+d) - \sum _{i=0}^{n-1} \alpha _i y(t-i) -\sum _{i=1}^{m+d-1} \beta _i u(t-i) \right] ; \end{aligned}$$

in the absence of a disturbance, and assuming that this controller is applied for all $t \in \mathbf{Z}$, we have $y (t) = y^* (t)$ for all $t \in \mathbf{Z}$. Of course, if the plant parameters are unknown, we need to use estimates; also, the adaptive version of the d-step-ahead control law is only applied after some initial time, i.e. for $t \ge t_0$.

2.1 Initialization

In most adaptive control results, the goal is to prove asymptotic behaviour, so the details of the initial condition are unimportant. Here, however, we wish to get a bound on the transient behaviour so we must proceed carefully. In the pole placement setting of [20], this was relatively straight-forward: the delay plays no role, the controller is strictly causal, and we start the plant estimator off at time $t_0$, with an initial “plant state” of $\phi (t_0) = \phi _0$. Here we have a more complicated situation, even in the case of $d=1$, since the proposed controller is not strictly causal.

To proceed, observe that if we wish to solve (2) for y(t) starting at time $t_0$, then it is clear that we need an initial condition of

$$\begin{aligned} x_0:= & {} \left[ \begin{array}{cccccc} y( t_0 -1)&\quad \cdots&\quad y(t_0 -n-d+1)&u(t_0 -1 )&\quad \cdots&\quad u( t_0 -m-2d+1 ) \end{array} \right] ^T \nonumber \\&\in \mathbf{R}^{n+m + 3d - 2}. \end{aligned}$$

(3)

Observe that this is sufficient information to obtain $\{ \phi (t_0-1 ) ,\ldots , \phi (t_0 -d) \}$.

2.2 Parameter estimation

We can rewrite the plant (2) as

$$\begin{aligned} y(t) = \phi ( t-d ) ^T \theta ^* + \bar{w} (t-d) ,\quad t \ge t_0, \end{aligned}$$

(4)

with an initial condition of $x_0$. Given an estimate $\hat{\theta } (t)$ of $\theta ^*$ at time t, we define the prediction error by

$$\begin{aligned} e(t+1) := y(t+1) - \phi (t-d+1)^T \hat{\theta } (t) ; \end{aligned}$$

(5)

this is a measure of the error in $\hat{\theta } (t)$. A common way to obtain a new estimate is from the solution of the optimization problem

$$\begin{aligned} argmin_{\theta } \{ \Vert \theta - \hat{\theta } (t) \Vert : y(t+1) = \phi (t-d+1)^T {\theta } \} , \end{aligned}$$

yielding the ideal (projection) algorithm

$$\begin{aligned} \hat{\theta }(t+1) = \left\{ \begin{array}{ll} \hat{\theta }(t) &{} \quad \text{ if } \phi (t-d+1) = 0 \\ \hat{\theta }(t) + \frac{\phi (t-d+1)}{\Vert \phi (t-d+1)\Vert ^2} \, e (t+1) &{} \quad \text{ otherwise; } \end{array} \right. \end{aligned}$$

(6)

at this point, we can also constrain the estimate to $\mathcal{S}$ by projection. Of course, if $\phi (t-d+1)$ is close to zero, numerical problems can occur, so it is very common in the literature (e.g. [5, 6]) to add a constant to the denominator and possibly another gain in the numerator: with $0< \bar{\alpha } < 2$ and $\bar{\beta } > 0$, consider the classical algorithm⁴

$$\begin{aligned} \hat{\theta }(t+1) = \hat{\theta }(t) + \frac{\bar{\alpha } \phi (t)}{ \bar{\beta } + \phi (t)^T \phi (t)} e(t+1) . \end{aligned}$$

(7)

However, as pointed out in [19, 20, 25], this can lead to the loss of exponential stability and a loss of a bounded gain on the noise.

We propose a middle ground: as proposed in [20, 25], we turn off the estimation if it is clear that the disturbance signal $\bar{w} (t)$ is swamping the estimation error.⁵ More specifically, if we examine the update law in (6) when $\phi (t-d+1) \ne 0$, we see that

$$\begin{aligned} \Vert \hat{\theta } (t+1) - \hat{\theta } (t) \Vert = \frac{| e(t+1)|}{\Vert \phi (t-d+1) \Vert } . \end{aligned}$$

Suppose that $\theta _0 \in \mathcal{S}$ and $\hat{\theta } (t) \in \mathcal{S}$; if this update quantity is large but less than $2 \Vert \mathcal{S }\Vert$, then it could very well be that $\hat{\theta } (t+1) \in \mathcal{S}$ and it could be that the large update is due to $\hat{\theta } (t)$ being very inaccurate; on the other hand, if this quantity is larger than $2 \Vert \mathcal{S }\Vert$, then it is clear that $\hat{\theta } (t+1) \notin \mathcal{S }$ and probably quite inaccurate—in this case the disturbance may be fairly large relative to the other signals. To this end, with $\delta \in (0, \infty ]$, we turn off the estimator if the update is larger than $2 \Vert \mathcal{S} \Vert + \delta$ in magnitude; so define ${\rho _{\delta }}: \mathbf{R}^{n+m+d} \times \mathbf{R}\rightarrow \{ 0,1 \}$ by

$$\begin{aligned} {\rho _{\delta }}( \phi (t-d+1) , e (t+1) ) := \left\{ \begin{array}{ll} 1 &{} \quad \text{ if } | e(t+1) | < ( 2 \Vert \mathcal{S} \Vert + \delta ) \Vert \phi (t-d+1) \Vert \\ 0 &{} \quad \text{ otherwise }; \end{array} \right. \end{aligned}$$

given $\hat{\theta } (t_0 -1) = \theta _0$, for $t \ge t_0-1$ we define⁶

$$\begin{aligned} \check{\theta } (t+1) = \hat{\theta } (t) + {\rho _{\delta } ( \phi (t-d+1) , e(t+1))}\times \frac{ \phi (t-d+1)}{\Vert \phi (t-d+1) \Vert ^2} e(t+1) , \end{aligned}$$

(8)

which we then project onto $\mathcal{S}$:

$$\begin{aligned} \hat{\theta } (t+1):= \pi _\mathcal{S} ( \check{\theta } (t+1) ). \end{aligned}$$

(9)

Remark 4

We label this approach vigilant estimation for two reasons.

• (i) First of all, suppose that the disturbance is zero, i.e. $w(t)=0$, and $\phi (t-d+1) \ne 0$. Then a careful examination of the update quantity reveals that ${\rho _{\delta }}( \cdot , \cdot ) =1$ and

  $$\begin{aligned} {\rho _{\delta }}( \cdot , \cdot ) \frac{ \phi (t-d+1)}{\Vert \phi (t-d+1) \Vert ^2} e(t+1) = - \frac{ \phi (t-d+1) \phi (t-d+1)^T}{\Vert \phi (t-d+1) \Vert ^2} [ \hat{\theta } (t) - \theta ^* ] ; \end{aligned}$$

  so we see that the gain on the parameter estimate error $\hat{\theta } (t) - \theta ^*$ is exactly

  $$\begin{aligned} -\frac{ \phi (t-d+1) \phi (t-d+1)^T}{\Vert \phi (t-d+1) \Vert ^2}, \end{aligned}$$

  which is scale invariant—if we replace $\phi (t-d+1)$ by $c \phi (t-d+1)$ for any non-zero c, then the quantity is the same. Hence, the estimator is as alert when $\phi$ is small as when it is large; this differs from the classical algorithm, wherein the gain gets small when $\phi$ is small.

• (ii) Second of all, as discussed above, the update algorithm turns off if it is clear that the disturbance is over-whelming the estimation process.

2.3 Properties of the estimation algorithm

Analysing the closed-loop system will require a careful analysis of the estimation algorithm. We define the parameter estimation error by $\tilde{\theta } (t): = \hat{\theta } (t) - \theta ^*$ and the corresponding Lyapunov function associated with $\tilde{\theta } (t)$, namely $V(t) : = \tilde{\theta } (t)^T \tilde{\theta } (t)$. In the following result, we list a property of V(t); it is a straight-forward generalization of what holds in the pole placement setup of [20, 25].

Proposition 1

For every $t_0 \in \mathbf{Z}$, $x_0 \in \mathbf{R}^{n+m+3d-2}$, ${\theta }_0 \in \mathcal{S}$, $\theta _{ab}^* \in \mathcal{S}_{ab}$, $y^*, w \in {l_{\infty }}$, and $\delta \in ( 0, \infty ]$, when the estimator (8) and (9) is applied to the plant (1), the following holds:

$$\begin{aligned} \Vert \hat{\theta } (t+1) - \hat{\theta } (t) \Vert\le & {} {\rho _{\delta } ( \phi (t-d+1) , e(t+1))}\times \frac{ |e(t+1)| }{ \Vert \phi (t-d+1) \Vert } , \; t \ge t_0-1 ,\nonumber \\ V(t)\le & {} V( \underline{t} ) + \sum _{j= \underline{t}}^{t-1} {\rho _{\delta } ( \phi (j-d+1) , e(j+1))}\nonumber \\&\times \left[ -\frac{1}{2} \frac{[e (j+1) ]^2}{ \Vert \phi (j-d+1) \Vert ^2} + 2 \frac{[ \bar{w}(j-d+1)]^2}{ \Vert \phi (j-d+1) \Vert ^2}\right] , \;\; t \ge \underline{t} \ge t_0 -1.\nonumber \\ \end{aligned}$$

(10)

2.4 The control law

The elements of $\hat{\theta } (t)$ are partitioned in a natural way as

$$\begin{aligned} \left[ \begin{array}{cccccc} \hat{\alpha }_0 (t)&\cdots&\hat{\alpha }_{n-1} (t)&\hat{\beta }_0 (t)&\cdots&\hat{\beta }_{m+d-1} (t) \end{array} \right] ^T . \end{aligned}$$

The d-step-ahead adaptive control law is that of

$$\begin{aligned} y^*(t+d) = \hat{\theta } (t)^T \phi (t) , \; t \ge t_0 , \end{aligned}$$

or equivalently

$$\begin{aligned} \sum _{i=0}^{m+d-1} \hat{\beta }_{i} (t) u(t-i) = y^*(t+d) - \sum _{i=0}^{n-1} \hat{\alpha }_{i} (t) y(t-i) , \; t \ge t_0 . \end{aligned}$$

(11)

Hence, as is common in this setup, we assume that the controller has access to the reference signal $y^*(t)$exactly d time units in advance.

Remark 5

With this choice of control law, it is easy to prove that the prediction error e(t) and the tracking error

$$\begin{aligned} {\varepsilon }(t) := y (t) - y^* (t) \end{aligned}$$

are different if $d \ne 1$. Indeed, it is easy to see that

$$\begin{aligned} {\varepsilon }(t)= & {} -\phi (t-d)^T \tilde{\theta } (t-d) + \bar{w} (t-d) , \; t \ge t_0 + d, \end{aligned}$$

(12)

$$\begin{aligned} e(t)= & {} - \phi (t-d)^T \tilde{\theta } (t-1) + \bar{w} (t-d) , \; t \ge t_0. \end{aligned}$$

(13)

Notice, in particular, that (12) provides a nice closed-form expression for the tracking error ${\varepsilon }(t)$ only for $t \ge t_0 + d$; the reason is that the tracking error for $t= t_0 ,\ldots , t_0+d-1$ is determined by $x_0$, w and $y^*$.

The goal of this paper is to prove that the adaptive controller consisting of the estimator (8), (9) together with the control equation (11) yields highly desirable linear-like convolution bounds on the closed-loop behaviour as well as provides good tracking of $y^*$. In the next section, we develop several models used in the development, after which we state and prove the main result.

Remark 6

While the proposed adaptive controller which consists of the estimator (8), (9) together with the controller (11) is nonlinear, when it is applied to the plant it turns out that the closed-loop system enjoys the homogeneity property. While it does not enjoy the additivity property needed for linearity, we will soon see that we are still able to prove linear-like convolution bounds on the closed-loop behaviour.

3 Preliminary analysis

In the pole-placement adaptive control setup of our earlier work [20, 25], a key closed-loop model consists of an update equation for $\phi (t)$, with the state matrix consisting of controller and plant estimates; this was effective—the characteristic polynomial of this matrix is time-invariant and has all roots in the open unit disk. If we were to mimic this in the d-step-ahead setup, the characteristic polynomial would have roots which are time-varying, with some at zero and the rest at the zeros of the naturally defined polynomial $\hat{\beta } (t, z^{-1})$, which is time-varying and may not have roots in the open unit disk. Hence, at this point we make an important deviation from the approach of [20, 25]: we construct three different models for use in the analysis.

3.1 A good closed-loop model

In the first model, we obtain an update equation for $\phi (t)$ which avoids the use of plant parameter estimates, but which is driven by the tracking error. Only two elements of $\phi$ have a complicated description:

$$\begin{aligned} \phi _1 (t+1)= & {} y(t+1) = {\varepsilon }(t+1) + y^*(t+1) , \; t \ge t_0-1, \end{aligned}$$

and the $u(t+1)$ term, for which we use the original plant model to write

$$\begin{aligned} \phi _{n+1}(t+1)= & {} u(t+1) \\= & {} \frac{1}{b_0} \left[ \sum _{i=0}^d a_i ( {\varepsilon }(t+d+1-i) + y^* (t+d+1-i) )\right. \\&\left. +\sum _{i=d+1}^n a_i y(t+d+1-i) - \sum _{i=0}^{m-1} b_{i+1} u(t-i) - w ( t+d+1 ) \right] . \end{aligned}$$

With $e_i \in \mathbf{R}^{n+m+d}$ the $i^{th}$ normal vector, if we now define

$$\begin{aligned} B_1:= e_1 , \;\; B_2 := e_{n+1} , \end{aligned}$$

(14)

then it is easy to see that there exists a matrix $A_g \in \mathbf{R}^{(n+m+d) \times (n+m+d )}$ (which depends implicitly on $\theta _{ab}^* \in \mathcal{S}_{ab}$) so that the following equation holds:

$$\begin{aligned} \phi (t+1)= & {} {A}_g \phi (t) + B_1 {\varepsilon }(t+1) + B_2 \sum _{j=0}^d \left[ \frac{a_{d-j}}{b_0} {\varepsilon }(t+1+j) + \frac{a_{d-j}}{b_0} y^* (t+1+j) \right] \nonumber \\&+B_1 y^*(t+1) - \frac{1}{b_0} B_2 w ( t+d+1 ) , \; t \ge t_0-1 . \end{aligned}$$

(15)

The characteristic equation of $A_g$ equals $\frac{1}{b_0} z^{n+m+d} B( z^{-1} )$, so all of its roots are in the open unit disk.

3.2 A crude closed-loop model

At times, we will need to use a crude model to bound the size of the growth of $\phi (t)$ in terms of the exogenous inputs. Once again, only two elements of $\phi (t)$ have a complicated description: to describe $y(t+1)$ we use the plant model (1):

$$\begin{aligned} \phi _1 (t+1)= & {} y(t+1) \\= & {} - \sum _{i=1}^{n} a_{i} y(t+1-i) + \sum _{i=0}^{m} b_{i} u(t+1-d-i) + w(t+1) \\=: & {} \bar{\theta }_{ab}^* \phi (t) + w(t+1), \end{aligned}$$

and to describe $u(t+1)$ we use the control law:

$$\begin{aligned} y^*(t+d)= & {} \hat{\theta } (t) ^T \phi (t) \\ \Rightarrow \; y^* (t+d+1)= & {} \hat{\theta } (t+1) ^T \phi (t+1) , \; t \ge t_0 -1 ; \end{aligned}$$

it is easy to define $\bar{\theta }_{\alpha \beta } (t)$ in terms of the elements of $\hat{\theta } (t+1)$ so that

$$\begin{aligned} y^* (t+d+1) = \bar{\theta }_{\alpha \beta } (t)^T \phi (t) + \hat{\alpha }_0 (t+1) y(t+1) + \hat{\beta }_0 (t+1) u(t+1) , \; t \ge t_0-1 . \end{aligned}$$

If we combine this with the formula for $y(t+1)$ above, we end up with

$$\begin{aligned} u(t+1)= & {} \frac{1}{ \hat{\beta } _0 (t+1)} [ - \bar{\theta }_{\alpha \beta } (t) - \hat{\alpha }_0 (t+1) \bar{\theta }_{ab}^* ] \phi (t) \\&+ \frac{1}{\hat{\beta }_0 (t+1)} y^* (t+d+1) - \frac{\hat{\alpha }_0 (t+1)}{\hat{\beta }_0 (t+1)} w(t+1) , \; t \ge t_0-1 . \end{aligned}$$

Hence, we can define matrices $A_b (t)$, $B_3 (t)$ and $B_4 (t)$ so that

$$\begin{aligned} \phi (t+1)= & {} A_b (t) \phi (t) + B_3 (t) y^* (t+d+1) + B_4 (t) w(t+1), \; t \ge t_0-1; \qquad \end{aligned}$$

(16)

due to the compactness of $\mathcal{S}_{ab}$, $\mathcal{S}_{\alpha \beta }$ and $\mathcal{S}$, the following is immediate:

Proposition 2

There exists a constant $c_1$ so that for every $t_0 \in \mathbf{Z}$, $x_0 \in \mathbf{R}^{n+m+3d-2}$, ${\theta }_0 \in \mathcal{S}$, $\theta _{ab}^* \in \mathcal{S}_{ab}$, $y^*,w \in {l_{\infty }}$, and $\delta \in ( 0, \infty ]$, when the adaptive controller (8), (9) and (11) is applied to the plant (1), the following holds:

$$\begin{aligned} \Vert A_b (t) \Vert \le c_1 , \; \Vert B_3 (t) \Vert \le c_1 , \; \Vert B_4 (t) \Vert \le c_1 , \; t \ge t_0-1 . \end{aligned}$$

3.3 A better closed-loop model

The good closed-loop model (15) is driven by future tracking error signals. We can now combine this with the crude closed-loop model (16) to create a new model which is driven by perturbed versions of the present and past values of $\phi$, with the weights associated with the parameter update law. Motivated by the form of the term in the parameter estimator, we first define

$$\begin{aligned} \nu (t-1) := \rho _{\delta } ( \phi (t-d) , e(t)) \times \frac{ \phi (t-d)}{\Vert \phi (t-d) \Vert ^2} e(t) , \; t \ge t_0. \end{aligned}$$

(17)

The following result plays a pivotal role in the analysis of the closed-loop system.

Proposition 3

There exists a constant $c_2$ so that for every $t_0 \in \mathbf{Z}$, $x_0 \in \mathbf{R}^{n+m+3d-2}$, ${\theta }_0 \in \mathcal{S}$, $\theta _{ab}^* \in \mathcal{S}_{ab}$, $y^*, w \in {l_{\infty }}$, and $\delta \in ( 0, \infty ]$, when the adaptive controller (8), (9) and (11) is applied to the plant (1), the following holds:

$$\begin{aligned} \phi (t+1) = A_g \phi (t) + \sum _{j=0}^{d-1} \Delta _j (t) \phi (t-j) + \eta (t) , \; t \ge t_0+d-1 , \end{aligned}$$

with

$$\begin{aligned} \Vert \eta (t) \Vert\le & {} c_2 ( 1 + \Vert \nu ( t+2) \Vert + \cdots + \Vert \nu (t+d+1) \Vert ) \\&\times \left[ \sum _{j=1}^{d+1} | y^* ( t+j) | + \sum _{j=1}^{d+1} ( | w(t+j) | + | \bar{ w} ( t+2-j ) | ) \right] \end{aligned}$$

and

$$\begin{aligned} \Vert \Delta _j (t) \Vert \le c_2 ( \Vert \nu ( t-d+1) \Vert + \cdots + \Vert \nu (t+d) \Vert ) , \;\; \; j=0,\ldots ., d-1 . \end{aligned}$$

Proof

See Appendix. $\square$

To make the model of Proposition 3 amenable to analysis, we define a new extended state variable and associated matrices:

$$\begin{aligned} \bar{\phi } (t) := \left[ \begin{array}{c} \phi (t) \\ \phi (t-1) \\ \vdots \\ \phi (t-d+1) \end{array} \right] , \; \bar{A}_g := \left[ \begin{array}{cccc} A_g &{} \quad &{} \quad &{} \\ I &{}\quad &{} \quad &{} \\ &{} \quad \ddots &{} \quad &{} \\ &{} \quad &{}\quad I &{}\quad 0 \end{array} \right] , \end{aligned}$$

(18)

and

$$\begin{aligned} \bar{B}_1 := \left[ \begin{array}{c} {I} \\ {0} \\ {\vdots } \\ {0} \end{array} \right] , \Delta (t) = \left[ \begin{array}{cccc} \Delta _0 (t) &{}\quad \Delta _1 (t) &{} \quad \cdots &{} \quad \Delta _{d-1} (t) \\ 0 &{} \quad \cdots &{} \quad \cdots &{} \quad 0 \\ \vdots &{} \quad \cdots &{} \quad \cdots &{} \quad \vdots \\ 0&{} \quad 0 &{} \quad 0 &{} \quad 0 \end{array} \right] , \end{aligned}$$

(19)

which gives rise to a state-space model which will play a key role in our analysis:

$$\begin{aligned} \bar{\phi } (t+1) = [ \bar{A}_g + \Delta (t) ] \bar{\phi } (t) + \bar{B}_1 \eta (t) , \; t \ge t_0+2d-2 . \end{aligned}$$

(20)

Now $A_g$ arises from $\theta _{ab}^* \in \mathcal{S}_{ab}$ and lies in a corresponding compact set $\mathcal{A}$; furthermore, its eigenvalues are at zero and at the zeros of $B(z^{-1})$, which has all of its roots in the open unit disk, so we can use classical arguments to prove that there exist constants $\gamma$ and $\sigma \in (0,1)$ so that for all $\theta _{ab}^* \in \mathcal{S}_{ab}$, we have

$$\begin{aligned} \Vert \bar{A}_g ^i \Vert \le \gamma \sigma ^i , \; i \ge 0 ; \end{aligned}$$

(21)

indeed, for every $\sigma$ larger than

$$\begin{aligned} \underline{\lambda } := \max _{\theta _{ab}^* \in \mathcal{S}_{ab}} \{| \lambda | : \lambda \in \mathbf{C} \text{ and } B( \lambda ^{-1} ) =0 \} , \end{aligned}$$

we can choose $\gamma$ so that (21) holds.

Equations of the form given in (20) arise in classical adaptive control approaches. While we can view (20) as a linear time-varying system, we have to bear in mind that both $\Delta (t)$ and $\eta (t)$ are (nonlinear) implicit functions of all of the data: $\theta _{ab}^*$, $\theta _0$, $x_0$, $y^*$ and w. That being said, the linear time-varying interpretation is very convenient for analysis; to this end, we let $\Phi _{ {A}}$ denote the state transition matrix of a general time-varying square matrix A. The following result will prove useful in analysing our closed-loop systems on sub-intervals for which the constraints hold.

Proposition 4

With $\sigma \in ( \underline{\lambda } , 1)$, suppose that $\gamma \ge 1$ is such that (21) is satisfied for every $A_g \in \mathcal{A}$. For every $\mu \in ( \sigma , 1 )$, $\beta _0 \ge 0$, $\beta _1 \ge 0$, and

$$\begin{aligned} \beta _2 \in \left[ 0 , \frac{1}{\gamma } ( \mu - \sigma )\right) , \end{aligned}$$

there exists a constant $\bar{\gamma } \ge 1$ so that for every $A_g \in \mathcal{A}$ and $\Delta \in s( \mathbf{R}^{( n+m+d)d \times ( n+m+d)d )} )$ satisfying

$$\begin{aligned} \sum _{i = \tau }^{t-1} \Vert \Delta (i) \Vert \le \beta _0 + \beta _1 ( t- \tau )^{1/2} + \beta _2 ( t- \tau ) , \; \underline{t} \le \tau \le t-1 \le \bar{t} , \end{aligned}$$

(22)

we have

$$\begin{aligned} \Vert \Phi _{\bar{A}_g + \Delta } (t, \tau ) \Vert \le \bar{\gamma } \mu ^{t - \tau } , \; \underline{t} \le \tau < t \le \bar{t} . \end{aligned}$$

(23)

Proof

Fix $\sigma \in ( \underline{\lambda } , 1)$ and $\gamma \ge 1$ so that (21) is satisfied for every $A_g \in \mathcal{A}$. For every $\mu \in ( \sigma , 1 )$, $\beta _0 \ge 0$, $\beta _1 \ge 0$, and

$$\begin{aligned} \beta _2 \in \left[ 0 , \frac{1}{\gamma } ( \mu - \sigma )\right) , \end{aligned}$$

it follows from the lemma of Kreisselmeier [10] that there exists a constant $\bar{\gamma }$, which is independent of $A_g \in \mathcal{A}$ (though dependant on $\beta _2$, $\gamma$, $\mu$, and $\sigma$), so that if (22) holds then (23) holds as well. $\square$

In the next section, we prove that the closed-loop system is exponentially stable and that there is a convolution bound on the closed-loop behaviour. Following that, we analyse robustness and address the tracking problem.

4 Closed-loop stability

Theorem 1

For every $\delta \in ( 0 , \infty ]$ and $\lambda \in ( \underline{\lambda } ,1)$, there exists a constant $c>0$ so that for every $t_0 \in \mathbf{Z}$, plant parameter ${\theta }_{ab}^* \in \mathcal{S}_{ab}$, exogenous signals $y^*, w \in \ell _{\infty }$, estimator initial condition $\theta _0 \in \mathcal{S}$, and plant initial condition

$$\begin{aligned} x_0 = \left[ \begin{array}{cccccc} y( t_0 -1)&\cdots&y(t_0 -n-d+1)&u(t_0 -1 )&\cdots&u( t_0 -m-2d+1 ) \end{array} \right] ^T , \end{aligned}$$

when the adaptive controller (8), (9) and (11) is applied to the plant (1), the following bound holds:

$$\begin{aligned} \Vert \phi (k) \Vert \le c \lambda ^{k- t_0} \Vert x_0 \Vert + \sum _{j=t_0}^{k} c \lambda ^{k-j} ( | y^* (j+d) | + | w(j)| ) , \;\; k \ge t_0 . \end{aligned}$$

(24)

Remark 7

Theorem 1 implies that the system has a bounded gain (from $y^*$ and w to y) in every p-norm.

Remark 8

Most adaptive controllers are proven to yield a weak form of stability, such as boundedness (in the presence of a non-zero disturbance) or asymptotic stability (in the case of a zero disturbance), which means that details surrounding initial conditions can be ignored. Here the goal is to prove a stronger, linear-like, convolution bound as well as exponential stability, so it requires a much more detailed analysis.

Proof

Fix $\delta \in (0, \infty ]$ and $\lambda \in ( \underline{\lambda }, 1)$, and let $t_0 \in \mathbf{Z}$, $\theta _{ab}^* \in \mathcal{S}_{ab}$, $y^*, w\in {l_{\infty }}$, $\theta _0 \in \mathcal{S}$, and $x_0 \in \mathbf{R}^{n+m+3d-2}$ be arbitrary. Now choose $\sigma \in ( \underline{\lambda } , \lambda )$. Observe that $x_0$ gives rise to $\phi (t_0 -1)$,..., $\phi (t_0 - d+1)$, and therefore $\bar{\phi } (t_0 -1)$, which we label $\bar{\phi }_0$; it is clear that $\Vert \bar{\phi }_0 \Vert \le d \Vert x_0 \Vert$ and

$$\begin{aligned} \Vert \phi ( t_0-j) \Vert \le \Vert x_0 \Vert , \; j=1,\ldots , d-1 . \end{aligned}$$

Step 1 Preamble and preliminary results

To proceed we will analyse (20), namely

$$\begin{aligned} \bar{\phi } (t+1) = [ \bar{A}_g + \Delta (t) ] \bar{\phi } (t) + \bar{B}_1 \eta (t) , \; t \ge t_0+2d-2 , \end{aligned}$$

(25)

and obtain a bound on $\bar{\phi } (t)$ in terms of $\eta (t)$, $\bar{w} (t)$, and $y^* (t)$, which we will then convert to the desired form. First of all, we see from Proposition 3 that there exists a constant $\gamma _1$ so that⁷

$$\begin{aligned} \Vert \eta (t) \Vert\le & {} \gamma _1 ( 1 + \Vert \nu ( t+2) \Vert + \cdots + \Vert \nu (t+d+1) \Vert ) \nonumber \\&\times \left[ \sum _{j=1}^{d+1} | y^* ( t+j) | + \sum _{j=1}^{d+1} ( | w(t+j) | + | \bar{ w} ( t+2-j) | ) \right] \nonumber \\\le & {} \gamma _1 ( 1 + \Vert \nu ( t+2) \Vert + \cdots + \Vert \nu (t+d+1) \Vert ) \nonumber \\&\times \underbrace{\left[ \sum _{j=1}^{d+1} | y^* ( t+j) | + \sum _{j=1-d}^{d+1} ( | w(t+j) | + | \bar{ w} ( t+j) | ) \right] }_{=: \tilde{w} (t)} , \end{aligned}$$

(26)

and

$$\begin{aligned} \Vert \Delta (t) \Vert \le \gamma _1 ( \Vert \nu ( t-d+ 1) \Vert + \cdots + \Vert \nu (t+d) \Vert ) , \;\;t \ge t_0 + d - 1 . \end{aligned}$$

(27)

Second of all, following Sect. 3.3 we see that there exists a constant $\gamma _2$ so that for every $A_g \in \mathcal{A}$, we have that the corresponding matrix $\bar{A}_g$ satisfies

$$\begin{aligned} \Vert \bar{A}_g ^i \Vert \le \gamma _2 \sigma ^i , \; i \ge 0 . \end{aligned}$$

Before proceeding, we provide several preliminary results. The first shows that we can always obtain a nice bound on the closed-loop behaviour on a short interval.

Claim 1

There exists a constant $\gamma _3$ so that for every $\underline{t} \ge t_0 -1$, we have

$$\begin{aligned} \Vert \phi (t) \Vert \le \gamma _3 \lambda ^{t - \underline{t}} \Vert \phi ( \underline{t} ) \Vert + \gamma _3 \sum _{j= \underline{t}}^{t-1} \lambda ^{t - 1 - j } | \tilde{w} (j) | , \; t= \underline{t} , \; \underline{t}+1 ,\ldots , \underline{t} + 4d . \end{aligned}$$

Proof of Claim 1

Using the crude model given in (16) together with Proposition 2, we see that there exists a constant $c_1 \ge 1$ so that

$$\begin{aligned} \Vert \phi (t+1) \Vert \le c_1 \Vert \phi (t) \Vert + c_1 | y^* ( t+d+1) | + c_1 | w(t+1) | , \; t \ge t_0 -1. \end{aligned}$$

Using the definition of $\tilde{w} (t)$, this immediately implies that

$$\begin{aligned} \Vert \phi (t+1) \Vert \le c_1 \Vert \phi (t) \Vert + c_1 | \tilde{w} (t) | , \; t \ge t_0 -1. \end{aligned}$$

(28)

Now let $\underline{t} \ge t_0 -1$ be arbitrary. By solving (28) from $t = \underline{t}$, we have

$$\begin{aligned} \Vert \phi (t+1) \Vert\le & {} c_1 ^{t- \underline{t}} \Vert \phi ( \underline{t} ) \Vert + \sum _{j=\underline{t}}^{t-1} c_1 ^ {t-1-j} | \tilde{w} (j) | \\\le & {} \left( \frac{c_1}{ \lambda } \right) ^{t - \underline{t} } [ \lambda ^{t - \underline{t} } \Vert \phi ( \underline{t} ) \Vert + \sum _{j = \underline{t}}^{t-1} \lambda ^{t-1-j} | \tilde{w} (j) | ] , \; t \ge \underline{t} . \end{aligned}$$

If we set $\gamma _3 := \left( \frac{c_1}{ \lambda } \right) ^{4d }$, then the result follows. $\square$

In order to apply Proposition 4, we need to compute a bound on the sum of $\Vert \Delta (t) \Vert$ terms; the following result provides an avenue.

Claim 2

There exists a constant $\gamma _4$ so that

$$\begin{aligned} \sum _{j=t_1}^{t_2-1} \Vert \Delta (j) \Vert \le \gamma _4 [ \sum _{j=t_1-d+1}^{t_2+d-1}\Vert \nu (j) \Vert ^2 ]^{1/2} (t_2- t_1 )^{1/2} , \; t_2 > t_1 \ge t_0+d-1 . \end{aligned}$$

Proof of Claim 2

Since there are 2d terms in the RHS of (27), it is easy to see that

$$\begin{aligned} \sum _{j=t_1}^{t_2-1} \Vert \Delta (j) \Vert \le 2 d \sum _{j=t_1-d+1}^{t_2+d-1} \Vert \nu (j) \Vert . \end{aligned}$$

If we apply the Cauchy–Schwarz inequality, then we have

$$\begin{aligned} \sum _{j=t_1-d+1}^{t_2+d-1} \Vert \nu (j) \Vert \le \left[ \sum _{j=t_1-d+1}^{t_2+d-1} \Vert \nu (j) \Vert \right] ^{1/2} (t_2- t_1 + 2d-1 )^{1/2} . \end{aligned}$$

But

$$\begin{aligned} (t_2-t_1+2d-1)^{1/2} \le (2d)^{1/2} ( t_2 - t_1 )^{1/2} , \; t_2 > t_1 , \end{aligned}$$

so the result follows. $\square$

Step 2 Partition the time-line.

Now we consider the closed-loop system behaviour. To proceed, we partition the timeline into two parts: one in which the noise is small and one where it is not; the idea is that when the noise is small, the closed-loop behaviour should be similar to that when the noise is zero. Of course, here we have to choose the notion of “small” carefully: we do so by using the scaled version of the noise, namely $\frac{ | \bar{w} (t) |}{\Vert \phi (t) \Vert }$, which appears in the bound on V given in Proposition 1. To this end, with $\xi >0$ to be chosen shortly, partition $\{ j \in \mathbf{Z}: j \ge t_0 \}$ into

$$\begin{aligned} S_\mathrm{good}&:= \left\{ j \ge t_0 : \phi (j) \ne 0 \text{ and } \frac{[ \bar{w}(j)]^2}{ \Vert \phi (j) \Vert ^2} < \xi \right\} ,\\ S_\mathrm{bad}&:= \left\{ j \ge t_0 : \phi (j) = 0 \text{ or } \frac{[ \bar{w}(j)]^2}{ \Vert \phi (j) \Vert ^2} \ge \xi \right\} ; \end{aligned}$$

clearly $\{ j \in \mathbf{Z}: \;\; j \ge t_0 \} = S_\mathrm{good} \cup S_\mathrm{bad}$.⁸ Observe that this partition implicitly depends on the system parameters $\theta _{ab}^* \in \mathcal{S}_{ab}$, as well as the initial conditions. We will apply Proposition 4 to analyse the closed-loop system behaviour on $S_\mathrm{good}$; on the other hand, we will easily obtain bounds on the system behaviour on $S_\mathrm{bad}$. Before doing so, we partition the time index $\{ j \in \mathbf{Z}: j \ge t_0 \}$ into intervals which oscillate between $S_\mathrm{good}$ and $S_\mathrm{bad}$. To this end, it is easy to see that we can define a (possibly infinite) sequence of intervals of the form $[ k_i , k_{i+1} )$ satisfying:

• (i) $k_1 = t_0$;

• (ii) $[ k_i , k_{i+1} )$ either belongs to $S_\mathrm{good}$ or $S_\mathrm{bad}$; and

• (iii) if $k_{i+1} \ne \infty$ and $[ k_i , k_{i+1} )$ belongs to $S_\mathrm{good}$ (respectively, $S_\mathrm{bad}$), then the interval $[ k_{i+1} , k_{i+2} )$ must belong to $S_\mathrm{bad}$ (respectively, $S_\mathrm{good}$).

Now we analyse the behaviour during each interval.

Step 3 The closed-loop behaviour on $S_\mathrm{bad}$.

Let $j \in [ k_i , k_{i+1} )$ be arbitrary. In this case, either $\phi (j) = 0$ or $\frac{[ \bar{w} (j)]^2}{ \Vert \phi (j) \Vert ^2} \ge \xi$ holds. In either case, we have

$$\begin{aligned} \Vert \phi (j) \Vert \le \frac{1}{\xi ^{1/2}} | \bar{w}(j) |, \; j \in [ k_i , k_{i+1} ) . \end{aligned}$$

(29)

From the crude model (16) and Proposition 2, we have

$$\begin{aligned} \Vert \phi (j+1) \Vert\le & {} \frac{c_1}{\xi ^{1/2}} | \bar{w}(j) | + c_1 | y^* ( j+d+1 ) | + c_1 | w ( j+1 ) | \\\le & {} \left( \frac{c_1}{\xi ^{1/2}} + c_1 \right) | \tilde{w} (j) | , \; j \in [ k_i , k_{i+1} ) . \end{aligned}$$

If we combine this with (29), we end up with

$$\begin{aligned} \Vert \phi (j) \Vert \le \left\{ \begin{array}{ll} \frac{1}{\xi ^{1/2}} | \tilde{w}(j) | &{} \;\text{ if } j=k_i \\ c_1 \left( 1 + \frac{1}{ \xi ^{1/2} } \right) | \tilde{w}(j-1) | &{} \; \text{ if } j = k_i+1,\ldots , k_{i+1} . \end{array} \right. \end{aligned}$$

(30)

Step 4 The closed-loop behaviour on $S_\mathrm{good}$.

Suppose that $[ k_i , k_{i+1} )$ lies in $S_\mathrm{good}$; this case is much more involved than in the proof of [20, 25] since the bound on $\Vert \Delta (t) \Vert$ provided by Claim 2 extends both forward and backward in time, occasionally outside $S_\mathrm{good}$. Furthermore, the difference equation for $\bar{\phi }$ given in (25) only holds for $t \ge t_0 + 2d-2$, so if $k_i = t_0$ then we cannot use it until $k_i + 2d -2$. For this reason, we will handle the first 2d and last 2d time units separately.

To this end, first suppose that $k_{i+1} \le k_i + 4d$. Then by Claim 1, we see that there exists a constant $\gamma _5$ so that

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _5 \lambda ^{k-k_i} \Vert \phi (k_i) \Vert + \sum _{j=k_i}^{k-1} \gamma _5 \lambda ^{k-1-j} | \tilde{w} (j) | , \; k_i \le k \le k_{i+1} . \end{aligned}$$

(31)

Now suppose that $k_{i+1} > k_i+4d$. Define $\bar{k}_i:= k_i +2d$ and $\underline{k}_{i+1}:= k_{i+1} -2d$. By the definition of $S_\mathrm{good}$ and the fact that $\rho _{\delta } ( \cdot , \cdot ) \in \{ 0 , 1 \}$, it follows that

$$\begin{aligned} {\rho _{\delta }}( \phi (j) , e( j+d)) \frac{ \bar{w} (j)^2}{\Vert \phi (j) \Vert ^2} < \xi , \; j \in [ k_i , k_{i+1} ) , \end{aligned}$$

so

$$\begin{aligned} {\rho _{\delta } ( \phi (j-d+1) , e(j+1))}\frac{ \bar{w} (j-d+1)^2}{\Vert \phi (j-d+1) \Vert ^2} < \xi , \; j \in [ k_i+d-1 , k_{i+1}+d-1 ) . \end{aligned}$$

(32)

By Proposition 1, we see that

$$\begin{aligned} V(\bar{k})\le & {} V( \underline{k} ) + \sum _{j= \underline{k}}^{\bar{k}-1} {\rho _{\delta } ( \phi (j-d+1) , e(j+1))}\\&\times \left[ -\frac{1}{2} \frac{[e (j+1) ]^2}{ \Vert \phi (j-d+1) \Vert ^2} + 2 \frac{[ \bar{w}(j-d+1)]^2}{ \Vert \phi (j-d+1) \Vert ^2}\right] , \;\ k_i \le \underline{k} < \bar{k} \le k_{i+1} . \end{aligned}$$

Using the fact that the first term in the sum is $\nu ( j)$, using (32) to provide a bound on the second term in the sum, and using the fact that

$$\begin{aligned} V( \underline{k} ) = \Vert \hat{\theta } (k) - \theta ^* \Vert \le 4 \Vert \mathcal{S} \Vert ^2, \end{aligned}$$

it follows that

$$\begin{aligned} \sum _{j=\underline{k}}^{\bar{k}-1} \Vert \nu (j) \Vert ^2 \le 8 \Vert \mathcal{S } \Vert ^2 + 4 \xi ( \bar{k}- \underline{k}) , \; k_i +d-1 \le \underline{k} < \bar{k} \le k_{i+1}+d-2 . \end{aligned}$$

(33)

We would like to leverage this bound on $\nu (j)$ to obtain a bound on $\Vert \Delta (j) \Vert$. From Claim 2

$$\begin{aligned} \sum _{j=\underline{k}}^{\bar{k}-1} \Vert \Delta (j) \Vert \le \gamma _4 \left[ \sum _{j=\underline{k}-d+1}^{\bar{k}+d-1} \Vert \nu (j) \Vert ^2 \right] ^{1/2} (\bar{k}- \underline{k})^{1/2} , \; \bar{k}> \underline{k}\ge t_0+d-1 ; \end{aligned}$$

as long as we keep

$$\begin{aligned} \underline{k}-d+1 \ge k_i+d-1 \ge t_0 + d-1 \text{ and } \bar{k}+d-1 \le k_{i+1} +d-2 \end{aligned}$$

or equivalently

$$\begin{aligned} \underline{k}\ge k_i+2d-2 \ge t_0+2d-2 \text{ and } \bar{k}\le k_{i+1} - 1 , \end{aligned}$$

then we can use (33) to provide a bound on the RHS; this will definitely be the case if we restrict

$$\begin{aligned} \bar{k}_i \le \underline{k}< \bar{k}\le \underline{k}_{i+1} , \end{aligned}$$

resulting in

$$\begin{aligned} \sum _{j=\underline{k}}^{\bar{k}-1} \Vert \Delta (j) \Vert \le \gamma _4 [ 8 \Vert \mathcal{S } \Vert ^2 + 4 \xi ( \bar{k}- \underline{k}+ 2d -1) ]^{1/2} ( \bar{k}- \underline{k})^{1/2} , \; \bar{k}_i \le \underline{k} < \bar{k} \le \underline{k}_{i+1}. \end{aligned}$$

If we restrict $\xi \le 1$, then we obtain

$$\begin{aligned} \sum _{j=\underline{k}}^{\bar{k}-1} \Vert \Delta (j) \Vert\le & {} \gamma _4 [ 8 \Vert \mathcal{S } \Vert ^2 + 4 \xi (2d-1) + 4 \xi ( \bar{k}- \underline{k}) ]^{1/2} ( \bar{k}- \underline{k})^{1/2} \\\le & {} \gamma _4 [ 8 \Vert \mathcal{S } \Vert ^2 + 4 (2d-1) ]^{1/2} ( \bar{k}- \underline{k})^{1/2} \\&+ 2 \gamma _4 \xi ^{1/2} ( \bar{k}- \underline{k}) , \; \bar{k}_i \le \underline{k}< \bar{k}\le \underline{k}_{i+1} ; \end{aligned}$$

if we define

$$\begin{aligned} \gamma _6 := \gamma _4 [ 8 \Vert \mathcal{S } \Vert ^2 + 4 (2d-1) ]^{1/2} + 2 \gamma _4 , \end{aligned}$$

then for $\xi \le 1$ we have

$$\begin{aligned} \sum _{j=\underline{k}}^{\bar{k}-1} \Vert \Delta (j) \Vert\le & {} \gamma _6 ( \bar{k}- \underline{k}) ^{1/2} + \gamma _6 \xi ^{1/2} ( \bar{k}- \underline{k}) , \;\; \bar{k}_i\le \underline{k}< \bar{k}\le \underline{k}_{i+1}. \end{aligned}$$

Now we will apply Proposition 4: we set

$$\begin{aligned} \beta _0 = 0 , \; \beta _1 = \gamma _6 , \; \beta _2 = \gamma _6 \xi ^{1/2} , \; \mu = \lambda , \; \gamma = \gamma _2; \end{aligned}$$

we need ${\beta _2} < \frac{1}{ \gamma } ( \mu - \sigma )$, or equivalently

$$\begin{aligned} \gamma _6 \xi ^{1/2}< & {} \frac{1}{\gamma _2} ( \lambda - \sigma ) \\ \Leftrightarrow \; \xi< & {} \left( \frac{ \lambda - \sigma }{ \gamma _2 \gamma _6 } \right) ^2, \end{aligned}$$

so we set

$$\begin{aligned} \xi := \min \left\{ 1 , \frac{1}{2} \left( \frac{ \lambda - \sigma }{ \gamma _2 \gamma _6 } \right) ^2 \right\} . \end{aligned}$$

So from Proposition 4, we see that there exists a constant $\gamma _7$ so that the state transition matrix $\Phi _{\bar{A}_g + \Delta } (t , \tau )$ satisfies

$$\begin{aligned} \Vert \Phi _{\bar{A}_g + \Delta } (t, \tau ) \Vert \le \gamma _7 \lambda ^{t - \tau } , \; \bar{k}_i\le \tau \le t \le \underline{k}_{i+1}. \end{aligned}$$

In order to solve (25), we need a bound on $\eta (t)$. But (33) implies that

$$\begin{aligned} | \nu (j) | ^2 \le 8 \Vert \mathcal{S} \Vert ^2 + 4 \xi \le 8 \Vert \mathcal{S} \Vert ^2 + 4 , \; \bar{k}_i\le j \le \underline{k}_{i+1}, \end{aligned}$$

so from (26) we see that

$$\begin{aligned} \Vert \eta (t) \Vert \le \gamma _1 [ 1 + d ( 8 \Vert \mathcal{S} \Vert ^2 + 4 ) ^{1/2} ] | \tilde{w} (t) | , \;\; \bar{k}_i \le t \le \underline{k}_{i+1} . \end{aligned}$$

If we use this in the difference equation (25), we see that there exists a constant $\gamma _8$ so that

$$\begin{aligned} \Vert \bar{\phi }(k) \Vert \le \gamma _8 \lambda ^{k- \bar{k}_i} \Vert \bar{\phi } ( \bar{k}_i) \Vert + \sum _{j=\bar{k}_i}^{k-1} \gamma _8 \lambda ^{k-1-j} | \tilde{w} (j)| , \; \bar{k}_i\le k \le \underline{k}_{i+1}. \end{aligned}$$

(34)

However, we would like a bound on the whole interval $[k_i , k_{i+1} )$, and we’d like it on $\phi$ rather than $\bar{\phi }$.

Claim 3

There exists a constant $\gamma _9$ so that

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _9 \lambda ^{k- k_i} \Vert \phi (k_i) \Vert + \sum _{j=k_i}^{k-1} \gamma _9 \lambda ^{k-1-j} | \tilde{w} (j)| , \; k_i \le k \le k_{i+1}. \end{aligned}$$

Proof of Claim 3

First of all, on the interval $[k_i , \bar{k}_i]$ we can apply Claim 1:

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _3 \lambda ^{k-k_i} \Vert \phi (k_i ) \Vert + \sum _{j=k_i}^{k-1} \gamma _3 \lambda ^{k-1-j} | \tilde{w} (j) | , \; k_i \le k \le \bar{k}_i . \end{aligned}$$

This provides a bound of the desired form on the first sub-interval of $[k_i , k_{i+1})$.

Next, from (34) we have

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _8 \lambda ^{k- \bar{k} _i} \Vert \bar{\phi }(\bar{k}_i ) \Vert + \sum _{j=\bar{k}_i}^{k-1} \gamma _8 \lambda ^{k-1-j} | \tilde{w} (j) | , \; \bar{k}_i \le k \le \underline{k}_{i+1} . \end{aligned}$$

(35)

Using the definition of $\bar{\phi }$ and Claim 1 (with $\underline{t} = k_i$), we have

$$\begin{aligned} \Vert \bar{\phi }(\bar{k}_i ) \Vert\le & {} \Vert \phi ( \bar{k}_i) \Vert + \Vert \phi ( \bar{k}_i -1 ) \Vert + \cdots + \Vert \phi ( \bar{k}_i - d + 1 ) \Vert \\\le & {} \gamma _3 ( \lambda ^{\bar{k}_i - k_i} + \lambda ^{\bar{k}_i - k_i +1} + \cdots + \lambda ^{\bar{k}_i - k_i+d-1} ) \Vert \phi ( k_i ) \Vert \\&+\gamma _3 \left[ \sum _{j=k_i}^{\bar{k}_i-1} \lambda ^{ \bar{k}_i -1-j} | \tilde{w} (j) | + \sum _{j=k_i}^{\bar{k}_i-2} \lambda ^{ \bar{k}_i -2-j} | \tilde{w} (j) | + \cdots + \sum _{j=k_i}^{\bar{k}_i-d} \lambda ^{ \bar{k}_i -d-j} | \tilde{w} (j) | \right] \\\le & {} \underbrace{\frac{\gamma _3 d}{ \lambda ^{d-1}}}_{=: \bar{\gamma }_3} \lambda ^{\bar{k}_i - k_i } \Vert \phi (k_i) \Vert + \gamma _3 \left[ \sum _{j=k_i}^{\bar{k}_i-1} \lambda ^{ \bar{k}_i -1-j} | \tilde{w} (j) | \right. \\&\left. + \frac{1}{\lambda } \sum _{j=k_i}^{\bar{k}_i-2} \lambda ^{ \bar{k}_i -1-j} | \tilde{w} (j) | + \cdots + \frac{1}{\lambda ^{d-1}} \sum _{j=k_i}^{\bar{k}_i-d} \lambda ^{ \bar{k}_i -1-j} | \tilde{w} (j) | \right] \\\le & {} \bar{\gamma }_3 \lambda ^{\bar{k}_i - k_i } \Vert \phi (k_i) \Vert + \bar{\gamma }_3 \sum _{j=k_i}^{\bar{k}_i-1} \lambda ^{ \bar{k}_i -1-j} | \tilde{w} (j) | . \end{aligned}$$

If we now substitute this into (35), then we have

$$\begin{aligned} \Vert \phi (k) \Vert\le & {} \gamma _8 \bar{\gamma }_3 \lambda ^{k - k_i} \Vert \phi (k_i) \Vert + \gamma _8 \bar{\gamma }_3 \lambda ^{k - \bar{k}_i} \sum _{j=k_i}^{\bar{k}_i-1} \lambda ^{ \bar{k}_i -1-j} | \tilde{w} (j) | \\&+ \gamma _8 \sum _{j=k_i}^{k-1} \lambda ^{ {k} -1-j} | \tilde{w} (j) | , \;\; \bar{k}_i \le k \le \underline{k}_{i+1} ; \end{aligned}$$

if we define $\bar{\gamma }_8 := \gamma _8 + \gamma _8 \bar{\gamma }_3$, then it follows that

$$\begin{aligned} \Vert \phi (k) \Vert \le \bar{\gamma }_8 \lambda ^{k-k_i} \Vert \phi (k_i) \Vert + \bar{\gamma }_8 \sum _{j= k_i}^{k-1} \lambda ^{k-1-j} | \tilde{w} (j) | , \; \bar{k}_i \le k \le \underline{k}_{i+1} . \end{aligned}$$

(36)

This provides a bound of the desired form on the second sub-interval of $[k_i , k_{i+1} ]$.

Last of all, we would like to obtain a bound of the desired form on $[ \underline{k}_{i+1} , k_{i+1} ]$. By Claim 1 we have

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _3 \lambda ^{k - \underline{k}_{i+1}} \Vert \phi ( \underline{k}_{i+1} ) \Vert + \sum _{j = \underline{k}_{i+1}}^{k-1} \gamma _3 \lambda ^{k-1-j} | \tilde{w} (j) | , \; \underline{k}_{i+1} \le k \le k_{i+1} . \end{aligned}$$

Using (36) to obtain a bound on $\Vert \phi ( \underline{k}_{i+1} ) \Vert$, we obtain

$$\begin{aligned} \Vert \phi (k) \Vert\le & {} \gamma _3 \lambda ^{k - \underline{k}_{i+1}} \left[ \bar{\gamma }_8 \lambda ^{\underline{k}_{i+1} - k_i} \Vert \phi (k_i) \Vert + \bar{\gamma }_8 \sum _{j=k_i}^{\underline{k}_{i+1}-1} \lambda ^{\underline{k}_{i+1}-1-j} | \tilde{w} (j) | \right] \\&+ \sum _{j = \underline{k}_{i+1}}^{k-1} \gamma _3 \lambda ^{k-1-j} | \tilde{w} (j) | \\\le & {} \gamma _3 \bar{\gamma }_8 \lambda ^{k-k_i} \Vert \phi (k_i) \Vert + ( \gamma _3 \bar{\gamma }_8 + \gamma _3) \sum _{j=k_i}^{k-1} \lambda ^{k-1-j} | \tilde{w} (j) |, \; \underline{k}_{i+1} \le k \le k_{i+1}. \end{aligned}$$

So if we set

$$\begin{aligned} \gamma _9 := \max \{ \gamma _3 , \bar{\gamma }_8 , \gamma _3 \bar{\gamma }_8 + \gamma _3 \} , \end{aligned}$$

then the result holds. $\square$

Step 5 Analysing the whole time-line.

At this point, we glue together the bounds obtained on $S_\mathrm{bad}$ and $S_\mathrm{good}$ together to obtain a bound which holds on all of $[ t_0 , \infty )$.

Claim 4

There exists a constant $\gamma _{10}$ so that the following bound holds:

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _{10} \lambda ^{k-t_0} \Vert \phi ( t_0 ) \Vert + \sum _{j=t_0}^{k} \gamma _{10} \lambda ^{k-j} | \tilde{w} ( j ) | , \;\; k \ge t_0 . \end{aligned}$$

(37)

Proof of Claim 4

If $[k_1 , k_2 ) = [t_0 , k_2) \subset S_\mathrm{good}$, then (37) holds for $k \in [t_0 , k_2 ]$ by Claim 3 as long as

$$\begin{aligned} \gamma _{10} \ge \max \left\{ \gamma _9 , \frac{\gamma _9}{\lambda } \right\} . \end{aligned}$$

(38)

If $[k_1 , k_2 ) = [t_0 , k_2) \subset S_\mathrm{bad}$, then from (30) we see that the bound holds as long as

$$\begin{aligned} \gamma _{10} \ge \max \left\{ \frac{1}{ \xi ^{1/2}} , \frac{c_1}{\lambda } \left( 1 + \frac{1}{\xi ^{1/2}} \right) \right\} . \end{aligned}$$

(39)

We now use induction - suppose that (37) holds for $k \in [k_1 , k_i ]$; we need to prove that it holds for $k \in ( k_i, k_{i+1} ]$ as well. If $[k_i, k_{i+1}) \subset S_\mathrm{bad}$, then from (30) we see that the bound holds on $(k_i , k_{i+1} ]$ as long (39) holds. On the other hand, if $[k_i, k_{i+1}) \subset S_\mathrm{good}$, then $k_i -1 \in S_\mathrm{bad}$; from (30) we have that

$$\begin{aligned} \Vert \phi ( k_i) \Vert \le c_1 \left( 1 + \frac{\gamma _3}{\xi ^{1/2}}\right) | \tilde{w}(k_i-1) | ; \end{aligned}$$

combining this with Claim 3, which provides a bound on $\Vert \phi (k)\Vert$ for $k \in [k_i , k_{i+1} )$, we have

$$\begin{aligned} \Vert \phi (k) \Vert\le & {} \gamma _9 \lambda ^{k-k_i} \Vert \phi (k_i ) \Vert + \sum _{j=k_i}^{k-1} \gamma _9 \lambda ^{k-1-j} | \tilde{w} (j) | \\\le & {} \gamma _9 \lambda ^{k-k_i} c_1 \left( 1 + \frac{\gamma _3}{\xi ^{1/2}}\right) | \tilde{w} (k_i -1 ) |+ \sum _{j=k_i}^{k-1} \gamma _9 \lambda ^{k-1-j} | \tilde{w} (j) | \\\le & {} \left[ \gamma _9 c_1 \left( 1 + \frac{\gamma _3}{\xi ^{1/2}}\right) + \gamma _9 \right] \sum _{j=k_i-1}^{k-1} \gamma _9 \lambda ^{k-1-j} | \tilde{w} (j) | , \; k \in [k_i , k_{i+1} ]. \end{aligned}$$

So the bound holds in this case as long as

$$\begin{aligned} \gamma _{10} \ge \frac{1}{\lambda } \left[ \gamma _9 c_1 \left( 1 + \frac{\gamma _3}{\xi ^{1/2}}\right) + \gamma _9 \right] . \end{aligned}$$

$\square$

Step 6 Obtaining a bound of the desired form

The last step is to convert the bound proven in Claim 4 to one of the desired form, i.e. we need to replace $\tilde{w}$ with w and $y^*$. First of all, using the definition of $\tilde{w}$ given in (26), we see that

$$\begin{aligned} \tilde{w} (t) = \sum _{j=1}^{d+1} | y^* ( t+j) | + \sum _{j=1-d}^{d+1} ( | w(t+j) | + | \bar{ w} ( t+j) | ) . \end{aligned}$$

From the definition of $\bar{w} (t)$, we have that

$$\begin{aligned} | \bar{w} (t) | \le | f_0 | | w (t+d) | + \cdots + | f_{d-1} | | w(t+1) | ; \end{aligned}$$

the $f_i's$ arise from long division and are continuous functions of $\theta _{ab}^* \in \mathcal{S}_{ab}$, so it follows that exists a constant $\gamma _{11}$ so that for all $\theta _{ab}^* \in \mathcal{S}_{ab}$, we have

$$\begin{aligned} | \tilde{w} (t) | \le \sum _{j=1}^{d+1} | y^* ( t+j) | + \gamma _{11} \sum _{j=1-d}^{2d+1} | w(t+j) | . \end{aligned}$$

It turns out that some of the terms in the sum are superfluous:

• (i) We see from the control law (11) that $y^* (t)$ affects $\phi (t)$ only via u(t). Indeed, u(t) explicitly depends on $y^* (t+d)$ which means, by causality, that $y^*( t+d+1)$ has no effect on $\phi (t)$.

• (ii) We see from the original plant equation (1) that w(t) affects $\phi (t)$ via y(t). Indeed, y(t) explicitly depends on w(t), which means, by causality, that $\sum _{j=1}^{2d+1} | w(t+j) |$ can have no effect on $\phi (t)$.

If we combine these observations with Claim 4, we see that the bound becomes

$$\begin{aligned} \Vert \phi (k) \Vert\le & {} \gamma _{10} \lambda ^{k-t_0} \Vert \phi (t_0) \Vert + \sum _{j=t_0}^{k} \gamma _{10} \lambda ^{k-j} [ | y^* (j+1) | + \cdots + | y^* ( j+d) | \\&+ \gamma _{11} | w( j - d + 1) | + \cdots + \gamma _{11} | w (j) | ]; \end{aligned}$$

if we examine each term in the summation, it is straight-forward to verify that

$$\begin{aligned} \Vert \phi (k) \Vert\le & {} \gamma _{10} \lambda ^{k-t_0} \Vert \phi (t_0) \Vert + \frac{\gamma _{10} d}{\lambda ^{d-1}} \sum _{j=t_0-d+1}^{k} \lambda ^{k-j} | y^*(j+d) | \\&+\frac{\gamma _{10} \gamma _{11} d}{\lambda ^{d-1}} \sum _{j=t_0-d+1}^{k} \lambda ^{k-j} | w (j) | \\\le & {} \gamma _{10} \lambda ^{k-t_0} \Vert \phi (t_0) \Vert + \frac{\gamma _{10} d ( 1 + \gamma _{11} ) }{\lambda ^{d-1}} \sum _{j=t_0}^{k} \lambda ^{k-j} (|y^*(j+d) | + | w (j) | ) | \\&+ \underbrace{\frac{\gamma _{10} d }{\lambda ^{d-1}} \sum _{j=t_0-d+1}^{t_0-1} \lambda ^{k-j} |y^*(j+d)| }_{\psi _1 ( k )} + \underbrace{\frac{\gamma _{10} \gamma _{11} d }{\lambda ^{d-1}} \sum _{j=t_0-d+1}^{t_0-1} \lambda ^{k-j} | w (j ) | }_{=: \psi _2 (k)}. \end{aligned}$$

Now $y^*$ affects $\phi$ via the control signal, and it is clear that $y^* (k)$ for $k < t_0 + d$ has no effect on $\phi (k)$, $k \ge t_0$, so the $\psi _1 (k)$ term can be ignored.⁹ On the other hand, the $\psi _2 (k)$ term does have an effect: first observe that $\psi _2$ can be rewritten as

$$\begin{aligned} \psi _2 (k) = \frac{\gamma _{10} \gamma _{11} d}{\lambda ^{d-1}} \left[ \sum _{j=t_0-d+1}^{t_0-1} \lambda ^{t_0-j} | w (j ) | \right] \lambda ^{k-t_0} ; \end{aligned}$$

second of all, it follows from the plant equation (1) that each of $\{ w(t_0 -d+1),\ldots , w(t_0-1) \}$ can be rewritten as a linear function of $x_0$, so it follows that there exists a constant $\gamma _{12}$ so that

$$\begin{aligned} \Vert \psi _2 (k) \Vert \le \gamma _{12} \lambda ^{k-t_0} \Vert x_0 \Vert , \; k \ge t_0 . \end{aligned}$$

Since $\Vert \phi (t_0 ) \Vert \le \Vert x_0 \Vert$, we conclude that

$$\begin{aligned} \Vert \phi (k) \Vert\le & {} ( \gamma _{10} + \gamma _{12} ) \lambda ^{k-t_0} \Vert x_0 \Vert \\&+ \frac{\gamma _{10} d ( 1 + \gamma _{11}) }{\lambda ^{d-1}} \sum _{j=t_0}^{k} \lambda ^{k-j} (|y^*(j+d) | + | w (j) | ) , \; k \ge t_0 , \end{aligned}$$

as desired. $\square$

5 Robustness to time-variations and unmodelled dynamics

It turns out that the exponential stability property and the convolution bounds proven in Theorem 1 will guarantee robustness to a degree of time-variations and unmodelled dynamics; in this way, the approach has a lot in common with an LTI closed-loop system, which also enjoys this feature. Indeed, as we have recently proven in [36], this is true even in a more general situation than that considered here. At this point, we will state the key result and then simply refer to that paper for the proof.

To proceed, consider a time-varying version of the reparameterized plant (2), in which $\theta ^*$ is now time-varying and there are some unmodelled dynamics which enter the system via $\bar{w} _{\Delta } (t)$:

$$\begin{aligned} y(t+d) = \theta ^*(t)^T \phi (t) + \bar{w} (t) + \bar{w} _{\Delta } (t) . \end{aligned}$$

(40)

• (i) Time variation model Since the mapping from $\mathcal{S}_{ab}$ to $\mathcal{S}_{\alpha \beta }$ is analytic and both sets are compact, we may as well consider the time-variations in the latter setting. We adopt a common model of acceptable time-variations used in adaptive control, e.g. see [10]: with $c_0 \ge 0$ and $\epsilon >0$, we let ${s} ( \mathcal{S}_{ \alpha \beta } , c_0, \epsilon )$ denote the subset of ${l_{\infty }}( \mathbf{R}^{n+m+d})$ whose elements $\theta ^*$ satisfy $\theta ^* (t) \in \mathcal{S}_{ \alpha \beta }$ for every $t \in \mathbf{Z}$ as well as

  $$\begin{aligned} \sum _{t=t_1}^{t_2-1} \Vert \theta ^* (t+1) - \theta ^* (t) \Vert \le c_0 + \epsilon ( t_2 - t_1 ) , \; t_2 > t_1 \end{aligned}$$

  (41)

  for every $t_1 \in \mathbf{Z}$.

• (ii) Unmodelled dynamics We also adopt a common model of unmodelled dynamics:

  $$\begin{aligned} {m} (t+1)= & {} \beta {m} (t) + \beta \Vert \phi (t) \Vert , \; m(t_0)= m_0 \; \end{aligned}$$

  (42)
  $$\begin{aligned} \bar{w} _{\Delta } (t)\le & {} \mu m(t) + \mu \Vert \phi (t) \Vert . \end{aligned}$$

  (43)

  As argued in [25], this encapsulates a large class of additive, multiplicative and uncertainty in a coprime factorization, which is common in the robust control literature, e.g. see [46], and is commonly used in the adaptive control literature, e.g. see [11].

We will now show that if the time-variations are slow enough and the size of the unmodelled dynamics is small enough, then the closed-loop system retains exponential stability as well as the convolution bounds.

Theorem 2

For every $\delta \in ( 0 , \infty ]$, $c_0 \ge 0$ and $\beta \in (0,1)$, there exist an $\epsilon >0$, $\mu > 0$, ${\lambda } \in ( \max \{ \beta , \underline{\lambda }) \} ,1)$ and ${c} >0$ so that for every $t_0 \in \mathbf{Z}$, plant parameter ${\theta }^* \in s ( \mathcal{S}_{\alpha \beta }, c_0 , \epsilon )$, exogenous signals $y^*, w \in \ell _{\infty }$, estimator initial condition $\theta _0 \in \mathcal{S}$, and plant initial condition

$$\begin{aligned} x_0 = \left[ \begin{array}{cccccc} y( t_0 -1)&\cdots&y(t_0 -n-d+1)&u(t_0 -1 )&\cdots&u( t_0 -m-2d+1 ) \end{array} \right] ^T , \end{aligned}$$

when the adaptive controller (8), (9) and (11) is applied to the plant (40) with $\bar{w}_{\Delta }$ satisfying (42), (43), the following bound holds:

$$\begin{aligned} \Vert \phi (k) \Vert \le c \lambda ^{k- t_0} \Vert \left[ \begin{array}{c} x_0 \\ m_0 \end{array} \right] \Vert + \sum _{j=t_0}^{k} c \lambda ^{k-j} ( | y^* (j+d) | + | w(j)| ) , \;\; k \ge t_0 . \end{aligned}$$

(44)

Proof

This was proven in [25] for the case of pole placement and then extended to a more general setting in Theorems 1 and 3 of [36]; the setup here is a special case of the latter, so the result follows immediately from that. $\square$

6 Tracking

We now move from the stability problem to the much harder tracking problem. We first derive a very useful bound on the tracking error in terms of the prediction error. Following that, we analyse the case when the disturbance is absent: we start with the original LTI case, and then we move to the situation in which the parameters are slowly time-varying. Last of all, we consider the original LTI case with a disturbance.

6.1 A useful bound

The d-step-ahead control law (11) can be rewritten as

$$\begin{aligned} y^*(t)=\hat{\theta }(t-d)^\top \phi (t-d),\quad t\ge t_0+d. \end{aligned}$$

Since the tracking error is $\varepsilon (t)=y(t)-y^*(t)$, we have

$$\begin{aligned} \varepsilon (t)=y(t)-\hat{\theta }(t-d)^\top \phi (t-d),\quad t\ge t_0+d. \end{aligned}$$

Combining the above with the prediction error definition in (5), we easily obtain

$$\begin{aligned} \varepsilon (t) = e(t) + \phi (t-d)^\top \left[ \hat{\theta }(t-1) - \hat{\theta }(t-d) \right] ,\;t\ge t_0+d. \end{aligned}$$

(45)

Observe that the relationship in (45) is true irrespective of the plant model, i.e. it need not satisfy (1) or (2).

Now we turn to the prediction and tracking errors scaled by the state $\phi$. For $t\ge t_0+d$, if $\Vert \phi (t-d)\Vert \ne 0$ then it follows from (45) that

$$\begin{aligned} \frac{|\varepsilon (t)|}{\Vert \phi (t-d)\Vert } \le \frac{|e(t)|}{\Vert \phi (t-d)\Vert } + \Vert \hat{\theta }(t-1) - \hat{\theta }(t-d) \Vert ; \end{aligned}$$

multiplying both sides by $\rho _{\delta }(\phi (t-d),e(t))$ yields

$$\begin{aligned} \rho _{\delta }(\phi (t-d),e(t)) \times \frac{|\varepsilon (t)|}{\Vert \phi (t-d)\Vert }\le & {} \rho _{\delta }(\phi (t-d),e(t)) \times \frac{|e(t)|}{\Vert \phi (t-d)\Vert }\\&+ \rho _{\delta }(\phi (t-d),e(t)) \times \Vert \hat{\theta }(t-1) - \hat{\theta }(t-d) \Vert \\\le & {} \rho _{\delta }(\phi (t-d),e(t)) \times \frac{|e(t)|}{\Vert \phi (t-d)\Vert } \\&+ \Vert \hat{\theta }(t-1) - \hat{\theta }(t-d) \Vert , \\&\quad t\ge t_0+d. \end{aligned}$$

It turns out that the estimator property in (10) holds irrespective of the plant model; if we use this to yield a bound on the second term on the right-hand side above, then we obtain

$$\begin{aligned}&\rho _{\delta } (\phi (t-d),e(t)) \frac{|\varepsilon (t)|}{\Vert \phi (t-d)\Vert }\\&\quad \le \sum _{j=0}^{d-1} \rho _{\delta }(\phi (t-d-j),e(t-j))\frac{|e(t-j)|}{\Vert \phi (t-d-j)\Vert }, \; t\ge t_0+d. \end{aligned}$$

By Cauchy–Schwartz

$$\begin{aligned}&\rho _{\delta }(\phi (t-d),e(t)) \frac{|\varepsilon (t)|^2}{\Vert \phi (t-d)\Vert ^2}\\&\quad \le \left( \sum _{j=0}^{d-1} \rho _{\delta }(\phi (t-d-j),e(t-j))\frac{|e(t-j)|}{\Vert \phi (t-d-j)\Vert }\right) ^2 \\&\quad \le \left( \sum _{j=0}^{d-1} \rho _{\delta }(\phi (t-d-j),e(t-j))\frac{|e(t-j)|^2}{\Vert \phi (t-d-j)\Vert ^2}\right) \left( \sum _{j=0}^{d-1}1\right) \\&\quad = d\sum _{j=0}^{d-1} \rho _{\delta }(\phi (t-d-j),e(t-j)) \frac{|e(t-j)|^2}{\Vert \phi (t-d-j)\Vert ^2}, \; t\ge t_0+d. \end{aligned}$$

Hence, it follows that for $\bar{t}\ge t_0+2d-1$ we obtain

$$\begin{aligned}&\sum _{j=\bar{t}}^{t} \rho _{\delta }(\phi (j-d),e(j)) \frac{|\varepsilon (j)|^2}{\Vert \phi (j-d)\Vert ^2}\nonumber \\&\quad \le \sum _{j=\bar{t}}^{t} \left( d\sum _{q=0}^{d-1} \rho _{\delta }(\phi (j-d-q),e(j-q)) \frac{|e(j-q)|^2}{\Vert \phi (j-d-q)\Vert ^2}\right) \nonumber \\&\quad \le d^2 \sum _{j=\bar{t}-d+1}^{t} \rho _{\delta }(\phi (j-d),e(j)) \frac{|e(j)|^2}{\Vert \phi (j-d)\Vert ^2}, \nonumber \\&\qquad \;t\ge \bar{t} \ge t_0+2d-1. \end{aligned}$$

(46)

The inequality in (46) will prove to be useful in the forth-coming analysis.

In the next two sub-sections, we analyse the case when the disturbance is absent; we start with the case with the original LTI case, and then we move to the situation in which the parameters are slowly time-varying. After that, we anlyse the general case.

6.2 The LTI case: no disturbance

In the literature, it is typically proven that the tracking error is square summable, e.g. see [5]. Here we can prove an explicit bound on the 2-norm of the error signal in terms of the plant initial condition and the size of the reference signal, which is a significant improvement.

Theorem 3

For every $\delta \in ( 0 , \infty ]$ and $\lambda \in ( \underline{\lambda } ,1)$ there exists a constant $c>0$ so that for every $t_0 \in \mathbf{Z}$, plant parameter ${\theta }_{ab}^* \in \mathcal{S}_{ab}$, exogenous signal $y^*\in \ell _{\infty }$, estimator initial condition $\theta _0 \in \mathcal{S}$, and plant initial condition

$$\begin{aligned} x_0 = \left[ \begin{array}{cccccc} y( t_0 -1)&\cdots&y(t_0 -n-d+1)&u(t_0 -1 )&\cdots&u( t_0 -m-2d+1 ) \end{array} \right] ^T , \end{aligned}$$

when the adaptive controller (8), (9) and (11) is applied to the plant (1) in the presence of a zero disturbance w, the following bound holds:

$$\begin{aligned} \sum _{k=t_0+2d-1}^{\infty } {\varepsilon }(k)^2 \le c ( \Vert x_0 \Vert ^2 + \sup _{j \ge t_0+d} | y^* (j) |^2 ). \end{aligned}$$

Proof

Fix $\delta \in ( 0 , \infty ]$ and $\lambda \in (\underline{\lambda },1)$. Let $t_0 \in \mathbf{Z}$, ${\theta }_{ab}^* \in \mathcal{S}_{ab}$, $y^*\in \varvec{\ell }_{\infty }$, $\theta _0 \in \mathcal{S}$, and $x_0$ be arbitrary. Now suppose that $w=0$; for this case, by the definition of the function $\rho _{\delta }$, for $t\ge t_0+d$ we have

$$\begin{aligned} \rho _{\delta }(\phi (t-d),e(t))=0 \quad \Leftrightarrow \quad \Vert \phi (t-d)\Vert =0. \end{aligned}$$

If we incorporate this into the relation (46) with $\bar{t} = t_0 + 2d-1$, then for $T > t_0 + 2d-1$ we obtain

$$\begin{aligned} \sum _{t=t_0+2d-1, \phi (t-d)\ne 0}^{T} \frac{|\varepsilon (t)|^2}{\Vert \phi (t-d)\Vert ^2}&\le d^2 \sum _{t=t_0+d, \phi (t-d)\ne 0}^{T} \frac{|e(t)|^2}{\Vert \phi (t-d)\Vert ^2} \\&\le d^2 \sum _{t=t_0+d, \phi (t-d)\ne 0}^{\infty } \frac{|e(t)|^2}{\Vert \phi (t-d)\Vert ^2} \\&\le 8d^2\Vert \mathcal{S}\Vert ^2 \text{(by } \text{ Proposition }~1). \end{aligned}$$

Since ${\varepsilon }(t) = 0$ if $\phi (t-d) = 0$, if we now apply the bound on $\phi (t)$ proven in Theorem 1, we conclude that there exists constants $c_1 > 0$ and $\lambda \in (0,1)$ so that

$$\begin{aligned} \sum _{t=t_0+2d-1}^{\infty } {\varepsilon }(t)^2\le & {} 8 d^2 \Vert \mathcal{S} \Vert ^2 \times \sup _{j \ge t_0 } \Vert \phi (j) \Vert ^2 \\\le & {} 16 d^2 \Vert \mathcal{S} \Vert ^2 c_1^2 \left[ \Vert x_0 \Vert ^2 + \left( \frac{1}{1- \lambda }\right) ^2 \sup _{j \ge t_0 +d } | y^* (j) |^2 \right] , \end{aligned}$$

which yields the desired result. $\square$

6.3 The slowly time-varying case: no disturbance

Now we turn to the case in which the plant parameter is slowly time-varying (with no jumps in the parameters) and the disturbance w(t) is zero. We should not expect to get exact tracking; we will be able to prove, roughly speaking, that the average tracking error is small on average if the time-variation is small. To proceed, we consider the time-varying plant of (40) without the unmodelled dynamics and with zero noise:

$$\begin{aligned} y(t+d) = \theta ^*(t)^T \phi (t) . \end{aligned}$$

(47)

Theorem 4

For every $\delta \in ( 0 , \infty ]$, there exist constants $\bar{\epsilon } >0$ and $\gamma >0$ so that for every $t_0 \in \mathbf{Z}$, $\epsilon \in ( 0, \bar{\epsilon })$, $\theta ^*\in s(\mathcal{S}_{\alpha \beta },0,\epsilon )$, $y^*\in \varvec{\ell }_{\infty }$, $\theta _0 \in \mathcal{S}$, and plant initial condition

$$\begin{aligned} x_0 = \left[ \begin{array}{cccccc} y( t_0 -1)&\quad \cdots&\quad y(t_0 -n-d+1)&\quad u(t_0 -1 )&\quad \cdots&\quad u( t_0 -m-2d+1 ) \end{array} \right] ^T , \end{aligned}$$

when the adaptive controller (8), (9) and (11) is applied to the time-varying plant (47), the following holds:

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j= t_0}^{t_0+T-1} |\varepsilon (j)|^2\le & {} \gamma {\epsilon }^{2/3} \Vert y^*\Vert _\infty ^2 . \end{aligned}$$

Proof

Fix $\delta \in ( 0 , \infty ]$ and $\lambda _1\in (\underline{\lambda },1)$, and set $w=0$. By Theorem 2, there exist constants $\gamma _1>0$ and

$$\begin{aligned} \bar{\epsilon } \in (0, \max \{ 2 \Vert \mathcal{S } \Vert , 2^{3/2} {d}^{1/2} \Vert \mathcal{S} \Vert \} ) \end{aligned}$$

so that for every $t_0\in \mathbf{Z}$, $y^*\in \varvec{\ell }_{\infty }$, $\theta _0 \in \mathcal{S}$, initial condition $x_0$, and $\theta ^*\in s(\mathcal{S}_{\alpha \beta },0,\bar{\epsilon })$, when the adaptive controller (8), (9) and (11) is applied to the plant (47), the following holds:

$$\begin{aligned} \Vert \phi (t)\Vert \le \gamma _1 \lambda _1^{t-t_0} \Vert x_0\Vert + \frac{\gamma _1}{1-\lambda _1} \sup _{j\in [t_0,t]} |y^*(j+d)|, \qquad t\ge t_0. \end{aligned}$$

(48)

Now, let $t_0\in \mathbf{Z}$, $y^*\in \varvec{\ell }_{\infty }$, $\theta _0 \in \mathcal{S}_{ab}$, $x_0$, $\epsilon \in ( 0 , \bar{\epsilon } )$ and $\theta ^*\in s(\mathcal{S}_{\alpha \beta },0,{\epsilon })$ be arbitrary. We first want to find a bound on the tracking error in terms of the prediction error. Note that the relationship in (45) and (46) holds irrespective of the plant model. Since $w=0$, it follows that for $t \ge t_0 +d$:

$$\begin{aligned} \rho _{\delta }(\phi (t-d),e(t))=0 \quad \Leftrightarrow \quad \Vert \phi (t-d)\Vert =0. \end{aligned}$$

Now apply (46); by changing the index to facilitate analysis, we obtain

$$\begin{aligned} \sum _{j=\bar{t}+d-1, \phi (j)\ne 0}^{t-1} \frac{|\varepsilon (j+d)|^2}{\Vert \phi (j)\Vert ^2} \le d^2 \sum _{j=\bar{t}, \phi (j)\ne 0}^{t-1} \frac{|e(j+d)|^2}{\Vert \phi (j)\Vert ^2}, \; t\ge \bar{t}+d,\; \bar{t} \ge t_{0}. \end{aligned}$$

(49)

Now we incorporate time-variation. Let $t_{i}\ge t_{0}$ be arbitrary; then from plant equation (47) we have

$$\begin{aligned} y(t+d)= & {} \phi (t)^\top \theta ^*(t_i) + \underbrace{ \phi (t)^\top \left[ \theta ^*(t) - \theta ^*(t_i) \right] }_{=:\Delta _i(t)}. \end{aligned}$$

(50)

Note from (41) that $\Vert \Delta _i(t) \Vert \le \epsilon \Vert \phi (t)\Vert \left( t-t_i \right) .$ Define $\tilde{\theta }_i(t):= \hat{\theta }(t)-\theta ^*(t_i)$. Since $w=0$, by applying Proposition 1 to the plant (50), we obtain¹⁰

$$\begin{aligned} \sum _{j=t_i, \Vert \phi (j)\Vert \ne 0 }^{t-1} \frac{|e(j+d)|^2}{\Vert \phi (j)\Vert ^2}\le & {} 2\Vert \tilde{\theta }(t_i) \Vert ^2+ \sum _{j=t_i, \Vert \phi (j)\Vert \ne 0}^{t-1} \frac{4\Vert \Delta _i(j)\Vert ^2}{\Vert \phi (j)\Vert ^2} \\\le & {} 2\Vert \tilde{\theta }_i(t_i) \Vert ^2 + 4 \epsilon ^2 \sum _{j=t_i}^{t-1} (j-t_i)^2\\= & {} 2\Vert \tilde{\theta }_i(t_i) \Vert ^2 + 4 \epsilon ^2 \sum _{k=0}^{t-t_i-1} k^2 \\\le & {} 8\Vert \mathcal{S} \Vert ^2 + 4 \epsilon ^2 (t-t_i-1)^3, \quad t\ge t_i+1,\; t_i\ge t_0. \end{aligned}$$

Using the above bound in (49) with $\bar{t} = t_i$, we obtain

$$\begin{aligned} \sum _{j=t_i+d-1, \phi (j)\ne 0}^{t-1} \frac{|\varepsilon (j+d)|^2}{\Vert \phi (j)\Vert ^2}&\le d^2 \sum _{j=t_i, \phi (j)\ne 0}^{t-1} \frac{|e(j+d)|^2}{\Vert \phi (j)\Vert ^2} \nonumber \\&\le d^2 \left[ 8\Vert \mathcal{S} \Vert ^2 + 4 \epsilon ^2 (t-t_i-1)^3 \right] , \;\; t \ge t_i + d,\; t_i \ge t_0. \end{aligned}$$

(51)

Since the disturbance is zero here, it follows that $\Vert \phi (j)\Vert =0$ implies that $\varepsilon (j+d)=0$.¹¹ So from (51), we conclude that

$$\begin{aligned} \sum _{j=t_i+d-1}^{t-1} |\varepsilon (j+d)|^2&\le 4d^2 \left[ 2\Vert \mathcal{S}\Vert ^2 + \epsilon ^2 (t-t_i-1)^3\right] \nonumber \\&\quad \times \sup _{j\in [t_i+d-1,t) } \Vert \phi (j)\Vert ^2, \;\; t\ge t_i+d,\quad t_i\ge t_0. \end{aligned}$$

(52)

As $t_i\ge t_0$ is arbitrary, we can relabel the indexes and obtain

$$\begin{aligned} \sum _{j=t_i}^{t-1} |\varepsilon (j+d)|^2&\le 4d^2 \left[ 2\Vert \mathcal{S}\Vert ^2 + \epsilon ^2 (t-t_i-1 + d-1 )^3\right] \times \sup _{j\in [t_i,t) } \Vert \phi (j)\Vert ^2, \nonumber \\&\quad t\ge t_i+1,\quad t_i\ge t_0+d-1. \end{aligned}$$

(53)

We now analyse the average tracking error. From (53), we obtain

$$\begin{aligned} \frac{1}{t-t_i} \sum _{j=t_i}^{t-1} |\varepsilon (j+d)|^2&\le 4d^2 \left[ \frac{2\Vert \mathcal{S}\Vert ^2 }{t-t_i} + \epsilon ^2 \frac{(t-t_i+ d-2 )^3}{t-t_i} \right] \times \sup _{j\in [t_i,t) } \Vert \phi (j)\Vert ^2, \nonumber \\&\quad t\ge t_i+1,\quad t_i\ge t_0+d-1. \end{aligned}$$

(54)

Now define

$$\begin{aligned} \beta _\epsilon := \left( \epsilon \times d\Vert \mathcal{S}\Vert ^2 \right) ^\frac{2}{3} \end{aligned}$$

(55)

and $T_{\beta }\in \mathbf{N}$ by

$$\begin{aligned} T_{\beta }:= \left\lceil \frac{2d \Vert \mathcal{S}\Vert ^2 }{\beta _\epsilon } \right\rceil ; \end{aligned}$$

this means that

$$\begin{aligned} \frac{2 d\Vert \mathcal{S}\Vert ^2 }{T_{\beta }}\le \beta _\epsilon . \end{aligned}$$

Since $\epsilon \le 2\Vert \mathcal{S}\Vert$ by design, we can easily check that $T_\beta \ge d$, which means that

$$\begin{aligned} \frac{(T_\beta + d-2 )^3}{T_\beta } \le 8T_\beta ^2. \end{aligned}$$

Incorporating this and the definition of $T_\beta$ into (54), by choosing $t=t_i+T_\beta$ we have

$$\begin{aligned} \frac{1}{T_{\beta }} \sum _{j=t_i}^{t_{i}+T_\beta -1} |\varepsilon (j+d)|^2&\le 4d \left[ \frac{2d \Vert \mathcal{S}\Vert ^2 }{T_{\beta }} + 8\epsilon ^2d T_{\beta }^2\right] \times \sup _{j\in [t_i,t_{i}+T_\beta ) } \Vert \phi (j)\Vert ^2 \nonumber \\&\le 4d \left[ \beta _\epsilon + 8\epsilon ^2 d T_{\beta }^2\right] \times \sup _{j\in [t_i,t_{i}+T_\beta ) } \Vert \phi (j)\Vert ^2 , \; t_i\ge t_0+d-1. \end{aligned}$$

(56)

We would like to obtain a bound on $\epsilon ^2 T_{\beta }^2$. But it follows from (55) that

$$\begin{aligned} \beta _{\epsilon }^3 = \epsilon ^2 d^2 \Vert \mathcal{S} \Vert ^4 , \end{aligned}$$

so

$$\begin{aligned} \epsilon ^2 = \beta _{\epsilon } \left( \frac{ \beta _{\epsilon }}{d \Vert \mathcal{S} \Vert ^2} \right) ^2 = 4 \beta _{\epsilon } \left( \frac{ \beta _{\epsilon }}{2 d \Vert \mathcal{S} \Vert ^2} \right) ^2 ; \end{aligned}$$

if we define $x = \frac{ \beta _{\epsilon }}{2 d \Vert \mathcal{S} \Vert ^2}$, then we see that

$$\begin{aligned} \epsilon ^2 T_{\beta }^2= & {} 4 \beta _{\epsilon } x^2 \left( \lceil \frac{1}{x} \rceil \right) ^2 \\\le & {} 4 \beta _{\epsilon } x^2 \left( \frac{1}{x} + 1 \right) ^2 \\= & {} 4 \beta _{\epsilon } ( x+1 )^2 . \end{aligned}$$

But $\epsilon \in ( 0 , 2^{3/2} d^{1/2} \Vert \mathcal{S } \Vert )$ by hypothesis, so

$$\begin{aligned} x = \frac{ \beta _{\epsilon }}{2 d \Vert \mathcal{S} \Vert ^2} = \frac{ ( \epsilon d \Vert \mathcal{S} \Vert ^2 )^{2/3} }{2 d \Vert \mathcal{S} \Vert ^2} < \frac{(2^{3/2} d^{1/2} \Vert \mathcal{S} \Vert \times d \Vert \mathcal{S} \Vert ^2)^{2/3}}{ 2 d \Vert \mathcal{S} \Vert ^2 } = 1, \end{aligned}$$

so

$$\begin{aligned} \epsilon ^2 T_{\beta }^2 \le 16 \beta _{\epsilon } . \end{aligned}$$

Substituting this into (56) and simplifying yields

$$\begin{aligned} \frac{1}{T_{\beta }} \sum _{j=t_i}^{t_{i}+T_\beta -1} |\varepsilon (j+d)|^2&\le 516d^2 \beta _\epsilon \times \sup _{j\in [t_i,t_{i}+T_\beta ) } \Vert \phi (j)\Vert ^2,\qquad t_i\ge t_0+d-1. \end{aligned}$$

(57)

We now analyse the average tracking error over the whole time horizon; we do so by considering time intervals of length $T_\beta$. From (57) we easily obtain

$$\begin{aligned} \frac{1}{iT_{\beta }} \sum _{j=\bar{t}}^{\bar{t}+iT_\beta -1} |\varepsilon (j+d)|^2&\le 516d^2 \beta _\epsilon \times \sup _{j\in [\bar{t},\bar{t}+iT_\beta ) } \Vert \phi (j)\Vert ^2, \; i\in \mathbf{N},\; \bar{t}\ge t_0+d-1. \end{aligned}$$

(58)

The bound in (58) provides a bound on the average tracking error over time intervals of lengths that are multiples of $T_\beta$. To extend this to intervals of arbitrary length, first observe that (58) can be rewritten as

$$\begin{aligned} \sum _{j= \bar{t}}^{\bar{t} + i T_{\beta } -1} |\varepsilon (j+d)|^2 \le i T_{\beta } \left( \underbrace{516 d^2}_{=: \gamma _2} \beta _{\epsilon } \right) \sup _{j\in [\bar{t},\bar{t}+iT_\beta ) } \Vert \phi (j)\Vert ^2, \; i\in \mathbf{N},\; \bar{t}\ge t_0+d-1. \end{aligned}$$

For $k \in \{ 0,1,\ldots , T_{\beta }-1 \}$, this inequality implies that

$$\begin{aligned} \sum _{j= \bar{t}+k}^{\bar{t} + i T_{\beta } -1+k} |\varepsilon (j+d)|^2 \le i \gamma _2 T_{\beta } \beta _{\epsilon } \sup _{j\in [\bar{t}+k,\bar{t}+iT_\beta +k ) } \Vert \phi (j)\Vert ^2, \; i\in \mathbf{N},\; \bar{t}\ge t_0+d-1; \end{aligned}$$

adding these two inequalities and simplifying yields

$$\begin{aligned}&\sum _{j= \bar{t}}^{\bar{t} + i T_{\beta } -1+k} |\varepsilon (j+d)|^2 \le 2i \gamma _2 T_{\beta } \beta _{\epsilon } \sup _{j\in [\bar{t},\bar{t}+iT_\beta +k ) } \Vert \phi (j)\Vert ^2, \; i\in \mathbf{N}, \\&\quad k \in \{ 0,1,\ldots , T_{\beta }-1 \}, \; \bar{t}\ge t_0+d-1. \end{aligned}$$

Changing variables to enhance clarity, we see that this implies that

$$\begin{aligned} \sum _{j= \bar{t}}^{\bar{t} + T -1} |\varepsilon (j+d)|^2 \le 2 \gamma _2 T \beta _{\epsilon } \sup _{j\in [\bar{t},\bar{t} + T-1 ) } \Vert \phi (j)\Vert ^2, \; T \ge T_{\beta } , \; \bar{t}\ge t_0+d-1, \end{aligned}$$

which means that

$$\begin{aligned} \frac{1}{T} \sum _{j= \bar{t}}^{\bar{t} + T -1} |\varepsilon (j+d)|^2 \le 2 \gamma _2 \beta _{\epsilon } \sup _{j\in [\bar{t},\bar{t} + T-1 ) } \Vert \phi (j)\Vert ^2, \; T \ge T_{\beta } , \; \bar{t}\ge t_0+d-1. \end{aligned}$$

(59)

This means that

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j=\bar{t}}^{\bar{t}+T-1} |\varepsilon (j+d)|^2 \le 2 \gamma _2 \beta _\epsilon \times \limsup _{j\rightarrow \infty } \Vert \phi (j)\Vert ^2 , \; \bar{t} \ge t_0 + d - 1. \end{aligned}$$

From (48), see that

$$\begin{aligned} \limsup _{j\rightarrow \infty } \Vert \phi (j)\Vert \le \frac{\gamma _1}{1-\lambda _1} \Vert y^*\Vert _\infty ; \end{aligned}$$

the boundedness of the tracking error ensures that for every $\bar{t} \ge t_0$ we have

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j= \bar{t}}^{\bar{t}+T-1} |\varepsilon (j+d)|^2 = \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j= t_0}^{ t_0+T-1} |\varepsilon (j+d)|^2 , \; \bar{t} \ge t_0 + d - 1 , \end{aligned}$$

so we conclude that

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j= t_0}^{ t_0+T-1} |\varepsilon (j+d)|^2 \le \left( \frac{\gamma _ 1}{1-\lambda _1}\right) ^2 2 \gamma _2 \beta _\epsilon \times \Vert y^*\Vert _\infty ^2. \end{aligned}$$

Since $\beta _\epsilon = ( d \Vert \mathcal{S} \Vert ^2)^{2/3} \epsilon ^{2/3}$, the result follows. $\square$

6.4 Tracking in the presence of a disturbance

Now we turn to the much harder problem of tracking in the presence of a disturbance; throughout this sub-section, we assume that the plant is LTI. Our goal is to show that if the noise is small, then the tracking error is small; this is a stringent requirement, since in adaptive control it is usually only proven that if the noise is bounded, then the error is bounded. We can, of course, measure signal sizes in a variety of ways, with the 2-norm and the $\infty$-norm the most common; given that a large disturbance can lead the estimator astray and cause “temporary instability”, the 2-norm seems to be the most appropriate here.

If the closed-loop system were LTI, then by Parseval’s Theorem we could conclude that the average power of the tracking error is bounded by the average power of the disturbance, i.e. there exists a constant c so that

$$\begin{aligned} \limsup _{T \rightarrow \infty } \frac{1}{T} \sum _{j=t_0}^{t_0 + T-1} [ {\varepsilon }(t) ]^2 \le {c} \times \limsup _{T \rightarrow \infty } \frac{1}{T} \sum _{j=t_0}^{t_0 + T-1} [ w (t) ]^2 ; \end{aligned}$$

(60)

unfortunately, while the closed-loop system has some desirable linear-like closed-loop properties, the controller is nonlinear so the closed-loop system is clearly not LTI. However, we can prove this bound in two extreme cases:

• if $y^* = 0$, then $y= {\varepsilon }$, so with c and $\lambda$ as given in Theorem 1, it is easy to see that

  $$\begin{aligned} \limsup _{T \rightarrow \infty } \frac{1}{T} \sum _{j=t_0}^{t_0 + T-1} [ {\varepsilon }(t) ]^2 \le \frac{c^2}{(1- \lambda )^2} \times \limsup _{T \rightarrow \infty } \frac{1}{T} \sum _{j=t_0}^{t_0 + T-1} [ w (t) ]^2 ; \end{aligned}$$

• on the other hand, if $y^* \ne 0$ and $w =0$, then from Theorem 3 we see that

  $$\begin{aligned} \limsup _{T \rightarrow \infty } \frac{1}{T} \sum _{j=t_0}^{t_0 + T-1} [ {\varepsilon }(t) ]^2 = 0. \end{aligned}$$

In the general case, we will prove something weaker than (60), but with much the same flavour; it is, however, much stronger than the standard result in the literature.

Theorem 5

For every $\delta \in ( 0 , \infty ]$, there exists a $\gamma >0$ so that for every $t_0 \in \mathbf{Z}$, ${\theta }_{ab}^* \in \mathcal{S}_{ab}$, $y^*,w\in \varvec{\ell }_{\infty }$, $\theta _0 \in \mathcal{S}$, and plant initial condition

$$\begin{aligned} x_0 = \left[ \begin{array}{cccccc} y( t_0 -1)&\quad \cdots&\quad y(t_0 -n-d+1)&u(t_0 -1 )&\quad \cdots&\quad u( t_0 -m-2d+1 ) \end{array} \right] ^T , \end{aligned}$$

when the adaptive controller (8), (9) and (11) is applied to the plant (1) with $\liminf _{t\rightarrow \infty } |y^*(t)|>0$ then the following holds:

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j= t_0}^{ t_0+T-1} |\varepsilon (j)|^2\le & {} \gamma \times \limsup _{T\rightarrow \infty } \frac{1}{T} \sum _{j= t_0}^{ t_0+T-1} |w(j)|^2\nonumber \\&\times \frac{\limsup _{t\rightarrow \infty } |y^*( t)|^2+ \limsup _{t \rightarrow \infty } |w( t)|^2}{\liminf _{t\rightarrow \infty } |y^*( t)|^2}. \qquad \end{aligned}$$

(61)

Remark 9

So we see that the bound proven here is similar to that of (60) which holds in the LTI case, although we have an extra term multiplied on the RHS:

$$\begin{aligned} \frac{\limsup _{t\rightarrow \infty } |y^*( t)|^2+ \limsup _{t\rightarrow \infty } |w(t)|^2}{\liminf _{t\rightarrow \infty } |y^*(t)|^2}. \end{aligned}$$

If the reference signal is larger than the noise, which is what one would normally expect, then this would be bounded by

$$\begin{aligned} 2 \frac{\limsup _{t\rightarrow \infty } |y^*( t)|^2}{\liminf _{t\rightarrow \infty } |y^*(t)|^2}; \end{aligned}$$

if $| y^* (t) | \in \{ -1, 1 \}$ then this is exactly two. It is curious that the quantity gets large if $y^* (t)$ gets close to zero; we suspect that this is an artifact of the proof, since all simulations indicate that the LTI-like bound (60) holds.

Proof

Fix $\delta \in ( 0 , \infty ]$ and $\lambda \in (\underline{\lambda },1)$. Let $t_0 \in \mathbf{Z}$, ${\theta }_{ab}^* \in \mathcal{S}_{ab}$, $y^*,w\in \varvec{\ell }_{\infty }$, $\theta _0 \in \mathcal{S}$, and $x_0$ be arbitrary, but so that $\liminf _{t \rightarrow \infty } | y^* (t) | > 0$. Before proceeding, choose $\underline{t} \ge t_0 + 2d-1$ so that

$$\begin{aligned} \inf \{ | y^* (t) | : \; t \ge \underline{t} \} > 0. \end{aligned}$$

Now, by using (46) and applying Proposition 1, for $\bar{t}\ge t_0+2d-1$ we obtain

$$\begin{aligned}&\sum _{j=\bar{t}}^{t} \rho _{\delta }(\phi (j-d),e(j)) \frac{|\varepsilon (j)|^2}{\Vert \phi (j-d)\Vert ^2} \nonumber \\&\quad \le d^2 \sum _{j=\bar{t}-d+1}^{t} \rho _{\delta }(\phi (j-d),e(j)) \frac{|e(j)|^2}{\Vert \phi (j-d)\Vert ^2} \nonumber \\&\quad \le 8d^2\Vert \mathcal{S}\Vert ^2 + 4d^2 \sum _{j=\bar{t}-d+1}^{t} \rho _{\delta }(\cdot ,\cdot ) \frac{|\bar{w} (j-d)|^2}{\Vert \phi (j-d)\Vert ^2} \nonumber \\&\quad = 4d^2\Vert \mathcal{S}\Vert ^2 \left( 2 + \frac{1}{\Vert \mathcal{S}\Vert ^2} \sum _{j=\bar{t} -d +1}^{t} \rho _{\delta }(\cdot ,\cdot ) \frac{|\bar{w} (j-d)|^2}{ \Vert \phi (j-d)\Vert ^2} \right) \nonumber \\&\quad = 4d^2\Vert \mathcal{S}\Vert ^2 \left( 2 + \sum _{j=\bar{t}-d+1}^{t} \rho _{\delta }(\cdot ,\cdot ) \frac{|\bar{w} (j-d)|^2}{ \left( \Vert \mathcal{S}\Vert \Vert \phi (j-d)\Vert \right) ^2} \right) , \nonumber \\&\qquad t\ge \bar{t} \ge t_0+2d-1. \end{aligned}$$

(62)

From the controller equation (11), we have

$$\begin{aligned} y^*(t) = \hat{\theta }(t-d)^\top \phi (t-d), \qquad t\ge t_0+d, \end{aligned}$$

which means that

$$\begin{aligned} |y^*(t)| \le \Vert \hat{\theta }(t-d)\Vert \Vert \phi (t-d) \Vert \le \Vert \mathcal{S} \Vert \times \Vert \phi (t-d) \Vert , \qquad t\ge t_0+d; \end{aligned}$$

if we substitute this into (62), then we obtain

$$\begin{aligned}&\sum _{j=\bar{t}}^{t} \rho _{\delta }(\phi (j-d),e(j)) \frac{|\varepsilon (j)|^2}{\Vert \phi (j-d)\Vert ^2}\nonumber \\&\quad \le 4d^2\Vert \mathcal{S}\Vert ^2 \left( 2 + \sum _{j=\bar{t}-d+1}^{t} \rho _{\delta }(\phi (j-d),e(j)) \frac{|\bar{w} (j-d)|^2}{ |y^*(j)| ^2} \right) , \nonumber \\&\qquad t\ge \bar{t} \ge \underline{t} . \end{aligned}$$

(63)

Now we analyse the above bound for two cases: when the estimator is turned on, i.e. when $\rho _{\delta } ( \cdot , \cdot ) =1$ and when the estimator is turned off, i.e. when $\rho _{\delta } ( \cdot , \cdot ) =0$. Before proceeding, we define some notation: for $t_2\ge t_1\ge t_0$, we define

$$\begin{aligned} {{\underline{\varvec{y}}}}^*_{[t_1,t_2]} := \inf _{j\in [t_1,t_2],\, \rho _{\delta }(\phi (j-d),e(j))=1 } |y^*(j)|^2. \end{aligned}$$

Case 1 The estimator is turned on: $\rho _{\delta } ( \phi ( j-d ) , e(j) ) =1$.

From (63), we have

$$\begin{aligned} \sum _{j=\bar{t},\,\rho _{\delta }(\phi (j-d),e(j))=1}^{t} \frac{|\varepsilon (j)|^2}{\Vert \phi (j-d)\Vert ^2}&\le 4d^2\Vert \mathcal{S}\Vert ^2 \left( 2 + \frac{1}{ \underline{\varvec{y}}^*_{[\bar{t}-d+1,t]} } \sum _{j=\bar{t}-d+1}^{t} |\bar{w}(j-d)|^2 \right) , \nonumber \\&\quad t\ge \bar{t} \ge \underline{t} , \end{aligned}$$

(64)

which means that

$$\begin{aligned} \sum _{j=\bar{t},\rho _{\delta }(\phi (j-d),e(j))=1}^{t} |\varepsilon (j)|^2&\le 4d^2\Vert \mathcal{S}\Vert ^2 \left( \sup _{j\in [\bar{t}-d,t-d]} \Vert \phi (j)\Vert ^2 \right) \nonumber \\&\quad \times \left( 2 + \frac{1}{\underline{\varvec{y}}^*_{[\bar{t}-d+1,t]} } \sum _{j=\bar{t}-d+1}^{t} |w(j-d)|^2 \right) , \; t\ge \bar{t}\ge \underline{t}. \end{aligned}$$

(65)

Case 2 The estimator is turned off : $\rho _{\delta } ( \phi ( j-d) , e(j) ) =0$.

In this case, we know from the definition of $\rho _{\delta }$ that when $\rho _{\delta } ( \phi (t-d) , e(t))=0$:

• if $\delta = \infty$ then $\phi (t-d) = 0$, so

  $$\begin{aligned} \Vert \phi (t-d) \Vert \le \frac{1}{\delta } | \bar{w} ( t-d ) |; \end{aligned}$$

• if $\delta \in (0 , \infty )$, then we have that

  $$\begin{aligned} |e(t)| \ge (2\Vert \mathcal{S}\Vert +\delta )\Vert \phi (t-d) \Vert ; \end{aligned}$$

  using the formula for the prediction error given in (13) we see that

  $$\begin{aligned} | e(t) |\le & {} \Vert \phi (t-d) \Vert \times \Vert \tilde{\theta } (t-1) \Vert + | \bar{w} (t-d) | \\\le & {} 2 \Vert \mathcal{S} \Vert \times \Vert \phi (t-d) \Vert + | \bar{w} (t-d) | ; \end{aligned}$$

  combining these two equations yields

  $$\begin{aligned} \Vert \phi (t-d) \Vert \le \frac{1}{\delta } | \bar{w} (t-d) | . \end{aligned}$$

Using the formula for the tracking error given in (12), we have

$$\begin{aligned} |\varepsilon (t)|&\le \Vert \phi (t-d)\Vert \Vert \tilde{\theta }(t-d)\Vert + |\bar{w} (t-d)| \\&\le \frac{2 \Vert \mathcal{S}\Vert }{\delta } |\bar{w} (t-d)| + |\bar{w} (t-d)| ,\quad t\ge t_0+2d-1. \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{j=\bar{t},\,\rho _{\delta }(\phi (j-d),e(j))=0}^{t} |\varepsilon (j)|^2&\le \left( 1 + \frac{2 \Vert \mathcal{S}\Vert }{\delta }\right) ^2 \sum _{j=\bar{t},\,\rho _{\delta }(\phi (j-d),e(j))=0}^{t} |\bar{w}(j-d)|^2 \nonumber \\&\le \left( 1 + \frac{2 \Vert \mathcal{S}\Vert }{\delta }\right) ^2 \sum _{j=\bar{t}}^{t} |\bar{w}(j-d)|^2 , \quad t\ge \bar{t}\ge t_0+2d-1. \end{aligned}$$

(66)

We can now combine (65) and (66) of Case 1 and Case 2, respectively, to yield

$$\begin{aligned} \sum _{j=\bar{t}}^{t} |\varepsilon (j)|^2&\le 8d^2\Vert \mathcal{S}\Vert ^2 \left( \sup _{j\in [\bar{t},t]} \Vert \phi (j+d)\Vert ^2 \right) \nonumber \\&\quad +\max \left\{ \left( 1 + \tfrac{2 \Vert \mathcal{S}\Vert }{\delta }\right) ^2, 4d^2\Vert \mathcal{S}\Vert ^2 \left( \tfrac{\sup _{j\in [\bar{t},t]} \Vert \phi (j+d)\Vert ^2}{\underline{\varvec{y}}^*_{[\bar{t}-d+1,t]}} \right) \right\} \nonumber \\&\quad \times \left( \sum _{j=\bar{t}-d+1}^{t} |\bar{w} (j-d)|^2 \right) , \quad t\ge \bar{t}\ge \underline{t}. \end{aligned}$$

(67)

By Theorem 1, there exists constants $c>0$ and $\lambda \in (0,1)$ so that

$$\begin{aligned} \Vert \phi (t+d)\Vert \le c \lambda ^{t+d-t_0} \Vert x_0\Vert + \sum _{j=t_0}^{t+d} c \lambda ^{t+d-j} (|y^*(j)|+|w(j)|) , \; t \ge \underline{t} , \end{aligned}$$

so we can choose $\bar{t} \ge \underline{t}$ (which depends implicitly on $x_0$, $y^*$, $\theta _0$, and $\theta ^*$) such that

$$\begin{aligned} \Vert \phi (t+d)\Vert \le \frac{2c}{1-\lambda } \limsup _{k \rightarrow \infty } (|y^*(\bar{t}+k)|+|w(\bar{t}+k)|), \; t\ge \bar{t} , \end{aligned}$$

as well as

$$\begin{aligned} | y^* (t) |^2 \ge \underbrace{ \frac{1}{2} \liminf _{k \rightarrow \infty } | y^* (k) |^2 }_{=: \underline{y}^*} , \; t \ge \bar{t} - d + 1 . \end{aligned}$$

If we incorporate this into (67), then we obtain

$$\begin{aligned} \sum _{j=\bar{t}}^{t} |\varepsilon (j)|^2&\le 8d^2\Vert \mathcal{S}\Vert ^2 \left( \sup _{j\in [\bar{t},t]} \Vert \phi (j+d)\Vert ^2 \right) \\&\quad + \max \biggl \{ \left( \tfrac{2 \Vert \mathcal{S}\Vert }{\delta }+1\right) ^2, \left( \tfrac{4cd\Vert \mathcal{S}\Vert }{1-\lambda }\right) ^2 \times \tfrac{ \limsup _{k\rightarrow \infty } (|y^*(\bar{t}+k)|^2+|\bar{w}(\bar{ t}+k)|^2)}{ 0.5 \underline{y}^*} \biggr \}\\&\quad \times \left( \sum _{j=\bar{t}-d+1}^{t} |\bar{w}(j-d)|^2 \right) , \; t \ge \bar{t} - d + 1, \end{aligned}$$

which means that

$$\begin{aligned}&\limsup _{ T\rightarrow \infty } \frac{1}{ T} \sum _{j=\bar{t}}^{\bar{t}+ T-1} |\varepsilon (j)|^2 \le \limsup _{ T\rightarrow \infty } \frac{1}{ T} \sum _{j=\bar{t}-d+1}^{\bar{t}+ T-1} |\bar{w}(j-d)|^2\\&\qquad \times \max \biggl \{ \left( \tfrac{2 \Vert \mathcal{S}\Vert }{\delta }+1\right) ^2, \left( \tfrac{4cd\Vert \mathcal{S}\Vert }{1-\lambda }\right) ^2 \times \tfrac{ \limsup _{k\rightarrow \infty } (|y^*(\bar{t}+k)|^2+|w(\bar{t}+k)|^2)}{ 0.5 \underline{y}^*} \biggr \}. \end{aligned}$$

But $\bar{w} (t)$ is a weighted sum of $\{ w(t+1) ,\ldots , w ( t+d) \}$, and the boundedness of all variables makes the starting point of the average sums irrelevant, so the desired bound (61) follows. $\square$

7 A simulation example

Here we provide several simulation examples to illustrate the results of this paper. Consider the second-order time-varying plant with relative degree one:

$$\begin{aligned} y(t+1)=-a_1(t)y(t)-a_2(t)y(t-1) +b_0(t)u(t)+b_1(t)u(t-1)+w(t) \end{aligned}$$

with $a_1(t)\in [-3,3], a_2(t)\in [-4,4], b_0(t)\in [1.5,5]$ and $b_1(t)\in [-1,1]$. When the parameters are fixed, we see that the corresponding system has a zero in $[- \frac{2}{3} , \frac{2}{3} ]$ and poles which may be stable or unstable.

7.1 Simulation 1: the benefit of vigilant estimation

In the first simulation, we illustrate that the vigilant estimation algorithm provides better performance than the classical algorithm does. More specifically, we compare the adaptive controller using the vigilant estimator (8), (9) (with $\delta = \infty$) with the adaptive controller using the classical estimation algorithm (7) suitably modified to incorporate projection onto $\mathcal{S}$ (and with $\bar{\alpha } = \bar{\beta } = 1$). In each case, we apply the adaptive controller to this plant with the parameters chosen as

$$\begin{aligned} a_1(t)&=3\cos (0.01t), \\ a_2(t)&=4\sin (0.007t), \\ b_0(t)&=3.25-1.75\cos (0.0045t), \\ b_1(t)&= - \cos (0.002t). \end{aligned}$$

We set $y^*=0$ (so $\varepsilon (t)=y(t)$) and the noise to

$$\begin{aligned} w(t) = \left\{ \begin{matrix} 0 &{}&{} \quad 0 \le t\le 100 \\ 0.05\cos (10t) &{}&{} \quad \text {otherwise;} \end{matrix} \right. \end{aligned}$$

we set $y(-1)=y(0)=-0.1$, $u(-1)= u(-2)=0$, and the initial parameter estimates to the midpoint of the respective intervals. Fig. 1 shows tracking errors during the transient phase of 200 steps, and Fig. 2 shows the tracking error and parameter estimation for the rest of the simulation time of 2000 steps. We can clearly see that the proposed controller provides better transient performance as well as better disturbance rejection than the classical algorithm. Furthermore, you can see that the proposed controller does a much better job of tracking the parameter variations.

Fig. 1

The left plot shows the tracking error for Simulation 1 for $t\le 200$ using vigilant estimation; the right plot shows the tracking error for Simulation 1 for $t\le 200$ using classical estimation

Fig. 2

Column a shows results using vigilant estimation, and column b shows results using classical estimation. In each column, the upper plot shows the tracking error for $t\ge 200$; the next plot shows the control signal for $t \ge 200$; the last four plots show the parameter estimates (solid) and actual parameters (dashed) for $t\ge 200$

7.2 Simulation 2: illustrating robustness

In the second simulation, we illustrate the tolerance to time-variation and unmodelled dynamics. We apply the proposed adaptive controller (with $\delta = \infty$) to the plant when the parameters are time-varying:

$$\begin{aligned} a_1(t)&=-3\cos (0.002t), \\ a_2(t)&=-4\sin (0.0015t), \\ b_0(t)&=3.25-1.75\cos (0.0035t), \\ b_1(t)&= \left\{ \begin{matrix} 0.5 &{} &{} \quad 0 \le t \le 1500 \\ -0.5 &{} &{} \quad 1500< t \le 3000 \\ 1 &{} &{} \quad 3000 < t , \end{matrix} \right. \end{aligned}$$

and when the unmodelled dynamics (in the associated plant model (40)) are described by

$$\begin{aligned} m(t+1)= & {} 0.5m(t) + 0.5 \Vert \phi (t)\Vert , \quad m(0)=0 \\ \bar{w}_\Delta (t)= & {} \left\{ \begin{matrix} 0.1m(t)+0.1 \Vert \phi (t)\Vert &{}&{}\quad t\ge 2500 \\ 0 &{}&{}\quad \text {otherwise}. \end{matrix} \right. \end{aligned}$$

We set the reference signal to

$$\begin{aligned} y^*(t)= \cos (0.015 t) \end{aligned}$$

and the noise signal to

$$\begin{aligned} w(t)=0.01\cos (10t); \end{aligned}$$

we choose initial conditions of $y(-1)=y(0)=-1$ and $u(-1)= u(-2)=0$, and the initial parameter estimates to $\theta _0=[-2 \;\; -2 \;\; 2 \;\; 1]^\top$; Fig. 3 shows the results. The adaptive controller clearly shows robust performance to both unmodelled dynamics and time-variations, including parameter jumps: the tracking is quite good, and the parameter estimator (approximately) tracks the time-varying parameters.

Fig. 3

The upper plot shows both the output signal (solid) and the reference signal (dashed) for Simulation 2; the next four plots show the parameter estimates (solid) and actual parameters (dashed) for Simulation 2

7.3 Simulation 3: tracking with no noise

Theorem 3 says that there exists a constant c so that

$$\begin{aligned} \sum _{j=t_0+2d-1}^\infty \varepsilon (j)^2 \le c (\Vert y^*\Vert _\infty ^2+\Vert x_0\Vert ^2), \end{aligned}$$

i.e. the 2-norm of the tracking error is not only finite, but is bounded by a constant time the sizes of the reference signal and plant initial condition. In this simulation, we apply the proposed adaptive controller (with $\delta = \infty$) to the plant when

$$\begin{aligned} a_1(t)=-2,\quad a_2(t)=3,\quad b_0(t)=3.25,\quad b_1(t)=-1. \end{aligned}$$

We set the disturbance signal to zero and the reference signal to

$$\begin{aligned} y^*(t)=A_0\cos (0.025t) \end{aligned}$$

with amplitudes of

$$\begin{aligned} A_0\in \left\{ 10^{-3},10^{-2},0.1,1,10,10^2,10^3,10^4\right\} ; \end{aligned}$$

we set the plant initial condititon to $y(-1)=y(0)=-1$ and $u(-1)=u(-2)=0$, and we set the initial parameter estimate to the midpoint of the respective intervals. We simulate for 100, 000 steps. Because there is no noise, we get asymptotic tracking; we compute the square sum of the tracking error and compare it to the square of the reference amplitude and the square of the norm of the plant initial condition; the results are in Table 1. We see that the result is consistent with Theorem 3: the gain is bounded above by approximately 1000.

Table 1 Simulation 3 results

7.4 Simulation 4: tracking with slowly varying parameters

In our fourth simulation, we illustrate the result in Theorem 4; we show that the average tracking error is proportional to the speed of the parameter variation. We apply the proposed controller (with $\delta = \infty$) with plant parameters of

$$\begin{aligned}&a_2(t) =1, \quad b_0(t) =3.25,\quad b_1(t) = 1, \\&a_1(t) =2\sin \left( \omega _0 t\right) , \end{aligned}$$

with

$$\begin{aligned} \omega _0\in \left\{ 0.001,0.002,0.005,0.01 \right\} . \end{aligned}$$

We choose plant initial conditions of $y(-1)=y(0)=-1$ and $u(-1)= u(-2)=0$, and the initial parameter estimate equal to the midpoint of the respective intervals. With a zero disturbance and

$$\begin{aligned} y^*(t)=\cos (0.015t) , \end{aligned}$$

we simulate the closed-loop system for $T=5000$ steps; we plot the tracking error for the last 3000 steps in Fig. 4, i.e. after the transient effect has been eliminated. We see that, consistent with Theorem 4, average tracking error increases with the speed of the plant parameter variation.

Fig. 4

The plots show the tracking error for Simulation 4

7.5 Simulation 5: tracking with noise

In the final simulation, we illustrate the tracking result in the presence of noise, namely Theorem 5. We show that, on average, the tracking error is proportional to the size of the exogenous noise. We apply the proposed adaptive controller (with $\delta = \infty$) to the plant when

$$\begin{aligned} a_1=-2, \quad a_2=3,\quad b_0=3.25,\quad b_1=-1. \end{aligned}$$

We choose an initial condition of $y(-1)=y(0)=-1$ and $u(-1)=u(-2)=0$ and set the initial parameter estimates to the midpoint of the respective intervals. We set the noise to

$$\begin{aligned} w(t)=W_0\cos (10t) \end{aligned}$$

with different amplitudes:

$$\begin{aligned} W_0\in \left\{ 0.001,0.01,0.1,1\right\} ; \end{aligned}$$

we choose the reference signal $y^*$ to be a square wave of amplitude one and period 300; observe that $\liminf _{t\rightarrow \infty } |y^*(t) |=1$, $\Vert y^*\Vert _\infty =1$ and $\Vert w\Vert _\infty =|W_0|$. We simulate for $T=5000$ steps; in Fig. 5, we plot the tracking error for the last 3000 steps, so that we focus on the “steady-state behaviour”. We clearly see that the average tracking error magnitude is roughly proportional to the average noise signal magnitude.

Fig. 5

The “steady-state” tracking error for Simulation 5 for different noise magnitudes

8 Summary and conclusions

Under common assumptions on the plant model, in this paper we use a modified version of the original, ideal, projection algorithm (termed a vigilant estimator) to carry out parameter estimation; the corresponding d-step-ahead adaptive controller guarantees linear-like convolution bounds on the closed-loop behaviour, which confers exponential stability and a bounded noise gain, unlike almost all other parameter adaptive controllers. This is then leveraged in a modular way to prove tolerance to unmodelled dynamics and plant parameter variation. We examine the tracking ability of the approach and are able to prove properties which most adaptive controllers do not enjoy:

• (i) in the absense of a disturbance, we obtain an explicit 2-norm on the size of the tracking error in terms of the size of the initial condition and the reference signal;

• (ii) if there is no noise but there are slow time-variations, then we prove that we can bound the size of the average tracking error by the size of the time-variation;

• (iii) if there is noise, then under some technical conditions we bound the size of the average tracking error in terms of the size of the average disturbance times another complicated quantity.

We are working on several extensions of the approach. First of all, we would like to use a multi-estimator approach to reduce the amount of structural information on the plant; we have proven this already in the case of first-order systems [35], but extending this to the general case has proven to be challenging. Second of all, we would like to obtain a crisper bound on the average tracking error than that discussed in (iii) above, i.e. prove that the size of the average tracking error is bounded above by a constant time the size of the average disturbance; while all of our simulations confirm this, as of yet we have not been able to prove it.

Appendix

Proof of Proposition 3

To proceed, we analyse the good closed-loop model of Sect. 3.1. From (15), it is clear that we need to obtain a bound on the terms $B_1 {\varepsilon }(t+1)$ and $B_2 {\varepsilon }( t+j)$ for $j=1,\ldots ,d+1$. It will be convenient to define an intermediate quantity¹²:

$$\begin{aligned} \bar{\nu } (t-1) := \rho _{\delta } ( \phi (t-d) , e(t)) \times \frac{ \phi (t-d)}{\Vert \phi (t-d) \Vert ^2} {\varepsilon }(t) , \; t \ge t_0 . \end{aligned}$$

Step 1 Obtain a desirable bound on $B_i {\varepsilon }(t)$ in terms of $\bar{\nu } (t-1)$, $\phi (t-d)$ and $\bar{w} (t-d)$.

First of all, for $i=1,2$ define

$$\begin{aligned} \bar{\Delta }_i (t) := \rho _{\delta } ( \phi (t-d) , e(t)) \frac{ {\varepsilon }(t) }{ \Vert \phi (t-d)\Vert ^2} B_i \phi (t-d)^T , \; t \ge t_0 . \end{aligned}$$

It is easy to see that

$$\begin{aligned} \bar{\Delta }_i (t) \phi (t-d) = \rho _{\delta } ( \phi (t-d) , e(t)) B_i { {\varepsilon }(t) } . \end{aligned}$$

So

$$\begin{aligned} B_i {\varepsilon }(t)= & {} \rho _{\delta } ( \phi (t-d) , e(t)) B_i {\varepsilon }(t) + \underbrace{[ 1 - \rho _{\delta } ( \phi (t-d) , e(t)) ] {\varepsilon }(t)}_{=: \eta _0 (t)} B_i \nonumber \\= & {} \bar{\Delta }_i (t) \phi (t-d) + B_i \eta _0 (t) , \; t \ge t_0 . \end{aligned}$$

(68)

Using (12) and (13) and the definition of $\rho _{\delta } ( \phi (t-d) , e(t))$, it is easy to show that

$$\begin{aligned} | \eta _0 (t) | \le \left( 1 + \frac{ 4 \Vert \mathcal{S} \Vert }{ \delta } \right) | \bar{w} (t-d) | , \; t \ge t_0 + d; \end{aligned}$$

(69)

furthermore, it is clear that

$$\begin{aligned} \Vert \bar{\Delta }_i (t) \Vert = \rho _{\delta } ( \phi (t-d) , e(t)) \frac{ | {\varepsilon }(t) | }{ \Vert \phi (t-d)\Vert } = \Vert \bar{\nu } (t-1) \Vert , \; t \ge t_0 . \end{aligned}$$

(70)

Step 2 Bound $\bar{\nu } (t-1)$ in terms of $\nu (t) ,\ldots , \nu (t-d)$.

It follows from the formulas for ${\varepsilon }(t)$ and e(t) given in (12) and (13) that

$$\begin{aligned} {\varepsilon }(t)= & {} e(t) + \phi (t-d)^T [ \hat{\theta } (t-1) - \hat{\theta } (t-d) ] , \; t \ge t_0 + d . \end{aligned}$$

Using the definition of $\bar{\nu } (t-1)$, we have

$$\begin{aligned} \Vert \bar{\nu } (t-1) \Vert\le & {} \rho _{\delta } ( \phi (t-d) , e(t)) \frac{ | e (t) | }{ \Vert \phi (t-d)\Vert } + \Vert \hat{\theta } (t-1) - \hat{\theta } (t-d) \Vert \\= & {} \Vert \nu (t-1) \Vert + \Vert \hat{\theta } (t-1) - \hat{\theta } (t-d) \Vert , \; t \ge t_0 + d . \end{aligned}$$

Now it follows from the estimator update law that

$$\begin{aligned} \Vert \hat{\theta } (t-1) - \hat{\theta } (t-d) \Vert\le & {} \Vert \hat{\theta } (t-1) - \hat{\theta } (t-2 ) \Vert + \cdots + \Vert \hat{\theta } (t-d+1) - \hat{\theta } (t-d ) \Vert \\\le & {} \rho _{\delta } ( \phi (t-d-1), e (t-1) ) \frac{| e( t-1)|}{\Vert \phi (t-d-1) \Vert } + \cdots \\&+ \rho _{\delta } ( \phi ( t-2d+1) , e (t-d+1)) \frac{| e( t-d+1)|}{\Vert \phi (t-2d+1) \Vert } \\\le & {} \sum _{j=2}^{d} \Vert \nu ( t-j ) \Vert . \end{aligned}$$

We conclude that

$$\begin{aligned} \Vert \bar{\nu } (t-1) \Vert\le & {} \sum _{j=1}^{d} \Vert \nu ( t-j ) \Vert , \; t \ge t_0 + d . \end{aligned}$$

(71)

Step 3 Obtain a bound on $B_i {\varepsilon }(t)$ in terms of $\{ \nu (t) ,\ldots , \nu (t-d) \}$, $\phi (t-d)$ and $\bar{w} (t-d)$.

If we combine (68), (69), (70) and (71), we see that

$$\begin{aligned} B_i {\varepsilon }(t) = \bar{\Delta }_i (t) \phi (t-d) + B_i \eta _0 (t) \end{aligned}$$

with

$$\begin{aligned} \Vert \bar{\Delta } _i (t) \Vert \le \sum _{j=1}^{d} \Vert \nu ( t-j ) \Vert \end{aligned}$$

and

$$\begin{aligned} | \eta _0 (t) | \le \left( 1 + \frac{4 \Vert S \Vert }{ \delta } \right) | \bar{w} (t-d) | , \; t \ge t_0+d . \end{aligned}$$

Step 4 Apply the result of Step 3 to (15).

We can apply the above result to each of the terms on the RHS of (15) containing ${\varepsilon }( \cdot )$. So from Step 3, we have

$$\begin{aligned} B_1 {\varepsilon }(t+1) = \bar{ \Delta }_1 ( t+1 ) \phi (t+1-d) + B_1 \eta _0 (t+1) \end{aligned}$$

(72)

and

$$\begin{aligned} \frac{a_{d-j}}{b_0} B_2 {\varepsilon }( t+1+j)= & {} \frac{a_{d-j}}{b_0} \bar{ \Delta }_2 ( t+1+j ) \phi (t+1-d+j) \nonumber \\&+ \frac{a_{d-j}}{b_0} B_2 \eta _0 (t+1+j) , \; j =0,1,\ldots , d. \end{aligned}$$

(73)

Each term except one is of the desired form: the case of $j=d$ is problematic since it contains a $\phi (t+1)$ term. However, we can use the crude model given in (16) to see that

$$\begin{aligned}&\frac{a_0}{b_0} \bar{ \Delta }_2 ( t+d+1 ) \phi (t+1) \nonumber \\&\quad = \frac{a_0}{b_0} \bar{ \Delta }_2 ( t+d+1 ) \times [ A_b (t) \phi (t) + B_3 (t) y^* (t+d+1) + B_4 (t) w (t+1) ] . \nonumber \\ \end{aligned}$$

(74)

If we now combine (72), (73) and (74), we see that we should define

$$\begin{aligned} \Delta _0 (t)= & {} \frac{a_0}{b_0} \bar{ \Delta }_2 ( t+d+1 ) A_b (t) + \frac{a_1}{b_0 } \bar{ \Delta }_2 ( t+d ),\\ \Delta _j (t)= & {} \frac{a_{j+1}}{b_0} \bar{\Delta }_2 ( t+d -j ) , \; j = 1,\ldots , d-2 , \end{aligned}$$

and

$$\begin{aligned} \Delta _{d-1} (t) = \bar{\Delta }_1 (t+1) + \frac{a_d}{b_0} \bar{\Delta }_2 ( t +1 ). \end{aligned}$$

It is clear from Step 3 that this choice of $\Delta _i$ has the desired property for $t \ge t_0 + d - 1$. Last of all, we group all of the remaining terms into $\eta (t)$:

$$\begin{aligned} \eta (t):= & {} B_1 y^*(t+1) + B_2 \frac{1}{b_0} \sum _{j=0}^d a_{d-j} y^* ( t+1 +j ) - \frac{1}{b_0} B_2 w(t+d+1) \\&+ B_1 \eta _0 (t+1) + \frac{a_0}{b_0} \bar{\Delta }_2 (t+d+1) [ B_3 (t) y^* (t+d+1) \\&+ B_4 (t) w (t+1) ] + B_2 \sum _{j=0}^{d-1} \frac{a_{d-j}}{b_0} \eta _0 (t+1+j). \end{aligned}$$

If we apply Proposition 2 and use the bound on $\eta _0 (t)$ given in Step 3, then we see that $\eta (t)$ has the desired property for $t \ge t_0 + d -1$ as well. $\square$