On the notions of normality, locality, and operational stability in ADRC

Abstract

Treating plant dynamics as an ideal integrator chain disturbed by the total disturbance is the hallmark of active disturbance rejection control (ADRC). To interpret its effectiveness and success, to explain why so many vastly different dynamic systems can be treated in this manner, and to answer why a detailed, accurate, and global mathematical model is unnecessary, is the target of this paper. Driven by a motivating example, the notions of normality and locality are introduced. Normality shows that, in ADRC, the plant is normalized to an integrator chain, which is called local nominal model and locally describes the plant’s frequency response in the neighborhood of the expected gain crossover frequency. Locality interprets why ADRC can design the controller only with the local information of the plant. With normality and locality, ADRC can be effective and robust, and obtain operational stability discussed by T. S. Tsien. Then viewing proportional-integral-derivative (PID) control as a low-frequency approximation of second-order linear ADRC, the above results are extended to PID control. A controller design framework is proposed to obtain the controller in three steps: (1) choose an integrator chain as the local nominal model of the plant; (2) select a controller family corresponding to the local nominal model; and (3) tune the controller to guarantee the gain crossover frequency specification. The second-order linear ADRC and the PID control are two special cases of the framework.

1 Introduction

Active disturbance rejection control (ADRC), conceived by Han [1,2,3] as a general purpose control technology and an alternative to the industry-dominant proportional-integral-derivative (PID) control, has developed rapidly in recent years, in both engineering practice (see, for example, [4,5,6]) and theoretical studies (see, for example, [7, 8]).

The idea of ADRC can be traced to T. S. Tsien. In Chap. 15 of his epic book titled “Engineering Cybernetics” [9], Tsien flatly said that the mathematical model of a physical plant can never be known exactly in practice and should not be the basis on which to design the controller. Furthermore, with the example of airplane under icing conditions, Tsien emphasizes that the control system design must face large, unpredictable variations of the plant and maintain its operational stability. Unfortunately, his advice has been largely ignored in academic studies, where rigor was attained at the expense of shifting the object of study. The object shifted from the real physical processes, with all their uncertainties and imperfections, to a set of mathematical equations that are assumed to accurately described the dynamics of the plant to be controlled. The result has been the ever-widening divide between theory and practice witnessed by all. The later developments, such as those in the area of adaptive control [10], attempt to mediate the discrepancies between the model and the actual dynamics but offer few tangible improvements.

In China, however, Tsien’s penetrating insight was not entirely lost. In a survey paper titled “Certain issues in modern control theory” and published in 1980 [11], Guan points out the issue of model dependency in modern control theory and the problem of disturbance it mostly ignored. He asserts that the frequency response method favored by engineers is based on the fundamental principle that the closed-loop system behavior largely depends on open-loop characteristics near the crossover frequency. He further suggests that such deep engineering insight must be somehow combined with the theoretical studies of optimality and stability. In essence, what Guan implies that, for the purpose of feedback design, open loop dynamics needs to be known only locally, in the neighborhood of the gain crossover frequency.

Tsien returned to China shortly after the publication of [9] and never returned to the field of control theory. It was Han who answered Tsien call in 1989 [12] and flatly called the modern control theory a theory about model, not necessarily control. He insists that a physical process should be controlled based on its characteristics local in time and space, not some mathematical model assumed to be detailed and accurate the entire time, through all phases of operations. It would take him the next twenty years to conceive and develop an epic solution to this challenge, in the form of ADRC.

Key to ADRC, above all, is the proposition that the physical plants are to be treated as an ideal integrator chain disturbed by total disturbance. The total disturbance includes external disturbance and internal disturbance, which is Tsien’s notion and can be understood here as the lumped result of the dynamics and uncertainties internal to the plant and make the plant different from the integrator chain. In other words, in ADRC, model is redefined as one that describes the ideal dynamics of the integrator chain, instead of actual dynamics of a particular physical process.

With an integrator chain and total disturbance, ADRC provides a framework to solve the control problem. It establishes an extended state observer (ESO) to estimate the total disturbance in real time. Then, the estimation is canceled and the plant is controlled as an integrator chain. With continuously estimating and canceling, ADRC forces the plant to behave like the ideal integrator chain, while the controller design becomes straightforward.

Even though ADRC has found successful applications in many fields of engineering practice, its universality has yet to be established theoretically. To this end, it is shown in [13] that any linear finite-dimensional controller can be implemented via the linear ADRC (LADRC) structure, but this still left one wondering what makes such structure so prevalence. What is hidden in ADRC that captured the hidden commonalities among different fields of control engineering? This question provides the main motivation for this paper.

To explain the mechanism of ADRC, this paper introduces the notions of normality and locality. Normality refers to the property of the design methods to normalize those physical plants as an integrator chain. While locality, as discussed by Han and Guan, means for the purpose of control design, the design methods such as ADRC and PID control can obtain controller mainly with the plant’s local information. That is, the dynamics of the physical plants only need to be described as an integrator chain near the expected gain crossover frequency. Furthermore, it illustrates with examples that operational stability discussed by Tsien is a result of normality and locality.

The rest of this paper is organized as follows. Section 2 revisits a motivating example and introduces the second-order LADRC. The example is proposed by [14] and sparks persistent interest in frequency response and robustness research of ADRC [15,16,17,18,19,20,21]. Section 3 proposes the concept of local nominal model and discusses the notions of locality, normality, and operational stability. Section 4 illustrates the locally shaping ability of the second-order LADRC and the PID control. Section 5 establish the locality of the second-order LADRC and the PID control, and proposes a new design framework. The paper ends with a few concluding remarks in Sect. 6.

2 The motivating example

In this section, we briefly revisit the example in [14, 16], which is typically used in robust control research of ADRC. Using it as an motivating example, we introduce the second-order LADRC and illustrate how it guarantees stability and robustness for the plant with parametric uncertainty.

2.1 The plant

Consider the plant

$$\begin{aligned}{} & {} \left\{ \begin{aligned}&{\dot{x}}_1 = x_2,\\&{\dot{x}}_2 = - a_2 x_1 -a_1 x_2 + b (u +w),\\ \end{aligned}\right. \end{aligned}$$

(1)

$$\begin{aligned}{} & {} y=x_1, \end{aligned}$$

(2)

where $x_1,x_2$ are the state, u, y, and w are, respectively, the input, output, and external disturbance. The parameter $b=206.25$, while $a_1,a_2 \ge 0$ but uncertain.

Obviously, the plant (1)–(2) has transfer function

$$\begin{aligned} P(s)=\frac{Y(s)}{U(s)+ W(s)} = \frac{b}{s^2 + a_1 s + a_2}. \end{aligned}$$

(3)

2.2 Second-order LADRC and its transfer function

Now we introduce the second-order LADRC and control (1)–(2) with it. The second-order ADRC views the plant as

$$\begin{aligned} {\ddot{y}}=b_0 u +f, \end{aligned}$$

(4)

where $b_0$ is a tuning parameter, while f is called as total disturbance. For (1)–(2), we have

$$\begin{aligned} f=- a_2 x_1 -a_1 x_2 + (b -b_0)u + bw. \end{aligned}$$

Introducing extended state $x_3=f$, equation (4) is written as

$$\begin{aligned}{} & {} \left\{ \begin{aligned}&{\dot{x}}_1 = x_2,\\&{\dot{x}}_2 = x_3 + b_0 u,\\&{\dot{x}}_3 = {\dot{f}}, \end{aligned}\right. \\{} & {} y=x_1. \end{aligned}$$

Then a linear ESO (LESO) is established as

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{\hat{x}}_1 &{} = &{} \beta _1(y-\hat{x}_1)+\hat{x}_2,\\ \dot{\hat{x}}_2 &{} = &{} \beta _2(y-\hat{x}_1)+\hat{x}_3+{b_0} u,\\ \dot{\hat{x}}_3 &{} = &{} \beta _3(y-\hat{x}_1), \end{array}\right. \end{aligned}$$

(5)

where $\beta _1,\beta _2,\beta _3$ are tuning parameters. And the controller is

$$\begin{aligned} u=\frac{1}{b_0}[l_2(r-\hat{x}_1) - l_1 \hat{x}_2 - \hat{x}_3], \end{aligned}$$

(6)

where $l_1,l_2$ are the tuning parameters. LESO (5) and controller (6) are the second-order LADRC.

LADRC (5)–(6) has six tuning parameters. To simplify, reference [14, 16]suggest to generate the parameters $\beta _1,\beta _2,\beta _3$ and $l_1,l_2$ with

$$\begin{aligned}&\beta _1=3\omega _o,~~\beta _2=3\omega _o^2,~~\beta _3=\omega _o^3, \end{aligned}$$

(7)

$$\begin{aligned}&l_1=2\omega _o,~~l_2=\omega _o^2, \end{aligned}$$

(8)

where $\omega _o$ is a parameter called as ESO bandwidth. Thus, the LADRC has only two parameters $\omega _o$ and $b_0$.

Substituting (6) into (5) and with (7)–(8), we have

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\hat{x}}_1 = -3 \omega _o \hat{x}_1 +\hat{x}_2 + 3 \omega _o y, \\ \dot{\hat{x}}_2 = -4\omega _o^2 \hat{x}_1 -2\omega _o \hat{x}_2 + 3\omega _o^2 y +\omega _o^2 r,\\ \dot{\hat{x}}_3 = -\omega _o^3 \hat{x}_1 +\omega _o^3 y, \end{array}\right. \end{aligned}$$

(9)

Viewing y and r as two inputs of (9), while u in (6) as the output, we have the transfer functions

$$\begin{aligned} \frac{U(S)}{ Y(s)}&=-\frac{\omega _o^3(10s^2+5\omega _o s+\omega _o^2)}{b_0s(s^2+5\omega _os+10\omega _o^2)},\\ \frac{U(S)}{ R(s)}&= \frac{\omega _o^2(s + \omega _o)^3 }{b_0 s(s^2+5\omega _os+10\omega _o^2) }, \end{aligned}$$

where U(s), Y(s), and R(s) are respectively the Laplace transform of u, y, and r. Let

$$\begin{aligned}&C(s)=\frac{\omega _o^3(10s^2+5\omega _os+\omega _o^2)}{b_0s(s^2+5\omega _os+10\omega _o^2)}, \end{aligned}$$

(10)

$$\begin{aligned}&C_1(s)= \frac{(s + \omega _o)^3}{\omega _o(10 s^2+5\omega _os+\omega _o^2)}, \end{aligned}$$

(11)

the second-order LADRC has equation

$$\begin{aligned} U(s) = C(s) [C_1(s) R(s) - Y(s)]. \end{aligned}$$

(12)

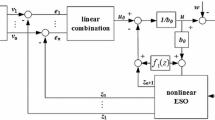
Equation (12) describes how to generate u with r and y, while (3) describes how the plant generates y with u and w. With them, the second-order LADRC system has a block diagram shown in Fig. 1.

Fig. 1

Block diagram of the second-order LADRC system

Remark 1

Note here we say the second-order LADRC “views” the plant as (4). It emphasizes in (4), the order two and the parameter $b_0$ are selected by the engineer. For the second-order LADRC, the plant (1)–(2) is a special case whose order and relative degree are both two. Such a plant is suitable to introduce the second-order LADRC because the total disturbance can be clearly described, while it is well known that the second-order LADRC can be used for the more complicated plants.

Remark 2

Fig. 1 illustrates an advantage of viewing the plant as (4). Suppose we have a plant whose transfer function is P(s). By viewing it as (4), we obtain LADRC (5)–(6) and Fig. 1. Note in the procedure we do not use the plant’s information such as order, relative degree, and time-delay. That is, no matter what the plant’s order, relative degree, and time-delay are, it can be controlled by the second-order LADRC, while the stability and performance of the closed-loop system can be analyzed with Fig. 1.

2.3 Stability and robustness

With Fig. 1, the stability and robustness of the LADRC system depends on the closed-loop made of C(s) and P(s).

In LADRC (5)–(8), let $b_0=206.25$, $\omega _o=100$. For the following five typical pairs:

$$\begin{aligned} \begin{aligned} (a_1,a_2) \in \{&(3.085,0),(3.085,10),(3.085,100),\\&(1,0),(100,0)\}, \end{aligned} \end{aligned}$$

(13)

the Bode plots of P(s)C(s) are drawn in Fig. 2. Let

$$\begin{aligned} P_0(s) = \frac{b}{s^2}. \end{aligned}$$

the Bode plot of $P_0(s)C(s)$ is also drawn. Obviously, all the five pairs are stable. When

$$\begin{aligned} \begin{aligned}&(a_1,a_2) \\&\in \{(3.085,0),(3.085,10),(3.085,100),(1,0)\}, \end{aligned} \end{aligned}$$

(14)

the gain crossover frequency is near 100 rad/s, the phase margins is near $31.9^\circ$. For the pair $(a_1,a_2)=(100,0)$, the gain crossover frequency is 53.2 rad/s, while phase margin is $81.2^\circ$.

Fig. 2

Bode plots of P(s)C(s) and $P_0(s)C(s)$

Figure 2 shows the second-order LADRC is robust subject to the plant’s significant variation. Such robustness is also reported by [15], where the plant may be unstable. In the rest of this paper, we interpret the robustness with the frequency response method.

3 Normality, locality, and operational stability

In this section, we introduce the concept of the local nominal model and show integrator chain can be widely used as a local nominal model. Then we discuss normality, locality, and operational stability of LADRC.

3.1 Local nominal model

Definition 1

(Local nominal model) Suppose we have a plant P(s) while $P_0(s)$ is another transfer function. $P_0(s)$ is said a local nominal model of P(s) at frequency $\omega _\gamma \ge 0$, if when $\omega \approx \omega _\gamma$, we have $P(j \omega ) \approx P_0(j \omega )$.

The purpose of a local nominal model is to describe the plant at $\omega _\gamma$ with a simple model, where $\omega _\gamma$ is usually the expected gain crossover frequency of the loop transfer function to design. Thus, because of its simplicity, the integrator chain

$$\begin{aligned} P_0(s) = \frac{b}{s^n} \end{aligned}$$

(15)

is a suitable candidate for a local nominal model. In this paper, we only use (15) as local nominal model.

When (15) is a local nominal model at $\omega _\gamma$, the plant’s frequency response is similar to (15) in the band near $\omega _\gamma$. Or, intuitively, the plant can be viewed as a distorted integrator chain but the distortion is ignorable near $\omega _\gamma$. Thus, a simple approach to check if (15) is a local nominal model is to draw the plant’s Bode diagram. Note (15) has

$$\begin{aligned}{} & {} |P_0(j\omega ) |= \frac{b}{\omega ^n}, \\{} & {} \angle P_0(j\omega ) = -n \cdot 90^\circ . \end{aligned}$$

If near $\omega _\gamma$, the slope of the magnitude-frequency plot approximates $-n$ while the phase approximates $-n\!\cdot \!90^\circ$, then (15) is a local nominal model at $\omega _\gamma$.

In ADRC, local nominal model (15) corresponds to Han canonical form

$$\begin{aligned} \frac{{\mathrm d}^n}{{\mathrm d}t^n} y = b_0u+f, \end{aligned}$$

(16)

where f is total disturbance. That is, when the plant is written as (16), the local nominal model (15) is implicitly used.

The following are two special cases of $n=2$, where integrator chain (15) becomes double integrator

$$\begin{aligned} P_0(s) = \frac{b}{s^2}. \end{aligned}$$

(17)

In this paper, we mainly focus on and illustrate the special case of $n=2$, while the results can be generalized to the integrator chains with other orders.

Example 1

Consider the plant in Sect. 2.1. With (3), it has frequency response

$$\begin{aligned} P({\mathrm j}\omega )=\frac{b}{({\mathrm j}\omega )^2 + a_1 ({\mathrm j}\omega ) + a_2}. \end{aligned}$$

When $\omega \rightarrow +\infty$, the term $({\mathrm j}\omega )^2$ is dominant in the denominator so that

$$\begin{aligned} P({\mathrm j}\omega ) \approx \frac{b}{({\mathrm j}\omega )^2 }=P_0({\mathrm j}\omega ). \end{aligned}$$

Thus, when $\omega$ is large enough, the frequency response of (3) approximates that of double integrator (17). For the five pairs in (13), the Bode plots of (3) are drawn in Fig. 3. With (17) and $b = 206.25$, Bode plot of $P_0 (s)$ is also drawn with black line. Obviously, all six plots are close in high-frequency. At frequency $\omega _\gamma =100$, the plants with the four pairs in (14) have (17) as a local nominal model. Even for the pair $(a_1,a_2)=(100,0)$, double integrator (17) can be viewed as a local nominal model.

Fig. 3

Bode plots of P(s) and $P_0(s)$ in Example 1

Example 2

Consider the plant

$$\begin{aligned} P_1(s)= & {} \frac{1}{(s+1)^3}, \end{aligned}$$

(18)

$$\begin{aligned} P_2(s)= & {} \frac{0.40}{(s+0.1)(s+0.3)}\textrm{e}^{-0.18s}, \end{aligned}$$

(19)

$$\begin{aligned} P_3(s)= & {} \frac{0.36}{s(s-0.2)}, \end{aligned}$$

(20)

$$\begin{aligned} P_4(s)= & {} \frac{0.0191(20-s)}{s(s+0.5)}, \end{aligned}$$

(21)

and let

$$\begin{aligned} P_0(s)= & {} \frac{0.38}{s^2}. \end{aligned}$$

(22)

The Bode plots of (18)–(22) are shown in Fig. 4. It is shown that the plant (22) is a local nominal model of plant (18)–(21) respectively at $\omega _1 =1.7$, $\omega _2 =2.0$, $\omega _2 =6.0$, and $\omega _4 =3.0$. It means if we control $P_1(s)$, $P_2(s)$, $P_3(s)$, and $P_4(s)$ and specify their loop transfer functions’ gain crossover frequency respectively at $\omega _1 =1.7$, $\omega _2 =2.0$, $\omega _2 =6.0$, and $\omega _4 =3.0$, we can use (22) as their local nominal model.

Fig. 4

Bode plots of P(s) and $P_0(s)$ in Example 2

Remark 3

Definition 1 uses “$\approx$” instead of inequality constraint. The reasons are the following two. First, for engineering practice, “$\approx$” is clear enough and used in classic textbooks such as [22]; second, we have not found a suitable strict inequality constraint. Empirically and with Bode plot, we suggest that at $\omega _\gamma$, if the slope of the magnitude-frequency plot is in $(-n-0.5,-n+0.5)$ and the phase is in $(-n \cdot 90^\circ -15^\circ ,-n \cdot 90^\circ +45^\circ ]$, then (15) can be used as a local nominal model.

Remark 4

When (15) is a local nominal model, its parameter b is not unique. For example, in Example 1, if we let $b = 200$, the plants with pairs of (13) all have the local nominal model (17) at frequency $\omega _\gamma =100$.

Remark 5

Example 1 can be generalized to that for all stable minimum-phase plants with relative degree n, integrator chain (15) is a local nominal model at a large enough frequency. This property is why ADRC usually chooses the plant’s relative degree as its order.

Remark 6

Note (18)–(21) are four typical plants. The plant (18) is a stable and minimal-phase plant whose order and relative degree are not two. The plant (19) has time-delay. The plant (20) has an unstable zero, while (21) is unstable. Example 2 shows that the local nominal model provides a unified approach to deal with them.

3.2 Normality

Now we discuss normality. Suppose we have a method to design controller. We say the method has normality if it first normalizes the plant to a local nominal model. For example, with Example 1 and Sect. 2, we conclude the second-order LADRC has normality because it normalizes the plant to double integrator (17) first. PID control also has normality and we illustrate it later.

Normality partly explains why so many vastly different plants in various fields of engineering can be treated as Han canonical form (4). The reason is, these plants can have local nominal model (17) at the expected gain crossover frequency. Thus, the second-order LADRC normalize them to (17) and control them.

Normality has two advantages. First, it simplifies the controller design to obtain a controller for integrator chain (15), which is relatively easy to control. Second, it guarantees the robustness of the method. It means several plants, maybe quite different, can share a common local nominal model and a common controller. That is, the method can obtain a controller with perfect robustness.

3.3 Locality

Locality is also a property of the design method. We say the method has locality if it is mainly based on local information to design and can guarantee stability when used for the plant. Both the second-order LADRC and the PID control have locality. They design the controller with the local nominal model (17), which contains the local information of the plant around the expected gain cross-over frequency.

Normality and locality are the reason why the second-order LADRC and the PID control can be widely used. As shown in Example 1 and Example 2, double integrator (17) can be a local nominal model for a huge class of plants, including the plants with time-delay, unstable poles, and unstable zeros. with normality and locality, the second-order LADRC and the PID control are widely applicable for these plants.

Locality is a property to be proven. In Sects. 4 and 5, we prove the locality of the second-order LADRC and the PID control.

3.4 Operation stability

Operational stability is a concept Tsien proposes in Chapter 15 of [9]. It means the control system can stably work when the plant has large unpredictable variations. It implies perfect robustness and seems difficult.

Normality and locality can guarantee operational stability. With normality, the method may normalize two significantly different plants to the same local nominal model. With locality, the two plants obtain the same controller. If the two plants are respectively the plant before and after variation, operational stability is realized.

Example 3

Consider the plant (1)–(2) controlled by (5)–(8). Suppose at beginning, $(a_1,a_2)=(1,0)$. Then at $t=0.3s$, the plant suddenly changes and $(a_1,a_2)=(3.085,100)$. It is a large variation because the plant loses its integrator. But with Fig. 2, we conclude the stability of the LADRC system is maintained, even the gain crossover frequency and phase margin vary little.

The time-domain simulation is shown in Figs. 5 and 6. The effect of the suddenly change on the state and control signals is indeed slight. That is, the system is operationally stable.

Fig. 5

The state and control signals of Example 3

Fig. 6

The state and control signals of Example 3, around the variation moment $t=0.3$

4 Locally loop shaping

This section analyzes the locally loop-shaping ability of the second-order LADRC and the PID control, which is the foundation of the locality of the two approaches. Here locally loop shaping means to shape the loop transfer function’s frequency response mainly with local information. We analyze the second-order LADRC first, then extend the results to the PID control.

4.1 Second-order LADRC

For the second-order LADRC (5)–(8), its controller (10) can be re-written as

$$\begin{aligned} C(s)&= \frac{\omega _o^3(10s^2 + 5\omega _o s + \omega _o^2)}{b_0 s(s^2+5\omega _o s +10 \omega _o^2)}\\&= {\frac{\omega _o^2}{b_0}} \cdot \frac{10 {\frac{s^2}{\omega _o^2}} + 5{\frac{s}{\omega _o}} +1}{{\frac{s}{\omega _o}}\left( {{\frac{s^2}{\omega _o^2}} + 5{\frac{s}{\omega _o}} +10}\right) }. \end{aligned}$$

It has two terms. The first term ${\omega _o^2}/{b_0}$ is the gain, while the second term is a function of ${s}/{\omega _o}$ and can compensate phase.

The Bode plot of ${b_0} C(s) / {\omega _o^2}$ is drawn in Fig. 7, where the red line is the approximation of the magnitude plot. It has two break frequencies, $\omega _o/\sqrt{10}$ and $\sqrt{10} \omega _o$, which divide the Bode plot of C(s) into three parts. The first is low frequency $\omega <\omega _o/\sqrt{10}$, where the magnitude descends with a slope approximating $-1$, while the phase approximates $-90^\circ$. The second is middle frequency $\omega _o/\sqrt{10}<\omega < \sqrt{10} \omega _o$, where the magnitude increases with a slope approximating $+1$, while the phase increases then descends with a peak up to $31.9^\circ$. The third is high frequency $\omega >\sqrt{10} \omega _o$, where the magnitude descends with a slope approximating $-1$, while the phase approximates $-90^\circ$.

Note that in low and high frequency, the phase of C(s) is almost fixed. Only in middle frequency, the phase can be adjusted in a wide range. Or, only in middle frequency, by tuning $\omega _o$ and $b_0$, C(s) can provide phase and gain compensation freely.

Fig. 7

Bode plot of ${b_0} C(s) / {\omega _o^2}$

Because of its frequency response, C(s) has a wonderful ability of locally loop shaping. Suppose P(s) is the plant and consider the loop transfer function

$$\begin{aligned} L(s) = P(s) C(s). \end{aligned}$$

With Fig. 7, we conclude that in low frequency $|L({\mathrm j}\omega ) |$ is enlarged, while large $|L({\mathrm j}\omega ) |$ is helpful to guarantee stability and reject the low-frequency external disturbance; In middle-frequency, the slope of $|L({\mathrm j}\omega ) |$ and $\angle L({\mathrm j}\omega )$ are both adjusted to guarantee enough stability margin; In high frequency, $|L({\mathrm j}\omega ) |$ decreases quickly enough to be robust subject to unmodeled dynamics and filter measurement noise.

Furthermore, we have the following theorem.

Theorem 1

If double integrator (17) is controlled by LADRC (5)–(8) with $b_0=b$, then the system is stable. And the loop transfer function $P_0(s) C(s)$ has gain crossover frequency $\omega _o$ and phase margin $31.9^\circ$, while the magnitude plot has slope $-1$ at $\omega _o$.

Proof

Let double integrator (17) be the plant in Fig. 1. The LADRC system’s stability depends on the loop transfer function

$$\begin{aligned} P_0(s) C(s)= & {} \frac{\omega _o^3(10s^2 +5\omega _o s +\omega _o^2)}{s^3 (s^2 + 5\omega _o s +10\omega _o^2)} \nonumber \\= & {} \frac{10 \left( \dfrac{s}{\omega _o}\right) ^2 + 5 {\dfrac{s}{\omega _o}} +1 }{(\dfrac{s}{\omega _o})^3 \left[ \left( \dfrac{s}{\omega _o}\right) ^2 + 5 {\dfrac{s}{\omega _o}} + 10\right] }, \end{aligned}$$

(23)

which is a function of $\dfrac{s}{\omega _o}$ and has $|P_0({\mathrm j}\omega _o)C({\mathrm j}\omega _o) |=1$. Furthermore,

$$\begin{aligned} \begin{aligned}&\angle P_0({\mathrm j}\omega _o)C({\mathrm j}\omega _o)\\&=-180^\circ + \arctan \left( \frac{9}{5}\right) -\arctan \left( \frac{5}{9}\right) = -148.1^\circ . \end{aligned} \end{aligned}$$

Drawing the Bode diagram of $P_0(s) C(s)$ in Fig. 8, we conclude that the system is stable and $P_0(s) C(s)$ has unique gain crossover frequency. Thus, the gain crossover frequency is $\omega _o$, while the phase margin is $31.9^\circ$. And it is easy to verify that the magnitude plot has slope $-1$ at $\omega _o$. $\square$

Fig. 8

Bode diagram of (23)

Theorem 1 and Fig. 8 establish a connection between double integrator (17) and LADRC (5)–(8). When $b_0=b$, the controller (10) and the double integrator (17) make an ideal controller-plant pair. The transfer function $P_0({\mathrm j}\omega _o)C({\mathrm j}\omega _o)$ has an ideal shape. Especially, its gain crossover frequency is exactly the second tuning parameter $\omega _o$, which can be arbitrarily tuned.

4.2 From second-order LADRC to PID control

Now we re-write (10) as

$$\begin{aligned} C(s)= & {} {\frac{\omega _o^2}{b_0}} \cdot \frac{10 {\frac{s^2}{\omega _o^2}} + 5{\frac{s}{\omega _o}} +1}{{\frac{s}{\omega _o}}\left( {{\frac{s^2}{\omega _o^2}} + 5{\frac{s}{\omega _o}} +10}\right) }\\= & {} {\frac{\omega _o^2}{10 b_0}}\left( 5+ \frac{1}{\frac{s}{\omega _o}} + 10 {\frac{s}{\omega _o}} \right) \cdot {\frac{10}{{\frac{s^2}{\omega _o^2}} + 5{\frac{s}{\omega _o}} +10}}. \end{aligned}$$

Ignoring the term

$$\begin{aligned} {\frac{10}{{\frac{s^2}{\omega _o^2}} + 5{\frac{s}{\omega _o}} +10}} \end{aligned}$$

(24)

and defining

$$\begin{aligned} K_P ={\frac{\omega _o^2}{2 b_0}},~~T_I ={\frac{5}{\omega _o} },~~T_D ={\frac{2}{\omega _o}}, \end{aligned}$$

C(s) can be simplified as a PID controller

$$\begin{aligned} \begin{aligned} C_{\textrm{PID}}(s)&={\frac{\omega _o^2}{10 b_0}}\left( 5+ {\frac{\omega _o}{s}} + 10 {\frac{s}{\omega _o}}\right) \\&= K_P \left( 1 + \frac{1}{T_I s} + T_D s\right) . \end{aligned} \end{aligned}$$

(25)

Similarly, writing the pre-filter $C_1 (s)$ as

$$\begin{aligned} C_1(s)= \frac{\omega _o^2}{10s^2 +5\omega _o s +\omega _o^2} \cdot \frac{(s +\omega _o)^3}{\omega _o^3}. \end{aligned}$$

and ignoring the term

$$\begin{aligned} \frac{(s +\omega _o)^3}{\omega _o^3}, \end{aligned}$$

(26)

$C_1(s)$ can be simplified as

$$\begin{aligned} F_r(s)&= \frac{\omega _o^2}{10s^2 +5\omega _o s +\omega _o^2}. \end{aligned}$$

(27)

Replacing C(s) and $C_1(s)$ respectively with $C_{\textrm{PID}}(s)$ and $F_r(s)$, we obtain the block diagram shown in Fig. 9.

Fig. 9

Block diagram of the PID control

Remark 7

If further ignoring the term $\frac{\omega _o^2}{10\,s^2 +5\omega _o s +\omega _o^2}$ of $F_r(s)$, i. e., $F_r(s)=1$, the PID control in Fig. 9 becomes a classical unity feedback PID control.

4.3 PID control

Note both (25) and (27) have two tuning parameters $b_0$ and $\omega _o$, which are the two tuning parameters of the second-order LADRC. The Bode plots of ${b_0}C(s)/{\omega _o^2}$ and ${b_0C_{\textrm{PID}}(s)/{\omega _o^2}}$ are draw in Fig. 10, while the Bode plots of $C_1(s)$ and $F_r(s)$ are drawn in Fig. 11. Since (24) and (26) have unity gain in low frequency, the two pairs are indeed close in low frequency. Note the phase plot of ${b_0}C_{\textrm{PID}}(s)/{\omega _o^2}$ illustrates the phase compensation is mainly in middle frequency around $\omega _o$. In low and high frequency, $C_{\textrm{PID}}(s)$ has phase respectively approximating $-90^\circ$ and $90^\circ$.

Fig. 10

Bode plots of $b_0 C(s)/\omega _o^2$ and $b_0 C_{\textrm{PID}}(s)/\omega _o^2$

Fig. 11

Bode plots of $C_1(s)$ and $F_r(s)$

Similar to the second-order LADRC, PID control has the following theorems.

Theorem 2

Suppose double integrator (17) is controlled in Fig 9 as the plant. Then, with

$$\begin{aligned} b_0=\frac{\sqrt{106}}{10} b, \end{aligned}$$

(28)

the system is stable, while the loop transfer function $P_0(s) C_{\textrm{PID}}(s)$ has gain crossover frequency $\omega _o$ and phase margin $60.9^\circ$, and the magnitude plot’s slope approximates $-1$ at $\omega _o$.

Proof

When (17) is controlled by $C_{\textrm{PID}}(s)$, the loop transfer function is

$$\begin{aligned} P_0(s) C_{\textrm{PID}}(s)= & {} {\frac{b}{s^2}} \cdot \frac{\omega _o^2}{10 {\frac{\sqrt{106}}{10} } b}\left( 5+ \frac{\omega _o}{s} + 10 {\frac{s}{\omega _o}} \right) \nonumber \\= & {} \frac{\omega _o^2}{{\sqrt{106}} s^2}\left( 5+ \frac{\omega _o}{s} + 10 {\frac{s}{\omega _o}} \right) . \end{aligned}$$

(29)

It is a function of $\dfrac{s}{\omega _o}$ and has $|P_0({\mathrm j}\omega _o)C_{\textrm{PID}}({\mathrm j}\omega _o) |=1$, $\angle P_0({\mathrm j}\omega _o) C_{\textrm{PID}}({\mathrm j}\omega _o)=-119.1^\circ$. Drawing the Bode diagram of $P_0(s) C_{\textrm{PID}}(s)$ in Fig. 12, we conclude that the system is stable and $P_0(s) C_{\textrm{PID}}(s)$ has unique gain crossover frequency. Thus, the gain crossover frequency is $\omega _o$, while the phase margin is $60.9^\circ$. And it is easy to verify that the magnitude plot’s slope approximates $-1$ at $\omega _o$. $\square$

Fig. 12

Bode plot of $P_0(s)C_{\textrm{PID}}(s)$

5 The ADRC inspired design framework

In this section, we establish the locality of the second-order LADRC and the PID control. Then a design framework inspired by ADRC is proposed by generalization.

5.1 Locality as shown in second-order ADRC

Now we consider to control a plant P(s) with the second-order LADRC. We assume

A1 the plant P(s) has a local nominal model (17) at frequency $\omega _\gamma > 0$ and has no differentiator.

Theorem 3

Suppose A1 holds. If P(s) is controlled by LADRC (5)–(8) with

$$\begin{aligned} b_0 = b,~~\omega _o = \omega _\gamma , \end{aligned}$$

(30)

then there exists $\omega _{\textrm{cut}} \approx \omega _\gamma$ such that

$$\begin{aligned}&|P({\mathrm j}\omega _{\textrm{cut}})C({\mathrm j}\omega _{\textrm{cut}})|=1, \end{aligned}$$

(31)

$$\begin{aligned}&\angle (P({\mathrm j}\omega _{\textrm{cut}})C({\mathrm j}\omega _{\textrm{cut}})) \approx -148.1^\circ . \end{aligned}$$

(32)

Proof

Consider the loop transfer function P(s)C(s). Since P(s) has no differentiator, it does not take place unstable pole-zero cancelation between C(s) and P(s). Because P(s) has a local nominal model (17) at $\omega _\gamma$, we conclude near $\omega _\gamma$, $P({\mathrm j}\omega )$ is continuous and has similar value and slope with $P_0({\mathrm j}\omega )$. Then we have

$$\begin{aligned} P({\mathrm j}\omega )C({\mathrm j}\omega ) \approx P_0({\mathrm j}\omega )C({\mathrm j}\omega ),~~\omega \approx \omega _\gamma . \end{aligned}$$

(33)

Because of Theorem 1,

$$\begin{aligned}&|P({\mathrm j}\omega _\gamma )C({\mathrm j}\omega _\gamma ) |\approx 1, \end{aligned}$$

(34)

$$\begin{aligned}&\angle P({\mathrm j}\omega _\gamma )C({\mathrm j}\omega _\gamma ) \approx -148.1^\circ , \end{aligned}$$

(35)

and $|P({\mathrm j}\omega _\gamma )C({\mathrm j}\omega _\gamma ) |$ has slope about $-1$. Thus, we conclude that $|P({\mathrm j}\omega )C({\mathrm j}\omega ) |$ passes downstairs 0dB once near $\omega _\gamma$. Let the passing frequency be $\omega _{\textrm{cut}}$, we have (31) and (32). $\square$

Theorem 3 establishes the locality of the second-order LADRC, which means the second-order LADRC (5)–(8) can be tuned based on local nominal model (17) and be used to control the plant P(s). Suppose P(s) is a typical engineering plant controlled by (5)–(8). The Bode plots of P(s)C(s) and $P_0(s)C(s)$ are drawn in Fig. 13. Theorem 3 guarantees in the band near the expected gain crossover frequency $\omega _\gamma$, P(s)C(s) is close to $P_0(s)C(s)$. There exists $\omega _{\textrm{cut}}$ satisfying (31) and (32). Recalling Fig. 7, in low frequency we have $|P({\mathrm j}\omega )C({\mathrm j}\omega ) |>1$, while in high frequency we have $|P({\mathrm j}\omega )C({\mathrm j}\omega ) |<1$. Thus, $|P({\mathrm j}\omega )C({\mathrm j}\omega ) |$ only passes 0dB once at $\omega _{\textrm{cut}}$, the LADRC system is stable and has phase margin about $31.9^\circ$.

Fig. 13

Typical Bode plots of P(s)C(s) and $P_0(s)C(s)$

Theorem 3 should be used as a condition to try the second-order LADRC. When the plant satisfies A1, it is worth trying the second-order LADRC and has a great possibility to succeed.

Example 4

Consider the plant (18) in Example 2. Controlling it with LADRC (5)–(8), where $b_0=0.38$, $\omega _o=1.7$, the Bode plots of P(s)C(s) and $P_0(s)C(s)$ are what drawn in Fig. 13. It is easy to conclude that the LADRC stabilizes P(s), although the Bode plots of P(s) and $P_0(s)$ are quite different in low and high frequency.

Example 5

Re-consider the plant in Sect. 2.1. With Example 1 and Theorem 3, we conclude when $(a_1,a_2)$ satisfying (14), the gain crossover frequency is near $100 {\mathrm {rad/s}}$, while the phase margin is near $31.9^\circ$. For the pair of $(a_1,a_2)=(100,0)$, the phase margin is significantly larger. That is what illustrated in Fig. 2.

Remark 8

Theorem 3 enlarges the scope to use the second-order LADRC. For example, the plants in Example 2 all can be controlled by the second-order LADRC.

Remark 9

With Theorem 3, ESO is an unnecessary high-gain in LADRC. High-gain means in ESO (5), the parameters $\beta _1,\beta _2,\beta _3$ are large enough. Or, when the three parameters are generated with (7), $\omega _o$ is large enough. In the existing ADRC literature, ESO is usually high-gain to guarantee the stability. But high-gain ESO is difficult to realize in practice. Theorem 3 proves that $\omega _o=\omega _\gamma$ is enough to guarantee stability, thus ESO is unnecessary high-gain.

5.2 Locality of PID control

Similar with Theorem 3, we have the following theorem, which establishes the locality for and is a trying condition of PID control.

Theorem 4

Suppose the plant P(s) satisfies A1 and is controlled in Fig 9 as the plant. Then, with

$$\begin{aligned} b_0=\frac{\sqrt{106}}{10} b, ~~\omega _o=\omega _\gamma , \end{aligned}$$

(36)

then there exists $\omega _{\textrm{cut}} \approx \omega _\gamma$ such that

$$\begin{aligned}&|P({\mathrm j}\omega _{\textrm{cut}})C({\mathrm j}\omega _{\textrm{cut}})|=1, \end{aligned}$$

(37)

$$\begin{aligned}&\angle (P({\mathrm j}\omega _{\textrm{cut}})C({\mathrm j}\omega _{\textrm{cut}})) \approx -119.1^\circ . \end{aligned}$$

(38)

Proof

The proof is similar to the proof of Theorem 3. We consider the loop transfer function $P(s)C_{\textrm{PID}}(s)$. Since P(s) has no differentiator, it does not take place unstable pole-zero cancelation between $C_{\textrm{PID}}(s)$ and P(s). And we have

$$\begin{aligned} P({\mathrm j}\omega )C_{\textrm{PID}}({\mathrm j}\omega ) \approx P_0({\mathrm j}\omega )C_{\textrm{PID}}({\mathrm j}\omega ),~~\omega \approx \omega _\gamma . \end{aligned}$$

(39)

That is, in Bode diagram, the plot of $P(s)C_{\textrm{PID}}(s)$ is close to that of $P_0(s)C_{\textrm{PID}}(s)$. Thus,

$$\begin{aligned}&|P({\mathrm j}\omega _\gamma )C_{\textrm{PID}}({\mathrm j}\omega _\gamma ) |\approx 1, \end{aligned}$$

(40)

$$\begin{aligned}&\angle P({\mathrm j}\omega _\gamma )C_{\textrm{PID}}({\mathrm j}\omega _\gamma ) \approx -119.1^\circ , \end{aligned}$$

(41)

and $|P({\mathrm j}\omega _\gamma )C_{\textrm{PID}}({\mathrm j}\omega _\gamma ) |$ has slope about $-1$. Because the Bode plot is continuous, we conclude that $|P({\mathrm j}\omega )C_{\textrm{PID}}({\mathrm j}\omega )|$ passes downstairs 0dB once near $\omega _\gamma$. Let the passing frequency be $\omega _{\textrm{cut}}$, we have (37) and (38). $\square$

Example 6

Consider the plant in Example 1. Let $b=206.25$, $\omega _\gamma =100$, and generate PID control with (36). The Bode plots of $P(s)C_{\textrm{PID}}(s)$ for the five typical pairs are drawn in Fig. 14, while that of $P_0(s)C_{\textrm{PID}}(s)$ is also drawn. All five pairs are stable. For the four pairs of (14), the gain crossover frequency approximate $\omega _\gamma$ and phase margins are near $60.9^\circ$. While the pair $(a_1,a_2)=(100,0)$ has a phase margin greater than $90^\circ$.

Fig. 14

Bode plots of $P(s)C_{\textrm{PID}}(s)$ and $P_0(s)C_{\textrm{PID}}(s)$ in Example 6

Remark 10

Theorem 4 clarifies when the differentiator (D) term is necessary. When the plant has the local nominal model (17) at the expected gain crossover frequency $\omega _\gamma$, its phase approximates $-180^\circ$ there. In this situation, proportional-integral (PI) control can not obtain enough phase margin and D-term is necessary.

Remark 11

Theorem 4 implies the normality of PID control. With A1, PID control can be viewed as to normalize the plant to double integrator (17) first.

Remark 12

Theorem 4 can be used as a new tuning approach for PID control. It has only two tuning parameters and is similar with self-coupling PID in [24].

5.3 The design framework

The design framework is a generalization of the results of the second-order LADRC and the PID control. It obtains the controller in three steps.

Step 1   To establish a local nominal model (15) at the expected a gain crossover frequency $\omega _\gamma$. In practice, such a $\omega _\gamma$ is usually given in the specification and by experienced engineers. Thus, complicated dynamics such as resonant peak are carefully avoid so that (15) can be a local nominal model and well describe the plant near $\omega _\gamma$.

Step 2   To choose the corresponding controller based on local nominal model (15). For example, when $n=1$ in (15), the first-order LADRC and the PI control are candidates; When $n=2$, the second-order LADRC and the PID control are candidates; When $n=3$, the third-order LADRC and the $\hbox {PIDD}^2$ control are candidates.

Step 3   To generate the controller’s parameters. With these parameters, the controller provide gain and phase compensation at $\omega _\gamma$ exactly to local nominal model (15), and approximately to the plant. For LADRC, if $\omega _c=\omega _o=\omega _\gamma$ can not meet the phase margin specification, let $\alpha >1$ be a tuning parameter and let

$$\begin{aligned} \omega _c = \frac{\omega _\gamma }{\alpha },~~\omega _o = {\alpha } {\omega _\gamma }, \end{aligned}$$

(42)

then generate the parameters. For example, for the second-order LADRC, the parameters can be tuned with

$$\begin{aligned}&\beta _1 =3\omega _o,~~\beta _2=3\omega _o^2,~~\beta _3=\omega _o^3,\\&l_1 =2\omega _c,~~l_2=\omega _c^2. \end{aligned}$$

By increasing $\alpha$, the controller C(s) can provide enough phase margin compensation at $\omega _\gamma$. Then to tune $b_0$ to guarantee $\omega _\gamma$ is exactly the gain crossover frequency of the closed-loop. The details of tuning can be found in [25]. In this way, the controller can guarantee enough phase margin.

With the three steps, most plants can be controlled with enough phase margin, while to check stability and robustness is necessary in practice.

The following is an example to illustrate the design framework.

Example 7

Suppose to control the plant $P_2(s)$ in (19) with LADRC, the gain crossover frequency is specified as 2rad/s with phase margin $45^\circ$. Step 1, with Example 2, the local nominal model is (22). Step 2, the second-order LADRC is selected. Step 3, since $45^\circ$ is obviously larger than $31.9^\circ$, we use $\alpha =4$ in (42) and tune $b_0$ to 0.4479. The Bode diagram of $P_2(s)C(s)$ is drawn in Fig. 15. It indeed has gain crossover frequency 2rad/s and phase margin $45^\circ$. And the step response of the LADRC system is drawn in Fig. 16.

Fig. 15

Bode plots of $P_2(s)C(s)$ in Example 7

Fig. 16

Step response of Example 7

Remark 13

The controllers in Step 2 all have an integrator. If the integrator is not allowed because of the plant’s differentiator or the type number specification, how to choose the candidate controllers is an open problem. Some preliminary work can be found in [26].

6 Conclusions

This paper showcases an ADRC-inspired design framework, combining insights from Tsien, Guan, and Han to justify and explain its inner workings. This framework rests on the notion of normality and locality as summarized below:

1. Normality. A large class of physical plants can be normalized in the form of an integrator chain, on which the controller is to be designed with ease and effectiveness. In ADRC design, once the order of the plant is determined, the plant is implicitly normalized as an integrator chain with the same order.

2. Locality. It is shown that the second-order LADRC and the PID control operate with locality. That is, these two approaches can obtain their controllers mainly with the local nominal model of the plant, while these controllers simultaneously compensate for the gain and phase freely only in the middle frequency, the neighborhood of the crossover.

3. A three-step design procedure is established: 1) establish the plant’s local nominal model; 2) choose the corresponding controller, and 3) loop-shaping gain and phase in middle-frequency range. The second-order LADRC and the PID control are interpreted as two special examples in the new framework based on the same local nominal model of (17), leading to insight as to why the two control approaches have been used widely in practice.

4. Operational stability. Because the control design is not premised on the detailed and global model, the resulting closed-loop system proves to be robust in the presence of large variations in plant dynamics, as long as they do not alter the plant dynamics in the middle-frequency range. It is in this sense that the operational stability as defined by Tsien is attained.