Classical pole placement adaptive control revisited: linear-like convolution bounds and exponential stability

Abstract

While the original classical parameter adaptive controllers do not handle noise or unmodelled dynamics well, redesigned versions have been proven to have some tolerance; however, exponential stabilization and a bounded gain on the noise are rarely proven. Here we consider a classical pole placement adaptive controller using the original projection algorithm rather than the commonly modified version; we impose the assumption that the plant parameters lie in a convex, compact set, although some progress has been made at weakening the convexity requirement. We demonstrate that the closed-loop system exhibits a very desirable property: there are linear-like convolution bounds on the closed-loop behaviour, which confers exponential stability and a bounded noise gain, and which can be leveraged to prove tolerance to unmodelled dynamics and plant parameter variation. We emphasize that there is no persistent excitation requirement of any sort; the improved performance arises from the vigilant nature of the parameter estimator.

1 Introduction

Adaptive control is an approach used to deal with systems with uncertain or time-varying parameters. The classical adaptive controller consists of a linear time-invariant (LTI) compensator together with a tuning mechanism to adjust the compensator parameters to match the plant. The first general proofs that adaptive controllers could work came around 1980, e.g. see [1,2,3,4,5]. However, such controllers were typically not robust to unmodelled dynamics, did not tolerate time variations well, and did not handle noise or disturbances well, e.g. see [6]. During the following two decades, a great deal of effort was made to address these shortcomings. The most common approach was to make small controller design changes, such as the use of signal normalization, deadzones, and $\sigma$-modification, to ameliorate these issues, e.g. see [7,8,9,10,11]. Quite surprisingly, it turns out that simply using projection (onto a convex set of admissible parameters) has proved quite powerful, and the resulting controllers typically provide a bounded-noise bounded-state property, as well as tolerance of some degree of unmodelled dynamics and/or time variations, e.g. see [12,13,14,15,16,17]. Of course, it is clearly desirable that the closed-loop system exhibits LTI-like system properties, such as a bounded gain on the noise¹ and exponential stability. As far as the author is aware, in the classical approach to adaptive control a bounded gain on the noise is proven only in [12, 13]; however, a crisp exponential bound on the effect of the initial condition is not provided, and a minimum phase assumption is imposed. While it is possible to prove a form of exponential stability if the reference input is sufficiently persistently exciting, e.g. see [18], this places a stringent requirement on an exogenous input.

There are several non-classical approaches to adaptive control which provide LTI-like system properties. First of all, in [19, 20] a logic-based switching approach is used to sequence through a predefined list of candidate controllers; while exponential stability is proven, the transient behaviour can be quite poor and a bounded gain on the noise is not proven. A more sophisticated logic-based approach, labelled supervisory control, was proposed by Morse; here a supervisor switches in an efficient way between candidate controllers—see [21,22,23,24,25]. In certain circumstances a bounded gain on the noise can be proven—see [26, 27], and the Concluding Remarks section of [22]. A related approach, called localization-based switching adaptive control, uses a falsification approach to prove exponential stability as well as a degree of tolerance of disturbances, e.g. see [28].

Another non-classical approach, proposed by the first author, is based on periodic probing, estimation, and control: rather than estimate the plant or controller parameters, the goal is to estimate what the control signal would be if the plant parameters and plant state were known and the ‘optimal controller’ were applied. Exponential stability and a bounded gain on the noise are achieved, as well as near optimal performance, e.g. see [29,30,31]; a degree of unmodelled dynamics and time variations can be allowed. Roughly speaking, the idea is to estimate the ‘optimal control signal’ at every step; this differs from the classical approach to adaptive control wherein the goal is to (at best) obtain an asymptotic estimate of the ‘optimal control signal’. In order to carry out this estimation, a sampled data approximation of a differentiator is used, with optimality being achieved as the sampling period tends to zero. The drawback is that while a bounded gain on the noise is always achieved, it tends to increase dramatically the closer that one gets to optimality. Because of the nature of the approach, it only works in the continuous-time domain.

In this paper we consider the discrete-time setting and we propose an alternative approach to obtaining LTI-like system properties. We return to a common approach in classical adaptive control—the use of the projection algorithm to carry out parameter estimation together with the certainty equivalence principle. In the literature it is the norm to use a modified version of the ideal projection algorithm in order to avoid division by zero;² in this paper we prove that an unexpected consequence of this minor adjustment is that some inherent properties of the scheme have been destroyed. Here we use the original version of the projection algorithm coupled with a pole placement certainty equivalence-based controller. In the general case we impose compactness and convexity assumptions on the set of admissible parameters; however, some progress has been made at weakening the convexity requirement. We obtain linear-like convolution bounds on the closed-loop behaviour, which immediately confers exponential stability and a bounded gain on the noise; such convolution bounds are, as far as the authors are aware, a first in adaptive control, and it allows us to use a modular approach to analyse robustness and tolerance to time-varying parameters, which is a highly desirable feature. Indeed, this allows us to utilize all of the intuition that we have developed for LTI systems in the adaptive setting, something which has not been present using other techniques. To this end, the results will be presented in a very pedagogically desirable fashion: we first deal with the ideal plant (with disturbances); we then leverage that result to prove that a large degree of time variations is tolerated; we then demonstrate that the approach tolerates a degree of unmodelled dynamics, in a way familiar to those versed in the analysis of LTI systems.

In a recent short paper we consider the first-order case [32]. Here we consider the general case, which requires much more sophisticated analysis and proofs. Furthermore, in comparison to [32], here we (i) present a more general estimation algorithm, which alleviates the classical concern about dividing by zero, (ii) prove that the controller achieves the objective in the presence of a more general class of time variations, and (iii) prove robustness to unmodelled dynamics. An early version of this paper has appeared in a conference [33].

Before proceeding, we present some mathematical preliminaries. Let $\mathbf{Z}$ denote the set of integers, $\mathbf{Z}^+$ the set of non-negative integers, $\mathbf{N}$ the set of natural numbers, $\mathbf{R}$ the set of real numbers, and $\mathbf{R}^+$ the set of non-negative real numbers. We let ${\mathbf{D}}^0$ denote the open unit disc of the complex plane. We use the Euclidean 2-norm for vectors and the corresponding induced norm for matrices, and denote the norm of a vector or matrix by $\Vert \cdot \Vert$. We let ${l_{\infty }}( \mathbf{R}^n)$ denote the set of $\mathbf{R}^n$-valued bounded sequences; we define the norm of $u \in {l_{\infty }}( \mathbf{R}^n)$ by $\Vert u \Vert _{\infty } := \sup _{k \in \mathbf{Z}} \Vert u(k) \Vert$. Occasionally, we will deal with a map $F: {l_{\infty }}( \mathbf{R}^n) \rightarrow {l_{\infty }}( \mathbf{R}^n)$; the gain is given by $\sup _{ u \ne 0 } \frac{\Vert Fu \Vert _{\infty }}{\Vert u \Vert _{\infty } }$ and denoted by $\Vert F \Vert$. With $T \in \mathbf{Z}$, the truncation operator $P_T: {l_{\infty }}( \mathbf{R}^n) \rightarrow {l_{\infty }}( \mathbf{R}^n)$ is defined by

$$\begin{aligned} (P_T x) (t) = \left\{ \begin{array}{ll} x(t) &{} \quad {t \le T} \\ 0 &{} \;\; t > T. \end{array} \right. \end{aligned}$$

We say that the map $F: {l_{\infty }}( \mathbf{R}^n) \rightarrow {l_{\infty }}( \mathbf{R}^n)$ is causal if $P_T F P_T = P_T F$ for every $T \in \mathbf{Z}$.

If ${{\mathcal {S}}} \subset \mathbf{R}^p$ is a convex and compact set, we define $\Vert {{\mathcal {S}}} \Vert := \max _{x \in {{\mathcal {S}}} } \Vert x \Vert$ and the function $\pi _{{\mathcal {S}}} : \mathbf{R}^p \rightarrow {{\mathcal {S}}}$ denotes the projection onto ${{\mathcal {S}}}$; it is well known that $\pi _{{\mathcal {S}}}$ is well defined.

2 The setup

In this paper we start with an nth-order linear time-invariant discrete-time plant given by

$$\begin{aligned} y(t+1)= & {} - \sum _{i=0}^{n-1} a_{i+1} y(t-i) + \sum _{i=0}^{n-1} b_{i+1} u(t-i) + d(t) \nonumber \\= & {} \underbrace{ \left[ \begin{array}{cccccc} y(t)&\cdots&y(t-n+1)&u(t)&\cdots&u(t-n+1) \end{array} \right] }_{=: \phi (t)^T} \underbrace{ \left[ \begin{array}{c} -a_1 \\ \vdots \\ -a_n \\ b_1\\ \vdots \\ b_n \end{array} \right] }_{=: \theta ^*} + d(t) , \nonumber \\ \;\;\;\;\;\; \phi (t_0)= & {} \phi _0 , \quad t \ge t_0 , \end{aligned}$$

(1)

with $y(t) \in \mathbf{R}$ being the measured output, $u(t) \in \mathbf{R}$ the control input, $\phi (t)$ a vector of input–output data, and $d(t) \in \mathbf{R}$ the disturbance (or noise) input. We assume that $\theta ^*$ is unknown but belongs to a known set ${{\mathcal {S}}} \subset \mathbf{R}^{2n}$. Associated with this plant model are the polynomials

$$\begin{aligned} A(z^{-1} ) := 1 + a_1 z^{-1} + \cdots + a_n z^{-n} , \quad B(z^{-1} ) := b_1 z^{-1} + \cdots + b_n z^{-n} \end{aligned}$$

and the transfer function $\frac{B(z^{-1} )}{A(z^{-1} )}$.

Remark 1

It is straightforward to verify that if the system has a disturbance at both the input and output, then it can be converted to a system of the above form.

We impose an assumption on the set of admissible plant parameters.

The convexity part of the above assumption is common in a branch of the adaptive control literature—it is used to facilitate constrained parameter estimation, e.g. see [34], and it is a key assumption in arguably the simplest technique to ensuring that the associated pole placement adaptive controller has tolerance to a degree of unmodelled dynamics and to noise, e.g. see [12,13,14,15,16,17, 35]. That being said, in Sect. 8 we will show that it is possible to weaken this to assuming that $\theta ^* \in {{\mathcal {S}}}_1 \cup {{\mathcal {S}}}_2$ with each $S_i$ convex and compact, and for each $\theta ^* \in {{\mathcal {S}}}_1 \cup {{\mathcal {S}}}_2$, the corresponding pair of polynomials $A(z^{-1} )$ and $B(z^{-1} )$ are coprime; however, we will require that all closed-loop poles be placed at zero, and a more complicated controller will be required. The boundedness part of the assumption is less common, but it is quite reasonable in practical situations; it is used here to ensure that we can prove uniform bounds and decay rates on the closed-loop behaviour.

The main goal here is to prove a form of stability, with a secondary goal that of asymptotic tracking of an exogenous reference signal $y^* (t)$; since the plant may be non-minimum phase, there are limits on how well the plant can be made to track $y^*(t)$. To proceed, we use a parameter estimator together with an adaptive pole placement control law. At this point, we discuss the most critical aspect—the parameter estimator.

2.1 Parameter estimation

We can write the plant as

$$\begin{aligned} y(t+1) = \phi (t)^T \theta ^* + d(t) . \end{aligned}$$

Given an estimate ${\hat{\theta }} (t)$ of $\theta ^*$ at time t, we define the prediction error by

$$\begin{aligned} e(t+1) := y(t+1) - \phi (t)^T {\hat{\theta }} (t) ; \end{aligned}$$

this is a measure of the error in ${\hat{\theta }} (t)$. The common way to obtain a new estimate is from the solution of the optimization problem

$$\begin{aligned} \hbox {argmin}_{\theta } \{ \Vert \theta - {\hat{\theta }} (t) \Vert : y(t+1) = \phi (t)^T {\theta } \} , \end{aligned}$$

yielding the ideal (projection) algorithm

$$\begin{aligned} \hat{\theta }(t+1) = \left\{ \begin{array}{ll} \hat{\theta }(t) &{} \text{ if }~ {\phi (t) = 0 } \\ \hat{\theta }(t) + \frac{\phi (t)}{\phi (t)^T \phi (t)} \, e (t+1) &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(2)

Of course, if $\phi (t)$ is close to zero, numerical problems can occur, so it is the norm in the literature (e.g. [3, 34]) to replace this by the following classical algorithm: with $0< \alpha < 2$ and $\beta > 0$, define³

$$\begin{aligned} \hat{\theta }(t+1) = \hat{\theta }(t) + \frac{\alpha \phi (t)}{ \beta + \phi (t)^T \phi (t)} e(t+1) . \end{aligned}$$

(3)

This latter algorithm is widely used and plays a role in many discrete-time adaptive control algorithms; however, when this algorithm is used, all of the results are asymptotic, and exponential stability and a bounded gain on the noise are never proven. It is not hard to guess why—a careful look at the estimator shows that the gain on the update law is small if $\phi (t)$ is small. A more mathematically detailed argument is given in the following example.

Remark 2

Consider the simple first-order plant

$$\begin{aligned} y(t+1)= - a_1 y(t) + b_1 u(t) + d(t) \end{aligned}$$

with $a_1 \in [-2, -1]$ and $b_1 \in [1,2]$. We use the estimator (3) with $\alpha \in (0,2)$ and $\beta >0$, and, as in [12,13,14,15,16,17], we use projection to keep the parameters estimates inside ${{\mathcal {S}}}$ so as to guarantee a bounded-input bounded-state property. Further suppose that $y^*=d=0$, and that a classical pole placement adaptive controller places the closed-loop pole at zero: $u(t) = {\frac{{\hat{a}}_1 (t)}{ {\hat{b}}_1 (t)}} y(t) =: {\hat{f}} (t) y(t)$. Suppose that

$$\begin{aligned} y(0) = y_0 = {\varepsilon }\in (0,1), \quad {\hat{\theta }} (0) = \left[ \begin{array}{c} - {\hat{a}}_1 (0) \\ {\hat{b}}_1 (0) \end{array} \right] = \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] , \quad \theta ^* = \left[ \begin{array}{c} 2 \\ 1 \end{array} \right] \end{aligned}$$

so that ${\hat{f}} (0) = - 0.5$ and $-a_1 + b_1 {\hat{f}} (0 ) = 1.5$, i.e. the system is initially unstable. An easy calculation verifies that ${\hat{f}} (t) \in [-2, - 0.5]$ and $- a_1 + b_1 {\hat{f}} (t) \in [ 0, 1.5 ]$ for $t \ge 0$, which leads to a crude bound on the closed-loop behaviour: $| y(t) | \le (1.5)^t {\varepsilon }$ for $t \ge 0$. With $N( {\varepsilon }) := \text{ int } [ \frac{1}{2 \ln (1.5)} \ln ( \frac{1}{{\varepsilon }} ) ]$, it follows that

$$\begin{aligned} | y(t) | \le {\varepsilon }^{1/2} , \quad t \in [0, N( {\varepsilon }) ] . \end{aligned}$$

A careful examination of the parameter estimator shows that

$$\begin{aligned} \Vert {\hat{\theta }} (t) - \theta _0 \Vert \le 20 (2)^{1/2} \frac{{\varepsilon }}{\beta } , \quad t \in [0, N( {\varepsilon }) ] . \end{aligned}$$

From the form of ${\hat{f}} (t)$, it is easy to prove that if $\frac{{\varepsilon }}{\beta }$ is small enough,⁴ then we have $| -a + b_1 {\hat{f}} (t) | \ge 1.25$ for $t \in [0, N( {\varepsilon }) ]$, in which case

$$\begin{aligned} | y (N({\varepsilon }) ) | \ge ( 1.25 )^{N({\varepsilon })} {\varepsilon }\;\; \Rightarrow \;\; \left| \frac{y ( N( {\varepsilon }))}{{\varepsilon }} \right| = \left| \frac{y ( N( {\varepsilon }))}{y(0) } \right| \ge (1.25)^{N({\varepsilon })} ; \end{aligned}$$

since $N({\varepsilon }) \rightarrow \infty$ as ${\varepsilon }\rightarrow 0$, we see that exponential stability is not achieved. A similar kind of analysis can be used to prove that a bounded gain on the noise is not achieved either.

Now we return to the problem at hand—analysing the ideal algorithm (2). We will be using the ideal algorithm with projection to ensure that the estimate remains in ${{\mathcal {S}}}$ for all time. With an initial condition of ${\hat{\theta }} (t_0) = \theta _0 \in {{\mathcal {S}}}$, for $t \ge t_0$ we set

$$\begin{aligned} {\check{\theta }} (t+1) = \left\{ \begin{array}{ll} {\hat{\theta }} (t) &{} \;\; \text{ if }~ {\phi (t) = 0 } \\ \hat{\theta }(t) + \frac{\phi (t)}{\phi (t)^T \phi (t)} \, e (t+1) &{} \;\; \text{ otherwise, } \end{array} \right. \end{aligned}$$

(4)

which we then project onto ${{\mathcal {S}}}$:

$$\begin{aligned} {\hat{\theta }} (t+1):= \pi _{{\mathcal {S}}} ( {\check{\theta }} (t+1) ). \end{aligned}$$

(5)

Because of the closed and convex property of ${{\mathcal {S}}}$, the projection function is well defined; furthermore, it has the nice property that, for every $\theta \in \mathbf{R}^{2n}$ and every $\theta ^* \in {{\mathcal {S}}}$, we have

$$\begin{aligned} \Vert \pi _{{\mathcal {S}}} ( \theta ) - \theta ^* \Vert \le \Vert \theta - \theta ^* \Vert , \end{aligned}$$

i.e. projecting $\theta$ onto ${{\mathcal {S}}}$ never makes it further away from the quantity $\theta ^*$.

2.2 Revised parameter estimation

Some readers may be concerned that the original problem of dividing by a number close to zero, which motivates the use of classical algorithm, remains. Of course, this is balanced against the soon-to-be-proved benefit of using (4)–(5). We propose a middle ground as follows. A straightforward analysis of $e(t+1)$ reveals that

$$\begin{aligned} e(t+1) = - \phi (t)^T [ {\hat{\theta }} (t) - \theta ^* ] + d (t) , \end{aligned}$$

which means that

$$\begin{aligned} | e(t+1) | \le 2 \Vert {{\mathcal {S}}} \Vert \times \Vert \phi (t) \Vert + | d(t) | . \end{aligned}$$

Therefore, if

$$\begin{aligned} | e(t+1) | > 2 \Vert {{\mathcal {S}}} \Vert \times \Vert \phi (t) \Vert , \end{aligned}$$

then the update to ${\hat{\theta }} (t)$ will be greater than $2 \Vert {{\mathcal {S}}} \Vert$, which means that there is little information content in $e(t+1)$—it is dominated by the disturbance. With this as motivation, and with $\delta \in (0, \infty ]$, let us replace (4) with

$$\begin{aligned} {\check{\theta }} (t+1) = \left\{ \begin{array}{ll} \hat{\theta }(t) + \frac{\phi (t)}{\phi (t)^T \phi (t)} \, e (t+1) &{} \quad \text{ if }~ {| e(t+1) | < ( 2 \Vert {{\mathcal {S}}} \Vert + \delta ) \Vert \phi (t) \Vert } \\ {\hat{\theta }} (t) &{} \quad \text{ otherwise; } \end{array} \right. \end{aligned}$$

(6)

in the case of $\delta = \infty$, we will adopt the understanding that $\infty \times 0 = 0$, in which case the above formula collapses into the original one (4). In the case that $\delta < \infty$, we can be assured that the update term is bounded above by $2 \Vert {{\mathcal {S}}} \Vert + \delta$, which should alleviate concerns about having infinite gain. We would now like to rewrite the update to make it more concise. To this end, we now define ${\rho _{\delta }}: \mathbf{R}^{2n} \times \mathbf{R}\rightarrow \{ 0,1 \}$ by

$$\begin{aligned} {\rho _{\delta }}( \phi (t) , e (t+1) ) := \left\{ \begin{array}{ll} 1 &{} \quad \text{ if } | e(t+1) | < ( 2 \Vert {{\mathcal {S}}} \Vert + \delta ) \Vert \phi (t) \Vert \\ 0 &{} \quad \text{ otherwise, } \end{array} \right. \end{aligned}$$

yielding a more concise way to write the estimation algorithm update:

$$\begin{aligned} {\check{\theta }} (t+1) = {\hat{\theta }} (t) + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ \phi (t)}{ \phi (t)^T \phi (t)} e(t+1) ; \end{aligned}$$

(7)

once again, we project this onto ${{\mathcal {S}}}$:

$$\begin{aligned} {\hat{\theta }} (t+1):= \pi _{{\mathcal {S}}} ( {\check{\theta }} (t+1) ). \end{aligned}$$

(8)

Remark 3

If the disturbance $d( t )=0$, then the estimation algorithm (7)–(8) has a nice scaling property. In this case, if $\phi (t) \ne 0$ then ${\rho _{\delta } ( \phi (t) , e(t+1))}=1$, so (7) becomes

$$\begin{aligned} {\check{\theta }} (t+1) = {\hat{\theta }} (t) + \frac{ \phi (t) \phi (t)^T}{ \phi (t)^T \phi (t)} [ \theta ^* - {\hat{\theta }} (t) ]; \end{aligned}$$

so if $\phi (t)$ is replaced by $\gamma \phi (t)$ with $\gamma \ne 0$, then ${\check{\theta }} (t+1)$ (and ${\hat{\theta }} (t+1)$) remains the same. Hence, scaling the pair (y(t), u(t)) makes no difference to the estimator, which is clearly a desirable feature; notice that the classical algorithm (3) does not enjoy that property. This is the first clue that this algorithm may provide closed-loop properties not provided by the classical algorithm (3).

2.3 Properties of the estimation algorithm

Analysing the closed-loop system behaviour will require a careful examination of the estimation algorithm. We define the parameter estimation error by

$$\begin{aligned} {\tilde{\theta }} (t): = {\hat{\theta }} (t) - \theta ^* , \end{aligned}$$

and the corresponding Lyapunov function associated with ${\tilde{\theta }} (t)$, namely $V(t) : = {\tilde{\theta }} (t)^T {\tilde{\theta }} (t)$. In the following result we list a property of V(t); it is a generalization of what is well known for the classical algorithm (3).

Proof

See Appendix. $\square$

2.4 The control law

The elements of ${\hat{\theta }} (t)$ are partitioned in a natural way as

$$\begin{aligned} {\hat{\theta }} (t) =: \left[ \begin{array}{cccccc} - {\hat{a}}_1 (t)&\cdots&- {\hat{a}}_n (t)&{\hat{b}}_1 (t)&\cdots&{\hat{b}}_n (t) \end{array} \right] ^T . \end{aligned}$$

Associated with ${\hat{\theta }} (t)$ are the polynomials

$$\begin{aligned} {\hat{A}} (t, z^{-1} ):= & {} 1 + {\hat{a}}_1 (t) z^{-1} + \cdots + {\hat{a}}_n (t) z^{-n} , \\ {\hat{B}}(t,z^{-1} ):= & {} {\hat{b}}_1 (t) z^{-1} + \cdots + {\hat{b}}_n (t) z^{-n} . \end{aligned}$$

While we can use an $(n-1)$th-order proper controller to carry out pole placement, it will be convenient to use an nth-order strictly proper controller, such as in [15, 16, 36,37,38]. In particular, we first choose a 2nth-order monic polynomial

$$\begin{aligned} A^* (z^{-1} ) = 1 + a_1^* z^{-1} + \cdots + a_{2n}^* z^{-2n} \end{aligned}$$

so that $z^{2n} A^* (z^{-1} )$ has all of its zeros in ${\mathbf{D}}^o$. Next, we choose two polynomial

$$\begin{aligned} {\hat{L}} (t, z^{-1} )= & {} 1 + {\hat{l}}_1 (t) z^{-1} + \cdots + {\hat{l}}_n (t) z^{-n} \\&\text{ and } \quad {\hat{P}} (t,z^{-1} ) = {\hat{p}}_1 (t) z^{-1} + \cdots + {\hat{p}}_n (t) z^{-n} \end{aligned}$$

which satisfy the equation

$$\begin{aligned} {\hat{A}} ( t , z^{-1} ) {\hat{L}} (t, z^{-1} ) + {\hat{B}} ( t , z^{-1} ) {\hat{P}} (t,z^{-1} ) = A^* ( z^{-1} ) ; \end{aligned}$$

(10)

given the assumption that the ${\hat{A}} ( t , z^{-1} )$ and ${\hat{B}} ( t , z^{-1} )$ are coprime, it is well known that there exist unique ${\hat{L}} (t, z^{-1} )$ and ${\hat{P}} (t,z^{-1} )$ which satisfy this equation. Indeed, it is easy to prove that the coefficients of ${\hat{L}} (t, z^{-1} )$ and ${\hat{P}} (t,z^{-1} )$ are analytic functions of ${\hat{\theta }} (t) \in {{\mathcal {S}}}$.

In our setup we have an exogenous signal $y^* (t)$. At time t we choose u(t) so that

$$\begin{aligned} u(t)= & {} - {\hat{l}}_1 (t-1) u(t-1) - \cdots - {\hat{l}}_n (t-1) u(t-n) \nonumber \\&- {\hat{p}}_1 (t-1) [ y(t-1)- y^* (t-1) ]\nonumber \\&- \cdots - {\hat{p}}_n (t-1) [ y(t-n)- y^* (t-n) ] . \end{aligned}$$

(11)

So the overall controller consists of the estimator (7)–(8) together with (11).⁵

It turns out that we can write down a state-space model of our closed-loop system with $\phi (t) \in \mathbf{R}^{2n}$ as the state. Proceeding as in Kreisselmeier [37], only two elements of $\phi$ have a complicated description:

$$\begin{aligned} \phi _1 (t+1)= & {} y(t+1) = e(t+1) + {\hat{\theta }} (t)^T \phi (t) ,\\ \phi _{n+1}(t+1)= & {} u(t+1) = - \sum _{i=1}^{n} \left\{ {\hat{l}}_i (t) u(t+1-i) + {\hat{p}}_i (t) [ y(t+1-i) - y^* (t+1-i) ] \right\} \\= & {} \left[ \begin{array}{cccccc} - {\hat{l}}_1 (t)&\cdots&- {\hat{l}}_n (t)&- {\hat{p}}_1 (t)&\cdots&- {\hat{p}}_n (t) \end{array} \right] \phi (t) + \sum _{i=1}^n {\hat{p}}_i (t) y^* ( t+1 - i ) . \end{aligned}$$

With $e_i \in \mathbf{R}^{2n}$ the ith normal vector, if we now define

$$\begin{aligned} {\bar{A}} (t) := \left[ \begin{array}{cccccccc} -{\hat{a}}_1 (t) &{} -{\hat{a}}_2 (t) &{} \cdots &{} -{\hat{a}}_n (t) &{} {\hat{b}}_1 (t) &{} \cdots &{} \cdots &{} {\hat{b}}_n (t) \\ 1 &{} 0 &{} \cdots &{} 0 &{} 0 &{} \cdots &{} \cdots &{} 0 \\ &{} \ddots &{} &{} \vdots &{} \vdots &{} \cdots &{} \cdots &{} \vdots \\ &{} &{} 1 &{} 0 &{} 0 &{} \cdots &{} \cdots &{} 0 \\ - {\hat{p}}_1 (t) &{} - {\hat{p}}_2 (t) &{} \cdots &{} -{\hat{p}}_n (t) &{} - {\hat{l}}_1 (t) &{} -{\hat{l}}_2 (t) &{} \cdots &{} - {\hat{l}}_n (t) \\ 0 &{} \cdots &{} \cdots &{} 0 &{} 1 &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \cdots &{} \cdots &{} \vdots &{} &{} \ddots &{} &{} \vdots \\ 0 &{} \cdots &{} \cdots &{} 0 &{} &{} &{} 1 &{} 0 \end{array} \right] , \end{aligned}$$

$$\begin{aligned} B_1:= e_1 , \quad B_2 := e_{n+1} , \quad r(t) := \sum _{i=1}^{n} {\hat{p}}_i (t) y^* (t+1-i) , \end{aligned}$$

(12)

then the following key equation holds:

$$\begin{aligned} \phi (t+1) = {\bar{A}} (t) \phi (t) + B_1 e(t+1) + B_2 r(t) ; \end{aligned}$$

(13)

notice that the characteristic equation of ${\bar{A}} (t)$ always equals $z^{2n} A^* ( z^{-1} )$. Before proceeding, define

$$\begin{aligned} {\bar{a}} := \max \{ \Vert {\bar{A}} ( {\hat{\theta }} ) \Vert : {\hat{\theta }} \in {{\mathcal {S}}} \} . \end{aligned}$$

Remark 4

While the proposed adaptive controller (7)–(8) together with (11) is nonlinear, when it is applied to the plant the closed-loop system enjoys the homogeneity property. More precisely, fix the initial parameter estimate $\theta _0$ and starting time $t_0 \in \mathbf{Z}$; suppose that an initial condition, reference signal, and disturbance signal combination $( \phi _0, r, d)$ yields a system response of $\phi$, and with $\gamma \in \mathbf{R}$ suppose that an initial condition, reference signal, and disturbance signal combination of $( \gamma \phi _0, \gamma r, \gamma d)$ yields a system response of $\phi ^{\gamma }$. Using induction it is easy to prove that⁶

$$\begin{aligned} \phi ^{\gamma } (t) = \gamma \phi (t) , \; t \ge t_0 . \end{aligned}$$

Hence, with minimal effort we see that the closed-loop behaviour enjoys one of the two required properties of a linear system, namely that of homogeneity. While it does not enjoy the other property needed for linearity, we will soon see that we are still able to prove linear-like convolution bounds on the closed-loop behaviour.

3 Preliminary analysis

The closed-loop system given in (13) arises in classical adaptive control approaches in slightly modified fashion, so we will borrow some tools from there. More specifically, the following result was proven by Kreisselmeier [37], in the context of proving that a slowly time-varying adaptive control system is stable (in a weak sense); we are providing a special case of his technical lemma to minimize complexity.⁷

Remark 5

We apply the above proposition in the following way. Suppose that $\sigma \in (0,1)$, $\gamma _1 >1$, $\alpha _i \ge 0$, $\beta _i \ge 0$ are such conditions (i) and (ii) hold. If $\mu \in ( \sigma , 1 )$, then it follows that $\frac{\mu }{\gamma _1^{1/N}} - \sigma > 0$ for large enough $N \in \mathbf{N}$, so condition (iii) will hold as well as long as $\alpha _2$ and $\beta _2$ are small enough.

In applying Proposition 2, the matrix ${\bar{A}} (t)$ will play the role of $A_{nom} (t)$. A key requirement is that Condition (i) holds: the following provides relevant bounds. Before proceeding, let

$$\begin{aligned} {\underline{\lambda }} \; := \; \max \{ | \lambda | : \lambda \; \text{ is } \text{ a } \text{ root } \text{ of } z^{2n} A^* (z^{-1}) \}. \end{aligned}$$

Proof

See Appendix. $\square$

4 The main result

Remark 6

We see from (12) that r(t) is a weighted sum of $\{ y^* (t) ,..., y^* ( t-n+1 ) \}$. Hence, there exists a constant ${\bar{c}}$ so that the bound (14) can be rewritten as

$$\begin{aligned} \Vert \phi (k) \Vert \le c \lambda ^{k- t_0} \Vert \phi _0 \Vert + \sum _{j=t_0-n+1}^{k-1} {\bar{c}} \lambda ^{k-1-j} | y^*(j)| + \sum _{j=t_0}^{k-1} c \lambda ^{k-1-j} | d (j) | , \;\; k \ge t_0 . \end{aligned}$$

Remark 7

Theorem 1 implies that the system has a bounded gain (from d and r to y) in every $p-$norm. More specifically, for $p= \infty$ we see immediately from (14) that

$$\begin{aligned} \Vert \phi (k) \Vert \le c \Vert \phi _0 \Vert + \frac{c}{1- \lambda } \sup _{ \tau \in [t_0 , k] } [ | r( \tau ) | + | d( \tau ) | ) ] , \;\; k \ge t_0 . \end{aligned}$$

Furthermore, for $1 \le p < \infty$ it follows from Young’s Inequality applied to (14) that

$$\begin{aligned}&\left[ \sum _{j=t_0}^k \Vert \phi (j) \Vert ^p \right] ^{1/p} \le \frac{c}{(1 - \lambda ^p)^{1/p}} \Vert \phi _0 \Vert \\&+ \frac{c}{1 - \lambda } \left\{ \left[ \sum _{j=t_0}^k \Vert r (j) \Vert ^p \right] ^{1/p} + \left[ \sum _{j=t_0}^k \Vert d (j) \Vert ^p \right] ^{1/p} \right\} , \; k \ge t_0 . \end{aligned}$$

Remark 8

Most pole placement adaptive controllers are proven to yield a weak form of stability, such as boundedness (in the presence of a nonzero disturbance) or asymptotic stability (in the case of a zero disturbance), which means that details surrounding initial conditions can be ignored. Here the goal is to prove a stronger, linear-like, convolution bound, so it requires a more detailed and nuanced analysis. A key tool is Proposition 2, which was introduced by Kreisselmeier [37] to analyse slowly time-varying adaptive pole placement problems. It has been used in a number of places in the adaptive control literature, including the work of [15, 16, 35], all of whom utilize the classical projection algorithm (3). However, as pointed out in Remark 2, an adaptive controller based on the classical projection algorithm (3) does not, in general, provide exponential stability or a bounded gain on the noise, regardless of how small the parameter $\beta >0$ is; indeed, what is proven in [15, 16] is that for every set of initial conditions and every pair of exogenous disturbance and reference signal inputs, the state $\phi (t)$ is bounded, i.e. the system enjoys the bounded-input bounded-state property. What is surprising and unexpected is that for $\beta =0$, the closed-loop system enjoys much nicer properties, and clearly this does not follow in any obvious way by taking the limit as $\beta \rightarrow 0$ of what is proven in the classical setup of [15, 16].

Remark 9

The approach taken in our proof is motivated by our earlier work on the first-order one-step-ahead adaptive controller [32]; here we use Kreisselmeier’s result on time-varying systems given in Proposition 2 in place of a lemma used in [32] for time-varying first-order systems. While the layout of our proof has a superficial similarity to that to [15, 16], in that we both partition the timescale in terms of the size of state (in the case of [15, 16]) or the size of the disturbance scaled by the state (here), on closer inspection it is clear that they differ significantly.

Remark 10

With ${\hat{G}} (t, z^{-1} ) =\sum _{i=1}^{2n} {\hat{g}}_i (t) z^{-i} := {\hat{B}} (t, z^{-1} ) {\hat{P}} (t,z^{-1} )$ it is possible to use arguments like those in [34] to prove, when the disturbance d is identically zero, a weak tracking result of the form

$$\begin{aligned} \lim _{t \rightarrow \infty } \left[ \sum _{i=0}^{2n} a_i^* y(t-i) - \sum _{i=1}^{2n} {\hat{g}}_i (t) y^* ( t-i) \right] = 0 . \end{aligned}$$

Since the main goal of the paper is on stability issues, we omit the proof. However, we do discuss step tracking in a later section.

Proof

Fix $\delta \in (0, \infty ]$ and $\lambda \in ( {\underline{\lambda }}, 1)$. Let $t_0 \in \mathbf{Z}$, $\theta _0 \in {{\mathcal {S}}}$, $\theta ^* \in {{\mathcal {S}}}$, $\phi _0 \in \mathbf{R}^{2n}$, and $y^*, d\in {l_{\infty }}$ be arbitrary. Define r via (12). Now choose $\lambda _1 \in ( {\underline{\lambda }} , \lambda )$.

We have to be careful in how to apply Proposition 2 to (13)—we need the $\Delta (t)$ term to be something which we can bound using Proposition 1. So define

$$\begin{aligned} \Delta (t):= {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{e(t+1)}{\Vert \phi (t) \Vert ^2} B_1 \phi (t)^T ; \end{aligned}$$

(15)

it is easy to check that

$$\begin{aligned} \Delta (t) \phi (t) = {\rho _{\delta } ( \phi (t) , e(t+1))}B_1 e(t+1) \end{aligned}$$

and that

$$\begin{aligned} \Vert \Delta (t) \Vert = {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{| e(t+1)|}{\Vert \phi (t) \Vert } , \end{aligned}$$

which is a term which plays a key role in Proposition 1. We can now rewrite (13) as

$$\begin{aligned} \phi (t+1) = [ {\bar{A}} (t) + \Delta (t) ] \phi (t) + B_1 \underbrace{[ 1 - {\rho _{\delta } ( \phi (t) , e(t+1))}] e(t+1) }_{=: \eta (t)} + B_2 r(t) . \nonumber \\ \end{aligned}$$

(16)

If ${\rho _{\delta } ( \phi (t) , e(t+1))}=1$ then $\eta (t) =0$, but if ${\rho _{\delta } ( \phi (t) , e(t+1))}= 0$ then

$$\begin{aligned} | e(t+1) | \ge ( 2 \Vert {{\mathcal {S}}} \Vert + \delta ) \Vert \phi (t) \Vert ; \end{aligned}$$

but we also know that

$$\begin{aligned} e(t+1) = - {\tilde{\theta }} (t) \phi (t) + d(t) \; \Rightarrow \; | e(t+1) | \le 2 \Vert {{\mathcal {S}}} \Vert \times \Vert \phi (t) \Vert + | d(t) | ; \end{aligned}$$

(17)

combining these equations we have

$$\begin{aligned} ( 2 \Vert {{\mathcal {S}}} \Vert + \delta ) \Vert \phi (t) \Vert \le 2 \Vert {{\mathcal {S}}} \Vert \times \Vert \phi (t) \Vert + | d(t) | , \end{aligned}$$

which implies that $\Vert \phi (t) \Vert \le \frac{1}{\delta } | d(t) |$; it is easy to check that this holds even when $\delta = \infty$. Using (17) we conclude that

$$\begin{aligned} | \eta (t) | \le \left( \frac{2 \Vert {{\mathcal {S}}} \Vert }{\delta } +1 \right) | d(t) | , \quad t \ge t_0 . \end{aligned}$$

(18)

We now analyse (16). We let $\Phi (t, \tau )$ denote the transition matrix associated with ${\bar{A}} (t) + \Delta (t)$; this matrix clearly implicitly depends on $\theta _0$, $\theta ^*$, d and r. From Lemma 1 there exists a constant $\gamma _1$ so that

$$\begin{aligned} \Vert {\bar{A}} (t)^i \Vert \le \gamma _1 \lambda _1^i, \;\; i \ge 0, \; t \ge t_0 , \end{aligned}$$

(19)

and for every $t > k \ge t_0$, we have

$$\begin{aligned}&\sum _{j=k}^{t-1} \Vert {\bar{A}} (j+1) - {\bar{A}} (j) \Vert \nonumber \\&\le \gamma _1 \left[ \sum _{j=k}^{t-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ | e(j+1)|^2}{ \Vert \phi (j) \Vert ^2 } \right] ^{1/2} ( t-k)^{1/2} . \end{aligned}$$

(20)

Using the definition of $\Delta$ given in (15) and the Cauchy–Schwarz inequality, we also have

$$\begin{aligned}&\sum _{j=k}^{t-1} \Vert \Delta (j) \Vert \nonumber \\&\le \left[ \sum _{j=k}^{t-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ | e(j+1)|^2}{ \Vert \phi (j) \Vert ^2 } \right] ^{1/2} ( t-k)^{1/2} , \; t > k \ge t_0 . \end{aligned}$$

(21)

At this point we consider two cases: the easier case in which there is no noise, and the harder case in which there is noise.

Case 1: $d(t) = 0$, $t \ge t_0$.

Using the bound on $\eta (t)$ given in (18), in this case (16) becomes

$$\begin{aligned} \phi (t+1) = [ {\bar{A}} (t) + \Delta (t)] \phi (t) + B_2 r(t), \quad t \ge t_0 . \end{aligned}$$

(22)

The bound on V(t) given by Proposition 1 simplifies to

$$\begin{aligned} V(t) \le V ( t_0 ) - \frac{1}{2} \sum _{j=t_0}^{t-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ [e(j+1)]^2}{ \Vert \phi (j) \Vert ^2} , \quad t \ge t_0 +1 . \end{aligned}$$

Since $V( \cdot ) \ge 0$ and $V( t_0 ) = \Vert \theta _0 - \theta ^* \Vert ^2 \le 4 \Vert {{\mathcal {S}}} \Vert ^2$, this means that

$$\begin{aligned} \sum _{j=t_0}^{t-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ [e(j+1)]^2}{\Vert \phi (j)\Vert ^2} \le 2 V( t_0 ) \le 8 \Vert {{\mathcal {S}}} \Vert ^2. \end{aligned}$$

Hence, from (20) and (21) we conclude that

$$\begin{aligned}&\sum _{j=k}^{t-1} \Vert {\bar{A}} (j+1) - {\bar{A}} (j) \Vert \le 8^{1/2} \gamma _1 \Vert {{\mathcal {S}}} \Vert ( t-k)^{1/2} ,\\&\sum _{j=k}^{t-1} \Vert \Delta (j) \Vert \le 8^{1/2} \Vert {{\mathcal {S}}} \Vert ( t-k)^{1/2} , \; t > k \ge t_0 . \end{aligned}$$

Now we apply Proposition 2: we set

$$\begin{aligned} \alpha _0 = \beta _0 = \alpha _2 = \beta _2 = 0 , \quad \alpha _1 = 8^{1/2} \gamma _1 \Vert {{\mathcal {S}}} \Vert , \quad \beta _1 = 8^{1/2} \Vert {{\mathcal {S}}} \Vert , \quad \mu = \lambda . \end{aligned}$$

Following Remark 3 it is now trivial to choose $N \in \mathbf{N}$ so that $\frac{\lambda }{ \gamma _1^{1/N}} - \lambda _1 > 0$, namely

$$\begin{aligned} N = \text{ int } \left[ \frac{\ln ( \gamma _1 )}{\ln ( \lambda ) - \ln ( \lambda _1 ) } \right] + 1 , \end{aligned}$$

(23)

which means that

$$\begin{aligned} 0 = \alpha _2 + \frac{\beta _2}{N} < \frac{1}{N \gamma _1 } \left( \frac{\lambda }{ \gamma _1^{1/N}} - \lambda _1 \right) . \end{aligned}$$

From Proposition 2 we see that there exists a constant $\gamma _2$ so that the state transition matrix $\Phi ( t, \tau )$ corresponding to ${\bar{A}} (t) + \Delta (t)$ satisfies

$$\begin{aligned} \Vert \Phi (t, \tau ) \Vert \le \gamma _2 \lambda ^{t - \tau } , \quad t \ge \tau \ge t_0 . \end{aligned}$$

If we now apply this to (22), we end up with the desired bound:

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _2 \lambda ^{k- t_0} \Vert \phi ( t_0) \Vert + \sum _{j=t_0}^{k-1} \gamma _2 \lambda ^{k-1-j} | r (j) | , \quad k \ge t_0 . \end{aligned}$$

Case 2: $d(t) \ne 0$ for some $t \ge t_0$.

This case is much more involved since noise can radically affect parameter estimation. Indeed, even if the parameter estimate is quite accurate at a point in time, the introduction of a large noise signal (large relative to the size of $\phi (t)$) can create a highly inaccurate parameter estimate. To proceed, we partition the timeline into two parts: one in which the noise is small versus $\phi$ and one where it is not; the actual choice of the line of division will become clear as the proof progresses. To this end, with ${\varepsilon }>0$ to be chosen shortly, partition $\{ j \in \mathbf{Z}: j \ge t_0 \}$ into two sets:

$$\begin{aligned} S_{\mathrm{good}}:= & {} \left\{ j \ge t_0 : \phi (j) \ne 0 \text{ and } \frac{[ d(j)]^2}{ \Vert \phi (j) \Vert ^2} < {\varepsilon }\right\} , \\ \;\; S_{\mathrm{bad}}:= & {} \left\{ j \ge t_0 : \phi (j) = 0 \text{ or } \frac{[ d(j)]^2}{ \Vert \phi (j) \Vert ^2} \ge {\varepsilon }\right\} ; \end{aligned}$$

clearly $\{ j \in \mathbf{Z}: \;\; j \ge t_0 \} = S_{\mathrm{good}} \cup S_{\mathrm{bad}}$. Observe that this partition clearly depends on $\theta _0$, $\theta ^*$, $\phi _0$, d and $r/y^*$. We will apply Proposition 2 to analyse the closed-loop system behaviour on $S_{\mathrm{good}}$; on the other hand, we will easily obtain bounds on the system behaviour on $S_{\mathrm{bad}}$. Before doing so, we partition the time index $\{ j \in \mathbf{Z}: j \ge t_0 \}$ into intervals which oscillate between $S_{\mathrm{good}}$ and $S_{\mathrm{bad}}$. To this end, it is easy to see that we can define a (possibly infinite) sequence of intervals of the form $[ k_i , k_{i+1} )$ satisfying:

• (i) $k_1 = t_0$, and

• (ii) $[ k_i , k_{i+1} )$ either belongs to $S_{\mathrm{good}}$ or $S_{\mathrm{bad}}$, and

• (iii) if $k_{i+1} \ne \infty$ and $[ k_i , k_{i+1} )$ belongs to $S_{\mathrm{good}}$ (respectively, $S_{\mathrm{bad}}$), then the interval $[ k_{i+1} , k_{i+2} )$ must belong to $S_{\mathrm{bad}}$ (respectively, $S_{\mathrm{good}}$).

Now we turn to analysing the behaviour during each interval.

Sub-Case 2.1: $[ k_i , k_{i+1} )$ lies in $S_{\mathrm{bad}}$.

Let $j \in [ k_i , k_{i+1} )$ be arbitrary. In this case either $\phi (j) = 0$ or $\frac{[ d(j)]^2}{ \Vert \phi (j) \Vert ^2} \ge {\varepsilon }$ holds. In either case we have

$$\begin{aligned} \Vert \phi (j) \Vert \le \frac{1}{{\varepsilon }^{1/2}} | d(j) |, \; j \in [ k_i , k_{i+1} ) . \end{aligned}$$

(24)

From (13) and (17) we see that

$$\begin{aligned} \Vert \phi (j+1) \Vert\le & {} {\bar{a}} \Vert \phi (j) \Vert + ( 2 \Vert {{\mathcal {S}}} \Vert \times \Vert \phi (j) \Vert + | d(j) | + | r(j) | ) \nonumber \\\le & {} [ 1+ \underbrace{( {\bar{a}} + 2 \Vert {{\mathcal {S}}} \Vert )}_{=: \gamma _3} \frac{1}{{\varepsilon }^{1/2}} ] | d(j) | + | r(j) | , \; j \in [ k_i , k_{i+1} ) . \end{aligned}$$

(25)

If we combine this with (24), we conclude that

$$\begin{aligned} \Vert \phi (j) \Vert \le \left\{ \begin{array}{ll} \frac{1}{{\varepsilon }^{1/2}} | d(j) | &{} \;\; j=k_i \\ ( 1 + \frac{\gamma _3}{ {\varepsilon }^{1/2} } ) | d(j-1) | + | r(j-1) | &{} \;\; j = k_i+1,..., k_{i+1} . \end{array} \right. \end{aligned}$$

(26)

Sub-Case 2.2: $[ k_i , k_{i+1} )$ lies in $S_{\mathrm{good}}$.

Let $j \in [ k_i , k_{i+1} )$ be arbitrary. In this case $\phi (j) \ne 0$ and

$$\begin{aligned} \frac{[ d(j)]^2}{ \Vert \phi (j) \Vert ^2} < {\varepsilon }, \;\; j \in [k_i , k_{i+1} ) , \end{aligned}$$

which implies that

$$\begin{aligned} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ d(j)^2}{\Vert \phi (j) \Vert ^2} < {\varepsilon }, \quad j \in [k_i , k_{i+1} ). \end{aligned}$$

(27)

From Proposition 1 we have that

$$\begin{aligned} V( {\bar{k}}) \le V( {\underline{k}}) + \sum _{j={\underline{k}}}^{{\bar{k}}-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ - \frac{1}{2} e(j+1)^2 + 2 d(j)^2}{\Vert \phi (j) \Vert ^2} , \quad k_i \le {\underline{k}}< {\bar{k}}\le k_{i+1} ; \end{aligned}$$

using (27) and the fact that $0 \le V( \cdot ) \le 4 \Vert {{\mathcal {S}}} \Vert ^2$, we obtain

$$\begin{aligned} \sum _{j={\underline{k}}}^{{\bar{k}}-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ e(j+1)^2 }{ \Vert \phi (j)\Vert ^2}\le & {} 2 V( {\underline{k}}) + 2 \sum _{j={\underline{k}}}^{{\bar{k}}-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{ 2 d(j)^2}{\Vert \phi (j)\Vert ^2} \\\le & {} 8 \Vert {{\mathcal {S}} } \Vert ^2 + 4 {\varepsilon }( {\bar{k}}- {\underline{k}}) , \quad k_i \le {\underline{k}}< {\bar{k}}\le k_{i+1} . \end{aligned}$$

Hence, using this in (20) and (21) yields

$$\begin{aligned}&\sum _{j={\underline{k}}}^{{\bar{k}}-1} \Vert {\bar{A}} (j+1) - {\bar{A}} (j) \Vert \le \gamma _1 [ 8 \Vert {{\mathcal {S}} } \Vert ^2 + 4 {\varepsilon }( {\bar{k}}- {\underline{k}})]^{1/2} ( {\bar{k}}- {\underline{k}})^{1/2} \\&\quad \le \gamma _1 8^{1/2} \Vert {{\mathcal {S}} } \Vert ( {\bar{k}}- {\underline{k}})^{1/2} + 2 \gamma _1 {\varepsilon }^{1/2} ( {\bar{k}}- {\underline{k}}) , \quad k_i \le {\underline{k}}< {\bar{k}}\le k_{i+1} , \end{aligned}$$

as well as

$$\begin{aligned} \sum _{j={\underline{k}}}^{{\bar{k}}-1} \Vert \Delta (j) \Vert\le & {} [ 8 \Vert {{\mathcal {S}} } \Vert ^2 + 4 {\varepsilon }( {\bar{k}}- {\underline{k}})]^{1/2} ( {\bar{k}}- {\underline{k}})^{1/2} \\\le & {} 8^{1/2} \Vert {{\mathcal {S}} } \Vert ( {\bar{k}}- {\underline{k}}) ^{1/2} + 2 {\varepsilon }^{1/2} ( {\bar{k}}- {\underline{k}}) , \quad k_i \le {\underline{k}}< {\bar{k}}\le k_{i+1} . \end{aligned}$$

Now we will apply Proposition 2: we set

$$\begin{aligned} \alpha _0= & {} \beta _0 = 0 , \quad \alpha _1 = \gamma _1 8^{1/2} \Vert {{\mathcal {S}} } \Vert , \quad \beta _1 = 8^{1/2} \Vert {{\mathcal {S}} } \Vert , \\ \alpha _2= & {} 2 \gamma _1 {\varepsilon }^{1/2} , \quad \beta _2 = 2 {\varepsilon }^{1/2} , \quad \mu = \lambda . \end{aligned}$$

With N chosen as in Case 1 via (23), we have that ${\underline{\delta }} := \frac{\lambda }{ \gamma _1^{1/N}} - \lambda _1 > 0$; we need

$$\begin{aligned} \alpha _2 + \frac{\beta _2}{N} < \frac{1}{N \gamma _1} {\underline{\delta }} , \end{aligned}$$

which will certainly be the case if we set ${\varepsilon }:= \frac{ {\underline{\delta }}^2}{8 \gamma _1^2 ( \gamma _1 N + 1 )^2}$. From Proposition 2 we see that there exists a constant $\gamma _4$ so that the state transition matrix $\Phi (t , \tau )$ corresponding to ${\bar{A}} (t) + \Delta (t)$ satisfies

$$\begin{aligned} \Vert \Phi (t, \tau ) \Vert \le \gamma _4 \lambda ^{t - \tau } , \; k_i \le \tau \le t \le k_{i+1} . \end{aligned}$$

If we now apply this to (16) and use (18) to provide a bound on $\eta (t)$, we end up with

$$\begin{aligned}&\Vert \phi (k) \Vert \le \gamma _4 \lambda ^{k- k_i} \Vert \phi ( k_i) \Vert \nonumber \\&\quad + \left( 2 \frac{\Vert {{\mathcal {S}}} \Vert }{\delta } +1 \right) \sum _{j=k_i}^{k-1} \gamma _4 \lambda ^{k-1-j} ( | r (j) | + | d(j) | ) , \;\; k_{i} \le k \le k_{i+1} . \end{aligned}$$

(28)

This completes Sub-Case 2.2.

Now we combine Sub-Case 2.1 and Sub-Case 2.2 into a general bound on $\phi (t)$. Define

$$\begin{aligned} \gamma _5 := \max \left\{ 1, 1 + \frac{\gamma _3}{{\varepsilon }^{1/2}}, \gamma _4 , \gamma _4 \left( 2 \frac{\Vert {{\mathcal {S}}} \Vert }{\delta } +2 + \frac{\gamma _3}{{\varepsilon }^{1/2}} \right) \right\} . \end{aligned}$$

It remains to prove

Claim

The following bound holds:

$$\begin{aligned} \Vert \phi (k) \Vert \le \gamma _5 \lambda ^{k-t_0} \Vert \phi _0 \Vert + \sum _{j=t_0}^{k-1} \gamma _5 \lambda ^{k-1-j} ( |r(j) | + | d(j) | ) , \;\; k \ge t_0 . \end{aligned}$$

(29)

Proof of the Claim

If $[k_1 , k_2 ) = [t_0, k_2) \subset S_{\mathrm{good}}$, then (29) holds for $k \in [t_0 , k_2 ]$ by (28). If $[t_0 , k_2 ) \subset S_{\mathrm{bad}}$, then from (26) we obtain

$$\begin{aligned} \Vert \phi (j) \Vert \le \left\{ \begin{array}{ll} \Vert \phi ( k_1 ) \Vert = \Vert \phi _0 \Vert &{}\quad j=k_1 = t_0 \\ ( 1 + \frac{\gamma _3}{{\varepsilon }^{1/2}}) | d(j-1) | + | r(j-1) | &{}\quad j = k_1+1,..., k_{2} , \end{array} \right. \end{aligned}$$

which means that (29) holds for $k \in [t_0 , k_2 ]$ for this case as well.

We now use induction—suppose that (29) holds for $k \in [k_1 , k_i ]$; we need to prove that it holds for $k \in ( k_i, k_{i+1} ]$ as well. If $[k_i, k_{i+1}) \subset S_{\mathrm{bad}}$ then from (26) we have

$$\begin{aligned} \Vert \phi ( j ) \Vert \le \left( 1 + \frac{\gamma _3}{{\varepsilon }^{1/2}}\right) | d(j-1) | + | r(j-1) | , \; j = k_i+1,..., k_{i+1} , \end{aligned}$$

which means that (29) holds for $k \in ( k_i, k_{i+1} ]$. On the other hand, if $[k_i, k_{i+1}) \subset S_{\mathrm{good}}$, then $k_i -1 \in S_{\mathrm{bad}}$; from (26) we have that

$$\begin{aligned} \Vert \phi ( k_i) \Vert \le \left( 1 + \frac{\gamma _3}{{\varepsilon }^{1/2}}\right) | d( k_i-1 ) | + | r (k_i -1 ) | . \end{aligned}$$

Using (28) to analyse the behaviour on $[k_i , k_{i+1}]$, we have

$$\begin{aligned} \Vert \phi (k ) \Vert\le & {} \gamma _4 \lambda ^{k-k_i} \Vert \phi ( k_i ) \Vert + \left( 2 \frac{ \Vert {{\mathcal {S}}} \Vert }{\delta } + 1 \right) \gamma _4 \sum _{j=k_i}^{k-1} \lambda ^{k-1-j} ( | r(j) | + | d(j) | ) \\\le & {} \gamma _4 \lambda ^{k-k_i } [ ( 1 + \frac{\gamma _3}{{\varepsilon }^{1/2}}) | d( k_i-1 ) | + | r (k_i -1 ) | ] +\\&+\gamma _4 \left( 2 \frac{ \Vert {{\mathcal {S}}} \Vert }{\delta } + 1 \right) \sum _{j=k_i}^{k-1} \lambda ^{k-1-j} ( | r(j) | + | d (j) | ) \\\le & {} \left[ \gamma _4 \left( 1 + \frac{\gamma _3}{{\varepsilon }^{1/2}}\right) + \gamma _4 ( 2 \frac{ \Vert {{\mathcal {S}}} \Vert }{\delta } + 1 ) \right] \sum _{j=k_i-1}^{k-1} \lambda ^{k-1-j} ( | r(j) | + | d(j) | ) \\\le & {} \gamma _5 \sum _{j= t_0 } ^{k-1} \lambda ^{k-1-j} ( | d(j) | + | r(j) | ) , \quad k = k_i+1 ,..., k_{i+1} , \end{aligned}$$

as desired. $\square$

This completes the proof. $\square$

5 Tolerance to time variations

The linear-like bound proven in Theorem 1 can be leveraged to prove that the same behaviour will result even in the presence of slow time variations with occasional jumps. So suppose that the actual plant model is

$$\begin{aligned} y(t+1) = \phi (t)^T \theta ^* (t) +d(t) , \; \phi (t_0) = \phi _0 , \end{aligned}$$

(30)

with $\theta ^* (t) \in {{\mathcal {S}}}$ for all $t \in \mathbf{R}$. We adopt a common model of acceptable time variations used in adaptive control: with $c_0 \ge 0$ and ${\varepsilon }>0$, we let $s( {{\mathcal {S}}} , c_0, {\varepsilon })$ denote the subset of ${l_{\infty }}( \mathbf{R}^{2n})$ whose elements $\theta ^*$ satisfy $\theta ^* (t) \in {{\mathcal {S}}}$ for every $t \in \mathbf{Z}$ as well as

$$\begin{aligned} \sum _{t=t_1}^{t_2-1} \Vert \theta ^* (t+1) - \theta ^* (t) \Vert \le c_0 + {\varepsilon }( t_2 - t_1 ) , \quad t_2 > t_1 \end{aligned}$$

(31)

for every $t_1 \in \mathbf{Z}$. We will now show that, for every $c_0 \ge 0$, the approach tolerates time-varying parameters in $s( {{\mathcal {S}}} , c_0, {\varepsilon })$ if ${\varepsilon }$ is small enough.

Proof

Fix $\delta \in ( 0, \infty ]$, $\lambda _1 \in ( {\underline{\lambda }} ,1)$, $\lambda \in ( {\underline{\lambda }} , \lambda _1 )$ and $c_0 > 0$. Let $t_0 \in \mathbf{Z}$, $\theta _0 \in {{\mathcal {S}}}$, $\phi _0 \in \mathbf{R}^{2n}$, and $y^*, d \in \ell _{\infty }$ be arbitrary. With $m \in \mathbf{N}$, we will consider $\phi (t)$ on intervals of the form $[t_0 + im , t_0 + (i+1)m ]$; we will be analysing these intervals in groups of m (to be chosen shortly); we set ${\varepsilon }= \frac{c_0}{m^2}$, and let $\theta ^* \in s( {{\mathcal {S}}} , c_0, {\varepsilon })$ be arbitrary.

First of all, for $i \in \mathbf{Z}^+$ we can rewrite the plant equation as

$$\begin{aligned} y(t+1)= & {} \phi (t)^T \theta ^* (t_0 + im) + d(t) + \underbrace{ \phi (t)^T [\theta ^* ( t) - \theta ^* (t_0 + im) ]}_{=: {\tilde{n}} (t)} , \;\nonumber \\&\;\;\;\; t \in [ t_0 + im , t_0+ (i+1)m ] . \end{aligned}$$

(32)

Theorem 1 applied to (32) says that there exists a constant $c>0$ so that

$$\begin{aligned}&\Vert \phi (t) \Vert \le c \lambda ^{ t - t_0 - im } \Vert \phi (t_0 + im ) \Vert + \sum _{j=t_0 + im }^{t-1} c \lambda ^{t-1-j} ( | r (j) | + | d(j) | + | {\tilde{n}} (j) | ) , \;\\&\;\;\;\;\;\;\;\;\;\; t \in [ t_0 + im , t_0+ (i+1)m ] . \end{aligned}$$

The above is a difference inequality associated with a first-order system; using this observation together with the fact that $c \ge 1$, we see that if we define

$$\begin{aligned} \psi (t+1) = \lambda \psi (t) + | r(t) | + | d(t) | + | {\tilde{n}} (t) | , \quad t \in [ t_0 + im , t_0+ (i+1)m-1 ] , \end{aligned}$$

with $\psi (t_0 + im) = \Vert \phi (t_0 + im ) \Vert$, then

$$\begin{aligned} \Vert \phi (t) \Vert \le c \psi (t) , \quad t \in [ t_0 + im , t_0+ (i+1)m ] . \end{aligned}$$

Now we analyse this equation for $i =0,1,..., m-1$.

Case 1: $|{\tilde{n}} (t) | \le \frac{1}{2c} ( \lambda _1 - \lambda ) \Vert \phi ( t ) \Vert$ for all $t \in [ t_0 + im , t_0+ (i+1)m ]$.

In this case

$$\begin{aligned} \psi (t+1)\le & {} \lambda \psi (t) + |r(t)| + | d(t) | + | {\tilde{n}} (t) | \\\le & {} \lambda \psi (t) + |r(t)| + | d(t) | + \frac{1}{2c} ( \lambda _1 - \lambda ) c \psi (t) \\\le & {} \left( \frac{\lambda + \lambda _1 }{2} \right) \psi (t) + | r(t) | + | d(t) | , \; t \in [ t_0 + im , t_0+ (i+1)m ] , \end{aligned}$$

which means that

$$\begin{aligned}&| \psi (t) | \le \left( \frac{\lambda + \lambda _1 }{2} \right) ^{t-t_0-im} | \psi ( t_0 + im ) | + \sum _{j=t_0+im}^{t-1} \left( \frac{\lambda + \lambda _1 }{2} \right) ^{t-1-j} ( | r (j) | + | d(j) | ) ,\\&\;\;\;\;\; t=t_0+im,..., t_0+ (i+1)m . \end{aligned}$$

This, in turn, implies that

$$\begin{aligned} \Vert \phi ( t_0+ (i+1)m ) \Vert\le & {} c \left( \frac{\lambda + \lambda _1 }{2} \right) ^m \Vert \phi ( t_0 + im) \Vert \nonumber \\&+ \sum _{j=t_0 + im}^{t_0 + (i+1)m-1} c \left( \frac{\lambda + \lambda _1 }{2} \right) ^{t_0 + (i+1)m-1-j} ( | r(j) | + | d(j) | ) .\nonumber \\ \end{aligned}$$

(33)

Case 2: $|{\tilde{n}} (t) | > \frac{1}{2c} ( \lambda _1 - \lambda ) \Vert \phi ( t ) \Vert$ for some $t \in [ t_0 + im , t_0+ (i+1)m ]$.

Since $\theta ^* (t) \in {{\mathcal {S}}}$ for $t \ge t_0$, we see

$$\begin{aligned} |{\tilde{n}} (t) | \le 2 \Vert {{\mathcal {S}}} \Vert \times \Vert \phi ( t ) \Vert , \; t \in [ t_0 + im , t_0+ (i+1)m ] . \end{aligned}$$

This means that

$$\begin{aligned} \psi (t+1)\le & {} \lambda \psi (t) + | r(t)|+ | d(t) | + | {\tilde{n}} (t) | \\\le & {} \lambda \psi (t) + | r(t)|+ | d(t) | + 2 \Vert {{\mathcal {S}}} \Vert c \psi (t) \\\le & {} \underbrace{( 1+2c \Vert {{\mathcal {S}}} \Vert )}_{=: \gamma _1} \psi (t) + |r(t)| + | d(t) | , \; t \in [ t_0 + im , t_0+ (i+1)m ] , \end{aligned}$$

which means that

$$\begin{aligned}&| \psi (t) | \le \gamma _1^{t-t_0-im} \Vert \psi ( t_0 + im ) \Vert \\&\quad + \sum _{j=t_0+im}^{t-1} \gamma _1^{t-j-1} (|r(j)| + | d (j) |) , \; t=t_0+im,..., t_0+ (i+1)m . \end{aligned}$$

This, in turn, implies that

$$\begin{aligned} \Vert \phi ( t_0+ (i+1)m ) \Vert\le & {} c \gamma _1 ^m \Vert \phi ( t_0 + im) \Vert \nonumber \\&+ c \sum _{j=t_0 + im}^{t_0 + (i+1)m-1} ( \gamma _1 )^{t_0 + (i+1)m-j-1} ( | r(j) | + | d(j) | ) \nonumber \\\le & {} c \gamma _1^m \Vert \phi ( t_0 + im) \Vert \nonumber \\&+ c \left( \frac{ 2 \gamma _1}{ \lambda + \lambda _1 } \right) ^m \sum _{j=t_0 + im}^{t_0 + (i+1)m-1}\nonumber \\&\left( \frac{ \lambda + \lambda _1}{2} \right) ^ {t_0 + (i+1)m -j-1 } ( | r(j) | + | d(j) | ) . \end{aligned}$$

(34)

On the interval $[t_0 , t_0 + m^2]$ there are m subintervals of length m; furthermore, because of the choice of ${\varepsilon }$ we have that

$$\begin{aligned} \sum _{j=t_0}^{t_0 + m^2-1} \Vert \theta ^* (j+1) - \theta ^* (j) \Vert \le c_0 + {\varepsilon }m^2 \le 2 c_0 . \end{aligned}$$

A simple calculation reveals that there are at most $N_1 := \frac{4 c_0 c}{ \lambda _1 - \lambda }$ subintervals which fall into the category of Case 2, with the remaining number falling into the category of Case 1. Henceforth, we assume that $m > N_1$. If we use (33) and (34) to analyse the behaviour of the closed-loop system on the interval $[t_0 , t_0 + m^2]$, we end up with a crude bound of

$$\begin{aligned}&\Vert \phi (t_0 + m^2) \Vert \le c^{m} \gamma _1^{N_1 m} \left( \frac{ \lambda _1 + \lambda }{2} \right) ^{m (m- N_1)} \Vert \phi ( t_0 ) \Vert \nonumber \\&\quad +\, (\frac{ 2 \gamma _1 }{ \lambda {+} \lambda _1 } )^{ m} ( c \gamma _1^m)^m \left( \frac{2}{ \lambda {+} \lambda _1 } \right) ^{m^2} \sum _{j=t_0}^{t_0 +m^2-1} \left( \frac{ \lambda _1 {+} \lambda }{2} \right) ^{t_0 +m^2-j-1} ( | r(j) | + | d(j) | ) . \nonumber \\ \end{aligned}$$

(35)

At this point we would like to choose m so that

$$\begin{aligned} c^{m} \gamma _1^{N_1 m} \left( \frac{ \lambda _1 + \lambda }{2} \right) ^{m^2 - m N_1} \le \lambda _1^{m^2} \; \Leftrightarrow \; c^{m} \gamma _1^{N_1 m} \left( \frac{2}{ \lambda + \lambda _1 }\right) ^{m N_1} \le \left( \frac{2 \lambda _1}{\lambda _1 + \lambda } \right) ^{m^2}; \end{aligned}$$

notice that $\frac{2 \lambda _1}{\lambda _1 + \lambda } > 1$, so if we take the log of both sides, we see that we need

$$\begin{aligned} m \ln (c) + N_1 m \ln ( \gamma _1 ) + N_1 m \ln \left( \frac{2}{ \lambda + \lambda _1 } \right)\le & {} m^2 \ln \left( \frac{2 \lambda _1}{\lambda _1 + \lambda } \right) , \end{aligned}$$

which will clearly be the case for large enough m, so at this point we choose such an m. It follows from (35) that there exists a constant $\gamma _2$ so that

$$\begin{aligned} \Vert \phi (t_0 + m^2) \Vert \le \lambda _1^{m^2} \Vert \phi (t_0) \Vert + \gamma _2 \sum _{j=t_0}^{t_0 +m^2-1} \lambda _1^{t_0 +m^2-j-1 } ( | r(j) | + | d(j) | ) . \end{aligned}$$

Indeed, the same bound holds regardless of the interval of analysis:

$$\begin{aligned} \Vert \phi ({\bar{t}} + m^2) \Vert \le \lambda _1^{m^2} \Vert \phi ( {\bar{t}}) \Vert + \gamma _2 \sum _{j={\bar{t}}}^{{\bar{t}} +m^2-1} \lambda _1^{{\bar{t}} +m^2-j-1 } ( | r(j) | + | d(j) | ) , \quad {\bar{t}} \ge t_0 . \end{aligned}$$

Solving iteratively yields

$$\begin{aligned}&\Vert \phi (t_0 + i m^2) \Vert \nonumber \\&\le \lambda _1^{im^2} \Vert \phi (t_0) \Vert + \gamma _2 \sum _{j=t_0}^{t_0 +im^2-1} \lambda _1^{t_0 +im^2-j-1 } ( | r(j)| + | d(j) | ) , \quad i \ge 0 . \end{aligned}$$

(36)

We now combine this bound with the bounds which hold on the good intervals (33) and the bad intervals (34) and conclude that there exists a constant $\gamma _3$ so that

$$\begin{aligned} \Vert \phi (t ) \Vert \le \gamma _3 \lambda _1^{t- t_0} \Vert \phi (t_0 ) \Vert + \gamma _3 \sum _{j=t_0}^{t-1} \lambda _1^{t-j-1} (| r(j) | + | d(j) | ) , \quad t \ge t_0 , \end{aligned}$$

as desired. $\square$

6 Tolerance to unmodelled dynamics

Due to the linear-like bounds proven in Theorems 1 and 2, we can use the Small Gain Theorem to good effect to prove the tolerance of the closed-loop system to unmodelled dynamics. However, since the controller, and therefore the closed-loop system, is nonlinear, handling initial conditions is more subtle: in the linear time-invariant case we can separate out the effect of initial conditions from that of the forcing functions ($r/y^*$ and d), but in our situation they are intertwined. We proceed by looking at two cases—with and without initial conditions. In all of the cases we consider the time-varying plant (30) with $d_{\Delta } (t)$ added to represent the effect of unmodelled dynamics:

$$\begin{aligned} y(t+1) = \phi (t)^T \theta ^* (t) +d(t) + d_{\Delta } (t) , \quad \phi (t_0) = \phi _0 . \end{aligned}$$

(37)

To proceed, fix $\delta \in (0, \infty ]$, $\lambda _1 \in ( {\underline{\lambda }} ,1)$ and $c_0 \ge 0$; from Theorem 2 there exists a $c_1>0$ and ${\varepsilon }>0$ so that for every $t_0 \in \mathbf{Z}$, $\phi _0 \in \mathbf{R}^{2n}$, $\theta _0 \in {{\mathcal {S}}}$, $y^*, d \in \ell _{\infty }$, and $\theta ^* \in s( {{\mathcal {S}}} , c_0, {\varepsilon })$, when the adaptive controller (7), (8) and (11) is applied to the time-varying plant (37), the following bound holds:

$$\begin{aligned} \Vert \phi (k) \Vert \le c_1 \lambda _1^{k- t_0} \Vert \phi _0 \Vert + \sum _{j=t_0}^{k-1} c_1 \lambda _1^{k-1-j} {( | r(j) | + | d(j)| + | d_{\Delta } (j) | )} , \;\; k \ge t_0 . \quad \end{aligned}$$

(38)

6.1 Zero initial conditions

In this case we assume that $\phi (t) = 0$ for $t \le t_0$; we derive a bound on the closed-loop system behaviour in the presence of unmodelled dynamics. Suppose that the unmodelled dynamics is of the form $d_{\Delta } (t) = ( \Delta \phi )(t)$ with $\Delta : {l_{\infty }}( \mathbf{R}^{2n}) \rightarrow {l_{\infty }}(\mathbf{R}^{2n})$ a (possibly nonlinear time-varying) causal map with a finite gain of $\Vert \Delta \Vert$. It is easy to prove that if $\Vert \Delta \Vert < \frac{1 - \lambda _1}{c_1 }$, then

$$\begin{aligned} \Vert \phi (k) \Vert \le \frac{c_1}{1 - \lambda _1 - c_1 \Vert \Delta \Vert } ( \sup _{t \ge t_0} \Vert r (t) \Vert + \sup _{t \ge t_0} \Vert d(t) \Vert ) , \quad k \ge t_0 , \end{aligned}$$

i.e. a form of closed-loop stability is attained. Following the approach of Remark 7, we could also analyse the closed-loop system using $l_p$-norms with $1 \le p < \infty$.

6.2 Nonzero initial conditions

Now we consider the case of unmodelled LTI dynamics when the plant has nonzero initial conditions, and we develop convolution-like bounds on the closed-loop system. To this end suppose that the unmodelled dynamics are of the form

$$\begin{aligned} d_{\Delta } (t) := \sum _{j=0}^{\infty } \Delta _j \phi (t-j) , \end{aligned}$$

(39)

with $\Delta _j \in \mathbf{R}^{1 \times 2n }$; the corresponding transfer function is $\Delta (z^{-1}) := \sum _{j=0}^{\infty } \Delta _j z^{-j}$. It is easy to see that this model subsumes the classical additive uncertainty, multiplicative uncertainty, and uncertainty in a coprime factorization, which is common in the robust control literature, e.g. see [39], with the only constraint being that the perturbations correspond to strictly causal terms. In order to obtain linear-like bounds on the closed-loop behaviour, we need to impose more constraints on $\Delta (z)$ than in the previous subsection: after all, if $\Delta (z^{-1}) = \Delta _p z^{-p}$, it is clear that $\Vert \Delta \Vert = \Vert \Delta _p \Vert$ for all p, but the effect on the closed-loop system varies greatly—a large value of p allows the behaviour in the far past to affect the present. To this end, with $\mu >0$ and $\beta \in (0,1)$, we shall restrict $\Delta (z^{-1})$ to a set of the form

$$\begin{aligned} {{\mathcal {B}}} ( \mu , \beta ) := \left\{ \sum _{j=0}^{\infty } \Delta _j z^{-j} : \Delta _j \in \mathbf{R}^{1 \times 2n} \text{ and } \Vert \Delta _j \Vert \le \mu \beta ^j , \; j \ge 0 \right\} . \end{aligned}$$

It is easy to see that every transfer function in ${{\mathcal {B}}} ( \mu , \beta )$ is analytic in $\{ z \in \mathbf{C}: | z | > \beta \}$, so it has no poles in that region.

Now we fix $\mu >0$ and $\beta \in (0,1)$ and let $\Delta ( z^{-1})$ belong to ${{\mathcal {B}}} ( \mu , \beta )$; the goal is to analyse the closed-loop behaviour of (37) for $t \ge t_0$ when $d_{\Delta }$ is given by (39). We first partition $d_{\Delta }(t)$ into two parts—that which depends on $\phi (t)$ for $t \ge t_0$ and that which depends on $\phi (t)$ for $t < t_0$:

$$\begin{aligned} d_{\Delta }(t)= & {} \sum _{j=0}^{\infty } \Delta _j \phi (t-j) = \sum _{j= - \infty }^{t} \Delta _{ t-j} \phi (j) = \underbrace{\sum _{j=- \infty }^{t_0-1} \Delta _{ t-j} \phi (j)}_{=: d_{\Delta }^- (t)} + \underbrace{\sum _{j=t_0}^{t} \Delta _{ t-j} \phi (j)}_{=: d_{\Delta }^+ (t) } . \end{aligned}$$

It is clear that

$$\begin{aligned} \Vert d_{\Delta }^+ (t) \Vert\le & {} \sum _{j=t_0}^{t} \mu \beta ^{t-j} \Vert \phi (j) \Vert , \\ \Vert d_{\Delta }^- (t) \Vert\le & {} \sum _{j=- \infty }^{t_0-1} \mu \beta ^{t-j} \Vert \phi (j) \Vert = \mu \beta ^{t-t_0} \sum _{j=1}^{ \infty } \beta ^j \Vert \phi ( t_0 - j ) \Vert , \quad t \ge t_0 . \end{aligned}$$

If $\phi (t)$ is bounded on $\{ t \in \mathbf{Z}: t < t_0 \}$ then $\sum _{j=1}^{\infty } \beta ^{j} \Vert \phi ( t_0-j) \Vert$ is finite, in which case we see that $d_{\Delta }^- (t)$ goes to zero exponentially fast; henceforth, we make the reasonable assumption that this is the case. It turns out that we can easily bound $d_{\Delta }(t)$ with a difference equation. To this end, consider

$$\begin{aligned} {m} (t+1) = \beta {m} (t) + \beta \Vert \phi (t) \Vert , \quad t \ge t_0 , \end{aligned}$$

(40)

with ${m} (t_0) = m_0 := \sum _{j=1}^{\infty } \beta ^{j} \Vert \phi ( t_0-j) \Vert$; it is straightforward to prove that

$$\begin{aligned} | d_{\Delta }(t) | \le | d_{\Delta }^+ (t) | + | d_{\Delta }^- (t)| \le \mu {m} (t) + \mu \Vert \phi (t) \Vert , \quad t \ge t_0 . \end{aligned}$$

(41)

This model of unmodelled dynamics is similar to that used in the adaptive control literature, e.g. see [10].

Proof

Fix $\beta \in (0,1)$ and $\lambda _2 \in ( \max \{\lambda _1 , \beta \} , 1 )$. The first step is to convert difference inequalities to difference equations. To this end, consider the difference equation

$$\begin{aligned} \tilde{\phi }(t+1)= & {} \lambda _1 \tilde{\phi }(t) + c_1 | r(t) | + c_1 | d(t) | \nonumber \\&+ c_1 \mu {\tilde{m}} (t) + c_1 \mu {\tilde{\phi }}(t) , \; \tilde{\phi }(t_0) = c_1 \Vert \phi (t_0) \Vert , \end{aligned}$$

(42)

together with the difference equation based on (40):

$$\begin{aligned} {\tilde{m}} (t+1) = \beta {\tilde{m}} (t) + \beta \tilde{\phi }(t) , \quad {\tilde{m}} (t_0) = | {m}_0 | . \end{aligned}$$

(43)

It is easy to use induction together with (38), (40), and (41) to prove that

$$\begin{aligned} \Vert \phi (t) \Vert \le \tilde{\phi }(t) , \quad | m(t) | \le {\tilde{m}} (t) , \quad t \ge t_0 . \end{aligned}$$

(44)

If we combine the difference equations (42) with (43), we end up with

$$\begin{aligned} \left[ \begin{array}{c} \tilde{\phi }(t+1) \\ {\tilde{m}}(t+1) \end{array} \right] = \underbrace{ \left[ \begin{array}{cc} \lambda _1 + c_1\mu &{} c_1 \mu \\ \beta &{} \beta \end{array} \right] }_{A_{cl} ( \mu )} \left[ \begin{array}{c} \tilde{\phi }(t) \\ {\tilde{m}}(t) \end{array} \right] + \left[ \begin{array}{c} c_1 \\ 0 \end{array} \right] ( | d(t) | + | r(t) | ), \quad t \ge t_0 . \qquad \end{aligned}$$

(45)

Now we see that $A_{cl} ( \mu ) \rightarrow \left[ \begin{array}{cc} \lambda _1 &{} 0 \\ \beta &{} \beta \end{array} \right]$ as $\mu \rightarrow 0$, and this matrix has eigenvalues of $\{ \lambda _1 , \beta \}$. Now choose ${\bar{\mu }} > 0$ so that all eigenvalues are less than $( \frac{\lambda _2}{2} + \frac{1}{2}\max \{ \lambda _1 , \beta \} )$ in magnitude for $\mu \in (0 , {\bar{\mu }} ]$, and define ${\varepsilon }:= \frac{\lambda _2}{2} - \frac{1}{2}\max \{ \lambda _1 , \beta \}$. Using the proof technique of Desoer in [40], we can conclude that for $\mu \in (0 , {\bar{\mu }} ]$, we have

$$\begin{aligned} \Vert A_{cl} ( \mu ) ^k \Vert \le \underbrace{\left( \frac{3 + 2\beta + 2 c_1 {\bar{\mu }}}{ {\varepsilon }^2} \right) }_{=: \gamma _1} \lambda _2^k , \;\; k \ge 0 ; \end{aligned}$$

if we use this in (45) and then apply the bounds in (44), it follows that

$$\begin{aligned} \Vert \phi (k) \Vert \le c_1 \gamma _1 \lambda _2 ^{ k - t_0} ( \Vert \phi _0 \Vert + | m_0 | ) + \sum _{j=t_0}^{k-1} c_1 \gamma _1 \lambda _2^{k-1-j} ( | d (j) | + | r(j) | ) , \quad k \ge t_0, \end{aligned}$$

as desired. $\square$

7 Step tracking

If the plant is non-minimum phase, it is not possible to track an arbitrary bounded reference signal using a bounded control signal. However, as long as the plant does not have a zero at $z=1$, it is possible to modify the controller design procedure to achieve asymptotic step tracking if there is no noise/disturbance. So at this point assume that the corresponding plant polynomial $B( z^{-1} )$ has no zero at $z=1$ for any plant model $\theta ^* \in {{\mathcal {S}}}$. To proceed, we use the standard trick from the literature, e.g. see [34]: we still estimate $A(z^{-1} )$ and $B( z^{-1})$ as before, but we now design the control law slightly differently. To this end, we first define

$$\begin{aligned} {\tilde{A}} (t, z^{-1} ) := (1- z^{-1} ) {\hat{A}} ( t, z^{-1} ) , \end{aligned}$$

and then let $A^* ( z^{-1} )$ be a $2 (n+1)$th monic polynomial (rather than a 2nth one) of the form

$$\begin{aligned} A^* (z^{-1} ) = 1 + a_1^* z^{-1} + \cdots + a_{2n+2}^* z^{-2n-2} \end{aligned}$$

so that $z^{2(n+1)} A^* (z^{-1} )$ has all of its zeros in ${\mathbf{D}}^o$. Next, we choose two polynomial

$$\begin{aligned}&{{\tilde{L}}} (t, z^{-1} ) = 1 + {\tilde{l}}_1 (t) z^{-1}+ \cdots + {\tilde{l}}_{n+1} (t) z^{-n-1} \; \\&\quad \text{ and } \; {\hat{P}} (t,z^{-1} ) = {\hat{p}}_1 (t) z^{-1} + \cdots + {\hat{p}}_{n+1} (t) z^{-n-1} \end{aligned}$$

which satisfy the equation

$$\begin{aligned} {\tilde{A}} ( t , z^{-1} ) {\tilde{L}} (t, z^{-1} ) + {\hat{B}} ( t , z^{-1} ) {\hat{P}} (t,z^{-1} ) = A^* ( z^{-1} ) ; \end{aligned}$$

(46)

since ${\tilde{A}} ( t , z^{-1} )$ and ${\hat{B}} ( t , z^{-1} )$ are coprime, there exist unique ${\tilde{L}} (t, z^{-1} )$ and ${\hat{P}} (t,z^{-1} )$ which satisfy this equation. We now define

$$\begin{aligned} {\hat{L}} (t, z^{-1} ) = 1 + {\hat{l}}_1 (t) z^{-1} + \cdots + {\hat{l}}_{n+2} (t) z^{-n-2} := (1-z^{-1} ) {\tilde{L}} (t, z^{-1} ) ; \end{aligned}$$

at time t we choose u(t) so that

$$\begin{aligned} u(t)= & {} - {\hat{l}}_1 (t-1) u(t-1) - \cdots - {\hat{l}}_{n+2} (t-1) u(t-n-2)\\&- {\hat{p}}_1 (t-1) [ y(t-1)- y^* (t-1) ]\\&- \cdots - {\hat{p}}_{n+1} (t-1) [ y(t-n-1)- y^* (t-n-1) ] . \end{aligned}$$

We can use a modified version of the argument used in the proof of Theorem 1 to conclude that a similar type of result holds here; we can also prove that asymptotic step tracking will be attained if the noise is zero and the reference signal $y^*$ is constant. The details are omitted.

8 Relaxing the convexity requirement

The convexity and coprimeness assumptions on the set of admissible plant parameters play a crucial role in obtaining the nice closed-loop properties provided in Theorems 1–3. Here we will show that it is possible to weaken the convexity requirement if the goal is to place all closed-loop poles at zero, although it is at the expense of using a more complicated controller. Our proposed approach is modelled on the first-order one-step-ahead control setup (see [32, 41]) which is deadbeat in nature; of course, here the plant may not be first order, which increases the complexity. While we would like to remove the convexity requirement completely, at present we are only able to weaken it. So in this section we replace Assumption 1 with

The idea is to use an estimator for each of ${{\mathcal {S}}}_1$ and ${{\mathcal {S}}}_2$, and at each point in time we choose which one to use in the control law. Before proceeding, define

$$\begin{aligned} \bar{\mathbf{s}}:=\max \{\Vert {{\mathcal {S}}}_1\Vert ,\Vert {{\mathcal {S}}}_2\Vert \}. \end{aligned}$$

8.1 Parameter estimation

For each ${{\mathcal {S}}}_{i}$ and ${{{\hat{\theta }}}}_i(t_0)\in {{\mathcal {S}}}_{i}$, we construct an estimator which generates an estimate ${\hat{\theta }}_{i}(t)\in {{\mathcal {S}}}_{i}$ at each $t>t_{0}$. Motivated by (4) and (5), the associated prediction error is defined as

$$\begin{aligned} e_i (t+1)=y(t+1)-\phi (t)^{T}{\hat{\theta _i}} (t), \end{aligned}$$

(47)

and the parameter update law is given by

$$\begin{aligned} {{\check{\theta }}}_i(t+1)= & {} \left\{ \begin{matrix} {\hat{\theta _i}}(t)+\frac{\phi (t)}{\Vert \phi (t)\Vert ^2}e_i(t+1) &{} \text {if } \phi (t)\ne 0 \\ {\hat{\theta _i}}(t) &{} \text {if } \phi (t)=0, \end{matrix}\right. \end{aligned}$$

(48)

$$\begin{aligned} {\hat{\theta }}_i (t+1)= & {} \pi _{{{\mathcal {S}}}_i} ( {\check{\theta }}_i (t+1) ). \end{aligned}$$

(49)

(For ease of exposition, we do not use the more general version of the estimator equation in (7) and (8).) Associated with this estimator is the parameter estimation error ${{\tilde{\theta }}}_i(t):= {\hat{\theta _i}}(t)-\theta ^*$ as well as the corresponding Lyapunov function $V_i(t):={{\tilde{\theta }}}_i(t)^T {{\tilde{\theta }}}_i(t)$.

8.2 The switching control law

The elements of ${\hat{\theta }}_i(t)$ are partitioned as

$$\begin{aligned} {\hat{\theta }}_i(t)=:[-{{\hat{a}}}_{i,1}(t) \;\; \cdots \;\; -{{\hat{a}}}_{i,n}(t) \;\; {{\hat{b}}}_{i,1}(t) \;\; \cdots \;\; {{\hat{b}}}_{i,n}(t) ]^T; \end{aligned}$$

associated with these estimates are the polynomials

$$\begin{aligned} {{\hat{A}}}_i(t,z^{-1})= & {} 1+{{\hat{a}}}_{i,1}(t)z^{-1}+{{\hat{a}}}_{i,2}(t)z^{-2}\cdots +{{\hat{a}}}_{i,n}(t)z^{-n}, \\ {{\hat{B}}}_i(t,z^{-1})= & {} {{\hat{b}}}_{i,1}(t)z^{-1}+{{\hat{b}}}_{i,2}(t)z^{-2}\cdots +{{\hat{b}}}_{i,n}(t)z^{-n}. \end{aligned}$$

Next, we choose the following polynomials

$$\begin{aligned} {{\hat{L}}}_i(t,z^{-1})= & {} 1+{{\hat{l}}}_{i,1}(t)z^{-1}+{{\hat{l}}}_{i,2}(t)z^{-2}+\cdots +{{\hat{l}}}_{i,n}(t)z^{-n}, \\ {{\hat{P}}}_i(t,z^{-1})= & {} {{\hat{p}}}_{i,1}(t)z^{-1}+{{\hat{p}}}_{i,2}(t)z^{-2}+\cdots +{{\hat{p}}}_{i,n}(t)z^{-n} \end{aligned}$$

to place all closed-loop poles at zero, so we need

$$\begin{aligned} {{\hat{A}}}_i(t,z^{-1}){{\hat{L}}}_i(t,z^{-1})+{{\hat{B}}}_i(t,z^{-1}){{\hat{P}}}_i(t,z^{-1})=1. \end{aligned}$$

Given the assumption that the ${{\hat{A}}}_i ( t , z^{-1} )$ and ${{\hat{B}}}_i ( t , z^{-1} )$ are coprime, we know that there exist unique ${{\hat{L}}}_i (t, z^{-1} )$ and ${{\hat{P}}}_i (t,z^{-1} )$ which satisfy this equation; it is also easy to prove that the coefficients of ${{\hat{L}}}_i (t, z^{-1} )$ and ${{\hat{P}}}_i (t,z^{-1} )$ are analytic functions of ${\hat{\theta _i}} (t) \in {{\mathcal {S}}}_i$.

We can now discuss the candidate control law to be used. Define the controller gain by

$$\begin{aligned} {{\hat{K}}}_i(t):= [-{{\hat{p}}}_{i,1}(t) \;\; \cdots \;\; -{{\hat{p}}}_{i,n}(t) \;\; -{{\hat{l}}}_{i,1}(t) \;\; \cdots \;\; -{{\hat{l}}}_{i,n}(t) ]^T \end{aligned}$$

and a switching signal $\sigma :{\mathbf{Z}}\mapsto \{1,2\}$ that decides which gain to use at any given point in time. A natural choice for a control law is

$$\begin{aligned} u(t)={{\hat{K}}}_{\sigma (t-1)}(t-1)^T\phi (t-1)+\sum _{j=1}^{n}{{\hat{p}}}_{\sigma (t-1),j}(t-1)y^*(t-j); \end{aligned}$$

(50)

the above control law is similar to that given in (11) but with the controller gains chosen between the two choices at each point in time.

The most obvious choice of $\sigma (t)$ is to define it by

$$\begin{aligned} \hbox {argmin} \{ |e_1 (t) | , | e_2 (t) | \}. \end{aligned}$$

While this works in every simulation that we have tried, the proof remains elusive.

Hence, we try another approach, which is based on our earlier work in the first-order one-step-ahead setting [41], and exploits the deadbeat nature of the problem. Using the natural notation of ${{\bar{A}}}_{\sigma (t)}(t)$ to represent the ${{\bar{A}}}(t)$ matrix of (12) as well as ${{\hat{r}}}(t):=\sum _{j=1}^{n} {{\hat{p}}}_{\sigma (t),j}(t)y^*(t-j+1)$, the closed-loop behaviour is captured by

$$\begin{aligned} \phi (t+1)={{\bar{A}}}_{\sigma (t)}(t)\phi (t)+B_1e_{\sigma (t)}(t+1)+B_2 {{\hat{r}}}(t). \end{aligned}$$

(51)

While ${{\bar{A}}}_{\sigma (t)}(t)$ is a deadbeat matrix for every t, the product

$$\begin{aligned} {{\bar{A}}}_{\sigma (t)}(t)\times {{\bar{A}}}_{\sigma (t-1)}(t-1)\times \cdots \times {{\bar{A}}}_{\sigma (t_0)}(t_0),\qquad t\ge t_0 \end{aligned}$$

will not usually have all eigenvalues at zero. Hence, the method of analysis used in [41] will not work for the proposed control law (50). A natural attempt to alleviate the problem is to hold $\sigma (t)$ constant in (50) for 2n steps at a time; the difficulty now is that ${{\bar{A}}}_{\sigma (t)}(t)$ is still changing since ${\hat{\theta }}_{i}(t)$ still changes. A natural solution to this problem is to update the estimators every 2n steps as well; the difficulty here is that we end up with no information about $e_{i}(t+1)$ between the updates, so the closed-loop system is not amenable to analysis. So our proposed solution procedure will need to be different: we are going to change $\sigma (t)$ every $N\ge 2n$ steps; we keep the estimators running, but adjust the control parameters every $N\ge 2n$ steps as well. The effect of this will become clear in the proof of the main result of this section. To this end, we define a sequence of switching times as follows: we initialize ${{\hat{t}}}_0:=t_0$ and then define

$$\begin{aligned} {{\hat{t}}}_\ell :=t_0+\ell N,\qquad \ell \in \mathbf{N}. \end{aligned}$$

So now define the associated controller parameters by

$$\begin{aligned} K_i(t):= [-{{\hat{p}}}_{i,1}({{\hat{t}}}_\ell ) \;\; \cdots \;\; -{{\hat{p}}}_{i,n}({{\hat{t}}}_\ell ) \;\; -{{\hat{l}}}_{i,1}({{\hat{t}}}_\ell ) \;\; \cdots \;\; -{{\hat{l}}}_{i,n}({{\hat{t}}}_\ell ) ]^T, \;\; t\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}),\;\ell \in \mathbf{Z}^+, \end{aligned}$$

(52)

the switching signal by

$$\begin{aligned} \sigma (t)=\sigma ({{\hat{t}}}_\ell ),\;\; t\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}),\;\ell \in \mathbf{Z}^+, \end{aligned}$$

(53)

and the suitably revised definition of $r(\cdot )$:

$$\begin{aligned} r(t):=\sum _{j=1}^{n} {{\hat{p}}}_{\sigma ({{\hat{t}}}_\ell ),j}({{\hat{t}}}_\ell )y^*(t-j+1),\;\; t\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}),\;\ell \in \mathbf{Z}^+. \end{aligned}$$

We now define the control law as

$$\begin{aligned} u(t)=K_{\sigma (t-1)}(t-1)^T\phi (t-1)+r(t-1),\qquad t\ge t_0. \end{aligned}$$

(54)

What remains to be defined is the choice of switching signal $\sigma ({{\hat{t}}}_\ell )$. To this end, we define a performance signal $J_i:\{{{\hat{t}}}_0,{{\hat{t}}}_1,\ldots \}\mapsto \mathbf{R}$ for estimator i, which produces a measure of “accuracy” of estimation; for $\ell \in \mathbf{Z}^+$, we define

$$\begin{aligned} J_i({{\hat{t}}}_\ell ):=\left\{ \begin{array}{cl} 0 &{} \qquad \text {if }\phi (j)=0 \text { for all } j\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}), \\ \underset{{j\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1})},\phi (\cdot )\ne 0}{\max } \frac{|e_i(j+1)|}{\Vert \phi (j)\Vert } &{}\qquad \text {otherwise. } \end{array}\right. \end{aligned}$$

(55)

Before proceeding, assume that $\theta ^*\in {{\mathcal {S}}}$, so there exists one or more $j\in \{1,2\}$ so that $\theta ^{*}\in {{\mathcal {S}}}_{j}$; throughout the remainder of this section, let $i^{*}$ denote the smallest such j. With $\sigma ({{\hat{t}}}_0)=\sigma _0$, we use the following switching rule:

$$\begin{aligned} \sigma ({{\hat{t}}}_{\ell +1}) =\underset{i\in \{1,2\}}{\text {argmin}}\;J_i({{\hat{t}}}_\ell ), \qquad \ell \in \mathbf{Z}^+; \end{aligned}$$

(56)

for the case when $J_1({{\hat{t}}}_\ell )=J_2({{\hat{t}}}_\ell )$, we (somewhat arbitrarily) select $\sigma ({{\hat{t}}}_{\ell +1})$ to be 1. Before presenting the main result of this section, we first show that the logic in (56) yields a desirable closed-loop property.

Proof

Fix $t_0\in \mathbf{Z}$, ${\phi _0 \in {\mathbf{R}}^{2n}}$, $\sigma _{0}\in \{1,2\}$, $N\ge 1,$ ${\theta ^{*}\in {{\mathcal {S}}}}$, ${\hat{\theta _i}} (t_0)\in {{\mathcal {S}}}_{i}$ ($i=1,2$), and $y^*,d \in \ell _{\infty }$; let $\ell \ge 0$ be arbitrary. We know that $\theta ^{*}\in {{\mathcal {S}}}_{i^*}$. Assume that (a) does not hold, i.e. $J_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_{\ell }) > J_{i^*}({{\hat{t}}}_{\ell })$; then according to (56), this means that $\sigma ({{\hat{t}}}_{\ell +1})=i^*$, i.e. (b) will hold. $\square$

In the above we do not make any claim that $\theta ^{*}\in {{\mathcal {S}}}_{\sigma (t)}$ at any time; it only makes a statement about the size of the prediction error. It turns out that this is enough to ensure that closed-loop stability is attained. Next, we present the main result of this section.

8.3 The result

Proof

See Appendix. $\square$

Remark 11

The approach taken in this proof differs a fair bit from that of Theorem 1 and does not make use of Kreisselmeier’s result given in Proposition 2. Indeed, we spend the first half of the proof converting the closed-loop system into a first-order difference inequality which describes the closed-loop system every 2N steps, and the remainder of the proof consists of a modification of the arguments from our earlier work on the first-order one-step-ahead controller [32] to fit this new setting.

Remark 12

It turns out that the controller presented in this section enjoys the same tolerance to slowly time-varying parameters and to unmodelled dynamics as the one designed for the case of ${{\mathcal {S}}}$ convex. First of all, the proof for the case of unmodelled dynamics is identical to that of Theorem 3. Second of all, the proof for the case of time-varying parameters given in Theorem 2 just requires a small adjustment: simply choose the free parameter $m > N_1$ to be an integer multiple of N. Here we have made use of one of the most desirable features of the approach, namely that of modularity.

Remark 13

It is natural to ask if the proposed approach would work if ${{\mathcal {S}}}\subset \bigcup _{i=1}^p {{\mathcal {S}}}_i$ with each ${{\mathcal {S}}}_i$ compact and convex sets and for which the corresponding pair of polynomials $A(z^{-1} )$ and $B(z^{-1} )$ are coprime. (After all, if ${{\mathcal {S}}}$ is simply compact we can use the Heine–Borel Theorem to prove the existence of such ${{\mathcal {S}}}_i$’s.) While the proposed controller (48), (49), (54), (55) and (56) is well defined in this case, we have been unable to prove that it will work; a potential problem is that the switching algorithm could oscillate between two bad choices and never (or rarely) choose the correct one. We are presently working on a more complicated switching algorithm which does not have that problem.

9 Some simulation examples

Here we start with an example which satisfies Assumption 1; in Sect. 9.1 we focus on stability and in Sect. 9.2 we expand this to step tracking. We then move to an example which satisfies Assumption 2 and illustrate the switching controller of Sect. 8.

9.1 Stability

Here we provide an example to illustrate the benefit of the proposed adaptive controller. To this end, consider the second-order plant

$$\begin{aligned} y(t+1) = - a_1(t) y(t) - a_2 (t) y(t-1)+ b_1 (t) u(t) + b_2 (t) u (t-1) + d(t) \end{aligned}$$

with $a_1 (t)\in [0 , 2]$, $a_2 (t) \in [1, 3 ]$, $b_1 (t) \in [0,1]$, and $b_2 (t) \in [-5, -2]$. If the parameters were fixed, then every admissible model is unstable and non-minimum phase, which makes this a challenging plant to control; indeed, it has two complex unstable poles together with a zero that can lie anywhere in $[2, \infty )$. Last of all, for simplicity set $\delta = \infty$.

In this subsection we consider the problem of stability only—we set $y^* = 0$. First, we compare the ideal algorithm (4)–(5) (with projection onto ${{\mathcal {S}}}$) with the classical one (3) (suitably modified to have projection onto ${{\mathcal {S}}}$); in both cases we couple the estimator with the adaptive pole placement controller (11) where we place all closed-loop poles at zero. In the case of the classical estimator (3), we arbitrarily set $\alpha = \beta =1$. Suppose that the plant parameters are constant: $(a_1,a_2,b_1,b_2) = (2,3,1,-2)$, but the initial estimate is set to the midpoint of the interval. In the first simulation we set $y(0) = y(-1) =0.01$ and $u(-1)=0$ and set the noise d(t) to zero—see the top plot of Fig. 1. In the second simulation we set $y(0)= y(-1)=u(-1)=0$ and the noise to $d(t) = 0.01*\sin (5 t)$—see the bottom plot of Fig. 1. In both cases the controller based on the ideal algorithm (4)–(5) is clearly superior to the one based on the classical algorithm (3).

Fig. 1

A comparison of the ideal algorithm (solid) and the classical algorithm (dashed) with a nonzero initial condition and no noise (top plot) and a zero initial condition and noise (bottom plot)

Now we compare the two adaptive controllers when applied to a time-varying version of the plant with unmodelled dynamics, a zero initial condition, and a nonzero noise. More specifically, we set

$$\begin{aligned} a_1 (t)= & {} 1 + \sin (.001t), \; a_2 (t) = 2 + \cos (.001t) , \; b_1 (t) = 0.5 + 0.5 \sin ( .005t) , \\ b_2 (t)= & {} -3.5 +1.5 \sin (.005t) , \;\; d(t) = 0.01 \sin (5t) . \end{aligned}$$

For the unmodelled part of the plant, we use a term of the form discussed in Sect. 6.2:

$$\begin{aligned} m(t+1)= & {} 0.75 m(t) + 0.75 \Vert \phi (t) \Vert , \;\; m(0) = 0 ,\\ d_{ \Delta } (t)= & {} \left\{ \begin{array}{ll} 0 &{} \;\; t=0,1,..., 4999 \\ 0.025 m(t) + 0.025 \Vert \phi (t) \Vert &{} \;\; t \ge 5000. \end{array} \right. \end{aligned}$$

We plot the result in Fig. 2. We see that the controller based on the ideal algorithm is clearly superior to the one based on the classical algorithm, in the sense that the average size of the output y(t) is smaller (by a factor of about three), and the parameter estimates are more accurate; the latter property stems from the fact that the classical estimator tends to have a low gain when the signals are small, unlike the ideal estimator.

Fig. 2

The system behaviour with time-varying parameters and unmodelled dynamics; the parameters are dashed and the estimates are solid. The ideal algorithm is used in the left-most plots, while the classical algorithm is used in the right-most plots

9.2 Step tracking

The plant in the previous subsection has a large amount of uncertainty, as well as a wide range of unstable poles and non-minimum phase zeros, which means that there are limits on the quality of the transient behaviour even if the parameters were fixed and known. Hence, to illustrate the tracking ability we look at a subclass of systems: one with $a_1$ and $b_1$ as before, namely $a_1 (t)\in [0 , 2]$ and $b_1 (t) \in [0,1]$, but now with $a_2 = 1$ and $b_2 = -3.5$. With fixed parameters the corresponding system is still unstable and non-minimum phase.

We simulate the closed-loop pole placement step tracking controller of Sect. 7 with a zero initial condition, initial parameter estimates at the midpoints of the admissible intervals, and with time-varying parameters:

$$\begin{aligned} a_1 (t) = 1 + \sin (.002t), b_1 (t) = 0.5 + 0.5 \cos ( .005t) , \end{aligned}$$

with a nonzero disturbance:

$$\begin{aligned} d(t) = \left\{ \begin{array}{ll} 0.01 \sin (5t) &{} \;\; t =0,1,..., 2499 \\ 0.05 \sin (5t) &{} \;\; t = 2500,..., 4999, \end{array} \right. \end{aligned}$$

and a square wave reference signal of $y^*(t) = \text{ sgn } [ sin (0.01t)]$. We plot the result in Fig. 3; we see that the parameter estimates crudely follows the system parameters, with less accuracy than in the previous subsection, partly due to the fact that the constant setpoint dominates the estimation process and leads to higher inaccuracy. As a result, y(t) does a good job of following $y^*$ on average, but with the occasional flurry of activity when the parameter estimates are highly inaccurate. When the noise is increased fivefold at $k=2500$, the behaviour degrades only slightly.

Fig. 3

The pole placement tracking controller with time-varying parameters and small noise; the parameters are dashed and the estimates are solid

9.3 Removing convexity assumption

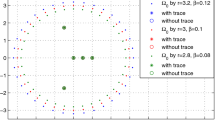
Next we illustrate the case when the set of admissible plant parameters satisfies Assumption 2 but not Assumption 1; we will consider a second-order plant with $\theta ^*$ belonging to ${{\mathcal {S}}}\subset {{\mathcal {S}}}_1 \cup {{\mathcal {S}}}_2$, with ${{\mathcal {S}}}_1$ equal to the set ${{\mathcal {S}}}$ of the previous example and ${{\mathcal {S}}}_2$ equal to ${{\mathcal {S}}}_1$ but with a sign added on the $b_i$ parameters:

$$\begin{aligned} {{\mathcal {S}}}_1:= & {} \left\{ \left[ {\begin{matrix}a_1 \\ a_2 \\ b_1 \\ b_2\end{matrix}} \right] \in {\mathbf{R}}^4: a_1\in [0,2],a_2\in [1,3],b_1\in [0,1],b_2\in [-5,-2]\right\} , \\ {{\mathcal {S}}}_2:= & {} \left\{ \left[ {\begin{matrix}a_1 \\ a_2 \\ b_1 \\ b_2\end{matrix}} \right] \in {\mathbf{R}}^4: a_1\in [0,2],a_2\in [1,3],b_1\in [-1,0],b_2\in [2,5]\right\} ; \end{aligned}$$

notice that convex hull of ${{\mathcal {S}}}_1 \cup {{\mathcal {S}}}_2$ includes the case of having $b_1 = b_2=0$, which means that the corresponding system is not stabilizable. We will apply the proposed controller of Sect. 8 to the time-varying plant with a zero initial condition and reference signal, and a nonzero noise. Specifically, we set $a_1(t)$ and $a_2(t)$ as in Sect. 9.1:

$$\begin{aligned} a_1 (t) = 1 + \sin (.001t), \quad a_2 (t) = 2 + \cos (.001t) , \; \end{aligned}$$

but now we set $b_1(t)$ and $b_2(t)$ to be

$$\begin{aligned} b_1 (t) = \left\{ \begin{array}{ll} -0.5 -0.5 \sin (.005t) &{} 1500\le t<8000 \\ 0.5 +0.5 \sin (.005t) &{} \text {otherwise,} \end{array} \right. \\ b_2 (t) = \left\{ \begin{array}{ll} 3.5 -1.5 \sin (.005t) &{} 1500\le t<8000 \\ -3.5 +1.5 \sin (.005t) &{} \text {otherwise.} \end{array} \right. \end{aligned}$$

We apply the proposed switching controller consisting of the estimator (48), (49), the control law (54), the performance signal (55) and the switching rule (56); we choose $N=2n=4$. Here we also set $y^{*}=0$, $y(0)=y(-1)=u(-1)=0$ and the noise to $d(t)=0.01\sin (5t)$. Initial parameter estimates ${\hat{\theta }}_i(0)$ are set to the midpoints of each respective interval, and we set $\sigma _0=2$.

The result for this case is plotted in Fig. 4; we see that the controller does a reasonable job, even though the switching algorithm often chooses the wrong model. Larger transients (than in the simulation of Sect. 9.1) occasionally ensue, but on average the adaptive controller provides good performance. Furthermore, the estimator does a fairly good job of tracking the time-varying parameter.

Fig. 4

The upper plot shows the system output. The next four plots show the parameter estimates ${\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )$ (dashed) and actual plant parameters (solid). The bottom plot shows the switching signal $\sigma ({{\hat{t}}}_\ell )$ (dashed) and the correct index (solid)

10 Summary and conclusions

Here we show that if the original, ideal, projection algorithm is used in the estimation process (subject to the assumption that the plant parameters lie in a convex, compact set), then the corresponding pole placement adaptive controller guarantees linear-like convolution bounds on the closed-loop behaviour, which confers exponential stability and a bounded noise gain (in every p-norm with $1 \le p \le \infty$), unlike almost all other parameter adaptive controllers. This can be leveraged to prove tolerance to unmodelled dynamics and plant parameter variation. We emphasize that there is no persistent excitation requirement of any sort; the improved performance arises from the vigilant nature of the ideal parameter estimation algorithm.

As far as the author is aware, the linear-like convolution bound proven here is a first in parameter adaptive control. It allows a modular approach to be used in analysing time-varying parameters and unmodelled dynamics. This approach avoids all of the fixes invented in the 1980s, such as signal normalization and deadzones, used to deal with the lack of robustness to unmodelled dynamics and time-varying parameters.

In the present paper the standard assumption is that the set of plant parameters lies in a compact and convex set. In Sect. 8 we relaxed the convexity requirement a bit: there the goal is to place all poles at the origin, and the convexity requirement is weakened to requiring that the set of admissible parameters lie in the union of two convex sets; two parameter estimators are used together with a switching algorithm to choose which estimator to use at each point in time. We are working at removing the convexity requirement altogether: the idea is to utilize the Heine–Borel theorem to prove that the compact set of admissible parameters lies in a finite union of convex set (for which the corresponding numerator and denominator polynomials are coprime), use a parameter estimator for each, and then design a switching algorithm to switch between them. While the (natural extension of) the switching algorithm for the case of two convex sets does not appear to work in the general case, we are presently analysing a more complicated algorithm.

We are presently working on extending the approach to the model reference adaptive control setting; the analysis is turning out to be more complicated than here, in large part due to the facts that the controller is not strictly causal (as it is here) and that a system delay (or the relative degree of the plant transfer function) creates additional complexity. Extending the approach to the continuous-time setting may prove challenging, since a direct application would yield a non-Lipschitz continuous estimator, which brings with it mathematical solvability issues.

11 Appendix

Proof of Proposition 1:

Since projection does not make the parameter estimate worse, it follows from (7) that

$$\begin{aligned} \Vert {\hat{\theta }} (t+1) - {\hat{\theta }} (t) \Vert \le \Vert {\check{\theta }} (t+1) - {\hat{\theta }} (t) \Vert\le & {} \Vert {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ \phi (t)}{ \phi (t)^T \phi (t)} e(t+1) \Vert \\\le & {} {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ |e(t+1)| }{ \Vert \phi (t) \Vert } , \quad t \ge t_0 . \end{aligned}$$

so the first inequality holds.

We now turn to energy analysis. We first define $\tilde{{\check{\theta }}} (t):= {\check{\theta }} (t) - \theta ^*$ and ${\check{V}} (t) := {\tilde{\check{\theta }}}(T)^T {\tilde{\check{\theta }}}(t)$. Next, we subtract $\theta ^*$ from each side of (7), yielding

$$\begin{aligned} {\tilde{\check{\theta }}}(t+1)= & {} {\tilde{\theta }} (t) + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ \phi (t)}{ \phi (t)^T \phi (t)} [ -\phi (t)^T {\tilde{\theta }} (t) + d(t) ] \\= & {} \left[ I - \underbrace{{\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ \phi (t) \phi (t)^T}{ \phi (t)^T \phi (t)}}_{=: W_1 (t)} \right] {\tilde{\theta }} (t) + \underbrace{ {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ \phi (t)}{ \phi (t)^T \phi (t)}}_{=: W_2 (t)} d(t) . \end{aligned}$$

Then

$$\begin{aligned} {\check{V}} (t+1)= & {} [ (I-W_1(t)) \tilde{\theta }(t) + W_2 (t) d(t) ]^T \times [ (I-W_1(t)) \tilde{\theta }(t) + W_2 (t) d(t) ] \\= & {} \tilde{\theta }(t)^T [ I - W_1(t)] [ I - W_1(t)] \tilde{\theta }(t) \\&+ 2 \tilde{\theta }(t)^T [I - W_1(t)] W_2(t) d(t) + W_2(t)^T W_2(t) d(t)^2 . \end{aligned}$$

Now let us analyse the three terms on the RHS: the fact that $W_1(t)^2= W_1(t)$ allows us to simplify the first term; the fact that $W_1 (t) W_2 (t) = W_2 (t)$ means that the second term is zero; $W_2 (t)^T W_2 (t) = {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{1}{ \phi (t)^T \phi (t)}$, which simplifies the third term. We end up with

$$\begin{aligned} {\check{V}} (t+1)= & {} \tilde{\theta }(t)^T [ I - W_1(t)] \tilde{\theta }(t) + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{d(t)^2}{ \phi (t)^T \phi (t) } \\= & {} V(t) - {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ [ \tilde{\theta }(t)^T \phi (t)]^2}{ \phi (t)^T \phi (t)} + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{d(t)^2}{ \phi (t)^T \phi (t)} \\= & {} V(t) + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ d(t)^2 - [d (t)-e(t+1)]^2}{ \phi (t)^T \phi (t)} \\\le & {} V(t) + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ - \frac{1}{2} e(t+1)^2 + 2 d(t)^2}{\phi (t)^T \phi (t)} . \end{aligned}$$

Since projection never makes the estimate worse, it follows that

$$\begin{aligned} V(t+1) \le V(t) + {\rho _{\delta } ( \phi (t) , e(t+1))}\frac{ - \frac{1}{2} e(t+1)^2 + 2 d(t)^2}{\phi (t)^T \phi (t)} . \end{aligned}$$

$\square$

Proof of Lemma 1:

Fix $\delta \in ( 0 , \infty ]$ and $\sigma \in ( {\underline{\lambda }} , 1)$. First of all, it is well known that the characteristic polynomial of ${\bar{A}} (t)$ is exactly $z^{2n} A^* (z^{-1})$ for every $t \ge t_0$. Furthermore, it is well known that the coefficients of ${\hat{L}} (t, z^{-1} )$ and ${\hat{P}} (t,z^{-1} )$ are the solution of a linear equation, and are analytic functions of ${\hat{\theta }} (t) \in {{\mathcal {S}}}$. Hence, there exists a constant $\gamma _1$ so that, for every set of initial conditions, $y^* \in {l_{\infty }}$ and $d \in {l_{\infty }}$, we have $\sup _{t \ge t_0} \Vert {\bar{A}} (t) \Vert \le \gamma _1$.

To prove the first bound, we now invoke the argument used in [40], who considered a more general time-varying situation but with more restrictions on $\sigma$. By making a slight adjustment to the first part of the proof given there, we can prove that with $\gamma _2 := \sigma \frac{ (\sigma + \gamma _1 )^{2n-1}}{ ( \sigma - {\underline{\lambda }} )^{2n}}$, then for every $t \ge t_0$ we have $\Vert {\bar{A}} (t) ^k \Vert \le \gamma _2 \sigma ^{k} , \;\; k \ge 0$, as desired.

Now we turn to the second bound. From Proposition 1 and the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \sum _{j=k}^{t-1} \Vert {\hat{\theta }} (j+1) - {\hat{\theta }} (j) \Vert\le & {} \sum _{j=k}^{t-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{| e(j+1) |}{\Vert \phi (j)\Vert } \\\le & {} \left[ \sum _{j=k}^{t-1} {\rho _{\delta } ( \phi (j) , e(j+1))}\frac{e(j+1)^2}{\Vert \phi (j)\Vert ^2} \right] ^{1/2} ( t-k)^{1/2} . \end{aligned}$$

Now notice that

$$\begin{aligned}&\Vert {\bar{A}} (t+1) - {\bar{A}} (t) \Vert \le \Vert {\hat{\theta }} (t+1) - {\hat{\theta }} (t) \Vert \\&\quad + \sum _{i=1}^n ( | {\hat{l}}_i (t+1) - {\hat{l}}_i (t) | + | {\hat{p}}_i (t+1) - {\hat{p}}_i (t) | ) . \end{aligned}$$

The fact that the coefficients of ${\hat{L}} (t, z^{-1} )$ and ${\hat{P}} (t,z^{-1} )$ are analytic functions of ${\hat{\theta }} (t) \in {{\mathcal {S}}}$ means that there exists a constant $\gamma _3 \ge 1$ so that

$$\begin{aligned} \sum _{j=k}^{t-1} \Vert {\bar{A}} (j+1) - {\bar{A}} (j) \Vert \le \gamma _3 \sum _{j=k}^{t-1} \Vert {\hat{\theta }} (j+1) - {\hat{\theta }} (j) \Vert , \end{aligned}$$

so we conclude that the second bound holds as well. $\Box$

In order to prove Theorem 4, we need some preliminary results. The first step is to extend Proposition 1 to the case when $\theta ^*$ may not lie in ${{\mathcal {S}}}_{i}$.

Proof

Since projection does not make the parameter estimate worse, it follows from (48) and (49) that when $\phi (t)\ne 0$,

$$\begin{aligned} \Vert {\hat{\theta }}_i (t+1) - {\hat{\theta }}_i (t) \Vert \le \Vert {\check{\theta }}_i (t+1) - {\hat{\theta }}_i (t) \Vert\le & {} \left\| \frac{\phi (t)e_i(t+1)}{\Vert \phi (t)\Vert ^2}\right\| \le \frac{ |e_i(t+1)| }{ \Vert \phi (t) \Vert }, \end{aligned}$$

(59)

and when $\phi (t)=0$,

$$\begin{aligned} \Vert {\hat{\theta }}_i (t+1) - {\hat{\theta }}_i (t) \Vert =0. \end{aligned}$$

The result follows by iteration. $\square$

The next result produces a crude bound on the closed-loop behaviour.

Proposition 4

Consider the plant (1) and suppose that the controller consisting of the estimator (48), (49) and the control law (54) is applied.⁸ Then for every $p\ge 0$, there exists a constant ${{\bar{c}}}\ge 1$ such that for every $t_0\in \mathbf{Z}$, $t\ge t_0$, $\phi _0\in \mathbf{R}^{2n}$, ${\theta ^{*}\in {{\mathcal {S}}}}$, ${\hat{\theta _i}} (t_0)\in {{\mathcal {S}}}_{i}$ ($i=1,2$) and $y^*,d \in {\varvec{\ell }}_{\infty }$:

$$\begin{aligned} \Vert \phi (t+p)\Vert \le {{\bar{c}}}\Vert \phi (t)\Vert + {{\bar{c}}} \sum _{j=0}^{p-1} (|d(t+j)|+|r(t+j)|). \end{aligned}$$

(60)

Proof

Fix $p\ge 0$. Let $t_0\in \mathbf{Z}$, $t\ge t_0$, $\phi _0\in \mathbf{R}^{2n}$, ${\theta ^{*}\in {{\mathcal {S}}}}$, ${\hat{\theta _i}} (t_0)\in {{\mathcal {S}}}_{i}$ ($i=1,2$) and $y^*,d \in {\varvec{\ell }}_{\infty }$ be arbitrary. From (1) we see that

$$\begin{aligned} |y(t+1)|\le \Vert {{\mathcal {S}}}\Vert \Vert \phi (t)\Vert +|d(t)|. \end{aligned}$$

From (54) and Assumption 2, we have that there exists a constant $\gamma$ so that

$$\begin{aligned} |u(t+1)|\le \gamma \Vert \phi (t)\Vert +|r(t)|. \end{aligned}$$

From the definition of $\Vert \phi (t+1)\Vert$, we have that

$$\begin{aligned} \Vert \phi (t+1)\Vert \le \Vert \phi (t)\Vert +|y(t+1)|+|u(t+1)|. \end{aligned}$$

Combining these three bounds, we end up with

$$\begin{aligned} \Vert \phi (t+1)\Vert \le \underbrace{\left( 1+\Vert {{\mathcal {S}}}\Vert +\gamma \right) }_{=:{{\bar{a}}}} \Vert \phi (t)\Vert +|r(t)|+|d(t)|. \end{aligned}$$

Solving iteratively, we have

$$\begin{aligned} \Vert \phi (t+p)\Vert\le & {} {{\bar{a}}}^{p}\Vert \phi (t)\Vert +\sum _{j=0}^{p-1} {{\bar{a}}}^{p-j-1} (|d(t+j)|+|r(t+j)|) \\\le & {} {{\bar{a}}}^{p}\Vert \phi (t)\Vert + {{\bar{a}}}^{p-1} \sum _{j=0}^{p-1} (|d(t+j)|+|r(t+j)|). \end{aligned}$$

Put ${{\bar{c}}}:={{\bar{a}}}^{p}$ to conclude the proof. $\square$

We now state a technical result which we used in [32] to analyse the first-order one-step-ahead adaptive control problem.

Proof of Theorem 4:

Fix $\lambda \in (0,1)$ and $N\ge 2n$. Let $t_0\in \mathbf{Z}$, ${\phi _0 \in {\mathbf{R}}^{2n}}$, $\sigma _{0}\in \{1,2\}$, ${\theta ^{*} \in {{\mathcal {S}}}}$, ${\hat{\theta _i}} (t_0)\in {{\mathcal {S}}}_{i}$ ($i=1,2$), and $y^*,d \in \ell _{\infty }$ be arbitrary; as usual, we let $i^*$ denote the smallest $j\in \{1,2\}$ which satisfies $\theta ^{*}\in {{\mathcal {S}}}_{j}$.

As mentioned at the beginning of Sect. 8, the proposed controller is based on the first-order one-step-ahead control setup [41], although it is more complicated. The proof also uses similar ideas as those used in [41], but as our system is more complicated, it should not be surprising that the proof is significantly different and much more complicated. Hence, before proceeding we provide a proof outline: using the definition of ${{\hat{t}}}_\ell$ given in Sect. 8.2:

• 1. first, we define a state-space equation describing $\phi (t)$ which holds on intervals of the form $[{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1})$;

• 2. second, we analyse this equation, getting a bound on $\Vert \phi ({{\hat{t}}}_{\ell +1})\Vert$ in terms of $\Vert \phi ({{\hat{t}}}_{\ell })\Vert$ and the exogenous inputs;

• 3. we apply Lemma 2 and Proposition 4 to obtain a bound on $\Vert \phi ({{\hat{t}}}_{\ell +2})\Vert$ in terms of $\Vert \phi ({{\hat{t}}}_{\ell })\Vert$; i.e. we analyse two intervals at a time;

• 4. fourth, we then analyse the associated difference inequality (relating $\Vert \phi ({{\hat{t}}}_{\ell +2})\Vert$ in terms of $\Vert \phi ({{\hat{t}}}_{\ell })\Vert$) in a way similar (though not identical) to that used in [41].

Step 1: $\underline{\hbox {Obtain a state-space model describing } \phi (t) \hbox { for } t\in [{{\hat{t}}}_{\ell },{{\hat{t}}}_{\ell +1}).}$

By definition of the prediction error (47) and by the property of the switching signal (53) being constant on $[{{\hat{t}}}_{\ell },{{\hat{t}}}_{\ell +1})$, we have

$$\begin{aligned} y(t+1)= & {} \phi (t)^T{\hat{\theta }}_{\sigma (t)}(t)+e_{\sigma (t)}(t+1) \nonumber \\= & {} \phi (t)^T{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}(t)+e_{\sigma ({{\hat{t}}}_\ell )}(t+1) + \phi (t)^T{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )-\phi (t)^T{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell ) \nonumber \\= & {} {\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )^T\phi (t)+\left[ {\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}(t)-{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\right] ^T\phi (t)\nonumber \\&+e_{\sigma ({{\hat{t}}}_\ell )}(t+1),\;\; t\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}). \end{aligned}$$

(61)

From the control law (54) and the control gains (52), we have

$$\begin{aligned} u(t+1)= & {} K_{\sigma (t)}(t)^T\phi (t)+r(t) \nonumber \\= & {} K_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )^T\phi (t)+r(t),\qquad t\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}). \end{aligned}$$

(62)

We now derive a state-space equation for $\phi (t)$ in much the same way as (13) was derived; we first define

$$\begin{aligned}&{{{\bar{A}}}_{\sigma (j)}(j)}\\&\quad :=\begin{bmatrix} -{\hat{a}}_{\sigma (j),1}(j)&-{\hat{a}}_{\sigma (j),2}(j)&\cdots&-{\hat{a}}_{\sigma (j),n}(j)&{\hat{b}}_{\sigma (j),1}(j)&\cdots&\cdots&{\hat{b}}_{\sigma (j),n}(j) \\ 1&0&\cdots&0&0&\cdots&\cdots&0 \\&\ddots&\vdots&\vdots&\cdots&\cdots&\vdots \\&1&0&0&\cdots&\cdots&0 \\ - {\hat{p}}_{\sigma (j),1}(j)&- {\hat{p}}_{\sigma (j),2}(j)&\cdots&-{\hat{p}}_{\sigma (j),n}(j)&- {\hat{l}}_{\sigma (j),1}(j)&-{\hat{l}}_{\sigma (j),2}(j)&\cdots&- {\hat{l}}_{\sigma (j),n}(j) \\ 0&\cdots&\cdots&0&1&0&\cdots&0 \\ \vdots&\cdots&\cdots&\vdots&\ddots&\vdots \\ 0&\cdots&\cdots&0&&1&0 \end{bmatrix}; \end{aligned}$$

then, in light of (61) and (62), the following holds:

$$\begin{aligned}&\phi (t+1)={{\bar{A}}}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\phi (t)\nonumber \\&\quad + B_1 \left( \left[ {\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}(t)-{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\right] ^T\phi (t) + e_{\sigma ({{\hat{t}}}_\ell )}(t+1)\right) +B_2r(t),\nonumber \\&t\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}),\ell \in \mathbf{Z}^+; \end{aligned}$$

(63)

notice the additional term $\left[ {\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}(t)-{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\right]$ on the right-hand side which (13) does not have.

Step 2: $\underline{\hbox {Obtain a bound on } \Vert \phi ({{\hat{t}}}_{\ell +1})\Vert \hbox { in terms of } \Vert \phi ({{\hat{t}}}_{\ell })\Vert .}$

In (63) we have ${{\bar{A}}}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\in \mathbf{R}^{2n\times 2n}$ to be a constant matrix with all eigenvalues equal to zero; since $N\ge 2n$, clearly

$$\begin{aligned} \left[ {{{\bar{A}}}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )}\right] ^{{{\hat{t}}}_{\ell +1}-{{\hat{t}}}_{\ell }}=\left[ {{{\bar{A}}}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )}\right] ^N=0. \end{aligned}$$

So, solving (63) for $\phi ({{\hat{t}}}_{\ell +1})$ yields

$$\begin{aligned}&\phi ({{\hat{t}}}_{\ell +1})\nonumber \\&=\sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \left[ {{{\bar{A}}}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )}\right] ^{{{\hat{t}}}_{\ell +1}-j-1} \biggl ({B}_1 \biggl (\left[ {\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}(j)-{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\right] ^T\phi (j)+ e_{\sigma ({{\hat{t}}}_\ell )}(j+1)\biggr )\nonumber \\&\quad +B_2r(j)\biggr ). \end{aligned}$$

(64)

It follows from the compactness of ${{\mathcal {S}}}$ and the ${{\mathcal {S}}}_i$’s that $\left\| \left[ {{{\bar{A}}}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )}\right] ^j\right\| ,\; j=0,1\ldots ,N-1$, is bounded above by a constant which we label $c_1$. Using this fact together with Proposition 3 which provides a bound on the difference between parameter estimates at two different points in time, we obtain

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{\ell +1})\Vert\le & {} c_1 \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \left( \left\| {\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}(j)-{\hat{\theta }}_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\right\| \Vert \phi (j)\Vert +|e_{\sigma ({{\hat{t}}}_\ell )}(j+1)|+|r(j)| \right) \\\le & {} c_1 \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \left( \left[ \sum _{q={{\hat{t}}}_\ell ,\phi (q)\ne 0}^{j-1}\frac{|e_{\sigma ({{\hat{t}}}_\ell )}(q+1)|}{\Vert \phi (q)\Vert } \right] \Vert \phi (j)\Vert +|e_{\sigma ({{\hat{t}}}_\ell )}(j+1)|+|r(j)| \right) . \end{aligned}$$

By definition of the prediction error, if $\phi (j)=0$ then

$$\begin{aligned} |e_i(j+1)|=|d(j)|, \end{aligned}$$

and if $\phi (j)\ne 0$, then

$$\begin{aligned} |e_i(j+1)|=\frac{|e_i(j+1)|}{\Vert \phi (j)\Vert }\Vert \phi (j)\Vert . \end{aligned}$$

Incorporating this into the above inequality yields

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{\ell +1})\Vert\le & {} c_1 \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \left( \left[ \sum _{q={{\hat{t}}}_\ell ,\phi (q)\ne 0}^{j}\frac{|e_{\sigma ({{\hat{t}}}_\ell )}(q+1)|}{\Vert \phi (q)\Vert } \right] \Vert \phi (j)\Vert +|d(j)|+|r(j)| \right) \nonumber \\\le & {} c_1 \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \left( \left[ \sum _{q={{\hat{t}}}_\ell ,\phi (q)\ne 0}^{{{\hat{t}}}_{\ell +1}-1}\frac{|e_{\sigma ({{\hat{t}}}_\ell )}(q+1)|}{\Vert \phi (q)\Vert } \right] \Vert \phi (j)\Vert +|d(j)|+|r(j)| \right) \nonumber \\= & {} c_1\left[ \sum _{q={{\hat{t}}}_\ell ,\phi (q)\ne 0}^{{{\hat{t}}}_{\ell +1}-1}\frac{|e_{\sigma ({{\hat{t}}}_\ell )}(q+1)|}{\Vert \phi (q)\Vert } \right] \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \Vert \phi (j)\Vert +c_1\sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1}(|d(j)|+|r(j)|) \nonumber \\\le & {} c_1({{\hat{t}}}_{\ell +1}-{{\hat{t}}}_{\ell }) \left[ \underset{{j\in [{{\hat{t}}}_\ell ,{{\hat{t}}}_{\ell +1}), \phi (j)\ne 0}}{\max } \frac{|e_{\sigma ({{\hat{t}}}_\ell )}(j+1)|}{\Vert \phi (j)\Vert } \right] \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \Vert \phi (j)\Vert \nonumber \\&\quad +c_1\sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1}(|d(j)|+|r(j)|). \end{aligned}$$

(65)

Since ${{\hat{t}}}_{\ell +1}-{{\hat{t}}}_{\ell }=N$, it follows from Proposition 4 that there exists a constant $c_2$ so that the following holds:

$$\begin{aligned} \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} \Vert \phi (j)\Vert\le & {} c_2\Vert \phi ({{\hat{t}}}_\ell )\Vert +c_2\sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-2} (|d(j)|+|r(j)|); \end{aligned}$$

(66)

so, substituting (66) into (65) and using the definition of the performance signal $J_{\sigma ({{\hat{t}}}_\ell )}(\cdot )$ given in (55) it follows that there exists a constant $c_3$ so that

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{\ell +1})\Vert\le & {} c_1N J_{\sigma ({{\hat{t}}}_\ell )} \left( c_2\Vert \phi ({{\hat{t}}}_\ell )\Vert +c_2\sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-2} (|d(j)|+|r(j)|) \right) \nonumber \\&+ c_1\sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1}(|d(j)|+|r(j)|) \nonumber \\\le & {} c_3 J_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell ) \Vert \phi ({{\hat{t}}}_\ell )\Vert +c_3\left( 1+ J_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_\ell )\right) \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} (|d(j)|+|r(j)|).\nonumber \\ \end{aligned}$$

(67)

Step 3: $\underline{\hbox {Apply Lemma}~2 \hbox { and Proposition}~4 \hbox { to obtain a bound on } \Vert \phi ({{\hat{t}}}_{\ell +2})\Vert \hbox { in terms of }}$ $\underline{\Vert \phi ({{\hat{t}}}_{\ell })\Vert .}$

From Lemma 2 either

$$\begin{aligned} J_{\sigma ({{\hat{t}}}_\ell )}({{\hat{t}}}_{\ell })\le J_{i^*}({{\hat{t}}}_{\ell }) \end{aligned}$$

(68)

or

$$\begin{aligned} J_{\sigma ({{\hat{t}}}_{\ell +1})}({{\hat{t}}}_{\ell +1})\le J_{i^*}({{\hat{t}}}_{\ell +1}). \end{aligned}$$

(69)

If (68) is true, then we can substitute this into (67) to obtain a bound on $\Vert \phi ({{\hat{t}}}_{\ell +1})\Vert$ in terms of $J_{i^*}({{\hat{t}}}_{\ell })$ and then apply Proposition 4 to get a bound on $\Vert \phi ({{\hat{t}}}_{\ell +2})\Vert$ in terms of $\Vert \phi ({{\hat{t}}}_{\ell +1})\Vert$ and the exogenous inputs; it follows that there exists a constant $c_4$ so that

$$\begin{aligned}&\Vert \phi ({{\hat{t}}}_{\ell +2})\Vert \le c_3c_4 J_{i^*}({{{\hat{t}}}_\ell }) \Vert \phi ({{\hat{t}}}_\ell )\Vert \nonumber \\&\quad + c_3c_4\left( 1+ J_{i^*}({{{\hat{t}}}_\ell })\right) \sum _{j={{\hat{t}}}_\ell }^{{{\hat{t}}}_{\ell +1}-1} (|d(j)|+|r(j)| )+c_4 \sum _{j={{\hat{t}}}_{\ell +1}}^{{{\hat{t}}}_{\ell +2}-1} (|d(j)|+|r(j)|). \end{aligned}$$

(70)

On the other hand, if (69) is true, we can use (67) to get a bound on $\Vert \phi ({{\hat{t}}}_{\ell +2})\Vert$ in terms of $J_{i^*}({{\hat{t}}}_{\ell +1})$, and then apply Proposition 4 to get a bound on $\Vert \phi ({{\hat{t}}}_{\ell +1})\Vert$ in terms of $\Vert \phi ({{\hat{t}}}_{\ell })\Vert$; it follows that there exists a constant $c_5$ so that

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{\ell +2})\Vert \le c_3 c_5 J_{i^*}({{\hat{t}}}_{\ell +1}) \Vert \phi ({{\hat{t}}}_\ell )\Vert+ & {} c_3 c_5 J_{i^*}({{\hat{t}}}_{\ell +1}) \sum _{j={{\hat{t}}}_{\ell }}^{{{\hat{t}}}_{\ell +1}-1} (|d(j)|+|r(j)|)\nonumber \\+ & {} c_3\left( 1+ J_{i^*}({{\hat{t}}}_{\ell +1})\right) \sum _{j={{\hat{t}}}_{\ell +1}}^{{{\hat{t}}}_{\ell +2}-1} (|d(j)|+|r(j)|).\nonumber \\ \end{aligned}$$

(71)

If we define $\alpha ({{\hat{t}}}_\ell ):= \max \{J_{i^*}({{\hat{t}}}_\ell ),J_{i^*}({{\hat{t}}}_{\ell +1})\}$, then there exists a constant $c_6$ so that (70) and (71) can be combined to yield

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{\ell +2})\Vert \le c_6 \alpha ({{\hat{t}}}_{\ell }) \Vert \phi ({{\hat{t}}}_\ell )\Vert + c_6\left( 1+\alpha ({{\hat{t}}}_{\ell })\right) \sum _{j={{\hat{t}}}_{\ell }}^{{{\hat{t}}}_{\ell +2}-1}( |d(j)|+|r(j)|),\qquad \ell \in \mathbf{Z}^+. \end{aligned}$$

(72)

Step 4: Analyse the first-order difference inequality (72).

First, we change notation in (72) to facilitate analysis:

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{2j+2})\Vert \le c_6 \alpha ({{\hat{t}}}_{2j}) \Vert \phi ({{\hat{t}}}_{2j})\Vert + c_6\left( 1+\alpha ({{\hat{t}}}_{2j})\right) \sum _{q={{\hat{t}}}_{2j}}^{{{\hat{t}}}_{2j+2}-1} (|d(q)|+|r(q)|),\qquad j\in \mathbf{Z}^+ . \end{aligned}$$

(73)

Next, we will analyse (73) to obtain a bound on the closed-loop behaviour; we consider two cases—one with noise and one without.

Case 1: $d(t)=0$ for all $t\ge t_0$.

From Proposition 1 and the definition of $\alpha (\cdot )$, we have

$$\begin{aligned} \sum _{q=0}^{j-1} \alpha ({{\hat{t}}}_{2q})^2\le & {} \sum _{p=t_0,\phi (p)\ne 0}^{t_0+jN-1} \frac{|e_{i^*}(p+1)|^2}{\Vert \phi (p)\Vert ^2}\nonumber \\\le & {} 2[V(t_0)-V(t_0+jN)] \le 2V( t_0) \le 8\Vert {{\mathcal {S}}}_{i^*}\Vert ^2\nonumber \\\le & {} 8{\bar{\mathbf{{s}}}}^2 =:c_7, \; j\ge 1. \end{aligned}$$

(74)

If we use this bound in the second occurrence of $\alpha ({{\hat{t}}}_{2j})$ in (73), we obtain

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{2j+2})\Vert \le c_6 \alpha ({{\hat{t}}}_{2j}) \Vert \phi ({{\hat{t}}}_{2j})\Vert + \underbrace{c_6(1+\sqrt{c_7})}_{=:c_8} \underbrace{\sum _{q={{\hat{t}}}_{2j}}^{{{\hat{t}}}_{2j+2}-1} |r(q)|}_{=:{{\bar{r}}}(j)},\qquad j\in \mathbf{Z}^+ . \end{aligned}$$

(75)

Since $\lambda \in (0,1)$ and $c_6\ge 1$, then it follows that $\lambda _1:=\frac{\lambda ^{2N}}{c_6}\in (0,1)$. By Lemma 3(i) if we define $c_9:=c_7^{\frac{c_7+1}{2}}(\frac{1}{\lambda _1})^{\frac{c_7}{\lambda _1^2}+1}$ and use the fact that $\alpha ({{\hat{t}}}_{2j})\ge 0$, we see that

$$\begin{aligned} {\prod }_{q=0}^{j-1} \alpha ({{\hat{t}}}_{2q})\le c_9 \lambda _1^{j}\;\; j\in \mathbf{Z}^+, \end{aligned}$$

(76)

which, in turn, implies that

$$\begin{aligned} {\prod }_{q=0}^{j-1} [c_6 \alpha ({{\hat{t}}}_{2q})] \le c_9 \lambda ^{2j N},\;\; j\in \mathbf{Z}^+. \end{aligned}$$

(77)

Solving (75) iteratively and using this bound, we obtain

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{2j})\Vert \le c_9 \lambda ^{2jN} \Vert \phi ({{\hat{t}}}_0)\Vert + \sum _{q=0}^{j-1} c_9c_8 \left( \lambda ^{2N} \right) ^{j-1-q} {{\bar{r}}}(q),\;\; j\in \mathbf{Z}^+. \end{aligned}$$

(78)

Using Proposition 4 to obtain a bound on $\phi (t)$ between ${{\hat{t}}}_{2j}$ and ${{\hat{t}}}_{2j+2}$, we conclude that there exists a constant $c_{10}$ so that

$$\begin{aligned} \Vert \phi (t)\Vert \le c_{10} \lambda ^{t-t_0} \Vert \phi (t_0)\Vert +\sum _{j=t_0}^{t-1}c_{10}\lambda ^{t-j-1}|r(j)|,\qquad t\ge t_0. \end{aligned}$$

(79)

Case 2: $d(t)\ne 0$ for some $t\ge t_0$.

We now analyse the case when there is noise entering the system. Here the analysis will use a similar (but not identical) approach to that of Case 2 in the proof of Theorem 1. Motivated by Case 1, in the following we will be applying Lemma 3(ii) with a larger bound than in (74); define $c_{11}:=8(1+N){\bar{\mathbf{{s}}}}^2$. We also define $\lambda _{1}=\frac{\lambda ^{2N}}{c_6}$ and $\nu := \left\lceil { \frac{ {\frac{c_{11}+1}{2}}\ln {(c_{11})} +(4{\frac{c_{11}}{\lambda _1^2}}+1)(\ln {(2)}-\ln {(\lambda _1)})}{\ln {(2)}}}\right\rceil .$

We now partition the timeline into two parts: one in which the noise is small versus $\phi$ and one where it is not. With $\nu$ defined above, we define

$$\begin{aligned} S_{\mathrm{good}}= & {} \left\{ j\ge t_0:\phi (j)\ne 0 \text { and } \tfrac{|d(j)|^2}{\Vert \phi (j)\Vert ^2}<\tfrac{{\bar{\mathbf{{s}}}}^2}{\nu }\right\} ,\\ S_{\mathrm{bad}}= & {} \left\{ j\ge t_0:\phi (j)=0 \text { or } \tfrac{|d(j)|^2}{\Vert \phi (j)\Vert ^2}\ge \tfrac{{\bar{\mathbf{{s}}}}^2}{\nu }\right\} ; \end{aligned}$$

clearly $\{ j \in \mathbf{Z}: \;\; j \ge t_0 \} = S_{\mathrm{good}} \cup S_{\mathrm{bad}}$. We can clearly define a (possibly infinite) sequence of intervals of the form $[k_l,k_{l+1})$ which satisfy:

• (i) $k_{0}=t_0$ serves as the initial instant of the first interval;

• (ii) $[k_l,k_{l+1})$ either belongs to $S_{\mathrm{good}}$ or $S_{\mathrm{bad}}$; and

• (iii) if $k_{l+1}\ne \infty$ and $[k_l,k_{l+1})$ belongs to $S_{\mathrm{good}}$ then $[k_{l+1},k_{l+2})$ belongs to $S_{\mathrm{bad}}$ and vice versa.

Now we analyse the behaviour during each interval.

Sub-Case 2.1: $[k_l,k_{l+1})$ lies in $S_{\mathrm{bad}}$.

Let $j\in [k_l,k_{l+1})$ be arbitrary. In this case

$$\begin{aligned} \frac{|d(j)|^2}{\Vert \phi (j)\Vert ^2} \ge \frac{{\bar{\mathbf{{s}}}}^2}{\nu } \qquad \text {or}\qquad \Vert \phi (j)\Vert =0; \end{aligned}$$

in either case

$$\begin{aligned} \Vert \phi (j)\Vert \le \underbrace{\frac{\nu ^{\frac{1}{2}}}{{\bar{\mathbf{{s}}}}}}_{=:c_{12}}|d(j)|. \end{aligned}$$

Also, applying Proposition 4 for one step, there exists constant $c_{13}$ so that

$$\begin{aligned} \Vert \phi (j)\Vert \le c_{13} (|d(j-1)|+|r(j-1)|). \end{aligned}$$

Then for $j\in [k_l,k_{l+1})$, we have

$$\begin{aligned} \Vert \phi (j)\Vert \le \left\{ \begin{array}{ll} c_{12}|d(j)| &{} { j=k_l } \\ c_{13}(|d(j-1)|+|r(j-1)|) &{} j=k_l+1,k_l+2,\ldots ,k_{l+1}. \end{array} \right. \end{aligned}$$

(80)

Sub-Case 2.2: $[k_l,k_{l+1})$ lies in $S_{\mathrm{good}}$.

Let $j\in [k_l,k_{l+1})$ be arbitrary. First, suppose that $k_{l+1}-k_l\le 4N$. From Proposition 4 it can be easily proven that there exists a constant $c_{14}$ so that

$$\begin{aligned} \Vert \phi (t)\Vert \le c_{14} \lambda ^{t-k_l} \Vert \phi (k_l)\Vert + c_{14} \sum _{j=k_{l}}^{t-1} \lambda ^{t-j-1} (|d(j)|+|r(j)|), \qquad t\in [k_l,k_{l+1}]. \end{aligned}$$

(81)

Now suppose that $k_{l+1}-k_l>4N$. This means, in particular, that there exist $j_1<j_2$ so that

$$\begin{aligned} k_l\le {{\hat{t}}}_{2j_1} \le {{\hat{t}}}_{2j_2}\le k_{l+1}. \end{aligned}$$

To proceed, observe that $\Vert \phi (j)\Vert \ne 0$ and

$$\begin{aligned} \frac{|d(j)|^2}{\Vert \phi (j)\Vert ^2} < \frac{{\bar{\mathbf{{s}}}}^2}{\nu }, \; j \in [k_l,k_{l+1}) . \end{aligned}$$

(82)

With $0\le j_1<j_2$, it follows from Proposition 1 and the definition of $\alpha (\cdot )$ that

$$\begin{aligned} \sum _{q=j_1}^{j_2-1} \alpha ({{\hat{t}}}_{2q})^2\le & {} \sum _{p=t_0+2j_1N,\phi (p)\ne 0}^{t_0+2j_2N-1} \frac{|e_{i^*}(p+1)|^2}{\Vert \phi (p)\Vert ^2}\nonumber \\\le & {} 2V({{\hat{t}}}_{2j_1})+4\sum _{p={{\hat{t}}}_{2j_1},\phi (p)\ne 0}^{{{\hat{t}}}_{2j_2}-1}{\frac{|d(p)|^2}{\Vert \phi (p)\Vert ^2}}; \end{aligned}$$

(83)

using the bound given in (82) which holds on $[k_l,k_{l+1})$, this becomes

$$\begin{aligned}&\sum _{q=j_1}^{j_2-1} \alpha ({{\hat{t}}}_{2q})^2\nonumber \\&\le 8{\bar{\mathbf{{s}}}}^2+8N(j_2-j_1)\frac{{\bar{\mathbf{{s}}}}^2}{\nu }, \;\;\text { for all }j_1,j_2\in {\mathbf{Z}}^+\text { s.t. } k_l\le {{\hat{t}}}_{2j_1} < {{\hat{t}}}_{2j_2} \le k_{l+1}. \end{aligned}$$

(84)

If $j_2-j_1\le \nu$ then

$$\begin{aligned} \sum _{q=j_1}^{j_2-1} \alpha ({{\hat{t}}}_{2q})^2 \le 8{\bar{\mathbf{{s}}}}^2+8N\nu \frac{{\bar{\mathbf{{s}}}}^2}{\nu }= (8+8N){\bar{\mathbf{{s}}}}^2=c_{11}; \end{aligned}$$

(85)

so by Lemma 3(i), with $\lambda _1$ defined above, if we define $c_{15}:=c_{11}^{\frac{c_{11}+1}{2}}(\frac{2}{\lambda _1})^{\frac{4c_{11}}{\lambda _1^2}+1}$, then

$$\begin{aligned} {\prod }_{q=j_1}^{j_2-1} [c_6 \alpha ({{\hat{t}}}_{2q})] \le c_{15} \lambda ^{2N(j_2-j_1)},\;\;\text { for all } j_1,j_2\in {\mathbf{Z}}^+\;\text {s.t. }k_l\le {{\hat{t}}}_{2j_1} < {{\hat{t}}}_{2j_2}\le k_{l+1}. \end{aligned}$$

(86)

If $j_2-j_1>\nu$, then by Lemma 3(ii) and our choice of $\nu$ we have that

$$\begin{aligned} {\prod }_{q=j_1}^{j_2-1} [c_6 \alpha ({{\hat{t}}}_{2q})] \le c_{15} \lambda ^{2N(j_2-j_1)},\;\;\text { for all } j_1,j_2\in {\mathbf{Z}}^+\;\text {s.t. }k_l\le {{\hat{t}}}_{2j_1} < {{\hat{t}}}_{2j_2}\le k_{l+1}, \end{aligned}$$

(87)

as well.

Now we can proceed to solve (73). The first step is to use (85) to bound the second occurrence of $\alpha ({{\hat{t}}}_{2j})$ in (73), yielding

$$\begin{aligned} \Vert \phi ({{\hat{t}}}_{2j+2})\Vert \le c_6 \alpha ({{\hat{t}}}_{2j}) \Vert \phi ({{\hat{t}}}_{2j})\Vert + \underbrace{c_6(1+\sqrt{c_{11}})}_{=:c_{16}} \underbrace{\sum _{q={{\hat{t}}}_{2j}}^{{{\hat{t}}}_{2j+2}-1} (|r(q)|+|d(q)|)}_{=:{{\bar{w}}}(j)} . \end{aligned}$$

(88)

If we solve this iteratively and use the bounds in (86) and (87), we see that

$$\begin{aligned}&\Vert \phi ({{\hat{t}}}_{2j_2})\Vert \le c_{15} \lambda ^{2N(j_2-j_1)} \Vert \phi ({{\hat{t}}}_{2j_1})\Vert + \sum _{q=j_1}^{j_2-1} c_{16} c_{15} \left( \lambda ^{2N} \right) ^{j_2-1-q} {{\bar{w}}}(q),\nonumber \\&\text { for all } j_1,j_2\in {\mathbf{Z}}^+\;\text {s.t. }k_l\le {{\hat{t}}}_{2j_1} < {{\hat{t}}}_{2j_2}\le k_{l+1}. \end{aligned}$$

(89)

We can now use Proposition 4:

• to provide a bound on $\Vert \phi (t)\Vert$ between consecutive ${{\hat{t}}}_{2j}$’s;

• to provide a bound on $\Vert \phi (t)\Vert$ on the beginning part of the interval $[k_l,k_{l+1})$ (until we get to the first admissible ${{\hat{t}}}_{2j}$);

• to provide a bound on $\Vert \phi (t)\Vert$ on the last part of the interval $[k_l,k_{l+1})$ (after the last admissible ${{\hat{t}}}_{2j}$).

We conclude that there exist a constant $c_{17}\ge c_{14}$ so that

$$\begin{aligned} \Vert \phi (t)\Vert \le c_{17} \lambda ^{t-k_l} \Vert \phi (k_l)\Vert + c_{17} \sum _{j=k_{l}}^{t-1} \lambda ^{t-j-1} (|d(j)|+|r(j)|), \qquad t\in [k_l,k_{l+1}]. \end{aligned}$$

(90)

Now we combine Sub-Case 2.1 and Sub-Case 2.2 into a general bound on $\phi$. The following analysis is almost identical to the one at the end of the proof of Theorem 1. Define $c_{18}:=\max \{c_{17},c_{13}, c_{13}c_{17}\}$.

Claim

The following bound holds:

$$\begin{aligned} \Vert \phi (t)\Vert \le c_{18}\lambda ^{t-t_0}\Vert \phi (t_0)\Vert +\sum _{j=t_0}^{t-1} c_{18} \lambda ^{t-j-1}(|d(j)|+|r(j)|), \qquad t\ge t_0. \end{aligned}$$

(91)

Proof of the Claim

If $[k_0,k_1)=[t_0,k_1)\subset S_{\mathrm{good}}$, then (91) is true for $t\in [k_0,k_1]$ by (90). If $[k_0,k_1)\subset S_{\mathrm{bad}}$, then from (80) we obtain

$$\begin{aligned} \Vert \phi (j)\Vert \le \left\{ \begin{array}{ll} \Vert \phi (k_0)\Vert =\Vert \phi _0\Vert &{} { j=k_0=t_0 } \\ c_{13}(|d(j-1)|+|r(j-1)|) &{} j=k_0+1,k_0+2,\ldots ,k_{1}, \end{array} \right. \end{aligned}$$

which means that (91) holds on $[k_0,k_1]$ for this case as well.

We now use induction: suppose that (91) is true for $t\in [k_0,k_l]$; we need to prove it holds for $t\in (k_l,k_{l+1}]$ as well. If $k\in [k_l,k_{l+1}) \subset S_{\mathrm{bad}}$, then from (80) we see that

$$\begin{aligned} \Vert \phi (j)\Vert \le c_{13}(|d(j-1)|+|r(j-1)|), \; j=k_l+1,k_l+2,\ldots ,k_{l+1}, \end{aligned}$$

which means (91) holds on $(k_l,k_{l+1}]$. On the other hand, if $[k_l,k_{l+1}) \subset S_{\mathrm{good}}$, then $k_{l}-1\in S_{\mathrm{bad}}$; from (80) we have that

$$\begin{aligned} |\phi (k_l)|\le c_{13}(|d(k_l-1)|+|r(k_l-1)|). \end{aligned}$$

Using (90) to analyse the behaviour on $[k_l,k_{l+1}]$, we have

$$\begin{aligned} \Vert \phi (k)\Vert\le & {} c_{15}\lambda ^{k-k_l}[c_{13}(|d(k_l-1)|+|r(k_l-1)|)]+\sum _{j=k_l}^{k-1} c_{17} \lambda ^{k-j-1}(|d(j)|+|r(j)|),\nonumber \\\le & {} c_{18}\sum _{j=k_l-1}^{k-1} \lambda ^{k-j-1}(|d(j)|+|r(j)|),\qquad k\in [k_l,k_{l+1}], \end{aligned}$$

(92)

which implies that (91) holds. $\square$

This concludes the proof. $\square$