1 Introduction

Saltwater intrusion is a natural phenomenon in estuary tidal river network regions. However, in recent years, intensive human activity, such as dredging, damming and bulkheading, has significantly changed the natural pattern of previous channel characteristics. This has given rise to the extended incursion of saltwater, which deteriorates the water quality and ecosystems of tidal rivers (Cai et al. 2012; Zhu et al. 2015), and high salinity levels induced by saltwater intrusion are a major concern because they exert a significant adverse effect on the ecological environment and urban drinking water (Rengasamy 2006). In several tidal rivers, water is pumped and withdrawn for irrigation, industry and drinking purposes, but it is unavailable when the river water is contaminated and salified by saltwater intrusion from the ocean. Therefore, accurate predictions of estuary salinity are critical in water resource management to alleviate the adverse effects caused by these changes.

In the last few years, computer modelling has been widely used for the prediction of dynamic salinity variation processes because of its ability to perform complex simulations. Considering a variety of physical processes and a wide range of spatial and temporal scales, conventional numerical models are an important tool for solving critical environmental problems and have also been applied for salinity prediction (Hamrick 1992; Sheng 1987; Sun et al. 2016). However, the models require detailed information on the boundary and initial conditions covering freshwater flow, tide, wind effects and riverway terrain. Although these numerical models are available to provide detailed solutions to several critical problems, a large amount of field data and effort are also required to calibrate and verify the parameters for model application. When reliable forecasts are needed but there are inadequate data reflecting influential factors, the machine learning (ML) approach, which emphasises higher nonlinear fitting and efficiency, is more effective than conventional numerical methods (Qiu et al. 2008; Qiu and Wan 2013). Dozens of researchers have used ML models for various applications. For instance, Suen and Lai (2013) used back-propagation neural networks (NN) to simulate and forecast salinity changes at several locations in a Taiwanese river under assumed climate change influences; Rohmer and Brisset (2017) set up a support vector machine-based (SVM) model to predict the short-term (3 h) occurrence of the forthcoming conductivity peak’s characteristics for detecting and analysing water salinity. More salinity prediction studies based on other ML approaches can be found in the literature (Bowden et al. 2005b; Fang et al. 2017; Huang and Foo 2002).

Although ML models can map nonlinear relationships, the effective information embedded in nonstationary data sequences is often hard to capture sufficiently. As a consequence, the ability of regular ML models to forecast nonstationary time series is limited (Belayneh et al. 2014). To address this issue, forecasting hydrological time series using hybrid ML models with decomposition techniques has been proposed and is becoming a very active field of hydrological research in recent years (Nourani et al. 2014). Empirical mode decomposition (EMD) and wavelet decomposition (WD) are mathematical technologies used to analyse signals by decomposing them into various frequencies. These two decomposition techniques are widely recommended and applied to decompose nonstationary and nonlinear signals into a series of simpler components, which improves simulation accuracy. A significant body of literature has reported that EMD and WD have been combined with classic ML models, such as NN, SVM and adaptive neuro fuzzy inference system (ANFIS), to forecast urban water demand (Adamowski et al. 2012; Campisi-Pinto 2013), stream flow (Kisi et al. 2014; Shiri and Kisi 2010), precipitation (Feng et al. 2015; Ouyang and Lu 2018), groundwater levels (Moosavi et al. 2013) and water quality including parameters such as temperature and dissolved oxygen (Alizadeh and Kavianpour 2015; Liu et al. 2016; Yang et al. 2014). The ML models developed from EMD and WD pre-processed data have demonstrated better performance than models provided with raw data. As the generalization form of WD, wavelet packet decomposition (WPD) is able to capture more details of the signal than WD, thereby offering a richer range of features for signal analysis. In recent years, the conjunction of WPD and ML approaches has also been successfully applied for prediction problems (Moosavi et al. 2017; Seo et al. 2016).

Owing to the interaction of marine and terrestrial elements, salinity time series often present complex and nonstationary characteristics. For example, there are some short-term factors such as wind and storm surge, which can bring about abrupt shift of salinity (Shu et al. 2014; Wong 2003). In addition, human activities (e.g., river topography change induced by dredging) and the sea level rise are found to have been aggravating intrusion in the long run (i.e., an increasing trend of salinity) (Liu et al. 2017; Xinfeng and Jiaquan 2010). Thus, it is difficult to establish a reliable model for accurate prediction. In this regard, decomposition techniques can be used as pre-processing tools to simplify the characteristics of raw data in the framework of a hybrid ML model, which may accurately predict salinity levels in water. Recently, two outstanding ML approaches, random forest (RF) models and extreme learning machine (ELM) models, have been recognised in the field of hydrology. They have been successfully applied in numerous hydrological cases (Abdullah et al. 2015; Shortridge et al. 2016; Wang et al. 2015; Yang et al. 2017; Yaseen et al. 2016) such as stream-flow prediction, evapotranspiration prediction and flood hazard risk management. It is possible that the RF and ELM approaches have distinct advantages over other ML models (e.g. NN, SVM and General Regression Neural Network (GRNN)) owing to their lower computational power consumption yet higher generalisation ability in modelling complex nonlinear data. However, very few studies have been conducted on forecasting the salinity time series with either RF or ELM modelling. More specifically, there are few studies on coupling RF/ELM with decomposition techniques in hydrology and water resource literature (Barzegar et al. 2017). Hence, this study proposes and evaluates RF and ELM models and their hybrid models coupled with EMD, WD and WPD techniques for multistep lead time salinity prediction in the Modaomen waterway located in the Pearl River Delta of China, and then further examines and compares the performance of all the forecast models to determine their potential.

2 Study area and data

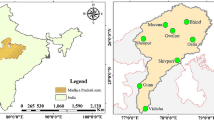
The Pearl River Delta (PRD) in China is located between \(21^\circ 30{\prime}\) N and \(23^\circ 42{\prime}\) N latitude, and between \(112^\circ 26{\prime}\) E and \(114^\circ 24{\prime}\) E longitude, lying in a subtropical region with features of a subtropical monsoon climate. Its annual precipitation ranges from 1200 to 2200 mm, and the precipitation of April–September accounts for 82–85% of the annual total. It is considered to be one of the most complicated river networks in the world, with a drainage density per unit area of 0.68–1.07 km/km2 and a catchment area of 9750 km2 (Chen and Chen 2002; Zhang et al. 2010). There are three main tributaries that merge in the PRD region: West River, North River and East River. The runoff discharges into the South China Sea through eight outlets, which are, in sequence from east to west, the Humen, Jiaomen, Hongqimen, Hengmen, Modaomen, Jitimen, Hutiaomen and Yamen waterways.

Figure 1 presents the Modaomen waterway (MW) in the PRD and the Pinggang (PG) salinity gauge station from which salinity time series data have been used for this study. MW is located in the downstream part of the West River, which has the largest amount of runoff among the eight outlets. Flows from the West River and North River combine to provide critical freshwater resources for MW. The PG station is one of the major pumping stations for water supply to Macao and Zhuhai City, located at approximately 35 km upstream of the MW outlet. Over the past three decades, dramatic anthropogenic activities in MW, including abundant and frequent reservoir construction, an enormous amount of sand excavation and large-scale extension of land reclamation, have greatly altered both the hydrological and hydrodynamic conditions of the river system (Wei et al. 2010). As a result, the water salinity at the PG station is severely intensified by the worsening saltwater intrusion problem during the dry season (from October to March in the following year) even with an upstream flow of more than 3900 m3/s (Gong et al. 2012). Specifically, the duration in hours for salinity exceeding the water supply criterion of 250 mg/L at PG has been increasing. For example, the duration with elevated salinity levels was less than 400 h before 2003, but was more than 700 h thereafter, and even more than 1200 h during the dry seasons of 2005–2006, 2007–2008 and 2009–2010 (Liu et al. 2014a). The increased high-salinity duration has posed a significant threat to water supply for almost 15 million people in the region.Footnote 1

Fig. 1
figure 1

Study area and PG station at the Modaomen waterway

Full size image

In this study, the average daily salinity time series covering nine drought periods at the PG station along MW were used. The data were obtained from the Hydrological Bureau of Guangdong Province. The periods of the datasets for the prediction range from October 2001 to February 2010. Generally, the collected data should be divided into two parts for both model development (training) and model evaluation (testing). In this study, the full set in a total of 1107 data records was divided into 935 records covering the first seven drought periods (85% of the set) for the training phase and 172 records covering the remaining two drought periods (15% of the set) for the testing phase. Table 1 displays the statistical characteristics, including the training, testing and complete data span.

Table 1 Statistical characteristics for average daily salinity of PG station at the MW
Full size table

3 Methodology and model development

3.1 Framework of hybrid modeling

To convert nonstationary sequences into relatively stationary versions, a hybrid modelling framework of ‘decomposition–prediction–reconstruction’ was used to combine ML approaches with decomposition techniques and included the following three steps:

  • Step 1: Applying the decomposition technique to pre-process and convert the original salinity time series into several components. In this step, three decomposition techniques were adopted: EMD, WD and WPD.

  • Step 2: Developing ML models for all the decomposed components to make multistep forecasts. In this step, two approaches were used: RF and ELM.

  • Step 3: Accumulating all the forecasted components from the RF/ELM model of a certain forecast lead time to obtain the final predicted result. In this study, models were developed for one-, three- and five-day lead time salinity prediction.

The primary objective of this study was to find and compare the performance of the RF and ELM approaches together with their hybrid models using decomposition techniques for salinity prediction. Hence, except for the hybrid models, the regular models were also constructed, and comparison analysis was used for the following forecast models: RF, ELM, EMD-RF, EMD-ELM, WD-RF, WD-ELM, WPD-RF and WPD-ELM. Section 3.2 introduces the principle of the three decomposition techniques used and the determination of decomposition level, and Sect. 3.3 presents the principles of the two ML models used in this study and the hyperparameter optimisation with the model input variables.

3.2 Decomposition technique

3.2.1 Empirical mode decomposition

EMD is an adaptive and efficient signal decomposition method that is often applied to smooth the nonlinear time series (Huang 1998; Huang and Wu 2008). Using the EMD method, any complicated datasets can be decomposed into a collection of oscillatory functions called intrinsic mode functions (IMFs) and one residue. An IMF is defined as a function that satisfies two conditions (Rato et al. 2008): (1) in the entire time series, the number of zero crossings and the number of maximum and minimum values must either be equal to or differ at most by one; and (2) at any point, the average of the envelope defined by the local maxima and minima must be zero.

EMD performs the decomposition of time series into IMFs by an iterative process called ‘sifting’, which can be organised into the following six steps:

  • Step 1: Let \(\left\{ {\left. {s\left( t \right), t = 1,2, \ldots ,n} \right\}} \right.\) denote a raw time series that will serve as the input for the sifting process.

  • Step 2: Identify all the local maxima and minima in {s(t)}. Then, obtain the upper envelope \(\left\{ {\left. {u\left( t \right)} \right\}} \right.\) by connecting all the local maxima using a cubic spline interpolation (Rilling et al. 2011). Similarly, the lower envelope {d(t)}. could be obtained with all the local minima.

  • Step 3: Calculate the difference between {s(t)}. and the mean value of two envelopes found in step 2 to obtain the first sub time series \(\left\{ {\left. {p\left( t \right)} \right\} } \right.\).

  • Step 4: Check whether \(\left\{ {\left. {p\left( t \right)} \right\} } \right.\) satisfies the IMF criteria. If not, steps 1–3 are iterated by replacing \(\left\{ {\left. {p\left( t \right)} \right\} } \right.\) with {s(t)}, and the process is repeated until the sub time series satisfies the criteria.

  • Step 5: The final series \(\left\{ {\left. {p\left( t \right)} \right\} } \right.\) from step 4 is defined as IMFi, and the resulting residue is \(R_{i}\)(\(R_{i} = R_{i - 1} - IMF_{i}\), where \(R_{0} = s\left( t \right)\)).

  • Step 6: Repeat steps 1–5 a total of N times until the residue Ri remains nearly unchanged, or just repeat N times set in accordance with practical needs and limitations. The original time series can therefore be expressed as

    $$s\left( t \right) = \mathop \sum \limits_{i = 1}^{N} IMF_{i} \left( t \right) + R_{N} \left( t \right)$$
    (1)

3.2.2 Wavelet decomposition

Wavelet transform is a time–frequency technique widely used in signal processing applications (Rao 1998). It allows a time series to be decomposed at multiple resolutions by dividing a given function into different scale components, where one can also assign a frequency range for each scale component (Partal and Kişi 2007). Different from the EMD method, wavelet transform is not adaptive because the wavelet shape should be chosen or designed to match the outline of the time series signal (Walden 2001). Wavelet transform is usually divided into two groups: continuous (CWT) and discrete wavelet transform (DWT).

CWT for an original signal f(t) with respect to a mother wavelet function ψ(t) can be defined as

$$CWT_{f} \left( {a,b} \right) = \left\langle {f\left( t \right),\psi_{a,b} \left( t \right)} \right\rangle = \mathop \int \limits_{ - \propto }^{ + \propto } f\left( t \right)\frac{1}{{\sqrt {\left| a \right|} }}\psi^{*} \left( {\frac{t - b}{a}} \right)dt$$
(2)

where a is a scale coefficient, b is a translation coefficient, and *  denotes complex conjugation. The wavelet function ψ(t) is designed with the following properties:

  1. 1.

    The wavelet must have a zero mean.

    $$\mathop \int \limits_{ - \propto }^{ + \propto } \psi \left( t \right)dt = 0$$
    (3)
  2. 2.

    The wavelet must be localised in both time and frequency space with a finite energy.

    $$\mathop \int \limits_{ - \propto }^{ + \propto } \left| {\psi \left( t \right)} \right|^{2} dt < \infty$$
    (4)

In CWT, the scale and translation coefficients are continuous, which makes CWT very slow because of the redundant additional data. Therefore, CWT is not used often for prediction. Instead, the wavelet of DWT is scaled and translated using certain scales and positions that can provide the necessary information while reducing the calculation cost (Percival and Walden 2000). In detail, DWT uses scale and position values based on powers of two, and the scale and translation coefficients are discretely expressed as

$$\left\{ {\begin{array}{*{20}l} {a = 2^{j} } \\ {b = k2^{j} } \\ \end{array} } \right.$$
(5)

where j, k are integers that control the scale and translation, respectively.

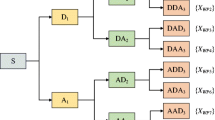
Mallat’s multiresolution theory is typically executed for multisolution DWT computations (Mallat 1989). The theory is made up of two primary components: decomposition and reconstruction. In the decomposition phase (Fig. 2a), the original signal is divided into high- and low-frequency components. Then, low frequencies are again divided into new high- and low-frequency components. The high and low frequencies are referred to as the detail and approximation of the signal, respectively. In each division, a high-pass filter (H) and a low-pass filter (L) are used to downsample the original signal. The approximation (A1, A2, A3) and detail \(\left( {D_{1} ,D_{2} ,D_{3} } \right)\) signals are therefore half the length of the original signal. Then, in the reconstruction phase (Fig. 2b), operations are reversed in a combination step without losing any information. Like decomposition, high- and low-pass filters are also applied, and the decomposed signals (detail and approximation) are upsampled and then summed to obtain the original signal. The reconstructed original signal can be found in the following way:

$$f = A_{1} + D_{1} = A_{2} + D_{1} + D_{2} = A_{3} + D_{1} + D_{2} + D_{3}$$
(6)
Fig. 2
figure 2

Mallat’s multiresolution theory for signal decomposition. a Decomposition tree of 3 levels. b Reconstruction tree of 3 levels

Full size image

Several wavelet bases have been used as the ‘mother wavelet’ for prediction in previous study (Maheswaran and Khosa 2012). It is recommended that wavelets with compact support such as Haar could be employed for time series having short memory and transient features, while wavelets with wide support for time series having long term memory and nonlinear features. In the present study, three commonly wide-support mother wavelets were applied for the time series decomposition: Daubechies (db8) (Daubechies and Heil 1992), Coiflets (coif5) (Daubechies and Heil 1992) and Symlets (sym8) (Misiti et al. 1996).

3.2.3 Wavelet packet decomposition

WPD can be regarded as a special format of DWT. Whereas DWT decomposes only the approximation signals, WPD can capture the information of both the detail and approximation signal components (Fig. 3). Hence, WPD derives more detailed frequency resolution from the signal being decomposed. To facilitate comparative analysis with DWT, the same wavelet bases (i.e. db8, coif5 and sym8) were used for WPD.

Fig. 3
figure 3

Wavelet packet decomposition tree of 3 levels

Full size image

3.2.4 Determination of decomposition level

The predictability of the decomposed components largely depends on the appropriate decomposition level for EMD, WD and WPD. In early WD studies, a trial-and-error approach was usually performed to determine the optimum decomposition level, but an empirical formula in relation to the size of the time series has also been introduced (Nourani et al. 2009; Wang and Jing 2003). In general, when the decomposition level is too small, the residue term by EMD and the approximation (e.g. A3/AAA3 for three levels of decomposition) by WD/WPD will be insufficiently stationary, which is not conducive to the final forecast accuracy; yet, they will be too simple (e.g. increase monotonously) for ML models (i.e. RF and ELM) to accurately forecast owing to the excessive amount of decomposition. In addition, the most suitable levels vary for different models according to their different capabilities of extracting information from data. In this study, the trial-and-error method was used for decomposition level optimisation. With the criteria of the best final forecast results, the original time series was decomposed as follows: 5 IMFs and 1 residue for the EMD-RF/ELM hybrid models; 5 levels (generating 1 approximation and 5 detail signals) for the WD-RF/ELM models; and 4 and 3 levels (yielding 16 and 8 decomposed components) for the WPD-RF and WPD-ELM models, respectively.

The decomposition results of the salinity time series using the three techniques are given in Fig. 4, which presents the components from WD and WPD using the coif5 wavelet. The elusive fluctuations of salinity data with sharp shifts and a trend across the study period are depicted in Fig. 4a. However, the extraction from the original time series separates the complex characteristics and allocates the relatively regular properties for several decomposed components. For instance, the residue term of EMD and approximations (i.e. A5/AAA3/AAAA4) of WD/WPD can all roughly reflect the shape of the original time series, displaying a trend without a sharp rise or fall (Fig. 4b–e). All other components had an individual specific and narrow range of vibrational frequencies, which displayed no trend and remained virtually stationary. Therefore, the exertion of the decomposition techniques can contribute to the stabilisation and simplification of the nonstationary salinity time series.

Fig. 4
figure 4

Decomposition of the observed salinity time series of the PG station. Subfigure a shows the original salinity time series. The decomposition results are presented with b EMD results, c WD results using coif5 wavelet, and d, e 3 and 4 levels WPD results using coif5 wavelet respectively. Hereinto, 3 components out of all the 8 components from 3 levels WPD results are shown while 6 out of 16 from 4 levels WPD

Full size image

3.3 Machine learning approach

3.3.1 Random forests

RF is an ensemble learning method operated by constructing multiple decision trees, where every individual tree contributes to the final classification and regression results. Each tree of the RF is grown using randomly selected samples and features. This method has two major characteristics: randomness and ensemble learning. The details of each are described below (Biau and Scornet 2016; Breiman 2001).

Given a training dataset of N samples with M features, the randomness in RF refers to the random sampling of the entire dataset and features to build every single decision tree. The bootstrap resampling method was adopted to randomly form a sample set of size N (the same size as the original dataset). In this process, around one-third of the data in the formed sample set are not used, which is referred to as out-of-bag data. The remaining data are called in-bag data. The random selection from the features of the entire dataset is also performed through the selection of \(m\) (m < M) features from the M features as a subset. Generally, parameter m needs to be adjusted for optimal performance. However, the model performance is not very sensitive to the parameter practically, and sometimes the RF model performs stably even when m = 1 (Yu et al. 2017). In this study, the adjustment for m showed little effect on the model performance; hence, the parameter m was uniformly set as M, which is equal to the number of model input variables. It could be said that the established RF in the study took only the randomness of training samples into account.

The subset of size N with m features obtained from the random selection is then used to build a single decision tree. The tree is built following the classification and regression trees model, but without pruning. This process is repeated K times to grow a ‘forest’ consisting of K trees. Every decision tree inside the ensemble ‘forest’ contributes to the final prediction, which is referred to as ensemble learning. For classification tasks, the final predicted class is decided based on the majority rule. The class that receives the most votes is the final result of prediction. For regression tasks, the final predicted value is derived by averaging the results from all trees. This process is also known as bagging (bootstrap aggregating). In general, increasing the K value is beneficial to obtain better performance, yet there is a threshold of \(K_{threshold}\) beyond which significant improvement will not be observed (Mayumi Oshiro et al. 2012). In this study, all the developed RF models have no significant improvement when the K value is larger than 2000. Therefore, \(K_{threshold} = 2000\) was adopted. The python scikit-learn package was applied to perform RF in this study.

3.3.2 Extreme learning machine

ELM is an emerging learning algorithm for the generalised single-hidden layer feed forward neural network (SLFN) (Huang et al. 2012), which has only three layers of neurons: the input layer, the single-hidden layer and the output layer (Fig. 5). The input layer acquires the input variables but performs no computations, and the output layer is linear without any transform function. The single-hidden layer of nonlinear neurons links two other layers and performs computations with transform functions.

Fig. 5
figure 5

The topological structure of the extreme learning machine network

Full size image

In the ELM model, the input layer weights W and biases \(b\) are both initialised randomly and then fixed. The output layer weights β are therefore independent and could be solved directly without an iteration process. Compared with traditional learning algorithms, the ELM generally performs well with an extremely fast learning speed.

A mathematical description of an ELM is as follows. Assuming a set of N training samples (xt, yt, t = 1, 2, …, N) with xt, yt ∊ Rm, Rn, an SLFN model with Λ number of hidden neurons could be expressed as

$$\mathop \sum \limits_{i = 1}^{\varLambda } \beta_{i} f\left( {w_{i} \cdot x_{t} + b_{i} } \right) = y_{t}$$
(7)

where \(w_{i} = \left[ {w_{i1} ,w_{i2} , \ldots ,w_{im} } \right]^{T}\) are the input weights, bi are the biases, and \(\beta_{i} = \left[ {\beta_{i1} ,\beta_{i2} , \ldots ,\beta_{in} } \right]^{T}\) are the output weights. Here,\(w_{i} \cdot x_{t} + b_{i}\) could also be expressed as WX, where X represents the inputs. The activation function f in a hidden neuron transforms the projected data (which is equal to WX) into different representations. In general, a nonlinear activation function can significantly improve the learning ability of an ELM. After transformation in hidden neurons, the data are then used to solve the output weights.

In practice, an ELM can be written compactly in matrix form by gathering outputs of all the hidden neurons into a matrix H. One may estimate the matrix β directly with the input and output dataset based on a system of linear equations (Huang et al. 2006):

$$Y = H\beta$$
(8)

such that:

$$H = f\left( {WX} \right) = \left[ {\begin{array}{*{20}c} {f\left( {x_{1} } \right)} \\ \cdots \\ {f\left( {x_{N} } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f\left( {w_{1} \cdot x_{1} + b_{1} } \right)} & \cdots & {f\left( {w_{\varLambda } \cdot x_{1} + b_{\varLambda } } \right)} \\ \vdots & \ddots & \vdots \\ {f\left( {w_{1} \cdot x_{N} + b_{1} } \right)} & \cdots & {f\left( {w_{\varLambda } \cdot x_{N} + b_{\varLambda } } \right)} \\ \end{array} } \right]_{N \times \varLambda }$$
(9)

and

$$\beta = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ \vdots \\ {\beta_{\varLambda }^{T} } \\ \end{array} } \right]_{\varLambda \times n} \quad {\text{and}}\quad Y = \left[ {\begin{array}{*{20}c} {y_{1}^{T} } \\ \vdots \\ {y_{N}^{T} } \\ \end{array} } \right]_{N \times n}$$
(10)

From Eqs. (8) and (9), an ELM can be viewed as two projections with a transformation between them, and the number of hidden neurons determines the size of matrices \(H, \beta\) and W. In most situations, the number of training samples xt is more than that of hidden neurons, which is an overdetermined problem. A unique solution for the problem is adopted by minimising L2, which is the norm of the training error. The output weights can be deduced by the Moore–Penrose generalised inverse function (+) (Huang et al. 2006):

$$\hat{\beta } = H^{ + } Y$$
(11)

where \(\hat{\beta }\) represents the estimated output weights.

Appropriate model structure optimisation is necessary because it prevents the ELM from learning noise data, which results in overfitting and reduces model performance. In most cases, a validation set could be used to measure it. The hyperparameter, which governs the effective parameters and the model structure, is the number of hidden neurons. For hyperparameter optimisation, an effective ‘optimal pruning’ method was adopted for this study (Miche et al. 2008, 2010), which can be used to add and remove hidden neurons or rank the parameters by relevance to the problem automatically. And the hyperparameter optimisation is performed using the results of the leave-one-out validation in this study.

The activation function f′(x) was defined by a logarithmic sigmoid transfer function as the following equation:

$$f^{\prime}\left( x \right) = \frac{1}{{1 + exp\left( { - x} \right)}}$$
(12)

For data-driven models, scaling of the input time series y(t) is necessary to avoid data patterns and attributes with large numerical ranges dominating the role of the smaller numerical ranges via:

$$y_{i, normalized} = \frac{{y_{i} - y_{min} }}{{y_{max} - y_{min} }}$$
(13)

The random generation of matrices W in the hidden layer makes each ELM distinct; hence, the ELM was run 100 times with the same inputs, and then the outputs were averaged to produce the final results. Sun et al. (2008) and Liu and Wang (2010) indicated that the average values are more stable than the values from a regular ELM. The high-performance ELM Toolbox (Akusok et al. 2015) was applied in this study, and the source code is available at ‘https://pypi.python.org/pypi/hpelm’.

3.3.3 Model input variable

The determination of input variables is a significant step in developing a reasonable data-driven model for prediction (Bowden et al. 2005a; Maier and Dandy 2000; Nourani et al. 2012). However, there is no ‘rule-of-thumb’ for input variable selection in forecasting problems. In the literature, three common methods have been frequently used for input selection (Galelli and Castelletti 2013; Maier et al. 2010; Taormina et al. 2016): (1) determining inputs using filter approaches with statistical analysis; (2) determining inputs through wrapper or embedded approaches with model driving; and (3) determining the number of time series lagged values that provide the best forecasting performance using exhaustive search over all potential combinations. In this study, the last method was used to explore the best results by setting several potential input combinations, where the most appropriate combination yields the best forecast output, which is subsequently considered for further analysis. For the hybrid models, the final forecast result is calculated using the accumulation of all the best component forecast outputs.

Successively, the potential input combinations were designed for one-day ahead prediction:

$$C_{1}^{\left( 1 \right)} : S\left( t \right) = f\left[ {S\left( {t - 1} \right)} \right]$$
(14)
$$C_{2}^{\left( 1 \right)} : S\left( t \right) = f\left[ {S\left( {t - 1} \right), S\left( {t - 2} \right)} \right]$$
(15)
$$C_{14}^{\left( 1 \right)} : S\left( t \right) = f\left[ {S\left( {t - 1} \right),S\left( {t - 2} \right), \ldots ,S\left( {t - 14} \right)} \right]$$
(16)

three-days ahead prediction:

$$C_{1}^{\left( 3 \right)} : S\left( t \right) = f\left[ {S\left( {t - 3} \right)} \right]$$
(17)
$$C_{2}^{\left( 3 \right)} : S\left( t \right) = f\left[ {S\left( {t - 3} \right),S\left( {t - 4} \right)} \right]$$
(18)
$$C_{12}^{\left( 3 \right)} : S\left( t \right) = f\left[ {S\left( {t - 3} \right),S\left( {t - 4} \right), \ldots ,S\left( {t - 14} \right)} \right]$$
(19)

and five-days ahead prediction:

$$C_{1}^{\left( 5 \right)} : S\left( t \right) = f\left[ {S\left( {t - 5} \right)} \right]$$
(20)
$$C_{2}^{\left( 5 \right)} : S\left( t \right) = f\left[ {S\left( {t - 5} \right),S\left( {t - 6} \right)} \right]$$
(21)
$$C_{10}^{\left( 5 \right)} : S\left( t \right) = f\left[ {S\left( {t - 5} \right),S\left( {t - 6} \right), \ldots ,S\left( {t - 14} \right)} \right]$$
(22)

where the difference between combinations lies in the inclusion of past information; S(t) represents the value of the target time series, S(t − 1) represents the lagged input, etc., and f refers to the RF or ELM model.

  1. 1.

    Results and comparison analysis

Each of the hybrid models coupled with WD or WPD was tested based on three kinds of mother wavelets. All the developed models generated predictions with one-, three- and five-day lead times. Specifically, when the forecast lead time is only one day, it could be a reference for PG station to pump and store freshwater if high salinity is predicted. When the forecast lead time is either three or five days, reservoir in West River and North River could apply the forecast results for water diversion to restrain saltwater intrusion.

To evaluate the performance of the models, three statistical indicators were used: the coefficient of determination (R2), the root-mean-square error (RMSE) and the Nash–Sutcliffe efficiency (NSE) coefficients. These statistics are widely used for the evaluation of hydrological and hydrodynamic models (Legates and McCabe 1999; Moriasi et al. 2007). The statistical parameters can be denoted mathematically as follows:

$$R^{2} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \bar{O}} \right)\left( {P_{i} - \bar{P}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \bar{O}} \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - \bar{P}} \right)^{2} }}} \right]^{2}$$
(23)
$$NSE = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - P_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \bar{O}} \right)^{2} }}$$
(24)
$$RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - P_{i} } \right)^{2} }}{n}}$$
(25)

where n is the total number of da samples for evaluation, Oi and Pi denote the observed and predicted daily salinity, respectively,\(\bar{O}\) is the mean of the observed daily salinity, and \(\bar{P}\) is the mean of the predicted daily salinity. R2 is an indicator measuring the percent of variation of observed salinity data, which is explained by the predicted data. NSE can be used to measure the proximity between the observed and predicted time series plots, ranging from −∞ to 1.0, with NSE = 1 corresponding to a perfect match. RMSE represents the deviation between the observed and predicted values, with units of \({\text{mg}}/{\text{L}}\) (units are omitted) for salinity in this study. The relatively small RMSE and large R2, NSE values signify an efficient model.

The performance statistical indicators for all the regular and hybrid models in the testing phase at the PG station are tabulated in Table 2. Comparison analyses of hybrid models are made after the description of model forecast results.

Table 2 Performance statistics of one, three and five days forecast horizons of all developed models during the testing phase
Full size table

3.4 Regular model forecast results

A comparison between the RF and ELM models showed that the ELM model worked better than the RF one in terms of all the evaluation indicators with respect to all three forecast horizons (Table 2). For the one-day lead time forecast, the performances of both the RF and ELM models are acceptable with high R2 and NSE values greater than 0.95 and 0.90, respectively. As expected, it is quite usual for a certain degree of decrease in accuracy with increasing lead time in real-time forecasting (Rezaie-Balf et al. 2017). However, for the three- and five-day lead times, both the R2 and NSE values of the two regular models decreased significantly, whereas the RMSE value displayed a substantial increase, indicating distinct reductions in model accuracy.

From the time series plots displayed in Fig. 6, the observed values closely coincided with the forecasted values obtained from the two models with respect to the one-day horizon, in which the peak and bottom values were also well matched with only a few time shift errors. From the scatter plots in Fig. 6, the distribution of scatter points is relatively far from the trend line for both the three- and five-day lead times, demonstrating a certain level of underestimation and overestimation of the RF and ELM model forecast results that was also reflected in the time series plot. Further, from the scatter plots, the forms of prediction deviation were different between the high and low intervals of the observed salinity values. One can observe that the predicted results of the salinity in high value intervals were prone to underestimation, whereas the results in low intervals tended to be overestimated.

Fig. 6
figure 6

Forecasted and observed time series with respect to one, three and five days forecast horizons during the testing period using ELM and RF models. The left panel shows time series plots, while the right panel shows scatter plots

Full size image

3.5 Hybrid model forecast results

  1. (1)

    EMD-RF/ELM

As shown in Table 2, the R2, NSE and \(RMSE\) values for the one-day ahead EMD-ELM model were 0.961, 0.922 and 184.946, respectively, which underperformed the corresponding regular ELM model with values 0.970, 0.941 and 161.700, respectively. Except for that, the performance of the hybrid EMD-RF/ELM models demonstrated a significant improvement compared with the regular models, especially for the three- and five-day lead times. For instance, after integrating EMD, the NSE values for the RF and ELM models for five-day lead times improved by 62.17% and 18.75% and then reached 0.793 and 0.779, respectively (Table 2). Moreover, with the longer forecast horizon, the EMD method can improve the regular RF/ELM models better. This improvement is associated with the low prediction accuracy of the regular models in the forecast of three- and five-day lead times, and it occurs with other hybrid models for the same reason. Overall, the performance statistics in Table 2 suggest that the EMD-RF model performed better than the EMD-ELM model for all the three forecast lead times, although the difference between the EMD-RF and EMD-ELM models was very small with RMSE values of 184.051 and 184.946, respectively, for the one-day lead time. However, the performance of the EMD-RF model for the three- and five-day lead times is distinctly superior to that of the EMD-ELM model.

The time series plots in Fig. 7 show that the observed and forecasted values generally fit well for each forecast horizon, in comparison with the plots of regular models in Fig. 6. However, it should be pointed out that the significant common fitting errors are presented at the end of the time series plot for all the EMD hybrid models, which should reduce the prediction accuracy. The scatter plots in Fig. 7 indicate that, although the points were closer to the trend line after using EMD for each forecast lead time, there was still significant overestimation or underestimation with respect to the three- and five-day horizons.

Fig. 7
figure 7

Forecasted and observed time series with respect to one, three and five days forecast horizons during the testing period using EMD-RF and EMD-ELM models. The left panel shows time series plots, while the right panel shows scatter plots

Full size image
  1. (2)

    WD-RF/ELM

The use of WD greatly improves the prediction accuracy of regular models. From Table 2, WD hybrid models yield excellent outputs for salinity prediction, with the RMSE values ranging between 19.942 and 288.951 over all three forecast horizons. With the WD technique, models can achieve good results for forecast horizons of more than one day, as the R2 and NSE values are not less than 0.935 and 0.869 for three-day lead times and 0.903 and 0.810 for five-day lead times, respectively. Besides, the WD-RF model with any one of the wavelet bases demonstrated better forecasting ability than the EMD-RF model, and it is the same for WD-ELM versus EMD-ELM. Table 2 also illustrates that the WD hybrid model with coif5 demonstrated the best forecast ability compared with the model with the other two wavelet bases (i.e. \(db8\) and sym8) using either the RF or ELM model. Moreover, WD-ELM models outperformed WD-RF models with any of the wavelet bases being used for decomposition.

Figure 8 presents the observed data versus forecasted results from the most suitable coif5 WD-ELM/RF models. From the time series plots, the performances of the WD-RF/ELM models are superior to those of the EMD-RF/ELM and regular RF/ELM models, particularly for the peaks of the salinity time series for all the forecast horizons. In addition, relatively smaller fitting errors were observed near the end of the predicted time series. In the right panels of Fig. 8, the scatters of observed values with forecasted values are distributed symmetrically on both sides of the trend line for each lead time. Furthermore, the overestimation and underestimation problems associated with the predicted outputs from the EMD-RF/ELM models were largely resolved.

Fig. 8
figure 8

Forecasted and observed time series with respect to one, three and five days forecast horizons during the testing period using coif5 wavelet based WD-RF and WD-ELM models. The left panel shows time series plots, while the right panel shows scatter plots

Full size image
  1. (3)

    WPD-RF/ELM

When using the same wavelet basis, the prediction accuracy of the WPD hybrid model was higher than that of the WD hybrid model with either RF or ELM across all three forecast lead times. As shown in Table 2, the evaluation indicators R2and \(NSE\) of the WPD hybrid models were not less than 0.913 and 0.831, respectively, each of which was larger than that of the corresponding WD hybrid models. The study results also suggest that the WPD model demonstrated the most significant improvement over the regular RF/ELM model among the three decomposition techniques used. Like the WD hybrid models, coif5 was considered as the most suitable wavelet for the WPD hybrid models obtaining the best prediction results. Furthermore, when the forecasted lead time results from all the WPD-RF and WPD-ELM models were compared, the latter was superior to the former when using the same wavelet basis.

Consistent with the results of statistical indicators, the time series and scatter plots of the coif5-based WPD-RF/ELM models in Fig. 9 also demonstrated the superiority of the WPD hybrid models as their predicted results mirror the observed results more closely than the WD hybrid models in Fig. 8, across the vast majority of the testing phase.

Fig. 9
figure 9

Forecasted and observed time series with respect to one, three and five days forecast horizons during the testing period using coif5 wavelet based WPD-RF and WPD-ELM models. The left panel shows time series plots, while the right panel shows scatter plots

Full size image

3.6 Comparison analysis

In this study, the two regular ML models (i.e. RF and ELM) demonstrated satisfactory performance in terms of the one-day lead time prediction. However, the forecasting ability declined substantially when the forecast horizon was extended to three- and five-day lead times. The use of decomposition techniques (i.e. EMD, WD and WPD) can help to smooth out the salinity time series, thus improving the forecast accuracy for the regular models to varying degrees. As might be expected, the forecast performance of all the models worsened as the forecast lead time increased. Forecast horizons longer than one day did not result in poor results from hybrid RF and ELM models as measured by the values of R2 and NSE, which were respectively not less than 0.886 and 0.779 for the three-day lead time, as well as 0.820 and 0.669 for the five-day lead time.

  1. (1)

    EMD versus WD versus WPD

On comparison of the effectiveness among all three decomposition techniques, the WPD model is considered the most effective one to improve the RF and ELM models, whereas the EMD model had the least significant effect. As for the WPD model, Table 2 indicates that each WPD-RF/ELM model outperformed the WD-RF/ELM model with the same wavelet basis, and the only difference between the two kinds of hybrid models is in the decomposed components. Although the decomposition level of the WPD model was less than that of the WD model, the former provided a more stationary representation of data through further decomposition of the detailed components (shown in Fig. 3). Both the RF and ELM models can hence yield more accurate component outputs to obtain better final results. As for EMD, we explore it by analysing the predicted results of EMD components. As the evaluation indicators of the predicted components suggested in Table 3, the IMF1 components of all the models performed significantly worse than any other component (e.g. IMF2, IMF3) for all the forecast horizons, indicating that the predicted IMF1 only exerted a limited positive effect (or even an adverse effect) on the final prediction results. Previous studies have suggested that IMF1 extracted by EMD is the most unsystematic and nonstationary component among all the decomposed components, resulting in a significant increase in the difficulty of prediction (Guo et al. 2012; Huang et al. 2014). Some researchers have also reported that the more nonlinear the original series, the more chaotic IMF1 will be (Liu et al. 2014b; Napolitano et al. 2011). This study also shows that in addition to IMF1, the first few components are not highly predictable, especially when the forecast horizon is more than one day, where the prediction accuracy significantly decreased. Accordingly, the limitedly predictable components decomposed by EMD may explain why EMD hybrid models underperformed either WD or WPD hybrid models and why the hybrid EMD-ELM model underperformed the regular ELM model for the one-day lead time.

Table 3 Performance statistics of decomposed components of EMD-RF and EMD-ELM models for one, three and five days lead times forecasts during the testing phase
Full size table
  1. (2)

    RF versus ELM

The results from all the forecast models generally showed that ELM had superior performance than RF. There was also a comparative study regarding environmental regression problems that reported the superiority of ELM over RF (Lima et al. 2015). In this study, the superiority of ELM was reflected in most of the 48 developed models (Table 2), except that the EMD-RF models outperformed the EMD-ELM models. Several components with large prediction errors by EMD may also explain the less accurate final results of the EMD-ELM model, especially for three- and five-day lead times.

Figure 10 shows the flowchart for forecasting salinity using hybrid models and the comparison analysis.

Fig. 10
figure 10

Flowchart of hybrid models coupling RF/ELM with decomposition techniques

Full size image

4 Summary

Under the influence of the intense anthropogenic activities, high levels of salinity induced by intensified saltwater intrusion phenomena are becoming a major concern in river systems, which can contaminate drinking water sources and cause several other environmental problems. Hence, it is critical to use effective and accurate approaches for salinity prediction, thus improving the water resources management of the tidal river network area. The potential of both RFs and ELM use in forecasting the salinity time series for multistep lead times (i.e. one, three and five days) was investigated. To convert the chaotic salinity time series into relatively stationary data that are more predictable, the ‘decomposition–prediction–reconstruction’ hybrid modelling framework was used to decompose a salinity time series into several components and forecast them individually, followed by the reconstruction of all the predicted components yielding final predicted outcomes. Three widely applied time–frequency techniques, EMD, WD and WPD, were used for salinity time series decomposition.

4.1 Conclusions

Based on the forecast results and comparison analysis provided in this study, the following can be concluded: (1) The regular RF and ELM models provided effective prediction for the one-day horizon with an NSE value greater than 0.90, but were not able to yield acceptable results for the forecast lead times of three (NSE less than 0.66) and five days (NSE less than 0.40). (2) Overall, hybrid RF and ELM models coupled with decomposition techniques were found to provide better results than regular RF and ELM models for each forecast lead time except for only one single case. (3) Hybrid models using WPD performed better than WD because the former generates more detailed and stationary components for prediction, whereas hybrid models using EMD underperform WPD and WD because of the nonstationary IMF1 and several other components that are limitedly predictable. For both the WPD and WD hybrid models, the coif5 wavelet basis was found to be particularly effective. (4) The ELM approach demonstrated better performance than the RF approach for the regular and WD/WPD hybrid models; the contrary was true for the EMD hybrid models. In general, developing hybrid RF and ELM models coupled with decomposition techniques can capture more valuable information from highly nonlinear data to give reasonably good results for salinity time series prediction (i.e., even for five days lead time, the NSE values still range from 0.669 to 0.921).

4.2 Study limitations

In this study, the hybrid modelling framework using ML models coupled with decomposition techniques can be an effective approach for multistep salinity prediction. However, the EMD technique has yet to be improved because the nonstationary IMF1 component and even other components could limit the accuracy promotion for regular RF/ELM models. Based on this, further pre-processing could be implemented for IMF1 and other insufficiently decomposed components to obtain more stationary components, thus improving the beneficial effect of EMD in hybrid models. In doing so, the secondary decomposition method in Yin et al. (2017) could be considered for reference in future research.

The investigated forecast models yielded results of salinity based on past data of salinity itself and hence did not include the exogenous drivers (e.g. stream flow, tide, rainfall and wind speed/direction) that could influence variations in the salinity time series. Because the research for response of the estuarine systems to anthropogenic and natural changes is significant in water resource management (Qiu and Wan 2013), it is worth investigating the effectiveness of the RF/ELM models in combination with decomposition techniques considering the exogenous physical factors as inputs. In this regard, a hybrid modelling strategy, including multiple driving factors for groundwater level prediction applied in Rezaie-Balf et al. (2017), could be taken into account.

In terms of the prediction outputs, we focus only on point prediction (i.e. only one predicted value at one moment) in this study. As a matter of fact, the outputs of a forecasting model are generally influenced by lots of uncertainty sources such as model parameters, model structure and observed data (Zhang et al. 2011). Hence, it is more reasonable to evaluate one model considering both point and probabilistic prediction results, while probabilistic results are the final expression of various uncertainties. To our best knowledge, there are still few studies incorporating the uncertainty quantification into “decomposition–prediction–reconstruction” hybrid wavelet forecasting framework (Bogner and Pappenberger 2011). The uncertainties of the forecasting framework can be attributed to model parameters, model structure, wavelet decomposition levels, wavelet bases and data samples, etc. In order to generate reliable uncertainty quantification for the proposed model, further research should also be made to effectively dump all possible uncertainties into the prediction outputs. For this purpose, an uncertainty estimation framework, that is applicable to any deterministic scheme and avoids model likelihood computation, can probably be used for reference (Montanari and Koutsoyiannis 2012).