1 Introduction

Water resources not only are essential for the human survival but also are a very important segment of socio-economic conservation (Chu and Huang 2020). Iran is located in arid and semi-arid regions of the world and therefore rainfall plays a significant role in meeting water demands. However, most of the rainfall events occur in the cold seasons of the year when the agricultural activities are in their lowest levels. Hence, there is a substantial need to store water in reservoir dams to supply water needs in the hot seasons (Khalili et al. 2016; Ahmadi et al. 2018; Pour et al. 2020; Salehi et al. 2020; Sharafi and Karim 2020).

An accurate estimation of inflows to dams is of particular importance for the short-term and long-term exploitation and plays a very important role in sustainable agriculture, floods and droughts management (Afan et al. 2020). For this purpose, many models have been proposed and a lot of research is being done for developing models to estimate complex hydrological phenomenon as accurately as possible (Rahmani-Rezaeieh et al. 2020). In this regard, the main problem is the involvement and impacts of different parameters like evaporation, rainfall, temperature, and other climatic factors, which should be taken into consideration in the hydrological studies (Nayak et al. 2004).

For modeling the inflows to the reservoirs, due to the non-linear nature, different perspectives have been proposed for the development and improvement of inflow predictive models (Rahmani-Rezaeieh et al. 2020). In general, two techniques including conceptual (white box) and systemic (black box) models have been recommended when modeling hydrological phenomena. The white box models are developed based on governing mathematical equations and existing physical parameters (Singh 2018). On the other side, it is not possible to present mathematical relationships in the black box models and the physical variables affecting the target parameter could not be easily recognized. The black box models include the potential of estimating the intended output by receiving the possible inputs and then performing a series of mathematical operations on them. The performance of black box models is significantly dependent on the quantity and quality of the data used (Mehr et al. 2017). Artificial intelligence (AI) model is a typical type of black box-based models that has been extensively used in recent years to solve various hydrological problems such as rainfall-runoff modeling (Vidyarthi et al. 2020; Adnan et al. 2021a; Herath et al. 2020; Molajou et al. 2021), estimating the rainfall (Nourani et al. 2019; Mehdizadeh 2020), river streamflow forecasting (Mehdizadeh and Sales 2018; Fathian et al. 2019; Mohammadi et al. 2020; Adnan et al. 2021b), and inflows to the dams reservoirs (Santos et al. 2019; Apaydin et al. 2020Lee et al. 2020).

One of the AI models is random forest (RF), which uses multiple iterative algorithms. It can be utilized as a powerful technique for evaluating the hydrological issues (Booker and Snelder 2012). The RF can learn complex patterns and consider the non-linear relationships between the independent and dependent variables. Besides, identifying the most effective input parameters influencing the target desired output is one of the important features of the RF. The aforementioned benefits have led to the use of RF when forecasting hydrological parameters (e.g., see Ali et al. 2020; Ghorbani et al. 2020; Hussain and Khan 2020; Pham et al. 2020; Tang et al. 2020).

In the application of AI-based models such as RF, determining the optimal input data always plays a major role in their final performance. Moreover, introducing the maximum number of inputs will not necessarily lead to achieving the highest accuracy of the relevant model. The Shannon's entropy theory is one of the approaches proposed in recent years for selecting the optimal inputs of the AI models (Ahmadi et al. 2021a). This theory shows that an event with a high probability of occurrence could provide less information; otherwise, if an event is less likely to occur, more information may be achieved (Saray et al. 2020). Indeed, the uncertainties are reduced through capturing the new information and the value of new information is equivalent to the amount of reduced uncertainty (Pei-Yue et al. 2010). Therefore, by weighting each of the inputs by the entropy method, the most effective ones can be selected and used in the modeling procedure. Such methodology has been already used in various studies when selecting the optimal input predictors (Darbandsari and Coulibaly 2020; Roy 2021; Ray and Chattopadhyay 2021).

Most of the recorded hydrological data have some noises so that they prevent the proper transfer of information to the models. Data pre-processing methods have been proposed to overcome this problem, which wavelet theory (W) and empirical mode decomposition (EMD) belong to such methods. The wavelet analysis is more sensitive to the proper choice of the mother wavelet type, but there is no such limitation in the EMD method and it can be therefore applied to the data without any special preconditions. EMD is a spectral analysis method, which was firstly introduced by Huang et al. (1998). After introducing the initial version (i.e., EMD), Wu and Huang (2009) proposed ensemble EMD (EEMD) due to the problem of mode composition existing in the EMD. Torres et. al. (2011) then introduced complete EEMD (i.e., CEEMD) to eliminate the imperfection of the previous versions (i.e., EMD and EEMD). Each of these methods has properties that make them suitable for decomposing the different original data. Data decomposition utilizing each of the EMD, CEMD and CEEND divides it into sections called as intrinsic modes, each of which contains parts of the same scale of data. Diverse coupled models have been proposed in literature to forecast hydrological parameters with the aim of this feature of EMD (e.g., see Chen and Dong 2020; Nazir et al. 2020; Ouarda et al. 2021).

As mentioned above, knowing the inflow time series to a dam reservoir could be of significant use for the optimal management and optimal allocation of water resources. The main objectives of present study are as follows: to (1) apply a pre-processing approach based on the entropy technique when implementing input patterns related to inflow estimation, (2) develop classic RF and then propose novel hybrid models through hybridizing the RF with the CEEMD and W, (3) evaluate the efficiency of six mother wavelets in developing the hybrid W-RF models, (4) compare the performance of whole the models proposed in the current study. According to the best knowledge of the authors, this study is the first try in the literature to propose the hybrid CEEMD-RF and compare its performance with the coupled W-RF ones when estimating the monthly reservoir inflow.

2 Materials and methods

2.1 Study area and data used description

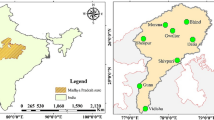
The Maroon River originates in the Nil Mountains and springs in the foothills of the Sadat Mountains of the Zagros in Kohgoluyeh and Boyer-Ahmad Province in Iran. It reaches the Maroon Dam Lake after a distance of 120 km and enters the Behbahan plain through the Takab Strait. The Maroon Reservoir Dam is located 19 km northeast of Behbahan with a height of 165 m, a length of 345 m, a width of 15 m and a total volume of the reservoir up to 1200 million cubic meters. This dam is of sandy gravel type with clay core. The geographical position of study location is shown in Fig. 1.

Fig. 1
figure 1

Geographical position of study location

Full size image

Idanak hydrometric station, located in Idanak village and upstream of the Maroon Reservoir Dam, records the required data. The data sets applied in the current study were comprised of the minimum, maximum, and mean air temperatures (Tmin, Tmax, T), rainfall (R), reservoir evaporation (E), and reservoir inflow (Q) during 1982–2017 on a monthly time-scale. From whole the available data (i.e., 420 data), 300 data were used to train the models while 120 data were applied when testing the developed models. Figure 2 demonstrates the time series of monthly data used in this study during both the training and testing periods. Some of the statistical properties of the data used consisting of minimum (Min), maximum (Max), Average (Avg), standard deviation (SD), and coefficient of variation (CV) for both the train and test phases are summarized in Table 1.

Fig. 2
figure 2

Time series of the monthly climatic data as possible inputs and reservoir inflow as the target during the study period

Full size image
Table 1 Statistical parameters of the data used in this study
Full size table

3 Models applied overview

3.1 Entropy-based input selection

In modeling of an intended problem using the artificial intelligence-based approaches, defining the effective parameters as the models inputs plays a significant role in improving their performances. In addition, in the time series modeling of the hydrological phenomena, considering the effective lags of the investigated problem can lead to an acceptable result (Ahmadi et al. 2021a). The models inputs were discerned in this study through the Shannon's entropy measure. This method derived from the information theory was initially introduced by Shannon (1948). Entropy is a measure of disorder in a system and is also a measure of the amount of uncertainty expressed by a discrete probability distribution in information theory; so that, this uncertainty is greater if the frequency distribution is well distributed than when the frequency distribution is sharper (Bednarik et al. 2010). This technique requires a matrix based on criteria and options. If the decision matrix data are known, the entropy technique can be employed to evaluate the weights.

Here, the monthly minimum, maximum, and mean air temperatures, monthly rainfall, and monthly reservoir evaporation were considered as the possible inputs effective on the monthly reservoir inflow. The most important variables were then identified using the entropy method. In most of the previous studies, a systematic method is not provided to specify the optimal lags when modeling the intended problem. In the present study, the entropy technique was also applied to select the appropriate lags of the considered inputs.

3.2 Random forest

Random forest (RF) as a data-driven method is firstly proposed by Breiman (2001). Indeed, it is developed for solving problems based on the regression and clustering through the development of decision trees (Fathian et al. 2019). An RF is comprised of a collection of un-pruned trees in which each tree is obtained by a recursive segmentation algorithm. In other words, the RF is a combined form of some decision trees so that several self-organizing samples of data are involved in its construction (Friedman et al. 2001). To create a regression tree, recursive segmentation and multiple regressions are used. The decision process is repeated at each internal node of the root node according to the tree rule until the pre-determined stop condition is met (Breiman 2001).

In the RF, a random vector \(X_{n}\) is generated for the nth tree, which is independent of random vectors \(X_{1} ,X_{2} ,....,X_{n - 1}\). Tree regression generates a set of trees utilizing the training dataset and achieved \(X_{n}\) as follows (Breiman 2001):

$$X_{n} = \left\{ {h_{1} (x),h_{2} (x),...,h_{n} (x)} \right\}$$
(1)
$$h_{n} = h(x,X_{n} ),x = \left\{ {x_{1} ,x_{2} ,...,x_{p} } \right\}$$
(2)

The above P-dimensional vector forms a forest and the outputs for each tree are provided as (Breiman 2001):

$$y_{1} = h_{1} (x),y_{2} = h_{2} (x),...,y_{n} = h_{n} (x)$$
(3)

where \(y_{n}\) denotes the output of nth tree.

To obtain the final output, the average of predictions of all the tress is calculated (Breiman 2001). The prediction error is also computed according to Eq. (4) as (Breiman 2001):

$$MSE = \frac{{\sum\limits_{i = 1}^{n} {\left[ {y(x_{i} ) - y_{i} } \right]^{2} } }}{n}$$
(4)

where \(y(x_{i} )\) illustrates the computational value, \(y_{i}\) denotes the observational value, n is the total number of observations, and MSE shows the mean square error rate between the observational and computational values.

3.3 Wavelet theory

A wavelet is a class of mathematical functions used to decompose a continuous signal into its frequency components. This method is a time-independent spectral analysis that separates time series in a time–frequency space in order to describe the time scale of processes and their relationships. Wavelet transform, like the Fourier transform, considers the time series as a linear combination of several base functions. One of the most important characteristics of the wavelet transform is its ability to obtain information in time, frequency, and position, simultaneously (Misiti et al. 1996). Continuous wavelet transform includes the capability to operate at any scale. However, the difficulty of calculating the wavelet coefficients as well as the need for high computational time and the production of large volumes of data are some of the problems of this type of wavelet transform. Discrete wavelet transform (DWT) method can be used to solve this problem (Chen et al. 1999).

To implement the DWT method, the Mallat algorithm or the Multi Resolution Analysis (MAR) method is presented (Mallat 2009). In this approach, the decomposed signal is passed through low-pass and high-pass filters. The low and high frequency contents of the signal are named as approximation and details, respectively (Mehdizadeh et al. 2020a; Ahmadi et al. 2021b). This filtering paradigm can be applied to obtain a time-scale display of a signal (Polikar 1999). In the DWT, the primary signal could be reconstructed via the synthesizing of the wavelet coefficients. This operation starts from the last level of decomposition and the original signal could be reconstructed through assembling the approximation and details series.

3.4 Complete ensemble empirical mode decomposition

Empirical mode decomposition (EMD) is a method of spectral data analysis, which was firstly proposed by Huang et al. (1998). This method has evolved several stages since its introduction. Wu and Huang (2009) then introduced ensemble EMD (EEMD) due to the problem of mode composition. Finally, Torres et al. (2011) solved the problem of imperfection of the EMD and EEMD methods by proposing the complete EEMD (CEEMD).

In the CEEMD method, intrinsic mode functions are displayed as \(\overline{IMF}_{k}\). If we assume that the \(E_{j} (.)\) operator provides the jth intrinsic mode computed by the EMD, \(\omega^{i}\) is the white noise with standard deviation N(0,1), x denotes the original data, and \(\varepsilon_{0}\) illustrates an initial constant, the different steps of CEEMD are as follows:

The first intrinsic mode \(x + \varepsilon_{0} \omega^{i}\) is calculated via the EMD and the first intrinsic mode of CEEMD is computed as shown in Eq. (5) (Torres et al. 2011):

$$\overline{IMF}_{1} = \frac{1}{I}\sum\limits_{i = 1}^{I} {IMF_{1}^{i} }$$
(5)

The first residual value is then calculated from Eq. (6) as (Torres et al. 2011):

$$r_{k} = r_{k - 1} - \overline{IMF}_{k}$$
(6)

In the next step, the second intrinsic mode function is obtained as (Torres et al. 2011):

$$\begin{gathered} \overline{IMF}_{2} = \frac{1}{I}\sum\limits_{i = 1}^{I} {E_{1} (r_{1} + \varepsilon_{1} E_{1} (\omega^{i} ))} \hfill \\ {\text{where }}r_{1} = r_{k - 1} + \varepsilon_{1} E_{1} (\omega^{i} )\;{\text{and}}\;i = 1, \ldots, I. \hfill \\ \end{gathered}$$
(7)

The residual value is computed as the Eq. (6) for \(k = 2,.....k\).

The (k + 1)th intrinsic mode function is obtained from the following Eq. (8) as (Torres et al. 2011):

$$\overline{IMF}_{(k + 1)} = \frac{1}{I}\sum\limits_{i = 1}^{I} {E_{1} (r_{k} + \varepsilon_{k} E_{k} (\omega^{i} ))}$$
(8)

where \(i = 1,.....,I\) As long as the residual has more than three extremes, the procedure of extracting the intrinsic mode functions continues.

3.5 Models development

Firstly, an entropy approach was used to discern the most important climatic data to apply them when defining the inputs of the models. This technique was also utilized to determine the appropriate lags of the most effective inputs.

After determining the inputs patterns, the single RF and then hybrid CEEMD-RF and W-RF models were implemented. Firstly, the classic RF models were implemented taking into consideration of the mean squared error obtained in training and testing datasets. The optimal number of trees was then used when modeling the intended parameter using the RF so that no change in the mean squared error was observed by increasing the number of trees (Shataee et al. 2012). Besides, the data decomposition through the wavelet functions and CEEMD technique was utilized to generate the hybrid models. For this aim, the selected inputs by the entropy method were processed (using five mother wavelet functions with appropriate decomposition levels and CEEMD approach) and then introduced as inputs to the RF model; thus, the coupled W-RF and CEEMD-RF models were developed.

3.6 Performance assessment metrics

This study used four evaluation metrics including root mean square error (RMSE), mean absolute error (MAE), Kling-Gupta efficiency (KGE), and Willmott index (WI) to investigate the estimation accuracy of single RF and coupled CEEMD-RF and W-RF models. These statistical metrics can be formulated as the following equations:

$$RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {\left( {Q_{o,i} - Q_{e,i} } \right)^{2} } }}{N}}$$
(9)
$$MAE = \frac{{\sum\nolimits_{i = 1}^{N} {\left| {Q_{o,i} - Q_{e,i} } \right|} }}{N}$$
(10)
$$KGE = 1 - \sqrt {(CC - 1)^{2} + (\alpha - 1)^{2} + (\beta - 1)^{2} }$$
(11)
$$WI = \left| {1 - \left[ {\frac{{\sum\nolimits_{i = 1}^{N} {(Q_{o,i} - Q_{e,i} )^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {\left| {Q_{o,i} - \overline{{Q_{o} }} } \right| + \left| {Q_{e,i} - \overline{{Q_{o} }} } \right|} \right)^{2} } }}} \right]} \right|,0 \le WI \le 1$$
(12)

where \(Q_{o,i}\) and \(Q_{e,i}\) denote the ith observed and estimated monthly reservoir inflows, respectively, \(\overline{{Q_{o} }}\) illustrates the mean of observed inflows, \(N\) is the total number of observational values, \(CC\) indicates the correlation coefficient among the observed and estimated monthly inflows, \(\alpha\) is the standard deviation ration for the observed and estimated monthly inflows, and finally \(\beta\) shows the mean ratio for the observed and estimated monthly inflows. As it is apparent, lower amounts of the RMSE and MAE as well as higher amounts of KGE and WI metrics verify better performance of respective model in estimating the monthly inflow time series.

In addition to the evaluation statistical metrics mentioned above, scatter and violin plots were also provided to visually investigate the estimation accuracy of standalone RF and hybrid CEEMD-RF and W-RF models.

4 Results and discussion

In all models based on artificial intelligence, the correct choice of inputs plays a significant role in achieving the desired performance in order to estimate the target parameter (e.g., monthly reservoir inflow in this research). Therefore, before modeling, it is necessary to examine the importance of each of the input parameters affecting the output parameter by preprocessing methods. Here, an entropy-based pre-processing technique was employed. Possible input variables influencing the monthly reservoir inflow in this study were comprised of monthly minimum air temperature (Tmin), monthly maximum air temperature (Tmax), monthly mean air temperature (T), reservoir evaporation (E), and rainfall (R).

In the entropy method, a certain weight is assigned to each of the input variables, which indicates the impact factor and the importance of this parameter on the output target parameter. Figure 3 shows the values of the weights (in percent) assigned to the considered input parameters in the form of a radar chart. As it can be clearly seen, rainfall (R) is the most important parameter affecting the monthly reservoir inflow due to having the highest weight (64.71%). After R, the evaporation (E) parameter gained more weight (21.13%) while the air temperature parameters had the lowest assigned weight values. Hence, only the rainfall variable was chosen among the variables considered when defining the input patterns. In the present study, three different types of input scenarios were taken into consideration including antecedent Q-based, antecedent R-based, and combined antecedent Q and R-based patterns. The entropy approach was used again to determine the appropriate lags of rainfall and inflow. In this regard, five lags of rainfall and inflow were considered. The values of weights (in percent) assigned to the different lags of rainfall and inflow are depicted schematically in Fig. 4. As shown, the first three lags have the highest weights in both the rainfall and inflow variables, which indicates their greater impacts on the target parameter.

Fig. 3
figure 3

Radar graph indicating the weights (in percent) assigned to each of the inputs

Full size image
Fig. 4
figure 4

The values of weights (in percent) assigned to the lagged rainfall and inflow data

Full size image

Initially, a classic RF was applied to estimate the monthly reservoir inflow of current month under the input patterns mentioned above. It is worth mentioning that the number of trees was selected in such a way that increasing the number of trees from the intended number had no significant effect on the performance RF-based models. The values of statistical metrics of RMSE, MAE, KGE, and WI computed for the single RF are summarized in Tables 2, 3, 4. As clear, the RF includes the potential of estimating the current month inflow as a function of intended inputs (i.e., antecedent Q in Table 2, antecedent R in Table 3, and combined antecedent Q and R in Table 4).

Table 2 Statistical performance of conventional RF and hybrid CEEMD-RF models under the lagged Q-based patterns
Full size table
Table 3 Statistical performance of conventional RF and hybrid CEEMD-RF models under the lagged R-based patterns
Full size table
Table 4 Statistical performance of conventional RF and hybrid CEEMD-RF models under the lagged Q and R-based patterns
Full size table

An attempt was then made in this study to enhance the accuracy of monthly reservoir inflow estimations via developing two types of coupled models. At first, a novel hybrid model was proposed by coupling the CEEMD on the classic RF. A performance comparison of the single RF and hybrid CEEMD-RF models in Tables 2–4 confirms the reliable potential of proposed coupled model compared to the classic RF. For an instance, considering the best hybrid model in Table 2 under the antecedent Q-based patterns during the test phase, it can be seen that the statistical measures of coupled CEEMD-RF3 are as RMSE = 16.723 m3/s, MAE = 11.380 m3/s, KGE = 0.434, WI = 0.752 while the mentioned error metrics of single RF3 were as RMSE = 39.152 m3/s, MAE = 25.942 m3/s, KGE = 0.354, WI = 0.435. This conclusion was also obtained for the other scenarios of this pattern as well as antecedent R-based and combined Q and R-based patterns (in Tables 3 and 4). The better estimation accuracy of hybrid CEEMD-RF models than the classical RF ones can be explained considering the fact that decomposing the original data via the CEEMD can provide the decomposed data so that they can be used successfully as the new inputs for improving the classic models performances.

In addition to proposing a new hybrid model called as CEEMD-RF, this study also developed another type of hybrid model using the hybridization of W theory and RF. Six various mother wavelets including Haar, Daubechies2 (db2), Daubechies4 (db4), Symlet (Sym), Coifflet (Coif), and Fejer-Korovkin (FK) were used during the development of coupled W-RF models. Based on the total number of observational data used for the modeling procedure (i.e., 420 data in the current study), certain levels of decomposed data should be used (Mehdizadeh et al. 2020a, 2020b). Here, two levels of data decomposition were taken into consideration (\(Int\left[ {Log(420)} \right] = 2\)). The numbers in the parenthesis mentioned after the name of used mother wavelet in Tables 5, 6, 7 (i.e., 1 and 2) denote the level of decomposition applied when developing the coupled W-RF models. A comparative assessment of the classic RF with error metrics mentioned in Tables 2–4 and hybrid W-RF models with error metrics tabulated in Tables 5–7 clearly verifies that hybridizing the W and RF could lead to more accurate estimates of monthly reservoir inflow. As an example, the values of statistical metrics achieved for the single RF2 during the test period of Q and R-based patterns in Table 4 (i.e., RMSE = 30.462 m3/s, MAE = 21.622 m3/s, KGE = 0.526, WI = 0.529) were improved to RMSE = 15.418 m3/s, MAE = 10.825 m3/s, KGE = 0.806, WI = 0.764 in the hybrid W-RF2 model utilizing Sym(2) mother wavelet. The dependable performance of hybrid W-RF models than the classical RF can be justified by explaining the fact that the wavelet analysis provides useful subsets of the original observations series, which can increase the model's potential to estimate the desired target parameter by extracting suitable information produced by these new sub-series.

Table 5 Statistical performance of hybrid W-RF models utilizing various mother wavelets under the lagged Q-based patterns
Full size table
Table 6 Statistical performance of hybrid W-RF models utilizing various mother wavelets under the lagged R-based patterns
Full size table
Table 7 Statistical performance of hybrid W-RF models utilizing various mother wavelets under the lagged Q and R-based patterns
Full size table

In a review paper, Nourani et al. (2014) evaluated the ability of the wavelet-artificial neural networks (W-ANN) hybrid model in various hydrological contexts (including rainfall-runoff) at short- and long-term time scales. They found out that due to the use of subsets resulting from the wavelet transform as the inputs of neural network models, the model performance increases significantly, which is completely consistent with the results of the present study.

A performance evaluation of six different mother wavelets when coupling them on the classic RF (Tables 5–7) clearly affirms that Sym and Coif are the best wavelets because of having lowest error values of the corresponding hybrid W-RF models; therefore, these wavelets could be suggested to be used as the suitable mother wavelets when estimating the monthly reservoir inflow through the hybrid W-RF technique. On the contrary, least-performing wavelets were the Haar and FK, which are not recommended. As mentioned above, two levels of decomposition were employed in the development of W-RF models. According to the values of statistical indicators mentioned in Tables 5–7, it can be clearly concluded that the estimation accuracy of coupled W-RF models was generally improved through applying the two decomposition levels in comparison to the use of one decomposition level. The wavelet transform by decomposing the original time series at higher decomposition levels helps to better interpret the structure of the original observational series and obtain useful information about its history; hence, this issue can be one of the reasons for improving the performance of W-RF models with increasing the level of data decomposition (Mehr et al. 2014).

Comparing the modeling accuracy of monthly reservoir inflow utilizing the hybrid CEEMD-RF and W-RF models demonstrates that CEEMD-RF models outperformed the W-RF ones for some cases and vice versa W-RF showed superior results than the CEEMD-RF for other cases. However, the W-RF models generally surpass the CEEMD-RF ones. The superior models for the estimation of monthly reservoir inflow time series of study location in the test stage were W-RF3 via Sym(2) wavelet under the antecedent Q-based patterns, W-RF2 through the Sym(2) wavelet under the antecedent R-based patterns, and W-RF2 via Sym(2) wavelet under the antecedent Q and R-based patterns. The values of statistical metrics for the mentioned superior models are bolded in Tables 5–7.

Regarding the ability of the intended input patterns, it can be seen from Tables 2–7 that the single RF and hybrid CEEMD-RF and W-RF models provided lower performances under the antecedent R-based input patterns. On the other side, using patterns based on the combined antecedent Q and R data is highly recommended to achieve the more accurate estimates of monthly reservoir inflow time series.

Besides the statistical error metrics used in the present study including the RMSE, MAE, KGE, and WI, two descriptive charts were also prepared and taken into consideration to visually evaluate the estimation accuracy of classic RF and coupled CEEMD-RF and W-RF models. In this context, scatter and violin diagrams were provided.

Figure 5 depicts the scatter plots of observed and estimated inflow data through the best models considering the different input patterns. According to this figure, it can be observed that the data dispersion around the dashed 1:1 line is significant for the single RF models, which indicates that the classic RF could not perform well in estimating the observed monthly reservoir inflow data. However, coupling the RF with the CEEMD and W techniques has improved the accuracy of monthly inflow estimates. In this regard, W(Sym)(2)-RF3 hybrid model developed under the lagged Q-based pattern could present the highest convergence around the perfect 1:1 line.

Fig. 5
figure 5

Scatter plots of the observed and estimated monthly reservoir inflows via the best classic RF and hybrid CEEMD-RF and W-RF models for the considered input patterns during the test phase

Full size image

One of the drawbacks of the scatter plot is that it does not provide any possibility to compare the distribution of estimated and observed data. In other words, through the scatter plot, it is not possible to find out whether the mean and variance of the observational data are correctly estimated by the developed models or not. To solve this problem, a violin diagram can be taken into consideration. It is better to mention that a violin diagram is another form of a box plot. Box plots only illustrate the minimum, maximum, mean, and quarters of the data; but, the violin diagram is used to visualize the data distribution and its possible density. The violin graphs for the optimal single and coupled models are given in Fig. 6. It can be seen that the single RF models with different inputs have not been able to estimate the maximum values well, but overestimation has occurred for the minimum and average data. The average of the estimated data is skewed. And therefore have a higher mean than the observational data. A comparison of the violin diagrams for the hybrid models of CEEMD-RF under the different input patterns shows that they could not be able to estimate the maximum values correctly. The hybrid W(Sym)(2)-RF3 model implemented under the lagged Q data-based pattern illustrated the best performance in estimating the observational inflow data so that the minimum and maximum values are estimated proportionally and the average of the estimated data is very close to the average of the observed values.

Fig. 6
figure 6

Violin plots of the observed and estimated monthly reservoir inflows via the best classic RF and hybrid CEEMD-RF and W-RF models for the considered input patterns during the test phase

Full size image

5 Conclusion

In the present study, improved models of RF were developed and proposed for the estimation of monthly reservoir inflow time series. To reach this goal, CEEMD and W were hybridized with the classic RF (i.e., CEEMD-RF and W-RF coupled models). To implement the hybrid W-RF, six various mother wavelets were employed under two decomposition levels. It is worthy to mention that an entropy-based pre-processing technique was used to determine the input patterns. The attained outcomes can be summarized as follows:

  • Results of entropy approach revealed that the rainfall was the most important variable influencing the monthly inflow time series.

  • Among the three different input patterns intended for the development of simple and hybrid models (i.e., antecedent Q-based, antecedent R-based, and combined antecedent Q and R-based patterns), whole the models developed via the application of combined antecedent Q and R data generally illustrated the better performance.

  • Hybridizing the CEEMD and W techniques on the RF led to better estimations of the monthly inflow time series compared with the classic RF. Among the best-performing hybrid models of CEEMD-RF and W-RF, the best W-RF models demonstrated superior performances than the other hybrid ones.

  • Testing the six different mother wavelets to couple them on the classic RF showed that Sym and Coif were generally the suitable wavelets to improve the estimation accuracy of monthly inflow through the hybrid W-RF models. On the other hand, Haar and FK wavelets were the least-performing wavelets.

  • It was concluded that the estimation accuracy of W-RF models was significantly improved through increasing the decomposition levels from one to two when decomposing the input data.

This study applied the developed hybrid models for estimating the monthly reservoir inflow. It is recommended that the proposed hybrid models, specifically the new hybrid CEEMD-RF one, could be of use and tested for modeling the other hydrological phenomena like rainfall, river streamflow, evaporation, drought, etc. Besides the hybrid CEEMD-RF and W-RF models proposed in the current study, more efforts could be made to introduce other types of coupled techniques via hybridizing the artificial intelligence models with the time series analysis and nature-inspired optimization algorithms.