1 Introduction

The data, including all forms of hydro, called hydrologic data, has vast importance on the scientific studies which have purposes like observing the water cycle and distribution in the world, physical and chemical characteristics of water and also the relationship between water and the whole ecologic system. This data has non-linear and non-stationary characteristics, as a results of water’s nature (Alvisi and Franchini 2011). Forecasting of hydrological variable is necessary for optimal design of water structures, planning and management of water storage, energy production and control of extreme events, such as floods.

Auto Regressive Moving Average (ARMA) and Auto Regressive Integrated Moving Average (ARIMA) models are two of the general time series parametric models (Alvisi and Franchini 2011). The ARIMA model, a generalization of an ARMA model, has been widely applied in forecasting the hydrological data (Alvisi and Franchini 2011; Brillinger et al. 1983; Ch et al. 2013). This model is limited as it is a linear model and assumes that the data is stationary.

With the recent development of artificial techniques, several methods, including Artificial Neural Network (ANN) (Chauhan and Shrivastava 2009; Chen et al. 2012; Cheng et al. 2004; Citakoglu et al. 2014; Guo et al. 2011; Haykin 1999; Hipel and McLeod 1994; Huang et al. 1998; Huang et al. 1999; Huang et al. 2009a), fuzzy logic methods (Huang et al. 2009b; Katambara and Ndiritu 2009; Kim et al. 2012), support vector machine (Kim et al. 2013; Kim et al. 2014; Kisi 2004a; Kisi 2004b) have been utilized that work more effectively than the traditional linear model in hydrological data forecasting problems. In these studies, it was shown that the artificial techniques have more advantages compared to the other classic techniques on learning the complex and non-linear relationships,Most proposed models are combinations of several of the above methods (Chauhan and Shrivastava 2009; Chen et al. 2012; Cheng et al. 2004; Citakoglu et al. 2014; Guo et al. 2011; Haykin 1999; Hipel and McLeod 1994; Huang et al. 1998; Huang et al. 1999; Huang et al. 2009a; Huang et al. 2009b; Katambara and Ndiritu 2009; Kim et al. 2012; Kim et al. 2013; Kim et al. 2014; Kisi 2004a; Kisi 2004b). A hybrid model based on the EMD and the ANN can be an effective way to forecast hydrological data.

There are some studies including Empirical Mode Decomposition (EMD) that uses empirical approach (Kisi 2008; Kisi and Cimen 2011; Kumar et al. 2005). This method, firstly proposed by Huang et al., is perfectly suitable for analysis of nonlinear and non-stationary signal, that represents the local characteristic of the given signal (Lin et al. 2012; Machiwal et al. 2012). Even the most complex signal can be decomposed into finite and limited number of Intrinsic Mode Function (IMFs). These IMFs; not only have stronger correlations and easier frequency components, but also provide easier and more accurate estimations. The EMD method has been used in many scientific branches what else like non-stationary ocean wave motions, earthquake signals and structure analyses, monitoring of bridges and buildings, diagnosis of mechanical failures, etc. (Mohammad 2013; Napolitano et al. 2011; Partal and Kisi 2007; Sang et al. 2012; Valipour et al. 2013). Also, Wei et al. used EMD-ANN to predict the short-term passenger flow in metro systems. Chen et al. proposed to predict tourism demand (i.e. the number of arrivals) based on EMD and neural networks (Vincent et al. 1999; Wang and Van Gelder 2006). Yu et al. designed an EMD based neural network for forecasting of crude oil price (Wei and Chen 2012). Lin et al. studied on forecasting foreign exchange rates using the EMD based least squares support vector regression (Yegnanarayana, “Artificial Neural Networks” and Prentice Hall of India 2006). To the best knowledge of the authors, the application of EMD-ANN approach for estimating monthly streamflows has not been studied and/or reported in the literature.

Our Approach

In our study, we used the EMD-ANN and the ANN models to predict monthly stream flows and compared the performances of these models. First, we applied EMD algorithm to decompose the original stream flow data into five IMFs. Secondly, these IMFs are modeled and forecasted using the ANN. Finally, these prediction results were integrated to get a final forecasting value. The EMD-ANN model was compared to the single ANN approach. The purpose of this study is to find a simple and reliable hybrid forecasting model for the stream flow data.

The rest of this paper is organized as follows. In Section 2, materials and methods including the EMD and the ANN methodology are presented. İn Section 3, the proposed model is described and the experimental results are presented. İn Section 4, the conclusions are presented.

2 Materials and Methods

2.1 Description of the Data

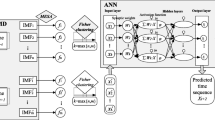
The data set consists of 32 years (380 months) of mean monthly stream flow in (m3/s), from Yamula station on the Kizilirmak river in Kayseri, Turkey. Drainage basin is shown in Fig. 1. This data set was obtained from Electrical Power Resources Survey Administration (EIEI), in Turkey (Fig. 2). The drainage area at this site is 15581,6 km2. In the applications, the first 260 month of flow data were used for training (calibration) and the remaining 120 month of the data set were used for testing. The statistical parameters of the monthly stream flow data set are presented in Table 1. In this table, x mean , S x , C sx , x min , x max , r 1 , r 2 , r 3 denote the overall mean, standard deviation, skewness, minimum, maximum, lag-1,lag-2, and lag-3 auto-correlation coefficients respectively. As seen in Table 1 the observed monthly flows show a high positive skewness (Csx = 1.29) and the auto-correlations are quite low, showing low persistence (e.g. r1 = 5650, r2 = 0.3384 and r3 = 0.0205). In this study hydrological time series signal is decomposed sing EMD method and these components have been forecasted using ANN. The prosedure of proposed model is seen in the flow chart.

Fig. 1
figure 1

The Yamula Station on Kizilirmak River

Full size image
Figure 2
figure 2

Monthly stream flow data

Full size image
Table 1 The monthly statistical parameters of stream flow data set
Full size table

2.2 The Empirical Mode Decomposition Method

The EMD method, first proposed by (Huang et al. 1998), is an adaptive and empirical approach for data analysis. This data driven method is designed for the data having non-linear and nonstationary characteristics. This method decomposes original time series into “mono component functions” called intrinsic mode functions (IMFs).

IMFs satisfy two conditions: (a) in the whole data set, the number of extreme and the number of zero crossings must either equal or differ at most by one, namely function should be symmetric in time, (b) the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero at any point. The IMFs are obtained by the superposition of the different frequency and amplitude waves and locally eliminating asymmetric signals with respect to the zero level. Due to the nature of the IMF, this functions are suitable for defining instantaneous frequency calculations using the Hilbert Transform and provide analyses of non-linear and nonstationary data (Machiwal et al. 2012; Mohammad 2013). The EMD technique decomposes the signals into the IMFs with an iterative procedure, including extreme identification and shifting process which is the core of the EMD algorithm. The shifting procedure is explained below;

  1. 1.

    All the local maxima and minima of the signal (x(t)) are identified.

  2. 2.

    Lower (emin) and upper (emax) envelopes are obtained by interpolation of x(t) signal between the local maxima and minima.

  3. 3.

    The mean value of the envelopes is computed, defined as below;

  4. 4.

    \( m(t)=\frac{e_{\min }+{e}_{\max }}{2} \)The resulting m(t) signal is subtracted from x(t) signal so that extracted detail signal is defined as; h 1(t) = x(t) − m(t).If m(t) is equal to zero or smaller than a fixed threshold, h1(t) is accepted as the first IMF and labeled as c1(t). Otherwise, steps 1–3 are repeated until h1(t) fulfills the properties of an IMF.

Resulting c1(t) is subtracted from x(t) signal, h 2(t) = x(t) − c 1(t). The shifting process (1- is repeated until the resulting signal meets the IMF criteria, which is the number of extremes not being larger than two. . The x(t) signal can be expressed in terms of IMFs, defined below equation;

$$ x(t)={\displaystyle \sum_{i=1}^n{c}_i(t)+ r(t)} $$
(1)

In this equation c i (t) represents the IMF components which are nearly orthogonal to each other and periodic, and r(t)is the final residue which is a constant or a trend. By the sifting process, each IMF is independent and specific for expressing the local characteristics of the original time series data. The IMFs components are derived from high frequency to low frequency as seen Fig. 3. In addition, EMD acts as a filter of high pass, band pass or low pass.

Fig. 3
figure 3

Five level EMD components obtained from the a Training stream flow data set, b Testing stream flow data set

Full size image

In our study; monthly stream flow data set was decomposed into five levels named IMF1 to IMF5 for the training and testing of ANN as seen in Fig. 3. This IMF data set is obtained from high frequency component to low frequency component as seen in Fig. 3.

2.3 The Artificial Neural Networks Method

The ANN has recently been used in a number of different ways in hydrology recently (Chauhan and Shrivastava 2009; Chen et al. 2012; Cheng et al. 2004; Citakoglu et al. 2014; Guo et al. 2011; Haykin 1999; Hipel and McLeod 1994; Huang et al. 1998; Huang et al. 1999; Huang et al. 2009a). The advantages of ANNs are that they are able to generalize adapting to signal distortion and noise, and that they have been trained by the sample and do not require precise description of patterns to be classified or criteria for forecasting.

Multilayer perceptron (MLP) is one of the most commonly used neural networks, organized in layers. The layers consist of a number of interconnected nodes which is named as neuron and contain an activation function. The architecture of MLP is presented as an input layer which communicates to one or more hidden layers where the actual processing is done via a system of weighted connections and an output layer where the answer is output. The MLP contains many interacting nonlinear nerons in multiple layers, therefore it can capture complex phenomone and has the capability of complex mapping between inputs and outputs. Although there are many different kinds of learning rule, which modifies the weights of the connections according to the input patterns, Back-propagation (BP) learning algorithm is used in this study. Because the BP algorithm is one of the most popular learning algorithms adopted in MLP. The weights and biases parameters of MLP are determined sing BP algorithm iteratively by a process of minimizing the global error or the total square error. This algorithm process as follows; The input neurons receive a feature vector x = [x 1, x 2, …, x n ] from the input dataset and propogate it to all neurons in hidden layers. Each hidden neuron j firstly compute the network input net j and generates the output of neuron y j , calculated using below equation;

$$ {y}_j={f}_j\left( ne{t}_j\right) $$
$$ ne{t}_j={\displaystyle \sum_{i=1}^n{w}_{i j}{x}_i+{w}_{j0}} $$
(2)

In the above eqation, w ij represents the weight between the ith neuron of the input layer and jth neuron of the hidden layera and w j0is the bias weight of neuron. The f j represents the activation function, also named as transfer function, determines the relationship between inputs and outputs of a node and network.

The most commonly used function in an MLP trained with back-propagation algorithmis the sigmoid function. The characteristics of the sigmoid function are that it is bounded above and below, it is monotonically increasing, and it is continuous and differentiable everywhere. The sigmoid function most often used for ANNs is the logistic function is defined as;

$$ f\left({y}_j\right)=\frac{1}{1-{e}^{y_j}} $$
(3)

Each output neuron j receives outputs of hidden layer as inputs, and continuously repeats all the operations described above process until the target mean sqare error is met. The iteration of otput according to termination condition is describes as below eqation;

$$ {O}_k= f\left({\displaystyle \sum_{j=1}^m} f\left({\displaystyle \sum_{i=1}^n{x}_i{w}_{i j}}\right){w}_{j k}\right) $$
(4)

In the above equation n is the number of input neuron, m is the number of output neuron (Valipour et al. 2013; Vincent et al. 1999; Wang and Van Gelder 2006).

In or study, hydrological time series data has been forecasted using MLP with a back-propagation algorithm. The BP algorithm is a supervised learning algorithm which minimizes the global error by using the generalized delta rule and the gradient steepest descent method. In our study, Levenberg–Marquardt technique, one of the BP algorithms, was used because of being more powerful and faster than the conventional gradient descent techniques. The learning procedure of a back-propagation neural network (BPN) with Levenberg–Marquardt technique is described as follows;

Firstly, Input data, at tth time, normalization is performed, and input data presents to the input layer.

Secondly, the network architecture and parameters including learning rate, activation function and bias, initial weights are determined.

Thirdly, The error (e) is computed over output neurons by comparing the generated outputs with the desired outputs.

Fourthly; The weight changes is computed. The error is applied to compute the weight change between the hidden layer and output.

Lastly, The weights are updated according to equation given below;

$$ \begin{array}{l}\mathrm{Hidden}\ \mathrm{layer}\ \mathrm{to}\ \mathrm{output}\ \mathrm{layer}:{w}_{kj}^{h+1}={w}_{kj}-{\left[ H+\mu I\right]}^{-1}{J}^T e\hfill \\ {}\mathrm{Input}\ \mathrm{layer}\ \mathrm{to}\ \mathrm{hidden}\ \mathrm{layer}:{w}_{ij}^{h+1}={w}_{ij}-{\left[ H+\mu I\right]}^{-1}{J}^T e\hfill \end{array} $$
(5)

In equation 6, H represents the Hessian matrix and calculated Jacobian matrices, as given below;

$$ H\approx {J}^T J $$

The Jacobian matrix composed of all first-order partial derivatives of a vector-valued function. In the neural networks, It is N by W matrix, where N is the number of entries in the training set and W is the total number of parameters (weights + biases) of the networks. It is defined as below;

$$ J=\left[\begin{array}{l}\frac{\partial f\left({x}_1, w\right)}{\partial {w}_1}\kern1em \cdots \cdots \kern1em \frac{\partial f\left({x}_1, w\right)}{\partial {w}_w}\\ {}\kern1em \vdots \cdots \cdots \kern3.1em \vdots \\ {}\frac{\partial f\left({x}_N, w\right)}{\partial {w}_N}\kern1em \cdots \cdots \kern1em \frac{\partial f\left({x}_N, w\right)}{\partial {w}_w}\end{array}\right] $$
(6)

In equation 6, the μ is the damping factor and adjusted at each iteration and guides the optimization process. If reduction of e is rapid, a smaller vale can be used, bringing the algorithm closer to the to the Gauss–Newton algorithm, whereas if an iteration gives insufficient reduction in the residual, μ can be increased, giving a step closer to the gradient descent direction.

After the weights are updated, if the sum of squared errors has not decreased, μ has been increased, else μ has been decreased.

Finally, steps are repeated until the global error satisfies a predefined threshold (Valipour et al. 2013; Vincent et al. 1999; Wang and Van Gelder 2006).

3 Application and Results

In this study, the proposed hybrid EMD–ANN approach is compared to the single ANN model based on the mean square error (MSE), mean absolute error (MAE) and correlation coefficient (R) statistics. The MSE, MAE and R statistics are given in the following equations.

$$ MSE=\frac{1}{N}{{\displaystyle {\sum}_{i=1}^N\left( Y{i}_{observed}- Y{i}_{estimated}\right)}}^2 $$
(3)
$$ MAE=\frac{1}{N}{\displaystyle {\sum}_{i=1}^N\Big| Y{i}_{observed}- Y{i}_{estimated}}\Big| $$
(4)
$$ R=\left(\frac{{\displaystyle {\sum}_{i=1}^N\left( Y{i}_{observed}- Y{m}_{observed}\right)}\left( Y{i}_{estimated}- Y{m}_{estimated}\right)}{\sqrt{{{\displaystyle {\sum}_{i=1}^N\left( Y{i}_{observed}- Y{m}_{observed}\right)}}^2{\displaystyle {\sum}_{i=1}^N{\left( Y{i}_{estimated}- Y{m}_{estimated}\right)}^2}}}\right) $$
(5)

where Yiobserved and and Yiestimated denote the observed and the corresponded estimated river flow, respectively, Ymobserved is mean of observational values, and Ymestimated is mean value of the estimations.

3.1 Forecasting Stream Flow Data with EMD-ANN Model

In the EMD–ANN model, there are three stages including data decomposition by the EMD and forecasting by the ANN.

Step 1. Use the EMD to decompose the original stream flow data into a five set of IMFs, seen in Fig. 3.

Step 2. Apply ANN models to forecast next month of the IMFs.

Step 3. Obtain the forecasted stream flow data by the summation of the predicted IMFs.

The effects of various EMD decomposition levels on model efficiency were also investigated to optimize the result, but no definitive improvements were found for further decomposition. Therefore, stream flow data set was decomposed into five levels labeled as IMF1 to IMF5.

Because the EMD decomposition acts a dyadic filter bank, the obtained IMFs are in frequency range from high to low and indicate the local characteristic time scale by itself. Therefore, these components of stream flow data have a periodic pattern as seen in Fig. 3 (Mohammad 2013).

In the second stage of this part of the study, a three-layer feed-forward ANN with a logistic activation function was chosen. There were no general rules for the definition of network topology. The selection was usually based on the trial and error method. Number of input data of ANN is important for computational requirements. In this study, the previous one to five months were selected as inputs to the ANN and using these inputs the ANN was trained and tested. The network is iterated for single hidden layer with combinations of one to ten neurons in this layer. The values of the internal weights and biases were adjusted so as to minimize the error between the actual output of the network and the desired output during training layer and learning rates. The ANN underwent supervised learning to perform successful forecasting of the stream flow data set. The best results were accomplished with the combination of one hidden layer with sigmoid function and linear function for output layer. The weight learning function used was the Levenberg-Marquardt algorithm and the performance function used was mean square error during definition of the network structure. The ANN training was stopped when the mean square error reached 0.0001.

In Table 2, the MSE, MAE and R values during forecasting of each IMFs are listed. One to five differing numbers of inputs derived from IMFs to ANN were tried to obtain the best forecasting performance.

Table 2 Performance values of the ANN model in forecasting of IMFs during test period
Full size table

The IMF components were forecasted successfully, as seen in Table 2 and in Fig. 4. However, forecasting performance of IMF1 component is worse than the others. Because, the IMF1 component is characterized by higher mean frequencies and include noise component because EMD acts a filter bank for Gaussian noise, white noise and turbulence of time series (Sang et al. 2012). Therefore, forecasting of IMF1 component is difficult.

Fig. 4
figure 4

Forecasted IMFs with ANN and Observed IMFs using four inputs during the test period

Full size image

It is observed in Table 2 that, the EMD-ANN model with three inputs resulted in better forecasting performance than the other counts of inputs.

In the third stage of this part of the study, predicted stream flows were obtained by summing all forecasted IMFs (IMF1 to IMF5). Table 3 summarizes the results of EMD-ANN models for each input combination. The three-input EMD-ANN model whose inputs were obtained by summation of the IMF1 to IMF5 series performed better than the other models based on the performance measures. Forecasted stream flows by the optimum EMD-ANN model are shown in Fig. 5. It is clear from the figure that the model closely follows the observed monthly time series.

Table 3 Performance values of the EMD-ANN models during the test period
Full size table
Fig. 5
figure 5

Observed and predicted stream flow data by using the three-input EMD-ANN model during the test period

Full size image

3.2 Forecasting of Stream Flow Data with ANN

In ANN forecasting models, the previous stream flow values from one to five months were used as inputs to the network to predict next month’s value. The optimum ANN models for each input combination was determined after trying various combinations. Table 4 gives the results of ANN models in the test period. Comparison of Table 3 and 4 indicates that the EMD-ANN model performs much better than the ANN model. The proposed hybrid model reduced the MSE, MAE values and increased the R value relatively by 36, 13 and 24.7 % respectively. The predicted stream flow data obtained from three-input ANN model in the test period are seen in Fig. 6. In this figure, the underestimation of the monthly peak values for the ANN model can be seen visually.

Table 4 Performance values of the ANN models in the test period
Full size table
Fig. 6
figure 6

Observed and predicted stream flow data by using the three-input ANN model during the test period

Full size image

4 Conclusion

In our study, the EMD-ANN model was investigated for the forecasting of stream flow data. Time series data was decomposed and five level sub-time series named IMF1-IMF5 were obtained for the purpose of forecasting. Each IMF component was used as input to the EMD-ANN model. After forecasting IMF’s, predicted results were obtained by summation of all forecasted IMFs. The proposed model were tested by applying previous one to five months input combinations of the stream flow data of Yamula station on Kizilirmak River in Turkey. The test results of the EMD-ANN model were compared with the single ANN model. The optimal test results were obtained for the three-input to EMD-ANN model. Comparison results showed that the EMD-ANN model provided a superior alternative to the ANN model by reducing the MSE and MAE values by 36 and 13 % respectively and increasing the R value by % 24.7.