1 Introduction

In geostatistical applications, regionalized variables exhibiting a spatial trend may not be modeled with second-order stationary random fields, i.e., random fields whose first and second-order moments exist and are invariant through a translation in space, nor with random fields whose increments are second-order stationary (intrinsic random fields of order 0, also known as stationary intrinsic random fields). This is the case, for instance, in geothermal reservoir modeling, where the temperature and the pressure tend to increase with depth, whereas porosity and permeability tend to decrease (Chilès and Gable 1984). In petroleum reservoir modeling, geometrical characteristics or petrophysical properties such as rock porosity often present trends that cannot be dealt with stationarity hypotheses (Chilès and Gable 1984; Dimitrakopoulos 1990). In ore body modeling, the distribution of geological properties such as rock types, mineral types or alteration types, also exhibit spatial zonations and trends, depending on the geological setting and paragenesis of the ore body, making difficult the representation of these properties with second-order stationary or intrinsic stationary random fields (Madani and Emery 2017).

The theory of intrinsic random fields of order k (for short, IRF-k) has been introduced when the assumption of second-order stationarity is not satisfied, but generalized increments filter out the trend and fulfill the assumptions of second-order stationarity (Chilès and Delfiner 2012; Christakos 1992; Matheron 1973). These random fields have been used in the past decades for spatial prediction purposes in geothermal fields (Chilès and Gable 1984; Suárez Arriaga and Samaniego 1998), oil reservoirs (Haas and Jousselin 1976), aquifers (Dong et al. 1990; Kitanidis 1999), soil (Buttafuoco and Castrignano 2005) and environmental sciences (Christakos and Thesing 1993), among other applications.

Apart from prediction, there is a growing interest in quantifying the uncertainty at locations with no direct observation, or jointly over several locations, for which conditional simulation techniques have been developed (Chilès and Delfiner 2012). In this respect, several algorithms have been proposed to simulate intrinsic random fields of order k, under the assumption that their generalized increments have multivariate-Gaussian distributions (Arroyo and Emery 2015; Chilès and Delfiner 2012; Christakos 1992; Dimitrakopoulos 1990; Emery and Lantuéjoul 2006, 2008; Pardo-Igúzquiza and Dowd 2003). Among these algorithms, the continuous spectral and turning bands approaches have proved to be successful in accurately reproducing the spatial correlation structure of the generalized increments, while being computationally efficient. However, they are still limited to the simulation of scalar random fields and are therefore not suitable for multivariate applications. The aim of this paper is to extend the continuous spectral algorithm to the simulation of vector random fields representing co-regionalized variables.

The outline of the paper is the following: Sect. 2 is devoted to an overview of the IRF-k theory, Sect. 3 introduces the spectral simulation algorithms for generating non-conditional simulations of an univariate IRF-k and of a vector IRF-k. Section 4 is devoted to applications to synthetic case studies. Conclusions follow in Sect. 5.

2 Concepts and notations

In IRF-k theory, the spatial trend is represented by a combination of basic drift functions \(\{f^l\}_{l\in {0,\ldots , L}}\) that are monomials of the spatial coordinates. The number L of such basic functions depends on the degree k of the drift and on the dimension d of the working space.

A generalized increment of order k, also referred to as an authorized linear combination of order k (for short, ALC-k), of a spatial random field \( {Y} \) is defined as a weighted sum of the form \(\sum _{i\in I}\lambda _i Y(\mathbf {x}_i)\) for a system of weights and locations \(\lambda = \{\lambda _i,\mathbf {x}_i\}_{i\in I}\) such that, for any basic drift function \(f^l\), one has

$$\begin{aligned} \sum _{i\in I}\lambda _if^l(\mathbf {x}_i)=0. \end{aligned}$$
(1)

In the following, the set of weights and locations \(\lambda = \{\lambda _i,\mathbf {x}_i\}_{i\in I}\) fulfilling Eq. (1) will be denoted as \(\Lambda _k\) and the ALC-k will be denoted as \(Y(\lambda )\).

A random field defined in the \(d-\)dimensional Euclidean space, say \(Y=\{Y(\mathbf {x}): \mathbf {x}\in \mathbb {R}^d\}\), is an intrinsic random field of order k if its ALC-k have zero mean and are second-order stationary, i.e., if the following conditions are satisfied for any \(\lambda =\{\lambda _i,\mathbf {x}_i\}_{i\in I} \in \Lambda _k\) and \(\mu =\{\mu _j,\mathbf {x}_j'\}_{j\in J}\in \Lambda _k\) (Chilès and Delfiner 2012):

  1. (1)

    \(\displaystyle {E\left\{ Y(\lambda )\right\} =0}\)

  2. (2)

    Cov\(\displaystyle {\left\{ Y(\lambda ),Y(\mu )\right\} } = \sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j\mathbf {K}(\mathbf {x}_i-\mathbf {x}_j')\),

where \(\mathbf {K}\) is a generalized covariance function defined up to an even polynomial of degree less than or equal to 2k.

A property of generalized covariances is that they are k-conditionally positive definite, that is, for any \(\lambda =\{\lambda _i, \mathbf {x}_i\}_{i\in I} \in \Lambda _k\), one has

$$\begin{aligned} \sum _{i\in I}\sum _{j\in I}\lambda _i\lambda _j\mathbf {K}(\mathbf {x}_i-\mathbf {x}_j)\ge 0. \end{aligned}$$

The generalized covariance has the following spectral representation (Chilès and Delfiner 2012):

$$\begin{aligned} \mathbf {K}(\mathbf {h})=\int _{\mathbb {R}^d}\frac{\cos \left( 2\pi \langle \mathbf {h},\mathbf {u}\rangle \right) -\mathbf {1}_\mathbf {B}(\mathbf {u})P_k(2\pi \langle \mathbf {h},\mathbf {u}\rangle )}{\left( 4\pi ^2\Vert \mathbf {u}\Vert ^2\right) ^{k+1}}\chi (\mathrm {d}\mathbf {u})+Q_k(\mathbf {h}), \end{aligned}$$

where:

  • \(P_k\) is the Taylor expansion of the cosine up to order 2k, that is

    $$\begin{aligned} P_k(x)=1-\frac{x^2}{2!}+\cdots +(-1)^k\frac{x^{2k}}{(2k)!}, \quad x\in \mathbb {R}\end{aligned}$$

  • \(\mathbf {1}_\mathbf {B}(\mathbf {u})\) is the indicator function of an arbitrary neighborhood \(\mathbf {B}\) of \(\mathbf {u}_0=\mathbf {0}\)

  • \(\chi (\mathrm {d}\mathbf {u})\) is a positive symmetric measure, with no atom at the origin (that is, \(\chi (\{\mathbf {0}\})=0\)) and satisfying

    $$\begin{aligned} \int _{\mathbb {R}^d}\frac{\chi (\mathrm {d}\mathbf {u})}{\left( 1+4\pi ^2\Vert \mathbf {u}\Vert ^2\right) ^{k+1}}<\infty \end{aligned}$$

  • \(Q_k\) is an arbitrary even polynomial of degree \(\le 2k\).

Without loss of generality, one can choose \(\mathbf {B} = \mathbb {R}^d\) and \(Q_k = 0\), which simplifies the spectral representation as follows:

$$\begin{aligned} \mathbf {K}(\mathbf {h})=\int _{\mathbb {R}^d}\frac{\cos \left( 2\pi \langle \mathbf {h},\mathbf {u}\rangle \right) -P_k(2\pi \langle \mathbf {h},\mathbf {u}\rangle )}{\left( 4\pi ^2\Vert \mathbf {u}\Vert ^2\right) ^{k+1}}\chi (\mathrm {d}\mathbf {u}). \end{aligned}$$
(2)

This representation is the generalization of Bochner’s theorem (Bochner 1933) according to which a continuous function is positive definite (thus, an ordinary covariance function) if and only if it is the Fourier transform of a positive bounded symmetric measure. A representation similar to Eq. (2) exists for the variogram of a stationary intrinsic random field, which corresponds to the case of an IRF-0 (\(k = 0\) and \(P_k\) = 1) (Chilès and Delfiner 2012).

If \(\chi (\mathrm {d}\mathbf {u})\) is absolutely continuous, the previous representation can be rewritten as follows:

$$\begin{aligned} \mathbf {K}(\mathbf {h})=\int \left[ \cos \left( 2\pi \langle \mathbf {h},\mathbf {u}\rangle \right) -P_k(2\pi \langle \mathbf {h},\mathbf {u}\rangle )\right] f(\mathbf {u})\,\mathrm {d}\mathbf {u}, \end{aligned}$$
(3)

with

$$\begin{aligned} f(\mathbf {u})\,\mathrm {d}\mathbf {u}=\frac{\chi (\mathrm {d}\mathbf {u})}{\left( 4\pi ^2\Vert \mathbf {u}\Vert ^2\right) ^{k+1}} \ge 0. \end{aligned}$$

In the following, \( {f} \) will be referred to as the spectral density of the generalized covariance \(\mathbf {K}\). Unless \( {Y} \) is a second-order stationary random field (i.e., \(\mathbf {K}\) is an ordinary covariance function), \( {f} \) is not integrable, so it is not a genuine probability density function.

Another tool used for modeling the spatial structure of an intrinsic random field of order k is the generalized variogram of order k, defined as (Chilès and Delfiner 2012)

$$\begin{aligned} \varUpsilon (\mathbf {h})=\frac{1}{M_k}\mathrm {Var}\left[ \Delta _\mathbf {h}^{k+1}Y(\mathbf {x})\right] \end{aligned}$$
(4)

with,

$$\begin{aligned} M_k= & {} \left( {\begin{array}{c}2k+2\\ k+1\end{array}}\right) \\ \Delta _\mathbf {h}^{k+1}Y(\mathbf {x})= & {} (-1)^{k+1}\sum _{q=0}^{k+1}(-1)^q\left( {\begin{array}{c}k+1\\ q\end{array}}\right) Y(\mathbf {x}+q\mathbf {h}). \end{aligned}$$

\(\Delta _\mathbf {h}^{k+1}Y(\mathbf {x})\) is the generalization of the forward finite difference \(Y(\mathbf {x}+\mathbf {h})-Y(\mathbf {x})\).

In the same way that the variogram is related to the covariance in the case of second-order stationary random fields, the generalized variogram of order k is related to the generalized covariance of order k, as follows (Chilès and Delfiner 2012):

$$\begin{aligned} \varUpsilon (\mathbf {h})=\frac{1}{M_k}\sum _{q=-(k+1)}^{k+1}(-1)^q\left( {\begin{array}{c}2k+2\\ k+1+q\end{array}}\right) \mathbf {K}(q\mathbf {h}). \end{aligned}$$
(5)

3 Non-conditional simulation

This section focuses on the non-conditional simulation of intrinsic scalar and vector random fields of order k. In the presence of conditioning data, any non-conditional realization can be converted into a conditional one (i.e., a realization that reproduces the conditioning data, in addition to the desired generalized covariance model) by means of a post-processing step based on intrinsic kriging (univariate case) or cokriging (multivariate case) with the same generalized covariance model and basic drift functions (Chilès and Delfiner 2012; de Fouquet 1994; Emery 2010).

3.1 Univariate case

To simulate an intrinsic scalar random field of order k (denoted as \(Y\)) with a generalized covariance function \(\mathbf {K}\) associated with the spectral density \(f\), let us consider a random field \(Y_S\) defined as

$$\begin{aligned} \forall \, \mathbf {x}\in \mathbb {R}^{d},\,Y_S(\mathbf {x})=\sqrt{\frac{2\,f(\mathbf {U})}{g(\mathbf {U})}}\cos (2\pi \langle \mathbf {x}, \mathbf {U}\rangle +\phi ), \end{aligned}$$
(6)

where \(\langle \,,\rangle\) represents the inner product in \(\mathbb {R}^d\), \(\mathbf {U}\) is a random vector (frequency) with probability density \(g: \mathbb {R}^d \rightarrow \mathbb {R}_+\) with a support containing that of f and \(\phi\) is a random scalar (phase) uniformly distributed over the interval \(\left[ 0, 2\pi \right)\). The demonstration that \(Y_S\) is an IRF-k with \(\mathbf {K}\) as its generalized covariance function of order k is deferred to the next subsection, which addresses the more general case of intrinsic vector random fields.

Based on the central limit theorem, to obtain an intrinsic random field of order k with the same generalized covariance \(\mathbf {K}\) and approximately Gaussian generalized increments of order k, it suffices to add and to rescale many of such independent random fields:

$$\begin{aligned} \forall \, \mathbf {x}\in \mathbb {R}^{d},\,\mathbf {Y}_S(\mathbf {x})=\frac{1}{\sqrt{N}}\sum _{n=1}^{N}\sqrt{\frac{2\,f(\mathbf {U}_n)}{g(\mathbf {U}_n)}}\cos (2\pi \langle \mathbf {x}, \mathbf {U}_n\rangle +\phi _n), \end{aligned}$$
(7)

where \(N\) is a large integer, \(\{\mathbf {U}_n: n=1, \ldots , N\}\) are mutually independent random vectors with probability density \(g\) and \(\{\phi _n: n=1, \ldots , N\}\) are mutually independent random variables uniformly distributed in \([0, 2\pi )\), independent of \(\{\mathbf {U}_n: n=1, \ldots , N\}\). Without loss of generality, one can also shift the random field by a constant, so that its value is zero at the origin \(\mathbf {x}= \mathbf {0}\):

$$\begin{aligned} \forall \, \mathbf {x}\in \mathbb {R}^{d},\,\mathbf {Y}_S(\mathbf {x})=\frac{1}{\sqrt{N}}\sum _{n=1}^{N}\sqrt{\frac{2\,f(\mathbf {U}_n)}{g(\mathbf {U}_n)}}\left[ \cos (2\pi \langle \mathbf {x}, \mathbf {U}_n\rangle + \phi _n)-\cos (\phi _n)\right] . \end{aligned}$$
(8)

A particular case of this algorithm has been proposed in Emery and Lantuéjoul (2008) for simulating IRF-k with power or spline generalized covariances. In contrast, the algorithm presented here (Eq. 8) is applicable to any generalized covariance model whose spectral density is absolutely continuous.

3.2 Multivariate case

One can extend the previous spectral algorithm to the simulation of an intrinsic vector random field of order k (denoted as \(\mathbf {Y}\)) with P cross-correlated scalar components, by considering a \(P \times P\) matrix of spectral densities \(\mathbf {f}\) (a Hermitian, positive semi-definite matrix) instead of a scalar spectral density f. In the case when this matrix is real-valued, it is associated with a \(P \times P\) matrix \(\mathbf {K}\) containing the generalized direct and cross-covariances of the components of \(\mathbf {Y}\), in a way similar to Eq. (3) (Cassiani and Christakos 1998; Chilès and Delfiner 2012; Christakos 1992), that is:

$$\begin{aligned} \mathbf {K}(\mathbf {h})=\int _{\mathbb {R}^d}{\left[ \cos \left( 2\pi \langle \mathbf {h},\mathbf {u}\rangle \right) -P_k(2\pi \langle \mathbf {h},\mathbf {u}\rangle )\right] \mathbf {f}(\mathbf {u})\mathrm {d}\mathbf {u}}, \end{aligned}$$
(9)

where \(P_k\) is the Taylor expansion of the cosine up to order 2k.

Specifically, let us define a vector random field as follows:

$$\begin{aligned} \mathbf {Y}_S(\mathbf {x})=\sum _{p=1}^{P}\alpha _p(\mathbf {U}_p)\cos (2\pi \langle \mathbf {x}, \mathbf {U}_p\rangle +\phi _p), \end{aligned}$$
(10)

where \(\left\{ \mathbf {U}_p: p=1, \ldots , P\right\}\) are mutually independent random vectors with probability density \(g:\mathbb {R}^d\rightarrow \mathbb {R}_+\), \(\left\{ \phi _p: p=1, \ldots , P\right\}\) are mutually independent random variables uniformly distributed over the interval \([0, 2\pi )\), independent of the \(\mathbf {U}_p\), and \(\left\{ \alpha _p: p=1, \ldots , P\right\}\) are vector-valued mappings (to be determined) with P real-valued components.

Considering \(\lambda =\{\lambda _i, \mathbf {x}_i\}_{i\in I} \in \Lambda _k\), one can define an ALC-k of the simulated vector random field \(\mathbf {\mathrm {\mathbf {Y}}}_S(\lambda )\) as follows:

$$\begin{aligned} \mathbf {\mathrm {\mathbf {Y}}}_S(\lambda )=\sum _{i\in I}\lambda _i\sum _{p=1}^{P}\alpha _p(\mathbf {U}_p)\cos (2\pi \langle \mathbf {x}_i, \mathbf {U}_p\rangle + \phi _p). \end{aligned}$$
(11)

Accounting for the fact that \(\left\{ \phi _p: p=1, \ldots , P\right\}\) are independent and uniformly distributed in \([0, 2\pi )\), the conditional expectation of \(\mathrm {\mathbf {Y}}_S(\lambda )\) given \(\mathbf {U}_p=\mathbf {u}_p\) is

$$\begin{aligned} \mathbb {E}\left[ \mathrm {\mathbf {Y}}_S(\lambda )|\mathbf {U}_p=\mathbf {u}_p\right] =\mathbf {0}. \end{aligned}$$

Therefore, the prior expectation is

$$\begin{aligned} \mathbb {E}\left[ \mathrm {\mathbf {Y}}_S(\lambda )\right]&= {} \mathbb {E}\left\{ \mathbb {E}\left[ \mathrm {\mathbf {Y}}_S(\lambda )|\mathbf {U}_p\right] \right\} \\& = {} \mathbf {0}. \end{aligned}$$

Now, consider \(\lambda =\{\lambda _i, \mathbf {x}_i\}_{i\in I}\in \Lambda _k\) and \(\mu =\{\mu _j, \mathbf {x}_j'\}_{j\in J}\in \Lambda _k\). If it exists, the matrix of direct and cross-covariances between \(\mathrm {\mathbf {Y}}_S(\lambda )\) and \(\mathrm {\mathbf {Y}}_S(\mu )\) is

$$\begin{aligned} \mathbb {E}\left[ \mathbf {Y}_S(\lambda )\mathbf {Y}_S(\mu )\right]&= {} \mathbb {E}\left[ \sum _{i\in I}\sum _{j\in J}\sum _{p=1}^{P}\sum _{q=1}^{P}\lambda _i\mu _j\alpha _p(\mathbf {U}_p)\alpha _q^\mathrm{T}(\mathbf {U}_q)\cos (2\pi \langle \mathbf {x}_i, \mathbf {U}_p\rangle + \phi _p)\cos (2\pi \langle \mathbf {x}_j', \mathbf {U}_q\rangle + \phi _q)\right] \\&= {} \mathbb {E}\left[ \sum _{i\in I}\sum _{j\in J}\sum _{p=1}^{P}\sum _{q=1}^{P}\lambda _i\mu _j\alpha _p(\mathbf {U}_p)\alpha _q^\mathrm{T}(\mathbf {U}_q)\times \frac{1}{2}\left[ \cos (2\pi \langle \mathbf {x}_i, \mathbf {U}_p\rangle +2\pi \langle \mathbf {x}_j', \mathbf {U}_q\rangle +\phi _p+\phi _q)\right. \right. \\&+\,\left. \left. \cos (2\pi \langle \mathbf {x}_i, \mathbf {U}_p\rangle -2\pi \langle \mathbf {x}_j', \mathbf {U}_q\rangle +\phi _p-\phi _q)\right] \right] . \end{aligned}$$

Accounting for the fact the phases \(\{\phi _p, p=1, \ldots , P\}\) are independent and uniformly distributed in \([0, 2\pi )\), all the cosine terms have a zero expectation except when \(p=q\), so that the previous equation simplifies into

$$\begin{aligned} \mathbb {E}\left[ \mathbf {Y}_S(\lambda )\mathbf {Y}_S(\mu )\right] = \frac{1}{2}\mathbb {E}\left[ \sum _{i\in I}\sum _{j\in J}\sum _{p=1}^{P}\lambda _i\mu _j\alpha _p(\mathbf {U}_p)\alpha _p^\mathrm{T}(\mathbf {U}_p)\left[ \cos (2\pi \langle \mathbf {x}_i+\mathbf {x}_j', \mathbf {U}_p\rangle +2\phi _p)+\cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {U}_p\rangle )\right] \right] . \end{aligned}$$
(12)

The first cosine term has a zero expectation because \(\phi _p\) is uniform on \([0,2\pi )\) and is independent of \(\mathbf {U}_p\), for all \(p=1, \ldots , P\). Therefore, Eq. (12) reduces to

$$\begin{aligned} \mathbb {E}\left[ \mathbf {Y}_S(\lambda )\mathbf {Y}_S(\mu )\right]= & {} \mathbb {E}\left[\sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j\sum _{p=1}^{P} \alpha _p(\mathbf {U}_p)\alpha _p^\mathrm{T}(\mathbf {U}_p)\frac{\cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {U}_p\rangle )}{2}\right] \\= & {} \int _{\mathbb {R}^d}\sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j\sum _{p=1}^{P}\alpha _p(\mathbf {u})\alpha _p^\mathrm{T}(\mathbf {u})\frac{\cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {u}\rangle )}{2}g(\mathbf {u})\,\mathrm {d}\mathbf {u}\\= & {} \int _{\mathbb {R}^d}\sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j\frac{\mathbf {A}(\mathbf {u})\mathbf {A}^\mathrm{T}(\mathbf {u})}{2}\cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {u}\rangle )g(\mathbf {u})\,\mathrm {d}\mathbf {u}, \end{aligned}$$

where \(\mathbf {A}(\mathbf {u})\) is the \(P\times P\) matrix whose p-th column is \(\alpha _p(\mathbf {u})\).

Since the weights \(\{\lambda _i\}_{i \in I}\) and \(\{\mu _j\}_{j \in J}\) filter out the polynomials of degree less than or equal to 2k (Eq. 1), one can subtract the Taylor expansion \(P_k\) of the cosine without modifying the integrand, as follows:

$$\begin{aligned} \mathbb {E}\left[ \mathbf {Y}_S(\lambda )\mathbf {Y}_S(\mu )\right] = \int _{\mathbb {R}^d}\sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j\frac{\mathbf {A}(\mathbf {u})\mathbf {A}^\mathrm{T}(\mathbf {u})}{2}\left[ \cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {u}\rangle )-P_k(2\pi \langle \mathbf {x}_i-\mathbf {x}_j',\mathbf {u}\rangle )\right] g(\mathbf {u})\,\mathrm {d}\mathbf {u}. \end{aligned}$$
(13)

For the simulated vector random field \(\mathrm {\mathbf {Y}}_S\) to be an intrinsic vector random field of order k with a matrix of generalized direct and cross-covariances \(\mathbf {K}\) associated with the spectral density matrix \({\mathbf {f}}\) (Eq. 9), it suffices that the following condition is satisfied for any frequency vector \(\mathbf {u}\):

$$\begin{aligned} \frac{\mathbf {A}(\mathbf {u})\mathbf {A}^\mathrm{T}(\mathbf {u})}{2}g(\mathbf {u})=\mathbf {f}(\mathbf {u}), \end{aligned}$$

or, equivalently,

$$\begin{aligned} \mathbf {A}(\mathbf {u})\mathbf {A}^\mathrm{T}(\mathbf {u})=\frac{2\mathbf {f}(\mathbf {u})}{g(\mathbf {u})}. \end{aligned}$$
(14)

This condition, which is analogous to that found for the simulation of intrinsic vector random fields of order 0 (Arroyo and Emery 2017), ensures that the improper integral

$$\begin{aligned} \frac{\mathbf {A}(\mathbf {u})\mathbf {A}^\mathrm{T}(\mathbf {u})}{2}\int _{\mathbb {R}^d}\left[ \cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {u}\rangle )-P_k(2\pi \langle \mathbf {x}_i-\mathbf {x}_j',\mathbf {u}\rangle )\right] g(\mathbf {u})\,\mathrm {d}\mathbf {u} \end{aligned}$$

is convergent, insofar as it coincides with the spectral representation of the generalized covariance \(\mathbf {K}(\mathbf {x}_i-\mathbf {x}_j')\). The summations and integral signs in Eq. (13) can therefore be permuted, which yields

$$\begin{aligned} \mathbb {E}\left[ \mathbf {Y}_S(\lambda )\mathbf {Y}_S(\mu )\right]= & {} \sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j\frac{\mathbf {A}(\mathbf {u})\mathbf {A}^\mathrm{T}(\mathbf {u})}{2}\int _{\mathbb {R}^d}\left[ \cos (2\pi \langle \mathbf {x}_i-\mathbf {x}_j', \mathbf {u}\rangle )-P_k(2\pi \langle \mathbf {x}_i-\mathbf {x}_j',\mathbf {u}\rangle )\right] g(\mathbf {u})\,\mathrm {d}\mathbf {u} \\= & {} \sum _{i\in I}\sum _{j\in J}\lambda _i\mu _j \mathbf {K}(\mathbf {x}_i-\mathbf {x}_j'). \end{aligned}$$

For instance, \(\mathbf {A}(\mathbf {u})\) can be chosen as the principal square root matrix of \(\frac{2\mathbf {f}(\mathbf {u})}{g(\mathbf {u})}\). The knowledge of \(\mathbf {A}(\mathbf {u})\) determines the vector-valued mappings \(\left\{ \alpha _p: p=1, \ldots , P\right\}\) to be used in Equation (10), which completes the specification of the algorithm.

Finally, based on the central limit theorem, to obtain an intrinsic vector random field with approximately Gaussian increments of order k and with zero value at the origin \(\mathbf {x}= \mathbf {0}\), it suffices to shift, add and rescale many of such independent random fields:

$$\begin{aligned} \mathbf {Y}_S(\mathbf {x})=\frac{1}{\sqrt{N}}\sum _{n=1}^{N}\sum _{p=1}^{P}\alpha _p(\mathbf {U}_{n,p})\left[ \cos (2\pi \langle \mathbf {x}, \mathbf {U}_{n,p}\rangle +\phi _{n,p})-\cos (\phi _{n,p})\right] , \end{aligned}$$
(15)

where \(N\) is a large integer, \(\{\mathbf {U}_{n,p}: n=1, \ldots , N; p=1, \ldots , P\}\) are mutually independent random vectors with probability density \(g\) and \(\{\phi _{n,p}: n=1, \ldots , N; p=1, \ldots , P\}\) are mutually independent random variables uniformly distributed as \(\phi _p\).

This algorithm (Eq. 15) generalizes the ones proposed in Emery et al. (2016) and in Arroyo and Emery (2017), which are restricted to the simulation of stationary and intrinsic vector random fields of order \(k = 0\), respectively. The density \(g\) can be chosen freely, provided that its support contains the support of each component of the spectral density matrix \({\mathbf {f}}\) (this necessary condition is implied by Eq. 14). Note that the spectral representation under consideration (Eq. 9) is restricted to generalized cross-covariances that are even functions of the lag vector \(\mathbf {h}\). A more general representation allowing the incorporation of an odd component is presented in Chilès and Delfiner (2012) for the case when \(k = 0\) and in Huang et al. (2009) for any non-negative integer k. The design of non-even generalized cross-covariance models together with algorithms for simulating vector IRF-k with such covariance models is a topic of further research.

4 Examples

In this section, the proposed spectral algorithm is tested to simulate random fields on a set of 250, 000 locations on a regular two-dimensional grid G with a unit mesh along each coordinate axis (\(d=2\)). The simulation is performed by using \(N = 500\) basic random fields in Eqs. (8) or (15). The density \(g\) is chosen as the spectral density of a stationary isotropic Matérn covariance with a unit sill (Lantuéjoul 2002):

$$\begin{aligned} \mathbf {M}(\mathbf {h},a,\nu )=\frac{2^{1-\nu }}{\varGamma (\nu )}\left( \frac{\Vert \mathbf {h}\Vert }{a}\right) ^{\nu }K_{\nu }\left( \frac{\Vert \mathbf {h}\Vert }{a}\right) , \end{aligned}$$
(16)

that is:

$$\begin{aligned} g(\mathbf {u},a,\nu )=\frac{(2\pi a)^d\varGamma \left( \nu +\frac{d}{2}\right) }{\varGamma (\nu )\pi ^{d/2}}\frac{1}{\left( 1+(2\pi a)^2\Vert \mathbf {u}\Vert ^2\right) ^{\nu +d/2}}, \end{aligned}$$
(17)

where \(\varGamma (\cdot )\) is the gamma function and \(K_{\nu }(\cdot )\) is the modified Bessel function of the second kind of order \(\nu\).

In the following, the scale parameter will be set to \(a=30\) and the shape parameter to \(\nu =\min (\alpha _1,\alpha _2)/2\), where \(\alpha _1\) and \(\alpha _2\) will be defined in each example. These values of \(a\) and \(\nu\) correspond to a heuristic choice that provides a good sampling of both large and small frequencies when generating the random vectors \(\{\mathbf {U}_{n}: n=1, \ldots , N\}\) (Eq. 8) or \(\{\mathbf {U}_{n,p}: n=1, \ldots , N; p=1, \ldots , P\}\) (Eq. 15). However, as proved in the previous sections, the algorithm is applicable with any other choice for these scale and shape parameters, insofar as the support of the Matérn density is the whole space \(\mathbb {R}^d\).

4.1 Example 1: Simulating a scalar random field with power generalized covariance in \(\mathbb {R}^d\)

Let us consider the simulation of a scalar intrinsic random field with a power generalized covariance of the form

$$\begin{aligned} \forall \, \mathbf {h}\in \mathbb {R}^d,\,\mathbf {K}(\mathbf {h})=(-1)^{1+\lfloor \alpha /2\rfloor }\left\| \frac{\mathbf {h}}{b}\right\| ^{\alpha }, \end{aligned}$$

where \(\lfloor \cdot \rfloor\) is the floor function, \(b\) is a positive real number and \(\alpha\) is a positive real number different from an even integer. The order of the intrinsic random field with such a generalized covariance is \(k=\lfloor \alpha /2\rfloor\).

The spectral density of \(\mathbf {K}(\mathbf {h})\) is (Chilès and Delfiner 2012):

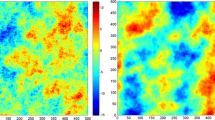
$$\begin{aligned} \forall \, \mathbf {u}\in \mathbb {R}^d,\, f_P(\mathbf {u}, b, \alpha )=\frac{b^d\varGamma \left( \frac{\alpha }{2}+1\right) \varGamma \left( \frac{\alpha +d}{2}\right) }{\varGamma \left( \frac{\alpha }{2}-k\right) \varGamma \left( 1-\frac{\alpha }{2}+k\right) \pi ^{\alpha +d/2}\Vert b\mathbf {u}\Vert ^{\alpha +d}}. \end{aligned}$$
(18)

As an example, Fig. 1 (left) shows the map of one realization obtained by using Eq. (8) with \(\alpha =5\) (therefore, \(k = 2\)) and \(b=100\). The simulated field (an IRF-2) exhibits a quadratic drift, which makes difficult to visually assess whether or not the desired spatial correlation structure is accurately reproduced. Since this structure is related to the generalized increments of order 2, one option to unveil it is to focus on the generalized variogram of order 2 of the simulated field, that is (Eq. 4):

$$\begin{aligned} \varUpsilon (\mathbf {h})=\frac{1}{20}E\left\{ \left[ Y(\mathbf {x}+3\mathbf {h})-3Y(\mathbf {x}+2\mathbf {h})+3Y(\mathbf {x}+\mathbf {h})-Y(\mathbf {x})\right] ^2 \right\} . \end{aligned}$$
(19)

\(\varUpsilon (\mathbf {h})\) can be expressed as a function of the generalized covariance \(\mathbf {K}(\mathbf {h})\) (Eq. 5). Experimentally, it can be estimated for each realization \(\left\{ y(\mathbf {x}): \mathbf {x}\in G\right\}\) by replacing the expectation in the previous equation by an average of the form

$$\begin{aligned} \hat{\varUpsilon }(\mathbf {h})=\frac{1}{20}\frac{\displaystyle {\sum _{\mathbf {x}\in G\cap G_{-\mathbf {h}}\cap G_{-2\mathbf {h}}\cap G_{-3\mathbf {h}}}}\left[ y(\mathbf {x}+3\mathbf {h})-3y(\mathbf {x}+2\mathbf {h})+3y(\mathbf {x}+\mathbf {h})-y(\mathbf {x})\right] ^2}{\mathrm {card}\left\{ G\cap G_{-\mathbf {h}}\cap G_{-2\mathbf {h}}\cap G_{-3\mathbf {h}}\right\} }, \end{aligned}$$
(20)

where \(G_{-\mathbf {h}}, G_{-2\mathbf {h}}\) and \(G_{-3\mathbf {h}}\) stand for the grid G shifted by vector \(-\mathbf {h}, -2\mathbf {h}\) and \(-3\mathbf {h}\), respectively, while card\(\{.\}\) indicates cardinality. Such an experimental generalized variogram is expected to fluctuate without bias around the theoretical generalized variogram (Chilès and Delfiner 2012). Accordingly, on average over a large set of realizations (so that statistical fluctuations become negligible), it is expected that the experimental generalized variogram matches the theoretical generalized variogram. This effectively happens when considering one hundred realizations (Fig. 1 right), confirming that the simulated field accurately reproduces the target power generalized covariance.

Fig. 1
figure 1

Left: map of one realization of an IRF-2 with power generalized covariance of exponent \(\alpha = 5\) and scale factor \(b = 100\). Right: experimental generalized variograms of order 2 of 100 realizations (green dashed lines) calculated for lag separation vectors oriented along the abscissa axis, average of experimental generalized variograms (blue stars) and theoretical generalized variogram (black solid line)

Full size image

4.2 Example 2: Simulating a vector random field with power generalized direct and cross-covariances

Let us now simulate an intrinsic vector random field \(\mathbf {Y}\) with \(P = 2\) components with the following \(2\times 2\) matrix of generalized direct and cross-covariances:

$$\begin{aligned} \forall \, \mathbf {h} \in \mathbb {R}^d,\, \mathbf {K}(\mathbf {h}) = \left( \begin{array}{cccc} (-1)^{1+\lfloor \alpha _1/2\rfloor }\left\| \frac{\mathbf {h}}{b_1}\right\| ^{\alpha _1} &{} &{} &{} \rho \,(-1)^{1+\lfloor \alpha _{12}/2\rfloor }\left\| \frac{\mathbf {h}}{b_{12}}\right\| ^{\alpha _{12}} \\ \rho \,(-1)^{1+\lfloor \alpha _{12}/2\rfloor }\left\| \frac{\mathbf {h}}{b_{12}}\right\| ^{\alpha _{12}} &{} &{} &{} (-1)^{1+\lfloor \alpha _2/2\rfloor }\left\| \frac{\mathbf {h}}{b_2}\right\| ^{\alpha _2} \end{array} \right) , \end{aligned}$$
(21)

where \(\rho \in \mathbb {R}\), \((b_1, b_2, b_{12}, \alpha _1, \alpha _2, \alpha _{12}) \in (\mathbb {R}_{+}^*)^{6}\), such that \(\alpha _1\) and \(\alpha _2\) are not even integers. The orders of the first and second components of the vector random field are \(k_1 = \lfloor \alpha _1/2\rfloor\) and \(k_2 = \lfloor \alpha _2/2\rfloor\), respectively, while the overall order of the intrinsic vector random field is \(k = \max (k_1,k_2)\).

The corresponding spectral density matrix for a given frequency vector \(\mathbf {u} \in \mathbb {R}^d\) is:

$$\begin{aligned} \mathbf {f}(\mathbf {u}) = \left( \begin{array}{cccc} f_P(\mathbf {u},b_1,\alpha _1) &{} &{} &{} \rho \,f_P(\mathbf {u},b_{12},\alpha _{12}) \\ \rho \,f_P(\mathbf {u},b_{12},\alpha _{12}) &{} &{} &{} f_P(\mathbf {u},b_2,\alpha _2) \end{array} \right) . \end{aligned}$$
(22)

The conditions under which this matrix is Hermitian positive semi-definite for any \(\mathbf {u} \in \mathbb {R}^d\) are detailed in "Appendix 1".

As an illustration, Fig. 2 shows the map of one realization obtained by using Eq. (15) with \(\alpha _1=2.5\) (\(k_1 = 1\)), \(\alpha _2=4.5\) (\(k_2=k=2\)), \(\alpha _{12}=3.5\), \(b_1=100\), \(b_2=90\), \(b_{12}=70\) and \(\rho =0.4\). Figure 3 compares the experimental generalized direct and cross-variograms of order 2 of one hundred realizations with the theoretical generalized direct and cross-variograms of order 2. The generalized cross-variogram is defined by substituting the covariance or the product of generalized increments for the variance (Eq. 4) or the squared value (Eqs. 19, 20) of generalized increments. As for the previous subsection, on average over the realizations, the experimental generalized variograms match the theoretical generalized variograms, which corroborates that the proposed spectral simulation algorithm accurately reproduces the spatial correlation structure of the desired vector random field.

Fig. 2
figure 2

Realizations of a bivariate intrinsic random field whose first component is an IRF-1 (on the left) and the second component is an IRF-2 (on the right). Generalized direct and cross-covariances are power models with \(\alpha _1=2.5\) (\(k_1 = 1\)), \(\alpha _2=4.5\) (\(k_2 = 2\)), \(\alpha _{12}=3.5\), \(b_1=100\), \(b_2=90\), \(b_{12} = 70\) and \(\rho =0.4\)

Full size image
Fig. 3
figure 3

Experimental generalized variograms of order 2 for 100 realizations (green dashed lines) calculated for lag separation vectors oriented along the abscissa axis, average of experimental generalized variograms (blue stars) and theoretical models (black solid lines). From left to right and top to bottom: generalized direct variograms for first component, generalized direct variograms for second component, and generalized cross-variograms. Generalized direct and cross-covariances are power models with \(\alpha _1=2.5\) (\(k_1 = 1\)), \(\alpha _2=4.5\) (\(k_2 = 2\)), \(\alpha _{12}=3.5\), \(b_1 = 100\), \(b_2 = 90\), \(b_{12} = 70\) and \(\rho =0.4\)

Full size image

4.3 Example 3: Simulating a vector random field with power and spline generalized direct covariances and Matérn generalized cross-covariance

Let us now simulate an intrinsic vector random field of order k, \(\mathbf {Y}\), with \(P = 2\) components by using the following \(2\times 2\) matrix of generalized direct and cross-covariances:

$$\begin{aligned} \forall \, \mathbf {h} \in \mathbb {R}^d,\, \mathbf {K}(\mathbf {h}) = \left( \begin{array}{cccc} (-1)^{1+\lfloor \alpha _1/2\rfloor }\left\| \frac{\mathbf {h}}{b_1}\right\| ^{\alpha _1} &{} &{} &{} \rho \,\mathbf {M}(\mathbf {h},a_{12},\nu _{12}) \\ \rho \,\mathbf {M}(\mathbf {h},a_{12},\nu _{12}) &{} &{} &{} (-1)^{1+k_2}\left\| \frac{\mathbf {h}}{b_2}\right\| ^{\alpha _2}\ln \left( \left\| \frac{\mathbf {h}}{b_2}\right\| \right) \end{array} \right) , \end{aligned}$$
(23)

where \(\rho \in \mathbb {R}\), \((b_1, b_2, \alpha _1, a_{12},\nu _{12}) \in (\mathbb {R}_{+}^*)^5\) such that \(\alpha _1\) is not an even integer, \(k_2 \in \mathbb {N}^{*}\) and \(\alpha _2 = 2k_2\). The orders of the first and second components of the vector random field are \(k_1 = \lfloor \alpha _1/2\rfloor\) and \(k_2\), respectively, while the overall order of the intrinsic vector random field is \(k = \max (k_1,k_2)\). \(\mathbf {M}(\mathbf {h},a_{12},\nu _{12})\) is the stationary Matérn covariance with sill \(\rho\), scale parameter \(a_{12}\) and shape parameter \(\nu _{12}\) (Lantuéjoul 2002); therefore, this is also a valid generalized covariance for any order k (Chilès and Delfiner 2012).

The corresponding spectral density matrix for a given frequency vector \(\mathbf {u} \in \mathbb {R}^d\) is:

$$\begin{aligned} \mathbf {f}(\mathbf {u}) = \left( \begin{array}{cccc} f_P(\mathbf {u},b_1,\alpha _1) &{} &{} &{} \rho \,g(\mathbf {u},a_{12},\nu _{12}) \\ \rho \,g(\mathbf {u},a_{12},\nu _{12}) &{} &{} &{} f_S(\mathbf {u},b_2,k_2) \end{array} \right) , \end{aligned}$$
(24)

where \(f_S(\mathbf {u}, b_2, k_2)\) is the spectral density of the spline generalized covariance \((-1)^{1+k_2}\Vert \frac{\mathbf {h}}{b_2}\Vert ^{2k_2}\ln \left( \Vert \frac{\mathbf {h}}{b_2}\Vert \right)\). The expression of this spectral density can be obtained by considering the spline generalized covariance as the limit, as \(\epsilon\) tends to zero, of a power generalized covariance of exponent \(2k_2+\epsilon\) divided by \(\epsilon\) (Emery and Lantuéjoul 2008). This implies

$$\begin{aligned} \forall \, \mathbf {u}\in \mathbb {R}^d,\, f_S(\mathbf {u}, b_2, k_2)=\lim _{\epsilon \rightarrow 0} \left( \frac{f_P(\mathbf {u}, b_2, 2k_2+\epsilon )}{\epsilon }\right) = \frac{b_2^d\varGamma \left( k_2+1\right) \varGamma \left( \frac{2k_2+d}{2}\right) }{2\pi ^{2k_2+d/2}\Vert b_2\mathbf {u}\Vert ^{2k_2+d}}. \end{aligned}$$
(25)

The conditions under which the spectral density matrix in Eq. (24) is Hermitian positive semi-definite for any \(\mathbf {u} \in \mathbb {R}^d\) (therefore, the defined generalized direct and cross-covariances constitute a valid model) are indicated in "Appendix 2".

As an illustration, Fig. 4 shows the map of one realization obtained by using Eq. (15) with \(\alpha _1=3\) (\(k_1 = 1\)), \(\alpha _2=2\) (\(k_2=1\)), \(b_1=180\), \(b_2=100\), \(a_{12}=80\), \(\nu _{12}=1.25\) and \(\rho =0.55\). Figure 5 compares the experimental generalized direct and cross-variograms of order 1 of one hundred realizations with the theoretical generalized direct and cross-variograms of order 1. On average over the realizations, the experimental generalized variograms match the theoretical generalized variograms, corroborating that the spatial correlation structure of the target vector random field is accurately reproduced.

Fig. 4
figure 4

Realizations of a bivariate intrinsic random field whose components are IRF-1 (first component on the left, second component on the right). Generalized direct and cross-covariances are power, spline and Matérn models with \(\alpha _1=3\) (\(k_1 = 1\)), \(\alpha _2=2\) (\(k_2 = 1\)), \(b_1=180\), \(b_2=100\), \(a_{12}=80\), \(\nu _{12} = 1.25\) and \(\rho =0.55\)

Full size image
Fig. 5
figure 5

Experimental generalized variograms of order 1 for 100 realizations (green dashed lines) calculated for lag separation vectors oriented along the abscissa axis, average of experimental generalized variograms (blue stars) and theoretical models (black solid lines). From left to right and top to bottom: generalized direct variograms for first component, generalized direct variograms for second component, and generalized cross-variograms. Generalized direct and cross-covariances are power, spline and Matérn models with \(\alpha _1=3\) (\(k_1 = 1\)), \(\alpha _2 = 2\) (\(k_2=1\)), \(b_1 = 180\), \(b_2 = 100\), \(a_{12} = 80\), \(\nu _{12}=1.25\) and \(\rho =0.55\)

Full size image

5 Conclusions

This paper presented an algorithm for simulating intrinsic vector random fields of order k with given generalized direct and cross-covariances and multivariate Gaussian generalized increments. The algorithm relies on the spectral decomposition of the generalized covariances, in order to reproduce the spatial correlation structure of the desired random field, and on the central limit theorem, in order to obtain generalized increments whose finite-dimensional distributions are approximately Gaussian.

The implementation of the algorithm is straightforward, with no restriction on the number of components of the vector random field, space dimension, number and positions of the locations targeted for simulation, or number of desired realizations, other than hardware and software capacities. The presented examples show the versatility of the algorithm and its applicability to simulate random fields with a complex covariance structure.