1 Introduction

Interface adhesion anisotropy is widely present in nature. This phenomenon can be found for example in pads of lizards and insects, which have been investigated both experimentally and theoretically [1,2,3] by researchers in the area of biomechanics, leading to numerous applications, such as bio-mimetic adhesive materials [4, 5]. Some of them incorporate anisotropic interface properties of adhesion [6,7,8]. In the area of anisotropic friction modelling, recent contributions have led to numerous orthotropic interface models. We cite in particular the development of orthotropic slip functions [9,10,11], orthotropic dry interface model [12] and elasto-plastic interface model [13]. Konyukhov et al. proposed a series of contributions which implement anisotropic interface adhesion based on covariant description of the interface kinematics [14,15,16].

In the field of numerical modelling, many efforts have been exerted to develop adhesive contact algorithms [17,18,19], however, literature on modelling schemes accounting for interface adhesion anisotropy is still in initial state [20, 21]. Achieving such models requires first, an appropriate description of the contact laws in both normal and tangential directions with a proper account for adhesion anisotropy, and secondly, a robust and stable resolution algorithm, that can deal with the computational difficulties inherent to the problem non-linearities. Furthermore, reversibility of the interface adhesion should also be considered to meet requirements of real applications. In this regard, both bonding and de-bonding processes including the interplay between adhesion forces and the state of damage of the adhesive bonds must be taken care of. It has been demonstrated that numerous factors during the bonding process may affect the final state of adhesion anisotropy [22]. Therefore, properly modelling the bonding and de-bonding processes becomes one of our main focuses.

In this work, we simulate complex interface behaviours with reversible adhesion orthotropy based on our extension of the Raous–Cangémi–Cocu (RCC) model, which is a cohesive interface model incorporating adhesion within unilateral and tangential contact scenarios [23,24,25]. It makes use of an adhesion intensity parameter \(\beta \), which was presented for the first time in the work of Frémond [26]. With its value varying between 0 and 1, \(\beta \) indicates the level of damage of the interface adhesion bonds (0 refers to complete separation, while 1 refers to complete bonding). Then the adhesive interface behaviour, evolving with \(\beta \), derives from a free surface energy and a pseudopotential of the surface dissipation, which describes the reversible de-bonding and bonding process as function of the geometrical configuration of the contact interface [27]. Derivatives of the free surface energy yields a straightforward description of the interface adhesion orthotropy, whose stiffness components are conveniently expressed according to the local coordinate system. A set of extended unilateral and tangential contact rules incorporating the interface adhesion orthotropy is then formulated.

Another difficulty lies in the inherently severe non-linearities due to contact dynamics. In fact, the non-smooth and multivalued nature of the orthotropic adhesive interface law gives rise to significant challenges in numerical resolution. It is thus necessary to adopt robust, and stable algorithms to ensure iteration convergence, solution accuracy and balanced efficiency. Methods based on penalty [28], Lagrange multiplier [29] approaches and augmented Lagrangian method [30, 31] are all general candidates for numerical treatment of contact constraints. Here, we propose a bi-potential theory based on the augmented Lagrangian method for solving contact problems which was developed to deal with implicit standard materials (ISM) [32, 33]. In comparison to the classical methods, the bi-potential framework combines two variational inequalities of the unilateral contact and friction law into a single displacement based variational principle with a single inequality. First introduced in the 1990s, it has recently been extended to problems involving hyperelastic or elastic-plastic contact and impact [34,35,36,37], and interface wear [38, 39]. The bi-potential contact algorithm implemented in this work, according to the basic relations of contact geometry, belongs to the category of “node-to-segment” (NTS) approaches. These approaches represent a relatively balanced solution combining implementation simplicity and resolution accuracy. Comparative contact algorithms include sequential multi-pass NTS approaches which also offer satisfactory accuracy, and more recently, the virtual-slave-node-to-segment (VTS) approach developed by Zavarise et al. [40,41,42,43], which opens a new way to the accurate assessment of contact interface forces requiring only single-pass scheme.

In this work, an orthotropic extension of the RCC surface energy model is proposed. The extended tangential adhesive law can be graphically interpreted by a cone with elliptical cross section. Then, we incorporate adhesion into the classical unilateral law and Coulomb friction rule to form a complete contact law. The problem of orthotropic adhesive contact is then solved using bi-potential method. The article is organized as follows: in Sect. 2, after a brief description of the contact kinematics, we present the complete framework of the orthotropic adhesion model of contact, which includes an extended formulation of the unilateral and tangential rules of contact involving interface adhesion orthotropy. Then, we present its implementation within the bi-potential framework, and provide the formulation of the hyperelastic material used to model soft bodies. In Sect. 3, the complete finite element formulation, including the resolution algorithm, is provided. To validate the framework, we present numerical examples in Sect. 4. In the end, a few concluding remarks are drawn in Sect. 5.

2 Problem setting

2.1 Contact kinematics

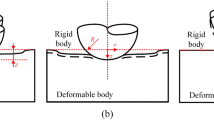
We provide in this section geometric descriptions of the contact kinematics and the relative notations. Let’s consider two deformable bodies \(B^{\alpha }, \alpha = 1, 2\) coming into contact. Deformation of the two bodies is represented by \(\varphi ^{\alpha }\), as shown in Fig. 1, which maps the initial configuration to positions of the current configuration. We assume that contact occurs at the boundaries \(\varphi (\Gamma _{c}^{\alpha })\) in the current configuration where \(\Gamma _{c}^{\alpha } \subset \partial B^{\alpha }\) are possible contact surfaces of bodies \(B^{\alpha }\).

Fig. 1
figure 1

Finite deformation contact

Full size image

Contact conditions need to be developed according to the current configuration. We note contact point \(P_2\) on \(B^{2}\) and its projection point \(P_1\) on \(B^{1}\) in the current configuration, as shown in Fig. 2.

Fig. 2
figure 2

The closest-point projection procedure and coordinate system

Full size image

By assuming that the contact boundary describes, at least in the vicinity of the contact point, a convex region, we can relate \(P_2\) to \(P_1\) by prescribing a minimum distance problem [44]:

$$\begin{aligned} d\big (\xi ^1, \xi ^2\big )=\left\| \mathbf{x }^2-\mathbf{x }^1(\varvec{\xi }) \right\| , \end{aligned}$$
(1)

where \(\mathbf{x }^2\) and \(\mathbf{x }^1\) are position vectors of the two points in global Cartesian coordinates xyz. \(\varvec{\xi } = (\xi ^1, \xi ^2)\) denotes parametrization of the boundary \(\varphi (\Gamma _{c}^{1})\) via the convective coordinates [45,46,47,48]. \(d(\xi ^1, \xi ^2)\) can be used to define the gap between the two bodies. To make Eq.(1) valid, \(\mathbf{x }^1\) needs to satisfy the following condition:

$$\begin{aligned}&\frac{\partial }{\partial \xi ^{\alpha }}d\big (\xi ^1, \xi ^2\big )=\frac{\mathbf{x }^2-\mathbf{x }^1\big (\xi ^1, \xi ^2\big )}{\left\| \mathbf{x }^2-\mathbf{x }^1\big (\xi ^1, \xi ^2\big ) \right\| } \cdot \mathbf{x }_{, \alpha }^1\big (\xi ^1, \xi ^2\big )=0,\nonumber \\&\quad \mathrm{with} \alpha = 1, 2, \end{aligned}$$
(2)

where \(\mathbf{x }_{, \alpha }^1(\xi ^1, \xi ^2)\) is the tangent vector \(\mathbf{a }_{\alpha }\). Be applying cross product between tangent vectors, we can write the normal vector \(\mathbf{n }\) as follows:

$$\begin{aligned} \mathbf{n }=\frac{\mathbf{a }_1 \times \mathbf{a }_2}{||\mathbf{a }_1 \times \mathbf{a }_2||}, \end{aligned}$$
(3)

once the first term of Eq. (2) is aligned to the same direction as \(\mathbf{n }\), we consider that \(P_1\) is the projection point of \(P_2\) on \(B^{1}\). Therefore, the normal relative displacement or gap \(g_{n}\) is:

$$\begin{aligned} g_{n}= \left( \mathbf{x }^2-\mathbf{x }^1\right) \cdot \mathbf{n }. \end{aligned}$$
(4)

In the of tangential movement, the path following which \(P_2\) slides on the contact surface of \(B^1\) is a priori unknown. We know however the relative velocity vector on \(P_2\). Therefore, the path of \(P_2\) can be obtained by integrating velocity over time. The increment of tangential relative displacement, as shown in Fig. 3, is:

$$\begin{aligned} d\mathbf{g }_{t}= \mathbf{a }_{\alpha } d\xi ^{\alpha }, \end{aligned}$$
(5)

with , tangential relative displacement can be calculated as:

(6)

where \(t_0\) refers to initial time, and t the current time.

Fig. 3
figure 3

Increment of tangential path

Full size image

Based on Eq. (5) and in order to obtain \(\mathbf{g }_{t}\), we need to first calculate by using the following relation

(7)

where . We have , Eq. (7) can be developed as an expression containing :

(8)

with

$$\begin{aligned} \left\{ \begin{array}{c} g_{n}\mathbf{n }=\mathbf{x }^2-\mathbf{x }^1\\ a_{\alpha \beta }=\mathbf{a }_{\alpha } \cdot \mathbf{a }_{\beta }\\ b_{\alpha \beta } = \mathbf{x }^{\alpha }_{,\alpha \beta } \cdot \mathbf{n } \end{array} \right. \; , \end{aligned}$$
(9)

where \(a_{\alpha \beta }\) and \(b_{\alpha \beta }\) represent respectively the metric tensor and curvature tensor. Substituting from Eq. (8) into Eq. (6), we can solve the tangential slip \(\mathbf{g }_{t}\).

Then the contact force vector \( {\mathbf {r}}\) is defined as a covariant vector, which is expressed via the contravariant basis surface vectors \(\mathbf{a }_{\alpha }\) and \(\mathbf{n }\):

$$\begin{aligned} {\mathbf {r}} = {\mathbf {r}}_{t}+{\mathbf {r}}_{n} = r^{\alpha }_{t}\mathbf{a }_{\alpha }+r_{n}\mathbf{n },\ \alpha =1,2, \end{aligned}$$
(10)

where \({\mathbf {r}}_{t}\) and \({\mathbf {r}}_{n}\) are respectively tangential and normal component of the contact force vector.

Let’s denote the local and global contact force vectors with respectively \( {\mathbf {r}}\) and \( {\mathbf {R}}\). The relation between contact force vectors expressed in local and global coordinate systems writes:

$$\begin{aligned} {\mathbf {R}} = {\mathbf {H}}^T {\mathbf {r}}, \end{aligned}$$
(11)

where \({\mathbf {H}}\) is the transition matrix. Here, due to the presence of adhesion on the contact interface, contact reaction \({\mathbf {r}}\) is composed of the cumulative effects due to both dry contact and the interface adhesion, hence

$$\begin{aligned} {\mathbf {r}} = \bar{{\mathbf {r}}} + \tilde{{\mathbf {r}}}, \end{aligned}$$
(12)

in which we use \(\bar{{\mathbf {r}}}\) to denote dry contact reactions, and \(\tilde{{\mathbf {r}}}\) contact forces due to interface adhesion. Note that the above relation can be projected to the local coordinate system according to the normal and tangential directions:

$$\begin{aligned} \left\{ \begin{array}{c} {r}_n = \bar{{r}}_{n} + \tilde{{r}}_{n} \\ {\mathbf {r}}_t = \bar{{\mathbf {r}}}_{t} + \tilde{{\mathbf {r}}}_{t} \end{array} \right. \; . \end{aligned}$$
(13)

Generalization of the RCC model is described in Cartesian coordinates.

2.2 RCC contact model with adhesion orthotropy

We develop an improved RCC contact model to describe the effect of orthotropic adhesion between contact surfaces. Introduced by Raous et al. [25], the original RCC model accounts for unilateral contact, friction and adhesion, based on an energy description of the contact interface, involving a free surface energy \(\varPsi \) and a pseudo-potential of the surface dissipation \(\varPhi \). Here, energy expressions \(\varPsi \) and \(\varPhi \) are formulated based on displacements that we project to the local system \((\mathbf{a }_1, \mathbf{a }_2, \mathbf{n })\), leading to tangential and normal components \(g_{t1}\), \(g_{t2}\) and \(g_n\):

$$\begin{aligned}&\varPsi (g_{t1},g_{t2}, g_n, \beta ) = \frac{C_{n}}{2}g_{n}^{2}\beta ^{2}+\frac{C_{t1}}{2}{g}_{t1}^{2}\beta ^{2}\nonumber \\&\quad +\frac{C_{t2}}{2}{g}_{t2}^{2}\beta ^{2}-w\beta +\bigcup _{\mathfrak {R}+}(g_{n})+ \bigcup _{Q}(\beta ) \quad , \end{aligned}$$
(14)
$$\begin{aligned}&\varPhi \big (\dot{{\mathbf {g}}}_{t},{g}_{n},{\dot{\beta }}\big ) = \mu |r_{n}-C_{n}g_{n}\beta ^{2}| ||\dot{{\mathbf {g}}}_{t}|| + \frac{b}{2}|{\dot{\beta }}|^{2} \quad . \end{aligned}$$
(15)

In the above expressions, \(\beta \) is a scalar parameter that measures the intensity of adhesion [26], with \(\beta \in [0,1]\). Specifically, \(\beta = 0\) indicates the absence of adhesion, \(\beta \) = 1 refers to perfect adhesion. Hence, any \(\beta \in (0,1)\) implies partial adhesion between contact surfaces. Other parameters in Eqs. (14, 15) include: \(C_{t1}\), \(C_{t2}\) and \(C_{n}\): parameters characterizing the initial adhesive stiffness when adhesion is complete, w: decohesion energy threshold, \(\bigcup \): indicator function that assures unilateral contact (\(g_{n}\geqslant 0\)), and meaningful values of the degree of adhesion. The subscript Q indicates \(Q=\{\eta \mid 0 \leqslant \eta \leqslant 1\}\), \(\mu \): friction coefficient, b: surface viscosity.

Deriving the surface free energy Eq. (14), we obtain the expression of the normal force of adhesion:

$$\begin{aligned} r^{ad}_n = C_n g_n \beta ^2 \; , \end{aligned}$$
(16)

and the tangential forces of adhesion:

$$\begin{aligned} \left\{ \begin{array}{ll} r^{ad}_{t1} = C_{t1} g_{t1} \beta ^2 \; \\ r^{ad}_{t2} = C_{t2} g_{t2} \beta ^2 \; . \end{array} \right. \end{aligned}$$
(17)

Both adhesion forces are dependent on the degree of adhesion \(\beta \). Then deriving energy functions Eqs. (14) and (15) with respect to \(\beta \) and \({\dot{\beta }}\) yields the incremental expression of \(\beta \) which gives its evolution in time:

$$\begin{aligned} \left\{ \begin{array}{ll} b {\dot{\beta }} \ge 0 &{} \mathrm{with} \quad {\beta }=0 \\ b {\dot{\beta }} = w - \Big (C_{n}g_{n}^{2}+C_{t1}{g}_{t1}^{2}+C_{t2}{g}_{t2}^{2}\Big ) {\beta } &{} \mathrm{with} \quad 0<\beta <1 \\ b {\dot{\beta }}\le w - \Big (C_{n}g_{n}^{2}+C_{t1}{g}_{t1}^{2}+C_{t2}{g}_{t2}^{2}\Big ) &{} \mathrm{with} \quad {\beta }=1 \;\;\; . \end{array} \right. \nonumber \\ \end{aligned}$$
(18)

In Eq. (18), we can see that two components may influence \(\beta \): the decohesion energy w, and the elastic energy of the interface \(\sum _{i=n,t1,t2} C_{i}{g}_{i}^{2}\). When interface elastic energy prevails, \({\dot{\beta }}\) becomes negative, which leads to decreasing \(\beta \). Otherwise, \({\dot{\beta }}\) is positive, then \(\beta \) increases.

We can view Eq. (14) as a variant of the penalty function method. Both methods are based on spring models with zero rest length, except that the two springs are stretched in opposite directions.

Therefore, this adhesive model can be seen as being based on a system of spring whose elasticity incorporates damage and self-recoverability. In this regard, the value of \(\beta \) measures the degree of damage of the spring, whose stiffness is adjustable based on \(\beta \). Therefore, decrease of \(\beta \) corresponds to the process of spring damage, leading to its rupture. On the contrary, the inverse process results in the recovery of spring stiffness.

2.3 Adhesive contact law and friction rule

2.3.1 Modified Signorini law with adhesion

We recall the unilateral contact law, also called Signorini law, which for classical dry contact is characterized by conditions of non-penetration and non adhesion. By using \(\bar{r}_{n}^{\alpha }\) to denote local normal contact force on the point \(\alpha \) due to dry contact, and the contact distance \(g_n\), we express the classical Signorini law as:

$$\begin{aligned} \left\{ \begin{array}{ll} g_n^{\alpha } = 0, &{} \bar{r}_{n}^{\alpha } \geqslant 0\\ g_n^{\alpha } > 0, &{} \bar{r}_{n}^{\alpha } = 0 \; \end{array} \right. \; \Rightarrow \; g_n^{\alpha } \bar{r}_{n}^{\alpha } = 0 \; . \end{aligned}$$
(19)

The first relation eliminates geometric penetration between contact surfaces. The second inequality indicates the absence of adhesion forces between dry contact surfaces once they are separated. For adhesive contact, since contact forces result from both the effects of dry contact and adhesion, the classical conditions of unilateral contact should be modified by considering Eq. (12), hence

$$\begin{aligned} \left\{ \begin{array}{ll} g_n^{\alpha } = 0, &{} r_n^{\alpha } - \tilde{r}_{n}^{\alpha } \geqslant 0\\ g_n^{\alpha } > 0, &{} r_n^{\alpha } = \tilde{r}_{n}^{\alpha } \end{array} \right. \; \Rightarrow \; g_n^{\alpha } \Big (r_n^{\alpha } - \tilde{r}_{n}^{\alpha }\Big ) = 0 \; . \end{aligned}$$
(20)

Here, adhesive forces \(\tilde{r}_{n}^{\alpha }\) are zeros with surfaces in contact. They will appear when contact surfaces start to separate (the second relation), and \(\tilde{r}_{n}^{\alpha }\) will tend to maintain the contact surfaces together. By considering Eq. (16), a modified Signorini condition with account for adhesion writes

$$\begin{aligned} \left\{ \begin{array}{ll} g_n^{\alpha } = 0, &{} r_n^{\alpha } - C_n g_n^{\alpha } \beta ^2 \geqslant 0\\ g_n^{\alpha } > 0, &{} r_n^{\alpha } = C_n g_n^{\alpha } \beta ^2 \end{array} \right. \; \Rightarrow \; g_n^{\alpha } \Big (r_n^{\alpha } - C_n g_n^{\alpha } \beta ^2\Big ) = 0 \; . \nonumber \\ \end{aligned}$$
(21)

The obtained unilateral contact law that incorporates the effect of interface adhesion [Eq. (21)] can be graphically represented by Fig. 4.

Fig. 4
figure 4

Modified Signorini law with adhesion: graphic representation of normal adhesion forces and the level of damage evolving with contact distance

Full size image

By assuming perfect adhesion (\(\beta =1\)) at \(g_n = 0\), the state of interface adhesion that evolves with \(g_n\) can be distinguished by three major phases:

  1. (1)

    Fully bonded adhesion Adhesion bonds remain intact (\(\beta = 1\)), although minor interface detachment \(g_n > 0\) is tolerable. Elastic energy due to \(g_n\) does not exceed the decohesion threshold w. Hence, linear relationship dominates the adhesion force vs. displacement curve (light green area in Fig. 4).

  2. (2)

    Adhesion with damage \(\beta \) decreases as the decohesion energy w is surpassed. Damage starts to accumulate on the adhesion bonds. Adhesion force \( \tilde{r}_{n}^{\alpha } = C_n g_n^{\alpha } \beta ^2\) continues to rise with \(g_n\) for a while since \( 0 \ll \beta < 1\) during the emergence of damage, before it decreases under the effect of the quadratic term \(\beta ^2\), with further reduced \(\beta \) (light cyan area in Fig. 4).

  3. (3)

    Separation \(\beta \) drops to zero, indicating completely broken adhesion bonds.

2.3.2 Modified Coulomb slip rule with adhesion

Classically, tangential problems are studied using the Coulomb model which is characterized by a set of rate-independent slip rules. The original Coulomb model describes tangential force that evolves with normal forces:

$$\begin{aligned} \left\{ \begin{array}{ll} \Vert \bar{{\mathbf {r}}}_t^{\alpha } \Vert \leqslant \mu \bar{r}_n^{\alpha } &{} \forall \; \Vert {\mathbf {g}}_t^{\alpha } \Vert = 0 \quad (\mathrm sticking) \\ \bar{{\mathbf {r}}}_t^{\alpha } = -\mu \bar{r}_n^{\alpha } \frac{{\mathbf {g}}_t^{\alpha }}{\Vert {\mathbf {g}}_t^{\alpha } \Vert } &{} \forall \; \Vert {\mathbf {g}}_t^{\alpha } \Vert \ne 0 \quad (\mathrm sliding) \; . \end{array} \right. \end{aligned}$$
(22)

Here, with the consideration of adhesion, both tangential and normal forces are supplemented by contributions due to interface adhesion as shown in Eq. (12), the above rules become

$$\begin{aligned} \left\{ \begin{array}{ll} \Vert {\mathbf {r}}_t^{\alpha } \Vert \leqslant \mu r_n^{\alpha } &{} \forall \; \Vert {\mathbf {g}}_t^{\alpha } \Vert = 0 \quad (\mathrm sticking) \\ {\mathbf {r}}_t^{\alpha } = -\mu (r_n^{\alpha } - \tilde{r}_n^{\alpha } ) \frac{{\mathbf {g}}_t^{\alpha }}{\Vert {\mathbf {g}}_t^{\alpha } \Vert } + \tilde{{\mathbf {r}}}_t^{\alpha } &{} \forall \; \Vert {\mathbf {g}}_t^{\alpha } \Vert \ne 0 \quad (\mathrm sliding) \; , \end{array} \right. \nonumber \\ \end{aligned}$$
(23)

in which \(\tilde{{\mathbf {r}}}_t^{\alpha }\), the adhesive tangential force on the contact point \(\alpha \) can be calculated by considering Eq. (17), and the orthotropic adhesive stiffness parameters \(C_{t1}\) and \(C_{t2}\) defined in Eq. (14)

$$\begin{aligned} \tilde{{\mathbf {r}}}_t^{\alpha } = - C_{t1}{\mathbf {g}}_{t1}^{\alpha } \beta ^2- C_{t2}{\mathbf {g}}_{t2}^{\alpha } \beta ^2= \left\{ \begin{array}{ll} - C_{t1}g_{t1}^{\alpha } \beta ^2\\ - C_{t2}g_{t2}^{\alpha } \beta ^2 \end{array} \right\} \; . \end{aligned}$$
(24)

With the consideration of interface adhesion, tangential forces are contributed by two mechanisms. The first mechanism is comparable to static friction by the classical Coulomb model. It vanishes once slip occurs. The second, arising from the effects of interface adhesion and defined by Eq. (24), gives rise to adhesive tangential force \(\tilde{{\mathbf {r}}}_t^{\alpha } \) which emerges with surface slip.

The obtained rule of tangential contact with interface adhesion [Eqs. (23, 24)] can be graphically interpreted by Fig. 5.

Fig. 5
figure 5

Modified Coulomb rule with adhesion: evolution of tangential adhesive forces and the level of damage versus slip

Full size image

By assuming perfect adhesion (\(\beta =1\)) at \(g_t = 0\), the state of interface adhesion that evolves with \(g_t\) can be distinguished, similar to the normal scenario described in the previous section, by three major phases: (1) fully bonded adhesion, (2) adhesion with damage, and (3) separation. Here, since both the slip vector \({\mathbf {g}}_t^{\alpha } \) and the tangential adhesion force vector \(\tilde{{\mathbf {r}}}_t^{\alpha } \) lie in the local plane \(({\mathbf {a}}_1, {\mathbf {a}}_2)\), their projection in the local system gives rise to expressions of tangential displacement and forces according to axis \({\mathbf {a}}_1\) and \({\mathbf {a}}_2\). Furthermore, in orthotropic adhesion, distinct adhesion stiffness parameters \(C_{t1}\) and \(C_{t2}\) can be defined in the two principal axes. Hence, the critical tangential forces are:

$$\begin{aligned} \tilde{r}_{t1}^{crit} = - C_{t1} g_{t1} \beta ^2 \; \quad and \quad \quad \tilde{r}_{t2}^{crit} = - C_{t2} g_{t2} \beta ^2 \; . \end{aligned}$$
(25)

The two critical forces are at the extreme points of the tangential forces ellipse, given by the equation:

$$\begin{aligned} \frac{{(\tilde{r}^{\alpha }_{t1})}^2}{{(C_{t1}\beta ^2 g_{t})}^2}+ \frac{{(\tilde{r}^{\alpha }_{t2})}^2}{{(C_{t2}\beta ^2 g_{t})}^2}=1 \; . \end{aligned}$$
(26)

The ellipse intersects the x-axis at \(C_{t1}\beta ^2 g_{t}\) and \(-C_{t1}\beta ^2 g_{t}\). It intersects the y-axis at \(C_{t2}\beta ^2 g_{t}\) and \(-C_{t2}\beta ^2 g_{t}\). To represent the adhesion orthotropy, any vector of adhesion force can be indicated on the ellipse, pointing from its centre to one point on the periphery. Then for any given slip value \(g_t\), one distinct ellipse can be drawn, which graphically gives a conic representation of the adhesion force by swiping \(g_t\) from 0 to \(+\infty \) as shown in Fig. 5.

2.3.3 Complete contact law with adhesion

By combining the modified Signorini law and Coulomb rule, we obtain the complete contact law with the account for interface adhesion as follows:

$$\begin{aligned} \begin{array}{lll} \mathrm{Separation}: &{} g_n^{\alpha }> 0 , &{} {\mathbf {r}}^{\alpha } = \tilde{\mathbf{r }}^{\alpha } \\ \mathrm{Sticking}: &{} g_n^{\alpha } = 0 \; \mathrm and \; \Vert {\mathbf {g}}_{\textit{t}}^{\alpha } \Vert = 0 , &{} {\mathbf {r}}^{\alpha } = \bar{{\mathbf {r}}}^{\alpha } \\ \mathrm{Sliding}: &{} g_n^{\alpha } = 0 \; \mathrm and \; \Vert {\mathbf {g}}_{\textit{t}}^{\alpha } \Vert > 0 , &{} {\mathbf {r}}_n^{\alpha } = \bar{{\mathbf {r}}}_n^{\alpha } \\ &{} &{} {\mathbf {r}}_t^{\alpha } = -\mu \bar{r}_n^{\alpha } \frac{{\mathbf {g}}_t^{\alpha }}{\Vert {\mathbf {g}}_t^{\alpha } \Vert } \\ &{} &{}-C_{t1}{\mathbf {g}}_{t1}^{\alpha } \beta ^2- C_{t2}{\mathbf {g}}_{t2}^{\alpha } \beta ^2, \end{array} \nonumber \\ \end{aligned}$$
(27)

in which \(\bar{{\mathbf {r}}}_n^{\alpha } \) refers to the normal contact force on point \(\alpha \) when surfaces are in contact. In the Sticking situation, since no relative motion occurs, adhesive forces are absent, contact force vector \(\bar{{\mathbf {r}}}^{\alpha }\) lies in the classical Coulomb cone \({\mathbf {K}}_{\mu }\), defined by

$$\begin{aligned} {\mathbf {K}}_{\mu } = \left\{ \bar{{\mathbf {r}}}^{\alpha } \in {\mathbb {R}}^3 \; | \quad r_n^{\alpha } \geqslant 0, \; \Vert {\mathbf {r}}_t^{\alpha } \Vert - \mu r_n^{\alpha } \leqslant 0 \right\} . \end{aligned}$$
(28)

However, with the appearance of relative motion, either following the normal direction (Separation case), or the tangential direction (Sliding case), the contact force vector \({\mathbf {r}}^{\alpha } \) exceeds the boundary of the classical Coulomb cone \({\mathbf {K}}_{\mu }\) due to the adhesive forces \(\tilde{{\mathbf {r}}}^{\alpha }\). Contrary to the classical Coulomb model for dry friction, the resultant contact force \({\mathbf {r}}^{\alpha }\) will not remain on the boundary of the Coulomb Cone since the relation between \(\Vert {\mathbf {r}}_t^{\alpha }\Vert \) and \({r}_n^{\alpha }\) is no longer linear, but subject to variations due to evolving \(\beta \), \( {\mathbf {g}}_t^{\alpha }\) and \({g}_n^{\alpha }\). We cannot conclude an explicit expression relating \( {\mathbf {r}}\) to \({\mathbf {g}}\). A unified superpotential for adhesive contact law does not exist. However, adhesive contact laws obeying Eq. (27) can be perfectly handled by extending the augmented Lagrangian method to the bipotential framework [33].

2.4 Contact law within the bipotential method

The classical penalty function method is a common algorithm for solving constrained optimization problems. However, contact boundary conditions and friction laws represent significant numerical difficulty, then it is tricky for the user to choose appropriate penalty factor. The method may become unstable with numerical oscillations when the system approaches the state of contact. In contrary, the Augmented Lagrangian Method is a convenient variant that overcomes the aforementioned disadvantages of the penalty method. The Augmented Lagrangian Method was first introduced to deal with constrained minimization problems. Since friction problems are not a minimization problem, the method has been extended by Alart and Curnier [30], Simo and Laursen [31] to suit for problems of contact and friction. Then based on augmented Lagrangian method, the bi-potential method has been developed to deal with contact and friction problems using a reduced system and a predictor-corrector Uzawa algorithm. For unilateral frictional contact, compared to classical methods that requires resolution of two minimum problems or variational inequalities: the first for unilateral contact and the second for friction, the bi-potential resolution unifies unilateral contact and friction, thus requires one single, unique inequality. From the perspective of contact geometry relations, the bi-potential algorithm can be attributed to the category of “node-to-segment” (NTS) contact algorithms. Comparative algorithms include sequential multi-pass NTS approaches, and more recently, the improved virtual-slave-node-to-segment (VTS) approach [40], which guarantees accurate assessment of contact interface pressure requiring only a single-pass scheme. Comparison of the presented bi-potential method with other contact algorithms is provided in “Appendix” section.

Here, the bipotential fuction and inequality of contact law is as follows:

$$\begin{aligned}&b_{c}\big (-\mathbf{g }^{\alpha },\mathbf{r }^{\alpha }\big )=\bigcup _{\mathfrak {R}-}\big (-g_{n}^{\alpha }\big )+\bigcup _{\mathbf{K }_{\mu }}\big (\mathbf{r }^{\alpha }\big )+\mu r_{n}^{\alpha }||-\mathbf{g }_{t}^{\alpha }|| \end{aligned}$$
(29)
$$\begin{aligned}&b_{c}\big (-\mathbf{g }^{\alpha },\mathbf{r }'^{\alpha }\big )-b_{c}\big (-\mathbf{g }^{\alpha },\mathbf{r }^{\alpha }\big )\ge -\mathbf{g }^{\alpha }\cdot \big (\mathbf{r }'^{\alpha }-\mathbf{r }^{\alpha }\big ), \forall \;\mathbf{r }'^{\alpha }\in \mathbf{K }_{\mu } \ , \nonumber \\ \end{aligned}$$
(30)

where \(\bigcup \) is indicator function. \(\mathfrak {R}-\) and \(\mathbf{K }_{\mu }\) represent respectively the negative real numbers and Coulomb cone.

The indicator functions become null when the variables \(-\mathbf{g }^{\alpha }\) and \(\mathbf{r }^{\alpha }\) comply with the restraining conditions.

We multiply both sides of the inequality (30) a parameter \(\rho \), which is used to ensure numerical convergence, and substitute (29) into (30):

$$\begin{aligned} \rho \mu \big ({r'}_{n}^{\alpha }-r_{n}^{\alpha }\big )||-\mathbf{g }_{t}^{\alpha }||+\big [\mathbf{r }^{\alpha }-\big (\mathbf{r }^{\alpha }-\rho \mathbf{g }^{\alpha }\big )\big ]\cdot \big (\mathbf{r }'^{\alpha }-\mathbf{r }^{\alpha }\big )\ge 0 \ .\nonumber \\ \end{aligned}$$
(31)

Taking into account the decomposition \(\mathbf{g }=\mathbf{g }_{t}+g_{n}\mathbf{n }\), the following inequality has to be satisfied:

$$\begin{aligned} \big (\mathbf{r }^{\alpha }-\mathbf{r }^{*\alpha }\big )\cdot \big (\mathbf{r }'^{\alpha }-\mathbf{r }^{\alpha }\big )\ge 0,\ \forall \;\mathbf{r }'^{\alpha }\in \mathbf{K }_{\mu } \ , \end{aligned}$$
(32)

where the modified augmented contact force \(\mathbf{r }^{*\alpha }\) is defined by:

$$\begin{aligned} \mathbf{r }^{*\alpha }=\mathbf{r }^{\alpha }-\rho \big (\mathbf{g }+\mu ||-\mathbf{g }_{t}^{\alpha }||\mathbf{n }\big ) \ , \end{aligned}$$
(33)

\(\mathbf{r }^{\alpha }\) is the projection of \(\mathbf{r }^{*\alpha }\) onto the closed convex Coulomb cone:

$$\begin{aligned} \mathbf{r }^{\alpha }=Proj\big (\mathbf{r }^{*\alpha },\mathbf{K }_{\mu }\big ) . \end{aligned}$$
(34)

According to the three different contact states, the projection procedure becomes:

$$\begin{aligned} \begin{array}{lll} \mathrm{if} &{} \quad \mu ||\mathbf{r }_{t}^{*\alpha }||<-r_{n}^{*\alpha } \quad \mathrm{then} \quad \mathbf{r }^{\alpha }=0 \quad &{} \mathrm{separating}\\ \mathrm{elseif} &{} \quad ||\mathbf{r }_{t}^{*\alpha }||\le \mu r_{n}^{*\alpha } \quad \mathrm{then} \quad \mathbf{r }^{\alpha }=\mathbf{r }^{*\alpha } \quad &{}\mathrm{sticking}\\ \mathrm{else} &{} \quad \mathbf{r }^{\alpha }=\mathbf{r }^{\alpha *}-\left( \frac{||\mathbf{r }_{t}^{\alpha *}||-\mu r_{n}^{\alpha *}}{1+\mu ^{2}}\right) \left( \frac{\mathbf{r }_{t}^{\alpha *}}{||\mathbf{r }_{t}^{\alpha *}||}+\mu \mathbf{n }\right) \quad &{} \mathrm{sliding } .\\ \end{array}\nonumber \\ \end{aligned}$$
(35)

2.5 Blatz-Ko hyperelastic model for soft materials

Blatz-Ko hyperelastic model [49] is widely used to describe behaviours of compressible foam type soft materials. In practical situations, such materials undergo large deformations. To deal with the geometrical transformation with large deformation, we use the deformation gradient tensor \(\mathbf{F }\) for the soft bodies in contact:

$$\begin{aligned} \mathbf{F } = \mathbf{I } + \nabla \mathbf{u }, \end{aligned}$$
(36)

where I is the unity tensor and u the displacement vector. The right Cauchy-Green deformation tensor C is defined as \(\mathbf{C }=\mathbf{F }^{T}\mathbf{F }\), and the Green-Lagrange strain tensor \({\mathbf {E}}=\frac{1}{2}({\mathbf {C}}-{\mathbf {I}})\). In the case of hyperelastic law, there exists a strain energy density function W which is a scale function of one of the strain tensors, whose derivative with respect to a strain component determines the corresponding stress component. This can be expressed by

$$\begin{aligned} \mathbf{S }=2\frac{\partial {{W}}}{\partial {{C}}}, \end{aligned}$$
(37)

where S is the second Piola-Kirchhoff stress tensor. In the particular case of isotropic hyperelasticity [50], Eq. (37) can be written by

$$\begin{aligned} \mathbf{S }=2\left[ \textit{I}_{3}\frac{\partial {{W}}}{\partial {I}_{3}}\mathbf{C }^{-1} + \left( \frac{\partial {{W}}}{\partial {I}_{1}}+ \textit{I}_{1}\frac{\partial {{W}}}{\partial {I}_{2}}\right) \mathbf{I } - \frac{\partial {{W}}}{\partial {I}_{2}}\mathbf{C } \right] , \end{aligned}$$
(38)

where \(I_i\) denotes the three invariants of the right Cauchy-Green deformation tensor C:

$$\begin{aligned} \textit{I}_{1}=C_{ii};\ \textit{I}_{2}=(\textit{I}^{2}_{1}-C_{ij}C_{ij})/2;\ \textit{I}_{3}=det(\mathbf{C }). \end{aligned}$$
(39)

The Blatz-Ko strain energy density function is given as follows:

$$\begin{aligned} {{W}}=\frac{G}{2}\left( \frac{{I}_{2}}{{I}_{3}}+2\sqrt{{I}_{3}}-5 \right) , \end{aligned}$$
(40)

where G is the shear modulus. By deriving the energy density (40) with respect to the three invariants, we obtain

$$\begin{aligned} \frac{\partial {{W}}}{\partial {I}_{1}}=0;\ \frac{\partial {{W}}}{\partial {I}_{2}}=\frac{G}{2\textit{I}_{3}};\ \frac{\partial {{W}}}{\partial {I}_{3}}=\frac{G}{2}\left( -\frac{{I}_{2}}{{I}_{3}^{2}}+\frac{1}{\sqrt{{I}_{3}}}\right) . \end{aligned}$$
(41)

Reporting the result in the second Piola-Kirchhoff stress tensor (38) gives

$$\begin{aligned} \mathbf{S }=G\left( \textit{J}\mathbf{C }^{-1}-\mathbf{C }^{-2}\right) , \end{aligned}$$
(42)

where \(\textit{J} = det(\mathbf{F })\). The Cauchy stress tensor \(\varvec{\sigma }\) is calculated from the second Piola-Kirchhoff stress tensor as follows:

$$\begin{aligned} {\varvec{\sigma }}=\frac{1}{\textit{J}}\mathbf{F }\mathbf{S }\mathbf{F }^{T}. \end{aligned}$$
(43)

3 Numerical implementation

3.1 Finite element formulation of the nonlinear problem

Since contact between soft bodies involves treatment of nonlinear kinematic relations and hyperelastic constitutive models (Sect. 2.5), we formulate the nonlinear finite element problem within the framework of large deformations. In this work, we use Green-Lagrange strain tensor \({\mathbf {E}}\) which comprises both linear and nonlinear terms, as function of nodal displacements \({\mathbf {u}}\):

$$\begin{aligned} {\mathbf {E}}=\left( {\mathbf {B}}_{L}+\frac{1}{2}{\mathbf {B}}_{NL}({\mathbf {u}})\right) {\mathbf {u}} , \end{aligned}$$
(44)

where \({\mathbf {B}}_{L}\) is the matrix relating the linear strain term to nodal displacements, and \({\mathbf {B}}_{NL}({\mathbf {u}})\), relates the nonlinear strain term to nodal displacements. From Eq. (44), the incremental form of the strain-displacement relationship can be written as:

$$\begin{aligned} \delta {\mathbf {E}}=\big ({\mathbf {B}}_{L}+{\mathbf {B}}_{NL}({\mathbf {u}})\big )\delta {\mathbf {u}} . \end{aligned}$$
(45)

Using the principle of virtual displacement, we can write the virtual work \(\delta U\) of the problem as:

(46)

where the second Piola–Kirchhoff stress tensor \({\mathbf {S}}\), in the case of Blatz-Ko material model is given in Sect. 2.5 by Eq. (42). The vector of contact reaction force \({\mathbf {R}}\) is expressed in the global coordinate system. It is obtained by considering Eqs. (11, 12) and includes in particular contributions due to adhesion:

$$\begin{aligned} {\mathbf {R}} = {\mathbf {H}}^T ( \bar{{\mathbf {r}}} + \tilde{{\mathbf {r}}} ) , \end{aligned}$$
(47)

with \(\bar{{\mathbf {r}}}\) and \(\tilde{{\mathbf {r}}}\) determined according to the contact and friction rules given in Sect. 2.3. Other notations in Eq. (46) include \(V_{0}\), volume of the initial configuration; \({\mathbf {F}}_{ext}\), vector of external loads; \({\mathbf {M}}\), mass matrix; \({\mathbf {A}}\), damping matrix; \(\dot{{\mathbf {u}}}\), vector of velocity, and , vector of acceleration. Substituting \(\delta {\mathbf {E}}\) from Eq. (45) into Eq. (46) results in

(48)

We can identify in Eq. (48) the vector of internal force:

$$\begin{aligned} {\mathbf {F}}_{int}=\int _{V_{0}}\big ({\mathbf {B}}_{L}+{\mathbf {B}}_{NL}({\mathbf {u}})\big )^{T}{\mathbf {S}}dV. \end{aligned}$$
(49)

Since \(\delta {\mathbf {u}}\) is arbitrary, a set of nonlinear equations can be obtained as

(50)

It is noted that the stiffness effect is taken into account by the internal force vector \({\mathbf {F}}_{int}\). Eq. (50) can be transformed into

(51)

with the initial conditions at \(t=0\)

(52)

Taking the derivative of with respect to the nodal displacements \({\mathbf {u}}\) gives the tangent stiffness matrix as

(53)

In addition, by considering Eqs. (45, 42), the tangent stiffness matrix can be written as the sum of the elastic stiffness matrix \({\mathbf {K}}_{e}\), the geometric stiffness (or initial stress stiffness) matrix \({\mathbf {K}}_{\sigma }\) and the initial displacement stiffness matrix \({\mathbf {K}}_{u}\):

$$\begin{aligned} {\mathbf {K}}={\mathbf {K}}_{e}+{\mathbf {K}}_{\sigma }+{\mathbf {K}}_{u}, \end{aligned}$$
(54)

with

$$\begin{aligned} \begin{aligned} {\mathbf {K}}_{e}&=\int _{V_{0}}{\mathbf {B}}_{L}^{T}{\mathbf {D}}{\mathbf {B}}_{L}\,dV \\ {\mathbf {K}}_{\sigma }&=\int _{V_{0}}\frac{\partial {\mathbf {B}}_{NL}^{T}}{\partial {\mathbf {u}}}{\mathbf {S}}\,dV \\ {\mathbf {K}}_{u}&=\int _{V_{0}}\left( {\mathbf {B}}_{L}^{T}{\mathbf {D}}{\mathbf {B}}_{NL}+{\mathbf {B}}_{NL}^{T} {\mathbf {D}}{\mathbf {B}}_{L}+{\mathbf {B}}_{NL}^{T}{\mathbf {D}}{\mathbf {B}}_{NL}\right) dV .\\ \end{aligned} \end{aligned}$$
(55)

3.2 Numerical integration algorithm

Now we need to integrate Eq. (51) between consecutive time configuration t and \(t+\Delta {t}\). The Newmark method is the most common method which is based on a second order algorithm. However, higher order approximation does not necessarily mean better accuracy and may even be redundant in impact problems. When the contact conditions suddenly change (impact, release of contact), the velocity and acceleration are not continuous, and excessive regularity constraints may lead to serious errors. For this reason, Jean [51] has proposed a first order algorithm which is used in this work, Eq. (51) can be transformed into:

$$\begin{aligned} {\mathbf {M}}\,d{\dot{\mathbf {u}}}={\mathbf {F}}\,dt+{\mathbf {R}}\,dt\ . \end{aligned}$$
(56)

This algorithm is based on the following approximations:

$$\begin{aligned}&\int _{t}^{t+\Delta t}{{{\mathbf {M}}}\,d{\dot{\mathbf {u}}}}={{\mathbf {M}}}\left( {{\dot{\mathbf {u}}}^{t+\Delta t}-{\dot{\mathbf {u}}}^{t}}\right) \end{aligned}$$
(57)
$$\begin{aligned}&\int _{t}^{t+\Delta t}{{\mathbf {F}}}\,dt=\Delta t\left( {\left( {1-\xi }\right) {{\mathbf {F}}}^{t}+\xi \,{{\mathbf {F}}}^{t+\Delta t}}\right) \end{aligned}$$
(58)
$$\begin{aligned}&\int _{t}^{t+\Delta t}\,{\mathbf {R}}\,dt=\Delta t\,{\mathbf {R}}^{t+\Delta t} \end{aligned}$$
(59)
$$\begin{aligned}&{{\mathbf {u}}}^{t+\Delta t}-{{\mathbf {u}}}^{t}=\Delta t\left[ {\left( {1-\theta }\right) {{\dot{\mathbf {u}}}}^{t}+\theta \,{\dot{\mathbf {u}}}^{t+\Delta t}}\right] \ , \end{aligned}$$
(60)

where \(0\le \xi \le 1;\,\,\,0\le \theta \le 1\). In the iterative solution procedure, all the values at time \(t+\Delta {t}\) are replaced by the values of the current iteration \(i+1\); for example, \({\mathbf {F}}^{t+\Delta {t}}={\mathbf {F}}^{i+1}\). A standard approximation of \({\mathbf {F}}^{i+1}\) gives

(61)

Finally, we obtain the recursive form of (56) in terms of displacements:

(62)

where the so-called effective terms are given by

$$\begin{aligned}&{{\bar{\mathbf{K}}}}^{i}=\xi \,{{\mathbf {K}}}^{i}+\frac{\xi }{{\theta \,\Delta t}}{{\mathbf {A}}}^{i}+\frac{1}{{\theta \,\Delta t^{2}}}{{\mathbf {M}}}^{i} \end{aligned}$$
(63)
$$\begin{aligned}&{{\bar{\mathbf{F}}}}_{acc}^{i}=-\frac{1}{{\theta \Delta t^{2}}}\,{{\mathbf {M}}}^{i}\Big ( {{{\mathbf {u}}}^{i}-{{\mathbf {u}}}^{t}-\Delta t\,{\dot{\mathbf {u}}}^{t}}\Big ) \end{aligned}$$
(64)
$$\begin{aligned}&{{\bar{\mathbf{F}}}}^{i}=\left( {1-\xi }\right) \left( {{{\mathbf {F}}}_{int}^{t}+{{\mathbf {F}}}_{ext}^{t}}\right) +\xi \left( {{{\mathbf {F}}}_{int}^{i}+{{\mathbf {F}}}_{ext}^{t+\Delta t}}\right) \ . \end{aligned}$$
(65)

At the end of each time step, the velocity is updated by

$$\begin{aligned} {\dot{\mathbf {u}}}^{t+\Delta t}={\displaystyle \Big (1-\frac{1}{\theta }\Big )\,{\dot{\mathbf {u}}}^{t}+\frac{1}{\theta \,\Delta t}\Big ({\mathbf {u}}^{t+\Delta t}-{\mathbf {u}}^{t}\Big )}\ . \end{aligned}$$
(66)

By setting \(\theta =\frac{1}{2}\), this scheme is then called the implicit trapezoidal rule and it is equivalent to the Tamma–Namburu method in which the acceleration need not be computed [52].

It is noted that Eq. (62) is strongly non-linear, because of large rotations and large displacements of solid, for instance in multibody contact/impact problems. Besides, as mentioned above, the constitutive law of contact with friction is usually represented by inequalities and the contact potential is even non differentiable. Instead of solving this equation in consideration of all nonlinearities at the same time, Feng [53] has proposed a solution strategy which consists in separating the nonlinearities in order to overcome the complexity of calculation and to improve the numerical stability. As \(\Delta {\mathbf {u}}\) and \({\mathbf {R}}\) are both unknown, Eq. (62) cannot be directly solved. First, the vector \({\mathbf {R}}\) is determined by the bi-potential method and the adhesive model in a reduced system, which only concerns contact nodes. Then, the vector \(\Delta {\mathbf {u}}\) can be computed in the whole structure, using adhesive contact reactions as external loading.

The iterative solution procedure involving contact modeling is written as Fig. 6.

Fig. 6
figure 6

The iterative solution procedure

Full size image

4 Numerical results

The algorithm presented above has been implemented within the in-house finite element code FER/Contact. In this section, three numerical examples based on contact simulations are presented to show orthotropic behaviours of the adhesive contact interface.

4.1 Orthotropic adhesion under compression

In this first example, we investigate the orthotropic interface adhesion of a hyperelastic soft body submitted to compressive load against a rigid surface. As shown in Fig. 7, a vertical displacement is constantly prescribed on the upper surface of the soft body, pressing it against a fixed, rigid plate. The test scenario allows observing consecutively two phenomena: first, the bonding process on the adhesive interface that takes place when contact is set up, then, initiation of the de-bonding process on the contact interface where sliding occurs due to compression induced section expansion of the soft body. We investigate how the de-bonding area evolves with the compressive load, and how the evolution is affected by the interface adhesion orthotropy. Characteristics of the system are described in the following. The soft body is \(6 \mathrm{mm} \) high with a square section of \(10 \times 10\ \mathrm mm\). It is modelled by Blatz-Ko hyperelastic material with a shear modulus of \(G= 2.1 \times 10^{5}\ \mathrm MPa\). Adhesive interface parameters are: \(w = 100\ \mathrm J\,m^{-2}\), \(C_{tx} = 1\times 10^{11}\ \mathrm N\,m^{-3}\), \(C_{ty} = 1\times 10^{10}\ \mathrm N\,m^{-3}\) and \(b= 0.1\ \mathrm N\,s\,m^{-1}\). Therefore, interface adhesive behaviour is orthotropic, with adhesive stiffness along x direction significantly stronger than that along y direction. We suppose that the system does not involve initial adhesion on the interface (adhesion strength parameter \(\beta = 0\) at time 0).

Fig. 7
figure 7

Orthotropic adhesion of a soft body under compression on a rigid surface

Full size image

As soon as the two bodies are in contact, adhesive bonds on the contact interface begin to form. Figure 8 depicts evolution of the adhesion strength parameter \(\beta \), calculated on 6 nodes on the contact interface, along the diagonal from the centre to the periphery. At time \(= 0.0015\ \mathrm s\), \(\beta \) increases to 1.0, indicating the achievement of complete bonding (Zone 1 in Fig. 8) of the adhesive interface. In Zone 2, as we continue to apply compression on the soft body, its section increases due to incompressible volume. The section expansion produces tangential interface effects involving shear stresses, which tend to weaken the interface adhesion. However, since the adhesives bonds are undamaged on this stage (\(\beta = 1.0\)), the soft body and the rigid surface remain stuck together, and we do not observe effective sliding on the contact interface. As the load increases, the effect of adhesion damages becomes noticeable starting from \(t= 0.011\ \mathrm s\), which corresponds to Zone 3 in Fig. 8. On this stage, tangential effects have been sufficiently accumulated, leading to initiation of damages to the adhesive bonds. As a result, \(\beta \) significantly decreases, especially on remote nodes with respect to the centre, on which \(\beta \) falls back to 0, indicating rupture of the adhesive bonds. We also find contours of \(\beta \) plotted on the contact surface in Fig. 8, where the effect of adhesion orthotropy can be distinguished. Since the adhesion stiffness in x axis \(C_{tx}\) is 10 times stronger than in y axis, significant resistance to interface sliding can be expected in x axis. Therefore, rupture of the adhesive bonds first appears on the upper and lower peripheries of the contact interface, and gradually propagates towards the centre area. Meanwhile, peripheral areas near the left and right edges remain adhered due to stronger adhesion stiffness \(C_{tx}\) in x axis.

Similar effects of adhesion orthotropy can be observed in Fig. 9, which shows the distribution of the Euclidean norm of tangential adhesive forces on the contact surface and its evolution with time. We note that within areas where de-bonding is initiated, particularly near the upper and lower edges, the adhesion forces decrease quickly to zero. On the contrary, we observe important adhesion forces in areas near the left and right edges since the adhesion orthotropy results in stronger resistance to sliding motions along the x axis. In conformity with the contours of \(\beta \) given in Fig. 8, distribution of the adhesion forces in Fig. 9 reflects identical effects of adhesion orthotropy, demonstrating better resistance to tangential interface effects in x axis compared to y axis.

Fig. 8
figure 8

Orthotropic adhesion under compression: a Evolution of \(\beta \) calculated on 6 nodes on the contact interface, along the diagonal from the centre to the periphery. b Evolution of \(\beta \) on the contact interface and variation in the shape of the contact surface in debonding process. In each square area, the colour progresses from dark red to blue, which represents the damage of the adhesive strength \(\beta \) from perfect adhesion (\(\beta = 1\)) to complete separation (\(\beta = 0\)). (Color figure online)

Full size image
Fig. 9
figure 9

Orthotropic adhesion under compression: Distribution of the Euclidean norm of tangential adhesive forces \(\left\| \tilde{\mathrm{R}}_{t}\right\| \) on the contact surface and its evolution with time in the debonding process. In each square area, the colour progresses from dark red to blue, which represents the variation of the Euclidean norm of tangential adhesion from maximum to zero. (Color figure online)

Full size image

4.2 Orthotropic adhesion in shear sliding

We investigate in this example behaviours of orthotropic adhesion in a test scenario involving shear sliding along varying orientations. Similar experimental setup which demonstrates microstructure based orthotropic adhesion has been explored in [54]. Here, we model the interface adhesion orthotropy by considering distinctive tangential adhesive stiffnesses \(C_{tx}\) and \(C_{ty}\), in x and y axis. The tested system is composed of an elastomer cylinder that slides on a rigid surface under tangential load, which is oriented along varying orientations on each test. As shown in Fig. 10, the elastomer cylinder is \(2\ \mathrm mm \) high, and has a radius of \(5\ \mathrm mm\). The elastomer is modelled by Blatz-Ko material with shear modulus \(G= 2.1 \times 10^{5}\ \mathrm MPa\). The adhesive interface parameters are: \(w = 100\ \mathrm J\,m^{-2}\), \(C_{tx} =5\times 10^{9}\ \mathrm N\,m^{-3}\), \(C_{ty} =1\times 10^{10}\ \mathrm N\,m^{-3}\) and \(b= 0.1\ \mathrm N\,s\,m^{-1}\). The simulation scenario involves 2 stages. On the first stage, we prescribe a slight compression on the elastomer by descending its upper surface by \(0.1\ \mathrm mm\) after contact. The compression activates the bonding process which leads to complete bonding on the adhesive interface. On the second stage, a lateral motion at the velocity of \(0.1\ \mathrm m/s\) is applied on the cylinder’s upper surface. Under the tangential effect on the contact interface, de-bonding is initiated and progresses until the rupture of adhesive bonds, which allows the cylinder to slide on the support surface. A group of 10 tests have been performed. On each test, we align the lateral motion to a new direction whose angle with respect to x axis, \(\theta \), increases from \( 0^\circ \) to \( 90^\circ \) by increments of \( 10^\circ \).

Figure 11 presents the evolution of adhesion parameters calculated on the centre node that belongs to the contact surface of the elastomer cylinder, for the 10 calculations performed with \(\theta \) ranging from \(0^\circ \ \mathrm to\ 90^\circ \). Positions of the centre node at the moment of adhesion rupture are reported in Fig. 11a. Blue circles represent results based on orthotropic adhesion properties with \(C_{tx}=0.5 C_{ty}\). Red circles are obtained considering the assumption of isotropic adhesion. For the isotropic cases, all the red circles are arranged at the same distance from the initial position, which conforms to expectations since the problem becomes perfectly symmetric with isotropic interface properties. For the cases with orthotropic interface adhesion, directions presenting stronger adhesive stiffness lead to increased resistance to sliding. Consequently, distance travelled by the centre node before de-bonding is the lowest in the case of \( 90^\circ \) sliding (along y axis), and highest in the \( 0^\circ \) case (along x axis). Intermediate cases can be considered based on adhesion whose stiffness results from the combination of \(C_{tx}\) and \(C_{ty}\). Norms of the maximum adhesion forces \(||\tilde{{\mathbf {R}}}_{t}^{max}||\) at the onset of de-bonding initiation for the 10 test cases are reported in Fig. 11b. Here, Monotonous trend can be observed for the adhesion forces as function of the sliding orientation angle \(\theta \). This observation is within our expectations because as the sliding motion approaches y axis, adhesion force increases since \(C_{ty}\) is significantly higher compared to \(C_{tx}\). We underline 4 of the tested cases, corresponding to sliding angles \( \theta = 0^\circ , 30^\circ , 60^\circ \) and \(90^\circ \), and we report for the underlined cases evolutions of the adhesion damage parameter \(\beta \) (Fig. 11c) and adhesion forces \(||\tilde{{\mathbf {R}}}_{t}||\) (Fig. 11d) for a complete load cycle involving bonding and de-bonding. In Fig. 11c, we note indistinguishable time history of \(\beta \) during the stage of adhesion bonding. However, initiation of de-bonding does not take place simultaneously for all the cases. It arises first in the case of sliding along x axis, in which direction the adhesion stiffness is the lowest. For the same reason, this scenario also exhibits the lowest adhesion force at the onset of de-bonding process (blue curve in Fig. 11d). Comparatively, with the sliding direction approaching y axis, stronger adhesion stiffness is involved. We observe accordingly retarded initiation of de-bonding, accompanied by increased adhesion forces (red, yellow and purple curves in Fig. 11d).

Fig. 10
figure 10

Orthotropic adhesion in shear sliding: Problem setup and loading sequence (Step 1, compression and adhesion process; Step 2, sliding and de-bonding process), where \(\theta \) represents angle between sliding direction and \( x \) axis

Full size image
Fig. 11
figure 11

Orthotropic adhesion in shear sliding: a Final positions of center contact point in isotropic/orthotropic cases with sliding angle \(\theta = 0^\circ \) to \(90^\circ \) respectively. b Maximum tangential adhesion norms \( ||\tilde{{\mathbf {R}}}_{t}^{max}||\) of center contact point with sliding angle \(\theta = 0^\circ \) to \(90^\circ \) respectively. c \(\beta \) evolutions of center contact point with 4 different \(\theta \) (\(0^\circ , 30^\circ , 60^\circ , 90^\circ \)). d Tangential adhesion force evolutions of center contact point with 4 different \(\theta \)

Full size image

4.3 Orthotropic adhesive twisting

In this example, we investigate the evolution of interface behaviours of a 3D twist tribosystem (Fig. 12) by considering both isotropic and orthotropic adhesions. The system is composed of an elastomer block that slides on a rigid surface under twisting load. The elastomer block is \(3\ \mathrm mm \) high, and has a \(10 \times 10\ \mathrm mm\) square section. For the isotropic case, the tangential adhesive stiffness \(C_{t} = 1\times 10^{10}\ \mathrm N\,m^{-3}\), and for the orthotropic case \(C_{tx} = 5\times 10^{10}\ \mathrm N\,m^{-3}\), \(C_{ty} = 1\times 10^{10}\ \mathrm N\,m^{-3}\). The other adhesive interface parameters are: \(w = 100\ \mathrm J\,m^{-2}\), \(b= 0.1\ \mathrm N\,s\,m^{-1}\). The simulation scenario involves 2 stages. On the first stage, we slightly compress the elastomer by lowering its upper surface by \(0.1\ \mathrm mm\). Then, on the second stage, a twisting motion is applied to the upper surface at a rate of \(20\ \mathrm rad/s\), driving the compressed elastomer block to twist clockwise. Blatz-Ko material is used to model the elastomer. To prevent excessive shear deformation of the elastomer body during the twist, we apply a significant shear modulus \(G= 2.1 \times 10^{5}\ \mathrm MPa\).

We begin by investigating the effect of interface adhesion by comparing cases with and without the interface adhesion orthotropy. Figures 13 and 14 compare respectively the evolution of adhesion damage parameter \(\beta \), and the tangential adhesion forces \(\left\| \tilde{\mathrm{R}}_{t}\right\| \), between the isotropic and orthotropic cases during the twisting process. For each group of comparison, 5 frames of result are extracted in chronological order to represent the evolving twist process. This allows us to highlight for each time instant, differences between the isotropic and orthotropic cases in terms of \(\beta \) and \(\left\| \tilde{\mathrm{R}}_{t}\right\| \) distributions. In Fig. 13, we use dark red colour to indicate complete bonding of the interface adhesives. As we apply twist kinematics to the elastomer body, tangential interface effects start to appear on the contact interface. They become first noticeable on the outskirts of the contact area where interface sliding is most significant. Damage to the adhesive bonds is thus initiated with decreasing \(\beta \) emerging at the corners of the contact interface, where also the first de-bonded area is observed. Then with the increasing load, de-bonding propagates from the outskirt area towards the centre, whereas the bonded region gradually shrinks until complete disappearance. During the process, the bonded region appears within a round area in the isotropic case. However, when adhesion orthotropy is involved, since stronger resistance to de-bonding is encountered in the x axis where tangential adhesive stiffness is more significant, delayed de-bonding is observed following the x axis, leading to an elliptical bonded region.

We also investigate the evolution of tangential forces on the same setup. In Fig. 14, Euclidean norms of tangential forces are depicted, allowing us to observe the evolving intensity of tangential forces on the contact interface. Chronologically, at the beginning of load, tangential forces are most significant on the outskirts of the contact area since linear velocity is higher. This is also where de-bonding is initiated and propagates towards the centre. Consequently, the peak of tangential forces appears in the form of an evolving circular band, whose radius decreases with the twist load, until gradually disappears in the centre of rotation, leading to complete de-bonding of the interface adhesives. In the case of orthotropic adhesion, the circular band appears in the form of an ellipse since stronger tangential adhesive stiffness is involved in x axis, following which de-bonding requires more efforts. This observation is in accordance with the evolution of \(\beta \) during the simulation.

Fig. 12
figure 12

Comparison between isotropic and orthotropic adhesive twisting: Problem setup and loading sequence (Step 1, compression and adhesion process; Step 2, twisting and de-bonding process)

Full size image
Fig. 13
figure 13

Comparison between isotropic and orthotropic adhesive twisting: Evolution of the adhesion intensity \(\beta \) in isotropic case and orthotropic case during the debonding process and their shape variation of the contact surface. In each square area, the colour progresses from dark red to blue, which represents the damage of the adhesive strength \(\beta \) from perfect adhesion (\(\beta = 1\)) to complete separation (\(\beta = 0\)). (Color figure online)

Full size image
Fig. 14
figure 14

Comparison between isotropic and orthotropic adhesive twisting: Evolution of tangential adhesion forces \(\left\| \tilde{\mathrm{R}}_{t}\right\| \) in two cases during the debonding process. In each square area, the colour progresses from dark red to blue, which represents the variation of the Euclidean norm of tangential adhesion from maximum to zero. (Color figure online)

Full size image

5 Conclusions

In this work, we proposed an orthotropic adhesion model to deal with problems of adhesive contact with orthotropic interface properties between hyperelastic bodies. This model has been implemented within the bi-potential method, based on a set of extended unilateral and tangential contact laws. The behaviour of orthotropic adhesion is described by adhesion stiffness, whose components can be expressed according to the local coordinate system. In this model, the strength of interface adhesive bonds and the effect of interfacial damage are characterized by a scalar parameter \(\beta \), therefore an entire bonding and debonding process of the adhesive links with the account for orthotropic interface effects can be modelled. The proposed approach has been tested on cases involving both tangential and unilateral contact kinematics, which allowed emergence of orthotropic interface effects between soft bodies. Owing to the straightforward description of the contact rules, the presented approach can be easily implemented. Therefore, immediate implementation of this orthotropic adhesion model within a third-party software can be suggested for direct application on real problems.