Uzawa algorithm to solve elastic and elastic–plastic fretting wear problems within the bipotential framework

Abstract

This paper deals with elastic and elastic–plastic fretting problems. The wear gap is taken into account along with the initial contact distance to obtain the Signorini conditions. Both the Signorini conditions and the Coulomb friction laws are written in a compact form. Within the bipotential framework, an augmented Lagrangian method is applied to calculate the contact forces. The Archard wear law is then used to calculate the wear gap at the contact surface. The local fretting problems are solved via the Uzawa algorithm. Numerical examples are performed to show the efficiency and accuracy of the proposed approach. The influence of plasticity has been discussed.

1 Introduction

Fretting arises when two bodies in contact become subject to reciprocating motion with small amplitudes. It is a common phenomenon in many mechanical elements such as bolted joints, clamping devices, rolling bearings, etc. Fretting may cause the loss of contact surface of concerned bodies and thus lead to fretting fatigue and fracture.

Extensive research has been conducted on fretting problems. Some experimental research is devoted to explore the mechanism of fretting. This leads to wear models where the wear coefficient is determined. Vingsbo and Söderberg established the “fretting map” to describe the three fretting regimes [1]. Zhou et al. [2] developed two kinds of “fretting map” which distinguished running conditions and the material response. Pearson and Shipway [3] proposed that elastic deformation of system and threshold energy should be considered when calculating the wear coefficient.

From the point of numerical simulation. Fretting problems include contact, friction and wear. Not only the contact pressure influences the wear rate, but the wear process changes the contact surface and influences the contact properties as a consequence. This creates an additional coupled relationship between contact and friction. The accuracy of contact calculation is the base to simulate wear process [4].

Many scholars used commercial finite element codes, such as ABAQUS and ANSYS, to obtain the contact pressure and partial relative displacements, and then applied wear models to compute the wear value accordingly. McColl et al. [5] simulated wear procedure under elastic deformation. Garcin et al. [6] studied the wear effect of crack nucleation. Hu et al. and Tobi et al. [7, 8] studied the interaction of plastic deformation and wear procedure. Yue et al. and Arnaud et al. [9, 10] considered the effect of third body layer.

Others applied their own method to solve the couple problem of contact, friction and wear. Johansson [11] studied the evolution of contact pressure in fretting, pioneering numerical work in this field. Strömberg used the augmented Lagrangian method to calculate contact forces and the Newton method to solve the nonlinear equilibrium equations. Lengiewicz and Stupkiewicz [14] developed the so-called “rigid-wear model” to deal with the pin-on-disc problem. Rodríguez-Tembleque et al. [15] studied the influence of anisotropy on 3D rolling wear problems. Carbonell et al. [16] developed particle finite element method to deal with wear problem of rock cutting tool.

In our paper, local contact and fretting problems are solved via the Uzawa algorithm within the bipotential framework. The bipotential theory which complies the contact boundary conditions and the contact laws naturally, was promoted by de Saxcé and Feng [17, 18] to deal with the so-called implicit standard materials (ISM). It has been successfully applied to deal with contact problems involving anisotropy [19], dynamics [20], etc. The present work extends the bi-potential method to fretting problems by using the Archard wear law [21] and by considering the normal wear gap of the contact surface as an internal state variable [13], which can be taken into account by the Archard wear law. For numerical formulations and simulations, the post two popular wear models are Archard wear law [21] and friction energy approaches [22]. As we only consider the constant friction coefficient, these two approaches are equivalent [10]. So the Archard wear law is chosen to calculate the normal wear gap. This is based on the hypothesis that the wear debris of contact surfaces disappears immediately instead of existing as a third-body between the two contact bodies. For elastic wear problems, the wear gap increment is calculated by means of the Archard wear law in every increment step after convergence of the contact state. But the wear gap increment is calculated in every increment step after convergence of the plastic iteration. The Uzawa algorithm is successfully applied to solve the three-dimensional elastic frictional contact problems and displays good performance both in simplicity and robustness [23]. Thus, it is suitable to extend the Uzawa algorithm to the fretting problem. Numerical examples are conducted to show the performance of this method of two different materials.

Fig. 1

Contact kinematics

2 Contact kinematics and Archard wear law

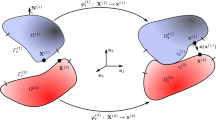
Let us consider two deformable bodies $\varOmega _1$ and $\varOmega _2$ coming into contact as in Fig. 1, where $M_1$ and $M_2$ are two corresponding contact points; $\mathbf {t}_1$, $\mathbf {t}_2$ and $\mathbf {n}$ denote respectively the tangential, orthogonal and normal direction vectors. The local relative position vector $\mathbf {x}^\alpha$ of each contact point $\alpha$ ($\alpha =1,2,\ldots ,N_c$) can be determined by the global vector $\mathbf {X}$:

$$\begin{aligned} \mathbf {x}^\alpha = \mathbf {H}_\alpha \mathbf {X} \end{aligned}$$

(1)

where $\mathbf {H}_\alpha$ represents the transition matrix. Conversely, the reverse rotation form of the contact force vector is:

$$\begin{aligned} \mathbf {R}^\alpha = \mathbf {H}_\alpha ^\mathrm{{T}} \mathbf {r}^\alpha \end{aligned}$$

(2)

where $\mathbf {R}^\alpha$ and $\mathbf {r}^\alpha$ are contact force vectors in global frame and local frame respectively. The gap vector between two contact points is derived from the incremental form of Eq. (1):

$$\begin{aligned} {\mathbf {x}}_{i+1}^\alpha ={\mathbf {H}}_\alpha \varDelta {\mathbf {X}}_i+{\mathbf {g}}^\alpha , \quad {\text { }}{\mathbf {g}}^\alpha =\left( {\text {0} \text { } \text {0} \text { } g^\alpha } \right) ^{\text {T}} \end{aligned}$$

(3)

where $\mathbf {g}^\alpha$ is the initial gap vector; $g^\alpha = {g_0^\alpha }+{g_w^\alpha }$ and it stands for the initial normal gap consisting in the addition of the initial motion gap ${g_0^\alpha }$ and the wear gap ${g_w^\alpha }$ (see Fig. 2).

Fig. 2

Initial normal gap

The wear gap is governed by the Archard wear law as follows

$$\begin{aligned} \dot{g}_w^\alpha = kP_n^\alpha \sqrt{\left( {\dot{x}_{t_1 }^\alpha } \right) ^2 + \left( {\dot{x}_{t_2 }^\alpha } \right) ^2 } \end{aligned}$$

(4)

where k stands for the wear coefficient, empirically determined, and $P_n^{\alpha }$ represents the normal contact pressure. The superimposed dot notation indicates a time derivative. The Archard wear law describes how the wear rate is proportional to both the normal contact traction and the relative tangential velocity. For the quasi-static problem, the approximate form (5) can be obtained by adopting a backward Euler time-discretization of Eq. (4)

$$\begin{aligned} g_w^{\alpha \left( {k + 1} \right) } = g_w^{\alpha \left( k \right) }+ kP_n^{\alpha \left( {k + 1} \right) } \sqrt{\left( {\varDelta x_{t_1 }^{\alpha \left( k \right) } } \right) ^2 + \left( {\varDelta x_{t_2 }^{\alpha \left( k \right) }} \right) ^2 }\ \end{aligned}$$

(5)

where ${\varDelta x_{t_j }^{\alpha \left( k \right) } } = x_{t_j }^{\alpha \left( {k + 1} \right) } - x_{t_j }^{\alpha \left( k \right) }, j=1,2$ . Assembling all the $N_c$ equations of Eqs. (2) and (3) leads to the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbf {x}} = {\mathbf {H}}\varDelta {\mathbf {X}} + {\mathbf {g}} \\ {\mathbf {R}} = \sum \limits _{\alpha = 1}^{N_c } {{\mathbf {R}}^\alpha = {\mathbf {H}}^\mathrm{{T}} {\mathbf {r}}} \end{array} \right. \end{aligned}$$

(6)

with the following complementary notations:

$$\begin{aligned} {\mathbf {H}} = \left[ \begin{array}{c} {\mathbf {H}}_1 \\ \vdots \\ {\mathbf {H}}_{N_c } \\ \end{array} \right] ,\text { }{\mathbf {x}} = \left[ \begin{array}{c} {\mathbf {x}}^1 \\ \vdots \\ {\mathbf {x}}^{N_c } \\ \end{array} \right] ,\text { }{\mathbf {r}} = \left[ \begin{array}{c} {\mathbf {r}}^1 \\ \vdots \\ {\mathbf {r}}^{N_c } \\ \end{array} \right] ,\text { }{\mathbf {g}} = \left[ \begin{array}{c} {\mathbf {g}}^1 \\ \vdots \\ {\mathbf {g}}^{N_c } \\ \end{array} \right] \end{aligned}$$

(7)

3 The complete contact law

For wear problems, and because of the wear gap $\text {g}_w^\alpha$ (see Fig. 2), the unilateral contact laws also known as Signorini conditions become

$$\begin{aligned} \left\{ \begin{array}{l} x_n^\alpha = \varDelta x_n^\alpha + g_0^\alpha + g_w^\alpha = 0 \quad \text{ if } \quad r_n^\alpha \ge 0 \\ x_n^\alpha = \varDelta x_n^\alpha + g_0^\alpha + g_w^\alpha > 0 \quad \text{ if } \quad r_n^\alpha = 0 \end{array} \right. \end{aligned}$$

(8)

The positive contact distance $x_n^\alpha \ge 0$ means that there is no interpenetration between contact surfaces. The second inequation means that there is no adhesion when the bodies are separated. For quasi-static problems, the time interval can be taken as being equal to the time unit interval. Coulomb friction laws are regularly used for rate-independent dry-friction problems and summarize in :

$$\begin{aligned} \left\{ \begin{array}{l} \left\| {{\mathbf {r}}_t^\alpha } \right\| \le \mu r_n^\alpha \quad \forall \ \left\| {{\mathbf { x}}_t^\alpha } \right\| = 0 \\ {\mathbf {r}}_t^\alpha = - \mu r_n^\alpha \frac{{{\mathbf { x}}_t^\alpha }}{{\left\| {{\mathbf {\ x}}_t^\alpha } \right\| }} \quad \forall \ \left\| {{\mathbf { x}}_t^\alpha } \right\| \ne 0 \\ \end{array} \right. \end{aligned}$$

(9)

where $\mu$ is the friction coefficient. The Coulomb friction laws in Eq. (9) can be rewritten in the form of a Coulomb cone $\mathbf {K}_\mu$

$$\begin{aligned} \mathbf {K}_\mu = \left\{ {{\mathbf {r}}^\alpha \in \mathbb {R}^3 \quad | \ r_n^\alpha \ge 0 ,\ \left\| {{\mathbf {r}}_t^\alpha } \right\| - \mu {\text {r}}_n^\alpha \le 0} \right\} \ . \end{aligned}$$

(10)

The combination of Signorini conditions with Coulomb friction laws leads to the complete contact law :

$$\begin{aligned} \begin{array}{rcl} &{}&{}\text {Separating: } x_n^\alpha >0,\ \mathbf {r} = 0 \\ &{}&{}\text {Sticking: } \left\| {{\mathbf {x}}_t^\alpha }\right\| = 0,\ \mathbf {r} \in \text {int} \left( {\mathbf {K}_\mu } \right) \\ &{}&{}\text {Sliding: } \left\| {{\mathbf {x}}_t^\alpha } \right\| \ne 0,\ \mathbf {r} \in \text {bd}\left( {\mathbf {K}_\mu } \right) \ |\ {\mathbf {r}}_t^\alpha = -\mu r_n^\alpha \frac{{{\mathbf {x}}_t^\alpha }}{{\;\left\| {{\mathbf {x}}_t^\alpha } \right\| }} \end{array} \end{aligned}$$

(11)

where ‘int’ and ‘bd’ represent the interior and the boundary of the Coulomb cone, respectively. Note that there is no explicit relationship between $\mathbf {x}$ and $\mathbf {r}$ because of the multivalued character in the separating and sticking contact states. Therefore, a superpotential for the contact law does not exist. The materials obeying these rules are called ISM (implicit standard materials) and can be perfectly handled with through extending the augmented Langrangain method to the bipotential framework [17, 18].

4 The implicit standard materials and the bipotential method

The bipotential method is a good strategy proposed by De Saxcé and Feng [17, 18] to deal with the so-called ISM. The derivation of this method is based on Fenchel’s inequalities :

$$\begin{aligned} \varphi (\varvec{\xi }) + \chi (\varvec{\zeta }) \ge \varvec{\xi } \cdot \varvec{\zeta } \end{aligned}$$

(12)

where $\varphi$ and $\chi$ are superpotentials and the right hand side of this equation stands for the dissipation energy. Only when the dual variables $\varvec{\xi }$ and $\varvec{\zeta }$ comply with the dissipative law, can the equality be satisfied

$$\begin{aligned} \varphi (\varvec{\xi }') + \chi (\varvec{\zeta }') = \varvec{\xi '} \cdot \varvec{\zeta '} \ . \end{aligned}$$

(13)

By letting $\varvec{\zeta }'=\varvec{\zeta }$ and by subtracting Eq. (13) from Eq. (12), it can be deduced that

$$\begin{aligned} \forall \varvec{\zeta } ,\quad \varphi (\varvec{\xi }) - \varphi (\varvec{\xi }') \ge \varvec{\zeta } \cdot (\varvec{\xi }-\varvec{\xi }') \ . \end{aligned}$$

(14)

The solution of $\varvec{\zeta }$ is called the subdifferential of $\varphi$ at $\varvec{\xi }'$. Letting $\varvec{\xi }'$ be equal to $\varvec{\xi }$ and conducting a similar operation as with $\varvec{\zeta }$, the subnormally law can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{\xi } \in \partial \chi (\varvec{\zeta })\\ \varvec{\zeta } \in \partial \varphi (\varvec{\xi })\\ \end{array} \right. \ . \end{aligned}$$

(15)

Fig. 3

Coulomb cone projection and contact states

The materials that conform to such subnormally laws are called explicit standard materials (ESM). But De Saxcé and Feng [18] have proven that there does not exist a superpotential for the contact law. Therefore, the concept of bipotential is developed to deal with the implicit relationship between dual variables such as

$$\begin{aligned} b_c (\varvec{\xi } \text {, } \varvec{\zeta }) \ge \varvec{\xi } \cdot \varvec{\zeta } \end{aligned}$$

(16)

where the bipotential function $b_c (\varvec{\xi } \text {, } \varvec{\zeta })$ is convex with respect to the dual variables $\varvec{\xi }$ and $\varvec{\zeta }$. Only when the dual variables satisfy the constitutive law, can inequation (16) satisfy the equality. Then, the corresponding implicit subnormally laws become

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{\xi } \in \partial _{\varvec{\zeta }} {b_c (\varvec{\xi } \text {, } \varvec{\zeta })}\\ \varvec{\zeta } \in \partial _{\varvec{\xi }} {b_c (\varvec{\xi } \text {, } \varvec{\zeta })} \\ \end{array} \right. \ . \end{aligned}$$

(17)

Obviously, when taking the following form :

$$\begin{aligned} b_c (\varvec{\xi } \text {, } \varvec{\zeta })= \varphi (\varvec{\xi }) + \chi (\varvec{\zeta }) \end{aligned}$$

(18)

the implicit inequation (16) becomes the same as the explicit one (12). So the ESM could be seen as a special form of the ISM.

5 The contact law within the bipotential framework

For any contact point $\alpha \ ({\alpha \in 1, \ldots ,N_c })$, the bipotential function of the contact law is as follows :

$$\begin{aligned} b_c (-\mathbf {x}^\alpha , \mathbf {r}^\alpha )= \bigcup \limits _{\mathbb {R}_-}(-x_n^\alpha )+ \bigcup \limits _{\mathbf {K}_\mu }(\mathbf {r}^\alpha )+ \mu r_n^\alpha \Vert {-\mathbf {x}_t^\alpha }\Vert \end{aligned}$$

(19)

where $\bigcup \nolimits _{\mathbb {R}_-}(-x_n^\alpha )$ and $\bigcup \nolimits _{\mathbf {K}_\mu }(\mathbf {r}^\alpha )$ are indicator functions. The restraining conditions $\mathbb {R}_-$ and $\mathbf {K}_\mu$ represent the negative orthant and the admissible Coulomb cone respectively. The indicator functions become null when the variables $-x_n^\alpha$ and $\mathbf {r}^\alpha$ comply with the restraining conditions; otherwise their value is infinite. Replacing the potentials in inequality (14) by $b_c (-\mathbf {x}^\alpha , \mathbf {r}^\alpha )$ leads to

$$\begin{aligned} b_c (-\mathbf {x}^\alpha , \mathbf {r}^{\alpha *})- b_c (-\mathbf {x}^\alpha , \mathbf {r}^{\alpha }) \ge -\mathbf {x}^\alpha \cdot (\mathbf {r}^{\alpha *}-\mathbf {r}^{\alpha }) \ . \end{aligned}$$

(20)

Inequality (20) can be multiplied by any positive real coefficient $\rho$. Thus, for any $\mathbf {r}^{\alpha *}$, it can be deduced that

$$\begin{aligned}&\rho b_c (-\mathbf {x}^\alpha , \mathbf {r}^{\alpha *}) - \rho b_c (-\mathbf {x}^\alpha , \mathbf {r}^{\alpha }) \nonumber \\&\quad +\,[ {\mathbf {r}^\alpha -(\mathbf {r}^\alpha -\rho \mathbf {x}^\alpha )} ] \cdot (\mathbf {r}^{\alpha *}-\mathbf {r}^{\alpha }) \ge 0 \end{aligned}$$

(21)

which means that $\mathbf {r}^\alpha$ is the proximal point of the augmented stress $\mathbf {r}^{\alpha *}$ :

$$\begin{aligned} \mathbf {r}^{\alpha *}=\mathbf {r}^\alpha -\rho \mathbf {x}^{\alpha *} \quad | \ \mathbf {x}^{\alpha *}=\mathbf {x}^\alpha + \mu \Vert {-\mathbf {x}_t^\alpha } \Vert \mathbf {n} \end{aligned}$$

(22)

where $\mathbf {r}^{\alpha *}$ represents the trial contact forces in the predictor-corrector step, and the corrector step is within the Coulomb cone $\mathbf {K}_\mu$ (see Fig. 3) :

$$\begin{aligned} \mathbf {r}^{\alpha }=\text {Proj}_{\mathbf {K}_\mu } (\mathbf {r}^{\alpha *}) \end{aligned}$$

(23)

where $\mathbf {K}_\mu ^{*}$ is the polar cone of $\mathbf {K}_\mu$. According to the three different contact states in Eq. (11), noting that the projection is normal to the boundary of the Coulomb cone when sliding, the projection procedure becomes:

$$\begin{aligned} \begin{array}{lll} \text {Separating: } \text {Proj}_{\mathbf {K}_\mu }(\mathbf {r}^{\alpha *})=\mathbf {0} \quad \text {if } \Vert \mu \mathbf {r}_t^{\alpha *} \Vert \le -r_n^{\alpha *} \\ \text {Sticking: } \text {Proj}_{\mathbf {K}_\mu }(\mathbf {r}^{\alpha *})=\mathbf {r}^{\alpha *} \quad \text {if } \Vert \mathbf {r}_t^{\alpha *} \Vert \le \mu r_n^{\alpha *} \\ \text { Sliding: } \text {Proj}_{\mathbf {K}_\mu }(\mathbf {r}^{\alpha *})= \mathbf {r}^{\alpha *}-\left( {\frac{{ \Vert \mathbf {r}_t^{\alpha *} \Vert - \mu r_n^{\alpha *} }}{{1 + \mu ^2 }}} \right) \left( {\frac{\mathbf {r}_t^{\alpha *} }{\Vert \mathbf {r}_t^{\alpha *} \Vert } - \mu \mathbf {n}} \right) \ \text {else} \end{array} \end{aligned}$$

(24)

where the explicit correcting procedure needs only one step. This shows the good stability and accuracy during the numerical calculation [18]. Thus, the contact forces can be calculated via a trial-correct step in Eqs. (22–24).

6 The equilibrium equations and Uzawa algorithm

For quasi-static fretting problems, considering the transform of contact forces in Eq. (6), the Newton–Raphson iterative form of the equilibrium equations can be written as

$$\begin{aligned} \mathbf {K}_T \varDelta \mathbf {X}=\mathbf {F}_\text {int} +\mathbf {F}_\text {ext}+\mathbf {H}^\text {T} \mathbf {r} \end{aligned}$$

(25)

where $\mathbf {F}_\text {int}$ stands for the internal forces vector and $\mathbf {F}_\text {ext}$ stands for the external loads vector, both in the global configurations. $\mathbf {K}_\text {T}$ represents the tangent stiffness matrix of the whole system. By combining Eq. (25) with Eq. (6) and by eliminating the global displacement increments vector $\varDelta \mathbf {X}$, the total relative position can be expressed in the local frame as :

$$\begin{aligned} \mathbf {x}=\mathbf {H} \mathbf {K}_T^{-1} (\mathbf {F}_\text {int}+\mathbf {F}_\text {ext})+\mathbf {g}+ \mathbf {H} \mathbf {K}_T^{-1} \mathbf {H}^\text {T} \mathbf {r} \ . \end{aligned}$$

(26)

By setting

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf {W}=\mathbf {H} \mathbf {K}_T^{-1} \mathbf {H}^\text {T} \\ \tilde{\mathbf {x}}=\mathbf {H} \mathbf {K}_T^{-1} (\mathbf {F}_\text {int}+\mathbf {F}_\text {ext})+\mathbf {g} \end{array} \right. \end{aligned}$$

(27)

the local equilibrium equation of contact and wear becomes

$$\begin{aligned} \mathbf {x}=\mathbf {Wr}+\tilde{\mathbf {x}} \ . \end{aligned}$$

(28)

Thus, the local fretting problem can be described by three equations : the Archard wear law (5); the trial-correct contact forces (23); and the local equilibrium equation (28) as follows

$$\begin{aligned} \begin{aligned}&\mathbf {x} =\mathbf {Wr}+\tilde{\mathbf {x}} \\&\mathbf {r}^{\alpha } =\text {Proj}_{\mathbf {K}_\mu ^\alpha } (\mathbf {r}^{\alpha *}) \\&g_w^{\alpha (k + 1)} = g_w^{\alpha (k)} + kP_n^{\alpha (k + 1)} \sqrt{\left( \varDelta x_{t_1 }^{\alpha (k + 1)} \right) ^2 + \left( \varDelta x_{t_2 }^{\alpha (k + 1)} \right) ^2 } \ . \end{aligned} \end{aligned}$$

(29)

For the fretting problem described within the bipotential framework, the Uzawa algorithm is a suitable choice to solve these local implicit equations, since many contact examples showed the accuracy and stability of this algorithm [23]. The Uzawa algorithm used to solve the elastic local wear problems is shown in Algorithm 1, where $\varTheta$ denotes the maximum iteration number; $\mathbf {W}_{\alpha \beta }=\mathbf {H}_\alpha \mathbf {K}_T^{-1} \mathbf {H}_\beta ^T$ represents the influence matrix of the relative position of contact point $\alpha$ due to a contact point $\beta$; $\tilde{\mathbf {x}}^{\alpha (k)}$ denotes the relative local displacement of contact point $\alpha$ at iteration step (k) caused by the initial gap, wear gap, internal and external forces. So $\mathbf {x}^{\alpha \beta (k)}$ could be seen as result of the effects caused by $\tilde{\mathbf {x}}^{\alpha (k)}$ plus the influence of contact forces of the remaining ($N_c - 1$) contact points. The value of positive coefficient $\rho$ will influence the speed of convergence but not the results. The condition of convergence in Eq. (34) is controlled by the total contact forces $\mathbf {r}$. The wear gap of each node $g_\text {w}^\alpha$ is assumed to be additional normal distance as illustrated in Fig. 2. It is considered to be constant in the current load step (k). After convergence of this step, the wear gap is calculated and updated by using Eq. (35).

Fig. 4

Solution strategy of elastic–plastic contact and wear

7 Plasticity

As many researches showed that the plastic deformation will effect wear process [7, 8]. We also use the elastic–plastic materials to compare with the elastic materials For elastic–plastic wear problem, each load step (k) needs Newton-Raphson iterations. Uzawa iterations of the contact solution are performed inside each Newton-Raphson iteration. For one load step (k), the wear gap of each node $g_\text {w}^\alpha$ is assumed to be constant and is actualized after convergence of the Newton-Raphson equilibrium loop. The iteration of elastic–plastic contact and wear is shown in Fig. 4, where $\delta _1$ and $\delta _2$ represent the convergence coefficient of the residual stress vector ${\mathbf {F}}_{r}$ and the total position increment vector $\mathbf {X}$. Both numerical examples are shown in the following section.

8 Numerical examples

The bipotential method has been applied in many academic and industrial examples regarding contact problems.

Fig. 5

Mesh and boundary conditions of the elastic block contact

Table 1 Parameters of elastic block contact

Fig. 6

Wear gap and contact pressure during the first cycle for 4 different loading pressures; S represents Strömberg’s results

Fig. 7

Wear gap and contact pressure during 9000 cycles at the 80th increment; S represents Strömberg’s results

8.1 Example 1: elastic block wear and deformation

The first example is considered to show the performance of the presented method in dealing with the elastic fretting wear problems. An elastic block comes into contact with a rigid plate which is the same as that chosen by Strömberg [12]. 80 increments are applied during one loading cycle. Four-node plane strain elements are used to build the mesh. The size of the elastic block is $50 \times 50$ mm. It is fixed at its top with a negative initial gap u at the bottom, and the right side is subject to an alternating pressure q. The mesh and boundary conditions are shown in Fig. 5 . The bottom of the block will come into contact and have a micro reciprocating motion with the rigid plate. Table 1 summarizes numerical parameters. The evolution of the wear gap and the normal contact pressure during the first cycle are shown in Fig. 6. Through the first cycle, we could see that the distribution of the contact pressure and the wear rate are obviously influenced by the path of displacement. The evolution of the wear gap during 9000 cycles and the normal contact pressure of loading path $q=0 \ \text {MPa}$ (increment = 80) during 3000 cycles are shown in Fig. 7. Over 3000 cycles, the normal contact pressure becomes almost zero due to the fact that the negative initial gap u is almost worn away. As wear goes, the edges of both sides are worn away and the normal contact pressure becomes zero. The normal contact pressure of the contact surface, where the wear gap is the smallest, increases gradually because of stress concentration and then becomes zero because the surface wears away. As the contact surface wears away, the normal contact pressure caused by the preload u decreases gradually. The wear rate is diminished according to the Archard wear law (4) despite of the non-dominating parameter which is the tangential velocity.

It is worthy noting that the evolution of the wear gap and contact pressure in the first cycle and during 9000 loading cycles are in good concordance with that found by Strömberg [12] as shown in Figs. 6 and 7.

Two points (see Fig. 5) are chosen to show the evolution of wear state during different loading pathes in one cycle. The evolution of wear state of point A is shown in Fig. 8.

Fig. 8

Evolution of wear state of Point $\text {A}$: $\text {st}^*$, $\text {sl}^*$ and $\text {se}^*$ represent sticking, sliding and separating states respectively. a Point A, first cycle, b Point A, 5000th cycle, c Point A, 10000th cycle

Fig. 9

Evolution of wear states of Point $\text {B}$: $\text {sl}^*$ and $\text {se}^*$ represent sliding and separating states respectively. a Point B, first cycle, b Point B, 5000th cycle, c Point B, 10000th cycle

Fig. 10

Mesh and boundary conditions of cylinder-flat contact

If we focus on the figure of point A during the first cycle, there are three different states : separating, sliding and sticking. When separating, the normal gap $x_n>0$ and the contact pressures $P_n$ and $P_t$ become zero; when sliding, the normal gap $x_n=0$ and the relative tangential displacement increment $\varDelta x_t\ne 0$, the relationship between contact pressures is $\frac{\left\| P_t \right\| }{P_n} =\frac{\left\| r_t/A \right\| }{r_n/A} =\frac{\left\| r_t \right\| }{r_n}=\mu$; when sticking, the normal gap $x_n=0$ and the relative tangential displacement increment $\varDelta x_t=0$, the relationship between contact pressures is $\frac{\left\| P_t \right\| }{P_n} =\frac{\left\| r_t/A \right\| }{r_n/A} =\frac{\left\| r_t \right\| }{r_n}<\mu$. The last state often takes place when the loading direction q changes. According to the Archard wear law, the wear gap increases only when the sliding state takes place. We note that the contact pressure and relative displacement suddenly change between two different contact states, making it difficult to describe this intermediate period. As wear increases, the contacting and sliding states both become shorter, and the maximum values of normal and tangential pressures decrease. The reason for this is that the surface of the body wears away gradually. Point B wear state evolution is shown in Fig. 9. This point displays no sticking state because it constantly moves. As the description of the right figure in Fig. 7, Point B is in the region where the contact pressure suddenly increases and decreases at the 80th increment of each cycle during the first 3000 cycles. After 3000 cycles, the maximum values of normal and tangential pressures decrease. These results of both points make a good agreement with the complete contact law (11) and the Archard wear law (5).

8.2 Example 2: two-dimensional cylinder-flat contact

In this numerical example, the constitutive models of elastic material and elastic–plastic material are compared. The basic cylinder-flat wear model is chosen in which it exits usually plastic deformation in the contact zone. The geometrical size and local mesh size of contact zone are the same as in McColl [5] which are shown in Fig. 10. The diameter of the cylinder is 12 mm with a preload displacement u and a reciprocating displacement $\delta$ at the top. The bottom of the flat is fixed. The element size in the contact area is about 10 $\mu m$.

Table 2 summarizes numerical parameters defined according to [8]. Only linear isotropic hardening is considered for the elastic–plastic model.

Table 2 Parameters of cylinder-flat contact

Fig. 11

Load history of cylinder-flat contact

The preload displacement u is applied in the first step. Then the reciprocating displacement $\delta$ is applied in the subsequent steps. The load history is shown in Fig. 11. When only the preload displacement $u=0.008$ mm is applied, the total normal forces is about 199.24 N. The maximum contact pressure and the half-width of contact area can be obtained analytically [24]. The comparison of normal contact pressure between Hertzian solution and our solution is shown in Fig. 12. The results demonstrates the accuracy of our method. Additionally, the contact bodies do not enter the yield stage in the preload step, as the maximum value of Von Mises stress is about 272.7 MPa. So the normal contact pressure distribution of elastic and elastic–plastic material are the same in the preload step. For the sake of description, all the following normal contact pressure distribution is in the position of the end of load cycle.

Fig. 12

Comparison of normal contact pressure

Fig. 13

Wear gap and normal contact pressure in the first cycle

Fig. 14

Evolution of wear state of the center point in the first cycle

Fig. 15

Wear gap and normal contact pressure during 100 cycles

Fig. 16

Wear gap and normal contact pressure of hypothetic wear coefficient during 100 cycles

8.2.1 Gross slip condition

For gross slip condition, the reciprocating displacement is $\delta =0.03$ mm. Each cycle is divided into 80 increments. The wear value and normal contact pressure distribution of two materials in the first cycle are shown in Fig. 13. The normal contact pressure distribution of elastic material is almost the same but moves a little to the left. But the maximum value of normal contact pressure of elastic–plastic material decreases to 747.4 MPa. The maximum wear gap of elastic–plastic material is less than that of elastic material, while the wear width reversely. In order to explore the reason of these differences, the center point of the contact region is chosen to show the evolution of wear state in the first cycle. The evolution of wear state of the center point in the first cycle is shown in Fig. 14. The initial relative tangential movement of elastic material is a little ahead of elastic–plastic material. The normal contact pressure is decreased, where major plastic deformation happened, before initial relative tangential movement. In these steps, the plastic deformation could be seen as the resistance of initial relative tangential movement. In the next steps, the relative tangential displacement of both materials are almost the same. But the normal contact pressure of elastic–plastic material is still varied while the normal contact pressure of elastic material changed a little. So the finial wear value of elastic–plastic material is less than the case of elastic material in the first cycle, mainly due to the reduction of normal contact pressure. The evolution of wear gap and normal contact pressure of two materials during 100 cycles are shown in Fig. 15. The comparison of maximum wear gap and wear width of both materials during 100 cycles is similar as that in the first cycle. The normal contact pressure distribution of both materials decrease a little in the end of 100 cycle compared with the first cycle because of the small wear gap in the order of $10^{-5}$ mm. In order to investigate the influence of wear to both materials and speed up the computation, the wear coefficient is assumed to enlarge hundredfold becoming $8.5 \times 10^{-7}\, \text {MPa}^{-1}$. The evolution of wear gap and normal contact pressure of two materials of new hypothetic wear coefficient during 100 cycles are shown in Fig. 16. The results of hypothetic wear coefficient will not be very accurate, but exhibit the tendency of evolution of wear gap and normal contact pressure distribution of more wear cycles. 100 wear cycle of the hypothetic wear coefficient case is corresponding to 10000 cycles of the case of real wear coefficient. We could see that after 10 cycles (corresponding to 1000 cycle of real wear coefficient), the maximum normal contact pressure of both materials decreased obviously. The peak value of normal contact pressure decreases, while the contact width increases, along with the wear cycle increases. Especially, in the end of 100 cycle, the normal contact pressure distribution of both materials become similar. So when the wear gap is minor, the influence of plasticity on contact pressure distribution will not be ignored. And when the wear gap becomes major, the influence of plasticity on contact pressure distribution is not so important than the influence of wear process.

Fig. 17

Wear gap and normal contact pressure in the first cycle

Fig. 18

Wear gap and normal contact pressure during 100 cycles

In the literature [11, 13, 25], numerical investigations indicate that increasing the wear depth increment using a fictitious wear coefficient (i.e. 100 times bigger than the real one) speed up the solution and will lead to insignificant errors. They studied the influence of the wear depth-increment over the CPU time and solution errors in fretting-wear problems under gross slip and partial slip conditions.

Fig. 19

Wear gap and normal contact pressure of hypothetic wear coefficient during 100 cycles

8.2.2 Partial slip condition

For partial slip condition, the reciprocating displacement $\delta =0.01$ mm is applied. Each cycle is divided into 64 increments. The wear value and normal contact pressure distribution of two materials in the first cycle are shown in Fig. 17. The normal contact pressure distribution of elastic material is almost the same as the preload step. For elastic–plastic material, the maximum value of normal contact pressure decreases a little to 788.3 MPa with a minor increase in the edge of contact region. The maximum wear gap of elastic–plastic material is bigger than that of elastic material which is different from gross slip condition. Because in partial slip condition, the wear region moving close to the edge of contact region and the normal contact pressure is bigger in this region. The evolution of wear gap and normal contact pressure of two materials during 100 cycles are shown in Fig. 18. The normal contact pressure distribution of elastic material remains almost the same during 100 cycles. While for elastic–plastic material, the normal contact pressure distribution decreases a little in wear region and increases a little in other contact region. The maximum wear gap of elastic–plastic material becomes smaller gradually compare to elastic material during 100 cycles. The wear coefficient is also assumed to enlarge hundredfold becoming $4.5 \times 10^{-6}\, \text {MPa}^{-1}$ to see the influence of wear to both materials in bigger wear depth. The evolution of wear gap and normal contact pressure of two materials of new hypothetic wear coefficient during 100 cycles in partial slip condition are shown in Fig. 19. With the hypothetic wear coefficient, the normal contact pressure distribution decreases continually of both materials around the maximum wear depth region because of the increase of wear depth. But the normal contact pressure distribution in sticking region increases along with the reduction of contact area. Especially, the peak value of normal contact pressure of elastic material will occur in the position between sticking and sliding regions. The peak value of elastic–plastic material does not exist because of plastic deformation. The maximum wear gap of elastic–plastic material will catch up and exceed elastic material gradually during 100 cycles. So the influence of plasticity in partial slip condition during wear process is the main contribution to smooth normal contact pressure.

9 Conclusions

In the present work, the bipotential method with Uzawa algorithm is extended to deal with elastic and elastic–plastic fretting wear problems. A finite element program in C++ is specially developed to this issue. The numerical application with the example of Strömberg [12] and the comparison with Hertzian solution show the good accuracy and stability of our method. The evolution of contact nodes during one cycle in example 1 is in good agreement with the complete contact law and the Archard wear law. It showed that the contact state depends on the wear procedure; at the same time, the wear rate depends on the contact state. The comparison of the elastic–plastic material with the elastic material showed the coupled influence of plasticity and wear gap on the normal contact pressure distribution under an assumption of constant friction coefficient. However in many actual engineering applications, the friction coefficient may depend on contact pressure, etc. This issue will be addressed in future works.