1 Introduction

Computational cardiovascular fluid mechanics and fluid–structure interaction (FSI) have seen major advances in the last 15 years. Some of the earliest patient-specific arterial FSI computations [1–4] were with a space–time (ST) FSI method, specifically the Deforming-Spatial-Domain/Stabilized ST (DSD/SST) method [5, 6].

The majority of the cardiovascular fluid mechanics and FSI computations in the last 15 years have been with non-ST methods, with the Arbitrary Lagrangian–Eulerian (ALE) method [7] having the largest share in the computations reported (see, for example, [8–29]). A large number of computations with the ST methods were also reported in the last 15 years, including computations in the first 10 years for FSI of abdominal aorta [30], FSI of carotid artery [30], and FSI of cerebral aneurysms [31–37]. The work with ST methods reported in the last 5 years focused on even more challenging aspects of cardiovascular fluid mechanics and FSI, including comparative studies of cerebral aneurysms [38], stent treatment of cerebral aneurysms [39–42], heart valve flow computation [43–45], FSI analysis of thoracic aorta [46], and coronary arterial dynamics [47]. Advances in core methods for moving boundaries and interfaces (MBI) and FSI (see, for example, [20, 21, 48–52] and references therein) and development of special methods targeting cardiovascular MBI and FSI (see, for example, [20, 37, 41, 42, 53] and references therein) helped address a large number of computational challenges. In this article, we focus on a challenge related to how we use the image-based arterial geometry in patient-specific arterial FSI computations.

In patient-specific arterial FSI computations the image-based arterial geometry does not come from a zero-stress state (ZSS). Special methods targeting cardiovascular MBI and FSI include those designed to take that into account. The attempt to find a ZSS for the artery was first made in a 2007 conference paper [54], where the concept of estimated zero-pressure (EZP) arterial geometry was introduced. The method introduced in [54] for calculating an EZP geometry was also included in a 2008 journal paper on ST arterial FSI methods [31] as “a rudimentary technique” for addressing the issue. It was pointed out in [31, 54] that quite often, the image-based geometries were used as arterial geometries corresponding to zero blood pressure, and that it would be more realistic to use the image-based geometry as the arterial geometry corresponding to the time-averaged value of the blood pressure. Given that arterial geometry at the time-averaged pressure value, an estimated arterial geometry corresponding to zero blood pressure needed to be constructed. Special methods developed to address the issue include the newer EZP versions [20, 33, 36, 37, 53] and the prestress technique introduced in [16], which was further refined in [18] and presented also in [20, 53].

A method for estimation of the element-based ZSS (EBZSS) was introduced in [55] in the context of finite element discretization of the arterial wall. The method has three main components. 1. An iterative method, which starts with a calculated initial guess, is used for computing the EBZSS such that when a given pressure load is applied, the image-based target shape is matched. 2. A method for straight-tube segments is used for computing the EBZSS so that we match the given diameter and longitudinal stretch in the target configuration and the “opening angle.” 3. An element-based mapping between the artery and straight-tube is extracted from the mapping between the artery and straight-tube segments. This provides the mapping from the arterial configuration to the straight-tube configuration, and from the estimated EBZSS of the straight-tube configuration back to the arterial configuration, to be used as the initial guess for the iterative method that matches the image-based target shape. The method was used successfully in [55] in test computations based on straight-tube configurations with single and three layers, and a curved-tube configuration with single layer. The method was used successfully also in [47] in coronary arterial dynamics computations with medical-image-based time-dependent anatomical models.

In a recent article [56], we have introduced the version of the EBZSS estimation method with isogeometric wall discretization. With isogeometric discretization, we can obtain the element-based mapping directly, instead of extracting it from the mapping between the artery and straight-tube segments. That is because all we need for the element-based mapping, including the curvatures, can be obtained within an element. With NURBS basis functions, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and much fewer elements. Higher-order NURBS basis functions allow representation of more complex shapes within an element. The 2D test computations with straight-tube configurations presented in [56] were intended to explain how the new EBZSS estimation method works and to demonstrate how it performs. In this expanded, journal version of that article, we also show how the method can be used in a 3D computation where the target geometry is coming from medical image of a human aorta.

In Sect. 2, we describe, in the context of isogeometric discretization, the Element-Based Total Lagrangian (EBTL) method, including the EBZSS concept. Section 3, extracted from [55], is an overview of the analytical relationship between the ZS and reference states of straight-tube segments, and here we call that relationship “straight-tube ZSS template”. The 2D test computations are presented in Sect. 4, and the 3D computation in Sect. 5. The concluding remarks are given in Sect. 6.

2 Element-Based Total Lagrangian (EBTL) method

In this section we provide an overview of the EBTL method [55], including the EBZSS concept, and describe the version of the method with NURBS wall discretization.

Let \(\varOmega _0\in \mathbb {R}^3\) be the material domain of a structure in the ZSS, and let \(\varGamma _0\) be its boundary. Let \(\varOmega _t\in \mathbb {R}^3\), \(t \in (0,T)\), be the material domain of the structure in the deformed state, and let \(\varGamma _{t}\) be its boundary. The structural mechanics equations based on the total Lagrangian formulation can be written as

$$\begin{aligned}&\int _{\varOmega _0} \mathbf {w}\cdot \rho _0\frac{\mathrm{d}^2 \mathbf {y}}{\mathrm{d}t^2}~\mathrm{d}\varOmega + \int _{\varOmega _0} \delta \mathbf {E}: \mathbf {S}~\mathrm{d}\varOmega - \int _{\varOmega _0} \mathbf {w}\cdot \rho _0\mathbf {f}~\mathrm{d}\varOmega \nonumber \\&\quad = \int _{\left( \varGamma _t\right) _{\mathrm{h}}} \mathbf {w}\cdot \mathbf{h}~\mathrm{d}\varGamma . \end{aligned}$$
(1)

Here, \(\mathbf {y}\) is the displacement, \(\mathbf {w}\) is the virtual displacement, \(\delta \mathbf {E}\) is the variation of the Green–Lagrange strain tensor, \(\mathbf {S}\) is the second Piola–Kirchhoff stress tensor, \(\rho _0\) is the mass density in the ZSS, \(\mathbf {f}\) is the body force per unit mass, and \(\mathbf{h}\) is the external traction vector applied on the subset \(\left( \varGamma _t\right) _{\mathrm{h}}\) of the total boundary \(\varGamma _{t}\).

2.1 EBZSS

In the EBTL method the ZSS is defined with a set of positions \(\mathbf {X}_0^e\) for each element e. Positions of nodes from different elements mapping to the same node in the mesh do not have to be the same. In the reference state, \(\mathbf {X}_{{\mathrm {REF}}}\), all elements are connected by nodes, and we measure the displacement \(\mathbf {y}\) from that connected state. The implementation of the method is simple. The deformation gradient tensor \(\mathbf {F}\) is evaluated for each element:

$$\begin{aligned} \mathbf {F}^e&\equiv \frac{\partial \mathbf {x}}{\partial \mathbf {X}_0^e}, \end{aligned}$$
(2)
$$\begin{aligned}&= \frac{\partial \left( \mathbf {X}_{{\mathrm {REF}}}+ \mathbf {y}\right) }{\partial \mathbf {X}_0^e}. \end{aligned}$$
(3)

The deformation gradient tensors for different elements are on different states, but the terms in Eq. (1), including the second term, do not depend on the orientation. Therefore the rest of the process is the same as it is in the total Lagrangian formulation.

2.2 NURBS basis functions

In representation of the EBZSS with NURBS basis functions, we may be able to use larger and fewer elements compared to linear basis functions. Higher-order NURBS basis functions allow representation of more complex shapes within an element. Curvature representation requires at least quadratic NURBS, and to have a continuous curvature, cubic or higher-order NURBS is required.

In the case of 1D parametric space, a curve segment can be represented by NURBS as

$$\begin{aligned} \mathbf {z}(\xi )&= \sum _{a=1}^{n_{\mathrm{en}}}R_a(\xi ) \mathbf {z}_a, \end{aligned}$$
(4)

where \(n_{\mathrm{en}}\) is the number of control points in the element, \(\mathbf {z}_a\) is the position of the control point (node) a,

$$\begin{aligned} R_a(\xi ) = \frac{N_a(\xi ) w_a}{\displaystyle \sum \nolimits _{b=1}^{n_{\mathrm{en}}}N_b(\xi )w_b}, \end{aligned}$$
(5)

\(N_a(\xi )\) is the B-spline basis function for point a, and \(w_a\) is the NURBS weight for point a. An equivalent form can be obtained by using the homogeneous coordinates [57], where \(\mathbf {z}_a\) is augmented as

$$\begin{aligned} \mathbf {z}_a^\mathrm {w}&= \left[ \begin{array}{ll} w_a \mathbf {z}_a \\ w_a \\ \end{array}\right] . \end{aligned}$$
(6)

With that, we represent the curve segment as

$$\begin{aligned} \mathbf {z}^\mathrm {w}(\xi )&= \sum _{a=1}^{n_{\mathrm{en}}}N_a(\xi ) \mathbf {z}_a^\mathrm {w}, \end{aligned}$$
(7)

and

$$\begin{aligned} \mathbf {z}(\xi )&= \begin{bmatrix} 1&\quad 0&\quad 0&\quad 0 \\ 0&\quad 1&\quad 0&\quad 0 \\ 0&\quad 0&\quad 1&\quad 0 \\ \end{bmatrix} \frac{\mathbf {z}^\mathrm {w}(\xi )}{\displaystyle \sum \nolimits _{a=1}^{n_{\mathrm{en}}}N_a(\xi ) w_a}. \end{aligned}$$
(8)

The forms given by Eqs. (4) and (8) are equivalent.

As proposed in [57], we represent the B-spline basis functions with the Bernstein basis functions \(B_b(\xi )\):

$$\begin{aligned} N_a (\xi )&= \sum _{b=1}^{n_{\mathrm{en}}} C_{ab} B_b (\xi ), \end{aligned}$$
(9)

where \(C_{ab}\) denotes the components of the Bézier extraction operator. See [57] for how to obtain the operator from the B-spline knots. With that,

$$\begin{aligned} \mathbf {z}^\mathrm {w}(\xi )&= \sum _{a=1}^{n_{\mathrm{en}}} \sum _{b=1}^{n_{\mathrm{en}}} C_{ab} B_b(\xi ) \mathbf {z}_a^\mathrm {w}. \end{aligned}$$
(10)

From that, we can first operate with \(C_{ab}\), and obtain the Bézier control positions as

$$\begin{aligned} \hat{\mathbf {z}}_b&= \sum _{a=1}^{n_{\mathrm{en}}} \mathbf {z}_a^\mathrm {w} C_{ab}. \end{aligned}$$
(11)

The extension to multi-dimensional parametric spaces is straightforward.

Given the control position \(\mathbf {z}_a\) for a point a, the corresponding homogeneous coordinates \(\mathbf {z}^\mathrm {w}_a\), its Bézier representation \(\hat{\mathbf {z}}_a\), and the Bézier extraction operator components \(C_{ab}\), we move to an array notation where

$$\begin{aligned}&\mathbf {Z} = \left[ \mathbf {z}_a\right] , \end{aligned}$$
(12)
$$\begin{aligned}&\mathbf {Z}^\mathrm {w} = \left[ \mathbf {z}_a^\mathrm {w}\right] , \end{aligned}$$
(13)
$$\begin{aligned}&\hat{\mathbf {Z}} = \left[ \hat{\mathbf {z}}_a\right] , \end{aligned}$$
(14)
$$\begin{aligned}&\mathbf {C} = \left[ C_{ab}\right] . \end{aligned}$$
(15)

Then, Eq. (11) can be written as

$$\begin{aligned} \hat{\mathbf {Z}} = \mathbf {Z}^\mathrm {w} \mathbf {C}. \end{aligned}$$
(16)

With that, the transformation from the Bézier representation to NURBS representation becomes

$$\begin{aligned} \mathbf {Z}^\mathrm {w}&= \hat{\mathbf {Z}} \mathbf {C}^{-1}. \end{aligned}$$
(17)

2.3 EBZSS representation with NURBS basis functions

When we are designing a ZSS, we have the corresponding reference state \(\mathbf {X}_{{\mathrm {REF}}}\). Therefore we have \(\left( \mathbf {X}_{{\mathrm {REF}}}\right) _a\), \(w_a\), and the Bézier extraction operator corresponding to the element. We obtain the homogeneous coordinates \(\left( \mathbf {X}_{{\mathrm {REF}}}\right) _a^\mathrm {w}\) and then convert that to \(\left( \hat{\mathbf {X}_{{\mathrm {REF}}}}\right) _a\). From that and the Bernstein basis functions, we can design the EBZSS as \(\left( \hat{\mathbf {X}_0^e}\right) _a\). For implementation convenience, we convert the control points to \(\left( \mathbf {X}_0^e\right) _a^\mathrm {w}\) by using Eq. (17).

Remark 1

Although in the ZSS we could have element-based \(w_a\) values, that would in general require using different basis functions between the ZS and reference states. Here we do not consider that option.

2.4 An iterative method

With the EBZSS, under a given load we would like to reach a configuration that matches the target shape, and we take \(\mathbf {X}_{{\mathrm {REF}}}\) as the target state. Here we assume that we have a reasonably good initial guess for the EBZSS, and explain the iterative method used in calculating the EBZSS that results in the target state associated with the given load. In doing that, we use many pieces of the method described in [55] for linear elements.

In our iterative method, we estimate \(\mathbf {F}\) from the \(i\mathrm{th}\) solution. We use the notation

$$\begin{aligned} \mathbf {F}\left( \mathbf {x}, \mathbf {X}\right)&= \mathbf {R\left( \mathbf {x}, \mathbf {X}\right) }\mathbf {U}\left( \mathbf {x}, \mathbf {X}\right) , \end{aligned}$$
(18)

which is the polar decomposition of \(\mathbf {F}\) into rotation \(\mathbf {R}\) and right stretch tensor \(\mathbf {U}\). The arguments in the tensors represent the numerator and denominator in the partial derivatives. With that, \(\mathbf {F}\) at \((i+1)\mathrm{th}\) iteration is expressed as

$$\begin{aligned} \mathbf {F}^{i+1}&= \mathbf {R}\left( \mathbf {X}_{{\mathrm {REF}}}, \mathbf {x}^i\right) \mathbf {F}^{i} \mathbf {R}\left( (\mathbf {X}_0^e)^i, (\mathbf {X}_0^e)^{i+1}\right) . \end{aligned}$$
(19)

With the approximation

$$\begin{aligned} \mathbf {R}\left( (\mathbf {X}_0^e)^i, (\mathbf {X}_0^e)^{i+1}\right) = \mathbf {I}, \end{aligned}$$
(20)

we obtain

$$\begin{aligned} \mathbf {F}^{i+1}&= \mathbf {R}\left( \mathbf {X}_{{\mathrm {REF}}}, \mathbf {x}^i\right) \mathbf {F}^{i}, \end{aligned}$$
(21)

and from that we obtain

$$\begin{aligned} \left( \mathbf {F}^{i+1} \right) ^{-1}&= \left( \mathbf {F}^{i} \right) ^{-1} \mathbf {R}(\mathbf {x}^i, \mathbf {X}_{{\mathrm {REF}}}), \end{aligned}$$
(22)
$$\begin{aligned}&= \left( \mathbf {U}^{i} \right) ^{-1} \mathbf {R}((\mathbf {X}_0^e)^i, \mathbf {X}_{{\mathrm {REF}}}) . \end{aligned}$$
(23)
Fig. 1
figure 1

The representative parametric position \(\pmb {\xi }_a\) assigned to the Bézier control point a, and the straight path from \(\mathbf {0}\) to \(\pmb {\xi }_a\). When performing the integration with the midpoint rule, the evaluation point is \(\pmb {\xi }_a/2\)

Full size image

In this article, in calculating \((\mathbf {X}_0^e)^{i+1}\), instead of doing the tensor evaluations at \(\pmb {\xi }\) = \(\mathbf {0}\), we do integrations from \(\pmb {\xi }\) = \(\mathbf {0}\) to the corresponding positions:

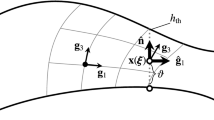
$$\begin{aligned}&\left. (\mathbf {X}_0^e)^{i+1}\right| _{\pmb {\xi }=\pmb {\xi }_a} - \left. {(\mathbf {X}_0^e)^{i+1}}\right| _{\pmb {\xi }=\mathbf {0}} =\int _ {\left. {\mathbf {X}_{{\mathrm {REF}}}^e}\right| _{\pmb {\xi }=\mathbf {0}}} ^{\left. {\mathbf {X}_{{\mathrm {REF}}}^e}\right| _{\pmb {\xi }=\pmb {\xi }_a}} \left( \mathbf {F}^{i+1}\right) ^{-1} \mathrm{d}\mathbf {X}_\mathrm {REF}. \end{aligned}$$
(24)

Here \(\pmb {\xi }_a\) is the representative parametric position assigned to the Bézier control point for a (see Fig. 1), and we use a straight path from \(\mathbf {0}\) to \(\pmb {\xi }_a\). The representative parametric positions are equally spaced. The first approximation here is performing the integration with the midpoint rule:

$$\begin{aligned}&\left. (\mathbf {X}_0^e)^{i+1}\right| _{\pmb {\xi }=\pmb {\xi }_a} - \left. {(\mathbf {X}_0^e)^{i+1}}\right| _{\pmb {\xi }=\mathbf {0}}\nonumber \\&\quad \approx \left. \left( \mathbf {F}^{i+1} \right) ^{-1} \right| _{\pmb {\xi }=\pmb {\xi }_a/2} \left( \left. \mathbf {X}_\mathrm {REF}^e\right| _{\pmb {\xi }=\pmb {\xi }_a} - \left. {\mathbf {X}_{{\mathrm {REF}}}^e} \right| _{\pmb {\xi }=\mathbf {0}} \right) . \end{aligned}$$
(25)

The second approximation is to assume that the relationship given by Eq. (25) between \(\left. (\mathbf {X}_0^e)^{i+1}\right| _{\pmb {\xi }=\pmb {\xi }_a}\) and \(\left. \mathbf {X}_\mathrm {REF}^e\right| _{\pmb {\xi }=\pmb {\xi }_a}\) can also be used between the control points \((\hat{\mathbf {X}_0^e)}^{i+1}_a\) and \((\hat{\mathbf {X}_\mathrm {REF}^e})_a\):

$$\begin{aligned}&(\hat{\mathbf {X}_0^e)}^{i+1}_a - \left. (\mathbf {X}_0^e)^{i+1}\right| _{\pmb {\xi }=\mathbf {0}}\nonumber \\&\quad \approx \left. \left( \mathbf {F}^{i+1} \right) ^{-1} \right| _{\pmb {\xi }=\pmb {\xi }_a/2} \left( (\hat{\mathbf {X}_\mathrm {REF}^e})_a - \left. {\mathbf {X}_{{\mathrm {REF}}}^e} \right| _{\pmb {\xi }=\mathbf {0}} \right) . \end{aligned}$$
(26)

This is the new version of the “direct-update (DU)” process (see [55] for the original DU process). The “recursive-update (RU)” process is given as

$$\begin{aligned}&(\hat{\mathbf {X}_0^e)}^{i+1}_a - \left. (\mathbf {X}_0^e)^{i+1}\right| _{\pmb {\xi }=\mathbf {0}}\nonumber \\&\quad \approx \left. \left( \mathbf {F}^{i+1} \right) ^{-1} \right| _{\pmb {\xi }=\pmb {\xi }_a/2} \left. \mathbf {F} \left( \mathbf {X}_{{\mathrm {REF}}}, (\mathbf {X}^e_0)^{i} \right) \right| _{\pmb {\xi }=\pmb {\xi }_a/2}\nonumber \\&\qquad ~\left( \hat{(\mathbf {X}_0^e)^i}_a - \left. {{(\mathbf {X}_0^e)^i}} \right| _{\pmb {\xi }=\mathbf {0}} \right) \end{aligned}$$
(27)
$$\begin{aligned}&\quad = \left. \left( \mathbf {U}^{i}\right) ^{-1} \right| _{\pmb {\xi }=\pmb {\xi }_a/2} \left. \mathbf {U} \left( \mathbf {X}_{{\mathrm {REF}}}, (\mathbf {X}^e_0)^{i} \right) \right| _{\pmb {\xi }=\pmb {\xi }_a/2}\nonumber \\&\qquad ~ \left( \hat{(\mathbf {X}_0^e)^i}_a - \left. {{(\mathbf {X}_0^e)^i}} \right| _{\pmb {\xi }=\mathbf {0}} \right) . \end{aligned}$$
(28)

We note that the tensor–vector operations in Eqs. (26), (27) and (28) actually involve the augmented versions of the tensors, where the augmented version of a tensor \(\mathbf {F}\) is defined as

$$\begin{aligned} \begin{bmatrix} \mathbf {F}&\quad \mathbf{0}\\ \mathbf{0}^T&\quad 1 \\ \end{bmatrix}, \end{aligned}$$
(29)

and the augmented versions of the vectors \(\left. (\mathbf {X}_0^e)^{i+1}\right| _{\pmb {\xi }=\mathbf {0}}\), \(\left. {\mathbf {X}_{{\mathrm {REF}}}^e} \right| _{\pmb {\xi }=\mathbf {0}}\) and \(\left. {{(\mathbf {X}_0^e)^i}} \right| _{\pmb {\xi }=\mathbf {0}}\), as defined by Eq. (7).

In the actual computations, we start from the “ZSS template”: \((\mathbf {X}^e_0)^{0} = (\mathbf {X}^e_0)_\mathrm {TEMP}\) (see Sect. 3). In the steady-state structural mechanics computations, it is reasonable to start from displacement \(\mathbf {y}\) = \(\mathbf{0}\). However, it is unlikely for that to be a good match for the ZSS. To improve the convergence of the structural mechanics solution for i = 0, we use an incremental loading and modify the initial guess for the EBZSS based on that ramping:

$$\begin{aligned} \left( (\mathbf {X}^e_0)^{0}\right) ^{j} = (1-t^j) \mathbf {X}_{{\mathrm {REF}}}+ t^j (\mathbf {X}^e_0)_\mathrm {TEMP}. \end{aligned}$$
(30)

Here \(0 < t^1 \le t^2 \le \ldots \le t^N = 1\), N is the number of nonlinear-iteration steps used in computing \(\mathbf {y}^0\), and the iterations start with \((\mathbf {y}^0)^0\) = \(\mathbf{0}\). We also ramp the load:

$$\begin{aligned} (\mathbf{h}^h)^j = t^j\mathbf{h}^h, \end{aligned}$$
(31)

where \(\mathbf{h}^h\) is the target load. The ramping options include having a ramping profile where the \(t^j\) values change at every certain number of nonlinear-iteration steps. With that, we obtain the steady-state solution \(\mathbf {y}^0\) for \((\mathbf {X}^e_0)^{0} = (\mathbf {X}^e_0)_\mathrm {TEMP}\) based on the full load. For i = 1 and beyond, \((\mathbf {X}^e_0)^i\) is calculated from Eq. (28), and the nonlinear iterations used in computing \(\mathbf {y}^i\) start with \((\mathbf {y}^i)^0\) = \(\mathbf{0}\).

3 Modeling the artery ZSS: straight-tube ZSS template

An analytical relationship between the ZS and reference states of straight-tube segments was given in [55]. Here we will call that relationship “straight-tube ZSS template.” We describe the straight tube in the target state, which is here the reference state, with three lengths: \(\overline{\ell }\), h and L. They are the circumferential length of the arterial-wall midsurface, wall thickness, and the longitudinal length. The tube volume is

$$\begin{aligned} V&= \overline{\ell } h L. \end{aligned}$$
(32)

For an artery, beyond having a target shape under a given load, there are some significant properties. One of them is the opening angle, \(\phi \), seen after a longitudinal cut, which we call the “LC state”. Figure 2 summarizes the template.

Fig. 2
figure 2

Straight tube in the target (left) and ZS (right) states. The dashed lines denote the arterial-wall midsurface in each state

Full size image

Remark 2

We note that in general it is not necessary for the LC state to be a ZSS.

4 2D test computations

We define a parameter \(\alpha \):

$$\begin{aligned} \overline{\ell _0} = \alpha \ell _\mathrm {I}, \end{aligned}$$
(33)

where \(\ell _\mathrm {I}\) is the circumferential length of the inner tube surface in the target state. The task of calculating \(\overline{\ell _0}\) becomes the task of calculating \(\alpha \).

4.1 Meshes

In the test computations here, we use quadratic and cubic NURBS basis functions. Although NURBS can represent a circular arc exactly, it cannot do that throughout a full circle while retaining the \(C^1\) continuity of the basis functions. Therefore, here we simplify the basis functions to uniform B-splines. Figures 3 and 4 show the meshes used. We evaluate how well the meshes represent the circular arcs. For that, we inspect the radius of curvature, \(\rho \). Figures 5 and 6 show \(\rho /\overline{\rho }\) as a function of the circumferential parametric coordinate, \(\xi \), where \(\overline{\rho }\) is the average radius.

Fig. 3
figure 3

Quadratic B-spline meshes with 4, 8, 16, 32, 64, and 128 elements. The red circles are the control points and the gray part is the actual tube. (Color figure online)

Full size image
Fig. 4
figure 4

Cubic B-spline meshes with 4, 8, 16, 32, 64, and 128 elements. The red circles are the control points and the gray part is the actual tube. (Color figure online)

Full size image
Fig. 5
figure 5

Representation of the radius of curvature within an element with quadratic B-splines. The curves are for the six meshes, \(\xi \) is the circumferential parametric coordinate, and \(\overline{\rho }\) is the average radius

Full size image
Fig. 6
figure 6

Representation of the radius of curvature within an element with cubic B-splines. The curves are for the six meshes, \(\xi \) is the circumferential parametric coordinate, and \(\overline{\rho }\) is the average radius

Full size image

Remark 3

The highest shape function value is at \(\xi =0\) for the quadratic B-splines, and at \(\xi =-1\) and \(\xi =1\) for the cubic B-splines. From that, and from Figs. 5 and 6, we conclude that the radius of curvature will be lowest at points closest to the control points, and highest between those points.

Figure 7 shows the standard deviation of \(\rho /\overline{\rho }\), as a function of the arc angle \(\varDelta \theta \) represented by an element, where \(\varDelta \theta \) = \(2 \pi /n_{\mathrm{el}}\), and \(n_{\mathrm{el}}\) is the number of elements. We note that both quadratic and cubic B-splines have second-order accuracy.

Fig. 7
figure 7

Standard deviation of \(\rho /\overline{\rho }\) as a function of the arc angle \(\Delta \theta \) represented by a B-spline element, where \(\overline{\rho }\) is the average radius

Full size image

4.2 Curvature matching in the ZSS

Curvature matching in the ZSS is done by first converting the B-spline element in the target state to Bézier representation. After that, for the specified \(\phi \), we generate element configurations with the objective of having a constant radius of curvature in the ZSS. Then we convert that back to B-spline representation. Figures 8 and 9 show examples of the process for \(\phi = 5\pi /2\), which results in Bézier elements with \(\varDelta \theta = (2\pi -\phi )/n_{\mathrm{el}}= - \pi /(2n_{\mathrm{el}})\), and for a given value of \(\alpha \). The negative value implies that the outer surface is smaller than the inner surface.

Fig. 8
figure 8

Curvature matching in the ZSS. Quadratic basis functions with eight elements. The B-spline mesh in the target state (top left) is converted to Bézier representation (top right). From that, for the specified \(\phi \) and for a given value of \(\alpha \), we generate element configurations with the objective of having constant radius of curvature in the ZSS (bottom right). Then we convert that back to B-spline representation (bottom left)

Full size image
Fig. 9
figure 9

Curvature matching in the ZSS. Cubic basis functions with eight elements. The B-spline mesh in the target state (top left) is converted to Bézier representation (top right). From that, for the specified \(\phi \) and for a given value of \(\alpha \), we generate element configurations with the objective of having constant radius of curvature in the ZSS (bottom right). Then we convert that back to B-spline representation (bottom left)

Full size image

In the case of quadratic Bézier functions, we choose the middle control point to be on the tangents to the inner surface at the two other control points. This determines the curvature in the ZSS. For cubic Bézier functions, we have an additional degree of freedom, and we use that by choosing the control points to be also at equally-spaced angular positions. Figure 10 shows quadratic convergence of the standard deviation of \(\rho _0/\overline{\rho _0}\) for the Bézier elements, where \(\overline{\rho _0}\) is the average radius. We note from Figs. 7 and 10 that Bézier elements yield the same representation quality as the B-spline elements for quadratic functions, and slightly better quality for cubic functions.

Fig. 10
figure 10

Curvature matching in the ZSS. Standard deviation of \(\rho _0/\overline{\rho _0}\) as a function of the arc angle \(\varDelta \theta \) represented by a Bézier element, where \(\overline{\rho _0}\) is the average radius

Full size image

4.3 Computational results

For a range of \(\alpha \) values, we go through the process described in Sect. 4.2 and, using the B-spline elements with curvature matching in the ZSS, we do structural mechanics computations. We obtain the steady-state solutions corresponding to a constant pressure value of \(p_0 = 92~\mathrm {mm~Hg}\). In these computations, the arterial wall is made of hyperelastic (Fung) material. The material constants \(D_1\) and \(D_2\) are \(2.6447 \times 10^3~\mathrm {N/m^2}\) and 8.365, and the penalty Poisson’s ratio is 0.45. We note that, because of the process in Sect. 4.2, the inner-surface shapes obtained from the computations will be at the best as good as those in the upper-left picture in Figs. 8 and 9, for whatever the number of elements are.

The structural mechanics computations generate a relationship between the curvature in the deformed state and \(\alpha \), and from that we select the \(\alpha \) value that matches the curvature in the target state. Figures 11 and 12 show the average curvature of the inner surface in the deformed state as a function of \(\alpha \) for the six meshes with quadratic and cubic B-splines. For quadratic functions, with the mesh made of four elements, the \(\alpha \) value that matches the target curvature is very different than the value obtained with the other meshes. For cubic functions, except for the mesh made of four elements, curves for all the meshes coincide. Figure 13 shows, for all the meshes, the \(\alpha \) value that matches the target curvature.

Fig. 11
figure 11

Average curvature in the deformed state as a function of \(\alpha \) for the six meshes with quadratic B-splines, where \(\overline{\kappa }\) is the curvature in the target state

Full size image
Fig. 12
figure 12

Average curvature in the deformed state as a function of \(\alpha \) for the six meshes with cubic B-splines, where \(\overline{\kappa }\) is the curvature in the target state

Full size image
Fig. 13
figure 13

For all the meshes, the \(\alpha \) value that matches the target curvature

Full size image

With all the meshes and the \(\alpha \) values displayed in Fig. 13, we compute the steady-state structural mechanics solutions to examine the stretches. We evaluate the stretches at the \(4{\times }4\) Gaussian quadrature points (see Fig. 14).

Fig. 14
figure 14

Schematic display of the integration points

Full size image

Remark 4

In the structural mechanics computations with quadratic functions, we use \(3{\times }3\) quadrature points.

Remark 5

The integration points are defined over the ZSS.

Fig. 15
figure 15

Radial stretches for the meshes with eight elements and quadratic (top) and cubic (bottom) B-splines

Full size image

Because of the circular symmetry, the stretches should depend only on the radial position. Here we check that by examining their values along different radial lines in the element, which are called “inner” and “outer” in Fig. 14. Figure 15 shows, for the meshes with eight elements, the radial stretches. For the meshes with 16 or more elements, the radial stretches along the inner and outer lines are basically indistinguishable.

Remark 6

The precise definitions of the radial and circumferential directions for the stretch components are based on the parametric coordinates.

Figure 16 shows, for the meshes with 16 elements, the circumferential stretches. For the meshes with 32 or more elements, the circumferential stretches along the inner and outer lines are basically indistinguishable.

Fig. 16
figure 16

Circumferential stretches for the meshes with 16 elements and quadratic (top) and cubic (bottom) B-splines

Full size image

Table 1 shows, for the mesh with 128 elements and cubic B-splines, the stretch values at the integration points. We assume the values in Table 1 to be the actual values and calculate based on that the relative error for the other meshes. Figure 17 shows the relative error in the radial and circumferential stretches at all eight integration points for all those other meshes.

Fig. 17
figure 17

Relative error in the radial and circumferential stretches at all eight integration points for the meshes with quadratic (top) and cubic (bottom) B-splines. The colors represent different meshes, with the same color convention used in Fig. 11. The relative error is calculated based on the value obtained from the mesh with 128 elements and cubic B-splines. (Color figure online)

Full size image

5 3D computation

Here we show how the method we have presented can be used in a 3D computation where the target geometry is coming from medical image of a human aorta. The first step is to generate a mesh for the target geometry, and we do the volume mesh generation in a special fashion, taking into account the radial stretch. As seen in Fig. 15, in the 2D computations \(\lambda _r\) was linear in \(\eta \), the parametric coordinate in the radial direction in the ZSS. In that computational setting, in the ZSS, the parametric and physical coordinates in the radial direction also had a linear relationship. Consequently, in the ZSS, \(\lambda _r\) was linear in the physical coordinate in the radial direction. Based on these considerations, we do the volume mesh generation for the target geometry with the objective of having in the ZSS a linear relationship between the parametric and physical coordinates in the radial direction. In this example, we use cubic B-splines.

5.1 Surface and volume mesh generation for the target geometry

The surface geometry can be obtained from the medical images using techniques such as those described in [37]. Then, we generate a surface mesh as shown in Fig. 18.

Table 1 Stretch values at the integration points for the mesh with 128 elements and cubic B-splines
Full size table
Fig. 18
figure 18

Surface geometry

Full size image
Fig. 19
figure 19

Volume geometry

Full size image

Next we generate the volume mesh. We have only one element in the radial direction, with four control points radially. The control points of the inner surface of the artery are the control points of the surface mesh in Fig. 18. To locate the control points of the outer surface, for each control point of the inner surface, we take a distance equal to the wall thickness in the direction normal to the surface at the collocation point corresponding to that control point. Figure 19 shows the volume geometry. In this example, the inner diameter at the inlet is 27.3 mm, and use a constant wall thickness of 2.5 mm. The two interior control points do not effect the arterial volume geometry. However, as mentioned above, we determine their locations in a special fashion, based on considerations related to the radial stretch. We will explain that in the next subsection.

5.2 Mesh generation for \((\mathbf {X}^e_0)^{0}\)

To obtain \((\mathbf {X}^e_0)^{0}\), we use the straight-tube ZSS template with the data obtained in Sect. 4. We first calculate the principal curvature directions for the elements of the inner surface. Figure 20 shows the directions of maximum principal curvature. As expected, in most places, the direction of maximum principal curvature coincides with the circumferential direction. Figure 21 shows the distribution of the maximum principal curvature.

Fig. 20
figure 20

Directions of maximum principal curvature

Full size image
Fig. 21
figure 21

Distribution of the maximum principal curvature

Full size image
Fig. 22
figure 22

Physical and ideal elements. The grey colored shape represents the physical element, and the lines and points represent the corresponding ideal Bézier control element. Target state (left) and ZSS (right)

Full size image

Using those two directions and their cross product, we create an “ideal element” as shown in Fig. 22. We see the direction of maximum principal curvature as the circumferential direction \(\theta \), the other principal direction as the longitudinal direction z, and the cross-product direction as the radial direction r. The ideal element is defined with its inner surface having those principal curvatures in the \(\theta \) and z directions, and expanding in all three directions to cover the physical element. To define the EBZSS for the ideal element, we use the straight-tube ZSS template with the data obtained in Sect. 4. The curvature in the circumferential direction comes from \(\phi = 5 \pi /2\) and \(\alpha = 0.870\), and for the z direction we assume \(\lambda _z = 1.0\) (no stretch) in this example. What we do in the radial direction is based on having the \(\lambda _r\) distribution from Fig. 15. To that end, as mentioned in the earlier parts of this section, we prefer to have a linear relationship between the parametric and physical coordinates in the radial direction in the ZSS. For that reason, the control points are equally spaced in the radial direction in the ZSS, but not in the target state.

With the ideal elements from the target state and ZSS, by using a least-squares projection, we map the physical element from the target state to the ZSS. Here we face a second choice to make, and that is for the control-point spacing in the radial direction for the physical element in the target state and ZSS. We choose the spacing in the target state to be proportional to the spacing for the ideal element in the target state, leading to a distribution in the ZSS that is not far from being equally spaced. Figure 23 shows the control mesh in the target state.

Fig. 23
figure 23

Control mesh in the target state, with the blue lines representing the mesh we use, which is based on the control-point spacing we chose in the radial direction, and with the black lines representing equal spacing of control points in the radial direction. (Color figure online)

Full size image

Remark 7

We expect that having proportionality between the spacings for the physical and ideal elements will facilitate accurate representation of the radial stretch.

Figure 24 shows the elements of \((\mathbf {X}^e_0)^{0}\) obtained with the process we have described. From \((\mathbf {X}^e_0)^{0}\) and \(\mathbf {X}_{{\mathrm {REF}}}\), we calculate the circumferential, longitudinal and radial stretches, defined based on the parametric coordinates in the ideal element, with the three directions corresponding to the directions of maximum and minimum principal curvatures and the cross product of the two directions. Figures 25, 26 and 27 show those stretches.

Fig. 24
figure 24

Elements of \((\mathbf {X}^e_0)^{0}\)

Full size image
Fig. 25
figure 25

Circumferential stretch from \((\mathbf {X}^e_0)^{0}\) and \(\mathbf {X}_{{\mathrm {REF}}}\)

Full size image
Fig. 26
figure 26

Longitudinal stretch from \((\mathbf {X}^e_0)^{0}\) and \(\mathbf {X}_{{\mathrm {REF}}}\)

Full size image
Fig. 27
figure 27

Radial stretch from \((\mathbf {X}^e_0)^{0}\) and \(\mathbf {X}_{{\mathrm {REF}}}\)

Full size image

5.3 Iterations to calculate \(\mathbf {X}^e_0\)

In computation of \(\mathbf {y}^0\) from \((\mathbf {X}^e_0)^0\), we use the ramping method described in Sect. 2.4, for reasons also described in that section. Figure 28 shows \((\mathbf {X}^e_0)^0\) and \(\mathbf {y}^0\). Figures 29, 30, 31 and 32 show \((\mathbf {X}^e_0)^i\) and \(\mathbf {y}^i\) for i = 1, 2, 300, and 1000. Figure 33 shows the maximum of \(\Vert \mathbf {y}^i\Vert \) as a function of i. There are some very-low-magnitude oscillations, but the solution converges very well.

Fig. 28
figure 28

Elements of \((\mathbf {X}^e_0)^0\) (left) and \(\mathbf {y}^0\) (right)

Full size image
Fig. 29
figure 29

Elements of \((\mathbf {X}^e_0)^1\) (left) and \(\mathbf {y}^1\) (right)

Full size image
Fig. 30
figure 30

Elements of \((\mathbf {X}^e_0)^2\) (left) and \(\mathbf {y}^2\) (right)

Full size image
Fig. 31
figure 31

Elements of \((\mathbf {X}^e_0)^{300}\) (left) and \(\mathbf {y}^{300}\) (right)

Full size image
Fig. 32
figure 32

Elements of \((\mathbf {X}^e_0)^{1000}\) (left) and \(\mathbf {y}^{1000}\) (right)

Full size image
Fig. 33
figure 33

Maximum of \(\Vert \mathbf {y}^i\Vert \) as a function of i (EBZSS iteration counter)

Full size image

5.4 Observations on the results

From converged \(\mathbf {X}^e_0\) and \(\mathbf {X}_{{\mathrm {REF}}}\), we calculate the circumferential, longitudinal and radial stretches, defined based on the parametric coordinates in the ideal element in the target state, with the three directions corresponding to the directions of maximum and minimum principal curvatures and the cross product of the two directions. The stretches are shown in Figs. 34, 35 and 36. In most places the stretches are very comparable to what we obtained from \((\mathbf {X}^e_0)^{0}\) and \(\mathbf {X}_{{\mathrm {REF}}}\) (see Figs. 25, 26 and 27). However, there are some differences locally, such as at the high-curvature region of the descending aorta. The high curvature might be due to the surrounding tissues. We also note the template used in the computation was based on the straight part of the aorta. Improving our method for determining the EBZSS might require more observed data, and additional boundary conditions representing the surrounding tissues.

Fig. 34
figure 34

Circumferential stretch from converged \(\mathbf {X}^e_0\) and \(\mathbf {X}_{{\mathrm {REF}}}\)

Full size image
Fig. 35
figure 35

Longitudinal stretch from converged \(\mathbf {X}^e_0\) and \(\mathbf {X}_{{\mathrm {REF}}}\)

Full size image
Fig. 36
figure 36

Radial stretch stretch from converged \(\mathbf {X}^e_0\) and \(\mathbf {X}_{{\mathrm {REF}}}\)

Full size image

6 Concluding remarks

We have presented the version of the EBZSS estimation method with isogeometric wall discretization and have successfully applied the method to patient-specific modeling of a human aorta. The EBZSS estimation method, originally introduced in the context of finite element wall discretization, will help us estimate the ZSS in patient-specific arterial FSI computations, where the image-based arterial geometry does not come from a ZSS. The method consists of three main components. 1. An iterative method, which starts with a calculated initial guess, is used for computing the EBZSS such that under a given load, the image-based target shape is matched. 2. A method for straight-tube segments is used for computing the EBZSS so that the given diameter and longitudinal stretch in the target configuration are matched together with the opening angle. 3. An element-based mapping between the artery and straight-tube configurations. This provides the mapping from the arterial configuration to the straight-tube configuration, and from the estimated EBZSS of the straight-tube configuration back to the arterial configuration, to be used as the initial guess for the iterative method that matches the target shape. With isogeometric discretization, we obtain the element-based mapping directly, instead of extracting it from the mapping between the artery and straight-tube segments. That is because all we need for the element-based mapping, including the curvatures, can be obtained within an element. With NURBS basis functions, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and much fewer elements. Higher-order NURBS basis functions allow representation of more complex shapes within an element. To demonstrate how the new EBZSS estimation method performs, we first presented 2D test computations with straight-tube configurations, carried out with quadratic and cubics basis functions and meshes made of different number of elements. Then we showed how the method can be used in a 3D computation where the target geometry is coming from medical image of a human aorta.