Estimation of element-based zero-stress state for arterial FSI computations

Abstract

In patient-specific arterial fluid–structure interaction (FSI) computations the image-based arterial geometry comes from a configuration that is not stress-free. We present a method for estimation of element-based zero-stress (ZS) state. The method has three main components. (1) An iterative method, which starts with an initial guess for the ZS state, is used for computing the element-based ZS state such that when a given pressure load is applied, the image-based target shape is matched. (2) A method for straight-tube geometries with single and multiple layers is used for computing the element-based ZS state so that we match the given diameter and longitudinal stretch in the target configuration and the “opening angle.” (3) An element-based mapping between the arterial and straight-tube configurations is used for mapping from the arterial configuration to the straight-tube configuration, and for mapping the estimated ZS state of the straight tube back to the arterial configuration, to be used as the initial guess for the iterative method that matches the image-based target shape. We present a set of test computations to show how the method works.

1 Introduction

Computational mechanics has been experiencing a rapid expansion in computational cardiovascular fluid mechanics (see, for example, [1–40]),with much emphasis on fluid–structure interaction (FSI) between the blood flow and cardiovascular wall. The expansion has partly been due to the advances in core FSI methods (see, for example, [36, 37, 41] and references therein) and the development of special methods targeting cardiovascular FSI (see, for example, [29, 33, 36] and references therein).

The special methods include those designed to take into account the fact that in patient-specific arterial FSI computations the image-based arterial geometry comes from a configuration that is not stress-free. Until recently, no attempt was made to find a zero-stress (ZS) configuration for the artery. The concept of estimated zero-pressure (EZP) arterial geometry was introduced in [9]. It was pointed out in [9] that quite often, the image-based geometries were used as arterial geometries corresponding to zero blood pressure, and that it would be more realistic to use the image-based geometry as the arterial geometry corresponding to the time-averaged value of the blood pressure. Given that arterial geometry at the time-averaged pressure value, an estimated arterial geometry corresponding to zero blood pressure needed to be constructed.

The original version of the technique for calculating an EZP geometry was introduced in a 2007 conference paper [42] and the 2008 journal paper [9] as “a rudimentary technique” for addressing the issue. Newer techniques were introduced after that. They include the newer EZP versions introduced in [17, 26, 29], which were also presented in [33, 36]. They also include the prestress technique introduced in [24] and further refined in [30], which also was presented in [33, 36]. In the approach given in [24, 30], a prestress state is found, which puts the artery in equilibrium with the time-averaged blood pressure (and viscous forces). The prestress is then directly employed for the arterial wall modeling in the FSI computations.

Arterial wall is a sophisticated multilayered composite with nonlinear stress–strain relationship. Moreover, because the arterial wall is a living tissue, its mechanical characteristics vary in time, and tissue growth over long time results in residual stress. A typical way to investigate the residual stress is to cut the arterial wall open and measure its “opening angle” [43–47]. Opening-angle measurements for various species were reported in [48]. The opening angle can then be used in the computations (see, for example, [49]) as part of the given data.

In this paper, we present a method for estimation of element-based ZS state. The method has three main components. The first component is an iterative method, which starts with an initial guess for the ZS state. It is used for computing the element-based ZS state such that when a given pressure load is applied, the image-based target shape is matched. The second component is a method for straight-tube geometries with single and multiple layers. It is used for computing the element-based ZS state so that we match the given diameter and longitudinal stretch in the target configuration and the opening angle. The third component is an element-based mapping between the arterial and straight-tube configurations. It is used for mapping from the arterial configuration to the straight-tube configuration, and for mapping the estimated ZS state of the straight tube back to the arterial configuration, to be used as the initial guess for the iterative method that matches the image-based target shape.

The first component is presented in Sect. 2. The second and third components are presented in Sect. 3. In Sect. 4, we present a set of test computations to show how the method works. The concluding remarks are given in Sect. 5.

2 Element-based zero-stress state

Let $\varOmega _0\in \mathbb R ^3$ be the material domain of a structure in the ZS configuration, and let $\varGamma _0$ be its boundary. Let $\varOmega _t\in \mathbb R ^3,\,t \in (0,T)$, be the material domain of the structure in the deformed configuration, and let $\varGamma _{t}$ be its boundary. The structural mechanics equations based on the total Lagrangian formulation can be written as

$$\begin{aligned}&\int _{\varOmega _0} \mathbf w \cdot \rho _0\frac{\mathrm{d}^2 \mathbf y }{\mathrm{d}t^2}~\mathrm{d}\varOmega + \int _{\varOmega _0} \delta \mathbf E : \mathbf S ~\mathrm{d}\varOmega - \int _{\varOmega _0} \mathbf w \cdot \rho _0\mathbf f ~\mathrm{d}\varOmega \nonumber \\&\quad = \int _{\left( \varGamma _t\right) _\mathrm{h}} \mathbf w \cdot \mathbf{h}~\mathrm{d}\varGamma . \end{aligned}$$

(1)

Here, $\mathbf y$ is the structural displacement, $\mathbf w$ is the virtual displacement, $\delta \mathbf E$ is the variation of the Green–Lagrange strain tensor, $\mathbf S$ is the second Piola–Kirchhoff stress tensor, $\rho _0$ is the mass density in the ZS configuration, $\mathbf f$ is the body force per unit mass, and $\mathbf{h}$ is the external traction vector applied on the subset $\left( \varGamma _t\right) _\mathrm{h}$ of the total boundary $\varGamma _{t}$.

2.1 Representation of the element-based ZS state

Typically the prestress is taken into account with the second Piola–Kirchhoff stress tensor as $\mathbf S +\mathbf S _0$. Applications in arterial FSI with prestress and a technique for finding the prestress can be found in [24, 30]. Here, instead of finding a prestress, we look for a ZS shape, but for each element.

In the method we propose here, we define the ZS state with a set of positions $\mathbf{X }_0^e$ for each element $e$. Positions of nodes from different elements mapping to the same node in the mesh do not have to be the same. In the reference configuration, $\mathbf{X }_\mathrm{REF }$, all elements are connected by nodes, and we measure the displacement $\mathbf y$ from that connected configuration.

The implementation of this method is quite simple.The deformation gradient tensor $\mathbf F$ can be evaluated for each element:

$$\begin{aligned} \mathbf F ^e&\equiv \frac{\partial \mathbf x }{\partial \mathbf{X }_0^e}, \end{aligned}$$

(2)

$$\begin{aligned}&= \frac{\partial \left( \mathbf{X }_\mathrm{REF }+ \mathbf y \right) }{\partial \mathbf{X }_0^e}. \end{aligned}$$

(3)

The deformation gradient tensors for different elements are on different configurations, but the terms in Eq. (1), including the second term, do not depend on the orientation. Therefore the rest of the process is the same as it is in the total Lagrangian formulation. We call this method the “element-based total Lagrangian (EBTL)” formulation.

2.2 An iterative method for finding the ZS state for a given load

One of the objectives of having prestress in arterial FSI computations is that we would like to have a configuration that matches the target shape under a given load. Here $\mathbf{X }_\mathrm{REF }$ represents the target shape. Suppose the element-based ZS state from the $i$th iteration is $(\mathbf{X }_0^e)^i$. We solve the steady-state structural mechanics equations with the EBTL formulation and obtain the displacement $\mathbf y ^{i}$. If $\mathbf y ^{i}$ is zero, then $(\mathbf{X }_0^e)^i$ is the converged solution. If not, then we follow the process below.

To explain the process, we first expand the definition of the deformation gradient tensor $\mathbf F$ to any two states $\mathbf x$ and $\mathbf X$, used as function arguments:

$$\begin{aligned} \mathbf F \left( \mathbf x , \mathbf X \right)&= \dfrac{\partial \mathbf x }{\partial \mathbf X }. \end{aligned}$$

(4)

We decompose this into rotation $\mathbf R$ and the right and left stretch tensors $\mathbf U$ and $\mathbf V$:

$$\begin{aligned} \mathbf F \left( \mathbf x , \mathbf X \right)&= \mathbf R \left( \mathbf x , \mathbf X \right) \mathbf U \left( \mathbf x , \mathbf X \right) ,\end{aligned}$$

(5)

$$\begin{aligned} \mathbf F \left( \mathbf x , \mathbf X \right)&= \mathbf V \left( \mathbf x , \mathbf X \right) \mathbf R \left( \mathbf x , \mathbf X \right) . \end{aligned}$$

(6)

The decompositions can be obtained by using the following equations:

$$\begin{aligned} \mathbf U ^2&= \mathbf F ^T \mathbf F ,\end{aligned}$$

(7)

$$\begin{aligned} \mathbf V ^2&= \mathbf F \mathbf F ^T. \end{aligned}$$

(8)

The relationship between the unit vectors $\mathbf a _0$ and $\mathbf a$ in the ZS and target configurations can be expressed as

$$\begin{aligned} \lambda _a \mathbf a = \mathbf F \mathbf a _0, \end{aligned}$$

(9)

where $\lambda _a$ is the stretch. Suppose we have the following relationship at $i$th iteration:

$$\begin{aligned} \lambda _a^{i} \mathbf a ^i = \mathbf F ^{i} \mathbf a _0^i, \end{aligned}$$

(10)

where $\mathbf a _0^i$ is an arbitrary unit vector in $(\mathbf{X }_0^e)^i$, and

$$\begin{aligned} \mathbf F ^{i}&\equiv \mathbf F \left( \mathbf x ^i, (\mathbf{X }_0^e)^i\right) . \end{aligned}$$

(11)

We also write a similar relationship between the next-iteration and target states $(\mathbf{X }_0^e)^{i+1}$ and $\mathbf{X }_\mathrm{REF }$:

$$\begin{aligned} \lambda _a \mathbf a = \mathbf F ^{i+1} \mathbf a _0^{i+1}, \end{aligned}$$

(12)

where $\mathbf a _0^{i+1}$ is an arbitrary unit vector in $(\mathbf{X }_0^e)^{i+1}$, and

$$\begin{aligned} \mathbf F ^{i+1}&\equiv \mathbf F \left( \mathbf{X }_\mathrm{REF }, (\mathbf{X }_0^e)^{i+1}\right) . \end{aligned}$$

(13)

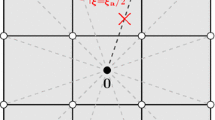
Figure 1 shows the configurations we are working with.

Fig. 1

Configurations we are working with

Here we assume

$$\begin{aligned} \lambda _a = \lambda _a^i. \end{aligned}$$

(14)

We write the relationship between the directions in $(\mathbf{X }_0^e)^{i+1}$ and $(\mathbf{X }_0^e)^i$ as follows:

$$\begin{aligned} \mathbf a _0^{i} = \mathbf R \left( (\mathbf{X }_0^e)^i, (\mathbf{X }_0^e)^{i+1}\right) \mathbf a _0^{i+1}. \end{aligned}$$

(15)

Now, we also assume that the direction we get from

$$\begin{aligned} \mathbf a = \mathbf R \left( \mathbf{X }_\mathrm{REF }, \mathbf x ^i\right) \mathbf a ^i \end{aligned}$$

(16)

is the same as the direction given by Eq. (12). Substituting Eq. (15) into Eq. (10), premultiplying both sides by $\mathbf R \left( \mathbf{X }_\mathrm{REF }, \mathbf x ^i\right)$, and using Eqs. (14) and (16), we get

$$\begin{aligned} \lambda _a \mathbf a = \mathbf R \left( \mathbf{X }_\mathrm{REF }, \mathbf x ^i\right) \mathbf F ^{i} \mathbf R \left( (\mathbf{X }_0^e)^i, (\mathbf{X }_0^e)^{i+1}\right) \mathbf a _{0}^{i+1}. \end{aligned}$$

(17)

Because $\mathbf a _0^{i+1}$ is an arbitrary vector, we obtain the following relationship from Eqs. (12) and (17):

$$\begin{aligned} \mathbf F ^{i+1} = \mathbf R \left( \mathbf{X }_\mathrm{REF }, \mathbf x ^i\right) \mathbf F ^{i} \mathbf R \left( (\mathbf{X }_0^e)^i, (\mathbf{X }_0^e)^{i+1}\right) . \end{aligned}$$

(18)

Now, we assume that the following approximation is a reasonable one:

$$\begin{aligned} \mathbf R \left( (\mathbf{X }_0^e)^i, (\mathbf{X }_0^e)^{i+1}\right) = \mathbf I . \end{aligned}$$

(19)

Thus,

$$\begin{aligned} \mathbf F ^{i+1} = \mathbf R \left( \mathbf{X }_\mathrm{REF }, \mathbf x ^i\right) \mathbf F ^{i}, \end{aligned}$$

(20)

and

$$\begin{aligned} \left( \mathbf F ^{i+1} \right) ^{-1}&= \left( \mathbf F ^{i} \right) ^{-1} \mathbf R (\mathbf x ^i, \mathbf{X }_\mathrm{REF }),\end{aligned}$$

(21)

$$\begin{aligned}&= \left( \mathbf U ^{i} \right) ^{-1} \mathbf R ((\mathbf{X }_0^e)^i, \mathbf{X }_\mathrm{REF }) . \end{aligned}$$

(22)

With this tensor, we calculate $(\mathbf{X }_0^e)^{i+1}$ from the target state $\mathbf{X }_\mathrm{REF }$.

Remark 1

Inspecting $\mathbf F ^{i+1}$, as obtained from Eq. (22):

$$\begin{aligned} \mathbf F ^{i+1} = \mathbf R (\mathbf{X }_\mathrm{REF }, (\mathbf{X }_0^e)^i) \mathbf U (\mathbf x ^i, (\mathbf{X }_0^e)^i), \end{aligned}$$

(23)

we observe that the rotation is based on $(\mathbf{X }_0^e)^i$ and $\mathbf{X }_\mathrm{REF }$, but the stretch is based on $\mathbf x ^i$ and $(\mathbf{X }_0^e)^i$.

In this paper we use hexahedral elements, and we evaluate the tensors at the element center. With that, we compute explicitly as follows:

$$\begin{aligned}&(\mathbf{X }_0^e)^{i+1}_a - \overline{(\mathbf{X }_0^e)^{i+1}}\nonumber \\&\quad = \underbrace{ \left( \overline{\mathbf{U }^e}^{i} \right) ^{-1} \overline{\mathbf{R }^e}((\mathbf{X }_0^e)^i, \mathbf{X }_\mathrm{REF })}_{\mathbf{K }^i} \left( ({\mathbf{X }}_\mathrm{REF }^e)_a - \overline{\mathbf{X }_\mathrm{REF }^e}\right) , \quad \quad \end{aligned}$$

(24)

with an overbar indicating the element-center value. What we see in Eq. (24) is that the ZS state is obtained using a transformation matrix $\mathbf K ^i$, which gives us only six degrees of choice, from the target state, which is already set. To increase the degrees of choice, we propose an alternative method:

$$\begin{aligned}&(\mathbf{X }_0^e)^{i+1}_a - \overline{(\mathbf{X }_0^e)^{i+1}}\nonumber \\&\quad = \underbrace{ \mathbf K ^i \overline{\mathbf{F }^e}(\mathbf{X }_\mathrm{REF }, (\mathbf{X }_0^e)^i) }_{\hat{\mathbf{K }}^i} \left( (\mathbf{X }_0^e)^i- \overline{(\mathbf{X }_0^e)^i}\right) ,\end{aligned}$$

(25)

$$\begin{aligned}&\quad = \hat{\mathbf{K }}^i \hat{\mathbf{K }}^{i-1} \cdots \hat{\mathbf{K }}^{1} \hat{\mathbf{K }}^{0} \left( (\mathbf{X }_0^e)^0_a- \overline{(\mathbf{X }_0^e)^0}\right) . \end{aligned}$$

(26)

Again the ZS state is obtained using a transformation matrix, but from the initial guess for the ZS state, which gives us additional degrees of choice. We note that Eq. (26) is only for better understanding of the method, and we implement Eq. (25). We will call the iterations given by Eq. (24), with direct update from the target state, “direct-update (DU)” process, and the iterations given by Eq. (25), with recursive update from the previous iteration, “recursive-update (RU)” process. The RU process is our preferred method, and unless specified otherwise, that is what we use in the computations reported in this paper.

Remark 2

If we do not approximate Eq. (22) by using the element-center values, the two processes are identical.

3 Modeling of the ZS state for an artery

3.1 Tube shape

We describe a tube-shaped model in the target state with three lengths: $\overline{\ell },\,h$ and $L$. They are the circumferential length at the arterial-wall center, wall thickness, and the length in the longitudinal direction. The volume of the tube is

$$\begin{aligned} V = \overline{\ell } h L. \end{aligned}$$

(27)

There are significant properties for an artery beyond having a target shape under a certain load. One of them is the opening angle, $\phi$, seen after a longitudinal cut, which we call the “LC state.”

Remark 3

We note that it is not necessary for the LC state to be a ZS state.

To describe the LC representation, we define $\phi$ as shown in Fig. 2. With that $\phi$ definition, the curvature can be written as follows:

$$\begin{aligned} \kappa = \frac{2 \pi - \phi }{\ell _0 }, \end{aligned}$$

(28)

where the subscript $0$ indicates a value at the LC state.

Fig. 2

Straight-tube ($left$) and opening-angle ($right$) definitions

3.1.1 Single-layer model

In this model we assume that the LC state is a ZS state. The subscripts “I” and “E” indicate values corresponding to the internal (lumen) and external surfaces. The radii of curvature are given as follows:

$$\begin{aligned}&\left( r_\mathrm{I }\right) _0 = \frac{\left( \ell _\mathrm{I }\right) _0}{\left| 2 \pi - \phi \right| }, \end{aligned}$$

(29)

$$\begin{aligned}&\left( r_\mathrm{E }\right) _0 = \frac{\left( \ell _\mathrm{E }\right) _0}{\left| 2 \pi - \phi \right| }, \end{aligned}$$

(30)

and the thickness is

$$\begin{aligned} h_0 = \left| \left( r_\mathrm{E }\right) _0 - \left( r_\mathrm{I }\right) _0 \right| . \end{aligned}$$

(31)

Remark 4

We note that the expressions provided by Eqs. (29) and (30) give infinite radii for $\phi = 2 \pi$.

The volume of the LC state is

$$\begin{aligned} V_0&= \frac{2\pi - \phi }{2} \left( \left( r_\mathrm{E }\right) _0^2 - \left( r_\mathrm{I }\right) _0^2 \right) L_0,\end{aligned}$$

(32)

$$\begin{aligned}&= \frac{2\pi - \phi }{2} \left( \left( r_\mathrm{E }\right) _0 - \left( r_\mathrm{I }\right) _0 \right) \left( \left( r_\mathrm{E }\right) _0 + \left( r_\mathrm{I }\right) _0 \right) L_0,\end{aligned}$$

(33)

$$\begin{aligned}&= \overline{\ell _0} h_0 L_0, \end{aligned}$$

(34)

where

$$\begin{aligned} \overline{\ell _0} = \frac{ \left( \ell _\mathrm{E }\right) _0 + \left( \ell _\mathrm{I }\right) _0 }{2}. \end{aligned}$$

(35)

Remark 5

We note that the expression given by Eq. (34) is applicable also for $\phi = 2 \pi$.

In the process of creating $\mathbf{X }_0^e,\,\phi$ is specified based on data, and the longitudinal stress, $\lambda _{z} = \frac{L}{L_0}$, is specified based on values from the literature. We iterate on the value of $\overline{\ell _0}$ to match $\overline{\ell }$ by solving the structural mechanics equations, and $h_0$ is a dependent parameter from the material incompressibility, which is enforced through Eqs. (27) and (34).

We introduce the parametric coordinate $-1 \le \eta \le 1$, and have the following linear relationship in the ZS state:

$$\begin{aligned} \ell _0(\eta )&= \left( \ell _\mathrm{I }\right) _0 \frac{1-\eta }{2} + \left( \ell _\mathrm{E }\right) _0 \frac{1+\eta }{2},\end{aligned}$$

(36)

$$\begin{aligned}&= \overline{\ell _0} + \frac{\varDelta \ell _0}{2}\eta , \end{aligned}$$

(37)

where

$$\begin{aligned} \varDelta \ell _0&= \left( \ell _\mathrm{E }\right) _0 - \left( \ell _\mathrm{I }\right) _0,\end{aligned}$$

(38)

$$\begin{aligned}&= \left( 2\pi - \phi \right) h_0. \end{aligned}$$

(39)

From the material incompressibility we write

$$\begin{aligned} 2 \pi r \mathrm{d}r L = \ell _0 \mathrm{d}\eta \frac{h_0}{2} L_0. \end{aligned}$$

(40)

Integrating both sides, we obtain

$$\begin{aligned} \pi \left( r^2 \!-\! r_\mathrm{I }^2\right) L \!&=\! \frac{h_0}{2} L_0 \left( \overline{\ell _0} (\eta \!+\! 1) \!+\! \frac{\varDelta \ell _0}{4} \left( \eta ^2 - 1\right) \right) . \end{aligned}$$

(41)

We solve this for $\eta$:

$$\begin{aligned} \eta&= 2 \frac{ \sqrt{ \left( \overline{\ell _0} - \frac{\varDelta \ell _0}{2} \right) ^2 + \varDelta \ell _0 \frac{2 \pi \left( r^2 - r_\mathrm{I }^2\right) L}{h_0 L_0} } - \overline{\ell _0} }{ \varDelta \ell _0},\end{aligned}$$

(42)

$$\begin{aligned}&= 2 \frac{ - \overline{\ell _0} + \frac{\varDelta \ell _0}{4} + \frac{2 \pi \left( r^2 - r_\mathrm{I }^2\right) L}{h_0 L_0} }{ \sqrt{ \left( \overline{\ell _0} - \frac{\varDelta \ell _0}{2} \right) ^2 + \varDelta \ell _0 \frac{2 \pi \left( r^2 - r_\mathrm{I }^2\right) L}{h_0 L_0} } + \overline{\ell _0} },\end{aligned}$$

(43)

$$\begin{aligned}&= 2 \frac{ 2\frac{r^2 - r_\mathrm{I }^2}{r_\mathrm{E }^2-r_\mathrm{I }^2} + \frac{\varDelta \ell _0}{4\overline{\ell _0}} -1 }{ \sqrt{ \left( 1 - \frac{\varDelta \ell _0}{2\overline{\ell _0}} \right) ^2 + 2\frac{\varDelta \ell _0}{\overline{\ell _0}} \frac{r^2 - r_\mathrm{I }^2}{r_\mathrm{E }^2-r_\mathrm{I }^2} } + 1 }. \end{aligned}$$

(44)

Equation (44) is applicable also for $\phi = 2 \pi$. We introduce $-\pi \le \theta \le \pi$ in the circumferential direction. Because of the circular symmetry in the deformed state, including the strain, the angle in the LC state can be written as

$$\begin{aligned} \theta _0 = \frac{2\pi - \phi }{2 \pi }\theta . \end{aligned}$$

(45)

We cannot use this expression for elements crossed by $\theta = \pm \pi$, and therefore we rearrange the mapping as

$$\begin{aligned} \theta _0^e = \frac{2\pi - \phi }{2 \pi }\left( \theta - \overline{\theta ^e}\right) , \end{aligned}$$

(46)

and that avoids $\theta = \pm \pi$ crossing the element. Here $\overline{\theta ^e}$ is the angle for the element center.

With the parameter set ($\eta ,\,\theta ,\,z$), we have the mapping

$$\begin{aligned} \mathbf{X }_0^e= \frac{h_0}{2} \eta \mathbf e _r \left( 0\right) + \frac{\overline{\ell _0}}{2}\frac{\theta }{\pi } \mathbf e _\theta \left( 0\right) + \frac{z}{\lambda _z} \mathbf e _z \end{aligned}$$

(47)

for $\phi =2 \pi$, and otherwise

$$\begin{aligned} \mathbf{X }_0^e&= \left( \frac{ \overline{\ell _0} }{2\pi - \phi } + \frac{h_0}{2} \eta \right) \mathbf e _r \left( \theta _0^e\right) \nonumber \\&\quad - \left( \frac{ \overline{\ell _0} }{2\pi - \phi }\right) \mathbf e _r(0) + \frac{z}{\lambda _z} \mathbf e _z,\end{aligned}$$

(48)

$$\begin{aligned}&= \frac{ \overline{\ell _0} }{2\pi - \phi } \left( \mathbf e _r \left( \theta _0^e\right) - \mathbf e _r(0) \right) \nonumber \\&\quad + \frac{h_0}{2} \eta \mathbf e _r \left( \theta _0^e\right) + \frac{z}{\lambda _z} \mathbf e _z. \end{aligned}$$

(49)

Because Eq. (49) is not valid for $\phi \rightarrow 2 \pi$, we rearrange the first term as

$$\begin{aligned} \frac{ \overline{\ell _0} }{2\pi - \phi } \left( \mathbf e _r \left( \theta _0^e\right) - \mathbf e _r(0) \right) = \frac{ \overline{\ell _0} }{2\pi - \phi } \begin{bmatrix} \cos \left( \theta _0^e\right) - 1\\ \sin \left( \theta _0^e\right) \\ \end{bmatrix},\nonumber \\ \end{aligned}$$

(50)

and approximate it by a Taylor series expansion:

$$\begin{aligned}&\frac{ \overline{\ell _0} }{2\pi - \phi } \left( \mathbf e _r \left( \theta _0^e\right) - \mathbf e _r(0) \right) \nonumber \\&\quad \approx \frac{ \overline{\ell _0} }{2\pi - \phi } \begin{bmatrix} \left( \theta _0^e \right) ^2 \left( - \frac{1}{2} + \frac{1}{24} \left( \theta _0^e \right) ^2 \right) \\ \theta _0^e \left( 1 - \frac{1}{6} \left( \theta _0^e\right) ^2 \right) \\ \end{bmatrix}\nonumber \\&\quad = \frac{\overline{\ell _0}}{2 \pi } \left( \theta -\overline{\theta ^e}\right) \begin{bmatrix} \theta _0^e \left( - \frac{1}{2} + \frac{1}{24} \left( \theta _0^e \right) ^2 \right) \\ \left( 1 - \frac{1}{6} \left( \theta _0^e\right) ^2 \right) \\ \end{bmatrix}. \end{aligned}$$

(51)

This form is valid for $\phi = 2\pi$, and if $\left| \phi - 2 \pi \right| < 2\times 10^{-4}$, the error in the approximation is within $10^{-16}$. Thus, Eq. (49) and its approximation by Eq. (51) can be used for creating $\mathbf{X }_0^e$.

3.1.2 Three-layer model

We extend the single-layer model to a three-layer model. We assume that the three layers are in a ZS state after they are separated. Then each layer has its own opening angle $\phi _{i}$, and we can simply use the single-layer model to create $\mathbf{X }_0^e$. We also assume that the model has an opening angle $\phi$ in the LC state, prior to the separation of the three layers. However, this angle cannot be specified directly. It can be matched iteratively by introducing an angle $\overline{\phi }$, which is related, by Eq. (39), to $\varDelta \ell _0$ indicated in Fig. 3. With that, we can calculate $\left( \overline{\ell _i}\right) _0$ as follows:

$$\begin{aligned} \left( \overline{\ell _i}\right) _0 = \overline{\ell _0} + \frac{\varDelta \ell _0}{2} \eta _i, \end{aligned}$$

(52)

where $\eta _i$ is the parametric coordinate of the center of the $i$th layer:

$$\begin{aligned} \eta _i = \frac{2}{h_0}\left( \sum _{k=1}^{i-1} \left( h_k\right) _0 + \frac{1}{2} \left( h_i\right) _0\right) - 1. \end{aligned}$$

(53)

In the process of creating $\mathbf{X }_0^e,\,(\lambda _z)_i$ is specified as before, and $\phi _i$ and $\frac{(h_i)_0}{h_0}$ are also specified. We iterate on the values of $\overline{\ell _0}$ and $\overline{\phi }$ to match $\overline{\ell }$ and $\phi$ by solving the structural mechanics equations, and $h_0$ is again a dependent parameter. While this is now a two-dimensional search, we know that $\phi$ depends mostly on $\overline{\phi }$, and less on $\overline{\ell }_0$.

Fig. 3

Three-layer model. Circumferential length as function of $\eta$

3.2 Arbitrary shape

We define centerlines for the artery. We can obtain the centerlines by using Vascular Modeling Toolkit [50]. A centerline consists of straight-line segments.

We first calculate the positions of the centerline nodes along the artery from the inlet, and this is the $z$-coordinate. We also introduce the basis vector $\mathbf e _r(0)$ orthogonal to the centerline, noting that the argument “0” is for $\theta = 0$.

We define the basis vectors from the inlet to the outlet sequentially. First we pick a basis vector at the inlet, and rotate it as we move along the centerline to make it perpendicular to the centerline segments.

With what we have from above, we define the following parameters for each element node: $z,\,\theta ,\,r,\,r_\mathrm{min }$, and $r_\mathrm{max }$. If there are branches, for each element we choose the closest one among the centerlines. We define $r_\mathrm{min }$ and $r_\mathrm{max }$ for each node as the coordinates of the closest internal and external surface positions, respectively. These are used for defining the mapped radius $\hat{r}$ as follows:

$$\begin{aligned} \hat{r} = r_\mathrm{I }+ \frac{r - r_\mathrm{min }}{r_\mathrm{max }- r_\mathrm{min }}\left( r_\mathrm{E }- r_\mathrm{I }\right) , \end{aligned}$$

(54)

where $r_\mathrm{I }$ and $r_\mathrm{E }$ are tube internal and external surface radii. These do not need to match $r_\mathrm{min }$ and $r_\mathrm{max }$. They are calculated from the centerline nodal values by interpolation at the projection point of the artery node. The centerline nodal values are calculated from the cross-sectional areas over planes orthogonal to the centerline at the centerline nodes. The orthogonality direction for a node is defined by averaging the orthogonality directions for the adjacent segments. With $\hat{r}$, we obtain the tube position $\mathbf{x }_\mathrm{T }$ as follows:

$$\begin{aligned} \mathbf{x }_\mathrm{T }= \hat{r}\mathbf e _r \left( \theta \right) + z \mathbf e _z. \end{aligned}$$

(55)

To construct the ZS state, we use either the single-layer or three-layer model. For example, in the case of the single-layer model, we first choose $\phi$ and $\lambda _z$ and find the proper $\overline{\ell _0}$ and $h_0$ from the straight-tube solution (described in Sect. 4), then we map $\hat{r}$ to $\eta$ by Eq. (44), and then we use Eq. (49) to obtain $(\mathbf{X }_0^e)_\mathrm{T }$. After that, we pull $(\mathbf{X }_0^e)_\mathrm{T }$ back onto the actual configuration with mappings similar to those in Sect. 2.2. Figure 4 shows the configurations of the process.

Fig. 4

Artery ($top~left$), straight tube ($top~right$), ZS state of the straight tube ($bottom~right$), and ZS state of the artery ($bottom~left$)

To pull $(\mathbf{X }_0^e)_\mathrm{T }$ back, we again start with the following assumption:

$$\begin{aligned} \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)\right) \!=\! \mathbf R \left( \mathbf x , \mathbf{x }_\mathrm{T }\right) \mathbf F \left( \mathbf{x }_\mathrm{T }, (\mathbf{X }_0^e)_\mathrm{T }\right) \mathbf R \left( (\mathbf{X }_0^e)_\mathrm{T }, \mathbf{X }_0^e\right) . \end{aligned}$$

(56)

Then we obtain

$$\begin{aligned}&\left( \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)\right) \right) ^{-1}\nonumber \\&\quad = \mathbf R \left( \mathbf{X }_0^e, (\mathbf{X }_0^e)_\mathrm{T }\right) \left( \mathbf F \left( \mathbf{x }_\mathrm{T }, (\mathbf{X }_0^e)_\mathrm{T }\right) \right) ^{-1} \mathbf R \left( \mathbf{x }_\mathrm{T }, \mathbf x \right) , \end{aligned}$$

(57)

again assume $\mathbf R \left( \mathbf{X }_0^e, (\mathbf{X }_0^e)_\mathrm{T }\right) = \mathbf I$, and obtain

$$\begin{aligned} \left( \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)\right) \right) ^{-1} = \left( \mathbf F \left( \mathbf{x }_\mathrm{T }, (\mathbf{X }_0^e)_\mathrm{T }\right) \right) ^{-1} \mathbf R \left( \mathbf{x }_\mathrm{T }, \mathbf x \right) . \end{aligned}$$

(58)

We obtain$(\mathbf{X }_0^e)_a$ from $\mathbf x _a^e$ as follows:

$$\begin{aligned} (\mathbf{X }_0^e)_a - \overline{\mathbf{X }_0^e}&= \left( \overline{\mathbf{F }^e}\left( \mathbf{x }_\mathrm{T }, (\mathbf{X }_0^e)_\mathrm{T }\right) \right) ^{-1} \overline{\mathbf{R }^e}\left( \mathbf{x }_\mathrm{T }, \mathbf x \right) \left( \mathbf x _a^e - \overline{\mathbf{x }^e}\right) .\nonumber \\ \end{aligned}$$

(59)

An alternative way of obtaining $\mathbf{X }_0^e$ is using the following relationship:

$$\begin{aligned}&\left( \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)\right) \right) ^{-1} \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)_\mathrm{T }\right) \nonumber \\&\quad = \left( \mathbf F \left( \mathbf{x }_\mathrm{T }, (\mathbf{X }_0^e)_\mathrm{T }\right) \right) ^{-1} \mathbf R \left( \mathbf{x }_\mathrm{T }, \mathbf x \right) \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)_\mathrm{T }\right) ,\end{aligned}$$

(60)

$$\begin{aligned}&\mathbf F \left( (\mathbf{X }_0^e), (\mathbf{X }_0^e)_\mathrm{T }\right) \nonumber \\&\quad = \mathbf F \left( (\mathbf{X }_0^e)_\mathrm{T }, \mathbf{x }_\mathrm{T }\right) \mathbf R \left( \mathbf{x }_\mathrm{T }, \mathbf x \right) \mathbf F \left( \mathbf x , (\mathbf{X }_0^e)_\mathrm{T }\right) ,\end{aligned}$$

(61)

$$\begin{aligned}&\quad = \mathbf V \left( (\mathbf{X }_0^e)_\mathrm{T }, \mathbf{x }_\mathrm{T }\right) \mathbf U \left( \mathbf x , (\mathbf{X }_0^e)_\mathrm{T }\right) , \end{aligned}$$

(62)

and calculating as follows:

$$\begin{aligned}&(\mathbf{X }_0^e)_a - \overline{(\mathbf{X }_0^e)}\nonumber \\&\quad = \overline{\mathbf{V }^e}\left( (\mathbf{X }_0^e)_\mathrm{T }, \mathbf{x }_\mathrm{T }\right) \overline{\mathbf{U }^e}\left( \mathbf x , (\mathbf{X }_0^e)_\mathrm{T }\right) \left( ((\mathbf{X }_0^e)_\mathrm{T })_a - \overline{((\mathbf{X }_0^e)_\mathrm{T })} \right) .\nonumber \\ \end{aligned}$$

(63)

We use $\mathbf{X }_0^e$ as the initial guess for the iterations described in Sect. 2.2. Our preferred mapping is the one given by Eq. (63), and that is what we use in the computations reported in this paper.

4 Test computations

The arterial wall is modeled with the continuum element made of hyperelastic (Fung) material. The Fung material constants $D_1$ and $D_2$ (from [51]) are 2.6447$\times$10$^3$ N/m$^2$ and 8.365, and the penalty Poisson’s ratio is 0.45. We set constant pressure $p_0 = 92~\text {mm~Hg}$.

We use the steady-state formulation. The boundary condition at the tube ends is free displacement in the radial direction from the centroid of those ends.

4.1 Straight tube

The target artery shape has 10 % thickness ratio, $\pi h /\ell _\mathrm{I }$, and longitudinal-length ratio $\pi L/\ell _\mathrm{I } = 3$. We note that the solution depends on $D_1/p_0$ and the thickness ratio, but not on the diameter or the longitudinal-length ratio. For the test computations, we define a parameter $\alpha$:

$$\begin{aligned} \overline{\ell _0} = \alpha \ell _\mathrm{I }. \end{aligned}$$

(64)

In the following test computations, we consider $\phi$ and $\lambda _z$ as given. We assume the $\alpha$ that gives 10 % thickness ratio after the structural mechanics computation is the proper $\alpha$. Based on this assumption, we iterate on $\alpha$ using a binary-search-like method. First we compute with two given $\alpha$: $\alpha ^1$ and $\alpha ^2$, and update $\alpha$ with the formula

$$\begin{aligned} \alpha ^{i+1} = \alpha ^{c} + \frac{ \alpha ^{+} - \alpha ^{-}}{ \ell _\mathrm{I }^{+} - \ell _\mathrm{I }^{-} } \left( \ell _\mathrm{I } - \ell _\mathrm{I }^c\right) , \end{aligned}$$

(65)

where $-$ and $+$ indicate the solutions closest to $\ell _\mathrm{I }$ approached from below and above among the set of all solutions, and $c$ is the closest one among the two. When $\left| \alpha ^{c} - \alpha ^{i}\right| \le 10^{-5}$, we consider the iterations converged.

Since we use a penalty form of the incompressibility constraint, we do not have the exact volume conservation. Therefore we adjust $h_0$ such that we have the correct volume at the target state. Within the iterations above, we adjust the thickness as follows:

$$\begin{aligned} h_0^{j+1} = \frac{V}{V^j} h_0^{j}, \end{aligned}$$

(66)

where $V$ and $V^{j}$ are the volumes of the target and the $j$th solution, respectively. The initial value of $h_0$ is set based on the volume conservation ($V_0 = V$) with Eq. (34), and we do this adjustment three times for each $\alpha ^i$.

In this paper, we present test computations for given values of $\phi$ = $13\pi /6,\,7\pi /3,\,5\pi /2$, and $8\pi /3$. For each opening angle, we consider $\lambda _z = \left\{ 1.0,1.1, \ldots , 1.5 \right\}$. So, we have a total of 24 test cases.

4.1.1 Single-layer model

The number of elements in the thickness, circumferential and longitudinal directions are $4,\,180$ and $6$, respectively. The mesh is shown in Fig. 5. In solving the steady-state structural mechanics equations, the number of nonlinear iterations is $75$, and the number of GMRES [52] iterations per nonlinear iteration is $200$. The values of $\alpha ^1$ and $\alpha ^2$, and the number of binary-search iterations, $n_\mathrm{b }$, are shown in Table 1.

Fig. 5

Mesh for the single-layer model

Table 1 Single-layer model. First two values of $\alpha$ and the number of binary-search iterations, $n_\mathrm{b }$

Figure 6 shows the converged values of $\alpha$. From Fig. 6, we can see that $\alpha$ has a rather weak dependence on $\phi$, and it is determined almost entirely by $\lambda _z$. We represent the relationship between $\phi ,\,\lambda _z$ and $\alpha$ with the following expression obtained by least-squares fit:

$$\begin{aligned} \alpha \!=\! \left( 0.011\phi \!+\! 1.887\right) \left( 0.807\lambda _z^2 \!-\! 1.496\lambda _z \!+\! 1.171\right) . \end{aligned}$$

(67)

Fig. 6

Single-layer model. Converged values of $\alpha$

Figure 7 shows the circumferential prestretch, $\lambda _\theta$, introduced by the element-based ZS state. Figure 8 shows the actual cut angle, $\phi _\mathrm{sol }$, obtained from the computation based on the ZS state. It is clear that $\phi _\mathrm{sol }$ is the same as the specified $\phi$, and therefore the following relationship holds:

$$\begin{aligned} \phi _\mathrm{sol } = \phi . \end{aligned}$$

(68)

Figure 9 shows, for the case $\lambda _z = 1.0$, the circumferential stretch for the LC state, and the constant value of 1.0 is also consistent with what we expect to see in the LC state. With Eqs. (67) and (68), we can model the ZS state for an arbitrary shape with single layer.

Fig. 7

Single-layer model. Circumferential prestretch introduced by the element-based ZS state for $\lambda _z = 1.0$. $Markers$ are the integration-point values and the $curves$ are after least-squares projection on to the nodes

Fig. 8

Single-layer model. Actual cut angle, $\phi _{\mathrm{sol }}$

Fig. 9

Single-layer model. For the case $\lambda _z = 1.0$, circumferential stretch for the LC state

In solving the steady-state structural mechanics equations for the LC state, the number of nonlinear iterations is 200, and the number of GMRES iterations per nonlinear iterations is 1,000.

4.1.2 Three-layer model

To construct the three-layer model, we also need the thickness ratio and opening angle for each layer at the ZS state. We use experimental data [47] for that, which is shown in Table 2. The number of elements in the thickness, circumferential and longitudinal directions are 9, 180 and 6, respectively. The mesh is shown in Fig. 10.

Fig. 10

Mesh for the three-layer model

Table 2 Thickness ratios and opening angles. Figure 3 was generated from this data

Just like in the single-layer model, we iterate on $\alpha$. In solving the steady-state structural mechanics equations, the number of nonlinear iterations is $100$, and the number of GMRES iterations per nonlinear iteration is $200$. The values of $\alpha ^1,\,\alpha ^2$ and $n_\mathrm{b }$ are shown in Table 3.

Table 3 Three-layer model. First two values of $\alpha$ and the number of binary-search iterations, $n_\mathrm{b }$

Figure 11 shows the converged values of $\alpha$, and the prestretch is shown in Fig. 12. From Fig. 11, we can see that $\alpha$ is almost independent of $\overline{\phi }$, like in the single-layer model. We represent the relationship between $\overline{\phi },\,\lambda _z$ and $\alpha$ with the following least-squares fit:

$$\begin{aligned} \alpha \!=\! \left( 0.008\overline{\phi } \!+\! 1.897\right) \left( 0.811\lambda _z^2 \!-\! 1.503\lambda _z \!+\! 1.176\right) . \end{aligned}$$

(69)

As we can see, Eqs. (67) and (69) are very close. Figure 13 shows the actual cut angle obtained from the computation based on the ZS state. As expected, $\phi _\mathrm{sol }$ is not equal to $\overline{\phi }$. We represent the relationship between $\overline{\phi },\,\lambda _z$ and $\phi _\mathrm{sol }$ with the following least-squares fit:

$$\begin{aligned} \phi _{\mathrm{sol }} = \left( \overline{\phi } - 7.968 \right) \left( 0.049 \lambda _z + 0.759 \right) + 7.943. \end{aligned}$$

(70)

Figure 14 shows, for the case $\lambda _z = 1.0$, the circumferential stretch for the LC state. With Eqs. (69) and (70), we can model the ZS state for an arbitrary shape with three layers.

Fig. 11

Three-layer model. Converged values of $\alpha$

Fig. 12

Three-layer model. Circumferential prestretch introduced by the element-based ZS state for $\lambda _z = 1.0$. Markers are the integration-point values and the curves are after least-squares projection on to the nodes

Fig. 13

Three-layer model. Actual cut angle, $\phi _{\mathrm{sol }}$

Fig. 14

Three-layer model. For the case $\lambda _z = 1.0$, circumferential stretch in the LC state

In solving the steady-state structural mechanics equations for the LC states with three layers, the number of nonlinear iterations is 300, and the number of GMRES iterations per nonlinear iterations is 1,000.

4.2 Arbitrary shape: a curved tube

We use a curved-tube shape as the target shape, shown in Fig. 15. The tube is based on $1/12$ of a torus with radius of curvature $5.8~r_\mathrm{I }$. The resulting length along the centerline is $L = 3.037~r_\mathrm{I }$. The thickness ratio is 10 %.

Fig. 15

A curved tube. Cross-sectional views at the tube center (left) and perpendicular to $\mathbf e _r(0)$ (right)

To obtain the ZS shape, we use the single-layer model and the results obtained in Sect. 4.1.1. For given $\phi$ and $\lambda _z$, we use Eq. (67) to obtain $\alpha$, and then obtain $\overline{\ell _0}$ by Eq. (64). We choose the basis vector $\mathbf e _r(0)$ as shown in Fig. 15, and it is constant along $z$ in the tube coordinates system.

We have a total of 4 test cases; $\phi = \left\{ \pi /2, 5\pi /2 \right\}$ and $\lambda _z = \left\{ 1.0, 1.2\right\}$. The mesh consists of 14,400 hexahedral elements with 18,900 nodes. The number of elements in the thickness, circumferential and longitudinal directions are $4,\,180$ and $20$, respectively.

4.2.1 ZS state

With the initial ZS state $(\mathbf{X }_0^e)^0$, we iterate using the method described in Sect. 2.2, until the $L_2$ norm$\left\| \mathbf y /r_\mathrm{I }\right\|$ is less than $10^{-5}$. In solving the steady-state structural mechanics equations for each iteration, the number of nonlinear iterations is $8$, and the number of GMRES iterations per nonlinear iteration is $300$. The number of iterations to obtain the converged solution for each case is given in Table 4.

Table 4 A curved tube. Number of iterations to obtain $\mathbf{X }_0^e$

We inspect the longitudinal prestretch, $\lambda _z$, as a function of $\eta$. As can be seen in Figs. 16, 17, 18 and 19, the prestretch introduced by $(\mathbf{X }_0^e)^0$ matches the specified prestretch very well. That is because the mapping that gives us $(\mathbf{X }_0^e)^0$, which is represented by Eq. (63), was designed with the objective to match the specified longitudinal prestretch. On the other hand, the prestretch introduced by $\mathbf{X }_0^e$, shown in Figs. 20, 21, 22 and 23, is close to the specified prestretch but does not match it. That is because the objective in the iterations that give us $\mathbf{X }_0^e$ is to match the target shape.

Fig. 16

A curved tube. For the case $\phi = \pi /2$ and $\lambda _z = 1.0$, the longitudinal prestretch introduced by $(\mathbf{X }_0^e)^0$

Fig. 17

A curved tube. For the case $\phi = \pi /2$ and $\lambda _z = 1.2$, the longitudinal prestretch introduced by $(\mathbf{X }_0^e)^0$

Fig. 18

A curved tube. For the case $\phi = 5\pi /2$ and $\lambda _z = 1.0$, the longitudinal prestretch introduced by $(\mathbf{X }_0^e)^0$

Fig. 19

A curved tube. For the case $\phi = 5\pi /2$ and $\lambda _z = 1.2$, the longitudinal prestretch introduced by $(\mathbf{X }_0^e)^0$

Fig. 20

A curved tube. For the case $\phi = \pi /2$ and $\lambda _z = 1.0$, the longitudinal prestretch introduced by $\mathbf{X }_0^e$

Fig. 21

A curved tube. For the case $\phi = \pi /2$ and $\lambda _z = 1.2$, the longitudinal prestretch introduced by $\mathbf{X }_0^e$

Fig. 22

A curved tube.For the case $\phi = 5\pi /2$ and $\lambda _z = 1.0$, the longitudinal prestretch introduced by $\mathbf{X }_0^e$

Fig. 23

A curved tube. For the case $\phi = 5\pi /2$ and $\lambda _z = 1.2$, the longitudinal prestretch introduced by $\mathbf{X }_0^e$

4.2.2 LC state

The LC state for the arbitrary shape depends on the cutting location. We test three locations: $\theta _\mathrm{c } = -\pi /2, 0, \pi /2$, which are shown in Fig. 24. We compute the LC state with the initial guess coming from the slit target shape, with zero pressure. We solve the structural mechanics problem based on the steady-state equations, using 288 nonlinear iterations. The number of GMRES iterations per nonlinear iteration is 100 for the first 80 nonlinear iterations, 500 for the next 80, and 1,500 for the last 128.

Fig. 24

A curved tube. Cutting locations $\theta _\mathrm{c }$ = $-\pi /2$, 0, $\pi /2$

Figures 25 and 26 show examples of the LC state. We compare the DU and RU processes by checking the opening angle as a function of $z$. For that, we define an opening angle for each layer of elements in the $z$ direction. For each layer, the opening angle is calculated by summing the angles between the two faces of each column of elements in the thickness direction, and subtracting that from $2\pi$. The unit vector associated with each face is calculated by area-weighted averaging of the unit vectors associated with the contributing element faces. Figures 27, 28, 29 and 30 show the opening angle for the cutting location $\theta _\mathrm{c } = \pi /2$, obtained from the ZS state given by $(\mathbf{X }_0^e)^0$ and by $\mathbf{X }_0^e$ computed with the DU and RU processes.

Fig. 25

A curved tube. LC state for the case $\phi = \pi /2$ and $\lambda _z = 1.0$. The lumen is colored red, and the cut edge, $\theta _\mathrm{c } = 0$, orange. (Color figure online)

Fig. 26

A curved tube. LC state for the case $\phi = 5\pi /2$ and $\lambda _z = 1.0$. The lumen is colored red, and the cut edge, $\theta _\mathrm{c } = 0$, orange. (Color figure online)

Fig. 27

A curved tube. Opening-angle comparison for the cutting location $\phi _\mathrm{c }=\pi /2$, for the case $\phi = \pi /2$ and $\lambda _z = 1.0$

Fig. 28

A curved tube. Opening-angle comparison for the cutting location $\phi _\mathrm{c }=\pi /2$, for the case $\phi = \pi /2$ and $\lambda _z = 1.2$

Fig. 29

A curved tube. Opening-angle comparison for the cutting location $\phi _\mathrm{c }=\pi /2$, for the case $\phi = 5\pi /2$ and $\lambda _z = 1.0$

Fig. 30

A curved tube. Opening-angle comparison for the cutting location $\phi _\mathrm{c }=\pi /2$, for the case $\phi = 5\pi /2$ and $\lambda _z = 1.2$

In evaluating the performance of the methods, the opening angle we are targeting is the one obtained from the ZS state given by $(\mathbf{X }_0^e)^0$. We note that, because of the mapping from $(\mathbf{X }_0^e)_\mathrm{T }$ to $(\mathbf{X }_0^e)^0$, that opening angle cannot be expected to match the specified opening angle. As can be seen from Figures 27, 28, 29 and 30, the opening angle obtained from $\mathbf{X }_0^e$ computed with the RU process is closer to the target opening angle. Figures 31, 32, 33 and 34 show the opening angle for all three cutting locations.

Fig. 31

A curved tube. Opening-angle comparison for all three cutting locations, for the case $\phi = \pi /2$ and $\lambda _z = 1.0$

Fig. 32

A curved tube. Opening-angle comparison for all three cutting locations, for the case $\phi = \pi /2$ and $\lambda _z = 1.2$

Fig. 33

A curved tube. Opening-angle comparison for all three cutting locations, for the case $\phi = 5\pi /2$ and $\lambda _z = 1.0$

Fig. 34

A curved tube. Opening-angle comparison for all three cutting locations, for the case $\phi = 5\pi /2$ and $\lambda _z = 1.2$

5 Concluding remarks

We have presented a method for estimation of element-based ZS state in arterial FSI computations. Using the ZS state in the computations takes into account the fact that in patient-specific arterial FSI modeling the image-based arterial geometry comes from a configuration that is not stress-free. The method has three components. The first component is an iterative method, which iterates on the ZS state to match the image-based target shape for a given pressure load. The initial guess needed for the iterations is generated by the second component, which is a method for straight-tube geometries with single and multiple layers. The element-based ZS state for the straight tube is computed to match the given diameter and longitudinal stretch in the target configuration and the opening angle. The opening angle, which is related to the circumferential residual stress and treated as part of the given data, is measured by cutting the arterial wall open. The third component is an element-based mapping between the arterial and straight-tube configurations. It is for mapping from the arterial configuration to the straight-tube configuration, and for mapping the estimated ZS state of the straight tube back to the arterial configuration, so that it can be used as the initial guess for the iterative method that matches the image-based target shape. We carried out a number of test computations with the method to show how it works. The test computations were based on straight-tube configurations with single and three layers, and a curved-tube configuration with single layer. The test computations support our belief that we have a good method for estimation of element-based ZS state.