Various contact approaches for the finite cell method

Abstract

The finite cell method (FCM) provides a method for the computation of structures which can be described as a mixture of high-order FEM and a special integration technique. The method is one of the novel computational methods and is highly developed within the last decade. One of the major problems of FCM is the description of boundary conditions inside cells as well as in sub-cells. And a completely open problem is the description of contact. Therefore, the motivation of the current work is to develop a set of computational contact mechanics approaches which will be effective for the finite element cell method. Thus, for the FCM method we are developing and testing hereby focusing on the Hertz problem the following algorithms: direct integration in the cell method, allowing the fastest implementation, but suffering from numerical artifacts such as the “stamp effect”; the most efficient scheme concerning approximation properties the cell-surface-to-analytical-surface contact element designed for contact with rigid bodies leading to cell-wisely contact elements; and finally the discrete-cell-to-cell contact approach based on the finite discrete method. All developed methods are carefully verified with the analytical Hertz solution. The cell subdivisions, the order of the shape functions as well as the selection of the classes for shape functions are investigated for all developed contact approaches. This analysis allows to choose the most robust approach depending on the needs of the user such as correct representation of the stresses, or only satisfaction of geometrical non-penetration conditions.

1 Introduction

The computation of complex structures in mechanics with the aid of computers based on the finite element method (FEM) started from the 50s of the 20th century. The method is spread through and is used in all fields of structural mechanics and is also applied to many other multifield problems.

However meshing of objects with complex geometry is a cumbersome task and may lead to very large numbers of elements. The fictitious domain method (FDM) has become an alternative to use objects of only simple geometry while meshing the object with linear elements of simple rectangular geometry. The error of the method was usually rather high. However recently, the finite cell method (FCM) has been developed based on high order approximations. It can be described as a method for the computation of structures based on a mixture of high-order FEM and a special integration technique. The method is one of the novel computational methods and is highly developed in numerous works of Düster and colleagues, see in [1–3]. A special attention within this method is given to the treatment of non-homogeneous Neumann boundary conditions—applied distributed forces, as well as Dirichlet boundary conditions—fixed boundary either inside the cell or on the cell boundary, see [4] and [5]. The general implementation of high-order finite element is given in the monograph of Solin et al. [6].

The contact problem can be seen a very specific problem for FCM. In order to give a more general overview for high-order finite element methods, contact has been implemented based on the covariant description in [7], the development of various aspects has been presented in [8]. Further computational contact mechanics methods have been analyzed in terms of iso-geometric analysis in various aspects, see [9–12]. The state of the art for the isogeometric contact is given in the recent review of De Lorenzis et al. [13]. The general background used in iso-geometric analysis is given in the monograph of Cottrell et al. [14].

The fundamental monographs on computational mechanics should also be mentioned here: the most recent book of Wriggers (second edition) [15] and Laursen [16]. Various numerical methods used in computational contact mechanics are summarized and represented in the book of Yastrebov [17]. A special, geometrically exact description in covariant form is given in the book of Konyukhov and Schweizerhof [18].

Despite many publications of various aspects in both computational mechanics and FCM, namely, the general contact problem for the FCM remains open. Current developments are mostly shown in 2D, for which the classical case of geometrically exact FEM contact is described in [19] and a special 2D reduction of the general covariant 3D case is shown in [20], also many 2D conventional computational contact mechanics algorithms are described in the monograph [21]. Classically, FCM is based on integrated Legendre polynomials, however, without any restriction other classes of functions can be taken. Thus, in the current work we compare results obtained with both Integrated Legendre polynomials and Bernstein polynomials, which are basis functions for NURBS. Using higher order functions allows to improve convergence (p-element), however, changing classes of functions from Legendre polynomials to Bernstein polynomials while keeping the high order allows to improve the approximation ability (less oscillations) which is more important for contact, see the discussion in [22]. Further it is necessary to mention here the monograph on NURBS of Piegl and Tiller [23] as a reference for various spline approximations.

1.1 Alternative contact approaches for FCM

The following alternative contact algorithms are developed and tested:

• DIC contact element (direct integration in the cell)—based on the straightforward idea to compute the contact integral by given integration points in the cell;

• CSTAS contact element (cell-surface-to- analytical- surface) for contact with rigid bodies;

• DCTC contact element (discrete-cell- to-cell)—based on the representation of the integration point as a discrete finite element for both deformable bodies.

In the numerical examples section then the investigations focus on the choice of the number of cells and integration points as well as on the selection of the class of approximation functions and also spline smoothing. All examples are analyzed for convergence, numerical error and special effects (smoothness) based on the verification with the Hertz problem possessing an analytic solution.

2 Geometrically exact theory of contact: necessary parts for FCM

In this section we shortly outline the main results of the geometrically exact theory of contact which will be necessary for our case of 2D geometry.

2.1 Kinematics of contact interaction

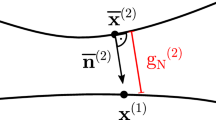
Contact within the geometrically exact theory is defined via the “Master–Slave” concept, where on the slave part a “slave point” is taken and is tested for the Closest Point Projection onto the “master surface”, see Fig. 1. A slave point $\varvec{r}_S$ is given numerically as an integration point, while the master surface is given exactly with Gaussian coordinates $\xi ^1$ und $\xi ^2$, defining a surface vector $\varvec{\rho }(\xi ^1,\xi ^2)$. The third spatial coordinate $\xi ^3$ is determined in the direction of the normal to a surface $\mathbf {n}$. In the 2D reduction we are going to have $\varvec{\rho }(\xi ^1)$ as a vector for the master curve, keeping the coordinate $\xi ^3$ in the normal direction, see Fig. 1.

Fig. 1

Idealization of contact problem with the “Master–Slave” concept and selection of the corresponding coordinate system $\xi ^1$, $\xi ^3$ on the master surface

The corresponding coordinate system on the master surface consists of the tangent vector in general form as a partial derivative $\dfrac{\partial \varvec{\rho }(\xi ^1)}{\partial \xi ^1} = \varvec{\rho }_{\xi ^1}$ (or the corresponding unit tangent vector $\varvec{\tau }$) and the normal vector $\varvec{n}$. This gives us the coordinate system as

$$\begin{aligned} \varvec{r}_S (\xi ^1,\xi ^3) = \varvec{\rho }(\xi ^1) + \xi ^3 \varvec{n}(\xi ^1) \ . \end{aligned}$$

(1)

While writing above mentioned equations, we implicitly assumed:

• A solution of the closest point projection (CPP) exists and is unique;

• The surfaces have necessary smoothness.

The existence and uniqueness of the CPP is fundamentally investigated for surfaces in [24] and for curves in [25]. Based on these theorems it is possible to represent any 3D domain as an overlapping of smooth domains in which the solution of the CPP is unique and exists. Within this process a hierarchical set of contact pairs is appearing: point-to-point, point-to-curve, curve-to-curve, point-to-surface, curve-to-surface, surface-to-surface, see more in the monograph [18].

2.1.1 Closest point projection procedure and measures of contact interactions

Initially a CPP procedure is set up as the following problem:

Find the minimum of the function corresponding to the distance between the slave point and the master curve, see Fig. 1

$$\begin{aligned} F(\xi ^1) = \frac{1}{2} \bigg \Vert \varvec{r}_S - \varvec{\rho }(\xi ^1) \bigg \Vert ^2 \rightarrow \mathrm{{min}}. \end{aligned}$$

(2)

The result is a coordinate $\xi ^1$ on the master curve. The solution is derived via the necessary condition of minimum as

$$\begin{aligned} F'(\xi ^1) = - \bigg ( \varvec{r}_S - \varvec{\rho }(\xi ^1) \bigg ) \cdot \frac{\mathrm{d} \varvec{\rho }}{\mathrm{d} \xi ^1} = 0 \ . \end{aligned}$$

(3)

In general, this problem is solved by the Newton method, for which it is necessary to compute the second derivative:

$$\begin{aligned} F''(\xi ^1) = - \bigg ( \varvec{r}_S - \varvec{\rho }(\xi ^1) \bigg ) \cdot \frac{\mathrm{d}^2 \varvec{\rho }}{\mathrm{d} (\xi ^1)^2} + \frac{\mathrm{d} \varvec{\rho }}{\mathrm{d} \xi ^1} \cdot \frac{\mathrm{d} \varvec{\rho }}{\mathrm{d} \xi ^1} \ . \end{aligned}$$

(4)

The Newton iterative scheme is constructed then as follows:

$$\begin{aligned} \xi ^1_{(n+1)}= & {} \xi ^1_{(n)} - F'(\xi ^1) \left( F''(\xi ^1) \right) ^{-1}\nonumber \\= & {} \xi ^1_{(n)} - \frac{\left( \varvec{r}_S - \varvec{\rho }(\xi ^1) \right) \cdot \varvec{\rho }_{\xi ^1}}{\left( \varvec{r}_S - \varvec{\rho }(\xi ^1) \right) \cdot \varvec{\rho }_{\xi ^1 \xi ^1} - \varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}} \ . \end{aligned}$$

(5)

Here, the first derivative of $\varvec{\rho }$ (a tangent vector to the master segment) with respect to $\xi ^1$ is abbreviated as $\varvec{\rho }_{\xi ^1} = \dfrac{\mathrm{d} \varvec{\rho }}{\mathrm{d} \xi ^1}$, and the second derivative is correspondingly as $\varvec{\rho }_{\xi ^1 \xi ^1}$.

Remark 1

In the case of a linear master segment, a closed form solution of the CPP procedure in Eq. (5) can be found, see details in [18, 20, 21].

Once the projection point is found, we can determine the relative velocity of the slave point in the coordinate system, Eq. (1).

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \varvec{r}_S (t,\xi ^1,\xi ^3)= & {} \frac{\mathrm{d}}{\mathrm{d} t} \varvec{\rho }(t,\xi ^1) + \frac{\mathrm{d}}{\mathrm{d} t} \left( \xi ^3 \varvec{n}(t,\xi ^1) \right) \nonumber \\= & {} \frac{\partial \varvec{\rho }}{\partial t} + \varvec{\rho }_{\xi ^1} \dot{\xi ^1} + \dot{\xi ^3} \varvec{n} + \xi ^3 \frac{\mathrm{d} \varvec{n}}{\mathrm{d} t}. \end{aligned}$$

(6)

Having introduced the new notations for the velocity of the projection point $\varvec{v} = \dfrac{\partial \varvec{\rho }}{\partial t}$ and for the velocity of the slave point S $\varvec{v}_S = \dfrac{\mathrm{d} \varvec{r}_S}{\mathrm{d} t}$, Eq. (6) is represented as

$$\begin{aligned} \varvec{v}_S = \varvec{v} + \varvec{\rho }_{\xi ^1} \dot{\xi ^1} + \dot{\xi ^3} \varvec{n} + \xi ^3 \frac{\mathrm{d} \varvec{n}}{\mathrm{d} t}. \end{aligned}$$

(7)

This equation contains rates of measures of the normal iteration $\xi ^3$ and for the tangential interaction $\xi ^1$ on the tangent plan at $\xi ^3=0$

$$\begin{aligned} \dot{\xi ^3}= & {} (\varvec{v}_S - \varvec{v}) \cdot \varvec{n} \ , \end{aligned}$$

(8)

$$\begin{aligned} \dot{\xi ^1}= & {} (\varvec{v}_S - \varvec{v}) \cdot \varvec{\tau } = \frac{(\varvec{v}_S - \varvec{v}) \cdot \varvec{\rho }_{\xi ^1}}{(\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1})} \ . \end{aligned}$$

(9)

The term $(\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1})$ is also geometrically describing the differential of an arc-length for the master curve

$$\begin{aligned} \mathrm{d}s = \sqrt{\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}} \; \mathrm{d} \xi ^1. \end{aligned}$$

(10)

For the weak form, Eqs. (8) and (9), are just represented by analogy:

$$\begin{aligned} \delta \xi ^3= & {} (\delta \varvec{r}_S - \delta \varvec{\rho }) \cdot \varvec{n} \ , \end{aligned}$$

(11)

$$\begin{aligned} \delta \xi ^1= & {} (\delta \varvec{r}_S - \delta \varvec{\rho }) \cdot \varvec{\tau } = \frac{(\delta \varvec{r}_S - \delta \varvec{\rho }) \cdot \varvec{\rho }_{\xi ^1}}{(\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1})} \ . \end{aligned}$$

(12)

2.2 Weak form

In order to formulate a weak form in the local coordinate system we need the representation for the vector of the relative virtual displacements on the tangent plane (via Eqs. (11) and (12)) as

$$\begin{aligned} \delta \varvec{r}_S - \delta \varvec{\rho } = \varvec{\rho }_{\xi ^1} \delta \xi ^1 + \varvec{n} \delta \xi ^3 \ , \end{aligned}$$

(13)

and the representation of the contact force in the local coordinate system as

$$\begin{aligned} \varvec{R} = \varvec{N} + \varvec{T} = N \varvec{n} + T^1 \varvec{\rho }_{\xi ^1} \ , \end{aligned}$$

(14)

where $T^1$ is a contravariant form of the tangent vector $\varvec{T}$. Then the weak form, reflecting the equilibrium of the contact forces $\varvec{R}_M$ and $\varvec{R}_S$ from both master and slave part respectively in the local form as $\varvec{R}_M ds_M = \varvec{R}_S ds_S$, see Fig. 2 is written as

$$\begin{aligned} \delta W_c= & {} \int _{s} \varvec{R} \cdot (\delta \varvec{r}_S - \delta \varvec{\rho }_M) \; \mathrm{d} s \nonumber \\= & {} \int _{s} \left[ N \; \delta \xi ^3 + T^1 (\varvec{\rho }_{\xi ^1} \varvec{\rho }_{\xi ^1}) \delta \xi ^1 \right] \; \mathrm{d} s \ . \end{aligned}$$

(15)

It should be noted that the integral is taken over the slave surface (by a set of slave integration points), while the force is given on the master surface. This allows to use covariant derivatives in the master coordinate surface for further linearization and formulation of the computational algorithms.

Fig. 2

Equilibrium of contact forces on the master $\varvec{R}_M$ and on the slave $\varvec{R}_S$ is written with respect to contact kinematics

2.2.1 Constitutive laws for N und T

Here, we employ the standard penalty method for the normal force (or one can say the one-sided linear elastic constitutive law for the normal force):

$$\begin{aligned} N = \varepsilon _N \xi ^3 H(-\xi ^3) \qquad \mathrm {mit} \qquad H(-\xi ^3) = {\left\{ \begin{array}{ll} 0, &{} \xi ^3 > 0 \\ 1, &{} \xi ^3 \le 0, \end{array}\right. }\nonumber \\ \end{aligned}$$

(16)

where $\varepsilon _N$ is a penalty parameter, $\xi ^3$ is the penetration and $H(-\xi ^3)$ is the Heaviside function, describing that the normal contact is active only if both bodies are in contact.

For the tangential force we employ here the standard return-mapping scheme for the Coloumb friction law. First, the trial force is computed as

$$\begin{aligned} T^{trial} = - \varepsilon _T \; \Delta \xi ^1 (\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}) \end{aligned}$$

(17)

where $\varepsilon _T$ is a tangential stiffness, and $\Delta \xi ^1 = \xi ^1_{current}- \xi ^1_{0}$ an incremental tangential displacement in the case of the simple update scheme. A more general updated scheme is discussed in detail in [18, 20, 21]. The real force is computed with regard to the Coulomb friction law

$$\begin{aligned} \frac{|T^{trial}|}{\sqrt{\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}}} \ge \mu |N| \end{aligned}$$

(18)

with $\mu$ as the coefficient of friction. The last equation leads to the following return-mapping algorithm:

$$\begin{aligned} T = {\left\{ \begin{array}{ll} T^{trial} = - \varepsilon _T \; \Delta \xi ^1 (\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}), &{} \frac{|T^{trial}|}{\sqrt{\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}}} < \mu |N| \ , \\ - sign(\Delta \xi ^1) \; \mu |N| \sqrt{\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}}, &{} \frac{|T^{trial}|}{\sqrt{\varvec{\rho }_{\xi ^1} \cdot \varvec{\rho }_{\xi ^1}}} \ge \mu |N| \ . \end{array}\right. } \end{aligned}$$

(19)

At this point we have to note that any further description is not limited to the penalty method for the normal force, thus, Lagrange multipliers based Mortar methods, see e.g. Wohlmuth [26], can be employed with some modifications which we will mention then.

2.3 Linearization

Since, mostly we will show non-frictional examples, the linearization is shown only for the normal part. This linearization is performed in a covariant form in the master coordinate system (1). Its derivation is available from many publications, see e.g. [20] and [19].

$$\begin{aligned} D \left( \delta W_c^N \right)= & {} \int _{s} \left( \frac{\mathrm{d} N}{\mathrm{d} t} \; \delta \xi ^3 + N \; \frac{\mathrm{d} (\delta \xi ^3)}{\mathrm{d} t} \right) \mathrm{d} s \nonumber \\= & {} \int _{s} \varepsilon _N (\delta \varvec{r}_S - \delta \varvec{\rho }) \cdot \varvec{n} \otimes \varvec{n} (\varvec{v}_S - \varvec{v}) \; \mathrm{d} s \end{aligned}$$

(20)

$$\begin{aligned}&- \int _{s} \varepsilon _N \xi ^3 \Bigl ( (\delta \varvec{r}_S - \delta \varvec{\rho }) \cdot \varvec{\tau } \otimes \varvec{n} \frac{\partial \varvec{\tau }}{\partial t}\nonumber \\&+ \, \delta \varvec{\tau } \cdot \varvec{n} \otimes \varvec{\tau } (\varvec{v}_S - \varvec{v}) \Bigr ) \mathrm{d} s \end{aligned}$$

(21)

$$\begin{aligned}&-\int _{s} \varepsilon _N \xi ^3 \kappa (\delta \varvec{r}_S - \delta \varvec{\rho }) \cdot (\varvec{\tau } \otimes \varvec{\tau }) (\varvec{v}_S - \varvec{v}) \; \mathrm{d} s. \nonumber \\ \end{aligned}$$

(22)

Remark 2

The tangent matrix derived after the linearization contains then the main part (20), the rotational part (21)) and the curvature part (22). The main part is representing the linearization of the linear constitutive law for the normal force in Eq. (16). In the case of the Lagrange multiplier method, this part is omitted and the corresponding tangent matrix will be composed from the rest the rotational and curvature parts. Details can be found in the monographs [18, 21].

2.4 Discretization and selection of the approach for FCM

For further development of the computational algorithm and a corresponding contact approach we will directly use the results of the current section, namely kinematics, weak form and its linearization. Various approaches listed in Sect. 1.1 will be varied just by selection of a certain discretization of these forms adapted to the FCM.

3 Analytical solutions for further verifications

Two analytical solutions are necessary in order to verify our results as well as to understand some artifacts appearing during the numerical solution.

3.1 Hertz solution

As discussed already earlier all contact approaches first of all, would be tested comparing to the Hertz solution, published by Heinrich Hertz in 1881 [27]. The Hertz solution is representing a solution for the contact of two cylinders, see Fig. 3 and is derived under the following assumptions, see also Johnson [28]:

• Contact surfaces are C2 smooth and contacting by their convex parts.

• No friction.

• Contact radius a is much smaller than the radius of both cylinders $R_1$ and $R_2$.

• The contacting bodies can be then approximated as elastic half-space. Linear elasticity theory is valid.

Fig. 3

2D Hertz problem: on the left—two cylinder problem under the force P; on the right–quarter of a cylinder and a plane section (cylinder with infinite radius) which is used in the current verification

The contact radius is determined as

$$\begin{aligned} a = \sqrt{\frac{4 P R_*}{\pi E_*}}. \end{aligned}$$

(23)

The contact pressure within this contact radius is distributed as

$$\begin{aligned} p(x) = \frac{2 P}{\pi a^2} \sqrt{a^2 - x^2}. \end{aligned}$$

(24)

Here P is the global force on the cylinder, and $R_*$, $E_*$ are relative radius and relative elastic module respectively:

$$\begin{aligned} \frac{1}{R_*}= & {} \frac{1}{R_1} + \frac{1}{R_2} \ , \Longrightarrow R_* = \dfrac{R_1 R_2}{R_1 + R_2} \end{aligned}$$

(25)

$$\begin{aligned} \frac{1}{E_*}= & {} \frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2} . \end{aligned}$$

(26)

In the current investigation contact of an elastic cylinder with a rigid body is considered. Thus, $R_2 \rightarrow \infty$ and $E_2 \rightarrow \infty$ leads to

$$\begin{aligned} R_*= & {} R_1 \ , \end{aligned}$$

(27)

$$\begin{aligned} E_*= & {} \frac{E_1}{1-\nu _1^2}. \end{aligned}$$

(28)

3.2 Rigid stamp problem

In order to understand some artifacts which are appearing during a numerical solution we have to understand also the solution of the rigid stamp problem presented in Fig. 4, first derived by Galin [29], see also Johnson [28].

Fig. 4

Representation of the rigid stamp problem subjected to a vertical force Q [28]

The distribution of the contact pressure has the following form

$$\begin{aligned} p(x) = \frac{Q}{\pi \sqrt{b^2 - x^2}}, \end{aligned}$$

(29)

which possesses two singular points at the boundary $x=b$ and $x=-b$; the minimal pressure is computed as $p_0 = \dfrac{Q}{\pi b}$. The pressure distribution with normalized quantities $Q=1$ and half-side $b=1$ is shown in Fig. 5.

Fig. 5

Distribution of the contact pressure for the stamp problem with force $Q = 1$ and half-side $b = 1$

4 Direct integration in the cell (DIC) contact element

The direct integration in the cell contact approach is based on the straightforward idea to compute a contact integral by given integration points in the cell. For simplicity we will start from contact with a rigid body, similar to the segment-to-analytical segment (STAS) approach, developed in detail in [30]. That is why, all proposed approaches will be verified by the Hertz solution [27]—contact of a cylinder with a rigid plane.

The straightforward idea to solve this contact problem is to test all integration points on the boundary for penetration and compute the corresponding penetration. However, even within this approach we will distinguish various types of computation of the contact integral. Due to the peculiarities of FCM, the density of integration points is quite high leading to the observation that at the boundary a layer of Gauss points may penetrate into the body, but not only boundary Gauss points.

4.1 Description of contact via a contact layer

In this scheme, we describe a proximity zone as an active contact zone with a parameter $\delta$, where $\delta$ is selected based on the density of Gauss points so that only one or optionally two layers of Gauss points are appearing in this zone. Nevertheless, the case of one layer is not a limitation of the method, and especially with a small value of penalty parameter $\varepsilon _N$ the second layer of Gauss points may appear (as shown in Fig. 7). In this case, we are working with an areal (or volumetric in 3D case) measure of contact. These types of contact measures are widely used in the dynamical simulation of rigid bodies contact, see Kane et al. [31] The selection of the contact zone is given for the Hertz contact case in Fig. 6, where one cell element of cubic order with nodes is shown (Bernstein type of polynomials) and the Gauss formula (red points) of forth order is used.

Fig. 6

Selection of possible active contact set by $\delta$: cubic element of Bernstein type, and Gauss points $4 \times 4$. Contact points are Gauss points in contact zone

Fig. 7

Computation of the contact integral via the penetrating area. Contact zone is determined by the value of penetration e into the rigid plane. 4 cells with $4\times 4$ int. points. Two layers of Gauss points are considered as an active contact zone

In this case, the contact boundary is not described by separate coordinates $\xi ^1$, instead the contact zone is determined by 2D integration points with coordinates $\xi$ and $\eta$. In order to determine them, the 2D approximation matrix $\varvec{A}(\xi ,\eta )$ is necessary, which is arising directly from the high-order approximation of the cell. This matrix consists of shape functions up to the k-th order either of the Lobatto (integrated Legendre polynomials), or of the Bernstein type depending on the analysis

$$\begin{aligned} {\varvec{\rho }}\!= & {} \! \varvec{A}(\xi ,\eta ) \varvec{x} \ \ \Longrightarrow \ \ \end{aligned}$$

(30)

$$\begin{aligned} \varvec{A} \!= & {} \! \left[ \begin{array}{lllllll} N_1(\xi , \eta ) &{}\quad \! 0 &{}\quad \! N_2(\xi , \eta ) &{}\quad \! 0 &{}\quad \! ... &{}\quad \! N_k(\xi , \eta ) &{}\quad \! 0 \\ 0 &{}\quad \! N_1(\xi , \eta ) &{}\quad \! 0 &{}\quad \! N_2(\xi , \eta ) &{}\quad \! ... &{}\quad \! 0 &{}\quad \! N_k(\xi , \eta ) \end{array}\right] .\nonumber \\ \end{aligned}$$

(31)

In the case of contact, only the main part of the tangent matrix will be used and we need a special integration scheme, organized as the subdivision into sub-cells. The active contact set is assembled as a set of penetrating Gauss points from this proximity zone. Another problem is the definition of the deformed normal: the normal is described as normal projection of Gauss points onto the un-deformed boundary. This is the most simple and straightforward approach.

4.1.1 Contact integral as an area integral

Since, a penetrating area is detected—a contacting boundary is represented by a layer—then the contact integral is reflecting the energy associated with the penalty method and is computed over this area, namely as a sum over these Gausss points, see representation in Fig. 7, in which two layers of Gauss points are penetrating.

Fig. 8

Subdivision of the cell element into sub-domains/sub-cells

Computation of the contact integral is similar to the domain integral for the finite cell, but only points included in the active contact set are taken into account:

$$\begin{aligned} \delta W_c= & {} \frac{1}{m \; n} \sum _{k=0}^{m-1} \sum _{l=0}^{n-1} \sum _{i=1}^{ngp} \sum _{j=1}^{ngp} \; N \delta \xi ^3 \; H(-\xi ^3) \;\nonumber \\&det\varvec{J}(\xi ,\eta ) \; w_i \; w_j, \end{aligned}$$

(32)

with N from Eq. (16). A cell element is split into $m \times n$ finite sub-domains/sub-cells, each of it is integrated by $ngp \times ngp$ Gauss integration formula. This sub-domain integration is shown in Fig. 8 The full domain A is split into sub-domains $A_{ij}$; $i=0,m$; $j=0,n$ and then in each sub-domain integration is performed, in due course, using high order integration formulas with $ngp \times ngp$ integration points. The global domain is discretized with high order functions using variables $\xi ,\eta$, while the local sub-domain/sub-cell is integrated using local variables $\xi _i,\eta _i$. The following transformation to the global domain coordinates is necessary

$$\begin{aligned} \xi= & {} \frac{\xi _i}{m} + \frac{2i+1}{m} - 1, \; \quad i = 0, 1, 2, \ldots m-1 \ , \end{aligned}$$

(33)

$$\begin{aligned} \eta= & {} \frac{\eta _j}{n} + \frac{2j+1}{n} - 1, \quad j = 0, 1, 2, \ldots n-1 \ . \end{aligned}$$

(34)

and then the full integral over the domain is represented as a composed formula for integration over sub-domains/sub-cells $A_{ij}$:

$$\begin{aligned}&\int \limits _{-1}^{+1} \int \limits _{-1}^{+1} f(\xi ,\eta ) \; \mathrm{d} \xi \; \mathrm{d} \eta = \sum _{k=0}^{m-1} \sum _{l=0}^{n-1} \int \limits _{A_{ij}} f(\xi ,\eta ) \; \mathrm{d} \xi \; \mathrm{d} \eta \nonumber \\&\quad = \frac{1}{m \; n} \sum _{k=0}^{m-1} \sum _{l=0}^{n-1} \int \limits _{-1}^{+1} \int \limits _{-1}^{+1}\nonumber \\&\qquad \times f \left( \frac{\xi _i}{m} \!+\! \frac{2i+1}{m} - 1 , \; \frac{\eta _j}{n} \!+\! \frac{2j+1}{n} - 1 \right) \; \mathrm{d} \xi \; \mathrm{d} \eta .\; \end{aligned}$$

(35)

This method has been also used in computational contact mechanics forming the Mortar method in order to satisfy the contact patch test, see in [32] as well as in high-order contact implementations [7, 18].

4.2 Spline approximation of the contact boundary via Gauss points

A more precise method includes the approximation of the boundary by a spline function. In this case, a contact line is determined via a spline over the penetrating points close to the boundary. A composed Bezier spline is used here, where only the boundary integration points (most left and most right in the cell) are used as approximation points, see Fig. 9.

Fig. 9

Approximation of the contact line as complex Bezier spline with the boundary integration points as approximation points

Fig. 10

Explanation of the integration over line. Contact boundary can be approximated as a line between cell boundaries

The advantages of the current approach are obvious:

• The deformed boundary can be fully taken into account;

• Contact kinematics in the sense of Sect. 2.1 are computed precisely.

Now the normal $\varvec{n}$ and tangent vector $\varvec{\tau }$ are computed based on the spline geometry. They are uniquely defined due to selection of a C1-smooth composed approximation spline. The quality of the approach is definitely depending on the number of integration points close to the real boundary.

4.2.1 Computation of the contact integral over a line

Integration over a contact line is a standard case for the computational contact mechanics fully related to the kinematics and weak form, described in Sect. 2.1. The precise computation will be given due to the geometry of the approximation spline described in Sect. 4.2. However, in order to decrease computational efforts, the boundary inside the cell can be assumed to be straight taking into account that during the realization of the FCM the number of sub-cells is quite large.

In this case the corresponding coordinates $x_i$ and $x_{i+1}$, $y_i$ and $y_{i+1}$ are computed relatively fast based on the deformed geometry, see Fig. 10. This is especially simple for the circular geometry in the current example. Therefore, the Jacobian for the line (arc-length) is computed as

$$\begin{aligned} \sqrt{det\varvec{M}} = \frac{1}{2} \sqrt{(x_i - x_{i+1})^2 + (y_i - y_{i+1})^2}. \end{aligned}$$

(36)

Afterwards, the contact integral is computed over line as

$$\begin{aligned} \delta W_c \!=\! \frac{1}{m} \sum _{k=0}^{m-1} \sum _{l=0}^{n-1} \sum _{i=1}^{ngp} \sum _{j=1}^{ngp} \; N \delta \xi ^3 \; H(-\xi ^3) \; \sqrt{det\varvec{M}} \; w_i, \end{aligned}$$

(37)

where m is the number of cell subdivision along OX and n is the number of cell subdivision along OY, where the sub-cell (sub-domain) integration is performed with $ngp \times ngp$ integration points.

4.2.2 Collocation method

So far, we simplified the computation of the integral as computation over a linear segment instead of a curve segment. Nevertheless, it is still possible to accelerate the computation by taking a value of the integral only as the value at the penetrating point—such a simple and fast method is known as collocation method in numerical mathematics. In this case, the contact integral is simplified as sum over the active contact Gauss points

$$\begin{aligned} \delta W_c = \sum _{k=0}^{m-1} \sum _{l=0}^{n-1} \sum _{i=1}^{ngp} \sum _{j=1}^{ngp} \; N \delta \xi ^3 \; H(-\xi ^3) \ . \end{aligned}$$

(38)

5 Verification of the DIC method with the analytical solution and discussion

The first set of the verification will contain the numerical analysis of the direct integration in the cell (DIC) contact element, developed in Sect. 4. For the numerical example we choose the Hertz problem, shown on the right side of the Fig. 3. The quarter of a circle is divided into 4 cell elements whereas the elements 1, 2 and 4 contain boundary points, see Fig. 11, and are represented by sub-cells ($5\times 5$ in Figure). The a-priori condition for the contact radius $a \ll R$ will be fulfilled within the cell element with number 1. Both, integrated Legendre and Bernstein polynomials will be used. The radius of the cylinder is $R = 4$, therefore using FCM a square with a side $b = 4$ is meshed into $2 \times 2$ elements. The plate thickness assuming a plane-stress state is taken as $d = 1$, however, it is well known that there is no influence of this parameter on the stress-distribution in the 2D plane system. The material is assumed to be linear elastic with $E = 10^6$ and Poisson’s ratio $\nu = 0.3$. The dimension system is assumed to be consistent, that is why all dimensions are intentionally omitted. The Penalty parameter is taken relatively high as $\varepsilon _N = 10^9$ providing a compromise between the value of penetration and the condition number of the matrix. All computations are displacement controlled, in which the final vertical displacement $v = 0.1$ is applied in 10 steps. Theoretically, it is possible to perform any force controlled loading if at least one integration point at the pseudo-time $t = 0$ (loading parameter) is active during the initial contact. The last case is requesting, however, special types of integration points such as Lobatto integration points, laying on the boundary as working with Gauss points is automatically leading to a kinematic system.

Fig. 11

Discretization for the Hertz problem with 4 elements and further adaptive cell subdivision $5 \times 5$ etc. of the boundary area

In our first example we are going to compare the contact stresses for various integration schemes. Since in all cases contact stresses cannot be computed as for the standard penalty method $N = \varepsilon _N \xi ^3$, then the stress components are computed at Gauss points and further extrapolated to the boundary using the same shape functions in the cell element. On the boundary then the normal stresses are computed with the Cauchy formula (39) for boundary stresses using either the un-deformed normal vector $\mathbf {n}$ for the area integration, or for the schemes, which are computed from the deformed boundary for the line type of integration. In all cases, the normal contact stresses are computed as:

$$\begin{aligned} \sigma _n = \sigma _x n_x^2 + 2 \tau _{xy} n_x n_y + \sigma _y n_y^2 \ . \end{aligned}$$

(39)

The resulting stresses for the representation are normalized such that both the maximal stress and the contact radius are equal to unit values $p_{max}=1$ and $a=1$. The following values are used for normalizing:

contact radius

$$\begin{aligned} a = \sqrt{\frac{4 P_{num} R (1-\nu ^2)}{\pi E}} \end{aligned}$$

(40)

and normal stress

$$\begin{aligned} p(x=0) = \frac{2 P_{num}}{\pi a}. \end{aligned}$$

(41)

The load $P_{num}$ is computed as global reaction force at elements 3 and 4 when the displacement v is applied.

5.1 Example—comparison of various integration schemes

In this example, the order of Bernstein polynomials is taken to be 5, subdivision into cells of the boundary elements 1, 2 and 4 is $7 \times 7$ sub-cells, see Fig. 11 in which $5 \times 5$ subdivision is shown exemplarily. Fig. 12 shows a comparison between the integration over an area (Sect. 4.1.1), the integration over a line (Sect. 4.2.1) and the collocation method (Sect. 4.2.2). The chosen penalty parameters for each method are shown in Fig. 12.

Fig. 12

Comparison of the normalized Hertz contact stresses for various integration methods: integration over an area ($\varepsilon _N = 10^9$); integration over a line ($\varepsilon _N = 10^9$) and the collocation method ($\varepsilon _N = 10^8$). Shape functions: Bernstein polynomials of 5th order. Cell subdivision of the bounding element is $7 \times 7$ cells

Fig. 13

Approximation of the circular profile via step-wise sets of Gauss points within the FCM method is causing “the stamp effect”

The main results can be summarized as follows:

• 1. All three integration methods are showing similar results.

• 2. They are showing a relatively good approximation of the analytical solution besides the area close to zero $x \rightarrow 0$. Here the minimum of the stresses is found.

• 3. Outside the contact area stresses are not zero.

As expected the various methods are showing different global force values $P_{num}$ used for scaling see Eq. (41): $P_{num} = 23690$ for the area integration, $P_{num} = 25130$ for the line integration and $P_{num} = 26250$ for the collocation method.

Fig. 14

Extreme appearance of the “stamp effect” for the Hertz problem: linear approximation of the elements with $2 \times 2$ cell subdivisions. Linear meshes with $20 \times 20$ and $40 \times 40$ elements

5.1.1 Stamp effect

The phenomenon of oscillations for high order finite element is a well known numerical artifact for the Hertz problem since the first publications [20] und [8], and various techniques have been developed for both high order finite element and isogeometric finite element interpolations, see the series of publications devoted especially to this problem [8–13]. Nevertheless, here another type of phenomena as numerical artifact (minimum at the center and shifted maximum) is appearing. This can be explained as a “stamp effect” due to a coarse cell discretization, namely if the element cell discretization resp. the cell subdivision is coarse the contact area is a straight line, see Fig. 13, and the stamp solution see Sect. 3.2 is prevailing rather than the Hertz solution see Sect. 3.1.

In order to reconstruct “the stamp effect” in its extreme fashion, the following measures are taken:

• Elements used in FCM are all with linear approximations.

• Each cell element is subdivided into $2 \times 2$ sub-cells.

• Area integration will be employed.

The result with different cell element subdivisions $20 \times 20$ and $40 \times 40$ compared to the analytical Hertz solution is shown in Fig. 14.

So far, we can summarize that “the stamp effect” is clearly prevailing

• if a coarse subdivision into sub-cells is used;

• if lower order functions are used for the FCM.

That is why, the next step is to investigate, how it is possible to improve the results controlling the above mentioned measures.

Fig. 15

Influence of the cell subdivision within the contacting boundary: $4 \times 4$, $7 \times 7$, $10 \times 10$ and $20 \times 20$ sub-cells. $2 \times 2$ cell elements of Bernstein type of 5th order

5.2 Influence of cell subdivision

The influence of cell subdivision will be studied with the fixed parameters from the first example in Sect. 5.1: number of cell element subdivision is $2 \times 2$, order of Bernstein polynomials is 5. The cell subdivisions are taken as $4 \times 4$, $7 \times 7$, $10 \times 10$ and $20 \times 20$ sub-cells in the bounding elements using $4 \times 4$, $7 \times 7$, $9 \times 9$ and $20 \times 20$ Gauss point integration formulas respectively. The result is shown in Fig. 15. Obviously, the cell refinement in the sense of increasing the number of sub-domains / sub-cells in the integration formula Eqs. (32), (35) allows to improve the result, though a small artifact concerning the “stamp effect” is still present even for a high refinement.

Fig. 16

Influence of the increasing order of the Bernstein polynomials: 3, 5, 7, 10. Bounding elements are subdivided into $10 \times 10$ sub-domains/sub-cells

5.3 Influence of the order of the shape functions

The influence of the order of the shape function will be studied with the following fixed parameters from the first example in Sect. 5.1: number of cell element subdivision $2 \times 2$, the contacting element is subdivided into $10 \times 10$ sub-cells, Bernstein type of approximation functions with increasing order 3, 5, 7 and 10 are used. The results are shown in Fig. 16. Obviously, increasing the order of approximation is not leading to a considerable improvement compared with increasing the cell subdivision, see Sect. 5.2.

Fig. 17

Trying to resolve “the stamp effect” using a smoothing of the contact boundary. Normal vector refer to initially smooth geometry—Bezier 1. Normal vector refers to deformed smooth geometry—Bezier 2. Lobatto integration points are used without any smoothing—Lobatto points. Cell subdivision $7 \times 7$ sub-cells, order of Bernstein polynomials is 5

Fig. 18

Changing the B-spline for smoothing during the penetration causing a relatively high error—the “stamp effect” is still present

5.3.1 Comparison of various spline smoothing techniques: a trial to resolve “the stamp effect”

Here we will compare a spline smoothing, described in Sect 4.2, with the goal to eliminate “the stamp effect”. We are going to distinguish the following approaches:

• 1. The boundary is approximated by a B-spline function as discussed in Sect 4.2, however, the normal vector (resp. tangent vector) is not updated and taken with respect to the initial undeformed configuration – curve “Bezier 1” in Fig. 17.

• 2. The boundary is approximated by a B-spline as discussed in Sect 4.2, all geometric parameters such as the normal vector (resp. tangent vector) are computed with respect to the deformed geometry of the spline – curve “Bezier 2” in Fig. 17.

• 3. No smoothing curve is employed, but Lobatto integration points are used within FCM. Since they are laying on the boundary, there is a ”hope” to eliminate “the stamp effect”. This is the curve “Lobatto points” in Fig. 17.

For all computation, the Bernstein polynomials of 5th order are used for the shape functions, cell subdivision of the bounding area is $7 \times 7$ sub-domains/sub-cells.

Obviously at a first look, “Bezier 1” is resolving the stamp effect in the best fashion. However, convergence in this case is very slow and with applied displacements larger than $v=0.08$ disconvergence is obtained unless the global residual tolerance is set artificially to $10^{-6}$ instead of standard $10^{-15}$. The disadvantage of smoothing using boundary Gauss points in the cell from the deformed geometry (Bezier 2) is explained in Fig. 18. Here we see that the normal vector approximations are distorted, because the curve is build by the boundary Gauss points, which are explicitly included into the active contact set. In this case, we are more approximating “the stamp” effect, rather than eliminating it.

Finally, it becomes obvious that the Lobatto integration is not resolving the problem at all, but rather producing new effects due to another active set of integration points laying exactly on the boundary.

5.4 Preliminary summary for the direct integration in the cell (DIC) contact approach

Direct usage a Gauss points from the Cell in FCM allows the simplest implementation of contact determination in its geometric fashion satisfying non-penetration. All proposed integration methods such as area integration, line integration and even collocation are leading to almost identical results for contact stresses. However, the main disadvantage of these methods is “the stamp effect”, which is an artifact due to the line-wise position of integration points. The classical smoothing of contact boundaries with B-spline functions is not resolving the problem: if the geometric parameters are computed with respect to the reference geometry, then severe convergence problems are arising; if the geometric parameters are computed with respect to the deformed smoothed geometry, then “the stamp effect” is not eliminated. The only reasonable way to resolve the stamp problem is a cell refinement in the sense of increasing the number of sub-domains / sub-cells in the integration formula eqns. (32), (35). Further, increasing the order of approximation plays not such an important role, see Fig. 15. In the next Section we propose a special “cell-surface-to-analytical-surface”, CSTAS contact element, which is free from “the stamp effect”.

Fig. 19

Cell-wisely construction of the contact element CSTAS laying exactly on the contact boundary

6 Cell-surface-to-analytical-surface (CSTAS) contact approach

In the previous sections we proposed the direct method based on using the given integration points inside cells within the finite cell method. Here, we are developing a special contact element cell-wisely, namely, the contact element will be based on the exact boundary inside the sub-domain/sub-cell. This requires more transformations inside each sub-domain/sub-cell, which will be illustrated using the Hertz problem.

The main idea of the CSTAS contact approach is the building of a linear contact element exactly on the contact boundary inside each sub-domain/sub-cell, see Fig. 19. This contact element will have its own parametrization, though it is defined in the coordinate system of the finite element cell-wisely.

6.1 Definition of the contact element in the local coordinate of the finite element

The most difficult issue constructing/designing the CSTAS contact element is the definition of the local finite element convective coordinates for the contact boundary $(\xi _i,\eta _i)$ and $(\xi _{i+1},\eta _{i+1})$ for each cell, see Fig. 19.

In the current specific example of the Hertz problem, it is possible to program this via a loop in $\xi$-direction. The $\xi _i$-coordinate for the cell is given by the cell subdivision, and the $\eta _i$-coordinate is simply computed from the circular cylinder equation:

$$\begin{aligned} \eta _i = \eta _M - \sqrt{R^2 - (\xi _i - \xi _M)^2} \ , \end{aligned}$$

(42)

where $\xi _M$ and $\eta _M$ are the coordinates of the cylinder center with radius R in the local element coordinate system.

6.1.1 More general approach to determine the local coordinates $\xi$ and $\eta$ for the contact element

In the general case of an arbitrary boundary inside the finite element, we first introduce a reparametrization of the finite element in the following form. For the linear finite element, shown in Fig. 19, we introduce the mid-point of the element $\varvec{\rho }$ together with corresponding coordinate vectors computed as derivative at mid-point $\varvec{\rho }_\xi$ and $\varvec{\rho }_\eta$.

$$\begin{aligned}&\varvec{\rho } = \frac{\varvec{x}_1 + \varvec{x}_2 + \varvec{x}_3 + \varvec{x}_4}{4} \ , \end{aligned}$$

(43)

$$\begin{aligned}&\varvec{\rho }_\xi = \frac{- \varvec{x}_1 + \varvec{x}_2 + \varvec{x}_3 - \varvec{x}_4}{4} \ , \end{aligned}$$

(44)

$$\begin{aligned}&\varvec{\rho }_\eta = \frac{- \varvec{x}_1 - \varvec{x}_2 + \varvec{x}_3 + \varvec{x}_4}{4}. \end{aligned}$$

(45)

Now the local element coordinate system is build as the description of any vector $\varvec{a}$ inside the element:

$$\begin{aligned} \varvec{a} = \xi \; \varvec{\rho }_\xi + \eta \; \varvec{\rho }_\eta \ . \end{aligned}$$

(46)

This procedure is possible because of the simple rectangular geometry of the cell element as the most efficient feature of the FCM method. In this cell-wise coordinate system, the coordinates of the boundary $(\xi _i,\eta _i)$ and $(\xi _{i+1},\eta _{i+1})$ should be defined.

Again we show this on the example of the circle. Let $\varvec{m}$ be a center of the circle with radius R. The equation of the circle is given as, see Fig. 19.

$$\begin{aligned} R = | \varvec{m} - \varvec{\rho } - \varvec{a} | \ . \end{aligned}$$

(47)

Since in this specific example the convective coordinate $\xi$ is given via the cell subdivision in the corresponding direction, then Eq. (47) can be resolved via $\eta$ as:

$$\begin{aligned}&\varvec{\rho }_\eta ^2 \; \eta ^2 + \left( 2 \varvec{\rho }_\xi \varvec{\rho }_\eta \; \xi + 2 \varvec{\rho } \varvec{\rho }_\eta - 2 \varvec{m} \varvec{\rho }_\eta \right) \eta \nonumber \\&\qquad + \left( \varvec{\rho }_\xi \; \xi + \varvec{\rho }-\varvec{m} \right) ^2 - R^2 = 0 \ . \end{aligned}$$

(48)

Finally $\eta$ is derived as a solution of this quadratic equation:

(49)

An additional geometric criterion is necessary for the final decision to select $\eta _1$ or $\eta _2$ as solution (either lower or upper semi-circle). In simple cases it is obvious a-priori.

Remark 3

One can see, that for more complex boundaries the analogues of Eqs. (47) and (48) can be non-linear and the solution will then require an additional inner solver to find the points $(\xi _i,\eta _i)$ and $(\xi _{i+1},\eta _{i+1})$.

6.2 Construction of the CSTAS contact element

Once the coordinates $(\xi _i,\eta _i)$ and $(\xi _{i+1},\eta _{i+1})$ of the segment are defined, we have to build the classical segment wise contact element, see details for 2D in [20]. For the segment-to-analytical-segment (STAS) approach in 2D (see also in [30]), we need the approximation matrix $\varvec{A}$ to obtain the relative displacement $(\delta \varvec{r}_S - \delta \varvec{\rho })$ at the contact element, which is necessary to describe all kinematic parameters of the contact element, see e.g. Eqs. (11), (12), see Sect. 2.1.

$$\begin{aligned} (\delta \varvec{r}_S - \delta \varvec{\rho }) = \varvec{A} \delta \varvec{x}. \end{aligned}$$

(50)

For the STAS approach the approximation matrix $\varvec{A}$ contains the linear shape functions only for the master segment $M_l(\xi ^1), l = 1 \ldots 2$:

$$\begin{aligned} \varvec{A} = \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} M_1(\xi ^1) &{} 0 &{} M_2(\xi ^1) &{} 0\\ 0 &{} M_1(\xi ^1) &{} 0 &{} M_2(\xi ^1) \end{array}\right] . \end{aligned}$$

(51)

Here, the local coordinate $\xi ^1$ is equivalent to $\zeta$ in Fig. 19: $\xi ^1 \equiv \zeta$.

In order to obtain the classical contact element, we need to construct the mapping of two pairs of coordinates $(\xi _i,\eta _i) ; (\xi _{i+1},\eta _{i+1})$ into the segment coordinate $\xi ^1$

$$\begin{aligned} \{ P \, \vert \, \{(\xi _i,\eta _i) ; (\xi _{i+1},\eta _{i+1}) \} \longrightarrow \{-1 \!\le \! \xi ^1 \le 1\} \}, \ \ i=0 ... n. \end{aligned}$$

(52)

This mapping is given by the following projection matrix $\varvec{P}$:

$$\begin{aligned} \varvec{P} = \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} N_1(\xi _i,\eta _i) &{}\quad 0 &{}\quad \cdots &{}\quad N_{nen}(\xi _i,\eta _i) &{}\quad 0 \\ 0 &{}\quad N_1(\xi _i,\eta _i) &{}\quad \cdots &{}\quad 0 &{}\quad N_{nen}(\xi _i,\eta _i) \\ N_1(\xi _{i+1},\eta _{i+1}) &{}\quad 0 &{}\quad \cdots &{}\quad N_{nen}(\xi _{i+1},\eta _{i+1}) &{}\quad 0 \\ 0 &{}\quad N_1(\xi _{i+1},\eta _{i+1}) &{}\quad \cdots &{}\quad 0 &{}\quad N_{nen}(\xi _{i+1},\eta _{i+1}) \end{array}\right] . \end{aligned}$$

(53)

Here $N_k(\xi _i,\eta _i), k = 1 \ldots nen$ are shape functions of high order for the 2D element, nen is the number of nodes reflecting the order of the approximation.

In this case, all geometric parameters containing the relative displacement (velocity), e.g. penetration (see Eq. (8)) is computed as

$$\begin{aligned} \xi ^3 = (\mathbf {r}_s - {\varvec{\rho }}) \cdot \mathbf {n}= \varvec{n}^T \varvec{A} \varvec{P} \varvec{x_{el}}, \end{aligned}$$

(54)

where $\varvec{x_{el}}$ is a nodal vector for the finite element.

The CSTAS contact is fully defined if both residual and corresponding tangent matrix are defined.

We present here only the main part of the tangent matrix, which is obtained after the discretization of Eq. (20):

$$\begin{aligned} \varvec{K}^N = \sum _{i=0}^{n-1} \sum _{j=1}^{ngp} \varepsilon _N \; \varvec{P}^T \varvec{A}^T \varvec{n} \otimes \varvec{n} \varvec{A} \varvec{P} \; \frac{w_j \sqrt{det\varvec{M}}}{n} \ . \end{aligned}$$

(55)

Here, the double sum is running over the number of cells n in $\xi$-direction within the finite element and over the number of Gauss points ngp for the cell contact element (CSTAS) with corresponding weights $w_j$. The Jacobian (arc-length) for the the cell contact element (CSTAS) is computed as

$$\begin{aligned}&\sqrt{det\varvec{M}} \nonumber \\&\quad = \frac{1}{2} \sqrt{(x(\xi _i,\eta _i) \!-\! x(\xi _{i+1},\eta _{i+1}))^2 \!+\! (y(\xi _i,\eta _i) \!-\! y(\xi _{i+1},\eta _{i+1}))^2}.\nonumber \\ \end{aligned}$$

(56)

Normally, we are going to use two Gauss points ($ngp = 2$) for each cell-wise contact segment, in which the weight is $w_j = 1$.

The rotational part following Eq. (21) is constructed by analogy, while the curvature part, see Eq. (22), is zero because the contact segment is linear.

The residual reflecting the discretization of the normal part of the weak form in Eq. (15) is computed respectively as:

$$\begin{aligned} \varvec{R}^N = \sum _{i=0}^{m-1} \sum _{j=1}^{ngp} \varepsilon _N \; \varvec{P}^T \varvec{A}^T \varvec{n} \; \frac{w_j \sqrt{det\varvec{M}}}{m} \ . \end{aligned}$$

(57)

Remark 4

Of course, both tangent matrix and residual are computed for the active contact set, i.e. if the penetration in Eq. (54) is negative, reflecting the constitutive law (or penetration method) in Eq. (16).

The normal vector $\varvec{n}$ to the segment (here the continuum is assumed to be above the contact element and the external normal is pointing downwards) is computed in global coordinates as

$$\begin{aligned} \varvec{n} = \frac{1}{2 \sqrt{det\varvec{M}}} \begin{pmatrix} y(\xi _{i+1},\eta _{i+1}) - y(\xi _i,\eta _i) \\ x(\xi _i,\eta _i) - x(\xi _{i+1},\eta _{i+1}) \end{pmatrix}, \end{aligned}$$

(58)

with the Jacobian $\sqrt{det\varvec{M}}$ computed in Eq. (56).

6.2.1 Summary of computational efforts for CSTAS contact element

The computational efforts for the construction of the CSTAS contact elements inside a single element cell are summarized as follows:

• Subdivision of a cell into n sub-cells and corresponding definition of the boundary coordinates $(\xi _i,\eta _i) ; (\xi _{i+1},\eta _{i+1})$ for each sub-division/sub-cell. This is given in the current example by the n times solution of Eqs. (47) or (48), or by a more complex solution in the case of arbitrary boundaries see Remark 3.

• The n contact elements are assembled using the projection matrix $\varvec{P}$ in Eq. 53, dimension of which $2 \times nen$ depends on the order of functions involved in the high order approximation of the cell element.

• Finally, the tangent matrix $\varvec{K}$ (see the normal part in Eq. (55)) and the residual $\varvec{R}^N$ are computed at the active contact set formed by ngp integration points for each sub-cell element.

Therefore, each cell element subdivided into n sub-division/sub-cells contains n contact elements, while forming of the contact active set is performed as penetration check at $ngp \times n$ integration points.

6.3 Verification of the CSTAS contact element

Again we will verify the solution comparing to the Hertz solution. The influence of the number of cell subdivisions, the order of approximation and the difference between classes of shape functions will be investigated.

6.3.1 Influence of cell subdivisions

We are still working with an example of meshing as given in Fig. 11. Here, Bernstein polynomials of 5th-order are used. The cell subdivisions of the bounding cell elements are $4 \times 4$, $7 \times 7$, $10 \times 10$ and $20 \times 20$ sub-domains/sub-cells with corresponding number of CSTAS contact elements. The results are given in Fig. 20. All material parameters are kept as in the previous example. The normal stresses are computed with regard to the stresses from the cells by using Eq. (39), that is why the stresses are still present even outside the contact zone. Obviously, by using the CSTAS contact approach “the stamp effect” is fully eliminated, however, we still need cell refinement in order to achieve “good correlation” of stresses within the contact zone. Further the results look somehow “stabilizing”, so there is only a small variance in stresses for $7 \times 7$, $10 \times 10$ and $20 \times 20$ cell subdivisions.

Fig. 20

Influence of the cell subdivision of bounding elements by $4 \times 4$, $7 \times 7$, $10 \times 10$ and $20 \times 20$ sub-cells. Finite element cells interpolated by Bernstein type shape functions of 5th order are given

6.3.2 Comparison of various orders of approximation for shape functions

As the starting position we will take $10 \times 10$ cell subdivisions. The order of shape functions is increasing as 3, 5, 7 and 10. Obviously, see Fig. 21, increasing the order introduces oscillations at the boundary similar to the well-known Gibbs phenomenon. Such an effect is also well known for high-order finite elements see in [7] as well as for isogeometric finite elements, see the review in [13].

Fig. 21

Comparison of various order of approximations for Bernstein shape functions: 3, 5, 7 and 10. Cell subdivision: $10 \times 10$ sub-cells

6.3.3 Comparison between Bernstein- and integrated Legendre polynomials for shape functions

As is known, the classical high-order FEM is employing integrated Legendre polynomials, while Bernstein polynomials are rather reflecting the iso-geometric finite element method, because the Bernstein polynomials are basis functions for NURBS elements. Here, we compare this in terms of the FCM. Using our example with $4 \times 4$ finite element cells by the following cases:

• 1. Bernstein polynomials of 5th order. Cell subdivision is $7 \times 7$ sub-cells for the bounding area.

• 2. Integrated Legendre polynomials of 5th order. Cell subdivision is $7 \times 7$ cells for the bounding area.

• 3. Bernstein polynomials of 7th order. Cell subdivision is $10 \times 10$ cells for the bounding area.

• 4. Integrated Legendre polynomials of 7th order. Cell subdivision is $10 \times 10$ cells for the bounding area.

Fig. 22

Comparison between Bernstein-and integrated Legendre polynomials for shape functions. In all cases $10 \times 10$ cell subdivision in contacting area

Obviously, see Fig. 22, the difference between integrated Legendre polynomials is rather small compared with Bernstein polynomials, though the quality of approximation using Bernstein polynomials is slightly better than using integrated Legendre polynomials. Nevertheless, it still valid that higher order approximations may lead to high oscillations around the point of loosing continuity.

6.3.4 Adaptive cell refinement with CSTAS method

As expected from the usage of finite elements in contact, the adaptive cell refinement will perform similar to an adaptive finite element refinement, see Wriggers and Scherf [33]. Since, within $h-p$ refinement the variety to combine various types of refinement is quite high, we exemplarily choose here only two examples of subdivisions:

• 1. Fairly high dense mesh with low order of approximation: $20 \times 20$ finite elements of 2th order (integrated Legendre polynomials) with additional $10 \times 10$ cell subdivision of the bounding area (more dense area in the Figure) with a corresponding CSTAS contact element, see the representation of the mesh by integration points in Fig. 23.

• 2. Medium dense mesh with higher order of approximation: $8 \times 8$ finite cell elements of 5th order (integrated Legendre polynomials) with additional $10 \times 10$ cell subdivision of the bounding area (more dense area in the Figure) with a corresponding CSTAS contact element, see the representation of the mesh by integration points in Fig. 24.

Fig. 23

$20 \times 20$ finite elements of 2nd order. Additional $10 \times 10$ cell subdivisions of the bounding area (more dense area in the Figure)

Fig. 24

$8 \times 8$ finite elements of 5th order. Additional $10 \times 10$ cell subdivisions of the bounding area (more dense area in the Figure)

Fig. 25

Comparison of adaptive cell refinement of two cases: Case 1: $20 \times 20$ finite cell elements of 2nd order. $10 \times 10$ cell subdivisions. Case 2: $8 \times 8$ finite cell elements of 5th order. $10 \times 10$ cell subdivisions

Fig. 26

Representation of discrete-cell-to-cell as contact between balls with radius $\chi$. Same radius $\chi$ is used for both contacting bodies in the case of the same cell density definition

The usage of integrated Legendre polynomials allows to simplify the meshing tremendously, together with the “adaptive cell refinement”, organized simply as separated cell subdivisions which is essentially identical to the separated integration formula with sub-domains, see Eq. 35 and also the theory in [18]. A comparison of the results is presented in Fig. 25 corresponding to the meshes shown in Figs. 23 and 24.

In both cases, see Fig. 25, there is good correlation with the analytical Hertz solution for both contact stress and contact radius, though the rule known from $h-p$ refinement is confirmed. For non-smooth functions and singularities it is better to use more elements (more sub-cells) with lower order rather than less elements with higher order. This rule is well represented here, in which case 2 shows a better correlation with the analytical Hertz solution.

6.4 Preliminary summary for the CSTAS contact approach

Using the cell-surface-to-analytical-surface (CSTAS) contact approach allows to eliminate fully such an artifact as “the stamp effect”, which is present for the direct integration in the cell (DIC) contact approach. Nevertheless, cell refinement is necessary in order to improve the result, keeping in mind that increasing the order of approximation is less effective. The best solution is given then by the adaptive mixed adaptive mesh and cell refinement.

7 Discrete cell to cell (DCTC) as the simplest contact algorithm for two deformable bodies

Up to now, we studied in detail all effects appearing during the development of the computational contact algorithm for contact of the deformable body with a rigid boundary. In the following, we would like to discuss the most simple implementation for contact between deformable bodies. This method is based on the nature of FCM—a set of Gauss points is represented as discrete elements and then a contact algorithm used for the finite discrete method (FDM) is employed. Details about FDM implementations are presented in the monograph of Munjiza [34].

The idea of the DCTC method is presented in Fig. 26 based on the assumption that a rather dense cell subdivision is employed. In this case, each cell is embedded in a circle with the radius $\chi$, allowing a ball-to-ball discrete contact, or (a discrete-cell-to-cell) method. The contact radius $\chi$ should be adjusted with regards to the distance between the neighboring integration points. Such an idea, using a ball fully filling a finite element with further ball-to-ball contact algorithm implementation, has been realized by Belytschko and Neal for explicit dynamics computations as the so-called pinball algorithm, see in [35].

Penetration in this case is computed as penetration between two circles with centers $\varvec{r}_{S_1}$ and $\varvec{r}_{S_2}$ describing in fact the position of integration points:

$$\begin{aligned} \xi ^3 = | \varvec{r}_{S_1} - \varvec{r}_{S_2} | - 2 \chi . \end{aligned}$$

(59)

By the selection of the value for the radius $\chi$ (here the size of cells and corresponding radius for contacting bodies are taken into account) the following facts should be taken into account:

• Convergence of the solution is better if the radius is larger;

• The radius $\chi$ should not be too large in order to avoid overlapping of the nearest integration points;

• The radius $\chi$ should not be too small in order to avoid loss of contact, if one circle (ball) would slide between other two without contact.

Fig. 27

Linear-Quadratic regularization of the contact force N, see [36]; penalty method

7.1 Regularization of the normal contact

For the regularization of normal contact we are selecting a revision of the penalty method, as proposed by Durville in [36]. This method is starting with zero derivative of the regularized contact force at zero penetration and combines quadratic regularization with a linear one. In order to combine the linear and the quadratic zone, an additional parameter $\xi ^3_{reg}$ is introduced, defining the boundary between the linear and the quadratic zone for the normal force N (see Fig. 27). For further linearization, it is necessary also to compute the derivative $N'$ depending on $\xi ^3_{reg}$. The force N and its derivative $N'$ are given then by the following formulas:

$$\begin{aligned} N= & {} {\left\{ \begin{array}{ll} 0 \; , &{} \xi ^3 > 0 \\ \frac{\varepsilon _N}{2 \; \xi ^3_{reg}} (\xi ^3)^2 \; , &{} -\xi ^3_{reg} \le \xi ^3 \le 0 \\ - \varepsilon _N \left( \xi ^3 + \frac{\xi ^3_{reg}}{2} \right) \; , &{} \xi ^3 < -\xi ^3_{reg} \end{array}\right. } \end{aligned}$$

(60)

$$\begin{aligned} N'= & {} {\left\{ \begin{array}{ll} 0, &{} \xi ^3 > 0 \\ \frac{\varepsilon _N}{\xi ^3_{reg}} (\xi ^3), &{} -\xi ^3_{reg} \le \xi ^3 \le 0 \\ - \varepsilon _N \; , &{} \xi ^3 < -\xi ^3_{reg} \end{array}\right. } \end{aligned}$$

(61)

Selection of $\xi ^3_{reg}$ is user dependent, however, the choice of this will influence the convergence.

7.2 Tangent matrix and residual

The proposed regularization in the previous section allows to build the residual and tangent matrix directly using the results from Sect. 2.2 and 2.3 as

$$\begin{aligned}&\varvec{f} = \varepsilon _N \; \xi ^3 \; [A]^T \varvec{n} = N \; [A]^T \varvec{n} \end{aligned}$$

(62)

$$\begin{aligned}&\varvec{K}^N = \varepsilon _N [A]^T \varvec{n} \otimes \varvec{n} [A] = N' \; [A]^T \varvec{n} \otimes \varvec{n} [A] \end{aligned}$$

(63)

where [A] is position matrix approximating the position of two integration points

$$\begin{aligned} \varvec{r}_{S_1} - \varvec{r}_{S_2} = [A] \{ \varvec{x} \} \end{aligned}$$

(64)

with $\varvec{x}$ as a nodal vector for the coordinates of two interacting integration points.

7.3 Verification with Hertz problem

The example for verification is shown in Fig. 28. In order to represent the DCTC contact elements we choose finite elements of 2nd order and $5 \times 5$ subdivisions leading to 3 Gauss points surrounded by circles for the DCTC contact element. The rigid line is subdivided element-wisely with Gauss points, see Fig. 28, however, with a trial to represent an arbitrary case, rather than point-to-point contact. The initial distance between bodies and radius $\delta$ is selected in such a way to avoid the initial penetration of circles.

Fig. 28

Example of the discretization for the Hertz problem. Element of the 2nd order and $5 \times 5$ subdivisions leading to 3 Gauss points surrounded by circles for DCTC contact element

In analogy to previous contact approaches, we analyze now the influence of cell subdivisions and order of approximation functions. The same geometry and material as before are used: $E = 10^6$, $\nu = 0.3$, $b = 4$, $R = 4$, $t = 1$. An uniform displacement $v = 0.1$ is applied at the upper boundary in 10 steps; the penalty parameter is chosen as $\varepsilon _N = 10^9$. The contact radius is taken as $\chi = 0.02$, the rigid line is represented with 11 Gauss points for all cases. The contact radius is chosen with regard to the Gauss points density in order to fulfill the ball-to-ball type contact. The initial distance between the bodies is given as $\delta = 0.04$.

7.3.1 Influence of cell subdivisions

In this example, the area is modeled with finite elements of Bernstein type shape functions of 5th order. The contacting area is split into $4 \times 4$, $7 \times 7$, $10 \times 10$ and $20 \times 20$ sub-domains/sub-cells consequently. A comparison of the results concerning contact pressure is given in Fig. 29.

Fig. 29

Influence of the cell subdivision for the DCTC contact element: $4 \times 4$, $7 \times 7$, $10 \times 10$ and $20 \times 20$. Finite elements of 5th order (Bernstein)

Obviously, the result is converging (stabilizing) starting from the $7 \times 7$ cell subdivision. No “stamp effect” is observed at all, however, the shape of the stress curve is concave instead of convex as for the Hertz problem. This is the direct effect of the selected penalty regularization of the force, presented in Sect. 7.1. If the regularization would be chosen directly following the analytical Hertz solution the stresses could be better approximated.

7.3.2 Influence of the order of approximation

In order to study the influence of the order of approximation, we select $10 \times 10$ cell subdivisions and compute with increasing order 3, 5, 7, 10. The results are shown in Fig. 30.

Fig. 30

Influence of the order of approximation with the DCTC contact element: 3, 5, 7, 10 order of the Bernstein polynomials. $10 \times 10$ cell subdivisions

Since, increasing the order of approximation within DCTC leads to the necessity of more integration points, then the results, as expected, are looking similar to increasing the cell subdivision in Sect. 7.3.1. The artifact of the specific penalty regularization is still present.

7.3.3 Self-contact in a pore

Since one of the advantages of the DCTC contact element is the possibility to describe contact between deformable bodies, we choose to compute the self-contact problem in a pore (Fig. 31).

Fig. 31

Representation of self-contact inside a pore; force controlled loading

Fig. 32

Computation of self contact inside a pore. 2 finite cell elements of 5th order Bernstein polynomials. Cell subdivision is $6 \times 6$ cells. Integration points are shown. The pore is not closed

As the most simple model, a half of the object with a pore is discretized. The pore is modeled with setting the material indicator within the FCM method to $\gamma = 10^{-12}$ inside the pore, however, only linear elastic material with $E = 10^6$, $\nu = 0.3$ is used. With setting the material indicator to a small value, the novel modeling type of contact modeling using the standard finite element is analyzed by Wriggers et al. in [37]. Since, the relatively large deformations are limited in this case, we intentionally choose an elliptic shape of the pore in order to reach contact faster. Half-size of the plate is $b = 2$, the height $h = 0.4$. The size of the elliptic pore is defined with the principle half-axes $R_1 = 1.8$ and $R_2 = 0.09$. In this case, the pore is more close to an open crack – otherwise we have to use a non-linear material law, which is suitable for large deformations. The distributed force at the boundary is then $q = 180$, which is applied in 6 load steps with $\Delta q = 30$ each. The penalty parameter for the DCTC contact element is $\varepsilon _N = 10^8$ with a contact radius of $\chi = 0.02$. The contact radius is chosen with regard to the Gauss points density in order to fulfill the ball-to-ball type contact. Obviously, the effectiveness is highly dependent on the cell subdivision. The pore is not closed in this case (stiff behavior) keeping the distance $\delta = 0.04$ in between computed via Eq. 59, see Fig. 32, which is directly the result of the control radius with this $6 \times 6$ subdivision.

In order to reach the state “self contact” better , the structure is subdivided into $24 \times 6$ sub-cells – 24 in horizontal direction – with contact radius $\chi = 0.006$ for the corresponding DCTC contact elements. As expected these parameters allow to detect self contact inside the pore, see Fig. 33. This final example is selected only to show the possibility to model self-contact with the DCTC contact element. A more appropriate model would require, of course, a more suitable material law for the continuum, allowing large deformations.

Fig. 33

Comparison of self contact in a pore. The cell subdivision into $24 \times 6$ cells and smaller contact radius allows to improve self-contact inside the pore (softer behavior)

7.3.4 Preliminary summary for the DCTC contact element

Using the DCTC contact element allows to model contact between deformable parts of bodies in a straightforward fashion. This rather simple method, however, requires careful selection of the contact radius $\chi$ for corresponding contacting circles. The verification on the Hertz problem shows that this type of contact is not suffering from “the stamp effect”, however, the results are depending on the type of the regularization for the contact force. Thus, the selected type of the regularization is delivering a concave shape of the contact Hertz stresses (fully in agreement with the chosen regularization) instead of convex shape in reality. A possible improvement would be the usage of a regularization in the form of Hertz solution exactly—a not very general procedure.

Nevertheless, the effectiveness of the proposed DCTC contact element in terms of satisfaction of the geometrical condition of non-penetration is illustrated by the example ”Self-contact in pore”, providing that the cell subdivision is initially important for the stiff behavior (locking) of the structure.

8 Summary

In the current work, several contact approaches have been developed for the FCM.

• DIC contact element (direct integration in the cell)—based on the straightforward idea to compute the contact integral by the given integration points in the cell;

• CSTAS contact element (cell-surface-to- analytical- surface) for contact with rigid bodies;

• DCTC contact element (discrete-cell- to-cell)—based on the representation of the integration point as a discrete finite element for both deformable bodies.

The Direct Integration in the Cell (DIC) contact approach can be chosen with several integration techniques: area, line integration and collocation method (for 2D problems). The DIC is the fastest method to implement contact for the FCM. In due course the collocation method is the fastest among the integration methods providing that all integration methods are delivering almost the same contact stresses. However, the DIC method is suffering from the “stamp effect” which can be resolved at least partially by cell refinement. The influence of the order of approximation as well as the classes of approximation functions (integrated Legengdre or Bernstein polynomials) is rather negligible.

The cell surface to analytical surface (CSTAS) is the most effective method concerning the approximation properties for contact stresses, however, the most complex one as it requires to build the contact element cell-wisely precisely on the contact boundary inside each sub-division/sub-cell containing the boundary. The CSTAS contact approach is free from “the stamp effect”. For best results, cell refinement or even adaptive cell refinement is, however, necessary.

The discrete cell to cell (DCTC) contact approach is particularly developed for two contacting deformable bodies. The method is build by analogy to the finite discrete element method and depends on additional parameters such as the radius of contacting circle $\chi$, which should be chosen with regard to the integration point density. The stress representation is, however, also highly depending on the way of the regularization of the contact force involved. Nevertheless, the method delivers good approximation and may fully satisfy the geometric condition of non-penetration. The results are illustrated concerning the self-contact in a pore.

It is expected that the best method for deformable bodies would be a Mortar type method cell surface to cell surface (CSTCS) in which a contact pair is build from the two possible contacting cells similar to the segment-to-segment mortar method in computational contact mechanics. However, this requires additional investigations and lays outside the scope of the current article.