Abstract
A powerful technique for the analysis of nonlinear oscillators is the rigorous reduction to phase models, with a single variable describing the phase of the oscillation with respect to some reference state. An analog to phase reduction has recently been proposed for systems with a stable fixed point, and phase reduction for periodic orbits has recently been extended to take into account transverse directions and higher-order terms. This tutorial gives a unified treatment of such phase reduction techniques and illustrates their use through mathematical and biological examples. It also covers the use of phase reduction for designing control algorithms which optimally change properties of the system, such as the phase of the oscillation. The control techniques are illustrated for example neural and cardiac systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nonlinear oscillators—dynamical systems with stable periodic orbits—arise in many systems of physical, technological, and biological interest. Examples from biology include pacemaker cells in the heart, the firing of action potentials in neurons, and circadian rhythms.
A powerful classical technique for the analysis of periodic orbits is the rigorous reduction to phase models, with a single variable describing the phase of the oscillation with respect to some reference state. Through reduction to phase models, one can understand the dynamics of high-dimensional and analytically intractable models in a more convenient form (see, e.g., [2, 33, 43, 53, 117]), and design useful phase-based control strategies (see, e.g., [15, 18, 48, 69, 75, 76, 95, 96, 106, 110, 118]). There are also situations for which extensions of phase reduction can improve the ability to understand and control the dynamics of a system with a periodic orbit [5, 37, 71, 105, 113]. Moreover, a useful analog to phase reduction can be formulated for systems with a stable fixed point, which allows novel control algorithms to be developed for such systems [112].
This tutorial gives a unified treatment of phase reduction for nonlinear oscillators and for systems with a stable fixed point and includes a discussion of recent developments, mathematical examples for which results can be found analytically, and biological examples for which numerical techniques must be employed. It also covers the use of phase reduction for the design of control algorithms which optimally change properties of the system, such as the phase of an oscillation, with examples for controlling neural and cardiac systems. Although by no means comprehensive, this tutorial illustrates the exciting potential of phase reduction and phase-based optimal control methods for biological applications, and it is hoped that it will provide a useful entry point for the reader who wishes to explore such methods further.
This tutorial is organized as follows. Section 2 describes the standard phase reduction and phase response curves for nonlinear oscillators and uses these to design energy-optimal phase control and time-optimal control of a thalamic neuron. Section 3 describes isostable reduction for systems with a stable fixed point and a method for controlling cardiac alternans based on this reduction. Section 4 covers an extension of standard phase reduction called augmented phase reduction which includes the concept of isostable response curves for nonlinear oscillators and applies this to energy-optimal phase control; it also describes an extension to second-order phase reduction. Section 5 discusses global isochrons and isostables and includes a control scheme for steering a trajectory from a stable periodic orbit to an unstable fixed point which uses knowledge of such global coordinates. Section 6 gives a brief introduction to phase-based control of oscillator populations. Concluding thoughts are given in Sect. 7.
2 Standard phase reduction and control
Consider an autonomous vector field
having a stable hyperbolic periodic orbit \(\mathbf {x}^\gamma (t)\) with period T. We define the set of all points in the basin of attraction as \({\mathcal {B}}\). For each point \(\mathbf {x}^*\) in \({\mathcal {B}}\), there exists a unique \(\theta (\mathbf {x}^*)\) such that [9, 33, 45, 53, 59, 115,116,117]
where \(\mathbf {x}(t)\) is a trajectory starting with the initial point \(\mathbf {x}^*\). The function \(\theta (\mathbf {x})\) is called the asymptotic phase of \(\mathbf {x}\) and takes values in \([0, 2\pi )\). Other conventions, related to this through a simple rescaling, define the asymptotic phase to take values in [0, T) or in [0, 1).
Let \(\mathbf{x}_0^\gamma \) be the point on the periodic orbit where the phase is zero. Our typical convention is to choose \(\mathbf{x}_0^\gamma \) as corresponding to the global maximum of the first coordinate on the periodic orbit. An isochron is a level set of \(\theta (\mathbf {x})\), that is, the collection of all points in the basin of attraction of \(\mathbf {x}^\gamma \) with the same asymptotic phase [115, 117]. We note that if \(\mathbf{x}(0)\) is a point on a periodic orbit, the isochron associated with that point is the set of all initial conditions \(\tilde{\mathbf{x}}(0)\) such that \(||\mathbf{x}(t) - \tilde{\mathbf{x}}(t)|| \rightarrow 0\) as \(t \rightarrow \infty \). Isochrons extend the notion of phase of a stable periodic orbit to the basin of attraction of the periodic orbit. It is conventional to define isochrons so that the phase of a trajectory on the periodic orbit advances linearly in time:
both on and off the periodic orbit. Points at which isochrons of a periodic orbit cannot be defined form the phaseless set [116].
Isochrons can be shown to exist for any stable hyperbolic periodic orbit. They are codimension one manifolds as smooth as the vector field, and transversal to the periodic orbit \(\mathbf {x}^\gamma \). Their union covers an open neighborhood of \(\mathbf {x}^\gamma \). This can be proved directly by using the implicit function theorem [9, 33] and is also a consequence of results on normally hyperbolic invariant manifolds [103].
Control theory seeks to design inputs to a dynamical system which change its behavior in a desired way. With this in mind, we consider the perturbed system
where \(\mathbf{U}(\mathbf{x},t)\) is a small control input. The evolution of this system in terms of isochrons is [2, 53]
Evaluating on the periodic orbit \(\mathbf{x}^\gamma \) for the unperturbed system gives, to leading order,
Here \(\mathbf{Z}(\theta ) \in {\mathbb {R}}^n\) is the gradient of phase variable \(\theta \) evaluated on the periodic orbit and is referred to as the (infinitesimal) phase response curve (PRC) [19, 24, 38, 78, 117]. It quantifies the effect of an external perturbation on the phase of a periodic orbit. We call (5) the standard phase reduction. In this tutorial we will consider inputs \(\mathbf{U}(t)\), with no dependence on \(\mathbf{x}\).
2.1 Calculating phase response curves
Given the importance of PRCs for phase reduction, we now describe several ways in which they can be calculated.
This is the classical way to compute the PRC, which is useful especially in experimental studies. Letting \(\mathbf{x} = (x_1, x_2, \ldots , x_n)\), by definition
where \(\varDelta \theta = \theta (\tilde{\mathbf{x}}^\gamma + \varDelta {x_i} \hat{i}) - \theta (\tilde{\mathbf{x}}^\gamma )\) is the change in \(\theta (\mathbf{x})\) resulting from the perturbation \(\tilde{\mathbf{x}}^\gamma \rightarrow \tilde{\mathbf{x}}^\gamma + \varDelta x_i \hat{i}\) from the base point \(\tilde{\mathbf{x}}^\gamma \) on the periodic orbit in the direction of the \(i{\mathrm{th}}\) coordinate. Since \(\dot{\theta } = 2 \pi /T\) everywhere in the neighborhood of \(\mathbf{x}^\gamma \), where the dot indicates \(\frac{d}{dt}\), the difference \(\varDelta \theta \) is preserved under the flow; thus, it may be measured in the limit as \(t \rightarrow \infty \), when the perturbed trajectory has collapsed back to the periodic orbit. That is, \(\left. \frac{\partial \theta }{\partial x_i} \right| _{\mathbf{x}^\gamma }\) can be found by comparing the phases of solutions in the infinite-time limit with initial conditions on and infinitesimally shifted from base points on \(\gamma \).
Practically, determination of the change in phase \(\varDelta \theta \) in computation of (6) can vary from relatively straightforward to quite complex depending on the particular features of the system of interest. For instance, when applying phase reduction strategies in neurons [78], the timing of a neural action potential is generally taken to correspond to \(\theta = 0\). In this case, the change in phase \(\varDelta \theta \) resulting from a perturbation can simply be inferred by measuring deviations from the expected timing between spikes. On the opposite end of the spectrum, phase estimation becomes difficult in more complicated models when there are no easily identifiable features that directly correspond to the phase. In these cases, more sophisticated methods need to be employed. For example, motivated by the problem of understanding the oscillatory biomechanics of cockroach running, the authors of [84] devise a methodology to estimate the phase of a population of phase-locked oscillators from multivariate data that is both robust to noise and measurement error. These ideas were later built upon in [85] to identify the dimension required to adequately characterize a periodic orbit using only measurement data. See [10] for other results on phase response curves for running cockroaches. Other phase inference algorithms [89] have been developed for use in low signal-to-noise environments, for instance, in electroencephalogram (EEG) recordings. Other methods have been developed that are applicable to multiple coupled oscillators which are not phase locked. For example, Kralemann et al. [50] develops a strategy to simultaneously measure the phases of two interacting oscillators using passive observations and uses this technique to analyze respiratory influence on heart rate variability [100]. Also, Wilson and Moehlis [111] developed a strategy for inferring the phase response curve of individual oscillators from aggregate population data, Kralemann et al. [51] proposes a method for determining directional connectivity in small populations of oscillators, and Krishnan et al. [52] investigates phase response curves that result when multiple perturbations are applied per cycle. While phase reduction methods are immensely useful for reducing the complexity of a complicated model displaying stable periodic oscillations, there are many practical considerations to be aware of when working with real, noisy, and possibly unreliable experimental data.
Adjoint method [2, 20, 23, 40]
Another technique for finding the PRC involves solving an associated adjoint equation, which we now derive following [2]. This adjoint equation can be solved numerically with the program XPP [20].
Consider an infinitesimal perturbation \(\varDelta \mathbf{x}\) to the trajectory \(\mathbf{x}^\gamma (t)\) at time \(t=0\). Let \(\mathbf {x}(t)\) be the trajectory evolving from this perturbed initial condition. Defining \(\varDelta \mathbf {x} (t)\) according to \(\mathbf {x}(t)=\mathbf {x}^{\gamma }(t) + \varDelta \mathbf {x} (t)\),
For the phase shift defined as \(\varDelta \theta = \theta (\mathbf {x}(t)) - \theta (\mathbf {x}^\gamma (t))\), we have
where \(\langle \cdot , \cdot \rangle \) defines the standard inner product and \(\nabla _{\mathbf{x^\gamma }(t)}\theta \) is the gradient of \(\theta \) evaluated at \({\mathbf{x^\gamma }(t)}\). We recall from above that \(\varDelta \theta \) is independent of time (after the perturbation at \(t=0\)) so that taking the time derivative of (8) yields, to lowest order in \(\Vert \varDelta \mathbf{x} \Vert \),
Here the matrix \(D \mathbf{F}^\mathrm{T}(\mathbf {x}^\gamma (t))\) is the transpose (i.e., adjoint) of the (real) matrix \(D \mathbf{F}(\mathbf {x}^\gamma (t))\). Since the above equalities hold for arbitrary infinitesimal perturbations \(\varDelta \mathbf{x}(t)\), we have
This follows from non-degeneracy of the inner product, which states that if \(<a,b> = 0\) for all b, then \(a=0\). To see this more rigorously, we can rearrange (9) to give
At any time t, by choosing \(\varDelta \mathbf{x}(t)\) to be a(t) we get \(\langle a,a \rangle = 0\) which from definite positivity of the inner product implies that \(a=0\). This can be rearranged to give (10).
Thalamic neuron model: Left panel shows how the spike time changes by \(\delta T\) under an external perturbation \(\delta v\). Here, black (resp., red) line shows the voltage under no (resp., \(\delta v\)) perturbation. In the right panel, the blue line (resp., red dots) shows the first component of the PRC computed from the adjoint (resp., the direct) method (color figure online)
Finally, note that
which in particular must hold at \(t=0\). Thus, we must solve (10) subject to the condition
Since \(\nabla _{\mathbf{x}^\gamma (t)} \theta \) evolves in \({\mathbb {R}}^n\), (11) supplies only one of n required initial conditions; the rest arise from requiring that the solution \(\nabla _{\mathbf{x}^\gamma (t)} \theta \) to (10) be T-periodic [20, 23, 40].
We note that [37] describes a method for calculating a generalization of phase response curves based on an invariance equation for planar systems and shows that this is equivalent to the adjoint method. This approach will be discussed in more detail in Sect. 5.
Example PRC calculation: thalamic neuron model
As an illustration, we calculate the PRC using both the direct method and the adjoint method for the thalamic neuron model [88] for the spiking behavior of neurons in the thalamus:
In these equations, \(I_\mathrm{b}\) is the baseline current, which we take as \(5\,\upmu \hbox {A/cm}^2\), v is the transmembrane voltage, and \(h,\ r\) are the gating variables of the neuron which describe the modulation of the flow of ions across the neural membrane. u(t) represents the applied current as the control input. For details of the currents (\(I_L, I_\mathrm{Na}, I_K, I_T\)), functions \(h_{\infty }, \tau _h,r_{\infty }, \tau _r\), and the rest of the parameters, see Appendix A. With no control input, these parameters give a stable periodic orbit with period \(T=8.3955\) ms.
The first (i.e., voltage) component of the PRC for this periodic orbit is shown in the right panel of Fig. 1. In this figure, we used XPP to calculate the first component of the PRC from the adjoint method. For the direct method, a MATLAB code was written where perturbations of size \(\delta v = -\,0.3\) were given at 20 points spread along the periodic orbit. Once the perturbed trajectories came reasonably close to the periodic orbit, spike time changes caused by the perturbations were scaled to obtain the corresponding phase changes, which when normalized by the magnitude of the perturbation gives the first component of the PRC.
Analytical results
There are certain dynamical systems for which PRCs can be calculated analytically. Here we consider three illustrative examples which can arise for simplified models of biological systems and physiological rhythms [24, 28, 117]: general radial isochron clocks which capture key characteristics of phase models, \(\lambda - \omega \) systems including the Hopf bifurcation normal form, and a system which has been used to model neurons undergoing a SNIPER bifurcation.
\(\bullet \) General radial isochron clocks
Consider planar dynamical systems that can be written in the form
where r and \(\phi \) are standard polar coordinates in two dimensions, \(K(\phi )>0\) for all \(\phi \), and there is a stable periodic orbit \(\mathbf{x}^\gamma \) with radius \(r_\mathrm{po}\) found by solving \(G(r_\mathrm{po}) = 0\). Such a periodic orbit will have period \(T=\int _0^{2\pi }d\phi /K(\phi )\). Because the dynamics of \(\phi \) are independent of r, the isochrons for such systems are radial lines. When \(K(\phi )\) is a constant, such a system is often referred to as a radial isochron clock [28, 41]. Because we allow K to be non-constant, we will refer to this system as a general radial isochron clock. The following calculation of PRCs for general radial isochron clocks generalizes previously published results in [28, 41] for radial isochron clocks.
For such systems, it is possible to find the PRC using the following geometrical argument. From Fig. 2, we see that
Taking the partial derivative of both sides with respect to x,
Rearranging and evaluating on the periodic orbit (i.e., using \(x = r_\mathrm{po} \cos \phi \) and \(y = r_\mathrm{po} \sin \phi \)),
PRCs are defined in terms of the change in the phase variable \(\theta \), and to obtain this, we recall that the isochrons are radial and note that
Therefore
Similarly,
We can rewrite the right-hand side of (17) and (18) in terms of the phase variable \(\theta \) by using (16) to give
where we take \(\theta =0\) at \(\phi = \phi _0\); inverting this will give \(\phi \) as a function of \(\theta \).
As an alternative derivation, we can start with (19) and differentiate with respect to r and \(\phi \) to give
Transforming to Cartesian coordinates using
and a similar expression for \(\frac{\partial \theta }{\partial y}\), we can obtain the PRC as
This is identical to (17) and (18). We note that PRCs for general radial isochron clocks take both positive and negative values, meaning that the same instantaneous, infinitesimal perturbation can either increase or decrease the phase, depending on when it is applied.
\(\bullet \,\lambda -\omega \) systems
Consider planar systems that can be written in the form
where r and \(\phi \) are again standard polar coordinates in two dimensions and there is a stable periodic orbit with nonzero radius \(r_\mathrm{po}\) (found by solving \(G(r_\mathrm{po}) = 0\)) and angular frequency \(\omega = H(r_\mathrm{po})\). We assume that \(G'(r_\mathrm{po}) \ne 0\). Note that these equations can be viewed as a polar coordinate representation of \(\lambda -\omega \) systems [24, 49] and include the normal forms for the Hopf bifurcation and the Bautin bifurcation [35, 54]. The PRC for examples of such systems has been calculated in references including [2, 5, 19, 22, 24, 37, 40, 68]. In general, we have
where
It is readily verified that this is solved by (cf. [46, 68])
Transforming to Cartesian coordinates \((x,y) = (r \cos \phi , r \sin \phi )\), and using the fact that \(\theta = \phi \) on the periodic orbit (since \(\partial \theta /\partial \phi = 1\), and choosing \(\theta =0\) to coincide with \(\phi =0\)), we obtain
cf. [22, 24], where \(\hat{x}\) and \(\hat{y}\) are unit vectors in the x and y directions, respectively. We note that PRCs for \(\lambda -\omega \) systems are appropriately scaled and shifted sinusoidal functions, which take both positive and negative values. As for the general radial isochron clocks, the same instantaneous, infinitesimal perturbation can either increase or decrease the phase, depending on when it is applied.
\(\bullet \)SNIPER example [2, 19]
The SNIPER (Saddle-Node Infinite PERiod) bifurcation [35, 54], also called SNIC (Saddle-Node on Invariant Circle) bifurcation, takes place when a saddle-node bifurcation of fixed points occurs on a periodic orbit. This bifurcation arises, for example, for Type I neurons [19]. Following the method of [19], we ignore the direction(s) transverse to the periodic orbit and consider the one-dimensional normal form for a saddle-node bifurcation of fixed points:
where x may be thought of as local arclength along the periodic orbit. For \(\eta >0\), the solution of (25) traverses any interval in finite time; as in [19], the period T of the orbit may be approximated by calculating the total time necessary for the solution to (25) to go from \(x = -\,\infty \) to \(x = +\,\infty \) and making the solution periodic by resetting x to \(-\,\infty \) every time it “fires” at \(x=\infty \). This gives \(T = \frac{\pi }{\sqrt{\eta }}\); hence, \(\omega = 2 \sqrt{\eta }\).
Since (25) is one-dimensional, Ermentrout [19] computes
where \(\frac{\mathrm{d}x}{\mathrm{d}t}\) is evaluated on the solution trajectory to (25). This gives
as first derived in [19], but with explicit \(\omega \)-dependence displayed as in [2]. In contrast to general radial isochron clocks and \(\lambda -\omega \) systems, the PRC for this SNIPER system is always positive. Thus instantaneous, infinitesimal perturbations will always increase the phase (or decrease the phase, depending on the sign of the perturbation) regardless of the time at which they are applied, although the magnitude of the phase change will be different. We will consider a different SNIPER example later in Sect. 4. Also note that the example in [21] shows that care must be used in relating bifurcations to PRCs.
It is also possible to calculate analytic approximations to the PRC near a homoclinic bifurcation [2], a heteroclinic orbit [90], and for relaxation oscillators [44].
2.2 Control based on standard phase reduction
Since phase-reduced models have lower dimension than the full models from which they came, optimal control problems for phase-reduced models give lower-dimensional boundary value problems and thus are simpler to solve. In this tutorial, we will consider control problems for which the control input only directly affects a single state variable. For example, in neural control applications one might apply control in the form of an injected electrical current which only affects the equation for the transmembrane voltage. Moreover, we assume that the control input only depends on time, and not on the state variables. That is, we take \(\mathbf{U(\mathbf{x},t)} = (u(t),0_{n-1})\), where without loss of generality we say that the control affects the first state variable \(x_1\), and \(0_{n-1}\) is a vector of \((n-1)\) zeros.
We consider three different problems. The first, energy-optimal phase control, illustrates the basics of how standard phase reduction can be used to find optimal control inputs. The second, energy-optimal phase control with a charge-balance constraint, illustrates how integral constraints can be incorporated into such problems. The third, time-optimal control with a charge- balance constraint, illustrates how the choice of a cost function affects the nature of the optimal control inputs.
Energy-optimal phase control [69]
Suppose at \(t=0\) our system starts at the point \(\mathbf {x_0^\gamma }\) on \(\mathbf{x}^\gamma (t)\). Without any control input, we expect the trajectory will return to the point \(\mathbf {x_0^\gamma }\) at time \(t=T\). Our objective here is to devise a control which returns the trajectory to its initial position after time \(t=T_1\), where \(T_1\ne T\). Possible motivations include changing the time at which a neuron fires (a first step toward controlling neural populations), shifting one’s circadian rhythm to adjust to a new time zone, or changing the phase of cardiac pacemaker cells to treat cardiac arrhythmias [71].
To do this, consider the standard phase reduction for the oscillator given by
where \(\omega \) is the oscillator’s natural angular frequency, \(Z(\theta )\) is the component of the phase response curve in the \(x_1\) direction, and u(t) is the control stimulus. We assume that \(Z(\theta )\) vanishes only at isolated points and that \(\omega > 0\), so orbits of full revolution are possible. We will assume that \(\theta =0\) corresponds to a special event for the oscillator, such as the firing of an action potential for a neuron, i.e., when a neuron’s transmembrane voltage is maximal.
Suppose that for the specified time \(T_1\) and for all stimuli u(t) which evolve \(\theta (t)\) via (27) from \(\theta (0) = 0\) to \(\theta (T_1) = 2 \pi \), we want to find the one which minimizes the cost function
that is, the square-integral cost on the current. For example, for a neural system this would correspond to causing a neuron which fires an action potential at \(t=0\) to fire another action potential at \(t=T_1\); if the system has resistance R obeying Ohm’s law, this corresponds to minimizing the power \(P \sim u^2 R\).
We apply calculus of variations (see Appendix B) to minimize [25]
with \(\lambda \) being the Lagrange multiplier (sometimes called a costate) which forces the dynamics to satisfy (27). The associated Euler–Lagrange equations are
where \(' = \hbox {d}/\hbox {d}\theta \). To find the optimal u(t), (31) and (32) need to be solved subject to the conditions
This is a two-dimensional two-point boundary value problem where the boundary conditions for \(\theta (t)\) are given in (33). The appropriate initial conditions \((\theta (0),\lambda (0))\) can be found, for example, by using a shooting method in which updated initial conditions are determined via Newton iteration; see Appendix C. The solution \((\theta (t),\lambda (t))\) using this initial condition can then be used in (30) to give the optimal stimulus u(t). Reference [69] shows under certain conditions that the optimal stimulus for this problem is unique.
Energy-optimal phase control for the thalamic neuron model: Left column shows the trajectory and time series, the middle column shows the evolution of phase \(\theta (t)\) and \(\lambda (t)\), and the right column shows the PRC and the control input. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)
Energy-optimal phase control example: thalamic neuron model
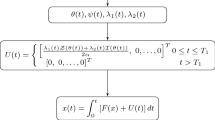
As an example, consider the thalamic neuron model given by Eqs. (12–14) with the same parameters as before. We set \(T_1=1.2T\) to demonstrate the control. We calculate the PRC of the model using XPP and then solve the Euler–Lagrange equations (31–32) as a two-point boundary value problem with boundary conditions given by Eq. (33). This gives \(\theta (t)\) and \(\lambda (t)\) as a time series, from which we obtain u(t) from (30). Then with the obtained input, we solve the full model (12–14) to see how the control algorithm based on reduced model performs when applied to the full model. The control algorithm based on standard phase reduction is outlined in the flowchart in Fig. 3, and the results are shown in Fig. 4. It can be seen that control input is of opposite sign of the PRC, which slows down the \(\theta \) dynamics; see (27). In fact, as shown in [69] for control objectives with \(T_1 \approx T\), the shape of the optimal input u(t) is very similar to the shape of the PRC (here the shape is “flipped” because our control objective was to slow down the oscillator). Since the control input is small, it does not drive the trajectory far away from the periodic orbit. The optimal control found with this procedure works very well when applied to the full model: The spike occurs at a time which differs from the desired time of 1.2T by only \(0.04\%\). The total control energy consumed (\(\int _0^{T_1} u(t)^2 \hbox {d}t\)) comes out to be 10.8 units. This is approximately \(25\%\) less power than what would be required to achieve the same \(T_1\) with a constant input \(u(t) = -\,1.19\), with a total control energy consumed of 14.3 units.
Note that if we applied optimal control theory to the full thalamic neuron model with the objective of changing the time at which the neuron fires, we would need to solve a six-dimensional boundary value problem: three dimensions for the variables V, h, and r, and three more dimensions for the corresponding Lagrange multipliers. Additionally, the transformation to phase variables allows for an intuitive definition of when the neuron spikes (i.e., when \(\theta = 0\)). By contrast, for the thalamic neural model, a hypersurface corresponding to the moment of a neural spike would need to be defined, ultimately resulting in a significantly more difficult optimal control problem to solve.
The above calculation assumes that we know the exact expression for the PRC for the system that we wish to control. In an experimental setting, one expects that the PRC which is found using the direct method will not be exactly correct, due to noise and other uncertainties. However, the following illustrates that the control which is found from an approximate PRC can still give good results, suggesting that the optimal control calculation has a good level of robustness.
Consider the left panel of Fig. 5, in which an approximate PRC is found by fitting a Fourier series to noisy data from the direct method; here the fit includes constant, \(\cos (\theta ), \sin (\theta ), \cos (2 \theta ), \sin (2 \theta ), \cos (3 \theta )\), and \(\sin (3 \theta )\) terms. We use the approximate PRC in (30–32) with \(T_1 = 1.2 T = 10.07\) to calculate the control input, which is shown in the right panel of Fig. 5. The next spike which occurs with this input is at \(t=9.95 = 1.185 T\), so it approximately achieves the desired control objective. Interestingly, the input found using the approximate PRC consumes less total energy (9.4 units) than the optimal input found for \(T_1 = 1.2 T\) using the exact PRC (10.8 units); this can be understood by noting that it should require less power to make the neuron fire at \(t=9.95\) than at \(t = 10.07\), since this is a milder objective. The optimal input calculated for a target time of \(T_1 = 9.95\) with the exact PRC would require even less power.
More rigorous investigations of the robustness of optimal control schemes for phase models can be found, for example, in [106, 107, 110]. However, there is still much work to be done to develop robust control algorithms for noisy, uncertain, heterogeneous biological systems.
The green dots in the left panel show noisy PRC measurements that might arise, for example, from applying the direct method to a thalamic neuron. The red line in the left panel shows the approximate PRC obtained by fitting a Fourier series to these data, while the blue line shows the exact PRC for this system. In the right panel, the red (resp., blue) line shows the control calculated using the approximate (resp., exact) PRC (color figure online)
We note that in optimal control problems, it is common to consider a Hamiltonian formulation which is equivalent to the Euler–Lagrange equations. In particular, one can define conjugate momenta \(p_i\) to the generalized coordinates \(q_i\) as \(p_i = \frac{\partial {{\mathcal {L}}}}{\partial \dot{q}_i}\). Then, the Legendre transformation [30] gives
from which one obtains Hamilton’s equations
For the present problem, \(q_i \in \{u,\lambda ,\theta \}\), and the only nonzero conjugate momentum is the conjugate momentum to \(\theta \) given by \(p_\theta = \frac{\partial L}{\partial \dot{\theta }} = \lambda \). Therefore,
From Hamilton’s equations, we then obtain
It is readily shown that these are the same as the Euler–Lagrange equations in (30–32).
Energy-optimal phase control with charge-balance constraint: [14, 74]
It may be desirable for energy-optimal phase control to restrict control inputs to obey the integral constraint \(\int _{0}^{T_1}u(t)\hbox {d}t=0\). If u(t) is an electrical input, this corresponds to a charge-balance constraint: The total amount of charge injected into the system over one control cycle is zero. We note that for neuroscience applications, charge-imbalanced inputs can cause Faradaic chemical reactions to take place near the stimulating electrode, which can result in damage to the tissue [67]. We can restate this constraint as follows: Let Q(t) be the amount of charge injected instantaneously at time t. Then, we get
Integrating both sides of this equation from 0 to \(T_1\), we obtain
For the charge-balance constraint to hold, we need the right-hand side of this equation to be zero. This means \(Q(T_1)=Q(0)\), and assuming that the input is being applied from time \(t=0\), which implies \(Q(0)=0\), we also have \(Q(T_1)=0\).
Similar to above, suppose that for a specified spike time \(T_1\), for all stimuli u(t) which evolve \(\theta (t)\) via (27) from \(\theta (0) = 0\) to \(\theta (T_1) = 2 \pi \), we want to find the stimulus which minimizes the cost function (28) and yields \(q(T_1)=0\). We apply calculus of variations to minimize [25]
where \({\varvec{\Phi }}(t)=[\theta (t), \; Q(t), \; \lambda _1(t), \; \lambda _2(t)]^\mathrm{T}\). The Lagrange multipliers \(\lambda _1(t)\) and \(\lambda _2(t)\) force the dynamics to satisfy Eqs. (27) and (35).
Using vector notation, the associated Euler–Lagrange equations are
so that
To find the optimal u(t), (38)–(41) need to be solved subject to the boundary conditions
This is a four-dimensional two-point boundary value problem where the boundary values for \(\theta (t)\) and Q(t) are given in (42).
Charge-balanced control example: thalamic neuron model
To demonstrate the control, we again consider the thalamic neuron model given by Eqs. (12–14) with same parameters as before. We set \(T_1=1.2T\) and show the results in Fig. 6. The steps taken to generate these results are similar to the ones given in Fig. 3.
Energy-optimal phase control with charge-balance constraint for the thalamic neuron model: Left column shows the trajectory and time series, the middle column shows the evolution of phase \(\theta (t)\) and instantaneous charge Q(t), and the right column shows the PRC and the control input. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit, whereas the red dashed line highlights the charge-balance constraint (color figure online)
It can be seen from Fig. 6 that control input takes both positive and negative values, as is necessary for charge balance. In order to slow down the oscillation, the input is most negative when the PRC is most positive. Moreover, when the input is most positive, it has little effect on the oscillation because the PRC is close to zero at those times; such positive inputs are necessary to achieve charge balance. The total control energy consumed (\(\int _0^{T_1} u(t)^2 \hbox {d}t\)) here is 37.9 units, which is almost 4 times the amount of energy consumed for the previous control without a charge-balance constraint. Since the control input is moderately large, it drives the trajectory away from the periodic orbit, which eventually returns back to the orbit once the control is turned off after time \(T_1\).
Note that if we applied optimal control theory to the full thalamic neuron model with the objective of changing the time at which the neuron fires and with the charge-balance constraint, we would need to solve an eight-dimensional boundary value problem: three dimensions for the variables V, h, and r, three more dimensions for the corresponding Lagrange multipliers, and two more dimensions for the charge-balance constraint.
This algorithm has been successfully applied to in vitro neurons in [76], showing that it is robust to noise and uncertainty inherent in real experimental systems. Moreover, an extension of such charge-balanced phase control to include constraints on the range of allowed control inputs is given without a charge-balance contraint in [15] and with a charge-balance constraint in [16].
Time-optimal control with charge-balance constraint: [75]
As an alternative control objective, suppose we want to find the control input u(t) that, when bounded to be less than a certain value \(\bar{u}\) in magnitude, i.e., \(|u(t)| \le \bar{u}\), would result in the minimum or maximum value of the timing of an event such as an action potential. For example, one might want a neuron to fire as quickly as possible subject to a constraint on the magnitude of the allowed input current; this could be used to increase the firing rate of neurons with a constraint due to hardware limitations and/or concern that large inputs might cause tissue damage. This is an optimization problem in which the next spike time \(T_1\) needs to be extremized. We will consider this problem with a charge-balance constraint imposed on the control input.
Time-optimal control with charge-balance constraint for the thalamic neuron model: Left column shows the trajectory and time series, the middle column shows the evolution of phase \(\theta (t)\) and instantaneous charge Q(t) under optimal control, and the right column shows the PRC and the control input. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)
In particular, we seek a control input u(t) which extremizes
with the following constraints:
Following a similar procedure to above, the Hamiltonian associated with this system is
where \(\lambda _1\) and \(\lambda _2\) are the Lagrange multipliers for this system. To obtain the necessary conditions for optimality, one can use the Hamiltonian in (45) to give
The optimal control for this problem is obtained from Pontryagin’s minimum principle [47, 57], which states that an optimal control must minimize the Hamiltonian. For the present problem, this gives
where \(\mathcal {M} \in \{\mathrm{min,max}\}\). This yields the following equations for the optimal control input, u(t), for the cases of minimizing the inter spike interval (or \(T_1\)) of the neuron and maximizing it:
Equations (46) and (47) indicate that the magnitude of the optimal control is always equal to its bound and that only its sign changes with respect to time. This solution, known as bang–bang control, is expected since the objective here is to achieve extreme final time, and thus, one expects maximum effort from the control stimulus.
The left panel shows isostable coordinates of (50) numerically calculated according to (49). Black lines denote level sets of isostables. Dashed white lines show two different trajectories starting from different initial conditions and ultimately approaching the fixed point (gray dot). In the right panel, the black trace takes longer to return to the fixed point than the red trace, as predicted from their initial isostable coordinate values (color figure online)
Time-optimal control with charge-balance constraint example: thalamic neuron model
To demonstrate the control, we again consider the thalamic neuron model given by Eqs. (12–14) with the same parameters as before. We set \(\bar{u}=1\) and consider the interspike interval minimization problem. We solve the optimal control equations subject to constraints given in Eq. (44) and plot the results in Fig. 7. Here as well, the steps taken to generate results are similar to the ones given in Fig. 3. With \(\bar{u}=1\), we get minimum \(T_1=0.93T\) under charge-balance constraint (the results from applying the optimal input to the phase model and the full model differ by only \(0.06\%\)). Since the control input is moderately small, the trajectory remains close to the periodic orbit. As can be seen from bottom panel of the right column of Fig. 7, the control input is positive and negative for equal amounts of time, thus giving zero net charge inflow at the end of the control.
Reference [75] shows for a different example neuron that the time-optimal control input obtained using this method gives good results when applied to the full non-reduced model for a range of input constraints \(\bar{u}\); see, for example, Fig. 6 from that reference.
3 Isostable reduction and control for systems with a stable fixed point
Before moving on to more sophisticated formulations of phase reduction for systems with a stable periodic orbit, we will first discuss a reduction which is analogous to the standard phase reduction, but for systems with a stable fixed point.
3.1 Isostables for a fixed point
Reference [112] proposed a method of phase reduction for systems with a stable fixed point, based on the notion of isostables [65], cf. [86]. Isostables are analogous to isochrons for asymptotically periodic systems and can be defined as sets of points in phase space that approach a fixed point together, in a well-defined sense described below. Isostables are related to the eigenfunctions of the Koopman operator [65].
The calculation of an isostable field, \(\mathcal {I}(\mathbf{x})\), exploits the linear nature of nonlinear dynamics near a fixed point \(\mathbf{x}_0\). For a linear system
and solutions \(\phi (t,\mathbf{x}(0))\) (also known as the flow) approach the fixed point as
where \(s_j(\mathbf{x})\) are the coordinates of the vector \(\mathbf{x}\) in the basis \(\{ \mathbf{v}_j | j = 1,\dots ,n \}\) of unit eigenvectors of A, with associated eigenvalues \(\{ \lambda _j| j = 1,\dots ,n \}\), sorted so that \(\lambda _1\) corresponds to a unique slowest direction of the stable manifold, i.e., \(\mathrm{Re}(\lambda _j)< \lambda _1 < 0, \; \forall \; j > 1\). Here, we assume that \(\lambda _1\) is real and unique, and as shown in [65], the magnitude of \(s_1(x)\) determines the infinite-time approach to the origin. In other words, hyperplanes of constant isostables, \(\mathcal {I}_\tau \equiv \{ {\mathbf {x}} \in {\mathbb {R}}^n | \mathcal {I}(\mathbf {x}) = \tau \}\), near a fixed point are parallel to the faster directions \(\mathbf {v}_2, \dots , \mathbf {v}_n\).
For nonlinear systems, the isostable field within the fixed point’s entire basin of attraction, \(\mathcal {I}( \mathbf{x})\), can be calculated by monitoring the infinite-time approach of \(\phi (t,\mathbf{x}) \) to the fixed point, \(\mathbf{x}_0\), by computing
where \(|| \cdot ||\) can be any norm; here we will be working with the 1-norm on \({\mathbb {R}}^n\). Intuitively, Eq. (49) compares the asymptotic approach to the fixed point along the slowest direction of the stable manifold, \(\mathbf{v}_1\), to an exponential function governed by the associated eigenvalue, \(\lambda _1\). We emphasize that Eq. (49) is valid for systems with a stable fixed point where \(\lambda _1\) is real and unique. In other cases, such as when \(\lambda _1\) is complex or the fixed point is unstable, isostables can still be calculated, and we refer the interested reader to [65] for a more complete discussion.
As an intuitive illustration of the notion of isostable coordinates, consider a FitzHugh–Nagumo-based model of an excitable system given in [87]:
Here the variables V and w are dimensionless and could be used to represent a cell membrane voltage and the state of a gating variable, respectively. In this example, we take \(a = 0.13, b = 0.013, c_1= 0.26, c_2 = 0.1,\) and \(d = 1\). With this choice of parameters, there is a stable fixed point at \((V,w) = (0,0)\). In the vicinity of the fixed point, small positive perturbations in the V variable result in large excursions. Numerically, \(\lambda _1\) is determined to be 0.013 and isostable coordinates are calculated directly according to (49) and shown in Fig. 8. As is characteristic of isostable coordinates, larger isostable values correspond to initial conditions that will take longer to approach the stable fixed point.
3.2 Isostable reduction
Isostables provide a useful coordinate system from which to define a reduced set of equations, similar to the phase reduction discussed in Sect. 2. To do so, consider an n-dimensional differential equation
where \(\mathbf{F}(\mathbf{x})\) is the vector field and \(\mathbf{U}(\mathbf{x},t)\) is an external stimulus. For a given set of initial conditions, suppose that the system follows the known trajectory \(\gamma \) to the stable fixed point \(\mathbf{x}_0\).
Our objective is to simplify (51) to a one-dimensional equation by defining scalar isostable coordinates \(\psi (\mathbf{x}) \in (-\infty , \infty ]\) for all \(\mathbf{x}\) in some neighborhood U of \(\mathbf{x}_0\) within its basin of attraction. It will be convenient to take \(\psi (\mathbf{x}) = -\log (\mathcal {I}(\mathbf{x}))\), where \(\mathcal {I}( \mathbf{x} )\) is defined in (49). Changing variables to isostable coordinates using the chain rule yields
where the final line is obtained by noting that \(\hbox {d} \psi / \hbox {d}t = -\lambda _1\) at all locations when \(\mathbf{U}(\mathbf{x,t}) = 0\) (see equation (2.3) of [112] for further explanation of this feature of isostable coordinates). Thus \( \frac{\partial \psi }{\partial \mathbf{x}} \cdot \mathbf{F}(\mathbf{x}) = \omega \), with \(\omega = -\lambda _1\) (recall that \(\lambda _1\) is negative). Reduction (52) for systems which approach a fixed point is directly analogous to standard phase reduction (5) for systems with a stable period orbit. Moreover, calculation of the gradient along a trajectory \(\mathbf{x}(t)\) is also similar, as shown in [112]:
with
where \(\mathbf{v}_j\) is the \(j{\mathrm{th}}\) right eigenvector of \(D\mathbf{F} (\mathbf{x}_0)\) when the eigenvalues are sorted in terms of increasing magnitude of their real parts. (Recall that \(\mathbf{x}_0\) is stable, so all eigenvalues have negative real part.) We refer to this gradient \(\nabla _{\mathbf{x} (t)}\psi \) as the isostable response curve (IRC); it gives a measure of the effect of a control input on the value of \(\psi \). In the absence of external stimuli, \(\frac{\hbox {d} \psi }{\hbox {d}t} = \omega \), i.e., \(\psi (\mathbf{x})\) increases at a constant rate. We note that \(\psi \) can be rescaled by a constant if desired, which will yield a different constant rate of change. By definition, \(\psi (\mathbf{x}) = \infty \) corresponds to \(\mathbf{x} =\mathbf{x}_0\), meaning that in the absence of external control, all trajectories in the domain of attraction of \(\mathbf{x}_0\) approach the fixed point in infinite time.
a The steady-state alternans behavior when pacing the FMG model at a rate of BCL \(=\) 175 ms with action potentials alternating between long and short durations. b APD restitution curves measured with different pacing histories. To measure one datapoint from the light blue curve, for instance, the model is paced at 250 ms until transient behavior dies out; the next action potential is initiated once the DI reaches a prescribed value. Different color curves highlight memory in the system [7, 99]. All curves increase monotonically with the DI
Example of control based on the isostable reduction: controlling alternans
Isostable reduction strategies have been shown to be useful in cardiological applications [112, 114] where the timing of the approach to the associated system’s fixed point is of interest. Cardiomyocytes are the electrically excitable cells within the heart which work together to produce a coordinated heartbeat. For these electrically coupled cells, small voltage perturbations from the resting state result in an action potential. The action potential duration (APD) is a (generally) increasing function of the diastolic interval (DI), i.e., time duration for which the cell remains quiescent preceding the next action potential [31]. This relationship is known as the APD restitution curve.
Under healthy conditions, a constant pacing interval, often referred to as the basic cycle length (BCL), produces steady-state period-1 behavior resulting in APDs which are constant on a beat-to-beat basis. However, pathological conditions can arise which result in period-2 behavior with action potentials of alternating duration. This phenomenon, known as alternans, has been well studied in the past decades and is generally viewed as a precursor to more deadly cardiac arrhythmia [77, 81]. Seminal work by Nolasco and Dhalen [79] showed that alternans can emerge as a result of a period doubling bifurcation when the slope of the APD restitution curve is greater than 1. The understanding of the exact cause of alternans has become more complicated in recent years as unstable calcium dynamics [82, 83] and memory of pacing history [7, 99] have been shown to play a contributing role.
In this example, cf. [112], we will consider the problem of eliminating alternans in the FMG model of cardiac action potentials [26]; see Appendix A. In this model, alternans ermeges primarily due to steep APD restitution. Using the nominal parameter set from [26], the single cell is paced at a BCL of 175 ms. Under steady-state conditions, alternans develops with action potentials of alternating duration, as shown in Panel A of Fig. 9. Previous work has focused on eliminating alternans by stabilizing the unstable period-1 behavior [8, 27, 114]. Isostable reduction allows one to investigate alternans elimination strategies in a weakly perturbed setting. Advantages of using this strategy as compared to others are that it can be implemented in high-dimensional models, does not require continuous feedback about state variables from the cell, and does not require the application of premature pulses.
Much like the analysis of the energy-optimal phase control of neural action potentials presented earlier, we begin with a standard isostable reduction (52)
In the context of controling cardiac arrhythmia, \(\psi \) represents the infinite-time decay of the smallest magnitude eigenvalue of the fixed point, \(\omega \) is determined by the rate of decay, and \(\mathcal {I}(\psi ) \equiv \hbox {d} \psi / \hbox {d} V\) is the isostable response curve to time varying voltage perturbations u(t). Here \(I(\psi )\) is a scalar function because we assume that the control only affects the voltage equation for the system. Note that while isostable coordinates are defined in terms of the ultimately linear infinite- time behavior near the fixed point, the reduction is valid in the entire basin of attraction of the fixed point. In this example, \(\psi = 0\) is defined to correspond to the moment that \(\hbox {d}V/\hbox {d}t = 0\) during the action potential plateau. Additionally, the isostable coordinates are scaled so that \(\omega = 1/2000\).
For this model, as is the case with most cardiac cells, the APD restitution curve is monotonically increasing as shown in Panel B of Fig. 9. We will also assume that in the absence of control, the APD is a monotonically increasing function of the isostable coordinate, i.e., \(\mathrm{APD}^{n} = \varLambda (\psi ^n)\) where \(\mathrm{APD}^n\) is the \(n{\mathrm{th}}\) APD and \(\psi ^n\) is the value of the isostable coordinate immediately preceeding the upstroke of the \(n{\mathrm{th}}\) action potential. Such a relation certainly holds in the unperturbed case, where longer DIs allow the system to travel closer to the fixed point resulting in larger values of \(\psi \) and longer APDs on the subsequent beat.
We will formulate our optimal control problem assuming that alternans is present and apply control on the \((n+1){\mathrm{th}}\) beat when \(\mathrm{APD}^{n}<\mathrm{APD}^{n-1}\). In other words, we will be applying control to modify a long APD. We define \(t = 0\) to correspond to the time the next action potential starts and define \(t_1\) to be the moment \(\psi (\mathbf{x}(t_1)) = 0\). Our objective will be to modify the isostable coordinate at \(t = \mathrm{BCL}\) (corresponding to the moment the following action potential occurs) in order to restore period-1 behavior. We do this by requiring
Intuitively, the above relation advances the isostable coordinate midway between isostable coordinates which produce long and short action potentials. Because we assume that the APD is a monotonically increasing function of the isostable coordinate immediately preceeding the upstroke in the action potential, satisfying this control objective will ultimately stabilize the unstable period-1 behavior in this system and eliminate alternans (see [112] for further explanation). Suppose that we also want to achieve this control objective using the stimulus u(t) which minimizes the cost functional
which is the same square-integral cost as (28). This optimal control formulation produces an analogous calculus of variations problem to the one posed in Sect. 2 resulting in similar Euler–Lagrange equations which can be solved for the appropriate boundary conditions using a shooting method.
Despite using different BCLs to obtain different action potentials for the FMG model, the IRCs are nearly identical. Dashed lines in a show bounds within which 90% of all measured IRCs fit. b The APD as a function of the beat number when control is applied (shaded regions) and without control (unshaded regions). Upon application of the optimal control, alternans is quickly eliminated resulting in period-1 behavior. When control is turned off, alternans reemerges in steady state
In order to calculate IRCs along trajectories of the FMG model we take the slowly varying sarcoplasmic reticulum calcium concentration \([\mathrm{Ca}^{2+}]_\mathrm{SR}\) to be equal to its average value of 318 \(\upmu \mathrm{mol}\) steady-state behavior using a BCL of 175 ms. We calculate IRCs using this reduced model for trajectories determined from action potentials in systems paced at BCLs ranging from 160 to 210 ms. Numerically, this is accomplished by integrating until the trajectory approaches the fixed point, determining the initial value of the IRC using both (54) and \(\frac{\mathrm{d} \phi }{\mathrm{d}t} = \frac{\partial \psi }{\partial \mathbf{x}} \cdot \mathbf{F}(\mathbf{x}) = \omega \), and integrating (53) backwards in time to determine the IRC. The IRC is similar over multiple trajectories, and the dashed lines in Panel A of Fig. 10 show boundaries within which 90 percent of the calculated IRCs fit. Because they are so similar, we use the average value of each calculated IRC in reduction (55). Optimal control is calculated by finding the u(t) which minimizes cost functional (57) subject to constraint (56). The resulting control is applied to the full 13-dimensional FMG model. Results are presented in panel B of Fig. 10, which show the measured APD as a function of the beat number. Without control (unshaded regions), alternans develops in the system. With control (shaded regions), alternans are quickly eliminated and the action potential does not change significantly on a beat-to-beat basis.
The control strategy documented above was investigated in greater detail in [112] and was shown to be effective for eliminating alternans in single-cell models. Later work [114] extended this general strategy for use in PDE models of cardiac tissue with one and two spatial dimensions. This and other alternans control elimination strategies [8, 27] require control to be given at multiple locations throughout the tissue when considering large domains, and it remains an open question whether alternans can be eliminated throughout the heart by applying local perturbation; [71] proposes a possible approach to do this by controlling cardiac pacemaker cells.
When compared to the wealth of the literature on optimal control methods using phase reduction (see, e.g., [15, 18, 48, 69, 75, 76, 95, 96, 106, 110, 118]), isostable coordinates are relatively new and control applications are still emerging. Preliminary applications, including the one presented above, have suggested that isostable control methods are particularly useful when the timing of a system’s approach to a fixed point or stationary solution is of practical interest. Additional applications include [62], which investigates optimal control input used to either speed or slow the convergence of a dynamical system to its fixed point. Also, [92, 108] develop control strategies to drive a population of excitable systems to the same isostable coordinate, thereby synchronizing their resulting convergence to a fixed point.
4 Augmented phase reduction for systems with a periodic orbit
Standard phase reduction (5) is valid only in a small neighborhood of the periodic orbit. Therefore, a control input derived based on the standard phase reduction can only be expected to be effective if its amplitude is small enough that it does not drive the system far away from the periodic orbit. This limitation becomes even more important if the nontrivial Floquet multiplier, which describes the rate of decay of perturbations transverse to the periodic orbit, has magnitude close to unity [71]. This limits the ability to achieve certain control objectives and necessitates the use of augmented phase reduction, to be described below. Augmented phase reduction uses the concept of isostables for a periodic orbit [113], which are coordinates that a give a sense of the distance in directions transverse to the periodic orbit; see Fig. 11. The addition of these transversal coordinates allows one to design control algorithms which, while achieving the desired control objective, also keep the controlled trajectory close to the periodic orbit [71]. Reference [71] devises an energy-optimal control algorithm to change the phase of a periodic orbit and shows how such a control algorithm is effective in situations where the control algorithm based on standard phase reduction fails; we will give a summary of this approach in Sect. 4.2. We note that augmented phase reduction is related to other proposed reductions given in [5, 34, 91, 101]; for more detail, see [71].
A sketch of the behavior of a two-dimensional system near its limit cycle \(\mathbf{x}^\gamma (t)\). The red and blue lines represent two trajectories which start on the isostable level set indicated as a dotted line, and after one period are on the isostable level set indicated as a dashed line. The isostable coordinate \(\psi _1\) decreases at an exponential rate governed by the Floquet multiplier \(\lambda _1\) (color figure online)
Toward defining isostable coordinates for (4) with a periodic orbit, consider a point \(\mathbf {x_0}\) on the periodic orbit \(\mathbf{x}^\gamma (t)\) with the corresponding isochron \(\varGamma _0\). The transient behavior of the system near \(\mathbf {x_0}\) can be analyzed by a Poincaré map P on \(\varGamma _0\),
Here \(\mathbf {x_0}\) is a fixed point of this map, and we can approximate P in a small neighborhood of \(\mathbf {x_0}\) as
where \(DP=\hbox {d}P/\hbox {d}x|_{\mathbf {x_0}}\). Suppose DP is diagonalizable with \(V \in {\mathbb {R}}^{n\times n}\) as a matrix with columns of unit length eigenvectors \(\{ v_k|k=1,\ldots ,n\}\) and the associated eigenvalues \(\{ \lambda _k|k=1,\ldots ,n\}\) of DP. These eigenvalues \(\lambda _i\) are the Floquet multipliers of the periodic orbit. For every nontrivial Floquet multiplier \(\lambda _i\), with the corresponding eigenvector \(v_i\), the set of isostable coordinates is defined as [113]
Here \(\mathbf {x}_\varGamma ^j\) and \(t_\varGamma ^j \in [0,T)\) are defined to be the position and the time of the \(j{\mathrm{th}}\) crossing of the isochron \(\varGamma _0\), and \(e_i\) is a vector with 1 in the \(i\mathrm{th}\) position and 0 elsewhere. Note that \(e_i^T V^{-1}\) is a left eigenvector of the linearization DP which selects for the appropriate component of \({\mathbf {x}}^j_\varGamma - {\mathbf {x}_0}\) in the basis of eigenvectors of DP. As shown in [113], cf. [5], we get the following equations for \(\psi _i\) and its gradient \(\nabla _{\gamma (t)} \psi _i\) under the flow \(\dot{\mathbf {x}}=\mathbf{F}(\mathbf {x})\):
where \(k_i=\log (\lambda _i)/T\) are Floquet exponents, \(D \mathbf{F}\) is the Jacobian of \(\mathbf{F}\), and Id is the identity matrix. We refer to this gradient \(\nabla _{\gamma (t)}\psi _i\equiv \mathbf{I}_i(\theta )\) as the isostable response curve (IRC). To ensure uniqueness of the IRC, along with its T-periodicity, we take the normalization condition \(\nabla _{\mathbf {x_0}}\psi _i \cdot v_i=1\). The IRC gives a measure of the effect of a control input in driving the trajectory away from the periodic orbit. The n-dimensional system can be realized as [113]
We refer to (61–62) as the augmented phase reduction. Here, the phase variable \(\theta \) indicates the position of the trajectory along the periodic orbit, and the isostable coordinate \(\psi _i\) gives information about transversal distance from the periodic orbit along the ith eigenvector \(v_i\). We note that, at this order, the phase (\(\theta \)) dynamics are unaffected by the isochron coordinates (\(\psi _i\)’s) and are identical to the phase dynamics for standard phase reduction (5). Therefore, the augmented phase reduction does not lead to any correction to the phase dynamics. In Sect. 4.3, we will show that this is no longer the case when the phase reduction is carried out to next order. The augmented phase reduction is identical to the two-dimensional system given by equation (22) in [5], in which \(\theta \) and \(\sigma \) describe the dynamics along, and transverse to the periodic orbit, respectively. It is evident from (61, 62) that the control input affects the oscillator’s phase through the PRC and its transversal distance to the periodic orbit through the IRC. In practice, isostable coordinates with nontrivial Floquet multiplier sufficiently close to 0 can be ignored as perturbations in those directions decay quickly under the evolution of the vector field. If all isostable coordinates are ignored, the augmented phase reduction reduces to the standard phase reduction. In this tutorial, we consider dynamical systems that only have one of the nontrivial Floquet multipliers close to one, and the remaining \(n-2\) nontrivial Floquet multipliers sufficiently close to zero. We then can write the augmented phase reduction as
Here we have removed the subscript for \(\psi \) and k, as we only have one isostable coordinate. Note that for planar systems, the eigenvector v is the unit vector along the one-dimensional projection of the isochron \(\varGamma _0\), and the nontrivial Floquet exponent k can then be computed, for example, from the divergence of the planar vector field as [29]
4.1 Calculating isostable response curves
Given the importance of IRCs for the augmented phase reduction, we now describe several ways in which they can be calculated.
Direct method: [113]
PRCs are calculated by the direct method by giving perturbations to the oscillator at various phases and recording the phase change caused by the perturbation as a function of the stimulation phase. IRCs can be measured in a similar way. We apply perturbations \((\tilde{\mathbf{x}}^\gamma + \varDelta {x_i} \hat{i})\) at various phases along the periodic orbit in the direction of the \(i{\mathrm{th}}\) coordinate. We record a time series of crossings of the \(\varGamma _0\) isochron, \(t_\varGamma ^j\), as well as the crossing locations, \({\mathbf {x}}_\varGamma ^j\), and use this information with the definition of isostable in (58) to calculate the isostable change \(\varDelta \psi \) caused by the perturbation, which when scaled by the magnitude of the perturbation yields the IRC.
Unlike solving for the PRC, backwards integration of (60) will result in positive Floquet exponents and hence a periodic solution that is unstable. To see why, consider the related adjoint equation (10), which yields Floquet exponents that are identical to those of the periodic orbit when integrated backwards in time. By contrast, the Floquet exponents of (60) will each be shifted by \(k_i\). Because (10) has a Floquet exponent of zero (corresponding to the periodic orbit itself), the shifted Floquet exponent in (60) will be positive, resulting in an unstable periodic orbit. We have therefore found it useful to formulate the calculation as a boundary value problem and solve it with Newton iteration; see Appendix C. The first step is to compute and save the periodic solution \(\mathbf{x}^\gamma (t)\) using an ODE solver. For the two-point boundary value formation, we take the boundary conditions as \(\mathbf{I}(0) = \mathbf{I}(T)\). For Newton iteration, we take
where Id is the identity matrix and J is the Jacobian matrix
which is computed numerically. Once a periodic solution is obtained, the computed IRC is scaled by the normalization condition \(\nabla _{\mathbf {x_0}}\psi \cdot v_i=1\).
Example IRC calculation: thalamic neuron model
As an illustration, we calculate the IRC using both the direct method and the adjoint method for the thalamic neuron model given by Eqs. (12–14) with the same parameters as before. Those parameters give a stable periodic orbit with time period \(T=8.3955\) ms and nontrivial Floquet multipliers 0.8275 and 0.0453. Since one of the nontrivial Floquet multipliers is close to 0, we only consider the isostable coordinate corresponding to the larger nontrivial Floquet multiplier in the augmented phase reduction. To calculate the IRC by the adjoint method, we solve the corresponding adjoint equation as a two-point boundary value problem. For the direct method, a MATLAB code was written where perturbations of size \(\delta v = -0.3\) were given at 20 points spread along the periodic orbit. Once the perturbed trajectories came reasonably close to the periodic orbit, the corresponding isostable change was calculated, which when normalized by the magnitude of the perturbation gives the first component of the IRC. The first (i.e., voltage) component of the IRC for the periodic orbit is shown in Fig. 12.
Analytical results
We now derive analytical results for IRCs for two illustrative examples which can arise for simplified models of biological systems and physiological rhythms: : \(\lambda -\omega \) systems and general radial isochron clocks. Some of these results are similar, but obtained using a different method, to the results in [37].
\(\bullet \) \(\lambda - \omega \) systems
Recall from (24) that the PRC for a \(\lambda - \omega \) system is
At a point \((x,y)=(r_\mathrm{po},0)\equiv (x_0,y_0)\), the isochron is in the direction orthogonal to the PRC (because surfaces of constant phase are orthogonal to the gradient of the phase). Thus, the eigenvector v is given as
We will use this vector in the normalization condition for the IRC below. The IRC (in polar coordinates: \(\frac{\partial \psi }{\partial r}~{\hat{r}}+ \frac{\partial \psi }{\partial \phi } {\hat{\phi }} \equiv I_r~{\hat{r}}+I_{\phi }~{\hat{\phi }}\)) can be found by solving the adjoint equation subject to T-periodicity and normalization condition as:
To find k, we note that near the periodic orbit we have the linear approximation \(\dot{r} = G'(r_0) r\), with solution \(r(t) = r_0 \exp [G'(r_0) t]\); since \(r(T) = r_0 \exp [G'(r_0) T]\), the Floquet exponent \(k = G'(r_0)\). Since \(I_{\phi }\) and \(I_r\) are T-periodic, we must have \(I_{\phi _0}=0\). Thus, the IRC in polar coordinates is
equivalently in Cartesian coordinates the IRC is
To find the constant \(I_{r_0}\), we use the normalization condition at point \((x_0,y_0)\)
This gives the IRC in polar and Cartesian coordinates as
or, equivalently,
We see that the Cartesian components of the IRC for a \(\lambda -\omega \) system each take positive and negative values, depending on the value of the phase \(\theta \). Thus, the same instantaneous, infinitesimal perturbation can either increase or decrease the isostable coordinate (moving the trajectory inward or outward from the periodic orbit, in the sense of isostables), depending on when it is applied.
We now consider two special cases of \(\lambda -\omega \) systems.
Hopf bifurcation normal form
The normal form for a Hopf bifurcation [35] in Cartesian coordinates is:
which can be written in polar coordinates as:
Thus, the Hopf normal form is a \(\lambda - \omega \) system, with \(G(r)=ar+cr^3\) and \(H(r)=b+dr^2\). With parameters \(c<0\) (corresponding to a supercritical Hopf bifurcation), and \(a<0\), the system has a stable fixed point. As a increases through 0, a stable periodic orbit is born, and the fixed point loses stability. For \(a>0\), the radius of the stable periodic orbit is \(r_\mathrm{po}=\sqrt{-a/c}\), and its time period is given by \(T=2\pi / \left( b+dr_\mathrm{po}^2\right) \). Using Eqs. (66, 67), we get the IRC as
We note that a special case of this problem was considered using different methods in Example 5.1 from [37].
Bautin bifurcation normal form
The Bautin normal form [36, 54] can capture a saddle-node bifurcation of periodic orbits, where an unstable branch of periodic orbits born out of a subcritical Hopf bifurcation turns around and gains stability. This can be written in polar coordinates as:
The Bautin normal form is thus a \(\lambda - \omega \) system with \(G(r)=ar+cr^3+fr^5\) and \(H(r)=b+dr^2+gr^4\). With parameters \(c>0\), \(f<0\), and \(a>0\), the system has an unstable fixed point and a stable periodic orbit. As a decreases through 0, an unstable periodic orbit is born in a subcritical Hopf bifurcation, and the fixed point becomes stable. As a decreases further, the stable and unstable periodic orbits annihilate in a saddle-node bifurcation of periodic orbits at \(a=c^2/4f\). The bifurcation diagram is shown in Fig. 13. Now consider the stable periodic orbit with radius \(r_\mathrm{po}=\sqrt{\frac{-c-\sqrt{c^2-4af}}{2f}}\) and time period \(T=2\pi / \left( b+dr_\mathrm{po}^2+gr_\mathrm{po}^4\right) \). Using Eqs. (66, 67), we get the IRC in polar and Cartesian coordinates as
We now consider the IRC for the thalamic neuron model for a parameter regime for which the system undergoes a saddle-node bifurcation of periodic orbits, and compare with the results for the Bautin normal form.
Example: IRC for thalamic neuron model near saddle-node bifurcation of periodic orbits
For the thalamic neuron model (12–14) with \(u=0\) and \(I_\mathrm{b}=0.3281\,\upmu \hbox {A/cm}^2\), there exists a stable periodic orbit near a saddle-node bifurcation of periodic orbits with time period \(T=88.6816\) ms and nontrivial Floquet multipliers 0.8415 and \(2.584 \times 10^{-8}\). Since one of the nontrivial Floquet multiplier is close to 0, we only consider the isostable coordinate corresponding to the larger nontrivial Floquet multiplier for the augmented phase reduction. The nontrivial Floquet exponent comes out to be \(k=-\,0.001946\). Figure 14 shows the periodic orbit for the thalamic neuron model with the given parameter values. Figure 15 shows the numerically computed IRC for the thalamic neuron model for these parameters. We see that the IRC along the voltage v and gating variable r match closely with a sinusoid, whereas the IRC along the gating variable h does not. This is because the Bautin normal form only captures the turning around of an unstable periodic orbit branch born out of a subcritical Hopf bifurcation and gaining stability in a saddle-node bifurcation of periodic orbits. However, it does not capture the relaxation nature of dynamics present in some models, including this one. That is why the IRC computed numerically for such models does not match closely in shape with the derived analytical expression, cf. [44]. The variables x and y in the Bautin normal form vary at a similar rate, but the variables v and h in the thalamic neuron model vary at a much faster rate than the variable r.
IRC for the thalamic neuron model near the saddle-node bifurcation of periodic orbits: The blue line shows the numerically computed IRCs, while the red line shows the best matching sinusoid curve. The left, middle, and right panels show the \(v, \ h\), and r components of the IRC and its closest matching sinusoid, respectively (color figure online)
\(\bullet \) General radial isochron clocks
Recall from (21) that the PRC for the general radial isochron clock is
which can be rewritten in terms of the phase variable \(\theta \) by using (16). To use adjoint Eq. (60) for the IRC (with \(\psi _i \rightarrow \psi \) and \(k_i \rightarrow k\)), we need an expression for the nontrivial Floquet exponent k, which must be negative for a stable periodic orbit. As for a \(\lambda -\omega \) system, \(k = G'(r_0)\).
The isochrons are radial lines, with eigenvector \(v={\hat{x}} + 0{\hat{y}}\) at point \((x,y)=(-r_\mathrm{po},0)\equiv (x_0,y_0)\). Thus, the adjoint equation for the IRC becomes:
Since the IRC is T-periodic, \(I_{\phi _0}=0\). Thus, we get the IRC in polar and Cartesian coordinates:
To find the constant \(I_{r_0}\), we use the normalization condition at point \((x_0,y_0)\)
Thus, it gives the IRC in polar and Cartesian coordinates as
We note that the Cartesian components of the IRC for a general radial isochron clock take both positive and negative values depending on the value of \(\phi \), which is related to the phase \(\theta \) through (16). Thus, as for \(\lambda -\omega \) systems, the same instantaneous, infinitesimal perturbation can either increase or decrease the isostable coordinate (moving the trajectory inward or outward from the periodic orbit in the sense of isostables), depending on when it is applied.
General radial isochron clock SNIPER example
A simple system which undergoes a SNIPER bifurcation is
where r and \(\phi \) are standard polar coordinates and \(\rho >0\). This is an example of a general radial isochron clock and was considered using different methods in Example 5.2 in [37]. As the bifurcation parameter \(\eta \) varies, two fixed points annihilate at \(\eta =1, \ \phi =\pi /2\), and \(r=\sqrt{\rho }\), giving rise to a periodic orbit for \(\eta >1\). The periodic orbit is stable with radius \(r_\mathrm{po}=\sqrt{\rho }\) and time period \(T=2\pi /\sqrt{\eta ^2-1}\). The phase variable \(\theta =f(\phi ;\eta )\) is found from (19) as
Thus, as \(\phi \) varies from \(-\,\pi \) to \(\pi \), \(\theta \) advances linearly in time from 0 to \(2\pi \). The bifurcation occurs at \(\phi =\pi /2\), which corresponds to \(\theta =\pi \). The periodic trajectory spends most of its time near \(\phi =\pi /2\) near the bifurcation, as shown in the left panel of Fig. 16. Thus, we expect the PRC to be large near \(\phi =\pi /2\) (i.e., \(\theta =\pi \)), and small elsewhere. From (20), we get the PRC as
which in terms of \(\theta \) is
It is clear from (72) that the PRC is always positive, and it blows up to infinity at \(\phi =\pi /2\) (i.e., \(\theta =\pi )\) at the bifurcation. This is evident from Fig. 16. Note: For \(\eta \gtrsim 1\), the expression in (73) reduces to \(\frac{\partial \theta }{\partial \phi }=\frac{1-\cos \theta }{\omega }\), which is consistent with the SNIPER example given in Sect. 2, cf. [2, 19].
\(\phi \) evolution and PRC for the general radial isochron clock SNIPER bifurcation model: The left panel plots the evolution of azimuthal angle \(\phi \) as a function of the phase \(\theta \) of the periodic orbit, which advances linearly in time. The middle (resp., the right) panel plots the PRC \(Z_\phi \) versus \(\theta \) (resp., \(\phi \)). The blue, red, green, and black lines correspond to \(\eta =20, \ 1.5, \ 1.05\), and 1.0005 respectively (color figure online)
Transforming to Cartesian coordinates \((x,y)=(r \cos \phi , r \sin \phi )\), we can write the PRC as
From (69–70), we get the IRC in polar and Cartesian coordinates:
IRC for the general radial isochron clock SNIPER bifurcation model: The left (resp., the right) column plots the IRC \(I_x\) (resp., \(I_y\)) versus \(\theta \). In both plots, the blue, red, green, and black lines correspond to \(\eta =20, \ 1.5, \ 1.05\), and 1.00001 respectively (color figure online)
At first glance, it seems that the IRC is sinusoidal. It is, but only far away from the bifurcation point. As we approach the bifurcation, \(\phi \) no longer varies linearly with phase (see the left panel of Fig. 16). The “sinusoidal” IRC gets expanded near the bifurcation point and squeezed away from the bifurcation point. This is seen in Fig. 17, which plots the IRC as the bifurcation parameter \(\eta \) varies. We see that near the bifurcation point, the IRC stays close to zero in the x direction and close to \(-\,1\) in the y direction. This observation agrees with the intuitive definition of IRC. Near the bifurcation point, the periodic trajectory points in the x direction, so the IRC, which is the gradient of \(\psi \) coordinate, is zero along that direction. On the other hand, the y coordinate is antiparallel to the isochron, along which the gradient of \(\psi \) is unity. We can write IRC as a function of phase as
We now consider a neural model for parameters near a SNIPER bifurcation and compare the PRC and IRC with the results from the preceding SNIPER example.
Example: Morris–Lecar model, cf. [37]
The Morris–Lecar model [72], a two-dimensional neuron model, is given as
In these equations, \(I_\mathrm{b}\) is the baseline current, v is the transmembrane voltage, and n is the gating variable. For details of the functions \(m_\infty (v), \ n_\infty (v), \ \tau _n(v)\) and the rest of the parameters, see Appendix A. For \(I_\mathrm{b}=39.9957\) mA, the system has a stable periodic orbit near a SNIPER bifurcation with time period \(T=1002.88\) ms, nontrivial Floquet multiplier \(\lambda =3.632 \times 10^{-45}\), with corresponding nontrivial Floquet exponent \(k=-\,0.1020\). The time series for one period is shown in Fig. 18. Figure 19 plots the PRC and IRC for the Morris–Lecar oscillator. The PRC is sinusoidal and does not change sign, just like the simple model (see Fig. 16 for comparison). The IRC looks like a sinusoid skewed to one side, similar to the IRC calculated for the simple model (see Fig. 17 for comparison).
Thalamic neuron model: Top row shows the uncontrolled periodic orbit, PRC, and IRC for the thalamic neuron model with parameters given in the main text. The middle (resp., bottom) row shows the trajectory, time series, and control input for control based on the augmented (resp., standard) phase reduction. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)
4.2 Energy-optimal phase control revisited [71]
As mentioned previously, when the control objective is more demanding, control based on standard phase reduction can fail because the controlled trajectory leaves the vicinity of the unperturbed periodic orbit where the reduction is valid. This can occur, for example, when trying to control cardiac pacemaker cells or circadian oscillators [71]. This motivates a control formulation based on the augmented phase reduction (63–64). This control algorithm minimizes not only the control energy, but also minimizes the oscillator’s transversal distance to the uncontrolled periodic trajectory. We take the following cost function: [71]
The first term in the cost function ensures that the control law uses a minimum energy input, and the second term minimizes the transversal distance (in the direction of the slow isostable coordinate \(\psi \)) from the uncontrolled periodic trajectory. The last two terms ensure that the system obeys the augmented phase reduction, with \(\lambda _1\) and \(\lambda _2\) being the Lagrange multipliers. The Euler–Lagrange equations are obtained from
which gives
where
These equations are solved as a four-dimensional two-point boundary value problem (see Appendix C) with the boundary conditions
The last boundary condition ensures that trajectory ends back on the periodic orbit. The corresponding optimal control problem with standard phase reduction, as described in Sect. 2, can be obtained by setting \(\beta =0\) and \(\lambda _2=0\) in the cost function.
Energy-optimal phase control example using augmented phase reduction: thalamic neuron model
To demonstrate the control, we again consider the thalamic neuron model given by Eqs. (12–14) with the same parameters as before and \(I_\mathrm{b}=5\upmu \hbox {A/cm}^2\). This gives a stable periodic orbit with time period \(T=8.3955\) ms and nontrivial Floquet multipliers 0.8275 and 0.0453. Since one of the nontrivial Floquet multipliers is close to 0, we only consider the isostable coordinate corresponding to the larger nontrivial Floquet multiplier in the augmented phase reduction. We set a more “aggressive” control objective \(T_1=0.5T\) and calculate the energy-optimal control based on both the augmented and standard phase reduction. The results are shown in Fig. 20. The numerical steps taken to generate these results are similar to the ones given by the flowchart in Fig. 3. To compare the control laws, we compute the control energy as \(\int _0^{T_1}u(t)^2 \hbox {d}t\) and the control error as the normalized Euclidean distance between the final position \(\mathbf {x}(T_1)\) and the initial position \(\mathbf {x}(0)\).
As seen in middle and bottom panels of the left column of this figure, the control based on the augmented phase reduction does better at keeping the trajectory close to the periodic orbit. On the other hand, with control based on the standard phase reduction, the trajectory moves far away from the periodic orbit. Since one of the Floquet multipliers is close to zero, the voltage state returns back quickly, but the other states still remain far away from the limit cycle. This is evident from the first two panels of the bottom row of Fig. 20. We also see that for the augmented phase reduction-based control, the control input is large when the IRC is near zero and is small when the IRC is large. This diminishes the effect of the control input on the isostable coordinate, and thus, the oscillator’s transversal distance from the periodic orbit remains small. This ensures that the augmented phase reduction represents the dynamics accurately, making the control more effective. The better performance of the augmented phase reduction- based control is also reflected in the control error, which is 0.023 and 0.045 for the augmented and standard phase reduction-based optimal control, respectively. The augmented phase reduction-based control does better at the expense of consuming more energy (434.82 units) compared to (329.25 units) in the standard phase reduction- based control.
Reference [71] gives other examples which illustrate how the use of the augmented phase reduction for energy-optimal phase control can give better results than the use of standard phase reduction, including cases where the standard phase reduction completely fails. It also considers the robustness of this algorithm to noise.
4.3 Second-order phase reduction [105]
Standard phase reduction (5) is valid for infinitesimal perturbations to a periodic orbit. In practice, however, provided the perturbations are small enough so that the system’s state does not travel too far from the unperturbed periodic orbit, (5) can be used in control problems where the applied control is certainly not infinitesimal (e.g., for phase- and time-optimal control problems from Sect. 2). In situations where the applied control must be larger, Eq. (62) can be used with the explicit goal of limiting the magnitude of the isostable coordinates so that the phase-reduced dynamics remain valid, as was done in Sect. 4.2. In this instance, the augmented phase-reduced equations (61–62) provide a reasonably simplified framework from which further analysis can be performed.
Note, however, that to a leading order approximation, the phase and isostable dynamics from (61–62) are uncoupled so that the phase dynamics of (61) are no different than those of (5). In many cases, it can be useful to employ a second- order approximation to the phase and isostable dynamics to better understand how the phase-reduced dynamics change as the system is perturbed from its stable periodic orbit. Previous authors have investigated the computation of second and higher-order approximations of isochrons near the periodic orbit [93, 94], which is useful for understanding the perturbed behavior of initial conditions from the periodic orbit itself. However, such strategies are difficult to apply to systems which have already been perturbed from the periodic orbit without explicit knowledge of the state with respect to the periodic orbit. As we show below, isostable coordinates can be used to bridge this gap resulting in a closed set of equations for a second-order accurate phase-amplitude reduction. This reduction framework was originally presented in [105] and is summarized below.
To begin, to leading order, the gradient of the phase and isostable coordinates near the stable periodic orbit can be written as
where \(H_{\theta ,\mathbf{x}^\gamma (\theta )}\) and \(H_{\psi _i,\mathbf{x}^\gamma (\theta )}\) are the Hessian matrices of second derivatives of \(\theta \) and \(\psi _i\) evaluated at \(\mathbf{x}^\gamma (\theta )\). Near the periodic orbit, Floquet theory [32, 35] allows us to write
where \(k_j\) are the Floquet exponents associated with the linearization of differential equation (1) by \(\varDelta \dot{\mathbf{x}} = D\mathbf{F}(\mathbf{x}^\gamma (t)) \varDelta \mathbf{x}\), \(\mathbf{q}_j\) are T-periodic vectors, and \(c_j\) are chosen to satisfy initial conditions. Using the definition of isostables (58), one can show that \(c_j = \psi _j\) so that the following relation can be derived as in [105]:
where \(\mathbf{p}_j(\theta (0) + \omega t) = \mathbf{q}_j(t)\). Recalling the fact that \(\hbox {d}\theta /\hbox {d}t = \partial \theta /\partial \mathbf{x} \cdot \hbox {d}{} \mathbf{x}/\hbox {d}t\), one can combine (82), (80) and perturbed system dynamics (4) to obtain a second- order correction to the phase reduction. Likewise, the relation \(\hbox {d}\psi _i/\hbox {d}t = \partial \psi _i/\partial \mathbf{x} \cdot \hbox {d}{} \mathbf{x}/\hbox {d}t\), along with Eqs. (82), (81) and (4), provides a second-order correction to the isostable dynamics. The augmented reduction to this order is given as
for \(i = 1,\dots ,n-1\), where \(\mathbf{B}^j(\theta ) \equiv H_{\theta ,\mathbf{x}^\gamma (\theta )} \mathbf{p}_j(\theta )\) and \(\mathbf{C}_i^j(\theta ) \equiv H_{\psi _i,\mathbf{x}^\gamma (\theta )} \mathbf{p}_j(\theta )\). Equation (83) is a second-order correction to the standard phase reduction (5). Unlike the augmented reduction (61–62), the phase dynamics depend on the isostable coordinates.
Ultimately, to find a second-order accurate augmented phase reduction, one must have knowledge of \(H_{\theta ,\mathbf{x}^\gamma (\theta )}\) and \(H_{\psi _i,\mathbf{x}^\gamma (\theta )}\). These can be obtained by noting that for an initial condition on the periodic orbit, perturbation results in the following changes to the phase coordinate:
If we consider a infinitesimal perturbation \(\varDelta \mathbf{x}\), to the trajectory \(\mathbf{x}^\gamma (t)\) at time \(t = 0\), letting \(\mathbf{x}(t)\) be the trajectory resulting from this initial condition and defining \(\varDelta \mathbf{x}(t) = \mathbf{x}^\gamma (t) + \varDelta \mathbf{x}(t)\), then to a second-order approximation,
where \(H_{i,\mathbf{x}^\gamma (t)}\) is the Hessian matrix of second partial derivatives of the \(i{\mathrm{th}}\) component of \(\mathbf{F}\). Similar to the process of obtaining (10) from both (8) and (7), one can take the time derivative of (85) (noting that \(d \varDelta \theta /dt = 0)\), substitute (86) into the result, and collect all \(\mathcal {O}(|\varDelta \mathbf{x}|^2)\) terms of the result to yield (cf. [105])
where \(Z_k(x(t)) \equiv \left. \partial \theta /\partial x_i \right| _{x(t)}\). The solution to (87) must be T-periodic with the additional normalization condition
in other words, for an initial perturbation along the periodic orbit the change in the PRC predicted according to adjoint equation (10) [i.e., the left-hand side of Eq. (88)] must be identical to the change predicted by using \(H_{\theta ,\mathbf{x}^\gamma (t)}\) [i.e., the right-hand side of Eq. (88)].
A Different level sets of \(\psi _1\) for the thalamic neural model (12–14). B The component of \(\mathbf{B}^1(\theta )\) associated with voltage perturbations. In C, the gradient of the phase coordinate is calculated using the direct method (dots) and estimated according to the reduced equation (solid lines) for locations corresponding to different values of \(\theta \) and \(\psi _1\)
As shown in [105], one can use similar arguments to those presented above to show \(H_{\psi _i,\mathbf{x}^\gamma (\theta )}\) can be obtained by finding the periodic solution of
subject to the normalizing condition
where \(I_{i,k}(\mathbf{x}^\gamma (t)) \equiv \left. \partial \psi _i/\partial x_k \right| _{\mathbf{x}^\gamma (t)}\). Notice that (87) requires knowledge of the PRC and that (89) requires knowledge of the IRC, both of which must be found, for instance, using (10) and (60), respectively.
As discussed in [105], the computational effort required to find the matrices \(H_{\theta ,\mathbf{x}^\gamma (t)}\) and \(H_{\psi _i,\mathbf{x}^\gamma (t)}\) using (87) and (89) grows with the square of the dimension of system (1). As such, this computation becomes a limiting factor in the reduction, especially in higher-dimensional systems. Preliminary results, however, suggest that it is possible to directly compute the terms \(\mathbf{B}^j(\theta )\) and \(\mathbf{C}_i^j\) as part of (83) and (84) using an alternative strategy with computational effort that scales with the dimension of the system. Such a method would be preferable especially when some of the isostable coordinates have small- magnitude Floquet multipliers and are neglected. Such investigations will be the subject of future work by the authors.
Example: second-order phase reduction for thalamic neuron model
Figure 21 gives an example of the second-order reduction methodology detailed above applied to the thalamic neural model considered earlier in Sect. 2 with parameters given in Appendix A. Nonunity Floquet multipliers associated with this periodic orbit are numerically determined to be \(\lambda _1 =0.8275\) and \(\lambda _2 = 0.0453\). Because \(\lambda _2\) is close to zero, we will only consider the decay of solutions associated with the more slowly decaying direction in this example. The solid line in panel A shows the periodic orbit, and curves of the form \(\mathbf{x}(\theta ,\psi _1) = \mathbf{x}^\gamma (\theta ) +\psi _1 \mathbf{p}_1(\theta )\) for \(\psi _1 = \pm \, 0.05\) are shown as dashed lines. The function \(\mathbf{B}^1(\theta )\) is numerically determined according to (83) by first calculating \(H_{\theta ,\mathbf{x}^\gamma (\theta )}\) using to (87). \(B_V^1(\theta )\), i.e., the component of \(\mathbf{B}^1(\theta )\) associated with voltage perturbations is shown in panel B. Panel C shows the gradient of the phase coordinate at locations \(\mathbf{x}(\theta ,\psi _1) = \mathbf{x}^\gamma (\theta ) +\psi _1 \mathbf{p}_1(\theta )\). Numerical calculations using direct method (6) are shown with dots, and the predicted values are shown according to the relation \(\frac{\partial \theta }{\partial V} = Z_V(\theta ) + \psi _1 B^1_V(\theta )\) where \(Z_V(\theta )\) is the components of \(\mathbf{Z}(\theta )\) associated with voltage perturbations. Practically, the neuron in this example might be perturbed from its limit cycle solution to a nonzero isostable coordinate; the reduction strategy suggested here gives a sense of how the effective phase response curve will change due to those perturbations. The ability to predict how a periodic dynamical system “adapts” to past inputs is important in many biological applications (cf., [11, 52, 99]). Additional control applications where this reduction strategy is useful are also shown in [105]. In general, it is expected that using the second-order reduction with optimal control algorithms will give improved accuracy over the standard or augmented phase reduction, particularly when the control input causes the trajectory to move away from the immediate neighborhood of the unperturbed periodic orbit.
5 Global isochrons and isostables
The phase dynamics associated with weak control inputs can typically be understood in terms of the phase reduction formulations presented so far. However, for stronger control inputs it might be necessary to consider the full global properties of the isochrons and isostables. The reduction in terms of global isochron and isostable coordinates is
which is identical to (63–64), except that we now have a global PRC and a global IRC instead of evaluating these on the periodic orbit. This reduction is exact in the full basin of attraction of the periodic orbit.
With this in mind, here we describe several methods which have been proposed to calculate isochrons and isostables throughout the basin of attraction of a periodic orbit.
(Brute force) forward integration method: [45]
Here one chooses an initial condition \({\mathbf {x}}_0 \in {\mathbf {x}}^\gamma \) and integrates forward for some large time \(\tau \). One then takes an intial condition \({\mathbf {x}}_\mathrm{test}\) in the basin of attraction of \({\mathbf {x}}^\gamma \) and integrates forward for the same time \(\tau \). Let \(\varPhi _t({\mathbf {x}})\) denote the flow of the dynamical system, i.e., the trajectory starting at \({\mathbf {x}}\). If
for some appropriately small tolerance \(\epsilon \), then \(\mathbf{x}_\mathrm{test}\) approximately lies on the isochron defined by \({\mathbf {x}}_0\). If not, one considers a different \({\mathbf {x}}_\mathrm{test}\) which is expected to give a smaller \(\left| \varPhi _\tau ({\mathbf {x}}_0) - \varPhi _\tau ({\mathbf {x}}_\mathrm{test}) \right| \) after time \(\tau \), for example based on a bisection algorithm. This is repeated for enough points \(\mathbf{x}_0\) and \(\mathbf{x}_\mathrm{test}\) in order to find the isochrons of interest. While this method can in principle be used for systems of any dimensionality, in practice one expects that it will be computationally very costly.
Backward integration method: [4]
Here one chooses an initial condition \({\mathbf {x}}_0 \in {\mathbf {x}}^\gamma \) and an initial condition \({\mathbf {x}}_\mathrm{test}\) near \({\mathbf {x}}_0\) on the local approximation to isochron as determined by the PRC. (Note that since the PRC is the gradient of the phase \(\theta \), it is perpendicular to the isochrons, which are level sets of \(\theta \).) The points \(\varPhi _{-\tau }({\mathbf {x}}_0)\) and \(\varPhi _{-\tau }({\mathbf {x}}_\mathrm{test})\), which can be obtained numerically through backward integration, approximately lie on same isochron. By choosing enough initial points, all isochrons of interest can be approximated numerically. In principle, this method can be used for systems of any dimensionality, but it typically has only been used for planar systems.
Boundary value problem formulation: [80]
It is possible to formulate the calculation of isochrons as a boundary value problem as follows. Truncating (7), we obtain the linearization about the periodic orbit \({\mathbf {x}}^\gamma \)
Now, notice that if \(\varDelta {\mathbf {x}}(0)\) is tangent to an isochron, then
where \(\mu \) is the Floquet multiplier for the periodic orbit. Thus, locally an isochron is given by the stable eigenvector of the linearization about the periodic orbit. This defines a boundary value problem, and one can trace out isochrons by using different (small-magnitude) vectors in the direction \(\varDelta {\mathbf {x}}(0)\).
We note that for fast–slow dynamical systems, which are common for biological oscillators, \(|\mu |\) can be quite small, in which case it can be numerically advantageous to let
Then
In [80], this was solved using the boundary value solver from the numerical continuation package AUTO. This method works well for fast–slow systems as often arise for biological problems and can allow isochrons to be calculated in beautiful detail [55, 56, 80], but thus far it has only been used for planar systems.
Method of Fourier averages: [64]
Reference [64] makes the observation that isochrons of a periodic orbit with angular frequency \(\omega = 2 \pi /T\) are level sets of the Fourier average defined by
where \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is a continuously differentiable observable function and \(\phi _t(x)\) is the flow induced by (1). This is related to the fact that Fourier averages are eigenfunctions of the Koopman semigroup of operators \(U^t\) which are defined by \(U^t f(\mathbf{x}) = f \circ \phi _t(\mathbf{x})\). The Fourier averages can be calculated numerically for specific trajectories using forward integration of a set of initial conditions, and interpolation is used to obtain the isochrons. This method can be used for systems with dimensionality two or greater; see, e.g., [66] for its application to bursting neurons. Reference [63] develops a related framework to calculate global isochrons and isostables for periodic orbits.
Invariance equation approach: [5, 37, 42]
This method is based on a parameterization \(K(\theta ,\sigma )\) of the stable manifold of a periodic orbit for a planar system which gives the simplified equations
where \(\lambda \) is the nontrivial Floquet exponent for the periodic orbit. These equations are equivalent apart from scaling to what we called the augmented phase reduction for a planar system in the absence of control input (in particular, \(\theta \) here is a rescaled version of the phase in the augmented phase reduction, and \(\sigma \) is a scaled version of the isostable coordinate \(\psi \)). This parametrization satisfies the invariance equation [3]
which is solved numerically in [37] using a series method and in [42] using a Newton method. Isochrons and isostables then can be deduced from the solution for K, as can the phase response curve and the isostable response curve generalized to be defined throughout the basin of attraction of the periodic orbit, rather than just in its neighborhood [5, 37]. Thus far, this approach has only been applied to planar systems.
Hamilton–Jacobi formulation: [17]
By definition of isochrons,
from which we obtain the (static) Hamilton–Jacobi equation for \(\theta (\mathbf{x})\):
which holds for all points \(\mathbf{x}\) in the basin of attraction of the periodic orbit. A simple boundary condition for this PDE is obtained by numerically finding the phase everywhere on the periodic orbit itself: One chooses an initial point on the periodic orbit and calculates the phase according to \(\hbox {d} \theta /\hbox {d}t = \omega \). After solving (93), any isochron can be visualized by taking an isocontour of \(\theta (\mathbf{x})\). Reference [17] demonstrates this approach by using a particular finite difference discretization of (93) and an iterative fast sweeping method which allows numerical calculation of isochrons for systems with dimensionality two or greater. Unlike the method of Fourier averages which solves for a number of specific trajectories, this is an Eulerian method which can often lead to faster computations for higher-dimensional systems.
Analytical results: global isostables and isochrons
We now derive the coordinate systems for global isostables and isochrons for two classes of planar dynamical systems which can arise for simplified models of biological systems and physiological rhythms: \(\lambda -\omega \) systems and general radial isochron clocks. Some of these results are similar, but obtained using a different method, to the results in [37].
\(\bullet \) \(\lambda -\omega \) systems
In general, the dynamics of the isostable coordinate in the polar coordinate system are given by
where k is the nontrivial Floquet exponent for the periodic orbit. Because \(\lambda -\omega \) systems are radially symmetric, \(\frac{\partial \psi }{\partial \phi }= 0\), i.e., \(\psi \) is a function of r only. Using this and (22), we can then rewrite (94) as:
with the condition that \(\psi (r_\mathrm{po}) = 0\) for all \(\phi \). Note that these results are consistent with (66), which says that the IRC (i.e., the gradient of \(\psi \) evaluated on the periodic orbit) points in the radial direction.
We can carry out a similar analysis to find global isochron coordinates, cf. Example 5.3 of [37]. Unlike the case of the isostable coordinate, the isochron coordinate has a dependence on both r and \(\phi \); this results from the requirement that \(\theta \) changes with \(\phi \) on the periodic orbit. We equate the time derivative to the appropriate partial derivatives:
Because \(\dot{\phi }\) depends only on r, it is constant along the periodic orbit; therefore, \(\dot{\phi }\left( r_\mathrm{po}\right) =\omega \) and we can without loss of generality specify that, along the periodic orbit, \(\theta = \phi \), meaning \(\frac{\partial \theta }{\partial \phi } = 1\). Furthermore, for a fixed value of \(r = r_1\), \(\theta \left( r_1,\phi \right) + 2\pi = \theta \left( r_1,\phi +2\pi \right) \) and \(\frac{\partial \theta }{\partial \phi }\) must be independent of \(\phi \) because of the system’s radial symmetry (the dynamics are completely independent of \(\phi \) so the phase dynamics should be similarly independent). Thus, we can extend the result on the periodic orbit and conclude that \(\frac{\partial \theta }{\partial \phi } = 1\) for all r and \(\phi \). As a result, we can again reduce the system to an ODE in r:
with the global isochron coordinate being given by:
We note that these results are consistent with (23) for the PRC (i.e., the gradient of the phase \(\theta \) evaluated on a periodic orbit) of a \(\lambda -\omega \) system.
Example: supercritical Hopf bifurcation
For the supercritical Hopf bifurcation, \(G(r) = ar + cr^3\) and \(H(r) = b+dr^2\); this is slightly more general than Example 4.1.1 from [5], which uses a different but related approach to find what we refer to as global isochrons and isostables. The ODE (95) for the global isostable coordinates is:
which has the general solution
where \(c_1\) is an arbitrary scaling coefficient that can be chosen to normalize as desired. To match the IRC given in (68), one would take
Note that rearranging (99) allows us to represent r in terms of \(\psi \) instead:
Now, substituting (99) into (98) and simplifying yields the IRC directly:
We now carry out a similar analysis to find the global isochron coordinates. Our ODE (96) is
which is solved as:
To enforce \(\phi = \theta \) on the periodic orbit, we select \(c_2=\frac{d}{2c}\log \left( -\frac{a}{c} \right) \). The relation between \(\phi \) and \(\theta \) can then be flipped and written as:
Lastly, by taking the gradient of (101), the global PRC is given by
Note that for \(r=r_\mathrm{po} = \sqrt{-\frac{a}{c}}\) and using the fact that \(\theta = \phi \) on the periodic orbit, this expression is equivalent to that obtained from (24). In general, the PRC can be put in terms of the coordinates \(\psi \) and \(\theta \) by substituting for r and \(\phi \) using (100) and (102), respectively.
Control to an unstable fixed point for the Hopf bifurcation normal form: The top panel shows the computed optimal input to reach \(r=0.01\) at \(T_1=12\), with the inset showing more detail. The bottom left panel shows the trajectory of the system which starts at \((x,y) = (r_\mathrm{po},0)\) until it reaches the target for r, and the bottom right panel shows the slow relaxation back to the periodic orbit after the control is turned off at \(T_1=12\)
Example: control to an unstable fixed point
A new frontier is the application of optimal control to systems for which the global isochrons and isostables are known; to our knowledge, the following is the first example of such a calculation. Typically, when we consider the phase reduction, one of the assumptions is that the trajectory remains close to the stable periodic orbit, i.e., \(\psi \approx 0\). There may be situations, however, where this is not desirable; in this case, the underlying assumptions of the non-global approach no longer hold and it is necessary to use global coordinates. For example, for the supercritical Hopf bifurcation there is an unstable fixed point interior to the stable periodic orbit; attempting to control to this point using the traditional augmented phase reduction analysis would yield an inaccurate result, but with the global coordinates we can effectively drive the system to the neighborhood of this unstable point. In terms of the stable periodic orbit’s isostable coordinates, the unstable fixed point corresponds to \(\psi \rightarrow \infty \); this can be seen from (99). Therefore, designing a control to reach the unstable point at time \(T_1\) would correspond to maximizing the value of \(\psi \) at \(T_1\).
To illustrate this, we consider the Hopf bifurcation normal form with the parameters \(a = 0.1, b = 1, c=d=-1\). Additionally, we assume we can only apply a control input in the \(\hat{x}\) direction. The components of the PRC and IRC in the \(\hat{x}\) direction are, respectively,
and
Note that for convenience, for (104) we have taken \(c_1=1\).
We now design a minimum energy control that brings the system close to the fixed point. Our cost function is given by (28), where u(t) is the control input and \(T_1\) is now the time at which we want the trajectory to be within a specified Euclidean distance from the unstable fixed point. We apply calculus of variations to minimize
The associated Euler–Lagrange equations are:
Because it is more convenient in general to represent the PRC and IRC in terms of the original polar coordinates, we calculate the partial derivatives with respect to \(\theta \) and \(\psi \) by utilizing the chain rule:
The partial derivatives of r and \(\phi \) are computed from (100) and (102). A shooting method on the reduced model was employed to obtain the values of \(\lambda _1\) and \(\lambda _2\) required to give the value of \(\psi \) corresponding to \(r=0.01\) at time \(T_1\); Fig. 22 shows the results of a realization for \(T_1 = 12\). Then, the original Hopf bifurcation normal form model was simulated using the input corresponding to these initial values for \(\lambda _1\) and \(\lambda _2\) for the reduced model. At the target time \(T_1\), the control was turned off (\(u=0\)) and the system was allowed to relax back to the periodic orbit. As can be seen, this control strategy effectively forces the system into the vicinity of the unstable fixed point.
We note that this method is computationally simpler than using a Hamilton–Jacobi–Bellman approach to achieve a similar goal of steering a trajectory to an unstable fixed point [13, 73]; however, it requires knowledge of the global PRC and IRC, which might not always be possible.
\(\bullet \) General radial isochron clock
Applying (94) to the general radial isochron clock system (15) gives
If we make the ansatz that the global isostable coordinate only depends on r, that is that \(\frac{\partial \psi }{\partial \phi } = 0\), then
If we can solve this under the condition that \(\psi (r_\mathrm{po}) = 0\), then the ansatz is confirmed.
The isochrons are radial for systems described by (15), and we can use (16) to determine how the phase variable \(\theta \) depends on \(\phi \).
General radial isochron clock SNIPER example
We now consider the planar general radial isochron clock SNIPER bifurcation example considered previously, cf. [37], with \(G(r) = \rho r-r^3\) and \(K(\phi ;\eta ) = \eta -\sin (\phi )\); here \(r_\mathrm{po} = \sqrt{\rho }\) and \(k = G'(r_\mathrm{po}) = -2 \rho \). From (113), the ODE for the global isostable coordinate is
This has the general solution:
which is of the same form as the isostables found in (99) up to a scaling factor. From here, we find that the global IRC is given as:
or, equivalently,
Assuming the system has a periodic orbit, the global isochrons are found by solving (72):
The resulting PRC is therefore given by:
or equivalently,
6 Phase-based control of a population of oscillators
Thus far, the control applications in this tutorial have been focused on individual oscillators. But phase-based control of oscillator populations can also be achieved.
As an example application, consider the hypothesis that pathological synchronization of spiking neurons in the basal ganglia–cortical loop within the brain is a factor contributing to tremors exhibited by patients with Parkinson’s disease [6, 58, 102]. For patients with advanced Parkinson’s disease who do not respond to drug therapy, there is an established treatment option called deep brain stimulation in which a neurosurgeon implants an electrode that can inject current into the brain tissue [1]. This suggests the control problem of designing a single electrical stimulus u(t) which desynchronizes a population of neural oscillators.
Various phase-based control methods have been proposed to accomplish such desynchronization; see, e.g., [48, 95,96,97]. Here we briefly describe an approach called chaotic desynchronization, which is based on the Lyapunov exponent associated with the phase difference between a pair of identical oscillators which both receive the same input u(t) [110]:
A control input u(t) with a positive Lyapunov exponent gives a desynchronizing effect. Note that the expression for the Lyapunov exponent in (119) depends on the derivative of the phase response curve for a single oscillator. Reference [110] formulates the desynchronization problem as an optimal control problem: Find the stimulus which maximizes the Lyapunov exponent while simultaneously minimizing the power used by the stimulus, the latter goal being desirable because it allows the battery which generates the electrical stimulus to have a longer life, thereby reducing the need for battery replacement surgery. This could also lessen the chance of undesirable side effects of deep brain stimulation, because it uses a weaker stimulus. The optimal control from this approach was found to be a very effective strategy for desynchronizing a neural population; moreover, this methodology is robust to weak coupling and heterogeneities of the neurons [110]. Chaotic desynchronization has been extended to the more realistic case of extracellular stimulation [109]. Other phase-based control schemes for neural populations include phasic burst stimulation [39] and stabilization of clusters [60, 61]. Also notable are control schemes which are inspired by phase reduction, in that they optimally drive a population of oscillators to the phaseless set [116], where the phase cannot be defined; noise then randomizes the phases of the oscillators, leading to desynchronization [12, 73].
A different approach to the control of oscillator populations is based on a partial differential equation for the distribution of phases. For example, suppose we have a population of N noise-free, identical, uncoupled oscillators all receiving the same control input u(t), with phase dynamics given by
Consider the probability distribution \(\rho (\theta ,t)\) for the limit \(N \rightarrow \infty \), with the interpretation that \(\rho (\theta ,t) \hbox {d}\theta \) is the probability that a neuron’s phase lies in the interval \([\theta ,\theta + \hbox {d} \theta )\) at time t. This distribution evolves according to the advection equation [2, 95]
Here desynchronization corresponds to a flat distribution \(\rho = 1/(2 \pi )\). Different ideas for controlling a phase distribution include controlling the distribution’s peak [110], control based on a generalization of the isostable reduction to partial differential equations [113, 114], and control which minimizes the norm between the current and target distributions [70].
7 Conclusion/outlook
The concepts of isochrons and phase reduction for nonlinear oscillators have a long history [33, 53, 115, 117], and their usefulness has been demonstrated for a number of systems of physical, technological, and biological interest over the last five decades. More recently, phase reduction techniques have been extended to include transverse directions and higher-order terms, and they have also been generalized to systems with stable fixed points. This tutorial presented a unified treatment of such phase reduction techniques and illustrated their use through various mathematical and biological examples.
This tutorial also covered the use of phase reduction for the design of control algorithms which optimally change properties of the system, such as the phase or period of an oscillation. By reducing the dimension of the system, phase reduction allows a more tractable approach to designing control algorithms than trying to do so for the full evolution equations for a system.
There is still much to be explored in this realm, and we note recent results on phase reduction for stochastic oscillators [98], and operational phase reduction which makes more natural ties to experimentally measurable quantities [104]. There are also ample opportunities to use phase reduction to design control algorithms for a variety of neural, cardiac, circadian, and other biological systems, and to investigate and design for robustness of such algorithms to noise, uncertainty, and heterogeneity. We hope that this tutorial has illustrated the promise of phase reduction and phase-based optimal control and will lead the reader down the path of applying such techniques to their own systems of interest.
References
Benabid AL, Pollak P, Gervason C, Hoffmann D, Gao DM, Hommel M, Perret JE, Rougemont JD (1991) Long-term suppression of tremor by chronic stimulation of the ventral intermediate thalamic nucleus. Lancet 337:403–406
Brown E, Moehlis J, Holmes P (2004) On the phase reduction and response dynamics of neural oscillator populations. Neural Comput 16:673–715
Cabré X, Fontich E, Llave RDL (2005) The parametrization method for invariant manifolds III: overview and applications. J Differ. Equs. 218:444–515
Campbell A, Gonzalez A, Gonzalez DL, Piro O, Larrondo HA (1989) Isochrones and the dynamics of kicked oscillators. Phys A Stat Theor Phys 155(3):565–584
Castejón O, Guillamon A, Huguet G (2013) Phase-amplitude response functions for transient-state stimuli. J Math Neurosci 3:1–26
Chen CC, Litvak V, Gilbertson T, Kuhn A, Lu CS, Lee ST, Tsai CH, Tisch S, Limousin P, Hariz M, Brown P (2007) Excessive synchronization of basal ganglia neurons at 20 Hz slows movement in Parkinson’s disease. Exp Neurol 205(1):214–221
Cherry EM, Evans SJ (2008) Properties of two human atrial cell models in tissue: restitution, memory, propagation, and reentry. J Theor Biol 254(3):674–690
Christini DJ, Riccio ML, Culianu CA, Fox JJ, Karma A Jr, G RF (2006) Control of electrical alternans in canine cardiac Purkinje fibers. Phys Rev Lett 96(10):104101
Coddington EA, Levinson N (1955) Theory of ordinary differential equations. McGraw-Hill, New York
Couzin-Fuchs E, Kiemel T, Gal O, Ayali A, Holmes P (2015) Intersegmental coupling and recovery from perturbations in freely running cockroaches. J Exp Biol 218:285–297
Cui J, Canavier CC, Butera RJ (2009) Functional phase response curves: a method for understanding synchronization of adapting neurons. J Neurophysiol 102(1):387–398
Danzl P, Hansen R, Bonnet G, Moehlis J (2008) Partial phase synchronization of neural populations due to random Poisson inputs. J Comput Neurosci 25(1):141–157
Danzl P, Hespanha J, Moehlis J (2009) Event-based minimum-time control of oscillatory neuron models: phase radnomization, maximal spike rate increase, and desynchronization. Biol Cybern 101:387–399
Danzl P, Nabi A, Moehlis J (2010) Charge-balanced spike timing control for phase models of spiking neurons. Discrete Contin Dyn Syst 28:1413–1435
Dasanayake I, Li JS (2011) Optimal design of minimum-power stimuli for phase models of neuron oscillators. Phys Rev E 83:061,916
Dasanayake I, Li JS (2015) Constrained charge-balanced minimum-power controls for spiking neuron oscillators. Syst Control Lett 75:124–130
Detrixhe M, Doubeck M, Moehlis J, Gibou F (2016) A fast Eulerian approach for computation of global isochrons in high dimensions. SIAM J Appl Dyn Syst 15:1501–1527
Efimov D, Sacre P, Sepulchre R (2009) Controlling the phase of an oscillator: a phase response approach. In: Proceedings of the 48th IEEE conference on decision and control. Shanghai, China, pp 7692–7697
Ermentrout B (1996) Type I membranes, phase resetting curves, and synchrony. Neural Comput 8:979–1001
Ermentrout G (2002) Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. SIAM, Philadelphia
Ermentrout G, Glass L, Oldeman B (2012) The shape of phase-resetting curves in oscillators with a saddle node on an invariant circle bifurcation. Neural Comput 24:3111–3125
Ermentrout G, Kopell N (1984) Frequency plateaus in a chain of weakly coupled oscillators. SIAM J Math Anal 15(3):215–237
Ermentrout G, Kopell N (1991) Multiple pulse interactions and averaging in coupled neural oscillators. J Math Biol 29:195–217
Ermentrout GB, Terman DH (2010) Mathematical foundations of neuroscience. Springer, Berlin
Forger DB, Paydarfar D (2004) Starting, stopping, and resetting biological oscillators: in search of optimal perturbations. J Theor Biol 230:521–532
Fox JJ, McHarg JL, Gilmour RF (2002) Ionic mechanism of electrical alternans. Am J Physiol Heart Circ Physiol 282(2):H516–H530
Garzón A, Grigoriev RO, Fenton FH (2014) Continuous-time control of alternans in long Purkinje fibers. Chaos Interdiscip J Nonlinear Sci 24(3):033124
Glass L, Mackey MC (1988) From clocks to chaos: the rhythms of life. Princeton University Press, Princeton
Glendinning P (1994) Stability, instability and chaos: an introduction to the theory of nonlinear differential equations. Cambridge texts in applied mathematics. Cambridge University Press, Cambridge
Goldstein H (1980) Classical mechanics, 2nd edn. Addison-Wesley, Reading
Gray RA (2014) Theory of rotors and arrhythmias. In: Zipes DP, Jalife J (eds) Cardiac electrophysiology: from cell to bedside, 6th edn. WB Saunders Co Ltd, New York, pp 341–350
Grimshaw R (1993) Nonlinear ordinary differential equations. CRC Press, Baca Raton
Guckenheimer J (1975) Isochrons and phaseless sets. J Math Biol 1:259–273
Guckenheimer J (1995) Phase portraits of planar vector fields: computer proofs. Exp Math 4(2):153–165
Guckenheimer J, Holmes PJ (1983) Nonlinear oscillations, dynamical systems and bifurcations of vector fields. Springer, New York
Guckenheimer J, Kuznetsov YA (2007) Bautin bifurcation. Scholarpedia 2(5):1853
Guillamon A, Huguet G (2009) A computational and geometric approach to phase resetting curves and surfaces. SIAM J Appl Dyn Syst 8(3):1005–1042
Hansel D, Mato G, Meunier C (1995) Synchrony in excitatory neural networks. Neural Comput 7:307–337
Holt A, Wilson D, Shinn M, Moehlis J, Netoff T (2016) Phasic burst stimulation: a closed-loop approach to tuning deep brain stimulation parameters for Parkinson’s disease. PLoS Comput Biol 13:e1005001
Hoppensteadt FC, Izhikevich EM (1997) Weakly connected neural networks. Springer, New York
Hoppensteadt FC, Keener J (1982) Phase locking of biological clocks. J Math Biol 15:339–349
Huguet G, de la Llave R (2013) Computation of limit cycles and their isochrons: fast algorithms and their convergence. SIAM J Appl Dyn Syst 12:1763–1802
Izhikevich E (2007) Dynamical systems in neuroscience: the geometry of excitability and bursting. MIT Press, London
Izhikevich EM (2000) Phase equations for relaxation oscillators. SIAM J Appl Math 60:1789–1804
Josic K, Shea-Brown ET, Moehlis J (2006) Isochron. Scholarpedia 1(8):1361
Kenig E, Cross M, Villanueva L, Karabalin R, Matheny M, Lifshitz R, Roukes M (2012) Optimal operating points of oscillators using nonlinear resonators. Phys Rev E 86:056207
Kirk DE (1970) Optimal control theory: an introduction. Dover Publications Inc., New York
Kiss IZ, Rusin CG, Kori H, Hudson JL (2007) Engineering complex dynamical structures: sequential patterns and desynchronization. Science 316:1886–1889
Kopell N, Howard L (1973) Plane wave solutions to reaction–diffusion equations. Stud Appl Math 52(4):291–328
Kralemann B, Frühwirth M, Pikovsky A, Rosenblum M, Kenner T, Schaefer J, Moser M (2013) In vivo cardiac phase response curve elucidates human respiratory heart rate variability. Nat Commun 4:2418
Kralemann B, Pikovsky A, Rosenblum M (2014) Reconstructing effective phase connectivity of oscillator networks from observations. New J Phys 16(8):085013
Krishnan GP, Bazhenov M, Pikovsky A (2013) Multipulse phase resetting curves. Phys Rev E 88(4):042902
Kuramoto Y (1984) Chemical oscillations, waves, and turbulence. Springer, Berlin
Kuznetsov Y (1998) Elements of applied bifurcation theory, 2nd edn. Springer, New York
Langfield P, Krauskopf B, Osinga H (2014) Solving Winfree’s puzzle: the isochrons in the FitzHugh-Nagumo model. Chaos 24:013131
Langfield P, Krauskopf B, Osinga H (2015) Forward-time and backward-time isochrons, and their interactions. SIAM J Appl Dyn Syst 14:1418–1453
Lenhart S, Workman JT (2007) Optimal control applied to biological models. Chapman and Hall/CRC, Boca Raton
Levy R, Hutchison WD, Lozano AM, Dostrovsky JO (2000) High-frequency synchronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor. J Neurosci 20(20):7766–7775
Malkin I (1949) The methods of Lyapunov and Poincare in the theory of nonlinear oscillations. Gostekhizdat, Moscow-Leningrad
Matchen T, Moehlis J (2017) Real-time stabilization of neurons into clusters. In: Proceedings of the 2017 American control conference. Seattle, pp 2805–2810
Matchen T, Moehlis J (2018) Phase model-based neuron stabilization into arbitrary clusters. J Comput Neurosci 44:363–378
Mauroy A (2014) Converging to and escaping from the global equilibrium: isostables and optimal control. In: Proceedings of the 53rd IEEE conference on decision and control. Los Angeles, pp 5888–5893
Mauroy A, Mezic I (2018) Global computation of phase-amplitude reduction for limit-cycle dynamics. Chaos. https://doi.org/10.1063/1.5030175
Mauroy A, Mezic I (2012) On the use of Fourier averages to compute the global isochrons of (quasi)periodic dynamics. Chaos 22:033112
Mauroy A, Mezić I, Moehlis J (2013) Isostables, isochrons, and Koopman spectrum for the action-angle representation of stable fixed point dynamics. Physica D 261:19–30
Mauroy A, Rhoads B, Moehlis J, Mezic I (2014) Global isochrons and phase sensitivity of bursting neurons. SIAM J Appl Dyn Syst 13:306–338
Merrill D, Bikson M, Jefferys J (2005) Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J Neurosci Methods 141:171–98
Moehlis J (2014) Improving the precision of noisy oscillators. Physica D 272:8–17
Moehlis J, Shea-Brown E, Rabitz H (2006) Optimal inputs for phase models of spiking neurons. ASME J Comput Nonlinear Dyn 1:358–367
Monga B, Froyland G, Moehlis J (2018) Synchronizing and desynchronizing neural populations through phase distribution control. In: Proceedings of the 2018 American control conference. Milwaukee, pp 2808–2813
Monga B, Moehlis J (2018) Optimal phase control of biological oscillators using augmented phase reduction. Biol Cybern. https://doi.org/10.1007/s00422-018-0764-z
Morris C, Lecar H (1981) Voltage oscillations in the barnacle giant muscle fiber. Biophys J 35(1):193–213
Nabi A, Mirzadeh M, Gibou F, Moehlis J (2013) Minimum energy desynchronizing control for coupled neurons. J Comput Neurosci 34:259–271
Nabi A, Moehlis J (2009) Charge-balanced optimal inputs for phase models of spiking neurons. In: Proceedings of the 2009 ASME dynamic systems and control conference. DSCC2009-2541
Nabi A, Moehlis J (2012) Time optimal control of spiking neurons. J Math Biol 64:981–1004
Nabi A, Stigen T, Moehlis J, Netoff T (2013) Minimum energy control for in vitro neurons. J Neural Eng 10(3):036005
Narayan SM (2006) T-wave alternans and the susceptibility to ventricular arrhythmias. J Am Coll Cardiol 47(2):269–281
Netoff T, Schwemmer M, Lewis T (2012) Experimentally estimating phase response curves of neurons: theoretical and practical issues. In: Schultheiss NW, Prinz AA, Butera RJ (eds) Phase response curves in neuroscience. Springer, pp 95–129
Nolasco JB, Dahlen RW (1968) A graphic method for the study of alternation in cardiac action potentials. J Appl Physiol 25(2):191–196
Osinga H, Moehlis J (2010) A continuation method for computing global isochrons. SIAM J Appl Dyn Syst 9:1201–1228
Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS (1999) Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation 99(10):1385–1394
Pruvot EJ, Katra RP, Rosenbaum DS, Laurita KR (2004) Role of calcium cycling versus restitution in the mechanism of repolarization alternans. Circ Res 94(8):1083–1090
Qu Z, Nivala M, Weiss JN (2013) Calcium alternans in cardiac myocytes: order from disorder. J Mol Cell Cardiol 58:100–109
Revzen S, Guckenheimer JM (2008) Estimating the phase of synchronized oscillators. Phys Rev E 78(5):051907
Revzen S, Guckenheimer JM (2012) Finding the dimension of slow dynamics in a rhythmic system. J R Soc Interface 9(70):957–971
Roberts AJ (1989) Appropriate initial conditions for asymptotic descriptions of the long term evolution of dynamical systems. J Aust Math Soc Ser B Appl Math 31(01):48–75
Rogers J, McCulloch A (1994) A collocation-Galerkin finite element model of cardiac action potential propagation. IEEE Trans Biomed Eng 41:743–757
Rubin J, Terman D (2004) High frequency stimulation of the subthalamic nucleus eliminates pathological thalamic rhythmicity in a computational model. J Comput Neurosci 16(3):211–235
Schwabedal JTC, Kantz H (2016) Optimal extraction of collective oscillations from unreliable measurements. Phys Rev Lett 116(10):104101
Shaw K, Park YM, Chiel H, Thomas P (2012) Phase resetting in an asymptotically phaseless system: on the response of limit cycles verging on a heteroclinic orbit. SIAM J Appl Dyn Syst 11:350–391
Shirasaka S, Kurebayashi W, Nakao H (2017) Phase-amplitude reduction of transient dynamics far from attractors for limit-cycling systems. Chaos 27:023119
Sootla A, Mauroy A, Ernst D (2017) An optimal control formulation of pulse-based control using Koopman operator. arXiv preprint arXiv:1707.08462
Suvak O, Demir A (2010) Quadratic approximations for the isochrons of oscillators: a general theory, advanced numerical methods, and accurate phase computations. IEEE Trans Comput Aided Des Integr Circuits Syst 29(8):1215–1228
Takeshita D, Feres R (2010) Higher order approximation of isochrons. Nonlinearity 23(6):1303–1323
Tass PA (1999) Phase resetting in medicine and biology. Springer, New York
Tass PA (2001) Effective desynchronization by means of double-pulse phase resetting. Europhys Lett 53:15–21
Tass PA (2003) A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biol Cybern 89(2):81–88
Thomas P, Lindner B (2014) Asymptotic phase for stochastic oscillators. Phys Rev Lett 113:254101
Tolkacheva EG, Schaeffer DG, Gauthier DJ, Krassowska W (2003) Condition for alternans and stability of the 1:1 response pattern in a memory model of paced cardiac dynamics. Phys Rev E 67(3):031904
Topçu C, Frühwirth M, Moser M, Rosenblum M, Pikovsky A (2018) Disentangling respiratory sinus arrhythmia in heart rate variability records. Physiol Meas 39(5):054002
Wedgwood K, Lin K, Thul R, Coombes S (2013) Phase-amplitude descriptions of neural oscillator models. J Math Neurosci 3(1):1–22
Wichmann T, DeLong MR, Guridi J, Obeso JA (2011) Milestones in research on the pathophysiology of Parkinson’s disease. Mov Disord 26(6):1032–1041
Wiggins S (1994) Normally hyperbolic invariant manifolds in dynamical systems. Springer, New York
Wilson D, Ermentrout B (2018) An operational definition of phase characterizes the transient response of perturbed limit cycle oscillators. SIAM J Appl Dyn Syst (In press)
Wilson D, Ermentrout B (2018) Greater accuracy and broadened applicability of phase reduction using isostable coordinates. J Math Biol 76(1–2):37–66
Wilson D, Holt AB, Netoff TI, Moehlis J (2015) Optimal entrainment of heterogeneous noisy neurons. Front Neurosci 9:192
Wilson D, Moehlis J (2014) An energy-optimal approach for entrainment of uncertain circadian oscillators. Biophys J 107:1744–1755
Wilson D, Moehlis J (2014) An energy-optimal methodology for synchronization of excitable media. SIAM J Appl Dyn Syst 13(2):944–957
Wilson D, Moehlis J (2014) Locally optimal extracellular stimulation for chaotic desynchronization of neural populations. J Comput Neurosci 37:243–257
Wilson D, Moehlis J (2014) Optimal chaotic desynchronization for neural populations. SIAM J Appl Dyn Syst 13:276–305
Wilson D, Moehlis J (2015) Determining individual phase response curves from aggregate population data. Phys Rev E 92:022902
Wilson D, Moehlis J (2015) Extending phase reduction to excitable media: theory and applications. SIAM Rev 57:201–222
Wilson D, Moehlis J (2016) Isostable reduction of periodic orbits. Phys Rev E 94:052213
Wilson D, Moehlis J (2017) Spatiotemporal control to eliminate cardiac alternans using isostable reduction. Phys D Nonlinear Phenom 342:32–44
Winfree A (1967) Biological rhythms and the behavior of populations of coupled oscillators. J Theor Biol 16:14–42
Winfree A (1974) Patterns of phase compromise in biological cycles. J Math Biol 1:73–95
Winfree A (2001) The geometry of biological time, 2nd edn. Springer, New York
Zlotnik A, Chen Y, Kiss I, Tanaka HA, Li JS (2013) Optimal waveform for fast entrainment of weakly forced nonlinear oscillators. Phys Rev Lett 111:024102
Acknowledgements
Support for this work by National Science Foundation Grants NSF-1635542 and NSF-1602841 is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Peter J. Thomas.
Appendices
Appendix A: Models
In this appendix, we give details of the mathematical models used in the main text.
Thalamic neuron model
The thalamic neuron model is given as
where
Morris–Lecar model
The Morris–Lecar model is given as
Fox–McHarg–Gilmour (FMG) model
The FMG model [26] describes the electrophysiological behavior of a canine ventricular myocytes with behavior governed by various potassium, sodium, and calcium currents. The transmembrane voltage dynamics are governed by the flow of ionic current across the cell membrane
Here \(I_{\mathrm{stim}}\) represents a stimulus current used to elicit action potentials, and \(I_{\mathrm{ion}}\) is the total membrane current density, both of which have units of \(\upmu \hbox {A}/\upmu \hbox {F}\). \(I_{\mathrm{ion}}\) is comprised of 13 individual currents, which are determined by 13 total state variables. A full description of the equations and nominal parameters is given in [26].
Appendix B: Derivation of the Euler–Lagrange equations
The Euler–Lagrange equations can be derived using the methods of analytical mechanics [30] or optimal control theory [47]. Suppose we want to find the function q(t) which extremizes the functional
The functional derivative has the property that for any function v(t),
where the last equation follows from integration by parts applied to the second term of the previous line. If we suppose that \(v(0) = v(T) = 0\), then
For this to be an extremum, it must hold for any v. Therefore, we obtain the Euler–Lagrange equation
To incorporate constraints into this approach, it is instructive to first consider the simpler optimization problem where one wants to find an extremum of the function \(\mathbf{f}(\mathbf{x})\) subject to the constraint that \(\mathbf{g}(\mathbf{x}) = \mathbf{c}\). Recognizing that at an extremum the level surface of \(\mathbf{f}(\mathbf{x})\) must be tangent to the surface defined by \(\mathbf{g}(\mathbf{x}) = \mathbf{c}\), we see that
for some scalar \(\lambda \), which is called the Lagrange multiplier. Finding the extremum of \(\mathbf{f}\) while simultaneously satisfying (124) is equivalent to finding the extremum of
Indeed,
In optimal control problems, it is necessary to minimize or maximize the cost function subject to the constraint that the dynamics must satisfy the appropriate evolution equation. For example, consider the energy-optimal phase control problem of designing the input u(t) such that the cost function \({{\mathcal {G}}}[u(t)]\) given by (28) is minimized, subject to the constraint that the solution must satisfy (27). We can rewrite (27) as
Integrating this, we obtain
We therefore want to find u(t) such that the following hold:
By analogy with the above constrained optimization example, the level surfaces of \({{\mathcal {G}}}[u(t)]\) will be tangent to surfaces for which \({{\mathcal {K}}}[u(t)] = 0\). Thus,
for some scalar function \(\lambda (t)\). [Without loss of generality, we have inserted a minus sign on the right-hand side of (125).]. Rearranging (125) gives
which is identical to the cost function (29). We now use (123) with q(t) taken in turn to be u(t), \(\lambda (t)\), and \(\theta (t)\), which gives Eqs. (30–32) in the main text.
Appendix C: Solving a two-point boundary value problem
Consider a general two-point boundary value problem
with the linear boundary condition
To solve such a boundary value problem, we integrate Eq. (126) with the initial guess \(c=y(0)\) and calculate the function g(c):
where y(b) is the solution at time b with the initial condition c. If we had chosen the correct initial condition c, g(c) would be 0. Based on the current guess \(c^\nu \), and the \(g(c^\nu )\) value, we choose the next initial condition by the Newton Iteration as
We compute the Jacobian \(J=\left. \frac{\partial g}{\partial c}\right| _{c^\nu }\) numerically as
where
\(J_i\) is the \(i\mathrm{th}\) column of J, \(\epsilon \) is a small number, and \(e_i\) is a column vector with 1 in the \(i\mathrm{th}\) position and 0 elsewhere.
Rights and permissions
About this article
Cite this article
Monga, B., Wilson, D., Matchen, T. et al. Phase reduction and phase-based optimal control for biological systems: a tutorial. Biol Cybern 113, 11–46 (2019). https://doi.org/10.1007/s00422-018-0780-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-018-0780-z