Phase model-based neuron stabilization into arbitrary clusters

Abstract

Deep brain stimulation (DBS) is a common method of combating pathological conditions associated with Parkinson’s disease, Tourette syndrome, essential tremor, and other disorders, but whose mechanisms are not fully understood. One hypothesis, supported experimentally, is that some symptoms of these disorders are associated with pathological synchronization of neurons in the basal ganglia and thalamus. For this reason, there has been interest in recent years in finding efficient ways to desynchronize neurons that are both fast-acting and low-power. Recent results on coordinated reset and periodically forced oscillators suggest that forming distinct clusters of neurons may prove to be more effective than achieving complete desynchronization, in particular by promoting plasticity effects that might persist after stimulation is turned off. Current proposed methods for achieving clustering frequently require either multiple input sources or precomputing the control signal. We propose here a control strategy for clustering, based on an analysis of the reduced phase model for a set of identical neurons, that allows for real-time, single-input control of a population of neurons with low-amplitude, low total energy signals. After demonstrating its effectiveness on phase models, we apply it to full state models to demonstrate its validity. We also discuss the effects of coupling on the efficacy of the strategy proposed and demonstrate that the clustering can still be accomplished in the presence of weak to moderate electrotonic coupling.

1 Introduction

Oscillators are an important component of numerous biological processes, including circadian rhythms, cardiac pacemaker cells, and motor control. Developing effective methods of controlling these oscillators is an important goal. This is especially true in neuroscience, where pathological activity may be linked to improper functioning of neural oscillators (Rosenblum and Pikovsky 2004). For example, evidence of the role of desynchronization of oscillators at the population level in the efficacy of deep brain stimulation (DBS) provides a compelling reason to investigate ways to improve our understanding of effective control strategies for oscillator populations.

DBS is a proven method for reducing certain symptoms related to Parkinson’s disease (PD), most notably tremors and dyskinesia, as well as tics associated with Tourette syndrome, essential tremor, and a number of other disorders (Savica et al. 2012; Benabid et al. 2002). In DBS, an electrode is implanted in either the subthalamic nucleus (STN) or globus pallidus pars interna (GPi) (Rodriguez-Oroz et al. 2005; The Deep-Brain Stimulation for Parkinson’s Disease Study Group 2001) in the case of Parkinson’s, or the thalamus for Tourette syndrome (Savica et al. 2012) or essential tremor (Benabid et al. 2002). Despite its proven effectiveness, the mechanisms by which DBS alleviates the symptoms are poorly understood. Additionally, there are risks associated with DBS, both related to the surgical procedure and hardware as well as to the chronic usage in combating the symptoms of PD (Rodriguez-Oroz et al. 2005; Beric et al. 2002). For these reasons, there have been various attempts in recent years to not only better understand the processes that allow for the success of DBS, but also to understand ways to reduce the possible negative side-effects. Many of these attempts suggest that DBS may function by modifying the behavior of oscillators to reduce synchronization.

Recent work (Uhlhaas and Singer 2006; Chen et al. 2007; Hammond et al. 2007; Levy et al. 2000; Schnitzler and Gross 2005) suggests that symptoms of Parkinson’s are associated with elevated synchrony of neurons in the basal ganglia, and there has been experimental and theoretical evidence (Tass 2003a; Wilson and Moehlis 2015; Wilson et al. 2011) that the reduction of this synchrony is correlated to the alleviation of symptoms. One approach to achieve partial desynchronization is to split the oscillator neurons into clusters, in which only a subpopulation of the neurons are spike-synchronized. In fact, Wilson and Moehlis (2015) suggests that the standard DBS protocol leads to clusters.

One promising approach to clustering, coordinated reset, involves using multiple electrode implants delivering a series of identical impulses separated by a time delay between implants. This has been studied extensively (Lücken et al. 2013; Lysyansky et al. 2011, 2013; Tass 2003a) with preliminary clinical success (Adamchic et al. 2014). Modeling and clinical results for coordinated reset suggest that relatively strongly clustered groups of neurons do not lead to pathological outcomes in the user and can be effective in treatment for Parkinson’s Disease. We note that the beneficial effects of clustering for Parkinson’s relief can also be inferred from Rubin and Terman (2004). Coordinated reset, however, relies on a number of electrodes equal to the number of clusters desired. This may not always be physically feasible in practice. It also requires the powering of multiple electrodes simultaneously, which additionally limits its energy efficiency.

Another approach is to design the control to maximize the desynchronization of the neurons. In Danzl et al. (2009), this is done using a high-amplitude input to drive neurons close to the unstable fixed point (a “phaseless set”) in the interior of the stable limit cycle. Wilson and Moehlis (2014) develops an optimal control strategy that is more energy-efficient than the method proposed in Danzl et al. (2009) but requires more frequent application of the control signal. In both cases, the energy cost represents a substantial improvement over conventional DBS and requires only a single input; total desynchronization, however, may not be preferable, as it can return to a synchronous state more quickly than in clustering (for comparison, see Wilson and Moehlis (2014) and Lysyansky et al. (2011); additionally, see Tass (2003b)). Furthermore, clustering behavior may contribute to longer-term reduction in pathological synchronization via increased plasticity in the relevant neural regions, cf. Zhao et al. (2011).

The references Wilson and Moehlis (2014), Zlotnik and Li (2014), Li et al. (2013), and Zlotnik et al. (2016) all employ precomputed signals to achieve their control objectives. Like Wilson and Moehlis (2014), Zlotnik and Li (2014) and Li et al. (2013) use optimization principles to derive lowest-energy control strategies for populations of neurons. In Zlotnik et al. (2016), heterogeneity in the natural frequencies of the neurons is exploited to entrain clusters of neurons. The use of precomputed, open-loop control signals in these methods reduces their flexibility in real-time application; there is no capacity for adjustment to error in the model. Additionally, the reliance on heterogeneity makes the control scheme highly model-specific, requiring a complete recalculation in the event of alterations to the model or neuron population.

In this paper we develop a control strategy for oscillators that provides a low-energy, single-input solution with minimal requirement for precomputed information. This strategy can be easily applied to any oscillatory neuron model to drive the population to a K-cluster state, where K is an arbitrary positive integer as desired for the control objective. The control strategy is designed based on a population of identical neurons subject to a single input; we note that while some of the underlying theory does not strictly hold for heterogeneous systems, modifications can be made to the strategy to accommodate small heterogeneities as well. Additionally, the control strategy is constructed to be sufficiently general as to be applicable to any oscillator with stable limit-cycle dynamics. We will begin in Section 2 by demonstrating that, provided certain assumptions are made about the oscillator population, the population may always be stabilized to a desired control state. With this established, we develop the control strategy in Section 3; the strategy is then applied to two different neuron populations subject to various conditions in the remainder of the paper.

As in some of the previously cited papers, we will make use of the phase model reduction for the dynamical system in designing our control strategy. The firing neuron has a fixed, stable limit cycle; following the work in Kuramoto (1984), Brown et al. (2004), and Sacrė and Sepulchre (2014) we can therefore reduce the dynamics when the neuron’s state is near the limit cycle to the representation:

$$ \dot{\theta_{j}}=\omega + Z\left( \theta_{j}\right) u\left( t\right), $$

(1)

where $\dot {\theta _{j}}$ describes the evolution of the j th neuron and the control input, $u\left (t\right )$, is proportional to the applied current I and is common to all neurons. $Z\left (\theta \right )$ is known as the phase response curve, and describes the sensitivity of the phase to a stimulus. The two models in this paper are examples of Type I and Type II neurons (Ermentrout and Terman 2010), respectively. For both models, the phase response curve was calculated by solving the appropriate adjoint equation using the dynamical modeling program XPPAUT (Ermentrout 2002). A preliminary version of these results has been published in Matchen and Moehlis (2017).

2 General stabilizability of N identical neurons

Before describing the specific control design we will employ, we start by showing that it is in general feasible to achieve a clustered state with a population of identical neurons. In particular, we demonstrate that any order-preserving clustering scheme for uncoupled, identical neurons is asymptotically stabilizable with an appropriate control input provided minor restrictions are placed on the phase response curve. Here we understand asymptotically stabilizable to mean that, for an appropriate choice of input u, the system of neurons approaches our desired state as $t\to \infty$. To do this, it must be shown that the control system is passive with a radially unbounded positive definite storage function and zero-state observable (Khalil 2015). These requirements are summarized as follows:

Radially Unbounded Positive Definite Storage Function :

A storage function $\mathcal {V}$ is any function which converts the state of the system into a scalar measure of the “energy” stored in the system; a simple physical example might be a function converting the position and velocity of an object into a total energy consisting of potential and kinetic energy components. In this case, we desire the storage function to equal 0 at exactly one point: our target state. The requirement that the function is positive definite means that everywhere else in the state space, the storage function’s value is greater than 0. Because the function is radially unbounded, we further require that as we move farther from this state, the value continually increases.

Passive :

A system is passive (Khalil 2015) if, for a given observable vector y and storage function $\mathcal {V}$ and any choice of u:

$$ u^{T} y \ge \dot{\mathcal{V}} , $$

(2)

where $\dot {\mathcal {V}}$ denotes the first time derivative of $\mathcal {V}$. This requires, for example, that if $u^{T} = \vec {0}$, $\dot {\mathcal {V}}\le 0$. Physically, this corresponds to the system not producing energy and instead being energy neutral or an energy consumer.

Zero-State Observable :

For a vector observable y to be zero-state observable, the target state must be the only point in state-space where $y=\vec {0}$ and remains zero for all future times. Although y may equal zero at other points in state-space, it must become nonzero in finite time. For example, if we used height as our observable for a bouncing ball, we would say the system is zero-state observable because, unless the velocity of the ball stays at zero (i.e., the ball has stopped bouncing), the height will not remain zero (the ball will bounce back up).

A system that meets these three criteria can be shown to be stabilizable with an appropriate choice of input (Khalil 2015). We demonstrate these requirements all generally hold for the case of N identical, uncoupled neurons in the reduced phase model formulation. We label the neurons such that, at time t = 0, the neuron phases are ordered as 𝜃₁ < 𝜃₂ < 𝜃₃ < ... < 𝜃 _N . Note that if the phases of two neurons are exactly the same, because the neurons are identical and receive identical inputs they are impossible to separate; therefore, we exclude the possibility of two phases being equal by assumption. Furthermore, since the neurons are identical, the response of a neuron is bounded by the neurons of phase initially less than the neuron and those greater than the neuron, so for t > 0, it follows from these assumptions that $\theta _{1}\left (t\right )<\theta _{2}\left (t\right )<...<\theta _{N}\left (t\right )$ (here we do not use the modulo 2π value for 𝜃 _j , so 𝜃 _j is allowed to be greater than 2π) (Li et al. 2013).

Typically when discussing stabilizability, the target state would be a specific coordinate in state-space, such as the origin. Here, however, we do not want the neurons to stop oscillating, so we do not wish to drive the system to specific values of 𝜃. Instead, we wish to instead reach a target state describing the relations between their phases as they continue to oscillate. It is therefore natural to define our storage function in terms of the differences between the phases of neurons rather than the individual phases (which are constantly evolving). More precisely, we construct our storage function as the linear combination of positive semidefinite functions, each prescribing the target separation for the phases of two neurons:

$$ v_{i} = v_{i}\left( \theta_{j} - \theta_{k}\right),\qquad \mathcal{V}\left( \theta_{1},...,\theta_{N}\right) = \sum\limits_{i = 1}^{l} \beta_{i} v_{i}, $$

(3)

with β _i > 0 and where 𝜃 _j and 𝜃 _k are the phases of any two neurons whose separation is to be prescribed by the function v _i . The value of l is arbitrary in this context; in Section 3, for the specific problem of clustering l = K. The individual storage function candidates have three properties:

• 1. At the target separation 𝜃 _j − 𝜃 _k = Δ𝜃^∗, $v_{i} \left ({\Delta }\theta ^{*}\right ) = 0$;

• 2. For 𝜃 _j − 𝜃 _k ≠Δ𝜃^∗, $v_{i}\left (\theta _{j} -\theta _{k}\right ) > 0$ and grows unbounded away from Δ𝜃^∗ within the interval $\theta _{j}-\theta _{k} \in \left (0,2\pi \right )$;

• 3. $\frac {\partial v_{i}}{\partial {\Delta }\theta }|_{{\Delta }\theta ^{*}}= 0$, $\frac {\partial v_{i}}{\partial {\Delta }\theta }|_{{\Delta }\theta \neq {\Delta }\theta ^{*}}\neq 0$.

Figure 1 illustrates the case of l = 2, Δ𝜃^∗ = π to demonstrate how these control objectives translate into a stabilized clustered configuration.

Fig. 1

Visualization of the control objective design. Each circle represents a neuron, and they oscillate around the unit circle. Here, l = 2, so two target separations are specified: the separation between the yellow and green neurons and the separation between the blue and red neurons. $\mathcal {V}= 0$ if and only if both of these separations are π (as is nearly the case in the circle to the right). Because the neurons are identical, the positions of the black neurons are bounded by the non-black neurons, and so they are guaranteed to be present in this clustered arrangement

We now calculate the value of $\dot {V}$. As each individual storage function is dependent on only one phase difference, we write $\dot {V}$ as:

$$ \dot{V} = \sum\limits_{i = 1}^{l} \beta_{i} \frac{\partial v_{i}}{\partial {\Delta}\theta_{i}} \dot{{\Delta}\theta_{i}}= \sum\limits_{i = 1}^{l} \beta_{i} \frac{\partial v_{i}}{\partial {\Delta}\theta_{i}}\left( \dot{\theta_{j}}-\dot{\theta_{k}}\right). $$

(4)

Substituting in from Eq. (1), $\dot {V}$ can be rewritten as:

$$ \dot{V} = u^{*}\sum\limits_{i = 1}^{l} \beta_{i} \frac{\partial v_{i}}{\partial {\Delta}\theta_{i}}\left( Z\left( \theta_{j}\right)-Z\left( \theta_{k}\right)\right), $$

(5)

where u^∗ is the common input received by every neuron. To satisfy passivity, we choose our observable to be a vector $y = \left [y_{1}, y_{2},\cdots ,y_{l}\right ]^{T}$ such that:

$$ y_{i}= \beta_{i} \frac{\partial v_{i}}{\partial {\Delta}\theta_{i}} \left( Z\left( \theta_{j}\right)-Z\left( \theta_{k}\right)\right). $$

(6)

Recognizing identical inputs as a special case of $u^{T}=\left [u_{1},u_{2},\cdots ,u_{l}\right ]$ where u _i = u^∗∀i, it follows that $u^{T} y = \dot {V}$ everywhere in the state-space. Therefore, the system as constructed is not only passive but also lossless. Additionally, y is zero-state observable: at the target state, $\frac {\partial v_{i}}{\partial {\Delta }\theta _{i}} = 0$; y = 0 otherwise only if $Z\left (\theta _{j}\right )-Z\left (\theta _{k}\right ) = 0$, but no such pair of neurons can stay indefinitely in the set y = 0. We can see this by considering:

$$ \frac{d}{dt}\left( Z\left( \theta_{j}\right)-Z\left( \theta_{k}\right)\right) = \frac{\partial Z}{\partial \theta}|_{\theta_{j}} \dot{\theta_{j}}-\frac{\partial Z}{\partial \theta}|_{\theta_{k}} \dot{\theta_{k}}. $$

(7)

Since $Z\left (\theta _{j}\right ) = Z\left (\theta _{k}\right )$, it follows from Eq. (1) that $\dot {\theta _{j}}=\dot {\theta _{k}}$ instantaneously, so the right side of Eq. (7) equalling 0 would require $\frac {\partial Z}{\partial \theta }|_{\theta _{j}} = \frac {\partial Z}{\partial \theta }|_{\theta _{k}}$. For y to equal 0 at all future times, this would further imply that this equality must hold over the entire period, i.e. $\exists \delta x \in \left (0,2\pi \right )$ such that $\frac {\partial Z}{\partial \theta } |_{x} = \frac {\partial Z}{\partial \theta } |_{x+\delta x} \forall x$. Graphically, this would mean that horizontally shifting the phase response curve reproduces the original curve. Since $\frac {\partial Z}{\partial \theta }|_{0} = \frac {\partial Z}{\partial \theta }|_{2\pi }$ and $Z\left (0\right ) = Z\left (2\pi \right )$, this is true if and only if $Z\left (\theta \right )$ is constant or has periodicity greater than 2π, which is physically not realized. Therefore, as the system is both passive with an unbounded storage function and zero-state observable, we can conclude that the system can be stabilized by the choice of $u=-\phi \left (y\right )$ where $\phi \left (y\right )$ is locally Lipschitz and $y\phi \left (y\right )>0$ (Khalil 2015). We note that this does not strictly hold for the case of an identical input; while $u^{T} = \left [u, u, \cdots , u\right ]$ does allow for locally Lipschitz solutions, there is a measure-0 set in which $y\phi \left (y\right )= 0$. In practice, however, we find this only forms an invariant set when the phase response curve is in some way degenerate or not physically realizable (such as having a higher than 2π periodicity) or the control objectives are poorly defined (such as when reaching the control state would require neurons to cross each other). Other instances of $y\phi \left (y\right )= 0$ are solely instantaneous and did not affect the computational outcome.

3 Control strategy for K clusters of neurons

Having shown that clustered states for identical neurons can be stabilized, we will now outline our design strategy for doing so. Our goals in developing a control strategy for clustering are threefold:

• 1. Create a flexible method such that the strategy functions in a way that is agnostic both to the specific neuron model used and the desired number of clusters K;

• 2. Require as little precomputing as possible so the method is robust to inaccuracies in modeling; and

• 3. Allow for the control to be easily tuned for parameters of interest, such as maximum input amplitude and speed with which clustering is achieved.

These three conditions can be seen as measures of robustness for the method. A control scheme that meets these three criteria can be altered on the fly by changing only a small number of target parameters, allowing the input to rapidly be tuned to the performance specifications desired. Additionally, deviations from expected results can be compensated for if the input is not constrained to precomputed values, as would be the case with optimal control strategies derived from, for example, variational principles.

The approach proposed here consists of considering what we propose to call the input of maximal instantaneous efficiency (IMIE) rather than precomputed data. Although not necessarily as efficient as true optimization strategies, IMIE requires only knowledge of the phase response curve of the neurons and the current state of the system.

The rest of this section will be structured as follows: first, we will define the two necessary functions for IMIE: a state function and a cost function. Next, we will lay out the details of the control strategy. Lastly, we will see how the reduction of the model for special cases returns results that agree with intuition and past results.

State Function :

The state function r, to be defined below, is functionally equivalent to a specific storage function which we will use to generate our control. Control of a system of N neurons into K clusters requires the direct control of 2K neurons, split into pairs of 2, with each pair of neurons adjacent to each other in phase order. The control is generated in such a way that each pair is driven apart to a target separation of $\frac {2\pi }{K}$ radians. In this way, K clusters are formed by exploiting the boundedness of response described in Section 2 and illustrated in Fig. 1. For example, if we wished to subdivide a population of 16 identical neurons into 4 clusters and the neurons were ordered by initial phase (𝜃₁ < 𝜃₂ < ... < 𝜃₁₆), the K control pairs would be {2, 3}, {6, 7}, {10, 11}, and {14, 15}, and the final clusters would be {15, 16, 1, 2}, {3, 4, 5, 6}, {7, 8, 9, 10}, and {11, 12, 13, 14}. We define a positive semidefinite function r_{i, j} for each control pair; this function is dependent only on the phase difference Δ𝜃_{i, j} = 𝜃 _j − 𝜃 _i and is identically zero at ${\Delta }\theta _{i,j} = \frac {2\pi }{K}$.

To allow for consistency in the definition of r_{i, j} across choices of K, the value of Δ𝜃_{i, j} is mapped by the function $g\left ({\Delta }\theta _{i,j}\right )$ so that $g\left (\frac {2\pi }{K}\right ) = \pi$. This is done using the piecewise definition:

$$ g\left( {\Delta}\theta_{i,j}\right) = \left\{\begin{array}{llllllllll} \frac{K}{2}{\Delta}\theta_{i,j} & 0\le{\Delta}\theta_{i,j}\le\frac{2\pi}{K} \\ K\frac{\left( {\Delta}\theta - 2\pi/K\right)}{\left( 2\left( K-1\right)\right)} + \pi & \frac{2\pi}{K}<{\Delta}\theta_{i,j}\le2\pi \end{array}\right.. $$

(8)

With this mapping, we define the positive-definite function for each pair as follows:

$$ r_{i,j} = \left\{\begin{array}{llllllllll}\frac{1}{g\left( {\Delta}\theta_{i,j}\right)^{p}} - \frac{1}{\pi^{p}} & 0<{\Delta}\theta_{i,j}\le\frac{2\pi}{K} \\ \frac{1}{\left( 2\pi-g\left( {\Delta}\theta_{i,j}\right)\right)^{p}} - \frac{1}{\pi^{p}} & \frac{2\pi}{K} < {\Delta}\theta_{i,j} < 2\pi \end{array}\right., $$

(9)

which is continuous and differentiable everywhere on the domain $\left (0,2\pi \right )$ except at ${\Delta }\theta _{i,j} = \frac {2\pi }{K}$. The value of the parameter p can be adjusted to meet control objectives; in the simulations in Section 4, p = 0.7. The function r_{i, j} can be made first-order differentiable by the replacement of the constant $\frac {1}{\pi ^{p}}$ with a term that is linear in g, though in practice this is not necessary. This replacement generates a function that does, however, serve as a valid storage function candidate in Eq. (3), while maintaining derivatives with the same sign as in Eq. (9). Clearly, Eq. (9) is greater than zero for all choices of p with ${\Delta }\theta _{i,j} \neq \frac {2\pi }{K}$ and grows unbounded as Δ𝜃_{i, j} → 0 or 2π.

From here we can define a state function of the system as:

$$ r = \frac{1}{K}\sum\limits_{l = 1}^{K}r_{2l-1,2l}. $$

(10)

Note that here we have omitted the neurons that are not being directly controlled, and as such our control pairs are relabelled as {1,2}, {3,4},...,{2K − 1,2K}. Since each component of the summation is greater than zero everywhere except at the desired target state, the combined function is also positive-definite and only equal to zero when all pairs of neurons achieve the target separation.

Cost Function :

With the state function defined, we turn our attention to the cost function. The purpose of the cost function is to prescribe the important characteristics of the control by penalizing undesired behavior. While any cost function can be used, we select one that penalizes energy usage and the time required to reach the target state. This can be accomplished by defining the cost function:

$$ C\left( t\right) = {{\int}_{0}^{t}} \left[{u\left( \tau\right)}^{2} + \alpha r\left( \tau\right)\right] \mathrm{d}\tau. $$

(11)

The first term introduces a quadratic cost to increased input amplitude; this is inspired by the general fact that the square of the input amplitude is proportional to power. The second term penalizes the value of r being large. The value of α can be adjusted to increase or decrease the relative importance of this penalty; the higher the value of α, the greater emphasis the control places on reducing the value of the state function quickly. The instantaneous cost associated with the state and input at a given time t can be given by taking the derivative and evaluating:

$$ \frac{dC}{dt} = {u\left( t\right)}^{2} + \alpha r\left( t\right) . $$

(12)

With the state and cost functions defined, the input of maximal instantaneous efficiency can be generated as follows. An optimal path is one that minimizes $C\left (t\right )$ as $t\to \infty$. While to truly optimize, the time-dependent input would need to be computed in advance, IMIE aims to produce a near-optimal input by minimizing the cost incurred at each time step instead. We rewrite $C\left (t\right )$ in terms of the value of r, which in the uncoupled case monotonically decreases at all times with the appropriate choice of u. Then the total cost as $t\to \infty$ is equal to:

$$ \lim_{t\to\infty} C\left( t\right) = {\int}_{r\left( 0\right)}^{0} \frac{dC}{dr} \mathrm{d}r; $$

(13)

by exploiting the chain rule, we equate $\frac {dC}{dr}$ to:

$$ \frac{dC}{dr} = \frac{{dC}/{dt}}{{dr}/{dt}}. $$

(14)

In this formulation, the input we choose is designed so that, at all times, the instantaneous magnitude of $\frac {dC}{dr}$ is minimized. This can be interpreted as the input that is most efficient in terms of cost relative to change in r. The value of $\frac {dC}{dt}$ is given by Eq. (12). Differentiating r with respect to time yields:

$$ \frac{dr}{dt} = \sum\limits_{l = 1}^{2K} \frac{\partial r}{\partial \theta_{l}}\frac{d\theta_{l}}{dt}. $$

(15)

As in Eq. (5), we can reorganize this and exploit the fact that in each neuron phase control pair 𝜃_2k, 𝜃_2k+ 1 the partial derivatives with respect to phase satisfy $\frac {\partial r}{\partial \theta _{2k}}=-\frac {\partial r}{\partial \theta _{2k + 1}}$ and express $\frac {dr}{dt}$ as:

$$ \frac{dr}{dt} = u\sum\limits_{l = 1}^{K}\frac{\partial r}{\partial\theta_{2l}}\left( Z\left( \theta_{2l}\right)-Z\left( \theta_{2l-1}\right)\right), $$

(16)

which has the characteristic form $-a\left (\theta _{1},...,\theta _{2K}\right )u\left (t\right )$. Therefore, $\frac {dC}{dr}$ is equal to:

$$ \frac{dC}{dr} = -\frac{u^{2}+\alpha r}{au}, $$

(17)

where the dependence of a and r on the state $\left [\theta _{1},...,\theta _{2K}\right ]$ is omitted from the equation for simplicity.

From this, the extrema can be found by differentiating with respect to u; the input used is then set equal to this calculated minimum. Differentiating and rearranging yields:

$$u\left( t\right) = \frac{\sqrt{a^{2}\alpha r\left( t\right)}}{a}=\text{sign}{\left( a\right)}\sqrt{\alpha r\left( t\right)}. $$

(18)

Note here the positive root is taken because $\frac {dC}{dr}$ is negative (since $\frac {dC}{dt}$ is always positive and $\frac {dr}{dt}$ is negative by construction), and therefore the quantity au must be positive for the entire expression to be negative.

Recalling the definition of $r\left (t\right )$, u evolves as a function of the average separation $\overline {{\Delta }\theta }$ of the control pairs as approximately ${\overline {{\Delta } \theta }}^{-{p}/{2}}\sqrt {\alpha }$. From this it can be seen that, holding p constant, increasing α corresponds to a $\sqrt {\alpha }$ increase of the maximum amplitude of the input signal. This in turn decreases the response time of the system at the cost, generally, of increasing total power usage and maximum input amplitude. In contrast, increasing the value of p while holding maximum amplitude constant (by adjusting α accordingly) will cause a sharper decline in the input signal, reducing power usage but increasing response time. As such, the system can be tuned to meet the desired control specifications– power usage, maximum amplitude, response time– simply by varying α and p accordingly, regardless of the neuronal model being used.

We now turn our attention to the case where α = 0 and demonstrate that the method returns a result that is consistent with intuition. In this case, no weight is placed on fast response time and the cost is entirely connected to minimizing the energy usage of the system. With α = 0, the original formulation of $\frac {dC}{dr}$ can be simplified greatly, yielding:

$$ \frac{dC}{dr} = \frac{-u}{a}. $$

(19)

Unlike the case where α≠ 0, this is linear and therefore has no minimum; since the only constraint is that $\frac {-u}{a}$ should be positive, a lower-cost control is always achieved by decreasing the magnitude of u. It can be seen that, as predicted by this result, using controller of constant amplitude takes longer (but requires less energy) when a smaller amplitude is used, thereby agreeing that the optimal control from an energy perspective is to use as small an input as possible.

In practice, we do not want the state to be reached in infinite time. If we abstract away from the physical representations of the phase model (which breaks down at high amplitudes of u) and consider only what will allow us to reach the target state in as little time as possible, we would expect that the solution would be to allow the input signal to be as large as possible for all times. We can model this by removing u² from the cost function so that $C^{*}\left (t\right ) = \alpha r\left (t\right )$. Now, $\frac {dC}{dr}$ is given as:

$$ \frac{dC}{dr} = \frac{-\alpha r}{au}. $$

(20)

As in the case where α = 0, this has no minimum, and instead approaches 0 as $u\to \infty$. Therefore, IMIE correctly predicts that for the fastest possible response, u should be allowed to be as large as allowed by the constraints on the system at all times. This trend, as well as the minimal-energy trend, are demonstrated in simulation and shown as solid lines in Fig. 5. While we do not propose IMIE as a fully optimal control strategy, this demonstrates that the method matches basic sanity checks in its application.

4 Application to uncoupled identical neurons

We now apply the IMIE approach to two different neural models: a two-dimensional reduced Hodgkin-Huxley model (Keener and Sneyd 2009; Hodgkin and Huxley 1952) and a three-dimensional model for periodically firing thalamic neurons (Rubin and Terman 2004). Unless otherwise stated, all simulations we present in this section utilized the parameters listed in Table 1. The dynamics for both models were initially represented using the phase model reduction, with all the neurons treated as identical (possessing the same natural frequencies and phase response curves). The dynamics for all neurons were given by:

$$ \dot{\theta}\left( t\right) = \omega + Z\left( \theta\right)u\left( t\right), $$

(21)

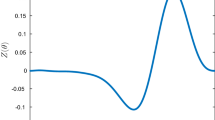
where the natural frequencies and phase response curves are appropriate to the models. The phase response curves for the two models were derived from the adjoint equation using XPPAUT and can be seen in Fig. 2. In addition to the distinctions between the initial dimensionality of the two models, they also differ in that the Hodgkin-Huxley model is an example of a Type II neuron, whereas the thalamic model is representative of a Type I neuron (Ermentrout and Terman 2010). This can be seen by the qualitative differences in their phase response curves: whereas Type II neurons have PRCs with positive and negative portions, Type I neurons have PRCs that are typically nonnegative (Galan et al. 2005).

Table 1 Default simulation parameters

Fig. 2

Phase response curves for the reduced Hodgkin-Huxley equations (top) and the thalamic model (bottom)

By using models of two different types of periodically firing neurons, we aim to show that the qualitative results of this control scheme are similar across qualitatively different base models. This agreement can be seen in Fig. 3, which shows the response of a population of neurons of each type to the proposed control strategy.

Fig. 3

Evolution of reduced Hodgkin-Huxley (top) and thalamic (bottom) phase models at three times for K = 4. a, b, and c show the projection of the phases onto the unit circle at times t = 0, t = 125, and t = 500 ms (0, 187.5, and 750 for thalamus), respectively. d shows the absolute value of the input over the length of the simulation. The differently-colored pairs represent neurons that are being actively controlled

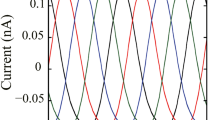
Figure 4 shows in finer detail the control signal applied to the Hodgkin-Huxley phase model to achieve clustering. Initially, when the neurons are still in a one-cluster configuration, the signal varies comparatively rapidly, both in amplitude and direction. However, as the system approaches the 4-cluster state, the signal becomes increasingly regular with a frequency four times that of the system’s natural frequency and with a signal that only slowly decreases in amplitude. We view these “maintenance” signals when the system is near the clustered state as especially feasible with current hardware. The results for the thalamic model are qualitatively equivalent to those presented here.

Fig. 4

Control signal over three time intervals, Hodgkin-Huxley model. The actual values of the signal (in contrast to the absolute values presented in Fig. 3) are presented over three 50-ms time intervals. The blue interval begins at t = 0 ms, the red at t = 200 ms, and the yellow at t = 450 ms. We note that the signal becomes increasingly regular as the system approaches a clustered state

Furthermore, IMIE improves upon the performance of strategies that similarly require only instantaneous state data to calculate a control. Using the same methodology of selecting whether to apply a positive or negative input based on the derivative of the state function r, the Hodgkin-Huxley neuron population was also simulated with the application of a constant-amplitude “bang-bang” control. In “bang-bang” control, the amplitude of the control signal is fixed while its direction (positive or negative) is allowed to switch. For a range of amplitudes, the constant-amplitude control and IMIE were simulated until the values of their state functions were within a tolerance of a 0 (r _{t o l} = 0.01). The “settling” time and value of ${{\int }_{0}^{T}} u^{2} dt$ was recorded for each trial; these results are shown in Fig. 5. For comparison between the two methods, in these simulations p was held constant and α was varied such that the initial value of u was equal to the listed max amplitude ($\alpha = \frac {u_{max}^{2}}{r\left (0\right )}$). Without an appreciable sacrifice of response time, IMIE achieves clustering at a dramatically reduced energy cost when compared to bang-bang control.

Fig. 5

Comparison of constant-amplitude control and IMIE. The solid lines denote the constant-amplitude control. The dashed lines represent the implementation of IMIE on the population of uncoupled, identical Hodgkin-Huxley neurons reduced to a phase model for control to the 4-cluster state. Note that the energy cost (in pink) is always lower for IMIE than the analogous constant-amplitude control, and despite these massive energy discrepancies the response time (in black) is always either better or approximately equal to that of constant-amplitude control, except in the extreme low-amplitude case. This demonstrates that IMIE represents a performance improvement over bang-bang control in terms of both energy cost and response time

With the effectiveness of the control established for phase models, the control was extended and applied to a full state model for both the Hodgkin-Huxley and thalamic neurons. The value of the state function r(t) was calculated based on an estimation of the phase corresponding to a neuron’s position in state-space. This rough approximation of the phase was found by identifying the point on the curve nearest to the neuron’s state’s position in state-space. Because the variation in V differs far more significantly than the variation in n or other gating variables, the distance to the curve was normalized in each dimension by the span of the limit cycle in that dimension. Example simulations for these full state-space models can be seen in Fig. 6. Note that there is a “jitter” in (d) in both plots; this can be attributed to inaccuracies inherent in estimating the phase of the neurons, which can result in large movement in the value of r(t) because of its large derivative at small values of Δ𝜃.

Fig. 6

Evolution of reduced Hodgkin-Huxley (top) and thalamic (bottom) state-space models over three time intervals. a, b, and c show three 25-millisecond voltage traces of the 50 neurons being simulated subject to the described control without coupling. As in the phase model simulations, the neurons initially become desynchronized, spreading out around the limit cycle before coalescing into clusters. d shows the absolute value of the input over the duration of the simulation, with general qualitative agreement to the plots in Fig. 3

Additionally, adjusting the values of p and α can alter the response characteristics of the populations of neurons in a consistent fashion. To illustrate this, a “settling time” and energy cost was calculated for different pairs of parameter values. Because p was varied between trials, to maintain a consistent benchmark of performance the system was simulated not to a specific value of r but rather to a specific average deflection from the target state. Δ𝜃 _{t o l} was defined as:

$$ {\Delta}\theta_{tol} = \frac{9}{10}{\Delta}\theta^{*}, $$

(22)

which subsequently was used to define a specific value of r _{t o l} dependent on the value of p as:

$$ r_{tol} = \frac{1}{g\left( {\Delta}\theta_{tol}\right)^{p}}-\frac{1}{\pi^{p}}. $$

(23)

The settling time T was defined as the time to reach r _{t o l} , and the energy cost was calculated as ${{\int }_{0}^{T}} u^{2}\left (t\right ) dt$.

The effect of variations in p and α on the phase model results can be seen in Fig. 7. As can be expected, for a given value of p, increasing α leads to a decreased response time but increased energy cost. Decreasing p corresponds to the input decreasing less sharply in time; despite a steeper rate of decrease, however, between 0 and Δ𝜃^∗ the value of r increases for a given Δ𝜃 as p increases. Therefore, increasing p corresponds to an increase in energy usage as well as a decrease in response time.

In practice, we may wish to prescribe a maximum amplitude for the control signal rather than just utilizing a scaling value of α arbitrarily. In the uncoupled phase model, we assume that r decreases at all times; from this, it follows that $\left |u\right |_{max}=\left |u(0)\right |$, as a decrease in r corresponds to a decrease in $\left |u\right |$. If, instead of varying α, $\left |u\right |_{max}$ is varied instead, the trend from Fig. 7 reverses. Here, the value of α is prescribed by its relationship to u and r:

$$ \sqrt{\alpha r\left( 0\right)} = \left|u\right|_{max} \qquad \Rightarrow \qquad \alpha = \frac{{u_{max}}^{2}}{r\left( 0\right)}, $$

(24)

where r is dependent on the choice of p. For a given maximum amplitude, an increase in the value of p now corresponds to a state function whose value drops more sharply, which in turn means an input whose magnitude drops more sharply. As such, energy usage decreases with increased p for a fixed u _{m a x} and response time increases in turn. This can be seen in Fig. 8.

Fig. 7

Effect of variations in p and α. The effect of varying the two parameters on settling time (with r _{t o l} set by the value of p) is shown in the left panel, while the integral of u² is shown to the right. Each curve represents a constant value of p, with α allowed to vary. These results maintain the correspondence between increasing energy cost and decreasing response time illustrated in Fig. 5

Fig. 8

Effect of variations in p and $\left |u\right |_{max}$. For a given maximum amplitude, increasing p leads to an increase in settling time (left) but a decrease in energy usage (right)

5 Application to coupled identical neurons

We now introduce coupling to the phase model reduction and adapt IMIE to accommodate its effects. We consider all-to-all electrotonic coupling; in the state-space model, this is introduced into the value of $\dot {V}$ as (Johnston and Wu 1995):

$$ {\Delta}\dot{V_{i}} = a_{e} \sum\limits_{j = 1}^{N} \left( V_{j}-V_{i}\right). $$

(25)

In the context of the phase model reduction, this can be rewritten as:

$$ \dot{\theta}_{i} = \omega + Z\left( \theta_{i}\right)u+a_{e}\sum\limits_{j = 1}^{N} \left( V\left( \theta_{j}\right)-V\left( \theta_{i}\right)\right)Z\left( \theta_{i}\right). $$

(26)

Here, a _e is the strength of the electrotonic coupling. This, however, is not a particularly convenient notation, as we would like to omit V from the phase model reduction. Assuming a _e is small (coupling is weak), we can further simplify this equation by selectively averaging the value of the coupling over one period (Schmidt et al. 2014), $\bar {f}\left (\theta _{j} - \theta _{i}\right ) = \bar {f}\left ({\Delta }\theta _{i,j}\right )$. This can be calculated as:

$$\begin{array}{@{}rcl@{}} \bar{f}\left( {\Delta}\theta_{i,j}\right) &=& \frac{1}{2\pi}{\int}_{0}^{2\pi} [(V(\theta_{j} + {\Theta}) \\ &&\left.\left.-V\left( \theta_{i}+{\Theta}\right)\right)Z\left( \theta_{i}+{\Theta}\right)\right]d{\Theta}; \end{array} $$

(27)

$\dot {\theta _{i}}$ can then be rewritten in terms of this averaged function instead.

Returning to Eq. (15), the expression for $\frac {d\theta _{l}}{dt}$ has changed, and Eq. (16) must include an additional term; $\frac {dr}{dt}$ is now computed as:

$$\begin{array}{@{}rcl@{}} \frac{dr}{dt} &=& \sum\limits_{l = 1}^{K}\frac{\partial r}{\partial \theta_{2l}} \left\{\left.\left.u\left( Z\left( \theta_{2l}\right)-Z\left( \theta_{2l-1}\right)\right)\right.\right.\right.\\ &&+ a_{e}\sum\limits_{m = 1}^{N} \left.\left[\bar{f}\left( \theta_{m}-\theta_{2l}\right)-\bar{f}\left( \theta_{m}-\theta_{2l-1}\right)\right]\right\}, \end{array} $$

(28)

which now has the characteristic form − au + b instead of simply − au. Rederiving the instantaneously optimal input yields:

$$ u\left( t\right) = \frac{b+\sqrt{b^{2}+a^{2}\alpha r}}{a}. $$

(29)

The problem presented by coupling is that a core assumption of the control design (namely, that $\frac {dr}{dt}$ monotonically decreases with the appropriate choice of sign for u) no longer holds; there is a measure-0 probability that the value of a is identically 0 at some time. If a approaches 0, the mandate that $\frac {dr}{dt}$ monotonically decrease proves excessively restrictive: the value of u grows unbounded, which both violates the regime in which the phase model reduction can be considered valid and runs counter to the goal of a cost-minimized strategy. To address this, we instead approach the problem by considering an averaged value of $\frac {dr}{dt}$, much as was done for the coupling function:

$$\begin{array}{@{}rcl@{}} \frac{dr}{dt}_{avg} &=& \frac{1}{2\pi}{\int}_{0}^{2\pi}\sum\limits_{l = 1}^{K}\frac{\partial r}{\partial \theta_{2l}} \left\{u\left( Z\left( \theta_{2l} +{\Theta}\right)\right.\right.\\ &&\left. -Z\left( \theta_{2l-1} + {\Theta}\right)\right)\\ &&+ a_{e}\sum\limits_{m = 1}^{N} \left.\left[\bar{f}\left( \theta_{m}{\Theta}-\theta_{2l}-{\Theta}\right)\right.\right.\\ &&\left.\left.-\bar{f}\left( \theta_{m}+{\Theta}-\theta_{2l-1}-{\Theta}\right)\right]\right\}d{\Theta}. \end{array} $$

(30)

Rearranging and recognizing that $\frac {1}{2\pi }{\int }_{0}^{2\pi } \bar {f}\left ({\Delta }\theta \right )d{\Theta } = \bar {f}\left ({\Delta }\theta \right )$, we simplify as:

$$\begin{array}{@{}rcl@{}} \frac{dr}{dt}_{avg} &=& -\bar{a}u+a_{e} \sum\limits_{l = 1}^{K}\frac{\partial r}{\partial\theta_{2l}}\sum\limits_{m = 1}^{N} \left[\bar{f}\left( \theta_{m}-\theta_{2l}\right)\right.\\ &&\qquad\qquad\qquad\qquad\quad\,\,\,\,\,\left.-\bar{f}\left( \theta_{m}-\theta_{2l-1}\right)\right], \end{array} $$

(31)

where:

$$\begin{array}{@{}rcl@{}} \bar{a} &=& \frac{-1}{2\pi}{\int}_{0}^{2\pi} \left|\sum\limits_{l = 1}^{K} \frac{\partial r}{\partial\theta_{2l}}\left( Z\left( \theta_{2l}+{\Theta}\right) \right.\right.\\ &&\left.- Z\left( \theta_{2l-1}+{\Theta}\right)\right)|d{\Theta}. \end{array} $$

(32)

The absolute value is taken to reflect the ability to choose at each time increment the appropriate sign of u, a feature that is otherwise not captured by this equation. The sign of u is still computed from the unaveraged value of a. As such, this equation still reduces to Eq. (18) in the limit b → 0.

Additionally, we can consider special cases that arise with the introduction of coupling and ensure that our intuition hold for these circumstances. We consider three cases: the limit where α is large compared to a and b, the limiting behavior as a²αr → 0, and the resulting equation for α = 0. If α is large, the magnitude of the input will similarly be large as the control objective will consist of approaching $r\left (t\right ) = 0$ as quickly as possible. In this case, $\left |u\right |\to \left |\frac {b}{\bar {a}} + \text {sign}\left (a\right )\sqrt {\alpha r}\right |$ when r is large. We include the absolute value on u to acknowledge the influence of a on the instantaneous sign of u. In this case only a relatively small correction term is applied to the control for the b = 0 case (amounting to, on average, matching the strength of the coupling), as the control dynamics are dominated by α instead of b. As we approach the target state, however, a²αr → 0 regardless of the choice of α, and the dynamics become instead dominated by the coupling; in this limit $\left |u\right |\to \left |\frac {b+\left |b\right |}{\bar {a}}\right |$.

This limiting behavior would be demonstrative of the response if our response time was irrelevant and energy was the only consideration, i.e. if α = 0. In that case, the response at all times would evolve as $\left |u\right | = \left |\frac {b+\left |b\right |}{\bar {a}}\right |$. When b < 0, coupling serves to pull the system toward the target state; in the presence of this favorable coupling, u = 0 as the most energy-efficient strategy is to input no additional energy. If b > 0, then $\left |u\right | = \left |\frac {2b}{a}\right |$. Whereas in the uncoupled case the optimal control input when α = 0 is to asymptotically approach a magnitude of 0, the presence of coupling allows for the presence of a local minimum instead with a value slightly higher than the averaged offset value of $\frac {b}{a}$.

Simulations with weak coupling (here, a _e = 0.01) were conducted for both the Hodgkin-Huxley and thalamic models. Results for the coupled state-space model can be seen in Fig. 9. Note that while the general shape of the input signal is consistent with the uncoupled case, the presence of weak coupling in addition to the uncertainty caused by the phase estimation leads to significant fluctuations in the amplitude of the control signal. Despite these fluctuations, the control scheme still is able to successfully cluster the population of neurons at a relatively low cost, albeit higher than in the uncoupled case.

Fig. 9

Simulation of thalamic state-space model with weak (a _e = 0.01) coupling for K = 4. Despite large fluctuations in the amplitude of the control signal, clustering proceeds similarly to in the uncoupled case: first, the system desynchronizes, and then strong clustering emerges

As can be seen by comparing Figs. 6 and 9, weak coupling does not significantly affect the response time of the system, only the energy cost. To demonstrate this, the population of neurons was simulated until reaching a value of r _{t o l} = 0.05 for different values of K, with p and α held constant. The results for the energy cost associated with these separate trials are shown in Table 2, while the settling times are shown in Table 3.

Table 2 Energy cost to reach K-cluster state

Table 3 Settling time (ms) to reach K-cluster state

As coupling strength moves out of the weak regime where the above averaging assumptions hold, the cost associated with achieving clustering increases unboundedly as the value of a _e approaches some asymptotic limit. To demonstrate this, the system was simulated for different coupling strengths varying from the weak regime to the moderate coupling regime. This was done for two different values of α to demonstrate robustness with respect to the choice of α. Figure 10 shows the energy cost for the reduced Hodgkin-Huxley phase model for α = 0.1 and α = 0.01 as a _e is varied. We consider $\log {a_{e}}$ to demonstrate it approaches an asymptotic limit; by using the log value, we treat the uncoupled case as the asymptotic behavior as $\log \left (a_{e}\right )\to -\infty$. The resulting plot is characteristic of a model of the form $\frac {1}{\left (a\log \left (x\right )+b\right )^{c}}+d$, suggesting an asymptotic limit in a _e rather than growth governed by an exponential or power law model. This is consistent with simulations failing to converge to the target state for a _e sufficiently large.

The inability to reach the target value of r _{t o l} should not, however, be seen as a complete failure to achieve clustering. Rather, as the coupling strength increases, the system reaches a state wherein the value of r fluctuates in a complicated manner about some average value. The stronger coupling is in this regime, the generally larger the variations between the maximum and minimum of the cycle; similarly, the range of inputs grows increasingly large as well. These phenomena are shown in Fig. 11. As can be seen, beyond a certain value for a _e , increasing the coupling strength actually causes the minima of $\left |u\right |$ and r to decrease; this is likely the result of the neurons reaching a configuration where the coupling actually aids in clustering instead of working against it, with the strength being high enough to reach much closer to the ideal state before coupling pulls the neurons away from the target state once more. This is consistent with Golomb and Hansel (2000), which found that depending on the initial configuration, coupled neuron networks could end in smeared one-cluster or multi-cluster states if there was sufficient connectivity between neurons, depending on the initial conditions. Here, the application of control effectively allows the system to transition from the basin of attraction of one of these configurations (the one-cluster state) to a different configuration (the multi-cluster state).

Fig. 10

Cost to reach r _{t o l} for varying coupling strengths at two different values of α for the Hodgkin-Huxley model (K = 4). As can be seen, in the weak coupling regime ($a_{e} \lesssim 0.01$) the system asymptotically approaches the uncoupled dynamics of the system (denoted by the dashed lines), but as moderate coupling is approached the required energy grows unbounded. This is consistent with the underlying assumptions used in the process of averaging, namely that perturbations are small

Fig. 11

Asymptotic behavior for Hodgkin-Huxley phase model, varying values of coupling strength. A population of Hodgkin-Huxley neurons (N = 50, K = 4) evenly spaced in phase space was simulated for 3000 ms; the final 1000 ms were averaged and analyzed to determine asymptotic behavior. The variation in the maximum and minimum magnitude for the input, as well as the average, is shown in the top panel, whereas the variation in the value of r is shown in the bottom figure

Beyond a certain value of a _e , IMIE as described cannot achieve clustering and the neurons instead coalesce. This is to be expected, as the fundamental assumption of its formulation– namely, that the effects of coupling are weak– is no longer accurate. As can be seen in Fig. 12, at higher coupling pronounced peaks and troughs can be seen in each cycle of the neuron population. The disparity between the peaks and troughs continues increasing as the coupling strength is increased. Below a critical value, these oscillations in r are damped as time progresses, leading to a relatively steady solution. Above a critical value, however, the oscillations instead increase, with each peak reaching a higher value of r than the previous peak, eventually tending toward $\infty$ and indicating clustering cannot be achieved with the averaged technique described.

Fig. 12

Evolution of Hodgkin-Huxley phase state models for weak (a _e = 0.005) and moderately strong (a _e = 0.27) coupling. The first 500 ms of simulation are shown in the top panel; The bottom figure expands the region of 2500 < t < 3000. When coupling is weak, the evolution of r is relatively smooth; however, as a _e increases the corresponding evolution of r becomes increasingly jagged, with each cycle containing peaks and troughs. Eventually, as a _e is increased farther, successive troughs and corresponding peaks increase in value instead of decreasing, and clustering cannot be achieved. This occurs in the Hodgkin-Huxley phase models around a _e ≈ 0.275

6 Conclusion

We have demonstrated a potentially effective strategy for designing controls for achieving clustering of populations of neuronal oscillators. Simulations of both phase models and full state models have demonstrated a significant improvement in cost when employing our input of maximal instantaneous efficiency (IMIE) as compared to other methods that make use of the same level of information when generating a closed-loop control strategy. Additionally, this method works not only for identical uncoupled neurons, but can be extended to accommodate weak to moderate coupling as well. Future work will focus in part on continuing to relax the restrictions on the heterogeneity of the neuron population. In the context of the phase model, variations in the natural frequency ω may be handled a manner similar to the method used in this paper to address weak coupling, provided these variations are sufficiently small. Heterogeneity that manifests in the phase response curve does not require a change in the overall structure of the control; it does, however, force us to relax the boundedness of the response. This may be handled by re-numbering neurons when their ordering changes. An exploration of the limits of this method is deferred to future work.

The use of two separate neural models, the Hodgkin-Huxley and thalamic models, demonstrates the robustness of the control strategy. While the Hodgkin-Huxley model is not physically relevant to the specific research areas of interest, the thalamic model provides a direct link to problems such as essential tremor. Research such as Hua et al. (1998) shows the correspondence between the firing behavior of singular neurons in the thalamus and the tremors in essential tremor, and Cagnan et al. (2013) indicates that DBS modifies and entrains the firing of oscillators in the thalamus. The flexibility of the control strategy we have presented allows it to achieve the same or similar results as conventional DBS, potentially at a fraction of the cost.

In the case of PD, the behavior of the basal ganglia is complex and involves the interplay of neurons in the STN, GPi, and other portions of the basal ganglia. As such, developing a control to generate desynchronization of firing activity is more complicated than in the case of the two models presented here. Ultimately, however, IMIE is sufficiently general that the only requirement for generating a control based on its principles is to extract the relevant oscillatory dynamics from the model of interest. While a full application to the clinical problem of PD is beyond the scope of this paper, there is no inherent limitation in the strategy described that bars its application to PD or other complex systems; the challenge lies instead in generating the appropriate modeling of these systems with which to employ IMIE.