Optimal phase control of biological oscillators using augmented phase reduction

Abstract

We develop a novel optimal control algorithm to change the phase of an oscillator using a minimum energy input, which also minimizes the oscillator’s transversal distance to the uncontrolled periodic orbit. Our algorithm uses a two-dimensional reduction technique based on both isochrons and isostables. We develop a novel method to eliminate cardiac alternans by connecting our control algorithm with the underlying physiological problem. We also describe how the devised algorithm can be used for spike timing control which can potentially help with motor symptoms of essential and parkinsonian tremor, and aid in treating jet lag. To demonstrate the advantages of this algorithm, we compare it with a previously proposed optimal control algorithm based on standard phase reduction for the Hopf bifurcation normal form, and models for cardiac pacemaker cells, thalamic neurons, and circadian gene regulation cycle in the suprachiasmatic nucleus. We show that our control algorithm is effective even when a large phase change is required or when the nontrivial Floquet multiplier is close to unity; in such cases, the previously proposed control algorithm fails.

1 Introduction

Periodic orbits, whose dynamics repeat in time, are ubiquitous in dynamical systems of biological interest, with cardiac rhythms, neural spikes, circadian rhythms, cell division, and the flowering cycle in plants being a few examples. “Standard” phase reduction (Winfree 1967; Guckenheimer 1975; Kuramoto 1997; Brown et al. 2004), a classical reduction technique based on isochrons (Winfree 1967; Guckenheimer 1975; Winfree 2001), has been instrumental in understanding such biological oscillators. It works by reducing the dimensionality of a dynamical system with a periodic orbit to a single-phase variable. This reduction captures the oscillator’s dynamics near the periodic orbit and the change in its phase due to an external stimulus through the phase response curve (PRC). Not only does it make the analysis of the high-dimensional systems more tractable, but it also has the potential to make their control (Moehlis et al. 2006; Wilson and Moehlis 2014; Zlotnik et al. 2013; Tass 2007; Minors et al. 1991) experimentally implementable; see, e.g., Stigen et al. (2011), Nabi et al. (2013b), Snari et al. (2015), Zlotnik et al. (2013). This is because although the whole state space dynamics of the system may not be known, PRCs can often be measured experimentally; see, e.g., Netoff et al. (2012); Minors et al. (1991).

This reduction is valid only in close proximity to the periodic orbit as noted, for example, by Guillamon and Huguet (2009). Consequently, the magnitude of the allowable stimulus is limited by the nontrivial Floquet multipliers (Guckenheimer and Holmes 1983) of the periodic orbit: in systems with a nontrivial Floquet multiplier close to 1, even a relatively small stimulus can drive the trajectory away from the periodic orbit, rendering the phase reduction inaccurate and control based on phase reduction ineffective. In most practical applications, the effectiveness of a control algorithm depends on the size of the allowable stimulus (Wilson and Moehlis 2014; Snari et al. 2015; Zlotnik et al. 2013). This suggests the use of a reduction technique called augmented phase reduction (Wilson and Moehlis 2016), which is an n-dimensional reduction based on both isochrons and isostables (Mauroy et al. 2013). The first dimension captures the phase of the oscillator along the periodic orbit, as for the standard phase reduction, while the other $n-1$ dimensions give a measure of the oscillator’s transversal distance from the periodic orbit along the $n-1$ isostable directions. The reduction captures the effect of an external stimulus on the change in the oscillator’s phase through the PRC, and the change in its transversal distance to the periodic orbit through the isostable response curve (IRC).

An equivalent reduction based on the Koopman operator is given by Shirasaka et al. (2017). This gives the same outcome as the phase-amplitude reduction devised by Castejón et al. (2013) for planar systems, but the augmented phase reduction does not require computationally intensive calculation of a coordinate system with respect to periodic orbit of dimensionality greater than 2. Moreover, the phase-amplitude description devised by Wedgwood et al. (2013) is not explicitly dependent on the Floquet multipliers of the system, whereas the augmented phase reduction is. This dependency on Floquet multipliers is advantageous in higher-dimensional systems, where the periodic orbit is weakly stable in only a few directions, as it allows us to reduce the dimensionality of the augmented phase reduction to capture transversal dynamics only along the weakly stable directions. The use of Floquet coordinates (Guckenheimer 1995) results in a similar reduction, but an additional step is required to quantify the effect of an external perturbation on the oscillator’s dynamics. It also requires the knowledge of the whole state space dynamics along the periodic orbit, which might not be observable in an electrophysiological setting. On the other hand, for our algorithm, the response functions that arise for augmented phase reduction in principle can be measured in an electrophysiological setting; indeed, we envision that IRCs can be measured experimentally just like PRCs, making the control based on the augmented phase reduction experimentally amenable as well. Control algorithms based on the augmented phase reduction are expected to be more effective than those based on just the phase coordinate, as they can be designed to allow a larger stimulus without the risk of driving the oscillator away from the periodic orbit (Wilson and Moehlis 2016).

In this paper, we develop a novel optimal control algorithm based on augmented phase reduction to advance (resp., delay) the phase of the oscillator, such that the oscillator completes one periodic trajectory sooner (resp., slower). Along with minimizing the total energy consumption, our control algorithm also minimizes a measure of the transversal distance of the oscillator from the unperturbed periodic orbit. This novel aspect of our control algorithm is crucial in ensuring that the controlled oscillator always stays close to the unperturbed periodic orbit, where phase reduction is valid, thus making our control algorithm effective. Note that this way of incorporating closeness of the controlled trajectory to the periodic trajectory in the cost function is possible due to the explicit formulation of transversal dynamics in terms of Floquet multipliers in the augmented phase reduction. This allows us to efficiently keep the perturbed trajectory close to the periodic orbit along weakly stable isostable directions, even in the presence of noise.

Moreover, we develop a novel strategy to eliminate cardiac alternans by connecting our control algorithm with the underlying physiological problem to change the phase of cardiac pacemaker cells. This strategy removes the need to excite the myocardium tissue at multiple sites. We also show how our control algorithm can be used to change the spike timing of neurons, which could be relevant to the problem of desynchronizing neurons for the treatment of essential and parkinsonian tremor (Nabi et al. 2013a; Nabi and Moehlis 2012). Such an optimal control is expected to consume less energy than the pulsatile current in the present deep brain stimulation (DBS) protocol, thus possibly prolonging the battery life of the stimulator, and also preventing tissue damage caused by the high-energy DBS stimuli. Finally, we apply our control algorithm to realign circadian rhythm with the new light and dark cycle to treat jet lag (Wever 1985) or adapt to night shift work (Czeisler et al. 1990; Eastman and Martin 1999).

We compare our new algorithm with a previous algorithm based on standard phase reduction proposed by Moehlis et al. (2006) by applying it to four different dynamical systems: the Hopf bifurcation normal form, cardiac pacemaker cells (motivated by suppressing alternans), thalamic neurons (motivated by desynchronizing neurons via spike timing control), and circadian gene regulation in the superchiasmatic nucleus (motivated by controlling circadian rhythm). We show that our algorithm effectively changes the phase in these dynamical systems while keeping the controlled oscillator close to the unperturbed periodic orbit. The previous algorithm drives the oscillator away from the periodic orbit and thus can fail. We also perform a parametric study to analyze the dependence of the control error on the nontrivial Floquet multiplier of the periodic orbit and on the amount of phase change desired. This study demonstrates the promising potential of our new algorithm over the previous algorithm, especially when a large change in phase is required or when a nontrivial Floquet multiplier of the oscillator is close to 1. In such cases, our algorithm does an order of magnitude better in terms of the calculated control error.

This article in organized as follows. In Sect. 2, we describe standard and augmented phase reduction. In Sect. 3, we devise our optimal control algorithm based on augmented phase reduction and also present the previously devised algorithm based on standard phase reduction. In Sect. 4, we compare the two control algorithms by applying them to four different dynamical systems and in turn develop strategies to suppress cardiac alternans, change the firing time of thalamic neurons, and shift the phase of a circadian rhythm. Section 5 analyzes the effect of noise on the performance of our control algorithm. Section 6 summarizes the results and gives concluding remarks. Numerical methods used in this article are detailed in “Appendix A.” “Appendix B” lists the mathematical models used in this article and also gives their augmented and standard phase reduction parameters.

2 Standard and augmented phase reduction

In this section, we give background on the concepts of isochrons, isostables, standard and augmented phase reduction. These concepts will be useful for devising our control algorithm in Sect. 3.

2.1 Standard phase reduction

The standard phase reduction is a classical technique used to describe dynamics near a periodic orbit by reducing the dimensionality of a dynamical system to a single-phase variable $\theta$ (Winfree 1967; Kuramoto 1984, 1997). Consider a general n-dimensional dynamical system given by

$$\begin{aligned} \frac{\mathrm{d} \mathbf {x}}{\mathrm{d}t} = F(\mathbf {x}), \qquad \mathbf {x} \in \mathbb {R}^n, \qquad (n \ge 2) . \end{aligned}$$

(1)

Suppose this system has a stable periodic orbit $\gamma (t)$ with period T. For each point $\mathbf {x}^*$ in the basin of attraction of the periodic orbit, there exists a corresponding phase $\theta (\mathbf {x}^*)$ such that

$$\begin{aligned} \lim _{t \rightarrow \infty } \left| \mathbf {x}(t) - \gamma \left( t+\frac{T}{2 \pi } \; \theta (\mathbf {x}^*) \right) \right| = 0, \end{aligned}$$

(2)

where $\mathbf {x}(t)$ is the flow of the initial point $\mathbf {x}^*$ under the given vector field. The function $\theta (\mathbf {x})$ is called the asymptotic phase of $\mathbf {x}$ and takes values in $[0, 2 \pi )$. Isochrons are level sets of this phase function. It is typical to define isochrons so that the phase of a trajectory advances linearly in time. This implies

$$\begin{aligned} \frac{\mathrm{d}\theta }{\mathrm{d}t} = \frac{2 \pi }{T} \equiv \omega \end{aligned}$$

(3)

both on and off the periodic orbit.

Now consider the system

$$\begin{aligned} \frac{\mathrm{d} \mathbf {x}}{\mathrm{d}t} = F(\mathbf {x})+U(t), \qquad \mathbf {x} \in \mathbb {R}^n, \end{aligned}$$

(4)

where $U(t) \in \mathbb {R}^n$ is an external perturbation. Standard phase reduction can be used to reduce this system to a one-dimensional system given by (Malkin 1949; Kuramoto 1984; Brown et al. 2004; Monga et al. 2018):

$$\begin{aligned} \dot{\theta }= \omega +\mathcal {Z}(\theta )^T U(t). \end{aligned}$$

(5)

Here $\mathcal {Z}(\theta ) \equiv \nabla _{\gamma (t)} \theta \in \mathbb {R}^n$ is the gradient of phase variable $\theta$ evaluated on the periodic orbit and is referred to as (infinitesimal) phase response curve (PRC). It quantifies the effect of control input on the phase of the periodic orbit. The PRC can be found by solving an adjoint equation numerically; see, eg., Ermentrout (2002); Brown et al. (2004); Monga et al. (2018). Alternative approaches for computing the PRC have been detailed in Efimov et al. (2009); Zlotnik and Li (2014); Wataru et al. (2013). Equation (5) is valid only in a close vicinity of the periodic orbit and diverges from the true dynamics as one goes further away from the periodic orbit. Therefore, the amplitude of the control input has to be small enough so that it does not drive the system far away from the periodic orbit, where the phase reduction is not accurate; see, e.g., Castejón et al. (2013). This limitation on control input becomes even more important if the nontrivial Floquet multiplier of the periodic orbit is close to 1. This limits achieving certain control objectives and thus suggests the use of the augmented phase reduction.

2.2 Augmented phase reduction

For a dynamical system with a periodic orbit, isostables (Wilson and Moehlis 2016) are coordinates which give a sense of the distance in directions transverse to the periodic orbit. Standard phase reduction can be augmented with these coordinates as follows.

Consider a point $\mathbf {x}_0$ on the periodic orbit $\gamma (t)$ with the corresponding isochron $\varGamma _0$. The transient behavior of the system (given by Eq. 4) near $\mathbf {x}_0$ can be analyzed by a Poincaré map P on $\varGamma _0$,

$$\begin{aligned} P:\varGamma _0 \rightarrow \varGamma _0; \qquad \mathbf {x} \rightarrow P(\mathbf {x}). \end{aligned}$$

(6)

Here $\mathbf {x}_0$ is a fixed point of this map, and we can approximate P in a small neighborhood of $\mathbf {x}_0$ as

$$\begin{aligned} P(\mathbf {x})=\mathbf {x}_0+DP(\mathbf {x}-\mathbf {x}_0)+\mathcal{} O\left( {||\mathbf {x}-\mathbf {x}_0||}^2\right) , \end{aligned}$$

(7)

where $DP=dP/dx|_{\mathbf {x}_0}$. Suppose DP is diagonalizable with $V \in \mathbb {R}^{n\times n}$ as a matrix with columns of unit length eigenvectors $\{ v_k|k=1,\ldots ,n\}$ and the associated real eigenvalues $\{ \lambda _k|k=1,\ldots ,n\}$ of DP. These eigenvalues $\lambda _i$ are the Floquet multipliers of the periodic orbit. For every nontrivial Floquet multiplier $\lambda _i$, with the corresponding eigenvector $v_i$, the set of isostable coordinates is defined as (Wilson and Moehlis 2016)

$$\begin{aligned} \psi _i(\mathbf {x})=e_i^TV^{-1}(\mathbf {x}_\varGamma ^j-\mathbf {x}_0)\exp (-\log (\lambda _i)t_\varGamma ^j/T), \end{aligned}$$

(8)

where $i=1,\ldots ,n-1$. Here $\mathbf {x}_\varGamma ^j$ and $t_\varGamma ^j \in [0,T)$ are defined to be the position and the time of the $j\mathrm{th}$ crossing of the isochron $\varGamma _0$, and $e_i$ is a vector with 1 in the $i\mathrm{th}$ position and 0 elsewhere. When an eigenvalue $\lambda _i$ has multiplicity $m>1$, and m linearly dependent eigenvectors (DP is nondiagonalizable), isostables can be defined in a similar way by multiplying Eq. (8) with ${(t_\varGamma ^j)}^{1-m}$, cf. Mauroy et al. (2013). Since DP is diagonalizable for the systems we consider in this article, we consider Eq. (8) as the isostable coordinate. As shown by Wilson and Moehlis (2016), cf. Castejón et al. (2013), we get the following equations for $\psi _i$ and its gradient $\nabla _{\gamma (t)} \psi _i$ under the flow $\dot{\mathbf {x}}=F(\mathbf {x})$:

$$\begin{aligned} \dot{\psi }_i= & {} k_i \psi _i, \end{aligned}$$

(9)

$$\begin{aligned} \frac{\mathrm{d}\nabla _{\gamma (t)} \psi _i}{\mathrm{d}t}= & {} \left( k_iI-DF(\gamma (t))^T\right) \nabla _{\gamma (t)}\psi _i, \end{aligned}$$

(10)

where $k_i=\log (\lambda _i)/T$ are Floquet exponents, DF is the Jacobian of F, and I is the identity matrix. We refer to this gradient $\nabla _{\gamma (t)}\psi _i\equiv \mathcal {I}_i(\theta )$ as the isostable response curve (IRC). Its T-periodicity along with the normalization condition $\nabla _{\mathbf {x}_0}\psi _i \cdot v_i=1$ gives a unique IRC. It gives a measure of the effect of a control input in driving the trajectory away from the periodic orbit. The n-dimensional system (given by Eq. 4) can be realized as (Wilson and Moehlis 2016)

$$\begin{aligned} \dot{\theta }= & {} \omega +\mathcal {Z}^T(\theta ) U(t), \end{aligned}$$

(11)

$$\begin{aligned} \dot{\psi }_i= & {} k_i\psi _i+\mathcal {I}_i^T(\theta ) U(t), \qquad \text {for} \ i=1,\ldots ,n-1. \end{aligned}$$

(12)

We refer to this reduction as the augmented phase reduction (APR). Here, the phase variable $\theta$ indicates the position of the trajectory along the periodic orbit, and the isostable coordinate $\psi _i$ gives information about the transversal distance from the periodic orbit along the ith eigenvector $v_i$. This reduction is similar to the 2-dimensional system given by Eq. 22 in the article of Castejón et al. (2013), in which $\theta$ and $\sigma$ describe the dynamics along, and transverse to the limit cycle, respectively. It is evident from Eqs. (11)–(12) that the control input affects the oscillator’s phase through the PRC, and its transversal distance to the periodic orbit through the IRC. In practice, isostable coordinates with nontrivial Floquet multiplier close to 0 can be ignored as perturbations in those directions are nullified quickly under the evolution of the vector field. If all isostable coordinates are ignored, the augmented phase reduction reduces to the standard phase reduction. In this article, we consider dynamical systems that only have one of the nontrivial Floquet multipliers close to one, and the remaining $n-2$ nontrivial Floquet multipliers close to zero. We then can write the augmented phase reduction as

$$\begin{aligned} \dot{\theta }= & {} \omega +\mathcal {Z}^T(\theta ) U(t), \end{aligned}$$

(13)

$$\begin{aligned} \dot{\psi }= & {} k\psi +\mathcal {I}^T(\theta ) U(t) . \end{aligned}$$

(14)

Since we are only considering one isostable coordinate, we have removed the subscript for $\psi$.

3 Optimal phase control

Suppose we start at the point $\mathbf {x}_0$ on $\gamma (t)$. Without any control input, we expect the trajectory will return to the point $\mathbf {x}_0$ at time $t=T$. Our objective here is to devise a control which returns the trajectory to its initial position after time $t=T_1$, where $T_1\ne T$. It should do so using minimal energy input and staying close to the uncontrolled periodic trajectory. An “easy” way of doing this is by taking the control input to be a scalar multiple of the vector field, $U(t)=sF(\mathbf {x})$. s would be positive (resp., negative) when phase advance (resp., delay) is the control objective. However, there are three problems with such a control in an experimental setting: first, the dynamical system under consideration may not be fully actuated (not all the states of the system can be perturbed), which is generally the case in practical situations; second, the entire state of the system may not be experimentally measurable; and third, the function $F(\mathbf {x})$ might be unknown.

Here we consider dynamical systems which only have one degree of actuation: the control input vector is $U(t) = [u(t), \ 0,\ldots ,0]^T$. Such a control input is motivated by the applications we consider in this article, where only one of the elements of the state vector is affected directly by the control input. So the standard phase reduction becomes

$$\begin{aligned} \dot{\theta }= \omega +\mathcal {Z}_{x_1}(\theta )u(t), \end{aligned}$$

(15)

and the augmented phase reduction is

$$\begin{aligned} \dot{\theta }= & {} \omega +\mathcal {Z}_{x_1}(\theta )u(t), \end{aligned}$$

(16)

$$\begin{aligned} \dot{\psi }= & {} k\psi +\mathcal {I}_{x_1}(\theta )u(t). \end{aligned}$$

(17)

Here $\mathcal {Z}_{x_1}$ and $\mathcal {I}_{x_1}$ correspond to the first component in the n-dimensional vector functions $\mathcal {Z}$ and $\mathcal {I}$, respectively. Without loss of generality, we will do away with the subscripts and write them as $\mathcal {Z}$ and $\mathcal {I}$. An optimal control law based on the augmented phase reduction is found by using the cost function C:

$$\begin{aligned} \begin{aligned} C=\int _0^{T_1} \left[ \alpha u^2 +\beta \psi ^2 +\lambda _1\left( \dot{\theta }-\omega -\mathcal {Z}(\theta )u(t)\right) \right. \\ \left. +\lambda _2\left( \dot{\psi }-k\psi -\mathcal {I}(\theta )u(t)\right) \right] dt. \end{aligned} \end{aligned}$$

(18)

The first term in the cost function ensures that the control law uses a minimum energy input. The second term minimizes the transversal distance (in the direction of the slow isostable coordinate $\psi$) from the uncontrolled periodic trajectory, thus ensuring that the controlled trajectory stays close to the periodic trajectory where the reduction is valid. The coefficients $\alpha$ and $\beta$ give us the freedom to weight energy minimization and transversal distance minimization differently for different problems. The last two terms ensure that the system obeys the augmented phase reduction, with $\lambda _1$ and $\lambda _2$ being the Lagrange multipliers. The Euler–Lagrange equations are obtained from

$$\begin{aligned} \frac{\partial P}{\partial q}=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial P}{\partial \dot{q}}\right) , \qquad q=\lambda _1, \lambda _2,\theta , \psi , u, \end{aligned}$$

(19)

where P is the integrand in the cost function C. This gives

$$\begin{aligned} \dot{\theta }= & {} \omega +\mathcal {Z}(\theta )u(t), \end{aligned}$$

(20)

$$\begin{aligned} \dot{\psi }= & {} k\psi +\mathcal {I}(\theta )u(t), \end{aligned}$$

(21)

$$\begin{aligned} \dot{\lambda }_1= & {} -u\left( \lambda _1\mathcal {Z}'(\theta )+\lambda _2\mathcal {I}'(\theta )\right) , \end{aligned}$$

(22)

$$\begin{aligned} \dot{\lambda }_2= & {} 2\beta \psi -k\lambda _2, \end{aligned}$$

(23)

where

$$\begin{aligned} u(t)=\frac{\lambda _1\mathcal {Z}(\theta )+\lambda _2\mathcal {I}(\theta )}{2\alpha }. \end{aligned}$$

(24)

These equations are solved as a two point boundary value problem (see “Appendix A”) with the boundary conditions

$$\begin{aligned} \theta (0)=0,\ \ \theta (T_1)=2\pi ,\ \ \psi (0)=0,\ \ \psi (T_1)=0. \end{aligned}$$

(25)

The last boundary condition makes sure that trajectory ends back on the periodic orbit.

The previously proposed optimal control problem based on standard phase reduction (Moehlis et al. 2006) can be obtained by setting $\beta =0$ and $\lambda _2=0$ in the cost function. This gives Euler–Lagrange equations for the variables $\theta$ and $\lambda _1$ as

$$\begin{aligned} \dot{\theta }= & {} \omega +\mathcal {Z}(\theta )u(t), \end{aligned}$$

(26)

$$\begin{aligned} \dot{\lambda }_1= & {} -u\lambda _1\mathcal {Z}'(\theta ), \end{aligned}$$

(27)

where

$$\begin{aligned} u=\frac{\lambda _1\mathcal {Z}(\theta )}{2\alpha }. \end{aligned}$$

(28)

These control laws (Eqs. 24 and 28) can then be applied to the full model $\dot{\mathbf {x}}=F(\mathbf {x})+U(t)$ to change the orbit’s phase. To compare the control laws, we compute the control energy as

$$\begin{aligned} \int _0^{T_1}u^2 \mathrm{d}t, \end{aligned}$$

(29)

and the control error as the normalized Euclidean distance between the final position and the initial position given as

$$\begin{aligned} \frac{|| x(T_1)-x(0)||}{\text {max} (||x(t)||)}, \end{aligned}$$

(30)

where ||x|| represents the standard Euclidean norm, and max (||x(t)||) represents the maximum value of the Euclidean norm of the periodic solution x(t). The control error arises because we apply the control input (Eqs. 24 and 28) based on the reduced model to the full model (Eq. 1).The control algorithm based on augmented phase reduction is outlined in the flowchart in Fig. 1. The algorithm based on standard phase reduction is implemented in a similar manner. We will see in Sect. 4 that our new control law is effective in circumstances in which the previously proposed control law fails since the novel attribute of our cost function minimizes the transversal distance, ensuring that the controlled trajectory is always close enough to the periodic orbit so that the phase reduction is valid. On the other hand, with the previously proposed control law, even a small control input can drive the trajectory away from the periodic orbit, thereby rendering the phase reduction invalid and the control law ineffective.

Fig. 1

Flowchart describing the control algorithm based on augmented phase reduction

4 Applications

We apply the new optimal control algorithm (based on the augmented phase reduction) and the previously proposed optimal control algorithm (based on the standard phase reduction) to four different dynamical systems: the Hopf bifurcation normal form, cardiac pacemaker cells, thalamic neurons, and circadian gene regulation in the suprachiasmatic nucleus. For all these systems, the PRC is numerically computed using the software XPP (Ermentrout 2002). We use Newton iteration to obtain the IRC as the periodic solution to Eq. (14). The control input is obtained by solving the Euler–Lagrange Eqs. (20)–(23) or (26)–(27) as a two point boundary value problem numerically. It is then applied to the full model to compute the resulting trajectory $\mathbf {x}(t)$. A parametric study is performed to compute this error as a function of the ratio $T_1/T$ and, for the Hopf bifurcation normal form, the nontrivial Floquet multiplier of the periodic orbit. A detailed description of the numerical procedures used is given in “Appendix A”.

4.1 Hopf bifurcation normal form

4.1.1 Motivation

Here we consider the normal form for a supercritical Hopf bifurcation (Guckenheimer and Holmes 1983), which occurs in several applications including biological and chemical oscillators (Winfree 2001; Marsden and McCracken 2012; Kopell and Howard 1973; Izhikevich 2007). This example allows us to explore in detail the interplay between the control objective and the nontrivial Floquet multiplier for the new and the previously proposed control algorithm.

4.1.2 Control strategy

We use our control algorithms to change the phase of a periodic orbit near a supercritical Hopf bifurcation. By varying parameters, we can calculate the control error for both algorithms as a function of the nontrivial Floquet multiplier and the target phase change, which gives a sense of which control algorithm would work better in what ranges of these quantities.

The normal form of the supercritical Hopf bifurcation with an external control input u(t) is:

$$\begin{aligned} \dot{x}= & {} ax-by+\left( x^2+y^2\right) (cx-dy)+u(t), \end{aligned}$$

(31)

$$\begin{aligned} \dot{y}= & {} bx+ay+\left( x^2+y^2\right) (dx+cy), \end{aligned}$$

(32)

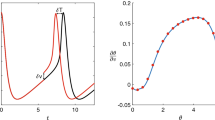
with $c<0$. With zero control input u(t), and $a<0$, the system has a stable fixed point. As a increases through 0, a stable periodic orbit is born, and the fixed point becomes unstable. With parameters $a=0.004,b=1,c=-1,d=1$, the system has a stable periodic orbit with the time period $T=6.2582$ and the nontrivial Floquet multiplier $\exp (-2aT)=0.9512$. The PRC and the IRC are sinusodial, cf. Castejón et al. (2013); Monga et al. (2018), with amplitudes $\sqrt{\frac{\mathrm{d}^2+c^2}{-ac}}$ and $\sqrt{1+\frac{\mathrm{d}^2}{c^2}},$ respectively. Here, $\theta =0$ corresponds to the initial condition $x=-0.0447,\ y=0.0447$. The top row of Fig. 2 shows the uncontrolled periodic orbit, PRC, and IRC for the given parameter values. The control parameters $\alpha$ and $\beta$ are both taken to be unity. We calculate the optimal control with $T_1=1.3T=8.1356$ both for our new algorithm and the previously proposed algorithm.

The resulting trajectories, time series, and control inputs are shown in the bottom two rows of Fig. 2. As seen in this figure, the new control algorithm does much better in changing the phase of the periodic orbit while also keeping the trajectory close to the periodic orbit for the uncontrolled system. This is because our algorithm minimizes the transversal distance, ensuring that the controlled trajectory is always close enough to the periodic orbit so that the phase reduction is valid. On the other hand, with the previously proposed control law, the control input drives the trajectory away from the periodic orbit, thereby rendering the phase reduction invalid and the control law ineffective. This is apparent from the control error (given by Eq. 30) as well, which is 0.1435 and 1.1394 for the new and the previous optimal control algorithms, respectively. However the new control algorithm does better at the expense of consuming more energy (given by Eq. 29), which comes out to be 0.0032 units, compared with 0.0015 units for the previous control algorithm. We note that the trajectory in the bottom row of Fig. 2 will eventually return to the stable uncontrolled periodic orbit, but will not have the corresponding desired phase shift.

Fig. 2

Hopf bifurcation normal form: Top row shows the uncontrolled periodic orbit, PRC, and IRC for the Hopf normal form with parameters given in the main text. The middle (resp., bottom) row shows the trajectory, time series, and control input for control based on our new (resp., the previously proposed) algorithm. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)

As the parameter a is further increased, the system moves away from the bifurcation point, resulting in a decreasing nontrivial Floquet multiplier. A parametric study is performed to analyze the dependence of the control error on the nontrivial Floquet multiplier and the ratio $T_1/T$. The top (resp., bottom) row of Fig. 3 shows this error for the new (resp., the previously proposed) control algorithm. The error for the previously proposed control algorithm increases as the nontrivial Floquet multiplier increases toward 1 and/or ratio $\frac{T_1}{T}$ moves away from 1 (the control objective becomes more extreme). This is because an extreme control objective requires a large control input, which drives the trajectory away from the periodic orbit, resulting in the phase reduction losing accuracy. However, when the nontrivial Floquet multiplier is close to zero, a trajectory kicked away from the periodic orbit returns quickly back to it, thereby nullifying the effect of a large control input on the accuracy of phase reduction. On the other hand, for the new control algorithm, the error remains small for all values of the ratio $\frac{T_1}{T}$ and nontrivial Floquet multiplier considered. Thus we can conclude that our new control algorithm is much more effective than the previously proposed control algorithm, especially when the control objective is extreme and/or the nontrivial Floquet multiplier of the periodic orbit is close to 1.

Fig. 3

Hopf bifurcation normal form: Top (resp., bottom) row shows the control error (Eq. 30) from the control based on our new (resp., the previously proposed) algorithm as a function of the nontrivial Floquet multiplier and the ratio $T_1/T$

We expect that the asymmetry in control error, as seen in the bottom panel of Fig. 3, can be explained by the inherent shear present in the model’s dynamics (Wang and Young 2003). For the parameters considered, we observe that when phase delay is the desired control objective, the trajectory is kicked inside the periodic orbit, i.e., the amplitude of the transient trajectory decreases. On the other hand, for a phase advance control objective, the trajectory is kicked out of the periodic orbit, i.e., the amplitude of the transient trajectory increases. The difference between this amplitude increase and decrease is magnified for the standard phase reduction-based control with a small Floquet multiplier. Shear present in the dynamics acts differently on these two cases, which is reflected as a small asymmetry in control error seen in the bottom panel of Fig. 3. For the new control algorithm, the difference between the amplitude increase and decrease stays relatively small, and thus, the control error is more symmetric as can be seen in the top panel of Fig. 3.

4.2 Controlling cardiac pacemaker cells

4.2.1 Motivation

The heartbeat is initiated by a collection of cells in the sinoatrial node (SA node), which acts as a pacemaker. These cells elicit periodic electrical pulses which polarize a collection of excitable and contractile cells called myocytes. In the process of depolarizing, myocytes contract and propagate action potentials to the neighboring cells. This well-coordinated process of excitation/depolarization and contraction enables the heart to pump blood throughout the body. Under normal conditions, with constant pacing, the action potential duration (APD), that is the time for which an action potential lasts, also remains constant. However, under some conditions, this 1:1 rhythm between pacing and the APD can become unstable, bifurcating into a 2:2 rhythm of alternating long and short APD, known as alternans (Mines 1913). Alternans is observed to be a possible first step leading to fibrillation (Pastore et al. 1999). Thus, a number of researchers have worked on suppressing alternans as a method of preventing fibrillation, thereby preventing the need for painful and damaging defibrillating shocks. Many of these methods (Hall and Gauthier 2002; Christini et al. 2006; Hall et al. 1997; Wilson and Moehlis 2015b) operate by exciting the myocardium tissue externally with periodic pulses and changing the period according to the alternating rhythm. However, such a control requires excitation at several sites in the tissue (Rappel et al. 1999).

Fig. 4

Suppression of alternans: the top panel shows the stable 2:2 rhythm of alternans. The bottom panel shows the 1:1 rhythm stabilized by reducing the BCL for one cycle

4.2.2 Control strategy

We devise a novel strategy to suppress alternans by changing the phase of the inherent pacemaker cells. Such a control strategy could eliminate the need to excite the tissue at multiple sites. We make use of the relation between APD, diastolic interval (DI), and basic cycle length (BCL) to devise our control strategy. DI is the time for which a myocyte cell remains depolarized, and BCL is the time between successive action potentials, which is dictated by the period of the pacemaker cells. In the simplest model (Guevara et al. 1984), APD is a function of the previous DI, given by the restitution curve: $\mathrm{APD}_i=f(\mathrm{DI}_{i-1})$. DI is a function of the current APD, given by what we call as the BCL curve: $\mathrm{APD}_i+\mathrm{DI}_i=\mathrm{BCL}$. The intersection of these two curves gives the normal 1:1 rhythm. If the slope of the restitution curve at this intersection is greater than 1, the 1:1 rhythm is unstable, giving rise to alternans. This was first shown by Nolasco and Dahlen (1968) and is illustrated in the top panel of Fig. 4. Given the current $\mathrm{DI}_i$, the next $\mathrm{APD}_{i+1}$ is given by the restitution curve. Traversing horizontally from this point to the BCL curve gives the next $\mathrm{DI}_{i+1}$. Repeating this analysis gives all the successive DIs and APDs. Under constant BCL, it is graphically illustrated in the top panel of Fig. 4 that when slope of the restitution curve is greater than 1, APDs and DIs alternate between two values, corresponding to alternans. If starting from point 2 in the bottom panel of Fig. 4, we reduce the BCL for one cycle such that the next DI corresponds to the unstable 1:1 state, this would stabilize the 1:1 rhythm, eliminating alternans. Thus our control strategy to eliminate alternans corresponds to decreasing the BCL for one cycle, i.e., advancing the phase of the SA node cells. Note that in a clinical setting, we may need to apply this control strategy multiple times, as the 1:1 rhythm is unstable. Applying control multiple times is physically realistic as long as the trajectory returns to the limit cycle before the next stimulus arrives. As we will see later, this is not the case with the previously proposed optimal control algorithm based on the standard phase reduction. This novel strategy should be clinically feasible as well, since an implanted battery could generate multiple stimuli.

To demonstrate our approach, we consider the SA node cell dynamics, instead of the discrete APD/DI dynamics. Our control objective is to change the phase of SA node cells; the amount of change required is linked to the amount by which the BCL curve needs to be shifted to stabilize the unstable APD/DI dynamics. Here we advance the phase by 20 % as an example. We consider the 7-dimensional YNI model of SA node cells in rabbit heart proposed by (Yanagihara et al. 1980). The model is of Hodgkin–Huxley type with 6 gating variables d, f, m, h, q, p and a transmembrane voltage variable V. The model is given as

$$\begin{aligned} \dot{V}= & {} \frac{I_{m}-I_{Na}-I_k-I_l-I_s-I_h}{C}+u(t), \end{aligned}$$

(33)

$$\begin{aligned} \dot{y}= & {} \alpha _y(1-y)-\beta _y y, \end{aligned}$$

(34)

where y represents the 6 gating variables. u(t) represents the applied current as the control input. For details of the currents ($I_{Na},I_k,I_l,I_s,I_h$) and the parameters, see “Appendix B.1.” With $I_{m}=1.0609$, we get a stable periodic orbit with time period $T=203.4552$ ms and nontrivial Floquet multipliers 0.7595, 0.1365, 0.0299, $\approx$ 0, $\approx$ 0, $\approx$ 0. Since one of the nontrivial Floquet multipliers is considerably larger than others, we only consider the isostable coordinate corresponding to it. The top row of Fig. 5 shows the uncontrolled periodic orbit, PRC, and IRC for the given parameter values. Control parameters $\alpha$ and $\beta$ are taken as 100 and 0.1, respectively. Here we give considerable more weight to minimizing energy, to overcome our new control algorithm’s tendency for this problem to require more energy than the previously proposed control algorithm. We calculate optimal control for the new and previously proposed algorithms with $T_1=0.8T=162.7641$ ms.

The resulting trajectories, time series, and control inputs are shown in the bottom two rows of Fig. 5. As seen in this figure, our new control algorithm successfully achieves the control objective while keeping the trajectory close to the uncontrolled periodic orbit. It is able to do so while giving considerable importance to energy minimization ($\alpha$ is significantly bigger than $\beta$). On the other hand, with the previous control algorithm, instead of staying close to the periodic orbit, the trajectory decays to the stable fixed point of the system. This is evident from the control error, which is 0.0858 and 0.3677 for our new and the previous optimal control algorithms, respectively. Our control does better at the expense of consuming more energy (6.3850 units) than the previous control (0.2100 units). Note that here we change the phase by 20% as an example. In a more realistic setting, we would require a more integrated model which combines the discrete APD/DI dynamics together with the dynamics of the SA node cell. This would automatically determine the phase change required.

Fig. 5

YNI model for cardiac pacemaker cells: top row shows the uncontrolled periodic orbit, PRC, and IRC for the YNI model with parameters given in the main text. The middle (resp., bottom) row shows the trajectory, time series, and control input for control based on our new (resp., the previously proposed) algorithm. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)

4.3 Controlling neurons

4.3.1 Motivation

Essential and parkinsonian tremor, the most common movement disorders, affect millions of people worldwide. These cause involuntary tremors in various parts of the body, disrupting the activities of daily living. Pathological neural synchronization in the thalamus and the STN brain region is hypothesized to be one of the causes of motor symptoms of essential and parkinsonian tremor, respectively (Kane et al. 2009; Kühn et al. 2009). Deep brain stimulation (DBS), an FDA-approved treatment, helps to alleviate these symptoms (Benabid et al. 1991, 2009) by stimulating the thalamus or the STN brain regions with a high-frequency high-energy pulsatile waveform. In the process, the high-frequency high-energy waveform has been hypothesized to desynchronize the synchronized neurons; see, e.g., Wilson et al. (2011); Wilson and Moehlis (2015a). This has motivated researchers to come up with efficient control techniques (Tass 2003; Nabi et al. 2013a) which not only desynchronize the neurons, but also consume less energy, thus prolonging the battery life of the stimulator and preventing tissue damage caused by the high-energy pulsatile stimuli.

4.3.2 Control strategy

At a single neuron level, desynchronization can be viewed as changing the phase of a neuron to be at a different phase than other neurons (Moehlis et al. 2006; Nabi and Moehlis 2012). With this in mind, we use our algorithm to change the phase of neuron spikes in thalamic neurons. To see the performance of our algorithm in an extreme scenario, we set the control objective to advance the phase by 60%. We demonstrate this by using the thalamic neuron model (Rubin and Terman 2004) given as

$$\begin{aligned} \dot{v}= & {} \frac{-I_L-I_{Na}-I_K-I_T+I_b}{C_m}+u(t), \end{aligned}$$

(35)

$$\begin{aligned} \dot{h}= & {} \frac{h_{\infty }-h}{\tau _h}, \end{aligned}$$

(36)

$$\begin{aligned} \dot{r}= & {} \frac{r_{\infty }-r}{\tau _r}. \end{aligned}$$

(37)

In these equations, $I_b$ is the baseline current, which we take as $5\upmu$A/$\mathrm{cm}^2$, v is the membrane voltage, and $h,\ r$ are the gating variables of the neuron. u(t) represents the applied current as the control input. For details of the currents ($I_L, I_{Na}, I_K, I_T$), functions $h_{\infty }, \tau _h,r_{\infty }, \tau _r$ and the rest of the parameters, see “Appendix B.2.” Under zero control input, these parameters give a stable periodic orbit with time period $T=8.3955~ms$ and nontrivial Floquet multipliers 0.8275 and 0.0453. Since one of the nontrivial Floquet multiplier is close to 0, we only consider the isostable coordinate corresponding to the larger nontrivial Floquet multiplier in the augmented phase reduction. The top row of Fig. 6 shows the uncontrolled periodic orbit, PRC, and IRC for the given parameter values. Control parameters $\alpha$ and $\beta$ are taken as unity. We calculate the optimal control for our new algorithm and the previously proposed algorithm with $T_1=0.4T=3.3582$ ms.

The resulting trajectories, time series, and control inputs are shown in the bottom two rows of Fig. 6. As seen in middle and bottom panels of the left column of this figure, our new control algorithm does better in keeping the trajectory close to the periodic orbit. On the other hand, with the previous control algorithm, the trajectory moves away from the periodic orbit. Looking at the central middle and bottom panels, it seems that the trajectory returns back to the periodic orbit even for the previously proposed optimal control algorithm, but this is not the case. Since one of the Floquet multipliers is close to zero, the voltage state returns back quickly, but the other states still remain far away from the limit cycle. This is evident from the first two panels of the bottom row of Fig. 6, as well as from the control error, which is 0.032 and 0.088 for our new and the previous optimal control algorithms, respectively. Our new control algorithm does better at the expense of consuming more energy (1119.15 units) compared to (784.16 units) in the previous control algorithm.

Fig. 6

Thalamic neuron model: top row shows the uncontrolled periodic orbit, PRC, and IRC for the thalamic neuron model with parameters given in the main text. The middle (resp., bottom) row shows the trajectory, time series, and control input for our new (resp., the previously proposed) control algorithm. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)

Fig. 7

Thalamic neuron model: blue $\Box$ (resp., red $*$) shows the control error for the control from our new (resp., the previously proposed) algorithm as a function of the ratio $T_1/T$ (color figure online)

We test the control algorithms for various target phase changes, corresponding to the range from $T_1=0.2T$ to $T_1=1.8T$. Fig. 7 shows control error for these phase changes for both our new and the previous optimal control algorithms. We see that the control error grows as the control objective becomes more extreme, which is expected. But it still remains relatively small for our new control algorithm. This again shows that our new control algorithm is more effective in changing the phase than the previously proposed control algorithm.

4.4 Controlling circadian oscillators

4.4.1 Motivation

Neurons in the suprachiasmatic nucleus (SCN) of the brain are responsible for maintaining the circadian rhythm in mammals. This rhythm is synchronized with the external day and night cycle under normal conditions. A disruption between these two rhythms can happen due to multiple reasons, such as travel across time zones, starting a night shift job, working in extreme environments (space, earth poles, underwater), etc. Such an asynchrony leads to several physiological disorders like insomnia, improper digestion, and even cancer and cardiovascular diseases (Rea et al. 2008; Klerman 2005), thus driving researchers to try to develop ways to remove this asynchrony. One way of doing this is by using a light stimulus, which affects the circadian rhythm (Czeisler et al. 1989). Therefore, many researchers have used appropriately timed exposure to light to entrain circadian rhythm with the new external cycle; see, e.g., Wever (1985); Czeisler et al. (1990); Eastman and Martin (1999).

4.4.2 Control strategy

Several control-theoretic approaches have been used in the past to determine timing and intensity of the light stimulus to synchronize the circadian rhythm with a new light–dark cycle (Dean et al. 2009; Forger and Paydarfar 2004; Zhang et al. 2012). One way of doing this is by changing the phase of one circadian oscillation so that the oscillation gets aligned with the external cycle after the end of the controlled oscillation. As an example, consider a person who is going on a vacation to London, traveling east from New York City. The day–night cycle in his new environment would be 5 h behind his internal rhythm. Thus, advancing the phase of his internal circadian rhythm by 20 percent ($\approx$ 5 h) for one cycle would realign his internal rhythm with the new environment. This would be equivalent of taking $T_1=0.8T$ in our control algorithm.

We use the 3-dimensional model of the clock gene regulation in SCN developed by Gonze et al. (2005) to demonstrate our control algorithm. This model has a negative feedback loop, where production of one gene leads to the inhibition of the other, thus causing oscillatory behavior. It is given as:

$$\begin{aligned} \dot{X}= & {} v_1\frac{K_1^4}{K_1^4+Z^4}-v_2\frac{X}{K_2+X} + L(t), \end{aligned}$$

(38)

$$\begin{aligned} \dot{Y}= & {} k_3X-v_4\frac{Y}{K_4+Y}, \end{aligned}$$

(39)

$$\begin{aligned} \dot{Z}= & {} k_5Y-v_6\frac{Z}{K_6+Z}. \end{aligned}$$

(40)

Here X represents mRNA concentration of a clock gene, per or cry, Y represents the resulting protein, PER or CRY (Gad et al. 2008), and Z is the active protein which inhibits production of the clock gene. L(t), the perturbation in ambient light, acts as the control input. Parameters $v_1,K_1,v_2,K_2,k_3,v_4,K_4,k_5,v_6,K_6$ are taken from Fig. 1 in the article of Gonze et al. (2005), and are given in “Appendix B.3.” These parameters give a stable periodic orbit with time period $T=23.5398$ hrs and the nontrivial Floquet multipliers 0.9509 and $\approx 0$. Since one of the nontrivial Floquet multipliers is approximately 0, we only consider the isostable coordinate corresponding to the larger nontrivial Floquet multiplier in the augmented phase reduction. The top row of Fig. 8 shows the uncontrolled periodic orbit, PRC, and IRC for the given parameter values. We have taken the control parameters $\alpha = 10$ and $\beta =0.1$. We again give more weight to minimizing energy to compensate for our new control algorithm’s tendency to require more energy than the previously proposed control algorithm for this problem.

Fig. 8

Circadian oscillator: top row shows the uncontrolled periodic orbit, PRC, and IRC for the circadian oscillator model with parameters given in the main text. The middle (resp., bottom) row shows the trajectory, time series, and control input for control based on our new (resp., the previously proposed) algorithm. Control is on (resp., off) for the portion shown by the thick black (resp., thin blue) line. The trajectory starts at the small red circle. The red horizontal line shows the amplitude of the uncontrolled periodic orbit (color figure online)

The resulting trajectories, time series, and control inputs are shown in the bottom two rows of Fig. 8. We see that our new control algorithm is able to advance the phase while keeping the trajectory close to the unperturbed periodic orbit. It is able to do so while giving considerable importance to energy minimization ($\alpha$ is 100 times bigger than $\beta$). On the other hand, with the previous control algorithm, the trajectory moves away from the unperturbed periodic orbit. This is apparent from the control error as well, which is 0.0099 and 0.0665 for our new and the previous optimal control, respectively. Our new control algorithm does better at the expense of consuming more energy (0.00096 units) than the previous control algorithm (0.00015 units).

Fig. 9

Circadian oscillator: blue $\Box$ (resp., red $*$) shows the control error from the control based on our new (resp., the previously proposed) algorithm as a function of the ratio $T_1/T$ (color figure online)

We also test our algorithm for more extreme cases of asynchrony, ranging from $T_1=0.5T$ (traveling west and gaining 12 h in time) to $T_1=1.4T$ (traveling east and losing 9 h in time). Figure 9 shows the control error for these cases for both our new and the previous control algorithm. The control error increases as the control objective becomes more extreme, but it still remains relatively small for our new control algorithm. This again demonstrates the effectiveness of our new control algorithm over the previously proposed control algorithm.

5 Effect of noise

So far we have demonstrated that our new control is effective in deterministic systems. However, real systems are subjected to noise, so here we analyze how such noise affects the performance of our new algorithm. We calculate control from the deterministic phase model (24 and 28) and apply it to the full model with added white noise. So in effect we consider noise to be an external disturbance that affects only the first state variable that we control directly. Thus we simulate the stochastic dynamical system

$$\begin{aligned} \frac{\mathrm{d} \mathbf {x}}{\mathrm{d}t} = F(\mathbf {x}) + [u(t)+\sigma \eta (t),\ldots ,0]^T. \end{aligned}$$

(41)

Here $\sigma \eta (t) = \sigma \mathcal {N}(0,1)$ is zero mean white noise with strength $\sigma$. To simulate this equation numerically, we rewrite it as

$$\begin{aligned} d \mathbf {x}= F(\mathbf {x})dt + [u(t)dt + \sigma dW(t) ,\ldots ,0]^T, \end{aligned}$$

(42)

where $dW(t)=\eta (t)dt$ and W(t) is the standard Weiner process. We use the second-order Runge–Kutta algorithm developed in (Honeycutt 1992) to simulate the above equation.

To analyze the effect of noise on the performance of our control algorithm, we perform a parametric study by calculating control error as a function of the nontrivial Floquet multiplier and the ratio $T_1/T$ for the Hopf bifurcation normal form. We take the noise strength $\sigma = 0.1r_{po}$, where $r_{po}=\sqrt{-a/c}$ is the radius of the periodic orbit. This ensures that the relative noise strength remains the same as the radius of the periodic orbit varies with the parameter a. The top (resp., bottom) row of Fig. 10 shows the control error for the new (resp., the previously proposed) control algorithm in presence of white noise. We see that this figure is very similar to Fig. 3 where we did not include white noise. The addition of white noise increases control errors for both the algorithms slightly, but the algorithm based on the augmented phase reduction still does much better than the algorithm based on standard phase reduction. Noise doesn’t affect the performance of the previous algorithm when the nontrivial Floquet multiplier is close to 0 and the ratio $T_1/T$ is close to one. This is because any perturbation caused by the noise is nullified quickly under the evolution of the vector field. However, the control error for our algorithm based on the augmented phase reduction remains small in the presence of noise for all analyzed values of the nontrivial Floquet multipliers and ratios $T_1/T$.

Fig. 10

Hopf bifurcation normal form with white noise: top (resp., bottom) row shows the control error (Eq. 30) from the control based on our new (resp., the previously proposed) algorithm for the system with white noise (color figure online)

Fig. 11

Circadian oscillator with noise: top left (resp., bottom left) panel shows the controlled trajectory in blue for control based on our new (resp., the previously proposed) algorithm, and the periodic orbit in black. The trajectory starts at the small red circle and reaches the small blue circle at time $T_1=0.8T$. Top right (resp., bottom right) panel shows the control input added to the noise for our new (resp., the previously proposed) algorithm (color figure online)

We also present results for controlling the circadian oscillator from Sect. 4.4 with white noise added to the X equation. Here we take the noise strength $\sigma = 0.004$, and the rest of the control parameters are the same as before. The corresponding results displayed in Fig. 11 show that white noise drives the controlled trajectory slightly further away from the periodic orbit for both algorithms, but our new control is still able to bring the trajectory close to where it started at time $T_1$. However, the previously proposed control algorithm fails to do so. Thus these results demonstrate the effectiveness of our new control algorithm in the presence of noise.

6 Discussion and conclusion

Standard phase reduction is a vital tool in the analysis and control of biological oscillators. It reduces the dimension of dynamical systems and can make their control experimentally feasible. However, it only allows a small stimulus without the risk of driving the oscillator away from the periodic orbit. This limitation makes it unsuitable for some control purposes, especially when a significant control stimulus is required or when a nontrivial Floquet multiplier of the periodic orbit is close to 1. This suggests the use of control techniques based on the augmented phase reduction. In this article, we have developed a novel optimal control algorithm based on the augmented phase reduction to change the phase of a periodic orbit. Our algorithm not only minimizes the total energy consumption but also reduces the controlled trajectory’s transversal distance from the uncontrolled periodic orbit. This is because of inclusion of both the “energy” ($u^2$) and the “transversal distance” terms ($\psi ^2$) in the cost function ensures that the control input remains small overall, and keeps the controlled trajectory from getting far away from the unperturbed periodic orbit.

Our algorithm is applicable to generic oscillators, which we have demonstrated for a diversity of applications. We compared the performance of our algorithm as a function of both the Floquet multiplier and the desired phase change by applying it to the normal form for the supercritical Hopf bifurcation. We devised a novel approach to eliminate alternans by changing the phase of the pacemaker cells and showed how our optimal control algorithm can be tied to the formulated geometrical approach. Such a control strategy could remove the need to excite the myocardium tissue at multiple sites. We also applied our algorithm to change the phase of thalamic neurons, which could be useful for desynchronizing pathologically synchronized neurons, thus holding potential to alleviate the motor symptoms of essential and parkinsonian tremor. Such an optimal control is expected to consume less energy than the pulsatile current used in present DBS protocol, thus prolonging the battery life of the stimulator, and also preventing tissue damage caused by the high-energy DBS stimuli. Additionally, we applied the algorithm to change the phase of the clock gene regulation in SCN, which has relevance to treating jet lag or to adapting to night shift work. Finally, we showed that our algorithm performs well even in the presence of noise.

For some systems, the previous control algorithm based on the standard phase reduction could not keep the trajectory close to the unperturbed periodic orbit and thus failed in achieving the desired control objective. We showed that our new algorithm works much better than the previous algorithm, especially when a nontrivial Floquet multiplier of the periodic orbit is close to 1 and/or a significant change in phase is required. In such cases, our new algorithm can do an order of magnitude better in terms of the calculated control error. From the right column of Figs. 2, 5, 6, and 8, we see that the control inputs for both of the control algorithms have similar shape, but are shifted in phase. As seen in these figures, for our new control algorithm, the control input is large when the IRC is near zero and is small when the IRC is large. This diminishes the effect of the control input on the isostable coordinate, and thus, the oscillator’s transversal distance from the periodic orbit remains small. This ensures that the augmented phase reduction represents the dynamics accurately, making the control more effective. Our new control algorithm does better at the expense of consuming more energy than the previously proposed control algorithm. We expect that by tuning the control parameters $\alpha$ and $\beta$, this energy difference can be reduced.

PRCs are measured experimentally by giving perturbations to the oscillator at various phases and recording the phase change caused by the perturbation as a function of the stimulation phase. We propose that IRCs can be measured in a similar way. One can apply perturbations at various phases and record the resulting “amplitude” change as a function of the stimulation phase, or one can record the time required for the trajectory to return to the periodic orbit as a function of the stimulation phase. Either of these approaches will give a measure of the IRC, which can be appropriately scaled to give the true IRC. Thus, just like the control algorithm based on standard phase reduction, we propose that our new algorithm from this paper can be applied in an electrophysiological setting.

Appendices

A Numerical Methods

In this appendix, we give details on the numerical methods we used to compute the Floquet multipliers, PRC, and IRC, and solve the Euler Lagrange equations and the full model equations.

1.1 A.1 Computation of PRC

For the normal form of the Hopf bifurcation, we can compute the PRC and its derivative w.r.t. $\theta$ analytically, see, e.g., Brown et al. (2004). For computing the PRCs (and their derivatives w.r.t. $\theta$) of the YNI, thalamic neuron, and the clock gene regulation model, we use the XPP package (Ermentrout 2002), which is widely used by the community working on nonlinear oscillators. This package solves the appropriate adjoint equation backward in time along the periodic orbit to compute the PRC as a function of time. We scale the PRC computed by this package by $\omega$, as we consider PRC as $\mathcal {Z}(\theta )=\frac{\partial \theta }{\partial \mathbf {x}}$, whereas the computed PRC from the XPP package is $\tilde{\mathcal {Z}}(t)=\frac{\partial t}{\partial \mathbf {x}}$. Note that the XPP computes the derivative of the PRC w.r.t. time $\left( \dot{\tilde{\mathcal {Z}}}(t)=\frac{\partial ^2 t}{\partial \mathbf {x}\partial t}\right)$, which is numerically equivalent to its derivative w.r.t. $\theta$$\left( \mathcal {Z}'(\theta )=\frac{\partial ^2 \theta }{ \partial \mathbf {x}\partial \theta }\right)$. The XPP package gives the PRC and its derivative as a time series. After appropriately scaling the time series, we write them as an analytical expression of $\theta$ by approximating them as a finite Fourier series, to be used in the numerical computation of the Euler–Lagrange equations.

1.2 A.2 Computation of Floquet multipliers

Once the PRC has been computed, we choose an arbitrary point on the periodic orbit as $\theta =0$ and approximate the isochron $\varGamma _0$ as an $n-1$ dimensional hyperplane orthogonal to the PRC at that point. To compute the Jacobian DF, we compute $\mathbf {x}_\varGamma ^j$ (as defined beneath Eq. 8 in the main text) for a large j, for a number of initial conditions $\mathbf {x}_0$ spread out on the isochron. Eigenvector decomposition of DF gives us the Floquet multipliers of the periodic orbit and the corresponding Floquet exponents $k_i$. Note that for planar systems, the nontrivial Floquet exponent can be directly computed from the divergence of the vector field as (Glendinning 1994)

$$\begin{aligned} k=\frac{\int _0^T{ \nabla \cdot F(\gamma (t))\mathrm{d}t}}{T}. \end{aligned}$$

(43)

1.3 A.3 Two point boundary value problem with Newton iteration

We calculate the IRC and solve the Euler–Lagrange equations as a two point boundary value problem using Newton iteration, which we briefly summarize. Consider a general two point boundary value problem

$$\begin{aligned} \dot{y} = f(t,y), \qquad y \in \mathbb {R}^n, \qquad 0\le t \le b, \end{aligned}$$

(44)

with the linear boundary condition

$$\begin{aligned} B_0y(0)+B_by(b)=a, \qquad B_0,\ B_b \in \mathbb {R}^{n\times n}. \end{aligned}$$

To solve such a boundary value problem, we integrate Eq. (44) with the initial guess $c=y(0)$ and calculate the function g(c):

$$\begin{aligned} g(c)=B_0c+B_by(b)-a, \end{aligned}$$

where y(b) is the solution at time b with the initial condition c. If we had chosen the correct initial condition c, g(c) would be 0. Based on the current guess $c^\nu$, and the $g(c^\nu )$ value, we choose the next initial condition by the Newton Iteration as

$$\begin{aligned} c^{\nu +1}=c^\nu -\left( \left. \frac{\partial g}{\partial c}\right| _{c^\nu }\right) ^{-1}g(c^\nu ). \end{aligned}$$

(45)

We compute the Jacobian $J=\left. \frac{\partial g}{\partial c}\right| _{c^\nu }$ numerically as

$$\begin{aligned} J_i=\frac{g^+-g^-}{2\epsilon }, \end{aligned}$$

where

$$\begin{aligned} g^+= & {} g\left( c^\nu +e_i \epsilon \right) ,\\ g^-= & {} g\left( c^\nu -e_i \epsilon \right) , \end{aligned}$$

$J_i$ is the $i\mathrm{th}$ column of J, $\epsilon$ is a small number, and $e_i$ is a column vector with 1 in the $i\mathrm{th}$ position and 0 elsewhere.

1.3.1 A.3.1 Computation of IRC

To calculate the IRC, we first compute and save the periodic solution $\gamma (t)$ using Matlab’s ODE solver ode45 with a relative error tolerance of $3e-12$, and an absolute error tolerance of $1e-15$. The next step is to solve the adjoint equation

$$\begin{aligned} \dot{\mathcal I} =\left( k_iI-DF(\gamma (t))^T\right) {\mathcal I}, \qquad 0\le t \le T, \end{aligned}$$

with periodic boundary conditions

$$\begin{aligned} {\mathcal I}(0)={\mathcal I}(T). \end{aligned}$$

We choose an initial guess ${\mathcal I}(0)$, and integrate the adjoint equation using Matlab’s ODE solver ode45 with a relative error tolerance of $3e-12$, and an absolute error tolerance of $1e-15$. For Newton iteration, we take

$$\begin{aligned} c^\nu= & {} {\mathcal I}(0), \end{aligned}$$

(46)

$$\begin{aligned} g(c^\nu )= & {} \underbrace{I}_{B_0}{\mathcal I}(0)-\underbrace{I}_{B_b}{\mathcal I}(T), \nonumber \\\Rightarrow & {} g(c^\nu )={\mathcal I}(0)-{\mathcal I}(T), \end{aligned}$$

(47)

$$\begin{aligned} \left. \frac{\partial g}{\partial c}\right| _{c^\nu }= & {} I-J, \end{aligned}$$

(48)

where I is the identity matrix, and J is the Jacobian matrix

$$\begin{aligned} J=\frac{\partial {\mathcal I}(T)}{\partial {\mathcal I}(0)}, \end{aligned}$$

which we compute numerically. We use Eqs. (46)–(48) together with Eq. (45) to compute the next initial condition. Once a periodic solution is obtained, the computed IRC is scaled by the normalization condition $\nabla _{\mathbf {x_0}}\psi _i \cdot v_i=1$ (Wilson and Moehlis 2016). Its derivative w.r.t. $\theta$ is obtained numerically by a central difference scheme

$$\begin{aligned} \mathcal {I}'(\theta _i)=\frac{\mathcal {I}(\theta _{i+1})-\mathcal {I}(\theta _{i-1})}{\theta _{i+1}-\theta _{i-1}}. \end{aligned}$$

The obtained IRC and its derivative w.r.t. $\theta$ are written as analytical expressions of $\theta$ by a finite Fourier series approximation, which is used in the computation of the Euler–Lagrange equations.

1.3.2 A.3.2 Solving Euler–Lagrange equations

For Euler Lagrange equations based on augmented phase reduction, we set the boundary conditions as $\theta (0)=0, \ \theta (T_1)=2\pi ,\ \psi (0)=0,\ \psi (T_1)=0$. We can write this as a two point boundary value problem with the function g as

$$\begin{aligned} g(c)= & {} \underbrace{\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}_{B_0}\underbrace{\begin{bmatrix}\theta (0)\\ \psi (0) \\ \lambda _1 (0)\\ \lambda _2 (0)\end{bmatrix}}_{c}+\underbrace{\begin{bmatrix}0&0&0&0\\0&0&0&0\\1&0&0&0\\0&1&0&0\end{bmatrix}}_{B_b}\begin{bmatrix}\theta (T_1)\\ \psi (T_1) \\ \lambda _1 (T_1)\\ \lambda _2 (T_1)\end{bmatrix}-\begin{bmatrix}0\\0 \\ 2\pi \\ 0\end{bmatrix},\\\Rightarrow & {} g(c)=\begin{bmatrix}0\\0 \\ \theta (T_1)-2\pi \\ \psi (T_1)-0\end{bmatrix}. \end{aligned}$$

Since $\theta (0)$, and $\psi (0)$ are fixed by our problem, g can be influenced by changing $\lambda _1(0)$ and $\lambda _2(0)$ only. So we get the following matrices for Newton Iteration:

$$\begin{aligned} c^\nu= & {} \begin{bmatrix}\lambda _1 (0)\\ \lambda _2 (0)\end{bmatrix}, \end{aligned}$$

(49)

$$\begin{aligned} g(c^\nu )= & {} \begin{bmatrix}\theta (T_1)-2\pi \\ \psi (T_1)\end{bmatrix}, \end{aligned}$$

(50)

$$\begin{aligned} \left. \frac{\partial g}{\partial c}\right| _{c^\nu }= & {} \begin{bmatrix}\frac{\partial \theta (T_1)}{\partial \lambda _1 (0)}&\frac{\partial \theta (T_1)}{\partial \lambda _2 (0)}\\ \frac{\partial \psi (T_1)}{\partial \lambda _1 (0)}&\frac{\partial \psi (T_1)}{\partial \lambda _2 (0)}\end{bmatrix}. \end{aligned}$$

(51)

In a similar way, we get the following matrices for Euler–Lagrange equations based on standard phase reduction:

$$\begin{aligned} c^\nu= & {} \lambda _1 (0), \end{aligned}$$

(52)

$$\begin{aligned} g(c^\nu )= & {} \theta (T_1)-2\pi , \end{aligned}$$

(53)

$$\begin{aligned} \left. \frac{\partial g}{\partial c}\right| _{c^\nu }= & {} \frac{\partial \theta (T_1)}{\partial \lambda _1 (0)}. \end{aligned}$$

(54)

All the integrations are done with Matlab ODE solver ode45 with relative error tolerance $\le 1e-10$ and absolute error tolerance $\le 1e-10$.

B Models

In this appendix, we give details of the mathematical models used and also their augmented and standard phase reduction models, which are necessary to reproduce the results of this article.

1.1 B.1 YNI model

Here we list the both full and reduced model parameters of the YNI model (Yanagihara et al. 1980) introduced in Sect. 4.2.2.

1.1.1 B.1.1 Full model equations and parameters

The full YNI model is given as

$$\begin{aligned} \dot{V}= & {} \frac{I_{m}-I_{Na}-I_k-I_l-I_s-I_h}{C}+u(t),\\ \dot{d}= & {} \alpha _d(1-d)-\beta _d d,\\ \dot{f}= & {} \alpha _f(1-f)-\beta _f f,\\ \dot{m}= & {} \alpha _m(1-m)-\beta _m m,\\ \dot{h}= & {} \alpha _h(1-h)-\beta _h h,\\ \dot{q}= & {} \alpha _q(1-q)-\beta _q q,\\ \dot{p}= & {} \alpha _p(1-p)-\beta _p p, \end{aligned}$$

where

$$\begin{aligned} \alpha _d= & {} \frac{0.01045(V+35)}{(1-\exp (-(V+35)/2.5))+\frac{0.03125V}{(1-\exp (-V/4.8))}},\\ \beta _d= & {} 0.00421(V-5)/(-1+\exp ((V-5)/2.5)),\\ \alpha _f= & {} 0.000355(V+20)/(-1+\exp ((V+20)/5.633)),\\ \beta _f= & {} 0.000944(V+60)/(1+\exp (-(V+29.5)/4.16)),\\ \alpha _m= & {} (V+37)/(1-\exp (-(V+37)/10)),\\ \beta _m= & {} 40\exp (-0.056(V+62)),\\ \alpha _h= & {} 0.001209(\exp (-(V+20)/6.534)),\\ \beta _h= & {} 1/(1+\exp (-(V+30)/10)),\\ \alpha _q= & {} 0.0000495+\frac{0.00034(V+100)}{(-1+\exp ((V+100)/4.4))},\\ \beta _q= & {} 0.0000845+0.0005(V+40)/(1-\exp (-(V+40)/6)),\\ \alpha _p= & {} 0.0006+0.009/(1+\exp (-(V+3.8)/9.71)),\\ \beta _p= & {} 0.000225(V+40)/(-1+\exp ((V+40)/13.3)),\\ i_s= & {} 12.5(\exp ((V-30)/15)-1),\\ I_s= & {} (0.95d+0.05)(0.95f+0.05)i_s,\\ I_{Na}= & {} 0.5m^3h(V-30),\\ I_h= & {} 0.4q(V+25),\\ I_k= & {} 0.7p(\exp (0.0277(V+90))-1)/\exp (0.0277(V+40)), \end{aligned}$$

$$\begin{aligned} I_l= & {} 0.8(-\exp (-(V+60)/20)+1),\\ C= & {} 1,\\ I_m= & {} 1.0609. \end{aligned}$$

1.1.2 B.1.2 Reduced model equations and parameters

For the augmented and standard phase reduction of the YNI model, we get $\omega =0.03088$, $k=-0.00135$. Once the PRC, IRC, and their derivatives w.r.t. $\theta$ are numerically computed (see “Appendix A”), we approximate them as finite Fourier series to be used as an analytical function in the numerical computation of Euler–Lagrange equations. $\theta =0$ corresponds to the initial condition $V=-19.2803, \ d= 0.6817, \ f=0.0236, \ m=0.8540, \ h=0.0013, \ q=0.0038, \ p= 0.6592$.

1.2 B.2 Thalamic neuron model

Here we list both full and reduced model parameters of the thalamus model (Rubin and Terman 2004) used in Section 4.3.2

1.2.1 B.2.1 Full model equations and parameters

The full thalamic neuron model is given as

$$\begin{aligned} \dot{v}= & {} \frac{-I_L-I_{Na}-I_K-I_T+I_b}{C_m}+u(t),\\ \dot{h}= & {} \frac{h_{\infty }-h}{\tau _h},\\ \dot{r}= & {} \frac{r_{\infty }-r}{\tau _r}, \end{aligned}$$

where

$$\begin{aligned} h_\infty= & {} 1/(1+\exp ((v+41)/4)),\\ r_\infty= & {} 1/(1+\exp ((v+84)/4)),\\ \alpha _h= & {} 0.128\exp (-(v+46)/18),\\ \beta _h= & {} 4/(1+\exp (-(v+23)/5)),\\ \tau _h= & {} 1/(\alpha _h+\beta _h),\\ \tau _r= & {} (28+\exp (-(v+25)/10.5)),\\ m_\infty= & {} 1/(1+\exp (-(v+37)/7)),\\ p_\infty= & {} 1/(1+\exp (-(v+60)/6.2)),\\ I_L= & {} g_L(v-e_L),\\ I_{Na}= & {} g_{Na}({m_\infty }^3)h(v-e_{Na}),\\ I_K= & {} g_K((0.75(1-h))^4)(v-e_K),\\ I_T= & {} g_T(p_\infty ^2)r(v-e_T),\\ C_m= & {} 1,\ g_L = 0.05,\ e_L = -70,\ g_{Na} = 3,\ e_{Na} = 50,\\g_K= & {} 5,\ e_K = -90,\ g_T = 5,\ e_T = 0, \ I_b = 5. \end{aligned}$$

1.2.2 B.2.2 Reduced model equations and parameters

For the augmented and standard phase reduction of the thalamic neuron model, we get $\omega =0.7484$, $k=-0.0225$. Once the PRC, IRC, and their derivatives w.r.t. $\theta$ are numerically computed (see “Appendix A”), we approximate them as finite Fourier series to be used as an analytical function in the numerical computation of Euler–Lagrange equations. $\theta =0$ corresponds to the initial condition $v=-57.5298,\ h=0.1424, \ r= 0.0017$.

1.3 B.3 Clock gene regulation model

Here we list the both full and reduced model parameters of the clock gene regulation model (Gonze et al. 2005) used in Sect. 4.4.2.

1.3.1 Full model equations and parameters

The full thalamus model is given as

$$\begin{aligned} \dot{X}= & {} v_1\frac{K_1^4}{K_1^4+Z^4}-v_2\frac{X}{K_2+X} + L(t),\\ \dot{Y}= & {} k_3X-v_4\frac{Y}{K_4+Y},\\ \dot{Z}= & {} k_5Y-v_6\frac{Z}{K_6+Z},\\ v_1= & {} 0.7,\ v_2 =0.35,\ v_4 = 0.35,\ v_6 = 0.35,\\ K_1= & {} 1,\ K_2 = 1,\ K_6 = 1,\ k_3 = 0.7,\ k_5 = 0.7. \end{aligned}$$

1.3.2 Reduced model equations and parameters

For the augmented and standard phase reduction of the clock gene regulation model, we get $\omega =0.2669$, $k=-0.0021$. Once the PRC, IRC, and their derivatives w.r.t. $\theta$ are numerically computed (see “Appendix A”), we approximate them as finite Fourier series to be used as an analytical function in the numerical computation of Euler–Lagrange equations. $\theta =0$ corresponds to the initial condition $X=0.1948, \ Y=0.4154,\ Z=1.8530$.