1 Introduction

Modern trend in designing carrying structures is facing the design process with complex requirements in terms of functionality, design, construction technology, etc. These features of supporting structures must comply with the required performance, while mass needs to be rationalized to the maximum degree. The performance of carrying structures is inversely proportional to their masses. When increasing the structure’s cross-sectional area, its carrying capacity and mass increase as well. The contradiction between these two parameters is solved by the method of optimization of the cross-sectional structure as discussed in the [1]. The main activity in the design process consists of finding the cross-sectional shape of structural element with the best carrying capacity for the given load conditions. Applying the optimal design method to steel structures has opened great opportunities in the application of thin-walled elements, which are sensitive to specific stress effects and loss of stability. Traditional deterministic optimization approaches are important in the design process, but they are insufficient because in most cases their models are limited and refer only to components of global stresses. In addition to global stresses, structures in actual operating conditions are also exposed to local stresses, as well as to certain modes of buckling.

Given the cumulative effect, the interaction of specific stress types leads to a significant capacity loss, especially when the influence of a single component prevails [2]. Research aimed at studying classical box-girders have shown that the local stress effect takes precedence over the global component, provided that the stability of flanges and webs (plates) of the girder is uncompromised [3]. The majority of research regarding the local stress was conducted on welded I-beams [4–10]. The reference length for analyzing the local effect is the length between two diaphragms [6]. Mathematical formulations of the stress–strain behaviour of girders are important for defining constraints in the optimal design procedure. The local stress phenomenon is closely related to the elastic behaviour of the girder’s compressed plate elements (flanges or webs) [11]. Under the influence of a partial load which can be either fixed (relying on the pillar) or moving (motion of wheels on the rail above the girder), the stress is localized around a relatively narrow girder zone, immediately around the area of action. Resistance of plate elements in thin-walled I-beams under the influence of concentrated load is analyzed in [5, 6]. The dominant stress mode is identified depending on the girder type (open or closed) and the position of the load. This fact is suggested by studying the bearing capacity of the thin-walled I-beam under a partially moving eccentric load [12–24]. Installing longitudinal stiffeners at the upper part of the pressed web of the thin-walled girder positively influences the bearing capacity [15, 16], enabling to reduce the structure’s mass by up to 21 % [17]. Typical forms of longitudinal stiffeners and their effect on the ultimate bearing capacity of longitudinally stiffened I-girders are discussed in [15–18]. The application of sophisticated, FEM-based (finite element method) procedures is an important tool in analyzing the girder’s stress state [19–21], where the dominant position in this respect is that of the ANSYS software [22].

2 Mathematical model

In [3] the problem of local stresses is discussed using the principle of decomposing the girder’s cross-section. The analysis of non-uniform structures, i.e. girders of more complex cross-section (multi-polygonal forms) requires modification of the principles of decomposition. This modification will include changes in the longitudinal direction and changes in loading conditions in the transverse direction of the girder. Therefore, the approach of “moving strip frame” has been developed, and its effect is twofold:

  • Enables analyzing non-uniform girders

  • Enables defining reaction moments as function of the external (active) load.

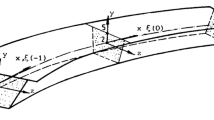
The mathematical model based on the methodology of decomposing the cross-section using the “moving strip frame” approach is considered for the case of a uniform beam with trapezoidal cross-section, and a patch loaded top flange plate (Fig. 1).

Fig. 1
figure 1

The trapezoidal girder segment

Full size image

The mathematical model of local stresses in girders of trapezoidal cross-section is formed on the basis of the following assumptions:

  • The girder segment’s length which is applicable for the analysis is determined in accordance with the recommendations outlined in [3].

  • The girder’s cross-sectional elements are considered as elastically restrained plates.

  • Displacements along the joints of the girder’s elements are negligible compared to their deflection.

  • Effects of plane forces are marginalized in relation to the active load and reaction moments elastic restraint.

  • The compressed girder plates are insensitive to the loss of stability.

Local stresses in the girder of trapezoidal cross-section were analyzed on a segment of length L, while mathematical formulation requires dividing the segment into three parts. The first and third girder segments are not directly exposed to the effects of external load and are symmetrical to the vertical girder axis. The second part is the girder segment which is directly exposed to the active load and its length L 2 equal to the length of the partial load u. Mathematical interpretation of the girder’s deflection and stress state implies that one always should start from the immediately loaded zone of the segment (second part), whereas the influence of the load is manifested on the first and third part through the corresponding boundary conditions.

2.1 Analyzing the behaviour of part 2 of the girder segment

The central girder segment zone is part of the structure through which the load is introduced and its geometrical performance characterizes the behaviour of the entire girder. The top flange plate of the central girder segment zone (part 2) is directly exposed to load effect. Through the moment of elastic restraint, the plate transfers the effect towards the other plates in the cross-section, due to resist any deformation. The mathematical model for local stress in part 2 of the underlying girder segment is formed in two phases. The first phase involves the application of the principle of decomposing the “strip frame” in an arbitrary cross section along part 2 of the girder segment (Fig. 2a). The second phase involves the implementation of solutions obtained by analyzing the “strip frame” for plates of which the box-shaped cross-section was formed.

Fig. 2
figure 2

Trapezoidal cross-section: geometry (a), reactive forces (b) and moments of elastic restraints (c)

Full size image

The term “strip frame” represents the cross-sectional geometry of the girder, the length of which is the same order as the plate thickness. Thus, girder plates in the transverse direction are considered through the model of line elements. This is a simple and exact method of relating the geometric properties of the cross section and the parameters of active and passive loads. In the local stress analysis, reactive compressive forces H i have marginal effect, which is in accordance with the introduced assumptions (Fig. 2b). The development of a partial load q(y) along the transverse direction in part v of the top flange plate is represented by a single trigonometric series of the following form [23]:

$$ q(y) = \frac{{4q_{0} }}{\pi }\sum\limits_{n = 1}^{\infty } \frac{1}{n} \sin \frac{n\pi v}{{2B_{1} }}\sin \frac{n\pi y}{{B_{1} }},\quad q_{0} = \frac{F}{uv} $$
(1)

where F—external load, u·v—surface exposed to the load, B 1—width of the plate no. 1.

Deflection of the line element as a result of the external load q(y) of the top flange plate is determined according to [23, 24], based on the following differential equation:

$$ \frac{{\partial^{4} w_{p} }}{{\partial x^{4} }} + 2\frac{{\partial^{4} w_{p} }}{{\partial x^{2} y^{2} }} + \frac{{\partial^{4} w_{p} }}{{\partial y^{4} }} = \frac{q(y)}{{D_{i} }} $$
(2)

where D i —flexural rigidity of the plates (i = 1, 2, 3, 4).

Deflection of the line element exposed to direct load effect q(y) is obtained by resolving differential Eq. (2) which determines the behaviour of other “strip frame” elements.

Functions of deflection, as well as those of the corresponding inclination for each “strip frame” line element are given in Table 1.

Table 1 Functions of deflection and inclination of the “strip frame” line elements
Full size table

Functions of deflection provided in Table 1 represent particular solutions for w p for deflections of plates of which the girder consists. These functions are intended to present deflections of the line girder in the form of single trigonometric series. The purpose of this procedure is that the particular solution should have the same form as the homogeneous solution for easy integration in the resulting expression for the plate deflection. In Table 1 two types of particular solutions were used: effects of external (active) load q(x, y) and reactive moments of the elastic restraint (passive load), which in the general case are denoted as M i and M i+1.

The active load q(y) = q 0 develops into a single trigonometric series using the following formulation:

$$ q(y) = \frac{2}{{B_{1} }}\sum\limits_{n = 1}^{\infty } {\sin \frac{n\pi y}{{B{}_{1}}}} \int\limits_{{\frac{1}{2}\left( {B_{1} - v} \right)}}^{{\frac{1}{2}\left( {B_{1} + v} \right)}} {q_{0} \sin \frac{n\pi y}{{B_{1} }}dy} = \frac{{4q_{0} }}{\pi }\sum\limits_{n = 1}^{\infty } {\frac{{\sin \left( {n\pi /2} \right)}}{n}} \sin \frac{n\pi v}{{2B_{1} }}\sin \frac{n\pi y}{{B_{1} }} $$
(3)

where q(y) is the partial load that results from the action of the constant-intensity force F on the (u·v) surface of the upper flange plate the width of which is B 1. The purpose of developing a single trigonometric series is to reduce dependence q(y) to a single independent variable y. Substituting (3) in (2) leads the differential Eq. (4) that defines the particular solution w p and it is independent of the variable x.

$$ \frac{{\partial^{4} w_{p} }}{{\partial y^{4} }} = \frac{{4q_{0} }}{{D_{1} \pi }}\sum\limits_{n = 1}^{\infty } {\frac{{\sin \left( {n\pi /2} \right)}}{n}} \sin \frac{n\pi v}{{2B_{1} }}\sin \frac{n\pi y}{{B_{1} }} $$
(4)

The particular solution w p is obtained by solving (4) and physically represents the deflection of line element no. 1 of the observed “strip frame” induced by the force F which has the following form:

$$ w_{p} (q) = w_{1} (q) = \frac{{4q_{0} B_{1}^{4} }}{{D_{1} \pi^{5} }}\sum\limits_{n = 1}^{\infty } {\frac{\sin (n\pi /2)}{{n^{5} }}} \sin \frac{n\pi v}{{2B_{1} }}\sin \frac{n\pi y}{{B_{1} }} $$
(5)

The slope of the elastic line of the no. 1 element represents the first derivative of the function (5) and its shape is given in Table 1.

Reactive moments of the elastic restrain represent the passive load—of intensities of M i and M i+1 in the general case—acting on the element no. 1 and the observed “strip frame.” This load is induced by the external force F and its role is to reduce the deflection of the directly loaded plate by transferring the load to other cross-sectional elements. Defining the particular solution w p (M i , M i+1) based on Eq. (2) is impossible, given that its right side is identically equal to zero when the plate is loaded with moments. Therefore, unlike in the previous case (when force F is acting), the inverse procedure need to be used, which includes defining the single trigonometric series based on the known expression for the elastic line of the ith element as function of variables M i and M i+1.

The function of deflection of the elastic line of the ith element under the effect of moments M i and M i+1 has the following form:

$$ w_{i} (M_{i} ,M_{i + 1} ) = \frac{1}{{6(EI)_{i} }}\frac{y}{{B_{i} }}\left[ {M_{i} \left( {2B_{i}^{2} - 3B_{i} y + y^{2} } \right) +\,M_{i + 1} \left( {B_{i}^{2} - y^{2} } \right)} \right] $$
(6)

Developing (6) into a single trigonometric series, we find the particular solution for deflection of the ith plate of width B i under the action of moments of elastic restraint M i and M i+1 which have the following form:

$$ w_{p} (M_{i} ,M_{i + 1} ) = w_{i} (M_{i} ,M_{i + 1} ) = - \sum\limits_{n = 1}^{\infty } {\frac{{2(M_{i} + M_{i + 1} )B_{i}^{2} }}{{D_{i} \pi^{3} n^{3} }}} \sin \frac{n\pi y}{{B_{i} }} $$
(7)

where B i —width of the ith plate.

The negative sign in (7) indicates that the function of deflection induced by reactive moments M i and M i+1 tends to reduce the deflection induced by the external load. If some of the reactive moment affects the increase of deflection, then the value of that moment should have a negative sign (−). This is the case with the moments M 2 acting on element no. 3 and the moment M 1 acting on elements no. 2 and 4.

Moments of elastic restraint (M 1 and M 2) of the loaded “strip frame” are determined based on the permanent conditions of frame elements in areas of mutual connection (Fig. 2c). These conditions imply that inclinations of each of two adjacent elements in the zone of their connections have the same values and character.

For the case of symmetrically loaded girder or frame as in examples considered, these conditions are defined by analyzing only two points and then the following applies:

$$ {\text{Point A}}: \left. {w_{{_{1} }}^{{\prime }} (q)} \right|_{y = 0} + \left. {w_{1}^{{\prime }} (M_{1} )} \right|_{y = 0} = \left. {w_{2}^{{\prime }} (M_{1} ,M_{2} )} \right|_{{y = B_{2} }} $$
(8)
$$ {\text{Point B}}:\quad \left. {w_{2}^{\prime } (M_{1} ,M_{2} )} \right|_{y = 0} = \left. {w_{3}^{\prime } (M_{2} )} \right|_{{y = B_{3} }} $$
(9)

By substituting the expression for deflection from Table 1 in (8) and (9) the required moment values are stated for the elastic restraints M 1 and M 2, which have the following forms:

$$ M_{1} = k_{1} s $$
(10)
$$ M_{2} = k_{2} s $$
(11)

where k 1 and k 2 are coefficients of elastic restraint at A and B, defined by (12) and (13).

$$ k_{1} = \frac{{0.25\pi^{2} n^{2} \left( {1 + 2\frac{{B_{3} }}{{B_{2} }}\frac{{D_{2} }}{{D_{3} }}} \right)}}{{\frac{{B_{1} }}{{D_{1} }}\left( {1 + 2\frac{{B_{3} }}{{B_{2} }}\frac{{D_{2} }}{{D_{3} }}} \right) + \frac{{B_{3} }}{{D_{3} }}}} $$
(12)
$$ k_{2} = \frac{{0.25\pi^{2} n^{2} }}{{\frac{{B_{1} }}{{D_{1} }}\left( {1 + 2\frac{{B_{3} }}{{B_{2} }}\frac{{D_{2} }}{{D_{3} }}} \right) + \frac{{B_{3} }}{{D_{3} }}}} $$
(13)

s—the absolute value of inclination above the supports of line element which is directly exposed to the load q(y); it is given through (14).

$$ s = \left( {\frac{n\pi }{{B_{1} }}} \right) \cdot a_{n,1} = \frac{{4q_{0} B_{1}^{3} }}{{D_{1} \pi^{4} }}\sum\limits_{n = 1}^{\infty } {\frac{\sin (n\pi /2)}{{n^{4} }}} \sin \frac{n\pi v}{{2B_{1} }} $$
(14)

Moment distributions along the girder plate are given by:

$$ \left. \begin{aligned} M_{1} (x) = (k_{1} s)\sin \frac{{n\pi x}}{{B_{1} }} \hfill \\ M_{2} (x) = (k_{2} s)\sin \frac{{n\pi x}}{{B_{1} }} \hfill \\ \end{aligned} \right\} $$
(15)

The differential equation for the elastic girder plate surface on part 2 is the following:

$$ \frac{{\partial^{4} w_{i} }}{{\partial x^{4} }} + 2\frac{{\partial^{4} w_{i} }}{{\partial x^{2} y^{2} }} + \frac{{\partial^{4} w_{i} }}{{\partial y^{4} }} = \frac{q(y)}{D} $$
(16)

where i represents the number of girder plates (i = 1, 2, 3 and 4).

Particular solutions of the Eq. (16) for individual girder elements (plates) corresponding to the zone of direct loading are equivalent to results obtained by analyzing the “strip frame.”

The homogeneous solution of the differential Eq. (16), according to [23] is:

$$ w_{h,i} = \sum\limits_{n = 1}^{\infty } {\left( \begin{aligned} A_{n,i} \cosh \frac{n\pi y}{{B_{i} }} + B_{n,i} \frac{n\pi y}{{B_{i} }}\sinh \frac{n\pi y}{{B_{i} }} \\ +\,C_{n,i} \sinh \frac{n\pi y}{{B_{i} }} + D_{n,i} \frac{n\pi y}{{B_{i} }}\cosh \frac{n\pi y}{{B_{i} }} \hfill \\ \end{aligned} \right)} \sin \frac{n\pi x}{{B_{i} }} $$
(17)

Functions of the girder plate deflection that apply to part 2 of the discussed segment are given by:

$$ w_{2,i} = w_{p,i} + w_{h,i} = \sum\limits_{n = 1}^{\infty } {\left( \begin{aligned} a_{n,i} + A_{n,i} \cosh \frac{n\pi y}{{B_{i} }} + B_{n,i} \frac{n\pi y}{{B_{i} }}\sinh \frac{n\pi y}{{B_{i} }} \hfill \\ +C_{n,i} \sinh \frac{n\pi y}{{B_{i} }} + D_{n,i} \frac{n\pi y}{{B_{i} }}\cosh \frac{n\pi y}{{B_{i} }} \hfill \\ \end{aligned} \right)} \sin \frac{n\pi x}{{B_{i} }} $$
(18)

where coefficients A n,i , B n,i , C n,i , and D n,i are functions of the n parameter and they are defined through the appropriate boundary conditions. Coefficients a n,i are defined by particular solution of Eq. (2) and they are presented through the deflection function in Table 1. The interaction of adjacent parts of the analyzed girder segment is determined through these conditions. Thus, it is necessary to define the behaviour of parts 1 and 3, which have a direct effect on part 2, as well as the boundary conditions along the contact zone for these girder segments.

2.2 Analyzing the behaviour of parts 1 and 3 of the girder segment

While parts 1 and 3 of the girder segment are not explicitly exposed to the load, the load effect is still transferred to these parts as a result of continuity of geometry and stress in girder plates. The behaviour of plates in unloaded girder segment parts is defined through the following forms of elastic surfaces [23]:

$$ w_{1,i} = \sum\limits_{n = 1}^{\infty } {\left( \begin{aligned} A_{n,i}^{'} \cosh \frac{n\pi y}{{B_{i} }} + B_{n,i}^{'} \frac{n\pi y}{{B_{i} }}\sinh \frac{n\pi y}{{B_{i} }} + \hfill \\ C_{n,i}^{'} \sinh \frac{n\pi y}{{B_{i} }} + D_{n,i}^{'} \frac{n\pi y}{{B_{i} }}\cosh \frac{n\pi y}{{B_{i} }} \hfill \\ \end{aligned} \right)} \sin \frac{n\pi x}{{B_{i} }} $$
(19)

and

$$ w_{3,i} = \sum\limits_{n = 1}^{\infty } {\left( \begin{aligned} A_{n,i}^{''} \cosh \frac{n\pi y}{{B_{i} }} + B_{n,i}^{''} \frac{n\pi y}{{B_{i} }}\sinh \frac{n\pi y}{{B_{i} }} \\+ \hfill C_{n,i}^{''} \sinh \frac{n\pi y}{{B_{i} }} + D_{n,i}^{''} \frac{n\pi y}{{B_{i} }}\cosh \frac{n\pi y}{{B_{i} }} \hfill \\ \end{aligned} \right)} \sin \frac{n\pi x}{{B_{i} }} $$
(20)

Boundary conditions in the contact zone of part 1 and 2 are formulated as follows:

$$ \left. \begin{aligned}& 1)\quad w_{1,i} = w_{2,i} \hfill \\ &2)\quad \frac{{\partial w_{1,i} }}{\partial x} = \frac{{\partial w_{2,i} }}{\partial x} \hfill \\ &3)\quad \frac{{\partial^{2} w_{1,i} }}{{\partial x^{2} }} = \frac{{\partial^{2} w_{2,i} }}{{\partial x^{2} }} \hfill \\ & 4)\quad \frac{{\partial^{3} w_{1,i} }}{{\partial x^{3} }} = \frac{{\partial^{3} w_{2,i} }}{{\partial x^{3} }} \hfill \\ \end{aligned} \right\}\quad {\text{for x}} = \, - \, u/2, $$
(21)

While supporting conditions at plate ends of part 1 are given by:

$$ \left. \begin{aligned} 5)\quad w_{1,i} = 0 \hfill \\ 6)\quad \frac{{\partial^{2} w_{1,i} }}{{\partial x^{2} }} = 0 \hfill \\ \end{aligned} \right\}\quad {\text{for x}} = \, - \, L/2 $$
(22)

The first two boundary conditions of the system (21) represent the geometric continuity (deflection and inclination), while the remaining two conditions define the continuity of acting forces (transverse force and bending moment) of plates in the zone connecting parts 1 and 2. Conditions 3 and 4 of the system (21) are valid for the case when the correspondent plate parts 1 and 2 are of the same thickness and when the connective line of these two is without concentrated loads (forces or moments). Conditions for supporting the plates on their ends is defined through the system (22), which corresponds to the properties of simply supporting (the support is stable, but the plate can rotate around it).

Conditions (22) are verified through experimental and numerical results [3] and they are reliable for local stress analysis. When substituting (18) and (19) into (21) and (22) for four girder plates, the required coefficients are determined, which are given through the following functions:

$$ \left. \begin{aligned} a_{n,1} & = \frac{{4q_{0} B_{1}^{4} }}{{D_{1} \pi^{5} }}\sum\limits_{n = 1}^{\infty } {\frac{\sin (n\pi /2)}{{n^{5} }}} \sin \frac{n\pi v}{{2B_{1} }} \\ A_{n,i} & = - \frac{{a_{n,i} }}{{\cosh \alpha_{n,i} }}\left[ {\cosh (\alpha_{n,i} - 2\beta_{n,i} ) +\,\beta_{n,i} \sinh (\alpha_{n,i} - 2\beta_{n,i} ) + \alpha_{n,i} \frac{{\sinh 2\beta_{n,i} }}{{2\cosh \alpha_{n,i} }}} \right] \\ B_{n,i} & = \frac{{a_{n,i} }}{{2\cosh \alpha_{n,i} }}\cosh (\alpha_{n,i} - 2\beta_{n,i} ) \\ B_{n,i}^{{\prime }} & = - \frac{1}{2}\left( {tgh\alpha_{n,i} \sinh 2\beta_{n,i} } \right) \cdot a_{n,i} \\ C_{n,i}^{{\prime }} & = \left( {\beta_{n,i} \cosh 2\beta_{n,i} - \sinh 2\beta_{n,i} } \right) \cdot a_{n,i} \\ D_{n,i}^{{\prime }} & = \frac{1}{2}\left( {\sinh 2\beta_{n,i} } \right) \cdot a_{n,i} \\ \end{aligned} \right\} $$
(23)

where: \( \alpha_{n,i} = \frac{{n\pi B_{i} }}{2L} \) and \( \beta_{n,i} = \frac{n\pi v}{4L} \)

Given the fact that the load is symmetrically distributed along the vertical girder axis, the contour conditions between parts 2 and 3 are analogous to systems (21) and (22); thus, the plate deflection function in part 3, which is given by (19), is symmetric to (20).

The intensity of von Mises stress is defined as:

$$ \sigma_{e,local} = \sqrt {\sigma_{x,l}^{2} + \sigma_{y,l}^{2} - \sigma_{x,l} \sigma_{y,l} + 3\tau_{xy,l}^{2} } $$
(24)

where

$$ \sigma_{x,local} = \frac{{6 \cdot M_{x} }}{{\delta_{i}^{2} }} = - \frac{{6D_{i} }}{{\delta_{i}^{2} }}\left( {\frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} + \upsilon \frac{{\partial^{2} w_{i} }}{{\partial y^{2} }}} \right) $$
(25)
$$ \sigma_{y,local} = \frac{{6 \cdot M_{y} }}{{\delta_{i}^{2} }} = - \frac{{6D_{i} }}{{\delta_{i}^{2} }}\left( {\frac{{\partial^{2} w_{i} }}{{\partial y^{2} }} + \upsilon \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}} \right) $$
(26)
$$ \tau_{xy,local} = \left( {\frac{{6 \cdot M_{xy} }}{{\delta_{i}^{2} }}} \right) = \frac{{6D_{i} (1 - \nu )}}{{\delta_{i}^{2} }}\left( {\frac{{\partial^{2} w_{i} }}{\partial x\partial y}} \right) $$
(27)

ν—Poisson’s ratio (=0.3 for steel), δ i —thickness of plates.

The tension due to the girder’s global stress is determined through (23).

$$ \sigma_{x,global} = \frac{FHl}{8I} $$
(28)

where: l is the actual girder length, H is the girder height, and I is the axial moment of the cross-sectional surface area.

The resulting stress state is given through the equivalent stress (29):

$$ \sigma_{e,total} = \sqrt {\left( {\sigma_{x,g} + \sigma_{x,l} } \right)^{2} + \sigma_{y,l}^{2} - \left( {\sigma_{x,g} + \sigma_{x,l} } \right)\sigma_{y,l} + 3\tau_{xy,l}^{2} } $$
(29)

The function of equivalent stress and that of the corresponding local stress components are provided in a diagram in Sect. 5.

Practical implications of the proposed model are characterized by the following three aspects: (1) identifying the local stress state of girders derived, (2) optimum design of the girder in order to balance local and global stress, and (3) identifying local stresses based on the function of plate deflection, which significantly reduces the measurement and the overall costs of the experiment. All three segments are contained in the present work, and the model developed can be used for box girders both with and without diaphragms. This method is particularly important for stress state analysis in carriers exposed to moving loads, such as truck-crane booms, main crane girders and the like. For functional reasons, some of the supporting structures cannot contain diaphragms, as in the case of a truck-crane boom, because its sections are meant to be pulled inside of each other. Due to the absence of diaphragms, the local stress effect in these carriers is very strong and makes the major cause of plastic deformation or damage. In this case, the intensity of local stress changes depending on the position of the load, regardless of the constant cross-section along the entire length. The developed model allows for application in girders with plates of stepwise variable thickness. This approach is important when the required stiffening cannot be achieved by using diaphragms; a typical example of this is the flange portion of the mobile crane boom segments. Likewise, most girders allow the use of the diaphragms; then, the length of the sample authoritative for the analysis of local stress corresponds to their spacing.

3 Analyzing the girder segment using the FEM procedure

In this chapter, the finite element method (FEM) is used to simulate the behaviour of the trapezoidal box girder segment, applicable to local stress analysis. The FEM analysis procedure was conducted using the Static Structural module of the ANSYS software [22]. The FEM approach is completely independent of mathematical model on which the analytical procedure is based, enabling comparative analysis of their results. Ends of the girder segments are simply supported, while the cross-section and the parameters of partial load correspond to the conditions defined in the mathematical model. Three-dimensional elements known as Solid 10node 187 were applied for generating finite elements meshes in accordance with the nomenclature of the library in the ANSYS software [22]. FEM simulation involves the analysis of two cases due to better identification of parameters that dominantly affect local carrying capacity of girder. The first case (alternative A) refers to the alternative when the 8 mm thick upper flange is directly exposed to the effects of load of 15 kN. The alternative B refers to the position of the girder which is rotated 180° relative to the first case (cross-sectional dimensions are identical in both cases). Thus, the thickness of the top flange plate is 4 mm, while the load has value 3 kN. The deflection and equivalent stress for the position of the girder that corresponds with alternatives A and B is shown in Figs. 3 and 4.

Fig. 3
figure 3

Overall girder deflection: alternative A (left) and alternative B (right)

Full size image
Fig. 4
figure 4

Equivalent stress of the girder: alternative A (left) and alternative B (right)

Full size image

The load corresponding to the variant A is five times higher than to the variant B, while the equivalent (von Mises) stress is identical in both cases. Under these conditions, the deflection corresponding to the variant A is 5.8 times smaller in regards to variant B. When comparing alternatives A and B it can be concluded that greater width and smaller thickness of flange which is directly exposed to the load have an adverse effect on the local stress state, i.e. carrying capacity of girder. Conditions of global carrying capacity, i.e. the cross-sectional geometric parameters, are exactly identical for both alternatives. This clearly indicates that the orientation of the cross section has a key role in the overall carrying capacity of the structure’s supporting elements.

Convergence results of FEM model (deflection and equivalent stress) implies a numerical approaching to exact values, starting from the previously obtained solutions. Convergence of solutions with FEM model is evaluated on the basis of finite elements mesh and the value of the results obtained. Proof of convergence is carried out by forming successive finite element meshes of different sizes. The degree of convergence defines the dependence of the number of finite elements from the accuracy of solution. Convergence of deflection and equivalent (von Mises) stress of the considered FEM models (Figs. 3, 4) is graphically illustrated via the diagrams, which are shown in Fig. 5. It can be concluded that for the adopted finite element size of 8 mm deviation from the true value is <2 %. This is an indication of the validity of the type and size of the finite elements.

Fig. 5
figure 5

Convergence solutions of the considered FEM models

Full size image

Verification of the FEM model for the analysis of the local stress state is carried out by experimental tests, which is important for identifying the influential parameters of carrying capacity.

4 Experimental analysis

Analytical and FEM procedure-based models are verified through experimental analysis. Tests were carried out on a carrier segment for two opposed positions of the cross-section (alternatives A and B), according to Fig. 6. Characteristics of the girder in terms of cross-sectional geometry, load and support are identical to those involved in the mathematical and the FEM model. In the present study, experimental testing is conducted in the domain of elastic material behaviour and the primary goal is to verify the presented method, which is based on the mathematical model discussed in Sect. 2.

Fig. 6
figure 6

Configuration of measurement points: a alternative A and b alternative B

Full size image

4.1 The test program

The program of experimental testing involves defining all characteristics of the sample, test device, organization procedure and data processing. The primary experimental parameters are related to the qualitative and quantitative characteristics of the cross-section, the loading surface area and its position relative to the girder. The relevant test requirements and procedure are given in this chapter.

4.1.1 The test subject

The test sample is a 1016 mm long trapezoidal box girder segment. The girder is formed by CO2 welding of 4, 5 and 8 mm plates in a longitudinal continuous manner, while sides of the boxes were closed by welding two, 8 mm thick diaphragms. Before welding, the box girder’s flange plates and webs were rolled to eliminate the initial geometric imperfections and calibrate them to the exact dimensions. Plates were made of structural steel S235JRG2, according to EN 10025.

4.1.2 Preparation of the test sample and the device

Immediately prior to the experiment it is necessary to carry out a range of activities related to the test sample and device. The sample’s bottom flange should entirely rely on cylindrical supports of the device in order to prevent the girder from bending and unpredictable dislocations. The girder’s measuring points along the line where extreme displacements are expected should be marked. The test device is a mechanical machine in which the load is introduced by simultaneously moving the top and bottom traverse. The central traverse is fixed and enables directing the load-inducing head. In order to remove residual stresses, at the beginning of the test the sample is exposed in several cycles to loads equal to ≈75 % of stress which corresponds to the elastic limit.

4.1.3 Organizing the test

The experimental tests were conducted on a general-purpose mechanical press, which is capable of simulating the maximum load of 400 kN. The test sample was mounted on a rotating base with roller-shaped supports, providing thereby the possibility to freely support the girder. The load was introduced manually through the control board. This board has the opportunity of working in two modes, which provides higher precision: the first is related to the range up to 40 kN (which was used in this study), whereas the second is related to the range of 40–400 kN. The relative deflection of plates is measured which allowed interpretation of local behaviour of carriers. Reading the achieved load is done via an analogous scale, while deflection is registered using a dial gauge.

4.1.4 Conducting the test

The procedure of testing the local stress was realized in two diametrically opposite position of the same girder. The top flange plate is loaded by applying directly the load-inducing head with the dimension 100 × 50 mm in its base. The load is registered through a measure cell located under the rotating base, on the mechanical scale of the control board. Relative deflections of girder plates are measured and identified using a mechanical dial gauge of 0.01 mm accuracy (Fig. 7). At the beginning and the end of each measurement the dial gauge displays zero value, which is a prerequisite for deflection measurement to be adequately realized, without any plastic deformation or unexpected dislocation.

Fig. 7
figure 7

Characteristic positions for testing the girder: alternative A (left) and alternative B (right)

Full size image

4.1.5 Results of the experimental analysis

Results of experimental tests are classified into two groups: direct and indirect. Direct test results are related to explicitly measured plate deflection values with the use of a measuring device, i.e. a dial gauge (Fig. 8). Relative deflection was measured at predefined points of the four girder plates. At each measuring point, the measurement is repeated 3 times, while the final value was determined as the geometric mean. Indirect results were obtained based on the direct results using specific calculation procedure. These results represent equivalent (von Mises) stresses. The detailed procedure based on which the stress values can be obtained, as well as the verification of the procedure are outlined in Sect. 4.2.

Fig. 8
figure 8

Measuring the deflection of the top flange plate of the girder for alternative A: left—point 13 (0.15 mm), centre: point 14 (0.08 mm) and right: point 15 (0.05 mm)

Full size image

4.2 Implicit stress state determination

Using the method of direct measurement, the relative deflections of girder plates are explicitly defined (Sect. 4.1.5). However, due to identify the phenomenon of local stress, it is necessary to define the values of equivalent stresses, in addition to deflection. This study is focused on the experimental–theoretical approach to analyzing the local stress which includes the following activities:

  • Direct measurement of deflection of girder plates.

  • Calculating the stress based on the measured deflection values.

The basic idea behind this approach is in the fact that defining the stress state of plates to the full extent also requires sufficient knowledge about the function of deflection [23, 24]. It is necessary to experimentally define the discontinuous deflection values, which can be further transformed into appropriate functional dependence using the extrapolation procedure. A convenient function for the extrapolation procedure for the ith plate is the following:

$$ w_{i} = \left( {A_{i} \cosh \frac{\pi x}{{B_{i} }} + B_{i} \frac{\pi x}{{B_{i} }}\sinh \frac{\pi x}{{B_{i} }}} \right)\sin \frac{\pi y}{{B_{i} }} $$
(30)

where A i and B i are coefficients determined from extrapolation conditions (the method of least squares).

Defining the patterns in which deflections are distributed is the basis for calculating the components and equivalent stress according to Eqs. (18–21). The proposed approach is verified in accordance with the experimentally obtained deflection values and equivalent stress in girder plates of rectangular cross section presented in [3]. In addition, the extrapolated deflection function is also necessary to identify the values of deflection under the loaded surface, which cannot be explicitly registered using a measuring device. This is of high practical importance when measuring the deflection of actual girders. In research [3], this problem is resolved by making openings on the girder, which is acceptable for experimental samples, but not for members of actual supporting structures. Deflection values determined in this way are shown as red rectangles in Fig. 9. The discussed experimental–theoretical approach to defining the girder’s stress state also has its practical importance because it allows identification of stress state implicitly on the basis of experimentally obtained deflection values, without using measuring tapes, auxiliary devices and without processing measurement signals. Thus, it is possible to identify stresses at close distance (a few millimetres), and this method greatly speeds up the process and reduces the cost of experimental testing.

Fig. 9
figure 9

Comparative diagram of deflection w 1 of plate “1” (longitudinal and transverse direction)

Full size image

5 Comparative analysis

This chapter is focused on comparative analysis of the analytical–theoretical, numerical and experimental procedures regarding the identification of local stresses in box girders. Results based on a methodological approach obtained through the mathematical model (Sect. 2) and finite element model formed in ANSYS software [22] (Sect. 3) are compared with the experimentally obtained values in terms of their verification. Distribution functions of deflections of plate “1” of a trapezoidal girder are shown in Fig. 9.

Functions of dominant stresses in components σ x and σ y of top flange plates are shown in Fig. 10. As a dimension, the shearing component τ xy is of lower order and its influence is negligible compared to normal stresses σ x and σ y . All presented diagrams are related to the position of girder corresponding to alternative A.

Fig. 10
figure 10

Comparative diagram of stress σ x and σ y of plate “1”

Full size image

6 Conclusion

The previous chapters of this study have identified the influential parameters of carrying capacity from the aspects of loading a trapezoidal box girder with global and local stress. The presented methodology for defining the local stress state of the trapezoidal girder is based on the principle of decomposing the cross-sectional elements and it is obtained by modifying the model presented in [3]. The importance of the above approach is of both theoretical and practical nature as it enables straightforward implementation on elements of carrying structures of more complex geometric shapes. Irrespective of the derived mathematical model, the relative deflection and the stress state of girder plates were also analyzed using the finite element method and the ANSYS software [22]. The analytical methodology (theoretical approach) and the finite element model were verified by experimental analysis. The test was carried out for two diametrically opposite positions of the same sample of trapezoidal cross-section. Dimensions obtained by experimental measurements refer to relative girder plate displacements, i.e. deflections. By combining the experimental results and theoretical approaches, the new methodology for local stress analysis of the trapezoidal box girders has been developed. In this implicit way, the girder’s stress image has been quantitatively and qualitatively defined, without the need for explicit measurements, which significantly simplifies the testing process and reduces its costs. The presented experimental/theoretical stress-determining approach has been verified through the experiment presented in [3]. The presented mathematical model is intended to identify the stress state of the quadrilateral box girder (rectangular and trapezoidal cross-section). The model is explicit in its form and enables to define displacements and local stresses of each plate for the given input parameters (geometry and load) in a simple way (without iterations). The mathematical model is based on the classical plate bending theory that takes into account the first-order shear stresses. Reliability of the proposed mathematical model is evaluated against the FEM approach and verified experimentally for two load cases (variants A and B). The published mathematical model is a useful engineering tool, specifically when designing new support structures and reconstructing the existing ones, given that it considers local stresses in interaction with the global load. The methodology presented in this paper provides a wide range of application in carriers of complex shape using the identical procedure and identical expressions that was presented in the paper. Thus, more complex cross-sections which consist of more than four plates e.g. hexagonal cross-sections can be analyzed. The main difference in that case is that a larger number of continuity conditions (8) and (9) are needed that should match the number plates for asymmetric load (if the load is symmetrical, the number of conditions is twice as small). This fact makes the basis for further studies in the field of local stresses in carriers, especially in cases of deformable longitudinal stiffeners. Especially important segment of future research from the aspect of rationality of the introduced mathematical model is its application in the process of cross-section optimization. The entire procedure of the proposed model is easy to develop as simple software with the purpose of automating and simplifying the work in engineering practice.