1 Introduction

Along with the rapid advance of science and technology, resonators have been widely utilized in engineering applications, especially in the micro/nanoelectromechanical systems (MEMS/NEMS), as sensors, actuators, frequency-filters, logic switches, energy collectors, and so on. Mechanical models of the most of resonators can be simplified as micro/nanoscale beams or plates. In order to design high performance MEMS, it needs to minimize the energy dissipation, or to get higher quality factor of the resonators. However, there exist inevitably various energy dissipation mechanisms in the resonators. Generally, the energy lost in the resonators is produced by two kinds of source, the external energy dissipation and the intrinsic energy dissipation. The external energy dissipation arising from the air damping and support damping can be minimized or eliminated through reasonable structural design and manufacturing process. However, the internal energy dissipation, such as the thermoelastic damping (TED) [1,2,3,4], is an energy dissipation mechanism of the system due to the thermoelastic coupling between the thermal field and the strain field in the vibrating solid structures. In the sense of the two-way coupled thermoelastic dynamics, TED originates from the irreversible heat flux flowing from the compressed parts with higher temperature to the stretched parts with lower temperature in vibrating microscale structures, like resonators with a positive thermal expansion coefficient [4]. Unfortunately, it has been consistently observed that the TED in the resonator will increase significantly with the decrease in the size and will not be eliminated by improving the external conditions [5]. So, TED is the dominant internal energy dissipation mechanism in the MEMS/NEMS. Therefore, to effectively and accurately estimate and evaluate TED in the resonators is of great importance in the design of high-quality resonators.

Zener [2, 3] firstly studied the TED in a thin microbeam with flexural vibration based on the one-way coupled heat conduction theory and Euler–Bernoulli beam theory. He developed an approximate analytical expression for TED in a thin rectangular cross-sectional metallic beam, which is known as Zener’s formula. Lifshitz and Roukes (L–R) [4] improved upon Zener’s work and developed exact and closed-form expressions for TED and frequency shift in the rectangular cross-sectional microbeams using the quasi-1-D heat conduction theory. Afterward, basis on Zener and L–R’s work, the quasi-1-D models are also used to estimate TED in micro-plate resonators. Nayfeh and Younis [5], Sun et al. [6, 7], Ali and Mohammadi [8] derived analytical solutions in the L–R’s form for the TED in plate resonators based on one-way coupled quasi-1-D heat conduction equation and classical plate theory. Salajeghe et al. [9] considered geometric nonlinearity effect on the quality factor of microcircular plate in the sense of von Karman’s plate theory. The numerical results quantitatively showed the effects of nonlinear deformation on the TED. Li et al. [10] carried out investigation on TED in fully clamped circular and rectangular plate resonators and derived the inverse quality factor in L–R’s analytical form by using the energy approach.

In order to improve the accuracy in evaluating the TED of micro- plate resonators, some authors used 2-D, even 3-D heat conduction theories in the solution of the temperature filed [11,12,13,14,15,16,17]. Based on fully coupled thermoelastic equations, Yi solved the complex eigenvalue problem related to TED of microcircular and elliptical plates under going in-plane vibrations [11] by using finite element method (FEM). By considering the temperature field changing simultaneously in the radial, circumferential and thickness directions, Pei [12] investigated the TED of a rotating flexible micro-annular plate in the flexural vibration by a semi-analytical approach. Adopting a 2-D and 3-D heat conduction theories, Fang et al. derived analytical solutions of TED in the axisymmetric vibration of circular plate resonators [13] and rectangular micro-plates [14].

All the above investigations on the TED are related to the resonators made of isotropic and homogenous materials. By considering stepwise inhomogeneity of material properties along the thickness direction, TED in laminated composite micro-plates was studied in the literature of [15,16,17,18,19,20,21,22], where the micro-plates were assumed to be composed by several isotropic and homogeneous layers with different material properties. Among them, as an excellent pioneering work on TED in the laminated composite microstructures was carried out by Bishop and Kinra [15, 16]. They extended Zener’s work to N-layer composite structures with thermally imperfect interfaces based on thermoelastic dynamics [15]. By using the thermal energy approach, Vengallatore obtained the TED in a symmetric three-layer laminated rectangular plate with thermally perfect interfaces [17]. Sun et al. [18] performed an analytical investigation on the TED in a symmetric three-layer microcircular plate. Furthermore, Liu et al. [19] carried out a theoretical analysis of thermoelastic damping in bilayered circular plate resonators with two-dimensional heat conduction. More recently, Zuo et al. [20] and Wang et al. [21] studied TED in a trilayered rectangular micro-plate with 1-D heat conduction and a bilayered rectangular micro-plate with 3-D heat conduction employing the thermal energy approach, where the physical neutral surface was introduced to delete the stretching-bending coupling. However, in the deriving of the physical neutral surface, the thermal membrane force which is produced from the asymmetric distribution of the material properties about the geometrically neutral surface is ignored.

Comparing the traditional laminated composite micro-plates, functionally graded material (FGM) microbeams and plates with tailored, or in advance designed continuous variation of the material properties in the thickness direction have the advantage of the material properties over the individual constituents and can satisfy many specific demands in different engineering applications. Moreover, in the micro/nanoengineering fields, FGM micro/nanobeam/plate structures have been found applications in the MEMS/NEMS [22,23,24,25,26,27,28,29,30,31,32,33,34]. As a result, studies on the static and dynamic responses of FGM microstructures have attracted extensive attentions of the researchers. In those investigations, free vibration of FGM microbeams [22, 23], circular and annular plates [24,25,26], and rectangular plates [27,28,29] were analyzed based on different plate theories by considering the size-dependent effect using the modified couple stress theory.

However, it can be found that in those investigations on the free vibration response of the microstructures, only a few contributions are focused on the effect of the thermoelastic coupling deformation on the vibration response of the microstructures [30,31,32,33,34]. Among these, Azizi et al. [30] investigated TED in a clamped-clamped FGM piezoelectric microbeam with the constituents of silicon and piezoelectric materials. They examined the effects of the volume fraction of the piezoelectric constituent, geometry and ambient temperature on the TED. Zhong et al. [31] performed an analytical study on the TED in a clamped FGM Euler–Bernoulli microbeam with material properties varying as exponential law through the thickness. However, in the mathematical modeling, they also ignored the stretching–bending coupling which should be considered when the material properties are asymmetric about the geometrical middle surface. Emami and Alibeigloo [32] present an analytical solution of TED in a simply supported FGM microbeam based on the one-way coupled heat conduction equation and Timoshenko beam theory. By expanding the variable coefficients and the temperature rise field in the forms of the Taylor series, the heat conduction equation with variable coefficients is solved analytically for temperature increment. By using the same approach to deal with the heat conduction equation, the authors [33] carried out a study on the TED in a simply supported rectangular FGM micro-plate based on the first-order shear deformation theory and the modified strain gradient theory. Recently, Li et al. performed theoretical analyses of TED in the vibrating FGM microbeams [34] and microcircular plates [35] with the mechanical and thermal properties continuous varying along the beam depth and plate thickness under different boundary conditions. A layer-wise homogenization approach was first developed and effectively used to solve the heat conduction equation with variable coefficients for arbitrary material gradient functions.

From the above review of the existing investigations on the TED of micro-plates we know that the most of the studies are related to homogenous or laminated microresonators. Only very a few papers referred to the non-homogenous micro-plates resonators with material properties varying continuously in the thickness directions. Comparing with the homogenous plate resonators, the coefficients of heat conduction equation for the FGM micro-plate resonators are variable, or functions of the thickness coordinate. Moreover, due to the distribution of material properties to be asymmetric about the geometrically neutral surface, there exists stretching–bending coupling in the thermal-elastic vibration. So, analysis on TED FGM micro-plates with arbitrary material gradient in the thickness direction and subjected to different boundary constraints is still the open research topic to be examined.

In the current research, we will carry out a theoretical analysis of TED in FGM micro-plates on the basis of the previous work [35]. Firstly, by using the one-way coupled thermoelastic dynamics and Kirchhoff’s plate theory, one-way coupled dynamic equations governing the free vibration and the heat conduction of the FGM micro-plates will be established by accurately considering the effects of stretching–bending coupling. Then, the resulted quasi-1-D heat conduction equation with variable coefficients will be approximately solved by using the layer-wise homogenization approach developed by the authors [35]. Furthermore, analytical expression for TED in FGM plates defined by the inverse quality factor is derived by using the complex frequency approach. We will show mathematically that the theory, the methodology and the solution presented will be suitable for evaluating the TED of thin FGM micro-plates with arbitrary through-thickness material gradient, geometry and boundary conditions. Finally, by specifying the material properties varying as power-law functions, numerical results of the TED in FGM rectangular plates are presented to show the validity of theory and methodology. Effects of the material gradient index, plate thickness, the aspect ratio, the vibration modes and boundary conditions on the TED and on the through thickness distribution of the temperature will be analyzed quantitatively. In addition, the temperature distribution along the plate thickness will be firstly illustrated for different material gradient profiles.

2 Mathematical formulation of the problem

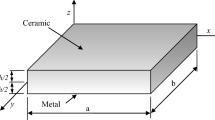
For the convenience of mathematical derivation, we consider a thin FGM micro rectangular plate with length a, width b and depth h. Cartesian coordinate system (x, y, z) is taken, as shown in Fig. 1, to describe the free vibration of the plate with TED. The \(x-y\) plane is located in the geometrically mid-surface of the plate, and the z-axis is normal to the mid-surface and in the thickness direction. Therefore, \(z=h/2\) and \(z=-\,h/2\) define the top and the bottom surface of the plate, respectively. It is assumed that the plate is made of two different homogenous material components with their volume fractions varying continuously in the thickness direction as arbitrary continuous functions. As a result, all the effective mechanical and thermal material properties are continuous functions of coordinate, z.

Fig. 1
figure 1

Geometry and coordinates of a functionally graded micro-plate

Full size image

2.1 Equations of motion

Herein, we consider the thin micro-plate with small vibration. So, the Kirchhoff’s plate theory is used to establish the governing equations of the FGM micro-plate in free vibration with TED. Based on this plate theory, considering the in-plane stretching, displacement field of the FGM micro-plates is given by [36,37,38]

$$\begin{aligned} u(x,y,z,t)= & {} u_{0} (x,y,t)-z\frac{\partial w_{0} }{\partial x} \end{aligned}$$
(1a)
$$\begin{aligned} v(x,y,z,t)= & {} v_{0} (x,y,t)-z\frac{\partial w_{0} }{\partial y} \end{aligned}$$
(1b)
$$\begin{aligned} w(x,y,z,t)= & {} w_{0} (x,y,t) \end{aligned}$$
(1c)

where t is time; u , v, and w are the components of the displacement in x, y, and z, directions, respectively; \(u_{0} \), \(v_{0} \) and \(w_{0} \)are the components at the points of geometrically middle surface, which are produced by the stretching–bending coupling deformation due to the asymmetric variation of the material properties in the thickness direction. If the plate is homogenous, or if it is functionally graded but the variation of the material properties is symmetrical about the geometrical middle surface, it gives \(u_{0} =v_{0} =0\).

By using the linear strain-displacement relations and the Hooke’s law [36], we can arrive at the following relations of the resultant membrane forces and the bending moments

$$\begin{aligned} \left( {\begin{array}{l} N_{x} \\ N_{y} \\ N_{xy} \\ \end{array}} \right) =\left[ {\begin{array}{l} A_{11} \;\;A_{12} \;\;0\;\;\; \\ A_{12} \;\;A_{11} \;\;0\;\;\; \\ \;0\;\;\;\;\,0\;\;A_{33} \;\,\; \\ \end{array}} \right] \left( {\begin{array}{l} \varepsilon _{x}^{0} \\ \varepsilon _{y}^{0} \\ \gamma _{xy}^{0} \\ \end{array}} \right) +\left[ {\begin{array}{l} B_{11} \;\;B_{12} \;\;\;\,0 \\ B_{12} \;\;B_{11} \;\;\;0 \\ \;0\;\;\;\;\,0\;\;\,\,\,B_{33} \; \\ \end{array}} \right] \left( {\begin{array}{l} \kappa _{x} \\ \kappa _{y} \\ \kappa _{xy} \\ \end{array}} \right) -\left( {\begin{array}{l} N_{T} \\ N_{T} \\ \;0 \\ \end{array}} \right) \end{aligned}$$
(2)
$$\begin{aligned} \left( {\begin{array}{l} M_{x} \\ M_{y} \\ M_{xy} \\ \end{array}} \right) =\left[ {\begin{array}{l} B_{11} \;\;B_{12} \;\;0 \\ B_{12} \;\;B_{11} \;\;0\;\,\, \\ \,0\;\;\;\;\,0\;\;B_{33} \\ \end{array}} \right] \left( {\begin{array}{l} \varepsilon _{x}^{0} \\ \varepsilon _{y}^{0} \\ \gamma _{xy}^{0} \\ \end{array}} \right) +\left[ {\begin{array}{l} \,D_{11} \;\;D_{12} \;\,0 \\ \,D_{12} \;\;D_{11} \;\;0 \\ \,\,\;0\;\;\;\,0\;\;\,\,D_{33} \\ \end{array}} \right] \left( {\begin{array}{l} \kappa _{x} \\ \kappa _{y} \\ \kappa _{xy} \\ \end{array}} \right) -\left( {\begin{array}{l} M_{T} \\ M_{T} \\ \;0 \\ \end{array}} \right) \end{aligned}$$
(3)

where\((\varepsilon _{x}^{0} ,\varepsilon _{y}^{0} ,\gamma _{xy}^{0} )\) and \((\kappa _{x} ,\kappa _{y} ,\kappa _{xy} )\)are the in-plane strain and curvature components respectively, given by

$$\begin{aligned} (\varepsilon _{x}^{0} ,\varepsilon _{y}^{0} ,\gamma _{xy}^{0} )= & {} \left( {\frac{\partial u_{0} }{\partial x},\frac{\partial v_{0} }{\partial y},\frac{\partial v_{0} }{\partial x}+\frac{\partial u_{0} }{\partial y}} \right) \end{aligned}$$
(4a)
$$\begin{aligned} (\kappa _{x} ,\kappa _{y} ,\kappa _{xy} )= & {} \left( {-\,\frac{\partial ^{2}w_{0} }{\partial x^{2}},-\frac{\partial ^{2}w_{0} }{\partial y^{2}},-2\frac{\partial ^{2}w_{0} }{\partial x\partial y}} \right) \end{aligned}$$
(4b)

The resultant membrane forces and the bending moments in Eqs. (2) and (3) are defined by

$$\begin{aligned}&(N_{x} ,N_{y} ,N_{xy} )=\int _{-h/2}^{h/2} {(\sigma _{x} \text{, }\sigma _{y} \text{, }\tau _{xy} )\text{ d }z} \end{aligned}$$
(5a)
$$\begin{aligned}&(M_{x} ,M_{y} ,M_{xy} )=\int _{-h/2}^{h/2} {(\sigma _{x} \text{, }\sigma _{y} \text{, }\tau _{xy} )z\text{ d }z} \end{aligned}$$
(5b)
$$\begin{aligned}&(N_{T} ,M_{T} )=\int _{-h/2}^{h/2} {\frac{\alpha (z)E(z)H}{1-\mu }(1\text{, }\,z)\text{ d }z} \end{aligned}$$
(5c)

where \(\sigma _{x} \), \(\sigma _{y}\) and \(\tau _{xy} \)are stress components; \(H(x,y,z,t)=T(x,y,z,t)-T_{0} \) is the variation in the temperature T with respect to the equilibrium temperature (or reference temperature) \(T_{0} \); E(z), \(\mu \) and \(\alpha (z)\) are the Young’s modulus, Poisson ratio and linear coefficient of thermal expansion, respectively. The stiffness coefficients in Eqs. (2) and (3) are given as follows

$$\begin{aligned} (A_{11} ,A_{12} ,A_{33} )= & {} \int _{-h/2}^{h/2} {\frac{E(z)}{1-\mu ^{2}}\left( {1,\mu ,\frac{1-\mu }{2}} \right) \text{ d }z} \end{aligned}$$
(6a)
$$\begin{aligned} (B_{11} ,B_{12} ,B_{33} )= & {} \int _{-h/2}^{h/2} {\frac{zE(z)}{1-\mu ^{2}}\left( {1,\mu ,\frac{1-\mu }{2}} \right) \text{ d }z} \end{aligned}$$
(6b)
$$\begin{aligned} (D_{11} ,D_{12} ,D_{33} )= & {} \int _{-h/2}^{h/2} {\frac{z^{2}E(z)}{1-\mu ^{2}}\left( {1,\mu ,\frac{1-\mu }{2}} \right) \text{ d }z} \end{aligned}$$
(6c)

It is easy to show that these stiffness coefficients satisfy relations of

$$\begin{aligned} A_{12} +2A_{33} =A_{11} , B_{12} +2B_{33} =B_{11} , \quad D_{12} +2D_{33} =D_{11} \end{aligned}$$
(7)

In the sense of the classical plate theory, by ignoring the in-plane inertia forces, equations of motion for the free vibration of the FGM micro-plates are given by [36]

$$\begin{aligned}&\frac{\partial N_{x} }{\partial x}+\frac{\partial N_{xy}}{\partial y}=0 \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\partial N_{xy} }{\partial x}+\frac{\partial N_{y} }{\partial y}=0, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{\partial ^{2}M_{x} }{\partial x^{2}}+2\frac{\partial ^{2}M_{xy} }{\partial x\partial y}+\frac{\partial ^{2}M_{y} }{\partial y^{2}}=I_{0} \frac{\partial ^{{2}}w_{0} }{\partial t^{2}} \end{aligned}$$
(10)

where\(I_{0} =\int _{-h/2}^{h/2} {\rho (z)\text{ d }z} \), \(\rho (z)\) is the mass density.

By substituting Eqs. (2)–(5) into Eqs. (8)–(10), and using the relations given in Eq. (7), we get equations of motion in terms of displacement components

$$\begin{aligned}&A_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}+A_{33} \frac{\partial ^{2}u_{0} }{\partial y^{2}}+(A_{12} +A_{33} )\frac{\partial ^{2}v_{0} }{\partial x\partial y}=B_{11} \frac{\partial }{\partial x}\nabla ^{2}w_{0} +\frac{\partial N_\mathrm{T} }{\partial x} \end{aligned}$$
(11)
$$\begin{aligned}&A_{11} \frac{\partial ^{2}v_{0} }{\partial y^{2}}+A_{33} \frac{\partial ^{2}v_{0} }{\partial x^{2}}+(A_{12} +A_{33} )\frac{\partial ^{2}u_{0} }{\partial x\partial y}=B_{11} \frac{\partial }{\partial y}\nabla ^{2}w_{0} +\frac{\partial N_\mathrm{T} }{\partial y} \end{aligned}$$
(12)
$$\begin{aligned}&D_{11} \nabla ^{4}w_{0} +I_{0} \frac{\partial ^{2}w_{0} }{\partial t^{2}}+\nabla ^{2}M_\mathrm{T} =B_{11} \nabla ^{2}\left( {\frac{\partial u{ }_{0}}{\partial x}+\frac{\partial v{ }_{0}}{\partial y}} \right) \end{aligned}$$
(13)

where \(\nabla ^{2}=\left( {\tfrac{\partial ^{2}}{\partial x^{2}}+\tfrac{\partial ^{2}}{\partial y^{2}}} \right) \) is the Laplace operator and \(\nabla ^{4}=\nabla ^{2}\nabla ^{2}\).

Calculating derivatives of Eqs. (11) and (12), respectively, with respect to x andy, adding respective sides, and using Eq. (7), we obtain

$$\begin{aligned} \nabla ^{2}\left( {\frac{\partial u_{0} }{\partial x}+\frac{\partial v_{0} }{\partial y}} \right) =z_{0} \nabla ^{4}w_{0} +\frac{1}{A_{11} }\nabla ^{2}N_\mathrm{T} \end{aligned}$$
(14)

Finally, by using Eq. (14) to eliminate the in-plane displacements in Eq. (13), we arrive at equation of motion only in terms of the transverse deflection \(w_{0}\) as follows:

$$\begin{aligned} D_\mathrm{eq} \nabla ^{4}w_{0} +I_{0} \frac{\partial ^{2}w_{0} }{\partial t^{2}}+\nabla ^{2}M_\mathrm{T} -z_{0} \nabla ^{2}N_\mathrm{T} =0 \end{aligned}$$
(15)

where\(D_\mathrm{eq} \)is the equivalent flexural rigidity; \(z_{0} \) represents position of the physical neutral surface. They are defined by

$$\begin{aligned} D_\mathrm{eq} =D_{11} -B_{11}^{2} /A_{11}, \quad z_{0} =B_{11}/A_{11} \end{aligned}$$
(16)

Notably, in Eq. (15) the thermal membrane force \(N_\mathrm{T} \) and bending moment \(M_\mathrm{T}\) depend on the temperature rise filed which is coupled with the strain field, or the kinematic parameters. They will be finally determined in terms of the deflection of the plate. However, in the analysis of vibration subjected to external thermal loadings, the temperature rise field is determined independently by solving the uncoupled heat conduction equation with its initial and boundary conditions.

In the absence of constraints at the boundaries to prevent the in-plane movements, the membrane forces will vanish. Thus, from Eq. (2), we have

$$\begin{aligned}&A_{11} \frac{\partial u_{0} }{\partial x}+A_{12} \frac{\partial v_{0} }{\partial y}-B_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}-B_{12} \frac{\partial ^{2}w_{0} }{\partial y^{2}}-N_\mathrm{T} =0 \ \end{aligned}$$
(17a)
$$\begin{aligned}&A_{12} \frac{\partial u_{0} }{\partial x}+A_{11} \frac{\partial v_{0} }{\partial y}-B_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}-B_{11} \frac{\partial ^{2}w_{0} }{\partial y^{2}}-N_\mathrm{T} =0 \end{aligned}$$
(17b)
$$\begin{aligned}&A_{33} \left( {\frac{\partial u_{0} }{\partial y}+\frac{\partial v_{0} }{\partial x}} \right) -2B_{33} \frac{\partial ^{2}w_{0} }{\partial x\partial y}=0 \end{aligned}$$
(17c)

Usually, the variation of the Poisson ratio of the FGM plate in the thickness direction changes very little comparing with other physical parameters. So, in order to facilitate the analysis, the Poisson ratio is assumed to be constant in the following analysis. Then, the stiffness parameters satisfy relations\(, A_{11} B_{12} =A_{12} B_{11}\) and \(A_{12} =\mu A_{11} \), \(B_{12} =\mu B_{11} \). Consequently, by solving Eq. (17) we can arrive at

$$\begin{aligned} \varepsilon _{x}^{0}= & {} \frac{\partial u_{0} }{\partial x}=z_{0} \frac{\partial ^{2}w_{0} }{\partial x^{2}}+\frac{N_\mathrm{T} }{A_{11} }, \end{aligned}$$
(18a)
$$\begin{aligned} \varepsilon _{y}^{0}= & {} \frac{\partial v_{0} }{\partial y}=z_{0} \frac{\partial ^{2}w_{0} }{\partial y^{2}}+\frac{N_\mathrm{T} }{A_{11} }, \end{aligned}$$
(18b)
$$\begin{aligned} \gamma _{xy}^{0}= & {} \frac{\partial u_{0} }{\partial y}+\frac{\partial v_{0} }{\partial x}=2z_{0} \frac{\partial ^{2}w_{0} }{\partial x\partial y} \end{aligned}$$
(18c)

Equation (18) shows that the membrane strains (strain at the geometrical middle surface) of the FGM plate consist of two part. The one is produced by stretching–bending coupling and the other is contributed by the thermal membrane force due to the thermally non-homogeneity of the material property and the non-symmetric temperature rise distribution about the geometrical middle surface as shown in Eq. (5c). Therefore, only for the homogenous material micro-plate, or the FGM micro-plate with the material properties varying symmetrically about the geometrical middle surface, the membrane strains will vanish due to \(z_{0} =0\) and \(N_\mathrm{T} =0\) at the same time. Otherwise, the thermal membrane force is not equal to zero and it will contribute to the membrane strains, and further to the TED.

2.2 Equation of heat conduction

In the case of absence of external thermal loads, temperature field in the FGM plates is governed by the one-way coupled heat conduction equation as follows [1]:

$$\begin{aligned} \frac{\partial }{\partial x}\left( {k\frac{\partial H}{\partial x}} \right) +\frac{\partial }{\partial y}\left( {k\frac{\partial H}{\partial y}} \right) +\frac{\partial }{\partial z}\left( {k\frac{\partial H}{\partial z}} \right) =\rho C\frac{\partial H}{\partial t}+\frac{\alpha ET_{0} }{1-2\mu }\frac{\partial e}{\partial t} \end{aligned}$$
(19)

where k and C are the thermal conductivity and the specific heat which are given functions of coordinate, z; e is the cubic dilation which is calculated by

$$\begin{aligned} e=\varepsilon _{xx} +\varepsilon _{yy} +\varepsilon _{zz} =\frac{1-2\mu }{1-\mu }\left( {\varepsilon _{0} -z\nabla ^{2}w} \right) +\frac{1+\mu }{1-\mu }\alpha H \end{aligned}$$
(20)

The derivation of Eq. (20) in detail is given in the Appendix.

For thin homogenous micro-plates, the previous researchers show that the difference between the value of the thermoelastic damping predicted by the 1-D heat conduction equation and that by 2-D, even 3-D heat conduction equation is very small [13, 14]. Therefore, by ignoring the terms of in-plane temperature gradient in Eq. (19) [5,6,7,8,9,10, 30,31,32,33,34,35] and considering the cubic dilation in Eqs. (20) and (19) reduces to the following quasi-one-dimensional heat conduction equation:

$$\begin{aligned} \frac{\partial }{\partial z}\left( {k\frac{\partial H}{\partial z}} \right) =\rho C\frac{\partial H}{\partial t}+\frac{\alpha ET_{0} }{1-\mu }\frac{\partial }{\partial t}\left( {\varepsilon _{0} -z\nabla ^{2}w} \right) \end{aligned}$$
(21)

It needs to noted that, herein a higher-order small quantity of\(\rho C\) is neglected in Eq. (21) [5,6,7,8,9,10, 17,18,19,20,21, 30,31,35]. It is obvious that the coefficients of Eq. (21) are variable because all the material parameters in it (except for the Poisson) are functions of the coordinate, z, for the FGM plates.

3 Harmonic response of the free vibration

By assuming the vibration is harmonic, the dynamically thermo-mechanical responses of the FGM plate resonator can be expressed by

$$\begin{aligned} (u_{0} ,v_{0} ,w_{0} ,H)=(\bar{{u}}(x,y),\bar{{v}}(x,y),\bar{{w}}(x,y),\bar{{H}}(x,y,z))e^{\text{ i }\omega t} \end{aligned}$$
(22)

where \(\omega \) is the complex natural frequency including TED; \(\text{ i }=\sqrt{-\,1} \); the quantities with a top bar are the amplitudes, or the shape modes, of the displacements and the temperature change, respectively. Substitution from Eq. (22) into Eqs. (15) and (21) yields

$$\begin{aligned}&D_\mathrm{eq} \nabla ^{4}\bar{{w}}+\nabla ^{2}\left( {\bar{{M}}_\mathrm{T} -z_{0} \bar{{N}}_\mathrm{T} } \right) -I_{0} \omega ^{2}\bar{{w}}=0 \end{aligned}$$
(23)
$$\begin{aligned}&\frac{\partial }{\partial z}\left( {\kappa \frac{\partial \bar{{H}}}{\partial z}} \right) =\text{ i }\omega \left[ {\rho C\bar{{H}}+\frac{\alpha ET_{_{0} } }{1-\mu }\left( {\bar{{\varepsilon }}_{0} -z\nabla ^{2}\bar{{w}}} \right) } \right] \end{aligned}$$
(24)

with

$$\begin{aligned}&\bar{{\varepsilon }}_{0} =\frac{\partial \bar{{u}}}{\partial x}+\frac{\partial \bar{{v}}}{\partial y} \end{aligned}$$
(25)
$$\begin{aligned}&(\bar{{N}}_\mathrm{T} ,\bar{{M}}_\mathrm{T} )=\int _{-h/2}^{h/2} {\frac{\alpha (z)E(z)}{1-\mu }\bar{{H}}(x,y,z)(1,z)\text{ d }z} \end{aligned}$$
(26)

4 Solution of the eigenvalue problem

Firstly, we solve the heat conduction equation (24) to find temperature modes in terms of the kinematic parameters related to the structural modes. Due to the inclusions of the variable coefficients, it is difficult to find analytical solution of it by direct analytical approach. Instead, we use a layer-wise homogenization approach developed by the authors [34, 35] to solve heat conduct equation (24) under the adiabatic boundary conditions at the top and bottom surfaces.

In the sense of the layer-wise homogenization approach, the transversely non-homogenous FGM plate is assumed to be divided into finite numbers (N) layers and the effective material properties in each layer are considered approximately to be constant. Accordingly, Eq. (24) is discretized into N differential equations with constant coefficients defined in the different divided layers as following

$$\begin{aligned} \frac{\partial ^{2}\bar{{H}}_{j} }{\partial z^{2}}+r_{j}^{2}\bar{{H}}_{j} =s_{j} \left( {\bar{{\varepsilon }}_{0} -z\nabla ^{2}\bar{{w}}} \right) , (z_{j}<z<z_{j+1} ,j=1,2,\ldots ,N) \end{aligned}$$
(27)

where \(\bar{{H}}_{j} (x,y,z)\) is the temperature amplitude defined in the j-layer; parameters \(r_{j} \) and \(q_{j} \) are defined by

$$\begin{aligned} r_{j} =\sqrt{\frac{-\,\text{ i }\omega \rho _{j} C_{j} }{k_{j} }} =(\text{ i }-1)\sqrt{\frac{\omega \rho _{j} C_{j} }{2k_{j} }}, s_{j} =\frac{\text{ i }\omega E_{j} \alpha _{j} T_{0} }{(1-\mu )k_{j} } \end{aligned}$$
(28)

The values of the mechanical and thermal parameters with subscripts, j, are evaluated at the middle surface, \(\bar{{z}}_{j} =(z_{j} +z_{j+1} )/2\). By solving Eq. (27) for each layer, and using the adiabatic boundary conditions at the top and bottom surfaces and continuation conditions at the interfaces, analytical solutions of the temperature rise field defining in the divined layers can be finally arrived at [34, 35]:

$$\begin{aligned} \bar{{H}}_{j} =\bar{{A}}_{j} \bar{{\varepsilon }}_{0} +\bar{{B}}_{j} \nabla ^{2}\bar{{w}}, (z_{j}<z<z_{j+1},\quad j=1,2,\ldots ,N) \end{aligned}$$
(29)

with

$$\begin{aligned} \bar{{A}}_{j}= & {} \bar{{A}}_{1j} \sin r_{j} z+\bar{{B}}_{1j} \cos r_{j} z+s_{j} /r_{j}^{2} \end{aligned}$$
(30a)
$$\begin{aligned} \bar{{B}}_{j}= & {} \bar{{A}}_{2j} \sin r_{j} z+\bar{{B}}_{2j} \cos r_{j} z-s_{j} z/r_{j}^{2} \end{aligned}$$
(30b)

where constants\(\bar{{A}}_{1j} \), \(\bar{{B}}_{1j}\), \(_{\mathrm { }}\bar{{A}}_{2j} \)and \(\bar{{B}}_{2j} \) are related to the geometry, the material properties and the frequency of the FGM micro-plate.

According to Eqs. (26) and (29), we obtain the amplitudes of the resultant thermal membrane force and bending moment

$$\begin{aligned} \bar{{N}}_\mathrm{T} =\beta _{11} \bar{{\varepsilon }}_{0} +\beta _{12} \nabla ^{{2}}\bar{{w}}, \quad \bar{{M}}_\mathrm{T} =\beta _{21} \bar{{\varepsilon }}_{0} +\beta _{22} \nabla ^{{2}}\bar{{w}} \end{aligned}$$
(31)

in which the analytical expressions of coefficients\(\beta _{ij} \)are given in the “Appendix”.

Furthermore, by using Eqs. (18), (22), (25) and (31), we can obtain the quantities \(\bar{{\varepsilon }}_{{0}}\), \(\bar{{N}}_\mathrm{T}\), and \(\bar{{M}}_\mathrm{T}\) in terms of \(\bar{{w}}\) as following

$$\begin{aligned} \bar{{\varepsilon }}_{0}= & {} \bar{{\beta }}\nabla ^{{2}}\bar{{w}}, \end{aligned}$$
(32a)
$$\begin{aligned} \bar{{N}}_\mathrm{T}= & {} f_{N} \nabla ^{{2}}\bar{{w}}, \end{aligned}$$
(32b)
$$\begin{aligned} \bar{{M}}_\mathrm{T}= & {} f_{M} \nabla ^{{2}}\bar{{w}} \end{aligned}$$
(32c)

where

$$\begin{aligned} f_{N} =\beta _{11} \bar{{\beta }}+\beta _{12} , \quad f_{M} =\beta _{21} \bar{{\beta }}+\beta _{22} , \quad \bar{{\beta }}=\frac{(1+\mu )B_{11} +2\beta _{12} }{(1+\mu )A_{11} -2\beta _{11}}. \end{aligned}$$
(33)

where \(f_{N} \) and \(f_{M}\) are functions of the complex frequency, \(\omega \). Then, by using Eqs. (32), we can rewrite the structural vibration equation, Eq. (23), in the standard form of

$$\begin{aligned} \nabla ^{4}\bar{{w}}-\lambda ^{{2}}\bar{{w}}=0 \end{aligned}$$
(34)

where

$$\begin{aligned}&\lambda =\left( {\frac{cI_{0} }{D_{r} (1+cf)}} \right) \omega , \end{aligned}$$
(35a)
$$\begin{aligned}&f(\omega )=\frac{f_{M} (\omega )-z_{0} f_{N} (\omega )}{D_{r} } \end{aligned}$$
(35b)
$$\begin{aligned}&c=\frac{D_{r} }{D_\mathrm{eq} }\quad , \end{aligned}$$
(35c)
$$\begin{aligned}&D_{r} =\frac{E_{r} h^{3}}{12(1-\mu ^{2})} \end{aligned}$$
(35d)

Herein, \(E_{r}\) and \(D_{r}\) are the Young’s modulus and the flexural rigidity of the reference homogenous material plate which it is assumed to be made from the bottom surface material of the FGM plate. Constant c represents effect of the material inhomogeneity on the flexural rigidity with \(c=\text{1 }\)corresponding to the reference homogenous plate; \(f(\omega )\) is a complex function of frequency, \(\omega \), the imaginary part of which measures the TED in the vibrating FGM micro-plate.

In the special case that the FGM plate reduces to the reference homogenous plate without TED \((f(\omega )=0)\), Eq. (35) reduces to

$$\begin{aligned} \nabla ^{4}\bar{{w}}^{{*}}_{{0}} -\lambda ^{{*2}}_{{0}}\bar{{w}}_{{0}}^{{*}} =0, \hbox { with } \lambda ^{{*2}}_{{0}}=\frac{I^{{*}}_{{0}} \omega _{{0}}^{{*2}}}{D_{r} } \end{aligned}$$
(36)

in which \(\omega _{{0}}^{{*}}\) is the isothermal frequency of the reference homogenous plate and \(\bar{{w}}_{{0}}^{{*}}\) is the related mode shape; \(I_{0}^{*} =\rho _{r} h\). For the same edge constraints, such as for the simply supported (S), the clamped (C) and the free (F) edges, we can show that the boundary conditions of Eq. (34) are the same with those of Eq. (36). The detail mathematical proofs of this conclusion can be found in the “Appendix”. Therefore, mathematical similarity between Eqs. (35) and (36) gives the relationship between the eigenvalues (frequencies) as follows [36]

$$\begin{aligned} \omega =\omega _{{0}} \sqrt{1+cf(\omega )} \end{aligned}$$
(37)

where \(\omega _{0} =\omega _{0}^{*} /\sqrt{c\bar{{\phi }}_{0} } \) is the natural frequency of isothermal FGM plate [36]; \(\bar{{\varphi }}_{0} =I_{0} /I_{0}^{*} \) is an inertial parameter. The corresponding mode shape function, \(\bar{{w}}\), of the FGM micro-plate is proportional to that of the reference homogenous plate, \(\bar{{w}}_{0}^{*}\). Examining the coefficients in Eq. (31) and the definition of Eq. (35b), one can see that Eq. (37) is a complicated transcendental equation about the complex frequency, \(\omega \). Therefore, it is difficult to find the root of this equation. However, due to the TED is very weak in the free vibration of the FGM micro-plate, we may approximately replace\(f(\omega )\) in the square root of Eq. (37) by\(f(\omega _{{0}} )\), the dissipation relation, Eq. (37), becomes [4, 6, 7, 35]

$$\begin{aligned} \omega =\omega _{0} \sqrt{1+cf(\omega _{0} )} \end{aligned}$$
(38)

The frequency of the reference homogenous plate can be expressed by

$$\begin{aligned} \omega _{0}^{*} =\frac{\Omega _{0}^{*} }{a^{2}}\sqrt{\frac{D_{r} }{\rho _{r} h}} \end{aligned}$$
(39)

where \(\Omega _{0}^{*}\) is a dimensionless frequency parameter only depending on the geometry and the boundary conditions of the reference homogenous plate which can be easily found in the literature [37, 38], or even in the text books [39]. It is well known that for a rectangular plate with the four edges simply supported (SSSS), analytical solution of \(\Omega _{0}^{*} \) is given by

$$\begin{aligned} \Omega _{0}^{*} =\left( {r^{2}+\frac{s^{2}}{\delta ^{2}}} \right) \pi ^{2}, (r,s=1,2,\ldots ,) \end{aligned}$$
(40)

where\(\delta =a/b\).

Finally, by using the complex frequency approach [4,5,6,7, 30,31,32,33,34,35], the TED is given in the terms of the inverse quality factor\(, Q^{-1}\), as follows

$$\begin{aligned} Q^{-1}=2\left| {\frac{\mathrm{Im}(\omega )}{\mathrm{Re}(\omega )}} \right| \end{aligned}$$
(41)

where \(\mathrm{Re}(\omega )\) and \(\text{ Im }(\omega )\) are the real and the imaginary parts of the complex frequency, respectively.

Herein, we should note that the above theoretical analyses or the mathematical formulations validate the thin FGM micro-plates with arbitrary through-thickness material gradient profile, arbitrary geometry and arbitrary boundary constraints.

5 Numerical results and discussions

In the following numerical computing, FGM micro-plate is assumed to be composited by the constituents of metal (Ni) and ceramic \((\hbox {Si}_{\mathrm {3}}\hbox {N}_{\mathrm {4}})\). Furthermore, material properties of the FGM micro-plate are assumed to vary along the thickness from the full ceramic to the full metal as the following power functions [33,34,35,36]

$$\begin{aligned} P=P_{m} \left[ {1+\left( {\frac{P_{c} }{P_{m} }-1} \right) \left( {\frac{1}{2}+\frac{z}{h}} \right) ^{n}} \right] \end{aligned}$$
(42)

where,\(\zeta =z/h\), \(n\in [0,\infty )\) represent the material gradient parameter with \(n=0\) and \(n\rightarrow \infty \) corresponding to the full ceramic and the full metal plates, respectively; \(P_{c} =P(h/2)\)and \(P_{m} =P(-\,h/2)\) refer to the thermal and mechanical properties of the full ceramic at the top surface and those of full metal at the bottom surface, respectively. Herein, we select the full metal plate as the reference homogenous material plate, i.e. \(P_{r} =P_{m} \). The mechanical and thermal properties of the metal (Ni) and ceramic \((\hbox {Si}_{\mathrm {3}}\hbox {N}_{\mathrm {4}})\) at reference temperature, \(T_{0} =300\,\text{ K }\), are listed in Table 1.

First, in order to check the convergence of the layer-wise homogenization approach, we plotted a curve of the TED of the FGM square plate with SSSS boundary conditions varying with the divided layer number, N in Fig. 2, from which it can be found that this method convergence speed is so quick that the TED is accurate enough once \(N>300\).

Table 1 Material properties of the constituents of the FGM micro-plate \((T_{0} =300\) K) [17, 35]
Full size table
Fig. 2
figure 2

TED in a SSSS square FGM micro-plate varying with the increasing divided layers, N (\(n=1\), \(a=b=200\,\upmu \)m, \(h=2\,\upmu \)m)

Full size image

By reducing the material to be full ceramic \((n=0)\), analytical solution of the TED for the SSSS homogenous plate was derived in the L–R’s form by Li et al. [10] by using the energy approach, which is expressed by

$$\begin{aligned} Q^{-1}=\frac{1+\mu }{1-\mu }\frac{E\alpha ^{2}T_{0} }{\rho C}\frac{6}{\xi ^{2}}\left( {1-\frac{1}{\xi }\frac{\sinh \xi +\sin \xi }{\cosh \xi +\cos \xi }} \right) , \quad \xi =h\sqrt{\frac{\omega _{0} \rho C}{2k}} \end{aligned}$$
(43)

Herein, values of physical parameters in Eq. (43) are given by those of the ceramic \((\hbox {Si}_{\mathrm {3}}\hbox {N}_{\mathrm {4}})\)in Table 1. A comparison between the values of TED for the full ceramic square micro-plate with SSSS boundary conditions estimated by Eq. (43) and by the present approach are listed in Table 2 for some specified values of the thickness. Moreover, in Fig. 3, we illustrated the continuous variation of the TED with the thickness, h. It can be seen obviously that a good agreement between the results shows the validity and effectiveness of the present approach to analyze the TED of the homogenous micro- plates.

Table 2 Values of the TED \((Q^{-1}\times 10^{5})\) of a homogenous (full ceramic) square micro-plate with SSSS edges obtained by the present approach and by the analytical solution in L–R’s form [10] (in the first mode, \(a=b=200\,\upmu \)m)
Full size table
Fig. 3
figure 3

Comparison of the TED for a full metal square plate with SSSS edges obtained by the present approach and by L–R’s analytical solution form [10] (in the first mode, \(a=b=200\,\upmu \)m)

Full size image

From the above analysis, we know that the TED comes from the thermal membrane force and bending moment produced by the temperature gradient in the thickness direction. So, we firstly analyze the variation of the temperature field along the plate thickness. By substituting Eq. (32a) into Eq. (29), the temperature field can be expressed stepwise as functions of coordinate, z, as follows

$$\begin{aligned} \bar{{H}}_{j} (x,y,z)=(\bar{{A}}_{j} \bar{{\beta }}+\bar{{B}}_{j} )\nabla ^{2}\bar{{w}}, (z_{j}<z<z_{j+1},\quad j=1,2,\ldots ,N) \end{aligned}$$
(51)

where \(\nabla ^{2}\bar{{w}}\) is a function of coordinates x and y given by the vibration modes of the FGM plate. So, the variation of the temperature field in the thickness direction can be determined by

$$\begin{aligned} \tau _{j} (z)=\frac{\bar{{H}}_{j} }{a\nabla ^{2}w}=\frac{1}{a}(\bar{{A}}_{j} \bar{{\beta }}+\bar{{B}}_{j} ),\quad (z_{j}<z<z_{j+1} ) \end{aligned}$$
(44)

For the specified value of the thickness, \(h=1\,\upmu \)m, \(3\,\upmu \)m and \(5\,\upmu \)m, Fig. 4 illustrates the real part of the through thickness temperature variation, \(\mathrm{Re}(\tau )\), of the FGM micro-plates with different values of the power index, n. Examining those curves corresponding to different values of n, it can be seen that the material gradient or the inhomogeneity in the materials has a significant influence on the distribution of the temperature filed along the thickness, which is produced by the complicated thermoelastic coupling dynamic deformations and strengthened by the material inhomogeneity. It is obvious that the curves of the FGM plates deviate from the geometric neutral surface where the temperature rise is negative due to the stretching–bending coupling and that they approach to the curves of the full ceramic \((n=0)\) and full metal \((n=10^{7})\) plates at the top and bottom surfaces, respectively. In addition, the distribution of the temperature field in the plate thickness direction also accords with the mechanism of the energy dissipation that the energy loss originates in the irreversible flow of heat from the hotter region to be compressed to the colder region to be stretched in the vibrating plate due to the thermoelastic coupling [1,2,3,4]. Moreover, along with the increase in the thickness, the temperature amplitudes at the top and the bottom surfaces increase.

Fig. 4
figure 4

Variation profiles of the temperature field along the thickness direction of FGM micro-plate and the homogenous micro-plates. a\(h=1\,\upmu \)m, b\(h=3\,\upmu \)m, c\(h=5\,\upmu \)m

Full size image

From Eqs. (30) and (41) one can seen that the TED depends closely on the isothermal frequency of the FGM micro-plate. Figure 5 shows continuous variation of the TED in the square FGM micro-plate versus \(\omega _{{0}} \)in the fundamental modes for different values of the material gradient index, n, under SSSS and CCCC (with all the four edges clamped) boundary conditions. From it one can see that as the increase in the value of \(\omega _{{0}} \) the TED firstly increases until it attains the maximum value, \(Q_{\max }^{-1} \), then decreases monotonously. The frequency corresponding to the peak value of TED gives a definite value of the plate thickness which is called the critical thickness, denoted by \(h_\mathrm{cr} \). Along with the increase in the material gradient index, n, or the increment of the volume fraction of metal, both the TED and the critical thickness increase.

Fig. 5
figure 5

Variation of TED with frequency \(\omega _{{0}}\) in the FGM micro-square plates in the first vibration mode for different values of n. a SSSS, b SSSS

Full size image

Figure 6 displays the characteristic curves of TED versus the material gradient index, n, for some specified values of plate thickness in a SSSS FGM square micro-plate. From it we can see that the TED reaches the minimum roughly at \(n =4.20\) for the very thin micro-plate \((h\leqslant 3\,\upmu \)m). So, it may be possible to design a higher quality plate resonator with the lowest TED smaller than that of the full ceramic plate.

Fig. 6
figure 6

\(\text{ TED }\) in a SSSS FGM micro-square plate varying continuously with parameter n for some specified values of the thickness \((a=b=200\,\upmu \)m). a\(h=1\,\upmu \)m; b\(h=2\,\upmu \)m; c\(h=3\,\upmu \)m; d\(h=4\,\upmu \)m; e\(h=\) 5–9 \(\upmu \)m

Full size image
Fig. 7
figure 7

TED varying continuously with the thickness in a SSSS FGM micro-plate vibrating in the first four modes \((n=1\), \(a=b=200\,\upmu \)m)

Full size image

Figure 7 shows the relation between the TED and the thickness of the SSSS square FGM micro-plate corresponding to the first four vibration modes. It can be seen that that the maximum values of TED of the micro-plate with different vibration modes are the equal. However, the values of the corresponding critical thickness decrease along with the increase in the order of the vibration modes. In Fig. 8, we plotted the curves of TED of a SSSS rectangular FGM micro-plate versus the thickness for different values of the aspect ratio, a/b. It can be seen that the maximum values of TED keep the same for the plates with different values of the aspect ratio, but the critical thickness decreases along with the increase in it.

Fig. 8
figure 8

Thickness dependence of TED in a SSSS FGM micro rectangular plate with different values of aspect ratio (a/b), in the first vibrating mode (\(n=1\), \(a=200\,\upmu \)m)

Full size image
Fig. 9
figure 9

TED versus the thickness in a FGM micro-plate with different boundary conditions in the first vibrating modes (\(n=1\), \(a=b=300\,\upmu \)m)

Full size image

Figure 9 shows the continuous variation of the TED versus the plate thickness of the FGM micro-plates with different boundary conditions which are CCCC, CFCF (clamped at \(x = 0\), a and free at \(y =0\), b), SSSS, SFSF (simply supported at \(x = 0\), a and free at \(y = 0\), b) and CFFF (clamped at \(x = 0\) and free at the other three edges). It is observed from this figure that the peak values of the TED remain the same for the four different edge constraints. However, the values of the related critical thicknesses decrease along with the increase in the rigidity of boundary constraints. The values of the dimensionless fundamental frequency parameter,\(\Omega _{0}^{*} \), of the related homogenous square plates with four kind boundary conditions as mentioned above are given in Table 3 [38, 39].

In order to further show the thermoelastic dissipation effect in the free vibration of the FGM micro-plate, the frequency shift, \([\mathrm{Re}(\omega )-\omega _{0} ]/\omega _{0} \), and attenuation, \(\mathrm{Im}(\omega )/\omega _{0} \), of the SSSS and the CCCC square FGM micro-plates with \(n =1\) and \(a=b=300\,\upmu \)m varying along with the thickness, h, are depicted in Fig. 10. We can see that the frequency shift increases monotonously with the increase in the plate thickness. However, the attenuation first increases and then decrease with the plate thickness, reaching the maximum value at the critical thickness (\(h_\mathrm{cr} =5.54\,\upmu \)m for CCCC plate and \(h_\mathrm{cr} =6.77\,\upmu \)m for SSSS plate) at which the frequency shift increases the most rapidly and the energy lost reaches the highest.

Furthermore, as a benchmark for other researchers to check the numerical results in their studies, for some specified increasing values of the material gradient index, n,  the values of the maximum TED and the corresponding values of the critical thickness for the square FGM micro-plate with the five boundary conditions are listed in Table 4. Again, similar with that illustrated in Figs. 5 and 9, we can see that the critical thickness increases along with the increase in the material gradient index, n, or with the increase in the volume fraction of the metal, for all the five kind boundary conditions. On the other hand, for a fixed value of n, the values of the critical thickness increase along with the decrease in the level of boundary constrains, however, the maximum values of the TED maintain constant. In other words, by enhancing the stiffness of the boundary constraints one could not change the maximum of the TED but can lower the critical thickness of the FGM micro-plate.

Finally, we quantitatively examine the influence of the stretching-bending coupling, or the thermal membrane force \(N_\mathrm{T} \), on the TED of the FGM micro-plates. In Table 5, we list the values of TED of a square FGM micro-plate (\(a=b=300\,\upmu \)m, \(h=4\,\upmu \)m) with and without [by setting \(f_{N} (\omega )=0\) in Eq. (39)] considering the stretching–bending coupling for some specified values of index, n, in the fundamental vibration mode under CCCC and SSSS boundary conditions, respectively. In this table, we also give the values of the relative error of the TED resulting from ignoring the thermal membrane force. Furthermore, in Fig. 11, we illustrate the continuous variation of the relative error versus the material gradient parameter,n, of the SSSS micro-plate for different values of the length, \(a=b=100\,\upmu \)m, \(200\,\upmu \)m, \(300\,\upmu \)m. From the numerical results, we can see that for a fixed value of the power-law index, n, the value of the TED of considering the stretching–bending coupling is larger than that of ignoring the coupling. In addition, the effects of thermal membrane force on the TED depend on the level of the inhomogeneity of the material property. The maximum relative error is about 1.4% which evaluated at \(n=1.5\). However, the relative errors keep almost the same for different values of the length. So, in order to get more accurate evaluation of TED for the FGM microbeam/plate resonators with the asymmetrical variation of the material properties through the thickness about the geometrical middle surface, the effects of the stretching-bending effect on the TED should be considered. Otherwise, the TED will be underestimated.

Table 3 The dimensionless fundamental frequencies of the homogenous square plate with different boundary conditions [37, 39]
Full size table
Fig. 10
figure 10

Frequency shift and attenuation versus the plate thickness in the CCCC and SSSS FGM micro-square plate in the first vibration mode. (\(n =\)1, \(a=b=300\,\upmu \)m)

Full size image
Table 4 Values of the maximum TED, \(Q_{\max }^{-1} \times \text{10 }^{{4}}\), and the related critical thickness, \(h_\mathrm{cr}\, (\upmu \)m), of a square FGM micro-plate for some specified values of n in the first vibration mode under different boundary conditions \((a=b=200\,\upmu \)m)
Full size table
Table 5 TED \((Q_{\max }^{-1} \times 10^{4})\) of a square FGM micro-plate with and without considering the effects of the thermal membrane force for some specified values of n in the first vibration mode (\(a=b=300\,\upmu \)m, \(h=4\,\upmu \)m)
Full size table
Fig. 11
figure 11

The relative error between the values of TED in a SSSS FGM micro-plate with and without considering the thermal membrane force versus the material gradient index

Full size image

6 Conclusions

Governing equations for thermoelastic coupling vibration of functionally graded micro-plates with arbitrary through-thickness material gradient profile are established based on the one coupled heat conduction theory and classical plate theory. Analytical solution of temperature rise field is obtained in terms of the kinematic parameters by solving the obtained constant coefficient heat conduction equations associated with the thermal boundary and continuation conditions using the layer-wise homogenization approach. Complex frequency for the free vibration of the FGM including TED is obtained utilizing the mathematical similarity between the eigenvalue problems of the FGM plate and that of the reference homogenous one. The theory and methodology developed in this paper can be used to deal with the thermoelastic coupling vibration and evaluate the TED in the thin FGM micro-plates with arbitrary through-thickness material gradient, geometry and boundary constraints.

The TED is influenced obviously by the material gradient. The material inhomogeneity also has a significant influence on the distribution of the temperature along the thickness. The temperature changes of the FGM plates at the geometric neutral surface are negative due to the stretching–bending coupling. The effects of the thermal membrane force, or the stretching–bending coupling, on the TED in FGM micro-plate are first accurately taken into account in the solution. The numerical results show that for the FGM micro-plate with material gradient profile being asymmetric about the geometric neutral surface, the stretching–bending coupling will lead to an increase in the value of the TED. Quantitatively, it is shown that the maximum value of the relative error between the values of the TED including the stretching–bending coupling and that ignoring the coupling is less than1.5%, which evaluates roughly at \(n=1.5\).