1 Introduction

Pipe conveying fluid (PCF) has become a subject of significant interest in both engineering and academic communities due to its widespread applications in various fields such as nuclear engineering, marine engineering and petroleum engineering [1, 2]. Researchers have focused on various aspects of PCF to address important concerns in the industry. One major area of study involves enhancing the resistance to flow corrosion of PCF, as highlighted in the work by Zeng et al. [3]. Additionally, researchers have analyzed failure mechanisms in different industrial pipes, as investigated by Xia et al. [4] and Wang et al. [5]. Furthermore, the dynamic response of PCF under special conditions has been a focus of research, as demonstrated in the work by Wang et al. [6, 23]. Another crucial aspect that draws attention is the stability of PCF. The internal fluid flow in PCF can induce self-excited/random vibrations or resonances, which can pose a threat to the structural integrity of the system being considered [7]. As pointed out by Paidoussis and Li [8], PCF exhibits rich dynamic behaviors, making it a new paradigm in dynamics. Therefore, understanding the underlying dynamic mechanisms of PCF is essential for mitigating or preventing adverse vibration occurrences.

PCF can be classified based on different boundary conditions, such as cantilevered PCF [9, 24], both ends supported PCF [10] and nonlinear supported PCF [11]. For a more in-depth understanding of the dynamics of PCF with these different boundary conditions, Oyelade and Oyediran [12] have provided valuable insights. Among the various types of PCF, cantilevered PCF is a notable non-conservative system, primarily due to the work done by the fluid on the end of the pipe. Despite its seemingly simple construction, cantilevered PCF exhibits extremely rich mechanical behaviors and vibration characteristics. Some of the underlying mechanisms discovered in the study of cantilevered PCF can be applied to more practical systems, including marine risers, oil pipelines and pipe bundles in heat exchangers. For the purpose of this study, we focus solely on cantilevered PCF. The excitation of internal fluid flow plays a significant role in the vibration of cantilevered PCF. When the flow velocity exceeds a critical value, aptly termed the critical velocity, the amplitude of vibration magnifies due to positive feedback in the system [13]. The study of structure stability has garnered increasing interest due to its substantial impact on the performance and robustness of structures [14, 15]. A thorough analysis of dynamical stability is essential for comprehensively understanding the mechanical characteristics of a structure. The critical velocity, influenced by various factors, serves as an indicator of the degree of stability of the structure, with higher critical velocities corresponding to stronger stability.

Over the years, a significant amount of research has been conducted to study the dynamical stability and response of cantilevered PCF, leading to various notable contributions from different researchers. Yoon and Son [16] conducted a detailed study on the influences of angular velocity, fluid velocity and tip mass on the stability of rotating flexible cantilevered PCF, providing valuable insights into this specific scenario. In the realm of nonlinear dynamics control, Zhou et al. [17] introduced a nonlinear energy sink (NES) to control the nonlinear vibration of a cantilevered PCF. Their work demonstrated that increasing the mass and damping of the NES leads to improved critical velocity, and the optimal position of the NES is closely related to the flutter mode. Taking into consideration tip mass and an array of intermediate springs, Ghayesh et al. [18] delved into the three-dimensional dynamics of a cantilevered PCF, using both theoretical and experimental methods. In cases where clearance constraints are present in cantilevered PCF, Paidoussis et al. [19] utilized a cubic spring model to approximate the impact force. However, they later developed a smoothed trilinear spring model [20] to overcome issues of wrong impact force estimation when the vibration amplitude is lower than the gap size. To better understand the effects of clearance constraints, Ni et al. [21] conducted a comparative study on the vibration response of cantilevered PCF, using both the cubic spring model and the smoothed trilinear spring model. Liu et al. [22, 35] focused on the theoretical study of the vortex-induced vibrations of a cantilevered PCF with clearance constraints, employing the smoothed trilinear spring model to describe the system. Recently, Wang et al. [6, 23] investigated the three-dimensional dynamics of a cantilevered PCF with pulsating fluid, providing further insights into this specific dynamic behavior.

To further enhance the critical velocity of cantilevered PCF and improve its stability, researchers have explored various approaches and configurations [9, 24]. Zhou et al. investigated the stability of composite PCF, where they specifically examined the influence of elastic boundary conditions on the critical velocity. Their study revealed that incorporating a rotation spring had a positive impact on the critical velocity, leading to a more stable system. In the pursuit of better understanding the effects of different materials on stability, Dai et al. [25] studied a cantilevered PCF composed of two different materials. They found that if the softer segment was mounted at the clamped end, the PCF exhibited a lower critical velocity. In a related study by Bahaadini et al. [26], they investigated a composite cantilevered PCF supported at the free end by springs. Using the extended Galerkin technique, they determined that decreasing the value of the fiber orientation angle could increase the critical velocity of the system. ElNajjar and Daneshmand [27] aimed to increase the critical velocity of both horizontal and vertical cantilevered PCFs by introducing lumped masses and/or springs at different locations. Their results indicated that the critical velocity could be significantly improved by strategically placing a spring and a lumped mass at specific locations. In addition to these stability-oriented studies, Jiang et al. [28] provided a detailed investigation into the dynamics of PCF subjected to external axial flow. Meanwhile, Abdelbaki et al. [29] conducted a study on the dynamics of a vertical hanging pipe subjected to both internal and external axial flows. Their proposed model allowed for obtaining quantitative insights into the dynamical behavior beyond the onset of instability. These studies collectively contribute to a comprehensive understanding of the behavior and stability of cantilevered PCF under different conditions and boundary constraints. Such research plays a crucial role in enhancing the safety and performance of various engineering systems involving cantilevered PCF.

From the extensive review of previous literature, it becomes evident that the dynamical stability of cantilevered PCF has been thoroughly investigated concerning various constraints, materials, external flow and lumped masses. These studies have provided valuable guidelines to improve the stability of cantilevered PCF in different scenarios. However, in real-world applications, cantilevered PCF often encounters lateral distributed loads due to auxiliary facilities, such as insulation layers wrapped on transfer pipes in solar power applications [30] or firefighting pipes in cold region highway tunnels [31]. The investigation of the effects of lateral distributed load on the dynamical stability of cantilevered PCF presents a worthwhile research topic that deserves attention. Understanding the impact of lateral distributed load on the stability of the structure is crucial. The exploration of different load patterns is particularly intriguing, as it has the potential to provide insights into optimizing the load distribution to enhance the stability of cantilevered PCF. Moreover, considering the limitations of composite PCF and ideal lumped masses or springs, studying the impact of lateral distributed load on the stability of cantilevered PCF could offer an alternative method to improve the critical velocity and overall performance of the structure. Therefore, investigating the dynamical stability of cantilevered PCF under lateral distributed load is an essential step toward gaining a more comprehensive understanding of the mechanical behavior of this type of structure.

Motivated by the aforementioned research gap, the primary objective of this study was to conduct a comprehensive investigation into the dynamical stability of a cantilevered PCF under different lateral distributed loads. To achieve this, we employ the powerful differential quadrature method (DQM), a numerical technique capable of solving partial differential equations (PDEs) by transforming them into matrix equations. Concretely, the influence of the load patterns on the critical velocity is probed. Moreover, enlightened by the regularities obtained above, some suggestions prompting the dynamical stability of cantilevered PCF are provided.

2 Mathematical formulations

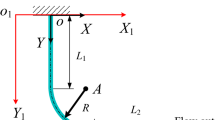
The problem under consideration involves a cantilevered PCF with various parameters, including pipe mass per unit length mp, Young’s modulus E, moment of inertia of principal section I, fluid mass per unit length mf and fluid flow velocity U. The governing equation of the system is derived using Newton’s second law, as previously done in Paidoussis’s work [1], with the additional contribution of a lateral distributed load. In this analysis, the fluid is assumed to be incompressible, and the flow is considered to be uniform and full developed in both the longitudinal and transverse cross sections of the pipe. In the absence of pipe extensibility, gravity, tension and structural damping, one obtains the governing equations for the lateral deflection of the cantilevered PCF based on the Euler–Bernoulli beam concept, as follows:

$${\text{EI}}\frac{{\partial^{4} w\left( {x,t} \right)}}{{\partial x^{4} }} + m_{{\text{f}}} U^{2} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} + 2m_{{\text{f}}} U\frac{{\partial^{2} w\left( {x,t} \right)}}{\partial x\partial t} + \left( {m_{{\text{p}}} + m_{{\text{f}}} } \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }}{ = }p\left( {x,t} \right)$$
(1)

where \(w\left( {x,t} \right)\) presents the lateral deflection relating to both longitudinal axis x and time t and\(p\left( {x,t} \right)\) denotes the time-dependent lateral distributed load.

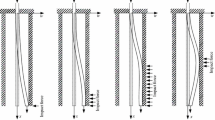
To investigate the influence of the lateral distributed load on the stability of the cantilevered PCF, we consider the presence of an auxiliary facility with a total mass M. To clarify the effects of the lateral distributed load, four different lad patterns are considered, namely uniform, descending, ascending and parabolic, as shown in Fig. 1a–d. These load patterns are defined as follows:

Fig. 1
figure 1

Four distributed loads

Full size image

Uniform distributed:

$$p_{1} \left( x \right) = - \frac{M}{L}\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }}$$
(2)

Descending distributed:

$$p_{2} \left( x \right) = - \frac{2M}{{L^{2} }}\left( {L - x} \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }}$$
(3)

Ascending distributed:

$$p_{3} \left( x \right) = - \frac{2M}{{L^{2} }}x\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }}$$
(4)

Parabolic distributed:

$$p_{4} \left( x \right) = - \frac{6M}{{L^{3} }}x\left( {L - x} \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }}$$
(5)

The following dimensionless quantities are introduced:

$$\begin{gathered} \xi = \frac{w}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} \eta = \frac{x}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta = \frac{{m_{{\text{f}}} }}{\Gamma },{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau = \frac{t}{{L^{2} }}\sqrt {\frac{{{\text{EI}}}}{{m_{{\text{f}}} + m_{{\text{p}}} + \frac{M}{L}}}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ u = {\text{UL}}\sqrt {\frac{{m_{{\text{f}}} }}{{{\text{EI}}}}} ,\sigma = \frac{\frac{M}{L}}{\Gamma },{\kern 1pt} {\kern 1pt} {\kern 1pt} \Gamma = m_{{\text{f}}} + m_{{\text{p}}} + \frac{M}{L} \hfill \\ \end{gathered}$$
(6)

As a result, the dimensionless formalizations of governing equations under four load patterns can be obtained by substituting Eqs. (2)–(6) into Eq. (1), namely

$$\frac{{\partial^{4} \xi }}{{\partial \eta^{4} }} + u^{2} \frac{{\partial^{2} \xi }}{{\partial \eta^{2} }} + 2\sqrt \beta u\frac{{\partial^{2} \xi }}{\partial \eta \partial \tau } + \frac{{\partial^{2} \xi }}{{\partial \tau^{2} }} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;\;0 \le \eta \le 1$$
(7)
$$\frac{{\partial^{4} \xi }}{{\partial \eta^{4} }} + u^{2} \frac{{\partial^{2} \xi }}{{\partial \eta^{2} }} + 2\sqrt \beta u\frac{{\partial^{2} \xi }}{\partial \eta \partial \tau } + \left[ {1 + \sigma \left( {1 - 2\eta } \right)} \right]\frac{{\partial^{2} \xi }}{{\partial \tau^{2} }} = 0,\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le \eta \le 1$$
(8)
$$\frac{{\partial^{4} \xi }}{{\partial \eta^{4} }} + u^{2} \frac{{\partial^{2} \xi }}{{\partial \eta^{2} }} + 2\sqrt \beta u\frac{{\partial^{2} \xi }}{\partial \eta \partial \tau } + \left[ {1 + \sigma \left( {2\eta - 1} \right)} \right]\frac{{\partial^{2} \xi }}{{\partial \tau^{2} }} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;0 \le \eta \le 1$$
(9)
$$\frac{{\partial^{4} \xi }}{{\partial \eta^{4} }} + u^{2} \frac{{\partial^{2} \xi }}{{\partial \eta^{2} }} + 2\sqrt \beta u\frac{{\partial^{2} \xi }}{\partial \eta \partial \tau } + \left[ {1 + \sigma \left( {6\eta - 6\eta^{2} - 1} \right)} \right]\frac{{\partial^{2} \xi }}{{\partial \tau^{2} }} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;\;0 \le \eta \le 1$$
(10)

As evident, when no additional lateral distributed loads are present (i.e., \(\sigma\) = 0), all these dimensionless equations reduce to the most conventional form describing the linear vibration behavior of PCF. Notably, varying load patterns result in different fourth terms on the left-hand sides of these equations, potentially leading to distinct stability characteristics of the cantilevered PCF.

The dimensionless boundary conditions of cantilevered PCF are expressed as:

$$\xi = \frac{\partial \xi }{{\partial \eta }} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \eta = 0$$
(11)
$$\frac{{\partial^{2} \xi }}{{\partial \eta^{2} }} = \frac{{\partial^{3} \xi }}{{\partial \eta^{3} }} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \eta = 1$$
(12)

3 Application of differential quadrature method

3.1 Description of DQM

The DQM has proven to be a highly effective method for solving eigenvalue problems in vibration systems, including beams and plates [32, 33]. By transforming the partial differential equation and the boundary conditions into a discrete matrix equation, the DQM eliminates the need for complicated integration calculations and the selection of trial functions typically required in weighted residual method, such as the Galerkin method. In this study, the DQM is used to solve the governing equation of the cantilevered PCF subjected to lateral distributed loads and to obtain the critical velocity. The lateral deflection of the cantilevered PCF is discretized at N nodes, and the fourth-order differential equation is transformed into a matrix equation with N by N dimensions. The eigenvalues of this matrix equation represent the squared natural frequencies of the system. By varying the flow velocity, we can determine the critical velocity at which the system undergoes a loss of stability.

Supposing that function f(x) is analytic and differentiable in the domain 0 ≤ x ≤ 1, we can divide this domain into N points. Let xi represent the ith point, where 1 ≤ i ≤ N. The rth-order derivative of function f(x) with respect to xi can be expressed as:

$$\left. {\frac{{{\text{d}}^{r} f\left( x \right)}}{{{\text{d}}x^{r} }}} \right|_{{x = x_{i} }} = \sum\limits_{j = 1}^{N} {A_{ij}^{\left( r \right)} f\left( {x_{j} } \right)} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,N$$
(13)

where Aij is the weighted coefficients. Obviously, the essence of DQM is that the derivative of function f(x) is approximated by a linear sum of the values at all discrete points.

If function f(x) is expressed by Lagrange polynomials, namely

$$f\left( x \right) = \sum\limits_{j = 1}^{N} {L_{j} \left( x \right)f\left( {x_{j} } \right)} = \sum\limits_{j = 1}^{N} {\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne j \end{subarray} }^{N} {\frac{{x - x_{k} }}{{x_{j} - x_{k} }}} f\left( {x_{j} } \right)}$$
(14)

Differentiating Eq. (14) with respect to x produces

$$f^{\left( 1 \right)} \left( x \right) = \sum\limits_{j = 1}^{N} {L_{j}^{\left( 1 \right)} \left( x \right)f\left( {x_{j} } \right)}$$
(15)

Comparing Eqs. (13) and (14), one obtains

$$A_{ij}^{\left( 1 \right)} = L_{j}^{\left( 1 \right)} \left( {x_{i} } \right) = \left\{ \begin{gathered} {{\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{N} {\left( {x_{i} - x_{k} } \right)} } \mathord{\left/ {\vphantom {{\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{N} {\left( {x_{i} - x_{k} } \right)} } {\left( {x_{i} - x_{j} } \right)\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne j \end{subarray} }^{N} {\left( {x_{j} - x_{k} } \right)} }}} \right. \kern-0pt} {\left( {x_{i} - x_{j} } \right)\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne j \end{subarray} }^{N} {\left( {x_{j} - x_{k} } \right)} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} i \ne j \hfill \\ - \sum\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{N} {A_{ik}^{\left( 1 \right)} } ,{\kern 1pt} {\kern 1pt} {\kern 1pt} i = j \hfill \\ \end{gathered} \right.$$
(16)

and the high-order derivatives are rendered by

$${\mathbf{A}}^{\left( r \right)} = {\mathbf{A}}^{{\left( {r - 1} \right)}} {\mathbf{A}}^{\left( 1 \right)} = {\mathbf{A}}^{\left( 1 \right)} {\mathbf{A}}^{{\left( {r - 1} \right)}}$$
(17)

where A is the assembled matrix of coefficients Aij.

To facilitate the treatment of boundary conditions, the ununiformed discrete points are defined in which the internal points are given by

$$x_{i} = \frac{1}{2}\left[ {1 - \cos \left( {\frac{i - 2}{{N - 3}}} \right)\pi } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 3,4, \cdots ,N - 2$$
(18)

and the rests are determined by

$$x_{1} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{2} = \delta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{N - 1} = 1 - \delta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{N} = 1$$
(19)

where \(\delta\) is a small enough value (10−4 in this study).

3.2 Formation of discrete matrix equation

Without loss of generality, application of DQM to Eq. (7) and the corresponding boundary conditions yields [34]

$$\ddot{\xi }_{j} + \sum\limits_{j = 1}^{N} {2\sqrt \beta uA_{ij}^{\left( 1 \right)} \dot{\xi }_{j} } + \sum\limits_{j = 1}^{N} {\left[ {A_{ij}^{\left( 4 \right)} + u^{2} A_{ij}^{\left( 2 \right)} } \right]} \xi_{j} = 0,{\kern 1pt} {\kern 1pt} \;\;\;{\kern 1pt} i = 3,4, \ldots ,N - 2$$
(20)
$$\xi_{1} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^{N} {A_{2j}^{\left( 1 \right)} \xi_{j} } = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^{N} {A_{N - 1j}^{\left( 2 \right)} \xi_{j} } = 0,{\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^{N} {A_{Nj}^{\left( 3 \right)} \xi_{j} } = 0$$
(21)

Combining these equations and rewriting in matrix form produce

$${\mathbf{M}{{\varvec{\ddot{\upxi}}} }} + {\mathbf{C}{\varvec{\dot{\upxi}}}} + {\mathbf{K}{\varvec{\upxi}} } = {\mathbf{0}}$$
(22)

in which M denotes the mass matrix, C the damping matrix, K the stiffness matrix and \({{\varvec{\upxi}}}\) the dimensionless lateral deflection vector.

In order to seek the eigenvalues, Eq. (22) is reformulated as

$$\left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{M}} \\ {\mathbf{M}} & {\mathbf{C}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{\ddot{\xi }}}} \\ {{\varvec{\dot{\xi }}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} { - {\mathbf{M}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{K}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{\dot{\xi }}}} \\ {\varvec{\xi }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {\mathbf{0}} \\ \end{array} } \right]$$
(23)

Therefore, it is converted to find the eigenvalues of the following matrix W [22, 35]

$${\mathbf{W}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{M}}^{{ - {\mathbf{1}}}} {\mathbf{K}}} & { - {\mathbf{M}}^{{ - {\mathbf{1}}}} {\mathbf{C}}} \\ \end{array} } \right]$$
(24)

Such eigenvalue \(\omega\) can be solved by QR decomposition, and it manifests the stability attributes of cantilevered PCF. Due to the presence of damping terms,\(\omega\) denotes generally complex number in which the imaginary part presents the vibration frequency and the real part refers to the trend of amplitude, and the stability of vibration system can thus be identified by the real part of \(\omega\), that is,

$$\left\{ {\begin{array}{*{20}l} {{\text{Re}} \left( \omega \right) > 0,{\kern 1pt} {\kern 1pt} } \hfill & {{\text{unstable}}} \hfill \\ {{\text{Re}} \left( \omega \right) < 0,} \hfill & {{\text{stable}}} \hfill \\ {{\text{Re}} \left( \omega \right) = 0,{\kern 1pt} } \hfill & {{\text{critical}}} \hfill \\ \end{array} } \right.$$
(25)

In the critical case, the dynamical stability of the cantilevered PCF can manifest in two types of instability: flutter and buckling. Flutter is a dynamic instability phenomenon characterized by two conjugate complex eigenvalues with zero real parts. This leads to periodical and non-decreasing motion caused by negative damping, resulting from positive feedback between the structure and fluid forces. As the fluid velocity increases, the motion magnifies due to this positive feedback, leading to flutter instability. This phenomenon is associated with non-conservative systems, such as the cantilevered PCF, where the presence of work done by the fluid on the end of the pipe enables flutter to occur once the fluid velocity reaches a critical value. On the other hand, buckling is a static instability phenomenon associated with a zero eigenvalue. In this case, the structure experiences a sudden collapse or deformation without any periodical vibration. Buckling generally occurs in conservative systems, but for cantilevered PCF, which is non-conservative, and buckling instability is not a concern.

4 Results and discussion

4.1 Convergence analysis

Prior to verifying the previously built model, a convergence analysis was carried out to determine the number of series terms required for accurate results. A program was executed to calculate the values of \(\omega\) for different N. Figure 2 illustrates the first four imaginary parts of \(\omega\), representing the first four natural frequencies of the cantilevered PCF under a uniform distributed load with \(\beta\) = 0.5 and u = 1.0, for varying values of N ranging from 9 to 30. It can be clearly seen that the first four natural frequencies converge rapidly as N reaches 15. To ensure accuracy, the present study set the relative error for convergence to be \(\varepsilon\) = 0.001, where \(\varepsilon = {{\left| {{\text{Im}} \left( {\omega^{\left( N \right)} } \right) - {\text{Im}} \left( {\omega^{{\left( {N - 1} \right)}} } \right)} \right|} \mathord{\left/ {\vphantom {{\left| {{\text{Im}} \left( {\omega^{\left( N \right)} } \right) - {\text{Im}} \left( {\omega^{{\left( {N - 1} \right)}} } \right)} \right|} {\left| {{\text{Im}} \left( {\omega^{\left( N \right)} } \right)} \right|}}} \right. \kern-0pt} {\left| {{\text{Im}} \left( {\omega^{\left( N \right)} } \right)} \right|}}\) and \(\omega^{\left( N \right)}\) is the circular frequency corresponding to N. According to this convergence examination, N = 15 is used for the uniform distributed load, as there are no further improvements observed beyond N = 15.

Fig. 2
figure 2

Convergence analysis for uniform distributed load

Full size image

Moreover, when u = 0, the cantilevered PCF essentially becomes a straight beam, and its natural frequencies can be calculated analytically. To illustrate the convergence of DQM, the first four natural frequencies when u = 0 and \(\beta\) = 0.5 are compared with exact solutions [36] in Table 1. The results show excellent agreement between the natural frequencies obtained by the DQM and the exact solutions, with a maximum relative error of only 0.02%.

Table 1 Natural frequencies when u = 0 and \(\beta\) = 0.5
Full size table

It should be pointed out that for different load patterns the value of N required for a convergent solution varies. Only the results are presented here: N = 16 for descending distributed load, N = 16 for ascending distributed load and N = 17 for parabolic distributed load. All subsequent studies in this work are conducted based on the convergent solutions.

4.2 Verification of model

In order to validate the proposed model for studying the stability of cantilevered PCF under different lateral loads, a validation procedure was performed. To fulfill this goal, the work by Dai et al. [25] was selected for comparison with our results, focusing on the scenario without lateral distributed load (\(\sigma\) = 0) and with a dimensionless parameter \(\beta\) = 0.5. For comparison purpose, a plot of the Argand diagram illustrating the relationship between \(\omega\) and u is displayed in Fig. 3. It was found that when u reaches 9.33, our model predicts that the real part of the third order mode becomes equal to zero. This result is remarkably close to the value obtained by Dai et al. [25]. Furthermore, the tendencies of the curves in this figure also exhibit a strong agreement with the findings reported by Dai et al. [25] in their corresponding figure (Fig. 3b). This close alignment between our model and the previously validated work by Dai et al. [25] provides robust evidence of the high reliability and accuracy of our model.

Fig. 3
figure 3

Relation between \(\omega\) and u when \(\beta\) = 0.5. a Our study, b Dai et al. [25]

Full size image

4.3 Comparisons with different load patterns

In order to investigate the dynamical stability of the targeted cantilevered PCF with different distributed load patterns. Some physical and geometrical quantities are defined as shown in Table 2. In this context, the key dimensionless parameters are calculated as:\(\beta\) = 0.1477and \(\sigma\) = 0.5804.

Table 2 Physical and geometrical quantities of cantilevered PCF
Full size table

Figure 4 presents the relation between \(\omega\) and u for different lateral load patterns. It can be seen that for all load ways,\({\text{Re}} \left( \omega \right)\) of the second order is the first to become positive as u increases, which means that the cantilevered PCF loses its stability firstly in the second order mode. In addition, as u continues to increase, \({\text{Re}} \left( \omega \right)\) of the fourth order tends to be positive as well. Consequently, at sufficiently high flow velocities, the vibration of the cantilevered PCF becomes divergent (flutter) due to the combined instabilities in the second- and fourth-order modes. To quantitatively study the influences of load patterns on the dynamical stability of the cantilevered PCF, the primary critical velocities are identified as illustrated in Fig. 5. An examination of Fig. 5 indicates that the critical velocities uc for various load patterns are 5.11, 6.23, 4.63 and 5.72, respectively. Comparing these critical velocities with the lowest value, we observe relative improvements of 10.37%, 34.56% and 23.54% for the uniform, descending and parabolic distributed load patterns, respectively. The results of this study suggest that the stability of the cantilevered PCF is strongly influenced by the type of lateral distributed load applied to it. The descending distributed load leads to the most significant improvement in dynamical stability, while the ascending distributed load results in the lowest critical velocity. The parabolic distributed load pattern provides even greater stability than the uniform distributed load. This study highlights the importance of considering different distributed load patterns in the design and optimization of cantilevered PCF systems. Practical applications, such as nuclear island pipes, could benefit from placing insulation layers or damping sandbags more at the restrained end of the pipe to achieve a higher critical velocity and enhance the dynamical stability of the system.

Fig. 4
figure 4

Argand diagrams for a uniform distributed load, b descending distributed load, c ascending distributed load and d parabolic distributed load

Full size image
Fig. 5
figure 5

Critical velocity with different load patterns

Full size image

In comparison with a study on the stability of a horizontal PCF with an additional lumped mass [27], our results underscore the significance of understanding the stability characteristics of cantilevered PCF under various distributed load patterns. By carefully considering and optimizing the load distribution, engineers can achieve improved stability and performance for cantilevered PCF in real-world applications.

4.4 Effect of lateral load on critical velocity

In the context above, we have established that the descending distributed load pattern exhibits the highest critical velocity compared to other load patterns. In this part, the influence of mass of auxiliary facility affiliated with the cantilevered PCF, represented by the parameter M/L, on the critical velocity uc within different load patterns is discussed in detail. Understanding this relationship is crucial for determining the amount of facility to deploy.

Figure 6 shows the plot of the critical velocities uc for different values of M/L where the scatters denote the calculated critical velocities and the dotted lines are the fitted curves defined by the following formulations:

Fig. 6
figure 6

Critical velocity versus M/L for a uniform distributed load, b descending distributed load, c ascending distributed load and d parabolic distributed load

Full size image

Uniform distributed:

$$u_{c} = \frac{{11.245 + 1.471\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}{{1 + 0.338\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}$$
(26)

Descending distributed:

$$u_{c} = \frac{{9.829 + 0.831\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}{{1 + 0.156\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}$$
(27)

Ascending distributed:

$$u_{c} = \frac{{12.553 + 2.509\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}{{1 + 0.614\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}$$
(28)

Parabolic distributed:

$$u_{c} = \frac{{9.595 + 1.289\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}{{1 + 0.253\left( {{M \mathord{\left/ {\vphantom {M L}} \right. \kern-0pt} L}} \right)}}$$
(29)

It should be pointed out that the predictions by the formulated critical velocity curves may not be reliable in the vicinity of M/L = 0. Therefore, caution should be exercised when interpreting the results in this range. Analyzing Fig. 6, we observe that for all load patterns, the critical velocities initially drop rapidly and then gradually decrease as M/L increases. Notably, when M/L < 30, the critical velocities exhibit high sensitivity to changes in M/L. However, as M/L continues to increase, the critical velocities tend to converge. Based on the tendencies of the fitted curves and the analysis of Eqs. (26)–(29), the convergent critical velocities for various load patterns are estimated to be approximately 4.37, 5.36, 4.10 and 5.11, respectively. In practical engineering scenarios, if the dimensionless velocities are lower than these convergent values, the affiliated facility can be deployed discretionarily as long as it does not result in any structural strength failure. However, if the dimensionless velocities exceed these convergent critical velocities, careful consideration should be given to the designation of the mass of the affiliated facility.

4.5 Critical velocity and instability mode

Observation of the dimensionless governing equations of cantilevered PCF in different load patterns reveals a strong relationship between the critical velocity and two key parameters:\(\beta\) and \(\sigma\). The variations of these parameters can lead to changes in the critical velocity and the corresponding instability mode. Therefore, it is essential to carefully investigate how the critical velocity and instability mode are affected by changes in \(\beta\) and \(\sigma\). Notably, the sum of \(\beta\) and \(\sigma\) is constrained by \(\beta + \sigma = 1 - \frac{{m_{p} }}{\Gamma }\) and the value of \(\beta\) is altered by changing the value of M/L. Figure 7 presents the values of \(\beta\) and \(\sigma\) for various M/L. It should be noted that only \(\beta\) will be emphasized here because \(\sigma\) changes with \(\beta\). For uniform distributed load, only \(\beta\) occurs.

Fig. 7
figure 7

Values of \(\beta\) and \(\sigma\) for different M/L

Full size image

In Fig. 8a, the relationship between critical velocity uc and \(\beta\) is depicted for the uniform distributed load pattern. It is observed that as the value of \(\beta\) increases, the critical velocity also rises. However, what is particularly interesting is the presence of three distinct jumps in the critical velocity curve at \(\beta\) = 0.29, 0.69 and 0.90. These points indicate that the critical velocity is highly sensitive to the value of \(\beta\). According to the instability mode, the figure can be divided into three distinct regions based on the value of \(\beta\). For the range 0.1 < \(\beta\) < 0.32 the instability arises from the flutter of the third mode. When 0.32 < \(\beta\) < 0.90, the instability arises from the flutter of the third mode. When 0.9 < \(\beta\), the cantilevered PCF experiences flutter associated with the fourth mode. The results in this figure indicate that for higher \(\beta\), namely lower auxiliary facility mass ratio, the stability of the cantilevered PCF could be enhanced and the instability modes are changeable as well.

Fig. 8
figure 8

Critical velocity versus \(\beta\) for a uniform distributed load, b descending distributed load, c ascending distributed load and d parabolic distributed load

Full size image

Figure 8b presents the critical velocity uc for different \(\beta\) in descending distributed load pattern. A notable positive correlation can be observed between \(\beta\) and the critical velocity uc. When \(\beta\) is less than approximately 0.195, the critical velocity increases almost linearly with \(\beta\). According to the instability mode, the \(\beta - u_{c}\) plane can be divided into two distinct regions: 0.01 < \(\beta\) < 0.0394 and 0.0394 < \(\beta\) < 0.34. In the range 0.01 < \(\beta\) < 0.0394, the cantilevered PCF loses its stability owing to the flutter of the first mode. When 0.0394 < \(\beta\) < 0.34, the instability is caused by the flutter of the second mode. Notably, there is a sensitive range of approximately 0.25 < \(\beta\) < 0.27, in which even a slight change of \(\beta\) results in significant alteration to the critical velocity. The results in this figure also indicate that for higher \(\beta\) the stability of cantilevered PCF could be enhanced, and the instability modes are also changeable.

Figure 8c presents the critical velocity uc for different \(\beta\) in ascending distributed load pattern. Similar to the previous figures, the critical velocity increases in direct proportion to the value of \(\beta\). What the difference from the previous load patterns is that the cantilevered PCF loses its stability in the second mode for whole range of \(\beta\). The sensitive range in ascending distributed load pattern is nearly 0.32 < \(\beta\) < 0.33. This figure also indicates that a higher \(\beta\) brings higher stability of cantilevered PCF but the instability modes are not changeable.

Figure 8d displays the critical velocity uc for different \(\beta\) in parabolic distributed load pattern. As can be seen, the distribution of the scatters is analogical with that of ascending distributed load. In this case, the cantilevered PCF switches to instability due to the second-mode flutter for the entire range of \(\beta\). Similar to the other load patterns, a higher value of \(\beta\) corresponds to higher stability of the cantilevered PCF, and the instability modes are settled. In addition, the sensitive range in this parabolic distributed load pattern is approximately 0.3 < \(\beta\) < 0.32.

5 Conclusions

This study focuses on investigating the dynamical stability of a cantilevered pipe conveying fluid (PCF) under different distributed lateral inertial load patterns. To this end, the differential quadrature method (DQM) was used to calculate the eigenvalues of the related problems. The reliability of the results was verified through exact solutions and published data. Based on the results of the calculations, several conclusions can be drawn:

  1. (1)

    The critical velocity and instability mode are significantly influenced by the parameter in the uniform distributed load pattern. For higher values of \(\beta\), the stability of the cantilevered PCF can be enhanced, and the instability modes are changeable. Three distinct regions are identified based on the value of \(\beta\), each corresponding to different instability modes.

  2. (2)

    For the ascending and parabolic distributed load pattern, the critical velocity increases as \(\beta\) rises. In this case, the cantilevered PCF becomes unstable due to the second-mode flutter for the entire range of \(\beta\).

  3. (3)

    For the descending distributed load pattern, the critical velocity also increases with \(\beta\), but the cantilevered PCF loses stability primarily through the first mode and then by the second mode.

  4. (4)

    The uniform load pattern is not a superior scheme for enhancing the stability. In order to improve the dynamical stability of cantilevered PCF, more loads should be deployed at the constrained end (descending) or at the middle part (parabolic).