Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints

Abstract

In this paper, the nonlinear dynamics of a cantilevered pipe conveying fluid interacting with two support walls on both sides is first investigated. The main goal of this study is to explore how the dynamics of a cantilevered pipe will perform in the presence of two support walls along the pipe axis. The interacting force is defined as impact in order to simulate the impacting effects for a pipe with various flow velocities. The impact force is modeled either by a cubic spring or by a trilinear spring. The nonlinear equations of motion are discretized via Galerkin’s method, and the discretized equations are solved by using a fourth-order Runge–Kutta method. Results show that the pipe would periodically impact the walls when the flow velocity is just beyond the critical value. When the flow velocity is sufficiently higher, however, the pipe may behave different patterns of contacting the walls, such as point contact and segments contact. Periodic, quasi-periodic motions, as well as chaotic oscillations are observed in such a pipe system.

1 Introduction

Pipes in heat exchangers have historically been the most used components in nuclear power plants and chemical process plants. They were also the most troublesome elements in these fields. These industries utilize high thermal efficiency shell and heat exchanger designs to avoid failure. Performance requirements often require the devices to be able to work under high coolant velocities and to be flexible tubes, which in turn would cause pipes to experience excessive flow-induced vibrations. A large number of studies have been made on flow-induced vibrations due to the corresponding significance [1–4]. Focuses of flow-induced vibrations were put on these fields in understanding the mechanisms of pipes conveying fluid.

Pipe/support system is often loose-fitting due to manufacturing considerations that require their clearances to facilitate pipe bundle assembly and to accommodate thermal expansion. The numbers and locations of supports are always chosen to control the vibration’s stability. When the flow-induced vibration exceeds the clearance in the supports, the pipe would collide the inner side of the support devices. According to the mutual theory of force, a similar effect would be exerted on the tube. Since destruction may occur during the vibrations, concentrations have been put on tube/support systems in the past decades to study the dynamical behaviors.

Indeed, extensive experimental researches have been conducted to study the nonlinear responses of pipe/support systems. Weaver and Schneider [5] conducted a wind-tunnel study to determine the effect of flat bar supports on the cross-flow-induced responses of heat exchanger U-tubes. Various support geometries were discussed. It was found that the geometry of supports can affect the dynamics of the tube due to variances in the contact configurations. Chen et al. [6] conducted three series of tests to evaluate the effects of tube to support clearance on the tube’s dynamic characteristics and instability phenomena for tube arrays in cross-flow. Vivid phenomena have been obtained to describe the interaction of the tube/support systems [7–9]. Experimental tests on the dynamical behaviors of pipe/support systems were also investigated by many other researchers. The interested reader is referred to Refs. [1–3].

On the other hand, numerical approaches, such as finite element method, have been utilized to simulate the nonlinear responses of the tube/support system. Roger and Pick [10] adopted the finite element method to simulate the vibration against the support plate of a heat exchanger tube. Simulation results obtained a good accuracy compared with the behavior of a cantilevered tube apparatus with two-dimensional sinusoidal excitation. Ghayesh et al. [11] have explored the three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring and an end-mass, both theoretically and experimentally. Two separated researches were combined by them, and the numerical solutions have shown good agreement with experiment results qualitatively and quantitatively. To understand the post-instability behavior of a tube array in cross-flow, Wang et al. [12–14] developed an improved model with the consideration of the nonlinearity associated with the mean axial extension of the tube array. The numerical results show that, when increasing flow velocity just beyond a critical value, a post-Hopf limit-cycle motion occurs. By using the proposed model, vibration amplitude can be predicted for amplitude of the limit-cycle motion. Sauve and Teper [15] have developed a solution strategy to solve the nonlinear equation of motion for nonlinear impact problems of tube/support systems. Single-span, two-span, and multi-span models are described and compared. Impact force occurs at only several points along the pipe while not anywhere throughout the pipe. The solution strategy is developed implicitly which is unconditionally stable. One of the salient features is that time step is variable, which ensures that solution errors are minimized. Rao et al. [16] considered friction and damping in their calculations which would make the results more approximate to practical. The model includes the effect of clearances and friction at supports, mass, stiffness, structural and fluid damping, and damping and mass associated with the fluid squeeze film phenomenon at supports. It predicts tube vibration for given excitation, tube displacements, reactions, and wear rate at tube supports.

The aforementioned investigations have made great experimental and numerical results that were useful for further studies and practical engineering. However, these researches only concentrated on the problems of single or several point contacts between the pipe and support. It means that, for a finite length pipe/support system, the contact locations lie on several points along the pipe axis. Hassan et al. [17] conducted calculations of single-span tube/support and multi-span tube/support systems to study the dynamic behavior due to point contact considering various contacting geometries. Results have obtained a good agreement to that made by Sauve and Teper which is the original work related to point contact. Another study performed by Hassan et al. [18] provided a means of representing tube/support contact as a combination of edge and segmental contact. The contact segment was unknown and determined artificially according to the researcher’s interests. The selection of the location of the segment could affect the performance of the tube/support system.

In this paper, the nonlinear impact dynamics of a pipe/support system is studied by considering a vertical cantilevered pipe conveying fluid subjected to support walls. The objective of this work is to explore various interesting dynamics of the fluid-conveying pipe when segments contacts rather than point impacts occur. It is expected that the obtained results are helpful in controlling the stability of vibro-impact systems in heat exchanger devices. The impact force is described as either a cubic spring or a smoothed trilinear spring force distributed along the pipe axis. Thus, unlike previous work, we assume that the contact may occur anywhere along the pipe at any time compared to Ref. [15]. To the author’s knowledge, this is the first study ever on such a system. To verify the effectiveness of the proposed model, results of the degenerated model are compared with those predicted by Païdoussis and Semler [21], to explore the effect of the distributed motion constraints.

2 Model development

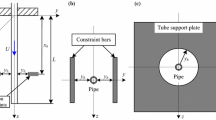
A schematic representation of the system is shown in Fig. 1a–d. The system consists of a tubular pipe of length $L$, flexural rigidity EI, density $\rho _\mathrm{p}$, mass per unit length $m$, and coefficient of Kelvin–Voigt damping $a$, conveying fluid of density $\rho _\mathrm{f}$ and mass per unit length $M$, with flow velocity $U$. The support walls are modeled as a cubic spring, which imposes the impact force continuously on the pipe when part of the pipe has a lateral displacement. The support walls are also modeled as a smoothed trilinear spring, which allows a gap between the pipe and walls. In this case, impact force occurs when the lateral displacement exceeds the gap.

Fig. 1

Schematic of the pipe/support contact configurations

There are several classifications of tube motion for this system. These motions may be classified as impact, sliding, or combined impact and sliding [19, 20]. Figure 1a shows a point contact. Contact or impact force occurs at the edge point of the tube tip. In the case of relatively low flow velocities, the vibration or impact pattern can be described by this configuration. Figure 1b–d shows three possible contacts of line contact during the pipe’s oscillation. Interesting dynamical phenomena for pipes conveying fluid would occur based on these different contact configurations.

Full derivations of the equation are presented, using a modified version of Hamilton’s principle. In the derivation of the equation, the following assumptions are included: (1) The fluid is incompressible; (2) the flow is of constant velocity and free from pulsation; (3) the pipe behaves like a nonlinear Euler–Bernoulli beam (the diameter is small compared to the length); (4) the strain in the pipe is considered small; (5) shear deformation is neglected; (6) the pipe centerline is inextensible; (7) taking into account of support walls, the impact forces are assumed to be imposed on the centerline of the pipe. Based on these conditions, the equation of motion of a cantilevered tube conveying fluid was given by Païdoussis and Semler [21], which was suitable for open system. The equation is modified here to take into account the contact force term, which is due to the impact between the pipe and support walls. The resultant equation of motion in dimensionless form of the pipe is given as follows:

$$\begin{aligned}&\alpha {\dot{\eta }}^{{\prime }{\prime }{\prime }{\prime }}+{\eta }^{{\prime }{\prime }{\prime }{\prime }}+2u\sqrt{\beta }{\dot{\eta }}^{\prime }\nonumber \\&\quad +\,{\eta }^{{\prime }{\prime }}\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] +\gamma {\eta }^{\prime }+\ddot{\eta } \nonumber \\&\quad +\,2u\sqrt{\beta }{\dot{{\eta }}^{\prime }}{\eta }^{\prime 2}+{\eta }^{{\prime }{\prime }}{\eta }^{\prime 2}\left[ {u^{2}-\frac{3}{2}\gamma \left( {1-\xi } \right) } \right] \nonumber \\&\quad -\,\frac{1}{2}\gamma {\eta }^{\prime 3}+3{\eta }^{\prime }{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }}+{\eta }^{{\prime }{\prime 3}} \nonumber \\&\quad +\,{\eta }^{\prime }\int _0^\xi \left\{ {\dot{\eta }}^{\prime 2}-2u\sqrt{\beta }{\eta }^{\prime }{\dot{\eta }}^{{\prime }{\prime }}\right. \nonumber \\&\quad \left. -{\eta }^{\prime }{\eta }^{{\prime }{\prime }{\prime }}\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] +{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }{\prime }} \right\} \mathrm{d}\xi \\&\quad -\,{\eta }^{{\prime }{\prime }}\int _\xi ^1 \int _0^\xi \left\{ {\dot{\eta }}^{\prime 2}-2u\sqrt{\beta }{\eta }^{\prime }{\dot{\eta }}^{{\prime }{\prime }}\right. \nonumber \\&\quad \left. -{\eta }^{\prime }{\eta }^{{\prime }{\prime }{\prime }}\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] +{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }{\prime }} \right\} \mathrm{d}\xi \mathrm{d}\xi \nonumber \\&\quad -\,{\eta }^{{\prime }{\prime }}\int _\xi ^1 {\!\left( \! {-\gamma {\eta }^{\prime 2}+2u\sqrt{\beta }{\eta }^{\prime }{\dot{\eta }}^{\prime }+u^{2}{\eta }^{\prime }{\eta }^{{\prime }{\prime }}+{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }}} \right) \mathrm{d}\xi }\nonumber \\&\quad +\,f\left( \eta \right) =0\nonumber \end{aligned}$$

(1)

In Eq. (1), $\eta$ ($\xi , \tau$) is the lateral deflection of the tube. $\alpha ,\beta , \gamma$, respectively, represent the coefficient of Kelvin–Voigt damping, mass ratio of the fluid and system, and gravity effect. $u$ denotes the dimensionless flow velocity of the internal fluid. The dot and prime on the variables, respectively, denote the derivatives with respect to time $\tau$ and the coordinate of the centerline of the tube $\xi$. The three integrals are a description of kinetic and potential energies, which are needed when using Hamilton’s principle. The dimensionless variables are of the following form in transforming between dimensional variables:

$$\begin{aligned} \xi= & {} \frac{x}{L},\eta =\frac{w}{L},\tau =\sqrt{\frac{{\textit{EI}}}{m+M}}\frac{t}{L^{2}},u=\sqrt{\frac{M}{{\textit{EI}}}}{\textit{LU}},\\ \alpha= & {} \sqrt{\frac{{\textit{EI}}}{m+M}}\frac{a}{L^{2}},\beta =\frac{M}{m+M},\gamma =\frac{m+M}{{\textit{EI}}}L^{3}g \end{aligned}$$

Compared to the equation used in [21], this equation is an extension of point impact to line impact along the pipe axis. $f$($\eta$) in Eq. (1) is the impact force due to impact of the tube and walls. Various mathematical models may be used to represent properly the impact forces. The first approximation used by Paidoussis et al. [22, 23] was to model the restraining forces by a cubic spring. A more realistic representation was that used by Paidoussis et al. involving a smoothed trilinear spring model. Impact force is described as

$$\begin{aligned} f\left( \eta \right) =\kappa _c \eta ^{3} \end{aligned}$$

(2)

or

$$\begin{aligned} f\left( \eta \right) =\kappa _t \left( {\eta -\frac{1}{2}\left( {\left| {\eta +\delta } \right| -\left| {\eta -\delta } \right| } \right) } \right) ^{r} \end{aligned}$$

(3)

in which $\kappa _\mathrm{c}$ and $\kappa _\mathrm{t}$ are the nondimensional stiffness for describing the impact force and $\delta$ is the nondimensional gap between the two walls. In this paper, $\kappa _\mathrm{c}=10^{5}$ for cubic spring model and $\kappa _\mathrm{t}=5.6\times 10^{5}, r=3$, and $\delta =0.044$ for smoothed trilinear spring model are chosen for calculations, which have been proved to be in good accordance with experiment results according to Paidoussis and Li [22].

3 Discretization

The infinite-dimensional model is discretized by the Galerkin’s technique, with the cantilevered beam eigenfunctions $\varphi _{j}$ ($\xi$). These eigenfunctions are used as a suitable set of base functions with $q_{j}$($\tau$) being the corresponding generalized coordinates; thus:

$$\begin{aligned} \eta \left( {\xi ,\tau } \right) =\sum _{j=1}^N {\varphi _j \left( \xi \right) q_j \left( \tau \right) }, \end{aligned}$$

(4)

where $N$ is the number of modes taken into calculations. Substituting Eq. (4) into Eq. (1), multiplying by $\varphi _{i}$($\xi$), and integrating from 0 to 1 leads to

$$\begin{aligned}&\ddot{q}_i +c_{ij} \dot{q}_j +k_{ij} q_j +\alpha _{ijkl} q_j q_k q_l +\beta _{ijkl} q_j q_k \dot{q}_l\nonumber \\&\quad +\,\gamma _{ijkl} q_j \dot{q}_k \dot{q}_l +f_i \left( {q_j ,q_k ,q_l } \right) =0 \end{aligned}$$

(5)

where $c_{ij}, k_{ij}, \alpha _{ijkl}, \beta _{ijkl}$, and $\gamma _{ijkl}$ are coefficients computed from the integrals of the eigenfunctions $\varphi _{i}$($\xi$), analytically or numerically [24, 25]. In this paper, we have calculated these nonlinear terms’ coefficients via matrix transformation method. All the nonlinear terms in Eq. (5) may be written in the following form

$$\begin{aligned}&\left[ {\sum _{j=1}^N {L_1 \left( {\varphi _j } \right) T_1 \left( {q_j } \right) } } \right] \left[ {\sum _{k=1}^N {L_2 \left( {\varphi _k } \right) T_2 \left( {q_k } \right) } } \right] \nonumber \\&\quad \times \left[ {\sum _{l=1}^N {L_3 \left( {\varphi _l } \right) T_3 \left( {q_l } \right) } } \right] \end{aligned}$$

(6)

$L_{1}, L_{2}, L_{3}$ and $T_{1}, T_{2}, T_{3}$ are differential operators related to space domain and time domain, respectively. If necessary, they can be the original function, first-order, second-order, third-order, or fourth-order derivatives of the space and time variables. Purpose of this proposal is to put the space coordinates on the left side and put the time coordinates on the right side. It may lead to convenient integration of the nonlinear terms in Eq. (1). By extending dimensions of the coefficient matrices

$$\begin{aligned}&\overline{\mathbf{L}_{1\times N^{3}} } \left( {\tilde{\varphi }_j ,\tilde{\varphi }_k ,\tilde{\varphi }_l } \right) \nonumber \\&\quad =\mathbf{A}_L \left[ {L_1 \left( {\varphi _j } \right) } \right] _{1\times N} \mathbf{B}_L \big [ {L_2 \left( {\varphi _k } \right) } \big ]_{N\times N^{2}}\nonumber \\&\quad \quad \times \mathbf{C}_L \big [ {L_3 \left( {\varphi _l } \right) } \big ]_{N^{2}\times N^{3}}\end{aligned}$$

(7)

$$\begin{aligned}&\overline{\mathbf{T}_{N^{3}\times 1} } \left( {\tilde{q}_j ,\tilde{q}_k ,\tilde{q}_l } \right) \nonumber \\&\quad =\mathbf{D}_T \left[ {T_1 \left( {q_j } \right) } \right] _{N^{3}\times N^{2}} \mathbf{E}_T \big [ {T_2 \left( {q_k } \right) } \big ]_{N^{2}\times N}\nonumber \\&\quad \quad \times \mathbf{F}_T \big [ {T_3 \left( {q_l } \right) } \big ]_{N\times 1} \end{aligned}$$

(8)

Equation (6) can be written as

$$\begin{aligned}&\left[ {L_1 \left( {\varphi _j } \right) T_1 \left( {q_j } \right) } \right] \left[ {L_2 \left( {\varphi _k } \right) T_2 \left( {q_k } \right) } \right] \left[ {L_3 \left( {\varphi _l } \right) T_3 \left( {q_l } \right) } \right] \nonumber \\&\quad =\overline{\mathbf{L}_{1\times N^{3}} } \left( {\tilde{\varphi }_j ,\tilde{\varphi }_k ,\tilde{\varphi }_l } \right) \overline{\mathbf{T}_{N^{3}\times 1} } \left( {\tilde{q}_j ,\tilde{q}_k ,\tilde{q}_l } \right) \end{aligned}$$

(9)

in which the sign “$\sim$” on the top of each variable has the same meaning as $L_{i }$ and $T_{i.}$ Left multiplying $\varphi _{i}$ and integrating along the pipe, we would get coefficients of the nonlinear terms, i.e., $\alpha _{ijkl}, \beta _{ijkl}$, and $\gamma _{ijkl}$. Applying these quantities to Eq. (5), the nonlinear equations of motion reduce to the following simple form

$$\begin{aligned} \ddot{\mathbf{q}}+\mathbf{C}{\dot{\mathbf{q}}}+\mathbf{Kq}+\mathbf{g}\left( \mathbf{q},{\dot{\mathbf{q}}} \right) +\mathbf{f}\left( \mathbf{q} \right) =\mathbf{0}, \end{aligned}$$

(10)

where $\mathbf{q}=\left[ {q_1 ;\;q_2 ;\;\cdots ;\;q_N } \right] , {\dot{\mathbf{q}}}=\left[ \dot{q}_1 ;\;\dot{q}_2 ;\;\cdots ;\dot{q}_N \right]$, and $\ddot{\mathbf{q}}=\left[ {\ddot{q}_1 ;\;\ddot{q}_2 ;\;\cdots ;\;\ddot{q}_N } \right]$ are the tube’s displacement, velocity, and acceleration vectors, respectively; C, K, g, and f denote the damp matrix (including the model damping terms and the gyroscopic force terms), stiffness matrix, nonlinear terms, and impact force vector, respectively. Elements expressions of these matrices and variables are given in “Appendix.” For the purpose of numerical computation, we define $\mathbf{p}= \dot{\mathbf{q}}$ and z=[q; p]; Eq. (10) is then reduced to its first-order form:

$$\begin{aligned} \dot{\mathbf{z}}=\mathbf{Az}+\mathbf{G}\left( \mathbf{z} \right) +\mathbf{F}\left( \mathbf{z} \right) , \end{aligned}$$

(11)

where

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{ll} \mathbf{0}&{}\quad \mathbf{I} \\ {-\mathbf{K}}&{}\quad {-\mathbf{C}} \\ \end{array} }} \right] , \quad \mathbf{G}=\left[ {{\begin{array}{l} \mathbf{0} \\ {-\mathbf{g}} \\ \end{array} }} \right] ,\,\hbox {and}\,\mathbf{F}=\left[ {{\begin{array}{l} \mathbf{0} \\ {-\mathbf{f}} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(12)

They are $2N\times 2N, 2N\times 1, 2N\times 1$ matrices, respectively. Solutions of q and p consist of the displacement and velocity at any point $\xi$ along the pipe.

As pointed out by Paidoussis and Li [23], simulation results from models with five modes and higher are qualitatively the same both in magnitude and in shape when the integration step size is sufficiently small, and thus, a five-mode model ($N=5$) will be used in all the simulations to follow. But, for the specialty of the impact problem, the $N=5$ model may not satisfy the accuracy of solutions. More extensive calculations have been done in the next section. It was found that $N=5$ is the more preferable. Solutions of Eq. (11) are obtained by using the fourth-order Runge–Kutta integration algorithm with variable step size. The initial conditions employed are $q_{1}(0)=0.001$ and $p_{i}(0)=0$. In the numerical scheme of the effective judgment of impact force on account of the proposed model in Eq. (3), a modified unit step function is adapted. In the case of ${\vert }\eta {\vert }<\delta$, no impact occurs, and in the case of ${\vert }\eta {\vert }>\delta$, impact occurs. It physically means that the pipe vibrates between the two walls without contacting them. If the absolute value of the lateral displacement is greater than half of the gap, impact force occurs and direction of the force is opposite to the displacement. Under this condition, impact force is obtained by integration from Eq. (3) during every time step and direction of the impact force is opposite to that of the displacement. Numerical results will be presented in the form of bifurcation diagrams, time traces, and vibration shapes.

4 Results

4.1 Validation of the algorithm

In this subsection, in order to validate the correctness of the present algorithm, the impact model is first degenerated from line contact to point contact, which is the case of a constrained pipe conveying fluid studied by Païdoussis and Semler [21]. The point impact in the work conducted by Païdoussis and Semler [21] is replaced by a microsegment of the wall supports. In this case, the length of the walls is set to be microscale, saying its length is $\delta =0.001$. Thus, the model is quite like that used in the work by Païdoussis. For comparison purpose, the cubic spring constraint is taken into calculation and $\kappa _\mathrm{c}=10^{5}$ is chosen. The system parameters are $\alpha =0.005, \beta =0.213$, and $\gamma =26.75$, and the impacting location is $\xi _\mathrm{b}=0.75$. The results in Fig. 2 are in good agreement with those obtained by Païdoussis and Semler [21], with relative error 2 %. This demonstrates the validation of the line contact model which will be used in the following analysis.

Fig. 2

Phase portraits and power spectral for $N=2, \kappa _\mathrm{c}=10^{5}, \xi _\mathrm{b}=0.75, \alpha =0.005, \beta =0.213, \gamma =26.75$, and for different values of flow velocity $u$

4.2 Validation of the $N=5$ model

In Sect. 3, it has been mentioned that Paidoussis and Li [22] had adopted the model number $N=5$ in their numerical computation for the reason of its good agreement with experiment. In this subsection, we will first discuss the possible choice of $N$ when studying the nonlinear dynamics of the present pipe model. For that purpose, numerical results are represented in Fig. 3 based on the trilinear spring model. As shown in Fig. 3, the system undergoes a change in bifurcation diagram with different model number $N$ and it has reached a stable state when $N$ is chosen to be 5 or greater than that. The system experiences chaotic motion with flow velocity 9.8 and then becomes periodic with flow velocity 12.3, under the model number of 5 and 6. From this perspective, it can be seen that in this paper, $N=5$ is a good choice both in approximation calculation and cutting the cost of calculation.

Fig. 3

Bifurcation diagram for a $N=3$, b $N=4$, c $N=5$, and d $N=6$ with the smoothed trilinear impact model and $\xi =1$

4.3 Case I: The impact force is modeled as a cubic spring

In this case, the impact force, which is described as a cubic spring, is imposed on the cantilevered pipe conveying fluid. Planar motion of impacting dynamics will be investigated with the same system parameters as that adopted in the work conducted by Païdoussis and Selmer [21].

Based on the research of Païdoussis and Selmer [21], the point impact is modified as line impact along the pipe. Any part on the pipe may be in contact with the one or two sides of the walls for the vibration induced by the fluid flowing in the pipe. Under this consideration, the nonlinear impact force is imposed on throughout the pipe. Once the amplitude of its lateral displacement satisfies impact condition, reactive forces from the walls will be exerted on the pipe. In this way, the pipe may exhibit many contact patterns. Several typical patterns have been shown in Fig. 1a–d. Figure 4 shows the bifurcation diagram of the displacement amplitudes of the tip of the pipe.

Fig. 4

Bifurcation diagram for the system with cubic impact model and $\xi =1$

Interesting behaviors of flow-induced vibration with impact effects come out as we can see in Fig. 4. The impact force is a cubic nonlinear spring approximation. Impact force occurs once the pipe has a very small lateral deflection. During the flow-induced vibration, the pipe suffers nonlinear forces throughout its axis. Using the cubic spring model, the pipe would undergo periodic motions when the flow velocity is beyond the critical value, as can be seen in Fig. 4. The pipe experiences a Hopf bifurcation at $u=8.05$. A period-1 oscillation occurs from this point. It is of interest to note that as shown in Fig. 4, the system jumps from a period-1 motion to a period-3 motion at $u=12.65$. After a period-3 motion with larger flow velocity at $u=13.15$, the system goes back to a period-1 motion.

Thus, we can obtain the point from Fig. 4 that, the system is easier to remain periodic with the cubic spring impact model. The impact force happens anywhere that has a nonzero lateral displacement, and the nonlinear impact force has a positive effect on eliminating the system’s complex behaviors such as chaotic motion.

The vibration shapes, phase portraits, and time traces for three different flow velocities are shown in Fig. 5.

Fig. 5

Time traces, phase portraits, and pipe shapes under various dimensionless flow velocities. a Flow velocity $u=10$, b flow velocity $u=12.8$, c flow velocity $u=13.9$

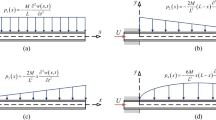
The support walls restrain the pipe and hence the pipe can only vibrate with limited displacement amplitudes. At some particular flow velocities, the system shows contact patterns of point contact and line contact. The contact is defined as a nonzero contact force, which is referred to the impact force. The line contact pattern is presented to a light extent for this force. Impact forces for flow velocity $u=13.9$ along the pipe at a particular time are shown in Fig. 6. The line contact patterns are demonstrated by the distribution of nonlinear impact forces.

Fig. 6

Impact forces and the corresponding contact patterns; the three contact patterns are in accordance with Fig. 1b, c, and d, respectively

4.4 Case II: The impact force is modeled as a smoothed trilinear spring

As pointed out in Sect. 4.3, the impact force occurs once the pipe has lateral deflection throughout its axis. In practice, there is always a gap between the pipe axis and the walls. No impact happens if the amplitude of displacement is smaller than the gap. Païdoussis and Li [21] commented that the cubic spring model is mathematically convenient, but it cannot model the physical situation perfectly.

In this subsection, therefore, the dynamical behaviors of the system will be re-examined by using a smoothed trilinear spring impact model. In the following calculations, the value of the impact model is the same as that adopted in Sect. 4.2. Numerical results have been obtained for the motions of the pipe based on the trilinear spring model. The bifurcation diagram for the response of the pipe at $\xi =1$ is shown in Fig. 7.

Fig. 7

Bifurcation diagram for the system with trilinear spring model and $\xi =1$

The gap between the pipe and wall is 0.044. Since the pipe is constrained by the walls, its amplitude will not become infinite. As shown in Fig. 7, the vibration response is periodic in a small range from 8.05 to 8.73. For flow velocity in this range, the pipe vibrates periodically with constraint or impact forces (see Fig. 8a). With increasing flow velocity, the amplitude of lateral deflections becomes larger and strong impacting effect occurs between the pipe and walls. Strictly speaking, no periodic motion can be found in the flow velocity range $8.73< u <12.52$. The pipe would again undergo periodic motions when the flow velocity reaches to 12.52. At $u=12.52$, the absolute value of the negative displacement of the pipe is smaller than that of the positive displacement. It is also noted that the absolute value of the negative displacement is smaller than the gap between the pipe and the wall. The pipe shape at this flow velocity is exactly the one when impacting occurs mainly on one side of the pipe, which is depicted in Fig. 8b.

Fig. 8

Pipe shape under various flow velocities; a $u=8.5$ and b $u=13$

Several other sample results for various flow velocities are illustrated in Fig. 9 for $\xi =1$. At $u=8.5$, the response of the pipe is periodic. For $u=11.5$, the pipe oscillates quasi-periodically due to the strong effect of impact force. At $u=13$, however, the pipe system becomes periodic again. It is seen in Fig. 9b that repeatedly impacting behavior happens when the pipe contacts the walls. The time trace of the pipe at $\xi =1$ indicates that the pipe tip is bouncing forth and back on the ‘edge’ of the walls. This behavior in this work may be also defined as an impacting action.

Fig. 9

Phase portrait and time traces for various flow velocities of the smoothed trilinear impact model and at $\xi =1$; a $u=8.5$, b $u=11.5$, and c $u=13$

Figure 10 shows the impact force’ envelop along the pipe when $u=13$. From this figure, it is easily seen that when the flow velocity is $u=13$, the impact action mainly happens on one side of the walls. The pipe has lateral deflection on both sides of course, which can be seen in Fig. 8b, but for a wide range of $\xi$, there is no impact force on the other side since a gap exists between the pipe and walls. If the vibration amplitude of the pipe is smaller than the gap, the impact force becomes zero.

Fig. 10

Envelop of the impact force acting on the system, with flow velocity $u=13$

5 Conclusion

In-plane dynamics of a cantilevered pipe conveying fluid interacting with two support walls on both sides is first investigated. In the current model, it is assumed that a pipe conveying fluid is restrained by two support walls which are modeled as two kind of nonlinear springs. This restraining/impact force is included in the nonlinear equation of motion. The equation of motion is integrated numerically, and the dynamical responses and impacting behaviors are examined. A degenerated model is introduced first to illustrating the effectiveness of the model and numerical scheme. Good agreement is obtained compared to those in [21].

Other interesting results have been obtained with impacting force modeled by either a cubic spring or a smoothed trilinear spring. By using the cubic spring impact model, nonlinear impact forces are distributed along the pipe even for very small displacement of the pipe. Results show that this impact-related force is one of the principle nonlinearities of the system. The pipe with cubic spring would undergo periodic motions even for sufficiently high flow velocities. Both period-1 and period-3 motions are observed. For the smoothed trilinear spring model, there is zero value of impact force when the lateral displacement is smaller than the gap. This model is more realistic in simulating the impact behaviors. Effective impact action happens only for amplitude of displacement exceeds the gap limit. Results show that the pipe undergoes periodic oscillations when the flow velocity is just beyond the critical value of flutter instability. However, complex behaviors such as quasi-periodic motion would occur for much higher flow velocities. Chaotic oscillations in a wide range of flow velocity are possible. It is shown that the effect of distributed motion constraints on the nonlinear dynamics of pipe conveying fluid is significant.

This project is a preliminary study of impact/contact dynamics of pipes conveying fluid subjected to wall supports. Further exploring of impact models between pipe bundles and supports will be conducted in the subsequent researches.

Appendix

In this part, we will give the elements of the matrices mentioned in Sect. 3. As described above, the nonlinear terms in Eq. (5) may be written in Eq. (6). As can be seen that, the nonlinear terms are the multiplication of three terms, which are all related to the eigenfuncitons, such as ${\eta }^{\prime }{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }}$ and ${\eta }^{{\prime }{\prime }}\int _\xi ^1 {\int _0^\xi {{\eta }^{\prime }{\dot{{\eta }}^{{\prime }{\prime }}}\mathrm{d}\xi } \mathrm{d}\xi }$. After applying the Galerkin’s technique, the multiplication has the form of (13). After using the transforming scheme, Eq. (6) would be of that form of Eqs. (7), (8), and (9). Expressions of the elements of matrices in these equations are given below (taking ${\eta }^{\prime }{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }}$, for example). As to the integrals of in some of the nonlinear terms, they could be applied on the corresponding terms when the transformation has been completed.

$$\begin{aligned} \mathbf{A}_L= & {} \left[ {{\begin{array}{lllll} {{\varphi }^{\prime }_1 }&{} {{\varphi }^{\prime }_2 }&{} \cdots &{} {{\varphi }^{\prime }_N } \\ \end{array} }} \right] _{1\times N} \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{B}_L= & {} \left[ {{\begin{array}{lllllllllllll} {{\varphi }^{{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }}_N }&{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }}_N }&{} &{} 0&{} &{} &{} \\ &{} &{} 0&{} &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N\times N^{2}} \end{aligned}$$

(14)

$$\begin{aligned} \mathbf{C}_L= & {} \left[ {{\begin{array}{llllllllllllllllllll} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N }&{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N }&{} &{} &{} &{} &{} &{} 0&{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N }&{} &{} &{} &{} &{} \\ &{} &{} &{} 0&{} &{} &{} &{} &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N^{2}\times N^{3}} \end{aligned}$$

(15)

$$\begin{aligned} \mathbf{D}_T= & {} \left[ {{\begin{array}{llllll} {{q}^{\prime }_1 }&{} &{} &{} &{} \\ &{} {{q}^{\prime }_1 }&{} &{} 0&{} \\ &{} &{} {{q}^{\prime }_1 }&{} &{} \\ &{} 0&{} &{} \ddots &{} \\ &{} &{} &{} &{} {{q}^{\prime }_1 } \\ {{q}^{\prime }_2 }&{} &{} &{} &{} \\ &{} {{q}^{\prime }_2 }&{} &{} 0&{} \\ &{} &{} {{q}^{\prime }_2 }&{} &{} \\ &{} 0&{} &{} \ddots &{} \\ &{} &{} &{} &{} {{q}^{\prime }_2 } \\ &{} &{} \cdots &{} &{} \\ {{q}^{\prime }_N }&{} &{} &{} &{} \\ &{} {{q}^{\prime }_N }&{} &{} 0&{} \\ &{} &{} {{q}^{\prime }_N }&{} &{} \\ &{} 0&{} &{} \ddots &{} \\ &{} &{} &{} &{} {{q}^{\prime }_N } \\ \end{array} }} \right] _{N^{3}\times N^{2}}\end{aligned}$$

(16)

$$\begin{aligned} \mathbf{E}_T= & {} \left[ {{\begin{array}{lllll} {{q}^{{\prime }{\prime }}_1 }&{} &{} &{} 0 \\ &{} {{q}^{{\prime }{\prime }}_1 }&{} &{} \\ &{} &{} \ddots &{} \\ 0&{} &{} &{} {{q}^{{\prime }{\prime }}_1 } \\ {{q}^{{\prime }{\prime }}_2 }&{} &{} &{} 0 \\ &{} {{q}^{{\prime }{\prime }}_2 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {{q}^{{\prime }{\prime }}_2 } \\ 0&{} \cdots &{} \cdots &{} \\ {{q}^{{\prime }{\prime }}_N }&{} &{} &{} 0 \\ &{} {{q}^{{\prime }{\prime }}_N }&{} &{} \\ &{} &{} \ddots &{} \\ 0&{} &{} &{} {{q}^{{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N^{2}\times N}\end{aligned}$$

(17)

$$\begin{aligned} \mathbf{F}_T= & {} \left[ {{\begin{array}{l} {{q}^{{\prime }{\prime }{\prime }}_1 } \\ {{q}^{{\prime }{\prime }{\prime }}_2 } \\ \vdots \\ {{q}^{{\prime }{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N\times 1} \end{aligned}$$

(18)

Substituting (13) to (18) into Eq. (9), left multiplying $\varphi _i \left( \xi \right)$ and integrating along the pipe, we would get the coefficients of the nonlinear terms.

$$\begin{aligned} \alpha _{ijkl}= & {} \int _0^1 {\left[ {u^{2}-\frac{3}{2}\gamma \left( {1-\xi } \right) } \right] \varphi _i } \varphi _j ^{\prime \prime }\varphi _k ^{\prime }\varphi _l ^{\prime }\mathrm{d}\xi \nonumber \\&-\,\frac{1}{2}\gamma \int _0^1 {\varphi _i } \varphi _j ^{\prime }\varphi _k ^{\prime }\varphi _l ^{\prime }\mathrm{d}\xi +3\int _0^1 {\varphi _i } \varphi _j ^{\prime }\varphi _k ^{\prime \prime }\varphi _l ^{\prime \prime \prime }\mathrm{d}\xi \nonumber \\&+\int _0^1 {\varphi _i } \varphi _j ^{\prime \prime }\varphi _k ^{\prime \prime }\varphi _l ^{\prime \prime }\mathrm{d}\xi \nonumber \\&-\int _0^1 {\varphi _i \varphi _j ^{\prime }\int _0^\xi {\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] \varphi _k ^{\prime }\varphi _l ^{\prime \prime \prime }\mathrm{d}\xi } } \mathrm{d}\xi \nonumber \\&+\int _0^1 {\varphi _i } \varphi _j ^{\prime }\int _0^\xi {\varphi _k ^{\prime \prime } \varphi _l^{{\prime }{\prime }{\prime }{\prime }}}\mathrm{d}\xi \mathrm{d}\xi \nonumber \\&+\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime }}\int _\xi ^1 \int _0^\xi \left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] \nonumber \\&\times \,\varphi _k ^{\prime }\varphi _l ^{{\prime } {\prime }{\prime }}\mathrm{d}\xi \mathrm{d}\xi \mathrm{d}\xi \nonumber \\&-\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime } }\int _\xi ^1 {\int _0^\xi {\varphi _k ^{{\prime }{\prime } }\varphi _l^{{\prime }{\prime }{\prime }{\prime }}\mathrm{d}\xi } } \mathrm{d}\xi \mathrm{d}\xi \nonumber \\&+\,\gamma \int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime }}\int _\xi ^1 {\varphi _k ^{\prime }\varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi \nonumber \\&-\,u^{2}\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime } }\int _\xi ^1 {\varphi _k ^{\prime }\varphi _l ^{{\prime }{\prime } }\mathrm{d}\xi } \mathrm{d}\xi \nonumber \\&-\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime }}\int _\xi ^1 {\varphi _k ^{{\prime }{\prime }}\varphi _l ^{{\prime }{\prime }{\prime }}\mathrm{d}\xi } \mathrm{d}\xi \end{aligned}$$

(19)

$$\begin{aligned} \beta _{ijkl}= & {} 2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{\prime }_j {\varphi }^{\prime }_k {\varphi }^{\prime }_l \mathrm{d}\xi }\nonumber \\&-\,2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{\prime }_j \int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime \prime }\mathrm{d}\xi } \mathrm{d}\xi } \nonumber \\&+\,2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{{\prime }{\prime }}_j \int _\xi ^1 {\int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime \prime }\mathrm{d}\xi } \mathrm{d}\xi } \mathrm{d}\xi }\nonumber \\&-\,2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{{\prime }{\prime }}_j \int _\xi ^1 {{\varphi }^{\prime }_k \varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi }\end{aligned}$$

(20)

$$\begin{aligned} \gamma _{ijkl}= & {} \int _0^1 {\varphi _i {\varphi }^{\prime }_j \int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi }\nonumber \\&-\int _0^1 {\varphi _i {\varphi }^{{\prime }{\prime }}_j \int _\xi ^1 {\int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi } \mathrm{d}\xi } \end{aligned}$$

(21)

Coefficients of the linear terms are defined as follows:

$$\begin{aligned} m_{ij}= & {} \int _0^1 {\varphi _i \varphi _j \mathrm{d}\xi } =\delta _{ij}\end{aligned}$$

(22)

$$\begin{aligned} c_{ij}= & {} \alpha \int _0^1 {\varphi _i \varphi _j ^{{\prime }{\prime } {\prime } {\prime } }\mathrm{d}\xi } +2u\sqrt{\beta }\int _0^1 {\varphi _i \varphi _j ^{\prime }\mathrm{d}\xi }\end{aligned}$$

(23)

$$\begin{aligned} k_{ij}= & {} \int _0^1 {\varphi _i \varphi _j ^{{\prime } {\prime } {\prime } {\prime } }\mathrm{d}\xi } +\int _0^1 {\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] \varphi _i \varphi _j ^{{\prime }{\prime } }\mathrm{d}\xi }\nonumber \\&+\,\gamma \int _0^1 {\varphi _i \varphi _j ^{\prime }\mathrm{d}\xi } \end{aligned}$$

(24)

As to elements in $\mathbf{f}\left( \mathbf{q} \right)$, it is obtained by left multiplying $\varphi _i \left( \xi \right)$ and integrating along the pipe. That is:

$$\begin{aligned} f_i =\int _0^1 {\varphi _i f\left( {\sum _{s=1}^N {\varphi _s q_s } } \right) \mathrm{d}\xi }. \end{aligned}$$

(25)