Nonlinear analysis of L-shaped pipe conveying fluid with the aid of absolute nodal coordinate formulation

Abstract

By adopting the absolute nodal coordinate formulation, a novel and general nonlinear theoretical model, which can be applied to solve the dynamics of combined straight-curved fluid-conveying pipes with arbitrary initially configurations and any boundary conditions, is developed in the current study. Based on this established model, the nonlinear behaviors of a cantilevered L-shaped pipe conveying fluid with and without base excitations are systematically investigated. Before starting the research, the developed theoretical model is verified by performing three validation examples. Then, with the aid of this model, the static deformations, linear stability and nonlinear self-excited vibrations of the L-shaped pipe without the base excitation are determined. It is found that the cantilevered L-shaped pipe suffers from the static deformations when the flow velocity is subcritical, and will undergo the limit-cycle motions as the flow velocity exceeds the critical value. Subsequently, the nonlinear forced vibrations of the pipe with a base excitation are explored. It is indicated that period-n, quasi-periodic and chaotic responses can be detected for the L-shaped pipe, which has a strong relationship with the flow velocity, excitation amplitude and frequency.

1 Introduction

The system of pipes conveying fluid, as a one of the typical and simplest fluid–structure interaction system, always appears in various engineering fields, including the nuclear industry, marine oil extraction, aerospace engineering and so on. However, due to the properties and working environment of the fluid-conveying pipe, it may suffer from the flow-induced vibrations or the forced vibrations under the action of the internal flow, external flow or external excitation. And these vibrations may cause catastrophic damage, so it is quite necessary to understand the mechanism of the pipes conveying fluid. In addition, the system of the fluid-conveying pipe can display rich dynamical behaviors and has become a new paradigm in the field of dynamics, which has been pointed out by Païdoussis [1]. Thus, due to these facts, the literature concerned with the dynamics of pipes conveying fluid has emerged in the past few decades [2,3,4,5,6,7,8,9].

The existing literature in this topic was mainly concerned with fluid–structure interaction of the straight or curved pipes conveying fluid. To predict the stability of the straight fluid-conveying pipes, the linear theoretical model was first developed. It was found that the cantilevered pipes would lose stability by flutter [10], while the buckling instability would occur in the system of the fluid-conveying pipes with both ends supported [11, 12]. Because of this found, the researchers hope to further determine the dynamic responses of the pipe when the flow velocity become sufficiently high. Inspired by this, the famous nonlinear theoretical model for the pipes conveying fluid, including the cantilevered pipes and pipes supported at both ends, was established in the study of Semler et al. [13], with the aid of the extended Hamilton’s principle. For a long time, this theoretical model has been widely used by researchers to study the dynamics of the fluid-conveying pipe system. Unfortunately, this pipe model could only deal with the situation when the deformation of the pipe was considered to be small. To solve this problem, several large-deformation-based theoretical models were developed based on the absolute nodal coordinate formulation (ANCF) [14, 15] or the geometrically accurate beam model [16, 17]. As another kind of pipe commonly used in engineering, the curved fluid-conveying pipe has also been received extensive attention from scholars [18,19,20,21,22,23,24,25,26,27]. In these studies, three different theories, including the conventional inextensible theory, the extensible theory and the modified inextensible theory, were mainly employed to develop the different theoretical models that could predict the stability and dynamics of a semi-circular pipe conveying fluid with both ends supported. However, it should be pointed out that these models can only simulate the pipe with an initially circular configuration, and are not suitable for the pipe with arbitrary initially configurations. This kind of pipe is also common in engineering. As a consequence, a few theoretical models, which could deal with the pipes with arbitrary shapes, were proposed [28,29,30,31,32,33]. For instance, based on the Hamilton’s extended principle, a nonlinear theoretical model was proposed by Sinir [28] to investigate the nonlinear dynamics of a slightly curved fluid-conveying pipe with both ends supported. It was found that the periodic and chaotic motions could be observed in this considered pipe system. To explore the three-dimensional dynamics of the curved fluid-conveying pipes, Łuczko and Czerwiński [29] developed a model, which is general and well applicable to analysis of a wide variety of systems. In addition, this proposed model could handle various boundary conditions easily. In quite recently, the statics and dynamics of the slightly curved cantilevered fluid-conveying pipes with four different initial shapes were first explored in the study of Zhou et al. [30] by employing the absolute nodal coordinate formulation. Some interesting and sometimes unexpected results were found based on their numerical calculations.

Although the above-mentioned literature covers a wide range of pipe models, including the straight-shaped pipes, circular-shaped pipes and even the pipes with special or arbitrary configurations, they all appeared singly and the combination of them was not taken into account. In fact, due to some site restrictions or special requirements, the straight-curved combination pipes may often be used in engineering, such as L-, U-, Z- and J-shaped pipes. Thus, it is worth to explore the dynamics of the straight-curved combination fluid-conveying pipe. Indeed, a few researchers have studied this kind of pipe [34,35,36,37,38,39,40,41,42,43]. In 1990, a linear analytical model that include the Poisson coupling was proposed by Lesmez et al. [34] to perform the modal analysis of vibrations in liquid-filled piping system. Two examples, including single pipe bend and piping system with U-bend, were given to verify this proposed model. The dynamic stiffness method of the wave approach was employed by Koo and Yoo [36] to determine the natural frequencies, frequency response functions and the stability of the Korea Advanced Liquid Metal Reactor (KALIMER) IHTS hot leg piping system. A 3D straight-curved combination pipe conveying fluid was taken into account in the study of Dai et al. [38], who mainly explored the influence of the internal flow velocity on the natural frequencies of the considered pipe system with the aid of transfer matrix method. In addition, it was found that the steady combined force could have a great impact on the vibration characteristics of the curved-shaped pipe. As pointed out by Wen et al. [40], the nonlinear force caused by the deformation of the straight pipe segment, static deformation and geometrical nonlinearity of the pipe could have a considerable influence on the dynamics of the straight-curved combination pipe. Unfortunately, this effect was not taken into account in the study of Koo and Yoo [36], and only the static axial force caused by static deformation of the pipe was contained in the Dai et al.’s model [38]. Thus, a modified four segmental kinetic theoretical model was established by Wen et al. [40] to explore the nonlinear static deformation and the linear stability of the straight-curved pipe conveying fluid. Their numerical results indicated that the effect of the static deformation of the pipe on the natural frequencies of the pinned–pinned pipe or the pinned-sliding bearing-pinned pipe was pronounced, while for pinned–pinned pipe, this effect could be ignored. Based on the active learning Kriging model, Zhao et al. [41] first investigated the resonance failure of the straight-curved combination pipe conveying fluid and a failure performance function was built. The finite volume method was applied by Guo et al. [42] to study fluid-induced vibrations of the Z-shaped pipe with different supports and the effects of the supports on the vibration amplitude of the pipeline. The corresponding results demonstrated that the elastic support could effectively reduce the vibration amplitude and was also relatively safe. More recently, the vibration and in-plane wave propagation analysis of a L-shaped fluid-conveying pipe with multiple supports was performed in the study of Wu et al. [43] with the help of impedance synthesis method. This method had been proved by the corresponding experiments. It was noted that the periodic supports could effectively suppress the vibration level of the considered pipe system for a given frequency window.

The present study focuses on exploring the static deformation, linear stability, nonlinear self-excited and nonlinear forced vibrations for a straight-curved combination fluid-conveying pipe with the aid of absolute nodal coordinate formulation (ANCF). The calculation method of ANCF is applied to establish an effective theoretical model to deal with nonlinear dynamical behaviors of arbitrary initial configurations of pipes (e.g., L-, Z-, U- and J-shaped pipes) conveying fluid, which is the uniqueness of this paper. It should be pointed out that the model developed in present work has four advantages compared with those models mentioned in Ref. [31,32,33,34,35,36,37,38,39,40]: (i) it can determine the extremely large-amplitude vibrations of the soft straight-curved combination pipes conveying fluid; (ii) it can be applied to the straight-curved combination pipes with arbitrary initially shapes, such as L-, Z-, U- and J-shaped pipes; (iii) it can be applied to any boundary conditions, such as pinned–pinned, clamped-free, pinned–pinned-free and so on; (iv) it can handle not only the self-excited vibrations but also the forced oscillations.

2 Theoretical model of the pipe system

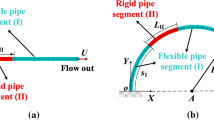
Figure 1 shows the schematic of the cantilevered L-shaped fluid-conveying pipe subjected to a base excitation. X₁ and Y₁ represent the global coordinates. The base excitation is in the X-direction, and can be expressed in the form of w_b = D₀sin(Ωt), where D₀ and Ω are the amplitude and frequency of the base excitation, respectively. In addition, it can be found in Fig. 1 that this pipe system consists of two straight pipe segments and one curved pipe segment. The length of the straight pipe segment near the clamped end is L₁, and the length near the free end is L₂. As for the curved pipe segment, it is a 1/4 arc of radius R. It should be mentioned that, in this paper, the three pipe segments are assumed to be equal in length, which means L₁ = L₂ = πR/2 = L/3, where L is the length of the whole L-shaped pipe. Moreover, the mass per unit length of the L-shaped pipe is m and the flexural rigidity is EI. The fluid flowing in the pipe has mass per unit length M and mean velocity U. The effects of structural damping and gravitational force are not considered, and the fluid is assumed to be plug flows and incompressible.

Fig. 1

Schematic of cantilevered L-shaped fluid-conveying pipe subjected to a base excitation

The absolute nodal coordinate formulation (ANCF) is employed here to establish a nonlinear theoretical model for the considered L-shaped fluid-conveying pipe. The L-shaped pipe in this paper is considered to be slender and can only vibrate in the X–Y plane; hence, the 2-node planar curved ANCF elements [44] are chosen to discretize this pipe system. Since we have chosen the ANCF to deal with this problem, correspondingly, the extended Lagrange equation introduced by Irschik and Holl [45] is required to derive the nonlinear governing equations of this L-shaped pipe system. And this equation can be written as follows [45]:

$$ \frac{{\text{d}}}{{{\text{d}}t}}\frac{\partial T}{{\partial {\dot{\mathbf{q}}}}} - \frac{\partial T}{{\partial {\mathbf{q}}}} + \int_{S}^{{}} {{\text{d}}{\mathbf{a}} \cdot \left( {{\mathbf{v}}_{{\mathbf{F}}} - {\mathbf{v}}_{{\mathbf{P}}} } \right)\frac{{\partial T^{\prime}}}{{\partial {\dot{\mathbf{q}}}}}} - \int_{S}^{{}} {{\text{d}}{\mathbf{a}} \cdot \left( {\frac{{\partial {\mathbf{v}}_{{\mathbf{F}}} }}{{\partial {\dot{\mathbf{q}}}}} - \frac{{\partial {\mathbf{v}}_{{\mathbf{P}}} }}{{\partial {\dot{\mathbf{q}}}}}} \right)T^{\prime}} = {\mathbf{Q}} $$

(1)

where T denotes the total kinetic energy of the system, q and ${\dot{\mathbf{q}}}$ are, respectively, the generalized coordinate vector and velocity vector, and Q represents the vector of generalized forces. The two surface integrals shown in Eq. (1) should be only evaluated at the pipe element boundaries S. In addition, v_F and v_P, respectively, denote the absolute velocities of the pipe and fluid; T ′ represents the kinetic energy per unit volume of the fluid; and da is an oriented surface element on S.

After determining all the terms shown in Eq. (1) and making a series of operations, we can obtain the nonlinear dynamic equation of the pipe element subjected to a base excitation, which can be found in Eq. (2). For the sake of brevity, we put the detailed process of formula derivation in Appendix A, and the interested readers can refer to it.

$$ {\mathbf{M}}_{e}^{*} {\ddot{\mathbf{q}}}^{*} + {\mathbf{C}}_{e}^{*} {\dot{\mathbf{q}}}^{*} + {\mathbf{K}}_{e}^{*} {\mathbf{q}}^{*} + {\mathbf{N}}_{e}^{*} ({\mathbf{q}}^{*} ) = {\mathbf{0}} $$

(2)

where ${\mathbf{M}}_{e}^{*}$, ${\mathbf{C}}_{e}^{*}$ and ${\mathbf{K}}_{e}^{*}$ are the linear mass, damping and stiffness matrices for the pipe element, respectively. The damping matrices C_e^* are derived from Coriolis fluid force.${\mathbf{N}}_{e}^{*} ({\mathbf{q}}^{*} )$ represents the vector of nonlinear terms. These matrices and the vector of nonlinear terms can be given as follows:

$$ \begin{aligned} & {\mathbf{M}}_{e}^{*} = \int_{0}^{l} {{\mathbf{S}}^{T} {\mathbf{S}}{\text{d}}x} \\ & {\mathbf{C}}_{e}^{*} = u\sqrt \beta \int_{0}^{l} {\frac{{{\mathbf{S}}^{T} {\mathbf{S}^{\prime}} - {\mathbf{S}^{\prime}}^{T} {\mathbf{S}}}}{{\sqrt {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } }}{\text{d}}x} + u\sqrt \beta L\left( {{\mathbf{S}}^{T} {\mathbf{S}}|_{x = l} - {\mathbf{S}}^{T} {\mathbf{S}}|_{x = 0} } \right) \\ & {\mathbf{K}}_{e}^{*} = - \left( {u^{2} + \frac{1}{2}\Pi_{0} } \right)\int_{0}^{l} {\frac{{{\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}}}}{{{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} }}{\text{d}}x} + u^{2} L\left( {\frac{{{\mathbf{S}}^{T} {\mathbf{S}^{\prime}}}}{{\sqrt {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } }}|_{x = l} - \frac{{{\mathbf{S}}^{T} {\mathbf{S}^{\prime}}}}{{\sqrt {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } }}|_{x = 0} } \right) \\ & {\mathbf{N}}_{e}^{*} ({\mathbf{e}}) = \frac{1}{2}\Pi_{0} \int_{0}^{l} {\frac{{{\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} {\mathbf{q}}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} }}{{\left( {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } \right)^{2} }}{\text{d}}x} \\ & + \int_{0}^{l} {\left( {\frac{{\left[ {\left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S}^{\prime\prime}} + {\mathbf{S^{\prime\prime}}}^{T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)} \right]{\mathbf{q}}^{*} {\mathbf{q}}^{*T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S^{\prime\prime}q}}^{*} }}{{\left( {{\mathbf{q}}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} } \right)^{3} }} - \frac{{3{\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} {\mathbf{q}}^{*T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S^{\prime\prime}q}}^{*} {\mathbf{q}}^{*T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S^{\prime\prime}q}}^{*} }}{{\left( {{\mathbf{q}}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} } \right)^{4} }}} \right){\text{d}}x} \\ & - \int_{0}^{l} {\frac{{{\mathbf{q}}_{0}^{*T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S^{\prime\prime}q}}_{0}^{*} }}{{\left( {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } \right)^{3/2} }}\left( {\frac{{\left[ {\left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S^{\prime\prime}}} + {\mathbf{S^{\prime\prime}}}^{T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)} \right]{\mathbf{q}}^{*} }}{{\left( {{\mathbf{q}}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} } \right)^{3/2} }} - \frac{{3{\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} {\mathbf{q}}^{*T} \left( {{{\tilde{\mathbf{I}}{\mathbf{S}}^{\prime}}}} \right)^{T} {\mathbf{S^{\prime\prime}q}}^{*} }}{{\left( {{\mathbf{q}}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}^{*} } \right)^{5/2} }}} \right){\text{d}}x} \\ & + \int_{0}^{l} {{\mathbf{S}}^{T} {\text{d}}x} \left[ {\begin{array}{*{20}c} { - a_{0} \omega^{2} \sin \left( {\omega t} \right)} \\ 0 \\ \end{array} } \right] - u\sqrt \beta \int_{0}^{l} {\frac{{{\mathbf{S}^{\prime}}^{T} }}{{\sqrt {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } }}{\text{d}}x} \left[ {\begin{array}{*{20}c} {a_{0} \omega \cos \left( {\omega t} \right)} \\ 0 \\ \end{array} } \right] \\ & + u\sqrt \beta \left( {\frac{{{\mathbf{S}}^{T} }}{{\sqrt {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } }}|_{x = l} - \frac{{{\mathbf{S}}^{T} }}{{\sqrt {{\mathbf{q}}_{0}^{*T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0}^{*} } }}|_{x = 0} } \right)\left[ {\begin{array}{*{20}c} {a_{0} \omega \cos \left( {\omega t} \right)} \\ 0 \\ \end{array} } \right] \\ \end{aligned} $$

(3)

In addition, in order to obtain the above expressions, we have introduced the following quantities:

$$ \begin{aligned} & \begin{array}{*{20}c} {\begin{array}{*{20}c} {\tau = \left( {\frac{EI}{{M + m}}} \right)^{\frac{1}{2}} \frac{t}{{L^{2} }},} & {{\mathbf{q}}^{*} = \frac{{\mathbf{q}}}{L},} & {{\mathbf{q}}_{0}^{*} = \frac{{{\mathbf{q}}_{0} }}{L},} \\ \end{array} } & {u = \left( \frac{M}{EI} \right)^{\frac{1}{2}} UL,} \\ \end{array} \\ & \begin{array}{*{20}c} {\beta = \frac{M}{M + m},} & {\Pi_{0} = \frac{{A_{P} L^{2} }}{I},} & {d_{0} = \frac{{D_{0} }}{L},} & {\omega = \Omega \sqrt {\frac{{\left( {M + m} \right)L^{4} }}{EI}} ,} \\ \end{array} \\ \end{aligned} $$

(4)

According to the concept of the traditional finite element method, these matrices and vector for those pipe elements can be assembled into the corresponding global matrices and vector, and then, we can have the nonlinear governing equation of the whole L-shaped pipe system

$$ {\mathbf{M}{\ddot{e}}} + {\mathbf{C}{\dot{e}}} + {\mathbf{Ke}} + {\mathbf{N}}({\mathbf{e}}) = {\mathbf{0}} $$

(5)

where e means the generalized coordinate vector; M, C and K are the assembled mass, damping and stiffness matrices for the whole pipe system, respectively; N(e) represents the assembled vector of nonlinearities. Then, based on this equation and with the aid of fourth-order Runge–Kutta integration algorithm, the nonlinear dynamic behaviors of the L-shaped pipe subjected to base excitation can be easily determined.

In addition to the nonlinear dynamic responses, the static deformations of the L-shaped pipe under the action of the internal flow also need to be determined since this considered pipe contains the curved pipe segments. According to the suggestion in Ref. [30], to determine the static deformation, we can divide the generalized coordinate vector e into two parts: a static part and a perturbation about the static part, leading to the following expression

$$ {\mathbf{e}} = {\mathbf{e}}_{s} + \Delta {\mathbf{e}} $$

(6)

where e_s is the generalized coordinate vector of the static equilibrium configuration, and Δe denotes the perturbation about the static equilibrium position. By substituting Eqs. (6) into Eqs. (5), and deleting all the time-dependent terms, the static equilibrium equation of the L-shaped pipe system can be obtained

$$ {\mathbf{Ke}}_{s} + {\mathbf{N}}({\mathbf{e}}_{s} ) = {\mathbf{0}} $$

(7)

Based on the equilibrium equation shown in Eq. (7), we can determine the static deformations of the L-shaped pipe with the help of Newton–Raphson method.

3 Results of the L-shaped pipe without the base excitation

In this section, the cantilevered L-shaped pipe without the base excitation will be investigated first, since the results of such a pipe system are rarely reported in the existing literature. In addition, the nonlinear mechanism of forced vibrations of the L-shaped pipe with a base excitation can be better understood based on the results shown in this section. Unless otherwise stated, several key system parameters are chosen to be: L = 1, β = 0.5 and Π₀ = 10,000 for numerical calculation. Since the base excitation is not taken into account in this section, the amplitude of the excitation is set to be zero, i.e., d₀ = 0. Moreover, it should be pointed out that 12 finite ANCF pipe elements will be employed in the current work to discrete the considered L-shaped fluid-conveying pipe. Appendix B will demonstrate that 12 elements are sufficient to predict the nonlinear responses of the pipe system under consideration.

3.1 Model validation

Before embarking some results of the cantilevered L-shaped pipe conveying fluid, two validation examples will be given first in this subsection to demonstrate the reliability of the proposed theoretical pipe model in simulating the dynamics of the L-shaped pipe without the base excitation.

The first validation example is to reproduce the natural frequencies of an empty cantilevered L-shaped pipe, which have been reported in researches of Jong [46] and Wu et al. [43]. For the convenience of comparison, the system parameters utilized in this example are selected to be the same as those applied in Refs. [46] and [43]: the length of the straight pipe segments is L₁ = L₂ = 0.9 m, the radius of curvature of the curved pipe segment is R = 0.127 m, Young’s modulus is E = 210G pa, mass density of the pipe is ρ_p = 7800 kg/m³, outer diameter of the pipe cross section is r_o = 0.1 m, and inner diameter of the pipe cross section is r_i = 0.09 m. Based on the present ANCF model and with these parameters, the first four natural frequencies of the empty L-shaped pipe are obtained, which are summarized in Table 1. In addition to the results obtained by the present model, in this table, the results obtained by four other models, including continuous bend model, discrete bend model, FEM model and impedance synthesis model, are also given. By comparing these results, it is found that the results of the present model are larger than those of other models, but the error is acceptable, within 10%. This can be understood since the Poisson effect is taken into account in these existing models but not in the present ANCF model. Besides, the first four vibration modes of the considered L-shaped pipe are plotted in Fig. 2 to further verify the present ANCF model. It is obvious that the mode shapes shown in Fig. 2 are consistent with those reported in Ref. [43].

Table 1 The first four natural frequencies of the empty cantilevered L-shaped pipe (Hz)

Fig. 2

The first four vibration modes of the empty cantilevered L-shaped pipe: a the first mode, b the second mode, c the third mode and d the fourth mode

The natural frequencies and mode shapes of empty cantilevered L-shaped pipe were reproduced by the present ANCF model in the first validation example, which only indicates that the present model can simulate the L-shaped pipe when the internal flow velocity is not considered. In the following, to demonstrate the present model can also deal with the problem of L-shaped pipe conveying fluid, a simulation model is established with the aid of CFD simulation as the second validation example. The system parameters of the simulation model are chosen to be: the length of the straight pipe segments is L₁ = L₂ = 0.1 m, the radius of curvature of the curved pipe segment is R = 0.0637 m, Young’s modulus is E = 10 MPa, mass density of the pipe is ρ_p = 7800 kg/m³, outer diameter of the pipe cross section is r_o = 0.004 m, inner diameter of the pipe cross section is r_i = 0.003 m, and the fluid flowing in the pipe is considered to be water. The CFD simulation is based on ANSYS WORKBENCH platform, the linear elastic model is used to build the pipe structure, while the fluid flowing in the pipe is simulated by the inviscid flow model. About meshing, the pipe structure is meshed by Solid186 elements and the dynamic grid technology is applied to mesh the fluid. In terms of solution, the modified k-ω turbulence model based on SST (shear stress transport) and bidirectional fluid–structure coupling technology are adopted in performing simulation. For comparison purpose, the physical and geometrical parameters used in the present ANCF model are considered to be the same as those applied in the simulation model. Accordingly, the results are given in Fig. 3, where the tip-end dimensionless static displacements of the cantilevered L-shaped fluid-conveying pipe in X-direction and Y-direction, obtained by the present ANCF model and the simulation model, for different dimensionless flow velocities are given. By inspecting this figure, it is clear that the tip-end static displacements of the L-shaped pipe obtained by the present model agree well with those obtained by the simulation model. Furthermore, the plotted results in Fig. 4 intuitively show the configuration of deformed pipe at different values of flow velocity (e.g., u = 1 and u = 3). The CFD simulation results are offered for qualitative comparison to state reliability of the present ANCF model. As can be seen that the deformed configurations of pipe obtained by both models are in good agreement. Combining Figs. 3 and 4, it is believed that the present ANCF model is able to simulate the cantilevered L-shaped pipe conveying fluid accurately.

Fig. 3

The tip-end dimensionless static displacements of the cantilevered L-shaped fluid-conveying pipe in a X dire and b Y-direction, obtained by the present ANCF model and the simulation model, for different dimensionless flow velocities

Fig. 4

The static deformations of the cantilevered L-shaped fluid-conveying pipe for two different dimensionless flow velocities: a u = 1 and b u = 3, obtained by the present ANCF model and the simulation model

Before leaving this subsection, it should be pointed out that the present ANCF model is superior to the simulation model in two aspects. The first is the calculation time. To determine the static deformation of pipe at one flow velocity, the calculation time required by the present ANCF model in this paper is 0.035835 s, while that required by the simulation model is about 8 h. In addition, the simulation model takes up ten cores of CPU when calculating, while the ANCF model only takes up one. The second advantage of the present ANCF model is that it can predict the extremely large static deformations and the nonlinear dynamic responses of the considered L-shaped fluid-conveying pipe, but the simulation model is hard to realize. This is due to that when flutter instability occurs in the pipe system, the deformation of the pipe is relatively large, and at this time, the grid distortion problem is prone to appear in the simulation model, which leads to the divergence of the simulation results. To solve the grid distortion problem, we can only increase the number of grids; however, this will greatly increase the simulation time. Thus, based on the above considerations, we believe that the present ANCF model has more advantages in dealing with the problem of the pipes conveying fluid.

3.2 Linear stability analysis around the static equilibrium configuration

As suggested by the previous study [30], the linear stability analysis of the fluid-conveying pipe should be performed around the corresponding static equilibrium configurations in the case of the considered pipe initially curved. Thus, the linear stability analysis in this subsection will be performed around the static equilibrium configuration since the L-shaped pipe contains the curved pipe segment. To achieve this goal, the static deformations of the L-shaped pipe must be determined first.

In Fig. 5a, the static displacement of pipe is obtained based on Eq. (7) through Newton–Raphson method. In order to make the interlaced curves easier to distinguish, we draw them with different colors, such as the red line represents the initially shapes of the pipe, the blue lines denote the static equilibrium configurations for the low flow velocities, while the static deformations for the high flow velocities are marked in black. By inspecting Fig. 5a, it is easy to see that each flow velocity corresponds to a static equilibrium configuration, and for a high flow velocity, the corresponding static deformation is quite large, which means that the flow velocity has a remarkable impact on the static deformations of the cantilevered L-shaped fluid-conveying pipe. In addition, with the increase in the flow velocity, the position of the free end of the L-shaped pipe in the local coordinate system X-o-Y first moves to the upper left, and then after reaching a critical point, it starts to move to the lower right. This phenomenon is similar to the results reported in Ref. [30], where the static deformations of the slightly curved cantilevered pipe were explored.

Fig. 5

a Static equilibrium configurations of the cantilevered L-shaped pipe conveying fluid, and b dimensionless complex frequencies of the lowest four modes of the pipe as a function of the dimensionless flow velocity

After determining the static equilibrium configurations of the considered L-shaped pipe, the nonlinear governing equation can be linearized around the static equilibrium position [30]:

$$ {\mathbf{M}}\Delta {\ddot{\mathbf{e}}} + {\mathbf{C}}\Delta {\dot{\mathbf{e}}} + \left( {{\mathbf{K}} + {\mathbf{K}}_{T} } \right)\Delta {\mathbf{e}} = {\mathbf{0}} $$

(8)

where K_T represents the tangential stiffness matrix at the static equilibrium configuration and can be given by [30]

$$ {\mathbf{K}}_{T} = \frac{{\partial {\mathbf{N}}\left( {\mathbf{e}} \right)}}{{\partial {\mathbf{e}}}}|_{{{\mathbf{e}} = {\mathbf{e}}_{s} }} $$

(9)

In Fig. 5b, the complex frequency of lowest four modes can be obtained by solving eigenvalues of Eq. (8). We show some dimensionless flow velocities (u = 0, 6, 12) and mark them in red point in Fig. 5b, and the interval flow velocity is 0.1 during calculations. In addition, it should be pointed out that the x-coordinate in Fig. 5b is the dimensionless frequency of the pipe, while the y-coordinate denotes the dimensionless damping. It is well known that when the damping of the fluid-conveying pipe is negative, the flutter instability occurs, and when the damping is zero, the corresponding flow velocity is the critical flow velocity. Bering this in mind and by inspecting Fig. 5b, it is easy to find that the flutter instability occurs in the second mode of the considered L-shaped pipe and the corresponding critical flow velocity is u_cr = 7.28.

3.3 Nonlinear dynamics

In this subsection, the self-excited vibrations of the L-shaped pipe without base excitation will be examined. To this end, the initial tip-end displacement of the pipe in the Y-direction is assumed to be 0.001 and the dimensionless flow velocity gradually increases from 7 to 13, in the progress of numerical calculations. Then, based on Eq. (5) and applying the fourth-order Runge–Kutta integration algorithm, the bifurcation diagram of the dimensionless tip-end displacements in X-direction of the cantilevered L-shaped pipe versus internal flow velocity is obtained, which can be found in Fig. 6. The black points in this bifurcation diagram denote the tip-end vibration amplitude when the pipe is vibrating at steady state. That is to say, when the oscillation of pipe becomes steady, the tip-end displacement will be recorded and obtained when the vibration velocity of pipe is zero at a certain flow velocity. The static equilibrium position of the pipe varying with flow velocity is obtained and added in red points. From this figure, it is immediately seen that the flutter instability occurs in the system of cantilevered L-shaped pipe, and the critical flow velocity is u_cr = 7.28, which is identical to the results predicted by the linear stability analysis. When the flow velocity is below the critical value, the considered pipe will only suffer from the static deformation, which corresponds to single point in the bifurcation diagram. Once the flow velocity is beyond the critical value, the limit-cycle oscillations take place, which leads to two points corresponding to one flow velocity in the bifurcation diagram. In order to further understand the nonlinear dynamic responses of the L-shaped pipe, the oscillating shapes of the pipe for two typical flow velocities, including u = 7.1 and 12, are added in Fig. 6, where the initially curved shapes of the pipe are highlighted in red, the static equilibrium configurations are marked in black and the blue lines denote the oscillating shapes of the pipe. It is found that in the case of u = 7.1, the pipe is stabilized at a static equilibrium position. However, when the flow velocity is beyond the critical flow velocity, such as u = 12, the pipe will vibrate around the corresponding static equilibrium configuration rather than the initially curved shape.

Fig. 6

Bifurcation diagram for the dimensionless tip-end displacements in X-direction of the cantilevered L-shaped pipe versus internal flow velocity

4 Results of the L-shaped pipe with the base excitation

After a brief investigation on the self-excited vibrations of L-shaped pipe conveying fluid in Sect. 3, the effect of base excitation on the nonlinear forced vibrations of the considered L-shaped pipe will be explored in this section. To this end, the range of the dimensionless excitation frequency is chosen to be 0–100, and three typical values of excitation amplitude, namely d₀ = 0.001, 0.01 and 0.05, are taken into account in the numerical simulations. The other system parameters are taken to be: L = 1, β = 0.5 and Π₀ = 10,000, which are the same as those utilized in Sect. 3. In addition, according to the discussions in the last section, the internal flow velocity could have remarkable impacts on the dimensionless complex frequencies and dynamical behaviors of the cantilevered L-shaped pipe in the absence of the base excitation. Thus, it is also interesting to explore the influence of the internal flow velocity on the nonlinear forced vibrations of the considered L-shaped pipe in the present of the base excitation. For that purpose, two subcritical flow velocities, namely u = 5 and 7, and two supercritical flow velocities, including u = 8 and 12, will be considered in this section. In addition, it should be noted that the software MATLAB R2019a is used for all the numerical calculations in this work; the interval excitation frequency is chosen to be 0.5 during numerical calculations.

4.1 Model validation

In Sect. 3.1, two examples were given to prove that the proposed ANCF model can be used to deal with the problem of the L-shaped pipe in the absence of the base excitation. However, whether this model can handle the problem of the L-shaped pipe with base excitation needs further verification. Unfortunately, there are almost no models in the existing literature that can be applied to simulate the nonlinear forced vibrations of the L-shaped pipe with the base excitation. As a consequence, we can only degenerate the cantilevered L-shaped pipe into to a straight cantilevered pipe, and compare the results obtained by using the present ANCF model and the Semler et al.’s model [13]. To this end, a straight cantilevered pipe subjected to base excitation is taken into account and the system parameters are selected to be: L = 1, β = 0.2, Π₀ = 10,000 and d₀ = 0.01. Based on extended numerical calculations, the bifurcation diagrams of the dimensionless tip-end displacements of pipe for two different values of flow velocity, namely, u = 3.6 and 6, are illustrated in Fig. 7. When the flow velocity is below the critical flow velocity (u_cr = 5.6), the results obtained by the two different models are almost the same, except for the difference in vibration amplitude when the excitation frequency is high, which can be found in Fig. 7a. When the flow velocity is beyond the critical value, it can be clearly seen from Fig. 7b that the bifurcation trends obtained by the two different models are basically the same, but the vibration amplitudes are slightly different in the considered rang of excitation frequency. Based on the discussions in Ref. [30], this difference is easy to be understood. Thus, it can be concluded that the present ANCF model can also deal with problems of the fluid-conveying pipe under base excitations.

Fig. 7

Bifurcation diagrams for the dimensionless tip-end displacements of the cantilevered straight pipe versus excitation frequency, for d₀ = 0.01, with a u = 3.6 and b u = 6

4.2 The case of the L-shaped pipe conveying subcritical fluid

First, we will pay our attention to the nonlinear forced vibrations of the L-shaped pipe conveying subcritical fluid under the base excitation. In the case of u = 5, the bifurcation diagrams of the dimensionless tip-end displacements in X-direction of the considered pipe for three different values of excitation amplitude, including d₀ = 0.001, 0.01 and 0.05, are given in Fig. 8. When the excitation amplitude is equal to 0.001, three peaks can be observed in the bifurcation diagram shown in Fig. 8a, although the vibration amplitude is quite small. Considering that the L-shaped pipe considered in this section is subjected to a base excitation, it is easy to think that these three peaks are caused by the resonance of the pipe. Indeed, the dimensionless excitation frequencies corresponding to these three peaks are 17.5, 30 and 78.5, which are consistent with the second-, third- and fourth-order natural frequencies of the pipe in the case of u = 5. This indicates that the second-, third- and fourth-mode resonance takes place in the considered pipe system under the action of the base excitation. The oscillating shapes of the pipe for these three resonance frequencies are further illustrated in Fig. 9, where the static equilibrium configuration is highlighted in red and the blue lines denote the oscillating shapes. It should be mentioned that the deformations of the pipe shown in Fig. 9 are magnified by the corresponding factors to show the vibration shapes more clearly, since the vibration amplitudes are quite small. From this figure, it is observed that the L-shaped pipe is always oscillating around the static equilibrium configuration. In addition, if we observe carefully, it can be found that each excitation frequency considered in Fig. 9 corresponds to different oscillating shapes of the pipe, which indicates that the main modes participating in the vibration of the pipe are different for these three excitation frequencies.

Fig. 8

Bifurcation diagrams for the dimensionless tip-end displacements in X-direction of the cantilevered L-shaped pipe versus excitation frequency, for u = 5, with a d₀ = 0.001, b d₀ = 0.01, and c d₀ = 0.05

Fig. 9

Oscillating shapes of the cantilevered L-shaped pipe for three typical values of excitation frequency: a ω = 17.5 (deformation is magnified by a factor of 20), b ω = 30 (deformation is magnified by a factor of 10) and c ω = 78.5 (deformation is magnified by a factor of 20), with u = 5 and d₀ = 0.001

The bifurcation diagram shown in Fig. 8b is the result for d₀ = 0.01, which is very similar to that for d₀ = 0.001. Two similarities can be summarized as: (i) the pipe always undergoes the period-1 motions within the excitation frequency under consideration; (ii) there are also three peaks in the bifurcation diagram, and the corresponding frequencies are also equal to the second-, third- and fourth-order natural frequencies of the pipe. Moreover, compared with Fig. 8a, it is also noted that the amplitudes of the forced vibrations of the considered L-shaped pipe are increased with the increase in excitation amplitude.

When the excitation amplitude is increased to 0.05, the situation is different, which can be immediately seen in Fig. 8c. From this bifurcation diagram, it seems that with the increase in excitation frequency, the pipe undergoes the period-1 (0 < ω < 27.5), period-n (28 < ω < 64), chaotic (64.5 < ω < 74.5), period-n (75 < ω < 77) and period-1 (77.5 < ω < 100) motions in sequence. This is not entirely true, however. To further analyze these dynamic behaviors, we plotted Fig. 10, in which the time histories, phase portraits and power spectra diagrams of the pipe for several typical values of excitation frequency, including ω = 17.5, 35, 70.5 and 76.5, are given. It is noted that the pipe undergoes the period-1 motions when the excitation frequency equals to 17.5 or 35, chaotic motion occurs in the case of ω = 70.5, and period-2 motion can be detected in the considered pipe system for ω = 76.5. In this way, based on extensive calculations, it is found that the pipe always undergoes the period-1 motions in the range of 28 < ω < 64 instead of the period-n motions as originally thought. This means the pipe actually undergoes the period-1 (0 < ω < 64), chaotic (64.5 < ω < 74.5), period-n (75 < ω < 77) and period-1 (77.5 < ω < 100) motions, successively. In addition, it is indicated that when the L-shaped pipe is subjected to a base excitation with large excitation amplitude, it may display rich dynamic responses.

Fig. 10

Time histories, phase portraits and power spectra diagrams of the cantilevered L-shaped pipe for several typical values of excitation frequency: a ω = 17.5, b ω = 35, c ω = 70.5 and d ω = 76.5, with u = 5 and d₀ = 0.05

Then, another subcritical flow velocity u = 7 is considered and the corresponding bifurcation diagrams are displayed in Fig. 11. When the excitation amplitude is small, e.g., d₀ = 0.001 and 0.01, the pipe always experiences the limit-cycle motions (period-1) in the range of 0 < ω < 100, which is similar with the results shown in Fig. 8a and b. However, only two peaks can be observed in the bifurcation diagrams shown in Fig. 11a and b, and the corresponding frequencies are identical to the second- and fourth-order natural frequencies of the pipe for u = 7. This means that the base excitation only excites the second- and fourth-order vibration modes of the pipe. By inspecting Fig. 11c, in which the results for d₀ = 0.05 are given, it is noted that period-1 and chaotic motions are the main dynamic responses of the pipe at this time. By further comparing Figs. 8 and 11, it can be concluded that when the flow velocity is below the critical value, increasing the flow velocity can simplify dynamic behaviors of the considered L-shaped pipe under the same base excitation.

Fig. 11

Bifurcation diagrams for the dimensionless tip-end displacements in X-direction of the cantilevered L-shaped pipe versus excitation frequency, for u = 7, with a d₀ = 0.001, b d₀ = 0.01 and c d₀ = 0.05

4.3 The case of the L-shaped pipe conveying supercritical fluid

Then, the situation to be discussed is the nonlinear forced vibrations of the L-shaped pipe conveying supercritical fluid subjected to a base excitation. The bifurcation diagrams for u = 8 and three different values of excitation amplitude are illustrated in Fig. 12. Clearly, it can be seen that the results for the pipe conveying supercritical fluid are quite different from those for the pipe conveying subcritical fluid. For instance, in the cases of d₀ = 0.001 and 0.01, the bifurcation diagrams shown in Fig. 12a and b indicate that the quasi-periodic motions are the main dynamic responses of the L-shaped pipe conveying supercritical fluid with the base excitation, except for some periodic- and chaotic-motion windows. However, only the period-1 motions would occur in the system of the pipe conveying subcritical fluid for d₀ = 0.001 and 0.01. To further show the characteristics of the quasi-periodic motions, Fig. 13 is given, where the time history, phase portrait, power spectra diagram and Poincare map of the oscillation for ω = 41.5 are illustrated. When the excitation amplitude is increased to 0.05, the main dynamic behaviors of the considered pipe have changed from quasi-periodic motions to periodic, quasi-periodic and chaotic motions, which can be observed in Fig. 12c. In other words, the strong base excitation can stimulate complex dynamic responses of the L-shaped pipe conveying the supercritical fluid.

Fig. 12

Bifurcation diagrams for the dimensionless tip-end displacements in X-direction of the cantilevered L-shaped pipe versus excitation frequency, for u = 8, with a d₀ = 0.001, b d₀ = 0.01 and c d₀ = 0.05

Fig. 13

Dynamic responses of the cantilevered L-shaped pipe for ω = 41.5 with d₀ = 0.01 and u = 8; a the time history, b phase portrait, c power spectra diagram and d Poincare map

Next, in the case for supercritical flow velocity, u = 12, the corresponding results for three different excitation amplitudes are plotted in Fig. 14. From this figure, some features can be observed: (i) when the excitation amplitude is relatively small, such as d₀ = 0.001 or 0.01, the mainly dynamic responses of the pipe are the quasi-periodic motions, expect for some periodic windows; (ii) increasing the excitation amplitude will increase the frequency range of limit-cycle motions, while that of quasi-periodic motions will decrease; (iii) the chaotic motion occurs in the considered pipe system when the excitation amplitude is increased to 0.05. It should be noted that these features are quite different from those for a straight fluid-conveying pipe under base excitations. According to ref. [47], the straight pipe only experiences limit-cycle vibrations over the considered excitation frequency range. However, as the excitation amplitude is small (e.g., d₀ = 0.001), the L-shaped pipe conveying subcritical fluid also just undergoes limit-cycle oscillations and has resonance peaks, which are similar with those of a straight pipe.

Fig. 14

Bifurcation diagrams for the dimensionless tip-end displacements in X-direction of the cantilevered L-shaped pipe versus excitation frequency, for u = 12, with a d₀ = 0.001, b d₀ = 0.01 and c d₀ = 0.05

5 Conclusions

In this paper, the nonlinear statics and dynamics of the cantilevered L-shaped fluid-conveying pipe subjected to a base excitation are systematically studied. To this end, a novel nonlinear theoretical model is proposed with the help of absolute nodal coordinate formulation (ANCF). The corresponding nonlinear governing equation of the considered pipe system is determined by employing the extended Lagrange equations. Based on this equation, the static deformations, linear stability and the nonlinear self-excited vibrations of the pipe without the base excitation are investigated first. Then, the nonlinear forced vibrations of the pipe under the base excitation are considered, devoting to exploring influences of the internal flow velocity, excitation amplitude and excitation frequency on dynamic responses of this L-shaped pipe system. Finally, the main conclusions of this present work are given as follows:

• (i) Based on the three validated examples, it is demonstrated that the present ANCF model is available for predicting the nonlinear self-excited and forced vibrations of L-shaped fluid-conveying pipes.

• (ii) The static deformations of L-shaped pipe fluid-conveying are strongly dependent on the internal flow velocity and can be extremely large when the flow velocity is sufficiently high. The L-shaped pipe without base excitations will lose stability by flutter and the main dynamic behaviors after instability are the limit-cycle vibrations.

• (iii) Under the action of base excitations, more complex dynamic responses, such as period-n, quasi-periodic and chaotic behaviors, will occur for the pipe system. It is found that the internal flow velocity, excitation amplitude and frequency can have great impacts on the forced vibration characteristics. Increasing the excitation amplitude results in enriching dynamical behaviors of the pipe.

Appendices

Appendix A

In this Appendix, the detailed derivations of Eqs. (2) and (3) will be given. As we mentioned before, since the ANC formulation was used in this study to establish the theoretical model of the considered L-shaped pipe, the equation shown in Eq. (1) should be employed to derive the nonlinear governing equation of the pipe system. Thus, each physical quantity in Eq. (1) needs to be determined.

First, the absolute velocity vector of the pipe element will be determined. Since the pipe is subjected to a base excitation in X-direction, the position vector r of an arbitrary point on the pipe element in the inertial coordinate system X₁-o₁-Y₁ consists of two parts: the position vector of this point in the local coordinate system X-o-Y, and the position vector of the local coordinate system in the inertial coordinate system. Thus, we have:

$$ {\mathbf{r}} = {\mathbf{r}}_{l} + {\mathbf{r}}_{i} = {\mathbf{Sq}} + \left[ {\begin{array}{*{20}c} {w_{b} } \\ 0 \\ \end{array} } \right] $$

(A.1)

where S and q, respectively, denote the shape function and the nodal coordinate vector of the ANCF pipe element, which have been defined in Ref. [30]. Then, according to Eq. (A.1), the absolute velocity vector of the pipe element can be easily defined:

$$ {\mathbf{v}}_{{\mathbf{P}}} = \frac{{{\text{d}}{\mathbf{r}}}}{{{\text{d}}t}} = {\dot{\mathbf{r}}} = {\mathbf{S\dot{q}}} + \left[ {\begin{array}{*{20}c} {\dot{w}_{b} } \\ 0 \\ \end{array} } \right] $$

(A.2)

According to the discussions in Ref. [30], the absolute velocity vector of the fluid element can be expressed as follows:

$$ {\mathbf{v}}_{{\mathbf{F}}} = {\mathbf{v}}_{{\mathbf{P}}} + Uf{{\varvec{\uptau}}} $$

(A.3)

where f is the longitudinal deformation gradient and τ denotes the tangential unit vector along the deformed pipe axis. Their expression can be given as follows [30]:

$$ f = \frac{{\sqrt {{\mathbf{r^{\prime}}}^{T} {\mathbf{r^{\prime}}}} }}{{\sqrt {{\mathbf{r^{\prime}}}_{0}^{T} {\mathbf{r^{\prime}}}_{0} } }},{{\varvec{\uptau}}} = \frac{{{\mathbf{r^{\prime}}}}}{{\sqrt {{\mathbf{r^{\prime}}}^{T} {\mathbf{r^{\prime}}}} }} $$

(A.4)

From the above expressions, we can quickly find that neither v_F nor v_P is a function of ${\dot{\mathbf{q}}}$, and hence, the second surface integration shown in Eq. (1) is found to be zero. Then, based on Eqs. (A.2), (A.3) and (A.4), we can obtain the following expressions of the total kinetic energy of the system and the density of kinetic energy of the fluid

$$ \begin{aligned} T = & \frac{1}{2}m\int_{0}^{l} {{\mathbf{v}}_{{\mathbf{P}}}^{T} } {\mathbf{v}}_{{\mathbf{P}}} {\text{d}}x + \frac{1}{2}M\int_{0}^{l} {{\mathbf{v}}_{{\mathbf{F}}}^{T} } {\mathbf{v}}_{{\mathbf{F}}} {\text{d}}x \\ & = \frac{1}{2}\left( {m + M} \right)\int_{0}^{l} {{\dot{\mathbf{q}}}^{T} {\mathbf{S}}^{T} {\mathbf{S\dot{q}}}{\text{d}}x} + MU\int_{0}^{l} {\frac{{{\dot{\mathbf{q}}}^{T} {\mathbf{S}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}}}{{\sqrt {{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} } }}{\text{d}}x} + \frac{1}{2}MU^{2} \int_{0}^{l} {\frac{{{\mathbf{q}}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}}}{{{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} }}{\text{d}}x} \\ & \; + \left( {m + M} \right)\int_{0}^{l} {\left[ {\begin{array}{*{20}c} {\dot{w}_{b} } \\ 0 \\ \end{array} } \right]^{T} {\mathbf{S\dot{q}}}{\text{d}}x} + MU\int_{0}^{l} {\left[ {\begin{array}{*{20}c} {\dot{w}_{b} } \\ 0 \\ \end{array} } \right]^{T} \frac{{{\mathbf{S}^{\prime}\mathbf{q}}}}{{\sqrt {{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} } }}{\text{d}}x} \\ & \; + \frac{1}{2}\left( {m + M} \right)l\left( {\dot{w}_{b} } \right)^{2} \\ \end{aligned} $$

(A.5)

$$ \begin{aligned} T^{\prime} = & \frac{1}{2}\rho_{F} {\mathbf{v}}_{F}^{T} {\mathbf{v}}_{F} \\ & = \frac{1}{2}\rho_{F} {\dot{\mathbf{q}}}^{T} {\mathbf{S}}^{T} {\mathbf{S\dot{q}}} + \rho_{F} U\frac{{{\dot{\mathbf{q}}}^{T} {\mathbf{S}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}}}{{\sqrt {{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} } }} + \frac{1}{2}\rho_{F} U^{2} \frac{{{\mathbf{q}}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}}}{{{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} }} \\ & \; + \rho_{F} \left[ {\begin{array}{*{20}c} {\dot{w}_{b} } \\ 0 \\ \end{array} } \right]^{T} {\mathbf{S\dot{q}}} + \rho_{F} U\left[ {\begin{array}{*{20}c} {\dot{w}_{b} } \\ 0 \\ \end{array} } \right]^{T} \frac{{{\mathbf{S}^{\prime}\mathbf{q}}}}{{\sqrt {{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} } }} + \frac{1}{2}\rho_{F} \left( {\dot{w}_{b} } \right)^{2} \\ \end{aligned} $$

(A.6)

where ρ_F is the density of the fluid, q₀ represents the nodal coordinate vector of the initial pipe element, and l is length of the pipe element. By substituting Eqs. (A.2), (A.3) and (A.6) into the first surface integration in Eq. (1), the following expression can be determined

$$ \begin{aligned} & \int_{S} {{\text{d}}{\mathbf{a}} \cdot \left( {{\mathbf{v}}_{{\mathbf{F}}} - {\mathbf{v}}_{{\mathbf{P}}} } \right)\frac{{\partial T^{\prime}}}{{\partial {\dot{\mathbf{q}}}}}} \\ & = aMU\left( {{\mathbf{S}}^{T} {\mathbf{S\dot{q}}} + U\frac{{{\mathbf{S}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}}}{{\sqrt {{\mathbf{q}}_{0}^{T} {\mathbf{S}^{\prime}}^{T} {\mathbf{S}^{\prime}\mathbf{q}}_{0} } }} + {\mathbf{S}}^{T} \left[ {\begin{array}{*{20}c} {\dot{w}_{b} } \\ 0 \\ \end{array} } \right]} \right)|_{0,l} \\ \end{aligned} $$

(A.7)

where a is a scalar and can be defined as a(x = 0) = -1 and a(x = l) = 1.

Finally, the vector of generalized forces of the system, Q, needs to be determined. Since the influence of gravity and damping is not taken into account in this article, we only need to determine the generalized elastic forces vector of the system. Recalling that the L-shaped pipe in this paper is considered to be slender, the Euler–Bernoulli beam theory is adopted. Due to this fact, the potential energy of the pipe element can be written as

$$ U_{el} = \frac{1}{2}\int_{0}^{l} {EA_{p} \varepsilon^{2} {\text{d}}x} + \frac{1}{2}\int_{0}^{l} {EI\left( {\kappa - \kappa_{0} } \right)^{2} {\text{d}}x} $$

(A.8)

where κ₀ denotes the initial curvature of the pipe element. For the straight pipe segments κ₀ = 0, and for the curved pipe segment κ₀ ≠ 0. Moreover, ε and κ are, respectively, the longitudinal strain and geometrical curvature of the deformed pipe element, which can be defined as follows [30]:

$$ \varepsilon = \frac{1}{2}\left( {f^{2} - 1} \right),\kappa = \frac{{\left| {{\mathbf{r^{\prime}}} \times {\mathbf{r^{\prime\prime}}}} \right|}}{{||{\mathbf{r^{\prime}}}||^{3} }} $$

(A.9)

According to Eq. (A.8), the vector of the generalized elastic forces is defined by

$$ {\mathbf{Q}} = - \frac{{\partial U_{el} }}{{\partial {\mathbf{q}}}} = - \int_{0}^{l} {EA_{p} \varepsilon \frac{\partial \varepsilon }{{\partial {\mathbf{q}}}}{\text{d}}x} - \frac{1}{2}\int_{0}^{l} {EI\left( {\kappa - \kappa_{0} } \right)\frac{\partial \kappa }{{\partial {\mathbf{q}}}}{\text{d}}x} $$

(A.10)

So far, all the terms in Eq. (1) have been determined. For the rest, we just need to substitute Eqs. (A.5), (A.7), (A.10) and (4) into Eq. (1) and perform some straightforward manipulations, so that nonlinear governing equations of the pipe element can be obtained.

Appendix B

It is well known that if the elements used to discretize the pipe is not enough, the numerical results will not converge, and if the number of elements is too large, the calculation cost will increase. Due to this fact, it is necessary to determine a suitable number of pipe elements. To this end, the static equilibrium configurations of the L-shaped pipe for u = 8 with four different numbers of pipe elements, including 6, 9, 12 and 15, are displayed in Fig. 15a. From this figure, it is found that the results for 12 and 15 pipe elements are almost the same, indicating that 12 pipe elements are sufficient for predicting the static equilibrium configurations of the L-shaped pipe. Furthermore, Fig. 15b shows the bifurcation diagrams of dimensionless tip-end displacements in X-direction of the pipe without the base excitation for different numbers of the pipe elements. Again, it is easy to find that the results of 12 pipe elements are almost consistent with those of 15 pipe elements. According to these two figures, therefore, it is believed that 12 pipe elements are sufficient to predict the nonlinear statics and dynamics of the considered L-shaped pipe conveying fluid.

Fig. 15

Convergence analysis on a the static equilibrium configurations of the L-shaped pipe for u = 8, and b the bifurcation diagrams of dimensionless tip-end displacements in X-direction of the pipe versus internal flow velocity