Rotating silver nanobeam subjected to ramp-type heating and varying load via Eringen’s nonlocal thermoelastic model

Abstract

The objectives of this article are to present a mathematical model that uses Eringen’s nonlocal elasticity theory to describe the free vibratory motion of rotating nanoscale beams. The Euler–Bernoulli beam theory, Eringen’s nonlocal elasticity theory, and generalized thermoelasticity with phase-lags are used to derive the system of equations for rotating thermoelastic nanobeams. The studied nanobeam is subjected to ramp-type heating and to a significantly exponentially decaying load. The analytical solution was derived using the Laplace transform method, and the transformation of the converted fields was performed by applying the residue calculus. The numerical results of the physical fields under investigation are collected and displayed graphically. The impacts of nonlocal parameters, different types of loads, and ramping-time parameters in addition to rotation were studied and analyzed.

1 Introduction

In a compact state including the micro/nano-electromechanical system (MEMS/NEMS), the advancement of electronic and mechanical structures is now more significant because this necessary part of the technology increases the efficiency and compactness of industrial machinery. In fact, MEMS/NEMS is a combination of mechanical, electrical sensors, and electronic elements. Nanomechanical resonators are a type of NEMS device, commonly used in high-speed and accuracy applications. The expression MEMS/NEMS was first used during the 1980s. This was first used in the USA and has been extended to include a wide variety of technologies with the aim of miniaturizing devices by combining functions into small packages [1]

These mechanical systems are small in size and have different applications. MEMS/NEMS has developed significantly in the past decade and has attracted great interest all over the world. This is due to the massive application of MEMS/NEMS in various fields such as medicine, transportation systems, medical engineering, and production processes [2, 3]. For designers of micro-electromechanical systems (MEMS), knowledge of the mechanical properties of elastic micro-components is important, bearing in mind the ultimate goal of predicting the amount of deflection from an applied load and vice versa to avoid cracking and breakage, enhance efficiency, and increase the lifespan of MEMS instruments [4].

When the sizes of these structures are very small, atomic study and reproduction calculations have revealed a large dimension effect on the mechanical features. During this research, the scale effect plays an important role in static and dynamic activities and behavior of micro- and nanostructures, and should not be disregarded. It is known that classical continuum mechanics in nano- and small-scale structures do not reflect these dimensional effects [5]. The stress at any point in the classical elasticity theory (local theory) depends only on the stress at the same point, while the stress at any point in the nonlocal elasticity theory is a function of the strains at all points in the continuum. In this manner, the nonlocal continuum theory includes data on the long-range forces between atoms, and the internal length scale is actually added as material parameters to represent the small-scale influence in the constitutive equations. In this context, it is not sufficient to apply classical continuity theory to analyze nanostructures, because classical theories lack transparency regarding the effects of small size. Recently, the use of nonlocal elasticity in micro- and nanomaterials has received great attention in the nanotechnology community, and the literature shows that the concept of nonlocal elasticity is increasingly being used for accurate and rapid nanostructure research [6].

Since the mechanical behavior of nanostructures strongly depends on size effects when the device is very small for molecular distances, classical continuity models must be updated to consider small-scale effects. In Eringen’s nonlocal theory [7, 8], small effects are incorporated across a single substance modulus into the constitutive equation. Due to Eringen’s theory [7, 8], for a broad class of multiphysics phenomena with the internal length scale ranging from atomistic to macroscopic size, an excellent approximation can be given. Hence, when analyzing nanostructures, using the classical continuum theory and ignoring small-scale effects and atomic forces lead to inaccurate results and thus to erroneous design. The nonlocal elasticity model of Eringen has been used in several papers to examine nanostructures [9,10,11,12,13,14,15,16]. Such works rely on Eringen’s theory of nonlocal elasticity and are seen innovative in the nanoparticles field.

To describe the mechanism of heat transfer in solids, several models of thermal conductivity have been established. In contrast to the experimental results, the classical thermoelastic theory (CTE) derived from the basis of the Fourier thermal conductivity law predicts an infinite velocity for the propagation of thermal turbulence. This defect stems from the fact that the heat transfer equation obtained from this theory is a parabolic partial differential equation. Although some researchers have applied unconventional models of thermal conductivity, generalized theories of thermal elasticity where the parabolic heat transfer equation is replaced by a hyperbolic equation do not suffer from this deficiency. As a well-known example, Lord and Shulman presented a model with a single-phase-lag coefficient which led to the hyperbolic thermal conductivity equation. The Lord–Shulman (LS) model [17] only takes into account the small effect in time. Tzou [18, 19] proposed a dual-phase-lag (DPL) model using an additional phase-lag parameter, capable of detecting the small effect in space and time. The aim of this work is to construct a mathematical model to explain the vibrational motion of nano-sized rotating beams that rely on the Euler–Bernoulli beam assumptions, the nonlocal elasticity theory of Eringen, and the two-phase delay (DPL) model proposed by Tzou [18].

Nano-machines are structures with movable parts in the nanometer realm. To be suitable for utilization in nano-turbomachinery and nano-robots, rotating beams that are commonly used in many turbomachinery and robotic applications need to be reduced to nanometer dimensions. Study papers dealing with the thermodynamics of rotating nanoscale beams are found to be little in the literature. The hope is that these nanostructure devices will receive significant attention in the coming years. So the researchers have documented the feasibility of rotating structures on the nanoscale. In the near future, these nanostructure devices are expected to garner a lot of interest. As a result, researchers have reported the possibility of nanoscale rotating structures. The rotating nanostructural device involves a rotating metal plate, with a multi-walled nanotube of carbon acting as the main moving feature. For the effective design of these rotating nanoscale devices, a deep understanding of their mechanical behavior, such as bending, vibration, twisting, and buckling, is required. Therefore, it is important to develop simplified models for the dynamics of complex nanoscale systems. This is because the complete atomistic simulations will be computationally costly and prohibitive in many situations [19].

Srivastava [20] mentioned the rotational dynamics of carbon nanotubes and carbon nanotubes gears within a single laser area of operation. Using the molecular dynamics (MD) approach, Lohrasebi and Tabar [21] developed a spinning nanomotor computational model consisting of three coaxial carbon nanotubes and a number of graphene blades. Ghafarian et al. [22] used the Euler–Bernoulli beam model of nonlocal Eringen elasticity theory to formulate the governing differential equation and boundary conditions characterizing the dynamic behavior of a rotating double-tapered AFGM nanobeam. Mohammadi et al. [23] investigated the hygro-mechanical vibration of a rotating viscoelastic nanobeam embedded in an elastic visco-Pasternak medium and in a nonlinear thermal environment. Ebrahimi and Dabbagh [24, 25] researched the study of smart rotating porous heterogeneous piezo-electric nanobeams and rotating heterogeneous magneto-electro-elastic nanobeams for wave propagation. Ebrahimi and Salari [26, 27] considered the nonlocal temperature-dependent thermomechanical vibration analysis, and the vibration analysis of functionally graded rotating nanobeams. Additionally, Eringen’s nonlocal elasticity principle has been applied in many works to analyze the rotating nanobeams [28,29,30,31].

The literature has been comprehensively based on applications in rotating microstructures encompassing different machinery systems for micro/nano-gears, micro/nano-turbines, micro/nano-blades, rotating micro/nano-rings, and micro/nano-robots. In atomic microscopes and accelerometers, for example, cantilever nanobeams and clamped–clamped beams in micro-mirror systems are used. Due to the rapid development of the current nanostructure, new mechanical tools such as wireless sensors, transistors, biological samples, actuators, and other mechanical structures are applied in the fields of biology, medicine, engineering, etc. However, throughout the working period, some nano-mechanical structures are affected by complex chemical and physical conditions which lead to problems such as work failure and fatigue. Therefore, it is important to examine the mechanical behavior of nano-machines in nano-design.

The present work analyzes the thermoelastic vibration behavior in a rotating nanobeam due to the lack of literature research on this topic. The nonlocal nanobeam model integrates the nonlocal parameter that is able to detect the effect at a small scale. On the basis of the Euler–Bernoulli beam theory and generalized thermal elasticity with phase-lag, the dynamic interaction of homogeneous and isotropic nanobeam resonators resulting from ramp-type heating that are subject to exponential time decay varying load was investigated. The technique used in the derivation is the Laplace transform. To obtain the results in the time domain, a modified inverse Laplace transform approach is also used. The results will be analyzed due to the parameters of rotation, point load, and ramping time. This also provides numerical results to demonstrate the small-scale effect on the nanobeam resonator. The results obtained based on the proposed analytical approach indicate a fair agreement based on numerical methods with the previously published data.

2 Nonlocal thermoelasticity model

Eringen’s theory of non-positional elasticity [7, 8, 32, 33] has been frequently used to model the vibration of nanobeams. In contrast to the classical beam theory, this theory includes a size-dependent term, which allows it to predict the oscillations of nanobeams. The nonlocal stress tensor ${\tau }_{ij}$ can be represented at every position ${\varvec{x}}$ in the body according to the theory of nonlocal elasticity as

$${\tau }_{ij}({\varvec{x}})=\int\limits_{V}K\left(\left|{{\varvec{x}},{\varvec{x}}}^{{{\prime}}}\right|,\xi \right){\sigma }_{ij}\left({\varvec{x}}^{{\prime}}\right)\mathrm{d}V({\varvec{x}}^{{\prime}})$$

(1)

where ${\sigma }_{ij}\left({\varvec{x}}^{{\prime}}\right)$ is the classical local stress tensor which is defined as

$${\sigma }_{ij}\left({\varvec{x}}^{{\prime}}\right)=2\mu {\varepsilon }_{ij}\left({\varvec{x}}^{{\prime}}\right)+\left(\lambda {\varepsilon }_{kk}\left({\varvec{x}}^{{\prime}}\right)-\gamma \theta \left({\varvec{x}}^{{\prime}}\right)\right){\delta }_{ij}$$

(2)

and ${\varepsilon }_{ij}$ is the strain tensor at two neighboring points ${{\varvec{x}}}^{{{\prime}}}$ and ${\varvec{x}}$ given by

$${\varepsilon }_{ij}\left({\varvec{x}}^{{\prime}}\right)=0.5\left(\frac{{\partial u}_{i}\left({\varvec{x}}^{{\prime}}\right)}{\partial {x}_{j}^{{{\prime}}}}+\frac{{\partial u}_{j}\left({\varvec{x}}^{{\prime}}\right)}{\partial {x}_{i}^{{{\prime}}}}\right)$$

(3)

In these equations, $\theta =T-{T}_{0}$, ${T}_{0}$ is the ambient temperature, $\gamma =\frac{{\alpha }_{t}E}{\left(1-2\nu \right)}={\alpha }_{T}E$, ${\alpha }_{t}$ is the linear thermal expansion, $E$ is Young’s modulus, $\nu$ is the ratio of Poisson, ${u}_{i}$ are the components of displacement, $K\left(\left|{{\varvec{x}},{\varvec{x}}}^{{{\prime}}}\right|,\xi \right)$ is a positive scalar kernel function, $\xi ={e}_{0}a/l$ is the nonlocal scale parameter, ${\delta }_{kl}$ is Kronecker delta function, $a$ and $l$ are the internal and external characteristic lengths respectively, while ${e}_{0}$ is a parameter which has been experimentally determined. The Lamé constants $\lambda$ and $\mu$ can be given as $\lambda =E\nu /(1+\nu )(1-2\nu )$ and $\mu =E/2(1+\nu )$.

When the kernel is selected as [34, 35]:

$$K\left(\left|{{\varvec{x}},{\varvec{x}}}^{{{\prime}}}\right|,\xi \right)=\frac{1}{2\pi {\xi }^{2}{l}^{2}}{K}_{0}\left(\frac{\Vert {{\varvec{x}}-{\varvec{x}}}^{{{\prime}}}\Vert }{\xi l}\right)$$

(4)

where ${K}_{0}$ is the modified Bessel function and $\Vert {{\varvec{x}}-{\varvec{x}}}^{{{\prime}}}\Vert$ is the Euclidean distance. Equation (1) may be reduced as follows:

$$\left(1-{\xi }^{2}{\nabla }^{2}\right){\tau }_{ij}({\varvec{x}})={\sigma }_{ij}\left({\varvec{x}}^{{\prime}}\right)$$

(5)

When Eq. (2) is presented in Eq. (5), we get the nonlocal constitutive stress–strain-temperature equations as

$$\left(1-{\xi }^{2}{\nabla }^{2}\right){\tau }_{ij}={C}_{ijkl}{\varepsilon }_{kl}-{\gamma }_{ij}\theta$$

(6)

Equation (6) is the Eringen differential model, which is related to nonlocal law and takes into consideration the influence of size on nanostructure response. It can be found that if the parameter $a$ is omitted, i.e., the elements of a medium are considered to be distributed continuously, then the parameter $\xi =0$ and Eq. (6) is reduced to the classical case to the constitutive Eq. (2).

Conventional thermoelasticity is founded on the ideas of classical heat conductivity theory, in particular on the classical Fourier law, which relates the heat flow vector ${\varvec{q}}\left({\varvec{x}},t\right)$ to the temperature gradient as

$${\varvec{q}}\left({\varvec{x}},t\right)=-K\nabla \theta \left({\varvec{x}},t\right),$$

(7)

where $K$ is the thermal conductivity. The energy equation is given by

$$\rho {C}_{E}\frac{\partial \theta }{\partial t}+\gamma {T}_{0}\frac{\partial e}{\partial t}=-\nabla \cdot {\varvec{q}}+Q,$$

(8)

where ${C}_{E}$ the specific heat per unit mass at constant strain, $Q$ is the heat source and $e={\varepsilon }_{kk}$ is the volumetric strain.

Tzou in [17, 18] has proposed the dual-phase-lag thermoelastic model. According to this new model, the classical Fourier law is replaced by a global relation relationship between the heat flux vector ${\varvec{q}}$ at any point ${\varvec{x}}$ of the material in the time $t+{\tau }_{q}$ and the temperature gradient $\nabla \theta$ at the same point in the time $t+{\tau }_{\theta }$

$${\varvec{q}}\left({\varvec{x}},t+{\tau }_{q}\right)=-K\nabla \theta \left({\varvec{x}},t+{\tau }_{\theta }\right),$$

(9)

where times ${\tau }_{\theta }$ and ${\tau }_{q}$ denote the temperature gradient phase-lag and the heat flow phase-lag, respectively [17]. A well-developed lagging response structure represented by Eq. (9) can be shown by expanding it in terms of time-related expansions of Taylor and holding the terms up to certain orders in the parameters ${\tau }_{q}$ and ${\tau }_{\theta }$

$$\left(1+{\tau }_{q}\frac{\partial }{\partial t}+\frac{{\tau }_{q}^{2}}{2}\frac{{\partial }^{2}}{\partial {t}^{2}}\right){\varvec{q}}=-K\left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)\nabla \theta$$

(10)

Thus, the modified Fourier law may be obtained as follows:

$$\begin{array}{c}\left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)\left[\rho {C}_{e}\frac{\partial \theta }{\partial t}+\gamma {T}_{0}\frac{\partial }{\partial t}\left(\mathrm{div}{\varvec{u}}\right)-Q\right]=K\left(1+{\tau }_{q}\frac{\partial }{\partial t}+\frac{{\tau }_{q}^{2}}{2}\frac{{\partial }^{2}}{\partial {t}^{2}}\right){\nabla }^{2}\theta \\ \end{array}$$

(11)

When ${\tau }_{\theta }=0$ and ${\tau }_{q}>0$, the Lord and Shulman model (LS) can be obtained, and in the case of ${\tau }_{q}={\tau }_{\theta }=0$, the classical coupled thermoelasticity theory (CTE) can be gotten.

3 Mathematical model and problem formulation

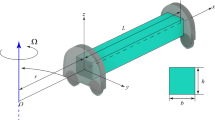
The schematic representation of a thin elastic rotating nanoscale beam is shown in Fig. 1. The nanobeam is of length, $\left(0\le x\le L\right)$, width $b$ $\left(-b/2\le y\le b/2\right)$ and thickness $h$ $\left(-h/2\le z\le h/2\right)$. We take the $x$-axis along the beam axis and the axes $y$ and $z$, respectively, to correspond to width and thickness of the beam.

Fig. 1

Schematic diagram for the nanobeam

Displacements may be written according to the Euler–Bernoulli beam theory as

$$u=-z\frac{\partial w}{\partial x}, v=0, w=w\left(x,t\right),$$

(12)

where $w$ is the lateral deflection.

The one dimensional nonlocal constitutive equation can be written as

$${\tau }_{xx}-{\xi }^{2}\frac{{\partial }^{2}{\tau }_{xx}}{\partial {x}^{2}}=E\frac{\partial u}{\partial x}-E{\alpha }_{T}\theta =-E\left(z\frac{{\partial }^{2}w}{\partial {x}^{2}}+{\alpha }_{T}\theta \right),$$

(14)

where ${\tau }_{xx}$ is the nonlocal axial stress.

The bending moment of cross section $A=bh$ is defined as follows:

$$M\left(x,t\right)={\int }_{-h/2}^{h/2}z{\tau }_{xx}\mathrm{d}z$$

(15)

Using Eqs. (14) and (15), we get

$$M\left(x,t\right)-{\xi }^{2}\frac{{\partial }^{2}M}{\partial {x}^{2}}=-EI\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+{\alpha }_{T}{M}_{T}\right)$$

(16)

where $I=b{h}^{3}/12$ is the moment of inertia of the cross section, $EI$ is the flexural stiffness and ${M}_{T}$ is the thermal moment of nanobeam. The thermal moment ${M}_{T}$ is defined by

$${M}_{T}=\frac{12}{{h}^{3}}{\int }_{-h/2}^{h/2}\theta \left(x,z,t\right)z\mathrm{d}z$$

(17)

It is assumed that the nanobeam rotates along an axial parallel to the $z$-axis with angular velocity $\Omega$. In this case, centrifugal tensile strength $R\left(x,t\right)$ is introduced as a result of the rotation. Additionally, if the beam is subjected to a distributed load $q\left(x,t\right)$, the Euler–Lagrange’s relation is written as [36, 37]:

$$\frac{{\partial }^{2}M}{\partial {x}^{2}}+\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)+q\left(x,t\right)=\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}$$

(18)

If $\Omega =0$; i.e., the centrifugal tension force $R$ vanishes since there is no rotation. At a distance $x$ from the origin (Fig. 1), the axial force $R(x)$ owing to centrifugal stiffening is [19, 25]

$$R(x) =\int\limits_{x}^{L}\rho A{\Omega }^{2}(r+x)dx$$

(19)

The distance between the rotating center and the first edge of the nanobeam is the constant $r$ (a hub radius) (see Fig. 1). After integration, Eq. (19) can be rewritten as

$$R(x) =\frac{1}{6L}\left[3L\rho A{\Omega }^{2}(L-x)(L+2r+x)\right]$$

(20)

Equations (16) and (18) may be used to compute the bending moment as:

$$M\left(x,t\right)={\xi }^{2}\left(\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}-q\left(x,t\right)-\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)\right)-EI\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+{\alpha }_{T}{M}_{T}\right).$$

(21)

Eliminating the moment $M$ from Eq. (18) using Eq. (21), the equation of motion of the nanobeams may be expressed as:

$$\left[\frac{{\partial }^{4}}{\partial {x}^{4}}+\frac{\rho A}{EI}\frac{{\partial }^{2}}{\partial {t}^{2}}\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\right]w-\frac{1}{EI}\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[q+\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)\right]+{\alpha }_{T}\frac{{\partial }^{2}{M}_{T}}{\partial {x}^{2}}=0$$

(22)

The modified heat conduction Eq. (11) in the absence of heat sources $\left(Q=0\right)$ is given by

$$K\left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)\left(\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}}{\partial {z}^{2}}\right)\theta =\left(1+{\tau }_{q}\frac{\partial }{\partial t}+\frac{{\tau }_{q}^{2}}{2}\frac{{\partial }^{2}}{\partial {t}^{2}}\right)\frac{\partial }{\partial t}\left(\rho {C}_{E}\theta -\gamma {T}_{0}z\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)$$

(23)

4 General solution along the thickness direction

We use a temperature increment solution that depends in terms of a sin function (sinusoidal variation) to solve governing system equations as:

$$\theta \left(x,z,t\right)=\Theta \left(x,t\right)\mathrm{sin}\left(pz\right), p=\frac{\pi }{h}$$

(24)

Using the relation (24), Eqs. (21)–(23) may be rewritten as:

$$\left[\frac{{\partial }^{4}}{\partial {x}^{4}}+\frac{\rho A}{EI}\frac{{\partial }^{2}}{\partial {t}^{2}}\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\right]w-\frac{1}{EI}\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[q+\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)\right]+\frac{24{\alpha }_{T}}{{\pi }^{2}h}\frac{{\partial }^{2}\Theta }{\partial {x}^{2}}=0$$

(25)

$$M\left(x,t\right)={\xi }^{2}\left(\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}-q-\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)\right)-EI\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\Theta \right)$$

(26)

$$\left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)\left(\frac{{\partial }^{2}\Theta }{\partial {x}^{2}}-\frac{{\pi }^{2}}{{h}^{2}}\Theta \right)=\left(1+{\tau }_{q}\frac{\partial }{\partial t}+\frac{{\tau }_{q}^{2}}{2}\frac{{\partial }^{2}}{\partial {t}^{2}}\right)\frac{\partial }{\partial t}\left(\frac{\rho {C}_{E}}{K}\Theta -\frac{\gamma {T}_{0}{\pi }^{2}h}{24K}\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)$$

(27)

For convenience, we will introduce the following dimensionless variables:

$$\begin{array}{c}\left\{{x}^{{\prime}},{w}^{{\prime}},{u}^{{\prime}},{z}^{{\prime}},{L}^{{\prime}},{h}^{{\prime}},{b}^{{\prime}}\right\}=\eta c\left\{x,w,u,z,L,h,b\right\}, \left\{{t}^{{\prime}},{\tau }_{q}^{{\prime}},{\tau }_{\theta }^{{\prime}}\right\}=\eta {c}^{2}\left\{t,{\tau }_{q},{\tau }_{\theta }\right\},{\Theta }^{{\prime}}=\frac{1}{{T}_{0}}\Theta ,\\ {\xi }^{{\prime}}={\eta }^{2}{c}^{2}\xi , {{\Omega {^{\prime}}}}^{2}=\frac{\rho \mathrm{A}{\Omega }^{2}}{{EI\eta }^{4}{c}^{4}}, {M}^{{\prime}}=\frac{1}{\eta cEI}M, {q}^{{\prime}}=\frac{A}{EI}q, {c}^{2}=\frac{E}{\rho }, \eta =\frac{\rho {C}_{E}}{K}.\end{array}$$

(28)

If non-dimensional quantities (28) are entered into the governing Eqs. (25)–(27), we can get (for convenience, dropping the primes):

$$\left[\frac{{\partial }^{4}}{\partial {x}^{4}}+\frac{12}{{h}^{2}}\frac{{\partial }^{2}}{\partial {t}^{2}}\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\right]w-\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[q+\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)\right]+\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\frac{{\partial }^{2}\Theta }{\partial {x}^{2}}=0,$$

(29)

$$\left(1+{\tau }_{\theta }\frac{\partial }{\partial t}\right)\left(\frac{{\partial }^{2}\Theta }{\partial {x}^{2}}-\frac{{\pi }^{2}}{{h}^{2}}\Theta \right)=\left(1+{\tau }_{q}\frac{\partial }{\partial t}+\frac{{\tau }_{q}^{2}}{2}\frac{{\partial }^{2}}{\partial {t}^{2}}\right)\frac{\partial }{\partial t}\left(\Theta -\frac{\gamma {\pi }^{2}h}{24K\eta }\frac{{\partial }^{2}w}{\partial {x}^{2}}\right),$$

(30)

$$M\left(x,t\right)=\frac{12{\xi }^{2}}{{h}^{2}}\frac{{\partial }^{2}w}{\partial {t}^{2}}-{\xi }^{2}\left[q+\frac{\partial }{\partial x}\left(R(x)\frac{\partial w}{\partial x}\right)\right]-\frac{{\partial }^{2}w}{\partial {x}^{2}}-\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\Theta.$$

(31)

Now, a special type of external transverse load is being studied. We investigate the time-varying exponential load running vertically downward in the direction of the beam thickness [38]

$$q\left(x,t\right)=-{q}_{0}\left(1-\delta {\mathrm{e}}^{-\beta t}\right)$$

(32)

where $\beta$ is the dimensionless decaying parameter of the applied load and ${q}_{0}$ is the dimensionless magnitude of the point load, respectively ($\delta =0$ for the uniformly distributed load).

In this study, we will assume that the nanobeam rotates at a constant angular velocity, and that the centrifugal tension force $R(x)$ is at its maximum value [19]. The rotating beam problem has now been turned into a case of an axially loaded beam. Although this averaging appears to be a rudimentary approximation, it may be used to analyze the wave dispersion properties of spinning nanobeams such as carbon nanotubes. Due to centrifugal stiffening at the root ($x=0$), the maximal axial force $R(x)$ has the form [19]:

$${R}_{max} =\int\limits_{0}^{L}\rho A{\Omega }^{2}\left(r+x\right)dx=\frac{1}{2}\rho A{\Omega }^{2}L\left(2r+L\right)$$

(33)

The governing equation may now be expressed as a nonlocal partial differential equation with constant coefficients.

As a result, the equation of motion (29) is a partial differential equation with constant coefficients that may be represented as:

$$\left[\frac{{\partial }^{4}}{\partial {x}^{4}}+\frac{12}{{h}^{2}}\frac{{\partial }^{2}}{\partial {t}^{2}}\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\right]w-\left(1-{\xi }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[q+\frac{6L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\frac{{\partial }^{2}w}{\partial {x}^{2}}\right]+\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\frac{{\partial }^{2}\Theta }{\partial {x}^{2}}=0$$

(34)

The specific bending moment $M$ in Eq. (31) can also be expressed as:

$$M\left(x,t\right)=\frac{12{\xi }^{2}}{{h}^{2}}\frac{{\partial }^{2}w}{\partial {t}^{2}}-{\xi }^{2}\left[q+\frac{6L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\frac{{\partial }^{2}w}{\partial {x}^{2}}\right]-\frac{{\partial }^{2}w}{\partial {x}^{2}}-\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\Theta$$

(35)

5 Boundary and initial conditions

The studied nanobeam was initially supposed to be homogeneous, at rest, undeformed. The initial conditions are considered as follows:

$${\left.w\left(x,t\right)\right|}_{t=0}={\left.\frac{\partial w\left(x,t\right)}{\partial t}\right|}_{t=0}=0, {\left.\Theta \left(x,t\right)\right|}_{t=0}={\left.\frac{\partial\Theta \left(x,t\right)}{\partial t}\right|}_{t=0}=0$$

(36)

We assume that the limit conditions of the nanobeam problem at both ends satisfy

$${\left.w\left(x,t\right)\right|}_{x=0,L}=0, {\left.\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}\right|}_{x=0,L}=0$$

(37)

Let us also consider that the nanobeam is thermally loaded at $x=0$. Hence, due to Eq. (24), we can put

$$\Theta ={\theta }_{0}f\left(x,t\right)\hbox{ on }x=0$$

(38)

where ${\theta }_{0}$ is a constant and $f\left(x,t\right)$ is a changing ramp-type function with the following mathematical description:

$${\left.f\left(x,t\right)\right|}_{x=0}=\left\{\begin{array}{l}0\quad t\le 0,\\ \frac{t}{{t}_{0}} \quad 0\le t\le {t}_{0},\\ 1\quad t>{t}_{0},\end{array}\right.$$

(39)

where ${t}_{0}>0$ is called ramp-type parameter, and it has the same dimensionless as the time $t$. Furthermore, the temperature at the end limit will satisfy the relationship:

$${\left.\frac{\partial\Theta }{\partial x}\right|}_{x=L}=0.$$

(40)

6 Solution in the Laplace transform space

In many areas of practical mathematics, the introduction of Laplace transforms is a topic of critical relevance. When working with linear systems defined by differential and partial equations, the Laplace transform is a valuable tool. We can do the Laplace transform of the various functions in order to research or evaluate a control system (function of time). The Laplace transform has the ability to convert analytic issues to algebraic problems, which is a useful characteristic. Even if the algebraic operation becomes more difficult, it is still easier to solve than the differential equation. The outcome of solving the algebraic problem in the frequency domain is then translated to the time domain form to get the final solution to the differential equation. To put it another way, the Laplace transformation is nothing more than a shortcut to solving differential and partial equations.

Employing the technique of the Laplace transform to Eqs. (30), (34) and (35), we get

$$\left[\left(1+\frac{6{\xi }^{2}L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\right)\frac{{\mathrm{d}}^{4}}{\mathrm{d}{x}^{4}}-\left(\frac{12{\xi }^{2}{s}^{2}}{{h}^{2}}+\frac{6L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\right)\frac{{\mathrm{d}}^{2}}{\mathrm{d}{x}^{2}}+\frac{12{s}^{2}}{{h}^{2}}\right]\overline{w }=-\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\frac{{\mathrm{d}}^{2}\overline{\Theta }}{\mathrm{d}{x }^{2}}-\overline{g }\left(s\right)$$

(41)

$$\left(1+{\tau }_{\theta }s\right)\left(\frac{{\mathrm{d}}^{2}\overline{\Theta }}{\mathrm{d}{x }^{2}}-\frac{{\pi }^{2}}{{h}^{2}}\overline{\Theta }\right)=s\left(1+{\tau }_{q}\mathrm{s}+{{s}^{2}\tau }_{q}^{2}/2\right)\left(\overline{\Theta }-\frac{\gamma {\pi }^{2}h}{24K\eta }\frac{{\mathrm{d}}^{2}\overline{w}}{\mathrm{d}{x }^{2}}\right)$$

(42)

$$\overline{M }\left(x,s\right)=\frac{12\xi {s}^{2}}{{h}^{2}}\overline{w }-\left(1+\frac{6{\xi }^{2}L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\right)\frac{{\mathrm{d}}^{2}\overline{w}}{\mathrm{d}{x }^{2}}-\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}\overline{\Theta }-\xi \overline{g }\left(s\right)$$

(43)

where $\overline{g }\left(s\right)={q}_{0}\left(\frac{1}{s}-\frac{\delta }{\beta +s}\right)$.

The differential equation for $\overline{w }$ is followed by the deletion of $\overline{\Theta }$ from Eqs. (41) and (42),

$$\left[\frac{{\mathrm{d}}^{6}}{\mathrm{d}{x}^{6}}-A\frac{{\mathrm{d}}^{4}}{\mathrm{d}{x}^{4}}+B\frac{{\mathrm{d}}^{2}}{\mathrm{d}{x}^{2}}-C\right]\overline{w }={A}_{5}\overline{g }\left(s\right)/{A}_{1}$$

(44)

where

$$\begin{array}{c}A=\frac{1}{{A}_{1}}\left({A}_{5}{A}_{1}+{A}_{2}+{A}_{4}{A}_{6}\right), B=\frac{1}{{A}_{1}}\left({A}_{5}{A}_{2}+{A}_{3}\right), C=\frac{{A}_{5}{A}_{3}}{{A}_{1}},\\ {A}_{1}=\left(1+\frac{6{\xi }^{2}L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\right), {A}_{2}=\left(\frac{12{\xi }^{2}{s}^{2}}{{h}^{2}}+\frac{6L{\Omega }^{2}\left(2r+L\right)}{{h}^{2}}\right), {A}_{4}=\frac{24{T}_{0}{\alpha }_{T}}{{\pi }^{2}h}, \\ {A}_{3}=\frac{12{s}^{2}}{{h}^{2}}, {A}_{5}=\frac{{\pi }^{2}}{{h}^{2}}+\frac{s\left(1+{\tau }_{q}\mathrm{s}+{{s}^{2}\tau }_{q}^{2}/2\right)}{1+{\tau }_{\theta }s}, {A}_{6}=\frac{s\left(1+{\tau }_{q}\mathrm{s}+{{s}^{2}\tau }_{q}^{2}/2\right)}{1+{\tau }_{\theta }s}\left(\frac{\gamma {\pi }^{2}h}{24K\eta }\right).\end{array}$$

(45)

By solving the differential Eq. (44), we obtain the general solution for $\overline{w }$ as follows:

$$\overline{w }\left(x,s\right)=\sum_{j=1}^{3}\left({C}_{j}{\mathrm{e}}^{-{m}_{j}x}+{C}_{j+3}{\mathrm{e}}^{{m}_{j}x}\right)-\frac{{A}_{5}\overline{g }\left(s\right)}{C{A}_{1}}$$

(46)

The unknown parameters ${C}_{j}, (j=\mathrm{1,2}..,6)$, can be calculated for the given boundary conditions. Also, the parameters ${m}_{1}^{2}$, ${m}_{2}^{2}$ and ${m}_{3}^{2}$ satisfies the following equation:

$${m}^{6}-A{m}^{4}+B{m}^{2}-C=0$$

(47)

Inserting Eq. (46) into Eq. (41), results in

$$\overline{\Theta }\left(x,s\right)=-\frac{1}{{A}_{4}{A}_{5}}\left[{A}_{1}\frac{{\mathrm{d}}^{4}\overline{w}}{\mathrm{d}{x }^{4}}-\left({A}_{2}+{{A}_{4}A}_{6}\right)\frac{{\mathrm{d}}^{2}\overline{w}}{\mathrm{d}{x }^{2}}+{A}_{3}\overline{w }+\overline{g }\left(s\right)\right]$$

(48)

General solutions of Eq. (48) can be simplified with the help of Eq. (46) as follows:

$$\overline{\Theta }\left(x,s\right)=\sum_{j=1}^{3}{H}_{j}\left({C}_{j}{\mathrm{e}}^{-{m}_{j}x}+{C}_{j+3}{\mathrm{e}}^{{m}_{j}x}\right)-{H}_{4},$$

(49)

where

$${H}_{j}=-\frac{1}{{A}_{4}{A}_{5}}\left[{A}_{1}{m}_{j}^{4}-\left({A}_{2}+{{A}_{4}A}_{6}\right){m}_{j}^{2}+{A}_{3}\right], {H}_{4}=\frac{\overline{g }\left(s\right)\left({A}_{4}-C\right)}{C{A}_{4}{A}_{5}}$$

(50)

By using expressions (46) and (49), the bending moment $\overline{M }$ can be calculated from (43) as:

$$\overline{M }\left(x,s\right)=\sum_{j=1}^{3}{L}_{j}\left({C}_{j}{\mathrm{e}}^{-{m}_{j}x}+{C}_{j+3}{\mathrm{e}}^{{m}_{j}x}\right)+{L}_{4}$$

(51)

where

$${L}_{j}=-\left({A}_{1}{m}_{j}^{2}+{A}_{4}{H}_{j}-{A}_{0}\right), {L}_{4}=\overline{g }\left(s\right)\left({A}_{4}{H}_{4}-\frac{{A}_{0}{A}_{5}}{C{A}_{1}}-\xi \right), {A}_{0}=\frac{12\xi {s}^{2}}{{h}^{2}}$$

(52)

By using Eq. (46), the axial displacement $\overline{u }$ can be simplified to:

$$\overline{u }=-z\frac{\mathrm{d}\overline{w}}{\mathrm{d}x }=z\sum_{j=1}^{3}{m}_{j}\left({C}_{j}{\mathrm{e}}^{-{m}_{j}x}-{C}_{j+3}{\mathrm{e}}^{{m}_{j}x}\right).$$

(53)

The boundary conditions in the Laplace transform domain given in Eqs. (37)–(40) are reduced to

$${\left.\overline{w }\left(x,s\right)\right|}_{x=0,L}=0, {\left.\frac{{\mathrm{d}}^{2}\overline{w }\left(x,s\right)}{\mathrm{d}{x}^{2}}\right|}_{x=0,L}=0,$$

(54)

$${\left.\overline{\Theta }\left(x,s\right)\right|}_{x=0}={\theta }_{0}\left(\frac{1-{\mathrm{e}}^{-{t}_{0}s}}{{t}_{0}{s}^{2}}\right)=\overline{G }\left(s\right),$$

(55)

$${\left.\frac{\mathrm{d}\overline{\Theta }}{\mathrm{d}x }\right|}_{x=L}=0.$$

(56)

We get the following system of equations by inserting the above boundary conditions to Eqs. (46) and (49):

$$\sum_{j=1}^{3}\left({C}_{j}+{C}_{j+3}\right)=\frac{{A}_{5}\overline{g }\left(s\right)}{C{A}_{1}}$$

(57)

$$\sum_{j=1}^{3}\left({C}_{j}{\mathrm{e}}^{-{m}_{j}L}+{C}_{j+3}{\mathrm{e}}^{{m}_{j}L}\right)=\frac{{A}_{5}\overline{g }\left(s\right)}{C{A}_{1}}$$

(58)

$$\sum_{j=1}^{3}{m}_{j}^{2}\left({C}_{j}+{C}_{j+3}\right)=\frac{{A}_{5}\overline{g }\left(s\right)}{C{A}_{1}}$$

(59)

$$\sum_{j=1}^{3}{m}_{j}^{2}\left({C}_{j}{e}^{-{m}_{j}L}+{C}_{j+3}{e}^{{m}_{j}L}\right)=\frac{{A}_{5}\overline{g }\left(s\right)}{C{A}_{1}}$$

(60)

$$\sum_{j=1}^{3}{H}_{j}\left({C}_{j}+{C}_{j+3}\right)={H}_{4}+\overline{G }\left(s\right),$$

(61)

$$\sum_{j=1}^{3}{{m}_{j}H}_{j}\left({C}_{j}{e}^{-{m}_{j}L}-{C}_{j+3}{e}^{{m}_{j}L}\right)=0,$$

(62)

The unknown parameters ${C}_{j}, (j=\mathrm{1,2}..,6)$, can be obtained by solving system (57)–(62).

Within the Laplace transform field, we have gotten all the analytical solutions for the physical. The Laplace transform inversion of complex transformed field variable expressions is difficult to achieve. The results will be calculated numerically in the next part using a Fourier series expansion method.

7 Inversion of the Laplace transforms

Numerical inversion of the Laplace transform is a helpful approach for pharmacokinetic modeling and parameter estimation when the model equations can be solved in the Laplace domain but the answers cannot be inverted back to the time domain. Various methods of numerical evaluation of the integral of the Laplace inversion have been discovered. For lateral vibration, thermal temperature, displacement, and stress distributions, the Riemann-sum approximation model is employed to get numerical results in the time domain. In this approach, any function $\overline{f }\left(x,s\right)$ in the domain of Laplace can be reversed to $f\left(x,t\right)$ in the time domain as [39, 40]:

$$f\left(x,t\right)=\frac{{\mathrm{e}}^{\zeta t}}{{t}_{1}}\left[\frac{1}{2} \mathrm{Re}\left\{ \overline{f }\left(x,\zeta \right)\right\}+\mathrm{Re}\left\{\sum_{n=0}^{N}{e}^{\frac{\mathrm{i}n\pi t}{{t}_{1}}}\overline{f }\left(x,\zeta +\frac{\mathrm{i}n\pi }{{t}_{1}}\right)\right\}\right],$$

(63)

where $\zeta$ is an arbitrary real number greater than real parts of all the singularities of $\overline{f }\left(x,s\right)$, $\mathrm{Re}$ is the real part and $\mathrm{i}=\sqrt{-1}$. We evaluated the proposed technique on a collection of known inverses of sample transform functions. To show the degree of precision, the findings of our numerical inversion approach are compared with the accurate estimates.

We will check two examples to illustrate the applicability of the suggested numerical inversion technique. We take the transformed function $\overline{{g }_{1}}\left(s\right)=\frac{1}{1+s+{s}^{2}}$ and $\overline{{g }_{2}}\left(s\right)=\frac{\mathrm{exp}\left(-1/s\right)}{{s}^{3/2}}$ which are the transforms of the functions ${g}_{1}\left(t\right)=\left(2/\sqrt{3}\right)\mathrm{exp}\left(-t/2\right)\mathrm{sin}\left(\sqrt{3}t/2\right)$ and ${g}_{2}\left(t\right)=\frac{\mathrm{sin}\left(2\sqrt{t}\right)}{\sqrt{\pi }}$. To invert the transform $\overline{{g }_{1}}\left(s\right)$, the parameter values of [6] were used, namely $\zeta =0.421$, $N=19$ and ${t}_{1}=7.5$ [41, 42]. Table 1 displays the numerical disparities between numerical values and exact values of $g\left(t\right)$ for the four approaches for time values ranging from 0.0 to 10.0. Comparison with the exact inverse Laplace transform shows a fairly good approximation.

Table 1 Comparison between the numerical inversion and the exact inverse Laplace transform

The enhanced approach can quickly achieve great accuracy without requiring large calculations. In addition, as compared to other algorithms with comparable high accuracy, the programming effort for the approach is modest [41, 42]. More importantly, by increasing processing effort by a linear amount, our inversion approach may make large improvements in accuracy. Our technique is thought to work well for a broader variety of functions.

8 Numerical results

We now present some numerical findings to explain our theoretical results in the above section and to demonstrate the influence of the nonlocal parameter and the decaying time-varying load. The numerical computations were carried out with the help of the Mathematica software. The material selected for numerical analysis was taken as silver, which is an excellent material, used in resonant devices. The physical data of silver at ${T}_{0}=293 K$ is given as:

$$\begin{array}{c}E=56 \mathrm{GPa}, \rho =10500 \mathrm{kg}/{\mathrm{m}}^{3}, {C}_{E}=234 \mathrm{J}/(\mathrm{kg K}),\\ {\alpha }_{T}=20\times {10}^{-6}(1/\mathrm{K}), \nu =0.36, K=429 \mathrm{W}/(\mathrm{mK}).\end{array}$$

The actual dimensions of the nanobeam are $\xi =2\ \mathrm{nm}$, $L=20\ \mathrm{nm}$, and $h=2b=4\ \mathrm{nm}$. The numerical results were computed using the non-dimensional variables set out in Eq. (28) for a wide range of beam lengths when $L=1$, $z=h/3$, $t=0.1$ and non-dimensional decay parameter $\beta =0.1$. Then, the aspect ratios of the nanobeam are taken as $L/h=5$ and $b/h=0.5$. For four cases, numerical calculations are carried out as follows.

8.1 The effect of the nonlocal parameter

The nonlocal theorem is achieved by adding the nonlocal coefficient to replace its variables in the conventional continuous medium and expressing the internal forces as nonlocal expressions. Some physical phenomena must also be considered while searching for mechanical behavior at the micro-nanoscale. Physical phenomena have a significant influence on the physical properties of the structure and the possibility of deformation, for example, surface, elastic electricity, etc. When examining the general elastic properties of nanostructures, it is not worth mentioning surface effects comprising surface energy, surface tension, and surface relaxation. However, due to their tiny size scales, such as lattice spacing between individual atoms, surface characteristics, and grain size, continuum models have lately received attention. It is quite difficult to establish a physically consistent model, which is based on such parameter significance using traditional continuous formulation.

In this subsection, we investigate how different dimensionless nonlocal parameter $\xi$ values influences the non-dimensional temperature, deflection, displacement, and moment of bending. Three specific values of $\xi$ are set in simulation, i.e., $\xi =0$ for local state, $\xi =0.01$ and $\xi =0.03$ for nonlocal one. In this case, one assumes that the angular velocity of rotation $\Omega$ remains constant, ramping time parameter ${t}_{0}$ as well as the phase-lags ${\tau }_{q}$ and ${\tau }_{\theta }$. We take $\Omega =0.3$, ${t}_{0}=0.1$, ${\tau }_{q}=0.02$, ${q}_{0}=0.1$ and ${\tau }_{\theta }=0.01$. Figures 2–5 demonstrate the influence of the nonlocal parameter $\xi$ on the vibration characteristics in the axial direction of nanobeam. Figures 2, 3, 4 and 5 present a comparison of the thermoelastic response of nanobeam obtained by the proposed method and those obtained by Abouelregal and Zenkour [40] based on the nonlocal model. In the case of a local model, the amplitudes of the values of the researched fields is more than in nonlocal models. From this estimate, the results indicate a strong agreement among the results. Studies have demonstrated that the mechanical characteristics of small-scale items are considerably different from or even entirely opposite nanoscales. Excellent approximations of a wide range of physical phenomena with characteristic lengths extending from the atomic scale to the macroscopic scale can be obtained by this theory.

Fig. 2

The deflection ${\varvec{w}}$ for different values of nonlocal parameter ${\varvec{\xi}}$

Fig. 3

The temperature ${\varvec{\theta}}$ for different values of nonlocal parameter ${\varvec{\xi}}$

Fig. 4

The isplacement ${\varvec{u}}$ for different values of nonlocal parameter ${\varvec{\xi}}$

Fig. 5

The bending moment ${\varvec{M}}$ for different values of nonlocal parameter ${\varvec{\xi}}$

The non-dimensional lateral vibration $w$, as shown in Fig. 2, first decreases, then reaches the bottom value about $x=0.3$ and then rises to zero. As can be expected, the lateral vibration distribution $w$ always starts and finishes at the zero values (i.e., disappears) and fulfills the limit conditions at $x=0$ and $x=L$. Due to the nature of the boundary conditions, the nanoscale beam often exerts the greatest deviation near the first edge of the beam as compared to other points on the axial axis. Also, it can be found that lateral vibration decreases with increasing nonlocal parameter $\xi$.

Figure 3 shows the variance of the distribution of temperature $\theta$ over distance $x$ for the three cases. The thermal temperature $\theta$ in this figure decreases as the distance $x$ increases in the wave propagation direction. This means that heat waves are traveling inside the medium at limited speeds, and this is consistent with the physical side. This phenomenon also illustrates the significance of generalized models of thermoelasticity as well as their use as an alternative to conventional models predicting an infinite velocity of the heat waves. It is further observed from the figure that the nonlocal parameter $\xi$ has a slight effect on temperature distribution. The increase in the value of $\xi$ leads to a decrease in temperature values.

Figure 4 illustrates the variability of the displacement $u$ in the presence and absence of the memory influence against the distance $x$. From the figure, we found that the displacement starts at the first edge with positive values and then slowly decreases until at $x=0.3$ becomes negative and reversed. The nonlocal parameter has a direct impact on the distribution of displacement. The displacement $u$ begins to decrease with the nonlocal parameter $\xi$ in the range $0\le x\le 0.3$. It is clear that raising the nonlocal term resulted in more deformation in the spinning system in both situations in the range $0.3\le x\le 1$.

Figure 5 is plotted against distance $x$ to analyze the nonlocality influence on the bending moment distribution $M$. From the figure, we see that the moment bending $M$ also increases along the beam as the distance $x$ increases. From the curves, it is noted that the curves describing the moment bending are convexly restricted. It begins at the first edge with its minimum value and then rises gradually until it reaches zero toward the last edge of the beam. We also noticed that the increase in the nonlocal parameter $\xi$ is intended to increase the distribution of the bending $M$.

The results presented generally indicate that the nonlocal parameter $\xi$ has a major effect on all physical fields studied. This clarifies the distinction between local thermoelasticity models and nonlocal thermoelasticity models in the event of a thermal field [41]. The effect of this parameter should also be taken into consideration when making nanoscale systems and devices. Moreover, the results of nonlocal continuum-based models are physically plausible results in the dynamics of nanobeams and simulations of molecular and other dynamics.

8.2 The impact of angular rotational velocity

In order to reduce rotating mechanical parts to micrometer or even to the nanoscale, many researchers have conducted research on rotating nano-devices, requirements and developments of intelligence, miniaturization and nano-metering. In this case, the effect of the angular velocity of rotation $\Omega$ on dimensionless field quantities has been carried out. As the magnitude of the non-dimensional speed of rotation rises, the thermal and mechanical waves become non-dispersive. The centrifugal force causes the angular velocity of the examined fields to fluctuate.

In this case, one assumes that the nonlocal parameter $\xi$ remains constant, ramping time parameter ${t}_{0}$ as well as the phase-lags ${\tau }_{q}$ and ${\tau }_{\theta }$. In the calculations, the fixed values $\xi =0.1$, ${t}_{0}=0.1$, ${q}_{0}=0.1$ ${\tau }_{q}=0.02$ and ${\tau }_{\theta }=0.01$ have been taken into account. Figures 6, 7, 8 and 9 demonstrate the difference in the quantities considered for three different angular velocity values ($\Omega =0, 0.1, 0.3$). In the case of non-rotation, we find that the rotation coefficient is equal to zero ($\Omega =0$) and this is known as a special case of current practice.

Fig. 6

The deflection ${\varvec{w}}$ for different values of the angular velocity ${\varvec{\Omega}}$

Fig. 7

The temperature ${\varvec{\theta}}$ for different values of the angular velocity ${\varvec{\Omega}}$

Fig. 8

The isplacement ${\varvec{u}}$ for different values of the angular velocity ${\varvec{\Omega}}$

Fig. 9

The bending moment ${\varvec{M}}$ for different values of the angular velocity ${\varvec{\Omega}}$

Figures 6 presents the angular velocity of rotation $\Omega$ that influences the nanoscale beam deflection $w$. It was found that in the case of presence and absence of rotation this parameter has a substantial effect on the distribution of deflection and variability in results. Through increasing the angular velocity $\Omega$, the deflection $w$ decreases. These results are consistent with those reported [43]. For different non-dimensional angular velocity values $\Omega$, the temperature variation $\theta$ of the nanobeam with the distance $x$ has been studied. Such variations are shown in Figs. 7. It is noticeable that the temperature distribution increases as the angular velocity $\Omega$ increases. The results and observations obtained in the preceding literature are consistent with the concordant results such as those obtained by the authors [44, 45].

To investigate the influence of angular velocity $\Omega$ on the displacement variance $u$, Fig. 8 is plotted. We found that there is a significant effect of the rotation coefficient on the curves representing the displacement field. It is noted from the figure that in some intervals, the distribution of the displacement $u$ decreases with increasing rotation $\Omega$ and increases with it at other intervals. Figure 9 shows the variance in the distribution of bending moment $M$ of the rotating nanobeam with different values of angular velocity $\Omega$. From the figure, it is observed that the rotation $\Omega$ has a great effect on the moment curves, and that the moment’s amplitude increases with the moment $M$. The stiffening influence of the centrifugal force, which is related to the square of the rotation speed, is attributed to the rise in the amount of deflection as angular velocity increases.

One of the aims of this study is to describe the temperature distribution behavior and the angular velocity effect, as it provides useful insight when designing the blades of certain nanoscale devices, such as nano-turbines [43]. We may also infer the prominent influence of rotation on the various physical distributions by means of the preceding discussions. These results are in strong agreement with the preceding results obtained in [46,47,48]. Given the number of studies that have shown the viability of nanoscale rotating systems, this topic is predicted to gain a lot of attention in the coming future; existing samples involve researching molecular gears and carbon nanotube gears.

8.3 The influence of ramping time parameter

The third case exploring how the non-dimensional deflection, displacement, temperature, and bending moment differ with the time parameter of the ramping ${t}_{0}$ when the nonlocal parameter $\xi$ remains constant, angular velocity $\Omega$ as well as the phase-lags ${\tau }_{q}$ and ${\tau }_{\theta }$. We take $\Omega =0.3$, ${t}_{0}=0.1$, ${q}_{0}=0.1$, and $\Omega =0.3$. The numerical results are graphically collected and displayed in Figs. 10, 11, 12 and 13.

Fig. 10

The deflection ${\varvec{w}}$ for different values of the ramping time parameter ${{\varvec{t}}}_{0}$

Fig. 11

The temperature ${\varvec{\theta}}$ for different values of the ramping time parameter ${{\varvec{t}}}_{0}$

Fig. 12

The isplacement ${\varvec{u}}$ for different values of the ramping time parameter ${{\varvec{t}}}_{0}$

Fig. 13

The bending moment ${\varvec{M}}$ for different values of the ramping time parameter ${{\varvec{t}}}_{0}$

In Fig. 10, the influence of the ramping time parameter ${t}_{0}$ on the dynamic deflection of the nanoscale beam is shown. The ramping time parameter ${t}_{0}$ can be seen to have a remarkable effect on the bottom value of the non-dimensional deflection, and the bottom value of the deflection decreases with an increase in ramping time parameter ${t}_{0}$ increase [11].

Figure 11 is drawn to demonstrate the essence of temperature $\theta$ behavior for a specific ramp time parameter values. The increase in the ramping time parameter’s value causes the temperature values to decrease which is very apparent in the curves’ peek points. Figure 12 shows the variance of displacement $u$ as regards distance $x$ due to the ramping time-varying heat. From the figure, we observed that the displacement $u$ values decreased with the ramping time parameter in the range $0\le x\le 0.3$, then increased in the range $0.3\le x\le 1$.

Figure 13 demonstrates the existence of the bending moment $M$ at any distance $x$ from the first edge of the nanobeam for specific ramping time parameter values. The ramping time parameter ${t}_{0}$ can be found to have significant effects on the bending moment distribution [49, 50].

8.4 The effect of the magnitude of the point load

Throughout this subsection, the analysis of the impact of the dimensionless magnitude of point load ${q}_{0}$ on field quantities along the axial distances of the nanobeams in the presence of rotation and a varying heat has been performed. Explaining the dynamical behavior of the surface across which the dispersed load is travelling was a critical topic for scientists, leading to the development of a new field of study. In this case, three different values are considered for the dimensionless magnitude of the point load ${q}_{0}$. We put $\delta =0$ for the uniformly distributed load, and for the varying load exponential decay with time, we take $\delta =1$. The lateral vibration, temperature, displacement, and the nanobeam bending moment are shown in Figs. 14, 15, 16 and 17 for a comparison of the results. In the calculations, the fixed values $\xi =0.1$, ${t}_{0}=0.1$, ${\tau }_{q}=0.02$, $\Omega =0.3$, and ${\tau }_{\theta }=0.01$ have been taken into account. Distributed load causes the nanobeam to soften or harden due to tension or compression states. The point load on the structure may cause torsion as would be expected in the context of continuous mechanics. The critical bending load in bending is defined as the limit value at which the amplitude is at its highest. Dynamic bending exhibits a variety of properties [51].

Fig. 14

The deflection ${\varvec{w}}$ for different values of the magnitude of point load ${{\varvec{q}}}_{0}$

Fig. 15

The temperature ${\varvec{\theta}}$ for different values of the magnitude of point load ${{\varvec{q}}}_{0}$

Fig. 16

The isplacement ${\varvec{u}}$ for different values of the magnitude of point load ${{\varvec{q}}}_{0}$

Fig. 17

The bending moment ${\varvec{M}}$ for different values of the point load ${{\varvec{q}}}_{0}$

Because increasing the temperature induces early internal stresses and strains in the nanotube, the temperature increase softens the structure and decreases the thermoelastic characteristics. As a result, raising the temperature reduces the system’s vibration and divergence flow velocity [52]. As a result, in the increasing point load condition, temperature rise has a lowering influence on dynamic behavior.

It should be noted that in the case of a uniformly distributed load, the absolute values of the distributions of the deflection, the displacement, temperature, and the bending moment are greater than in the case of the exponential and decreasing variable dependent on time (see Figs. 14, 15, 16 and 17). These figures also show that if the changing load exponential decays with time, the absolute values of the field variables grow with the magnitude of the point load ${q}_{0}$ [38, 53].

9 Conclusion

A new mathematical model has been developed in the present work which governs the generalized nonlocal thermoelasticity with phase-lag for rotating nanobeams subjected to dynamic transverse loads. The governing partial differential equations are developed by including the nonlocal scale effects, according to the nonlocal Euler–Bernoulli beam theory, dual-phase-lag thermoelastic model, and Eringen’s nonlocal theory. The vibration of thermoelastic for nanobeam subjected to ramp-type heating has been studied. The results of this study reveal new phenomena related to the vibration of nanobeams. The impact on field variables of the dynamic loads ${q}_{0}$, rotation, the nonlocal parameter $\xi$ somewhere and the ramping time parameter ${t}_{0}$ are investigated and graphically illustrated. The current work provides the possibility of nanobeams response behaviors to allow investigation in a general framework. The main observational conclusions are summarized as:

• The nonlocal parameter affects substantially all physical fields studied. With the increase in the parameter of the length scale, the rotating nanobeam deflection will increase.

• The temperature variance would have a major impact on the deflection response as the nonlocal parameter is greater.

• Thermoelastic deflection, displacement, and temperature strongly depend on the time parameter for the ramping.

• The effects of the dynamic loads are very significant for all field quantities.

• Major variations in physical quantity are found between the exponential decay load varying and the uniformly distributed load.

• A pattern of finite propagation velocities is found in all figures depicted. It is predictable since the thermal wave moves at a finite velocity.

• Nanobeam vibration is a significant topic in nanotechnology research as it concerns to the optical properties and electronic of multi-walled carbon nanotubes.

• In microelectromechanical applications including relay switches, mass flow sensors, frequency filters, resonators, and accelerometers, the present model can be used.

• This study can consider demands and applications under the loading environment in the design and development of rotating resonator devices.