1 Introduction

The celestial mechanics is the branch of astronomy which deals with the motions of astronomical objects in space. Different dynamical models of the celestial bodies are studied in celestial mechanics such as two-body, three-body, restricted three-body and N-body problem. A number of space missions have been successfully operated by using these mathematical models. A reduced model of the restricted N-body problem where the infinitesimal body oscillates in the perpendicular to the orbital plane of the primaries along the Z-axis is called Sitnikov problem.

The circular Sitnikov restricted three-body problem is a dynamical model that was first time originally introduced by [1]. Later on, the circular Sitnikov problem, admitted as the MacMillan problem, was discussed in detailed by [2]. According to [3], the restricted three-body problem has several applications in celestial mechanics and dynamical astronomy. This is a particular example that includes the Sitnikov problem. Long-standing awareness of the issue was rekindled by Sitnikov’s article, which established the presence of oscillating motion for the three-body problem [4]. Finding the third body’s motion down the perpendicular line while the primary bodies are being pulled apart by Newtonian gravity is the challenge at hand. A nonlinear second-order, ordinary differential equation can be used to model the problem which is not easily integrable. So, finding a precise solution to the problem is impossible. Therefore, many researchers have developed a number of different techniques to solve the differential equation of motion to know behavior of this problem. [5] investigated the mapping rather than the original differential equations and show that a hyperbolic invariant set exists. Also, found that the disorder region’s of theoretical forecast matches numerical findings very well and discussed LCEs and KS-entropy of the dynamical system .The stability of periodic orbits in vertical motion and bifurcations into three-dimensional families in the Sitnikov constrained N-body problem was discussed by [6]. Further, [7] investigated the stability of Sitnikov problem in periodic movements when the amplitude of periodic vertical movements is adjusted in a continuous monotone way, special emphasis is paid to the alternation of stability and instability within the family. The Sitnikov problem is simplified to a particular limited (\(N+1\))-body problem introduced by [8] and prove that a limited or unlimited amount of periodic solutions exist. After that symmetric regular solution in the circular Sitnikov problem is founded by [9]. Furthermore, Newton–Raphson(N-R) basins of convergence, which correspond to the libration points for the Sitnikov four-body problem, together with non-spherical primaries are numerically investigated by [10]. In the circular Sitnikov problem, for numerous approaches they compared the basins of attraction with spheroid primary [11, 12]. For the convex configuration, [13, 14] calculated the basin of convergence for the axial-symmetric five-body problem and [15] found the periodic solutions of a generalized Sitnikov problem.

The elliptical Sitnikov restricted three-body problem was first time investigated by [4], who show the subsistence of oscillatory form solution which is known as Sitnikov problem. In the elliptic Sitnikov problem, the families of symmetric periodic orbits were analytically obtained by [16]. The radiation pressure effect is studied in the elliptic Sitnikov problem of restricted four-body problem (RFBP) by [17]. Further, the elliptic Sitnikov five-body problem is studied by [18]. They examined the periodicity as well as stability of the problem by using Poincare surfaces of section (PSS). Moreover, the elliptical as well as circular case of Sitnikov problem of three and four-body problem are discussed by several authors [19,20,21,22,23]. Recently, [15, 24, 25] studies on the periodic solution in elliptic or circular Sitnikov four and five-body problem under several perturbation forces. By [26], the Sitnikov three-body problem is subjected to the method of multiple scales is investigated and produced an analytical result that is congruent with a numerical solution. In addition, [21] computed periodic solution of linear and nonlinear Sitnikov restricted three-body problem (SRTBP). The circular Sitnikov restricted four-body problem by taking perturbation theory and found the periodic orbits upto second- and fourth-order approximations is studied by [23].

The ambition of our present study is to utilize Multiple Scales Method in order to calculate analytical periodic solution for the Sitnikov restricted four-body problem (SRFBP) and comparing it with the numerical solution to demonstrate how important this perturbation approach. Our work is organized in the following way: We give a quick summary of the periodic solution of SRTBP as well as SRFBP in Sect. 1. We describe circular SRFBP equations of motion and its dynamical properties in Sect. 2. In Sect. 3, we describe linear stability of periodic solution using eigenvalue approach. Further, we investigate the zeroth-, first- and second-order approximated periodic solution with the help of Multiple Scales Method in Sect. 4. In Sect. 5, the results of the numerical simulations are examined as well as a comparison between the analytic and numerical solutions are presented. Finally, we added the conclusion of the paper in Sect. 6.

2 Descriptions and equations of motion of the proposed model

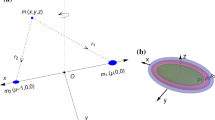
The Sitnikov motions are constructed from the RFBP by taking \(m_1 =m_2 =m_3=m = \frac{1}{3}\); \(x(t)=y(t)=0\) and \(r_1=r_2=r_3=\sqrt{z^2+\frac{1}{3}}\). The fourth primary body has mass \(m'\) which is less than the masses of the primaries, and it does not influence the motion of the primaries. All the primaries are at vertices of an equilateral triangle and moving in circular orbit around the center of mass of the system. Therefore, the distances of primaries from the center of mass of the system at any time remain in the same ratio [27] which is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the circular Sitnikov restricted four-body problem

Full size image

The equation of motion of the infinitesimal body along z-axis is given [23] by

$$\begin{aligned} \ddot{z}= & {} \Omega _{z}=\frac{-z}{(\frac{1}{3}+z^2)^\frac{3}{2}}. \end{aligned}$$
(1)

In this dynamical system, energy integral with one degree of freedom is given as

$$\begin{aligned} \dot{z}^2= \frac{2}{\sqrt{\frac{1}{3}+z^2}}-2C, \end{aligned}$$
(2)

where C is an arbitrary constant which depends on the initial conditions. The distance between either of the primaries or the fourth body is

$$\begin{aligned} r=\sqrt{\frac{1}{3}+z^2}. \end{aligned}$$

When we substitute these values into Eq. (2), we get the following expression

$$\begin{aligned} \dot{r}^2 =\left( \frac{2}{r}-\bar{C}\right) \left( 1-\frac{1}{3r^2}\right) , \end{aligned}$$
(3)

where \({\bar{C}}= 2C\). Eliminating fractional form of Eq. (3) with the help of following transformation

$$\begin{aligned} {\bar{u}}=\frac{1}{r}, \end{aligned}$$

as the dependent variable. Using this expression into Eq. (3), we have

$$\begin{aligned} \left( \frac{\hbox {d}{\bar{u}}}{\hbox {d}t}\right) ^2= {\bar{u}}^4 (2 {\bar{u}} -\bar{C})\left( 1-\frac{{\bar{u}}^2}{3}\right) . \end{aligned}$$
(4)

We change the scale by introducing \(u=\frac{{\bar{u}}}{\sqrt{3}}\) and \(c=\frac{{\bar{C}}}{2\sqrt{3}}\). The quadrature of Eq. (4) with this notation takes the form

$$\begin{aligned} \int _{1}^{u}\frac{\hbox {d}u}{\sqrt{6\sqrt{3}u^4(u-c)(1-u^2)}}=\int _{0}^{t}\hbox {d}t. \end{aligned}$$
(5)

The lower limit is so chosen in such a way that at \(t=0,~ u=1\) or \({\bar{u}}=\sqrt{3}\) or \(r=\frac{1}{\sqrt{3}}\) and \(\dot{z}=\sqrt{(2\sqrt{3}-{\bar{C}})}\). The infinitesimal body begins its motion at the origin of the reference system. If \({\bar{C}}>2 \sqrt{3}\) or \(c>1\), then motion is not possible at the origin. The quadrature given in Eq. (5) may be reduce to Legendre’s form by taking

$$\begin{aligned} v^2=\frac{1-u}{1-c} ~~\text {and}~~ k^2=\frac{1-c}{2}. \end{aligned}$$

In this connection, we get the integral

$$\begin{aligned} \int _{0}^{v}\frac{\hbox {d}v}{(1-2 k^2 v^2)^2\sqrt{(1-v^2)(1-k^2 v^2)}}=3\sqrt{3}\int _{0}^{t}\hbox {d}t, \end{aligned}$$
(6)

and can be solved in terms of the third kind of elliptical integral. The motion of the infinitesimal body in the direction of z-axis will be regular and periodic provided that \(0 <c\le 1\). Of course, the period is a function of the constant c, and by integrating Eq. (6), it can be obtained the quarter period between the limits 0 and 1. The period is given by

$$\begin{aligned} \int _{0}^{1}\frac{\hbox {d}v}{(1-2 k^2 v^2)^2\sqrt{(1-v^2)(1-k^2 v^2)}}=\sqrt{3\sqrt{3}}\int _{0}^{\frac{T}{4}}\hbox {d}t, \end{aligned}$$
(7)

where T is the period. The complete elliptic integral can be obtained by setting the upper bound of the integral to its maximum range, i.e., \(\sin \theta =1\) or \( \theta =\frac{\pi }{2}\) so that we put \(v=\sin \theta \), then the integral of Eq. (7) becomes

$$\begin{aligned} \int _{0}^{\frac{\pi }{2}}\frac{\hbox {d}\theta }{(1-2 k^2 \sin ^2\theta )^2\sqrt{(1-k^2 \sin ^2\theta )}}=\sqrt{3\sqrt{3}}{\frac{T}{4}}. \end{aligned}$$

Applying Binomial expansion, the above integral can be written as

$$\begin{aligned}{} & {} \int _{0}^{\frac{\pi }{2}} \left( 1+\frac{9}{2}k^2 \sin ^2\theta +\frac{115}{8}k^4 \sin ^4\theta +\frac{375}{48}k^6\sin ^6\theta +\dots \right) \hbox {d}\theta =\sqrt{3\sqrt{3}}{\frac{T}{4}}. \end{aligned}$$

Using reduction formula in this integral, we get

$$\begin{aligned} T=\frac{2\pi }{\sqrt{3\sqrt{3}}}\left( 1+\frac{9}{4}k^2 +\frac{345}{64}k^4 +\frac{5625}{2304}k^6+\dots \right) , \end{aligned}$$
(8)

and this expression converges for all values of \(k^2<\frac{1}{2}\) and \(k^2=\frac{1}{2}\left( 1-\frac{1}{\sqrt{\frac{1}{3}+z(0)^2}}\right) \). The general solution can be obtained by inverting the quadrature given in Eq. (6) as an elliptic integral of the third kind. But, it is not possible to reverse of Eq. (6) to find the expression of z(t). So that an approximation solution is needed for this problem. Further, if we multiply Eq. (8) by \(\sqrt{3\sqrt{3}}\), then it agree to get the period of MacMillan [2] work.

Table 1 Comparison between Sitnikov restricted three and four-body problem for period of oscillation
Full size table

With the help of Eq. (8), we obtained numerical values of the period, which is shown in Table 1. In this table, we observe that when the initial values of z(0) increase their corresponding period of oscillation also increases that means initial conditions play a vital role for period of oscillation.

Using Eqs. (1) and (2), the equation of motion upto \(O(z^3)\) can take the form

$$\begin{aligned} \ddot{z}+\omega _r^2z+\beta \omega _d^2 z^3=0, \end{aligned}$$
(9)

where \(\omega _r^2=3\sqrt{3}, ~\omega _d^2=\frac{27\sqrt{3}}{2}\) and \(\beta =-1\). Here, \(\beta =-1<0\), i.e., equation represents a “soft spring” and closed curves. Eq. (9) is known as duffing equation, which has a wide range of practical application such as non-harmonic oscillations and chaotic nonlinear behavior. Also, it is used in mechanical, electrical and physics. Further, Eq. (9) can be written as a system of first-order ordinary differential equations by assuming

$$\begin{aligned} \dot{z}=q,\ \dot{q}= -\omega _r^2z-\beta \omega _d^2 z^3. \end{aligned}$$
(10)

At fixed points \(\dot{z}=q=0\) so that \(q=0\) and \(\dot{q}= z(-\omega _r^2-\beta \omega _d^2 z^2)=0\). Therefore, the fixed points are (0, 0), \((\frac{\sqrt{2}}{3},0)\) and \((- \frac{\sqrt{2}}{3},0)\), respectively.

3 Linear stability analysis of periodic solution

Analysis of the stability of the fixed points can be done by linearizing Eq. (10) which gives

$$\begin{aligned}{} & {} \ddot{z}=\dot{q},\ \ddot{q}= (-\omega _r^2 -3\beta \omega _d^2 z^2)\dot{z}. \end{aligned}$$
(11)

The matrix for Eq. (11) can be written as

$$\begin{aligned} \begin{bmatrix} \ddot{z} \\ \ddot{q} \end{bmatrix}=\begin{bmatrix} 0 &{}1\\ (-\omega _r^2 -3\beta \omega _d^2 z^2)&{} 0 \end{bmatrix} \begin{bmatrix} \dot{z} \\ \dot{q} \end{bmatrix}. \end{aligned}$$

Examining the stability at the critical point (0, 0), the characteristics equation of the above matrix is given as

$$\begin{aligned} \begin{vmatrix} 0-\lambda&1\\ -\omega _{r}^{2}&0-\lambda \end{vmatrix}=0, \end{aligned}$$

and its eigenvalues are \(\lambda _{1,2}=\pm i \sqrt{\omega _r^2}=\pm i \sqrt{3\sqrt{3}}\). This shows that the critical point is center for which stability is ensured. Again, at the other two critical points \((\frac{\sqrt{2}}{3},0)\) and \((-\frac{\sqrt{2}}{3},0)\), the characteristics equation of the matrix is given by

$$\begin{aligned} \begin{vmatrix} 0-\lambda&1\\ -6\sqrt{3}&0-\lambda \end{vmatrix}=0, \end{aligned}$$

and its eigenvalues are \( \lambda _1= \sqrt{6\sqrt{3}}\) and \(\lambda _2=-\sqrt{6\sqrt{3}}\), respectively. This shows that the critical points are saddle points and the period is hyperbolic. Hence, Hartman–Grobman theorem concludes that we have critical points which lose stability at \((\frac{\sqrt{2}}{3},0)\) and \((-\frac{\sqrt{2}}{3},0)\), respectively, which is shown in Fig. 2.

The phase curves are given as

$$\begin{aligned} \frac{\hbox {d}q}{\hbox {d}z}=\frac{(-\omega _r^2z -\beta \omega _d^2 z^3)}{q}{.} \end{aligned}$$
(12)

Integrating Eq. (12), we get

$$\begin{aligned} \frac{q^2}{2}+\omega _r^2\frac{z^2}{2} +\beta \omega _d^2 \frac{z^4}{4}=K_1{,} \end{aligned}$$

where \(K_1\) is a constant and we may state that phase curves are on the function’s level sets.

$$\begin{aligned} G(z,q)=q^2+\omega _r^2 z^2 +\beta \omega _d^2 \frac{z^4}{2}. \end{aligned}$$
Fig. 2
figure 2

Phase curves of the restricted Sitnikov four-body problem

Full size image

4 Periodic solution using multiple scales method

The Multiple Scales Method is a technique for analyzing the impact of weak nonlinearities on the solution of ordinary and partial differential equations. Instead of a single variable, the original time is expressed in terms of numerous time scales, which are termed multiple independent variables or scales. In the form of perturbation series, we express the solution z(t) as

$$\begin{aligned} z(t)=\sum _{n=0}^{\infty } \epsilon ^{n} z_{n}(t,\tau ,\sigma ), \end{aligned}$$
(13)

where \(\tau =\epsilon t\) and \(\sigma =\epsilon ^2 t\) are slow variables, depends on t. The variable t, \(\tau \) and \(\sigma \) are correlated with each other. The purpose of Multiple Scales Method is to reduce the secular terms using two variables which are independent variables. We enlarged the ordinary differentiation in fast variable t to the differential operator \(D_t\), which contains partial derivative in regard fast variable t, slow variable \(\tau \) and \(\sigma \). The differential operator \(D_t\) is denoted by the chain rule as

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}=D_{t}=\left( \frac{\partial }{\partial t}+\epsilon \frac{\partial }{\partial \tau }+\epsilon ^2 \frac{\partial }{\partial \sigma }\right) , \end{aligned}$$
(14)

and hence

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}z(t)=D_{t}\sum _{n=0}^{\infty } \epsilon ^{n} z_{n}(t,\tau ,\sigma ). \end{aligned}$$
(15)

For all t and \(\frac{\hbox {d}}{\hbox {d}t}\tau =\epsilon \) and \(\frac{\hbox {d}}{\hbox {d}t}\sigma =\epsilon ^2\). Using the conditions that \(z_n(t,\tau ,\sigma )\) follow continuity as well as differentiability for \(t,\tau \) and \(\sigma \), respectively. Putting Eq. (14) into Eq. (15) with easy calculation, we obtain first and second derivative of z

$$\begin{aligned} \frac{\hbox {d}z}{\hbox {d}t}= & {} \frac{\partial z_0}{\partial t}+\epsilon \left( \frac{\partial z_1}{\partial t}+\frac{\partial z_0}{\partial \tau }\right) +\epsilon ^2\left( \frac{\partial z_2}{\partial t}+\frac{\partial z_1}{\partial \tau }+\frac{\partial z_0}{\partial \sigma }\right) +O(\epsilon ^3), \end{aligned}$$
(16)

and

$$\begin{aligned} \frac{\hbox {d}^2z}{\hbox {d}t^2}= & {} \frac{\partial ^2 z_0}{\partial t^2}+\epsilon \left( \frac{\partial ^2 z_1}{\partial t^2}+2\frac{\partial ^2 z_0}{\partial \tau \partial t}\right) +\epsilon ^2\left( \frac{\partial ^2 z_2}{\partial t^2}+2\frac{\partial ^2 z_1}{\partial \tau \partial t}+2\frac{\partial ^2 z_0}{\partial \sigma \partial t}+\frac{\partial ^2 z_0}{\partial \tau ^2}\right) +O(\epsilon ^3). \end{aligned}$$
(17)

With the help of Eqs. (13), (16), (17) and the initial conditions as \(z(0)=\alpha \) and \(\dot{z}(0)=0\) into Eq. (9), we have

$$\begin{aligned}{} & {} \left\{ \frac{\partial ^2 z_0}{\partial t^2}+\epsilon \left( \frac{\partial ^2 z_1}{\partial t^2}+2\frac{\partial ^2 z_0}{\partial \tau \partial t}\right) +\epsilon ^2\left( \frac{\partial ^2 z_2}{\partial t^2}+2\frac{\partial ^2 z_1}{\partial \tau \partial t}+2\frac{\partial ^2 z_0}{\partial \sigma \partial t}+\frac{\partial ^2 z_0}{\partial \tau ^2}\right) +O(\epsilon ^3)\right\} \\{} & {} \quad +\omega _r^2\left\{ z_0+\epsilon z_1+\epsilon ^2 z_2+O(\epsilon ^3)\right\} -\epsilon \omega _d^2\left\{ z_0+\epsilon z_1+\epsilon ^2 z_2+O(\epsilon ^3)\right\} ^3=0. \end{aligned}$$

Equating the coefficients of \(\epsilon ^0,\epsilon ^1\) and \(\epsilon ^2\) to zero, we obtained the following set of equations

$$\begin{aligned}{} & {} \frac{\partial ^2 z_0}{\partial t^2}+\omega _r^2 z_0=0,\nonumber \\{} & {} z_0(0,0,0)=\alpha , \frac{\partial }{\partial t} z_0(0,0,0)=0, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \frac{\partial ^2 z_1}{\partial t^2}+2\frac{\partial ^2z_0}{\partial \tau \partial t}+\omega _r^2 z_1-\omega _d^2 z_0^3=0,\nonumber \\{} & {} z_1(0,0,0)=0, \frac{\partial }{\partial \tau } z_0(0,0,0)+\frac{\partial }{\partial t} z_1(0,0,0)=0 \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \frac{\partial ^2 z_2}{\partial t^2}+2\frac{\partial ^2z_0}{\partial \sigma \partial t}+2\frac{\partial ^2z_1}{\partial \tau \partial t}+\frac{\partial ^2z_0}{\partial ^2 \tau }+\omega _r^2 z_2-3\omega _d^2 z_0^2 z_1=0,\nonumber \\{} & {} z_2(0,0,0)=0, \nonumber \\{} & {} \frac{\partial }{\partial \tau } z_1(0,0,0)+\frac{\partial }{\partial \sigma } z_0(0,0,0)+\frac{\partial }{\partial t} z_2(0,0,0)=0. \end{aligned}$$
(20)

The solution of Eq. (18) can be given as

$$\begin{aligned}{} & {} z_0(t,\tau ,\sigma )=z_0(\tau ,\sigma )e^{i\omega _r t}+{\bar{z}}_0(\tau ,\sigma )e^{-i\omega _r t}. \end{aligned}$$

Together with the initial constraints

$$\begin{aligned}{} & {} z_0(0,0)+{\bar{z}}_0(0,0)=\alpha , \nonumber \\{} & {} z_0(0,0)-\bar{z}_0(0,0)=0, \end{aligned}$$
(21)

where \({\bar{z}}_0(\tau , \sigma )\) be the complex conjugate of \(z_0(\tau , \sigma )\) and \(z_0(\tau , \sigma )\) is complex function in the slow variables \(\tau \) and \(\sigma \) that is arbitrary.

4.1 First-order approximated periodic solution

We compute the partial derivatives of \(z_0\) with respect to \(t, \tau \) and \( \sigma \), considering them as uncorrelated variables, and plug them into Eq. (19), we obtain

$$\begin{aligned} \frac{\partial ^2 z_1}{\partial t^2}+\omega _r^2 z_1= & {} \omega _d^2 \left[ z_0^3(\tau ,\sigma )e^{3i\omega _r t}+\bar{z}_0^3(\tau ,\sigma )e^{-3i\omega _r t}\right] +k_1(\tau ,\sigma )e^{i\omega _r t}+k_2(\tau ,\sigma )e^{-i\omega _r t}, \end{aligned}$$
(22)

where

$$\begin{aligned} k_1(\tau ,\sigma )= & {} 3\omega _d^2 z_0^2(\tau ,\sigma ){\bar{z}}_0(\tau ,\sigma )-2i\omega _r \frac{\partial z_0(\tau ,\sigma )}{\partial \tau },\\ k_2(\tau ,\sigma )= & {} 3\omega _d^2 z_0(\tau ,\sigma )\bar{z}_0^2(\tau ,\sigma )+2i\omega _r \frac{\partial \bar{z}_0(\tau ,\sigma )}{\partial \tau }. \end{aligned}$$

It is clear to see that the solution of Eq. (22) has secular terms, when the coefficients of \(e^{i\omega _r t}\) and \(e^{-i\omega _r t}\) are nonzero. As a result, to prevent secular terms in differential Eq. (22), the coefficient \(k_1(\tau ,\sigma )\) and \(k_2(\tau ,\sigma )\) must vanish.

$$\begin{aligned}{} & {} 3\omega _d^2 z_0^2(\tau ,\sigma ){\bar{z}}_0(\tau ,\sigma )-2i\omega _r \frac{\partial z_0(\tau ,\sigma )}{\partial \tau }=0, \end{aligned}$$
(23)
$$\begin{aligned}{} & {} 3\omega _d^2 z_0(\tau ,\sigma )\bar{z}_0^2(\tau ,\sigma )+2i\omega _r \frac{\partial \bar{z}_0(\tau ,\sigma )}{\partial \tau }=0. \end{aligned}$$
(24)

Here, we observe that Eq. (24) is complex conjugate of Eq. (23) and can be excluded. If \(z_0(\tau ,\sigma )\) satisfying these conditions, \(z_1(t,\tau ,\sigma )\) will be free from secular terms and no singularities appear in the first two term in the series of z(t) in Eq. (13). To solve Eq. (23) with the assistance of polar coordinate \((R,\theta )\), let

$$\begin{aligned} z_0(\tau ,\sigma )=R(\tau ,\sigma )e^{i\theta (\tau ,\sigma )}, (R,\theta ):R\rightarrow R. \end{aligned}$$

Substituting these values into Eqs. (23) and (24), we get

$$\begin{aligned}{} & {} z_0(\tau ,\sigma )=f_1(\sigma )e^{i\left( -\frac{81}{12}f_1^2(\sigma )\tau +f_2(\sigma )\right) },\nonumber \\{} & {} {\bar{z}}_0(\tau ,\sigma )=f_1(\sigma )e^{-i\left( -\frac{81}{12}f_1^2(\sigma )\tau +f_2(\sigma )\right) }, \end{aligned}$$
(25)

where \(f_1(\sigma )\) and \(f_2(\sigma )\) are functions (arbitrary) in the steady variable \(\sigma \) which is given as

$$\begin{aligned} \begin{aligned}{} & {} R(\tau ,\sigma )=f_1(\sigma ).\\ {}{} & {} \theta (\tau ,\sigma )=-\frac{81}{12}f_1^2(\sigma )\tau +f_2(\sigma ). \end{aligned} \end{aligned}$$
(26)

Substituting Eqs. (25) and (26), we get the zeroth-order approximated solution

$$\begin{aligned} z_0(t,\tau ,\sigma )=f_1(\sigma )\left[ e^{i\gamma _1(t,\tau ,\sigma )}+ e^{-i\gamma _1(t,\tau ,\sigma )}\right] , \end{aligned}$$

where

$$\begin{aligned} \gamma _1(t,\tau ,\sigma )=\omega _r t-\frac{81}{12}f_1^2(\sigma )\tau +f_2(\sigma ). \end{aligned}$$
(27)

Therefore, Eq. (22) will take the form

$$\begin{aligned} \frac{\partial ^2 z_1}{\partial t^2}+\omega _r^2 z_1= & {} \omega _d^2 \left[ z_0^3(\tau ,\sigma )e^{3i\omega _r t}+\bar{z}_0^3(\tau ,\sigma )e^{-3i\omega _r t}\right] , \end{aligned}$$

and its general solution is given as follow,

$$\begin{aligned} z_1(t,\tau ,\sigma )= & {} z_1(\tau ,\sigma )e^{i\omega _r t}+\bar{z}_1(\tau ,\sigma )e^{-i\omega _r t}-\frac{f_1^3(\sigma )\omega _d^2}{6\omega _r^2}\left[ e^{3i\gamma _1(t,\tau ,\sigma )}+ e^{-3i\gamma _1(t,\tau ,\sigma )}\right] , \end{aligned}$$

Together with initial conditions

$$\begin{aligned} z_1(0,0)+{\bar{z}}_1(0,0)= & {} \frac{f_1^3(0)\omega _d^2}{3\omega _r^2} \cos (3\gamma _{10}), \end{aligned}$$
(28)
$$\begin{aligned} z_1(0,0)-\bar{z}_1(0,0)= & {} f_1^3(0)i\left[ \frac{\omega _d^2}{3\omega _r^2}\sin (3\gamma _{10})+\frac{81}{6\omega _r} \sin (3\gamma _{10})\right] , \end{aligned}$$
(29)

where \(\sqrt{-1}=i\) and \(\gamma _{10}=\gamma _1(0)\).

4.2 Second-order approximated periodic solution

We compute the partial derivatives of \(z_0\) and \(z_1\) with respect to \(t, \tau \) and \(\sigma \), considering them as uncorrelated variables, and plug them into Eq. (20), we get

$$\begin{aligned} \frac{\partial ^2 z_2}{\partial t^2}+\omega _r^2 z_2= & {} \frac{-2187}{8\omega _r^2}f_1^5(\sigma )\left[ e^{5i \gamma _1(t,\tau ,\sigma )}+e^{-5i \gamma _1(t,\tau ,\sigma )}\right] +\left( \frac{81 \omega _d^2}{4\omega _r}-\frac{\omega _d^4}{\omega _r^2}\right) \nonumber \\{} & {} \times f_1^5(\sigma )\left[ e^{3i \gamma _1(t,\tau ,\sigma )}+e^{-3i \gamma _1(t,\tau ,\sigma )}\right] +3\omega _d^2f_1^2(\sigma )\left[ z_1(\tau ,\sigma )e^{i(\omega _r t+2 \gamma _1(t,\tau ,\sigma ))}\right. \nonumber \\{} & {} \left. +{\bar{z}}_1(\tau ,\sigma )e^{-i(\omega _r t+2 \gamma _1(t,\tau ,\sigma ))}\right] +k_3(\tau ,\sigma )e^{i\omega _r t}+k_4(\tau ,\sigma )e^{-i\omega _r t}, \end{aligned}$$
(30)

where

$$\begin{aligned} k_3(\tau ,\sigma )= & {} 6\omega _d^2 f_1^2(\sigma )z_1(\tau ,\sigma )-2i \omega _r \frac{\partial z_1(\tau ,\sigma )}{\partial \tau } +3\omega _d^2f_1^2(\sigma ){\bar{z}}_1(\tau ,\sigma ) e^{i2\theta (\tau ,\sigma )}\\ {}{} & {} +2\omega _r e^{i\theta (\tau ,\sigma )}\left[ \frac{-81}{6}f_1^2(\sigma )\frac{\partial f_1(\sigma )}{\partial \sigma }\tau +f_1(\sigma )\frac{\partial f_2(\sigma )}{\partial \sigma }-i\frac{\partial f_1(\sigma )}{\partial \sigma }\right] \\ {}{} & {} +\left[ \left( \frac{6561}{144}-\frac{\omega _d^4}{2\omega _r^2}\right) \frac{f_1^5(\sigma )}{2 \omega _r}\right] e^{i\theta (\tau ,\sigma )},\\ k_4(\tau ,\sigma )= & {} 6\omega _d^2 f_1^2(\sigma ){\bar{z}}_1(\tau ,\sigma )+2i \omega _r \frac{\partial {\bar{z}}_1(\tau ,\sigma )}{\partial \tau } +3\omega _d^2f_1^2(\sigma ) z_1(\tau ,\sigma ) e^{-i2\theta (\tau ,\sigma )}\\ {}{} & {} +2\omega _r e^{-i\theta (\tau ,\sigma )}\left[ \frac{-81}{6}f_1^2(\sigma )\frac{\partial f_1(\sigma )}{\partial \sigma }\tau +f_1(\sigma )\frac{\partial f_2(\sigma )}{\partial \sigma }+i\frac{\partial f_1(\sigma )}{\partial \sigma }\right] \\ {}{} & {} +\left[ \left( \frac{6561}{144}-\frac{\omega _d^4}{2\omega _r^2}\right) \frac{f_1^5(\sigma )}{2 \omega _r}\right] e^{-i\theta (\tau ,\sigma )}. \end{aligned}$$

Reducing the secular term \(k_3(\tau ,\sigma )=0\) and \(k_4(\tau ,\sigma )=0\), then Eq. (30) takes the form

$$\begin{aligned} \frac{\partial ^2 z_2}{\partial t^2}+\omega _r^2 z_2= & {} \frac{-2187}{8\omega _r^2}f_1^5(\sigma )\left[ e^{5i \gamma _1(t,\tau ,\sigma )}+e^{-5i \gamma _1(t,\tau ,\sigma )}\right] +\left( \frac{81 \omega _d^2}{4\omega _r}-\frac{\omega _d^4}{\omega _r^2}\right) \\ {}{} & {} \times f_1^5(\sigma )\left[ e^{3i \gamma _1(t,\tau ,\sigma )}+e^{-3i \gamma _1(t,\tau ,\sigma )}\right] +3\omega _d^2f_1^2(\sigma )\left[ z_1(\tau ,\sigma )e^{i(\omega _r t+2 \gamma _1(t,\tau ,\sigma ))}\right. \\ {}{} & {} \left. +\bar{z}_1(\tau ,\sigma )e^{-i(\omega _r t+2 \gamma _1(t,\tau ,\sigma ))}\right] , \end{aligned}$$

and its general solution is found as,

$$\begin{aligned} z_2(t,\tau ,\sigma )= & {} z_2(\tau ,\sigma )e^{i\omega _r t}+{\bar{z}}_2(\tau ,\sigma )e^{-i\omega _r t}+\frac{2187}{192\omega _r^4}f_1^5(\sigma )(e^{i5\gamma _1}+e^{-i5\gamma _1})\\{} & {} -\left( \frac{81\omega _d^2}{4\omega _r}-\frac{\omega _d^4}{\omega _r^2}\right) \frac{f_1^5(\sigma )}{8\omega _r^2}(e^{i3\gamma _1}+e^{-i3\gamma _1})-3\omega _d^2f_1^2(\sigma )\left[ z_1(\tau ,\sigma )\frac{e^{i(\omega _r t+2\gamma _1)}}{8\omega _r^2}\right. \\{} & {} \left. +{\bar{z}}_1(\tau ,\sigma )\frac{e^{-i(\omega _r t+2\gamma _1)}}{8\omega _r^2}\right] , \end{aligned}$$

with initial circumstance

$$\begin{aligned} z_2(0,0)+{\bar{z}}_2(0,0)= & {} \frac{-2187f_1^5(0)}{96\omega _r^4} \cos (5\gamma _{10})+\left( \frac{81\omega _d^2}{4\omega _r}-\frac{\omega _d^4}{\omega _r^2}\right) \frac{f_1^5(0)}{4\omega _r^2} \cos (3\gamma _{10}), \end{aligned}$$
(31)
$$\begin{aligned} z_2(0,0)-\bar{z}_2(0,0)= & {} \frac{-10935}{96\omega _r^4}f_1^5(0)i\sin (5\gamma _{10})+\frac{2i}{\omega _r} \frac{\partial f_1(0)}{\partial \sigma }. \end{aligned}$$
(32)

4.3 Periodicity conditions of Zeroth, first- and second-order approximated solution

With the initial circumstance in Eq. (21), the generalized zeroth-order estimated solution \(z_0\) is given as,

$$\begin{aligned} z_0(t,\tau ,\sigma )=2 f_1(\sigma )\cos \gamma _1(t,\tau ,\sigma ), \end{aligned}$$
(33)

where \(f_1(\sigma )=\frac{\alpha }{2}=\alpha _0, f_2(\sigma )=f_2(0)=2n\pi ,n\in Z\). The general first-order approximated solution \(z_1\) obtained as,

$$\begin{aligned} z_1(t,\tau ,\sigma )= & {} z_1(\tau ,\sigma )e^{i\omega _r t}+{\bar{z}}_1(\tau ,\sigma )e^{-i\omega _r t}-\frac{f_1^3(\sigma )\omega _d^2}{3\omega _r^2}\cos 3\gamma _1(t,\tau ,\sigma ), \end{aligned}$$
(34)

With the initial conditions given in Eqs. (28–29) and \(\gamma _1\) are defined in Eq. (27), while the estimated second-order solution \(z_2\) may be represented as

$$\begin{aligned} z_2(t,\tau ,\sigma )= & {} z_2(\tau ,\sigma )e^{i\omega _r t}+\bar{z}_2(\tau ,\sigma )e^{-i\omega _r t}+\frac{2187}{96\omega _r^4}f_1^5(\sigma )\cos 5\gamma _1(t,\tau ,\sigma )\nonumber \\{} & {} -\left( \frac{81\omega _d^2}{4\omega _r}-\frac{\omega _d^4}{\omega _r^2}\right) \frac{f_1^5(\sigma )}{4\omega _r^2}\cos 3\gamma _1(t,\tau ,\sigma )\nonumber \\{} & {} -\frac{3\omega _d^2f_1^2(\sigma )}{8\omega _r^2}\left[ z_1(\tau ,\sigma )e^{i(\omega _r t+2\gamma _1(t,\tau ,\sigma ))}+{\bar{z}}_1(\tau ,\sigma )e^{-i(\omega _r t+2\gamma _1(t,\tau ,\sigma ))}\right] , \end{aligned}$$
(35)

with the initial conditions are given in Eqs. (31-32). The solutions in Eqs. (33), (34) and (35) include four arbitrary functions \(z_1(\tau ,\sigma ), ~z_2(\tau ,\sigma ), ~f_1(\sigma )\) and \(f_2(\sigma )\) in slow variables \(\tau \) and \(\sigma \), respectively. The conditions in Eqs. (31-32) must be compatible with these three solutions. It is also evident that the function \(f_2(\sigma )\) has just one restriction: \(f_2(0)=2n\pi \), whereas \(f_1(\sigma )\) has none. We will treat these two functions as constants with \(f_1(\sigma )=\dfrac{\alpha }{2}=\alpha _0\) and \(f_2(\sigma )=2n\pi \), respectively. Initial circumstances can be chosen as follows to achieve harmony among the solutions:

$$\begin{aligned} z_1(\tau ,\sigma )= & {} {\bar{z}}_1(\tau ,\sigma )=\frac{f_1^3(0)\omega _d^2}{6\omega _r^2}\cos 3\gamma _{10},\nonumber \\ z_2(\tau ,\sigma )= & {} {\bar{z}}_2(\tau ,\sigma )= \frac{f_1^5(0)}{8\omega _r^2}\left[ \frac{-2187}{24\omega _r^2}\cos 5\gamma _{10}+\delta _1\cos 3\gamma _{10}\right] , \end{aligned}$$

where \(\delta _1=\left( \dfrac{81\omega _d^2}{4\omega _r}-\dfrac{\omega _d^4}{\omega _r^2}\right) .\) Therefore, the first three solutions in the perturbation series are controlled by

$$\begin{aligned} z_0(t,\tau )= & {} 2f_1(0)\cos \psi (t,\tau ), \end{aligned}$$
(36)
$$\begin{aligned} z_1(t,\tau )= & {} \frac{f_1^3(0)\omega _d^2}{3\omega _r^2}\left[ \cos \omega _r t-\cos 3 \psi (t,\tau )\right] , \end{aligned}$$
(37)
$$\begin{aligned} z_2(t,\tau )= & {} \frac{f_1^5(0)}{4\omega _r^2}\left[ \frac{2187}{24\omega _r^2}\left( \cos 5\psi (t,\tau )-\cos \omega _r t\right) +\delta _1(\cos \omega _r t-\cos 3 \psi (t,\tau ))\right. \nonumber \\{} & {} \left. -\frac{\omega _d^4}{2 \omega _r^2}\cos (\omega _r t+2 \psi (t,\tau ))\right] , \end{aligned}$$
(38)

where

$$\begin{aligned} \psi (t,\tau )=\omega _r t-\frac{81}{12}f_1^2(0)\tau +2n\pi . \end{aligned}$$

Since \(\cos (\theta +2n\pi )=\cos \theta ,~\sin (\theta +2n\pi )=\sin \theta \), then the solution of Eqs. (36), (37) and (38) can be written in a simplest form

$$\begin{aligned} z_0(t,\tau )= & {} 2f_1(0)\cos \omega _r\left( t-\frac{81f_1^2(0)}{12\omega _r}\tau \right) , \end{aligned}$$
(39)
$$\begin{aligned} z_1(t,\tau )= & {} \frac{f_1^3(0)\omega _d^2}{3\omega _r^2}\left[ \cos \omega _r t-\cos 3 \left( t-\frac{81f_1^2(0)}{12\omega _r}\tau \right) \right] , \end{aligned}$$
(40)
$$\begin{aligned} z_2(t,\tau )= & {} \frac{f_1^5(0)}{4\omega _r^2}\left[ \frac{2187}{24\omega _r^2}\left\{ \cos 5\omega _r\left( t-\frac{81f_1^2(0)}{12\omega _r}\tau \right) -\cos \omega _r t\right\} +\delta _1\right. \nonumber \\{} & {} \left. \times \left\{ \cos \omega _r t-\cos 3 \omega _r \left( t-\frac{81f_1^2(0)}{12\omega _r}\tau \right) \right\} -\frac{\omega _d^4}{2 \omega _r^2}\cos 3\omega _r\left( t-\frac{81f_1^2(0)}{18\omega _r}\tau \right) \right] . \end{aligned}$$
(41)

Using the slow variable \(\tau =\epsilon t\) and the parameter \(\epsilon \) can be replaced by unity in the technique of place maintaining parameters. With the help of Eqs. (39), (40) and (41), the zeroth-, first- and second-order estimated multiple scales method solution is given by

$$\begin{aligned} z^{(0)}(t)= & {} 2f_1(0)\cos \omega _r\left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t, \end{aligned}$$
(42)
$$\begin{aligned} z^{(1)}(t)= & {} 2f_1(0)\cos \omega _r\left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t +\frac{f_1^3(0)\omega _d^2}{3\omega _r^2}\left[ \cos \omega _r t-\cos 3 \left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t\right] , \end{aligned}$$
(43)
$$\begin{aligned} z^{(2)}(t)= & {} 2f_1(0)\cos \omega _r\left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t +\frac{f_1^3(0)\omega _d^2}{3\omega _r^2}\left[ \cos \omega _r t-\cos 3 \left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t\right] \nonumber \\{} & {} +\frac{f_1^5(0)}{4\omega _r^2}\left[ \frac{2187}{24\omega _r^2}\left\{ \cos 5\omega _r\left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t-\cos \omega _r t\right\} +\delta _1\left\{ \cos \omega _r t-\cos 3 \omega _r \left( 1-\frac{81f_1^2(0)}{12\omega _r}\right) t\right\} \right. \nonumber \\{} & {} \left. -\frac{\omega _d^4}{2 \omega _r^2}\cos 3\omega _r\left( 1-\frac{81f_1^2(0)}{18\omega _r}\right) t\right] . \end{aligned}$$
(44)

5 Numerical results

The findings of zeroth-, first-, and second-order approximation solutions of the SRFBP under various conditions (initial) are compared in this section. The numerical solutions of Eq. (1), as well as the zeroth-, first-, and second-order approximation solutions of Eq. (9) are derived using the Multiple Scales Method and are included in Eqs. (42), (43), and (44), respectively. Within the context of three alternative beginning positions (\(z(0)=0.1, ~0.2, ~0.3\)) and initial zero velocity (\(\dot{z}(0)=0\)), we compare the analytical and numerical solutions. The examination of infinitesimal mass motion will be separated into two major categories. Three alternative solutions are produced for three different conditions in the first group, as illustrated in the Fig. 3. The conditions \(z(0)=0.1, ~z(0)=0.2\) and \(z(0)=0.3\) are represented by the red, green, and blue curves in this diagram, respectively.

Fig. 3
figure 3

Solutions at the three various values of initial conditions

Full size image
Fig. 4
figure 4

Comparison of analytical and numerical solution

Full size image

On other hand, in the second important group, we compared numerically and analytically obtained solutions at the same initial conditions used in the group first. This group include four figures, (Fig. 4), where the red and blue curves denote the numerical solution (NS) and second-order approximations (SA) by the Multiple Scales Method. The motion of the infinitesimal body is periodic and can be seen in Fig. 3d. We observe that the infinitesimal body goes away from the center of mass, its amplitude increases and vice versa. The numerically calculated solution does not sustain periodicity patterns all over time. When the condition \(z(0)\le 0.31\) with \(\dot{z}(0)=0\), the motion is periodic but beyond this interval, it is not bounded and periodic. From Fig. 4, we see that the infinitesimal body begins to move with zero velocity and regard to the primary’s center of mass from three separate positions. Moreover, motion is regular within the interval \(0\le t \le 928\) with \(z(0)=0.1\). However, motion beyond this interval is not regular in numerical case. Again, in the interval \(0\le t\le 718\) with initial condition \(z(0)=0.2\), motion is periodic but when the interval \(t>718\) motion is non-periodic in numerical sense. Furthermore, in the interval \(0\le t\le 661\) with initial condition \(z(0)=0.3\), motion is periodic in analytically as well as numerically but when the interval \(t>661\) motion is not periodic numerically while analytically it maintains the periodicity patterns. On the other hand, when an infinitesimal body begins its motion far from its center of mass, we notice that motion might become chaotic. In addition, with rising values of beginning circumstances, periodicity becomes relatively slow to complete the path in the numerical simulation. Fig. 4d presents a comparison between zeroth-, first- and second-order analytical with numerical solution at the initial condition \(z(0)=0.1\).

Now, we compare the solutions by the multiple scales method of different orders with numerically computed solutions in the following items:

  • The solution by the multiple scales method is regular periodic all time whatever the initial conditions are taken.

  • The major difference between the obtained periodic solutions by the Multiple Scales Method and by the numerical solution is the difference in its frequency and period of time.

  • In the numerical solution, when the infinitesimal body starts its motion near the center of masses of the primaries, the period of time as well as the amplitude increases. On other hand, in analytical solution the period of time seems to be same but amplitude increases in the time interval [0, 20].

  • In the numerical solution for long time, we find that the motion is not periodic although by the multiple scales method, it is regular and periodic.

6 Conclusion

In the present article, we have discussed the motion of an infinitesimal body of the restricted four-body problem, which is known as particular circular Sitnikov problem by deleting the unbounded terms, known as secular terms. The periodic solutions for SRFBP were produced adopting the Multiple Scales Method. We compared these results to numerical results to see how important the perturbation approach.

One of the most important goal of eliminating secular terms is to determine the conditions that will compel motion to be periodic or to establish motion’s periodicity criteria. We can discover approximated periodic solutions form under these conditions in closed form. It was observed that the beginning circumstances (initial conditions) have a significant effect in the patterns of numerical and analytical periodic solutions. The motion was investigated numerically, and the estimated solution are computed using the Multiple Scales Method and compared by each other. We noticed that in the time interval \(0\le t\le 928\), the motion is periodic with condition \(z(0)=0.1\), but it is non-periodic in the numerical sense beyond this interval. Again, when \(z(0)=0.2\) and \(0\le t\le 718\), motion is periodic and as \(t>718\), it escape outside of the orbit so that motion is not periodic. Further, when \(z(0)=0.3\) and \(0\le t\le 661\), motion is periodic and whenever \(t>661\), orbit is escape far from its position which leads motion to non-periodicity. For the time \(t>0\), however, the Multiple Scales Method produces regular and periodic motion. Furthermore, we remark that whenever the test particle begins its motion near to the center of mass, the motion produced by the zeroth-, first-, and second-order approximation results is periodical and regularized. However, the test particle travels away from the center of mass, the numerical simulation solutions for a long period may not be periodic, even if all of the zeroth- to second-order approximation solutions come to be periodic. We showed that the Multiple scales technique yields the genuine motion of the circular Sitnikov RFBP, and that higher order approximation solutions are more accurate than lower order approximation solutions. Furthermore, since the numerical solution for a long time may not exhibit regular motion, the Multiple Scales technique provides a more realistic results than the numerical solution. A exact solution of this problem is also discussed and compared with MacMillan problem and observed that the time period of MacMillan problem is \(\sqrt{3\sqrt{3}}\) times of the time period of Sitnikov restricted four-body problem.