Periodic solutions of a generalized Sitnikov problem

Abstract

In this paper, we study the problem of determining whether a global family of even periodic solutions of a generalized Sitnikov problem, which emerges from a circular generalized Sitnikov problem, continues for all values of eccentricity in [0, 1) or ends in the equilibrium.

1 Introduction

The Sitnikov problem is a restricted three-body problem in which two bodies of equal positive mass, called primaries, move in circular or elliptic Keplerian orbits on a plane $\varPi$, and a massless body, called particle, moves on a straight line orthogonal to $\varPi$ passing through the primary bodies’ center of mass. If the units of mass, space and time are properly chosen, it can be assumed that the gravitational constant G is equal to 1, the mass of the primaries is 1/2, and the minimal period of their orbits is $2\pi$. Additionally, if the plane $\varPi$ is the plane x, y and the center of mass of the primary bodies is fixed at the origin of the system, the motion equation for the particle is

$$\begin{aligned} \ddot{z}(t)+\frac{z(t)}{\left( r^2(t,e)+z^2(t)\right) ^{\frac{3}{2}}}=0, \end{aligned}$$

(1)

where r(t, e) is the distance of the primaries to their center of mass at time t, and $e\in [0,1)$ is the eccentricity of their corresponding orbits. The function $r(\cdot ,e)$ is given implicitly by the equation

$$\begin{aligned} r(t,e)=\frac{1}{2}(1-e\cos (u(t,e))), \end{aligned}$$

where u(t, e) is the eccentric anomaly, which solves the Kepler equation

$$\begin{aligned} u(t,e)-e\sin (u(t,e))=t-{\bar{t}}. \end{aligned}$$

Here ${\bar{t}}$ is the time of passage through the pericenter, which can be assumed to be equal to zero. When $e=0$, the primaries move in the same circular orbit and in this case we have the circular Sitnikov problem.

The Sitnikov problem became relevant when K. Sitnikov showed in Sitnikov (1960) the existence of solutions, for small $e>0$, with chaotic behavior. Since then many authors have studied this problem, see Alekseev (1968), Alfaro and Chiralt (1993), Belbruno et al. (1994), Beltritti et al. (2018), Bountis and Papadakis (2009), Jiménez-Lara and Escalona-Buendía (2001), Corbera and Llibre (2000), Corbera and Llibre (2002), Dvorak (1993), Llibre and Ortega (2008), Llibre and Simó (1980), Marchesin and Vidal (2013), Moser (1973), Ortega (2016), Ortega and Rivera (2010), Pandey and Ahmad (2013), Perdios and Markellos (1987), Rivera (2013), Rivera and Andrés (2012), Soulis et al. (2008), Zanini (2003).

A question that arises in the literature referred to the Sitnikov problem is the study of families of periodic solutions that depend continuously of the parameter e. A special case is those families whose solutions are additionally even. One way to find them is to look for solutions of (1) satisfying the boundary conditions

$$\begin{aligned} {\dot{z}}(0)={\dot{z}}(M\pi )=0 \end{aligned}$$

(2)

for $M\in {\mathbb {N}}$, see Jiménez-Lara and Escalona-Buendía (2001), Corbera and Llibre (2000), Corbera and Llibre (2002), Llibre and Ortega (2008), Ortega and Rivera (2010), Rivera (2013). If these conditions hold then $z(t)=z(-t)$ and $z(t+2M\pi )=z(t)$ for every $t\in {\mathbb {R}}$.

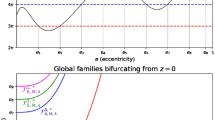
In Jiménez-Lara and Escalona-Buendía (2001), the authors study the above problem numerically. For $M=4$, Figure 9 in this work shows, among other things, certain families that originate from the circular Sitnikov problem and continue for all values of $e\in [0,1)$, and other families that emerge from the equilibrium $z=0$ at some eccentricity $e_{*}$ and continue for all values $e_{*}<e<1$. Later, Llibre and Ortega (2008) prove analytically, using the method of global continuation of Leray and Schauder, the existence of exactly $\nu _M:=[\sqrt{8}M]$ families of non-trivial periodic solutions of (1) (with initial condition $z(0)>0$), satisfying (2), families that emerge from the circular Sitnikov problem and continue for values of $e>0$. The corresponding solutions of each family have the same quantity of zeros in the interval $[0,M\pi ]$; this is because the zeros of these solutions are non-degenerate, and this fact allows to see, by a classical argument employed by Rabinowitz (1971), that the number of zeros in $[0,M\pi ]$ remain constant in these solutions. Then, every family is identified by the number of zeros that their solutions have in the interval $[0,M\pi ]$, and this number goes from $p=1$ to $p=\nu _M$, see Theorem 3.1 in Llibre and Ortega (2008). In the same theorem, the authors also prove that, fixed $\epsilon \in (0,1)$, for these families, one of the next alternatives holds: the first is that, called 4a) in that work, the family continues for all values of $e\in [0,1-\epsilon ]$, and the second is that, called 4b), the family ends in the equilibrium $z=0$ at some eccentricity value $E\in [0,1-\epsilon )$. (However, in Figure 9 of Jiménez-Lara and Escalona-Buendía 2001 these families are not observed.) Additionally, the authors demonstrate that if $p<M$ then 4a) holds, but if $p\ge M$ the alternative 4b) can hold at a value of eccentricity E, and a lower bound for E is given, see Theorem 3.2 in Llibre and Ortega (2008). Ortega and Rivera (2010) demonstrate analytically, using a slight variant of the Pitchfork bifurcation and the theory of global continuation, the existence of an infinite number of families that bifurcate from the equilibrium $z=0$ at adequate eccentricities $e_*$ and continue for all values $e_*<e<1$. The authors also improve the result in Theorem 3.2 in Llibre and Ortega (2008) demonstrating that the condition 4a) is satisfied if p is less than a value $p_0(M)$, which is greater than M, although there is not an estimate for $p_0(M)$, see Lemma 3.1 and Theorem 7.1 in Ortega and Rivera (2010). In addition, the authors show that conditions 4a) and 4b) cannot occur simultaneously; this is consequence of Proposition 3 therein.

The problems studied in Llibre and Ortega (2008) and Ortega and Rivera (2010) are approached by Rivera (2013) for a generalized Sitnikov problem in which there are N primary bodies, of equal mass and posed in the vertices of a N-polygon, moving around their center of mass in Keplerian orbits. Lastly, in Beltritti et al. (2018) the authors study a circular generalized Sitnikov problem, in which the primaries perform a rigid motion around their center of mass and form at all times an admissible planar central configuration (see Definition 2 in Beltritti et al. 2018).

The results of Section 2.3 in Llibre et al. (2015) and Theorem 1 in Beltritti et al. (2018) allow us to propose a generalized Sitnikov problem (GSP) in which the primary bodies orbit on the plane x, y around their center of mass, performing a planar homographic motion and forming at all times an admissible central configuration. Closely following the demonstration of the results in Llibre and Ortega (2008), Ortega and Rivera (2010), Rivera (2013), and taking into account Theorem 5 in Beltritti et al. (2018), we can extend the results of these papers to the instance where the primaries move as mentioned above. So, in this work our objective is to study if the families that continue from a circular generalized Sitnikov problem (CGSP) satisfy an alternative like 4a) or 4b) of Theorem 3.1 in Llibre and Ortega (2008). We have found evidence that the vast majority of the families satisfy a condition like 4a); in the case of the classical Sitnikov problem, these families represent the 99.4 percent of all families that emerge from the circular Sitnikov problem.

To prove our results, we study the linearized equation in equilibrium $z=0$ for the GSP via the polar coordinates and use the theory to count zeros of solutions of differential equations of the form $\ddot{h}(t)+q(t)h(t)=0$ in finite length intervals, see Sect. 5 in Chapter XI in Hartman (1982).

In the present paper, after introducing preliminary facts in Sect. 1, we describe in Sect. 2 the GSP that we consider in this work; we establish the motion equation for the particle, and we also state a similar result to Theorem 7.1 in Ortega and Rivera (2010), which refers to the continuation of families of even periodic solutions of the GSP that emerge from the CGSP. In Sect. 3, we establish some mathematical criteria that allow us to determine whether a family that emerges from the CGSP satisfies a condition like 4a) or, if it fulfills an alternative like 4b), provides an interval of possible values of eccentricities where it can end. In Sect. 4, we present some numerical results that indicate us that the vast majority of families emanating from the CGSP satisfy a condition like 4a). In Sect. 5, we analytically approach the problem that concern us regarding the classical Sitnikov problem. Finally, in the “Appendix”, some technical results used in Sect. 5 are expose and demonstrate.

2 A generalized Sitnikov problem

We begin this section by giving the definition of Central Configuration and by determining its relationship with planar homographic motion. We remark that some reasonings in this section are analogous to those made in Sect. 3 in Rivera (2013). Also, from now on the gravitational constant G is equal to 1.

Definition 1

Let $\eta =(\eta _1,\ldots ,\eta _N)$ be a N-tuple of positions in ${\mathbb {R}}^2$ and let $m=(m_1,\ldots ,m_N)$ be a vector of mass. We say that $(\eta ,m)$ is a Central Configuration if there exists $\alpha \in {\mathbb {R}}$ such that

$$\begin{aligned} \nabla _jU(\eta ,m)=-\alpha m_j\eta _j,\ \ j=1,2,\ldots ,N, \end{aligned}$$

where

$$\begin{aligned} U(\eta ,m)=\sum _{i<j}\frac{m_im_j}{|\eta _i-\eta _j|} \end{aligned}$$

and $\nabla _j$ denotes the 2-dimensional partial gradient with respect to $\eta _j$.

We have also that $\alpha =\frac{U(\eta ,m)}{I(\eta ,m)}$ where $I(\eta ,m)=\sum _{i=1}^{N}m_i|\eta _i-c|^2$, and c is the center of mass of the configuration $(\eta ,m)$ (see Section 2.3 in Llibre et al. 2015).

Fixing the center of mass at the origin of the coordinate system, by Proposition 2.3.4 in Llibre et al. (2015), if $r_1(t)$, $\theta _1(t)$ is any solution of

$$\begin{aligned}&\ddot{r}_1(t)-r_1(t)\left( {\dot{\theta }}_1(t)\right) ^2=-\frac{\alpha }{r_1^2(t)}\nonumber \\&\quad \frac{\mathrm{d}}{\mathrm{d}t}\left( r_1^2(t){\dot{\theta }}_1(t)\right) =0, \end{aligned}$$

(3)

and we define

$$\begin{aligned} \chi _j(t):=r_1(t)Q(\theta _1(t))\eta _j, \end{aligned}$$

where $Q(\theta )=\begin{pmatrix} \cos (\theta ) &{} -\sin (\theta )\\ \sin (\theta ) &{} \cos (\theta ) \end{pmatrix}$, then $\chi (t)=(\chi _1(t),\chi _2(t),\ldots ,\chi _N(t))$ is a planar homographic solution of the N-body problem. It is known that for, every $e\in [0,1)$ there exists $r_1(t)=r_1(t,e)$ and $\theta _1(t)=\theta _1(t,e)$ solutions of (3), such that the functions $\chi _j(t)$ describe an ellipse with eccentricity $e\in [0,1)$ and semimajor axis $s_j:=|\eta _j|$ (see Chapter 2 in Murray and Dermott (1999). In such a case, the minimal period of $\chi _j(t)$ is $\frac{2\pi }{\sqrt{\alpha }}$ and

$$\begin{aligned} r_1(t,e)=1-e\cos (u(t,e)), \end{aligned}$$

(4)

where

$$\begin{aligned} u(t,e)-e\sin (u(t,e))=\sqrt{\alpha }(t-{\bar{t}}), \end{aligned}$$

(5)

with ${\bar{t}}$ being the time of passage through the pericenter, which we suppose, without loss of generality, is equal to zero. We also choose appropriate units so that $\alpha =1$, then the functions $\chi _j(t)$ are $2\pi$-periodic. From now on, we identify an admissible central configuration with the value $\lambda :=\sum _{i=1}^{N}\frac{m_i}{8s_i^3}$; this definition of $\lambda$ is chosen to keep the analogy with the results in Rivera (2013). We do so because, as we can see in Rivera (2013) and we will see in this work, the results obtained for the considered problems depend on the value of $\lambda$.

By Theorem 1 in Beltritti et al. (2018), if $(\eta ,m)$ is an admissible central configuration, we can propose a generalized Sitnikov problem (GSP), in which the trajectories of primaries are the functions $\chi _j(t)$ with $r_1(t,e)$ as in (4), and the massless particle moves on a straight line orthogonal to the plane x, y; a line passing through the origin of the system. In this case, the differential equation that describes the movement of the particle is

$$\begin{aligned} \ddot{z}(t)+\sum _{i=1}^{N}\frac{m_iz(t)}{\left( 4s^2_ir^2(t,e)+z(t)^2\right) ^{\frac{3}{2}}}=0, \end{aligned}$$

(6)

where the definition $r(t,e):=r_1(t,e)/2$ is also chosen to keep the analogy with the results in Rivera (2013). At this point, we are interested in solutions of (6) satisfying the Neumann boundary conditions

$$\begin{aligned} {\dot{z}}(0)={\dot{z}}(M\pi )=0. \end{aligned}$$

(7)

Thus, a function z(t) that solves (6) and satisfies (7) is an even, $2M\pi$-periodic solution of the GSP. If we define $z(t,\xi ,\eta ,e)$ as the solution of (6) such that $z(0)=\xi$ and ${\dot{z}}(0)=\eta$, then finding solutions of (6) satisfying (7) is equivalent to looking for the zeros of the real analytic function

$$\begin{aligned} F_M^\lambda (\xi ,e):{\mathbb {R}}\times [0,1)\rightarrow {\mathbb {R}}, \ F_M^\lambda (\xi ,e):={\dot{z}}(M\pi ,\xi ,0,e). \end{aligned}$$

Due to the symmetries of the GSP, we can search for such zeros only in the set ${\mathbb {R}}_+\times [0,1)$.

For $e=0$, the primaries move in circular orbits and in this case the values $\xi _{p,M}^\lambda \in {\mathbb {R}}_+$ such that of $F_M^\lambda (\xi ,0)=0$ are those that satisfy

$$\begin{aligned} T^\lambda (\xi _{p,M}^\lambda )=\frac{2M\pi }{p},\ \text {for} p\in {\mathbb {N}}, \end{aligned}$$

(8)

where $T^\lambda (\xi )$ is defined as the minimum period of $z(t,\xi ,0,0)$. If (8) holds, then p is the number of zeros of $z(t,\xi _{p,M}^\lambda ,0,0)$ in $[0,M\pi ]$. From Theorem 5 in Beltritti et al. (2018), we have that $T^\lambda (\xi )$ is an increasing function, $\lim \limits _{\xi \rightarrow 0^{+}}T^\lambda (\xi )=2\pi \left( \sum _{i=1}^{N}\frac{m_i}{s_i^3}\right) ^{-\frac{1}{2}}$ and $\lim \limits _{\xi \rightarrow +\infty }T^\lambda (\xi )=+\infty$. Then (8) has a solution for all values of $p\in {\mathbb {N}}$ such that

$$\begin{aligned} p<M\left( \sum _{i=1}^{N}\frac{m_i}{s_i^3}\right) ^{\frac{1}{2}}=M\sqrt{8}\left( \sum _{i=1}^{N}\frac{m_i}{8s_i^3}\right) ^{\frac{1}{2}}=M\sqrt{8\lambda }. \end{aligned}$$

Therefore, if we define $M_\lambda :=\min \left\{ M\in {\mathbb {N}}:M\ge \frac{1}{\sqrt{8\lambda }}\right\}$ and

$$\begin{aligned} \nu _{M,\lambda }:=\left\{ \begin{array}{ll} \left[ \sqrt{8\lambda } M\right] &{}\quad \text {if}\ \sqrt{8\lambda }M\notin {\mathbb {N}}\\ \left[ \sqrt{8\lambda } M\right] -1 &{}\quad \text {if}\ \sqrt{8\lambda }M\in {\mathbb {N}}, \end{array}\right. \end{aligned}$$

then, for $M\ge M_\lambda$, the equation $F_M^\lambda (\xi ,0)=0$ has exactly $\nu _{M,\lambda }$ solutions in ${\mathbb {R}}_+$. Taking into account the previous reasoning, after the next definition, we conclude this section enunciating a result concerning families of solutions of the GSP that emerge from the CGSP. The notation we use is analogous to that in Ortega and Rivera (2010).

Definition 2

Let $\varSigma _M^\lambda :=\left\{ (\xi ,e)\in {\mathbb {R}}_+\times [0,1) : F_M^\lambda (\xi ,e)=0 \right\}$ and ${\mathcal {C}}^*$ be a connected component of $\varSigma _M^\lambda$ (which is actually arcwise connected because $F_M^\lambda$ is analytic). Then ${\mathcal {C}}:=\left\{ z(t,\xi ,0,e):(\xi ,e)\in {\mathcal {C}}^*\right\}$ is a global family of solutions of the GSP and ${\mathcal {C}}^*$ is the connected component associated with ${\mathcal {C}}$.

Proposition 1

Let $\lambda >0$. For every $M\ge M_\lambda$ and $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$, there exists a global family ${\mathcal {C}}_{p,M,\lambda }$ of non-trivial solutions of the GSP such that

• i) all solutions of ${\mathcal {C}}_{p,M,\lambda }$ have exactly p zeros in $[0,M\pi ]$.

• ii) ${\mathcal {C}}_{p,M,\lambda }^*\bigcap \{e=0\}=\{(\xi _{p,M}^\lambda ,0)\}$ where ${\mathcal {C}}_{p,M,\lambda }^*$ is the connected component associated with ${\mathcal {C}}_{p,M,\lambda }$.

Moreover, one and only one of the following conditions holds:

• D1) the projection of ${\mathcal {C}}_{p,M,\lambda }^*$ on e-axis is the interval [0, 1),

• D2) the projection of ${\mathcal {C}}_{p,M,\lambda }^*$ on e-axis is $[0,{\bar{e}})$, with ${\bar{e}}<1$. Furthermore, $cl({\mathcal {C}}_{p,M,\lambda }^*)\bigcap \{\xi =0\}=\{(0,{\bar{e}})\}$, where cl is the closure operator in ${\mathbb {R}}^2$.

Proof

Closely following the ideas in Llibre and Ortega (2008) and Ortega and Rivera (2010), if we adapt them to this instance we obtain the proof. $\square$

Note that if ${\mathcal {C}}_{p,M,\lambda }$ fulfills $\textit{D1}$, then the family continues for all values of $e\in [0,1)$, in such a case, we say that ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D1}$-condition. On the other hand, if ${\mathcal {C}}_{p,M,\lambda }$ fulfills $\textit{D2}$, then it ends in the equilibrium $z=0$ at a value of eccentricity ${\bar{e}}$, in this case we say that ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D2}$-condition at eccentricity value ${\bar{e}}$.

3 Mathematical criteria for the study of conditions $\textit{D1}$ and $\textit{D2}$

In this section, we introduce some mathematical criteria that allow us to approach the problem of determining whether a family ${\mathcal {C}}_{p,M,\lambda }$ satisfies the condition $\textit{D1}$ or, if it fulfills $\textit{D2}$-condition at an eccentricity value ${\bar{e}}$ to establish a lower and upper bound for ${\bar{e}}$. To introduce such criteria, we need to study the linearized equation in the equilibrium $z=0$ for the GSP, via the polar coordinates, and demonstrate some results about it.

We first remark that, throughout this paper, we always treat $\lambda$ as a fixed number and we study the problem that concerns us varying the values of $M\ge M_\lambda$ and $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$.

Following the ideas used in Llibre and Ortega (2008), we can see that if there exists a family ${\mathcal {C}}_{p,M,\lambda }$ that satisfies $\textit{D2}$-condition at an eccentricity value $e\in [0,1)$, then the solution y(t, e) of

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{y}(t,e)+ \lambda \frac{y(t,e)}{r^{3}(t,e)}=0\\ y(0,e)=1\\ {\dot{y}}(0,e)=0 \end{array} \right. \end{aligned}$$

(9)

is an even, $2M\pi$-periodic function, which has exactly p zeros in the interval $[0,M\pi ]$, and additionally

$$\begin{aligned} {\dot{y}}(M\pi ,e)=0. \end{aligned}$$

(10)

The differential equation in (9) is the linearized equation in the equilibrium $z=0$ for the GSP. Introducing polar coordinates

$$\begin{aligned} y(t,e)=\rho (t,e)\cos (\theta (t,e)),\ \ {\dot{y}}(t,e)=\rho (t,e)\sin (\theta (t,e)) \end{aligned}$$

we have that $\theta$ solves the problem

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\theta }}(t,e)=-\frac{\lambda }{r^{3}(t,e)}\cos ^{2}(\theta (t,e))-\sin ^2(\theta (t,e)) \\ \theta (0,e)=0. \end{array} \right. \end{aligned}$$

(11)

Note first that $y(t,e)=0$ if and only if $\theta (t,e)=(2{\bar{\kappa }}+1)\frac{\pi }{2}$ for some ${\bar{\kappa }}\in {\mathbb {Z}}$. Now, since ${\dot{\theta }}(t,e)<0$ for every $t\in {\mathbb {R}}$ the function $\theta$ can cross the $i\pi$-level, $i\in {\mathbb {Z}}$, only once and it does so from top to bottom, since also $\theta (0,e)=0$ then if $\theta ({\bar{t}},e)=-\kappa \pi$, with $\kappa \in {\mathbb {Z}}$, we have that actually $\kappa \in {\mathbb {N}}$ and the number of zeros of y(t, e) in $[0,{\bar{t}}]$ is $\kappa$. So, equality (10) and the condition that y(t, e) has p zeros in $[0,M\pi ]$ can be joined, in terms of the function $\theta$, in the following equation

$$\begin{aligned} \theta (M\pi ,e)=-p\pi . \end{aligned}$$

(12)

Remark 1

Due to the previous analysis, a necessary condition for a global family ${\mathcal {C}}_{p,M,\lambda }$ to satisfy $\textit{D2}$ at an eccentricity value $e\in [0,1)$ is that the solution of (11) satisfies (12). Then, the negation of this condition allow us to discard the possibility that ${\mathcal {C}}_{p,M,\lambda }$ ends in the equilibrium at a value of eccentricity for which (12) is not true. Since the falsity of (12) does not seem to be easy to check, through a series of changes of variable, we will analyze this condition in a mathematical framework that allows us to check it more easily.

Taking into account (5), if we apply the independent change of variable $u-e\sin (u)=t$ the problem (9) becomes

$$\begin{aligned} \left\{ \begin{array}{l} (1-e\cos (u))\ddot{y}(u,e)-e\sin (u){\dot{y}}(u,e)+8\lambda y(u,e)=0\\ y(0,e)=1\\ {\dot{y}}(0,e)=0 \end{array} \right. \end{aligned}$$

(13)

and the condition (10) remain equal. The differential equation involved in (13) is a particular case of the so called Ince’s equation, which has been an object of study of many scholars, see Magnus and Winkler (2013). An advantage of this equation over the equation in (9) is that the functions that multiply y(u, e) and its derivatives depend explicitly on the independent variable. For $\lambda =1$, at the end of Ortega and Rivera (2010), the authors pose a question that involves the differential equation in (13) and the Neumann boundary conditions ${\dot{y}}(0,e)={\dot{y}}(M\pi ,e)=0$, which in case of having an affirmative answer, it dismisses the possibility of the existence of a global family ${\mathcal {C}}_{p,M,1}$ satisfying $\textit{D2}$-condition. Reformulating the problem (13) in terms of polar coordinates

$$\begin{aligned} y(u,e)={\bar{\rho }}(u,e)\cos ({\bar{\theta }}(u,e)),\ \ {\dot{y}}(u,e)={\bar{\rho }}(u,e)\sin ({\bar{\theta }}(u,e)), \end{aligned}$$

we have that ${\bar{\theta }}$ solves the problem

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{\bar{\theta }}}(u,e)=-\frac{ 8\lambda \cos ^{2}({\bar{\theta }}(u,e))}{1-e\cos (u)}-\sin ^2({\bar{\theta }}(u,e))+\frac{e\sin ({\bar{\theta }}(u,e))\cos ({\bar{\theta }}(u,e))\sin (u)}{1-e\cos (u)} \\ {\bar{\theta }}(0,e)=0. \end{array}\right. \end{aligned}$$

(14)

Now we will show a relationship between $\theta (t,e)$ and ${\bar{\theta }}(u,e)$.

Lemma 1

Let $\theta$ and ${\bar{\theta }}$ be the solutions of the initial value problems (11) and (14), respectively. Then $\theta (t,e)=-\kappa \pi \Leftrightarrow {\bar{\theta }}(u,e)=-\kappa \pi$, for $\kappa \in {\mathbb {N}}$, where t and u are related by the equation $t=u-e\sin (u)$.

Proof

If $t=u-e\sin (u)$ we have that

$$\begin{aligned} {\dot{y}}(t,e)={\dot{y}}(u,e)\frac{\mathrm{d}u}{\mathrm{d}t}={\dot{y}}(u,e)\frac{1}{1-e\cos (u)}, \end{aligned}$$

then ${\dot{y}}(t,e)=0\Leftrightarrow {\dot{y}}(u,e)=0$. Thus $\theta (t,e)=-\kappa _1\pi \Leftrightarrow {\bar{\theta }}(u,e)=-\kappa _2\pi$, with $\kappa _1,\kappa _2\in {\mathbb {Z}}$. Since ${\dot{\theta }}(t,e)<0$ for every $t\in {\mathbb {R}}$ and $\dot{{\bar{\theta }}}(u,e)<0$, if ${\bar{\theta }}(u,e)=j\pi$ with $j\in {\mathbb {Z}}$, the functions $\theta$ and ${\bar{\theta }}$ can cross the $i\pi$-level, $i\in {\mathbb {Z}}$, only once and do so from top to bottom. Since additionally $\theta (0,e)={\bar{\theta }}(0,e)=0$ we conclude that $\kappa _1=\kappa _2$ and $\kappa _1,\kappa _2\in {\mathbb {N}}$. $\square$

Let w(u, e) be the function such that $y(u,e)=w(u,e)v(u,e)$, with $v(u,e)=\sqrt{1-e\cos (u)}$, then

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{w}(u,e)+q_\lambda (u,e) w(u,e)=0\\ w(0,e)=(1-e)^{-\frac{1}{2}}\\ {\dot{w}}(0,e)=0, \end{array}\right. \end{aligned}$$

(15)

where

$$\begin{aligned} q_\lambda (u,e)=\frac{(1-e\cos (u))^2+(32\lambda -4)(1-e\cos (u))+3(1-e^2)}{4(1-e\cos (u))^2}. \end{aligned}$$

(16)

Reformulating again the problem in terms of polar coordinates, we have that if

$$\begin{aligned} w(u,e)=\rho _w(u,e)\cos (\theta _w(u,e)),\ \ {\dot{w}}(u,e)=\rho _w(u,e)\sin (\theta _w(u,e)), \end{aligned}$$

then

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\theta }}_w(u,e)=-q_\lambda (u,e)\cos ^{2}(\theta _w(u,e))-\sin ^2(\theta _w(u,e)) \\ \theta _w(0,e)=0. \end{array}\right. \end{aligned}$$

(17)

Remark 2

For the next lemma, we will need that $q_\lambda (u,e)>0$ for every $e\in [0,1)$ and $u\in {\mathbb {R}}$, and this is true if and only if $\lambda \ge \frac{1}{8}$. Therefore, from this point on we study our problem for values of $\lambda \ge \frac{1}{8}$. In these cases, $M_\lambda =1$, so for every $M\in {\mathbb {N}}$ we have that $\nu _{M,\lambda }\ge 1$ (except if $\lambda =\frac{1}{8}$ and $M=1$; in this case $\nu _{M,\lambda }=0$), and thus, there always exists a family ${\mathcal {C}}_{p,M,\lambda }$ emanating from the CGSP. Note that the condition $\lambda >\frac{1}{8}$ is equivalent to the fact that the CGSP has a synchronous solution, see Corollary 2 in Beltritti et al. (2018).

Lemma 2

Let ${\bar{\theta }}$ and $\theta _w$ be the solutions of the problems (14) and (17), respectively. Then ${\bar{\theta }}(M\pi ,e)=-\kappa \pi \Leftrightarrow \theta _w(M\pi ,e)=-\kappa \pi$ for $M,\kappa \in {\mathbb {N}}$.

Proof

Let us first observe that

$$\begin{aligned} {\bar{\theta }}(u,e)=-(2\kappa -1)\frac{\pi }{2}\Leftrightarrow \theta _w(u,e)=-(2\kappa -1)\frac{\pi }{2}, \ \ \text {for}\ \ \kappa \in {\mathbb {N}}. \end{aligned}$$

(18)

In fact, since $y(u,e)=0\Leftrightarrow w(u,e)=0$ then ${\bar{\theta }}(u,e)=-(2\kappa _1-1)\frac{\pi }{2}\Leftrightarrow \theta _w(u,e)=-(2\kappa _2-1)\frac{\pi }{2}$, for some $\kappa _1,\kappa _2\in {\mathbb {Z}}$. Since $\dot{{\bar{\theta }}}(u,e)<0$ and ${\dot{\theta }}_w(u,e)<0$ if ${\bar{\theta }}(u,e)={\bar{\kappa }}_1\frac{\pi }{2}$ and $\theta _w(u,e)={\bar{\kappa }}_2\frac{\pi }{2}$, ${\bar{\kappa }}_1, {\bar{\kappa }}_2\in {\mathbb {Z}}$, the functions ${\bar{\theta }}$ and $\theta _w$ can cross the $i\frac{\pi }{2}$-level, with $i\in {\mathbb {Z}}$, only once and do so from top to bottom. Furthermore, since ${\bar{\theta }}(0,e)=\theta _w(0,e)=0$ then $\kappa _1=\kappa _2$ and $\kappa _1,\kappa _2\in {\mathbb {N}}$.

Since ${\dot{y}}(M\pi ,e)={\dot{w}}(M\pi ,e)v(M\pi ,e)+w(M\pi ,e){\dot{v}}(M\pi ,e)={\dot{w}}(M\pi ,e)v(M\pi ,e)$ we have that ${\dot{y}}(M\pi ,e)=0\Leftrightarrow {\dot{w}}(M\pi ,e)=0$, then

$$\begin{aligned} {\bar{\theta }}(M\pi ,e)=-{\tilde{\kappa }}_1\pi \Leftrightarrow \theta _w(M\pi ,e)=-{\tilde{\kappa }}_2\pi \end{aligned}$$

with ${\tilde{\kappa }}_1,{\tilde{\kappa }}_2\in {\mathbb {N}}$. Let us see that ${\tilde{\kappa }}_1={\tilde{\kappa }}_2$. Suppose without loss of generality that ${\tilde{\kappa }}_1>{\tilde{\kappa }}_2$, then there exists $u_1\in (0,M\pi )$ such that ${\bar{\theta }}(u_1,e)=-{\tilde{\kappa }}_1\pi +\frac{\pi }{2}$ and, due to (18), we have that $\theta _w(u_1,e)=-{\tilde{\kappa }}_1\pi +\frac{\pi }{2}$. Since $\theta _w$ can cross the ($-{\tilde{\kappa }}_1\pi +\frac{\pi }{2}$)-level once and does so from top to bottom then $\theta _w(M\pi ,e)\le -{\tilde{\kappa }}_1\pi$ which is an absurd because ${\tilde{\kappa }}_1>{\tilde{\kappa }}_2$. Then, ${\tilde{\kappa }}_1={\tilde{\kappa }}_2$. $\square$

Now let us define the function ${\bar{\varphi }}(u,e)$ as a smooth choice of the argument of the curve

$$\begin{aligned} u\rightarrow D(u,e)\left[ \begin{matrix} w(u,e)\\ {\dot{w}}(u,e) \end{matrix}\right] , \end{aligned}$$

(19)

where D(u, e) is the $2\times 2$ diagonal matrix with entries 1 and $q_\lambda ^{-\frac{1}{2}}(u,e)$. A definition like above can be found in Hartman (1982) (see formula (2.48) in Chapter XI) and it is useful to estimate the number of zeros of solutions of $\ddot{h}(t)+q(t)h(t)=0$ in an interval $[0,{\widetilde{T}}]$ with ${\widetilde{T}}>0$ (see Sect. 5 of Chapter XI in Hartman (1982). Also, as in Hartman (1982), we can see that

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{\bar{\varphi }}}(u,e)=-\sqrt{q_\lambda (u,e)}-\frac{1}{4}\sin (2{\bar{\varphi }}(u,e))\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)} \\ {\bar{\varphi }}(0,e)=0. \end{array}\right. \end{aligned}$$

(20)

Lemma 3

Let $\theta _w$ and ${\bar{\varphi }}$ be the solutions of (17) and (20), respectively. Then $\theta _w(u,e)=-\kappa \pi \Leftrightarrow {\bar{\varphi }}(u,e)=-\kappa \pi$ for $\kappa \in {\mathbb {N}}$.

Proof

From the definition of ${\bar{\varphi }}$, we have that $\theta _w(u,e)=-\kappa _1\pi \Leftrightarrow {\bar{\varphi }}(u,e)=-\kappa _2\pi$ for $\kappa _1,\kappa _2\in {\mathbb {Z}}$ . Now, $\kappa _1=\kappa _2$ and $\kappa _1,\kappa _2\in {\mathbb {N}}$ since both functions can cross the $i\pi$-level, $i\in {\mathbb {Z}}$, only once and do it from top to bottom, and also $\theta _w(0,e)={\bar{\varphi }}(0,e)=0$. $\square$

In order to facilitate the view of the subsequent calculations, we define $\varphi (u,e):=-{\bar{\varphi }}(u,e)$. Note that this function solves the problem

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\varphi }}(u,e)=\sqrt{q_\lambda (u,e)}-\frac{1}{4}\sin (2\varphi (u,e))\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)} \\ \varphi (0,e)=0. \end{array}\right. \end{aligned}$$

(21)

Now we enunciate the first theorem of this article.

Theorem 1

Let $\theta$ and $\varphi$ be the solutions of (11) and (21), respectively. Then

$$\begin{aligned} \theta (M\pi ,e)=-\kappa \pi \Leftrightarrow \varphi (M\pi ,e)=\kappa \pi \end{aligned}$$

for $\kappa ,M\in {\mathbb {N}}$.

Proof

The result is a consequence of all previous lemmas in this section. $\square$

The advantage of working, in this context, with the function $\varphi$ instead of $\theta$ is that the nonlinear term $\frac{1}{4}\sin (2\varphi (u,e))\frac{{\dot{q}}_\lambda ({\tiny {\tiny }}u,e)}{q_\lambda (u,e)}$ in (21) is very small compared to $\sqrt{q_\lambda (u,e)}$ (at least numerically, for $\left( \lambda > \frac{9}{64}\right)$, it seems to be). This suggests that $\varphi (M\pi ,e)\approx \int _{0}^{M\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u$. More precisely, as the function $q_\lambda (u,e)$ satisfies $q_\lambda (i\pi +u,e)=q_\lambda (i\pi -u,e)$ for $i\in {\mathbb {Z}}, e\in [0,1)$ and $u\in {\mathbb {R}}$; also,

$$\begin{aligned} {\dot{q}}_\lambda (u,e)=\frac{e \left( 3 e^{2} + \left( 16 \lambda - 2\right) e \cos (u) - (16 \lambda + 1)\right) \sin (u)}{2 \left( 1-e \cos (u) \right) ^{3}}<0 \end{aligned}$$

for $u\in (0,\pi )$, we have that

$$\begin{aligned} \left| \frac{1}{4}\int _{0}^{M\pi }\sin (2\varphi (u,e))\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\right| \mathrm{d}u\le & {} \frac{1}{4}\int _{0}^{M\pi }\left| \frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\right| \mathrm{d}u =\frac{M}{4}\int _{0}^{\pi }\left| \frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\right| \mathrm{d}u\\= & {} -\frac{M}{4}\int _{0}^{\pi }\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\mathrm{d}u =\frac{M}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) , \end{aligned}$$

hence

$$\begin{aligned} \begin{aligned} \varphi (M\pi ,e)&=\int _{0}^{M\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{1}{4}\int _{0}^{M\pi }\sin (2\varphi (u,e))\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\mathrm{d}u\\&=M\int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{1}{4}\int _{0}^{M\pi }\sin (2\varphi (u,e))\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\mathrm{d}u\\&>M\int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{M}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) , \end{aligned} \end{aligned}$$

(22)

and note that if $e=0$ the terms $\frac{1}{4}\int _{0}^{M\pi }\sin (2\varphi (u,e))\frac{{\dot{q}}_\lambda (u,e)}{q_\lambda (u,e)}\mathrm{d}u$ and $\frac{M}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right)$ are equal to 0, and the last expression grows up very slowly as function of e. So the expression

$$\begin{aligned} M\int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{M}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) \end{aligned}$$

(23)

could be a good approximation below of $\varphi (M\pi ,e)$. Taking into account this heuristic explanation, the Theorem 1 and inequality (22); once we fix $\lambda \ge \frac{1}{8}$, we will focus on finding those values of $M\in {\mathbb {N}}$, $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$ and $e\in [0,1)$ such that the inequality

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{1}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) >\frac{p}{M}\pi \end{aligned}$$

(24)

is true (note that this is a problem involving only elementary functions); indeed, if a global family ${\mathcal {C}}_{p_1,M_1,\lambda }$ satisfies $\textit{D2}$-condition at ${\bar{e}}\in [0,1)$, which implies that $\theta (M_1\pi ,{\bar{e}})=-p_1\pi$, and the above inequality holds for $M_1$, $p_1$ and some $e_1\in [0,1)$, then, by Theorem 1 and (22), $e_1\ne {\bar{e}}$. Therefore, inequality (24) allow us to discard values of eccentricities at which a global family ${\mathcal {C}}_{p,M,\lambda }$ could satisfy $\textit{D2}$-condition. Note that if there exists $M\in {\mathbb {N}}$ and $p\in \{1,2\ldots ,\nu _{M,\lambda }\}$ such that (24) is true for every $e\in [0,1)$ then ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D1}$-condition.

Since $\frac{\nu _{M,\lambda }}{M}<\sqrt{8\lambda }$ and $\lim \limits _{M\rightarrow \infty }\frac{\nu _{M,\lambda }}{M}=\sqrt{8\lambda }$ , a particular inequality that we will also analyze is

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{1}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) >\sqrt{8\lambda }\pi , \end{aligned}$$

(25)

which implies (24) for all $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$. So, if the above inequality holds for some ${\bar{e}}\in [0,1)$ then there is not a global family ${\mathcal {C}}_{p,M,\lambda }$ satisfying $\textit{D2}$-condition at ${\bar{e}}$.

Remark 3

A fundamental ingredient to demonstrate that $\varLambda ={\mathbb {N}}$, if $\lambda >\frac{9}{64}$, in Theorem 3 in Rivera (2013), the Theorem 6.1 in Llibre and Ortega (2008) and item (ii) of Lemma 3.1 in Ortega and Rivera (2010), is $\lim \limits _{e\rightarrow 1^{-}}\theta (M\pi ,e)=-\infty$, which is, in Rivera (2013), a consequence of Corollary 1 therein, and, in Llibre and Ortega (2008) and Ortega and Rivera (2010), is obtained from Proposition 6.4 in Llibre and Ortega (2008). Let us see that estimation (22) allow us to give another proof of $\lim \limits _{e\rightarrow 1^{-}}\theta (M\pi ,e)=-\infty$.

If $\lambda >\frac{1}{8}$ and $0<e<1$, then

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u> & {} \int _{0}^{\pi }\sqrt{\frac{8\lambda -1}{1-e\cos (u)}}\mathrm{d}u=\sqrt{8\lambda -1}\int _{-1}^{1}\frac{1}{\sqrt{1-ex}}\frac{1}{\sqrt{1-x^2}}\mathrm{d}x\\> & {} \frac{\sqrt{8\lambda -1}}{\sqrt{2}}\int _{0}^{1}\frac{1}{\sqrt{1-ex}}\frac{1}{\sqrt{1-x}}\mathrm{d}x\\> & {} \sqrt{\frac{8\lambda -1}{2}}\int _{0}^{1}\frac{1}{\sqrt{1-ex}}\frac{1}{\sqrt{1-ex}}\mathrm{d}x\\= & {} \sqrt{\frac{8\lambda -1}{2}}\int _{0}^{1}\frac{1}{1-ex}\mathrm{d}x\\= & {} \sqrt{\frac{8\lambda -1}{2}}\frac{1}{e}\ln \left( \frac{1}{1-e}\right) \\> & {} \sqrt{\frac{8\lambda -1}{2}}\ln \left( \frac{1}{1-e}\right) . \end{aligned}$$

Hence, if ${\widetilde{C}}:=\frac{16\lambda -1}{(16\lambda +1)2}$, due to (22), we infer that

$$\begin{aligned}&\frac{4}{M}\varphi (M\pi ,e)\\&\quad>4\int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) \\&\quad >\sqrt{64\lambda -8}\ln \left( \frac{1}{1-e}\right) -\ln \left( \frac{(16\lambda +1)2}{(1-e)(16\lambda -1)}\right) \\&\quad =\ln \left( \frac{{\widetilde{C}}}{(1-e)^{\sqrt{64\lambda -8}-1}}\right) . \end{aligned}$$

Thus, if $\lambda >\frac{9}{64}$ then $\sqrt{64\lambda -8}-1>0$, hence $\lim \limits _{e\rightarrow 1^{-}}\varphi (M\pi ,e)=+\infty$. By Theorem 1, we have that $\lim \limits _{e\rightarrow 1^{-}}\theta (M\pi ,e)=-\infty$.

Now we enunciate the second theorem of this work.

Theorem 2

Let $\lambda \ge \frac{1}{8}$, $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$. Consider ${\mathcal {C}}_{p,M,\lambda }$ as the global family that emerges from the CGSP. Then,

• i) if ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D2}$-condition at an eccentricity value ${\bar{e}}$, then ${\tilde{e}}_{p,M,\lambda }\le {\bar{e}}$ where ${\tilde{e}}_{p,M,\lambda }$ is the minimum solution of equation

  $$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{1}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) =\frac{p}{M}\pi \end{aligned}$$

  (26)

  in [0, 1). If additionally $\lambda >\frac{9}{64}$ then ${\bar{e}}\le {\hat{e}}_{p,M,\lambda }$ where ${\hat{e}}_{p,M,\lambda }$ is the maximum solution of (26) in [0, 1).

• ii) if (26) has no solution in [0, 1) then ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D1}$-condition.

Proof

Let $\lambda \ge \frac{1}{8}$, $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$. If ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D2}$-condition at an eccentricity value ${\bar{e}}$, by Theorem 1 we have that $\varphi (M\pi ,{\bar{e}})=p\pi$. Then, from (22) and the fact that $\int _{0}^{\pi }\sqrt{q_\lambda (u,0)}\mathrm{d}u=\sqrt{8\lambda }\pi >\frac{p}{M}\pi$, the equation (26) has a solution in [0, 1), and this proves the existence of ${\tilde{e}}_{p,M,\lambda }$. Since $\int _{0}^{\pi }\sqrt{q_\lambda (u,0)}\mathrm{d}u>\frac{p}{M}\pi$ then inequality (24) holds for every $0\le e<{\tilde{e}}_{p,M,\lambda }$, which implies that ${\tilde{e}}_{p,M,\lambda }\le {\bar{e}}$. If also $\lambda >\frac{9}{64}$ by Remark 3, we have that ${\hat{e}}_{p,M,\lambda }$ exists and that inequality (24) is also true for ${\hat{e}}_{p,M,\lambda }<e<1$. Then ${\bar{e}}\le {\hat{e}}_{p,M,\lambda }$.

If (26) has no solution, since $\int _{0}^{\pi }\sqrt{q_\lambda (u,0)}\mathrm{d}u>\frac{p}{M}\pi$, we have that (24) is true for every $e\in [0,1)$, then ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D1}$-condition. $\square$

Note that, since $\int _{0}^{\pi }\sqrt{q_\lambda (u,0)}\mathrm{d}u>\frac{p}{M}\pi$ for every $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$, the condition (26) has no solution in [0, 1), is equivalent to the condition (24) is true for every $e\in [0,1)$.

Considering what we have mentioned in this section, the condition the inequality (24) holds for every $e\in [0,1)$ is a mathematical criteria that allows us to assure, if this is true, that a global family ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D1}$-condition. Being the case that (24) is not true for all $e\in [0,1)$, the equality (26) allows us to give a lower bound, and if $\lambda >\frac{9}{64}$, we can give a higher bound for a possible value of eccentricity ${\bar{e}}$ at which the global family ${\mathcal {C}}_{p,M,\lambda }$ could satisfy $\textit{D2}$-condition.

4 Numerical results

In this section, we show numerical results about the veracity of the inequality (25) and

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u-\frac{1}{4}\ln \left( \frac{(1+e)(16\lambda +e)}{(1-e)(16\lambda -e)}\right) >\delta \pi , \end{aligned}$$

(27)

for values of $\delta$ less than and close to $\sqrt{8\lambda }$. Note that (27) implies (24) for every $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,\lambda }\}$ such that $\frac{p}{M}<\delta$.

Fig. 1

Inequality check (25)

For values of $\lambda =\frac{1}{8}+\frac{7}{8}\frac{j}{250}$, $j=1,2,\ldots ,250$ and $e=\frac{k}{250}$, for $k=1,2,\ldots ,249$, we check inequality (25) numerically. The results can be seen in Fig. 1, the colored points correspond to pairs $(\lambda ,e)$ such that (25) is true. A fact to highlight is that for every $\lambda \ge 0.1635$ there is an interval $J_\lambda :=\left[ b_\lambda ,0.996\right]$ such that the inequality (25) is true for $(\lambda ,e)$ with $e\in J_\lambda$. (note that the minimum $\lambda$ value for which the inequality (25) is true is greater than $\frac{9}{64}$; this happens because the maximum value of eccentricity that we consider is 0.996). When $\lambda =1$ we have the classical Sitnikov problem and in this case $b_1=0.34$. This fact, together with Theorem 1, implies that the question posed at the end of Ortega and Rivera (2010) has an affirmative answer for all $e\in [0.34,1)$.

Fig. 2

Inequality check (27)

An interesting fact can be seen when we analyze the veracity of (27) numerically, considering $\delta$ less than and close to $\sqrt{8\lambda }$. The results are in Fig. 2. In this case, we can see that for $\delta < \sqrt{8\lambda }$ fixed, there exists $x_\delta$ such that the inequality (27) is true for every pair $(\lambda ,e)\in [x_\delta ,1]\times [0,0.996]$; furthermore, $x_\delta$ goes quickly to 0.1635 when $\delta$ decreases. This suggests that $\textit{D1}$-condition is satisfied by most global families ${\mathcal {C}}_{p,M,\lambda }$. In the particular case $\lambda =1$ and $\delta =0.994\sqrt{8}$, the inequality (27) is true for all $e\in [0,0.996]$.

Remark 4

Note that numerical results about inequality (25) and (27), for $\lambda =1$, suggest that there is no possibility that a global family ${\mathcal {C}}_{p,M,1}$ satisfies D2-condition at any $e\ge 0.34$, or, if $\frac{p}{M}<0.994\sqrt{8}$ at any $e\in [0,1)$ (this suggests that 99.4 percent of ${\mathcal {C}}_{p,M,1}$ families satisfy $\textit{D1}$-condition). However, for ${\bar{e}} \in [0,0.34]$ there is still the possibility that a global family ${\mathcal {C}}_{p,M,1}$ exists, with $\frac{p}{M}\ge 0.994\sqrt{8}$, satisfying D2-condition at ${\bar{e}}$. In this case, the expression (23) is not good enough to estimate $\varphi (M\pi ,e)$ and analyze such situation. A similar fact happens for $\lambda \ge \frac{1}{8}$.

5 Global families that emerge from the classical circular Sitnikov problem

In this section, we explain analytically the numerical results obtained in Sect. 4 for the classical Sitnikov problem ($\lambda =1$). We remark that for such analysis we will need to use computationally obtained results.

We highlight that at all times in this section $\lambda =1$.

Lemma 4

The inequality (25) holds for every $e\in [0.96,1)$.

Proof

Let’s first observe that

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_1(u,e)}\mathrm{d}u>\frac{\sqrt{15}}{4}\pi +\frac{\sqrt{14}}{2}\ln \left( \frac{64}{75(1-e)}\right) +\frac{2}{\sqrt{3}}. \end{aligned}$$

(28)

In fact,

$$\begin{aligned}&\int _{0}^{\pi }\sqrt{q_1(u,e)}\mathrm{d}u\\&\quad =\frac{1}{2}\int _{-1}^{1}\sqrt{1+\frac{28}{1-ex}+\frac{3(1-e^2)}{(1-ex)^2}}\frac{\mathrm{d}x}{\sqrt{1-x^2}}\\&\quad >T_1+T_2+T_3 \end{aligned}$$

where

$$\begin{aligned} T_1= & {} \frac{1}{2}\int _{-1}^{0}\sqrt{1+\frac{28}{1-ex}}\frac{\mathrm{d}x}{\sqrt{1-x^2}},\\ T_2= & {} \frac{1}{2}\int _{0}^{\frac{2}{3-e}}\sqrt{\frac{28}{1-ex}}\frac{\mathrm{d}x}{\sqrt{1-x^2},}\\ T_3= & {} \frac{1}{2}\int _{\frac{2}{3-e}}^{1}\sqrt{1+\frac{28}{1-ex}+\frac{3(1-e^2)}{(1-ex)^2}}\frac{\mathrm{d}x}{\sqrt{1-x^2}}. \end{aligned}$$

Now

$$\begin{aligned} T_1>\frac{1}{2}\int _{-1}^{0}\sqrt{1+\frac{28}{2}}\frac{\mathrm{d}x}{\sqrt{1-x^2}}=\frac{\sqrt{15}}{4}\pi . \end{aligned}$$

(29)

On the other hand, if $0<e<1$ then

$$\begin{aligned} T_2> & {} \frac{1}{2}\int _{0}^{\frac{2}{3-e}}\sqrt{\frac{28}{1-ex}}\frac{\mathrm{d}x}{\sqrt{1-(ex)^2}}\\= & {} \frac{\sqrt{14}}{2}\frac{1}{e}\ln \left( \frac{\left( \sqrt{2}+\sqrt{1+ex}\right) ^2}{1-ex}\right) \Bigg |_{0}^{\frac{2}{3-e}}\\= & {} \frac{\sqrt{14}}{2}\frac{1}{e}\left( \ln \left( \frac{3-e}{3(1-e)}\left( \sqrt{2}+\sqrt{\frac{3+e}{3-e}}\right) ^2\right) -\ln \left( (\sqrt{2}+1)^2\right) \right) \\= & {} \frac{\sqrt{14}}{2}\frac{1}{e}\left( \ln \left( \frac{1}{3(1-e)}\left( \sqrt{2(3-e)}+\sqrt{3+e}\right) ^2\right) -\ln \left( (\sqrt{2}+1)^2\right) \right) . \end{aligned}$$

As the function $\sqrt{2(3-e)}+\sqrt{3+e}$ is decreasing in [0, 1] (since its derivative is equal to $\frac{1}{2 \sqrt{e + 3}} - \frac{1}{\sqrt{6 - 2 e}}$ which is negative for all $e\in [0,1]$), we have that

$$\begin{aligned} \begin{aligned} T_2&>\frac{\sqrt{14}}{2}\ln \left( \frac{16}{3(1-e)}\left( \sqrt{2}+1\right) ^{-2}\right) >\frac{\sqrt{14}}{2}\ln \left( \frac{16}{3(1-e)}\left( \frac{5}{2}\right) ^{-2}\right) \\&=\frac{\sqrt{14}}{2}\ln \left( \frac{64}{75(1-e)}\right) . \end{aligned} \end{aligned}$$

(30)

Finally, let us define for $e\in [0,1)$ that

$$\begin{aligned} \sigma (x,e):=\frac{1}{2}\sqrt{1+\frac{28}{1-ex}+\frac{3(1-e^2)}{(1-ex)^2}}\frac{1}{\sqrt{1-x^2}}. \end{aligned}$$

Since, for every $e\in [0,1)$, $\sigma (x,e)$ is an increasing function of x in [0, 1] then

$$\begin{aligned} (T_3)^2>\left( \sigma \left( \frac{2}{3-e},e\right) \left( 1-\frac{2}{3-e}\right) \right) ^2=\frac{e^3-5e^2-28e+96}{60-12e}, \end{aligned}$$

and since the last term of the above chain of inequalities is decreasing in [0, 1] (because its derivative is $- \frac{e^{3} - 10 e^{2} + 25 e + 22}{6 \left( e - 5\right) ^{2}}$ which is negative in [0, 1]) then

$$\begin{aligned} T_3>\frac{2}{\sqrt{3}}. \end{aligned}$$

(31)

Then, inequality (28) follows from inequalities (29), (30) and (31). Now, we have that

$$\begin{aligned} 4\int _{0}^{\pi }\sqrt{q_1(u,e)}\mathrm{d}u>\sqrt{15}\pi +\sqrt{56}\ln \left( \frac{64}{75(1-e)}\right) +\frac{8}{\sqrt{3}}. \end{aligned}$$

Then, a sufficient condition for (25) to hold is

$$\begin{aligned} \sqrt{15}\pi +\ln \left( \left( \frac{64}{75}\right) ^{\sqrt{56}}\frac{(16-e)}{(1-e)^{\sqrt{56}-1}(16+e)(1+e)}\right) +\frac{8}{\sqrt{3}}>4\sqrt{8}\pi . \end{aligned}$$

This inequality is true for $e=0.96$ and as the function $\frac{(16-e)}{(1-e)^{\sqrt{56}-1}(16+e)(1+e)}$ is increasing (since its derivative $\frac{34 e^{2} - \sqrt{14} \left( 2 e^{3} + 2 e^{2} - 512 e - 512\right) - 544}{\left( 1 - e\right) ^{-1 + 2 \sqrt{14}} \left( 1 - e\right) \left( e + 1\right) ^{2} \left( e + 16\right) ^{2}}$ is positive for $e\in [0,1)$) the above inequality is true for all $e\in [0.96,1)$. $\square$

The previous result guarantees that for every $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,1}\}$ the global family ${\mathcal {C}}_{p,M,1}$ cannot satisfy $\textit{D2}$-condition at an eccentricity value ${\bar{e}}\ge 0.96$. So, from now we will analyze the problem that concern us for $e\in [0,0.96]$.

Lemma 5

Let $q_1(u,e)$ be the function defined in (16). If $e\in [0,0.96]$ then

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_1(u,e)}\mathrm{d}u>\sqrt{8}\pi P(e), \end{aligned}$$

where

$$\begin{aligned} P(e)= & {} g_1(0)+g_1(1) e^2+g_1(2) e^4+g_1(3) e^6\\= & {} 1+\frac{703}{4096} e^2+\frac{6375537}{67108864}e^4+\frac{18015614935}{274877906944}e^6. \end{aligned}$$

Proof

Using the code described in Remark 5, in the “Appendix”, we can check, without error, that $\int _{0}^{\pi }c_{1,2\tau }(u)\mathrm{d}u>0$ for $0 \le \tau \le 35$. Now, if we take $e\in [0,0.96]$, from Lemma 8 and (34), we have that

$$\begin{aligned}&\sum _{\tau =0}^{\infty }\int _{0}^{\pi }c_{1,2\tau }(u)\mathrm{d}ue^{2\tau }\\&\quad =\pi P(e)+\sum _{\tau =4}^{35}g_1(\tau )\pi e^{2\tau }+ \sum _{\tau =36}^{\infty }\int _{0}^{\pi }c_{1,2\tau }(u)\mathrm{d}u e^{2\tau }\\&\quad> \pi P(e) +\pi \sum _{\tau =4}^{18}g_1(\tau ) e^{2\tau }\frac{e^{36-2\tau }}{(96/100)^{36-2\tau }}-\frac{\pi }{4}\sum _{\tau =36}^{\infty }e^{2\tau }\\&\quad = \pi P(e) +\pi e^{36}\sum _{\tau =4}^{18}g_1(\tau ) \left( \frac{100}{96}\right) ^{36-2\tau }-\frac{\pi e^{72}}{4}\sum _{\tau =0}^{\infty }e^{2\tau }\\&\quad = \pi P(e) +\pi e^{36}\left( \sum _{\tau =4}^{18}g_1(\tau ) \left( \frac{100}{96}\right) ^{36-2\tau }-\frac{1}{4}\frac{e^{36}}{1-e^2}\right) \\&\quad >\pi P(e) +\pi e^{36}\left( \sum _{\tau =4}^{18}g_1(\tau ) \left( \frac{100}{96}\right) ^{36-2\tau }-\frac{1}{4}\frac{\left( \frac{96}{100}\right) ^{36}}{1-\left( \frac{96}{100}\right) ^2}\right) . \end{aligned}$$

The term $\sum _{\tau =4}^{18}g_1(\tau ) \left( \frac{100}{96}\right) ^{36-2\tau }-\frac{1}{4}\frac{\left( \frac{96}{100}\right) ^{36}}{1-\left( \frac{96}{100}\right) ^2}$ can be computed with a software and we can check without error that it is positive. The code for such calculus is

$$\begin{aligned}&\text {sum(gt(tau,1)*Rational(100,96)**(36-2*tau) for tau in range(4,19))-Rational(1,4)}\\&\quad \text {*Rational(96,100)**36}/ \text {(1-Rational(96,100)**2)}. \end{aligned}$$

Hence, by Lemma 7, we have that

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_1(u,e)}\mathrm{d}u>\sqrt{8}\pi P(e) \end{aligned}$$

for all $e\in [0,0.96]$. $\square$

Now, from the previous lemma, a sufficient condition for inequality (25) to be satisfied for an eccentricity value $e\in [0,0.96]$ is

$$\begin{aligned} \sqrt{8}\pi P(e)-\frac{1}{4}\ln \left( \frac{(1+e)(16+e)}{(1-e)(16-e)}\right) >\sqrt{8}\pi . \end{aligned}$$

If we define $R(e):=\sqrt{8}\pi P(e)-\frac{1}{4}\ln \left( \frac{(1+e)(16+e)}{(1-e)(16-e)}\right)$, we can see that ${\dot{R}}(e)=\frac{R_1(e)}{R_2(e)}$ where $R_2(e)$ is positive for all $e\in [0,1)$ and $R_1(e)$ is a polynomial with three changes of sign; moreover, we can check that $R_1(0)<0$, $R_1(0.34)>0$, $R_1(1)<0$ and $R_1(16)>0$; then, by Descartes’ rule, ${\dot{R}}(e)$ has exactly two zeros in [0, 1). Also, the first one, $e_1\approx 0.173307$, corresponds to a local minimum and the second, $e_2\approx 0.972036$ corresponds to a local maximum. Now, since $R(0.34)>\sqrt{8}\pi$ then $R(e)>\sqrt{8}\pi$ for all $e\in [0.34,0.96]$, and taking into account Lemma 4, we have that (25) is true for every $e\in [0.34,1)$ (and therefore (24) holds for every $e\in [0.34,1)$, $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,1}\}$). Furthermore, $e_1$ is an absolute minimum of R(e) in [0, 0.34] and since

$$\begin{aligned} R(e_1)>0.9947\sqrt{8}\pi , \end{aligned}$$

then inequality (24) is true for every $e\in [0,1)$, $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,1}\}$ such that $\frac{p}{M}<0.9947\sqrt{8}$.

Therefore, if we define ${\bar{\nu }}_{M,1}:=[0.9947\sqrt{8}M]$, we can enunciate the next result:

Theorem 3

Let $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,\nu _{M,1}\}$. Then

• i) if $1\le p\le {\bar{\nu }}_{M,1}$ the global family ${\mathcal {C}}_{p,M,1}$ satisfies $\textit{D1}$-condition.

• ii) if ${\bar{\nu }}_{M,1}<p \le \nu _{M,1}$ and the global family ${\mathcal {C}}_{p,M,1}$ satisfies $\textit{D2}$-condition at an eccentricity value ${\bar{e}}$, then ${\bar{e}}\in (0,0.34)$. Moreover, ${\tilde{E}}_{p,M,1}<{\tilde{e}}_{p,M,1}\le {\hat{e}}_{p,M,1}<{\hat{E}}_{p,M,1}$, where ${\tilde{E}}_{p,M,1}$ and ${\hat{E}}_{p,M,1}$ are the only two roots of $R(e)-\frac{p}{M}\pi$ in (0, 0.34).

The reason why we introduce the ${\tilde{E}}_{p,M,1}$ and ${\hat{E}}_{p,M,1}$ values in this result is because we can find them numerically and be sure that another root of $R(e)-\frac{p}{M}\pi$ does not exist in (0, 0.34); note that we cannot guarantee it will happen if we look for the solutions of (26).

Proof

The item i) and the fact that ${\bar{e}}\in (0,0.34)$ in item ii) follow from the reasoning made in the above paragraph. Now, if ${\mathcal {C}}_{p,M,1}$ satisfies $\textit{D2}$-condition at ${\bar{e}}$, then equality (26) has a solution in (0, 0.34). Since $e_1$ is the only value in (0, 0.34) such that ${\dot{R}}(e)$ is equal to zero, $R(0)-\frac{p}{M}\pi >0$, $R(0.34)-\frac{p}{M}\pi >0$, and $\int _{0}^{\pi }\sqrt{q_1(u,e)}\mathrm{d}u>\sqrt{8}\pi P(e)$ for every $e\in [0,0.34]$, there are exactly two roots of $R(e)-\frac{p}{M}\pi$ in (0, 0.34), ${\tilde{E}}_{p,M,1}$ and ${\hat{E}}_{p,M,1}$, such that ${\tilde{E}}_{p,M,1}<{\tilde{e}}_{p,M,1}\le {\hat{e}}_{p,M,1}<{\hat{E}}_{p,M,1}$. $\square$

Now, we can see that ${\bar{\nu }}_{M,1}=\nu _{M,1}$ for $M=1,2,3,4,5,6,7,8,9,10,12,13$ and other 21 values of M less than 54. So, in these cases, every global family satisfies $\textit{D1}$-condition. In addition, for $M\le 80$ we have that ${\bar{\nu }}_{M,1}=\nu _{M,1}$ or ${\bar{\nu }}_{M,1}=\nu _{M,1}-1$. Therefore, if $M\le 80$, the only global family that could satisfy $\textit{D2}$-condition is ${\mathcal {C}}_{\nu _{M,1},M,1}$. For some values of M such that ${\bar{\nu }}_{M,1}=\nu _{M,1}-1$, in Table 1 we show the values of ${\tilde{E}}_{\nu _{M,1},M,1}$ and ${\hat{E}}_{\nu _{M,1},M,1}$.

Table 1 Values of ${\tilde{E}}_{\nu _{M,1},M,1}$ and ${\hat{E}}_{\nu _{M,1},M,1}$

Note that Theorem 3 improves Theorem 3.2 in Llibre and Ortega (2008), and we can check that the values of ${\tilde{E}}_{\nu _{M,1},M,1}$ are greater than the lower bound $\rho _M$ exposed therein, but in this case both ${\tilde{E}}_{\nu _{M,1},M,1}$ and ${\hat{E}}_{\nu _{M,1},M,1}$ are given implicitly.

Corollary 1

Let $M\in {\mathbb {N}}$ and $p\in \{1,2,\ldots ,{\bar{\nu }}_{M,1}\}$. Then for all $e\in [0,1)$ there exists an even $2M\pi$-periodic solution, which has p-zeros in $[0,M\pi ]$, of the classical Sitnikov problem in which the primaries orbit in ellipses of eccentricity e.

Conclusions. We study a generalized Sitnikov problem, in which the primary bodies are performing a planar homographic motion and forming at all times an admissible central configuration. This problem represents a generalization of the Sitnikov’s problems considered in Llibre and Ortega (2008), Ortega and Rivera (2010), Rivera (2013), and the results in these papers can be extended to this case closely following the ideas therein. The particular question that is studied in this work is the problem of determining if a global family ${\mathcal {C}}_{p,M,\lambda }$ of even periodic solutions which emerges from a CGSP continues for all values of eccentricities $e\in [0,1)$ ($\textit{D1}$-condition) or ends in the equilibrium at a value of eccentricity ${\bar{e}}$ ($\textit{D2}$-condition). The principal contribution of this paper, which represents an advance on what is already known in the literature, is some mathematical criteria to determine if a global family ${\mathcal {C}}_{p,M,\lambda }$ satisfies $\textit{D1}$-condition, or to give a lower bound and, if $\lambda >\frac{9}{64}$, to give an upper bound for a possible value of eccentricity ${\bar{e}}$ at which ${\mathcal {C}}_{p,M,\lambda }$ could satisfy $\textit{D2}$-condition. Such criteria allow us to find evidence that the vast majority of global families ${\mathcal {C}}_{p,M,\lambda }$ satisfy $\textit{D1}$-condition. For the classical Sitnikov problem ($\lambda =1$), these families represent the 99.4 per cent of all global families.

Appendix

In this section, we enunciate and demonstrate some technical lemmas, which deal with Taylor series of $\sqrt{q_\lambda (u,e)}$ and $\int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u$ and are used to demonstrate other results of the article.

Before enunciating the first lemma, it should be noted the definition of combinatory number, $\begin{pmatrix} \gamma \\ n \end{pmatrix}:=\frac{\prod _{i=1}^{n}(\gamma -i+1)}{n!}$, where $\gamma \in {\mathbb {R}}$ and $n\in {\mathbb {N}}$.

Lemma 6

Let $q_\lambda (u,e)$ be the function defined in (16). Then, for $u \in (0,\pi )$, we have that

$$\begin{aligned} \sqrt{q_\lambda (u,e)}=\sqrt{8\lambda }\sum _{l=0}^{\infty }c_{\lambda ,l}(u)e^{l}, \end{aligned}$$

where

$$\begin{aligned}&c_{\lambda ,l}(u)=\sum _{j=0}^{\left[ \frac{l}{2}\right] }\sum _{k=0}^{l-2j}\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_\lambda ^k(u)\cos ^{l-k-2j}(u)\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_\lambda ^{j}(u), \end{aligned}$$

(32)

with $a_\lambda (u)=\frac{\cos ^2(u)-3}{32\lambda }$, $b_\lambda (u)=-\frac{32\lambda -2}{32\lambda }\cos (u)$.

Proof

Let us first observe that

$$\begin{aligned} \sqrt{q_\lambda (u,e)}= & {} \frac{1}{2}\frac{\sqrt{32\lambda -(32\lambda -2)\cos (u)e+(\cos ^2(u)-3)e^2}}{1-e\cos (u)}\\= & {} \sqrt{8\lambda }\frac{\sqrt{1+b_\lambda (u)e+a_\lambda (u)e^2}}{1-e\cos (u)} \end{aligned}$$

where $a_\lambda (u)=\frac{\cos ^2(u)-3}{32\lambda }$ and $b_\lambda (u)=-\frac{32\lambda -2}{32\lambda }\cos (u)$. As $\sqrt{1+x}=\sum _{i=0}^{\infty }\begin{pmatrix} \frac{1}{2}\\ i \end{pmatrix}x^i$ for all $-1<x< 1$, we have that

$$\begin{aligned} \sqrt{q_\lambda (u,e)}=\sqrt{8\lambda }f_\lambda (u,e)\sum _{n=0}^{\infty }\cos ^n(u)e^n, \end{aligned}$$

where $f_\lambda (u,e):=\sum _{n=0}^{\infty }\begin{pmatrix} \frac{1}{2}\\ n \end{pmatrix}e^n(b_\lambda (u)+ea_\lambda (u))^n$.

Since $\sqrt{1+x}$ is analytic in $(-1,1)$ and $b_\lambda (u)e+a_\lambda (u)e^2$ is analytic, as a function of e in ${\mathbb {R}}$, we have that, for every $u\in (0,\pi )$, $\sqrt{1+b_\lambda (u)e+a_\lambda (u)e^2}=f_\lambda (u,e)$ is analytic, as a function of e, in $(-1,1)$. Then, for $e\in [0,1)$

$$\begin{aligned} f_\lambda (u,e)=\sum _{n=0}^{\infty }\frac{\partial ^nf_\lambda (u,0)}{\partial e^n}\frac{e^n}{n!}. \end{aligned}$$

Let us calculate $\frac{\partial ^nf_\lambda (u,0)}{\partial e^n}$.

$$\begin{aligned} \frac{\partial ^nf_\lambda (u,0)}{\partial e^n}= & {} \sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\begin{pmatrix} \frac{1}{2}\\ m \end{pmatrix}\frac{\partial ^n}{\partial e^n}(e^m(b_\lambda (u)+ea_\lambda (u))^m)\Big |_{e=0}\\= & {} \sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\begin{pmatrix} \frac{1}{2}\\ m \end{pmatrix}\sum _{i=0}^{n} \begin{pmatrix} n\\ i \end{pmatrix}\left( \frac{\partial ^ie^m}{\partial e^i}\frac{\partial ^{n-i}}{\partial e^{n-i}}(b_\lambda (u)+ea_\lambda (u))^m\right) \bigg |_{e=0}\\= & {} \sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\begin{pmatrix} \frac{1}{2}\\ m \end{pmatrix} \begin{pmatrix} n\\ m \end{pmatrix}\left( \frac{\partial ^me^m}{\partial e^m}\frac{\partial ^{n-m}}{\partial e^{n-m}}(b_\lambda (u)+ea_\lambda (u))^m\right) \bigg |_{e=0}\\= & {} \sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\begin{pmatrix} \frac{1}{2}\\ m \end{pmatrix} \begin{pmatrix} n\\ m \end{pmatrix}\frac{(m!)^2}{(2m-n)!}b_\lambda ^{2m-n}(u)a_\lambda ^{n-m}(u). \end{aligned}$$

Now,

$$\begin{aligned} \sqrt{q_\lambda (u,e)}=\sqrt{8\lambda }\sum _{l=0}^{\infty }c_{\lambda ,l}(u)e^l, \end{aligned}$$

where

$$\begin{aligned} c_{\lambda ,l}(u)=\sum _{n=0}^{l}\frac{\partial ^nf_\lambda (u,0)}{\partial e^n}\frac{\cos ^{l-n}(u)}{n!}. \end{aligned}$$

Considering $j=n-m$, and $k=n-2j$, we have that

$$\begin{aligned} c_{\lambda ,l}(u)= & {} \sum _{n=0}^{l}\sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\begin{pmatrix} \frac{1}{2}\\ m \end{pmatrix}\begin{pmatrix} n\\ m \end{pmatrix}\frac{(m!)^2}{(2m-n)!}\frac{b_\lambda ^{2m-n}(u)a_\lambda ^{n-m}(u)}{n!}\cos ^{l-n}(u)\nonumber \\= & {} \sum _{n=0}^{l}\sum _{m=\left[ \frac{n+1}{2}\right] }^{n} \left[ \prod _{s=1}^{m}\left( \frac{1}{2}-s+1\right) \right] \frac{b_\lambda ^{2m-n}(u)}{(2m-n)!}\frac{a_\lambda ^{n-m}(u)}{(n-m)!}\cos ^{l-n}(u)\nonumber \\= & {} \sum _{j=0}^{\left[ \frac{l}{2}\right] }\sum _{n=2j}^{l}\prod _{s=1}^{n-j}\left( \frac{1}{2}-s+1\right) \frac{b_\lambda ^{n-2j}(u)}{(n-2j)!}\cos ^{l-n}(u)\frac{a_\lambda ^j(u)}{j!}\nonumber \\= & {} \sum _{j=0}^{\left[ \frac{l}{2}\right] }\sum _{k=0}^{l-2j}\prod _{s=j+1}^{k+j}\left( \frac{1}{2}-s+1\right) \frac{b_\lambda ^k(u)}{k!}\cos ^{l-k-2j}(u)\prod _{i=1}^{j}\left( \frac{1}{2}-i+1\right) \frac{a_\lambda ^{j}(u)}{j!}\nonumber \\= & {} \sum _{j=0}^{\left[ \frac{l}{2}\right] }\sum _{k=0}^{l-2j}\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_\lambda ^k(u)\cos ^{l-k-2j}(u)\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_\lambda ^{j}(u). \end{aligned}$$

(33)

$\square$

Lemma 7

Let $q_\lambda (u,e)$ be the function defined in (16). Then

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u=\sqrt{8\lambda }\sum _{\tau =0}^{\infty }\int _{0}^{\pi }c_{\lambda ,2\tau }(u)\mathrm{d}ue^{2\tau }. \end{aligned}$$

Proof

Note first that $\begin{pmatrix} \frac{1}{2}\\ k \end{pmatrix}(-1)^k<0$ if $k\ge 1$, and $\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}(-1)^k>0$ if $j\ge 1$ and $k\ge 0$. Since the function $-1<\frac{a_\lambda (u)}{1+b_\lambda (u)} < 0$ for $u\in (0,\pi )$, and $\sum _{k=0}^{\infty }\begin{pmatrix} \gamma \\ k \end{pmatrix}\beta ^k=(1+\beta )^{\gamma }$ for $\gamma \in {\mathbb {R}}$ and $|\beta |<1$, if $u\in (0,\pi )$, we have that

$$\begin{aligned}&|c_{\lambda ,l}(u)|\\&\quad \le 1+ \sum _{k=1}^{l}\left| \begin{pmatrix} \frac{1}{2}\\ k \end{pmatrix}b_\lambda ^k(u)\right| \left| \cos ^{l-k}(u)\right| +\sum _{j=1}^{\left[ \frac{l}{2}\right] }\sum _{k=0}^{l-2j}\left| \begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_\lambda ^k(u)\right| \left| \cos ^{l-k-2j}(u)\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_\lambda ^{j}(u)\right| \\&\quad \le 1-\sum _{k=1}^{\infty }\begin{pmatrix} \frac{1}{2}\\ k \end{pmatrix}b_\lambda ^k(u)-\sum _{j=1}^{\infty }\sum _{k=0}^{\infty }\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_\lambda ^k(u)\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_\lambda ^{j}(u)\\&\quad =2-\sqrt{1+b_\lambda (u)}\sum _{j=0}^{\infty }\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}\left( \frac{a_\lambda (u)}{1+b_\lambda (u)}\right) ^j\\&\quad \le 2. \end{aligned}$$

Thus, by the dominated convergence theorem we have that

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u=\sqrt{8\lambda }\sum _{l=0}^{\infty }\int _{0}^{\pi }c_{\lambda ,l}(u)\mathrm{d}ue^l, \end{aligned}$$

for every $0\le e<1$. Taking into account the expression of $c_{\lambda ,l}(u)$, if l is an odd number then $\int _{0}^{\pi }c_{\lambda ,l}(u)\mathrm{d}u=0$. Therefore,

$$\begin{aligned} \int _{0}^{\pi }\sqrt{q_\lambda (u,e)}\mathrm{d}u=\sqrt{8\lambda }\sum _{\tau =0}^{\infty }\int _{0}^{\pi }c_{\lambda ,2\tau }(u)\mathrm{d}ue^{2\tau }. \end{aligned}$$

$\square$

Remark 5

From (33) in Lemma 6, if we define $h_\tau (u,\omega ):=\cos ^{2\tau -2\omega }(u)(3-\cos ^2(u))^\omega$, we have that

$$\begin{aligned}&c_{\lambda ,2\tau }(u) =\sum _{n=0}^{2\tau }\sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\begin{pmatrix} \frac{1}{2}\\ m \end{pmatrix}\begin{pmatrix} n\\ m \end{pmatrix}\frac{(m!)^2}{(2m-n)!}\frac{b_\lambda ^{2m-n}(u)a_\lambda ^{n-m}(u)}{n!}\cos ^{2\tau -n}(u)\\&\quad =\sum _{n=0}^{2\tau }\sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\left[ \prod _{s=1}^{m}\left( \frac{1}{2}-s+1\right) \right] \frac{(-1)^m}{(n-m)!}\frac{1}{(2m-n)!}\frac{(32\lambda -2)^{2m-n}}{(32\lambda )^m} h_{\tau }(u,n-m). \end{aligned}$$

Now, taking into account that $\int _{0}^{\pi }\cos ^i(x)\mathrm{d}x=\frac{i-1}{i}\int _{0}^{\pi }\cos ^{i-2}(x)\mathrm{d}x$ for $i\ge 2$, if $\tau \ge n-m\ge 0$ then

$$\begin{aligned}&\int _{0}^{\pi } h_{\tau }(u,n-m)\mathrm{d}u\\&\quad =\sum _{i=0}^{n-m}\begin{pmatrix} n-m\\ i \end{pmatrix}3^{i}(-1)^{n-m-i}\int _{0}^{\pi }\cos ^{2(\tau -i)}(u)\mathrm{d}u\\&\quad =\sum _{i=0}^{n-m}\begin{pmatrix} n-m\\ i \end{pmatrix}3^{i}(-1)^{n-m-i}\prod _{j=1}^{\tau -i}\frac{2\tau -2i-2j+1}{2\tau -2i-2j+2}\pi \\&\quad =:{\bar{g}}(\tau ,n-m)\pi . \end{aligned}$$

Hence,

$$\begin{aligned}&\int _{0}^{\pi }c_{\lambda ,2\tau }(u)\mathrm{d}u\nonumber \\= & {} \sum _{n=0}^{2\tau }\sum _{m=\left[ \frac{n+1}{2}\right] }^{n}\left[ \prod _{s=1}^{m}\left( \frac{1}{2}-s+1\right) \right] \frac{(-1)^m}{(n-m)!}\frac{1}{(2m-n)!}\frac{(32\lambda -2)^{2m-n}}{(32\lambda )^m}{\bar{g}}(\tau ,n-m)\pi \nonumber \\= & {} : g_\lambda (\tau )\pi . \end{aligned}$$

(34)

Note that $\int _{0}^{\pi }c_{\lambda ,2\tau }(u)\mathrm{d}u$ is always a product between a number $g_\lambda (\tau )$ and $\pi$, so we can calculate with a symbolic computation software the expression of $g_\lambda (\tau )$ without error. Thus, for example, we can verify that

$$\begin{aligned}&\int _{0}^{\pi }c_{\lambda ,0}(u)\mathrm{d}u=\pi \\&\quad \int _{0}^{\pi }c_{\lambda ,2}(u)\mathrm{d}u=\frac{768 \lambda ^{2} - 64 \lambda - 1}{4096 \lambda ^{2}}\pi \\&\quad \int _{0}^{\pi }c_{\lambda ,4}(u)\mathrm{d}u=\frac{3 \left( 2293760 \lambda ^{4} - 163840 \lambda ^{3} - 4608 \lambda ^{2} - 128 \lambda - 5\right) }{67108864 \lambda ^{4}}\pi . \end{aligned}$$

In general it seems to be that $\int _{0}^{\pi }c_{\lambda ,2\tau }(u)\mathrm{d}u>0$ for all $\lambda \ge \frac{1}{8}$ and $\tau \in {\mathbb {N}}_0$.

The code used in the Python library “Sympy” with which we calculate $\int _{0}^{\pi }c_{\lambda ,2\tau }(u)\mathrm{d}u$ is described below

$$\begin{aligned}&\text {def conv(m,n):}\\&\quad \text {return factorial(m)/factorial(m-n)/factorial(n)}\\&\quad \text { def intcos(s):}\\&\quad \text {return prod(Rational(2*s-2*j+1,2*s-2*j+2) for j in range(1,s+1))}\\&\quad \text {def bargt(t,s):}\\&\quad \text {return sum((-1)**(s-i)*3**(i)*conv(s,i)*intcos(t-i)\ for i in}\\&\quad \text {range(s+1))}\\&\quad \text {def gt(tau,lam):}\\&\quad \text {A=sum(sum((-1)**m*prod(Rational(1,2)-s+1}\\&\quad \text {for s in range(1,m+1))*1/factorial(n-m)/factorial(2*m-n)}\\&\quad \text {*(32*lam-2)**(2*m-n)/(32*lam)**m*bargt(tau,n-m) for m in}\\&\quad \text {range(floor(Rational(n+1,2)),n+1)) for n in range(2*tau+1))}\\&\quad \text {return A} \end{aligned}$$

The function $\text {gt(tau,lam)}$ calculates $g_\lambda (\tau )$ with error zero.

Lemma 8

Let $c_{1,l}(u)$ be the coefficient defined in (32). Then

$$\begin{aligned} \int _{0}^{\pi }c_{1,2\tau }(u)\mathrm{d}u\ge -\frac{\pi }{4}. \end{aligned}$$

for all $\tau \in {\mathbb {N}}_0$.

Proof

For $u\in (0,\frac{\pi }{2})$, we have that

$$\begin{aligned}&c_{1,2\tau }(u)\nonumber \\&\quad =\sum _{k=0}^{2\tau }\begin{pmatrix} \frac{1}{2}\\ k \end{pmatrix}b_1^k(u)\cos ^{2\tau -k}(u)+\sum _{j=1}^{\tau }\sum _{k=0}^{2\tau -2j}\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_1^k(u)\cos ^{2\tau -k-2j}(u)\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_1^{j}(u)\nonumber \\&\quad =\cos ^{2\tau }(u)\sum _{k=0}^{2\tau }\begin{pmatrix} \frac{1}{2}\\ k \end{pmatrix}\left( -\frac{15}{16}\right) ^k+\sum _{j=1}^{\tau }\sum _{k=0}^{2\tau -2j}\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_1^k(u)\cos ^{2\tau -k-2j}(u)\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_1^{j}(u)\nonumber \\&\quad \ge \cos ^{2\tau }(u)\sqrt{1-\frac{15}{16}}+\sum _{j=1}^{\tau }\left[ \sum _{k=0}^{2\tau -2j}\begin{pmatrix} \frac{1}{2}-j\\ k \end{pmatrix}b_1^k(u)\right] \begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}a_1^{j}(u)\nonumber \\&\quad =(1+b_1(u))^{\frac{1}{2}}\sum _{j=1}^{\infty }\begin{pmatrix} \frac{1}{2}\\ j \end{pmatrix}\left( \frac{a_1(u)}{1+b_1(u)}\right) ^{j}\nonumber \\&\quad =(1+b_1(u))^{\frac{1}{2}}\left( -1+\sqrt{1+\frac{a_1(u)}{1+b_1(u)}}\right) \nonumber \\&\quad =\frac{a_1(u)}{(1+b_1(u))^{\frac{1}{2}}}\frac{1}{1+\sqrt{1-\frac{-a_1(u)}{1+b_1(u)}}}. \end{aligned}$$

(35)

Since the function $\frac{a_1(u)}{(1+b_1(u))^{\frac{1}{2}}}$ is negative and increasing in $(0,\frac{\pi }{2})$ (because its derivative is equal to $\frac{ \left( 45 \cos ^{2}{\left( u \right) } - 64 \cos {\left( u \right) } + 45\right) \sin {\left( u \right) }}{16 \left( 16 -15 \cos {\left( u \right) }\right) ^{\frac{3}{2}}}$, which is positive for all $u\in (0,\frac{\pi }{2})$), and the function $\frac{-a_1(u)}{1+b_1(u)}$ is positive and decreasing in $(0,\frac{\pi }{2})$ (since its derivative $- \frac{\left( 15 \cos ^{2}{\left( u \right) } - 32 \cos {\left( u \right) } + 45\right) \sin {\left( u \right) }}{2 \left( 15 \cos {\left( u \right) } - 16\right) ^{2}}$ is negative for $u\in (0,\frac{\pi }{2})$), we have that the last expression in the chain of inequalities mentioned above is increasing. Then, it reaches its minimum in $\left[ 0,\frac{\pi }{2}\right]$ at $u=0$. Hence $c_{1,2\tau }(u)\ge c_{1,2\tau }(0)= - \frac{1}{4}$ for every $u\in (0,\frac{\pi }{2})$. Therefore

$$\begin{aligned} \int _{0}^{\pi }c_{1,2\tau }(u)\mathrm{d}u=2\int _{0}^{\frac{\pi }{2}}c_{1,2\tau }(u)\mathrm{d}u\ge - \frac{\pi }{4}. \end{aligned}$$

$\square$