1 Introduction

Dual rotor systems have been widely used in the aero-engine field. In many cases, dynamic behaviors of medium bearings of dual rotor systems of aero-engines are complex or maybe nonlinear [1]. The dynamic analysis of the aero-engine dual rotor system is an essential requirement and is vital to the aero-engine’s safety [2]. Due to the existence of uncertainties such as the change of operating temperature or assembly errors, the vibration amplitude of rotor systems may be too large or even malfunction may occur [3,4,5]. Due to the medium bearing connecting the inner and outer rotors, the vibrations of dual rotor systems of aeroengines become more complicated [6]. Considering this, Wang et al. [7] analyzed the effects of mass eccentricity, rotational speed ratio, initial clearance, and inner-shaft stiffness on the dynamic behaviors for a dual rotor system, which is beneficial for a better understanding rubbing faults of the aero-engine. Yi et al. [8] proposed a dynamic model of dual rotor systems with local defects on the inner ring of the inner-shaft bearing to investigate the amplitude–frequency response of dual rotor systems. Hou et al. [9] investigated the effects of the non-concentricity on the vibration characteristics of dual-rotor systems, and they pointed out that the natural frequencies of the bending modals decrease continuously with the increase in the magnitude of the non-concentricity. In order to consider the defect size and the corresponding uncertainty, Tian et al. [10] proposed a non-intrusive polynomial chaos expansion model and verified the validity of this model. These uncertainties of a real rotor system can be divided into two categories: parameter uncertainties and model uncertainties [11, 12]. The former can be caused by the lack of knowledge in description of the real system parameters, such as the Young's modulus of the rotating shaft and the exact value of the variation of the supporting stiffness under the influence of the ambient temperature during the operation of the rotor system, which is regarded as a variable. The latter are introduced by a series of simplifications and approximations during the modeling process, i.e., by modeling errors, such as simplifying a uniformly distributed mass axis to a discrete distribution with the order to speed up calculation [13,14,15,16].

For the vibration analysis of a designed rotor system or a real rotor system, there are two types of methods to consider the uncertainties. A possible choice consists in using the stochastic parameter methods, in which the stochastic parameters are random variables. Yang et al. [17], for example, studied the Polynomial Chaos Expansion method to describe the uncertainties introduced by crack. Fu et al. [18] proposed a method combining the Chebyshev Surrogate and the Polynomial Chaos Expansion to consider random parameters. However, the main disadvantage of this method is that model uncertainties cannot be considered because the stochastic representation of the uncertainties is constructed after the establishment of the dynamic model utilizing these methods [19,20,21]. Another choice consists in using the nonparametric stochastic modeling method with which both the parameter uncertainties and model uncertainties can be considered. Murthy et al. [22], for example, derived the dynamics model of a single-rotor system with model uncertainties utilizing the nonparametric stochastic modeling method based on maximum entropy and random matrix theory, and the effects of uncertainties on the eigenvalues of the system were analyzed, but the effects of the two uncertainties were not discussed respectively. Gan et al. [23, 24] studied the reliability calculation of the rotor subsystem based on the nonparametric modeling technique, which provides a reference for the design of complex rotor system. Huang [25] constructed a probabilistic model for a high-speed motorized spindle with model uncertainties using the nonparametric method combining with the finite element theory, and analyzed the vibration responses of the spindle. However, most previous studies on rotor systems with model and data uncertainties were based on the method of finite element theory combined with nonparametric modeling method, with which it is difficult to represent the uncertainties at specific elements (e.g., coupling elements of a dual rotor system). Therefore, it is necessary to explore the nonparametric dynamics modeling method for dual rotor systems with uncertainties and discuss the effects of two types of uncertainties.

In this paper, the method of nonparametric stochastic modeling combined with the Riccati whole transfer matrix is proposed for modeling the uncertainties at specific elements of a dual rotor system. The whole transfer matrix of a dual rotor system with model uncertainties is derived, and the uncertain dynamics model is established. Under different uncertainty levels, the first three-order critical speeds of this system were calculated and compared with the calculated results of the parametric model, and the effects of the two types of uncertainties on the eigenvalues were analyzed. At the same time, it provides theoretical reference for the study of vibration characteristics of multi-rotor systems with uncertainties.

2 Nonparametric modeling method for a dual rotor system with uncertainties

2.1 Construction method of asymmetric random matrix

The idea of stochastic modeling for concentrated mass point elements, massless elastic shaft elements, disk elements, supporting elements and coupling elements in a dual rotor system with model uncertainties is to replace these deterministic element matrices with random matrices, i.e., mean element matrices. It is necessary to express the random asymmetric element B into the form of the random symmetric element through matrix transformation. For positive definite and asymmetric matrices, and matrices that are neither positive definite nor symmetric, the transformation method is as follows

$${\varvec{B}} = \user2{AQ,}$$
(1)

in which Q is unitary matrix and can be an orthogonal matrix when B is a real matrix. A is a random symmetric positive definite matrix. With this transformation, the whole transfer matrix of each element of the dual rotor system can be transformed into a symmetric positive definite matrix. In order to calculate the matrices A and Q, singular value decomposition is performed on B:

$${\varvec{B}} = \user2{U\Lambda V}^{{T}} ,$$
(2)

Since the matrices U and V obtained by Eq. (2) are unitary matrices, there is U.TU = I, where I is the identity matrix. Thus, Eq. (2) can be rewritten as

$$\begin{gathered} {\varvec{B}} = \user2{U\Lambda U}^{{T}} {\varvec{UV}}^{{T}} \\ { = }\left( {\user2{U\Lambda U}^{{T}} } \right)\left( {{\varvec{UV}}^{{T}} } \right). \\ \end{gathered}$$
(3)

By comparing the forms of Eq. (1) and (3), it is easy to find that A and Q can be expressed as:

$${\varvec{A}} = \user2{U\Lambda U}^{{T}} ,$$
(4)
$${\varvec{Q}} = {\varvec{UV}}^{{T}} ,$$
(5)

From Eq. (1, 2, 3, 4, 5), it can be seen that the simulation of an arbitrary random matrix by using nonparametric modeling method can be transformed into the simulation of a random symmetric positive definite matrix. Entropy of the random matrix A represents the level of uncertainty under known constraints. When entropy is maximum, the level of uncertainty of A is maximum. According to Ref. [26, 27], the random matrix A can be expressed as

$${\varvec{A}} = {\varvec{L}}_{{A}}^{{T}} {\varvec{GL}}_{{A}} ,$$
(6)

where E{A} = A, and A = LATLA, in which LA is an upper triangular matrix, and G is a random matrix, which satisfies G = LG.TLG, E{G} = I, where I is the identity matrix. Each off-diagonal element of the upper triangular matrix LG is a Gaussian random variable with zero mean, and the standard deviation can be expressed as

$$\sigma = \frac{1}{{\left( {n + 2\lambda_{{A}} - 1} \right)^{1/2} }},$$
(7)

in which λ A can be calculated with the matrix A and the dispersion parameter δ A by

$$\lambda_{{A}} = \frac{{{tr}\left( {\underline{{\varvec{A}}}^{2} } \right) - \left( {n - 1} \right)\delta_{{A}}^{2} {tr}\left( {\underline{{\varvec{A}}}^{2} } \right) + \left( {{tr}\underline{{\varvec{A}}} } \right)^{2} }}{{2\delta_{{A}}^{2} {tr}\left( {\underline{{\varvec{A}}}^{2} } \right)}},$$
(8)

in which the dispersion parameter δA controls the level of dispersion degree of matrix A. The larger the δA is, the higher the level of dispersion degree of matrix A is, that is, the greater the uncertainty of the model. In particular, δA = 0 means there is no uncertainty, that is, G = I, and A = A.

The diagonal elements of matrix LG can be expressed as

$${\varvec{L}}_{{{G,}ii}} = \left( {\frac{{2V_{ii} \left( {\frac{{n + 2\lambda_{{A}} - i - 2}}{2}} \right)}}{{n + 2\lambda_{{A}} - 1}}} \right)^{\frac{1}{2}} ,$$
(9)

in which Vii is a gamma random variable, and its probability density function pVii(v) can be written as:

$$p_{{V_{ii} }} (v) = {1}_{{{\mathbb{R}}^{ + } }} (v)\frac{{v^{{\frac{{n + 1 - (i + 1)\delta_{{A}}^{2} }}{{2\delta_{{A}}^{2} }}}} {\text{e}}^{ - v} }}{{{\Gamma }\left( {\frac{{n + 1 + (1 - i)\delta_{{A}}^{2} }}{{2\delta_{{A}}^{2} }}} \right)}},$$
(10)

From Eq. (8), it can be derived that λ A increases as δ A decreases for n fixed. Thus, δA → 0 and A → A if λ A →  + ∞. For a given value of δ A, A can be simulated by the Monte Carlo method [28].

In order to compare the effects of parameter uncertainties and model uncertainties on the critical speeds of the dual rotor system, the model uncertainty at the same level as the parameter uncertainty should be introduced. According to Ref. [29], model uncertainties and parameter uncertainties can be estimated by using the statistical distribution of critical speeds and the actual model parameters. Since this paper is only to study the effects of model uncertainties and parameter uncertainties under the same level of uncertainty, the two types of uncertainty will not be estimated concretely, and the dispersion parameter δ A of matrix A is assumed to be at a known range in the example in Sect. 3.

2.2 Nonparametric whole transfer matrix of the uncertain dual rotor system

The dual rotor system can be divided into a finite number of ideal elements, including concentrated mass elements, massless elastic shaft elements, rigid disc elements, supporting elements and coupling elements [30,31,32]. The whole transfer matrix of the two rotors in the non-coupled axis section is only related to their respective state vectors, thus, it is easy to list the mean Riccati whole transfer matrix of each element, and the corresponding whole transfer matrices of specific elements, for instance, the mass elements are given in Appendix. The random matrix construction method in Sect. 2.1 can be used to construct the corresponding nonparametric Riccati whole transfer matrix.

The mean state vector (ZI, ZII)i+1T of decoupling element of the dual rotor system at the cross section i + 1 can be written as

$$\left( {{\varvec{Z}}_{{I}} ,{\varvec{Z}}_{{{II}}} } \right)_{i + 1}^{{T}} = \left( {M_{{I}} ,Q_{{I}} ,x_{{I}} ,\theta_{{I}} ,M_{{{II}}} ,Q_{{{II}}} ,x_{{{II}}} ,\theta_{{{II}}} } \right)_{i + 1}^{{T}} .$$
(11)

It is similar to Eq. (11), the mean state vector (ZI, ZII)iT of decoupling element of the dual rotor system at the cross section i can be written as

$$\left( {{\varvec{Z}}_{{I}} ,{\varvec{Z}}_{{{II}}} } \right)_{i}^{{T}} = \left( {M_{{I}} ,Q_{{I}} ,x_{{I}} ,\theta_{{I}} ,M_{{{II}}} ,Q_{{{II}}} ,x_{{{II}}} ,\theta_{{{II}}} } \right)_{i}^{{T}} .$$
(12)

The transitive relation of (ZI, ZII)i+1 T and (ZI, ZII)iT is

$$\left[ {\begin{array}{*{20}c} {\underline{{\varvec{Z}}}_{{I}} } \\ {\underline{{\varvec{Z}}}_{{{II}}} } \\ \end{array} } \right]_{i + 1} = \left[ {\underline{{\varvec{Z}}} } \right]_{i} \left[ {\begin{array}{*{20}c} {\underline{{\varvec{Z}}}_{{I}} } \\ {\underline{{\varvec{Z}}}_{{{II}}} } \\ \end{array} } \right]_{i} = \left[ {\begin{array}{*{20}c} {\underline{{\varvec{T}}}_{{{I}{,11}}} } & {\underline{{\varvec{T}}}_{{{I}{,12}}} } & {0} & {0} \\ {\underline{{\varvec{T}}}_{{{I}{,21}}} } & {\underline{{\varvec{T}}}_{{{I}{,22}}} } & {0} & {0} \\ {0} & {0} & {\underline{{\varvec{T}}}_{{{II}{,11}}} } & {\underline{{\varvec{T}}}_{{{II}{,12}}} } \\ {0} & {0} & {\underline{{\varvec{T}}}_{{{II},21}} } & {\underline{{\varvec{T}}}_{{{II},22}} } \\ \end{array} } \right]_{i} \left[ {\begin{array}{*{20}c} {\underline{{\varvec{Z}}}_{{I}} } \\ {\underline{{\varvec{Z}}}_{{{II}}} } \\ \end{array} } \right]_{i}$$
(13)

in which the block matrices (Tj, 11)i, (Tj, 12)i, (Tj, 21)i and (Tj, 21)i can be expressed as follows:

$$\left( {\underline{{\varvec{T}}}_{j,11} } \right)_{i} = \left[ {\begin{array}{*{20}c} 1 & {l_{j} } \\ 0 & 1 \\ \end{array} } \right]_{i} ,$$
(14)
$$\left( {\underline{{\varvec{T}}}_{j,12} } \right)_{i} = \left[ {\begin{array}{*{20}c} {l_{j} \left( {m_{j} \omega^{2} - k_{s,j} } \right)} & {\left( {\frac{{\Omega_{j} }}{\omega }J_{p,j} - J_{d,j} } \right)\omega^{2} } \\ {m_{j} \omega^{2} - k_{s,j} } & {0} \\ \end{array} } \right]_{i} ,$$
(15)
$$\left( {\underline{{\varvec{T}}}_{j,21} } \right)_{i} = \left[ {\begin{array}{*{20}c} {\frac{{\left( {l_{j} } \right)^{2} }}{{2\left( {EI} \right)_{j} }}} & {\frac{{\left( {l_{j} } \right)^{3} }}{{6\left( {EI} \right)_{j} }}} \\ {\frac{{l_{j} }}{{\left( {EI} \right)_{j} }}} & {\frac{{\left( {l_{j} } \right)^{2} }}{{2\left( {EI} \right)_{j} }}} \\ \end{array} } \right]_{i} ,$$
(16)
$$\left( {\underline{{\varvec{T}}}_{j,22} } \right)_{i} = \left[ {\begin{array}{*{20}c} {1 + \frac{{(m_{j} \omega^{2} - k_{s,j} )(l_{j} )^{3} }}{{6(EI)_{j} }}} & {l_{j} + \frac{{(l_{j} )^{2} (\frac{{\Omega_{j} }}{\omega }J_{p,j} - J_{d,j} )\omega^{2} }}{{2(EI)_{j} }}} \\ {\frac{{(l_{j} )^{2} (m_{j} \omega^{2} - k_{s,j} )}}{{2(EI)_{j} }}} & {1 + \frac{{(l_{j} )(\frac{{\Omega_{j} }}{\omega }J_{p,j} - J_{d,j} )\omega^{2} }}{{(EI)_{j} }}} \\ \end{array} } \right]_{i} ,$$
(17)

in which j = 1, 2, which representing the serial number of a rotor. The parameters mj, lj, Ej, Ij, Ωj, and Jp, j are respectively the concentrated mass, length of shaft segment, elastic modulus, moment of inertia of section, angular velocity of rotation and polar moment of inertia of rigid thin disk of rotor j in the ith element; ꞷ is the angular velocity of precession; k s is the stiffness of the supporting element. The mean Riccati whole transfer matrix of the decoupled element can be obtained with the method from Ref. [29]:

$$\underline{{\varvec{S}}}_{i + 1} = \left( {\left[ {\begin{array}{*{20}c} {\underline{{\varvec{T}}}_{{\text{I,11}}} } & 0 \\ 0 & {\underline{{\varvec{T}}}_{{\text{II,11}}} } \\ \end{array} } \right]_{i} \underline{{\varvec{S}}}_{i} + \left[ {\begin{array}{*{20}c} {\underline{{\varvec{T}}}_{{\text{I,12}}} } & 0 \\ 0 & {\underline{{\varvec{T}}}_{{\text{II,12}}} } \\ \end{array} } \right]_{i} } \right)\left( {\left[ {\begin{array}{*{20}c} {\underline{{\varvec{T}}}_{{\text{I,21}}} } & 0 \\ 0 & {\underline{{\varvec{T}}}_{{{\text{II,}}21}} } \\ \end{array} } \right]_{i} \underline{{\varvec{S}}}_{i} + \left[ {\begin{array}{*{20}c} {\underline{{\varvec{T}}}_{{\text{I,22}}} } & 0 \\ 0 & {\underline{{\varvec{T}}}_{{{\text{II,}}22}} } \\ \end{array} } \right]_{i} } \right)^{ - 1} ,$$
(18)

in which Si is a zero square matrix. Using the construction method of random matrix given in Eq. (6) in Sect. 2.1, the mean matrix in Eq. (13) can be replaced with the random matrix. The nonparametric Riccati whole transfer matrix of the dual rotor system with model uncertainties then can be derived by substituting this random matrix into Eq. (18):

$${\varvec{S}}_{i + 1} = \left( {\left[ {\begin{array}{*{20}c} {{\varvec{T}}_{{\text{I,11}}} } & 0 \\ 0 & {{\varvec{T}}_{{\text{II,11}}} } \\ \end{array} } \right]_{i} {\varvec{S}}_{i} + \left[ {\begin{array}{*{20}c} {{\varvec{T}}_{{\text{I,12}}} } & 0 \\ 0 & {{\varvec{T}}_{{\text{II,12}}} } \\ \end{array} } \right]_{i} } \right)\left( {\left[ {\begin{array}{*{20}c} {{\varvec{T}}_{{\text{I,21}}} } & 0 \\ 0 & {{\varvec{T}}_{{{\text{II,}}21}} } \\ \end{array} } \right]_{i} {\varvec{S}}_{i} + \left[ {\begin{array}{*{20}c} {{\varvec{T}}_{{\text{I,22}}} } & 0 \\ 0 & {{\varvec{T}}_{{{\text{II,}}22}} } \\ \end{array} } \right]_{i} } \right)^{ - 1} ,$$
(19)

in which the block matrices (T j,11)i, (T j,12)i, (T j,21)i and (T j,22)i have the same property as the matrix B in Eq. (1), thus, the random matrix (Aj,qr)i2 can be deduced and written as

$$\left( {{\varvec{A}}_{{j{\text{,qr}}}} } \right)_{i}^{2} = \left( {{\varvec{T}}_{{j{\text{,qr}}}} } \right)_{i}^{{T}} \left( {{\varvec{T}}_{{j{\text{,qr}}}} } \right)_{i} = \left( {{\varvec{P}}_{{j{\text{,qr}}}} } \right)_{i} \left( {{\varvec{\varLambda}}_{{j{\text{,qr}}}} } \right)_{i}^{2} \left( {{\varvec{P}}_{{j{\text{,qr}}}} } \right)_{i}^{ - 1} ,$$
(20)

The random matrix (Aj,qr)i can be obtained from Eq. (20) and can be expressed as

$$\left( {{\varvec{A}}_{{j{\text{,qr}}}} } \right)_{i} = \left( {{\varvec{P}}_{{j{\text{,qr}}}} } \right)_{i} \left( {{\varvec{\varLambda}}_{{j{\text{,qr}}}} } \right)_{i} \left( {{\varvec{P}}_{{j{\text{,qr}}}} } \right)_{i}^{ - 1} ,$$
(21)

in which the random matrix (Aj,qr)i satisfies the following relation:

$$\left( {{\varvec{A}}_{{j{\text{,qr}}}} } \right)_{i} = \left( {{\varvec{L}}_{{{A},j{\text{,qr}}}} } \right)_{i}^{{T}} \left( {{\varvec{G}}_{{{A},j{\text{,qr}}}} } \right)_{i} \left( {{\varvec{L}}_{{{A},j{\text{,qr}}}} } \right)_{i}^{ - 1} ,$$
(22)

For coupling element, the transfer relation between two mean state vectors (ZI, ZII)iT and (ZI, ZII)i+1T corresponding to the cross sections i and i + 1 of the dual rotor system is

$$\left[ {\begin{array}{*{20}c} {\underline{{\varvec{Z}}}_{{I}} } \\ {\underline{{\varvec{Z}}}_{{{II}}} } \\ \end{array} } \right]_{i + 1} = \left( {\underline{{{\varvec{TC}}}} } \right)_{i} \left[ {\begin{array}{*{20}c} {\underline{{\varvec{Z}}}_{{I}} } \\ {\underline{{\varvec{Z}}}_{{{II}}} } \\ \end{array} } \right]_{i} ,$$
(23)

in which (TC)i is the mean whole transfer matrix of the coupling element, and it can be expressed in the form of component block matrices as

$$\left( {\underline{{{\varvec{TC}}}} } \right)_{i} = \left[ {\begin{array}{*{20}c} {\underline{{{\varvec{TC}}}}_{{{11}}} } & {\underline{{{\varvec{TC}}}}_{{{12}}} } & {\underline{{{\varvec{TC}}}}_{{{13}}} } & {\underline{{{\varvec{TC}}}}_{{{14}}} } \\ {\underline{{{\varvec{TC}}}}_{{{21}}} } & {\underline{{{\varvec{TC}}}}_{{{22}}} } & {\underline{{{\varvec{TC}}}}_{{{23}}} } & {\underline{{{\varvec{TC}}}}_{{{24}}} } \\ {\underline{{{\varvec{TC}}}}_{{{31}}} } & {\underline{{{\varvec{TC}}}}_{{{32}}} } & {\underline{{{\varvec{TC}}}}_{33} } & {\underline{{{\varvec{TC}}}}_{{{34}}} } \\ {\underline{{{\varvec{TC}}}}_{{{41}}} } & {\underline{{{\varvec{TC}}}}_{{{42}}} } & {\underline{{{\varvec{TC}}}}_{{{43}}} } & {\underline{{{\varvec{TC}}}}_{{{44}}} } \\ \end{array} } \right]_{i} ,$$
(24)

in which the uncoupled terms (TC11)i, (TC22)i, (TC33)i and (TC44)i are all identity matrices, and where (TC13)i, (TC14)i, (TC23)i, (TC24)i, (TC31)i, (TC32)i, (TC41)i, (TC42)i are all zero matrices. The coupling terms can be written as

$$\left( {\underline{{{\varvec{TC}}}}_{{{12}}} } \right)_{i} { = }\left[ {\begin{array}{*{20}c} 0 & 0 \\ {m_{{I}} \omega^{2} - k_{s} } & 0 \\ \end{array} } \right]_{i} ,$$
(25)
$$\left( {\underline{{{\varvec{TC}}}}_{{{34}}} } \right)_{i} { = }\left[ {\begin{array}{*{20}c} 0 & 0 \\ {m_{{{II}}} \omega^{2} - k_{s} } & 0 \\ \end{array} } \right]_{i} ,$$
(26)
$$\left( {\underline{{{\varvec{TC}}}}_{{{14}}} } \right)_{i} { = }\left( {\underline{{{\varvec{TC}}}}_{{{32}}} } \right)_{i} { = }\left[ {\begin{array}{*{20}c} 0 & 0 \\ {k_{s} } & 0 \\ \end{array} } \right]_{i} .$$
(27)

The mean Riccati whole transfer matrix of the coupling element is

$$\left( {\underline{{{\varvec{SC}}}} } \right)_{i + 1} = \left( {\underline{{{\varvec{SC}}}} } \right)_{i} + \left[ {\begin{array}{*{20}c} {\underline{{{\varvec{TC}}}}_{{{12}}} } & {\underline{{{\varvec{TC}}}}_{{{14}}} } \\ {\underline{{{\varvec{TC}}}}_{{{32}}} } & {\underline{{{\varvec{TC}}}}_{34} } \\ \end{array} } \right]_{i} .$$
(28)

By replacing the mean matrices in Eq. (24) with random matrices, and substituting this equation into Eq. (28), the nonparametric Riccati whole transfer matrix of the coupling element can be derived:

$$\left( {{\varvec{SC}}} \right)_{i + 1} = \left( {{\varvec{SC}}} \right)_{i} + \left[ {\begin{array}{*{20}c} {{\varvec{TC}}_{{{12}}} } & {{\varvec{TC}}_{{{14}}} } \\ {{\varvec{TC}}_{{{32}}} } & {{\varvec{TC}}_{34} } \\ \end{array} } \right]_{i} ,$$
(29)

in which the random matrix (TCqr)i is such that

$$\left( {{\varvec{TC}}_{qr} } \right)_{i}^{T} \left( {{\varvec{TC}}_{qr} } \right)_{i} = \left( {{\varvec{AC}}_{qr} } \right)_{i}^{{2}} = \left( {{\varvec{P}}_{qr} } \right)_{i} \left( {{\varvec{\varLambda}}_{qr} } \right)_{i}^{{2}} \left( {{\varvec{P}}_{qr} } \right)_{i}^{ - 1} ,$$
(30)

where the random matrix (ACqr)i is such that

$$\left( {{\varvec{AC}}_{qr} } \right)_{i} { = }\left( {{\varvec{P}}_{qr} } \right)_{i} \left( {{\varvec{\varLambda}}_{qr} } \right)_{i} \left( {{\varvec{P}}_{qr} } \right)_{i}^{ - 1} ,$$
(31)
$$\left( {{\varvec{AC}}_{qr} } \right)_{i} = \left( {{\varvec{L}}_{{{AC,}qr}} } \right)_{i}^{{T}} \left( {{\varvec{G}}_{{{AC,}qr}} } \right)_{i} \left( {{\varvec{L}}_{{{AC,}qr}} } \right)_{i} .$$
(32)

In order to make rotor I have the same serial number as rotor II at the coupling node, and to facilitate the programming of the above formulas, virtual elements are considered, so that the serial numbers of the two rotors at both ends and at the coupling node are aligned. According to Eq. (19) and (29), the nonparametric Riccati whole transfer matrix Si of each element of the dual rotor system can be successively obtained. Thus, S2, S3, …, SN+1 can be obtained, and SN+1 is written as

$${\varvec{S}}_{N + 1} = \left[ {\begin{array}{*{20}c} {S_{11} } & {S_{12} } & {S_{13} } & {S_{14} } \\ {S_{21} } & {S_{22} } & {S_{23} } & {S_{24} } \\ {S_{31} } & {S_{32} } & {S_{33} } & {S_{34} } \\ {S_{41} } & {S_{42} } & {S_{43} } & {S_{44} } \\ \end{array} } \right]_{N + 1} .$$
(33)

Considering that virtual elements are added at the ends of each rotor. Since the length and mass of the virtual elements are equal to 0, the ends of each rotor become free ends. Thus, we have

$$\left( {M_{j} ,Q_{j} } \right)_{N + 1}^{{T}} { = }\left( {M_{j} ,Q_{j} } \right)_{1}^{{T}} = {\mathbf{0}}{\mathbf{.}}$$
(34)

The boundary conditions of the end sections of the dual rotor system are given by Eq. (34). In addition, the state vector (MI, QI, MII, QII)N+1T is such that

$$\left( {M_{{I}} ,Q_{{I}} ,M_{{{II}}} ,Q_{{{II}}} } \right)_{N + 1}^{{T}} { = }{\varvec{S}}_{N + 1} \left( {x_{{I}} ,\theta_{{I}} ,x_{{{II}}} ,\theta_{{{II}}} } \right)_{N + 1}^{{T}} .$$
(35)

With Eq. (34) and (35), we deduce that the synchronous precession equation of uncertain dual rotor system is such that

$$\left| {\begin{array}{*{20}c} {S_{11} } & {S_{12} } & {S_{13} } & {S_{14} } \\ {S_{21} } & {S_{22} } & {S_{23} } & {S_{24} } \\ {S_{31} } & {S_{32} } & {S_{33} } & {S_{34} } \\ {S_{41} } & {S_{42} } & {S_{43} } & {S_{44} } \\ \end{array} } \right|_{N + 1} = 0.$$
(36)

By solving Eq. (36), the synchronous precession angular velocities of the system can be obtained, and then the critical speeds can be obtained by using Eq. (37).

$$n_{{\text{c}}} = \frac{60}{{2{\uppi }}}\omega_{{\text{c}}} ,$$
(37)

in which ωc and nc are the synchronous precession angular velocity and critical speed respectively. Figure 1 is the flow chart of calculating the critical speed of the uncertain dual rotor systems using nonparametric method.

Fig. 1
figure 1

Flow chart of calculating the critical speeds of the uncertain dual rotor systems using nonparametric method

Full size image

3 Numerical examples of critical speeds analysis for the uncertain dual rotor system

In order to illustrate the effectiveness of nonparametric methods in the analysis or prediction of the critical speeds of the uncertain dual rotor systems, the dual rotor model provided in Ref. [31] was taken as the research object, and the effects of model uncertainties on the critical speeds with the parameter uncertainties such as the elastic modulus of the rotating shaft and the bearing stiffness were compared and analyzed.

3.1 Calculation model and the unit division of the dual rotor system

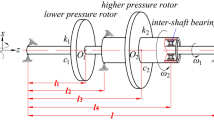
Figure 2 shows the initial calculation model of the dual-rotor system, with intermediate supports at nodes 3–8 and 5–12. In which the Roman numerals I and II are serial numbers of the two rotors, and where the Arabic numerals 1, 2, …, 12 are serial numbers of the nodes of this dual rotor system. See Ref. [31] for detailed data.

Fig. 2
figure 2

Calculation model of the dual rotor system

Full size image

According to the calculation model shown in Fig. 2, the rotor I is inconsistent with the number of nodes. Considering the virtual elements and adjusting the number of each unit, the unit division of this dual rotor system is shown in Fig. 3.

Fig. 3
figure 3

Unit division for the dual rotor system

Full size image

3.2 Effects of model and parameter uncertainties at intermediate supports on critical speeds

As shown in Fig. 3, the dual rotor system only has intermediate supports at the 6th and 14th elements. Thus, the uncertainties will affect the corresponding Riccati whole transfer matrices. In order to analyze the contribution of the two types of uncertainties to the critical speeds of this dual rotor system, it is necessary to consider the uncertainties of stiffness parameters of the intermediate supports at the same uncertainty level as model uncertainties. The previous nonparametric Riccati whole transfer matrix method is used for 40 calculations, and the results are compared with those of the parametric method. Figure 4 shows the envelopes of the first three-order critical speeds calculated by the nonparametric (blue lines) and parametric (red lines) methods for the dispersion parameter δTC, i of the whole transfer matrices of the coupling elements, i.e., the intermediate supporting stiffness elements, from 0.03 to 0.20. Specifically, the results for δTC, i = 0 represents the calculation results of mean dynamic model, that is, the calculation results when the two types of uncertainties are not considered.

Fig. 4
figure 4

The first three-order critical speeds of the dual rotor system with uncertainties: a Fluctuation of nc1 for δTC, i from 0.03 to 0.20; b Fluctuation of nc2 for δTC, i from 0.03 to 0.20; c Fluctuation of nc3 for δTC, i from 0.03 to 0.20

Full size image

The envelop of calculation results in Fig. 4 show that the results of the first-order critical speed nc1 of this uncertain system by nonparametric method completely cover the results of parametric method for δ TC, i from 0.03 to 0.20, which indicates that the uncertainty of the whole transfer matrices of the coupling unit makes the fluctuation degree of nc1 larger than that of the stiffness parameters of the intermediate supports. Moreover, for δTC, i from 0.03 to 0.20, with the increase of δTC, i, this phenomenon is more obvious. Therefore, the fluctuation of nc1 is more affected by model uncertainty than parameter uncertainty.

From Fig. 4, for the second-order critical speed nc2, and for δTC, i = 0.03, the fluctuation rate (relative to the results for δTC, i = 0) of nc2 is 0.26 and 0.25% due to model uncertainty and parameter uncertainty, respectively. The fluctuation rate of nc2 increases obviously when δ TC, i increases from 0.03 to 0.20. Due to model and parameter uncertainties, the fluctuation rate increases to 2.37 and 2.18% respectively for δTC, i = 0.20.

As for the third-order critical speed nc3, the contribution of two types of uncertainties to fluctuation of nc3 is different from that of nc1 and nc2. For δTC, i = 0.03 ~ 0.20, compared with model uncertainty, the effect of parameter uncertainty on the fluctuation of nc3 increases more obviously with the increase of δTC, i. The fluctuation rate of nc3 caused by model uncertainty and parameter uncertainty is 0.28 and 0.27% respectively for δTC, i = 0.03; the fluctuation rate increases to 1.14 and 2.12% respectively for δTC, i = 0.20.

From the above analysis for the results in Fig. 4, the following conclusions can be drawn: at the intermediate supports, the effects of model and parameter uncertainty in the whole transfer matrices on the first three-order critical speeds of the uncertain dual rotor system are different. Compared with parameter uncertainty, model uncertainty has a greater effect on the fluctuation of nc1. However, the effect of parameter uncertainty on nc3 is greater than that of model uncertainty.

In Ref. [24], the fluctuation of critical speeds of Jeffcott rotor system with model uncertainty was also studied by nonparametric method. The results show that the fluctuation rate of the first-order critical speed is different from the second one due to the uncertainties, which is consistent with the results in this section.

3.3 Effects of model and parameter uncertainties in the whole transfer matrices of rotating shaft elements on critical speeds

As is shown in Fig. 3, the dual rotor system consists of 19 elements. The 1st and 19th elements of rotor I and the 1st, 2nd, 3rd, 4th, 5th, 15th, 16th, 17th, 18th, and 19th elements of rotor II are virtual elements, that is, the axis length is 0. Since the two adjacent state vectors on a virtual element are actually transferred in the form of identity matrix, the identity matrices in the block identity matrices of the uncoupled elements can be considered as matrices with neither model uncertainty nor parameter uncertainty. In this section, the model uncertainty of the whole transfer matrices and the parameter uncertainty of elastic modulus E are considered to compare the effects of the two types of uncertainties on the fluctuation of nc1, nc2 and nc3. Figure 5 displays the envelopes of nc1, nc2 and nc3 calculated by the nonparametric (blue lines) and parametric (red lines) methods for δ T, i from 0.03 to 0.20. Similar to δ TC, i, δ T, i is a dispersion parameter of the whole transfer matrices of uncoupled elements. Specifically, the results with δ T, i = 0 represents the calculations without uncertainties.

Fig. 5
figure 5

The first three-order critical speeds of the dual rotor system: a Fluctuation of nc1 for δT, i from 0 to 0.20; b Fluctuation of nc2 for δT, i from 0.03 to 0.20; c Fluctuation of nc3 for δT, i from 0.03 to 0.20

Full size image

Figure 5 shows that for δ T, i = 0.03 ~ 0.20, the fluctuation of nc1, nc2 and nc3 calculated by the nonparametric method is different. The fluctuation band of nc1 gradually increases from [1659.95, 1694.33] rpm to [1522.35, 1781.23] rpm, and the fluctuation rate increases from 1.03 to 7.76%. The fluctuation band of nc2 increases from [3810.65, 3859.25] rpm to [3677.15, 4067.43] rpm, and the fluctuation rate increases from 0.63 to 5.10%. The fluctuation band of nc3 gradually increases from [4933.07, 4979.00] rpm to [4750.30, 5055.40] rpm, and the fluctuation rate increases from 0.46 to 3.08%. However, the calculation results with parameter uncertainty are quite different from those with model uncertainty: the upper envelopes of nc1, nc2 and nc3 coincide with their lower envelopes respectively, which indicates that nc1, nc2 and nc3 have no fluctuation. The main reason is that the stiffness of the two rotating shafts is larger than that of supports, which makes the critical speeds of the system insensitive to the variation of stiffness of the rotating shafts. This conclusion is also consistent with the description in Ref. [33].

In Ref. [20], the vibration characteristics of a double-disc and single-rotor system with uncertainties were studied by using the nonparametric modeling method, and the contribution of two types of uncertainties to the fluctuation of critical speeds of the uncertain rotor system was indirectly analyzed. The results show that the sensitivity of the first-order and second-order critical speeds of the rotor system to the parameter uncertainty of support stiffness and elastic modulus is different from that of model uncertainty with the same uncertainty level. If the stiffness of support is close to that of rotating shaft, the effects of parameter uncertainty (such as the uncertain elastic modulus) on the critical speeds is obvious. If the stiffness of rotating shaft is much greater than support stiffness, the parameter uncertainty of elastic modulus of rotating shaft has little effect on the fluctuation of critical speeds. This conclusion is consistent with that in this section.

3.4 Validation of the nonparametric method

In order to verify the nonparametric method, the critical speeds of this dual rotor system with uncertainties are calculated through Monte Carlo Simulation (MCS) for a comparison. In the uncertain dynamic modeling, the stiffness values of two intermediate supports are taken as uncertain parameters. Figure 6 shows the results obtained by MCS and nonparametric method for δTC, i from 0.03 to 0.20.

Fig. 6
figure 6

The comparison of critical speeds calculated by Monte Carlo Simulation and nonparametric method: a Fluctuation of nc1 for δTC, i from 0.03 to 0.20; b Fluctuation of nc2 for δTC, i from 0.03 to 0.20; c Fluctuation of nc3 for δTC, i from 0.03 to 0.20

Full size image

Figures 6(a, b and c depict the fluctuation of nc1, nc2 and nc3 obtained by MCS and nonparametric method. In Fig. 6(a), the results of nonparametric method completely envelop that of MCS. For δTC, i from 0.03 to 0.20, the fluctuation band of the first-order critical speed nc1 obtained by nonparametric method increases from [1659.86, 1684.88] rpm to [1620.90, 1740.65] rpm with the fluctuation rate increasing from 0.75 to 3.59%, whereas the fluctuation band obtained by MCS only increases from [1668.93, 1669.41] rpm to [1667.78, 1670.27] rpm with the fluctuation rate increasing from 0.01 to 0.07%. That is, compared with parameter uncertainty, model uncertainty has a greater effect on the fluctuation of nc1, which is consistent with the conclusion in Sect. 3.2. In Fig. 6(b), the fluctuation band of the second-order critical speed nc2 obtained by nonparametric method increases from [3824.88, 3844.45] rpm to [3718.78, 3900.12] rpm with the fluctuation rate increasing from 0.26 to 2.37%, while the fluctuation band obtained by MCS increases from [3821.15, 3835.00] rpm to [3751.93, 3883.71] rpm with the fluctuation rate increasing from 0.18% to 1.72% for δ TC, i = 0.03 ~ 0.20. In Fig. 6(c), the fluctuation band of the third-order critical speed nc3 obtained through nonparametric method increases from [4942.72, 4970.22] rpm to [4896.12, 5009.08] rpm with the fluctuation rate increasing from 0.28 to 1.14%, whereas the fluctuation band obtained by MCS increases from [4947.11, 4967.54] rpm to [4812.03, 5021.05] rpm with the fluctuation rate increasing from 0.21 to 2.11% for δTC, i = 0.03 ~ 0.20. In addition, Fig. 6(c) shows that parameter uncertainty plays a major role in the fluctuation of nc3 for δ TC, i = 0.03 ~ 0.20. To conclude, the main results shown in Fig. 6 are in agreement with Fig. 4, which means that it is effective to consider model uncertainty through nonparametric method.

4 Summary and conclusions

We consider a dual rotor system that is affected by two types of uncertainties, i.e., model uncertainty and parameter uncertainty, in the whole transfer matrices of coupling elements or uncoupled elements. By combining the nonparametric method based on the random matrix theory with the Riccati whole transfer matrix method, the whole transfer matrix of coupling and uncoupled elements of the dual rotor system with model uncertainty is obtained.

Numerical examples are employed to verify the proposed method. This validates that the nonparametric dynamic modeling method can be used to calculate the fluctuation band of critical speeds of uncertain dual rotor systems. From the calculation results, the contribution of both model uncertainty and parameter uncertainty can be obtained from the upper and lower envelopes of critical speeds. The main conclusions are as follows.

  1. (1)

    Due to model uncertainty of both coupling elements and uncoupled elements, the fluctuation degree of the first three-order critical speeds of the dual rotor system increases with the gradual increase of δTC, i and δTC, i. In addition, due to the large stiffness of rotating shafts, the uncertainty of the elastic modulus of rotating shafts has little effect on the first three-order critical speeds.

  2. (2)

    The uncertainty of the whole transfer matrices of the coupling unit makes the fluctuation degree of nc1 larger than that of the stiffness parameters of the intermediate supports. Compared with parameter uncertainty, model uncertainty has a greater effect on the fluctuation of nc1. However, the effect of parameter uncertainty on nc3 is greater than that of model uncertainty.

  3. (3)

    The model uncertainty of uncoupled elements has a more obvious impact on the first three-order critical speeds, compared with the uncertainty of elastic modulus of the two rotating shafts.