Research nonlinear vibrations of a dual-rotor system with nonlinear restoring forces

Abstract

A dual-rotor system is a core component of an aero-engine, and it is very important to study the nonlinear vibrational characteristics for the aero-engine’s development. Based on analyzing structural characteristics of aero-engine’s rotors, a novel and more practical dual-rotor dynamic coupling model with nonlinear restoring forces of high-pressure and low-pressure rotors is first proposed. In the linear dynamic coupling model, the coupling critical speed, natural frequencies and vibration responses of the low-pressure rotor are analyzed systematically. In the nonlinear dynamic coupling model, the vibrational characteristics of the dual-rotor system with different nonlinear parameters are simulated numerically based on the nonlinear dynamic theory. The improved shooting method combined the harmonic balance method, and the genetic algorithm is proposed to calculate theoretical solutions of the nonlinear dynamic coupling model. The stability of theoretical solutions is investigated by the Floquet theory. The research results show that the dual-rotor system appears very complicated nonlinear vibrations such as nonlinear multitudinal solutions, double period motions, almost periodic motions and chaotic motions. The transition between nonlinear vibrations occurs suddenly.

1 Introduction

There are many nonlinear excitation sources in rotating machinery, and a lot of complex nonlinear dynamical phenomena occur. In the engineering practice, it is necessary to analyze and explain these complicated nonlinear vibrations in order to avoid the serious dangerousness. Many scholars around the world have made a lot of researches in the field of nonlinear rotor dynamics. Yamamoto [1] and Ishida et al. [2, 3] studied vibration characteristics of a single rotor system with weak nonlinear spring characteristics by theoretical analyses and experiments. Ehrich [4, 5] observed various kinds of nonlinear resonances in aircraft engines and found a subharmonic resonance of order 1/9 and chaotic motions, which greatly enrich the rotor dynamics theory with a strong nonlinearity. The nonlinearities of above studies appeared due to the clearance of the bearings at supporting positions. Sinou [6, 7] emphatically investigated dynamic characteristics of a rotor system with a transverse crack, and axis orbits of harmonic resonances and the subharmonic resonance of order 1/2 were studied by the harmonic balance method. Liu et al. [8] proposed a novel crystal format model of a cracked rotor and researched vibration characteristics under the conditions that cracks were at different positions. In the above researches, the nonlinearities of rotor systems are caused by cracks. Jiang and Ulbrich [9, 10] modified the Jeffcott rotor with a given stator clearance and carried out an analytical study on the stability of full-annular rub solutions under an externally excited. They systematically explored effects of each parameter on the jump phenomenon, almost periodic motions, and so on. Chu and Zhang [11, 12] made a comprehensive exploration about the Jeffcott rotor with the rub-impact and found a lot of complex nonlinear vibrations, including the period doubling bifurcation, the grazing bifurcation, a sudden transition from the periodic motion to chaotic motions, and others. In these studies, the nonlinearities are generated by friction and the collision between the stator and rotor.

The above researches are based on a single rotor system, and the theory of nonlinear dynamics has been relatively mature. However, applications of the multi-rotor system are more extensive in rotating machinery. New methods are often needed in the study of multi-rotor systems. It is difficult to get the unbalance of rotors by directly adding a trial weight of a rotor in the dual-rotor system; Zhang et al. [13] proposed a new synchronization identification method for the unbalance of the dual-rotor system. Similarly, the nonlinear vibrations of multi-rotor systems become more complicated because of the complex coupling relationship between rotors. The nonlinear rotor dynamics theory based on a single rotor system has some limitations to explain nonlinear vibration characteristics of a multi-rotor system.

The aero-engine is a typical multi-rotor system, and the application of the dual-rotor system is most common. At present, many scholars have carried out a lot of researches about nonlinear vibration characteristics of the dual-rotor system. Deng et al. [14, 15] proposed mathematical model to formulate nonlinear displacements, elastic deformations and contact forces of bearings of the dual-rotor system, and systematically analyzed the dynamic characteristics of the dual-rotor system about influences of rotational speeds, clearance of the inter-shaft bearing, the number of rollers and geometry parameters of bearings. Luo et al. [16, 17] established a high-dimensional nonlinear dynamic model of a dual-rotor system by using the finite element software and fixed the interface modal synthesis method. They considered nonlinear forces of a squeeze film damper and the inter-shaft bearing and studied the nonlinear dynamic response characteristics of the counter-rotating dual-rotor system with varied unbalance forces. Jin et al. [18] presented a two-level model order reduction (MOR) method by combining component mode synthesis (CMS) method and proper orthogonal decomposition (POD) technique to rapidly and accurately analyze dynamic behaviors of the complex dual rotor-bearing system. Lu et al. [19] focused on nonlinear response characteristics of a dual-rotor system coupled by the cylindrical roller inter-shaft bearing, and discussed complex nonlinearities affected by the bearing radical clearance, the vertical constant force and the rotating speed ratio. In the above researches, the nonlinearities of the dual-rotor system are caused by the bearings. Hertz elastic contact theory and the bearing dynamics theory were applied to calculate the nonlinear force. When the nonlinear dynamic model of a dual-rotor system was established, the FEM is used or the high-pressure rotor is considered to be a rigid shaft. The FEM model pays more attention to vibrations at the supporting coupling node, which is not conducive to get global solutions of the rotor system. If the high-pressure rotor is rigid, the elastic deformation of the high-pressure rotor is ignored and the vibrational characteristics are obtained by the geometrical principle or the deflection equation. Due to the complexity of the dual-rotor system’s structure, most scholars paid more attention to nonlinear vibrations caused by faults in the rotor system. Sun and Chen [20, 21] investigated the steady-state responses of a rub-impact dual-rotor system based on simplified and complex structures, and found complicated nonlinear phenomena, such as combined harmonic vibrations, hysteresis and resonant peak shifting. Xu and Wang [22] calculated collision and friction forces based on Hertz contact theory and Coulomb model, and introduced a nonlinear spring model and friction coefficients to establish the one-dimensional finite element model of the dual-rotor system. Yang et al. [23] studied the coupling faults of pedestal looseness and rub-impact to obtain the potential effects on the dynamic characteristics of the dual-rotor system. Wang et al. [24] analyzed response characteristics of a dual-rotor system with unbalance-misalignment coupling faults, and discussed effects of the misalignment angle and parallel misalignment. Gao et al. [25] investigated nonlinear dynamic characteristics of a dual-rotor system affected by the local defect on the surface of the outer race or the inner race of the inter-shaft bearing, and found that there are four abnormal resonances on the amplitude frequency curves due to effects of the local defect.

In the researches of the dual-rotor system mentioned above, the nonlinear spring characteristics of rotors and the influence of rotor’s restoring forces are neglected. Based on the research of Yamamoto and Ishida [26], the spring characteristics of a rotor are inconsistent with Hooke’s law when the supporting conditions of both ends of a shaft are different. The study of nonlinear spring characteristics of rotors is helpful to further explain the complex nonlinear vibration characteristics of a dual-rotor system.

In this paper, referring to the structure of an aero-engine with a dual-rotor system and considering nonlinear spring characteristics of high-pressure and low-pressure rotors, the dynamic coupling model of the dual-rotor system is proposed and the dynamic equations are established. In the linear dynamic coupling model, the response curves of the dual-rotor system are obtained in the vicinities of critical speeds, and natural frequencies and the coupling critical speed are analyzed systematically. In the nonlinear dynamic strongly coupling model, vibrational characteristics of the dual-rotor system with the nonlinear coefficients β⁽⁰⁾ and ε⁽¹⁾ [27] are discussed emphatically. Numerical simulations are performed on the dual-rotor system by the Runge–Kutta method. Combined the harmonic balance method and the genetic algorithm, the improved shooting method is proposed to obtain theoretical solutions of the nonlinear dynamic coupling model. The stabilities of theoretical solutions are investigated allsidedly based on the Floquet theory. The theoretical solutions consist with the numerical simulation well. The nonlinear vibrations, such as double period motions, almost periodic motions and chaotic motions, are analyzed systematically and explained by the time history, FFT spectra and Poincare map at some rotational speeds. The bifurcation map and the largest Lyapunov exponent are applied to further explain chaotic motions. The results of this study put forward new research directions to analyze nonlinear vibration characteristics of the dual-rotor system.

2 Dual-rotor physical model and establishment of dynamics equations

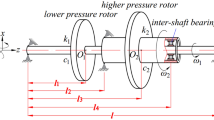
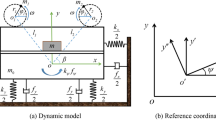
According to the structure characteristics of an aero-engine with a dual rotor, the physical model of the dual-rotor system with two disks and four supporting points is established as shown in Fig. 1a. The physical model is composed of the low-pressure rotor and the high-pressure rotor. The low-pressure rotor is supported by Fulcra A and D, and the high-pressure rotor is supported by Fulcrum B and inter-shaft bearing C shown in Fig. 1a.

Fig. 1

Dual-rotor system: a schematic diagram of a dual-rotor system, b rotor model and coordinate system of the low-pressure rotor, c rotor model and coordinate system of the high-pressure rotor, d dynamic clearance of the inter-shaft bearing and nonlinear restoring forces of the high-pressure rotor with dynamic and asymmetric characteristics

Based on the theory of rotor dynamics, the mathematical model is obtained by using the lumped mass system. The low-pressure rotor is composed of a massless elastic shaft supported at both ends and a rigid disk which is not mounted at the center of the shaft as shown in Fig. 1b. It is simplified to a 4DOF model where deflection motions and inclination motions couple with each other. The high-pressure rotor is also composed of a massless elastic shaft supported at both ends and a rigid disk which is mounted at the center of the shaft as shown in Fig. 1c. It is assumed that vibrations of the low-pressure rotor are small enough to ignore the inclinations of the disk of the high-pressure rotor. The high-pressure rotor is simplified to a 2DOF model to include deflection motions.

The coupling relationship of low-pressure and high-pressure rotors is the key of the model of the dual-rotor system. In the physical model, the high-pressure rotor is supported by the inter-shaft bearing on the low-pressure rotor. The support of the low-pressure rotor to the high-pressure rotor provides the restoring force of the high-pressure rotor. And the restoring force of the high-pressure rotor acts on the low-pressure rotor in the form of the reaction force of the supporting force of the low-pressure rotor. In addition, vibrations of the low-pressure rotor cause continuously small displacements and inclinations of the inter-shaft bearing in x–y plane. It means that the supporting condition of the high-pressure rotor is dynamic. According to studies by Yamamoto and Ishida [1], the clearance of a single-row deep-groove bearing can cause nonlinear restoring forces for the rotor. The clearance of the bearing is always presented by the angular clearance shown in Fig. 1d. Under the dynamic supporting condition, the angular clearance of the inter-shaft bearing changes with vibrational amplitudes of low-pressure rotor, and the nonlinear restoring forces of the high-pressure rotor are dynamic and asymmetric in x and y directions shown in Fig. 1d. The red and black lines in Fig. 1d, respectively, represent restoring forces in two limit cases, and restoring forces of the high-pressure rotor change between the two cases.

It is assumed that the restoring forces of the high-pressure rotor are equal to the supporting forces of the low-pressure rotor to the high-pressure rotor. Therefore, the coupling relationship of low-pressure and high-pressure rotors in this model is described by nonlinear restoring forces of the high-pressure rotor.

In order to facilitate the mathematical derivations, nonlinear restoring forces of the high-pressure rotor are considered to be linear, and the gravity of high-pressure and low-pressure rotors is neglected. The high-pressure rotor is a Jeffcott rotor, and it is easy to obtain dynamic equations. So, the following derivations are focused on the low-pressure rotor.

Considering deflection motions and inclination motions of the low-pressure rotor, the elastic potential energy can be expressed as follows:

$$\begin{aligned} V_{L1} &= \frac{ 1}{ 2}\left( {\hat{\alpha }r_{1}^{2} + 2\hat{\gamma }r_{1} \theta + \hat{\delta }\theta^{2} } \right) \\ & = \frac{ 1}{ 2}\left( {\hat{\alpha }\left( {x_{1}^{2} + y_{1}^{2} } \right) + 2\hat{\gamma }\left( {x_{1} \theta_{x} + y_{1} \theta_{y} } \right) + \hat{\delta }\left( {\theta_{x}^{2} + \theta_{y}^{2} } \right)} \right) \end{aligned}$$

(1)

In addition, considering the restoring force of the high-pressure rotor acting on the low-pressure rotor, the following potential energy can be obtained:

$$V_{L2} = Fr_{1} = \hat{k}x_{2} x_{1} + \hat{k}y_{2} y_{1}$$

(2)

The potential energy of the low-pressure rotor is got as follows:

$$V_{L} = V_{L1} + V_{L2}$$

(3)

The kinetic energy of the low-pressure rotor is composed of deflection motions and inclination motions. In Fig. 1b, the center of gravity of the low-pressure rotor is Point G(x_G1, y_G1, 0), and M(x₁, y₁, 0) is the geometrical center. The kinetic energy for the deflection motions is expressed as follows:

$$\begin{aligned} T_{L1} & { = }\frac{ 1}{ 2}\hat{m}_{1} \left( {\dot{x}_{G 1}^{2} + \dot{y}_{G 1}^{2} } \right) \\ & = \frac{ 1}{ 2}\hat{m}_{1} \left( {\dot{x}_{ 1}^{ 2} + \dot{y}_{ 1}^{ 2} + \left( {\hat{e}_{ 1} \hat{\omega }_{ 1} } \right)^{2} - 2\hat{e}_{ 1} \hat{\omega }_{ 1} \dot{x}_{ 1} \sin \left( {\hat{\omega }_{ 1} \hat{t}} \right) + 2\hat{e}_{ 1} \hat{\omega }_{ 1} \dot{y}_{ 1} \cos \left( {\hat{\omega }_{ 1} \hat{t}} \right)} \right) \\ \end{aligned}$$

(4)

The principal moments of inertia around principal axes X₁, Y₁ and Z₁ of the disk of the low-pressure rotor are I_P, I and I. The components of angular speeds are ω_X1, ω_Y1 and ω_Z1, respectively. The kinetic energy for inclination motions is expressed as follows, where the transformation relationships of angles are referred to Ref. [21]:

$$\begin{aligned} T_{L2} & = \frac{ 1}{ 2}\left( {\hat{I}_{P} \hat{\omega }_{z1}^{2} + \hat{I}\hat{\omega }_{x1}^{2} + \hat{I}\hat{\omega }_{y1}^{2} } \right) \\ & = \frac{ 1}{ 2}\left( {\hat{I}_{P} \hat{\omega }_{1} \left( {\hat{\omega }_{1} + \left( {\dot{\theta }_{1x} \theta_{1y} - \theta_{1x} \dot{\theta }_{1y} } \right)} \right) + I\left( {\dot{\theta }_{1x}^{2} + \dot{\theta }_{1y}^{2} } \right)} \right) \\ & = \frac{ 1}{ 2}\hat{\omega }_{1}^{2} \left( {\hat{I}_{P} \left( {1 - \hat{\tau }^{2} } \right) + \hat{I}\hat{\tau }^{2} } \right) + \frac{ 1}{ 2}\hat{I}_{P} \hat{\omega }_{1} \left( {\dot{\theta }_{x} \theta_{y} - \theta_{x} \dot{\theta }_{y} } \right) + \frac{ 1}{ 2}\hat{I}\left( {\dot{\theta }_{x}^{2} + \dot{\theta }_{y}^{2} } \right) \\ &\quad + \frac{ 1}{ 2}\left( {2\hat{I} - \hat{I}_{P} } \right)\tau \hat{\omega }_{1} \left( {\dot{\theta }_{x} \sin \left( {\hat{\omega }_{ 1} \hat{t} + \beta_{\tau } } \right) - \dot{\theta }_{y} \cos \left( {\hat{\omega }_{ 1} \hat{t} + \beta_{\tau } } \right)} \right) \\ & \quad + \frac{ 1}{ 2}\hat{I}_{P} \hat{\tau }\hat{\omega }_{1}^{2} \left( {\theta_{y} \sin \left( {\hat{\omega }_{ 1} \hat{t} + \beta_{\tau } } \right) + \theta_{x} \cos \left( {\hat{\omega }_{ 1} \hat{t} + \beta_{\tau } } \right)} \right) \\ \end{aligned}$$

(5)

Then, the kinetic energy of the low-pressure rotor is obtained as follows:

$$T_{L} = T_{L1} + T_{L2}$$

(6)

Based on Lagrange’s equation shown as follows, the dynamic equations of the low-pressure rotor can be obtained:

$$\frac{d}{dt}\left( {\frac{{\partial T_{L} }}{{\partial \dot{q}_{L} }}} \right) - \frac{{\partial T_{L} }}{{\partial q_{L} }} + \frac{{\partial V_{L} }}{{\partial q_{L} }} = 0$$

(7)

where q_L is the general coordinates.

Considering the damping, the dynamic equations of the low-pressure rotor can be expressed as follows:

$$\left\{ \begin{aligned} &\hat{m}_{1} \ddot{x}_{1} + \hat{c}_{11} \dot{x}_{1} + \hat{c}_{12} \dot{\theta }_{x} + \hat{\alpha }x_{1} + \hat{\gamma }\theta_{x} + \hat{k}x_{2} = \hat{m}_{1} \hat{e}_{1} \hat{\omega }_{1}^{2} \cos \hat{\omega }_{1} \hat{t} \hfill \\ & \hat{m}_{1} \ddot{y}_{1} + \hat{c}_{11} \dot{y}_{1} + \hat{c}_{12} \dot{\theta }_{y} + \hat{\alpha }y_{1} + \hat{\gamma }\theta_{y} + \hat{k}y_{2} = \hat{m}_{1} \hat{e}_{1} \hat{\omega }_{1}^{2} \sin \hat{\omega }_{1} \hat{t} \hfill \\& \hat{I}\ddot{\theta }_{x} + \hat{I}_{P} \hat{\omega }_{1} \dot{\theta }_{y} + \hat{c}_{21} \dot{x}_{1} + \hat{c}_{22} \dot{\theta }_{x} + \hat{\gamma }x_{1} + \hat{\delta }\theta_{x} = \left( {\hat{I}_{P} - \hat{I}} \right)\hat{\tau }\hat{\omega }_{1}^{2} \cos \left( {\hat{\omega }_{1} \hat{t} + \beta_{\tau } } \right) \hfill \\& \hat{I}\ddot{\theta }_{y} - \hat{I}_{P} \hat{\omega }_{1} \dot{\theta }_{x} + \hat{c}_{21} \dot{y}_{1} + \hat{c}_{22} \dot{\theta }_{y} + \hat{\gamma }y_{1} + \hat{\delta }\theta_{y} = \left( {\hat{I}_{P} - \hat{I}} \right)\hat{\tau }\hat{\omega }_{1}^{2} \sin \left( {\hat{\omega }_{1} \hat{t} + \beta_{\tau } } \right) \end{aligned} \right.$$

(8)

where $\hat{k}x_{2}$ and $\hat{k}y_{2}$ represent the reaction forces of the supporting force of the low-pressure rotor.

The dynamic equations of the high-pressure rotor can be expressed as follows:

$$\left\{ \begin{aligned} \hat{m}_{2} \ddot{x}_{2} + \hat{c}\dot{x}_{2} + \hat{k}x_{2} = \hat{m}_{2} \hat{e}_{2} \hat{\omega }_{2}^{2} \cos \hat{\omega }_{2} \hat{t} \hfill \\ \hat{m}_{2} \ddot{y}_{2} + \hat{c}\dot{y}_{2} + \hat{k}y_{2} = \hat{m}_{2} \hat{e}_{2} \hat{\omega }_{2}^{2} \sin \hat{\omega }_{2} \hat{t} \hfill \\ \end{aligned} \right.$$

(9)

where $\hat{k}x_{2}$ and $\hat{k}y_{2}$ represent the restoring forces of the high-pressure rotor, and they also represent supporting forces of the low-pressure rotor to the high-pressure rotor.

Introducing the parameters $\xi { = }\hat{m}_{2} g /\hat{k}$ and $\omega_{n}^{2} { = }\hat{k} /\hat{m}_{2}$, we can get the following dimensionless equations of motion:

$$\left\{ \begin{aligned}& \ddot{x}_{1} + c_{11} \dot{x}_{1} + c_{12} \dot{\theta }_{x} + \alpha x_{1} + \gamma_{1} \theta_{x} + \Delta x_{2} = e_{1} \omega_{1}^{2} \cos \omega_{1} t \hfill \\ &\ddot{y}_{1} + c_{11} \dot{y}_{1} + c_{12} \dot{\theta }_{y} + \alpha y_{1} + \gamma_{1} \theta_{y} + \Delta y_{2} = e_{1} \omega_{1}^{2} \sin \omega_{1} t \hfill \\ & \ddot{\theta }_{x} + I_{P} \omega_{1} \dot{\theta }_{y} + c_{21} \dot{x}_{1} + c_{22} \dot{\theta }_{x} + \gamma_{2} x_{1} + \delta \theta_{x} = \left( {I_{P} - 1} \right)\tau \omega_{1}^{2} \cos \left( {\omega_{1} t + \beta_{\tau } } \right) \hfill \\& \ddot{\theta }_{y} - I_{P} \omega_{1} \dot{\theta }_{x} + c_{21} \dot{y}_{1} + c_{22} \dot{\theta }_{y} + \gamma_{2} y_{1} + \delta \theta_{y} = \left( {I_{P} - 1} \right)\tau \omega_{1}^{2} \sin \left( {\omega_{1} t + \beta_{\tau } } \right) \hfill \\ \end{aligned} \right.$$

(10)

$$\left\{ \begin{aligned} \ddot{x}_{2} + c\dot{x}_{2} + x_{2} = e_{2} \omega_{2}^{2} \cos \omega_{2} t \hfill \\ \ddot{y}_{2} + c\dot{y}_{2} + y_{2} = e_{2} \omega_{2}^{2} \sin \omega_{2} t \hfill \\ \end{aligned} \right.$$

(11)

where $\alpha = \hat{\alpha } /\hat{m}_{1} \omega_{n}^{2}$, $\gamma_{1} { = }\hat{\gamma } /\hat{m}_{1} \omega_{n}^{2} \xi$, $c_{11} { = }\hat{c}_{11} /\hat{m}_{1} \omega_{n}$, $c_{12} { = }\hat{c}_{12} /\hat{m}_{1} \omega_{n} \xi$, $e_{1} { = }\hat{e}_{1} /\xi$, $I_{P} { = }\hat{I}_{P} /\hat{I}$, $c_{21} { = }\hat{c}_{21} \xi /\hat{I}\omega_{n}$, $c_{22} { = }\hat{c}_{22} /\hat{I}\omega_{n}$, $\gamma_{2} { = }\hat{\gamma }\xi /\hat{I}\omega_{n}^{2}$, $\delta { = }\hat{\delta } /\hat{I}\omega_{n}^{2}$, $c{ = }\hat{c} /\hat{m}_{2} \omega_{n}$, $e_{2} { = }\hat{e}_{2} /\xi$ and $\Delta { = }\hat{m}_{2} /\hat{m}_{1}$.

For convenience to deal with nonlinear spring characteristics in theoretical analyses, the nonlinear spring characteristics expressed by the power series of the shaft deflections x and y in Ref. [28] are introduced. The nonlinear terms of restoring forces of the 2DOF rotor are described as follows, where the N_X and N_Y express nonlinear terms in x and y directions, respectively:

$$\begin{aligned} N_{X} = 3\varepsilon_{30} x_{2}^{2} + 2\varepsilon_{21} x_{2} y_{2} + \varepsilon_{12} y_{2}^{2} + 4\beta_{40} x_{2}^{3} + 3\beta_{31} x_{2}^{2} y_{2} + 2\beta_{22} x_{2} y_{2}^{2} + \beta_{13} y_{2}^{3}\end{aligned}$$

(12)

$$\begin{aligned} N_{Y} = 3\varepsilon_{03} y_{2}^{2} + 2\varepsilon_{12} x_{2} y_{2} + \varepsilon_{21} x_{2}^{2} + 4\beta_{04} y_{2}^{3} + 3\beta_{13} x_{2} y_{2}^{2} + 2\beta_{22} x_{2}^{2} y_{2} + \beta_{31} x_{2}^{3}\end{aligned}$$

(13)

where $\varepsilon_{30} = \varepsilon_{c}^{\left( 1 \right)} + \varepsilon_{c}^{\left( 3 \right)}$, $\varepsilon_{21} = \varepsilon_{s}^{\left( 1 \right)} + 3\varepsilon_{s}^{\left( 3 \right)}$, $\varepsilon_{12} = \varepsilon_{c}^{\left( 1 \right)} - 3\varepsilon_{c}^{\left( 3 \right)}$, $\varepsilon_{03} = \varepsilon_{s}^{\left( 1 \right)} - \varepsilon_{s}^{\left( 3 \right)}$, $\beta_{40} = \beta^{\left( 0 \right)} + \beta_{c}^{\left( 2 \right)} + \beta_{c}^{\left( 4 \right)}$, $\beta_{04} = \beta^{\left( 0 \right)} - \beta_{c}^{\left( 2 \right)} + \beta_{c}^{\left( 4 \right)}$, $\beta_{31} = 2\beta_{s}^{\left( 2 \right)} + 4\beta_{s}^{\left( 4 \right)}$ and $\beta_{22} = 2\beta^{\left( 0 \right)} - 6\beta_{c}^{\left( 4 \right)}$. Nonlinear coefficients β⁽ⁱ⁾ (i = 0, 2, 4) and ε^(j) (j = 1, 3) refer to Ref. [28].

As mentioned above, nonlinear restoring forces of the high-pressure rotor change with the vibrational amplitudes of the low-pressure rotor. In fact, if we express the nonlinear restoring forces by the power series, the coefficients of nonlinear restoring forces change with the vibrational amplitudes of low-pressure rotor. To easily treat dynamic nonlinear restoring forces, inclinations of the inter-shaft bearing are ignored and the deflections P_L of the low-pressure rotor are introduced. In order to describe the nonlinear coupling relationship between low-pressure and high-pressure rotors easily, the nonlinear coupling coefficient μ is also introduced. The following nonlinear terms of the dual-rotor system can be described.

$$N_{x} { = }\mu P_{L} N_{X} { = }\mu \sqrt {x_{1}^{2} + y_{1}^{2} } N_{X}$$

(14)

$$N_{y} { = }\mu P_{L} N_{Y} { = }\mu \sqrt {x_{1}^{2} + y_{1}^{2} } N_{Y}$$

(15)

Combining Eqs. (10), (11), (14) and (15), we get dimensionless nonlinear coupling dynamic equations of the dual-rotor system as follows:

$$\left\{ \begin{aligned}& \ddot{x}_{1} + c_{11} \dot{x}_{1} + c_{12} \dot{\theta }_{x} + \alpha x_{1} + \gamma_{1} \theta_{x} + \Delta x_{2} + \Delta N_{x} = e_{1} \omega_{1}^{2} \cos \omega_{1} t \hfill \\ &\ddot{y}_{1} + c_{11} \dot{y}_{1} + c_{12} \dot{\theta }_{y} + \alpha y_{1} + \gamma_{1} \theta_{y} + \Delta y_{2} + \Delta N_{y} = e_{1} \omega_{1}^{2} \sin \omega_{1} t \hfill \\& \ddot{\theta }_{x} + I_{P} \omega_{1} \dot{\theta }_{y} + c_{21} \dot{x}_{1} + c_{22} \dot{\theta }_{x} + \gamma_{2} x_{1} + \delta \theta_{x} = \left( {I_{P} - 1} \right)\tau \omega_{1}^{2} \cos \left( {\omega_{1} t + \beta_{\tau } } \right) \hfill \\& \ddot{\theta }_{y} - I_{P} \omega_{1} \dot{\theta }_{x} + c_{21} \dot{y}_{1} + c_{22} \dot{\theta }_{y} + \gamma_{2} y_{1} + \delta \theta_{y} = \left( {I_{P} - 1} \right)\tau \omega_{1}^{2} \sin \left( {\omega_{1} t + \beta_{\tau } } \right) \hfill \\ \end{aligned} \right.$$

(16)

$$\left\{ \begin{aligned} \ddot{x}_{2} + c\dot{x}_{2} + x_{2} + N_{x} = e_{2} \omega_{2}^{2} \cos \omega_{2} t \hfill \\ \ddot{y}_{2} + c\dot{y}_{2} + y_{2} + N_{y} = e_{2} \omega_{2}^{2} \sin \omega_{2} t \hfill \\ \end{aligned} \right.$$

(17)

when μ = 0, Eqs. (16) and (17) are linear coupling dynamic equations of the dual-rotor system.

3 Analysis of the dual-rotor system with linear dynamic coupling

The counter-rotating dual-rotor system [16] is used, and the rotational speed ratio of the low-pressure rotor and the high-pressure rotor is − 1(ω = ω₁ = -ω₂) in numerical simulations. The dimensionless coefficients in the model are evaluated as shown in Table 1.

Table 1 Dimensionless coefficients in the model

3.1 Numerical simulation and analysis

Based on the dual-rotor model with the linear dynamic coupling, the Runge–Kutta method is applied to finish the numerical simulation. The resonance curves of the dual-rotor system are obtained and shown in Fig. 2. Abscissa shows rotational speed ω and ordinate shows amplitudes of rotors’ vibrations. The lines with red dots indicate the amplitude range, and both ends of the line are the maximum and the minimum values of amplitudes. The red circles indicate the constant amplitude of rotor’s vibrations.

Fig. 2

Resonance curves of the dual rotor with linear coupling: a (case of I_P< 1) and b (case of I_P> 1) for resonance curves of the low-pressure rotor, c resonance curve of the high-pressure rotor, and d resonance curve of the independent 4DOF rotor with I_P< 1

In the linear dynamic coupling model (μ = 0), the high-pressure rotor is independent of the low-pressure rotor and is equivalent to a Jeffcott rotor. The resonance curve has a peak at the major critical speed ω_H, as shown in Fig. 2c. According to Ref. [27], the major critical speed of the 4DOF rotor model is unique when I_P> 1 and there are two major critical speeds when I_P< 1. The resonance curve of the independent 4DOF rotor is shown in Fig. 2d, and the resonance curves of the low-pressure rotor are shown in Fig. 2a, b. Compared with the independent 4DOF rotor, the resonance curves of the low-pressure rotor have three peaks when I_P< 1 and there are two peaks when I_P> 1. The resonance curves of the low-pressure rotor always have a large peak at the major critical speed ω_H, and the position of the peak is same as the position of the peak shown in Fig. 2c. The other peaks occur at the major critical speeds ω_L1 and ω_L2. In addition, the amplitude P of the independent 4DOF rotor is constant, but the amplitude P_L of the low-pressure rotor changes within a certain range. The range of amplitude P_L is largest at the major critical speed ω_L1.

Figure 3 shows resonance curves of the low-pressure rotor deflections in x and y directions, respectively. When ω < ω_H, P_Lx< P_Ly. When ω = ω_H, P_Lx= P_Ly. When ω > ω_H, P_Lx> P_Ly. The difference between P_Lx and P_Ly is the largest when ω = ω_L1.

Fig. 3

Resonance curves of the low-pressure rotor in x and y directions

Combined with the above simulations and analyses, the linear dynamic coupling between low-pressure and high-pressure rotors leads to the difference between amplitudes of the low-pressure rotor in x and y directions. The amplitude P_L changes within a certain range.

3.2 Mathematical analysis

In order to explain the vibration response of the low-pressure rotor with the linear dynamic coupling, the low-pressure rotor is simplified to the 2DOF rotor to include deflection motions, and the following dynamic equations of high-pressure and low-pressure rotors are obtained without considering damping terms.

$$\left\{ \begin{aligned} \ddot{x}_{1} + \alpha x_{1} + \Delta x_{2} = e_{1} \omega_{1}^{2} \cos \omega_{1} t \hfill \\ \ddot{y}_{1} + \alpha y_{1} + \Delta y_{2} = e_{1} \omega_{1}^{2} \sin \omega_{1} t \hfill \\ \end{aligned} \right.$$

(18)

$$\left\{ \begin{aligned} \ddot{x}_{2} + x_{2} = e_{2} \omega_{2}^{2} \cos \omega_{2} t \hfill \\ \ddot{y}_{2} + y_{2} = e_{2} \omega_{2}^{2} \sin \omega_{2} t \hfill \\ \end{aligned} \right.$$

(19)

The following solutions of the dual rotor are assumed:

$$\left\{ \begin{aligned} x_{1} = P_{Lx} \cos \omega_{ 1} t,\;\;x_{2} = P_{H} \cos \omega_{2} t\; \hfill \\ y_{1} = P_{Ly} \sin \omega_{1} t,\;\;y_{2} = P_{H} \sin \omega_{2} t \hfill \\ \end{aligned} \right.$$

(20)

Substituting Eq. (20) in Eqs. (18) and (19), Eqs. (21) and (22) are obtained as follows:

$$\left\{ \begin{aligned} \left( {\left( {\alpha - \omega_{1}^{2} } \right)P_{Lx} - e_{1} \omega_{1}^{2} } \right)\cos \omega_{1} t = - \Delta P_{H} \cos \omega_{2} t \hfill \\ \left( {\left( {\alpha - \omega_{1}^{2} } \right)P_{Ly} - e_{1} \omega_{1}^{2} } \right)\sin \omega_{1} t = - \Delta P_{H} \sin \omega_{2} t \hfill \\ \end{aligned} \right.$$

(21)

$$\left( {P_{H} - P_{H} \omega_{2}^{2} - e_{2} \omega_{2}^{2} } \right)\cos \omega_{2} t = 0$$

(22)

According to Eq. (21), the amplitudes P_Lx and P_Ly are affected by the rotational speed and Δ. Because the rotational speed ratio is − 1, Eqs. (23) and (24) are obtained as follows:

$$\left\{ \begin{aligned} P_{Lx} = \frac{{e_{1} \omega_{1}^{2} - \Delta P_{H} }}{{\alpha - \omega_{1}^{2} }} \hfill \\ P_{Ly} = \frac{{e_{1} \omega_{1}^{2} + \Delta P_{H} }}{{\alpha - \omega_{1}^{2} }} \hfill \\ \end{aligned} \right.$$

(23)

$$P_{H} = \frac{{e_{2} \omega_{2}^{2} }}{{1 - \omega_{2}^{2} }} = \frac{{e_{1} \omega_{1}^{2} }}{{1 - \omega_{1}^{2} }}$$

(24)

The ratio of the P_Lx and P_Ly is shown as follows:

$$\frac{{P_{Lx} }}{{P_{Ly} }} = \left| {\frac{{e_{1} \omega_{1}^{2} - \Delta P_{H} }}{{e_{1} \omega_{1}^{2} + \Delta P_{H} }}} \right| = \left| {\frac{{1 - \Delta - \omega_{1}^{2} }}{{1 + \Delta - \omega_{1}^{2} }}} \right|$$

(25)

When Δ = 1, $\frac{{P_{Lx} }}{{P_{Ly} }} = \left| {\frac{{\omega_{1}^{2} }}{{\omega_{1}^{2} - 2}}} \right|$, and the relationship of the P_Lx and P_Ly holds the inequality shown as follows:

$$\left\{ \begin{aligned} P_{Lx} < P_{Ly} \;\;\;\left( {0 < \omega_{1} < 1} \right) \hfill \\ P_{Lx} = P_{Ly} \;\;\;\left( {\omega_{1} = 1} \right) \hfill \\ P_{Lx} > P_{Ly} \;\;\;\left( {\omega_{1} > 1} \right) \hfill \\ \end{aligned} \right.$$

(26)

The limit expressions (27) and (28) can be obtained. According to the limit expressions, P_Lx and P_Ly approach the same when the rotational speed approaches the low rotational speed or the high rotational speed. When ω = $\sqrt 2$, P_Lx≫ P_Ly. In the numerical simulation, ω_H= 1 and ω_L1 = $\sqrt 2$. The numerical simulation results are consistent with the above mathematical analysis results.

$$\mathop {\lim }\limits_{{\omega_{1} \to \infty }} \frac{{P_{Lx} }}{{P_{Ly} }} = \mathop {\lim }\limits_{{\omega_{1} \to \infty }} \left| {\frac{{\omega_{1}^{2} }}{{\omega_{1}^{2} - 2}}} \right| = \mathop {\lim }\limits_{{\omega_{1} \to 0}} \frac{{P_{Lx} }}{{P_{Ly} }} = \mathop {\lim }\limits_{{\omega_{1} \to 0}} \left| {\frac{{\omega_{1}^{2} }}{{\omega_{1}^{2} - 2}}} \right| = 1$$

(27)

$$\mathop {\lim }\limits_{{\omega_{1} \to \sqrt 2 }} \frac{{P_{Lx} }}{{P_{Ly} }} = \mathop {\lim }\limits_{{\omega_{1} \to \sqrt 2 }} \left| {\frac{{\omega_{1}^{2} }}{{\omega_{1}^{2} - 2}}} \right| = \infty$$

(28)

3.3 Analysis of natural frequency

Free vibrations in the dual-rotor system with no external force and no damping are governed by the following equations, which are given by putting e₁ = e₂ = 0, τ = 0, c₁₁ = c₁₂ = c₂₁ = c₂₂ = 0 into Eqs. (16) and (17).

$$\left\{ \begin{aligned}& \ddot{x}_{1} + \alpha x_{1} + \gamma_{1} \theta_{x} + \Delta x_{2} = 0 \hfill \\&\ddot{y}_{1} + \alpha y_{1} + \gamma_{1} \theta_{y} + \Delta y_{2} = 0 \hfill \\ & \ddot{\theta }_{x} + I_{P} \omega_{1} \dot{\theta }_{y} + \gamma_{2} x_{1} + \delta \theta_{x} = 0 \hfill \\ & \ddot{\theta }_{y} - I_{P} \omega_{1} \dot{\theta }_{x} + \gamma_{2} y_{1} + \delta \theta_{y} = 0 \hfill \\ \end{aligned} \right.$$

(29)

$$\left\{ \begin{aligned} \ddot{x}_{2} + x_{2} = 0\hfill \\ \ddot{y}_{2} + y_{2} = 0\hfill \\ \end{aligned} \right.$$

(30)

Equation (30) shows that the natural frequency of the high-pressure rotor is 1. So, the following illustration is focused on the analyses of natural frequencies of the low-pressure rotor.

Four variables x₁, y₁, θ_x and θ_y are coupled with each other in Eq. (29). In addition, displacements x₁ and y₁ on the low-pressure rotor are affected by displacements x₂ and y₂ on the high-pressure rotor. Based on component analyses of vibrations in the vicinity of the major critical speed in the numerical simulation, the following solutions of free oscillations are assumed.

$$\left\{ \begin{aligned} x_{1} = A\cos \left( {p_{1} t + \beta_{1} } \right),\;\;\theta_{x} = C\cos \left( {p_{1} t + \beta_{3} } \right),\;\;x_{2} = D\cos \left( {p_{ 1} t + \beta_{4} } \right) \hfill \\ y_{1} = B\cos \left( {p_{1} t + \beta_{2} } \right),\;\;\theta_{y} = C\sin \left( {p_{1} t + \beta_{3} } \right),\;\;y_{2} = D\sin \left( {p_{ 1} t + \beta_{4} } \right) \hfill \\ \end{aligned} \right.$$

(31)

Substituting Eq. (31) in Eq. (29) and comparing the coefficients of terms on the right- and left-hand sides, Eqs. (32) and (33) can be obtained as follows:

$$\left\{ \begin{aligned} \left( {\alpha - p_{1}^{2} } \right)\cos \left( {p_{1} t + \beta_{1} } \right) + \gamma_{ 1} \frac{C}{A}\cos \left( {p_{1} t + \beta_{3} } \right) + \Delta \frac{D}{A}\cos \left( {p_{ 1} t + \beta_{4} } \right) = 0 \hfill \\ \left( {\alpha - p_{1}^{2} } \right)\cos \left( {p_{1} t + \beta_{2} } \right) + \gamma_{ 1} \frac{C}{B}\sin \left( {p_{1} t + \beta_{3} } \right) + \Delta \frac{D}{B}\sin \left( {p_{ 1} t + \beta_{4} } \right) = 0 \hfill \\ \end{aligned} \right.$$

(32)

$$\left\{ \begin{aligned} \gamma_{ 2} \cos \left( {p_{1} t + \beta_{1} } \right) + \left( {\delta + I_{P} \omega_{1} p_{1} - p_{1}^{2} } \right)\frac{C}{A}\cos \left( {p_{1} t + \beta_{3} } \right) = 0 \hfill \\ \gamma_{ 2} \cos \left( {p_{1} t + \beta_{2} } \right) + \left( {\delta + I_{P} \omega_{1} p_{1} - p_{1}^{2} } \right)\frac{C}{B}\sin \left( {p_{1} t + \beta_{3} } \right) = 0 \hfill \\ \end{aligned} \right.$$

(33)

Equations (32) and (33) are sorted to get Eqs. (34) and (35).

$$\left\{ \begin{aligned} \cos \left( {p_{1} t + \beta_{1} } \right) = \frac{{ - f_{51} }}{{f_{4} }}\cos \left( {p_{1} t + \beta_{3} } \right) \hfill \\ \cos \left( {p_{1} t + \beta_{2} } \right) = \frac{{ - f_{52} }}{{f_{4} }}\sin \left( {p_{1} t + \beta_{3} } \right) \hfill \\ \end{aligned} \right.$$

(34)

$$\left\{ \begin{aligned} \cos \left( {p_{ 1} t + \beta_{4} } \right) = - \frac{{\frac{{ - f_{1} f_{51} }}{{f_{4} }} + f_{21} }}{{f_{31} }}\cos \left( {p_{1} t + \beta_{3} } \right) \hfill \\ \sin \left( {p_{ 1} t + \beta_{4} } \right) = - \frac{{\frac{{ - f_{1} f_{52} }}{{f_{4} }} + f_{22} }}{{f_{32} }}\sin \left( {p_{1} t + \beta_{3} } \right) \hfill \\ \end{aligned} \right.$$

(35)

where $f_{1} = \alpha - p_{1}^{2}$, $f_{21} = \gamma_{1} \frac{C}{A}$, $f_{31} = k\frac{D}{A}$, $f_{22} = \gamma_{1} \frac{C}{B}$, $f_{32} = k\frac{D}{B}$, $f_{4} = \gamma_{2}$, $f_{51} = \left( {\delta + I_{P} \omega_{1} p_{1} - p_{1}^{2} } \right)\frac{C}{A}$ and $f_{52} = \left( {\delta + I_{P} \omega_{1} p_{1} - p_{1}^{2} } \right)\frac{C}{B}$.

According to the relationship of trigonometric functions, Eq. (36) can be obtained as follows:

$$\left( { - \frac{{\frac{{ - f_{1} f_{51} }}{{f_{4} }} + f_{21} }}{{f_{31} }}} \right)^{2} \cos^{2} \left( {p_{1} t + \beta_{3} } \right) + \left( { - \frac{{\frac{{ - f_{1} f_{52} }}{{f_{4} }} + f_{22} }}{{f_{32} }}} \right)^{2} \sin^{2} \left( {p_{1} t + \beta_{3} } \right) = 1$$

(36)

Simplifying Eq. (36), we can get Eq. (37) to be shown as follows:

$$\left| {\left( {\alpha - p_{1}^{2} } \right)\left( {\delta + I_{P} \omega_{1} p_{1} - p_{1}^{2} } \right) - \gamma_{1} \gamma_{2} } \right| - \left| {\gamma_{2} \Delta \kappa } \right| = 0$$

(37)

where $\kappa = \frac{D}{C}$, $D = \frac{{e_{2} \omega_{2}^{2} }}{{\left| { 1- \omega_{2}^{2} } \right|}}$ and $C = \frac{{\left| {\left( { 1- I_{P} } \right)\tau \omega_{1}^{2} } \right|}}{{\left| {\delta { + }\left( {I_{P} - 1} \right)\omega_{1}^{2} } \right|}}$.

The following frequency equation of the low-pressure rotor can be given.

$$\begin{aligned} &\left| {\left( {\alpha - p_{1}^{2} } \right)\left( {\delta + I_{P} \omega_{1} p_{1} - p_{1}^{2} } \right) - \gamma_{1} \gamma_{2} } \right|\left| {\left( {1 - I_{P} } \right)\tau \left( {1 - p_{1}^{2} } \right)} \right|\\&\quad - \left| {\gamma_{2} \Delta e_{2} \left( {\delta + \left( {I_{P} - 1} \right)p_{1}^{2} } \right)} \right| = 0 \end{aligned}$$

(38)

The relationship between natural frequencies of the low-pressure rotor and the rotational speed is obtained by solving Eq. (38), and the results are shown in Fig. 4. The four natural frequencies p_1a, p_1b, p_1c and p_1d of the low-pressure rotor have the following characteristics:

Fig. 4

Natural frequency diagrams of the low-pressure rotor: a case of I_P< 1 and b case of I_P> 1

• 1. The relationship $p_{1a} > \sqrt \alpha > p_{1b} > p_{1c} > 0 > - \sqrt \alpha > p_{1d}$ holds. The positive p_1a, p_1b and p_1c respect forward whirling modes, and p_1d respects a backward whirling mode.

• 2. The natural frequencies p_1a, p_1b and p_1d change as a function of the rotational speed. As ω → ∞, they approach as p_1a→ I_Pω, p_1b→ $\sqrt \alpha$ and p_1d→ $- \sqrt \alpha$, asymptotically. In addition, the natural frequency p_1c= 1.

Compared with the independent 4DOF rotor, the low-pressure rotor has a new natural frequency p_1c, which is produced by the coupling between high-pressure and low-pressure rotors, and the natural frequency p_1c is equal to the natural frequency of the high-pressure rotor.

The line p₁ = ω₁ is drawn in Fig. 4a, b, and the different intersection points are created by the line p₁ = ω₁ and natural frequencies. The rotational speeds at the different intersections respect critical speeds of the low-pressure rotor. When I_P< 1, there are three intersections C₁, C₂ and C₃, and the low-pressure rotor has three critical speeds ω_H, ω_L1 and ω_L2 shown in Fig. 4a. The natural frequencies shown in 4a are consistent with the resonance curve shown in Fig. 2a well. When I_P> 1, there are two intersections C₁ and C₂, and the low-pressure rotor has two critical speeds ω_H and ω_L1 shown in Fig. 4b. The natural frequencies shown in 4b are also consistent with the resonance curve shown in Fig. 2b well.

4 Analysis of the dual-rotor system with nonlinear dynamic coupling

Reference [21] discussed systematically characteristics of nonlinear parameters β⁽ⁱ⁾ (i = 0, 2, 4) and ε^(j) (j = 1, 3) of Eqs. (12) and (13), and results show that nonlinear parameters β⁽⁰⁾ and ε⁽¹⁾ will cause the single rotor system to produce nonlinear vibrations in the vicinities of the harmonic resonance and the subharmonic resonance of order 1/2. Based on results mentioned above, influences of nonlinear parameters β⁽⁰⁾ and ε⁽¹⁾ on the vibration response of the dual-rotor system are studied in this paper. The parameter’s environment of numerical simulations and theoretical analyses in the nonlinear dynamic coupling model is the same with the condition in the linear dynamic coupling model, and the changed parameters are labeled in the following figures. For resonance to be shown clearly, the nonlinear coupling coefficient μ is set to a larger value. The nonlinear coefficients β⁽⁰⁾ and ε⁽¹⁾ shown in Figs. 5 and 6 are assigned, and the others are 0. The resonance curves are obtained by numerical simulations based on Eqs. (16) and (17). In figures, the red circles and the lines with red dots on both ends are numerical simulation results. The blue curves represent the theoretical solution curves, in which the solid lines are stable and the dotted lines are unstable.

Fig. 5

Resonance curves of the dual rotor with the nonlinear dynamic coupling (case of α = 2): a Resonance curves of the low-pressure rotor, b resonance curve of the high-pressure rotor

Fig. 6

Resonance curves of the dual rotor with the nonlinear coupling (case of α = 1.8): a Resonance curves of the low-pressure rotor, b resonance curve of the high-pressure rotor

4.1 Theoretical solution and analysis of stability

If the harmonic balance method is used to solve the nonlinear dynamic coupling model of the dual-rotor system, there will be so many uncertain parameters that make theoretical solutions be obtained difficultly. Because there are many parameters and a large amount of calculations, the improved shooting method is used to find theoretical solutions. The stabilities of those solutions are investigated based on the Floquet theory.

4.1.1 Derivation of theoretical solutions

When the complicated nonlinear differential equations are solved, the initial condition will directly affect the convergence of solutions and the calculation accuracy. Even though the initial values are adjusted by the Newton iterative method, the computational quantity is very large. In addition, the shooting method is often used to solve periodic solutions of a rotor system, and it is difficult to find maximum amplitudes of the system. In view of the above problems, the theoretical solutions of the nonlinear dynamic coupling model of the dual-rotor system are calculated by using the proposed shooting method systematically.

It is considered that the constant terms in the vibrational composition are small, and components of the harmonic resonance are focused on here. Therefore, we can assume solutions of the nonlinear dynamic coupling model to be expressed as follows:

$$\left\{ \begin{aligned} x_{1} = P_{L} \cos \left( {\omega_{1} t + \beta_{L} } \right),\;\;\theta_{x} = P_{\theta } \cos \left( {\omega_{1} t + \beta_{\theta } } \right),\;\;x_{2} = P_{H} \cos \left( {\omega_{2} t + \beta_{H} } \right) \hfill \\ y_{1} = P_{L} \sin \left( {\omega_{1} t + \beta_{L} } \right),\;\;\theta_{y} = P_{\theta } \sin \left( {\omega_{1} t + \beta_{\theta } } \right),\;\;y_{2} = P_{H} \sin \left( {\omega_{2} t + \beta_{H} } \right) \hfill \\ \end{aligned} \right.$$

(39)

Substitute Eq. (39) in Eqs. (16) and (17), and the rotating relationship is set as ω₁t = -ω₂t = 2nπ (n represents the number of cycles in the system response) to eliminate time parameter t in the system. The six-element nonlinear equations can be obtained as follows:

$$\left\{ \begin{aligned} &- P_{L} \omega_{1}^{2} \cos \beta_{L} - c_{11} P_{L} \omega_{1} \sin \beta_{L} - c_{12} P_{\theta } \omega_{1} \sin \beta_{\theta } + \alpha P_{L} \cos \beta_{L} \\ & \quad + \gamma_{1} P_{\theta } \cos \beta_{\theta } + \Delta P_{H} \cos \beta_{H} + \Delta N^{\prime}_{x} = e_{1} \omega_{1}^{2} \\& P_{L} \omega_{1}^{2} \sin \beta_{L} + c_{11} P_{L} \omega_{1} \cos \beta_{L} + c_{12} P_{\theta } \omega_{1} \cos \beta_{\theta } + \alpha P_{L} \sin \beta_{L} \\ & \quad + \gamma_{1} P_{\theta } \sin \beta_{\theta } + \Delta P_{H} \sin \beta_{H} + \Delta N^{\prime}_{y} = 0 \\& - P_{\theta } \omega_{1}^{2} \cos \beta_{\theta } + I_{P} \omega_{1} P_{\theta } \omega_{1} \cos \beta_{\theta } - c_{21} P_{L} \omega_{1} \sin \beta_{L} - c_{22} P_{\theta } \omega_{1} \sin \beta_{\theta } \\ & \quad + \gamma_{2} P_{L} \cos \beta_{L} + \delta P_{\theta } \cos \beta_{\theta } = \left( {I_{P} - 1} \right)\tau \omega_{1}^{2} \\& - P_{\theta } \omega_{1}^{2} \sin \beta_{\theta } + I_{P} \omega_{1} P_{\theta } \omega_{1} \sin \beta_{\theta } + c_{21} P_{L} \omega_{1} \cos \beta_{L} + c_{22} P_{\theta } \omega_{1} \cos \beta_{\theta } \\ & \quad + \gamma_{2} P_{L} \sin \beta_{L} + \delta P_{\theta } \sin \beta_{\theta } = 0 \\& - P_{H} \omega_{2}^{2} \cos \beta_{H} - cP_{H} \omega_{2} \sin \beta_{H} + P_{H} \cos \beta_{H} + N^{\prime}_{x} = e_{2} \omega_{2}^{2} \\& - P_{H} \omega_{2}^{2} \sin \beta_{H} + cP_{H} \omega_{2} \cos \beta_{H} + P_{H} \sin \beta_{H} + N^{\prime}_{y} = 0 \\ \end{aligned} \right.$$

(40)

Therefore, the optimal numerical solutions of each parameter in the equations are solved by using the genetic algorithm.

4.1.2 Analysis of the stability based on Floquet theory

The Floquet theory is the stability theory for analyzing solutions of linear differential equations with periodic variable coefficients. In the stability analysis for solutions of the dual-rotor system, some small disturbances are considered and the stability of solutions is investigated based on the stability principle of the Floquet theory.

Taking the deflection in x direction on the high-pressure rotor as an example, the following dynamics differential equation is presented.

$$\ddot{x}_{2} = f\left( {x_{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{x}_{2} ,{\kern 1pt} {\kern 1pt} t} \right)$$

(41)

A small disturbance $x^{\prime}$ is considered as follows:

$$x_{2} \left( t \right) = x_{2} \left( t \right) + x^{\prime}_{{}} \left( t \right)$$

(42)

where x₂(t) is the theoretical solution.

Substituting Eqs. (42) in (41), the power series of the disturbance $x^{'}$ are to be developed in the neighborhood of the solution x₂. The variation Eq. (43) is obtained by retaining the linear term as follows:

$$\begin{aligned} \ddot{x}_{ 2} + \ddot{x}^{\prime} & = f\left( {x_{ 2} + x^{\prime},\dot{x}_{ 2} + \dot{x^{\prime}},t} \right) \\ & = f\left( {x_{ 2} ,\dot{x}_{ 2} ,t} \right) + \frac{\partial f}{{\partial x_{ 2} }}x^{\prime} + \frac{\partial f}{{\partial \dot{x}_{ 2} }}\dot{x^{\prime}} \\ \end{aligned}$$

(43)

Therefore, the linear differential equation with periodic variable coefficients is obtained as follows:

$$\ddot{x}^{\prime} + p\left( t \right)\dot{x}^{\prime} + q\left( t \right)x^{\prime} = 0$$

(44)

where $p\left( t \right) = - \frac{\partial f}{{\partial \dot{x}_{ 2} }}$ and $q\left( t \right) = - \frac{\partial f}{{\partial x_{ 2} }}$.

The stability analysis can be carried out by the Floquet theory based on Eq. (44). If the stability of the disturbance $x^{\prime}$ is asymptotic stable, the theoretical solutions of the dual-rotor system are stable. Otherwise, the theoretical solutions are unstable. The stability is determined by the Floquet multiplier, which can be solved by the following process.

The solution of Eq. (44) is assumed as follows:

$$x^{\prime}\left( t \right) = a_{1} x^{\prime}_{1} \left( t \right) + a_{2} x^{\prime}_{2} \left( t \right)$$

(45)

According to the periodic solution, the solution of Eq. (45) can be characterized as follows:

$$\left\{ \begin{aligned} x^{\prime}_{1} \left( {t + T} \right) = a_{11} x^{\prime}_{1} \left( t \right) + a_{12} x^{\prime}_{2} \left( t \right) \hfill \\ x^{\prime}_{2} \left( {t + T} \right) = a_{21} x^{\prime}_{1} \left( t \right) + a_{22} x^{\prime}_{2} \left( t \right) \hfill \\ \end{aligned} \right.$$

(46)

Therefore, the following characteristic Eq. (47) can be obtained.

$$\left| \begin{aligned} a_{11} - \lambda \;\;\;\;a_{12} \hfill \\ a_{21} \;\;\;\;a_{22} - \lambda \hfill \\ \end{aligned} \right| = 0$$

(47)

The characteristic solutions of Eq. (47) are the Floquet multiplier λ_i which corresponds to a theoretical solution for the high-pressure rotor.

Based on the Floquet theory, the stability of theoretical solutions of the dual-rotor system can be judged as follows: If $\left| {\lambda_{i} } \right| > 1$, the corresponding theoretical solution is unstable. If $\left| {\lambda_{i} } \right| < 1$, the corresponding theoretical solution is stable. If $\left| {\lambda_{i} } \right| = 1$, the corresponding theoretical solution is within a critical condition.

4.2 Influence of nonlinear coefficient β⁽⁰⁾ on dynamic characteristics

Leading the nonlinear coefficient β⁽⁰⁾ to Eqs. (16) and (17), the dynamic characteristics of the dual-rotor system are studied with influences of the coefficient β⁽⁰⁾. Both cases of α = 2 and α = 1.8 are discussed. The major critical speed of the low-pressure rotor is slightly away from the major critical speed of the high-pressure rotor when α = 2, and the major critical speed of the low-pressure rotor is closer to the major critical speed of the high-pressure rotor when α = 1.8.

4.2.1 Analysis of numerical simulation

The resonance curves of the dual rotor obtained by numerical simulations are shown in Figs. 5 and 6. Considering the nonlinear coefficient β⁽⁰⁾, the resonance curves of the dual-rotor system have changed greatly. When the rotational speed moves in the vicinity of ω = ω_H (when α = 2, the rotational speed ω is between 0.965 and 1.185. When α = 1.8, the rotational speed ω is between 0.935 and 1.22), the variation range of amplitude of the low-pressure rotor becomes larger and the maximum amplitude suddenly increases as shown in Figs. 5a and 6a. In other rotational speed regions, the vibrational characteristics of the low-pressure rotor are the same to compare with the condition of the linear dynamic coupling model. As shown in Figs. 5b and 6b, vibrations of the high-pressure rotor do not have constant amplitudes and the almost periodic motions appear when the rotational speed goes in the vicinity of ω = ω_H. The maximum amplitudes are larger than amplitudes on other rotational speeds. In addition, the theoretical analysis shows that theoretical solutions of high-pressure and low-pressure rotors are unstable in the vicinity of ω = ω_H.

The time history, FFT spectra and Poincare map are used to further investigate nonlinear vibrations of the dual-rotor system, and the results are shown in Figs. 7 and 8.

Fig. 7

Results of numerical simulation (case of α = 2): time history, FFT spectra and Poincare map

Fig. 8

Results of numerical simulation (case of α = 1.8): time history, FFT spectra and Poincare map

Under the case of α = 2, the conditions of three rotational speeds ω = 1, 1.15 and 1.17 were selected for specific analyses. The analysis results are shown in Fig. 7. When ω = 1, the time history of the low-pressure rotor shows a beat vibration. The FFT spectra show that there are two very similar frequency components, which are distributed on both sides of ω = 1.414. The distribution of scattered points in the Poincare map is a ring. The above phenomena are shown in Fig. 7a₁. The time history of the high-pressure rotor shows a similar beat vibration, and the FFT spectra mainly show three kinds of frequency components which are distributed around ω = 1, ω = 1.414 and ω = 1.84, respectively. There are some small high-frequency components to make the distribution of scattered points in the Poincare map to become confused. The above phenomena are shown in Fig. 7a₂. When ω = 1.15, the time history of the low-pressure rotor shows a similar beat vibration. The FFT spectra mainly show two very similar frequency components which are distributed on both sides of ω = 1.414, and there are multiple kinds of frequency components with small amplitudes. The distribution of scatter points in the Poincare map is approximately ring. The above phenomena are shown in Fig. 7b₁. The vibrations of the high-pressure rotor are similar to the vibrations of the low-pressure rotor. However, it is more complex than the low-pressure rotor. Its FFT spectra show a series of frequency components, and the amplitudes of frequency components are relatively large. The distribution of scattered points in the Poincare map tends to be confused and presents chaotic motions. The above phenomena are shown in Fig. 7b₂. When ω = 1.17, the time histories of the low-pressure rotor and the high-pressure rotor exhibit almost periodic motions. The distribution of scattered points in the Poincare map shows a closed ring. The above phenomena are shown in Fig. 7c₁, c₂.

Under the case of α = 1.8, the conditions of four rotational speeds ω = 1, 1.12, 1.17 and 1.21 were selected for specific analyses. The analysis results are shown in Fig. 8. When ω = 1, the time history of the low-pressure rotor shows a beat vibration. The FFT spectra show that there are two very similar frequency components which are distributed on both sides of ω = 1.34. The distribution of scattered points in the Poincare map is a ring. The above phenomena are shown in Fig. 8a₁. The time history of the high-pressure rotor shows a similar beat vibration, and the FFT spectra mainly show three kinds of frequency components which are distributed around ω = 1, ω = 1.34 and ω = 1.69, respectively. There are some other frequency components with small amplitudes to make the distribution of scattered points in the Poincare map to become confused. The above phenomena are shown in Fig. 8a₂. When ω = 1.15, the time history of the low-pressure rotor also shows a similar beat vibration. The FFT spectra mainly show two very similar frequency components which are distributed on both sides of ω = 1.34, and there are multiple kinds of frequency components with small amplitudes. The distribution of the scatter points in the Poincare map still has the characteristics of a circular distribution. The above phenomena are shown in Fig. 8b₁. The vibrations of the high-pressure rotor are similar to the vibrations of the low-pressure rotor. However, it is more complex than the low-pressure rotor. Its FFT spectra show a series of frequency components, and the amplitudes of frequency components are relatively large. The Poincare map presents chaotic motions. The above phenomena are shown in Fig. 8b₂. When ω = 1.17, the time histories of the low-pressure rotor and the high-pressure rotor exhibit almost periodic motions. The distribution of scattered points in the Poincare map shows a closed annular. The above phenomena are shown in Fig. 8c₁, c₂. When ω = 1.21, the time histories of the low-pressure rotor and the high-pressure rotor show similar almost periodic motions. However, the FFT shows a series of complex frequency components, and the Poincare map presents chaotic motions. The above phenomena are shown in Fig. 8d₁, d₂.

According to the results of the FFT under different rotational speeds shown in Figs. 7 and 8, it can be seen that there is always an amplitude-maximizing frequency component when the dual-rotor system appears nonlinear vibrations. This frequency is equal to natural frequency ω_L1 of the low-pressure rotor. In addition, Figs. 7a₁ and 8a₁ show that the harmonic resonance frequency ω does not exist when the motion of the low-pressure rotor is a beat vibration, and Figs. 7c₁, 8c₁, d₁ show that the component of the harmonic resonance frequency ω is very small when the motions of the low-pressure rotor are almost periodic motions and chaotic motions. Furthermore, there are a series of frequency components which are generated by combinations of harmonic resonance frequency ω, the low-pressure rotor natural frequency ω_L1 and other frequencies. Based on the above analyses, not only the maximum amplitudes of the output response change suddenly, but also the frequency components of the output response change abruptly.

4.2.2 Theoretical analysis

Based on Eqs. (40) and (47), the shooting method and analyses of the Floquet theory are performed to obtain the theoretical solution curves of the dual-rotor system. The calculation results are shown in Figs. 5 and 6.

Under the case of α = 2, the theoretical solution curves of the low-pressure rotor are shown in Fig. 5a. The figure shows that the solution of the low-pressure rotor is unsteady, and the solution consists of two curves which are Curve A₁-B₁-C₁-D₁ starting from the low rotational speed and Curve H₁-G₁-F₁-E₁-C₁-D₁ starting from the high rotational speed. The curves of Sections A₁-B₁ and H₁-G₁-F₁-E₁ consist with the maximum amplitude of numerical simulation results. The two solution curves of Sections B₁-C₁ and E₁-C₁ increase and gradually approach each other. After the two solution curves approximately coincide at Point C₁, the growth trend suddenly turned into a downward trend, and the curves extend to Point D₁. In the rotational speed region of Segment F₁-E₁, there are three curves overlapping, indicating that the low-pressure rotor has triple theoretical solutions. In the rotational speed range of Segment C₁-D₁, there are two curves overlapping and the low-pressure rotor has double theoretical solutions. The theoretical solution curves of the high-pressure rotor are shown in Fig. 5b. The figure shows that the theoretical solutions of the high-pressure rotor have two types of stable and unsteady solutions. There are also two curves, which are Curve A₂-B₂-C₂-D₂ starting from a low rotational speed and Curve G₂-F₂-E₂-C₂-D₂ starting from a high rotational speed. The solutions of Sections A₂-B₂ and G₂-F₂ are stable, and the solutions are unstable in the other sections. The curves of Sections A₂-B₂ and G2-F₂-E₂ consist with the results of numerical simulation. Both curves of Sections B₂-C₂ and E₂-C₂ have a trend of increasing firstly and then decreasing. After the two solution curves approximately coincide at Point C₂, the downward trend suddenly turned into a growth trend, and the curves extend to Point D₂. In the rotational speed region of Segment F₂-E₂, there are three curves overlapping, and the high-pressure rotor has triple theoretical solutions. In the rotational speed range of Segment C₂-D₂, there are two curves overlapping, and the high-pressure rotor has double theoretical solutions.

Under the case of α = 1.8, the theoretical solution curves of the low-pressure rotor are shown in Fig. 6a. The characteristics of the theoretical solution curves are similar to the theoretical solution curves shown in Fig. 5a, but the two curves starting from a low rotational speed and a high rotational speed, respectively, are not coincident. In the rotational speed region of Segment F₁-E₁-D₁, there are three curves overlapping, and the low-pressure rotor has triple theoretical solutions. The theoretical solution curves of the high-pressure rotor are shown in Fig. 6b. The characteristics of theoretical solution curves are similar to theoretical solution curves shown in Fig. 5b, but the two curves starting from a low rotational speed and a high rotational speed, respectively, are also not coincident. In the rotational speed region of Segment G₂-F₂-E₂, there are three curves overlapping, and the low-pressure rotor has triple theoretical solutions.

4.3 Influence of nonlinear coefficients β⁽⁰⁾ and ε⁽¹⁾ on dynamic characteristics

The case of α = 2 is discussed. Considering the nonlinear coefficients β⁽⁰⁾ and ε⁽¹⁾, Eqs. (16) and (17) are solved and we discussed influences of the nonlinear coefficients β⁽⁰⁾ and ε⁽¹⁾ on the dual-rotor system.

4.3.1 Analysis of numerical simulation

The resonance curves obtained by numerical simulations and theoretical solution analyses are shown in Fig. 9. Figure 9a shows that variation ranges of amplitudes of the low-pressure rotor become larger abruptly and the maximum amplitude suddenly increases when the rotational speed locates in the vicinities of ω = ω_H, ω = ω_L1 and ω = 2ω_H (the rotational speed ω is between 0.87–1.105, 1.315–1.45 and 1.97–2.17, respectively). We can find that the vibrational characteristics of the high-pressure rotor do not meet the characteristics of harmonic vibrations from Fig. 9b. The vibration amplitude has a certain range of variations, and the maximum amplitude abruptly increases. In addition, the theoretical solutions of high-pressure and low-pressure rotors are whole unstable in the above three rotational speed regions.

Fig. 9

Resonance curves of the dual rotor with the nonlinear coupling: a Resonance curves of the low-pressure rotor, b resonance curves of the high-pressure rotor

The time history, FFT spectra and Poincare map are used to further investigate nonlinear vibrations of the dual-rotor system, and the calculation results are shown in Fig. 10.

Fig. 10

Results of numerical simulation: time history, FFT spectra and Poincare map

When ω = 0.95, the time histories of high-pressure and low-pressure rotors exhibit almost periodic motions. The distribution of scattered points in the Poincare map of the low-pressure rotor shows a closed annulus, and the distribution of scattered points in the Poincare map of the high-pressure rotor shows double closed rings. The above phenomena are shown in Fig. 10a₁, a₂. When ω = 1.08, the time histories of high-pressure and low-pressure rotors show a disorderly state. The FFT spectra show complex frequency components, and the Poincare maps exhibit chaotic motions. The above phenomena are shown in Fig. 10b₁, b₂. When ω = 1.4, the time histories of high-pressure and low-pressure rotors are confused. The FFT spectra show diverse frequency components, and the Poincare maps exhibit chaotic motions. The above phenomena are shown in Fig. 10c₁, c₂. When ω = 2.02, the time histories of high-pressure and low-pressure rotors show a kind of periodic motion similar to the harmonic motion. The FFT spectra show that there are harmonic frequencies ω, super-harmonic frequencies 2ω and 3ω, as shown in Fig. 10e₁, e₂. When ω = 2.05, the time histories of high-pressure and low-pressure rotors exhibit double period motions. The FFT spectra show frequency components of the harmonic frequency ω and the natural frequency ω_H of the high-pressure rotor. The Poincare maps all have two points. The above phenomena are shown in Fig. 10f₁, f₂.

As can be seen from the FFT spectra shown in Fig. 10, there is no constant term in the output response of the low-pressure rotor. But there is always a constant term in the output response of the high-pressure rotor shown in Fig. 10d₁, d₂. In addition, Fig. 10a₁, a₂ shows that the harmonic frequency ω is suppressed in the output response when the rotational speed moves in the vicinities of ω = ω_H and ω = ω_L1. When the system appears the nonlinear vibrations, the frequency components of the output response change abruptly. Furthermore, the super-harmonic frequency is excited when the rotational speed goes in the vicinity of ω = 2ω_H. As the rotational speed increases, the super-harmonic frequency component disappears and the natural frequency ω_H of high-pressure rotor is excited.

It is shown from the above analyses that the dual-rotor system appears chaotic motions in the vicinities of different major critical speeds. In order to further analyze chaotic motions, the bifurcation map and the largest Lyapunov exponent are calculated. The result is shown in Fig. 11. The Poincare section method is used to obtain the bifurcation map and the Lyapunov exponent λ is defined as follows. Let us consider two trajectories at distance d₀ at t = 0 in the phase space. We assume that the two points on these trajectories have a distance d expressed approximately by d(t) = d₀e^λt. The λ in this expression expresses the Lyapunov exponent. If the Lyapunov exponent has a positive value, these trajectories diverge rapidly. This means that the solution depends sensitively on the initial condition, and this sensitive dependence on the initial condition is a characteristic of chaotic vibration. Figure 11 shows the largest value of Lyapunov exponents, which was obtained based on the method proposed by Wolf [29]. When the rotational speed is in the vicinities of ω = 1.1 and ω = 1.4, the scattered points in the bifurcation map are confused and the largest Lyapunov exponents are positive. These phenomena mean the occurrence of chaotic motions. In addition, the bifurcation map shows that the vibration form has suddenly changed at ω = 0.87, ω = 1.11, ω = 1.31 and ω = 1.45.

Fig. 11

Bifurcation map and largest Lyapunov exponents (LET)

4.3.2 Theoretical analysis

Based on Eqs. (40) and (47), the improved shooting method and the analyses of the Floquet theory are performed to obtain the theoretical solution curves of the dual-rotor system. The calculation results are shown in Fig. 9.

The theoretical solution curves of the low-pressure rotor are shown in Fig. 9a. The theoretical solutions are all unstable, and Curves A₁-B₁, C₁-D₁, E₁-F₁, and G₁-H₁ consist with the maximum amplitude obtained by numerical simulations. In Segments B₁-C₁, D₁-E₁ and F₁-G₁ with nonlinear vibrations, the theoretical solution curves transition smoothly and there are no multiple solutions.

The theoretical solution curves of the high-pressure rotor are shown in Fig. 9b. The theoretical solution curves of the high-pressure rotor are composed of stable and unstable solutions. The theoretical solution curves consist with the results of numerical simulation in Sections A₂-B₂, C₂-D₂, E₂-F₂ and G₂-H₂. In addition, the theoretical solutions of Segments A₂-B₂, E₂-F₂, and G₂-H₂ are stable, and the others are unstable. In Segments B₂-C₂, D₂-E₂ and F₂-G₂ with nonlinear vibrations, the theoretical solution curves transition smoothly and there are no multiple solutions.

5 Conclusions

In this paper, the dynamic coupling models of the dual-rotor system with nonlinear restoring forces are first proposed. The influence of nonlinear spring characteristics on the dual-rotor system is discussed by numerical simulations and theoretical analyses. The following results are obtained.

• 1. Without considering the nonlinearity, the low-pressure rotor has a coupling natural frequency that is equal to the natural frequency of the high-pressure rotor in the linear dynamic coupling model. In addition, the vibrations of the low-pressure rotor change within a certain range when the rotor rotates at any rotational speeds. The vibration amplitudes of the low-pressure rotor in x and y directions are influenced by the mass and rotational speeds of high-pressure and low-pressure rotors.

• 2. Structural characteristics of the dual-rotor system with the inter-shaft bearing lead to dynamic support conditions of the high-pressure rotor, which mean that nonlinear spring characteristics of rotors caused by a clearance of the bearing cannot be ignored. The symmetric nonlinear coefficient β⁽⁰⁾ induces nonlinear vibrations of the dual-rotor system in the vicinity of the major critical speed of the high-pressure rotor (ω = ω_H). The nonlinear coefficients β⁽⁰⁾ and ε⁽¹⁾ induce nonlinear vibrations of the system in the vicinities of the major critical speed of the high-pressure rotor (ω = ω_H), the major critical speed of the low-pressure rotor (ω = ω_L1) and the critical speed of the subharmonic resonance of order 1/2 of the high-pressure rotor (ω = 2ω_H). The nonlinear vibrations always exhibit almost periodic motions and chaotic motions in the major critical speeds of high-pressure and low-pressure rotors.

• 3. When the dual-rotor system appears nonlinear vibrations, the frequency components of the vibration response are very complex. There are the natural frequency ω_H, the natural frequency ω_L1, super-harmonic frequencies and combinations of various frequencies due to the nonlinearity. The harmonic frequency ω is even suppressed. The frequency components change abruptly, and the transition between nonlinear vibrations occurs suddenly.