Nonlinear thermal behaviors of the inter-shaft bearing in a dual-rotor system subjected to the dynamic load

Abstract

This paper proposes a new theoretical method to investigate the thermal behaviors of the inter-shaft bearing considering the nonlinear dynamic characteristics of a dual-rotor system by combining heat transfer and nonlinear dynamics. The nonlinearities of the inter-shaft bearing, including the Hertzian contact and the radial clearance, are considered during the dynamic modeling for the system. The dynamic load of the inter-shaft bearing is defined according to the nonlinear dynamic responses of the system. Therefore, some fundamental nonlinear phenomena, i.e., jump and bi-stable phenomena happen to the dynamic load. It makes the dynamic load more appropriate to describe the actual load of the inter-shaft bearing than the static load. Furthermore, a steady-state heat transfer model for the inter-shaft bearing subjected to the dynamic load can be set up with the help of Palmgren’s empirical formula. The variation of temperatures with the rotation speed is obtained by using the Gauss–Seidel iteration. Temperatures of the inter-shaft bearing also show nonlinear thermal behaviors, i.e., jump and bi-stable phenomena. It implies the nonlinear dynamic behaviors of the system have a great impact on the thermal behaviors of the inter-shaft bearing. Moreover, an exhaustive parametric analysis for temperatures and nonlinear thermal behaviors of the inter-shaft bearing affected by dynamic parameters (including the rotation speed ratio, unbalances of rotors, the radial clearance, the stiffness and the roller number of the inter-shaft bearing) and thermal parameters (including the lubricant viscosity and the ambient temperature) is carried out. The results show that the rotation speed ratio has a significant influence on both temperatures and nonlinear thermal behaviors, other dynamic parameters mainly affect nonlinear thermal behaviors, while thermal parameters only affect temperatures. This unique discovery indicates the thermal behaviors of the inter-shaft bearing could be much more complex because of the nonlinear dynamic characteristics of the dual-rotor system. The obtained results will contribute to a better understanding of the nonlinear thermal behaviors of bearings and profoundly reveal the mechanism of the nonlinear thermal behaviors of bearings.

1 Introduction

With the development of the rotor system trending toward high-speed and heavy-load, higher requirements are put forward for dynamic and thermal performances of the supporting system. Dynamic and thermal behaviors of inter-shaft bearings [1], as essential support and transmission parts between the lower pressure (LP) rotor and the higher pressure (HP) rotor of dual-rotor systems especially in aero engines of fighters, are much more complex or maybe even nonlinear [2] in many cases. Nevertheless, the research about nonlinear thermal behaviors of the inter-shaft bearing is almost blank at present. Therefore, it is imperative to study nonlinear thermal behaviors of the inter-shaft bearing and clarify the effect of dynamic and thermal parameters.

The effect of bearings’ nonlinearities, including the Hertzian contact and the radial clearance on dynamic behaviors of the rotor system, have been discussed by many researchers so far. Yamamoto [3] studied the resonance of a rotor-bearing system affected by the radial clearance of the bearing and discovered that the frequency and amplitude of the resonance peak decrease with the increase of radial clearance. Fukata et al. [4] researched the radial vibration of a ball bearing under a constant radial load and revealed nonlinear vibrations, such as super-harmonic vibration and sub-harmonic vibration, are caused by the Hertzian contact and the radial clearance of bearings. The nonlinear dynamic behaviors, such as jump phenomenon, sub-harmonic and combination vibrations, in an actual dual-rotor assembly for a medium-size jet engine, were reproduced by Holmes [2] on a test facility. Mevel and Guyader [5] described two different routes, i.e., the sub-harmonic route and the quasi-periodic route, to the chaos of a lightly loaded ball bearing based on the same dynamic model of Fukata. A modified harmonic balance method was applied by Tiwari et al. [6, 7] to theoretically simulate the effect of the Hertzian contact and the radial clearance of bearings on nonlinear dynamic behaviors of horizontal rotors and was experimentally verified. Ghafari et al. [8] presented a lumped mass-damper-spring model considering the nonlinear stiffness of rolling elements to investigate the effect of the radial clearance on the equilibrium point of the bearing. Bai et al. [9] established a six degree-of-freedom (6DOF) model to investigate the sub-harmonic resonance of a symmetric ball bearing rotor system by numerical analysis and experiments. Based on the analytic method, also named as HB-AFT applied in Ref. [6, 7], Zhang et al. [10, 11] focused on the resonant hysteresis of a ball bearing rotor system with the Hertzian contact and the radial clearance of bearings. In all of the above works, they all concentrated on the nonlinear dynamic behaviors of bearing rotor system; none of them considered the thermal effect of the bearings.

There indeed exist some excellent research about the thermal behaviors of rolling bearings in the past decades. Palmgren [12] pioneered an empirical formula for calculating the friction torque through numerous experiments on various types and sizes of rolling bearings. Harris [13] utilized the basic concept of heat transfer among the main components of bearings to predict the steady-state temperatures by the lumped parameter method. Winer et al. [14] constructed an apparatus to simulate the thermal behaviors of a tapered roller bearing and offered formulas of thermal resistances between the shaft, the bearing and the housing. A 5DOF model of the rolling bearing was set up by DeMul et al. [15, 16] to describe the relationship between load and deflection by a matrix method. Jorgensen and Shin [17] presented a quasi-three-dimensional heat transfer model to predict the steady-state temperature distribution of the spindle bearing system considering thermal growth. Based on Palmgren’s empirical formula, Stein and Tu [18] proposed a state-space model for monitoring the preload of an angular contact ball bearing induced by the thermal expansion and analyzed the effect of the rotation speed and the initial preload. Sun et al. [19] developed an approach for blade loss simulation and established a thermal model to estimate thermal growths of the main components of bearings during the blade loss event. Takabi and Khonsari [20] put forward an unsteady-state heat transfer model for an oil bath lubrication deep-groove ball bearing to study the transient temperatures of the bearing. Ai et al. [21] concentrated on the thermal behaviors of double-row tapered roller bearings lubricated with grease and proposed a quasi-static model for the bearing to attain the load distribution and kinematic parameters. Than and Huang [22] offered a unified method, which is a combination of a quasi-static model and finite element method, to research nonlinear thermal behaviors of a high-speed spindle bearing under preload. Nevertheless, none of the above literatures considers the effect of dynamic characteristics on thermal behaviors of rolling bearings during modeling.

The motivation of this paper is to propose a new theoretical method to investigate the thermal behaviors of the inter-shaft bearing considering the nonlinear dynamic characteristics of a dual-rotor system by combining heat transfer and nonlinear dynamics. The dynamic load of the inter-shaft bearing is defined according to the nonlinear dynamic responses of the dual-rotor system, which can be substituted into the steady-state heat transfer model of the inter-shaft bearing with the help of Palmgren’s empirical formula. Therefore, the model enables us to investigate the thermal behaviors of the inter-shaft bearing affected by the nonlinear dynamic characteristics of the dual-rotor system through numerical simulations. The obtained results show that the nonlinear dynamic load from the dual-rotor system can make significant effect on the thermal behaviors of the inter-shaft bearing, e.g., the temperature frequency curve of the inter-shaft bearing has nonlinear features. In conclusion, the dynamic load defined in this paper is more appropriate than the static load employed in most of the references to describe the actual load of the inter-shaft bearing.

2 Dynamic load of the inter-shaft bearing

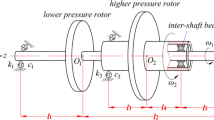
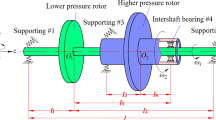
CFM56 is one of most widely used dual-rotor aero engines [23]. A two-disk dual-rotor system supported by four points is obtained Based on the basic structure of CFM56 and the simplified method of dynamic model [24]. Figure 1 displays the schematic diagram of a simple dual-rotor system with an inter-shaft bearing [24, 25]. Each rotor is composed of one disk and one shaft, both of which are bound together into one complete rotor. The inter-shaft bearing is located between the LP rotor and the HP rotor. Different from the supporting bearing, both the inner race and the outer race of the inter-shaft bearing rotate with the LP rotor and the HP rotor. Wherein, l_i (i = 1–5) are lengths of shafts, k_i and c_i (i = 1, 2, 3) are stiffness and damping coefficients of springs, ω₁ and ω₂ (rad/s) are rotation speeds of the LP rotor and the HP rotor. Assume that the LP rotor and the HP rotor operate at a constant ratio. Therefore, the rotation speed ratio is defined as $\lambda = \frac{{\omega_{2} }}{{\omega_{1} }}$. Since the HP rotor rotates faster than the LP rotor, $\lambda > 1$ for the co-rotating system and $\lambda < - 1$ for the counter-rotating system.

Fig. 1

Schematic diagram of a simple dual-rotor system with an inter-shaft bearing

The mathematical derivation of the dynamic equations for the dual-rotor system has been processed in Ref. [26, 27]. Thus the deduction process is omitted and the dynamic equations are given directly as

$$ \begin{aligned} & m_{1} \ddot{x}{}_{1} + c_{1} \left( {\dot{x}_{1} - \dot{\theta }_{y} l_{1} } \right) + c_{2} \left( {\dot{x}_{1} + \dot{\theta }_{y} l_{2} } \right) \\ & \quad + k_{1} \left( {x_{1} - \theta_{y} l_{1} } \right) + k_{2} \left( {x_{1} + \theta_{y} l_{2} } \right) \\ & \quad = m_{1} \omega_{1}^{2} e_{1} \cos \left( {\omega_{1} t} \right) - F_{x} - m_{1} g, \\ \end{aligned} $$

(1a)

$$ \begin{aligned} & m_{1} \ddot{y}{}_{1} + c_{1} \left( {\dot{y}_{1} + \dot{\theta }_{x} l_{1} } \right) + c_{2} \left( {\dot{y}_{1} - \dot{\theta }_{x} l_{2} } \right) \\ & \quad + k_{1} \left( {y_{1} + \theta_{x} l_{1} } \right) + k_{2} \left( {y_{1} - \theta_{x} l_{2} } \right) \\ & \quad = m_{1} \omega_{1}^{2} e_{1} \sin \left( {\omega_{1} t} \right) - F_{y} , \\ \end{aligned} $$

(1b)

$$ \begin{aligned} & J_{{d_{1} }} \ddot{\theta }_{x} + \omega_{1} J_{{p_{1} }} \dot{\theta }_{y} + c_{1} l_{1} \left( {\dot{y}_{1} + \dot{\theta }_{x} l_{1} } \right) \\ & \quad - c{}_{2}l_{2} \left( {\dot{y}_{1} - \dot{\theta }_{x} l_{2} } \right) + k_{1} l_{1} \left( {y_{1} + \theta_{x} l_{1} } \right) \\ & \quad - k_{2} l_{2} \left( {y_{1} - \theta_{x} l_{2} } \right) = F_{y} \left( {l_{2} - l_{5} } \right), \\ \end{aligned} $$

(1c)

$$ \begin{aligned} & J_{{{\text{d}}_{1} }} \ddot{\theta }_{y} - \omega_{1} J_{{{\text{p}}_{1} }} \dot{\theta }_{x} - c_{1} l_{1} \left( {\dot{x}_{1} - \dot{\theta }_{y} l_{1} } \right) \\ & \quad + c{}_{2}l_{2} \left( {\dot{x}_{1} + \dot{\theta }_{y} l_{2} } \right) - k_{1} l_{1} \left( {x_{1} - \theta_{y} l_{1} } \right) \\ & \quad + k{}_{2}l_{2} \left( {x_{1} + \theta_{y} l_{2} } \right) = - F_{x} \left( {l_{2} - l_{5} } \right), \\ \end{aligned} $$

(1d)

$$ \begin{aligned} & m_{2} \ddot{x}{}_{2} + c_{3} \left( {\dot{x}_{2} - \dot{\varphi }_{y} l_{3} } \right) + k_{3} \left( {x_{2} - \varphi_{y} l_{3} } \right) \\ & \quad = m_{2} \omega_{2}^{2} e_{2} \cos \left( {\omega_{2} t} \right) + F_{x} - m_{2} g, \\ \end{aligned} $$

(1e)

$$ \begin{aligned} & m_{2} \ddot{y}{}_{2} + c_{3} \left( {\dot{y}_{2} + \dot{\varphi }_{x} l_{3} } \right) + k_{3} \left( {y_{2} + \varphi_{x} l_{3} } \right) \\ & \quad = m_{2} \omega_{2}^{2} e_{2} \sin \left( {\omega_{2} t} \right) + F_{y} , \\ \end{aligned} $$

(1f)

$$ \begin{aligned} & J_{{d_{2} }} \ddot{\varphi }_{x} + \omega_{2} J_{{p_{2} }} \dot{\varphi }_{y} + c_{3} l_{3} \left( {\dot{y}_{2} + \dot{\varphi }_{x} l_{3} } \right) \\ & \quad + k_{3} l_{3} \left( {y_{2} + \varphi_{x} l_{3} } \right) = - F_{y} l_{4} , \\ \end{aligned} $$

(1g)

$$ \begin{aligned} & J_{{{\text{d}}_{2} }} \ddot{\varphi }_{y} - \omega_{2} J_{{{\text{p}}_{2} }} \dot{\varphi }_{x} - c_{3} l_{3} \left( {\dot{x}_{2} - \dot{\varphi }_{y} l_{3} } \right) \\ & \quad - k_{3} l_{3} \left( {x_{2} - \varphi_{y} l_{3} } \right) = F_{x} l_{4} , \\ \end{aligned} $$

(1h)

The physical significances and values of the parameters in Eq. (1) have been already claimed in Ref. [26, 27].

The inter-shaft bearing is a radial cylindrical roller bearing, especially in the dual-rotor aero engine of the fighter. The nonlinear factors, such as the radial clearance and the fractional exponential relationship of the Hertzian contact [13], are taken into consideration for calculating restoring forces of the inter-shaft bearing. The schematic diagram of the inter-shaft bearing and the picture of the NU1020 roller bearing are shown in Fig. 2.

Fig. 2

a Schematic diagram of the inter-shaft bearing. b The NU1020 roller bearing

The nonlinear vertical and horizontal restoring forces of the inter-shaft bearing [28] are expressed as

$$ \left[ {\begin{array}{*{20}c} {F_{x} } \\ {F_{y} } \\ \end{array} } \right] = K_{\text{b}} \sum\limits_{k = 1}^{{N_{\text{b}} }} {\delta_{k}^{10/9} H\left( {\delta_{k} } \right)} \left[ {\begin{array}{*{20}c} {\cos \theta_{k} } \\ {\sin \theta_{k} } \\ \end{array} } \right], $$

(2)

where K_b, N_b are the Hertz contact stiffness and the roller number of the inter-shaft bearing, $H\left( \cdot \right)$ represents the step function.

Assume that deformations are small enough, then the deformation between kth roller and races $\delta_{k}$ is expressed as

$$ \begin{aligned} \delta_{k} & = \left\{ {\left[ {x_{1} + \theta_{y} \left( {l_{2} - l_{5} } \right)} \right] - \left( {x_{2} + \varphi_{y} l_{4} } \right)} \right\}\cos \theta_{k} \\ & \quad + \left\{ {\left[ {y_{1} - \theta_{x} \left( {l_{2} - l_{5} } \right)} \right] - \left( {y_{2} - \varphi_{x} l_{4} } \right)} \right\}\sin \theta_{k} \\ & \quad - \delta_{0} \, \left( {k = 1, \, 2, \ldots ,N_{\text{b}} } \right), \\ \end{aligned} $$

where 2δ₀ is the radial clearance of the inter-shaft bearing.

The angular position of the kth roller is $\theta_{k} = \frac{2\pi }{{N_{\text{b}} }}\left( {k - 1} \right) + \omega_{\text{c}} t\;\left( {k = 1, \, 2, \ldots ,N_{\text{b}} } \right)$, where $\omega_{\text{c}} = \frac{{\omega_{ 1} r_{\text{i}} + \omega_{ 2} r_{\text{o}} }}{{r_{\text{i}} { + }r_{\text{o}} }}$ denotes the rotation speed of the cage, r_i, r_o are the radiuses of inner and outer races.

The NU1020 roller bearing of FAG^® is adopted as the inter-shaft bearing in this paper, and its important structural parameters are shown in Table 1.

Table 1 Structural parameters of the NU1020 roller bearing

The dynamic load of the inter-shaft bearing is introduced to estimate the actual load of the inter-shaft bearing when the system is operating at a certain rotation speed. The root-mean-square (RMS) [29] of the vertical and horizontal restoring forces is utilized to define the dynamic load; the formula is

$$ \begin{aligned} F_{\text{b}} & = \sqrt {\frac{{\int_{0}^{T} {\left( {\left( {F_{x} \left( t \right) - \bar{F}_{x} } \right)^{2} + \left( {F_{y} \left( t \right) - \bar{F}_{y} } \right)^{2} } \right)} {\text{d}}t}}{T}} \\ & \quad = \sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {\left( {F_{x} \left( i \right) - \bar{F}_{x} } \right)^{2} + \left( {F_{y} \left( i \right) - \bar{F}_{y} } \right)^{2} } \right)} }}{N}} , \\ \end{aligned} $$

(3)

where T is the period of the restoring forces, N is the number of discrete points in one period, $\bar{F}_{x}$ and $\bar{F}_{y}$ are average values of vertical and horizontal restoring forces.

3 Heat transfer modeling under the dynamic load

3.1 Friction heat (FH) under the dynamic load

Friction hinders motion and causes energy loss in the form of FH. During the operation of the inter-shaft bearing, FH causes the temperature to rise, which can be measured by the friction torque. The magnitude of friction torque considerably depends on the type of lubrication. For the oil lubrication roller bearing, the lubricant occupies a portion of the free space inside the bearing, and it will hinder the motion of rollers [13]. The friction torque is related to the lubricant performance, the filling amount in the free space, and the rolling speed of rollers.

Nevertheless, these factors are intensely coupled together and extremely difficult to distinguish from each other [18]. In 1959, Palmgren [12] attained an empirical formula for calculating the friction torque through numerous experiments on various types and sizes of rolling bearings. The empirical formula has been widely accepted as a precise method to predict the friction torque.

The inter-shaft bearing is a radial cylindrical roller bearing as shown in Fig. 2, the total friction torque M contains three parts: the load friction torque M_l, and the viscosity friction torque M_ν and the roller end-flange friction torque M_f. The inter-shaft bearing do not deliver axial load; thus, M_f can be ignored and M is simplified into

$$ M = M_{l} + M_{v} , $$

(4a)

the unit of above friction torque is N mm.

Different from the static load in previous research [17, 20, 22], the dynamic load of the inter-shaft bearing F_b is introduced to estimate the load friction torque M_l. The dynamic load shows nonlinear behaviors, which makes it much more complex than the static load. The dynamic load is more appropriate to describe the actual load of the inter-shaft bearing than the static load. Therefore, M_l subjected to the dynamic load can be expressed as

$$ M_{l} = f_{l} F_{\text{b}} D_{\text{m}} , $$

(4b)

where f_l is a coefficient depends on the type of roller bearing, its values are shown in Table 2.

Table 2 The coefficient f_l for the cylindrical roller bearing type [13]

The viscosity friction torque M_ν is related to the lubricant viscosity apparently. Herein, the kinematic viscosity ν in Centistoke (cSt, i.e., mm²/s) is applied to denote the lubricant viscosity. Both inner and outer races of the inter-shaft bearing rotate with LP and HP rotors; thus, the rotation speed difference between HP and LP rotors $\Delta n = \frac{60}{2\pi }\left| {\omega_{2} - \omega_{1} } \right| = \frac{60}{2\pi }\left| {\lambda - 1} \right|\omega_{1}$ (r/min, i.e., rpm) is introduced to estimate M_ν, as follows:

$$ M_{v} = \left\{ {\begin{array}{*{20}l} {10^{ - 7} f_{v} \left( {\nu \cdot \Delta n} \right)^{2/3} D_{\text{m}}^{3} } \hfill & {\nu \cdot \Delta n \ge 2000} \hfill \\ {160 \times 10^{ - 7} f_{v} D_{\text{m}}^{3} } \hfill & {\nu \cdot \Delta n < 2000} \hfill \\ \end{array} } \right., $$

(4c)

where f_ν is a coefficient depends on the type of roller bearing and the type of lubrication, its values are shown in Table 3.

Table 3 The coefficient f_ν versus cylindrical roller bearing type and lubrication type [13]

The total FH Q, the load FH Q_l and the viscosity FH Q_ν of the inter-shaft bearing are

$$ Q = Q_{l} + Q_{v} , $$

(5a)

$$ Q_{l} = 10^{ - 3} \left| {\omega_{2} - \omega_{1} } \right|M_{l} = 10^{ - 3} \left| {\lambda - 1} \right|\omega_{1} M_{l} , $$

(5b)

$$ Q_{\nu } = 10^{ - 3} \left| {\omega_{2} - \omega_{1} } \right|M_{\nu } = 10^{ - 3} \left| {\lambda - 1} \right|\omega_{1} M_{\nu } , $$

(5c)

the units of FHs are W.

3.2 Steady-state heat transfer modeling under the dynamic load

The lumped parameter method can be used to set up the steady-state heat transfer model for rollers, inner race and outer race of the inter-shaft bearing, because the Biot number [30] of bearing steel is rather small (Bi < 0.1). The inside temperatures of rollers, inner race and outer race are considered the same everywhere, thus the steady-state heat transfer model for the inter-shaft bearing is greatly simplified.

Figure 3 illustrates the thermal network for the inter-shaft bearing. The thermal nodes are labeled in Fig. 3a. There exists six lumped thermal nodes, including T_r, T_i and T_o are rollers, the inner race and the outer race of the inter-shaft bearing; T_LP and T_HP are portions of LP rotor contact the inner race and HP rotor contact the outer race; T_L is the lubricant. While T_∞ is the temperature of the ambient. The structure sizes of the inter-shaft bearing are also pictured; the values are listed in Table 1. The heat transfer network is depicted in Fig. 3b. R_ri, R_ro, R_i, R_o are thermal resistances of heat conduction while R_Lr, R_Li, R_Lo, R_LP, R_HP are thermal resistances of heat convection.

Fig. 3

Thermal network of the inter-shaft bearing. a Thermal nodes. b Heat transfer network

Assume that FH is generated at the contact zones between rollers and races, then distributed to rollers Q_r, inner race Q_i, and outer race Q_o. The distribution coefficients of the FH refer to Ref. [18]; therefore,

$$ Q = Q_{\text{r}} + Q_{\text{i}} + \, Q_{\text{o}} , $$

(6a)

$$ Q_{\text{r}} = 0.5Q, $$

(6b)

$$ Q_{\text{i}} = 0.25Q, $$

(6c)

$$ Q_{\text{o}} = 0.25Q. $$

(6d)

Considering the energy balance for every lumped thermal node, the governing equations of the steady-state heat transfer are expressed as

$$ \frac{{T_{\text{i}} - T_{\text{r}} }}{{R_{\text{ri}} }} + \frac{{T_{\text{o}} - T_{\text{r}} }}{{R_{\text{ro}} }} + \frac{{T_{\text{L}} - T_{\text{r}} }}{{R_{\text{Lr}} }} + Q_{\text{r}} = 0, $$

(7a)

$$ \frac{{T_{r} - T_{i} }}{{R_{ri} }} + \frac{{T_{LP} - T_{i} }}{{R_{i} }} + \frac{{T_{L} - T_{i} }}{{R_{Li} }} + Q_{i} = 0, $$

(7b)

$$ \frac{{T_{\text{r}} - T_{\text{o}} }}{{R_{\text{ro}} }} + \frac{{T_{\text{HP}} - T_{\text{o}} }}{{R_{\text{o}} }} + \frac{{T_{\text{L}} - T_{\text{o}} }}{{R_{\text{Lo}} }} + Q_{\text{o}} = 0, $$

(7c)

$$ \frac{{T_{\text{i}} - T_{\text{LP}} }}{{R_{\text{i}} }} + \frac{{T_{\infty } - T_{\text{LP}} }}{{R_{\text{LP}} }} = 0, $$

(7d)

$$ \frac{{T_{\text{o}} - T_{\text{HP}} }}{{R_{\text{o}} }} + \frac{{T_{\infty } - T_{\text{HP}} }}{{R_{\text{HP}} }} = 0, $$

(7e)

$$ \frac{{T_{\text{r}} - T_{\text{L}} }}{{R_{\text{Lr}} }} + \frac{{T_{i} - T_{\text{L}} }}{{R_{\text{Li}} }} + \frac{{T_{\text{o}} - T_{\text{L}} }}{{R_{\text{Lo}} }} = 0. $$

(7f)

The governing equations of the steady-state heat transfer Eq. (7) can be rewritten in a matrix form as follows:

$$ AT = B, $$

(8)

where $\varvec{T} = \left[ {\begin{array}{*{20}c} {T_{\text{r}} } & {T_{\text{i}} } & {T_{\text{o}} } & {T_{\text{LP}} } & {T_{\text{HP}} } & {T_{\text{L}} } \\ \end{array} } \right]^{\text{T}}$, $\varvec{B} = \left[ {\begin{array}{*{20}c} { - Q_{\text{r}} } & { - Q_{\text{i}} } & { - Q_{\text{o}} } & { - \frac{{T_{\infty } }}{{R_{\text{LP}} }}} & { - \frac{{T_{\infty } }}{{R_{\text{HP}} }}} & 0 \\ \end{array} } \right]^{\text{T}}$, the coefficient matrix A is seen in "Appendix".

3.3 Thermal resistance

• (1) Thermal resistance of heat conduction

  • (a) The thermal resistances of roller-inner race R_ri and roller-outer race R_ro.

The assumption of ideal line contact is applicable for contact pairs of roller-inner race and roller-outer race, the contact zones are treated as rectangles. The semiwidth of the contact zones [13] can be easily attained as

$$ \begin{aligned} b_{i} & = 3.35 \times 10^{ - 3} \left( {\frac{{F_{n} }}{{a_{r} \sum {\rho_{i} } }}} \right)^{{\frac{1}{2}}} , \\ b_{o} & = 3.35 \times 10^{ - 3} \left( {\frac{{F_{n} }}{{a_{r} \sum {\rho_{o} } }}} \right)^{{\frac{1}{2}}} , \\ \end{aligned} $$

where F_n is the normal force of roller-race; ∑ ρ_i is the curvature sum of roller-inner race contact pair; ∑ ρ_o is the curvature sum of roller-outer race contact pair.

The areas of the contact zones of roller-inner race and roller-outer race are

$$ A_{\text{i}} = 2a_{\text{r}} b_{\text{i}} ,\quad A_{\text{o}} = 2a_{\text{r}} b_{\text{o}} . $$

Considering that the contact zones of roller-inner race and roller-outer race are rectangles, it is not appropriate to use Peclet number [30] directly. The modified Peclet number Pe* [31], which accounts the effect of the shape and orientation of the contact zone, is introduced as follows:

$$ {\text{Pe}}^{*} = \left( {\varepsilon_{\text{m}} } \right)^{{\frac{1}{2}}} \;\;{\text{Pe}} = \left( {\varepsilon_{\text{m}} } \right)^{{\frac{1}{2}}} \frac{VL}{\alpha }, $$

where $\varepsilon_{\text{m}} = \frac{b}{a}$ is the aspect ratio, which describes the shape and orientation effect of the rectangular or elliptic heat source; V is the line speed; α is the thermal diffusivity; L is the characteristic length depends on the shape of the contact zone, its values are shown in Table 4.

Table 4 The characteristic length L for the shape of the contact zone [31]

Then the modified Peclet numbers for the contact zones of roller-inner race and roller-outer race are

$$ \begin{aligned} {\text{Pe}}_{\text{i}}^{ * } & = \left( {\varepsilon_{\text{m}} } \right)^{{\frac{1}{2}}} \cdot \frac{{\omega_{1} r_{\text{i}} \sqrt {A_{\text{i}} } }}{{\alpha_{\text{steel}} }}, \\ {\text{Pe}}_{\text{o}}^{ * } & = \left( {\varepsilon_{\text{m}} } \right)^{{\frac{1}{2}}} \cdot \frac{{\left| {\lambda \omega_{1} } \right|r_{\text{o}} \cdot \sqrt {A_{\text{o}} } }}{{\alpha_{\text{steel}} }}, \\ \end{aligned} $$

where α_steel is the thermal diffusivity of steel.

The thermal resistance of one roller-inner race and one roller-outer race [31] are

$$ \begin{aligned} R_{\text{i}}^{\text{one}} = \frac{1.13}{{k_{\text{steel}} \sqrt {A_{\text{i}} \cdot {\text{Pe}}_{\text{i}}^{ * } } }}, \hfill \\ R_{\text{o}}^{\text{one}} = \frac{1.13}{{k_{\text{steel}} \sqrt {A_{\text{o}} \cdot {\text{Pe}}_{\text{o}}^{ * } } }}, \hfill \\ \end{aligned} $$

(9)

where k_steel is the thermal conductivity of steel.

The stressed roller number of the inter-shaft bearing is represented as n_b, i.e., there are n_b (a number) $R_{\text{ri}}^{\text{one}}$, $R_{\text{ro}}^{\text{one}}$ in parallel [20]; thus, the total thermal resistances are

$$ \begin{aligned} R_{\text{ri}} = \frac{{R_{\text{i}}^{\text{one}} }}{{n_{\text{b}} }}, \hfill \\ R_{\text{ro}} = \frac{{R_{\text{o}}^{\text{one}} }}{{n_{\text{b}} }}. \hfill \\ \end{aligned} $$

(10)

• (b) The thermal resistances of inner race-LP rotor R_i and outer race-HP rotor R_o.

The inner race-LP rotor and the outer race-HP rotor are interference fit; therefore, the inner race and the portion of LP rotor contact the inner race is treated as singular-layer hollow cylinder; it is the same with the outer race and the portion of HP rotor contact the outer race. Thermal resistances are expressed as

$$ \begin{aligned} R_{\text{i}} & = \frac{{\ln \left( {{{d_{\text{i}} } \mathord{\left/ {\vphantom {{d_{\text{i}} } {d_{\text{L}} }}} \right. \kern-0pt} {d_{\text{L}} }}} \right)}}{{2\pi k_{\text{steel}} B}}, \\ R_{\text{o}} & = \frac{{\ln \left( {{{d_{\text{H}} } \mathord{\left/ {\vphantom {{d_{\text{H}} } {d_{\text{o}} }}} \right. \kern-0pt} {d_{\text{o}} }}} \right)}}{{2\pi k_{\text{steel}} B}}. \\ \end{aligned} $$

(11)

• (2) Thermal resistance of heat convection

In order to acquire the thermal resistance of heat convection under different conditions of heat convection [21], it is indispensable to predict the convective heat transfer coefficient h. Nevertheless, h can be expressed in terms of the fluid thermal conductivity k, the characteristic length L and the dimensionless Nusselt number Nu as follows:

$$ R_{\nu } = \frac{1}{Ah} = \frac{1}{A} \cdot \frac{L}{{k \cdot {\text{Nu}}}}. $$

(12)

Once the Nusselt number is determined, the thermal resistance of heat convection can be acquired based on Eq. (12). The Nusselt number is measured by the experiment in most cases. The Nusselt numbers under different conditions of heat convection are listed as follows:

• (a) The Nusselt number of lubricant roller Nu_Lr.

In 1965, Fand [32] presented a correlation by experimental investigation of forced convection from a cylinder to water in crossflow in the range $10^{ - 1} < {\text{Re}} < 10^{5}$. The heat exchange between the lubricant and the cylinder roller meets the requirements of the correlation, which is

$$ {\text{Nu}} = \left( {0.35 + 0.34 \, \text{Re}^{0.5} + 0.15 \, \text{Re}^{0.58} } \right)\Pr^{0.3} , $$

(13)

the correlation is valid for $10^{ - 1} < \text{Re} < 10^{5}$. Where $\text{Re} = \frac{VL}{\nu }$, $Pr = \frac{\nu }{\alpha }$ are the dimensionless Reynolds number and the dimensionless Prandtl number.

• (b) The Nusselt numbers of lubricant-inner race Nu_Li and lubricant-outer race Nu_Lo.

In 1958, Gazley [33] investigated on forced convection between two rotating concentric cylinders, the gap of which is filling with a fluid and air. The inner and outer races are just like two rotating concentric cylinders, which were separated by the lubricant. The Nusselt number is given in Ref. [21] as

$$ {\text{Nu}} = \left\{ {\begin{array}{*{20}l} 2 \hfill & {{\text{Ta}} < 41} \hfill \\ {0.167\;{\text{Ta}}^{0.69} \Pr^{0.4} } \hfill & {41 \le {\text{Ta}} < 100} \hfill \\ {0.401\;{\text{Ta}}^{0.5} \Pr^{0.4} } \hfill & {100 < {\text{Ta}}} \hfill \\ \end{array} } \right., $$

(14)

the Taylor number is $Ta = Re\sqrt {\frac{{\delta_{\text{io}} }}{r}}$, where $\delta_{\text{io}} = \frac{{d_{\text{o}} - d_{\text{i}} }}{2}$ is the gap between inner and outer races, r is the inside radius of race.

• (c) The Nusselt numbers of LP rotor-ambient Nu_LP and HP rotor-ambient Nu_HP.

Because LP and HP rotors are rotating, the heat exchange between two rotors and the ambient (air) are forced convection. The Nusselt number is given in Ref. [34] as

$$ {\text{Nu}} = \left\{ {\begin{array}{*{20}l} {0.00308 \, \text{Re} + 4.432} \hfill & {\text{Re} < 7300} \hfill \\ {\text{Re}^{0.37} } \hfill & {7300 \le \text{Re} < 9600} \hfill \\ {30.5 \, \text{Re}^{ - 0.0042} } \hfill & {9600 < \text{Re} } \hfill \\ \end{array} } \right.. $$

(15)

4 Results and discussion

4.1 Nonlinear behaviors of the dynamic load

The dynamic equations of the dual-rotor system Eq. (1) are nonlinear due to the nonlinearities of the restoring forces of the inter-shaft bearing. The fourth-order Runge–Kutta method is applied to solve dynamic equations Eq. (1), the dynamic responses are available with the help of the ode45 function in MATLAB^®. The RMS is used to express the amplitude in the amplitude frequency curve. Figure 4 displays the amplitude frequency curve of the LP rotor in the dual-rotor system. The dynamic parameters are taken as: the rotation speed ratio $\lambda = 1.2$, the LP rotor’s unbalance e₁ = 3 μm, the HP rotor’s unbalance e₁ = 2 μm. The run-up curve represents the rotation speed increases from a lower rotation speed to a higher rotation speed. On the contrary, the run-down curve represents the rotation speed decreases from a higher rotation speed to a lower rotation speed. The amplitude frequency curve of the HP rotor in the dual-rotor system is omitted because its shape is same with that of the LP rotor.

Fig. 4

Amplitude frequency curve of the LP rotor in the dual-rotor system. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 4, it can be seen that there are two resonance regions, which are caused by double unbalance excitations of HP and LP rotors in both run-up and run-down curves. In the run-up curve, the vibration amplitude increases sharply until the rotation speed reaches $\omega_{{{\text{A}}_{\text{up}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$, the jump phenomenon occurs, i.e., the vibration amplitude decrease abruptly; in the run-down curve, the jump phenomenon happens when the rotation speed reduces to $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{down}} }}$, i.e., the vibration amplitude increases abruptly. When the rotation speed $\omega_{1} \in \left[ {\omega_{{{\text{A}}_{\text{down}} }} , \omega_{{{\text{A}}_{\text{up}} }} } \right]$ and $\omega_{1} \in \left[ {\omega_{{{\text{B}}_{\text{down}} }} , \omega_{{{\text{B}}_{\text{up}} }} } \right]$, the vibration amplitude in run-up curve do not overlap with that in run-down curve, which means the bi-stable phenomenon occurs. In mathematics, it means Eq. (1) have two stable solutions among two “bi-stable interval” $\left[ {\omega_{{{\text{A}}_{\text{down}} }} , \omega_{{{\text{A}}_{\text{up}} }} } \right]$ and $\left[ {\omega_{{{\text{B}}_{\text{down}} }} , \omega_{{{\text{B}}_{\text{up}} }} } \right]$. Which stable solution the dynamic equations converge to depends on the initial state of motion. The initial states for the run-up curve and the run-down curve at “jump point” A_down, A_up, B_down and B_up are different; thus, the run-up curve and the run-down curve do not overlap among “bi-stable interval.”

In order to analyze the nonlinear behaviors of dynamic responses in detail, the vibration response analysis for ω₁ = 675 rad/s in the run-up curve and in the run-down curve are shown in Figs. 5 and 6. The analysis methods include the time histories for vertical and horizontal responses, orbit diagrams, Poincaré diagrams, and spectrum diagrams (wherein f_L is the frequency of the LP rotor; f_H is the frequency of the HP rotor; 2f_H − f_L, 3f_H − 2f_L and f_H + f_L are the combination frequencies of the HP rotor with the LP rotor; 2f_H is the double frequency of the HP rotor).

Fig. 5

Vibration response analysis for ω₁ = 675 rad/s in the run-up curve. a Vertical response. b Horizontal response. c Orbit diagram. d Poincaré diagram. e Spectrum diagram

Fig. 6

Vibration response analysis for ω₁ = 675 rad/s in the run-down curve. a Vertical response. b Horizontal response. c Orbit diagram. d Poincaré diagram. e Spectrum diagram

Comparing Figs. 5 and 6, the rotation speed are both ω₁ = 675 rad/s; the only difference between them is that Fig. 5 is located in the run-up curve while Fig. 6 is located in the run-down curve. However, the dynamic responses are very different from each other. In Fig. 5, the vertical and horizontal responses are almost harmonic signals, the orbit diagram is circular, the Poincaré diagram only has one point, and f_H is the dominant frequency, f_L is so small that it could be ignored. In Fig. 6, the vertical and horizontal responses are quasi-periodic signals, and look like beat vibrations. The orbit diagram is unclosed circle ring. The Poincaré diagram have six points. f_L and f_H are the dominant frequency, but the combination frequencies (2f_H − f_L, 3f_H − 2f_L and f_H + f_L) and the double frequency (2f_H) also occurs.

The restoring forces of the inter-shaft bearing can be attained by substituting the dynamic responses into Eq. (2). The restoring forces of the inter-shaft bearing for ω₁ = 675 rad/s in the run-up curve and in the run-down curve are displayed in Figs. 7 and 8. It can be found the force state of the inter-shaft bearing are very different from each other. The force of Fig. 7 is significantly greater than Fig. 8. Moreover, the restoring forces all vary periodically. The vertical and horizontal restoring forces are variable forces at a certain rotation speed. It is very difficult and inconvenient to describe the actual load of the inter-shaft bearing by using the vertical and horizontal restoring forces.

Fig. 7

The restoring forces of the inter-shaft bearing for ω₁ = 675 rad/s in the run-up curve. a Vertical restoring force. b Horizontal restoring force

Fig. 8

The restoring forces of the inter-shaft bearing for ω₁ = 675 rad/s in the run-down curve. a Vertical restoring force. b Horizontal restoring force

The dynamic load of the inter-shaft bearing can be obtained by substituting the restoring forces into the definition of the dynamic load Eq. (3). Figure 9 illustrates the variation of the dynamic load versus the rotation speed. It can be found that jump phenomenon also occurs at four “jump point” A_down, A_up, B_down and B_up, and bi-stable phenomenon occurs among two “bi-stable interval” $\left[ {\omega_{{{\text{A}}_{\text{down}} }} , \omega_{{{\text{A}}_{\text{up}} }} } \right]$ and $\left[ {\omega_{{{\text{B}}_{\text{down}} }} , \omega_{{{\text{B}}_{\text{up}} }} } \right]$. The dynamic load shows the same behaviors as the vibration amplitude. Comparing with restoring forces, the dynamic load is a constant force at a certain rotation speed. Thus, it is easier and more convenient to describe the actual load of the inter-shaft bearing.

Fig. 9

Variation of dynamic load with rotation speed. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In a word, the nonlinearities of the inter-shaft bearing, including the radial clearance and the fractional exponential relationship of the Hertzian contact, are considered during the dynamic modeling for the dual-rotor system. The dynamic load of the inter-shaft bearing is defined according to the nonlinear dynamic responses of the system. The dynamic load shows nonlinear behaviors, i.e., jump and bi-stable phenomena. It means the dynamic load can reflect the nonlinear dynamic characteristics of the system, which makes it much more complex than the static load. In conclusion, the dynamic load defined in this paper is more appropriate than the static load employed in most of the references to describe the actual load of the inter-shaft bearing.

4.2 Nonlinear thermal behaviors

The governing equations of steady-state heat transfer for the inter-shaft bearing Eq. (8) are linear matrix equations. The Gauss–Seidel iteration, an indirect method, is applied to solve the linear matrix equations, because the coefficient matrix A may be an ill condition [35] in many cases. The error of the Gauss–Seidel iteration for every rotation speed is set as $\left\| {T^{\left( n \right)} - T^{{\left( {n - 1} \right)}} } \right\| \le 10^{ - 12}$ (n denotes iteration time). The variation for temperatures of rollers, inner race and outer race with rotation speed, is plotted in Fig. 10. Thermal parameters are taken as: the lubricant viscosity $\nu = 5{\text{ mm}}^{2} /{\text{s}}$, the ambient temperature $T_{\infty } = 20\;^{\text{o}} {\text{C}}$.

Fig. 10

Variation for temperatures of rollers, inner race and outer race with rotation speed. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 10, it can be observed that the temperature of rollers T_r higher than the temperature of inner race T_i higher than the temperature of outer race T_o in both run-up and run-down curves, i.e., T_r > T_i > T_o. Nevertheless, the variation of T_r, T_i and T_o in both run-up and run-down curves with rotation speed are the same with each other. Therefore, we take T_r as an example to analyze nonlinear thermal behaviors of the inter-shaft bearing in the following sections. In the resonance regions A and B, T_r in run-up curve rises sharply until the rotation speed reaches $\omega_{{{\text{A}}_{\text{up}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$, the jump phenomenon happens, i.e., T_r declines abruptly; T_r in run-down curve declines gradually until the rotation speed reduces to $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{down}} }}$, the jump phenomenon happens, i.e., T_r rises abruptly. When the rotation speed $\omega_{1} \in \left[ {\omega_{{{\text{A}}_{\text{down}} }} , \omega_{{{\text{A}}_{\text{up}} }} } \right]$ and $\omega_{1} \in \left[ {\omega_{{{\text{B}}_{\text{down}} }} , \omega_{{{\text{B}}_{\text{up}} }} } \right]$, T_r in run-up curve do not overlap with T_r in run-down curve, which implies the bi-stable phenomenon happens.

In order to further analyze nonlinear thermal behaviors in the following sections, we introduce some symbols and parameters as: A_down, A_up, B_down and B_up are named as “jump point”; $\omega_{{{\text{A}}_{\text{down}} }}$, $\omega_{{{\text{A}}_{\text{up}} }}$, $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ are named as “frequency of jump point”; $\Delta T_{{{\text{A}}_{\text{down}} }}$, $\Delta T_{{{\text{A}}_{\text{up}} }}$, $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ are named as “jump amplitude”; $\Delta \omega_{\text{A}} = \left[ {\omega_{{{\text{A}}_{\text{down}} }} , \omega_{{{\text{A}}_{\text{up}} }} } \right]$ and $\Delta \omega_{\text{B}} = \left[ {\omega_{{{\text{B}}_{\text{down}} }} , \omega_{{{\text{B}}_{\text{up}} }} } \right]$ are named as “bi-stable interval.”

It is vital to carry out the FH analysis, including the total FH, the load FH and the viscosity FH, for exploring the inherent mechanism of nonlinear thermal behaviors of the inter-shaft bearing. Figure 11 displays the variation of the total FH, the load FH and the viscosity FH with rotation speed. The solid lines denote run-up curves and the dotted lines denote run-down curves.

Fig. 11

Variation of the total FH, the load FH and the viscosity FH with rotation speed. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 11, the blue line represents the viscosity FH Q_ν, Q_ν increases gradually with the increase of rotation speed, no nonlinear thermal behavior happens. The green line represents the load FH Q_l, Q_l shows jump phenomenon at “jump point” A_up and B_up in run-up curve while at “jump point” A_down and B_down in run-down curve; bi-stable phenomenon happens among two “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$. The red line represents the total FH Q, Q increases gradually with the increase of the rotation speed beyond $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$; Q shows jump phenomenon at A_up and B_up in run-up curve while at A_down and B_down in run-down curve; bi-stable phenomenon happens among $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$.

In a word, the direct reason why temperatures of the inter-shaft bearing show nonlinear thermal behaviors, i.e., jump and bi-stable phenomena, is the load FH shows nonlinear behaviors, while the root reason is the nonlinear dynamic characteristics of the dual-rotor system. The dynamic load of the inter-shaft bearing is introduced to calculate the load FH. The dynamic load can reflect the nonlinear dynamic characteristics of the dual-rotor system. This unique discovery cannot be found if the static load is applied to calculate the load FH.

4.3 Effect of rotation speed ratio

The effect of the rotation speed ratio on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section, the rotation speed ratio are $\lambda = 1.1$, $\lambda = 1.15$, $\lambda = 1.2$ and $\lambda = 1.25$. The variation for temperature of rollers with rotation speed under different rotation speed ratio are depicted in Fig. 12.

Fig. 12

Variation for temperature of rollers with rotation speed under different rotation speed ratio. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 12, with the increase of rotation speed ratio λ, the temperature of rollers T_r rises obviously; “frequency of jump point” $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ are still, but $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{A}}_{\text{up}} }}$ decrease obviously; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{down}} }}$, $\Delta T_{{{\text{A}}_{\text{up}} }}$, $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ all increase apparently; “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$ remain the original length, while $\Delta \omega_{\text{B}}$ is wider than $\Delta \omega_{\text{A}}$.

Comparing the values of $\omega_{{{\text{A}}_{\text{down}} }}$, $\omega_{{{\text{A}}_{\text{up}} }}$, $\omega_{{{\text{B}}_{\text{down}} }}$, $\omega_{{{\text{B}}_{\text{up}} }}$ with λ, the approximate relation is as follows:

$$ \frac{{\omega_{{{\text{B}}_{\text{down}} }} }}{{\omega_{{{\text{A}}_{\text{down}} }} }} \approx \lambda \approx \frac{{\omega_{{{\text{B}}_{\text{up}} }} }}{{\omega_{{{\text{A}}_{\text{up}} }} }}. $$

(16)

From Eq. (16), it can be seen that the rotation speed ratio has a crucial influence on $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{A}}_{\text{up}} }}$. In other words, the rotation speed ratio determines the relative position of four “jump point” and two “bi-stable interval” where nonlinear thermal behaviors happen.

4.4 Effect of rotors’ unbalances

The effect of the LP and HP rotors’ unbalances on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section. Firstly, the LP rotor’s unbalance are $e_{1} = 2{\upmu}{\text{m}}$, $e_{1} = 3{\upmu}{\text{m}}$, $e_{1} = 4{\upmu}{\text{m}}$ and $e_{1} = 5{\upmu}{\text{m}}$. The variation for temperature of rollers with rotation speed under different unbalances of LP rotor is depicted in Fig. 13.

Fig. 13

Variation for temperature of rollers with rotation speed under different unbalances of LP rotor. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 13, the temperature of rollers T_r under different LP rotor’s unbalances e₁ almost overlap except the resonance region B, which indicates e₁ mostly affects the region B. With the increase of e₁, “frequency of jump point” $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{A}}_{\text{up}} }}$ are still, but $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ increase sharply; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{down}} }}$ and $\Delta T_{{{\text{A}}_{\text{up}} }}$ barely change, while $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ increase apparently; “bi-stable interval” $\Delta \omega_{\text{A}}$ remains the original length, but $\Delta \omega_{\text{B}}$ becomes narrower.

Finally, the HP rotor’s unbalance are $e_{2} = 2{\upmu}{\text{m}}$, $e_{2} = 3{\upmu}{\text{m}}$, $e_{2} = 4{\upmu}{\text{m}}$ and $e_{2} = 5{\upmu}{\text{m}}$. The variation for temperature of rollers with rotation speed under different unbalances of HP rotor is depicted in Fig. 14.

Fig. 14

Variation for temperature of rollers with rotation speed under different unbalances of HP rotor. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 14, the temperature of rollers T_r under different HP rotor’s unbalances e₂ almost overlap except the resonance region A, which indicates e₂ mostly affects the region A. With the increase of e₂, “frequency of jump point” $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ are still, but $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{A}}_{\text{up}} }}$ increase sharply; “jump amplitude” $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ barely change, while $\Delta T_{{{\text{A}}_{\text{down}} }}$ and $\Delta T_{{{\text{A}}_{\text{up}} }}$ increase apparently; “bi-stable interval” $\Delta \omega_{\text{B}}$ remains the original length, but $\Delta \omega_{\text{A}}$ becomes narrower.

In summary, the unbalance of LP rotor only affects the resonance region B, while the unbalance of HP rotor only affects the resonance region A. With the increase of corresponding unbalance, the corresponding “frequency of jump point” and “jump amplitude” increase while the corresponding “bi-stable interval” becomes narrower.

4.5 Effect of inter-shaft bearings’ radial clearance

The effect of the inter-shaft bearings’ radial clearance on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section, the radial clearance are $\delta_{0} = 3{\upmu}{\text{m}}$, $\delta_{0} = 5{\upmu}{\text{m}}$, $\delta_{0} = 8{\upmu}{\text{m}}$ and $\delta_{0} = 10{\upmu}{\text{m}}$. The variation for temperature of rollers with rotation speed under different radial clearance are depicted in Fig. 15.

Fig. 15

Variation for temperature of rollers with rotation speed under different radial clearance. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 15, it can be seen that the radial clearance δ₀ has a significant influence on nonlinear thermal behaviors of the inter-shaft bearing. With the increase of δ₀, the highest temperature of T_r barely changes; “frequency of jump point” $\omega_{{{\text{A}}_{\text{up}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ decrease slightly, while $\omega_{{{\text{A}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{down}} }}$ decrease obviously; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{up}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ increase slightly, but $\Delta T_{{{\text{A}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{down}} }}$ increase apparently; “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$ become wider rapidly. It is worth noting that jump and bi-stable phenomena disappear when $\delta_{0} = 3{\upmu}{\text{m}}$.

In other words, the radial clearance of the inter-shaft bearing delays the contact between rollers and races, which is equivalent to reducing the stiffness of the inter-shaft bearing in another way [36]; thus, “frequency of jump point” decrease. Moreover, the radial clearance is an essential nonlinearity, thus reducing the radial clearance appropriately will significantly suppress nonlinear thermal behaviors, i.e., reduce “jump amplitude” and narrow “bi-stable interval.”

4.6 Effect of inter-shaft bearing’s stiffness

The effect of the inter-shaft bearings’ stiffness on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section; the stiffness are $K_{\text{b}} = 8K_{\text{b0}}$, $K_{\text{b}} = 10K_{\text{b0}}$, $K_{\text{b}} = 15K_{\text{b0}}$ and $K_{\text{b}} = 20K_{\text{b0}}$ ($K_{\text{b0}} = 10^{7} {\text{N}}/{\text{m}}^{10/9}$). The variation for temperature of rollers with rotation speed under different stiffness are depicted in Fig. 16.

Fig. 16

Variation for temperature of rollers with rotation speed under different stiffness. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 16, it can be seen that the stiffness K_b mostly affects nonlinear thermal behaviors of the inter-shaft bearing. With the increase of K_b, the highest temperature of T_r barely changes; “frequency of jump point” $\omega_{{{\text{A}}_{\text{down}} }}$, $\omega_{{{\text{A}}_{\text{up}} }}$, $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ all increase obviously; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{down}} }}$, $\Delta T_{{{\text{A}}_{\text{up}} }}$, $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ decrease slightly; “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$ become narrower slowly.

4.7 Effect of inter-shaft bearing’s roller number

The effect of the inter-shaft bearings’ roller number on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section; the roller number are $N_{\text{b}} = 12$, $N_{\text{b}} = 16$, $N_{\text{b}} = 20$ and $N_{\text{b}} = 24$. The variation for temperature of rollers with rotation speed under different roller numbers are depicted in Fig. 17.

Fig. 17

Variation for temperature of rollers with rotation speed under different roller numbers. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 17, it can be seen that the roller number N_b mostly affects nonlinear thermal behaviors of the inter-shaft bearing. With the increase of N_b, the highest temperature of T_r barely changes; “frequency of jump point” $\omega_{{{\text{A}}_{\text{down}} }}$, $\omega_{{{\text{A}}_{\text{up}} }}$, $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ all increase obviously; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{down}} }}$, $\Delta T_{{{\text{A}}_{\text{up}} }}$, $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ decrease slightly; “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$ become narrower slowly.

It is worth noting that the effect of the roller number on nonlinear thermal behaviors is very similar with the stiffness of the inter-shaft bearing. More roller number, more stressed roller number, greater dynamic load, and greater stiffness. Therefore, raising the stiffness and the roller number of the inter-shaft bearing moderately is helpful to suppress nonlinear thermal behaviors, i.e., reduce “jump amplitude” and narrow “bi-stable interval.”

4.8 Effect of the lubricant viscosity

The effect of the lubricant viscosity on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section; the lubricant viscosity are $\nu = 2\;{\text{mm}}^{2}/{\text{s}}$, $\nu = 5\;{\text{mm}}^{2}/{\text{s}}$, $\nu = 8\;{\text{mm}}^{2}/{\text{s}}$ and $\nu = 10\;{\text{mm}}^{2}/{\text{s}}$. The variation for temperature of rollers with rotation speed under different lubricant viscosity are depicted in Fig. 18.

Fig. 18

Variation for temperature of rollers with rotation speed under different lubricant viscosity. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 18, it can be seen that the lubricant viscosity ν has a significant influence on temperatures of the inter-shaft bearing. With the increase of ν, the temperature of rollers T_r rises sharply; “frequency of jump point” $\omega_{{{\text{A}}_{\text{down}} }}$, $\omega_{{{\text{A}}_{\text{up}} }}$, $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ are still; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{down}} }}$, $\Delta T_{{{\text{A}}_{\text{up}} }}$, $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ barely change; “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$ remains the original length.

4.9 Effect of the ambient temperature

The effect of the ambient temperature on temperatures and nonlinear thermal behaviors of the inter-shaft bearing is discussed in this section; the ambient temperature are $T_{\infty } = 20\;{}^{ \circ }{\text{C}}$, $T_{\infty } = 30\;{}^{ \circ }{\text{C}}$, $T_{\infty } = 40\;{}^{ \circ }{\text{C}}$ and $T_{\infty } = 50\;{}^{ \circ }{\text{C}}$. The variation for temperature of rollers with rotation speed under different ambient temperatures is depicted in Fig. 19.

Fig. 19

Variation for temperature of rollers with rotation speed under different ambient temperatures. (Solid lines represent run-up curves, dotted lines represent run-down curves)

In Fig. 19, it can be seen that the ambient temperature $T_{\infty }$ has a significant influence on temperatures of the inter-shaft bearing. With the increase of $T_{\infty }$, the temperature of rollers T_r rises sharply; “frequency of jump point” $\omega_{{{\text{A}}_{\text{down}} }}$, $\omega_{{{\text{A}}_{\text{up}} }}$, $\omega_{{{\text{B}}_{\text{down}} }}$ and $\omega_{{{\text{B}}_{\text{up}} }}$ are almost still; “jump amplitude” $\Delta T_{{{\text{A}}_{\text{down}} }}$, $\Delta T_{{{\text{A}}_{\text{up}} }}$, $\Delta T_{{{\text{B}}_{\text{down}} }}$ and $\Delta T_{{{\text{B}}_{\text{up}} }}$ barely change; “bi-stable interval” $\Delta \omega_{\text{A}}$ and $\Delta \omega_{\text{B}}$ remains the original length.

It is worthwhile to note that the effect of the lubricant viscosity and the ambient temperature is the same with each other. They both have a significant influence on temperatures of the inter-shaft bearing, while no effect on nonlinear thermal behaviors. Therefore, reducing the lubricant viscosity and the ambient temperature appropriately is contributive to control temperatures of the inter-shaft bearing.

5 Conclusions

In this paper, the dynamic load of the inter-shaft bearing has been defined according to the nonlinear dynamic responses of a dual-rotor system, based on which, a steady-state heat transfer model for the inter-shaft bearing subjected to the dynamic load has been set up with the help of Palmgren’s empirical formula. Thermal behaviors of the inter-shaft bearing affected by the nonlinear dynamic characteristics of the system have been studied in detail. Furthermore, an exhaustive parametric analysis for temperatures and nonlinear thermal behaviors of the inter-shaft bearing affected by dynamic and thermal parameters has been carried out. Some meaningful conclusions are drawn as follows:

• (1) The dynamic load can reflect the nonlinear dynamic characteristics of the dual-rotor system. It is more appropriate than the static load employed in most of the references to describe the actual load of the inter-shaft bearing.

• (2) Nonlinear thermal behaviors, i.e., jump and bi-stable phenomena, happen to temperatures of the inter-shaft bearing. There exists two “jump point” in both the run-up curve and the run-down curve, and two “bi-stable interval” are formed between the corresponding “jump point.”

• (3) The rotation speed ratio has a significant influence on both temperatures and nonlinear thermal behaviors of the inter-shaft bearing. Reducing the rotation speed ratio reasonably is not only helpful to curb temperatures, but also helpful to suppress nonlinear thermal behaviors.

• (4) Dynamic parameters mainly affect nonlinear thermal behaviors of the inter-shaft bearing. Reducing unbalances of rotors and the radial clearance or raising the stiffness and the roller number moderately are conducive to reduce “jump amplitude” and narrow “bi-stable interval.”

• (5) Thermal parameters only affect temperatures of the inter-shaft bearing. Reducing the lubricant viscosity and the ambient temperature appropriately are contributive to control temperatures at a lower level.

The unique discovery in this paper indicates the thermal behaviors of the inter-shaft bearing could be much more complex due to the nonlinear dynamic characteristics of the dual-rotor system. The future work will concentrate on the experimental verification of nonlinear thermal behaviors.

Appendix

The coefficient matrix A is a symmetric matrix, which is shown as follows:

$$A= \left[ {\begin{array}{*{20}c} { - \frac{1}{{R_{\text{ri}} }} - \frac{1}{{R_{\text{ro}} }} - \frac{1}{{R_{\text{Lr}} }}} & {\frac{1}{{R_{\text{ri}} }}} & {\frac{1}{{R_{\text{ro}} }}} & {} & {} & {\frac{1}{{R_{\text{Lr}} }}} \\ {\frac{1}{{R_{\text{ri}} }}} & { - \frac{1}{{R_{\text{ri}} }} - \frac{1}{{R_{\text{i}} }} - \frac{1}{{R_{\text{Li}} }}} & {} & {\frac{1}{{R_{\text{i}} }}} & {} & {\frac{1}{{R_{\text{Li}} }}} \\ {\frac{1}{{R_{\text{ro}} }}} & {} & { - \frac{1}{{R_{\text{ro}} }} - \frac{1}{{R_{\text{o}} }} - \frac{1}{{R_{\text{Lo}} }}} & {} & {\frac{1}{{R_{\text{o}} }}} & {\frac{1}{{R_{\text{Lo}} }}} \\ {} & {\frac{1}{{R_{\text{i}} }}} & {} & { - \frac{1}{{R_{\text{i}} }} - \frac{1}{{R_{\text{LP}} }}} & {} & {} \\ {} & {} & {\frac{1}{{R_{\text{o}} }}} & {} & { - \frac{1}{{R_{\text{o}} }} - \frac{1}{{R_{\text{HP}} }}} & {} \\ {\frac{1}{{R_{\text{Lr}} }}} & {\frac{1}{{R_{\text{Li}} }}} & {\frac{1}{{R_{\text{Lo}} }}} & {} & {} & { - \frac{1}{{R_{\text{Lr}} }} - \frac{1}{{R_{\text{Li}} }} - \frac{1}{{R_{\text{Lo}} }}} \\ \end{array} } \right] $$