1 Introduction

A capsule robot (capsubot) is a locomotion system that can move in a resistive environment without external propelling devices (legs, wheels, caterpillars, fins, water screws, etc.) due to the motion of internal bodies and interaction of the housing with the environment. A capsule robot consists of a rigid housing (capsule) and internal bodies that can be driven relative to the housing by actuators. The actuators provide interaction of the internal bodies with the robot’s housing. The forces applied by the actuators to an internal body cause the reaction force applied to the housing, due to which the velocity of the housing relative to the environment changes. The change in the velocity of the housing leads to a change in the resistance (friction) force applied to the housing by the environment. The forces generated by the actuators are internal forces for the mechanical system under consideration (the housing plus the internal bodies), whereas the friction force is an external force. Thus, by controlling the motion of the internal bodies by means of internal forces, we can control the external force applied to the robot, controlling thereby the motion of the entire system.

The main goal of our paper is to demonstrate new possibilities for control of a capsule robot provided by introducing an elastic element (a spring) that connects the internal body to the housing of the robot. The housing and the internal body connected by a spring form an oscillatory system that is characterized by a natural frequency and, therefore, resonance phenomena can be anticipated if the excitation force acting between the housing and the internal body changes periodically. These phenomena should be taken into account when forming the control mode. We confine ourselves to a simple model that can move along a straight line on a rough horizontal plane and involves single internal body connected to the housing by a spring with linear characteristic. We assume that the control force changes periodically in a piecewise constant pulse-width mode. Such a choice is justified by relative simplicity of this model for identification and analysis of the resonance-induced features in the behavior of the robot. It should be noted that the pulse-width mode of control is widely used in various engineering mechanical and electromechanical systems.

The main result of the paper is the identification of the phenomenon of change in the magnitude and direction of the average velocity of the capsule robot due to variation of the period or duty cycle of the excitation signal. These resonance-induced phenomena are characteristic of vibration-driven locomotors with elastic elements and can be used in control strategies.

The capsule robots with elastic elements have been studied by a number of researchers, and various designs of such systems have been considered. However, the resonant change in the average velocity due to variation of the period or duty cycle of the excitation signal was not reported previously.

The paper is structured as follows. Section 2 provides a review that outlines the state of the art and major research trends in the field of capsule-type vibration-driven robots. Sections 3 and 4 present a mathematical model of the capsule robot under investigation. Section 5 describes the analytical study and numerical simulation of the behavior of the robot according to its mathematical model; in this section, the basic observations and theoretical conclusions about the resonant behavior of the system are stated and discussed. Section 6 contains a description of the equipment and measurement techniques for experimental verification of the phenomena predicted theoretically and observed in computer simulation of the robot’s dynamic behavior. The experimental results are presented and discussed in Sect. 7.

2 State of the art

Capsule robots have a number of advantages over mobile systems of other types. They are simple in design, do not require complex mechanical chains for transmitting the motion from the motors to the propelling extremities, and are easy to miniaturize—qualities which are beneficial for the emerging challenges in mobile robotics for bio-medical applications and maintenance technology with limited space [4, 14, 40]. Capsule robots can be used inside narrow tubes, for example, for inspecting their technical state. The housing of the capsule robot can be made hermetic and smooth, without protruding parts, which enables it to be used for operations in vulnerable environments, in particular, in medicine for diagnostic inspection inside a human body or for delivering a drug to an affected organ [1, 42].

Capsule robots are a kind of vibration-driven locomotors [3, 48]. Vibration-driven locomotors can be defined as systems of bodies that in the general case interact between themselves and with the environment and perform oscillatory motions relative to each other. For a capsule robot, only the housing interacts with the environment; the internal bodies do not interact with the environment.

The effect of resonance is widely used in vibration-driven robots [2, 3, 21, 39].

The scientific base for designing capsule robots is provided by the investigations of dynamics and control of locomotion of systems that move in resistive media due to the motion of internal bodies. The motions that are generated by periodic motions of the internal bodies and occur with periodically changing velocities are of most interest for capsule robots. An important issue in these studies is the optimization of the motions with respect to speed and energy consumption.

An optimization problem for a body that moves in a resistive environment and is controlled by the motion of an internal body was first stated in [9, 10]. It is assumed that the main body (housing) moves along a straight line in a horizontal plane and that the friction between the supporting plane and the housing is dry friction that obeys Coulomb’s law. Periodic control modes are designed for the relative motion of the internal body, subject to which the housing moves with a periodically changing velocity and travels the same distance in a prescribed direction for each period. The internal body is allowed to move within fixed limits. It is assumed that at the beginning and the end of each period, the velocity of the housing is zero, while the internal body finds itself in its extreme positions. Velocity-based and acceleration-based control modes are considered. For the first case, the internal body moves forward and backward between its extreme positions at constant velocities. The magnitudes of these velocities are the design parameters. The acceleration-based control mode implies for each period three intervals during which the relative acceleration of the internal body is constant; a constraint is imposed on the absolute value of the relative acceleration of the internal body. The durations of the intervals and the magnitudes of the acceleration of the internal body in each of them are the design parameters. For both control modes, the optimal parameters that maximize the average velocity of the housing are found. Similar problems are also considered in [11]; unlike [9, 10], the assumption that the velocity of the housing vanishes when the internal body comes to its extreme positions is not imposed. The optimal parameters of the velocity-based control mode are found not only for dry-friction environments but also for the environments with piecewise linear and quadratic laws of resistance to the motion of the housing. The optimal parameters for the acceleration-based control mode are obtained numerically for the environment with a piecewise linear resistance law [17].

An optimal control problem is solved [19] for the rectilinear motion of the system described above along a horizontal line for the case where the friction between the housing and the plane obeys Coulomb’s law. The acceleration of the internal body relative to the housing is chosen as the control variable; the absolute value of this variable is subject to a constraint. A periodic control with zero average that provides a motion of the housing with periodically changing velocity and maximizes its average speed is designed. Using the designed control, one can restore the periodic law of motion of the internal body that generates the optimal motion of the system. A similar problem is solved [5] for the system with two internal bodies, one of which moves periodically along a horizontal line parallel to the line of motion of the housing, while the other body moves periodically along a vertical line. The internal body that moves vertically allows controlling the normal pressure of the housing on the supporting plane, controlling thereby the force of friction acting on the housing during its motion. An optimal control problem for the rectilinear motion of the body with a moving mass was studied in [6] for a wide class of nonlinear resistance laws; the performance index and the constraints coincide with those of [19]. An algorithm for calculating the optimal control is proposed, and characteristic features of the optimal motion are studied.

The energy-optimal control modes are designed and investigated for the motion of the system with one internal body in the environments with power-law resistance [15]. The energy consumption is measured by the work produced by the resistance forces for one period of the motion of the system. The optimal control is constructed for prescribed values of the period of the internal body motion and the average velocity of the system; no other constraints are imposed on the motion of the system. A similar problem is solved in [16] for the case where a hereditary model is used to account for the interaction of the housing with liquid environment.

A capsubot the control of which is based on the principles presented in [9, 10] is described in [29]. A prototype of this robot was designed and tested at Tokyo Denki University (Japan). The robot has an electromagnetic (solenoid) drive. The magnitude and direction of the force applied to the internal body are controlled by changing the magnitude and polarity of the voltage applied across the solenoid coil.

Various aspects of motion planning, modeling, and control for capsule robots are also considered in [18, 23, 24, 31, 45].

In all studies cited above, it is assumed that the only force that acts on the internal body of the robot in the direction of its motion is the control force generated by the system’s actuator. In the present paper, we consider a capsule robot the internal body of which is connected to the housing by a spring. In this case, an oscillatory link (housing–spring–internal body) appears in the system. This oscillatory link is characterized by its natural frequency, which essentially changes the dynamic behavior of the system; in particular, resonance phenomena can be observed if the control force changes periodically. A vibration-driven robot the bodies of which are connected by a spring is considered in [8, 20, 43]. This robot is designed for motion inside pipes. It consists of two bodies (modules) both of which have contact with the pipe surface. The system is actuated by an electromagnetic drive that provides a force interaction between the modules. The contact surfaces of the modules have mechanical devices [43] or coverings [8, 20] that provide anisotropy for friction against the pipe surface, due to which the friction force resisting the motion of the robot in the desired direction is substantially less than the friction force resisting the motion in the opposite direction. In [43], the general principle of the motion of the robot is outlined, the expressions for calculating the force of magnetic interaction between the modules are given, the parameters of the physical prototype of the robot built by the authors are presented, and the results of the experimental investigations are briefly described. In [8, 20], a mathematical model is constructed for a two-module vibration-driven in-pipe robot with an electromagnetic drive and an opposing spring. This model allows studying the dynamic behavior of the system. Computer simulation technique is used to investigate the robot’s dynamics, in particular, its steady-state behavior when the bodies of the robot oscillate periodically relative to each other and the force of interaction of the robot’s bodies changes periodically in a pulse-width mode. The average velocity of the robot is investigated as a function of the period and the duty cycle of the pulse-width excitation signal. The optimal parameters at which the robot moves at the maximal velocity are found. A physical prototype of this robot was built, and the experiments were performed. The experimental data agree with the simulation results. Unlike the system considered in [8, 20], for the system studied in the present paper, one of the bodies is an internal body and does not have contact with the surface and, in addition, the friction between the housing of the robot and the supporting forces is classical Coulomb’s friction that does not possess anisotropy.

A capsule-type mobile system with elastic and dissipative elements is studied in a series of papers [32,33,34,35,36, 44]. The authors of these papers consider a system that consists of a capsule (housing) and an internal body that can move inside the capsule. The internal body is attached to the housing by means of a spring and a damper connected in parallel. The spring has a nonlinear characteristic in the general case. Inside the capsule, there may be limiters that restrict the displacement of the internal body. The limiters are modeled as massless plates connected to the housing by springs. The housing interacts with the environment. The essential difference between the system considered in the cited papers and the system studied by us is that in [32,33,34,35,36, 44], the excitation force is an external force generated by a source located outside the capsule. For example, this force can be produced by an external electromagnet. The advantage of such systems is that they do not cause problems related to power supply. The capsule robot itself may have very small dimensions, but the energy supply system may have any dimensions and be powered from any source. This system is studied mostly as a special kind of nonlinear vibro-impact system. The authors concentrate on the classification of steady-state motions, stability of such motions, occurrence or absence of stick-slip modes, chaotic behavior, etc.

A capsubot that consists of a rigid housing and an inverted pendulum inside is considered in [30]. The housing moves along a straight line on a rough horizontal plane. Coulomb’s dry friction acts between the housing and the underlying plane. The pendulum is attached to the housing by a viscoelastic joint the axis of which is parallel to the underlying plane and perpendicular to the line of the motion of the housing. The motion of the system is excited by a harmonically changing torque applied to the joint of the pendulum. The behavior of this locomotion system is studied by means of nonlinear dynamics techniques. The influence of the stiffness and damping coefficients of the joint on the dynamical properties of the system is analyzed.

The capsubot considered in our paper contains one internal body that can move rectilinearly relative to the housing. Such a design allows the robot to move along a straight line. Most of the publications, including those cited above, deal with capsubots moving along a straight line. However, vibration-driven locomotors with internal bodies can perform more complex motions, in particular, planar motions in which both the position of the robot’s center of mass and its orientation are changing. To be able to perform controlled planar motions, capsubots must have an appropriate design.

In [22, 25, 26, 41, 47], capsule robots with two internal bodies moving along rectilinear guides that are parallel to each other and to the underlying surface are addressed. When the internal bodies move synchronously in phase, the capsubot translates along a straight line, as is the case for the system with one internal body. When the internal bodies move synchronously in anti-phase, the robot rotates changing its orientation. By alternating these two types of motions, a transfer of the robot between two arbitrary states (characterized by the position of the center of mass and the orientation of the robot) can be implemented. More complex control strategies that allow simultaneous change in the center of mass position and the orientation of the robot are also possible. Both theoretical and experimental studies are presented.

A planar locomotion robot driven by two internal bodies moving along rectilinear guides that are parallel to the underlying plane and perpendicular to one another is considered in [46].

In [12], an alternative design of the capsubot with two internal masses is proposed. The locomotion system consists of a rigid housing and two internal bodies—a point mass that is able to move along a horizontal line fixed in the housing and a rotor that may rotate about a vertical axis rigidly fixed to the housing. It is assumed that the guide for the motion of the point mass passes through the rotor’s rotation axis and that the center of mass of the rotor lies on the axis of its rotation which is a dynamic symmetry axis of the rotor. The system moves on a rough horizontal plane. Coulomb’s dry friction acts between the housing and the underlying plane. The internal bodies interact with the housing but do not interact with the underlying plane. The configuration of the system is defined by the position of its center of mass on the plane, the position of the internal point mass on the line of its motion relative to the housing, and the angle of rotation of the housing. The controllability of this system on a plane is proved, and a control strategy that drives the system between two prescribed configurations is designed.

A locomotion system with internal masses that move along straight lines relative to the housing and a rotor is also considered in [27]. However, unlike [12], the rotor revolves about a horizontal, rather than vertical, axis and is controlled by a torque applied to this axis. This torque causes an asymmetry in the distribution of the normal pressure over the contact surface of the system, which leads to a torque of the forces of friction applied to the housing of the robot when it is moving. Due to this torque, the housing of the robot changes its orientation relative to the underlying plane. A control strategy that provides a desired planar motion of the system under consideration is proposed.

In [13], it is shown that the control of planar motion of a capsubot can be provided by one internal body (point mass) that moves along a planar trajectory relative to the housing, and an appropriate control strategy is presented. According to this strategy, first, the internal body moves along a circumference relative to the housing as a result of which the housing rotates and acquires the desired orientation, and then, the housing moves along a two-link broken line to the desired position due to rectilinear relative motions of the internal body.

3 Mechanical model of the robot

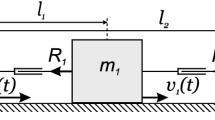
The robot consists of a rigid body (housing) and an electromagnetic (solenoid-type) drive located inside the housing.

Fig. 1
figure 1

Capsule-type robot. M—mass of the housing, m—mass of the core, c—spring rate \(F_e\)—control force, \(\mu \)—coefficient of dry friction

Full size image

The drive involves an electromagnetic coil (solenoid) that is rigidly attached to the housing and an internal body(core); the core is made of a ferromagnetic material and can move inside the solenoid along its axis. The core is attached to the housing by a spring, the axis of which is oriented along the solenoid’s axis. The solenoid’s axis is parallel to the axis of the housing. The housing interacts with a resistive environment in which the robot is moving. The robot is actuated by means of a magnetic force that acts on the core when an electric voltage is applied across the solenoid. The drive is designed so that the magnetic force acts in one direction and tends to pull the core inside the coil. The core returns to its initial position due to the spring. The schematic of the system described is shown in Fig. 1.

In this paper, we consider the model in which the force applied to the core by the solenoid is used as the control variable. The dynamics of the electric circuit of the solenoid is not taken into account. We assume that the robot moves on a horizontal plane along a straight line parallel to the axis of the robot’s housing. This model was suggested and derived in [7]. The current study extends the cited paper with experimental investigations.

4 Equations of motion

Let M denote the mass of the housing together with the solenoid, m the mass of the core, \(F_{{\mathrm{e}}}\) the force applied to the core by the solenoid, \(F_{{\mathrm{fr}}}\) the force with which the environment resists the motion of the housing, c the spring rate, x the coordinate that identifies the position of the housing’s center of mass relative to a fixed (inertial) reference frame, \(\xi \) the coordinate that identifies the position of the core’s center of mass relative to the housing. The variables x and \(\xi \) are measured along the line of motion of the robot. The coordinate \(\xi \) is chosen so that the spring is unstrained for \(\xi = 0\). Note that \(F_{{\mathrm{e}}}\) is an internal force for the system housing–solenoid–core, while \(F_{{\mathrm{fr}}}\) is an external force. We assume that the resistance force is a function of the velocity of the housing relative to the environment: \(F_{{\mathrm{fr}}} = F_{{\mathrm{fr}}}({\dot{x}})\), where the notation \({\dot{x}}\) indicates the time derivative of x.

By applying Newton’s second law separately to the housing and to the core, we obtain the governing equations for the system under consideration in the following form:

$$\begin{aligned} \begin{aligned}&M\ddot{x}(t) = c\,\xi (t) - F_{{\mathrm{e}}}(t) + F_{{\mathrm{fr}}}({\dot{x}}), \\&m\big (\ddot{x}(t) + \ddot{\xi }(t)\big ) = -c\,\xi (t) + F_{{\mathrm{e}}}(t). \end{aligned} \end{aligned}$$
(1)

Introduce the new variable

$$\begin{aligned} X(t) = x(t) + \frac{m}{M+m}\,\xi (t), \end{aligned}$$
(2)

that identifies the coordinate of the center of mass of the entire system in the inertial reference frame. The system (1) can be reduced to the form

$$\begin{aligned}&\displaystyle (M+m){\ddot{X}} = F_{{\mathrm{fr}}}\left( {\dot{X}} - \frac{m}{M+m}\,{\dot{\xi }}\right) , \nonumber \\&\frac{Mm}{M+m}\,\ddot{\xi } + c\,\xi = \, F_{{\mathrm{e}}} \, - \nonumber \\&\frac{m}{M+m}F_{{\mathrm{fr}}}\left( {\dot{X}} - \frac{m}{M+m}\,{\dot{\xi }}\right) . \end{aligned}$$
(3)

Consider the force generated by the drive as a periodic piecewise continuous function:

$$\begin{aligned} F_{{\mathrm{e}}} = \left\{ \begin{array}{ll} \displaystyle F_0, &{} \displaystyle {\left\{ \frac{t}{T}\right\} < \tau },\\[1em] \displaystyle 0, &{} \displaystyle {\left\{ \frac{t}{T}\right\} \ge \tau }, \end{array} \right. \end{aligned}$$
(4)

where T is the period, \(F_0\) is a positive constant that has a dimension of force, and \(\tau \) is a dimensionless positive constant from the interval \((0,\,1)\). The parameter \(\tau \) identifies the fraction of the period, during which the control force is not equal to zero. Curly brackets denote the fractional part of the expression enclosed in them. In physics and electronics, the excitation mode (4) is called a pulse-width mode, the parameter \(\tau \) being called the duty cycle of the pulse-width signal.

Assume that the resistance force \(F_{{\mathrm{fr}}}\) acting between the housing and the environment is the dry friction force that obeys Coulomb’s law:

$$\begin{aligned} \begin{array}{l} \displaystyle F_{{\mathrm{fr}}}({\dot{x}}) = \left\{ \begin{array}{ll} \displaystyle -N\mathrm{{sgn}}\,{\dot{x}}, &{}\quad {\dot{x}} \ne 0,\\[1em] \displaystyle -c\,\xi + F_{{e}}, &{}\quad {\dot{x}} = 0, \quad |\,c\,\xi - F_{{e}}| \le N, \\[1em] \displaystyle -N\mathrm{{sgn}}\,(c\,\xi - F_{{e}}), &{}\quad {\dot{x}} = 0, \quad |\,c\,\xi - F_{{e}}| > N, \end{array} \right. \\ \\ \displaystyle N=\mu (M+m)g, \end{array} \end{aligned}$$
(5)

where \(\mu \) is the coefficient of dry friction of the housing against the supporting plane and g is the acceleration due to gravity.

5 Simulation and analysis of the steady-state motion of the robot

For the robots of the type under consideration, of most interest is the motion mode in which the core is oscillating with period T relative to the housing, while the housing is moving relative to the environment at a rate that changes periodically with the same period T. We call such a mode of motion the steady-state mode. For steady-state motions, the functions \(\xi (t)\) and \({\dot{X}}(t)\) are T-periodic. An important characteristic of the steady-state motion of the robot is its average velocity V defined by

$$\begin{aligned} V = \frac{1}{T}\int \limits _0^T{\dot{X}}(t)\mathrm{d}t = \frac{X(T)-X(0)}{T}. \end{aligned}$$
(6)

The basic content of this section is the analysis of the dependence of the average velocity of the robot on the excitation parameters T and \(\tau \).

5.1 Simulation parameters

We assume that the robot moves along a horizontal rough plane. The simulation is performed for the invariable parameters of the robot presented in Table 1. These parameters correspond to the prototype of the capsule robot that will be discussed in the section devoted to the experiment.

Table 1 Parameters of the system
Full size table

5.2 Analysis of simulation results

The simulation results will be presented in dimensionless variables. Instead of V, t, and T, we will use the variables \(Vc/(F_0\omega )\), \(\omega t\), and \(\omega T\), respectively, preserving the previous notation for the normalized variables. The time scaling parameter \(\omega \) is defined by

$$\begin{aligned} \omega = \sqrt{\frac{c(M+m)}{Mm}}. \end{aligned}$$
(7)

This quantity is the natural frequency of the oscillatory system formed by the housing and core of the robot connected by a spring.

Figure 2 shows typical plots of the average velocity V versus the parameter \(\tau \) in the dimensionless units. The right plot corresponds to \(T = T_1 = 1.10 \cdot 2\pi \), while the left plot to \(T = T_2 = 0.66 \cdot 2\pi \). Notice that the excitation periods \(T_1\) and \(T_2\) satisfy the inequalities \(T_2< 2\pi < T_1\) and that \(2\pi \) is the dimensionless period of natural vibrations of the robot caused by the spring that connects the internal body (core) with the housing. Therefore, the excitation mode with period \(T_1\) can be called the pre-resonance mode and the excitation mode with period \(T_2\), the post-resonance mode.

Fig. 2
figure 2

Simulation results for variation of \(\tau \)

Full size image

Both curves demonstrate that the average velocity of the steady-state motion of the robot depends significantly on the duty cycle of the pulse-width excitation signal, which indicates the possibility of controlling the motion of the robot by changing only the parameter \(\tau \). For \(\tau = 0\), \(\tau = 1/2\), and \(\tau = 1\), the average velocity of the robot is equal to zero. Both curves possess a property of central symmetry about the point \((1/2, \, 0)\) of the coordinate plane \(\tau V\). This implies that changing the duty cycle of the excitation signal from \(\tau \) to \(1 - \tau \) at the same period leads to the change in the direction of motion of the capsule robot, with the magnitude of its velocity being preserved.

This property holds for all systems governed by Eq. (3), subject to the pulse-width excitation mode (4), provided that the function \(F_{{\mathrm{fr}}}(z)\) is an odd function of the argument \(\displaystyle z= {\dot{X}} - m{\dot{\xi }}/(M+m)\). We will prove a respective mathematical proposition. We will indicate the dependence of the quantities V and \(F_{{\mathrm{e}}}(t)\) on the parameter \(\tau \) by a superscript in the square brackets, i.e., instead of V and \(F_{{\mathrm{e}}}(t)\) we will write \(V^{[\tau ]}\) and \(F_{{\mathrm{e}}}^{[\tau ]}(t)\), respectively.

Definition (4) for the function \(F_e^{[\tau ]}(t)\) for \(F_0 = 1\) implies the relationship

$$\begin{aligned} F_{{\mathrm{e}}}^{[\tau ]}(t) = 1-F_{{\mathrm{e}}}^{[1-\tau ]}(t - \tau T). \end{aligned}$$
(8)

Proposition

The average velocities \(V^{[\tau ]}\) and \(V^{[1-\tau ]}\) are related by

$$\begin{aligned} V^{[\tau ]}=-V^{[1-\tau ]}. \end{aligned}$$
(9)

Proof

Perform in equations (3), where \(F_{{\mathrm{e}}} = F_{{\mathrm{e}}}^{[\tau ]}(t)\), the change of variables

$$\begin{aligned} Y(t) = -X(t+\tau T), \quad \eta (t) = -\xi (t+\tau T) + 1. \end{aligned}$$
(10)

Since the function \(F_{{\mathrm{fr}}}(z)\) is odd in the argument \(z = {\dot{X}} - m{\dot{\xi }}/(M+m)\) and relation (8) holds, we obtain

$$\begin{aligned}&(M + m)\,{\ddot{Y}} = F_{{\mathrm{fr}}}\left( {\dot{Y}} - \frac{m}{M+m}\,{\dot{\eta }}\right) , \nonumber \\&\frac{Mm}{M+m}\,\ddot{\eta } + c\,\eta = \, F_{{\mathrm{e}}}^{[1-\tau ]}(t) \, - \nonumber \\&\frac{m}{M+m}\,F_{{\mathrm{fr}}}\left( {\dot{Y}} - \frac{m}{M+m}\,{\dot{\eta }}\right) . \end{aligned}$$
(11)

This implies that if the functions X(t) and \(\xi (t)\) define a solution of system (3) for \(F_{{\mathrm{e}}} = F_{{\mathrm{e}}}^{[\tau ]}(t)\), then the functions Y(t) and \(\eta (t)\) define a solution of the same system for \(F_{{\mathrm{e}}} = F_{{\mathrm{e}}}^{[1-\tau ]}(t)\). If, in addition, the functions \({\dot{X}}(t)\) and \(\xi (t)\) are T-periodic, then the functions \({\dot{Y}}(t)\) and \(\eta (t)\) are also T-periodic. Differentiation of the first equation (10) yields the relation \({\dot{Y}}(t) = -{\dot{X}}(t+\tau T)\), which for the case of a T-periodic function \({\dot{X}}(t)\) implies the relations

$$\begin{aligned} \int \limits _0^T{\dot{Y}}(t)\mathrm{d}t = -\int \limits _0^T{\dot{X}}(t+\tau T)\mathrm{d}t = -\int \limits _0^T{\dot{X}}(t)\mathrm{d}t. \end{aligned}$$
(12)

Since

$$\begin{aligned} V^{[\tau ]} = \frac{1}{T}\int \limits _0^T{\dot{X}}(t)\mathrm{d}t, \quad V^{[1-\tau ]} = \frac{1}{T}\int \limits _0^T{\dot{Y}}(t)\mathrm{d}t, \end{aligned}$$
(13)

equations (12) imply relation (9). This completes the proof of the proposition.

Corollary

For \(\tau = 1/2\), the average velocity of the steady-state motion of the system is equal to zero: \(V^{[1/2]} = 0\).

The curves in Fig. 2 demonstrate an essential qualitative difference. In the right plot of Fig. 2, the function \(V(\tau )\) has a maximum in the interval (0, 1/2), and the value of this maximum is positive, while in the left plot of Fig. 2 this function has a minimum in the same interval and the value of this minimum is negative. Recall that the right plot of Fig. 2 corresponds to the pre-resonant excitation mode (\(T > 2\pi \)), while the left plot of Fig. 2 characterizes the post-resonant mode (\(T < 2\pi \)). This observation suggests a conjecture about the resonance effect that exhibits itself in the change in the direction of motion when the excitation period T passes through certain critical values close to multiples of the period of the natural elastic vibrations of the system.

The resonance-induced change in the direction of motion of a mobile vibration-driven system was observed previously in [49]. In the cited paper, a two-component locomotion system moving along a straight line on a horizontal plane is considered. The system consists of two identical modules, each of which involves a rigid body and an unbalanced vibration exciter. The unbalanced vibration exciter is a rotor the center of mass of which does not lie on the axis of the rotation. The modules are connected to each other by a spring with linear characteristic. The friction acting between the modules of the system and the plane along which the system is moving is Coulomb’s dry friction. The coefficient of friction is assumed to be small. The motion of the system is excited by rotation of both rotors with identical constant angular velocities but with a phase shift. (The perpendiculars dropped from the centers of mass of the rotors onto their axes of rotation are not parallel.) In the system described, the change in the direction of motion is observed when the excitation frequency passes through the resonance value that is equal to the natural frictionless vibration frequency of the modules connected by a spring.

Fig. 3
figure 3

Simulation results for \(\tau = 0.3\)

Full size image

The resonant change in the sign of the average velocity of the robot is clearly seen on the curve plotting the average velocity V versus the excitation period T. Figure 3 shows such a curve for \(\tau = 0.3\). In this case, the change in the average velocity sign occurs at \(T = 2\pi \), which corresponds to the resonance period, and at \(T = 1.14 \cdot 2\pi \).

Qualitatively, this behavior is preserved for other \(\tau \in (0,\,1/2)\). According to the proposition stated above, the plots of V versus T that correspond to the values \(\tau \) and \(1-\tau \) of the duty cycle of the pulse-width excitation signal are symmetric to each other relative to axis T.

The above observations imply that the motion of the robot can be controlled by changing either the duty cycle or the period of the excitation signal.

6 Experiment

The experiment was carried out to investigate the influence of the excitation parameters on the average velocity of the robot. The simulation demonstrates two interesting facts: first, that the change in only one parameter \(\tau \), which indicates the duty cycle of the excitation during the period time T, can result in the change in the direction of the average velocity, with the magnitude of this velocity being preserved; second, that the direction of the average velocity can be inverted by varying the period time T while \(\tau \) is fixed. To verify these facts on the physical prototype of the robot is the main purpose of the experiments described as follows.

6.1 Experimental setup

The experimental setup consists of three basic parts: a capsule robot, a rail guide, and a power source. The power source supports the discrete voltage supply mode; the minimal discretization step is \(1~\mathrm {ms}\). Figure 4 shows the experimental prototype of the capsule robot on the rail guide. The robot design includes a solenoid, a core, a spring, and a base. The solenoid and the base together form the housing of the robot. The robot is actuated due to motion of the internal body (core) with respect to the housing of the robot. The overall dimensions of the robot are \(L \times W \times H = 227 \times 30 \times 50 \, \mathrm {mm}\). The other parameters are given in Table 1. The rail guide prevents the robot housing from lateral motion. The rail guide, the housing, the coil, and the core are equipped with markers for motion tracking.

Fig. 4
figure 4

The prototype of capsule-type robot

Full size image

6.2 Experimental procedure and exemplary motion schemes

To provide the locomotion, the electromagnet is powered with a periodic piecewise continuous voltage \(U_{{\mathrm{e}}}\) created by the programmable power source:

$$\begin{aligned} U_{{\mathrm{e}}} = \left\{ \begin{array}{ll} \displaystyle U_0, &{}\quad \displaystyle {\left\{ \frac{t}{T}\right\} < \tau },\\[1em] \displaystyle 0, &{}\quad \displaystyle {\left\{ \frac{t}{T}\right\} \ge \tau }, \end{array} \right. \end{aligned}$$
(14)

where T is the period; \(U_0\) is a positive constant voltage; \(\tau \) is a dimensionless positive constant that belongs to the interval \((0,\,1)\) and identifies the fraction of the period during which the control voltage is not equal to zero; curly brackets denote the fractional part of the expression enclosed in them. The change in the magnitude of the voltage leads to the change in the magnitude of the force \(F_e\) acting on the core. The selected voltage control mode does not guarantee that the time history of the generated force \(F_e\) is identical to that defined in the mathematical model (4). Therefore, it is expected that the experimental and simulated data will not match quantitatively. However, the qualitative effects are expected to be observed.

The locomotion is analyzed by tracking the markers on the core and the coil. Two exemplary locomotion characteristics are given in Figs. 5 and 6. The presented video frames illustrate the motion of the system during one period T and its position after a number of cycles. The diagrams in Figs. 5 and 6 present the time histories of the positions of the coil and the core. It is apparent that the core performs a periodic motion relative to the housing that leads to a locomotion of the entire robot with a constant average velocity. Figure 5 presents the tracking results when the period of the excitation signal is below the predicted resonance period, while Fig. 6 shows the tracking results when the excitation period exceeds the resonance period.

Fig. 5
figure 5

Motion of the experimental system: \(T = 60\) ms, \(\tau = 0.70\)

Full size image
Fig. 6
figure 6

Motion of the experimental system: \(T = 100\) ms, \(\tau = 0.70\)

Full size image

7 Experimental analysis and results

The experimental analysis and results will be presented in the same dimensionless variables that were used in the section of the analysis of the simulation results. Instead of V, t, and T, we will use the variables \(Vc/(F_0\omega )\), \(\omega t\), and \(\omega T\), respectively, preserving the previous notation for the normalized variables. The time scaling parameter \(\omega \) is defined by (7), which is the natural frequency of the oscillatory system formed by the housing and the core of the robot connected by a spring.

7.1 Average velocity vs \(\tau \)

The first part of the experiment is aimed at the investigation of the dependence of the average velocity V of the robot on the excitation parameter \(\tau \) while the parameter T is fixed. The displacement of the housing of the robot \(x_t\) is measured for the time equal to t, and the average velocity is calculated as \(x_t/t\). Two values of T are selected as was the case for the previous mathematical analysis; one of them corresponds to the pre-resonance period (\(T = 1.10 \cdot 2\pi \)), while the other to the post-resonance period (\(T = 0.66 \cdot 2\pi \)).

Fig. 7
figure 7

The dependencies of average velocities on \(\tau \)

Full size image

Figure 7 shows the dependencies obtained from the experiment. From this figure, it is clear that the average velocity of the robot depends significantly on the duty cycle of the voltage control signal \(\tau \). For \(\tau = 0\), \(\tau = 1\), and near \(\tau = 0.5\), the average velocity of the robot is equal to zero. The difference between the magnitudes of the maximum and minimum of average velocities with respect to \(\tau \) for each fixed T is less than \(20\%\) (see Table 2).

Table 2 Extreme values of average velocity
Full size table

Therefore, the motion in any direction without significant reduction in the magnitude of the average velocity can be provided by controlling only one parameter \(\tau \) at a fixed period T.

7.1.1 Central symmetry property in the experimental data set

For the simulated data, the property \(V^{[\tau ]}=-V^{[1-\tau ]}\) holds for all systems governed by Eq. (3), subject to the pulse-width excitation mode (4), provided that the function \(F_{{\mathrm{fr}}}(z)\) is an odd function of the argument \(\displaystyle z= {\dot{X}} - m{\dot{\xi }}/(M+m)\).

To test this property for the physical prototype, we approximate the experimental data with a function that has the same property. In this research, we select this function as follows:

$$\begin{aligned} V = f(\tau ) = A\,\sin \Bigg (\frac{\pi (\tau - \tau _c)}{\omega _s}\Bigg ), \end{aligned}$$
(15)

where A, \(\tau _c\), and \(\omega _s\) are the parameters to be identified. The proposed function has a central symmetry property with respect to the point \((\tau _c, 0)\) in the interval [0,  1].

We assume the following model for the measurement process:

$$\begin{aligned} V(\tau ) = f(\tau ) + \xi , \end{aligned}$$
(16)

where \(V(\tau )\) is the result of measurement of the average velocity of the robot for the excitation signal duty cycle \(\tau \), \(f(\tau )\) is the true value of the average velocity for the duty cycle \(\tau \), and \(\xi \) is a random error of measurement. For the random variable \(\xi \), we assume the Gaussian distribution with zero expected value.

Let \(\{V\}\) denote the set of the values of V obtained as a result of n measurements: \(\{V\} = (V_1,\,V_2,\,\ldots ,\,V_n)\). The values of \(\tau \) for different measurements may be different or coincide. It is reasonable to select the parameters of the function \(f(\tau )\) so as to maximize the probability of the realization of the measurement data set \(\{V\}\) (the maximum likelihood principle). In this case, the parameters A, \(\tau _c\), and \(\omega _s\) of the function \(f(\tau )\) are defined as a result of minimization of the sum of the squares of the measurement errors realized in the respective series of experiments:

$$\begin{aligned} \sum \limits _{i=1}^n \xi _i^2 = \sum \limits _{i=1}^n \Big (V_i - f(\tau _i)\Big )^2 \rightarrow \min _{A, \tau _c, \omega _s}, \end{aligned}$$
(17)

where \(\tau _i\) is the value of \(\tau \) in the experiment number i and \(V_i\) is the average velocity measured in this experiment.

Fig. 8
figure 8

Fitting models

Full size image

This problem was solved using Levenberg–Marquardt algorithm [28, 37]. During calculations, the confidence level of \(95\%\) is used [38]. The fitting results are illustrated in Fig. 8; the corresponding statistical information is given in Table 3.

Table 3 Fitting parameters
Full size table

The estimated value of the parameter \(\tau _c\) is close to 0.5; therefore, it can be said that the property of central symmetry with respect to the point close to (0.5, 0) is observed in the experimental data as well as in the simulated data.

7.1.2 Qualitative matching

The comparison between the simulated and the experimental data is depicted in Fig. 9. It can be seen from this figure that the simulated data for the parameter \(T = 0.66 \cdot 2\pi \) fit the experimental curve well, whereas for \(T = 1.10 \cdot 2\pi \) the discrepancy between the simulated and the experimental data is significant. This significant discrepancy could be accounted for by the fact that in the computational model, we ignored the dynamics of the electric circuit of the solenoid. However, the qualitative coincidence is fairly well: The zeros of the respective simulated and experimental curves are close to each other, and the values of the average velocity coincide in sign for the majority of the values of \(\tau \). In the simulation, there is an essential qualitative difference between the curves for \(T = 0.66 \cdot 2\pi \) and \(T = 1.10 \cdot 2\pi \), which is reflected in the change in the sign of the average velocities for the same values of \(\tau \). The same qualitative difference is observed for the experimental data. For example, the average velocity in the interval \(0 \le \tau \le 0.5\) is nonnegative for \(T = 1.10 \cdot 2\pi > 2\pi \) and non-positive for \(T = 0.66 \cdot 2\pi < 2\pi \). This effect could be explained by the resonance phenomenon.

Fig. 9
figure 9

The dependencies of average velocities on \(\tau \)

Full size image

7.2 The resonance effect

The resonant change in the sign of the average velocity of the robot can be seen from the curve plotting the average velocity V versus the excitation period T. For this reason, the second part of the experiment is aimed at the investigation of the dependence of the average velocity V of the robot on the parameter T, with the parameter \(\tau \) being fixed. For the experiments, we took \(\tau = \tau _1 = 0.3\) and \(\tau = \tau _2 = 0.7\) (\(\tau _2 = 1 - \tau _1\)). These values of \(\tau \) were previously taken for the simulation on the basis of the mathematical model of the robot. The experimental results are depicted in Fig. 10. In the case of the curve for \(\tau = 0.3\), the change in the velocity sign occurs at \(T = 0.82 \cdot 2\pi \), while in the case of the curve for \(\tau = 0.7\) the change in the velocity sign occurs at \(T = 0.77 \cdot 2\pi \). Thus, the experiments record the resonant change in the average velocity of the robot as T changes, as is predicted by the mathematical simulation.

Fig. 10
figure 10

The dependencies of the average velocities on T

Full size image

8 Conclusion

This paper provides model-based and experimental investigations of a capsule-type robot motion with a periodic excitation force. The excitation law is controlled by two parameters: the period and the duty cycle. The mathematical modeling shows that the direction and magnitude of the average velocity of a capsule robot depend significantly on both parameters. The simulation reveals the resonance-induced change in motion as the excitation period monotonically increases. The resonance effect leads to the change in the direction of the robot’s average velocity and occurs near the natural vibration period of the oscillatory system formed by the housing and core connected by a spring. The computer simulation also reveals the symmetry property of the average velocity of the robot with respect to the duty cycle \(\tau \), implying that for the duty cycles \(\tau \) and \(1 - \tau \) the robot moves at the same average velocity in opposite directions. This property is proved on the basis of the mathematical model. Therefore, every feasible velocity can be provided by varying only one parameter \(\tau \) for T fixed to a value that corresponds to the absolute maximum of the average velocity. The experimental study validates the resonance effect and average velocity central symmetry property predicted by the mathematical model. This study concentrates on the research and validation of the qualitative behavior of the capsule-type robot; however, with the use of more realistic model of electromagnetic force, the quantitative validation could be anticipated.