1 Introduction

The most well-known locomotion principles for mobile robotic systems presume the use of external devices such as legs, wheels, tracks, propellers, etc., interacting with the exterior environment. However, the motion of a robotic system inside a resistive medium can be based also upon special motions of internal movable masses relative to the main body of the robot. This way of locomotion without external devices can be useful for motion inside hazardous and vulnerable environment.

Mobile robotic systems with internal movable masses are considered in a number of papers and used for micro- and nano-positioning [5, 6]. In [1], optimal periodic motions of systems subjected to dry friction forces and controlled by internal movable masses are analyzed. The obtained optimal control corresponds to the maximum average speed of the periodic motion under constraints imposed upon the relative displacement of the internal mass, its velocity, or acceleration. Experimental data [3, 4] confirm the obtained theoretical results. In earlier papers, only one-dimensional motions of systems with internal masses along a horizontal line are discussed.

In this paper, two-dimensional motions of a rigid body carrying internal movable masses are considered. The body contacts a horizontal plane at three support points where normal reactions and dry friction forces are applied to the body. Two versions of internal masses with two degrees of freedom are considered.

A short summary of results concerning optimal one-dimensional motions of a system with an internal mass is given. These results [1] are used for designing controls for two-dimensional motions. For two versions of mechanical systems, the controls are proposed that transfer the systems from any initial position and configuration in the horizontal plane to any prescribed terminal position and configuration in this plane.

2 Mechanical Systems

Consider a rigid body P of mass m 1 that can slide along a fixed horizontal plane OXY. Vertical axis OZ of the Cartesian coordinate system OXYZ is directed upwards. Body P called the main body contacts plane OXY at three support points A i, i = 1, 2, 3. Since in the case of three support points the system is statically determinate, normal reactions N i at points A i can be found univalently.

Dry friction forces F i acting between points A i and plane OXY obey Coulomb’s law. If point A i slides along the plane with velocity v i, the friction force is defined by equation

$$\displaystyle \begin{aligned} {\mathbf{F}}_{i}=-fN_{i}{\mathbf{v}}_{i}/v_{i}, \quad v_{i}=|{\mathbf{v}}_{i}|, \quad \text{if} \quad {v}_{i}\neq0. \end{aligned} $$
(1)

Here, f is the coefficient of friction. At the state of rest of body P, we have

$$\displaystyle \begin{aligned} \quad |{\mathbf{F}}_{i}| \leq f N_{i}, \quad \text{if} \quad v_{i}=0,\quad i=1,2,3. \end{aligned} $$
(2)

We consider two versions of mechanical systems.

Version 1

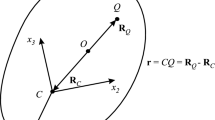
Main body P carries a point Q of mass m 2 that can move relative to the main body along a horizontal plane parallel to plane OXY (Fig. 1). The point mass Q has two degrees of freedom relative to the main body and is controlled by actuators installed on the body.

Fig. 1
figure 1

Two-dimensional motion (Version 1)

Full size image

Version 2

Two additional bodies are associated with the main body, namely, point Q of mass m 2 and rotor R of mass m 3. The rotor is a rigid body that can rotate about the vertical axis BZ′ which is parallel to OZ and passes through point B of body P. Rotor R is dynamically symmetric with respect to its axis BZ′. A horizontal line directed along the unit vector e is connected with the rotor and rotates with it. Point mass Q can move along this line; its displacement BQ is denoted by ξ (Fig. 2). As in Version 1, the internal bodies have two degrees of freedom relative to the main body: the angle of rotation of the rotor and displacement ξ. The relative motions of these bodies are controlled by two actuators: one of them rotates rotor R, and the second moves point Q along vector e.

Fig. 2
figure 2

Two-dimensional motion (Version 2)

Full size image

Version 2 can be implemented in different ways [2].

3 Optimal One-Dimensional Motion

Let us consider one-dimensional motion of a system that consists of a main body of mass M and an internal point mass m that can move relative to the main body (Fig. 3). Both masses move along a horizontal axis Ox. The main body interacts with the horizontal plane by means of dry friction forces, whereas the point mass equipped with an actuator interacts only with the main body. Denote by x the horizontal displacement of the main body, by v its velocity, by ξ the displacement of mass m relative to the main body, by u and w its relative velocity and acceleration, respectively. The kinematic equations can be written as follows:

$$\displaystyle \begin{aligned} \dot{x}=v,\quad \dot{\xi}=u, \quad \dot{u}=w. \end{aligned} $$
(3)

The dynamical equations can be reduced to the relationship:

$$\displaystyle \begin{aligned} (M+m)\dot{v}=-mw+F, \end{aligned} $$
(4)

where F is the dry friction force acting upon the main body. This force obeys Coulomb’s law (1):

$$\displaystyle \begin{aligned} F=-f(M+m)g\:\mathrm{sign}v\quad \mbox{if} \quad v\neq0;\quad |F|\leq f(M+m)g,\quad \mbox{if} \quad v=0, \end{aligned} $$
(5)

where g is the acceleration of gravity.

Fig. 3
figure 3

One-dimensional system

Full size image

Equations (4) and (5) can be presented in the normalized form:

$$\displaystyle \begin{aligned} \dot{v}=-\mu w-fg\:\mathrm{sign}v,\quad \mbox{if} \quad v\neq0;\quad |w|\leq fg\mu^{-1},\quad \mbox{if} \quad v=0, \end{aligned} $$
(6)

where μ = m∕(M + m). Let us consider relative acceleration w as a control subject to the constraint |w|≤ W, where the constant W must satisfy the inequality:

Y = μW(fg)−1 > 1. If this inequality does not hold, then the system cannot be controlled by the motion of the internal mass.

The relative displacement of the internal mass is subject to the constraint:

$$\displaystyle \begin{aligned} 0\leq \xi \leq L, \end{aligned} $$
(7)

where L is a given constant.

Let us consider periodic motions of our system satisfying the following boundary conditions:

$$\displaystyle \begin{aligned} x(0)=v(0)=\xi(0)=u(0)=0, \quad v(T)=\xi (T)=u(T)=0, \end{aligned} $$
(8)

where T is the period of motion. We consider the following optimal control problem.

Problem

Find control w(t) subject to constraint |w|≤ W and such that for the solution of system (3), (6) satisfying boundary conditions (8) and constraint (7), the average velocity V = x(T)∕T is maximum.

The solution of this problem (in the class of piecewise constant controls w(t)) is given in [1]. We describe this solution below for the case where 1 < Y < 2 + 51∕2.

The optimal control w(t) and the corresponding velocity v(t) are given by

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} w(t)=fg\mu^{-1} \times \begin{cases} 1, \quad t\in (0,t_{1}),\\ -Y, \quad t\in(t_{1},t_{2}),\\ 1, \quad t\in(t_{2},T),\\ \end{cases} \end{array} \end{aligned} $$
(9)
$$\displaystyle \begin{aligned}v(t)=fg\mu^{-1} \times \begin{cases} 0,\quad t\in (0,t_{1}),\\ (Y-1)(t-t_{1}),\quad t\in(t_{1},t_{2}),\\ {} [(Y-1)(t_{2}-t_{1})-2(t-t_{2})], \quad t\in(t_{2},t_{3}),\\ 0, \quad t\in(t_{3},T).\\ \end{cases} \end{aligned}$$

Here, the following denotations are introduced:

$$\displaystyle \begin{aligned}T=2\tau\sqrt{\frac{Y+1}{Y}},\quad \tau=\sqrt{\frac{2L\mu}{fg}},\end{aligned}$$
$$\displaystyle \begin{aligned}t_{1}=\tau\sqrt{\frac{Y}{Y+1}},\quad t_{2}=T-t_{1}, \quad t_{3}=\tau \left( \sqrt{\frac{Y}{Y+1}}+\sqrt{\frac{Y+1}{Y}}\right).\end{aligned}$$

The value of the maximum average speed V and the total displacement x 0 of the system over the period are given by

$$\displaystyle \begin{aligned} V=\sqrt{\frac{\mu Lfg}{2Y(Y+1)}}\:(Y-1), \quad x_{0}=VT=\mu L(Y-1)/Y. \end{aligned} $$
(10)

The control described above can be applied to the displacement of the system for a given distance X. First, let us represent this distance as follows: X = nx 0 + x 1, 0 ≤ x 1 < x 0, where n is an integer. The total displacement consists of n periods with duration T and displacement x 0 each and one additional interval with duration T 1 and displacement x 1. To determine the control for the additional interval, we consider the relationship similar to (10):

$$\displaystyle \begin{aligned} x_{1}=\mu L(Y_{1}-1)/Y_{1}. \end{aligned} $$
(11)

Since x 1 < x 0, we have 1 < Y 1 < Y . Hence, for the additional interval of length x 1, the control can be defined by the same formulas (9) as for the optimal period with the only replacement Y by Y 1 defined by Eq. (11).

Thus, we have determined the control of one-dimensional motion of our two-mass system that ensures its displacement for any given distance X.

The same control is also applicable to a two-body system in its rotational motion about a common axis. Here, the dry friction torque is applied to the main body, whereas the second body can rotate relative to the main one. Here, linear displacements should be replaced by angles of rotation about the axis, and the masses of bodies by their moments of inertia.

The control of one-dimensional motion can be used as a component part of the control for two-dimensional motions.

4 Control of Motion for Version 1

Let the initial and terminal positions of system P + Q be given, and system is at rest at these positions. This means that the initial and terminal positions of the triangle A 1A 2A 3 in plane OXY as well as the initial and terminal positions of point Q relative to this triangle are prescribed. The control problem is to find such motion of point Q relative to body P that transfers the system P + Q from the initial position to the terminal one.

Denote by C the center of mass of body P and assume that the vertical axis passing through point C is the principal central axis of inertia of the body. The projection C′ of point C onto plane OXY lies within triangle A 1A 2A 3. Point Q can move arbitrarily in a horizontal plane parallel to OXY within a circle |C′Q′|≤ R 0, where Q′ is the projection of Q onto OXY, with an acceleration w relative to body P bounded by the inequality |w|≤ w 0.

If point Q moves slowly so that its relative acceleration and velocity are small enough, then body P stays at rest. Hence, point Q can move slowly from any initial to any terminal position relative to the stationary body P.

Possible motion of point Q that solves our control problem consists of three stages.

First, point Q moves slowly from its initial position to some position where the distance C′Q′ is equal to l, l ∈ (0, R 0). Body P does not move.

At the second stage, point Q moves along a circle relative to body P so that the distance C′Q′ is equal to l. The relative velocity of this motion should be high enough so that body P rotates in the direction opposite to the rotation of point Q. To achieve the rotation of body P, the bound w 0 should be high enough. The motion of body P at this stage is not, generally speaking, a pure rotation; its center of mass C can also move. This stage ends, when body P comes to the rest, and the orientation of the triangle A 1A 2A 3 coincides with its terminal orientation.

At the third stage, point Q moves along horizontal straight lines such that its projection Q′ moves along lines C′A i, i = 1, 2, 3. Suppose point Q′ travels along line C′A 1; then body P moves translationally, and point C′ moves along the same line in the horizontal plane OXY. In this motion, all support points move along lines parallel to C′Q′A 1. This motion is feasible because the normal reactions N i at points A i, i = 2, 3, have equal and opposite torques with respect to line C′A 1 and thus counterbalance each other. The torques of friction forces F 2 and F 3 about point C are also equal in value and opposite in direction. Hence, the motion of point Q along line C′A 1 results in the translational motion of body P along this line. This motion can be performed using the control described in Sect. 3. Using two progressive motions of body P along two directions C′A i, it is possible to bring triangle A 1A 2A 3 to its terminal position. Point mass Q can reach its prescribed terminal position relative to body P by means of slow motion.

Therefore, it is proven that the system can be brought to the prescribed terminal position.

5 Control of Motion for Version 2

Let the initial and terminal positions of system P + Q + R be given, and the system is at rest at these positions. The problem is to find such motions of rotor R and point Q relative to body P that transfer the system from the initial position to the terminal one.

To simplify the problem, we suppose that the triangle A 1A 2A 3 is equilateral, the projection C′ of the center of mass C of the whole system P + Q + R (with zero displacement ξ = 0 of point Q) lies in the center of the triangle, and the vertical axis CZ′ passing through point C is the principal main axis of inertia of the system.

Under these assumptions, the explicit analytical solution of the control problem stated above is feasible [2]. This solution consists of three stages (Fig. 4).

Fig. 4
figure 4

Stages of motion

Full size image

At the first stage, point Q does not move, so that ξ = 0. Rotor R rotates about its axis. As a result, body P rotates about axis CZ′, whereas point C does not move. The rotation ends at the state of rest, in which projection B′ of point B onto plane OXY lies on a line that connects the projections of the initial and terminal positions of point C. At the end of this stage, vector e should be parallel to the same line.

At the second stage, rotor R stays fixed relative to body P, while point mass Q moves along vector e that keeps its direction. As a result, body P moves translationally along the same direction. At the end of the second stage, the center of mass C reaches its terminal position, and the whole system comes to the rest with ξ = 0.

At the third stage, as at the first one, the point mass Q stays at rest with ξ = 0. Due to the rotation of rotor R, body P rotates about the fixed vertical axis passing through its center of mass C that stays fixed. The rotation ends at the state of rest, in which triangle A 1A 2A 3 comes to its terminal position. Also, point B and vector e reach their terminal states.

At all three stages, the motions are essentially one-dimensional: rotations at the first and third stages, and translation at the second one. They can be described by formulas for controls given in Sect. 3. Thus, the solution of the control problem stated above is obtained.

6 Conclusions

It is shown that the mechanical system consisting of a main body and internal movable masses attached to it and controlled by actuators can be transferred from an initial state to any terminal state in the horizontal plane. The motion occurs in the presence of dry friction forces acting upon the main body. Two versions of internal masses associated with the main body are considered; both of them have two degrees of freedom relative to the body. The motions of internal masses that bring the system to the desired position include several stages, rotations and translations, that are reduced to one-dimensional motions considered earlier. The results obtained can be useful for mobile robots moving in hazardous or vulnerable environment; these robots have no external devices and may be hermetic.