Introduction

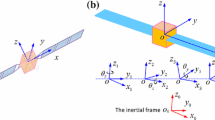
A maneuvering flexible spacecraft is often modeled as coupled rigid hub with attached flexible beam-like sub-structures. A widely used, albeit simplified model describing such systems is shown in Fig. 1 where a flexible rotating spacecraft is modeled as two symmetric flexible appendages with identical tip masses attached to a rotating rigid hub. Such models are described by coupled systems of Integro-Partial Differential Equations (IPDEs), [15–19, 21, 22, 28]. Solution techniques presented in these works are mainly numerical based on spatial discretization approaches that apply the finite element method or the assumed modes technique. Numerical solutions in general are approximate and the accuracy is a function of the number of elements/modes chosen, which can impose high computational cost, and also introduces truncation errors associated with the spatial discretization. Also in the case of the assumed modes technique the number of accurate modes can be limited by the numerical errors introduced by the matrix operation, [15, 28]. As a natural extension for such techniques, the control problem is developed in several works with emphasis on optimality and/or robustness, [2–4, 12, 13, 15, 23–25, 28, 29]. The effect of truncation errors and possible poor choice of basis functions on closed loop response characteristics including stability are issues that are difficult to assess in general.

Fig. 1
figure 1

Symmetric rotating spacecraft

Full size image

The control of a single axis rotating flexible spacecraft has been addressed extensively in the late 80’s through the 90’s utilizing several controls and modeling techniques. A simple quadratic cost function with the application of Euler-Lagrange equations is first introduced to control a slewing spacecraft, [4]. Based on the assumed modes solution open-loop and feedback control are developed to drive the spacecraft to rest while mitigating the vibrations of the flexible modes. As the number of modes is increased eigendecomposition is used to perform the matrix inversion. An experiment is also introduced to verify the numerical results. The optimal control problem of a rotating hub with symmetric four flexible appendages is presented as a numerical example with an admissible function that meets both physical and geometrical boundary conditions. The effectiveness of the minimization is shown to rely on the number of modes retained in the series of the chosen admissible function, [9]. Finite elements techniques and the assumed modes approach are both used to solve similar problems, [15, 28]. The natural frequencies are calculated and the two methods are compared in terms of accuracy and the required number of elements/modes. The optimal control problems for several other flexible structures are similarly addressed for various control schemes and penalty functions including free final time, free final angle and control rate penalty methods, [13]. Optimality conditions for large angle maneuvers of a flexible spacecraft comprising a rigid hub and four flexible appendages are derived and solved for, [25]. Moreover, a single stage continuation method is introduced for the two-point boundary value problems and kinematic nonlinearities, [24]. More recently, the adaptive control problem is investigated for a rigid-hub flexible-appendage model, [20]. Analytic solution of the integro-partial differential equation of motion is used with a control scheme that is independent of the truncation error generated from the numerical series approximations. The reader is referred to a comprehensive literature survey that covers the modeling and control of flexible appendages in the controls literature, [5]. Generally, both the aerospace and the control communities have been content with the numerical approximations following finite elements or assumed modes techniques for the past decade. Building on previous developments, this work presents a new approach for the dynamics and control of distributed parameters models by deriving the analytic transfer functions to obtain the system truncation-error-free frequency response, [6, 8, 26, 27]. The existence of the exact transfer functions is then utilized in frequency domain control for gains selection of a Lyapunov stable controller designed to drive the system from its initial state to a target state while suppressing the vibrations of the flexible appendages.

The paper is organized as follows; in “Dynamics of Multi-body Hybrid Coordinate Systems” a general framework for the derivation of multi-body dynamics is presented. Using that framework, the dynamical equations for the model in Fig. 1 are derived. In “The Generalized State Space Model” the concept of the Generalized State Space (GSS) is presented with the steps to obtain its closed form solution and the associated analytic transfer functions. Numerical results of the frequency response for the general system in Fig. 1 and the no tip-mass special case are presented in “Frequency Response Numerical Results” to validate two admissible assumed modes functions. In “The Control Problem” the control problem in the frequency domain is presented. The derived analytic transfer functions are utilized and numerical results are shown for the rigid and flexible coordinates responses. Finally, a brief discussion of the presented results and possible future extensions are discussed.

Dynamics of Multi-body Hybrid Coordinate Systems

A hybrid system of coordinates is described by m generalized coordinates describing the rigid body motion, denoted by q i =q i (t),i=1,…,m and n elastic coordinates, w j =w j (p,t),j=1,…,n, describing the relative elastic motion of a spatial position p, [15]. Hence, \(\textbf {q} = \left [q_{1},\ldots ,q_{m} \right ]^{\text {\tiny T}}\) and \(\textbf {w} = \left [w_{1},\ldots ,w_{n} \right ]^{\text {\tiny T}}\) constitute the configuration vector for this system.

For a general multi-body system of n beam-like flexible bodies and one spatial independent variable x i , the kinetic and potential energy are assumed to have the general structure,

$$ T = T_{D}(\textbf{q},\dot{\textbf{q}}) + \sum\limits_{i=1}^{n} {\int}_{l_{0i}}^{l_{i}} \hat{T}_{i}(\arg) \, \mathrm{d} x_{i} + T_{B}(\mathrm{arg_{B}}) $$
(1)
$$ V = V_{D}(\textbf{q},\dot{\textbf{q}}) + \sum\limits_{i=1}^{n} {\int}_{l_{0i}}^{l_{i}} \hat{V}_{i}(\arg) \, \mathrm{d} x_{i} + V_{B}(\mathrm{arg_{B}}) $$
(2)

where, (∗) D denotes the energy of the rigid body, \(\hat {(*)}\) denotes the energy in the elastic domain, (∗) B denotes the energy at the boundaries of the elastic domain, \(\arg = \left \{ \textbf {q}(t), \dot {\textbf {q}}(t), \textbf {w}_{i}(t,\textbf {p}_{i}), \dot {\textbf {w}}_{i}(t,\textbf {p}_{i}), \textbf {w}_{i}^{\prime }(t,\textbf {p}_{i}), \textbf {w}_{i}^{\prime \prime }(t,\textbf {p}_{i}) \right \}\), p i =p i (x i ), \(\mathrm {arg_{B}} = \left \{\textbf {q}(t),\dot {\textbf {q}}(t),\textbf {w}(t,l), \dot {\textbf {w}}(t,l), \textbf {w}^{\prime }(t,l), \dot {\textbf {w}}^{\prime }(t,l) \right \}\), \((\dot {*})\) denotes the time derivative and (∗)′ denotes the spatial derivative.

The Lagrangian can then be expressed as,

$$\begin{array}{@{}rcl@{}} \mathcal{L} &=& T - V \\ &=& L_{D} + \sum\limits_{i=1}^{n} {\int}_{l_{0i}}^{l_{i}} \hat{L}_{i} \, \mathrm{d} x_{i} + L_{B} \end{array} $$
(3)

where, \(\arg , \mathrm {arg_{B}}\) are dropped for brevity, L D ≡T D −V D , \(\hat {L}_{i} = \hat {T}_{i} - \hat {V}_{i}\), and L B =T B −V B . The non-conservative virtual work can then be expressed as,

$$ \delta W_{nc} = Q^{\text{\tiny T}} \delta \textbf{q} + \sum\limits_{i = 1}^{n} \left\{ {\int}_{l_{0i}}^{l_{i}} \hat{\textbf{f}}_{i}^{\text{\tiny T}}(x_{i}) \delta \textbf{w}_{i} \, \mathrm{d} x_{i} + \textbf{f}_{i}^{\text{\tiny T}} \delta \textbf{w}_{i}(l_{i}) + \textbf{g}_{i}^{\text{\tiny T}} \delta \textbf{w}^{\prime}_{i}(l_{i}) \right\} $$
(4)

where, Q is the non-conservative force associated with the rigid body coordinates q, f i is the non-conservative force associated with the elastic coordinates with f i and g i are the non-conservative force and torque, respectively, applied at the boundary, x i =l i . Hamilton’s extended principle, Eq. (5), is then applied to obtain the set of coupled hybrid ordinary and partial differential equations and the associated boundary conditions, Eq. (6) through Eq. (9)

$$ {\int}_{t_{1}}^{t_{2}} \left( \delta \mathcal{L} + \delta W_{nc} \right) = 0 \qquad \delta \textbf{q} = \delta \textbf{w}_{i} = 0 \quad \text{at} \quad t = t_{1}, t_{2} $$
(5)
$$ \frac{\, \mathrm{d}}{\, \mathrm{d} t} \left( \frac{\partial \mathcal{L}}{\partial \dot{\textbf{q}}} \right) - \frac{\partial \mathcal{L}}{\partial \textbf{q}} = Q^{\text{\tiny T}} $$
(6)
$$ \frac{\, \mathrm{d}}{\, \mathrm{d} t} \left( \frac{\partial \hat{L}_{i}}{\partial \dot{\textbf{w}}_{i}} \right) - \frac{\partial \hat{L}_{i}}{\partial \textbf{w}_{i}} + \frac{\partial}{\partial x_{i}} \left( \frac{\partial \hat{L}_{i}}{\partial \textbf{w}^{\prime}_{i}} \right) - \frac{\partial^{2}}{\partial {x_{i}^{2}}} \left( \frac{\partial \hat{L}_{i}}{\partial \textbf{w}^{\prime\prime}_{i}} \right) - \frac{\partial^{2}}{\partial x_{i} \partial t} \left( \frac{\partial \hat{L}_{i}}{\partial \dot{\textbf{w}}^{\prime}_{i}} \right) = \hat{\textbf{f}}_{i}^{\text{\tiny T}} $$
(7)
$$\begin{array}{@{}rcl@{}} \left. \left\{ \frac{\partial \hat{L}_{i}}{\partial \textbf{w}^{\prime}_{i}} - \frac{\partial}{\partial x_{i}} \left( \frac{\partial \hat{L}_{i}}{\partial {w}^{\prime\prime}_{i}} \right) \right\} \delta {w}_{i} \right|_{l_{0i}}^{l_{i}} &+& \left\{ \frac{\partial \mathcal{L}_{B}}{\partial {w}_{i}(l_{i})} - \frac{\mathrm{d}}{\mathrm{d}t } \left( \frac{\partial \mathcal{L}_{B}}{\partial \dot{{w}}_{i}(l_{i})} \right) \right\} \delta {w}_{i}(l_{i})\\ &+& \textbf{f}_{i}^{\text{\tiny T}} \delta \textbf{w}_{i}(l_{i}) = 0 \end{array} $$
(8)
$$ \left. \frac{\partial \hat{L}_{i}}{\partial \textbf{w}^{\prime\prime}_{i}} \delta \textbf{w}^{\prime}_{i} \right|_{l_{0i}}^{l_{i}} + \left\{ \frac{\partial \mathcal{L}_{B}}{\partial \textbf{w}^{\prime}_{i}(l_{i})} - \frac{\, \mathrm{d}}{\, \mathrm{d} t} \left( \frac{\partial \mathcal{L}_{B}}{\partial \dot{\textbf{w}}^{\prime}_{i}(l_{i})} \right) \right\} \delta \textbf{w}^{\prime}_{i}(l_{i}) + \textbf{g}_{i}^{\text{\tiny T}} \delta \textbf{w}^{\prime}_{i}(l_{i}) = 0 $$
(9)

where, \(\mathcal {L}_{B} \equiv L_{B} + \displaystyle \sum \limits _{i=1}^{n} {\int }_{l_{0i}}^{l_{i}} \hat {L}_{i} \, \mathrm {d} x_{i}\). Equation (6) through Eq. (9) are used to derive the dynamics of the hybrid model presented in Fig. 1.

Considering the deformation and the coordinate system presented in Fig. 2, the inertial position and velocity of a point on the i-th flexible appendage for the multi-body system is given by,

$$ \textbf{p}_{i}= \left( x_{i}+r\right) \hat{\textbf{b}}_{1} + y_{i} \hat{\textbf{b}}_{2} $$
(10)
$$ \textbf{v}_{i} = \dot{y}_{i}{\hat{\textbf{b}}_{2}} + \dot{\theta} {\hat{\textbf{b}}_{3}} \times \left[\left( x_{i}+r\right){\hat{\textbf{b}}_{1}} + y_{i} {\hat{\textbf{b}}_{2}}\right] $$
(11)

where, r is the rotating hub radius, L the length of the flexible appendage, \(x \in \left [0,L\right ]\) the position on the flexible appendage and y the transverse deflection of the flexible appendage. Neglecting the \(y\dot {\theta }\) term in the velocity and assuming that the two appendages have the same deflection profiles, y 1(x,t)=y 2(x,t), the kinetic and the potential energy for the model in Fig. 1 can be expressed as,

$$\begin{array}{@{}rcl@{}} T &=& T_{\text{hub}} + 2 T_{\text{appendage}} + 2 T_{\text{tip}} \\ T &=& \frac{1}{2}I_{\text{hub}}\dot{\theta}^{2} + {{\int}_{0}^{L}}\rho\left( \dot{y}+(x+r)\dot{\theta}\right)^{2} \mathrm{d}x \\ &&+ m_{\text{tip}}\left( (r+L)\dot{\theta}+\dot{y}(L)\right)^{2} + I_{\text{tip}}\left( \dot{\theta}+\dot{y}^{\prime}(L)\right)^{2} \end{array} $$
(12)
$$ V = {{\int}_{0}^{L}} EI\left( y^{\prime\prime}\right)^{2} \, \mathrm{d} x $$
(13)

The Lagrangian can then be constructed as,

$$\begin{array}{@{}rcl@{}} \mathcal{L} &=& \frac{1}{2}I_{\text{hub}}\dot{\theta}^{2} + {{\int}_{0}^{L}}\rho\left( \dot{y}+(x+r)\dot{\theta}\right)^{2} \, \mathrm{d} x - {{\int}_{0}^{L}} EI\left( y^{\prime\prime}\right)^{2} \mathrm{d}x\\ &&+ m_{\text{tip}}\left( (r+L)\dot{\theta}+\dot{y}(L)\right)^{2} + I_{\text{tip}}\left( \dot{\theta}+\dot{y}^{\prime}(L)\right)^{2} \end{array} $$
(14)

where from Eq. (6) and Eq. (7) we have, \(L_{D} = \frac {1}{2}I_{\text {hub}}\dot {\theta }^{2}\), \(\hat {L} = \rho \left (\dot {y}+(x+r)\dot {\theta }\right )^{2} - EI\left (y^{\prime \prime }\right )^{2}\), \(L_{B} = m_{\text {tip}}\left ((r+L)\dot {\theta }+\dot {y}(L)\right )^{2} + I_{\text {tip}}\left (\dot {\theta }+\dot {y}^{\prime }(L)\right )^{2}\) and \(\mathcal {L}_{B} = L_{B} + {{\int }_{0}^{L}} \hat {L} \, \mathrm {d} x\). The equations of motion and the boundary conditions are then derived from Eq. (6) through Eq. (9) as,

$$\begin{array}{@{}rcl@{}} && I_{\text{hub}}\ddot{\theta} + 2{{\int}_{0}^{L}}\rho (x+r) \left( \ddot{y}+(x+r)\ddot{\theta}\right) \, \mathrm{d} x \\ &&{\kern37pt}+ 2m_{\text{tip}}(L+r) \left( (L+r)\ddot{\theta} + \ddot{y}(L) \right) + 2 I_{\text{tip}}\left( \ddot{\theta}+\ddot{y}^{\prime}(L)\right) = u \\ &&\rho \left( \ddot{y} + (x+r)\ddot{\theta} \right) + EIy^{IV} = 0 \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} &&\text{at} \, x = 0 : y = 0 , \quad y^{\prime} = 0 \\ &&\text{at} \, x = L : \left. EI\frac{\partial^{3}y}{\partial x^{3}}\right|_{L} = m_{\text{tip}}\left( (L+r)\ddot{\theta}+\ddot{y}(L)\right) , \\ &&{\kern22pt}\left. EI\frac{\partial^{2}y}{\partial x^{2}}\right|_{L} = -I_{\text{tip}} \left( \ddot{\theta} + \ddot{y}^{\prime}(L) \right) \end{array} $$
(16)
Fig. 2
figure 2

Deformation & axis of flexible appendage

Full size image

It is noted that by setting m tip=I tip=0 a simpler no-tip-mass model dynamics and boundary conditions are obtained as,

$$\begin{array}{@{}rcl@{}} I_{\text{hub}}\ddot{\theta} + 2{{\int}_{0}^{L}}\rho (x+r) \left( \ddot{y}+(x+r)\ddot{\theta}\right) \, \mathrm{d} x& =& u \\ \rho \left( \ddot{y} + (x+r)\ddot{\theta} \right) + EIy^{IV} &=& 0 \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \text{at} \, x& =& 0 : y = 0 , \quad y^{\prime} = 0 \\ \text{at} \, x &=& L : \left. EI\frac{\partial^{3}y}{\partial x^{3}}\right|_{L} = 0 , \quad \left. EI\frac{\partial^{2}y}{\partial x^{2}}\right|_{L} = 0 \end{array} $$
(18)

The Generalized State Space Model

A generalized state space (GSS) model is developed by taking the Laplace transform of Eq. (15) such that,

$$\begin{array}{@{}rcl@{}} s^{2}J\bar{\theta} + 2 s^{2} \rho {{\int}_{0}^{L}} (r+x) \bar{y} \, \mathrm{d} x + 2 s^{2} m_{\text{tip}} (r+L) \bar{y}(L) + 2 s^{2} I_{\text{tip}}\bar{y}^{\prime}(L) &=&\bar{u} \\ s^{2} \rho \left( \bar{y} + (x+r)\bar{\theta} \right) + EI\bar{y}^{IV} &=& 0 \end{array} $$
(19)

where J is the total inertia of the system given by,

$$ J \equiv I_{\text{hub}} + 2 m_{\text{tip}} (r+L)^{2} + 2 I_{\text{tip}} + 2 {{\int}_{0}^{L}}\rho (r+x)^{2} \, \mathrm{d} x $$
(20)

\(\bar {\theta }\) is the rigid rotation in the Laplace domain and \(\bar {y}\) is the flexible deformation in the Laplace domain. Integration by parts is then utilized to decouple the deformation parameter \(\bar {y}\) from the spatial variable x such that,

$$ {{\int}_{0}^{L}} (r+x)\bar{y} \, \mathrm{d} x = (r+x){{\int}_{0}^{L}} \bar{y} \, \mathrm{d} x - \iint \bar{y} \, \mathrm{d} x \, \mathrm{d} x^{\prime} $$
(21)

Plugging Eq. (21) into Eq. (19) yields the generalized integral equation,

$$\begin{array}{@{}rcl@{}} s^{2}J\bar{\theta} + 2 s^{2} \rho \left( (x+r){{\int}_{0}^{L}} \bar{y} \, \mathrm{d} x - \iint \bar{y} \, \mathrm{d} x \, \mathrm{d} x^{\prime} \right)+ 2 s^{2} (r+L) \bar{y}(L) + 2 s^{2} I_{\text{tip}}\bar{y}^{\prime}(L) &=&\bar{u} \\ \frac{s^{2} \rho}{EI} \left( \bar{y} + (x+r)\bar{\theta} \right) + \bar{y}^{IV} &=& 0 \end{array} $$
(22)

Similar to the equations of motion, the boundary conditions are expressed in the Laplace/frequency domain as,

$$\begin{array}{@{}rcl@{}} \text{at} \, x &=& 0 : \bar{y} = 0 , \quad \bar{y}^{\prime} = 0 \\ \text{at} \, x &=& L : \bar{y}^{\prime\prime\prime}= \frac{s^{2} m_{\text{tip}}}{EI} \left[(r+L)\bar{\theta}+\bar{y}(L)\right] , \quad \bar{y}^{\prime\prime} = -\frac{s^{2} I_{\text{tip}}}{EI} \left[\bar{y}^{\prime}(L) + \bar{\theta} \right] \end{array} $$
(23)

and a generalized state space system can be constructed as,

$$ \begin{array}{lll} z_{1} = \iint\bar{y} \, \mathrm{d} x \, \mathrm{d} x^{\prime} & \qquad & z_{1}^{\prime} = z_{2} \\ z_{2} = \int \bar{y} \, \mathrm{d} x & \qquad &z_{2}^{\prime} = z_{3} \\ z_{3} = \bar{y} & \qquad & z_{3}^{\prime} = z_{4} \\ z_{4} = \bar{y}^{\prime} &\qquad & z_{4}^{\prime} = z_{5} \\ z_{5} = \bar{y}^{\prime\prime} &\qquad & z_{5}^{\prime} = z_{6} \\ z_{6} = \bar{y}^{\prime\prime\prime} & \qquad & z_{6}^{\prime} = -\beta\left( z_{3} + (r+x)\bar{\theta}\right) \end{array} \text{where,}\,\,\beta \equiv \frac{s^{2} \rho}{EI} $$
(24)

In state space representation Eq. (24) can be simply expressed as,

$$ \left\{\begin{array}{l} z_{1}^{\prime} \\ z_{2}^{\prime} \\ z_{3}^{\prime} \\ z_{4}^{\prime} \\ z_{5}^{\prime} \\ z_{6}^{\prime} \end{array}\right\} = \left[\begin{array}{llllll} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & -\beta & 0 & 0 & 0 \end{array}\right] \left\{\begin{array}{l} z_{1} \\ z_{2} \\ z_{3} \\ z_{4} \\ z_{5} \\ z_{6} \end{array}\right\} + \left\{\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ -\beta(r+x)\bar{\theta} \end{array}\right\} $$
(25)

or in the more compact form,

$$ \left\{ Z^{\prime} \right\} = A \left\{Z \right\} + \left\{b \right\} $$
(26)

The state space is generalized in the sense that the states consist of a distributed parameter variable, spatial partial derivatives, and first and second order integrals, which mix solutions at points in the flexible body domain with global response variables. The generalized state space model system of equations is solved by first developing the homogeneous and the forced solutions for the linear state space model in Eq. (26),

$$ \left\{Z(x)\right\} = \underbrace{\exp[Ax]\left\{Z(0)\right\}}_{Z_{H}} + \underbrace{{{\int}_{0}^{x}}{\exp \left[A(x-\tau)\right]\left\{b(\tau)\right\} \mathrm{d}\tau}}_{Z_{F}} $$
(27)

where the homogeneous solution Z H is given by,

$$ \left\{Z_{H}\right\} = \left\{\begin{array}{c} (1-f)z_{5}/\beta-(\beta x + f^{\prime\prime\prime})z_{6}/\beta^{2} \\ -f^{\prime}z_{5}/\beta+(1-f)z_{6}/\beta \\ -f^{\prime\prime}z_{5}/\beta-f^{\prime}z_{6}/\beta \\ -f^{\prime\prime\prime}z_{5}/\beta-f^{\prime\prime}z_{6}/\beta \\ fz_{5}-f^{\prime\prime\prime}z_{6}/\beta \\ f^{\prime}z_{5}+fz_{6}\end{array} \right\} $$
(28)

and the forced part is evaluated from,

$$\begin{array}{@{}rcl@{}} \left\{Z_{F} \right\} &=&{{\int}_{0}^{x}}{\exp \left[A(x-\tau)\right]\left\{b(\tau)\right\} \, \mathrm{d} \tau} \\ &=& -\beta \bar{\theta} {{\int}_{0}^{x}} {(r+\tau) \left\{ \begin{array}{c} \left( \beta(x-\tau)+f^{\prime\prime\prime}(x-\tau)\right)/\beta^{2} \\ \left( 1-f(x-\tau) \right)/\beta \\ -f^{\prime}(x-\tau)/\beta \\ -f^{\prime\prime}(x-\tau)/\beta \\ -f^{\prime\prime\prime}(x-\tau)/\beta \\ f(x-\tau) \end{array} \right\}\, \mathrm{d} \tau} \end{array} $$
(29)

The function f that represents the elements of the solution is derived from the matrix exponential solution of the flexible appendage sub-problem, [6, 27], and is given by

$$ f(x) = \cos\left( \frac{\beta^{1/4}x}{\sqrt{2}}\right)\cosh\left( \frac{\beta^{1/4}x}{\sqrt{2}}\right) $$
(30)

Observing that the function f represents the real part of the complex function

$$ f = Re\left\{\cos(\sigma x)\right\}, \quad \text{where,} \sigma \equiv \sqrt{i\sqrt{\beta}} $$
(31)

the homogeneous solution in Eq. (28) follows,

$$ \left\{Z_{H}\right\} = \left\{\begin{array}{c} (1-\cos(\sigma x))z_{5}/\beta + (\beta x + \sigma^{3} \sin(\sigma x))z_{6}/\beta^{2} \\ \sigma \sin(\sigma x) z_{5}/\beta+(1-\cos(\sigma x))z_{6}/\beta \\ \sigma^{2} \cos(\sigma x) z_{5}/\beta + \sigma \sin(\sigma x) z_{6}/\beta \\ -\sigma^{3} \sin(\sigma x) z_{5}/\beta + \sigma^{2} \cos(\sigma x) z_{6}/\beta \\ \cos(\sigma x) z_{5}-\sigma^{3} \sin(\sigma x) z_{6}/\beta \\ -\sigma \sin(\sigma x) z_{5}+ \cos(\sigma x) z_{6} \end{array} \right\} $$
(32)

Similarly, the forced part of the solution, Eq. (29), is obtained as the six integrals

$$\begin{array}{@{}rcl@{}} \left\{ Z_{F} \right\} &=& \left\{ \begin{array}{c} \frac{1}{6\beta}\left( -3\beta r x^{2} - \beta x^{3} + 6 \sigma^{2} r \cos(\sigma x) + 6 \sigma \sin(\sigma x) - 6 \sigma^{2} r - 6 \sigma^{2} x\right) \bar{\theta} \\ \frac{1}{2\sigma^{2}} \left( -2 \sigma^{2} r x - \sigma^{2} x^{2} + 2 \sigma r \sin(\sigma x) - 2 \cos(\sigma x) + 2 \right) \bar{\theta} \\ \frac{1}{\sigma} \left( \sigma r \cos(\sigma x) + \sin(\sigma x) - \sigma r - \sigma x \right) \bar{\theta}\\ \left( -\sigma r \sin(\sigma x) + \cos(\sigma x) - 1 \right) \bar{\theta} \\ -\sigma \left( \sigma r \cos(\sigma x) + \sin(\sigma x) - \sigma r - \sigma x \right) \bar{\theta} \\ -\frac{1}{\sigma^{2}}\left( \beta \left( \sigma r \sin(\sigma x) - \cos(\sigma x) +1 \right)\right) \bar{\theta} \end{array} \right\} \\ &=& \left\{ \begin{array}{c} I_{1}(x) \\ I_{1}(x) \\ I_{3}(x) \\ I_{4}(x) \\ I_{5}(x) \\ I_{6}(x) \end{array} \right\} \bar{\theta} \end{array} $$
(33)

Equations (32) and (33) are combined to produce the full GSS solution as a function of the GSS variables z 5 and z 6.

$$ \left\{Z(x)\right\} = \left\{\begin{array}{c} (1-\cos(\sigma x))z_{5}/\beta + (\beta x + \sigma^{3} \sin(\sigma x))z_{6}/\beta^{2} + I_{1}(x) \bar{\theta} \\ \sigma \sin(\sigma x) z_{5}/\beta+(1-\cos(\sigma x))z_{6}/\beta + I_{2}(x) \bar{\theta} \\ \sigma^{2} \cos(\sigma x) z_{5}/\beta + \sigma \sin(\sigma x) z_{6}/\beta + I_{3}(x) \bar{\theta} \\ -\sigma^{3} \sin(\sigma x) z_{5}/\beta + \sigma^{2} \cos(\sigma x) z_{6}/\beta + I_{4}(x) \bar{\theta} \\ \cos(\sigma x) z_{5}-\sigma^{3} \sin(\sigma x) z_{6}/\beta + I_{5}(x) \bar{\theta} \\ -\sigma \sin(\sigma x) z_{5}+ \cos(\sigma x) z_{6} + I_{6}(x) \bar{\theta} \end{array} \right\} $$
(34)

The expressions obtained can then be expressed in the general compact form as,

$$ \left\{Z(x)\right\} = \left\{ \begin{array}{c} g_{1}(x) \\ g_{2}(x) \\g_{3}(x) \\ g_{4}(x) \\ g_{5}(x) \\ g_{6}(x) \end{array} \right\} \bar{\theta} $$
(35)

where, g i (x) are the elements of the vector in Eq. (34). The solution of the GSS model in Eq. (34) is obviously invariant to many aspects of the modeling assumptions, and holds for all infinity of model parameters (e.g., E I,ρ,L,r), and clearly admits a variety of boundary conditions. By applying the specific model boundary conditions and solving for the unknown GSS variables, z 5,z 6, the solution is complete in terms of the known system parameters. This makes the GSS solution capable of handling a wide range of distributed parameters problems as the need to apply the model specific boundary conditions arises at the last step of the solution.

GSS Solution for the No-Tip-Mass Model

By setting the inertia and the tip mass to 0 and by applying the model dependent boundary conditions, Eq. (36), for the no-tip-mass model, z 5,z 6 are completely solved for as shown in Eq. (37)

$$\begin{array}{@{}rcl@{}} \text{at} \, x &=& 0 : \left\{ Z \right\} = \left[ \begin{array}{cccccc} 0 & 0 & 0 & 0 & z_{5} & z_{6} \end{array} \right]^{\mathrm{T}} \\ \text{at} \, x &=& L : z_{5}(L) = 0, \quad z_{6}(L) = 0 \end{array} $$
(36)
$$ \left\{\begin{array}{c} z_{5} \\z_{6} \end{array} \right\} = \frac{1}{\sigma^{4} \sin(\sigma L) / \beta - \cos(\sigma L)^{2}} \left[\begin{array}{ll} \cos(\sigma L) & \sigma^{3} \sin(\sigma L) / \beta \\ \sigma \sin(\sigma L) & \cos(\sigma L) \end{array}\right] \left\{\begin{array}{c} I_{5}(L) \\ I_{6}(L) \end{array}\right\} \bar{\theta} $$
(37)

For the no-tip-mass model, from Eq. (17) the rotation angle of the rigid hub is associated with the control torque by the transfer function,

$$\begin{array}{@{}rcl@{}} && s^{2} \left[ J_{1} + 2\rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \right] \bar{\theta} = \bar{u} \\ && \bar{\theta} = \frac{\bar{u}}{s^{2} \left[ J_{1} + 2\rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \right]} \end{array} $$
(38)

and from the GSS model, Eq. (24), the beam deformation is given by,

$$ \bar{y} = g_{3}(x)\bar{\theta} = \frac{g_{3}(x)}{s^{2} \left[ J_{1} + 2\rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \right]}\bar{u} $$
(39)

where, the total inertia J 1 is given by,

$$ J_{1} = I_{\text{hub}} + 2 {{\int}_{0}^{L}}\rho (r+x)^{2} \, \mathrm{d} x $$
(40)

GSS Solution for the Tip-mass Model

For the general model with tip mass shown in Fig. 1, the boundary conditions are expressed in terms of the GSS variables as,

$$\begin{array}{@{}rcl@{}} &&\text{at} \, x=0 : \left\{ Z \right\} = \left[ \begin{array}{cccccc} 0 & 0 & 0 & 0 & z_{5} & z_{6} \end{array} \right]^{\mathrm{T}} \\ &&\text{at} \, x=L : z_{5}(L) = -\alpha \left[z_{4}(L) + \bar{\theta} \right], \quad z_{6}(L) = \gamma \left[z_{3}(L) + (r+L)\bar{\theta} \right] \\ &&\text{where,} \alpha \equiv \frac{s^{2} I_{\text{tip}}}{EI} \quad \text{and} \quad \gamma \equiv \frac{s^{2} m_{\text{tip}}}{EI} \end{array} $$
(41)

where the unknown z 5,z 6 are obtained from,

$$\begin{array}{@{}rcl@{}} &&\left\{ \begin{array}{c} z_{5} \\ z_{6} \end{array} \right\} \,=\, \frac{1}{\sigma^{4}\sin(\sigma L)^{2} / \beta - \cos(\sigma L)^{2}} \left[\begin{array}{cc} -\alpha \cos(\sigma L) & \gamma \sigma^{3} \sin(\sigma L) / \beta \\ -\alpha \sigma \sin(\sigma L) &\gamma \cos(\sigma L) \end{array}\right] \left\{\begin{array}{c} z_{4}(L) \\ z_{3}(L) \end{array}\right\} \\ &&+ \left[\begin{array}{cc} \sigma^{3} \left( \gamma(r+L) - I_{6}(L)\right) / \beta & \left( -\alpha - I_{5}(L) \right) \\ \sigma\left( -\alpha-I_{5}(L) \right) & \gamma(r+L) - I_{6}(L) \end{array}\right] \left\{\begin{array}{c} \sin(\sigma L) \\ \cos(\sigma L) \end{array} \right\}\bar{\theta} \\ & \\ &&\left\{\begin{array}{c} z_{4}(L) \\ z_{3}(L) \end{array} \right\} = \frac{1}{\beta} \left[\begin{array}{ll} -\sigma^{3}\sin(\sigma L) & \sigma^{2}\cos(\sigma L) \\ \sigma^{2} \cos(\sigma L) & \sigma \sin(\sigma L) \end{array}\right] \left\{\begin{array}{c} z_{5} \\ z_{6} \end{array} \right\} + \begin{Bmatrix} I_{4}(L) \\ I_{3}(L) \end{Bmatrix} \bar{\theta} \end{array} $$
(42)

The beam deformation \(\bar {y}\) is represented as a function of the input torque \(\bar {u}\) as,

$$\begin{array}{@{}rcl@{}} && s^{2} \left[ J_{2} + 2m_{\text{tip}} (r+L)g_{3}(L) + 2I_{\text{tip}}g_{4}(L) + 2\rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \right] \bar{\theta} = \bar{u} \\ && \bar{\theta} = \frac{\bar{u}}{s^{2} \left[ J_{2} + 2m_{\text{tip}} (r+L)g_{3}(L) + 2I_{\text{tip}}g_{4}(L) + 2\rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \right]} \\ && \bar{y} = \frac{g_{3}(x)}{s^{2} \left[ J_{2} + 2m_{\text{tip}}(r+L)g_{3}(L) + 2I_{\text{tip}}g_{4}(L) + 2\rho \left( (r+x) g_{2}(x)-g_{1}(x) \right) \right]} \bar{u} \end{array} $$
(43)

where the total inertia in that case, J 2, is given by,

$$ J_{2} = I_{\text{hub}} + 2m_{\text{tip}}(r+L)^{2} + 2I_{\text{tip}} + 2{{\int}_{0}^{L}}\rho (r+x)^{2} dx $$
(44)

The analytic transfer functions obtained in Eq. (38), Eq. (39) and Eq. (43) are utilized to accurately obtain the frequency response of the hybrid system and in control of the flexible modes when performing large angle maneuvers as presented in the next sections.

Frequency Response Numerical Results

From Eq. (39) and Eq. (43), the transfer function of the no-tip-mass model, G 1(s,x), and the tip-mass model, G 2(s,x), are expressed as,

$$\begin{array}{@{}rcl@{}} G_{1}(s,x)\! &=&\! \frac{g_{3}(x)}{s^{2} \left[ J_{1} + 2\rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \right]} \\ G_{2}(s,x)\! &=&\! \frac{g_{3}(x)}{s^{2} \left[ J_{2}\! +\! 2m_{\text{tip}}(r+L)g_{3}(L)\! +\! 2I_{\text{tip}}g_{4}(L) + 2\rho \left( (r+x) g_{2}(x)-g_{1}(x) \right) \right]} \end{array} $$
(45)

The GSS transfer functions in Eq. (45) are used to validate the frequency response obtained from the classical assumed modes solution, [15]. The method assumes a decoupled spatial and time dependent beam response expressed by,

$$ y(x,t) = \sum\limits^{N}_{i=1}{q_{i}(t)\phi_{i}(x)} $$
(46)

The spatial function ϕ i (x) describes the i-th spatial “assumed mode” shape function of the flexible structure and is designed to meet the physical and the geometrical boundary conditions of the beam. A widely used admissible function that satisfies the boundary conditions is,

$$\begin{array}{@{}rcl@{}} &&\phi_{i}(x) = 1 - \frac{\cos(i\pi x)}{L} + \frac{1}{2}(-1)^{i+1}\left( \frac{i \pi x}{L}\right)^{2} \\ &&\text{where,} \, \,\,0 \leq x \leq L \end{array} $$
(47)

The admissible function in Eq. (47) is known to produce very accurate results and has been adopted widely, [15, 24]. However, the GSS transfer function solution can be used to validate any assumed numerical approximation. For that purpose another spatial spatial discretization is introduced as,

$$ \psi_{i}(x) = 1 + \frac{1}{2}(-1)^{i+1}\left( \frac{i \pi x}{L}\right)^{2} \\ $$
(48)

Notice that the simple polynomial basis function of Eq. (48) satisfies the geometric (left) boundary conditions at the rigid hub. Using Eq. (46) with Eq. (12) and Eq. (13) and following the Lagrangian approach,

$$ \frac{d}{dt} \left( \frac{\partial T}{\partial \dot{\textbf{x}}} \right) - \frac{\partial T}{\partial \textbf{x}} + \frac{\partial V}{\partial \mathrm{x}} = \textbf{F} $$
(49)

the system of equations of motion for the tip mass model is represented in the matrix form,

$$ \left[\begin{array}{ll} J_{2} & M^{\text{\tiny T}}_{\theta q} \\ M_{\theta q} & M_{qq} \end{array}\right] \ddot{\textbf{x}} + \left[\begin{array}{ll} 0 & 0 \\ 0 & K_{qq} \end{array}\right] \textbf{x} = \left\{ \begin{array}{c} u \\ 0 \end{array} \right\} $$
(50)

where the elements of the mass and the stiffness matrices are defined as,

$$\begin{array}{@{}rcl@{}} J_{2} &=& I_{\text{hub}} + 2m_{\text{tip}}(r+L)^{2} + 2I_{\text{tip}} + 2{{\int}_{0}^{L}}{\rho (r+x)^{2} \, \mathrm{d} x} \\ \left[M_{\theta q}\right]_{i} &=& 2 \left[\rho {{\int}_{0}^{L}}{(r+x)\phi_{i}(x) \, \mathrm{d} x} + m_{\text{tip}}(r+L) \phi_{i}(L) + I_{\text{tip}} \phi^{\prime}_{i}(L) \right] \\ \left[K_{qq}\right]_{ij} &=& 2 {{\int}_{0}^{L}}{\phi^{\prime\prime}_{i}(x) \phi^{\prime\prime}_{j}(x) \, \mathrm{d} x} \end{array} $$
(51)

where, for the function in Eq. (48), ϕ is simply replaced with ψ.

In order to obtain the no-tip-mass model equations, one can set m tip=I tip=0 in Eq. (51) to obtain the mass and stiffness matrices elements for the model. A comparison between the frequency response of the GSS analytic transfer functions and the numerical assumed modes method, assuming 10 modes, is presented at the beam mid-point at x=L/2 and at the beam tip at x=L. The set of parameters values used in this comparison are extracted from a physical model and are shown in Table 1, [15].

Table 1 System parameters values
Full size table

First, the spatial discretization presented in Eq. (48) is used and results are presented for the no-tip mass model at the beam mid-point and tip in Figs. 3 and 4, respectively. Whereas, the tip mass model frequency response is shown for the same two locations on the beam in Figs. 5 and 6.

Fig. 3
figure 3

Frequency response comparison no tip mass model at beam mid-point, x=L/2, using ψ i (x)

Full size image
Fig. 4
figure 4

Frequency response comparison no tip mass model at beam tip, x=L, using ψ i (x)

Full size image
Fig. 5
figure 5

Frequency response comparison tip mass model at beam mid-point, x=L/2, using ψ i (x)

Full size image
Fig. 6
figure 6

Frequency response comparison tip mass model at beam tip, x=L, using ψ i (x)

Full size image

For the admissible function in Eq. (47), the frequency reponse for the no-tip mass model is shown in Figs. 7 and 8 at x=L/2 and x=L, respectively. Similar results are obtained for the tip-mass model and are shown in Figs. 9 and 10.

Fig. 7
figure 7

Frequency response comparison no tip mass model at beam midpoint, x=L/2, using ϕ i (x)

Full size image
Fig. 8
figure 8

Frequency response comparison no tip mass model at beam tip, x=L, using ϕ i (x)

Full size image
Fig. 9
figure 9

Frequency response comparison tip mass model at beam midpoint, x=L/2, using ϕ i (x)

Full size image
Fig. 10
figure 10

Frequency response comparison tip mass model at beam tip, x=L, using ϕ i (x)

Full size image

It is shown that the numerical results obtained from the analytic transfer functions can be used to validate existing numerical approximations. In the case of the poor approximation in Eq. (48), the approximation clearly fails to capture the complete frequency response of the system. Whereas, the more accurate approximation in Eq. (47) is shown to agree more accurately with the GSS solution. It is also noted that in Figs. 7 and 9 for the beam mid-point the truncation error is more observable than at the beam tip in Figs. 8 and 10.

In the case of the function in Eq. (47), this assumed model has previously been selected because it is known to match experimental results, so it is not a huge surprise that the distributed parameter model, with zero truncation error, was in good agreement with the known to be reasonably well converged discretized model. Discretization can be considered the core of numerical analyses in structural dynamics, [1]. All finite elements software packages adopt a form of discretization as it offers a computationally efficient, easy to implement and a generally less involved solution. More generally however, it is important to note that the distributed parameter approach affords a rigorous means to address the issue of whether or not the discrete model has unacceptable truncation errors as in the case of the model in Eq. (48), and to design controllers, as shown below, which are free of truncation errors.

The Control Problem

For the general hybrid system of equations in Eq. (7), a globally stabilizing control law is developed, [14, 15]. A positive definite Lyapunov function based on the system total energy is defined as,

$$ U = T + V + af(e_{q}) $$
(52)

where, T is the kinetic energy as defined in Eq. (1), V is the potential energy in Eq. (2), a>0 is a constant coefficient, e q =q−q f is the error vector relative to a constant final state q f and f(e q )>0. By taking the time derivative of U and substituting the dynamics, Eq. (6) and Eq. (7), and the boundary conditions, Eq. (8) and Eq. (9), the following expression is obtained, [14, 15]

$$ \frac{\mathrm{d}U}{\mathrm{d}t} = \dot{q}^{\text{\tiny T}} \left[ Q + a \frac{\partial f(e_{q})}{\partial e_{q}} \right] + \sum\limits_{i=1}^{n} \left[ {\int}_{l_{0i}}^{l_{i}} \dot{\textbf{w}}_{i}^{\text{\tiny T}} \hat{\textbf{f}}_{i} \, \mathrm{d} x_{i} + \dot{\textbf{w}}_{i}^{\text{\tiny T}}(l_{i}) \textbf{f}_{i} + \dot{\textbf{w}}_{i}^{\prime}(l_{i}) \textbf{g}_{i} \right] $$
(53)

Lyapunov stability requires that \(\frac {\, \mathrm {d} U}{\, \mathrm {d} t} < 0\). Hence, a feedback control law can be established as,

$$\begin{array}{@{}rcl@{}} && Q = -K_{1} \dot{\textbf{q}} - a \frac{\partial f(e_{q})}{\partial e_{q}} \\ && \hat{\textbf{f}}_{i} = -K_{2i} \dot{\textbf{w}}_{i} \\ && \textbf{f}_{i} = -K_{3i} \dot{\textbf{w}}_{i}(l_{i}) \\ && \textbf{g}_{i} = -K_{4i} \dot{\textbf{w}}_{i}^{\prime}(l_{i}) \end{array} $$
(54)

where K 1,K 2,K 3 and K 4 are positive definite gain matrices which will guarantee that \(\frac {\, \mathrm {d} U}{\, \mathrm {d} t} \leq 0\). The control law in Eq. (54) is general and is not affected by any spatial discretization which makes it essential to the present development that does not include any spatial discretization or truncation errors.

Building on the analytical solution obtained for the more general tip mass model, the control problem is analyzed. To gain some insight on the system behavior, the unit step input Bode plots are generated at the midpoint of the appendage at x=L/2 for both the responses of the rigid body, \(\bar {\theta }(j\omega )\), and the flexible appendage, \(\bar {y}(j\omega )\), as shown in Figs. 11 and 12 respectively.

Fig. 11
figure 11

Bode plot \(\bar {\theta }\) at beam midpoint, x=L/2

Full size image
Fig. 12
figure 12

Bode plot \(\bar {y}\) at beam midpoint, x=L/2

Full size image

The resonant behavior of the system previously obtained from the GSS tranfer function, Eq. (45), is clearly present in this analysis with the phase angle shifting between +90∘ and −90∘ at those frequencies. For further insights, the assumed modes method is used to generate the model time response for a unit step input for 𝜃(t), \(\dot {\theta (t)}\), as shown in Figs. 13 and 14, and for y(x,t), \(\dot {y}(x,t)\), as shown in Figs. 15 and 16.

Fig. 13
figure 13

Step input response 𝜃(t)

Full size image
Fig. 14
figure 14

Step input response \(\dot {\theta }(t)\)

Full size image
Fig. 15
figure 15

Step input response at beam midpoint, y(x=L/2,t)

Full size image
Fig. 16
figure 16

Step input response at beam midpoint, \(\dot {y}(x = L/2,t)\)

Full size image

A case study is constructed for the more general tip mass model applying a Lyapunov stable controller, [12, 15]. First, Eq. (15) is rewritten as,

$$\begin{array}{@{}rcl@{}} && I_{\text{hub}}\ddot{\theta} = u + 2\left( M_{0} - rS_{0}\right) \\ && -\left( M_{0} - rS_{0}\right) \! =\! {{\int}_{0}^{L}}\rho (x+r) \left( \ddot{y}\! +\! (x+r)\ddot{\theta}\right) \, \mathrm{d} x + m_{\text{tip}}(L\! +\! r) \left( (L+r)\ddot{\theta} + \ddot{y}(L) \right) \\ && \rho \left( \ddot{y} + (x+r)\ddot{\theta} \right) + EIy^{IV} = 0 \end{array} $$
(55)

where, (M 0,S 0) represent the bending moment and shear force at the root of the beam. The effect of the tip mass inertia is left out for simplification and can be considered as a disturbance error or as part of the model uncertainty the controller needs to overcome. The set of boundary conditions in Eq. (16) can then be simplified as,

$$\begin{array}{@{}rcl@{}} &&\text{at} \, x = 0 : y = 0 , \quad y^{\prime} = 0 \\ &&\text{at} \, x = L : \left. EI\frac{\partial^{3}y}{\partial x^{3}}\right|_{L} = m_{\text{tip}}\left( (L+r)\ddot{\theta}+\ddot{y}(L)\right) , \quad \left. EI\frac{\partial^{2}y}{\partial x^{2}}\right|_{L} = 0 \end{array} $$
(56)

We are interested in large angle maneuvers with a target final state given by,

$$ \left[ \theta, \dot{\theta}, y(x,t), \dot{y}(x,t) \right]_{\text{Target}} = \left[\theta_{f}, 0, 0, 0 \right] $$
(57)

Following Lyapunov’s direct (second) method a weighted Lyapunov function is given by,

$$\begin{array}{@{}rcl@{}} 2U &=& w_{1}I_{\text{hub}}\dot{\theta}^{2} + w_{2}\left( \theta-\theta_{f} \right)^{2} \\ & +& 2w_{3}\left[{{\int}_{0}^{L}}\rho\left( \dot{y}+(x+r)\dot{\theta}\right)^{2} \, \mathrm{d} x + m_{\text{tip}}\left( (r+L)\dot{\theta}+\dot{y}(L)\right)^{2} + {{\int}_{0}^{L}} EI\left( y^{\prime\prime}\right)^{2} \, \mathrm{d} x \right] \end{array} $$
(58)

where an extra term that includes a penalty for the current state versus the target state, \(\left (\theta - \theta _{f} \right )\) is added to achieve the required maneuver. The Lyapunov function in Eq. (58) is continuous and positive definite for all the system states. We seek stability by differentiating the Lyapunov function, Eq. (58) w.r.t. time and substituting the dynamics, Eq. (55), and the boundary conditions, Eq. (56), \(\dot {U}\) can be expressed as,

$$\begin{array}{@{}rcl@{}} \dot{U} & = &w_{1} u \dot{\theta} + w_{2}\left( \theta - \theta_{f} \right) \dot{\theta} \\ &&+ 2\left( w_{3} - w_{1} \right) \left[ {{\int}_{0}^{L}}\rho (x+r) \left( \ddot{y}+(x+r)\ddot{\theta}\right) \, \mathrm{d} x + m_{\text{tip}}(L+r) \left( (L+r)\ddot{\theta} + \ddot{y}(L) \right) \right] \dot{\theta} \\ &=& \left[ w_{1} u + w_{2}\left( \theta - \theta_{f} \right) + 2\left( w_{3} - w_{1} \right)\left( rS_{0} - M_{0} \right) \right] \dot{\theta} \end{array} $$
(59)

In order to ensure stability, \(\dot {U}\) should meet the condition \(\dot {U} \leq 0\) and the control law is chosen as,

$$ u = \frac{-1}{w_{1}} \left[ w_{2}\left( \theta - \theta_{f} \right) + 2\left( w_{3} - w_{1} \right)\left( rS_{0} - M_{0} \right) + w_{4}\dot{\theta} \right] $$
(60)

By substituting Eq. (60) into Eq. (59), the negative semi-definite expression, \(\dot {U} = -w_{4}\dot {\theta }^{2} \leq 0\) is obtained which according to Lyapunov’s direct method ensures stability. Even though \(\dot {U} = -w_{4} \dot {\theta }^{2}\) is only negative semi-definite, we can substitute the control law of Eq. (59) into Eq. (55) and confirm that the only equilibrium state for which the acceleration state variables \(\left \{ \ddot {\theta }, \ddot {y}(x,t), \ddot {y}(L,t) \right \}\) is the desired fixed point, \(\left \{ \theta = \theta _{f}, \dot {\theta } = 0, y(x,t) = 0, \dot {y}(x,t) = 0 \right \}\). In order to simplify the gain choices associated with the control law, Eq. (60) can be re-written as,

$$ u = -\left[k_{1}\left( \theta - \theta_{f} \right) + k_{2}\left( rS_{0} - M_{0} \right) + k_{3}\dot{\theta} \right] $$
(61)

where, \(k_{1} \equiv \frac {w_{2}}{w_{1}}\), \(k_{2} \equiv \frac {2(w_{3}-w_{1})}{w_{1}}\) and \(k_{3} \equiv \frac {w_{4}}{w_{1}}\). By substituting Eq. (61) into Eq. (59), we obtain k 1≥0, k 2>−2 and k 3≥0 for stability. It should be noted that the shear and bending moment at the root of the beam can be measured by strain gauges. The sign and value of k 2 will determine whether the beam vibration energy, w 3>w 1, or the hub motion energy, w 1>w 3 is dissipated. To investigate the frequency domain response applying the control law, the Laplace transformation of Eq. (61) is expressed as,

$$\begin{array}{@{}rcl@{}} \bar{u} &=& -k_{1}\left( \bar{\theta} -\frac{ \theta_{f}}{s} \right) \\ &&- k_{2} s^{2}\left( \rho {{\int}_{0}^{L}}(x+r) \left( \bar{y} + (x+r)\bar{\theta} \right) \, \mathrm{d} x + m_{\text{tip}} (L+r) \left( (L+r)\bar{\theta} + \bar{y}(L) \right) \right) \\ && - k_{3} s \bar{\theta} \end{array} $$
(62)

Utilizing integration by parts the transformed control law is expressed in terms of the GSS state variables as,

$$\begin{array}{@{}rcl@{}} \bar{u} &=& \left[-k_{1} - k_{2} \rho s^{2} {{\int}_{0}^{L}} (r+x)^{2} \, \mathrm{d} x - k_{2} m_{\text{tip}} s^{2} (L+r)^{2} - k_{3} s \right] \bar{\theta} \\ &&+ k_{1}\frac{\theta_{f}}{s} - k_{2} \rho s^{2} \left( (x+r) g_{2}(x) - g_{1}(x) \right) - k_{2} m_{\text{tip}} s^{2} (L+r)g_{3}(L) \end{array} $$
(63)

Substituting Eq. (63) into the transfer function, Eq. (43), and collecting variables produced the transfer function for the hub angle \(\bar {\theta }\) as,

$$\begin{array}{@{}rcl@{}} && \bar{\theta} = \left[k_{1}\frac{\theta_{f}}{s} - k_{2} \rho s^{2} \left( (x+r) g_{2}(x) - g_{1}(x) \right) - k_{2} m_{\text{tip}} s^{2} (L+r)g_{3}(L) \right] / \\ && \, s^{2} \Bigg[ \frac{k_{1}}{s^{2}} + k_{2} \rho {{\int}_{0}^{L}} (r+x)^{2} \, \mathrm{d} x + k_{2} m_{\text{tip}} (L+r)^{2}+ \frac{k_{3}}{s} + J_{2} \\ && + m_{\text{tip}} (r+L)g_{3}(L) + I_{\text{tip}}g_{4}(L) + \rho \left( (r+x)g_{2}(x)-g_{1}(x) \right) \Bigg] \end{array} $$
(64)

The deformation transfer function can then be expressed in terms of \(\bar {\theta }\) as,

$$ \bar{y} = g_{3}(x)\bar{\theta} $$
(65)

After some trial and error the controller gains are adjusted to obtain a highly stable response. To illustrate the effect of gain changes on the system frequency response the gains are first set to k 1=1,k 2=1,k 3=1. Figures 17 and 18 show the amplitude and phase plots associated with the two transfer functions, Eq. (64) and Eq. (65), respectively, for unit gains. More generally, we can adapt a parameter optimization approach for optimizing the gains over the stable set defined by the constraints: k 1>0,k 3>0,k 2>−2 and selecting some specific performance metric for optimization. Such an approach constitutes a ”Lyapunov optimal control method”.

Fig. 17
figure 17

Bode plot \(\bar {\varTheta }\) with unit gains

Full size image
Fig. 18
figure 18

Bode plot \(\bar {y}\) with unit gains

Full size image

Clearly, the frequency response highlights potential resonant response with order of magnitude gain amplifications and a −180∘ phase angle. The gains are then adjusted to k 1=12,k 2=0,k 3=16. The amplitude and phase plots associated with the new set of gains are shown in Figs. 19 and 20.

Fig. 19
figure 19

Bode plot \(\bar {\varTheta }\) with designed gains

Full size image
Fig. 20
figure 20

Bode plot \(\bar {y}\) with designed gains

Full size image

With the reduced amplitude amplification, the chosen set of parameters can be suitable for a controller to drive the rigid hub to its target final angle while mitigating the vibrations effect of the flexible appendages. The time response plots for the system are shown for 𝜃(t), \(\dot {\theta }(t)\), in Figs. 21 and 22, and for y(x=L/2,t), \(\dot {y}(x=L/2,t)\) in Figs. 23 and 24.

Fig. 21
figure 21

Response 𝜃(t) with designed gains

Full size image
Fig. 22
figure 22

Response \(\dot {\theta }(t)\) with designed gains

Full size image
Fig. 23
figure 23

Response y(x=L/2,t) with designed gains

Full size image
Fig. 24
figure 24

Response \(\dot {y}(x=L/2,t)\) with designed gains

Full size image

The results show achieving the target state for 𝜃 and \(\dot {\theta }\) while reducing the vibrations in, y(x,t) and \(\dot {y}(x,t)\), It has to be noted that no controls are applied to the flexible appendage and the control torque is solely driving the hub while achieving acceptable results on the vibrations control. Several works discussed techniques of controlling the flexible structure by applying controls to the flexible appendages [10, 11].

Discussion & Conclusion

The generalized state space approach provides analytic transfer functions for the system frequency response for both the tip-mass and the no-tip-mass models, without introducing spatial discretization. The fact that nontrivial problems can be solved by these methods, using distributed parameter models, does not appear to be widely appreciated. These special case models and control design methods serve important roles in evaluating the applicability and validity of the approximations implicit in more generally applicable spatial discretization methods. Several other boundary conditions and constituitive assumptions can be applied and the analogous steps to those presented here can be followed in order to obtain the analytical distributed parameter solution. By utilizing the full transfer function solution provided by the GSS approach any control problem design in the frequency domain can be addressed. A case study is constructed for the gain selection of a Lyapunov stable control law. By looking at the frequency response and changing the gains an acceptable performance was achieved driving the structure from a stationary initial state to a target state while suppressing the beam vibrations. The GSS approach can be considered a platform through which distributed parameters models can be addressed. Recently, the more complex model following the Timoshenko beam theory is addressed with possible extensions to a variety of boundary conditions and control problems [7].

The presented control problem has potential for several extensions. Optimization was not considered in this work whereas several techniques exists for optimization in the frequency domain based on Parseval’s theorem. The GSS solution provides a general framework for any control scheme in the frequency domain. This is shown to be a very powerful tool. When it is possible to use discretization and truncation-free distributed parameter model transfer function solutions provided by the GSS approach, any control problem design in the frequency domain can be addressed rigorously.