Introduction

This study addresses the topic of modelling complex flow of micellar yield stress fluids in the 4:1:4 contraction–expansion benchmark flow problem. Here, two sources of plastic behaviour are considered: (i) through the solvent viscosity, offered by Bingham–Papanastasiou model (Papanastasiou 1987; Mitsoulis 2007; Belblidia et al. 2011; Al-Muslimawi et al. 2013), and (ii) through the polymeric viscoelastic contribution, introduced via Bautista–Manero models (Bautista et al. 1999; Manero et al. 2002; Boek et al. 2005; López-Aguilar et al. 2014a, b). The class of Bautista–Manero models has been derived to represent the characteristics of thixotropic wormlike micellar systems. Herein, low-solvent fractions and high-elasticity levels are accessible. This is achieved through a correction to the constitutive equation for these polymeric Bautista–Manero models, based on physical arguments for fluidity, in which absolute values of the dissipation function are adopted in complex flow (López-Aguilar et al. 2014b).

Yield stress concept

Although the concept of viscoplastic materials was first introduced by Bingham over nine decades ago (Bingham 1922), still this topic remains one of the most controversial in rheology today (Bingham 1922; Barnes 1999; Renardy 2010; Belblidia et al. 2011). Viscoplastic materials exhibit solid-like behaviour when the applied tension is ‘low’ and liquid-like behaviour at ‘high’ imposed stress. They are also termed yield stress materials, since it is common in engineering applications to model them by introducing a yield stress, τ 0, above which the material strains continuously, without recovery of strain upon removal of the applied tension. Under flow, these materials develop plastic plug-like flow zones, due to elastic resistance from the microstructure, in which any deformation essentially disappears. The controversy surrounding yield stress is associated with its existence, representation, experimental measurement and data interpretation. Note that, in practice, most materials weakly yield or creep in the limit of zero shear rate.

Barnes and Walters (1985) demonstrated that, through experimental data gathered from a constant stress rheometer, in this context, the yield stress concept was a pure idealisation. Thereby, given sufficiently accurate measurement, no ‘actual’ yield stress truly existed. Subsequently, the non-existence of yield stress, claimed by Barnes and Walters, was challenged by Hartnett and Hu (1989). These authors used a falling ball viscometer to demonstrate unambiguously that an aqueous Carbopol solution exhibited a yield stress—to an engineering approximation. To further complicate the situation, Møller et al. (2006) related the uncertainty in interpretation of some rheometrical measurement to material time dependency, that is, to thixotropic behaviour and time scale. Conspicuously, no single method has been universally accepted as the standard for measuring yield stress, and it is not unusual to find large variations in results obtained from different methods with the same material (Bonn 2006).

Theoretical and numerical modelling of viscoelastoplastic material

The so-called Bingham fluids display a distinct finite stress level (yield stress) at vanishingly low shear rates. In areas of intense deformation, above the yield stress limit, the material is observed to flow and behave as a Newtonian fluid. The presence of these unyielded and yielded regions across the flow domain provides a corresponding interface between them, or yield front, as an intrinsic discontinuity to the representation. Then, more complex shear viscous response may be included through power law-type rate dependency (Herschel–Bulkley or Casson models). A drawback to using these models is their discontinuous stress representation. This necessitates, using robust numerical techniques for discretisation, to accurately describe the yielded–unyielded regions and their corresponding interface (Belblidia et al. 2011).

To date, one successful approach proposed to deal with this discontinuous representation is the regularisation method of Papanastasiou (1987). As such, the resulting Papanastasiou viscoplastic model consists of a single unified, modified constitutive relation—applicable to both yielded and unyielded regions alike. Such an approach proffers the advantage that it eliminates the need for explicit tracking of the yield surface. Here, an exponential stress growth parameter is introduced to access numerical solutions, which, in limiting terms, may practically replicate ideal model results. This model has been successfully applied in a plethora of studies, to describe viscoplastic and viscoelastoplastic flows, in simple ideal and complex flow scenarios (Mitsoulis 2007). This would include a constitutive viscoelastoplastic model (as a combination of the Bingham viscoplastic and the Oldroyd viscoelastic models), which theoretically satisfies the second law of thermodynamics (Saramito 2007), entry–exit flows from dies, flow past objects and squeeze flows, steady Oldroyd-B 4:1:4 contraction–expansion flow (Belblidia et al. 2011), and steady die-swell flow for exponential Phan–Thien–Tanner models (EPTT, viscoelastic, shear thinning, strain hardening/softening; Al-Muslimawi et al. 2013). Here, the conventional yielded–unyielded regions across the flow domain were studied. Additionally, in Belblidia et al. (2011), vortex dynamics, excess pressure drop versus yield stress and enhancement with viscoelasticity were all reported, whilst in Al-Muslimawi et al. (2013), swelling ratio and excess pressure loss received attention.

Frigaard and Nouar (2005) presented a detailed analysis of the limitations of various regularisation schemes, including the Papanastasiou form. The challenge posed to predictive simulation is to depict the ‘appropriate’ level of exponential growth for the deformation in question. Undoubtedly, the subject matter of viscoplasticity/viscoelastoplasticity remains a hotly debated and challenging topic, which has provoked more than a thousand papers prior to 2005 (see Mitsoulis 2007). In addition, some authors have employed the augmented Lagrangian approach and applied it to problems of viscoplasticity (see, for example, Roquet and Saramito 2001, Huilgol and You 2005 and Muravleva et al. 2010). These authors have demonstrated the effectiveness of the augmented Lagrangian method for this type of problem.

Wormlike micelle solution systems

Wormlike micelle solution systems are a versatile family of fluids composed of mixtures of surfactants—typically of cetyltrimethylamonium bromide (CTAB) or cetylpyridinium chloride (CPyCl)—salts and sodium salicylate (NaSal), in water (López-Aguilar et al. 2014a; Yang 2002). These components interact physically, depending on concentration, temperature and pressure conditions, to form elongated micelles. These micelle networks entangle and provoke interactions of viscosity, elasticity and breakdown formation of internal structure (López-Aguilar et al. 2014a and b). Such complex system constitution generates highly complex rheological phenomena, which manifest features associated with thixotropy (Bautista et al. 1999), pseudo plasticity (Bautista et al. 1999; Manero et al. 2002; Boek et al. 2005; López-Aguilar et al. 2014a, b), shear banding (Bautista et al. 2000) and yield stress (Calderas et al. 2013). Advantage may be taken of these features to render micelle solutions as ‘smart fluids’ for varied processing and present-day applications, as in drilling fluids for enhanced oil reservoir (EOR) recovery (López-Aguilar et al. 2014a), and additives in household products, paints, cosmetics, health care products and drag reducing agents (López-Aguilar et al. 2014a; Yang 2002).

Micellar constitutive models

Many approaches have been pursued to model wormlike micelle flow behaviour. A family of models, coming from the original Bautista–Manero–Puig (BMP) model (Bautista et al. 1999; Manero et al. 2002), consists of a upper-convected Maxwell constitutive equation for stress evolution, coupled to a kinetic equation for structural flow-induced change (based on the rate of energy dissipation). This model can represent viscoelastoplastic characteristics in the limiting ideal state of infinite zero-shear viscosity (Calderas et al. 2013). Moreover, a variant micellar model has been proposed recently that interconnects viscoelasticity with the mechanical structure construction–destruction mechanism (López-Aguilar et al. 2014a, b). This model deals with modified Bautista–Manero (MBM) solution anomalies (Boek et al. 2005) for enhanced pressure drop (epd) estimation in contraction–expansion flow in the Stokesian limit (López-Aguilar et al. 2014a) and viscosity estimation across the flow field. Most significantly, this model is also able to capture highly elastic solutions in complex flow (López-Aguilar et al. 2014b). In addition, two variants for this model have been proposed, with energy dissipation given by as follows: (i) the polymer contribution exclusively (NM_τ p model) and (ii) polymer and solvent contributions combined (NM_T model). Such considerations introduce novel physics into the representation, by explicitly coupling the thixotropic and elastic nature of these fluids, alongside new key rheological characteristics, viz. declining first normal stress difference in simple shear flow (López-Aguilar et al. 2014a). De Souza (2009, 2011) has proposed an alternative thixotropic viscoelastoplastic model, based on a structure equation defined on the second invariant of the stress tensor τ p to drive the structure destruction mechanics. Then, the differential equation for their ‘structure parameter’ is introduced within and to form a generalised viscoelastic differential constitutive equation. In contrast, the family of Bautista–Manero models uses the dissipation function τ p : D (i.e. NM_τ p ) to this same end (López-Aguilar et al. 2014a, b). The De Souza model has been used in ideal simple and complex flow situations to represent thixotropic and viscoelastoplastic characteristics (see, for example, an overview for models representing viscoelastoplasticity (De Souza and Thompson 2012) and flow in an contraction–expansion setting (Hermany et al. 2013)).

The current contraction–expansion flow problem under study is now an accepted standard benchmark in experimental and computational rheology (Binding et al. 2006; Aguayo et al. 2008; Walters and Webster 2003; Rothstein and McKinley 2001). Its commending features relate to its vortex dynamics (re-entrant/salient), stress fields, flow kinematics and pressure drop measurement (López-Aguilar et al. 2014a). Here, diverse flow response may be found, relating to vortex dynamics and stress field evolution (extensional viscosity, N 2 effects), structure formation and numerical tractability (sharp-rounded corners) (Aboubacar et al. 2002a, b). One notes that pressure drop, which reflects the energy expended in a flow, is often studied through an epd measure (Binding et al. 2006; Aguayo et al. 2008) that itself offers a significant challenge to computational prediction (Binding et al. 2006).

Governing equations, constitutive modelling and problem specification

The governing equations under transient, incompressible and isothermal flow conditions may be expressed through those for mass conservation and momentum transport, coupled to a viscoelastic constitutive law for stress. Such a space–time partial differential equation set may be expressed in non-dimensional form as:

$$ \nabla \cdot \boldsymbol{u}=0, $$
(1)
$$ \mathrm{R}\mathrm{e}\frac{\partial \boldsymbol{u}}{\partial t}=\nabla \cdot \boldsymbol{T}-Re\boldsymbol{u}\cdot \nabla \boldsymbol{u}-\nabla p. $$
(2)

Here, field dependent variables u, p and T represent fluid velocity, hydrodynamic pressure and stress contributions, respectively, (t, x) represents space–time independent variables, and the gradient and divergence operators apply over the spatial domain. Then, stress is split into a solvent contribution τ s (viscous inelastic; plastic) and a polymeric contribution τ p (viscoelastic thixotropic; plastic) T = τ s  + τ p . In addition, D = (∇u + ∇u †)/2 is the rate of deformation tensor, with tensor transpose superscript notation †.

Dimensionless variables are defined through the following scaling choices:

$$ {\boldsymbol{x}}^{*}=\frac{\boldsymbol{x}}{L},\;{\boldsymbol{u}}^{*}=\frac{\boldsymbol{u}}{U},\;{t}^{*}=\frac{U}{L}t,\;{\boldsymbol{D}}^{*}=\frac{L}{U}\boldsymbol{D},\;{\boldsymbol{\tau}}_p^{*}=\frac{{\boldsymbol{\tau}}_p}{\left({\eta}_{p0}+{\eta}_s\right)\frac{U}{L}},\;{p}^{*}=\frac{p}{\left({\eta}_{p0}+{\eta}_s\right)\frac{U}{L}}. $$

Note that in all governing Eqs. (1)–(5), the * notation on dimensionless variable is discarded for concise form representation, retained by implication only. The Reynolds group number may be defined as Re = ρUL/(η p0 + η s ), with U a characteristic velocity scale (mean velocity, based on volume flow rate) and L a spatial scale (based on minimum contraction gap width). Then, ρ represents material density, and the zero-shear-rate viscosity (η 0 = η p0 + η s ) is the reference viscosity, whence \( \frac{\eta_{p0}}{\eta_{p0}+{\eta}_s}+\frac{\eta_s}{\eta_{p0}+{\eta}_s}=1.0 \). Here, η p0 is the zero-rate polymeric viscosity and η s is the solvent viscosity; the definition of solvent fraction is then β = η s /(η p0 + η s ).

The schematic representations of the 4:1:4 axisymmetric, rounded-corner contraction/expansion flow problem, alongside its corresponding mesh data, are reported elsewhere (López-Aguilar et al. 2014a; Aguayo et al. 2008) (see Aguayo et al. 2008 for further detail on this problem, which provides a full mesh refinement analysis for some typical case studies). Here, the lengths of the inlet and outlet regions are taken as 19.5H, where H is the upstream geometry radius divided by a factor of 4. Symmetry is enforced at the centreline. No-slip boundary conditions are enforced on the bounding wall. Entry flow kinematics is determined computationally for the equivalent entry-channel problem. These may be imposed through the time-stepping procedure, either as steady state or via a smooth transient build-up. Then, fully developed outflow conditions are established ensuring no change in streamwise and vanishing cross-stream kinematics. Once fully developed entry flow kinematics are known, stress may be determined pointwise through the derived corresponding ODE system.

Viscoelastoplastic Bingham–Papanastasiou model—solvent contribution form

In this study, non-Newtonian viscoplastic properties are introduced via a regularisation approach adopting the Bingham–Papanastasiou model (Papanastasiou 1987). Hence, yield stress contributions are recognised as entering through the solvent viscosity functionality alone. Note, there are other alternative formulation choices to embrace plastic behaviour via Papanastasiou regularisation (Papanastasiou 1987), namely (a) within polymeric viscosity functionality alone and (b) via both solvent and polymeric viscosity contributions. Studies illustrating the consequences of applying these various options have already been conducted and reported upon elsewhere, with polymeric representations under Oldroyd-B (Belblidia et al. 2011) and EPTT (Al-Muslimawi et al. 2013) models.

A general differential statement of the viscoelastic Bingham–Papanastasiou model employed here, with only solvent yield stress contribution, may be expressed in dimensionless form as follows:

$$ \boldsymbol{T}={\boldsymbol{\tau}}_s+{\boldsymbol{\tau}}_p $$
(3)
$$ {\boldsymbol{\tau}}_s=2\beta \varphi \left(I{I}_{\boldsymbol{D}};{m}_p,{\tau}_0\right)\boldsymbol{D} $$
(4)
$$ We{\overset{\nabla }{\boldsymbol{\tau}}}_p=2\left(1-\beta \right)\boldsymbol{D}-{f}_{\tau }{\boldsymbol{\tau}}_p, $$
(5)

where the upper-convected derivative of the extra-stress tensor is \( {\overset{\nabla }{\boldsymbol{\tau}}}_p=\frac{\partial {\boldsymbol{\tau}}_p}{\partial t}+\boldsymbol{u}\cdot \nabla {\boldsymbol{\tau}}_p-\nabla {\boldsymbol{u}}^T\cdot {\boldsymbol{\tau}}_p-{\boldsymbol{\tau}}_p\cdot \nabla \boldsymbol{u} \). Here, an elastic Weissenberg number, (We = λ 1 U/L), is introduced as a second dimensionless group number, arising as a product of a characteristic material relaxation time, λ 1, and a characteristic rate, U/L.

The Papanastasiou regularisation specifies an exponential functional form in its solvent viscosity contribution, based on the second invariant, \( I{I}_{\boldsymbol{D}}=\frac{1}{2}tr{\boldsymbol{D}}^2 \), of the rate of deformation tensor, viz

$$ \varphi \left(I{I}_{\boldsymbol{D}};{m}_p,{\tau}_0\right)={\eta}_0+\frac{\tau_0\left(1-{e}^{-{m}_p{\left|I{I}_{\boldsymbol{D}}\right|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right)}{2{\left|I{I}_{\boldsymbol{D}}\right|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}, $$
(6)

where parameters of {τ 0, m p } represent, τ 0 as the base cut-off yield stress factor and m p as the regularisation stress growth exponent (with scale of time). The τ 0 parameter expresses the stress level below which plastic behaviour is observed and is equivalent to a Bingham number, Bn, as expressed in Mitsoulis (2007).

Micellar NM_τ p _ABS Bingham–Papanastasiou model

To proceed to the micellar viscoelastoplastic representation, one needs to specify the generalised functional f τ , in Eqs. (3)–(5), imbuing a thixotropic networked nature to the fluid system. Recently, a new constitutive equation, based on the Bautista–Manero model class, has been proposed for modelling wormlike micellar systems that proposes the novel inclusion of viscoelasticity within the destruction mechanics of the fluid network structure (López-Aguilar et al. 2014a; corrects for epd undershoot at low deformation rates). Moreover, this formulation has been further developed to capture highly non-linear solutions in complex flows, of large We or low polymer concentration β forms (López-Aguilar et al. 2014b). This constitutes the base-level constitutive background upon which the present study is founded.

Using the Bautista–Manero–Puig (BMP) model (Bautista et al. 1999; Manero et al. 2002), with its MBM model counterpart (Boek et al. 2005), as the starting point, a non-linear dimensional differential structure equation for the fluidity (ϕ p  = η − 1 p ) is formed. Then, the polymeric viscosity function η p may be gathered. The evolving space–time fluidity provides the construction–destruction dynamics of the fluid network structure. Using the energy dissipated by the polymer under flow, this network structure may start from a fully structured state before being transformed into a completely unstructured state. The present investigation appeals to a version of this class of models, NM_τ p _ABS in Eqs. (3)–(5), which combines viscoelasticity into the thixotropic dependency and uses the absolute value of the dissipation function (guaranteeing accurate viscosity estimation; López-Aguilar et al. 2014b). As such, dependency on fluidity (ϕ p  = η − 1 p ) arises through its equivalent dimensionless structure functional f τ , of generalised differential form defined on the stress ζ variable (López-Aguilar et al. 2014a, b), viz.

$$ \frac{\partial {f}_{\tau }}{\partial t}=\frac{1}{\omega}\left(1-{f}_{\tau}\right)+{\xi}_{G_0} We\left|\boldsymbol{\zeta} :\boldsymbol{D}\right|. $$
(7)

Here, the dimensionless functional f τ is defined as f τ  = (η p0/η p), using η p0 as a viscous scaling factor on fluidity. Two distinct ζ versions of Eq. (7) arise and are documented elsewhere (López-Aguilar et al. 2014a), in one, considering the energy dissipated by the polymer constituent only to break the structure of the fluid (ζ = τ p , NM_τ p _ABS model), whilst, in the other, involving the polymer plus the solvent contributions to perform this same function (ζ = Τ, NM_T_ABS model). The dimensionless micellar parameters, which account for structural construction (ω = λ s U/L) and destruction \( \left[{\xi}_{G_0}=\left(k/{\eta}_{\infty}\right){G}_0\left({\eta}_{p0}+{\eta}_s\right)\right] \), appear in the corresponding terms for these dynamic mechanisms. Under steady-state conditions, the dynamic differential Eq. (7) reverts to its equivalent algebraic form,

$$ {f}_{\tau }=1+\omega {\xi}_{G_0} We\left|\boldsymbol{\zeta} :\boldsymbol{D}\right|. $$
(8)

Importantly, the dissipation function is the driving source of influence in departure from Oldroyd behaviour (f τ  = 1), which is modulated by the product of the construction and destruction parameters (thixotropy) with the Weissenberg number. Here, this expression for the f τ functional links directly with the viscosity, which is a positive physical quantity that should remain finite and above (or equal to) unity, under present scaling (ζ : D ≥ 0). As such, negative values (and less than unity) of this f τ functional are inadmissible. To avoid this eventuality arising (as previously exposed; López-Aguilar et al. 2014b) and consistent with the underlying ideal shear and extensional flow derivation theory, the ABS correction is utilised henceforth. This correction has the consequential effect of increasing the levels of non-linearity attained in numerical solutions, either via the relaxation time (high We; López-Aguilar et al. 2014b) or via the solvent fraction (low β) (present study).

Under such a description, the NM_τ p _ABS-Papanastasiou (named NM_τ p _ABS-Pap) dimensionless material functions for viscometric flow may be extracted as follows:

$$ {\eta}_{\mathrm{Shear}}=\beta \varphi \left(I{I}_{\boldsymbol{D}};{m}_p,{\tau}_0\right)+\frac{\left(1-\beta \right)}{f_{\tau }} $$
(9)
$$ {\eta}_E=3\beta \varphi \left(I{I}_{\boldsymbol{D}};{m}_p,{\tau}_0\right)+\frac{3\left(1-\beta \right){f}_{\tau }}{\left(f-2 We\dot{\varepsilon}\right)\left(f+ We\dot{\varepsilon}\right)} $$
(10)
$$ {N}_1=\frac{2\left(1-\beta \right) We{\overset{\cdot }{\gamma}}^2}{{f_{\tau}}^2} $$
(11)

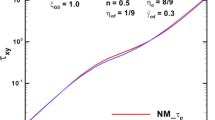
These material functions in Eqs. (9)–(11) provide the vital background and model reference against which to interpret anticipated complex flow response. One notes the extremely low levels of β-solvent fraction attained practically, those of β = {10−2, 10−3}; chosen to enhance the viscoelastoplastic characteristics inherent to these yield stress polymeric micellar fluids, under NM_τ p _ABS-pap modelling. Moreover, the micellar construction and destruction parameters are ω = 4.0 and ξ G0 = {1, 0.1125}. Here, at each solvent fraction level, fluids with {ω, ξ G0} = {4, 1} (relatively larger structure destruction parameter) display weaker strain-hardening characteristics (smaller peak in extensional viscosity) relative to those with {ω, ξ G0} = {4, 0.1125} (relatively reduced structure destruction parameter) (see Fig. 1). Consideration of the solvent viscoplastic Papanastasiou features is evaluated through variation of yield stress parameter τ 0 = {0.01, 0.1, 0.5, 1} and the regularisation stress growth exponent m p  = {10, 102, 103, 105, 107}. Also, viscoelastoplastic behaviour is pursued through β-variation for NM_τ p _ABS, with decreasing β = {0.9, 0.5, 1/9, 10−2, 10−2, 10−3, 10−4, 10−5} (Calderas et al. 2013). The special cases for which either τ 0 or m p attains null values characterise absence of viscoplasticity and thus collapse the fluid representation to that of the NM_τ p _ABS model. In Figs. 1, 2 and 3, dimensionless plots are provided of the material function against deformation rates in simple shear and uniaxial extension deformations.

Fig. 1
figure 1

Material functions against dimensionless rate; shear (η Shear) and extensional (η Ext) viscosities, N 1 and τ xy ; m p variation m p  = {10s; s = 1,2,…,7}; {β, τ 0, ω} = {10−2, 1, 4}; ξ G0 = 1 (top), ξ G0 = 0.1125 (bottom)

Full size image
Fig. 2
figure 2

Material functions against dimensionless rate; shear (η Shear) and extensional (η Ext) viscosities, N 1 and τ xy ; τ 0 variation τ 0 = {0.01, 0.1, 0.5, 1}; {β, m p , ω} = {10−2, 1, 4}; ξ G0 = 1 (top), ξ G0 = 0.1125 (bottom)

Full size image
Fig. 3
figure 3

Material functions against dimensionless rate; shear (η Shear) and extensional (η Ext) viscosities, N 1 and τ xy ; β-variation β = {0.9, 0.5, 1/9, 10−2, 10−3, 10−4, 10−5}; {τ 0, m p , ω} = {0, 0, 4}; ξ G0 = 1 (top), ξ G0 = 0.1125 (bottom)

Full size image

Yield stress m p variation {10s; s = 1,2,…,7}

Under {β, τ 0, ω, ξ G0} = {10−2, 1, 4, 1}, the shear stress against shear rate plot illustrates the influence of m p variation and also the effect of this low solvent fraction regime on the apparent polymeric plastic fluid characteristics (Fig. 1, top). Firstly, and as a consequence of the solvent viscoplastic characteristics at relatively low rates, the linear slope is gradually reduced as m p is increased, shifts of ~1 decade in rate for one decade increase in m p , once m p  ≥ 102. This shift leads to the appearance of a plateau (τ xy  = 10−2) at low rates, which is extended further into even lower-order rates as m p is increased, to the point in which the linear low-rate slope is practically lost. This position corresponds to the theoretical Papanastasiou prediction, in which m p → ∞ leads to an ideal yield stress viscoplastic response. The shear and extensional viscosities behave as expected, with shear thinning features, and strain hardening–softening (only at ξ G0 = 0.1125) features, as the deformation rate is increased. As m p is increased, the η 0 plateau value is incremented and thinning features onset at relatively low shear rates. Extensional viscosity curves reflect similar behaviour at low deformation rates, preserving the viscous factor of three units involved at each comparable m p level. Interestingly, the shear and extensional viscosity data curves ∀ m p converge at deformation rates of 10−1, before encountering either onset of shear thinning or onset of strain hardening–softening phenomena. Then, as the deformation rate is increased, these data curves appear to overlap, irrespective of their corresponding m p level. The first normal stress difference in shear (N 1) reflects invariance with m p change, as predicted by Eq. (11). Here, the quadratic slope at low shear rates is lost at a deformation rate of unity, evolving to a plateau of N 1 ~ 0.4.

As the thixotropic structure destruction parameter is decreased from ξ G0 = 1 to 0.1125, the upper-limiting plateau becomes N 1 ~ 4 units; extensional strain hardening–softening characteristics are exaggerated, with extensional viscosity peaks of ~6 units; both such effects apply irrespective of m p level. Moreover, as a consequence of this more structured fluid state at ξ G0 = 0.1125, the second viscoelastic plateau in τ xy is shifted to relatively larger shear rates (5 < \( {\lambda}_1\overset{\cdot }{\gamma } \) < 102) and higher levels of shear stress (~1 units).

Yield stress τ 0 variation {0.01, 0.1, 0.5, 1}

Alternatively, under {β, m p , ω, ξ G0} = {10−2, 102, 4, 1}, the shear stress against shear rate plot (Fig. 2, top) illustrates the influence of yield stress τ 0 variation. In contrast to m p variation, the effects of varying τ 0 on the shear stress are relatively milder. In particular, as τ 0 is elevated and at relatively low shear rate levels, the slope of linear dependency decreases. These data curves show united patterns at \( {\lambda}_1\overset{\cdot }{\gamma } \) ~ 10−1 units. In this moderate-to-high shear rate range, τ xy data curves follow the polymeric micellar behaviour described above: a plateau is attributed to non-linear thixotropic viscoelastoplasticity that extends into 1 < \( {\lambda}_1\overset{\cdot }{\gamma } \) < 102 range with further rise beyond \( {\lambda}_1\overset{\cdot }{\gamma } \) > 102. Shear and extensional viscosity are affected in their corresponding zero-rate plateaux as τ 0 is increased, whilst preserving their 3:1 extensional to shear viscosity ratio. Here, for low-rate shear viscosity, η 0 levels elevate from ~1 units for τ 0 = 0.01 to ~1.5 units at τ 0 = 1. Accordingly, this increase is reflected in extensional viscosity curves, for which the zero extension rate plateaux elevate from ~3 units for τ 0 = 0.01 to ~4.5 units at τ 0 = 1. As true for m p variation, the shear and extensional viscosity data curves ∀ τ 0 converge at deformation rates of 10−1, before encountering either decline due to shear thinning or strain hardening–softening phenomena.

Solvent fraction β-variation {0.9, 0.5, 1/9, 10−2, 10−3, 10−4, 10−5}

Finally, under {τ 0, m p , ω, ξ G0} = {0, 0, 4, 1}, the solvent fraction β-variation is analysed in Fig. 3 (top) that accounts for variation in polymer concentration. Here, the shear stress data curves illustrate the thixotropic NM_τ p _ABS property to generate a level τ xy plateau (value ~4.5) that applies over an ever wider shear rate range as the β-factor declines (at β = 10−5, plateau over \( 3<{\lambda}_1\overset{\cdot }{\gamma }<{10}^4 \)). Signs of plateau onset are observed at low solvent fractions, β ≤ 10−2 at \( {\lambda}_1\overset{\cdot }{\gamma } \) ~ 3 units. At larger rates and beyond the plateau period, the data curves return to a linear rise. One notes that the appearance of this thixotropic τ xy plateau, located in the moderate-to-high shear rate range, conforms to the current viscosity scale chosen under non-dimensionalisation η p0. It is desirable to shift such a polymeric feature to still lower shear rates and, henceforth, account for a realistic viscoelastoplastic plateau, as with the solvent viscoplastic Papanastasiou contribution. To achieve this, the characteristic viscosity scale should be fixed at the second Newtonian plateau η ∞ instead. This adjustment rescales the f τ functional, and hence viscosity, to the range \( \frac{\eta_{\infty }}{\eta_{p0}}\le {f}_{\tau}\le 1 \). Computational analysis to bear this out is due to appear subsequently. Analysis on N 1 reflects that, at low deformation rates (in the linear elastic regime), such β-variation provokes data curve translation by one-half decade for β-change from 0.9 to 1/9. At \( {\lambda}_1\overset{\cdot }{\gamma } \) ~ 6, these N 1 data curves unite, plateauing at N 1 ~ 0.4, independently of polymer concentration. The shear and extensional viscosity properties are also affected, with proportional decline in second Newtonian plateaux as β decreases. The Newtonian ratio of three is upheld between limiting extensional (dashed lines) and shear (continuous lines) viscosity plateaux.

Thixotropic ξ G0 variation

As the micellar structure destruction parameter is decreased from ξ G0 = 1 to 0.1125, again, the strain hardening–softening property is exaggerated, with peak values reaching ~6 units (Figs. 1, 2 and 3, bottom). Here, as the solvent fraction is decreased from β = 0.9 to 10−4, the appearance of an extensional viscosity peak is shifted to slightly lower deformation rates and reduces in size. Moreover, the plateaux in {τ xy , N 1} at ξ G0 = 0.1125 are shifted to larger levels of ~{1, 4}, relative to the less structured ξ G0 = 1 representation. These properties are unaffected by τ 0 or m p variation.

Numerical algorithm

The full detail of the hybrid finite element/finite volume numerical scheme used has appeared elsewhere, but for the sake of self-completeness and relevance to the present-yield stress–micellar implementation, a brief overview only is included.

Hybrid finite element/finite volume scheme

The hybrid finite element/volume scheme is a semi-implicit, time-splitting, fractional three-stage formulation, which draws upon finite element discretisation for velocity–pressure approximation and finite volume discretisation for stress. This combines the advantages and benefits offered by each approach, locally and to each component in the subsystem approximation (Matallah et al. 1998; Belblidia et al. 2008; Webster et al. 2005). Galerkin fe discretisation is imposed on the embedded Navier–Stokes system components, the momentum equation at stage 1, the pressure correction equation at stage 2 and the incompressibility satisfaction constraint at stage 3 (to ensure higher order precision). The subcell fv triangular tessellation is then constructed from the parent fe triangular grid by connecting the mid-side nodes. Such a tessellation is structured in nature. Stress variables are located at the vertices of fv subcells (cell vertex method, equivalent to linear interpolation). In contrast, quadratic velocity interpolation is enforced on the parent fe cell, alongside linear pressure interpolation. A direct Choleski solution method is utilised for the fe pressure correction stage 2, whilst for velocity stages (1, 3) under fe components, a space-efficient element-by-element Jacobi iteration is chosen.

Stress-finite volume cell vertex scheme

A cell vertex fv scheme is implemented for extra-stress, founded upon fluctuation distribution for fluxes (upwinding) and median-dual-cell treatment for source terms. Both provide nodal solution updates by distributing control volume residuals. Concisely, by rewriting the extra-stress equation in non-conservative form, with flux (R = u. ∇τ,) and absorbing remaining terms under the source (Q), one may obtain the following:

$$ \frac{\partial \boldsymbol{\tau}}{\partial t}+\boldsymbol{R}=\boldsymbol{Q}. $$
(12)

Here, each scalar stress component, τ, is considered as acting on an arbitrary volume \( \varOmega ={\displaystyle \sum_l{\varOmega}_l} \). Its variation is then controlled through corresponding fluctuation components of flux vector (R) and source term (Q),

$$ \frac{\partial }{\partial t}{\displaystyle \underset{\varOmega_l}{\int}\tau d\varOmega ={\displaystyle \underset{\varOmega_l}{\int }Rd\varOmega }}+{\displaystyle \underset{\varOmega_l}{\int }Q}d\varOmega . $$
(13)

According to the preferred strategy, the requirement is to evaluate the flux and source variations over each finite volume triangle (Ω l ) and construe their distribution to the three vertices of Ω l . The resulting nodal update for a particular node (l) is then obtained by accumulating the individual-cell contributions from its control volume Ω l , composed of all such fv triangles surrounding node (l). The flux and source residuals are evaluated over those control volumes associated with a given node (l) within the fv cell T, namely, the contribution governed over the fv triangle T, (R T , Q T ) from fluctuation distribution and that subtended over its counterpart median-dual-cell zone, (R mdc, Q mdc) from median dual cell approximation (Wapperom and Webster 1998). This procedure demands appropriate area weighting to maintain consistency, which for temporal accuracy has been extended to time terms likewise. First, the candidate stress equation is considered as split into three term groupings—those of time derivative, flux and source terms. Second, these are integrated over associated control volumes, for which the concise generalised fv nodal update equation per stress component may be expressed, viz.

$$ \left[{\displaystyle \sum_{\forall {T}_l}{\delta}_T{\alpha}_l^T{\varOmega}_T}+{\displaystyle \sum_{\forall MD{C}_l}\left(1-{\delta}_T\right){\widehat{\varOmega}}_l^T}\right]\frac{\varDelta {\uptau}_l^{n+1}}{\varDelta \kern0.1em t}={\displaystyle \sum_{\forall {T}_l}{\delta}_T{\alpha}_l^T{b}^T+}{\displaystyle \sum_{\forall MD{C}_l}\left(1-{\delta}_T\right){b}_l^{MDC}}, $$
(14)

where b T = (−R T  + Q T ), b MDC l  = (−R MDC + Q MDC)l. Here, Ω T is the area of the fv triangle T, whilst \( {\widehat{\varOmega}}_l^T \) is that of its associated median dual cell (MDC). The parameter δ T , 0 ≤ δ  T  ≤ 1, governs the balance allotted between the segregated contributions from the MDC and those from the fv triangle T (fluctuation distribution) (Webster et al. 2005). Hence, consistently and together, this formulation embeds fluctuation distribution/median-dual-cell contributions, area weighting and upwinding factors (α T l scheme dependent).

Vortex dynamics—τ 0 and We variation

As Weissenberg number (We) and yield stress (τ 0) are increased, and the kinematic nature of this complex flow is illustrated through the streamline patterns and graphs of vortex intensity of Fig. 4 and Table 1. Here, and basically if the flow rate is scaled to a value of unity, then the stream function is a variable flow rate, defined positively in the flow direction taking values between zero and unity, and where negative values may be meaningfully associated with recirculation (back-flow). Clearly, all results may be translated to percentage values of the flow rate. Concerning these streamline patterns, contours are plotted in core flow at equal increments of 0.05, covering contour levels of 0 ≤ Ψ ≤ 0.5; within vortices, the Ψ min peak value is recorded and there are six contour levels, covering the range 10−4 ≤ Ψ ≤ 10−4 in increments of 0.15 × 10−3. These data are generated under solvent Papanastasiou parameters of m p  = 102 and τ 0 = {0, 0.01, 0.05, 0.1}, which enforces the solvent plastic characteristics. In addition, the polymeric NM_τ p _ABS parameters used are ω = 4 and ξ = 1, with solvent fraction of β = 10−2. Conspicuously, vortex activity (size and intensity) decreases as either We is increased at a fixed τ 0 or τ 0 is increased at a fixed We.

Fig. 4
figure 4

Streamlines against τ 0 and We; {m p , β, ω, ξ G0} = {102, 10−2, 4, 1}

Full size image
Table 1 Vortex intensity (Ψ min = −Ψ min * × 10−4) against τ 0 and We; {m p , β, ω, ξ G0} = {102, 10−2, 4, 1}
Full size table

At We = 0.1 and τ 0 = 0 (viscoelastic NM_τ p _ABS, no solvent yield stress), the upstream and downstream vortex structures appear relatively symmetric in structure about the contraction. Here, the upstream vortex is slightly larger and more intense (Ψ min = −Ψ * min × 10−4 = 12) than the downstream vortex (Ψ min = 9.05). Larger yield stress levels under NM_τ p _ABS-Pap representation lead to vortex intensity suppression. In particular, at τ 0 = 0.01, both upstream (Ψ min = 5.88) and downstream (Ψ min = 4.35) vortex intensities drop by some 50 % away from the {NM_τ p _ABS, τ 0 = 0} reference solution. Notably, additional incrementation of τ 0 = {0.05, 0.1} generates even further vortex suppression of {96 %, 99 %}.

As We rises through {1, 10} at τ 0 = 0.01, this declining vortex behaviour is still further exaggerated, with percentage drop in intensity from each corresponding NM_τ p _ABS solution of {60 %, 65 %}.

At larger τ 0 values of {0.05, 0.1} at We = {1, 10}, this vortex suppression response from NM_τ p _ABS solution, and at each fixed We level, is even more marked, O (95 %), with the downstream vortex almost completely disappearing at {τ 0 = 0.1, We = 10}.

These trends are clearly illustrated in the graphical plots of Fig. 5 (top; m p  = 102), upstream–downstream vortex intensity versus τ 0 at each fixed We level (negative exponential form). The common trend across all three We = {0.1, 1, 10} curves is the drop in intensity to around the same intensity level by τ 0 = 0.05. Since the starting intensity at τ 0 = 0 for each We level rises with fall in We, this leads to ever increasing intensity drop rates as We rises. The upstream (left) trend graph versus the downstream (right) graph illustrates that the more marked intensity goes with the upstream vortex activity. Such trend adjustment is non-linear in change with We level, the largest being around We = 1.

Fig. 5
figure 5

Vortex intensity (Ψ min = −Ψ min * × 10−4) against τ 0 and We; {β, ω, ξ G0} = {10−2, 4, 1}; m p  = 102 (top), m p  = 103 (bottom)

Full size image

Regularisation stress growth exponent m p variation

The upper graphs for m p  = 102 versus the lower graphs for m p  = 103 of Fig. 5 illustrate the influence of increased yield stress characteristics and enhancement of plastic behaviour through the solvent (see material functions, Fig. 2). Here, there is steeper early decline in intensity, from τ 0 = 0.0 to τ 0 = 0.01, that is apparent in all instances of We. Asymptotic larger τ 0 behaviour is rather more rapidly assumed under m p  = 103 response, and this being quite evident even at the τ 0 = 0.01 level.

Solvent fraction β-variation

As above, polymeric concentration effects on vortex dynamics are illustrated in Fig. 6 through β = {10−2, 10−3} comparison. At such low solvent fraction levels, there are no significant differences in vortex dynamics to observe, only manifesting a slight increase in the vortex intensity for τ 0 < 0.05, which is larger with smaller We level.

Fig. 6
figure 6

Vortex intensity (Ψ min = −Ψ min * × 10−4) against τ 0 and We; {m p , ω, ξ G0} = {103, 4, 1}; β = 10−2 (continuous lines), β = 103 (dashed lines)

Full size image

Normal stress differences—τ 0 and We variation

Adopting the parametric study approach as above and under the setting {β, m p } = {10−2, 103}, the influence of plasticity and elasticity on normal stress difference is gathered through N 1 data fields of Fig. 7 and Table 2 and {τ 0, We} increase. Then, τ 0 incrementation at any fixed We = {0.1, 1, 10} level reveals little adjustment in N 1 magnitude or distribution. In contrast, at any fixed τ 0 = {0, 0.01, 0.1} level, N 1 extrema suffer a drop as We is elevated. This feature can be tied to the wall shear zones, and as such is a manifestation of shear thinning. In the extreme case of {τ 0 = 0.1, We = 1}, then {N 1max, N 1min} = {1.06, −0.94} are 62 % less intense relative to We = 0.1 data of {N 1max, N 1min} = {2.76,−2.50}. At We = 10, this trend is more abrupt, with We = 10 data of {N 1max, N 1min} = {0.59−0.46}, which represents a drop of 80 % relative to the same We = 0.1 extrema. Here, the red-positive and blue-negative regions, both upstream and downstream of the contraction, become less intense as We is elevated (as a consequence of shear thinning/strain softening, enhanced by low-β solvent fraction levels). Nevertheless, the domain occupation of the red-positive region grows in size, whilst the blue-negative zone contracts. Moreover, as We rises, the blue-negative zone at the centreline (and its local maxima) is convected downstream, as observed elsewhere (López-Aguilar et al. 2014b).

Fig. 7
figure 7

N 1 against τ 0 and We; {m p , β, ω, ξ G0} = {103, 10−2, 4, 1}

Full size image
Table 2 First normal stress difference (N 1) against τ 0 and We; {m p , β, ω, ξ G0} = {103, 10−2, 4, 1}
Full size table

In the upstream and downstream salient corner zones, N 1 data fields of Fig. 7 and Table 2 provide vortex-like structures, essentially identifying N 2 contributions to N 1, that evolve in the same fashion as do the true kinematic vortex structures (see Vortex dynamics—τ0 and We variation section above). Hence, these vortex-like N 2 structures shrink as τ 0 and We rise. One notes with look ahead that these structures are exaggerated when the effects of extensional viscosity are introduced via ξ G0 variation.

Yield fronts—yielded and unyielded regions, τ 0 and We variation

Figure 8 conveys the solution perimeter and division between yielded (red) and unyielded (blue) regions at {β, m p } = {10−2, 103} for the NM_τ p _ABS-Pap model. Once more, the effects of plasticity are analysed, via τ 0 = {0.01, 0.05, 0.1} and those due to elasticity, via We = {0.1, 1, 5, 10}. The cut-off criterion for these fields is based on the magnitude of stress (through its second invariant, see Mitsoulis 2007; Belblidia et al. 2011; Al-Muslimawi et al. 2013) exceeding τ 0 in each instance. The dominant and most interesting features to report here are those given in terms of τ 0 incrementation at fixed We level. For instance, at τ 0 = 0.01 and We = 0.1, red yielded regions are found near the tube wall, where the shear rates are relatively large. Approaching the geometry centreline, blue relatively slender unyielded regions appear around and along the centreline, upstream and downstream of the contraction. In shape, this unyielded centreline zone resembles a necking filament, with bulbous zones either side of the contraction. This structure pattern tapers to a sharp end that is directed towards the contraction, connected by a slender column-like thread that passes through the contraction along the centreline. In the recess zones (geometry salient corners), concave-shaped unyielded regions are also present.

Fig. 8
figure 8

Yield fronts against τ 0 and We; {m p , β, ω, ξ G0} = {103, 10−2, 4, 1}

Full size image

As yield stress level is raised to τ 0 = 0.05, the unyielded regions in the core flow have considerably expanded outwards, towards the tube walls; also, those in the recess zones have elongated upstream and downstream. This defines the perimeter of the yielded regions, which appear connected and are pinched by the expanding unyielded zones.

Finally, at even higher τ 0 = 0.1, the unyielded salient corner/core flow regions have now merged, surrounding and isolating the yielded zone, which is now restricted to a domain lying across and on either side of the contraction plane (shamrock shape). For {τ 0 = 0.1, We ≤ 1}, these regions preserve their characteristic sharp cusp tip at the centreline, a feature that is gradually being suppressed with rise in We (almost non-existent at We = 10). A significant new feature to note is the birth and growth of a half-moon-shaped unyielded region, just downstream of the contraction, emerging about the centreline. This feature is apparent in {τ 0 = 0.1, We ≥ 1} and {τ 0 = 0.05, We ≥ 5} solutions; subsequent to its appearance, it expands downstream, as either τ 0 or We rise.

Thixotropic destruction parameter ξ G0 variation—extensional viscosity effects

As illustrated in Figs. 1, 2 and 3, reduction of the ξ G0 destruction parameter (of polymeric NM_τ p _ABS model; López-Aguilar et al. 2014b) leads to the consideration of additional extensional viscosity features in this viscoelastoplastic context. Here, solutions generated under ξ G0 = 1 are contrasted against the relatively more strain-hardening configuration of ξ G0 = 0.1125.

Vortex dynamics

In Fig. 9 and Table 3, the streamline patterns reveal provocative results, when contrasting the two levels of strain hardening, ξ G0 = {1, 0.1125}, and elasticity levels, We = {0.1, 5}. At We = 0.1, ξ G0 solutions are graphically invariant to vortex structure adjustment, with ξ G0 change at each fixed τ 0 value. Here, under ξ G0 = 0.1125, larger upstream and downstream minimum vortex intensity values (Table 3) are predicted (vortex enhancement) relative to the solutions at ξ G0 = 1.

Fig. 9
figure 9

Streamlines against τ 0 and We = {0.1, 5}; {m p , β, ω} = {103, 10−2, 4}; ξ G0 = {1, 0.1125}

Full size image
Table 3 Vortex intensity (Ψ min = −Ψ min * × 10−4) against τ 0, ξ G0 and We; {m p , β, ω} = {103, 10−2, 4}
Full size table

In contrast, at We  = 5 and ξ G0 = 0.1125, notably larger upstream minimum vortex intensity values are obtained with respect to those under ξ G0 = 1. Here, the change in strain-hardening characteristics with ξ G0 = 0.1125 is now so dramatic that the downstream vortex structure is visually lost for τ 0 ≥ 0.01 and the upstream vortex takes on a convex shape. Moreover, the minimum upstream vortex intensity values for ξ G0 = 0.1125 solutions are conspicuously larger (by at least two orders of magnitude) than those under ξ G0 = 1.

Upstream vortex and the normal stress differences N 1 and N 2

In Fig. 10, comparisons of streamlines N 1 and N 2 data fields are provided under the strain-hardening setting of ξ G0 = 0.1125. Here, particular attention is paid to the close signature relationship between the kinematic upstream vortex structures and the vortex-like structures in N 2 fields (with its reflection/counterpart on N 1 data). Correspondence in shape and declining trends is identified amongst these structures, as the yield stress τ 0 is increased. This close relationship between vortex dynamics and N 2–N 1 data fields has already been commented upon elsewhere (López-Aguilar et al. 2014a; Tamaddon-Jahromi and Webster 2011).

Fig. 10
figure 10

Streamlines, N 1 and N 2, against τ 0; We = 5; {m p , β, ω, ξ G0} = {103, 10−2, 4, 0.1125}

Full size image

Excess pressure drop

In Fig. 11, the effects of m p and ξ G0 variation on epd are evaluated as the yield stress τ 0 is elevated and at three elasticity parameter levels, We = {0.1, 1, 5}. Consistently, it is evident from these data that any variation that leads to solid-like behaviour produces epd enhancement. Furthermore, these epd data curves adopt a linear trend with change in τ 0 (Belblidia et al. 2011). One notes here that the presence of viscoelasticity and pronounced strain-hardening characteristic does not change this trend in signature. The positive slope in the data curves for all We values reveals an increase in epd as τ 0 is elevated. Interestingly, the same effect is observed with m p variation; a growth in slope is observed when passing from m p  = 102 to 103. Amongst this epd enhancement evidence, the most prominent feature is that due to variation in ξ G0 (with its corresponding strain-hardening effects). For this parameter, shifting from ξ G0 = 1 to the relatively more strain-hardening level of 0.1125 translates into an increase of ~0.25 units in epd, covering the entire range of τ 0 examined. In contrast, rise through We provides smaller epd values, likely caused by marked shear thinning and strong N 1 characteristics of the viscoelastoplastic fluids analysed (see Figs. 1 and 2). One must also note, however, that the present model is constructed around the constant viscosity Maxwell/Oldroyd foundation, notorious for producing negative pressures in contraction flows. The present model variant has its deficiency of minimal strain-hardening response in elongation (see Figs. 1, 2 and 3), and it is the boosting of this feature that would be associated with high epd evaluation.

Fig. 11
figure 11

Epd against τ 0; We = {0.1, 1, 5}; {β, ω} = {10−2, 4}

Full size image

Yield fronts

The effects of ξ G0 variation on yield fronts are provided in Fig. 12. This illustrates the division between yielded (red) and unyielded (blue) regions at {β, m p } = {10−2, 103} for NM_τ p _ABS-Pap solutions. Here, at {τ 0 = 0.01, We = 0.1} and ξ G0 = 0.1125, the unyielded regions at the centre of the flow field appear larger than those for ξ G0 = 1. Such disparity is minimised with further rise in yield stress level, τ 0 ≥ 0.05.

Fig. 12
figure 12

Yield fronts against τ 0 and We = {0.1, 5}; {m p , β, ω} = {103, 10−2, 4}; ξ G0 = {1, 0.1125}

Full size image

At the higher elasticity level of We = 0.5, stronger strain-hardening characteristics through ξ G0 variation begin to influence yield front shape. Here, taking We = 0.5 solutions in comparison to We = 0.1 solutions, the unyielded {τ 0 = 0.01} regions at the centreline would appear wider in the radial direction, and their tip changes more abruptly. These characteristics are simply stretched out radially with further rise in τ 0. Strictly at We = 0.5 and in comparison across ξ G0 = {1, 0.1125} solutions, there are notable asymmetries in salient corner vortex zones. Moreover, at τ 0 = 0.1, the additional strain-hardening ξ G0 = 0.1125 solution is observed to suppress the half-moon-shaped unyielded region, present in the ξ G0 = 1 solution.

Conclusions

Yield stress elastic thixotropic solutions have been obtained through two different constitutive routes (and models thereby): (i) in the solvent contribution, via Papanastasiou regularisation, and (ii) in the polymeric contribution, via micellar thixotropic (NM_τ p _ABS-Pap) models. Numerical solutions have been reported whilst varying elastic and plastic contributions through parametric variation of yield stress cut-off τ 0 = {0.01, 0.05, 0.1}, regularisation stress growth exponent m p  = {102, 103}, polymeric concentration β = {10−2, 10−3} and thixotropic destruction parameter ξ G0 = {1, 0.1125}.

Numerical solutions under NM_τ p _ABS-Pap model reveal new and provocative findings on vortex dynamics, N 1 fields, yield front patterns and excess pressure drop, according to yield stress {τ 0, m p } parameter variation, strain-hardening (ξ G0) and polymeric concentration incrementation (β). Vortex intensity and size are observed to sharply reduce with increasing {τ 0, m p } (yield stress) and elasticity levels (strain softening). There is reduction in the initial negative slope of the vortex intensity curve versus τ 0, noted as We is elevated at the base-level m p  = 102. From this position, considering m p elevation at each fixed We level, there is an increased drop in vortex intensity with τ 0 rise. Clearly, enhancing solid-like features dampens the mobility of the material (vortex dynamics).

On structural influence

In contrast to these yield stress consequences above where ξ G0 = 1, now considering each fixed τ 0 level, the exaggerated strain-hardening properties observed when decreasing the thixotropic ξ G0 destruction parameter (from unity to 0.1125, characterising more mobile fluids) have a major impact on vortex activity. This is encapsulated through upstream vortex enhancement and downstream vortex suppression. The influence of change with elasticity (We rise, from 0.1 to 5) appears as a contra effect to that due to strain-hardening, with upstream vortex reduction for ξ G0 = 1 and enhancement for ξ G0 = 0.1125. This is true ∀ τ 0 solutions, though most emphasised at τ 0 = 0. Appealing to corresponding viscometric properties, this observation may be attributed to the influence of strain softening. It is particularly conspicuous that We rise promotes asymmetry in the streamline patterns about the contraction.

Patterns and trends in the normal stress difference fields reflect those in re-entrant corner vortex patterns, with elevation in yield stress, elasticity and strain hardening. Hence, these N 2 vortex-like features, in the upstream and downstream recess corner zones, contract as the yield stress τ 0 and the elasticity levels are increased. Interestingly, at the extreme setting {τ 0, We} = {0.1, 10}, downstream vortex activity practically disappears. Consistently, these trends are more exaggerated when strain hardening is enhanced through ξ G0 reduction, which represents more structured fluid states.

On yield front patterns

These reveal significant influence with yield stress τ 0 variation. Here, symmetric unyielded regions first appear at τ 0 = 0.01, with upstream and downstream slender core regions at the centreline and concave unyielded regions confined to recess zones. When the cut-off yield stress level (τ 0 value) is increased, the core region expands outwards towards the wall and approaches the recess unyielded zones, which now have elongated away from the corner. Further increase of the yield stress provokes unification, of core and recess yielded zones, to define a central single shamrock-shaped yielded region about the contraction gap. In contrast, elevation in elasticity through We provokes asymmetry in the recess unyielded zones. This is illustrated in the middle-to-high yield stress range (τ 0 ≥ 0.05) and for elasticity levels (We ≥ 5), when there is also formation of a new half-moon-shaped unyielded region, about the centreline just beyond the contraction plane. ξ G0 reduction (thixotropic structural influence) suppresses the formation of this half-moon-shaped unyielded region.

On epd

Here, findings versus increased yield stress (τ 0) follow linear functionality. The epd slopes slightly rise with elevation in m p . The epd intersection point at τ 0 = 0 (coinciding with NM_τ p _ABS solutions) is shifted to lower levels as We levels are increased. One associates this epd lowering for NM_τ p _ABS thixotropic solutions with its marked shear thinning and strong N 1 properties. One must acknowledge, however, that the present model variant has its deficiency of only minimal strain-hardening response in elongation, and it is the boosting of this feature that would be associated with high epd evaluation. Moreover, relatively more structured fluids, characterised with smaller ξ G0, display distinctly larger epd values throughout the τ 0 range covered.