On the modelling of the shear thickening behavior in micellar solutions

Abstract

The steady and transient nonlinear rheological behaviors of dilute rod-like micellar solutions are predicted here with a particular case of the generalized Bautista–Manero–Puig (BMP) model that consists of the upper-convected Maxwell constitutive equation and a dissipative power-dependent kinetic equation, which takes into account the formation and disruption of shear-induced structures (SISs). This model has been derived using the extended irreversible thermodynamic (EIT) formalism. In steady shear, the model predicts a Newtonian region at low shear rates and a characteristic shear rate (${\dot{\upgamma}}_{\mathrm{c}}$) at which shear thickening develops. In the shear thickening region, the model predicts either a reentrant zone, which is caused by multi-valued shear stresses when the data are collected with a shear stress-controlled mode or a continuous increase in the shear stress-shear rate flow curve, when the data are collected with a shear rate-controlled mode; in this region, two coexisting phases are predicted. The coexisting phases at the same shear rate in the two-phase envelope and the spinodal-like region were evaluated from the extended Maxwell equal-area criterion, which was calculated from the equal values of the two minima of the plot of the extended Gibbs free energy versus shear rate. At higher shear rates, the model predicts a transition to shear thinning, and under transient flows, an induction time and a saturation time are obtained from the predicted and the experimental data as detailed in the text. The magnitudes of both, the induction and the saturation times, diminish as the shear rate departs from ${\dot{\upgamma}}_{\mathrm{c}}$, but only the induction time decreases according to a power law with shear rate. The conditions under which these rheological responses arise are derived and justified in detail with the BMP model. The model predictions are compared with experimental data of two dilute micellar solutions. The model parameters were determined from a set of independent experiments without fitting.

Introduction

The shear thickening transition (STT) is characterized by a several-fold viscosity increase when dilute micellar solutions are sheared above a characteristic shear rate, ${\dot{\gamma}}_{\mathrm{c}},$ or a characteristic shear stress, σ _c (Hu et al. 1998a, b; Puig et al. 2007; Lerouge et al. 2010). For $\dot{\gamma}$ (or σ) larger than ${\dot{\gamma}}_{\mathrm{c}}$ (or σ _c ), an induction time (t _ind) is necessary for the inception of the viscosity growth. This induction time may range from seconds to several minutes (Hu et al. 1998a). After the induction time, another time, referred as the saturation time (t _sat), is detected before the steady state viscosity is attained (Berret et al. 2002). Both t _ind and t _sat become longer as the applied shear rate approaches ${\dot{\gamma}}_c$. A power law dependency of the form, t _ind ∼${\dot{\gamma}}^{-m}$, has been reported by several authors (Hu et al. 1993; Boltenhagen et al. 1997a; Pröztl and Springer 1997; Hu et al. 1998a; Barentin and Liu 2001; Berret et al. 2002; Macías et al. 2003); although other authors have reported a relationship of the form t _ind ~ ${\left(\dot{\gamma}-{\dot{\gamma}}_c\right)}^{-1}$ (Hu et al. 1993; Berret et al. 2002). Hu et al. (1993) found that t _ind ~${\dot{\upgamma}}^{-\mathrm{m}}$ is valid even far from ${\dot{\gamma}}_c$. Nevertheless, the dependence of t _ind on variables such as the surfactant concentration and chemical structure has not been explored so far.

Hu et al. (1998a) observed four regimens in the STT. The first one occurs below a characteristic shear stress, σ_c, where the shear rate increases monotonically with the stress and no shear thickening or shear-induced structures (SISs) are detected. The regime II appears when the stress is greater than σ_c but lesser than the saturation stress, σ_s, at which two coexisting states are observed. The steady state in this regime is detected only under stress-controlled conditions. The regime III is characterized by a second Newtonian region for σ _> σ _s followed by a shear thinning region at high shear rates (regime IV).

Shear thickening is caused by two mechanisms depending on the reference system. In associative polymers or in colloidal suspensions flocculated by reversible polymer bridging, shear thickening is attributed to nonlinear elasticity of flexible polymers, usually followed by forced desorption or disentanglement at large chain extensions, producing shear thinning of the flowing solutions (Séréro et al. 2000). On the other hand, shear thickening in dilute micellar solutions is caused by the formation of SIS, the morphology of which is still under debate (Pröztl and Springer 1997; Oda et al. 2000; Berret et al. 2001; Weber and Schoseller 2002; Macías et al. 2003, Marín-Santibañez et al. 2014). Upon their formation, these structures may remain for a long time producing rheopexy in addition to shear thickening (Lopez-Diaz et al. 2010).

Lerouge et al. (2010) suggested that the SISs are formed by supramolecular structures resulting from micellar association or by fusion that may occur under shear or extensional flow, as revealed by a reversible transition to a turbid gel phase that coexists with an isotropic fluid (Rehage and Hoffmann, 1982; Wunderlich et al. 1987; Boltenhagen et al. 1997b; Hu et al. 1998a, 1998b). The initiation of the process of SIS formation has also been attributed to local disturbances in wormlike concentration created by local velocity gradients (Dhont and Briels 2008).

Microscopic theories and models to analyze the STT in dilute surfactant solutions are scarce. Preliminary attempts to describe this phenomenon include theories that incorporate non-equilibrium shear-induced phase transitions and hydrodynamic instabilities (Porte et al. 1997; Olmsted and Lu 1999). Some models for shear thickening are based on shear-induced aggregation of rod-like micelles (Cates and Turner 1990; Wang et al. 1990). Models that couple a gelation transition to shear bands (Adjari 1998; Goveas and Olmsted 2001; Picard et al. 2002) or those that attribute shear thickening to electrokinetic or ionic phenomena (Barentin and Liu 2001) have also been forwarded, although shear thickening has been observed in nonionic micellar solutions as well (Hu and Matthys 1997). Early models have considered a growth mechanism involving the collinear fusion of flow-aligned micelles, but the predicted characteristic shear rate is not within the experimental range because interactions among micelles were not considered (Cates and Turner 1990; Wang 1991). Nevertheless, progress has been achieved in understanding the role of short-range attractive electrostatic interactions between rod-like particles bearing the same net charge (Ha and Liu 1997). Barentin and Liu (2001) attributed the shear gelation to counterion-mediated-induced intermicellar interactions by estimating the interaction potential between wormlike micelles; in this situation, the predicted ${\dot{\upgamma}}_{\mathrm{c}}$ is within the range of observed values. Cates and Candau (2001) proposed the existence of large ring-like micelles in the quiescent solutions as the precursors of the gel-like phase; however, experimental evidence of large ring-like micelles has not been reported. Aradian and Cates (2006) developed a model in which the instantaneous constitutive curve at fixed structure is non monotonic. To allow for spatial structuring, the homogeneous stress is replaced with one that can vary along the vorticity direction. They further incorporated a nonlocal gradient term in the stress to allow for the interfaces that are expected to arise. When the structural evolution is much slower than the stress relaxation, the model predicts oscillating shear bands. Recently, Castillo-Tejas et al. (2011) predicted shear thickening in micellar solutions using a molecular model that addresses the dynamics of interaction, orientation, and migration.

Other phenomenological models have been proposed such as the one by Goveas and Pine (1999) that considers the growth of a shear-induced gel phase in which there is no flow; this model predicts a reentrant region in the shear stress-shear rate flow curve only under stress-controlled conditions and a discontinuity under shear rate-controlled conditions. Another simple model, consisting of the upper-convected Maxwell constitutive equation coupled to a kinetic equation that accounts for the structural modifications induced by flow, has been proposed to explain the STT and the velocity variations observed in pipe and parallel-plate flows (Macías et al. 2003). This model predicts a continuous increase in the apparent viscosity with increasing shear rate as reported by several researchers (Boltenhagen et al. 1997a; Gámez-Corrales et al. 1999; Berret et al. 2000, 2002; Macías et al. 2001, 2003), but it cannot predict the reentrant region detected by Hu et al. (1998a) in regime II. In parallel-plate flow, the model can account for the average steady values of the viscosity in the structured thickened state, whereas in Poiseuille flow, it predicts a transition region between two parabolas where a change in curvature in the velocity profile is observed in the shear thickening regime. The shear rate in the vicinity of the wall is smaller than that resulting from extrapolation of the parabola positioned at the pipe center indicating that a more viscous liquid layer flows close to the walls, corresponding to the shear thickening regime of region III of high viscosity. This determines the pipe’s region where shear thickening develops. In the region of transition corresponding to that of regime II, fluctuations in the measured point velocities are detected, whereas the predictions depict the change in curvature in the transition region. In the vicinity of the wall, there is an apparent viscosity increase and the predictions of the model match the change in the curvature of the experiments. Other interesting predictions that agree with the experimental data are the flow curves for various values of the pipe length-to-diameter ratio (L/D): for small L/D, the fluid does not shear thicken because the residence time is smaller than the induction time and its behavior is Newtonian; as the pipe L/D and the residence time increases, a gradual manifestation of shear thickening occurs (Macías et al. 2003). These predictions illustrate the transient growth of the shear thickening phase, in which an induction time related to the residence time of the fluid in the pipe is a necessary condition for the development of shear thickening.

In this paper, we predict the steady and transient nonlinear rheology of dilute rod-like micellar solutions using a particular case of the generalized Bautista–Manero–Puig (BMP) model, which is deduced using the extended irreversible thermodynamic formalism (see Supplementary material (SM)). This model consists of the upper-convected Maxwell constitutive equation and a stress-dependent kinetic equation that takes into account the formation and disruption of the SIS. This extended model is an improvement of the one we used previously to describe the shear thickening behavior of cetyltrimethylammonium tosylate (CTAT) in parallel-plate and Poiseuille flows (Macías et al. 2003), inasmuch as it also describes the reentrant region and the shear-thinning region often observed at high shear rates. The predictions of the extended BMP model for shear thickening behavior are compared with experimental steady and transient rheological data of two cationic surfactant systems, CTAT, and cetyltrimethylammonium vinylbenzoate (CTAVB).

The model

The derivation of the generalized BMP model using the extended irreversible thermodynamic formalism is detailed in the SM, emphasizing the origin of the nonlinear reforming function, where higher order terms are included in the reforming and destruction functions. This model has been used successfully for shear (Manero et al. 2002) as well as extensional flows (Jahromi et al. 2011; López-Aguilar et al. 2014; Stukan et al. 2007). Here, we have considered additional nonlinear terms to build the tensor ${\underline {\underline {\mathrm{X}}}}_2$ and the scalar X₀ (see SM). Such additional nonlinear terms allow the prediction of the reentrant region and the shear thinning–shear thickening transition. Inasmuch as the shear stress is the controlling variable in shear thickening flow (Hu et al. 1998a; Puig et al. 2007), the kinetic parameter k is considered here to depend linearly only on the second invariant of the shear stress tensor, i.e., k = k ₀(1 – ψσ ₁₂), where k ₀ is the kinetic constant for structure modification (Macías et al. 2003). The parameter ψ is related to the reentrant region, i.e., the inhomogeneous–homogeneous flow transition (IHT). In this case, the characteristic structure time, λ, is given by $\frac{1}{\lambda }=\frac{1}{\lambda_0}\left(1-\chi \overline{\overline{\sigma}}:\overline{\overline{D}}\;\dot{\gamma}\right)$, i.e., λ is considered a function of the dissipation term multiplied by the shear rate, and λ ₀ is the characteristic structure recovery time. The characteristic structure time was defined in the BMP model previously (Bautista et al. 1999; Manero et al. 2007). The parameter χ represents the intensity of shear thickening–shear thinning transition (TTT), suggesting a novel approach to that exposed previously. As described before, the parameters ψ and χ accentuate the nonlinear character of the constitutive equations. The generalized model contains seven parameters (φ ₀, φ _∞, λ ₀, k ₀, G ₀, χ, and ψ). The first five ones can be obtained for single and independent measurements as shown elsewhere (Manero et al. 2002) whereas χ and ψ can be obtained without fitting as shown below, i.e., they are not adjustable parameters.

The governing equations are as follows:

$$ {\sigma}_{12}+\frac{1}{G_0\varphi}\frac{\mathrm{d}{\sigma}_{12}}{\mathrm{d}\mathrm{t}}=\frac{{\dot{\gamma}}_{12}}{\varphi } $$

(1)

$$ \frac{\mathrm{d}\varphi }{dt}=\frac{\varphi_0-\varphi }{\lambda_0}\left(1-\chi {\sigma}_{12}{\dot{\gamma}}_{12}^2\right)+{\mathrm{k}}_0\left(1+\psi {\sigma}_{12}\right)\left({\varphi}_{\infty }-\varphi \right){\sigma}_{12}{\dot{\gamma}}_{12} $$

(2)

(see Eqs. (SM16) and (SM17) in SM). Here, σ ₁₂ is the shear stress and ${\dot{\gamma}}_{12}$ the shear rate, φ is the inverse of shear viscosity (η) or fluidity, φ ₀ is the zero-shear rate fluidity, and φ _∞ is the minimum value of fluidity (i.e., maximum viscosity) reached at end of the thickening process as defined by Hartmann and Cressely (1997, 1998); in addition, G ₀ is the shear plateau modulus, λ ₀ is a structure reformation characteristic time, and χ and ψ are phenomenological coefficients (as indicated in SM), the significance of which will be disclosed later.

In Eq. (1) of the BMP model, the relation between the fluidity, the stress relaxation time τ, and the micellar length n is τ [=(G ₀ × φ)⁻¹ = τ ₀ (n/n ₀)], where τ ₀ is the stress relaxation time when φ = φ ₀. Substituting this relation into the evolution equation for the fluidity (Eq. (2)) yields an equation that can be expressed in terms of the average micellar length, which is the microstructural variable. The physical interpretation is that the micellar length n follows an evolution equation related to the breakage and reformation process of the micelles. This equation itself is coupled to the total stress, which contains the micellar contribution.

In steady, simple shear and since only the shear stress and the shear rate are considered, the subscript “₁₂” will be dropped and so, Eqs. (1) and (2) render a cubic expression in both σ and shear rate of the form:

$$ {k}_0{\lambda}_0{\varphi}_{\infty}\psi \dot{\gamma}{\sigma}^3+\left({\mathrm{k}}_0{\lambda}_0{\varphi}_{\infty}\dot{\gamma}-{\mathrm{k}}_0{\lambda}_0\psi {\dot{\gamma}}^2-\chi {\varphi}_0{\dot{\gamma}}^2\right){\sigma}^2+\left({\varphi}_0-{\mathrm{k}}_0{\lambda}_0{\dot{\gamma}}^2+\chi {\dot{\gamma}}^3\right)\sigma -\dot{\gamma}=0 $$

(3)

Inhomogeneous–homogeneous flow transition

It has been observed that at a characteristic shear rate and a characteristic shear stress, the homogeneous flow becomes inhomogeneous. That is, the flow becomes multivalued in the shear stress in a certain shear stress range, which is also referred as banded flow in the vorticity direction. The inhomogeneous character of the flow is associated to the appearance of SIS, suggesting a spinodal-type transition to a two-phase flow. However, Oda et al. (2000) observed that the characteristic shear rate at which this transition appears (${\dot{\gamma}}_c$) depends on the gap distance of the Couette cell employed, which ruled out the SIS phenomenon as a phase transition. Nucleation and growth of the SISs are therefore explained by Oda et al. (2000) as a transient inhomogeneous state, different to that observed in common shear banded flows, where a well-defined interface is apparent (Hu et al. 1998a, 1998b).

Considering that for 0 < ψ < ψ _IHT the fluid is homogenous, let us define ψ_IHT as the characteristic value at which the inhomogeneous–homogeneous transition (IHT) is observed, wherein the multivalued region or reentrant region appears. The flow becomes inhomogeneous when a characteristic stress is reached for values where ψ > ψ_IHT, which implies that the IHT conditions, d$\dot{\gamma}$/dσ = 0 and d² $\dot{\gamma}$/dσ ² = 0, must hold. The first and second partial derivatives of $\dot{\gamma}$ with respect to σ are as follows:

$$ \frac{d\dot{\gamma}}{d\sigma }=-\frac{\mathrm{k}{\varphi}_{\infty}\psi \dot{\gamma}3{\sigma}^2+\left(\mathrm{k}\dot{\gamma }{\varphi}_{\infty }-\left(\chi {\varphi}_0+\mathrm{k}\psi \right){\dot{\gamma}}^2\right)2\sigma +\left(\chi {\dot{\gamma}}^3-\mathrm{k}{\dot{\gamma}}^2+{\varphi}_0\right)}{\left(\mathrm{k}{\varphi}_{\infty}\psi {\sigma}^3+{\sigma}^2\left(\mathrm{k}{\varphi}_{\infty }-\left(\chi {\phi}_0+\mathrm{k}\psi \right)2\dot{\gamma}\right)+\sigma \left(3\chi {\dot{\gamma}}^2-2\mathrm{k}\dot{\gamma}\right)-1\right)} $$

(4)

$$ \begin{array}{l}0=\left(k{\varphi}_{\infty}\psi {\sigma}^3+\left(k{\varphi}_{\infty }-2\left({\varphi}_0\chi +k\psi \right)\dot{\gamma}\right){\sigma}^2+\left(3\chi {\dot{\gamma}}^2-2k\dot{\gamma}\right)\sigma -1\right)\frac{d^2\dot{\gamma}}{d{\sigma}^2}\\ {}-2\left(\left({\varphi}_0\chi +k\psi \right)\sigma -3\chi \dot{\gamma}+k\right)\sigma {\left(\frac{d\dot{\gamma}}{d\sigma}\right)}^2+2\left(2k{\varphi}_{\infty}\psi \sigma -4\left({\varphi}_0\chi +k\psi \right)\dot{\gamma}\sigma +3\chi {\dot{\gamma}}^2-2k\dot{\gamma}+k{\varphi}_{\infty}\right)\frac{d\dot{\gamma}}{d\sigma}\\ {}+6k{\varphi}_{\infty}\psi \dot{\gamma}\sigma +2\left(k{\varphi}_{\infty }-\left({\varphi}_0\chi +k\psi \right)\dot{\gamma}\right)\dot{\gamma}\end{array} $$

(5)

where k ₀ λ ₀ = k in Eqs. (4) and (5). From the IHT conditions, the two following equations hold:

$$ k{\varphi}_{\infty}\psi \dot{\gamma}6\sigma +\left(k\dot{\gamma}{\varphi}_{\infty }-\left(\chi {\varphi}_0+k\psi \right){\dot{\gamma}}^2\right)2=0 $$

(6)

$$ k{\varphi}_{\infty}\psi \dot{\gamma}3{\sigma}^2+\left(k\dot{\gamma}{\varphi}_{\infty }-\left(\chi {\varphi}_0+k\psi \right){\dot{\gamma}}^2\right)2\sigma +\left(\chi {\dot{\gamma}}^3-k{\dot{\gamma}}^2+{\varphi}_0\right)=0 $$

(7)

From Eqs. (6) and (7), a simple relationship is obtained:

$$ \psi =\left(\chi {\dot{\gamma}}^3-k{\dot{\gamma}}^2+{\varphi}_0\right)/k{\varphi}_{\infty}\dot{\gamma}3{\sigma}^2 $$

(8)

The characteristic shear stress and shear rate can be obtained as follows:

$$ {\sigma}_{IHT}={\left(\frac{\chi {\dot{\gamma}}_{IHT}^3-\mathrm{k}{\dot{\gamma}}_{IHT}^2+{\phi}_0}{3k{\varphi}_{\infty}\psi {\dot{\gamma}}_{IHT}}\right)}^{1/2} $$

(9)

Equation (9) can be used to evaluate, from experimental data, the criterion at which the IHT occurs.

Shear thickening–shear thinning transition

At high enough shear rates, a shear thickening–shear thinning transition (TTT) is observed in a number of systems (Hu et al. 1998a, Lerouge et al. 2010, Puig et al. 2007). To account for such transition, a new critical variable χ_TTT is defined here. For χ > χ _TTT, a shear thinning behavior for $\dot{\gamma}$ > ${\dot{\gamma}}_{TTT}$ is predicted. The condition for this transition is dη/d$\dot{\gamma}$ = 0 (where η = φ ⁻¹), which implies the condition dφ/d$\dot{\gamma}$ = 0. The implicit derivative of the fluidity with respect to the shear rate is given by

$$ \begin{array}{l}-\frac{1}{\lambda_0}\left(1-\frac{\chi {\dot{\gamma}}^3}{\varphi}\right)\frac{d\varphi }{d\dot{\gamma}}+\left(\frac{\varphi_0-\varphi }{\lambda_0}\right)\left(-\frac{\chi }{\varphi }3{\dot{\gamma}}^2+{\dot{\gamma}}^3\frac{\chi }{\varphi^2}\frac{d\varphi }{d\dot{\gamma}}\right)\\ {}+{\mathrm{k}}_0\left(1+\psi \frac{\dot{\gamma}}{\varphi}\right)\left(\left({\varphi}_{\infty }-\varphi \right)\left(-\frac{{\dot{\gamma}}^2}{\varphi^2}\frac{d\varphi }{d\dot{\gamma}}+\frac{1}{\varphi }2\dot{\gamma}\right)-\frac{{\dot{\gamma}}^2}{\varphi}\frac{d\varphi }{d\dot{\gamma}}\right)+\left({\varphi}_{\infty }-\varphi \right)\frac{{\dot{\gamma}}^2}{\varphi }{\mathrm{k}}_0\psi \left(-\frac{\dot{\gamma}}{\varphi^2}\frac{d\varphi }{d\dot{\gamma}}+\frac{1}{\varphi}\right)=0\end{array} $$

(10)

From the condition dφ/d$\dot{\gamma}$ = 0 in Eq. (10), the following equation holds:

$$ \left(\frac{\varphi_0-\varphi }{\lambda_0}\right)\left(-\frac{\chi }{\varphi }3{\dot{\gamma}}^2\right)+{\mathrm{k}}_02\dot{\gamma}\left(1+\psi \frac{\dot{\gamma}}{\varphi}\right)\left(\frac{\varphi_{\infty }-\varphi }{\varphi}\right)+\frac{{\mathrm{k}}_0\psi {\dot{\gamma}}^2\left({\varphi}_{\infty }-\varphi \right)}{\varphi^2}=0 $$

(11)

From this equation, an explicit expression for χ is obtained:

$$ \chi =\frac{{\mathrm{k}}_0{\lambda}_0\left({\varphi}_{\infty }-{\varphi}_{TTT}\right)\left(2{\varphi}_{TTT}+3\psi {\dot{\gamma}}_{TTT}\right)}{\left({\varphi}_0-{\varphi}_{TTT}\right)3{\dot{\gamma}}_{TTT}{\varphi}_{TTT}} $$

(12)

Equation (12) can be used to evaluate (from experimental data) the criterion at which the TTT occurs. It is noteworthy that no fitting is necessary to obtain ψ and χ, since they can be straight forwardly determined with Eqs. (9) and (12), respectively. For χ = 0, there is no TTT, independently of the value of ψ and hence φ _∞ = φ _TTT . Consequently, only a set of two equations determines the IHT (Eq. (9)) and the TTT (Eq. (12)).

Viscosity at high shear rates

In steady state at high shear rates, Eq. (3) becomes

$$ \left(-\chi \frac{\varphi_0-{\varphi}_A}{\lambda_0}+{\mathrm{k}}_0\left(\frac{\psi }{\varphi_A}\right)\left({\varphi}_{\infty }-{\varphi}_A\right)\right)\frac{{\dot{\gamma}}^3}{\varphi_A}=0 $$

(13)

where φ _A is the asymptotic value of the fluidity at high shear rates.

For χ = 0, we obtain

$$ \left({\mathrm{k}}_0\left(\frac{\psi }{\varphi_A}\right)\left({\varphi}_{\infty }-{\varphi}_A\right)\right)\frac{{\dot{\gamma}}^3}{\varphi_A}=0 $$

which yields φ _A  = φ _∞.

In addition, for ψ = 0,

$$ \left(-\chi \frac{\varphi_0-{\varphi}_A}{\lambda_0}\right)\frac{{\dot{\gamma}}^3}{\varphi_A}=0 $$

which yields φ ₀ = φ _A .

Consequently, for χ ≠ 0 and ψ ≠ 0, the following final expression is obtained:

$$ {\varphi}_A=\frac{\left({\mathrm{k}}_0{\lambda}_0\psi +\chi {\varphi}_0\right)\pm \sqrt{{\left({\mathrm{k}}_0{\lambda}_0\psi +\chi {\varphi}_0\right)}^2-4\chi {\mathrm{k}}_0{\lambda}_0\psi {\varphi}_{\infty }}}{2\chi } $$

(14)

Experimental section

CTAT, 98 % pure from SIGMA, was recrystallized from chloroform (analytical grade from Aldrich). CTAVB was synthesized by neutralization of a 1 wt% CTAOH aqueous solution (97 % pure, received as a 10 wt% aqueous solution from Fluka) with a concentrated solution of 4-vinylbenzoic acid (97 % pure from Fluka) in acetone (analytical grade from Fermont) as described elsewhere (Kline 1999). This surfactant was precipitated by adding absolute ethanol (Aldrich) and dried. The structure of CTAVB was confirmed by NMR spectroscopy.

Samples were prepared by weighing the appropriated amounts of surfactant and HPLC water in 20-ml glass vials, homogenized and placed in a temperature-controlled chamber at 30 °C for a week before performing the rheological tests. Samples with concentrations smaller than 0.1 wt% were made by dilution from a stock (0.1 wt% surfactant) solution.

Steady and transient shear rate measurements were performed at 30 °C in an ARES strain-controlled rheometer (TA Instruments), using a double-wall Couette geometry (bob internal and outer diameters of 29.5 and 32 mm, respectively, and cup internal and external diameters of 27.94 and 34 mm, respectively) and a humidification chamber to minimize water losses by evaporation.

The ODE45 “Matlab” library was used to solve Eq. (1) and (2). This library is based on a differential equations solver based in the Runge-Kutta fourth and fifth orders method. In addition, the “Matlab” library was employed to solve Eq. (3). Furthermore, near the critical value at which the IHT occurs, the Runge-Kutta method is sufficiently stable and hence, this method does not need further modifications (Dormand and Prince 1980).

Model predictions

The examination of the effect of the several model parameters on the flow curve requires a sensitivity analysis consisting in varying only one parameter while keeping the remainder ones constant.

Figure 1 depicts the effect of varying the intensity parameter of the IHT, ψ, on the steady shear flow curve (Fig. 1a) and the extended Gibbs free energy (derived from EIT) versus shear rate (Fig. 1b), keeping fixed the other parameters of the model (see legend of this figure). As detailed elsewhere (Bautista et al. 2007), the extended free energy, G, of a fluid system of volume V, under isothermal and isobaric conditions, subjected to simple shear flow caused by the application of a stress σ, is given by

$$ d\mathcal{G}=\frac{V\varphi }{2{G}_0{\varphi}_0}\underline {\underline{\sigma}}:d\underline {\underline{\sigma}} $$

(15)

Fig. 1

A Shear stress versus shear rate as a function of the parameter ψ (Pa⁻¹) while keeping the other parameters of the BMP model fixed (φ _∞ = 20 Pa⁻¹ s⁻¹, φ ₀ = 1000 Pa⁻¹ s⁻¹, k ₀ λ ₀ = 0.1 Pa⁻¹ s, χ = 0.001 Pa⁻¹ s²): a 0.1; b 1; c 2; d 10; e 100. B Plot of extended free energy versus shear stress. Two minima (curves d and e) are shown, indicating the position where the stable–metastable coexistence region is located. Points a ₁, a ₂, a ₃, e ₁, e ₂, and e ₃ are used in Fig. 10 to indicate the shear stress–shear rate values for the different structures that can develop in STT

For simple shear flow and performing the double dot product in Eq. (15), one obtains

$$ d\mathcal{G}=\kern0.62em \left(\frac{V\varphi }{2{G}_0{\varphi}_0}\right)\;\left(2{\sigma}_{12}d{\sigma}_{12}\kern0.5em +\kern0.5em {\displaystyle \sum_{i=1}^3{\sigma}_{ii}}d{\sigma}_{ii}\right) $$

(16)

Since in dilute shear-thickening micellar systems normal stresses are negligible, Eq. (16) becomes

$$ d\mathcal{G}=\kern0.62em \left(\frac{V\varphi }{2{G}_0{\varphi}_0}\right)\;\left(2{\sigma}_{12}d{\sigma}_{12}\right) $$

(17)

For simple steady shear flow, σ ₁₂ = $\dot{\gamma}/\varphi$, as deduced from Eq. (1). It is easy to show that Eq. (17) can be rewritten as

$$ d{\sigma}_{12}\kern0.5em =\kern0.5em \frac{1}{\varphi}\left(1\kern0.5em -\kern0.5em \frac{\dot{\gamma}}{\varphi}\frac{d\varphi }{d\dot{\gamma}}\right)d\dot{\gamma} $$

(18)

The substitution of Eq. (18) in Eq. (17) yields

$$ d\mathcal{G}\kern0.74em =\kern0.74em V\kern0.62em \left(\frac{4{\sigma}_{12}^3}{\varphi {G}_0^3}\kern0.5em \right)\kern0.36em d\dot{\gamma} $$

(19)

Figure 1A depicts that for low values of ψ, the flow curve increases monotonically, i.e., a no reentrant region is predicted (curves a and b); however, as the shear rate increases, the shear thickening increases sharply as a discontinuity at a given shear rate (curve c). Moreover, as ψ increases even further, a reentrant region develops with sigmoidal shape that becomes better defined as ψ becomes larger (curves d and e). It is noteworthy that curve c represents a characteristic value below which no reentrant region appears when the measurements are performed in stress-controlled mode (lines a and b in Fig. 1A), whereas above this characteristic line, a discontinuity in the shear rate is detected (lines d and e in Fig.1A). In fact, the curve (see dashed line in Fig. 1) obtained by calculating dσ/d$\dot{\upgamma}$ = 0, encloses the region at which the shear rate is discontinuous, given by dσ/d$\dot{\upgamma}$ > 0, as demonstrated elsewhere (Bautista et al. 2007). This behavior is akin to the unstable or spinodal region that appears whenever the condition, dP/dV < 0, is met in plots of pressure versus molar volume in the gas–liquid coexistence region (Sandler 2006). Figure 1B shows that the plot of G versus shear rate shows two minima (curves d and e), indicating the position where the stable–metastable coexistence region is located (see Fig. 1A). The plot of G versus shear is an EIT analog to the Maxwell equal-area criterion to obtain the coexistence pressure in liquid–vapor equilibrium (Sandler 2006). These plots depict two minima in the coexistence region and only one minimum outside it; the occurrence of the two minima indicates the positions of the coexisting shear rates when experiments are performed under applied shear rate. When the two minima in the plots of G versus $\dot{\gamma}$ meet into one (curve c in Fig. 1B), the characteristic shear stress, σ _c, and the characteristic shear rate, ${\dot{\upgamma}}_{\mathrm{c}},$occur where the coexisting region becomes indistinguishable, similar to the critical point in two-phase liquid–vapor equilibrium.

It is noteworthy to point out that our model can predict the homogeneous and the inhomogeneous coexistence regions, even though our model does not consider any inhomogeneous states. Interestingly, Onsager (1944) also predicted a spontaneous phase transition without additional information on inhomogeneous states with a partition function with a mean field potential of a homogeneous spins system.

These results are explained on the basis that ψ is related to the effect of the shear flow on the competition between the induction and destruction of the SIS. In fact, just above the characteristic shear stress (or shear rate), the SISs are nucleated non-homogeneously at the wall of the moving cylinder of the Couette geometry, or at stresses within region II near the moving plate in parallel plates, as described by Hu et al. (1998a). However, the structure (incipient wormlike micelles or a gel phase) formation becomes dominant as σ augments, which is regulated by the magnitude of ψ, as shown in Fig. 1. Clearly then, the parameter ψ is related to the reentrant zone that is often (but not always) detected during the shear thickening transition (Hu et al. 1998a; Macías et al. 2003) and it simply reflects the effect of the shear stress on the development of the SIS. Moreover, Eq. (9) predicts that ψ at the reentrant region transition is positive; χ is also restricted because the characteristic values of σ _c and ${\dot{\gamma}}_c$ must be positive. This result agrees with the simulations depicted in Fig. 1.

Figure 2 shows steady flow curves as a function of the parameter χ keeping the rest of the parameters fixed as indicated in the legend of this figure. Setting χ = 0 yields a shear thickening region at intermediate shear rates and Newtonian regions at low and high shear rates (curve a in inset of Fig. 2); however, as χ is increased, a Newtonian region is detected at low shear rates followed by shear thickening at intermediate shear rates, and then a well-defined shear thinning regions at high shear rates (curves b to e); moreover, the shear thickening intensity diminishes with increasing χ (inset in Fig. 2). Note also that the shear thinning region shifts to lower shear rates as χ augments. Hence, the value of χ determines the extent of the shear thickening intensity and the development of a shear-thinning region at high shear rates. Clearly, the parameters ψ and χ are related to the reentrant region and the shear thickening–thinning transition (TTT), respectively. A dashed line in the inset of this figure indicates the region at which the TTT develops at higher shear rates. Notice that both parameters, ψ and χ, are not fitting parameters since they can be obtained from Eqs. (9) and (12), respectively.

Fig. 2

Shear stress versus shear rate as a function of the parameter χ (Pa⁻¹ s²) while keeping the other parameters of the BMP model fixed: (φ _∞ = 20 Pa⁻¹ s⁻¹, φ ₀ = 1000 Pa⁻¹ s⁻¹, k ₀ λ = 1 Pa⁻¹ s, ψ = 0 Pa⁻¹): a 0; b 10⁻⁶; c 10⁻⁵; d 10⁻⁴; e 10⁻³. Inset: viscosity versus shear rate. The dashed line indicates the region at which the TTT develops at higher shear rates

Figure 3 depicts the effect of k ₀ λ ₀ on the steady shear flow curve. Two important effects are revealed as the value of k ₀ λ ₀ decreases: (1) ${\dot{\gamma}}_c$ shifts to larger values and (2) the shear thickening intensity decreases (inset). The factor k ₀ λ ₀ is related to the ratio of the destruction-to-formation of SIS under steady state. As this ratio decreases, the SISs form at higher shear rates and larger stresses corresponding to strong shear thickening intensity, so ${\dot{\gamma}}_c$ shifts to higher shear rates (curves c, d, and e) and t _ind decreases (see Fig. 4). The opposite situation corresponds to large values of k ₀ λ ₀, where t _ind is larger and the SISs form in a large shear rate span (curves a and b). In the latter case, the structures are labile and they can be easily disrupted by the flow.

Fig. 3

Shear stress versus shear rate as a function of k₀λ₀ (Pa⁻¹ s) while keeping the other parameters of the BMP model fixed (φ _∞ = 20 Pa⁻¹ s⁻¹, φ ₀ = 1000 Pa⁻¹ s⁻¹, ψ = 0 Pa⁻¹, χ = 10⁻⁵ Pa⁻¹ s²). a 100; b 10; c 1; d 10⁻¹; e 10⁻². Inset: viscosity versus shear rate

Fig. 4

Viscosity as a function of time for inception of flow at different applied shear rates (s⁻¹): a 200; b 250; c 300; d 400; e 600; f 800. The values of the other parameters of the BMP model are as follows: φ_∞ = 10 Pa⁻¹ s⁻¹, φ ₀ = 100 Pa⁻¹ s⁻¹, k ₀ = 10⁻² Pa s⁻², λ ₀ = 10 s, χ = 4 × 10⁻⁶ Pa⁻¹ s², ψ = 0 Pa⁻¹, and G ₀ = 0.37 Pa. Inset: induction and saturation times versus shear rate

Figure 4 depicts the simulations of start-up shear flow as a function of increasing shear rate ($\dot{\gamma}$ > ${\dot{\gamma}}_c$) for fixed values of the other parameters. This figure reveals that the model is capable to predict an induction time for the inception of shear thickening and a saturation time, after which the apparent steady state viscosity is reached, in agreement with experimental observations (Hu et al. 1998a; Berret et al. 2002; Macías et al. 2003). Moreover, the model is capable to predict the power law dependence of t_ind with $\dot{\gamma}$ of the form, t _ind ~ $\dot{\gamma}$ ^-m, as the applied shear stress (or shear rate) departs from the critical value (inset in Fig. 4). The linearity in the log–log plot of t _ind versus shear rate (inset of Fig.4) discloses that the exponent of the power law (m) is ca. 2.2, which is within the range of experimentally reported values (Boltenhagen et al. 1997b; Pröztl and Springer 1997; Hu et al. 1998a; Berret et al. 2002; Macías et al. 2003). In contrast, the saturation time increases with time but it does not follow a power law-dependence with time (inset in Fig. 4).

Determination of the parameters of the BMP model

The governing equations of the model, i.e., Eqs. (1) and (2), contain seven parameters, φ ₀, φ _∞, λ ₀, k ₀, G ₀, χ, and ψ, which, as we show in this section, are not adjustable parameters but they can be obtained from a closed system of equations. φ₀ is determined from the inverse of the shear viscosity in the Newtonian region before shear thickening develops, whereas φ_∞ is the inverse of the Newtonian viscosity at the end of shear thickening when no shear thinning develops or equal to the inverse of the Newtonian viscosity at very high shear rates once the shear thinning region turns into a Newtonian one.

The product of k ₀ and λ ₀ (k ₀ λ ₀) is obtained from the best fitting of the steady state flow curve employing Eq. (3).

G ₀ can be easily determined for semidilute and concentrated micellar solutions, from linear oscillatory shear measurements, and it is equal to the plateau modulus at high frequencies, i.e., ${G}_0=\underset{\omega \to \infty }{ \lim }G\hbox{'}$ (Soltero et al. 1996). However, for dilute micellar solutions, it is not possible to perform this kind of measurements since these dilute systems do not exhibit strong elastic properties. However, as it is demonstrated here, G ₀ can be straightforwardly obtained from shear flow relaxation, i.e., interruption of shear flow after the steady shear flow has been achieved. For this kind of flow, the right-hand side term of Eq. (1) is zero, and so, this equation reduces to

$$ {\sigma}_{12}+\frac{1}{G_0\varphi}\frac{\mathrm{d}{\sigma}_{12}}{dt}=0 $$

(21)

Here, the solution is given by

$$ \sigma ={\sigma}_{ss} \exp \left[-{G}_0\left({\varphi}_0t+{\lambda}_0\left({\varphi}_{ss}-{\varphi}_0\right)\left(1-{e}^{-t/{\lambda}_0}\right)\right)\right] $$

(22)

This curve exhibits two regions at inception of stress relaxation, one at short times and another at long times. At short times, the stress is given by

$$ \sigma ={\sigma}_{ss} \exp \left[-{G}_0\left({\varphi}_{ss}t\right)\right] $$

(23)

At long times, the stress is given by

$$ \sigma ={\sigma}_{ss} \exp \left[-{G}_0\left({\varphi}_{ss}t+{\lambda}_0\left({\varphi}_{\infty }-{\varphi}_0\right)\right)\right] $$

(24)

This set of simultaneous equations allows determining without fitting G ₀ and λ ₀. With λ₀, k ₀ can be easily calculated from the product k ₀ λ ₀ obtained from the steady flow curve, as described above.

Finally, the parameters ψ and χ are readily determined with Eq. (9) and (12), respectively.

Comparison with experimental results

Figure 5 shows experiments of stress relaxation after cessation of shear flow as a function of applied shear rate for a 0.4 wt% CTAT. The inset shows a magnification of the stress relaxation a short time, which reveals the first two relaxations of the three detected at short, intermediate, and long times. The relaxation is fast at short times and then it becomes much slower at longer times, and both, the short and the long times, become faster with increasing the applied shear rate before stopping the flow. The solid lines in this figure and in the inset indicate the predictions of the BMP model; clearly, there is good agreement between experimental data and predictions. From the predictions, the values of G ₀ and λ ₀ are readily obtained.

Fig. 5

Stress relaxation after the application of different shear rates for a 0.4 wt% CTAT micellar solution: 10, 30, 80, and 150 s⁻¹. Symbols and lines represent experimental data and predictions of the BMP model, respectively

Figure 6 presents experimental (symbols) and predicted (continuous lines) shear viscosity versus steady shear rate curves for CTAT and CTAVB micellar solutions at selected concentrations. CTAT micellar solutions exhibit shear thickening at concentrations from 0.1 and up to ca. 0.9 wt% above a characteristic shear rate ${\dot{\gamma}}_c$ (that is nearly concentration independent), followed by shear thinning at even higher shear rates (Berret et al. 2000; Macías et al. 2003; López-Díaz et al. 2010). For CTAVB micellar solutions, Newtonian behavior is detected up to a characteristic shear rate, above which shear thickening is observed, followed by strong shear thinning at higher concentrations, similar to the behavior observed for CTAT solutions. However, shear thickening is detected at much lower shear rates and concentrations in the CTAVB solutions compared to the CTAT system (Macías et al. 2003; Soltero et al. 2007). In fact, the shear thickening is observed in the CTAVB micellar solutions at concentrations as low as 0.02 wt% and at shear rates of the order of 0.8 s⁻¹, whereas in the CTAT system, shear thickening is detected for concentrations around 0.1 wt% and shear rates of ca. 100 s⁻¹ (Fig. 6). Moreover, ${\dot{\gamma}}_c$ shifts to lower values as the CTAVB concentration is increased, in contrast to the CTAT system. Interestingly, the effect of the counterion (in the absence of added electrolytes) has not been reported previously in the literature for the STT. Elsewhere, it has been reported that the hydrophobicity of the counterion displaces the critical micellar concentration, cmc; the sphere-to-rod transition, cmc ₂; and the entanglement concentration, c* (Hassan and Yakhmi 2000). Results have shown that the STT occurs at concentrations where locally cylindrical micelles exist, as deduced by SANS experiments in quiescent CTAT solutions (Berret et al. 1998) up to the neighborhood of c* and that electrostatic interactions play an important role (Truong and Walker, 2002). Our results suggest that the vinylbenzoate counterion binds more strongly to the micellar surface than the tosylate counterion does, shifting the STT to lower surfactant concentrations and critical shear rates. Predictions of the model (Eq. 3), setting ψ = 0 in Eqs. (9) and (12), since no reentrant region is evident, follow closely experimental data in both the shear thickening and the shear thinning regions for both CTAT and CTAVB micellar solutions. Model parameters for both micellar solutions are reported in Table 1, which were obtained experimentally as described elsewhere (Manero et al. 2002). Notice that the values of k ₀ λ ₀ are larger for CTAVB than those for CTAT. As mentioned in the previous section, an increase in k ₀ λ ₀ shifts ${\dot{\gamma}}_c$ to lower values, in agreement with the experimental results reported here. Notice also that shear thinning is more pronounced in CTAVB than in CTAT.

Fig. 6

Steady viscosity as a function of shear-rate for: CTAVB: (black square) 0.03; (black circle) 0.05; (black triangle) 0.1 wt%; CTAT: (white triangle) 0.4; (white square) 0.8 wt%. The values of the parameters of the model are reported in Table 1. Symbols and lines represent experimental data and predictions of the BMP model, respectively

Table 1 Values of the model parameters

Figure 7 depicts the time evolution of the shear viscosity upon inception of shear flow at various applied shear rates for a 0.4 wt% CTAT solution. When the applied shear rate is smaller than ${\dot{\gamma}}_c$, the steady shear Newtonian viscosity is reached almost immediately (not shown). However, when the applied shear rate is equal or larger than ${\dot{\gamma}}_c$, four features are evident in both systems: (1) the viscosity begins to grow only after a relatively long time has passed (t _ind); (2) t _ind becomes increasingly longer as the applied shear rate is closer to ${\dot{\gamma}}_c$; (3) another long time period is required to achieve steady state (t _sat); and (4) chaotic oscillations in the shear viscosity are observed. To reproduce the transient experiments, the BMP model (Eqs. (1) and (2)) requires independent values of k ₀ and λ ₀ as well as of the plateau modulus G ₀, which can be obtained as indicated above.

Fig. 7

Viscosity as a function of time for the inception of shear flow for a 0.4 wt% CTAT micellar solution at different applied shear rates (s⁻¹): (white triangle) 80; (white diamond) 150; (white square) 700. The parameters employed are k ₀ = 0.33 Pa⁻¹, λ ₀ = 0.18 s, and G ₀ = 0.37 Pa, whereas φ ₀, φ _∞, and χ are reported in Table 1. Symbols and lines represent experimental data and predictions of the BMP model, respectively

Figure 8 shows the experimental and predicted induction times as a function of the applied shear rate in a log–log plot for 0.4 wt% CTAT and 0.05 wt% CTAVB solutions. For both systems, the plots follow straight lines with a power law of the form t _ind∝${\dot{\gamma}}^{-m}$, where m = 1.5 ± 0.1 (for CTAT) and 1.9 ± 0.1 (for CTAVB); similar exponents were obtained for other CTAT and CTAVB concentrations (Macías et al. 2003; Soltero et al. 2007). Several researchers reported this power law dependency of the induction time with the shear rate (Boltenhagen et al. 1997a; Pröztl and Springer 1997; Hu et al. 1998a; Berret et al. 2000; Macías et al. 2003). The model predicts remarkably well these dependencies, as expected from the predictions of the transient behavior of these surfactant solutions (Fig. 7), except that the predicted power law exponent is larger (m = −2).

Fig. 8

Induction time as a function of applied shear rate for: CTABV: (black circle) 0.05; (black triangle) 0.1 wt%; CTAT: (⊲) 0.4 wt.%. Symbols and lines represent experimental data and predictions of the BMP model, respectively

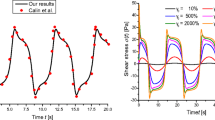
Figure 9 depicts experimental and predicted time-dependent complex flow histories produced by controlled shear rate rheometry in a linear increasing and decreasing mode, keeping the maximum shear rate constant and varying the ramp time required to reach the maximum shear rate (inset). Several features are revealed in this figure: (1) the amplitude of the hysteresis cycle decreases with increasing shear rate; (2) all the data collapse at the same decreasing shear rate path. Predicted values follow similar trends than the experimental ones, although they do not overlap. The reason is that the experimental and predicted steady-state data do not coincide exactly, especially at high shear rates as shown in Fig. 9, which causes shear thinning. Nevertheless, the predicted values follow the same tendency of the experimental data: (1) the increasing shear rate data shifts to lower values with increasing shear rate; (2) all the decreasing shear rate data collapse nearly in the same curve similarly to experimental data; and (3) the predicted area of the hysteresis loops also diminishes as the applied shear rate increases (see Fig. 9).

Fig. 9

Shear stress as a function of shear rate in linearly increasing and decreasing cycles for a 0.4 wt% CTAT micellar solution. Initial and final shear rates are the same in all the cycles (indicated in the inset), but the half time (t_1/2) of each cycle (i.e., time to reach the maximum shear rate) was varied: (black circle) 8; (black square) 15; (black triangle) 40 s. The parameters employed are k ₀ = 0.33 Pa⁻¹, λ ₀ = 0.18 s, and G ₀ = 0.37 Pa, whereas the values of φ ₀, φ _∞, and χ are reported in Table 1

The SIS formation as a function of applied stress, explained in this work as well as in previous reports and theories (Pröztl and Springer 1997, Dehmoune et al. 2011; Herle et al. 2008) is depicted in a cartoon (Fig. 10). Two types of rheological behavior are observed, monotonic (curves a, b, and c in Fig.1 ) and non-monotonic (curves d and e in Fig.1 ). Cartoons a ₁ , a ₂ , a ₃ , e ₁ , e ₂ , and e ₃ in Fig. 10 correspond to points indicated on the curves of Fig. 1. The first type (χ < χ_crit), for monotonic curves and σ < σ_aggr, involves small micellar associations. The average micellar length is not significantly larger than the one in a solution at rest, hence Newtonian behavior is observed. As the number and length of associated micelles increases, shear thickening arises, corresponding to a second stage where aggregation and entanglement formation occurs (here σ _aggr < σ < σ _orient). The length of the associated micelles increases substantially because of the fusion of shorter micelles. In the situation when σ _orient < σ, the micelles undergo breaking and orientation processes under flow, hence shear thinning arises in the third stage. In contrast, in non-monotonic curves (χ > χ _crit), the coexistence of two structures induces the banding in the vorticity direction (Dehmoune et al. 2011, Herle et al. 2008.

Fig. 10

Suggested SIS depending on applied stress and type of fluid. a χ < χ_c homogeneous flow, b χ_c < χ, inhomogeneous flow in the second stage. Points a ₁, a ₂, a ₃, e ₁, e ₂, and e ₃ are indicated for the different structures that can develop in STT

Concluding remarks

A simple model, derived from the extended irreversible thermodynamics formulation, consisting of the upper-convected Maxwell constitutive equation and a stress-dependent kinetic equation that accounts for nonlinear contributions in the breaking-and-reformation process of the SIS, predicts the steady and transient features of the STT in micellar solutions. It can predict either a reentrant region or a continuous increase in shear stress with shear rate, depending on whether rheological measurements are performed in a shear rate mode or in a stress mode. Plots of the extended Gibbs-free energy versus shear rate depict two minima in the coexistence region and only one minimum outside it; when experiments are performed by applying shear rate, the extended Gibbs-free energy minima indicate the positions of the coexisting shear rates. The model predicts a characteristic shear rate and an induction time for the appearance of shear thickening, and in addition, the rapid decrease of the induction time with increasing shear rate and a power law dependence with shear rate, in agreement with experimental observations. The predictions of the model compare remarkably well with experimental steady state and transient data for two dilute micellar solutions. Note the improvement attained with regard to the ability of the model to predict the observed phenomena. In particular, the regions of shear thinning and shear thickening regimes in steady and transient flows are clearly predicted.